Abstract
Real-world object size is a behaviorally relevant object property that is automatically retrieved when viewing object images: participants are faster to indicate the bigger of two object images when this object is also bigger in the real world. What drives this size Stroop effect? One possibility is that it reflects the automatic retrieval of real-world size after objects are recognized at the basic level (e.g., recognizing an object as a plane activates large real-world size). An alternative possibility is that the size Stroop effect is driven by automatic associations between low-/mid-level visual features (e.g., rectilinearity) and real-world size, bypassing object recognition. Here, we tested both accounts. In Experiment 1, objects were displayed upright and inverted, slowing down recognition while equating visual features. Inversion strongly reduced the Stroop effect, indicating that object recognition contributed to the Stroop effect. Independently of inversion, however, trial-wise differences in rectilinearity also contributed to the Stroop effect. In Experiment 2, the Stroop effect was compared between manmade objects (for which rectilinearity was associated with size) and animals (no association between rectilinearity and size). The Stroop effect was larger for animals than for manmade objects, indicating that rectilinear feature differences were not necessary for the Stroop effect. Finally, in Experiment 3, unrecognizable “texform” objects that maintained size-related visual feature differences were displayed upright and inverted. Results revealed a small Stroop effect for both upright and inverted conditions. Altogether, these results indicate that the size Stroop effect partly follows object recognition with an additional contribution from visual feature associations.
Public significance statement
When viewing an object, we quickly know its real-world size. Here, we show that this automatic retrieval of real-world object size knowledge partly depends on our ability to recognize the object, with stronger size retrieval effects for recognizable compared to non-recognizable objects. However, we also find evidence for an alternative route to extracting size knowledge that does not depend on recognition, based on visual feature-size associations.
Keywords: object size, familiar-size Stroop effect, conceptual knowledge, object categorization
Real-world object size, or familiar size, is a salient and behaviorally relevant object property. For example, small manmade objects (e.g., ball, paperclip) are often portable and manipulable, while large manmade objects (e.g., sofa, cabinet) are often stable and can serve as reliable landmarks (Bainbridge & Oliva, 2015). The relevance of familiar object size is reflected in visual cortex organization, with a familiar size dissociation in ventral temporal cortex (VTC; Konkle & Oliva, 2012a) that emerges quickly after stimulus onset (Khaligh-Razavi et al., 2018).
Interestingly, recent behavioral studies used a size Stroop paradigm to show that familiar object size may be automatically retrieved when viewing visual object images (Konkle & Oliva, 2012b; Long & Konkle, 2017; Long et al., 2019). This work built on the seminal work of Stroop (1935), which showed that an incongruent color name interfered with naming the word’s ink color (e.g., “red” in green font). These results have been interpreted as evidence that word reading occurs in parallel to color naming; because of our extensive experience with reading, processing in this pathway occurs quickly and without the need to allocate attention, thereby interfering with the ongoing color recognition task when the outputs of the two processes are in conflict (e.g., Cohen et al., 1990). Modified versions of the Stroop task have subsequently been used to assess the presumed automaticity of retrieving various forms of knowledge, including object color (Naor-Raz et al., 2003), numerical size (Henik & Tzelgov, 1982; Kaufmann et al., 2005), and familiar object size (Konkle & Oliva, 2012b). For familiar object size, Konkle and Oliva (2012b) presented large and small manmade objects to participants and asked them to select the object that was larger (or smaller) on the screen, ignoring familiar size (i.e., familiar size knowledge was in competition with the screen size task). Crucially, in congruent trials, the objects’ relative screen size was consistent with their relative familiar size, while in incongruent trials, the objects’ relative screen size was inconsistent with their relative familiar size. The main finding was a size Stroop effect, whereby participants were faster at selecting the large-on-screen (or small-on-screen) object in congruent than incongruent trials. From this, it was concluded that the familiar size of objects is automatically retrieved when viewing object images (Konkle & Oliva, 2012b).
These findings raise the question of how the familiar size of objects is retrieved automatically, such that it interferes with the screen size task. One possibility is that familiar size knowledge is automatically retrieved after recognizing the object at the “basic level” – for example, recognizing the object as a house or an apple triggers knowledge about the object’s size (e.g., Rosch et al. 1976; Konkle & Oliva, 2012b). A similar parallel recognition process may account for the word color Stroop effect. For example, simply turning the color words upside down – thereby slowing down automatic word recognition – reduces the classical word color Stroop effect (Liu, 1973). Recognition is also likely to explain the numerical size Stroop effect - the finding that participants are slower to indicate which of two digits is larger on the screen when the digits’ relative physical size is incongruent with the digits’ relative numerical size (e.g., 3 vs 5; Henik & Tzelgov, 1982). For this effect to emerge, participants must have recognized the digits’ numerical size in parallel to performing the screen size task. Physical and semantic information may thus be processed in parallel in multiple domains: color words, numbers, and objects. Conflicting output from these parallel pathways (e.g., about relative size) then leads to slower responses on the primary task.
Interestingly, a recent study proposed an alternative, or additional, route to real-world object size knowledge that “bypasses” high-level visual processing and basic-level recognition (Long & Konkle, 2017). Specifically, low-level “non-meaningful” perceptual features may directly activate familiar size information due to their natural covariance with real-world size. For example, large and small manmade objects differ systematically in terms of simple shape features, with for example large manmade objects typically having more rectilinear features than small objects (Long et al., 2016; Nasr et al., 2014). Long & Konkle (2017) rendered large and small manmade objects unrecognizable while maintaining some texture and form features (including differences in rectilinearity between large and small objects) to create “texforms” of large and small objects. Using the size Stroop paradigm, they found that participants were faster at selecting the texform that was larger (or smaller) on the screen when it was also the larger (or smaller) object in the real world, despite the fact that the texforms could not be recognized (e.g., people could not name the texforms in terms of meaningful categories). Thus, the object size Stroop effect could primarily be a feature-driven effect, with the automatic processing of real-world size relying on the low- or mid-level visual feature differences between large and small objects.
In the current study, we tested whether and to what extent visual feature differences and object recognition contribute to the size Stroop effect. In Experiment 1, we used object inversion to impair higher-level recognition processes by presenting the objects in a less familiar orientation while preserving low- and mid-level features (i.e., a rectilinear edge is equally rectilinear upright and inverted). In Experiment 2, we tested the role of rectilinearity in the size Stroop effect by comparing the effect for manmade objects and animals: large and small objects, but not large and small animals, differ in rectilinearity. Finally, in Experiment 3, we tested if recognition could play a role in the size Stroop effect for putatively unrecognizable texform objects, by presenting the texforms upright and inverted.
Experiment 1
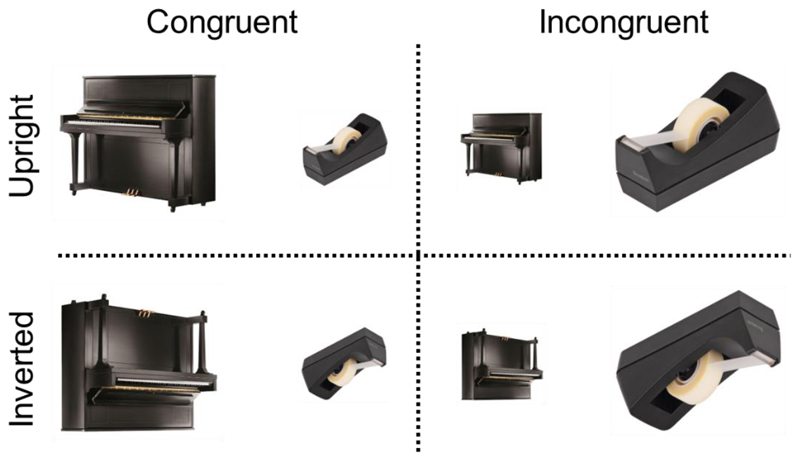
Experiment 1 examined the role of object recognition in the size Stroop effect. We used image inversion to impair recognition while preserving visual feature differences between objects (e.g., Yin, 1969). Previous research has shown that inversion slows down basic-level object recognition (Mack et al., 2008). Therefore, when objects are inverted, participants are more likely to complete the orthogonal screen-size task before recognizing the objects, and thus also before recognizing the objects’ real-world sizes. Crucially, the low- and mid-level features are not changed by image inversion (i.e., an inverted house is equally rectilinear as an upright house, and so this manipulation would not impair low- and mid-level visual processes). Inversion has previously been used to reduce the classic word color Stroop effect, reducing semantic interference by impairing word reading (Liu, 1973). If the size Stroop effect depends on object recognition, then it should be reduced in the inverted condition. In contrast, if the size Stroop effect is fully driven by visual feature differences between large and small objects, then the Stroop effect should be equal for upright and inverted trials.
Methods
Transparency and openness
For this and subsequent experiments, we report how we determined our sample size, all data exclusions (if any), all manipulations, and all measures in the study, and we follow JARS (Kazak, 2018). Data and research materials are available at the Open Science Framework (https://osf.io/ab3dy/). The experiment was programmed in PsychoPy (Peirce et al. 2019) and hosted online at Pavlovia (https://pavlovia.org/). Data were analyzed using Python (Python Software Foundation, Python Language Reference, version 3.9.13. Available at http://www.python.org). R Statistical Software (v4.2.3; R Core Team 2021) was used for power analyses, using the pwr R package (v1.3.0; Champely et al., 2017), and for Bayes Factor analyses, using the BayesFactor R package (v0.9.12-4.4; Morey & Rouder, 2022). The study design and its analysis were not pre-registered.
Participants
34 participants (M = 29.88 years; SD = 6.08 years; females = 18, males = 13; other = 1, undeclared = 2) took part in the study. This sample size was selected based on an a-priori power analysis ensuring 80% to detect an effect size of d = .5 (corresponding with np2 = .21) with p = .05 for the critical main effect of congruency. Previous studies found larger effect sizes for the main effect of congruency (e.g., Konkle & Oliva, 2012b; Long & Konkle, 2017). Participants were recruited online through Prolific (www.prolific.com) in return for monetary compensation. One participant was replaced due to low overall accuracy (72.27% > 3 SDs below the group mean). Informed consent was obtained electronically prior to the experiment. The study was conducted in compliance with the ethical principles and guidelines of the Research Ethics Committee of the Faculty of Science of the Radboud University and APA ethical standards. All data were collected in the year of 2022.
Constraints of generality
Participants were recruited from the US, UK and The Netherlands, with the requirement that they were fluent in English and were between the ages of 18 and 37 years old. While this is a more heterogeneous sample than in typical lab-based psychophysics experiments, the results may still be specific to this population and age group.
Stimuli
The stimuli comprised 60 unique images of 30 small (e.g., hole puncher) and 30 large (e.g., bed) manmade objects (available at https://osf.io/ab3dy/). The stimuli were found online and in publicly available stimulus sets (Konkle & Oliva, 2012a), downloaded from https://konklab.fas.harvard.edu/ImageSets/BigSmallObjects.zip. They were cropped from their background and pasted on a white uniform background of 500 x 500 pixels and displayed at 12 and 6 degrees of visual angle, as measured along the longest dimension of the object.
We used a computational model to quantify the rectilinearity in each manmade object image (for model description, see Li & Bonner, 2020). This analysis showed that large objects were more rectilinear than small objects, t(58) = 2.86, p = .006, np2 = .12, BF = 7.22. Moreover, we quantified the area-to-perimeter ratio for large and small manmade objects (Gayet et al., 2019). Area-to-perimeter ratio is a relevant dimension to object perception and visual cortex organization (Bao et al., 2020; Gayet et al., 2019; Coggan & Tong, 2023; but see Yargholi & Op de Beeck, 2023). Large and small objects did not differ on area-to-perimeter ratio, t(58) = 1.33, p = .190, np2 = .03, BF = .55.
Design
Participants completed a size Stroop task (Konkle & Oliva, 2012b), where each trial presented one large object and one small object (Figure 1). Thirty unique trials were created by pairing a large and small object based on similarity in height/width ratio, with each object image consistently paired with one other object image. In a congruent trial, the large object was presented at a larger size (12 deg. visual angle) than the small object (6 deg. visual angle). In an incongruent trial the large object was presented at a smaller size (6 deg. visual angle) than the small object (12 deg. visual angle). All trial pairs were presented in a congruent trial and an incongruent trial. Upon image presentation, participants were asked to respond by pressing either the ‘f’ or ‘j’ key on the keyboard to indicate the left or right image on the screen, respectively. Images were displayed until a response was given. Participants were instructed to respond as quickly and accurately as possible. All participants completed a block where they selected the large image on the screen and another block where they selected the small image on the screen, and the order of this was counterbalanced across participants. The position of the large and small image was randomly determined in each trial. In total, there were 480 trials (30 object pairs x 2 congruency x 2 orientation x 2 task instruction blocks x 2 repetitions per image in each instruction block). Self-paced breaks were interspersed at regular intervals. Prior to each instruction block (e.g., attend smaller), the participants completed a practice session consisting of eight trials, where feedback (“correct”,” incorrect”) was provided. No feedback was given during the main part of the experiment.
Figure 1. Paradigm: for both upright and inverted displays, participants selected the bigger (or smaller) image on the screen while disregarding their familiar size.
Representative image examples of the objects used in the study (actual images not shown for copyright reasons).
Analysis
Trials with RT less than 200 ms or greater than 1500 ms were excluded from the analysis (.79% of trials), following previous reports (Konkle & Oliva, 2012b; Long & Konkle, 2017). Given the main question of examining if the congruency effect was influenced by inversion, the data for each instruction block (attend larger; attend smaller) was averaged prior to statistical analysis. The data were first analyzed using a 2x2 repeated-measures analysis of variance (ANOVA) with congruency (congruent, incongruent) and orientation (upright, inverted) as within-subjects factors.
Next, to further characterize the size Stroop effect (incongruent – congruent), it was analyzed in an exploratory analysis as a function of how quickly participants responded. This analysis allows for testing whether the conflicting familiar size knowledge influenced both fast and slow responses during the orthogonal screen-size task, inspired by previous work testing conflict effects on both fast and slow RTs (e.g., Ridderinkhof, 2002) and work examining how visual object knowledge (e.g., object color and shapes) contributes to expert object recognition (Hagen et al., 2014; 2016; 2023). The faster the conflicting familiar size knowledge is processed in parallel, the more likely it is to influence fast reaction times. To examine the distribution of correct RTs, the trials of each participant were ranked from the fastest to the slowest, separately for each condition (i.e., by congruency [congruent, incongruent] x orientation [upright, inverted] x task [attend big, small]) before they were grouped into four bins containing the fastest 25% of the responses (quartile bin 1), the next fastest 25% of responses (quartile bin 2), the third fastest 25% of responses (quartile bin 3), and finally the slowest 25% of responses (quartile bin 4). Within each bin, the average correct RT for each condition was calculated (with each participant contributing one data point). Finally, a congruency effect (incongruent – congruent) was calculated for each bin. The congruency effect data were analyzed using a 2x4 repeated-measures ANOVA with orientation (upright, inverted) and bin (1, 2, 3, 4) as within-subjects factors.
In two additional exploratory analyses, we examined the relationship between the size Stroop effect and the rectilinearity difference of the two simultaneously presented objects. First, we ran a 2x2 repeated-measures ANOVA on the size Stroop effect for the RT data (incongruent – congruent) with inversion (upright, inverted) and rectilinearity difference (high, low) as within-subjects factors. The rectilinearity factor was created by ranking the trials based on the rectilinearity difference between the large and small objects on that trial, with image-level rectilinearity computed using a computational model (see Methods), and then performing a median split. In this ranking, trials where large objects were more rectilinear than small objects fall on one end of the spectrum, while trials where small objects were more rectilinear than large objects fall on the other end of the spectrum.
Second, we examined the correlation between the rectilinearity difference and the size Stroop effect. For each participant, we (1) averaged the RTs for each unique trial type (i.e., unique object pairs) separately for congruency (congruent, incongruent) and orientation (upright, inverted), (2) computed a size Stroop effect for each unique trial type (incongruent - congruent), (3) computed a rectilinearity index for each trial type by taking the difference between the rectilinearity measures of the large and small object of that trial type, in the direction that positive values indicate that large objects are more rectilinear than small objects, (4) correlated the size Stroop effect with the rectilinearity index, (5) Fisher transformed the correlations to create a more normal distribution, (6) across participants, tested the average correlation against 0 using a 1-sample t-test.
We report Bayes factors for all analyses. For isolated main and 2x2 interaction effects, we report Bayes factors using non-directional one-sample t-tests, with the standard settings of the BayesFactor R package. For 2x4 interactions in the response time distribution analysis, we report the Bayes factor for comparison of the full model (interaction and the two main effects) with the model containing only the two main effects. For all analyses, we report the Bayes factor in favor of the alternative hypothesis; for example, for a BF = 3, the alternative hypothesis predicts the data 3 times better than the null hypothesis.
Results
Accuracy
The overall accuracy was close to ceiling (M = 97.97%; SD = 2.52%). There was a size Stroop effect, as indicated by a main effect of congruency, with significantly higher accuracy in the congruent (M = 98.2%; SD = 2.6%) than incongruent (M = 97.7%; SD = 2.8%) condition, F(1, 33) = 6.71, p = .014, np2 = .17, BF = 3.21. This size Stroop effect did not differ for upright and inverted objects, as indicated by a non-significant interaction between congruency and orientation, F(1, 33) = 2.67, p = .112, np2 = .08, BF = .61. Accuracy for the upright and inverted objects did not differ, as indicated by a non-significant main effect of orientation, F(1, 33) = 3.6, p = .066, np2 = .1, BF = .91.
Response time
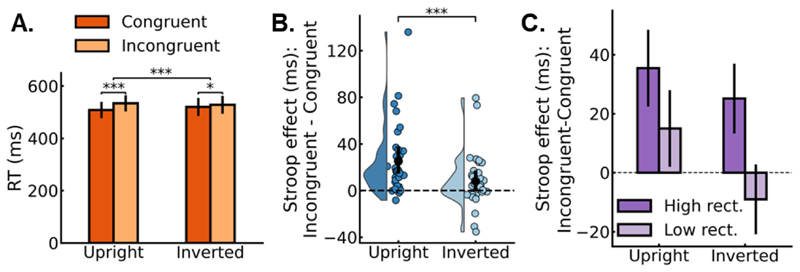
Figure 2A presents the mean RTs for correct trials as a function of congruency and orientation (see Figure 2B for size Stroop effect: incongruent - congruent). There was a size Stroop effect, as indicated by a main effect of congruency, with significantly faster RTs for the congruent (M = 514 ms; SD = 97 ms) than incongruent condition (M = 531 ms; SD = 102 ms), F(1, 33) = 17.39, p < .001, np2 = .35, BF = 130.83. Crucially, the size Stroop effect was larger for upright (M = 25 ms; SD = 29 ms) than inverted (M = 8 ms; SD = 23 ms) images, as indicated by a significant interaction between congruency and orientation, F(1, 33) = 16.92, p < .001, np2 = .34, BF = 112.96. For congruent trials, participants were faster in the upright (M = 508 ms; SD = 93 ms) than the inverted condition (M = 520 ms; SD = 102 ms; t(33) = 3.66, p < .001, np2 = .29, BF = 35.70), while for incongruent trials, participants did not differ in the upright (M = 534 ms; SD = 104 ms) and inverted conditions (M = 528 ms; SD = 100 ms; t(33) = 1.45, p = .158, np2 = .06, BF = .47). However, inversion did not entirely abolish the size Stroop effect (M = 8 ms; SD = 23 ms; t(33) = 2.11, p = .043, np2 = .12, BF = 1.2). Finally, the RTs for upright and inverted objects did not differ, as indicated by a non-significant main effect of orientation, F(1, 33) = 1.24, p = .274, np2 = .04, BF = .32.
Figure 2. Results of Experiment 1.
(A) Reaction times for correct responses as a function of congruency (congruent, incongruent) and orientation (upright, inverted). (B) Stroop effect in response times for correct responses, computed as incongruent trials minus congruent trials. The small colored markers represent individual participants, while the black markers represent the group averages. (C) Stroop effect in response time for correct responses as a function of rectilinearity split (high, low) and orientation (upright, inverted). All error bars represent 95% CIs. *, **, *** represent p < .05, .01, .001, respectively.
Influence of rectilinearity
The large and small objects included in the study differed in terms of rectilinearity, with large objects being on average more rectilinear than small objects (see Methods). In an additional exploratory analysis, we tested to what extent rectilinearity accounted for the size Stroop effect and whether this influence differed for upright and inverted objects. To this end, we ran a 2x2 repeated-measures ANOVA on the size Stroop effect for the RT data (incongruent – congruent) with inversion (upright, inverted) and rectilinearity (high, low) as within-subjects factors. We only report the statistics related to the rectilinearity factor. For the high-rectilinearity trials, the large objects were on average more rectilinear than the small objects (t(28) = 4.70, p < .001, np2 = .44, BF = 307.58), while there was no difference for the low-rectilinearity trials (t(28) = .93, p = .362, np2 = .03, BF = .48). The ANOVA showed that rectilinearity contributed to the size Stroop effect, as demonstrated by a main effect of rectilinearity, F(1, 33) = 19.53, p < .001, np2 = .37, BF = 18591.44. This effect was independent of inversion, as demonstrated by the lack of a 2-way interaction between inversion and rectilinearity, F(1, 33) = 2.53, p = .121, np2 = .07, BF = .54. As can be observed in Figure 2C, there was no size Stroop effect for inverted trials when rectilinearity was equated.
Correlation between Stroop effect and rectilinearity
In addition to the ANOVA involving rectilinearity, we analyzed whether the size Stroop effect correlated with rectilinearity differences between the large and small objects across trial types (i.e., object pairs). In line with the ANOVA results, for both upright and inverted objects, there was a small but reliable positive correlation (upright: r = .12, t(33) = 4.34, p < .001, np2 = .36, BF = 201.14; inverted: r = .19, t(33) = 5.23, p < .001, np2 = .45, BF = 2193.50), whereby increasing Stroop effects were associated with increasing rectilinearity differences in the direction that large objects are more rectilinear than small objects.
Response time distribution analysis
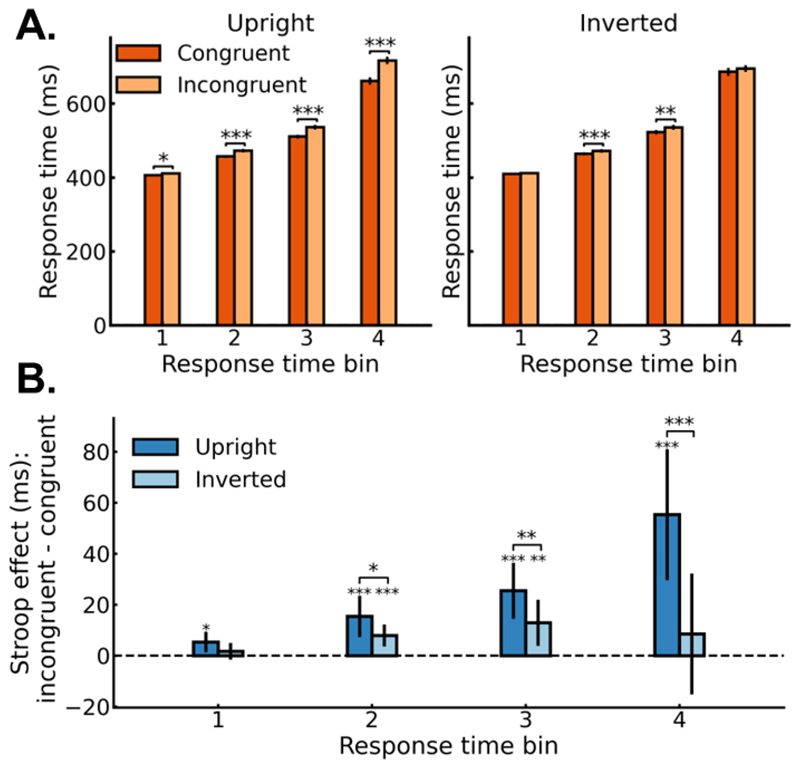
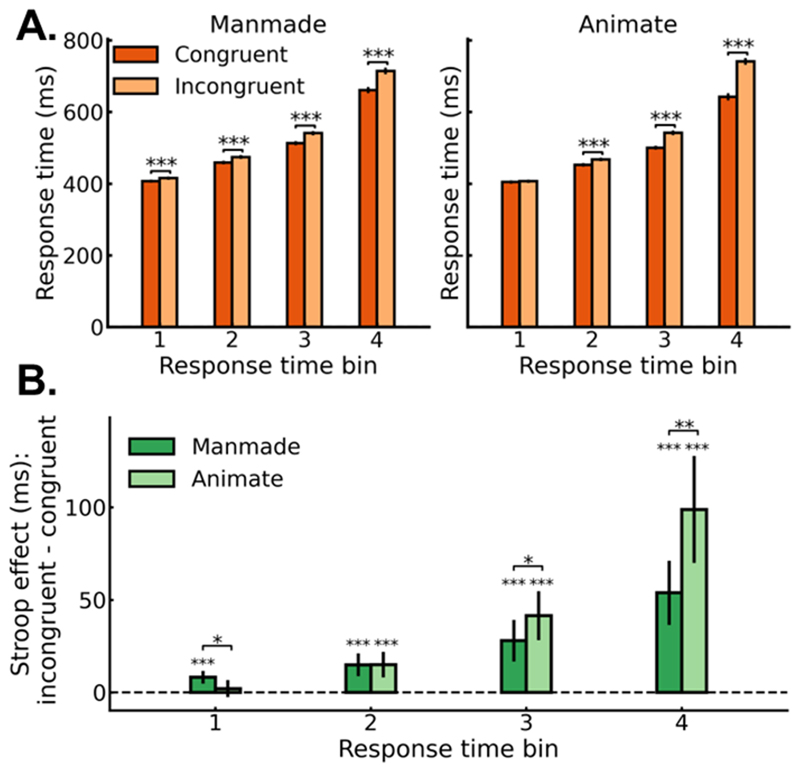
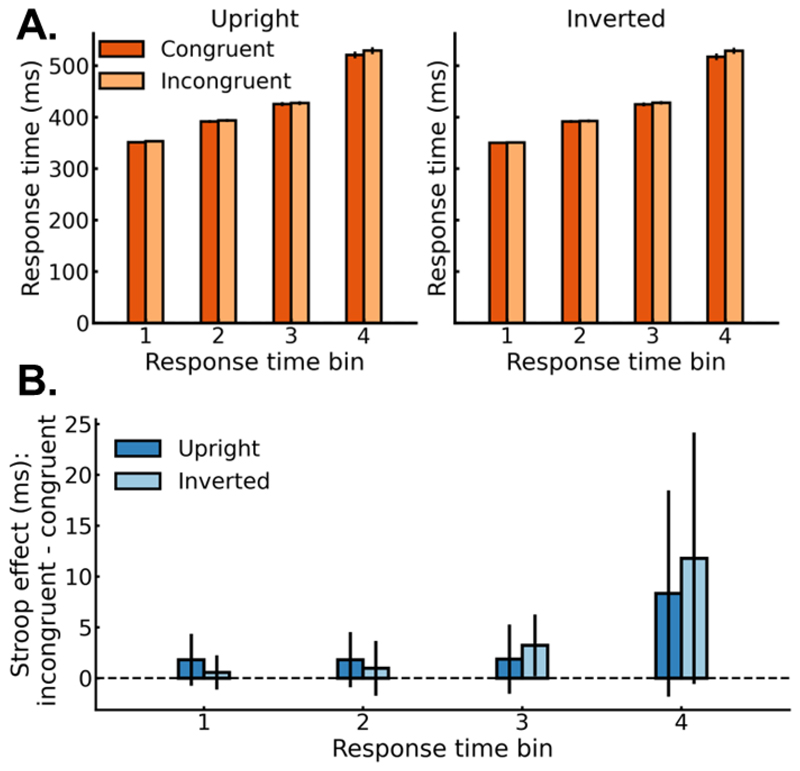
In a final exploratory analysis, we examined if the size Stroop effect depended on participants reaction times, with faster processing of the competing real-world size manifesting in Stroop effects in faster reaction times. Figure 3A shows the mean correct RTs as a function of congruency, orientation, and response time bin (see Figure 3B for size Stroop effect: incongruent – congruent). The significant interaction between orientation and bin, F(3, 99) = 12.32, p < .001, np2 = .27, BF = 18.92, indicated that orientation influenced the size Stroop effect differently across the RT distribution. Thus, we compared the size Stroop effect for upright and inverted conditions in each bin separately. The size Stroop effect for upright objects was larger than that for the inverted objects in all bins (t(33) > 2.59, p < .015, np2 > .17, BF > 3.18 for all tests) except the first bin (t(33) = -1.53, p = .136, np2 = .07, BF = .53). Finally, there was a congruency effect for upright objects in all bins (t(33) > 2.6, p < .014, np2 > .17, BF > 3.27, for all tests; Figure 3B). By contrast, only bins 2 and 3 showed a congruency effect for inverted displays (all sign. tests, t(33) > 2.79, p < .009, np2 > .19 BF > 4.90; all non-sign. tests for bins 1 and 4, t(33) < -1.02, p > .318, np2 < .03, BF < .30; Figure 3B).
Figure 3.
(A) Response time distribution for correct responses as a function of congruency, orientation, and response time bin. The y-axis scale is shared across panels. (B) Response time distribution for the size Stroop effect for correct responses as a function of orientation and response time bin. Bin 1 contains the 25% fastest responses of each participant. Bin 2 contains the next 25% fastest responses, and so on. All error bars represent 95% CIs. *, **, *** represent p < .05, .01, .001, respectively.
Summary
Overall, results of Experiment 1 show that the size Stroop effect was present for upright objects, replicating previous reports (Konkle & Oliva, 2012b). Importantly, the size Stroop effect was strongly reduced by object inversion. This reduction was most prominent on slower trials. Finally, differences in rectilinearity between large and small objects contributed to the size Stroop effect but did so equally for upright and inverted conditions, indicating a separate influence.
Experiment 2
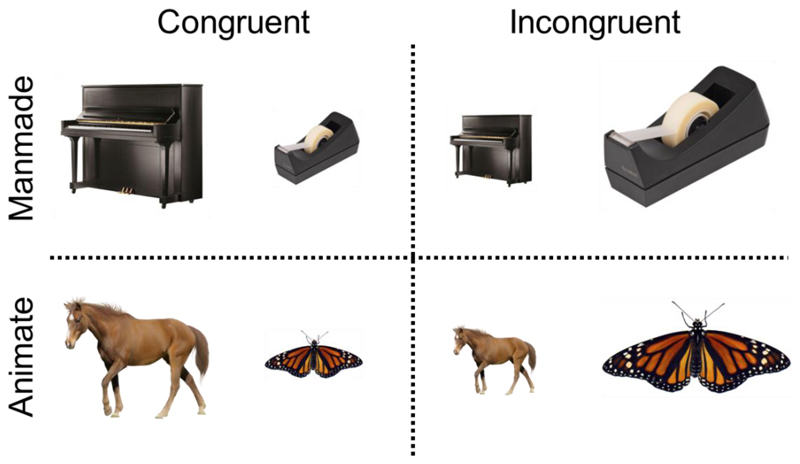
Experiment 1 showed that the size Stroop effect was almost abolished when recognition was made more difficult by object inversion and was fully abolished when objects did not differ in terms of rectilinearity (Figure 2C). Experiment 2 was designed to further test the role of differences in visual properties between large (e.g., rectilinear) and small (e.g., curvilinear) objects. In this experiment, we contrasted the size Stroop effect for large and small manmade objects, where there are systematic differences in rectilinearity (Long et al., 2016), to the Stroop effect for large and small animate objects, where there are no systematic differences in rectilinearity (see Methods). If differences in rectilinearity are necessary for the size Stroop effect, we would expect no size Stroop effect for animate objects. In contrast, if rectilinearity differences are not necessary for the size Stroop effect, we would expect a similar size Stroop effect for animate objects. Moreover, since animate objects may be recognized faster and more automatically than manmade objects (New et al. 2007), the size Stroop effect for animates could even be stronger than that for manmade objects. Finally, animate objects offer an interesting test since they do not (or only weakly, relative to manmade objects) show a real-world size organization in the human ventral temporal cortex as measured with functional magnetic resonance imaging (fMRI; Konkle & Caramazza, 2013; Luo et al., 2023).
Methods
Participants
34 participants (M = 33.0 years; SD = 10.49 years; females = 19; males = 15) took part in the study. As in Experiment 1, this sample size was selected based on an a-priori power analysis ensuring 80% to detect an effect size of d = .5 (corresponding with np2 = .21) with p = .05 for the critical main effect of congruency. Previous studies found larger effect sizes for the main effect of congruency (e.g., Konkle & Oliva, 2012b; Long & Konkle, 2017). Participants were recruited online through Prolific (www.prolific.com) in return for a monetary compensation. One participant was replaced due to low overall accuracy (77.93%; > 3 SDs below the group mean). Informed consent was obtained electronically prior to the experiment. The study was conducted in compliance with the ethical principles and guidelines of the Research Ethics Committee of the Faculty of Science of the Radboud University and APA ethical standards. All data were collected in the year of 2022.
Stimuli
The stimuli consisted of 120 unique images of 60 animate and 60 manmade objects, that were each divided into 30 large and 30 small objects (available at https://osf.io/ab3dy/). The manmade objects were the same as those used in the Experiment 1. The animate objects were found online and were cropped and pasted on a white uniform background of 500 x 500 pixels. All stimuli were displayed at 12 and 6 degrees of visual angle, as measured along the longest dimension of the object.
We used a computational model to quantify the rectilinearity in each animate object image (for model description, see Li & Bonner, 2020). Large and small animals did not differ in rectilinearity, t(58) = .61, p = .54, np2 = .006, BF = .31, unlike the manmade objects (see Experiment 1 for rectilinearity comparisons involving the manmade objects). The difference in rectilinearity between large and small manmade objects was larger than this difference in animate objects, t(58) = 2.31, p = .025, np2= .08, BF = 2.35.
Moreover, we quantified the area-to-perimeter ratio for large and small animals (see Experiment 1 for area-to-perimeter comparisons involving manmade objects). Large and small animals did not differ on area-to-perimeter ratio, t(58) = 1.14, p = .261, np2 = .02, BF = .45.
Design
The design and paradigm were the same as used in Experiment 1, with the exception that the trial composition consisted of: 30 trial pairs x 2 animacy x 2 congruency x 2 instruction block x 2 repetitions (Figure 4). This yielded a total of 480 trials.
Figure 4. Paradigm: for both manmade and animate displays, participants selected the bigger (or smaller) image on the screen while disregarding their familiar size.
Representative image examples of the objects used in the study (actual images not shown for copyright reasons).
Analysis
Trials with RT less than 200 ms and more than 1500 ms were excluded from the analysis (1.08% of total trials) (Konkle & Oliva, 2012b; Long & Konkle, 2017). Given the main question of examining if the congruency effect was modulated by animacy, the data for each instruction block (attend bigger; attend smaller) was averaged prior to statistical analysis. Similar exploratory analyses as in E1 were conducted, with the exception that the orientation factor was replaced by the animacy factor (see Experiment 1 for a detailed description of this analysis).
Results
Accuracy
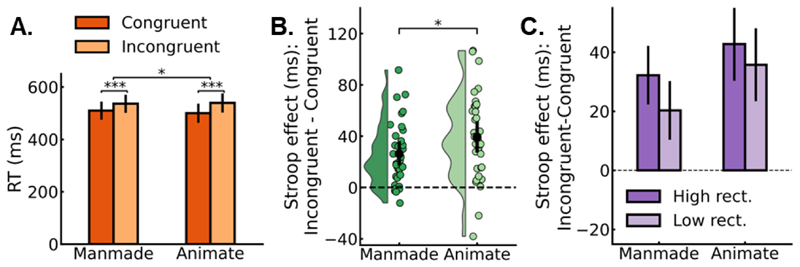
The overall accuracy was close to ceiling (M = 98.1%; SD = 1.78%). There was a size Stroop effect, as indicated by a main effect of congruency, with significantly higher accuracy in the congruent (M = 99.0%; SD = 1.4%) than incongruent (M = 97.2%; SD = 2.7%) condition, F(1, 33) = 31.58, p < .001, np2 = .49, BF = 6361.75. Moreover, the size Stroop effect was larger for animate (M = 2.5%; SD = 2.6%) than manmade objects (M = 1.3%; SD = 1.8%), as indicated by a significant interaction between congruency and animacy, F(1, 33) = 10.51, p = .003, np2 = .24, BF = 13.29. The accuracy for animate and manmade objects did not differ, as indicated by a non-significant main effect of animacy, F(1, 33) = 1.41, p = .244, np2 = .04, BF = .35.
Response time
Figure 5A present the mean RTs for correct trials as a function of congruency and animacy (see Figure 4B for size Stroop effect: incongruent – congruent). There was a size Stroop effect, as indicated by a main effect of congruency, with faster RTs in the congruent (M = 505 ms; SD = 105 ms) than incongruent (M = 538 ms; SD = 108 ms) condition, F(1, 33) = 55.63, p < .001, np2 = .63, BF = 928874.80. Interestingly, there was a larger size Stroop effect for animate (M = 39 ms; SD = 33 ms) than manmade (M = 26 ms; SD = 25 ms) objects, as indicated by a significant interaction between congruency and animacy, F(1, 33) = 7.26, p = .011, np2 = .18, BF = 3.98. The RTs for animate and manmade objects did not differ, as indicated by a non-significant main effect of animacy, F(1, 33) = 2.00, p = .167, np2 = .06, BF = .46.
Figure 5. Results of Experiment 2.
(A) Reaction times for correct responses as a function of congruency (congruent, incongruent) and animacy (manmade, animate). (B) Stroop effect in response times for correct responses, computed as incongruent trials minus congruent trials. The small colored markers represent individual participants, while the black markers represent the group averages. (C) Stroop effect in response time for correct responses as a function of rectilinearity split (high, low) and animacy (manmade, animate). All error bars represent 95% CIs. *, **, *** represent p < .05, .01, .001, respectively.
Influence of rectilinearity
Similar to Experiment 1, in an additional exploratory analysis we tested whether rectilinearity accounted for the size Stroop effect. For animals, in the high-rectilinearity trials, the large animals were on average more rectilinear than the small animals (see Experiment 1 for the same analysis involving the manmade objects), t(28) = 2.7, p = .012, np2 = .21. BF = 4.53. In contrast, in the low-rectilinearity trials, the large animals were on average less rectilinear than small animals, t(28) = -3.15, p = .004, np2 = .26, BF = 10.53. Thus, if rectilinearity evokes an association of “being large”, independent of recognition, then in the low rectilinearity trials, small objects should be associated with being large and therefore lead to a reversed or attenuated Stroop effect.
We ran a 2x2 repeated-measures ANOVA on the size Stroop effect for the RT data (incongruent – congruent) with animacy (manmade, animate) and rectilinearity (high, low) as within-subjects factors. We only report the stats related to the rectilinearity factor. Rectilinearity contributed to the size Stroop effect, as demonstrated by a main effect of rectilinearity, F(1, 33) = 4.96, p = .033, np2 = .13, BF = 1.47 (Figure 5C). This effect was independent of animacy, as demonstrated by the lack of a 2-way interaction between animacy and rectilinearity, F(1, 33) = .52, p = .478, np2 = .02, BF = .29.
Correlation between Stroop effect and rectilinearity
Similar to Experiment 1, we analyzed whether the trial-type (i.e., object pairs) Stroop effect correlated with trial-type rectilinearity differences between the large and small animals, or the large and small manmade objects. For manmade objects, there was a small but reliable positive correlation, r = .08, t(33) = 3.52, p = .001, np2 = .27, BF = 25.57, replicating Experiment 1. In contrast, for animate objects, there was a weak negative correlation, r = -.06, t(33) = -2.69, p = .011, np2 = .18, BF = 3.93, whereby larger size Stroop effects were associated with a rectilinearity difference in the direction that small objects were relatively more rectilinear.
Response time distribution
Figure 6A shows the mean correct RTs as a function of animacy and response time bin (see Figure 6B for size Stroop effect: incongruent - congruent). There was an interaction between animacy and response time bin (F(3, 99) = 13.63, p < .001, np2 = .29, BF = 203.50), indicating that animacy influenced the size Stroop effect differently across the RT distribution. Thus, we compared the size Stroop effect for manmade and animate conditions in each bin separately. In the first bin, the size Stroop effect was larger for manmade than animate objects (t(33) = 2.45, p = .020, np2 = .15, BF = 2.46), while in the slowest bins (3 and 4), the reverse was observed, with a larger size Stroop effect for animate than manmade objects (t(33) > 2.43, p < .021, np2 > .15, BF > 2.32 for both tests). Finally, there was a size Stroop effect for manmade displays in all bins (t(33) > 4.74, p < .001, np2 > .41, BF = 583.01, for all tests; Figure 6B). In contrast, the size Stroop effect for animate objects was significant in all bins (t(33) > 4.26, p < .001, np2 > .36, BF > 164.33 for all tests) except the first bin (t(33) = .9, p = .377, np2 = .02, BF = .27; Figure 6B).
Figure 6.
(A) Response time distribution for correct responses as a function of congruency, animacy, and response time bin. The y-axis scale is shared across panels. (B) Response time distribution for the size Stroop effect for correct responses as a function of animacy and response time bin. Bin 1 contains the 25% fastest responses of each participant. Bin 2 contains the next 25% fastest responses, and so on. All error bars represent 95% CIs. *, **, *** represent p < .05, .01, .001, respectively.
Summary
Overall, results of Experiment 2 show that animate objects evoked a larger size Stroop effect than manmade objects. Moreover, the larger size Stroop effect for animate objects was specific to the slower trials. In contrast, manmade objects evoked a larger size Stroop effect in the fastest trials. Similar to Experiment 1, the size Stroop effect for manmade objects was associated with rectilinearity differences between large and small objects, whereas this was not the case for animate objects.
Experiment 3
Experiment 1 provided evidence that the size Stroop effect depends on the ease of recognition (as manipulated by inversion), with a stronger Stroop effect for upright than inverted objects. The results of Experiment 2 provided further support for a role of recognition in driving the size Stroop effect, showing a stronger Stroop effect for animals than manmade objects. Because large and small animals were matched in terms of rectilinearity, Experiment 2 also provided evidence that rectilinearity is not necessary for evoking the size Stroop effect. At the same time, however, results from correlation analyses in both experiments pointed to a potential contribution of rectilinearity to the size Stroop effect for manmade objects. To further investigate the role of low- and mid-level features in driving the size Stroop effect, in Experiment 3 we aimed to replicate the previously observed size Stroop effect for texform objects (Long & Konkle, 2017) – objects that are made unrecognizable while maintaining texture and form features. In addition, to investigate whether the size Stroop effect could be driven by residual recognition of the texform objects, we examined if the size Stroop effect for texform objects was influenced by image inversion. If the size Stroop effect for texforms is driven by visual features, the effect should not differ for both upright and inverted trials. In contrast, if occasional recognition of texforms drives the size Stroop effect, then it should be reduced for inverted trials.
Methods
Participants
34 participants (M = 27.41 years; SD = 5.41 years; females = 20; males = 13; other = 1) took part in the study. As in Experiments 1 and 2, this sample size was selected based on an a-priori power analysis ensuring 80% to detect an effect size of d = .5 (corresponding with np2 = .21) with p = .05 for the critical main effect of congruency. Previous studies found larger effect sizes for the main effect of congruency (e.g., Konkle & Oliva, 2012b; Long & Konkle, 2017). Participants were recruited online through Prolific (www.prolific.com) in return for a monetary compensation. Two participants were replaced due to low overall accuracy (46.96%, 86.57% > 3 SDs below the group mean). Informed consent was obtained electronically prior to the experiment. The study was conducted in compliance with the ethical principles and guidelines of the Research Ethics Committee of the Faculty of Science of the Radboud University and APA ethical standards. All data were collected in the year of 2022.
Stimuli
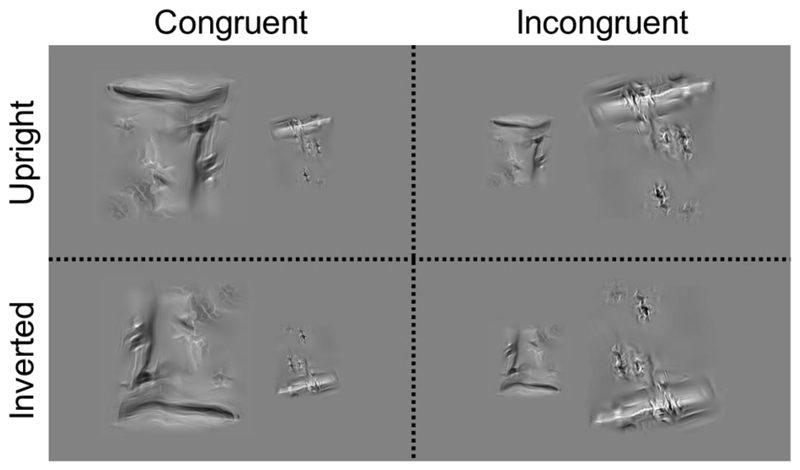
The stimuli consisted of 60 unique images that were divided into 30 small (e.g., dustpan) and 30 large (e.g., shopping cart) manmade objects, and taken from a previous study (Long et al., 2018). The stimuli were processed with a “texform” algorithm to render them unrecognizable while maintaining low-level shape and texture properties related to early and mid-level visual processing (Freeman & Simoncelli, 2011; Long et al., 2018). Specifically, within local pooling windows of the object image, low-level image measurements were computed (e.g., Gabor responses of different orientations, spatial frequencies, and spatial scales). Next, a white noise image was transformed to match the measured image statistics (for further details, see Long et al., 2018). The stimuli were pasted on a uniform gray background of 500 x 500 pixels and displayed at 12 and 6 degrees of visual angle, as measured along the longest dimension of the object. The stimuli were downloaded from the authors’ website (https://konklab.fas.harvard.edu/ImageSets/AnimSizeTexform.zip).
Similar to the manmade and animate objects, we used a computational model to quantify the rectilinearity in large and small texform objects (for model description, see Li & Bonner, 2020). This analysis showed that large texforms were more rectilinear than small texforms, t(58) = 2.88, p = .006, np2 = .13, BF = 7.58.
Design
The design and paradigm were the same as used in Experiment 1 (Figure 7). Specifically, the texforms were presented as a function of congruency (congruent, incongruent) and orientation (upright, inverted), using the same number of trials and breaks.
Figure 7. Paradigm: for both upright and inverted displays, participants selected the bigger (or smaller) image on the screen while disregarding their familiar size.
Analysis
Trials with response times shorter than 200 ms or longer than 1500 ms were excluded from the analysis (0.29% of total trial) (Konkle & Oliva, 2012b; Long & Konkle, 2017). Given the main question of examining the congruency effect and how it was influenced by inversion, the data for each instruction block (attend bigger; attend smaller) was averaged prior to statistical analysis. The data were analyzed as described for Experiment 1.
Results
Accuracy
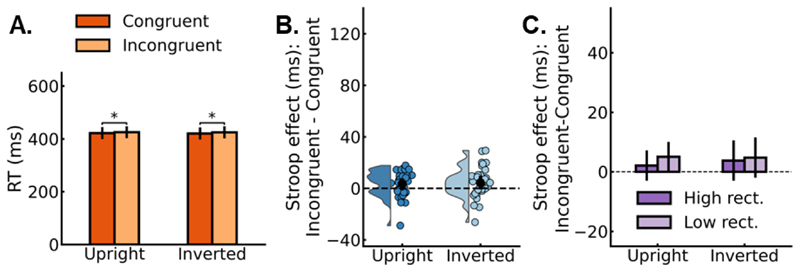
The overall accuracy was close to ceiling (M = 98.48%; SD = 1.43%). There was no overall size Stroop effect, as indicated by a non-significant effect of congruency, F(1, 33) = 1.6, p = .215, np2 = .05, BF = .38. Moreover, the size Stroop effect for upright and inverted trials did not differ, as indicated by a non-significant interaction between congruency and orientation, F(1, 33) = .17, p = .685, np2 = .005, BF = .20. The accuracy for upright and inverted objects also did not differ, as indicated by a non-significant effect of orientation, F(1, 33) = .32, p = .575, np2 = .01, BF = .21.
Response time
Figure 8A present the mean RTs for correct trials as a function of congruency and orientation (see Figure 8B for size Stroop effect: incongruent – congruent). There was a small size Stroop effect, with faster RTs for congruent (M = 421 ms; SD = 67 ms) than incongruent trials (M = 425 ms; SD = 65 ms), as indicated by a main effect of congruency, F(1, 33) = 6.42, p = .016, np2 = .16, BF = 2.87. The size Stroop effect for upright and inverted trials did not differ, as indicated by a non-significant interaction between congruency and orientation, F(1, 33) = .11, p = .742, np2 = .003, BF = .19, with small but significant size Stroop effects in both upright trials (M = 3.6 ms; SD = 10 ms; t(33) = 2.08, p = .046, np2 = .12, BF = 1.22) and inverted trials (M = 4.3 ms; SD = 12 ms; t(33) = 2.11, p = .043, np2 = .12, BF = 1.29). The RTs for upright and inverted objects did not differ, as indicated by a non-significant main effect of orientation, F(1, 33) = .7, p = .408, np2 = .02, BF = .25.
Figure 8. Results of Experiment 3.
(A) Reaction times for correct responses as a function of congruency (congruent, incongruent) and orientation (upright, inverted). (B) Stroop effect in response times for correct responses, computed as incongruent trials minus congruent trials. The small colored markers represent individual participants, while the black markers represent group averages. (C) Stroop effect in response time for correct responses as a function of rectilinearity split (high, low) and orientation (upright, inverted). All error bars represent 95% CIs. *, **, *** represent p < .05, .01, .001, respectively.
Influence of rectilinearity
Similar to Experiments 1 and 2, in an additional exploratory analysis we tested whether rectilinearity accounted for the size Stroop effect. In the high-rectilinearity trials, the large texforms were on average more rectilinear than the small texform, t(28) = 6.62, p < .001, np2 = .61. BF = 30089.17. In contrast, in the low-rectilinearity trials, the large and small texforms did not differ, t(28) = -1.31, p = .201, np2 = .06, BF = .66.
We ran a 2x2 repeated-measures ANOVA on the size Stroop effect for the RT data (incongruent – congruent) with orientation (upright, inverted) and rectilinearity (high, low) as within-subjects factors. We only report the stats related to the rectilinearity factor. Rectilinearity did not contribute to the size Stroop effect, as demonstrated by a non-significant main effect of rectilinearity, F(1, 33) = .34, p = .566, np2 = .01, BF = .24, and a non-significant 2-way interaction between orientation and rectilinearity, F(1, 33) = .2, p = .659, np2 = .01, BF = .25 (Figure 8C).
Correlation between Stroop effect and rectilinearity
We analyzed whether the trial-type (i.e., object pairs) Stroop effect correlated with trial-type rectilinearity differences between the large and small texform objects. There was no correlation for upright, r = -.01, t(33) = .31, p = .758, np2 = .003, BF = .19, or inverted texforms, r = - 0.1, t(33) = .26, p = .799, np2 = .002, BF = .19. Thus, while large and small texform objects differed in rectilinearity (see Methods), the variability in rectilinearity did not correlate with the variability in the size Stroop effect across trials. Note, however, that the size Stroop effect was numerically small (4 ms), such that this analysis may not have enough sensitivity to detect such a correlation.
Response time distribution
Figure 9A shows the mean correct RTs as a function of orientation and response time bin (see Figure 9B for size Stroop effect: incongruent - congruent). The significant main effect of bin, F(3, 99) = 3.82, p = .012, np2 = .10, BF = 4.50, reflected a Stroop effect in bins 3 (t(33) = 2.21, p = .031, np2 = .13, BF = 1.02) and 4 (t(33) = 2.48, p = .016, np2 = .16, BF = 1.62) but not in bins 1 (t(33) = 1.52, p = .134, np2 = .07, BF = .61) and 2 (t(33) = 1.44, p = .156, np2 = .06, BF = .38). However, there was no interaction between orientation and bin, F(3, 99) = .33, p = .803, np2 = .01, BF = .06, suggesting that orientation did not impact the Stroop effect across bins.
Figure 9.
(A) Response time distribution for correct responses as a function of congruency, orientation, and response time bin. The y-axis scale is shared across panels. (B) Response time distribution for the size Stroop effect for correct responses as a function of orientation and response time bin. Bin 1 contains the 25% fastest responses of each participant. Bin 2 contains the next 25% fastest responses, and so on. All error bars represent 95% CIs. *, **, *** represent p < .05, .01, .001, respectively.
Summary
Overall, the results of Experiment 3 showed a small size Stroop effect for texforms. This effect occurred for both upright and inverted objects. Analysis of the RT distribution revealed that the orientation-independent effect emerged in slower trials.
Discussion
This study investigated what drives the automatic retrieval of real-world object size knowledge, as reflected in the size Stroop effect (Konkle & Oliva, 2012b). While traditional perceptual and memory models propose that object recognition is the primary access point to object knowledge, such as an object’s familiar size (e.g., Collins & Quillan, 1969; Rosch et al., 1976), recent research showed that size knowledge, as reflected in the size Stroop effect, can be accessed directly from an object’s low- and mid-level visual features, without high-level object processing and recognition taking place (Long & Konkle, 2017). Here we shed novel light on this debate, by examining the role of recognition versus visual features in driving the size Stroop effect.
Experiments 1 and 2 replicated the original finding of a familiar-size Stroop effect for upright manmade objects (Konkle & Oliva, 2012b). Experiment 1 used image inversion to disrupt rapid object recognition while preserving the visual features in the objects (Mack et al., 2008). We reasoned that inversion should reduce or remove the size Stroop effect if the effect follows object recognition. The results showed that the large size Stroop effect for upright objects was nearly abolished for inverted objects, supporting our hypothesis. Moreover, to test if rectilinearity is necessary for the size Stroop effect, Experiment 2 used large and small animate objects since they, unlike manmade objects, do not differ systematically in rectilinearity (see Methods). We reasoned that animate objects should show a smaller size Stroop effect than manmade objects if the effect depends on rectilinearity. However, the larger Stroop effect for animate objects suggest that rectilinearity is not necessary for the size Stroop effect. Since animate objects may be recognized faster and more automatically than manmade objects (New et al. 2007), it could suggest that the larger Stroop effect for animate than manmade objects reflect larger competition due to object recognition evoking object related size knowledge. Overall, these findings indicate that the size Stroop effect partly depends on object recognition (Konkle & Oliva, 2012b).
In addition to showing that recognition plays a role in the size Stroop effect for manmade objects and animals, Experiment 3 replicated the size Stroop effect for unrecognizable texform objects (Long & Konkle, 2017). Texforms are manmade objects that are rendered unrecognizable and preserve some rectilinearity and texture properties that differ between large and small manmade objects. To test if the size Stroop effect for the texforms is modulated by inversion – for example because some exemplars were recognizable – Experiment 3 used the inversion manipulation of Experiment 1. The size Stroop effect was independent of inversion, suggesting that the Stroop effect did not follow residual recognition but was driven by orientation-independent visual features associated with large vs. small objects (e.g., rectilinearity). Consistent with this finding, the exploratory rectilinearity analysis of Experiments 1 and 2 showed an association between rectilinearity differences and the size Stroop effect, with larger Stroop effects for trials in which the large and small objects differed more strongly in rectilinearity. Importantly, this effect was independent of inversion, thus suggesting independent contributions of visual feature associations and object recognition to the size Stroop effect.
Analysis of the response time distributions further characterized the time course of the size Stroop effect evoked by manmade objects, animals, and texforms. In Experiment 1, we found that the size Stroop effect for upright and inverted manmade objects differed for relatively slower responses. In Experiment 2, in slower trials, animate objects evoked a larger size Stroop effect than manmade objects. Both of these Stroop effects are arguably driven by recognition, and the effect in the slower trials indicate that object recognition takes time before it completes and can interfere with the screen size task. Interestingly, for fast trials, in Experiment 1, there was no difference between upright and inverted trials, and in Experiment 2, manmade objects evoked a larger size Stroop effect than animals in the fastest responses. This suggests that the Stroop effect on these fast trials may have been driven by mid-level feature differences, which are equally present in upright and inverted trials, and more strongly present in manmade objects than animals.
Our findings are consistent with conventional theories for how perceptual stimuli evoke object knowledge. Rosch et al. (1976) proposed that a sensory stimulus’s “entry-point” to memory is at a so-called “basic” category level. They had participants verify if category labels at different levels of abstraction - e.g., “sparrow”, “bird”, or “animal” - matched a subsequent object image. They found that participants were fastest at verifying the object-label match at the level of “bird” than at the level of “animal” or “sparrow”. It was suggested that visual sensory stimuli are first categorized at the basic level before evoking associated object knowledge. This notion is consistent with other classic models of memory organization arguing for knowledge to be stored relative to basic-level categories (e.g., all birds can fly; a canary is a bird; therefore, it can fly) (e.g., Collins & Quillan, 1969; for reviews, see Yee et al. 2014). In the context of our task, and in line with the interpretation of the original study (Konkle & Oliva, 2012b), this implies that the automatic categorization of the objects (e.g., “car”, “ball”), in turn activates higher-order size knowledge (all cars are larger than balls). This would be a more accurate and generalizable mode of accessing real-world knowledge than using mid-level features such as rectilinearity, since large and small manmade objects often share such features (e.g., many small objects are rectilinear; small packages, cellphones, tablets, laptops, keys, etc.). The observation that a manipulation that disrupts our ability to categorize the object at a basic level greatly reduces the Stroop effect supports these classic views on how sensory stimuli activate conceptual knowledge.
What is the neural basis of the size Stroop effect? fMRI studies have shown that large and small objects evoke selective fMRI responses in medial and lateral ventral temporal cortex (VTC), respectively (Coutanche et al., 2019; Gabay et al., 2016; Julian et al., 2017; Konkle & Caramazza, 2013; Konkle & Oliva, 2012a; Khaligh-Razavi et al., 2018; Troiani et al., 2014; He et al., 2013). Part of this size organization has been causally linked to the size Stroop effect. That is, transcranial magnetic stimulation (TMS) to the lateral small-VTC area, but not a control area (vertex), reduced the size Stroop effect for manmade objects (Chiou & Lambon Ralph, 2016). However, it is unclear if this disrupted the recognition of the objects (and subsequent extraction of size information) or size knowledge independent of object recognition. Interestingly, the responses of large vs. small texforms overlap with responses to their real manmade object counterparts in VTC (Long et al., 2018), suggesting that the VTC size organization reflects visual feature differences between large and small objects. However, unlike real objects, there is currently no evidence linking the size Stroop effect of texforms to the ventral stream. Moreover, animate objects are processed in distinct regions of visual cortex compared to manmade objects, and visual cortex either does not show a size organization for animate objects (Konkle & Caramazza, 2013) or shows a relatively weak size organization for animate objects relative to manmade objects (Luo et al., 2023); and yet, we find stronger size Stroop effects for animate than manmade objects in the current study. These considerations suggest that the size Stroop effect does not directly map onto the object size organization of the ventral temporal cortex.
Our findings indicate that size knowledge is a salient object property that is automatically extracted after object recognition. What is the functional relevance of automatically extracting size? While it has been suggested that size is a relevant factor for determining how we interact with an object (e.g., grasping; Bainbridge & Oliva, 2015), our observation that animate objects also show a size Stroop effect suggests that interaction mode (e.g., grasping) is not the sole reason. Another possibility is that real-world size is rapidly extracted to support judging an object’s distance from the observer: a small object that is large on the retina must be relatively close. On this view, the size knowledge extracted after object recognition facilitates our judgments of distance, together with other distance cues.
In summary, our results indicate that the recognition of objects is a strong contributor to the automatic retrieval of real-world object size knowledge, as reflected in the size Stroop effect. However, our findings also provide evidence for an alternative route, where simple visual features can interfere with perceptual size judgments. Future work should examine how the size Stroop effect relates to mechanisms involved in cognitive control, for example, how recognition processes interact with processes involved in solving task conflict (e.g., Kalanthroff et al., 2018).
Acknowledgements
This project received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. 725970).
Footnotes
The authors declare no conflict of interest.
Author contributions: SH: conceptualization and design, data collection, analysis, writing. YZ: conceptualization and proof-reading. LM & NU: conceptualization, design, and proof-reading. MP: conceptualization and design, writing.
References
- Bainbridge WA, Oliva A. Interaction envelope: Local spatial representations of objects at all scales in scene-selective regions. Neuroimage. 2015;122:408–416. doi: 10.1016/j.neuroimage.2015.07.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bao P, She L, McGill M, Tsao DY. A map of object space in primate inferotemporal cortex. Nature. 2020;583(7814):103–108. doi: 10.1038/s41586-020-2350-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Champely S, Ekstrom C, Dalgaard P, Gill J, Weibelzahl S, Anandkumar A, De Rosario H. pwr: Basic functions for power analysis. 2017. https://CRAN.R-project.org/package=pwr|| .
- Chiou R, Ralph MAL. Task-related dynamic division of labor between anterior temporal and lateral occipital cortices in representing object size. Journal of Neuroscience. 2016;36(17):4662–4668. doi: 10.1523/JNEUROSCI.2829-15.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coggan DD, Tong F. Spikiness and animacy as potential organizing principles of human ventral visual cortex. Cerebral Cortex. 2023:bhad108. doi: 10.1093/cercor/bhad108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen JD, Dunbar K, McClelland JL. On the control of automatic processes: a parallel distributed processing account of the Stroop effect. Psychological review. 1990;97(3):332. doi: 10.1037/0033-295x.97.3.332. [DOI] [PubMed] [Google Scholar]
- Collins AM, Quillian MR. Retrieval time from semantic memory. Journal of verbal learning and verbal behavior. 1969;8(2):240–247. [Google Scholar]
- Coutanche MN, Thompson-Schill SL. Neural activity in human visual cortex is transformed by learning real world size. NeuroImage. 2019;186:570–576. doi: 10.1016/j.neuroimage.2018.11.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman J, Simoncelli EP. Metamers of the ventral stream. Nature neuroscience. 2011;14(9):1195–1201. doi: 10.1038/nn.2889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabay S, Kalanthroff E, Henik A, Gronau N. Conceptual size representation in ventral visual cortex. Neuropsychologia. 2016;81:198–206. doi: 10.1016/j.neuropsychologia.2015.12.029. [DOI] [PubMed] [Google Scholar]
- Gayet S, Stein T, Peelen MV. The danger of interpreting detection differences between image categories: A brief comment on “Mind the snake: Fear detection relies on low spatial frequencies”(Gomes, Soares, Silva, & Silva, 2018) 2019. [DOI] [PubMed] [Google Scholar]
- Hagen S, Vuong QC, Jung L, Chin MD, Scott LS, Tanaka JW. A perceptual field test in object experts using gaze-contingent eye tracking. Scientific Reports. 2023;13(1):11437. doi: 10.1038/s41598-023-37695-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagen S, Vuong QC, Scott LS, Curran T, Tanaka JW. The role of spatial frequency in expert object recognition. Journal of Experimental Psychology: Human Perception and Performance. 2016;42(3):413. doi: 10.1037/xhp0000139. [DOI] [PubMed] [Google Scholar]
- Hagen S, Vuong QC, Scott LS, Curran T, Tanaka JW. The role of color in expert object recognition. Journal of vision. 2014;14(9):9–9. doi: 10.1167/14.9.9. [DOI] [PubMed] [Google Scholar]
- He C, Peelen MV, Han Z, Lin N, Caramazza A, Bi Y. Selectivity for large nonmanipulable objects in scene-selective visual cortex does not require visual experience. Neuroimage. 2013;79:1–9. doi: 10.1016/j.neuroimage.2013.04.051. [DOI] [PubMed] [Google Scholar]
- Henik A, Tzelgov J. Is three greater than five: The relation between physical and semantic size in comparison tasks. Memory & cognition. 1982;10:389–395. doi: 10.3758/bf03202431. [DOI] [PubMed] [Google Scholar]
- Julian JB, Ryan J, Epstein RA. Coding of object size and object category in human visual cortex. Cerebral cortex. 2017;27(6):3095–3109. doi: 10.1093/cercor/bhw150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalanthroff E, Davelaar EJ, Henik A, Goldfarb L, Usher M. Task conflict and proactive control: A computational theory of the Stroop task. Psychological review. 2018;125(1):59. doi: 10.1037/rev0000083. [DOI] [PubMed] [Google Scholar]
- Kaufmann L, Koppelstaetter F, Delazer M, Siedentopf C, Rhomberg P, Golaszewski S, Ischebeck A. Neural correlates of distance and congruity effects in a numerical Stroop task: an event-related fMRI study. Neuroimage. 2005;25(3):888–898. doi: 10.1016/j.neuroimage.2004.12.041. [DOI] [PubMed] [Google Scholar]
- Kazak AE. Journal article reporting standards. 2018 doi: 10.1037/amp0000263. [DOI] [PubMed]
- Khaligh-Razavi SM, Cichy RM, Pantazis D, Oliva A. Tracking the spatiotemporal neural dynamics of real-world object size and animacy in the human brain. Journal of cognitive neuroscience. 2018;30(11):1559–1576. doi: 10.1162/jocn_a_01290. [DOI] [PubMed] [Google Scholar]
- Konkle T, Caramazza A. Tripartite organization of the ventral stream by animacy and object size. Journal of Neuroscience. 2013;33(25):10235–10242. doi: 10.1523/JNEUROSCI.0983-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konkle T, Oliva A. A real-world size organization of object responses in occipitotemporal cortex. Neuron. 2012a;74(6):1114–1124. doi: 10.1016/j.neuron.2012.04.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konkle T, Oliva A. A familiar-size Stroop effect: real-world size is an automatic property of object representation. Journal of Experimental Psychology: Human Perception and Performance. 2012b;38(3):561. doi: 10.1037/a0028294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li SPD, Bonner M. Curvature as an organizing principle of mid-level visual representation: a semantic-preference mapping approach; NeurIPS 2020 Workshop SVRHM; 2020. [Google Scholar]
- Liu AY. Decrease in Stroop effect by reducing semantic interference. Perceptual and Motor Skills. 1973;37(1):263–265. doi: 10.2466/pms.1973.37.1.263. [DOI] [PubMed] [Google Scholar]
- Long B, Konkle T. A familiar-size Stroop effect in the absence of basic-level recognition. Cognition. 2017;168:234–242. doi: 10.1016/j.cognition.2017.06.025. [DOI] [PubMed] [Google Scholar]
- Long B, Konkle T, Cohen MA, Alvarez GA. Mid-level perceptual features distinguish objects of different real-world sizes. Journal of Experimental Psychology: General. 2016;145(1):95. doi: 10.1037/xge0000130. [DOI] [PubMed] [Google Scholar]
- Long B, Moher M, Carey S, Konkle T. Real-world size is automatically encoded in preschoolers’ object representations. Journal of Experimental Psychology: Human Perception and Performance. 2019;45(7):863. doi: 10.1037/xhp0000619. [DOI] [PubMed] [Google Scholar]
- Long B, Yu CP, Konkle T. Mid-level visual features underlie the high-level categorical organization of the ventral stream. Proceedings of the National Academy of Sciences. 2018;115(38):E9015–E9024. doi: 10.1073/pnas.1719616115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo A, Wehbe L, Tarr M, Henderson MM. Neural Selectivity for Real-World Object Size In Natural Images. BioRxiv. 2023 March 17; doi: 10.1101/2023.03.17.533179. [DOI] [Google Scholar]
- Mack ML, Gauthier I, Sadr J, Palmeri TJ. Object detection and basic-level categorization: Sometimes you know it is there before you know what it is. Psychonomic Bulletin & Review. 2008;15(1):28–35. doi: 10.3758/pbr.15.1.28. [DOI] [PubMed] [Google Scholar]
- Morey R, Rouder J. BayesFactor: computation of Bayes factors for common designs. 2022:12–4. R package version 0.9. [Google Scholar]
- Naor-Raz G, Tarr MJ, Kersten D. Is color an intrinsic property of object representation? Perception. 2003;32(6):667–680. doi: 10.1068/p5050. [DOI] [PubMed] [Google Scholar]
- Nasr S, Echavarria CE, Tootell RB. Thinking outside the box: rectilinear shapes selectively activate scene-selective cortex. Journal of Neuroscience. 2014;34(20):6721–6735. doi: 10.1523/JNEUROSCI.4802-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- New J, Cosmides L, Tooby J. Category-specific attention for animals reflects ancestral priorities, not expertise. Proceedings of the National Academy of Sciences. 2007;104(42):16598–16603. doi: 10.1073/pnas.0703913104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peirce JW, Gray JR, Simpson S, MacAskill MR, Höchenberger R, Sogo H, Kastman E, Lindeløv J. PsychoPy2: experiments in behavior made easy. Behavior Research Methods. 2019 doi: 10.3758/s13428-018-01193-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ridderinkhof KR. Activation and suppression in conflict tasks: Empirical clarification through distributional analyses. Mechanisms in Perception and Action. 2002:494–519. [Google Scholar]
- Rosch E, Mervis CB, Gray WD, Johnson DM, Boyes-Braem P. Basic objects in natural categories. Cognitive psychology. 1976;8(3):382–439. [Google Scholar]
- Stroop JR. Studies of interference in serial verbal reactions. Journal of experimental psychology. 1935;18(6):643. [Google Scholar]
- Troiani V, Stigliani A, Smith ME, Epstein RA. Multiple object properties drive scene-selective regions. Cerebral cortex. 2014;24(4):883–897. doi: 10.1093/cercor/bhs364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yargholi E, Op de Beeck H. Category trumps shape as an organizational principle of object space in the human occipitotemporal cortex. Journal of Neuroscience. 2023;43(16):2960–2972. doi: 10.1523/JNEUROSCI.2179-22.2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yee E, Chrysikou EG, Thompson-Schill SL. In: The Oxford handbook of cognitive neuroscience. Ochsner KN, Kosslyn SM, editors. Vol. 1. Oxford University Press; 2014. Semantic memory; pp. 353–374. Core topics. [Google Scholar]
- Yin RK. Looking at upside-down faces. Journal of experimental psychology. 1969;81(1):141. [Google Scholar]