Nanoclusters of GPI-Anchored Proteins Are Formed by Cortical Actin-Driven Activity

Summary

Several cell-surface lipid-tethered proteins exhibit a concentration-independent, cholesterol-sensitive organization of nanoscale clusters and monomers. To understand the mechanism of formation of these clusters, we investigate the spatial distribution and steady-state dynamics of fluorescently tagged GPI-anchored protein nanoclusters using high-spatial and temporal resolution FRET microscopy. These studies reveal a nonrandom spatial distribution of nanoclusters, concentrated in optically resolvable domains. Monitoring the dynamics of recovery of fluorescence intensity and anisotropy, we find that nanoclusters are immobile, and the dynamics of interconversion between nanoclusters and monomers, over a range of temperatures, is spatially heterogeneous and non-Arrhenius, with a sharp crossover coinciding with a reduction in the activity of cortical actin. Cholesterol depletion perturbs cortical actin and the spatial scale and interconversion dynamics of nanoclusters. Direct perturbations of cortical actin activity also affect the construction, dynamics, and spatial organization of nanoclusters. These results suggest a unique mechanism of complexation of cell-surface molecules regulated by cortical actin activity.

Introduction

Functional lipid-tethered molecules at the cell surface, such as outer-leaflet glycosyl-phosphatidylinositol-anchored proteins (GPI-APs), the inner-leaflet Ras family of GTPases, and some glycolipids, are organized as cholesterol-sensitive nanoscale clusters and monomers (Fujita et al., 2007; Plowman et al., 2005; Sharma et al., 2004; Varma and Mayor, 1998). This nanoscale organization is necessary for the sorting of GPI-APs during endocytosis (Sharma et al., 2004) and associated with signaling functions of the Ras family of proteins (Plowman et al., 2005) at the cell surface. It is likely that the elaboration of a sorting and or signaling function from the nanoscale structures requires the construction of a larger-scale domain (Mayor and Rao, 2004).

In this context, it is significant that the ratio of nanoclusters to monomers is independent of concentration (Fujita et al., 2007; Plowman et al., 2005; Sharma et al., 2004). This characteristic, originally observed for GPI-APs (Sharma et al., 2004), is evidence for a violation of mass action and suggests that the nanocluster distribution on the surface of living cells is maintained away from chemical equilibrium (Mayor and Rao, 2004). This is difficult to reconcile with these components passively partitioning into “rafts” conceptualized as phase-segregated liquid-ordered domains akin to the equilibrium liquid-liquid phase coexistence in artificial multicomponent membranes (Edidin, 2003; Jacobson et al., 2007).

Our earlier measurements of the steady-state and time-resolved fluorescence-emission anisotropy arising from FRET between like fluorophores (homoFRET) over the whole cell gave information regarding the average short-scale organization of fluorescently tagged GPI-AP species (Rao and Mayor, 2005; Sharma et al., 2004; Varma and Mayor, 1998). By modeling the variation in FRET efficiency between GPI-APs upon photo-bleaching, we had arrived at a unique picture—a mixture of monomers and a small fraction (20%−40%) of nanoscale clusters (Sharma et al., 2004), whose ratio was independent of total levels of expression.

We now make an extensive analysis of the surface distribution and the dynamics of remodeling of GPI-AP nanoclusters in the unperturbed cell, by measuring FRET at a higher spatiotemporal resolution and correlating it with the remodeling dynamics of cortical actin (CA). We then study the effect of specific perturbations of the CA on the distribution and dynamics of nanoclusters. Finally we study the dynamics of recovery of the nanocluster distribution upon strong, localized perturbations of the CA in spontaneously blebbing cells. These studies suggest a model for lipid-tethered protein organization wherein the spatial organization and dynamics of lipid-tethered proteins in the steady state are a result of being driven by the activity of the CA.

Results

Spatial Distribution of Nanoclusters at Steady State

To study the spatial distribution of nanoscale clusters of GPI-APs at the surface of living cells, we used a custom designed wide-field or a line-scanning confocal microscope capable of measuring fluorescence anisotropy in real time to construct high-resolution (300 × 300 nm²), homoFRET-based spatial maps of the anisotropy of fluorescence emission of fluorescently labeled GPI-APs, PLF- or PLB^TMR-labeled folate receptors (PLF-FR-GPI or PLB^TMR-FR-GPI, respectively), or GFP tagged with a GPI anchor (GFP-GPI) in Chinese hamster ovary (CHO) and numerous other cell types (including NRK, 3T3, CaCo-2 cells; data not shown) (Figures S1A and S1B available online).

The images obtained consistently reveal two distinctive optically resolvable regions (Figure 1A). The first are regions with low average fluorescence anisotropy, most often associated with flatter, relatively undifferentiated regions of the cell membrane (Figure 1A; boxes i−iii). As established in Sharma et al. (2004) by examination of the change in anisotropy upon photo-bleaching, the low anisotropy corresponds to high nanocluster density (Figure S2C); the bleaching profiles closely resemble that seen in Sharma et al. (2004) and retain the crucial qualitative features of being flat initially and then increasing. From the images themselves, it is apparent that these low-anisotropy regions, highly enriched in nanoclusters, constitute a significant fraction of the cell surface. The second are regions with high average anisotropy, associated with membrane protrusions (Chhabra and Higgs, 2007) (e.g., microvilli; Figure S2B) or dynamic cell edges (e.g., membrane ruffles or leading edges of lamellipodia [Figure 1A(iv)]). To understand the nature of processes giving rise to nanoclusters in the unperturbed state of the cell, we focus our study on the low-anisotropy regions.

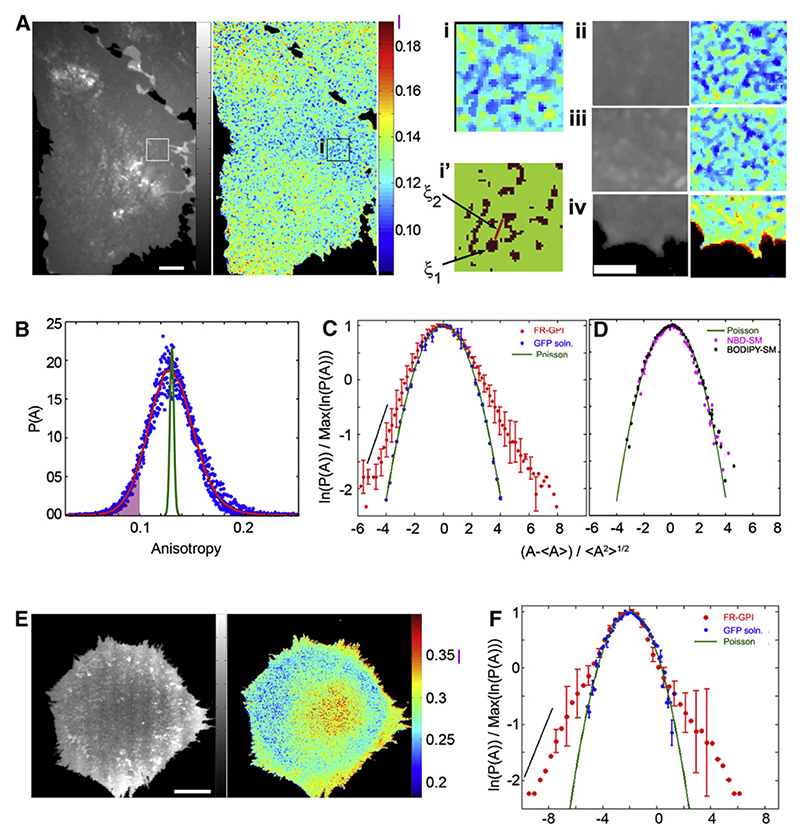
Figure 1. Quantitative Analysis of the Spatial Distribution of Nanoclusters.

CHO cells expressing FR-GPI were labeled with PLF (A) or PLB^TMR (E) and fluorescence intensity (grayscale) and anisotropy images (pseudocolored according to the indicated LUT) were recorded on a real-time wide-field anisotropy set-up at RT (A) or at 37°C on a line-scanning con-focal system (E). Anisotropy values from isolated monomeric proteins (A_∞) are indicated by a vertical line (magenta) at the right of the LUT bar. Note the presence of low-anisotropy regions in relatively constant intensity regions from flat regions of the cell shown (A, box i), and from different cells (A, boxes ii and iii). High-anisotropy structures (A, box iv) correspond to tips of lamellipodium, whereas the lamellum exhibits a low anisotropy. Graph (in panel B) shows normalized anisotropy distribution P(A) of flat regions of constant intensity from multiple FR-GPI-expressing cells (n = 11) including the region in box i shown in Figure 1A describing a typical distribution (red line). Comparison of P(A) with that expected by distributing the clusters and monomers according to a Poisson distribution (green line in B) shows significantly greater statistical weight in the low-anisotropy tails for the cell-derived distribution. Binary map (A, box i’) shows pixels, from the region shown in box i, with anisotropy values less than the cutoff represented by the shaded region in (B). Plots (C, D, and F) of ln(P(A)) versus $(A-\langle A\rangle )/\sqrt{\langle A^2\rangle }$ derived from anisotropy data from cells imaged in a wide-field (C and D) or confocal (F) microscope show a slower, exponentially decaying tail for FR-GPI-expressing cells (C and F, red dots), which appears as a linear decay (C and F, black line). In contrast, the simulated Poisson distribution (C, green line), the measured distribution in a 25 uM solution of GFP at RT (C, blue dots), or exogenously incorporated NBD-SM or BODIPY-SM (D, pink and black dots, respectively), at levels that give rise to homoFRET, coincide with a quadratic decay profile (D, green line). Scale bar: 8 μm (A), 4 μm (boxes ii, iii, and iv), 8 μm (E).

Analysis of the spatial FRET map in these flat regions (flat-cell-scapes) from a number of cells shows that the normalized anisotropy distributions overlap (Figure 1B). This permits us to ascribe a typical anisotropy distribution to cells grown under standard conditions (Figure 1B, red line). To check for correlations in the spatial distribution of nanoclusters, we compare the observed distribution of intensity and anisotropy with that expected by distributing the nanoclusters and monomers according to a Poisson process (Experimental Procedures), with the same mean intensity and anisotropy (Figure 1B, green line). We find that a large fraction of pixels exhibit very low and high anisotropy compared to that expected for a Poisson distribution of clusters and monomers, demonstrating significant spatial correlation of nanoclusters. Indeed, the observed distribution has a slower, exponentially decaying tail (Figure 1C, red dots) compared to the distribution of anisotropy of a solution of GFP (Figure 1C, blue dots). To ascertain whether this distribution is a characteristic of any lipid-anchored fluorophore, we examined the distribution of the anisotropy of fluorescent short fatty-acyl chain-containing lipids, NBD-SM (6-((N-(7-nitrobenz-2-oxa-1,3-diazol-4-yl)amino) hexanoyl) sphingosyl phosphocholine) or BODIPY-SM (N-(4,4-difluoro-5,7-dimethyl-4-bora-3a,4a-diaza-s-indacene-3-pentanoyl) sphingosyl phosphocholine), exogenously incorporated at the cell surface (Figure 1D, pink and black dots, respectively; images in Figure S3). Identical to the solution of GFP, the anisotropy distribution of NBD-SM shows a Gaussian tail (as expected from a random distribution; Figures 1C and 1D, green line). These observations of the spatial distribution (at a resolution of 300 nm) were made at room temperature (RT); at 37°C we use a line-scanning confocal microscope (Figure S1B) to focus at the cell surface. This imaging modality also allows one to exclude contributions from endocytosed fluorophores (Figure S4) and obtain similar results (Figures 1E and 1F).

To study the statistics of clustering, we map out regions highly enriched in nanoclusters by selecting pixels with anisotropy less than a calculated cutoff (corresponding to pixels where ≥ 75% of the proteins are in nanoclusters; Figure 1B, shaded portion). These rare configurations occur in patches (Figure 1A, box i’), corresponding to a mean size of ξ₁ ≤ 450 nm. Since our microscope resolution is 300 nm, this does not allow a lower bound on the size of these enriched domains. The pixels immediately surrounding these patches have high anisotropy. The regions of low anisotropy have a mean separation of order ξ₂ ≈ 800−1250 nm (Figure 1A, box i’), as determined by computing the radial distribution function (Chaikin and Lubensky, 1995). The value of ξ₂ is smaller than that expected from uniformly distributing these patches over the same sample area of the cell (data not shown). These observations suggest that nanoclusters of GPI-APs are highly enriched in specific domains of size ξ₁ ≥ 450 nm and that these domains are in turn further clustered, giving rise to a distinct hierarchical distribution of the nanoscale clustering.

Steady-State Dynamics of Nanoclusters: Diffusion and Interconversion

We next explored the steady-state dynamics of the GPI-AP monomers and nanoclusters, at temperatures ranging from 15°C−37°C, by a fluorescence intensity-anisotropy recovery setup (Figure S1C) based on a microphotolysis-type experiment (Peters et al., 1981). We locally perturbed the distribution of PLF-labeled folate receptor (FR-GPI) at the surface of CHO cells by multiphoton (MP) confocal excitation-induced photobleaching starting at time t = 0 up to t = t₁ (first illumination), when the laser is switched off for a waiting time, t_w, before being switched on again (second illumination). We follow the dynamical response both in homoFRET and fluorescence intensity from the same volume. During the first illumination period, the fluorescence emission intensity shows an initial rapid loss followed by a slower decay and significant recovery during t_w (Figure 2A, blue dots). The corresponding emission anisotropy trace, broadly, shows two kinds of behavior that significantly correlate with temperature. At 20°C, the anisotropy in the illuminated volume typically starts out at a depolarized value (Figure 2A, red line), characteristic of a mixture of nanoclusters and monomers (Sharma et al., 2004), and shows a sharp initial rise in fluorescence anisotropy (corresponding to rapid loss of homoFRET) before saturating to a high value, characteristic of isolated monomers in the membrane (A_∞; Figure 2, pink band). On the other hand, at 37°C (Figure 2B, red line), the anisotropy rises during t₁, as the fluorophores in the confocal volume bleach, and saturates to a value significantly lower than A_∞, obtained as described in Experimental Procedures.

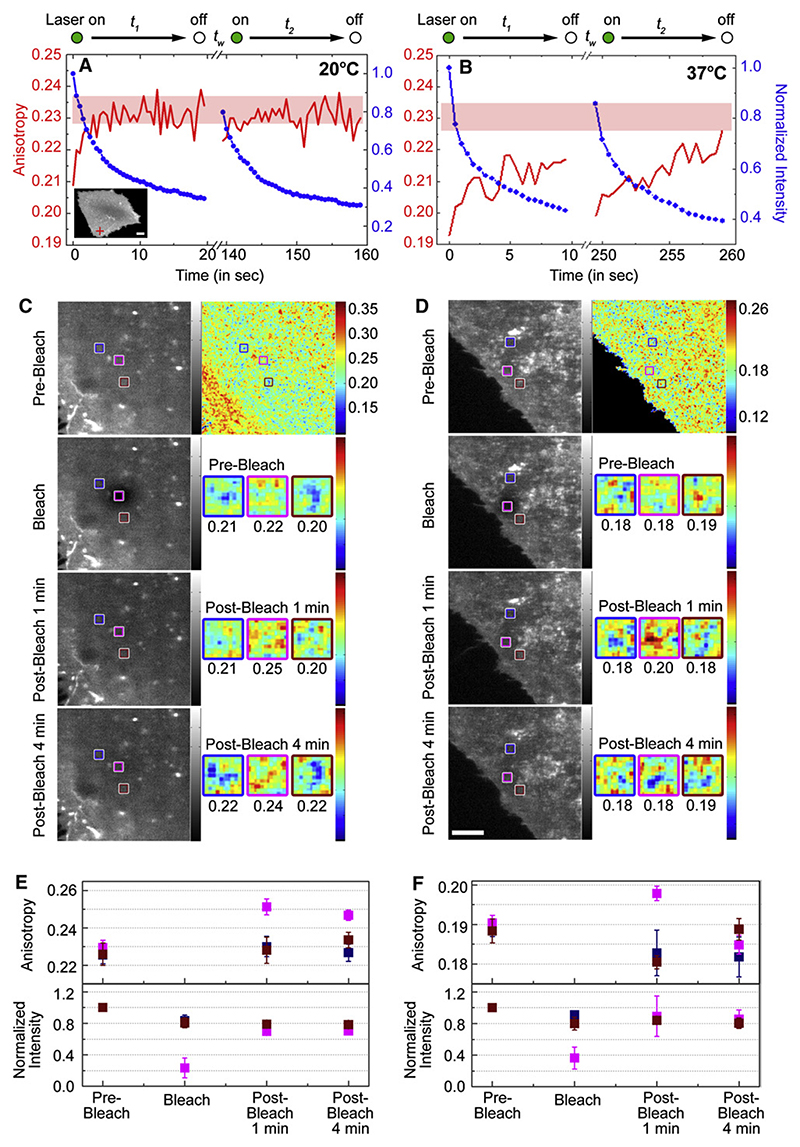
Figure 2. Intensity and Anisotropy Traces and Images from Cell-Surface-Labeled GPI-APs.

(A and B) PLF-labeled FR-GPI-expressing cells (A, inset), on a microscope stage maintained at 20°C (A) or at 37°C (B), were illuminated by multiphoton excitation at 790 nm. Intensity (blue line) and anisotropy (red line) traces were obtained simultaneously from the resultant confocal volume (e.g., red crosshair, inset in A) during the illumination sequence outlined at the top. The pink bands in the graphs are the range of A_∞ values obtained for each experiment.

(C and D) Fluorescence intensity (grayscale) and anisotropy (pseudocolored) images of PLB^TMR-labeled cells were recorded on line-scanning confocal microscope at 20°C (C) or at 37°C (D), prior to (Pre-Bleach), immediately post (Bleach, intensity only), or after 1 or 4 min of (Post-Bleach, 1 or 4 min, respectively) bleaching the region outlined in the magenta box. Average anisotropy values from the bleached (magenta) and unbleached (blue, brown) boxes are shown below pseudocolored anisotropy images from each colored box.

Graphs (E and F) show normalized fluorescence intensity (lower panel) and average (and standard error) anisotropy values (upper panel) from the respective colored boxes under the conditions indicated on the x axis, derived from measurements made on multiple cells (n ≥ 6) at 20°C (E) or at 37°C (F) in two independent experiments. Scale bar, 5 μm.

Regardless of the temperature, at the start of the second illumination, the recovery of fluorescence intensity in the observation volume depends on the durations, t₁ and t_w. If t₁ is small (<20 s) and t_w large (>30 s), the fluorescence intensity recovers significantly, implying that fluorophores diffuse in from the surrounding regions. However, at 20°C, the fluorescence anisotropy at the beginning of the second illumination starts out with the same saturation value obtained at the end of the first illumination and does not recover to that expected of the original mixture of nanoclusters and monomers (Figure 2A, red line). This implies that nanoclusters neither reform within nor are replenished from the reservoir of unbleached fluorophores present outside the illuminated volume. In contrast, at 37°C, there is an almost complete restoration of the original depolarized anisotropy value after t_w, implying that there is substantial reassembly of nanoclusters from monomers at 37°C (Figure 2B, red line). As a control, even at 20°C an exogenously added fluorescent lipid, BODIPY-SM, at concentrations high enough to record significant homoFRET recovers its intensity and depolarized anisotropy during an identical illumination sequence (Figure S5).

The lack of replenishment of unbleached nanoclusters of GPI-APs at 20°C could arise either from the absence of nanoclusters in the reservoir or their immobilization. To address this issue we analyzed the spatial distribution of monomers and nanoclusters in the reservoir outside the illuminated region by simultaneously measuring the intensity and anisotropy of FR-GPI in an area of the cell surface, prior to and after bleaching a central region in the imaging field (anisotropy recovery after photo-bleaching or ARAP). For this we labeled FR-GPI with a more photo-stable fluorescent analog of folic acid, PLB^TMR, and simultaneously imaged intensity and anisotropy in the line-scanning confocal anisotropy imaging set-up (Figure S1B). Initially, we detected significant depolarization in the whole illuminated area (Figure 2C; Pre-Bleach), characteristic of the steady-state distribution of nanoclusters and monomers. Following a bleaching of PLB^TMR-FR-GPI at the center of the illuminated area (Figure 2C; Bleach, magenta box), we find that while the fluorescence intensity recovers (Figure 2C; Post-Bleach 1 and 4 min), the anisotropy in the bleached spot does not (Figure 2C; Post-Bleach 1 and 4 min). However, the average intensity and anisotropy in the regions surrounding the bleached areas remain relatively unchanged during this time (Figure 2C; brown and purple boxes). Although the exact pattern of anisotropy in each of the boxes is not completely conserved, quantitative analyses from multiple runs of the same experiment (Figure 2E) confirm that only the monomeric species contribute to the replenishment of the intensity, whereas nanoclusters do not reform and are relatively immobile at this temperature.

In contrast, the ARAP experiment at 37°C shows that in conjunction with the rapid recovery of fluorescence intensity (Figure 2D, magenta boxes; bottom graph in F), the anisotropy recovers to its original depolarized anisotropy value, albeit after a long delay (Figure 2D, magenta boxes; top graph in F). However, we can halt the recovery of anisotropy at 37°C, if we perturb the formation of nanoclusters (see below). These studies reinforce the claim that while monomers are free to diffuse, nano-clusters are relatively immobile and formed in situ.

The dynamics of recovery of intensity and anisotropy cannot be accounted for by endocytic recycling of internalized labeled cell-surface GPI-APs. First, over the time of the experiment (~300 s), less than 10% of the cell-surface-labeled FR-GPI is endocytosed, and a smaller fraction recycled due to the slow kinetics of membrane recycling characterized previously (Chatterjee et al., 2001). Second, direct examination of the internalized fraction of FR-GPI by stripping away the cell-surface receptors shows no detectable fluorescence in the confocal volume (Figure S6).

We now systematically record the dynamical response to the sequence of local-pulsed illumination (detailed in Figures 2A and 2B) from different flat regions of cells, at temperatures ranging from 15°C−37°C. We theoretically model the time traces of fluorescence intensity and anisotropy from the confocal volume by reaction-diffusion type equations (Figure 3A; see Experimental Procedures and Supplemental Explanations A1−A3), incorporating diffusion of monomers and nanoclusters (diffusion coefficients, D₁ and D_c), bleaching of fluorophores (bleach rate, b), and the interconversion between monomers and nanoclusters (aggregation and fragmentation rates, k_a and k_f). Knowing the monomer and nanocluster anisotropy, A_m and A_c (Sharma et al., 2004), we obtain the intensity and anisotropy profiles by solving Equation 4 for C_nm(t) (Experimental Procedures), the fraction of nanoclusters having n proteins, m of which are un-bleached, present within the confocal volume at time t.

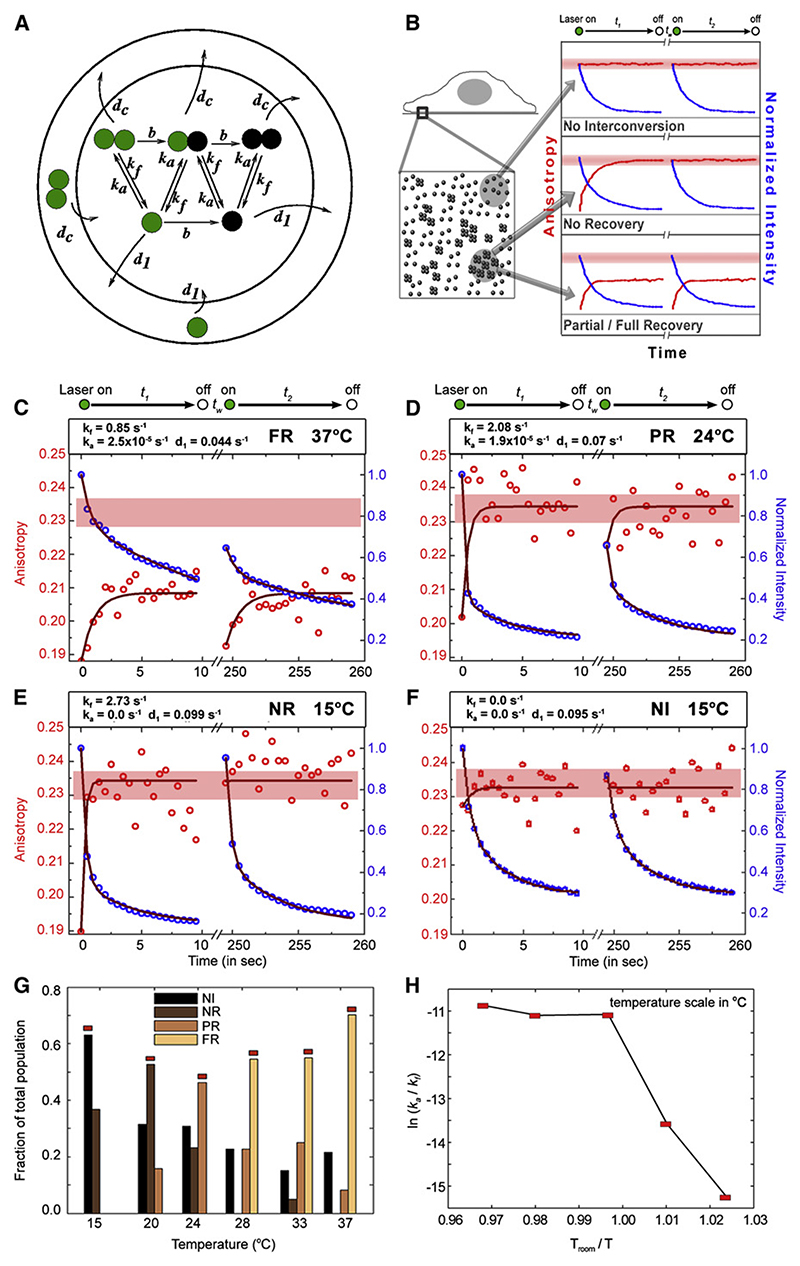
Figure 3. Temperature-Dependent Steady-State Dynamics of Nanoclusters.

(A) Schematic of the expected dynamics (bleaching, diffusion, and interconversion) of monomers and nanoclusters (depicted as dimers) within a confocal volume (inner circle). The colors of the circles represent the bleaching status of the fluorophores, green being active and black bleached. The arrows represent the transition rates between the species present. While the fluorophores diffuse both into and out of the confocal volume, the model assumes that the incoming fluorophores are predominantly unbleached. The outer circle represents the pool of unbleached monomers and nano-clusters that serves to replenish the confocal volume. The dynamics is modeled by reaction-diffusion equations, involving rates of bleaching (b), diffusion (monomer d₁ and cluster d_c), and cluster aggregation (k_a) and fragmentation (k_f) as detailed in the text.

(B) Schematic describes the relationship between the local organization of GPI-APs in a confocal volume and the type of fluorescence intensity and anisotropy traces obtained. Full recovery (FR) and partial recovery (PR) types would be expected from a region where there are nanoclusters and relatively robust monomer-nanocluster interconversion. No recovery type (NR) is expected from regions where there is significant fragmentation but no formation of nanoclusters, and the non-interconversion (NI) occurs where there are no nanoclusters to begin with.

(C−F) Typical time traces of intensity and anisotropy recovery of PLF-labeled FR-GPI during the illumination sequence indicated above each panel, recorded at different temperatures 37°C (C), 24°C (D), and 15°C (E and F), are modeled as described in (A). The fits (dark lines) provide the values of the parameters appearing in each panel. Extracted values of d_c were found to lie in the range (−10⁻⁵ s⁻¹ < d_c < 10⁻⁵ s⁻¹); this being 4 orders of magnitude smaller than d₁, we may safely take this as indicating immobilized clusters (consistent with Figure 2). Pink band represents the permissible range of A_∞ values.

(G) Histogram shows the relative population of each class (FR, PR, NR, and NI [where the anisotropy stays at a highly polarized value A_∞ at all times]) at different temperatures based on the classification scheme shown in (B); the representative class for each temperature is indicated by the red bar.

(H) Ratio of typical interconversion rates of the most probable distribution extracted as described in the text is represented in an Arrhenius plot, as ln k_a/k_f versus T_room/T. The line connecting the typical values of ln k_a/k_f in each representative class shows strong non-Arrhenius behavior and a sharp crossover at 24°C.

Using the model (Figure 3A), we fit the calculated intensity and anisotropy profiles to the experimental data and extract the best fit values for the parameters (Figures 3C−3F; Supplemental Explanation A2) at different temperatures. The diffusion coefficient of the nanoclusters, D_c, obtained from the fit, is vanishingly small (D_c ≈ 0) at all temperatures (Figures 3C−3F and S7A)— reasserting that while monomers are mobile, the nanoclusters are relatively immobile (Figures 2E and 2F).

We find that while the fit values of the interconversion rates show extensive variation at any given temperature (Figure S7B), the data neatly cluster into four qualitatively distinct classes: full recovery (FR), partial recovery (PR), no recovery (NR), and no interconversion (NI) (schematic in Figure 3B). Interconversion dynamics is typically absent at lower temperatures and present at higher temperatures (Figure S7B). As depicted in Figure 3B, these recovery classes reflect the spatial heterogeneity in the surface organization of nanoclusters. As shown in Figure 3G, we can define a representative class for each temperature (demarcated in red). We construct an Arrhenius plot from the typical value (Figure S8) in each representative class as a function of inverse temperature (Figure 3H). This plot is almost flat at temperatures above 24°C and changes sharply below this temperature, in a strongly non-Arrhenius manner, reaffirming the absence of interconversion below 24°C. From the near-horizontal curve above 28°C, one can extract a typical value for ΔE/k_BT ≈ 10⁻² from the slope of the curve above 24°C. This reflects the binding energy of nanoclusters (Israelachvili, 1992); this is 2−3 orders of magnitude lower than the minimal (van der Waals) interactions between molecules on a membrane at a similar intermolecular distance. In separate studies on the disruption of nanoclusters by crosslinking antibody binding (Sharma et al., 2004), we estimate a maximum nanocluster binding energy ≈ 10 k_BT.

These anomalous features in the spatial distribution and dynamics at steady state require explanation; to arrive at this, we perturbed the organization of nanoclusters in a variety of ways.

Interconversion Dynamics Is Sensitive to Cholesterol Perturbation

We investigated the spatial distribution and dynamics of GPI-AP nanoclusters upon perturbing cholesterol levels using methyl-β-cyclodextrin (mβCD). Treatment using high concentrations of mβCD completely abrogates nanoclusters (Sharma et al., 2004). On the other hand, mild perturbation of cholesterol levels (such that the overall fraction of nanoclusters remains unaltered) using low concentrations of mβCD (Sharma et al., 2004) has a measurable effect on the statistical distribution of nanoclusters. Both the net fraction of GPI-APs in the low-anisotropy region and the mean domain size (ξ₁) reduce, while the mean separation between domains (ξ₂) increases (Figures 4A−4E). Further, at 37°C, the interconversion rates of nanoclusters are drastically reduced (Figure 4F); cholesterol depletion also inhibits the recovery of anisotropy in ARAP experiments (Figure 4G). Thus, cholesterol is a major player in maintaining the spatial organization of the nanocluster enriched regions. This graded effect of cholesterol depletion on the organization of GPI-APs at different scales suggests that the interactions of cholesterol with GPI-APs occur at multiple levels—directly via passive cholesterol-GPI-AP attractive forces or via a coupling to the CA. Indeed, at these low levels of cholesterol depletion, we have observed significant reduction in the activity of CA (Chadda et al., 2007). These observations suggest that the perturbation of the spatial distribution and dynamics of nanoclusters by low levels of cholesterol removal may be mediated by alterations in the organization of CA, influencing CA-membrane interactions (Chadda et al., 2007; Kwik et al., 2003; Niggli, 2005).

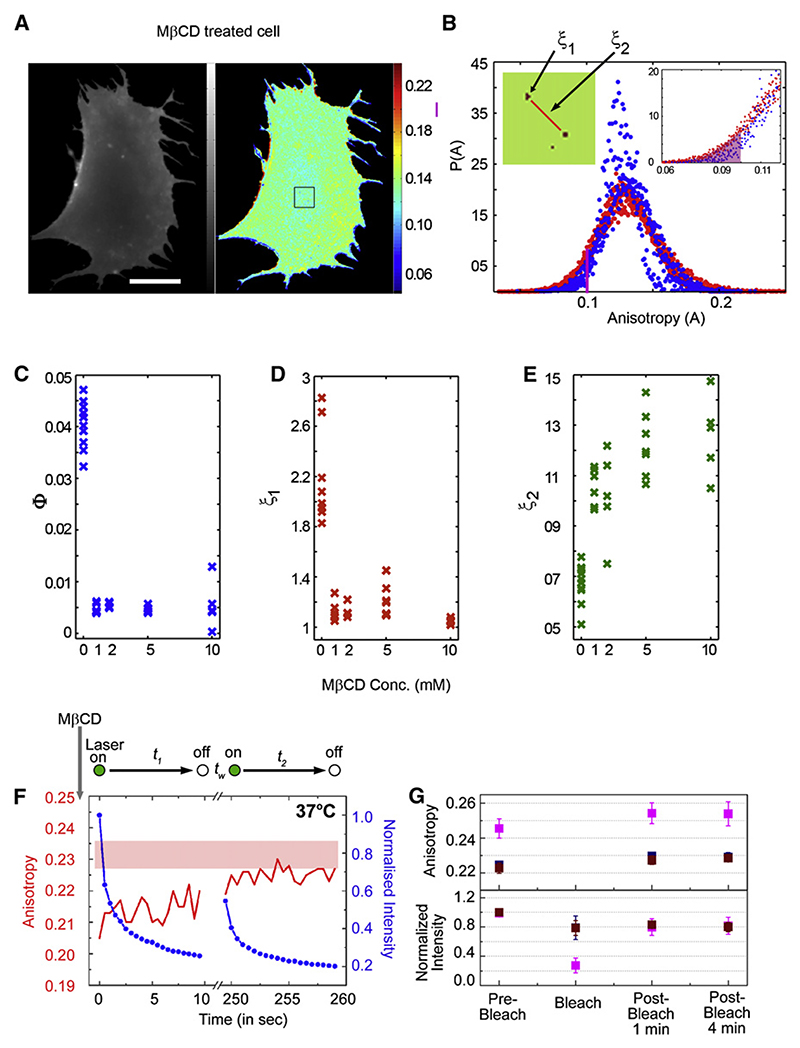
Figure 4. Influence of Cholesterol Depletion on Spatial Distribution and Nanocluster Formation at 37°C.

(A−E) Fluorescence intensity (grayscale) and anisotropy (pseudocolor) image (A) and graph (B) of normalized anisotropy distribution, P(A), of multiple FR-GPI-expressing cells (n = 7) including the cell shown in (A), obtained from cholesterol-depleted (B, blue dots; 10 mM mβCD, 30 min), show a lowering of the statistical weight, Φ, in the tails of P(A) derived from untreated cells (B, red dots; see right inset). Binary map (left inset in B) shows pixels from the region shown in box outlined in (A), with anisotropy values less than the cutoff represented by the shaded region in B (inset). The relative statistical weight of the rare regions (C, quantified as Φ, defined by shaded edge in B) and the cluster size ξ₁ (D, in units of 1 pixel = 160 nm) show a decrease while ξ₂ (E, in pixel units) increases with mβCD concentration.

(F) PLF-labeled FR-GPI-expressing cells incubated with mβCD (10 mM; 30 min) on a microscope stage maintained at 37°C were illuminated by multiphoton excitation at 790 nm. Intensity (blue line) and anisotropy (red line) traces were obtained simultaneously from the resultant confocal volume during the illumination sequence outlined at the top. After waiting time t_w, the traces were recorded from the same area of the cell during t₂. The pink band at the top indicates the range of A_∞ values obtained in the experiment.

(G) Graphs show normalized fluorescence intensity (lower panel) and average (and standard error) of anisotropy values (upper panel) from an ARAP experiment as described in Figure 2D, carried out at 37°C on PLB^TMR-labeled FR-GPI-expressing cells pretreated with mβCD (10 mM; 4 min). Magenta symbols represent data obtained from the area subject to photobleaching while blue and brown symbols are obtained from corresponding neighboring areas. Data were derived from measurements made on multiple cells (n ≥ 6) in two independent experiments. Scale bar = 10 μm.

Interconversion Dynamics Is Sensitive to Perturbation of Actin Polymerization and Myosin Activity

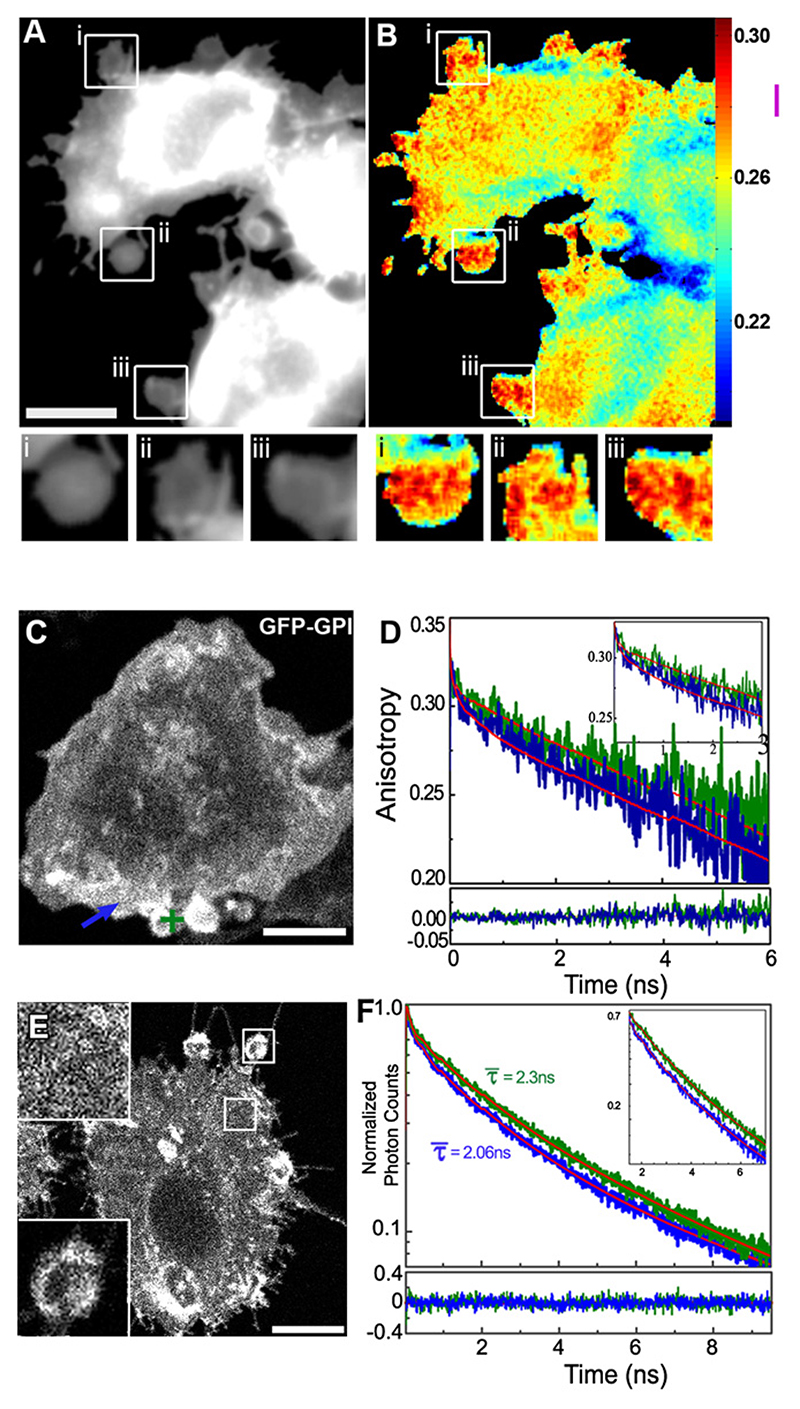
We perturbed the CA using Jasplakinolide (Jas) or Latrunculin (Lat) at 37°C to directly study the involvement of actin. Prolonged perturbations result in the generation of micron-sized blebs, devoid of CA (Figure S9A). The fully formed blebs lack GPI-AP nanoclusters, as we evince from the high value of anisotropy of GFP-GPI (Figures 5A and 5B) and confirm by time-resolved fluorescence decay, time-resolved anisotropy measurements, and fluorescence life-time imaging (Figures 5C−5F; For detailed explanations see Supplemental Explanation A5, Figures S10A− S10C, and Tables S1 and S2). The GPI-APs in these blebs also do not exhibit interconversion dynamics (Figures S9B and S9C). After removal of Lat, the Lat-generated blebs retract following re-establishment of local CA; the anisotropy and hence nanocluster concentrations recover to their pretreatment values (Movie S1).

Figure 5. Hetero- and HomoFRET Measurements Confirm Spatial Heterogeneity of Nanocluster Distribution; Actin Perturbation Generates Blebs Devoid of FRET Signals.

(A and B) Jas-treated (14 μM, 30 min at 37°C) GFP-GPI-expressing cells were imaged as described in Figure 1A. Fluorescence intensity (A) and anisotropy images (B), in grayscale and pseudocolor, respectively, show the formation of large-scale blebs (B boxes i−iii) that have high anisotropy values, approaching those of isolated monomers, A_∞, while flat regions are depolarized (blue areas in B). (C and D) GFP-GPI-expressing CHO cells (C) were treated with Lat A (25 μM, 30 min,37°C) to generate blebs, and at the indicated spot on a bleb (green cross), single point-time resolved anisotropy decay measurements were carried out using confocal multiphoton excitation at 37°C. Graph in (D) shows anisotropy decay profiles (green line) obtained from this region (green cross in panel C) compared with the anisotropy decay (blue line) from flat regions of cell in the same image (blue arrow in panel C), or from cell membranes treated with saponin to remove all nanoclusters (data not shown). Anisotropy decay profiles from blebs resemble those from saponin-treated membranes (see Table S1), confirming that GFP-GPI in bleb membranes are devoid of nanoclusters. (E and F) Fluorescence intensity distribution obtained by multiphoton confocal imaging of donor fluorophore PLF and acceptor fluorophore PLR-labeled FR-GPI-expressing cells. These cells exhibit blebs (bottom inset) and flat regions (top inset) after actin perturbation as in (C). (F) Fluorescence decay traces obtained from the same cells by positioning a multiphoton excitation volume over the bleb (bottom inset in E) exhibit a longer average donor lifetime (τ ~ 2.3 ns, green line) compared to that obtained in the flat region (top inset in E, blue trace), which is significantly shorter (τ ~ 2.0 ns, blue line). Residuals from the multicomponent fits (detailed in Table S2) are shown in the trace at the bottom. Scale bar, 5 μm.

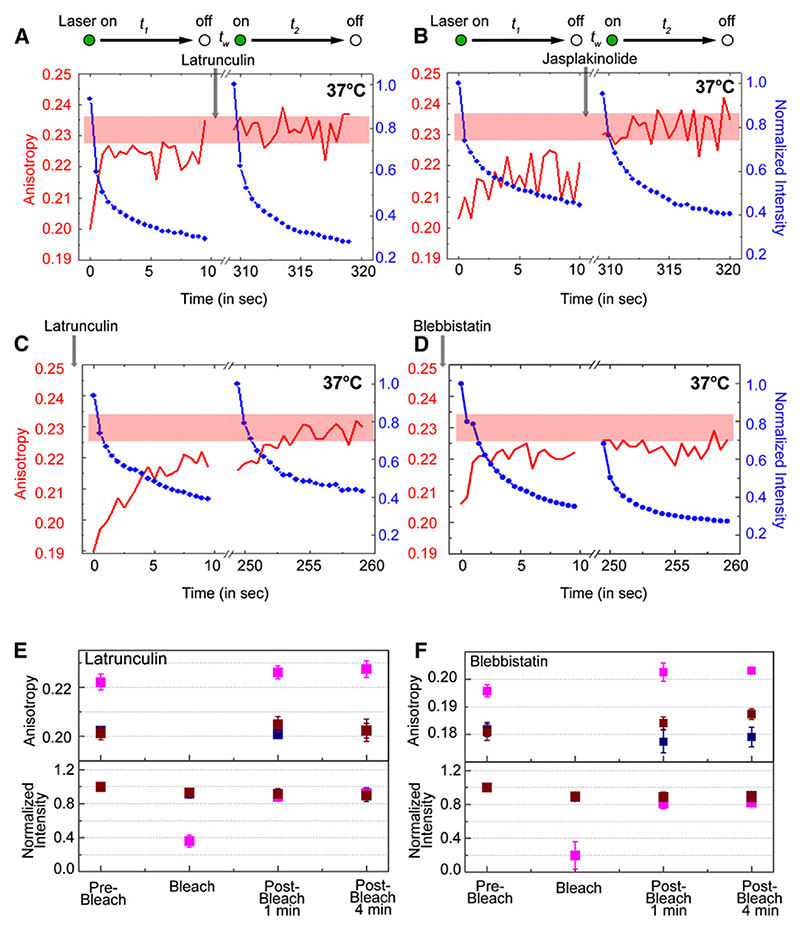
To directly test the role of CA in the dynamics of GPI-AP-nanocluster construction, we perturbed actin-polymerization activity by treatment with Jas and Lat for short periods of time. These treatments do not affect the average concentration of nanoclusters in the membrane as measured by a lack of an effect of the average anisotropy values of labeled GPI-APs (Figure 6A). At the same time these mild perturbations do not significantly deplete levels of CA (data not shown) but affect the dynamics of polymerization/depolymerization of actin near the membrane (Chadda et al., 2007) (Figure S11). In such situations, whereas the nanocluster concentration recovers completely after a time t₁ + t_w on control cells at 37°C (Figure 2B, red line), application of Lat or Jas during the waiting period (Figures 6A and 6B) or before the first laser pulse (Figure 6C) prevents the restoration of the original depolarized anisotropy value (Figures 6A−6C, red lines), although the fluorescence intensity recovers completely (Figures 6A−6C, blue lines). Furthermore, perturbation of myosin activity using Blebbistatin (Straight et al., 2003) inhibits the dynamics of interconversion (Figure 6D, red line). Mild treatment with Lat or Blebbistatin also prevents restoration of nanoclusters in the bleached area in the ARAP experiments (Figures 6E and 6F). These results directly implicate CA activity in maintaining the dynamic organization of cell-surface GPI-APs as nanoclusters and monomers.

Figure 6. Influence of Actin Cytoskeleton on Nanocluster Formation at 37°C.

(A and B) Multiphoton laser-excited intensity (blue) and anisotropy (red) traces of PLF-labeled FR-GPI-expressing cells obtained at 37°C from the illumination sequence indicated above each trace. After the first illumination period, t₁, Latrunculin (Lat, 6 μM; A) or Jasplakinolide (Jas, 5 μM; B) was added to cells on the stage. After waiting time t_w, the traces were recorded from the same area of the cell during t₂.

(C and D) PLF-labeled FR-GPI-expressing cells were preincubated with Lat (C; 6 μM for 5 min) or Blebistatin (D; 50 μM for 5 min) on a microscope stage maintained at 37°C and illuminated by multiphoton excitation at 790 nm. Intensity (blue line) and anisotropy (red line) traces were obtained simultaneously from the resultant confocal volume during the illumination sequence outlined at the top. The pink bands at the top of each panel indicate the range of A_∞ values obtained in the experiment.

(E and F) Graphs show normalized fluorescence intensity (lower panel) and average (and standard error) anisotropy values (upper panel) from an ARAP experiment as described in Figures 2C− 2F, carried out at 37°C on PLB^TMR-labeled FR-GPI-expressing cells, pretreated for 4 min with Lat (E; 6 μM) or Blebbistatin (F; 50 μM) at 37°C. Magenta symbols represent data obtained from the area subject to photobleaching while blue and brown symbols are obtained from corresponding neighboring areas. Data were derived from measurements made on multiple cells (n ≥ 8) in a single experiment and averaged over at least two independent experiments. The data show that recovery of nanoclusters in the bleached area depends on the integrity of actin as well as myosin activity. They also show that clusters formed outside the bleached area are relatively immobile at 37°C.

Dynamics of Nanocluster Recovery toward Steady State

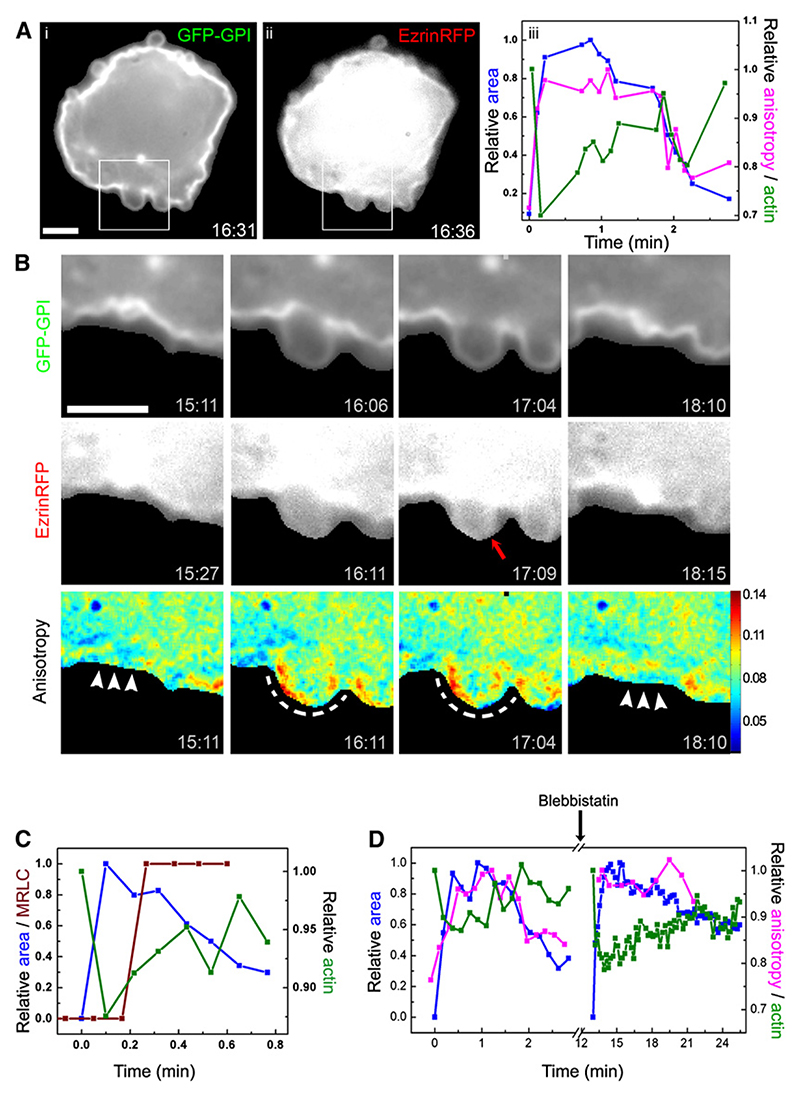
To explore the connection between CA and the composition of nanoclusters in membranes associated with CA, we examined a system wherein the cell membrane undergoes cycles of attachment and detachment from the underlying CA. Freshly plated fibroblasts (diameter ~30 μm) with a dynamically unstable CA meshwork spontaneously generate blebs (Charras et al., 2005; Keller et al., 2002). This presents a convenient system to temporally monitor CA detachment and reformation (Charras et al., 2006) and consequently the dynamics of loss and recovery of nanoclusters in the bleb membrane. Blebs form from the cell edge and grow to a maximum size of about 1−5 μm, after which they retract completely into the cell over a timescale of minutes (Figure 7A; see Movies S2−S4). We followed the dynamics of CA and GPI-AP nanoclusters as the bleb grows and retracts by monitoring the distribution of polymerized actin-binding protein, C-terminal-Ezrin (Bretscher et al., 1997), and GFP-GPI anisotropy, respectively (Figures 7A and 7B; Movie S4). The anisotropy starts out at a low value (due to the presence of nanoclusters); as the bleb grows, the anisotropy in that region increases and approaches a constant value close to that of isolated monomers, A_∞ (Figure S12). Observation of C-terminal-Ezrin-RFP and GFP-GPI anisotropy simultaneously (Movie S3) shows that the rim-located CA in the flat cell membrane first rapidly decreases so that the bleb grows and extends to its maximum diameter. CA then increases again at the rim of the bleb to retract the bleb (Figure 7A, graph; Figure S12B), as can be seen from the appearance of an enhanced rim staining of C-terminal-Ezrin-RFP (Figure 7B; compare also membrane outline [GFP-GPI fluorescence] and actin [C-terminal-Ezrin-RFP] in Movie S3). Simultaneous imaging of the C-terminal-Ezrin-RFP and the membrane rim during bleb formation and retraction confirm the sequence of rim localization of CA prior to bleb retraction (Movie S5).

Figure 7. Dynamics of Nanocluster Distribution and CA in Blebs from Freshly Plated Fibroblasts.

(A) Freshly plated CHO cells coexpressing GFP-GPI and RFP-Ezrin develop spontaneous blebs before they spread out and acquire a flat morphology at 37°C. GFP-GPI intensity (i) and RFP-ezrin distribution (ii) in the blebs were imaged on wide-field dual-camera set-up where images were collected sequentially for GFP and RFP fluorescence every 11 s. Graph in (iii) shows bleb-area (normalized to the maximum area), GFP-anisotropy (normalized to the maximum anisotropy value at the bleb), and RFP-Ezrin staining (normalized to the initial values) as a function of bleb growth and retraction.

(B) Montage taken from Movie S4; blebs appear spontaneously from the cell edge and grow to their maximum size in ~30 to 50 s and retract back in ~1 min−2 min. Note that blebs are initially devoid of rim staining for RFP-Ezrin and acquire it a few seconds (red arrow) after the bleb has reached its maximum size. Arrowheads and dashed line indicate regions of low and high anisotropy, respectively. Note that while RFP-ezrin staining is rapidly lost, the anisotropy (low to begin with) rapidly increases as the bleb grows. After the recovery of RFP-ezrin staining in the rim of the bleb, anisotropy reduces, as the bleb starts to shrink.

(C) Graph shows time course of MRLC-GFP recruitment (brown dots) during bleb growth and retraction in cells expressing MRLC-GFP, coincident with bleb retraction.

(D) Graph shows time course of bleb-area growth and retraction, anisotropy, and actin distribution before (left side) or after addition of Blebbistatin (50 μM) for 10 min to the same cells. Scale bar, 3.2 μm.

Bleb retraction is a consequence of the repolymerization of actin and subsequent myosin-based contractility (Charras et al., 2007). We confirm this by showing recruitment of myosin regulatory light chain (M-RLC) to the retracting bleb (Figures 7C, S12C, and S13) and inhibition of retraction by application of Blebbistatin (Figure 7D; Movie S6).

More interesting is the dynamics of the GFP-GPI anisotropy as the bleb retracts; the decrease in anisotropy from A_∞ (value at maximal bleb extension) follows the appearance of CA (Figure 7B; Movies S4 and S5) until it attains its steady-state depolarized value. This shows that the re-formation of nanoclusters is promoted by the presence of the CA. Inhibition of myosin activity with Blebbistatin slows down bleb retraction—many blebs fail to retract (Figure 7D; Movie S6) or retract with much slower kinetics (data not shown). In blebs that do not retract, Blebbistatin treatment inhibits the recovery of GFP-GPI anisotropy to its original depolarized value (Figure 7D; Movie S6), indicating that actomyosin contractility is required for nanocluster formation.

Discussion

Active Molecular Complexation Regulated by CA Activity

The experimental evidence presented here suggests that the spatial distribution and dynamics of formation and break-up of nanoclusters are mediated by the local CA and its active remodeling, driven by (de)polymerization and acto-myosin contractility. The statistical and dynamical characteristics of such molecular complexation in steady state are distinctive: (1) violation of mass action, (2) unusual nature of the probability distribution of anisotropy (Figures 1C and 1F), (3) spatial characteristics of domains enriched in nanoclusters and their dependence on actin, (4) variations in the spatial distribution and interconversion dynamics of nanoclusters arising from the spatial variation in levels of active CA (Figures 3G and S7B), (5) the near-horizontal nature of the Arrhenius plot at temperatures above 24°C, followed by a sharp crossover at 24°C (Figure 3H), and (6) the immobilization of nanoclusters. It is difficult to reconcile all these features with a molecular aggregation driven by lipid-lipid or protein-protein interactions based on models of membrane rafts formed by conventional thermodynamic forces (Simons and Vaz, 2004).

Instead, these feature may be best reconciled if the mechanism governing the formation of the nanoclusters is active. The involvement of actin and myosin activity in regulating the dynamics of nanoclusters explains the sharp crossover seen in the Arrhenius plot (Figure 3H): earlier studies have shown that acto-myosin activity exhibits a sharp crossover at ~24°C (Sheetz et al., 1984); our own data on the temperature dependence of blebbing and retraction, a process that requires actin polymerization and acto-myosin contractility (Charras et al., 2007), also suggest a crossover in the dynamics of the CA at ~24°C (Figure S14). The violation of mass action, the exponential tails of the anisotropy distribution, and the spatial distribution can all be attributed to the activity of a dynamic cortical actin cortex influencing molecules in the membrane overlying it (K.G. et al., unpublished data).

Molecular Players Involved in Nanocluster Formation

A critical issue, both in the generation of the nanoclusters and in the nanocluster-enriched domains associated with CA, concerns a molecular mechanism for the coupling of membrane components and acto-myosin activity. Currently, we do not know the detailed molecular links between the CA and the exoplasmic lipid-tethered protein that must exist in order to produce the effects we report here. However, cholesterol plays a key role in this process since levels of cholesterol in the membrane regulate the activity of many molecular players involved in the spatial remodeling of CA (Chadda et al., 2007; Kwik et al., 2003) and its removal disrupts these nanoclusters (Sharma et al., 2004) or drastically affects interconversion and its spatial distribution. This link must also involve additional protein and lipid components that associate with actin and drive the transbilayer clustering of GPI-APs. For example, long acyl-chain GPI-APs can dynamically interact with the CA via outer-leaflet components (e.g., long alkyl chain-containing sphingolipids), inner-leaflet membrane lipids (e.g., PIP2; Higgs and Pollard, 2000), and protein components involved in actin nucleation or binding (e.g., WASp and Arp2/3), with cholesterol playing a central role both in this coupling mechanism and in actin nucleation. Crosslinking extracellular GPI-APs induces transient anchoring and local remodeling of intracellular actin (Chen et al., 2006; Suzuki et al., 2007), suggesting that organization of specific membrane components regulates local CA and in turn is regulated by the same.

Active “Rafts”

The results presented here show that GPI-APs are organized on at least two length scales at steady state: at the nanoscale (<10 nm), and at optically resolvable scales (≤450 nm) wherein nanoclusters are further concentrated. The measurement of steady-state anisotropy probes structure at the nanometer scale, whereas the spatial map of anisotropy probes structure at the limits of optical resolution. Our measurements as such cannot rule out the possibility of a hierarchy of scales in between. For instance, there are at least two more scales: the distance between nanoclusters in optically resolved regions highly enriched in nanoclusters of size ξ₁ and the interdomain distance, ξ₂.

The large-scale domains may share some properties expected of “rafts” (Simons and Vaz, 2004). The graded response on both the size and distribution of these regions upon removal of membrane cholesterol suggests that these domains are cholesterol sensitive. Since nanoclusters composed of long alkyl-chain-containing GPI-APs are concentrated in these cholesterol-rich regions, it is likely that the local lipid composition is fairly specialized. Short-chain lipid-containing molecules (exogenously introduced lipids; e.g., NBD-SM) do not exhibit similar distributions and are most likely excluded from these regions. At this time, a precise correlation of nanocluster enrichment and local ordering of lipid tails is technically complex, requiring simultaneous measurement of GPI-AP clustering and lipid-order reporters (e.g., laurdan; Gaus et al., 2006). In spite of this possible resemblance of the local lipid configuration with liquid-ordered phases, we emphasize that these membrane regions enriched in nanoclusters are not an equilibrium thermo-dynamic phase. They represent a completely different mechanism of molecular complexation. Since the dynamics of formation and spatial distribution of nanoclusters is sensitive to perturbation of CA, actin must surely be involved. In addition, our observations with Blebbistatin application and in blebbing cells strongly suggest that myosin activity is required for the formation of nanoclusters. Thus, rafts of GPI-APs represent actively constructed domains (Mayor and Rao, 2004). The ability to actively construct domains of modified lipid composition in the cell membrane suggests regulatory control of domain formation by the cell. Spatial heterogeneity of the formation kinetics implies that specific sites may be chosen for generation of these domains. Consistent with this, we have shown that sites of cholesterol-sensitive cdc42 recruitment at the inner leaflet and its activation in the membrane are associated with a clustered distribution of GPI-APs on the outer leaflet (Chadda et al., 2007). Although rules behind the selection of these sites are yet to be elucidated, it is conceivable that local activation of guanine nucleotide exchange factors (GEFs) and GTPase-activating proteins (GAPs) that control GTPases involved in actin polymerization is an important component of this regulatory mechanism.

Conclusion

The formation and immobilization of native nanoclusters of GPI-APs represent a unique example of steady-state molecular complexation at the nanoscale regulated by the CA. The physical basis for this molecular nano-complexation may be understood in terms of the framework of active hydrodynamics of the membrane cytoskeleton composite (Hatwalne et al., 2004; Kruse et al., 2004; Ramaswamy and Rao, 2001, 2007), wherein cell-surface molecules, such as GPI-APs or transmembrane proteins, owing to their direct or indirect interactions with the CA, can transiently bind and unbind onto the CA. Such transiently bound molecules can be actively driven along the polar actin filaments resulting in local molecular clustering. The remodeling dynamics of the polar actin filaments induced by acto-myosin contractile forces and tread-milling can then dynamically reorganize this molecular clustering. A deeper understanding requires a detailed theoretical treatment (K.G. et al., unpublished data) to arrive at the statistics of clustering and other quantifiable features of the GPI-AP distribution described here.

These active complexes maybe a generic mechanism for local nanoclustering of a variety of cell-surface molecules such as GPI-APs (Sharma et al., 2004), Ras-isoforms, (Plowman et al., 2005), and gangliosides (Fujita et al., 2007). At the nanoscale (≤10 nm), these complexes could greatly enhance the rates of chemical reactions in living cells (Hancock, 2006). The larger-scale (≥100 nm) organization of these nanoclusters, also coupled to CA, in turn will facilitate the induction of functional membrane domains responsible for signaling and sorting functions (Mayor and Rao, 2004).

Lateral segregation of specific molecules in the construction of signaling complexes and sorting platforms is the central idea behind rafts (Simons and Ikonen, 1997). Here we show that this may be achieved by active mechanisms where the cell (via control of acto-myosin activity) could specify sites and regulate the extent of domain formation. This has implications in understanding the role of rafts, especially as regulatable membrane microdomains as envisaged by recent studies in cell signaling networks involved in regulating cell shape (Neves et al., 2008). It is also likely that such structures may exhibit distinct properties, quite distinct from those dictated by thermodynamic considerations as explored in artificial membranes.

Experimental Procedures

Cell Culture, Fluorescent Labeling, and Other Treatments

CHO cells, stably transfected with human folate receptor, were maintained in folic acid-free Ham’s F12 medium and imaged as described previously (Varma and Mayor, 1998). Cells were labeled with fluorescent analogs of folic acid N^α-pteroyl-N^ε-(4⁰-fluoresceinthiocarbamoyl)-L-lysine (PLF) or N^α-pteroyl-N^ε-Bodipy^TMR-L-lysine (PLB^TMR) or N^α-pteroyl-N^ε-Alexa⁵⁴⁶-L-lysine (PLA) with emission between 510−30 nm and 560−610 nm, respectively, at the cell surface at saturating concentration (10 to 50 nM) on ice for 1 hr and transferred to pre-warmed buffers (150 mM NaCl, 20 mM HEPES, 5 mM KCl, 1 mM CaCl₂, 1 mM MgCl₂, pH 7.2−7.4) before placing on a temperature-controlled microscope stage and imaged within 5−10 min. Cholesterol depletion was achieved by treatment with mβCD at indicated concentrations for 30 min; at 2 mM this treatment resulted in a loss of 15% of cell-surface fillipin staining (Chadda et al., 2007). Actin and myosin perturbation was carried out by incubating cells at 37°C for indicated lengths of time with Latrunculin A or B or Jasplakinolide at indicated concentrations for actin perturbation and Blebbistatin (50 μM) for myosin inhibition.

Fluorescence Traces

Fluorescence intensity and anisotropy traces were obtained from a parked multiphoton excitation (790 nm wavelength) confocal volume using Zeiss LSM 510 Meta microscope (Zeiss, Germany) with a 20×, 0.7NA objective to steer a femtosecond 80.09 MHz (12 ns) pulsed Tsunami Titanium:Sapphire (Ti:S) tunable laser (Newport, Mountain View, CA, USA). Ti:S laser was parked at a single point for continuous illumination at or near the cell periphery at the center of the field of observation. Time-correlated single-photon counting (TCSPC) statistics was maintained for acquisition of photons where binning time for photon collection was set to 0.5 s. TCSPC was accomplished using a Becker & Hickl 830 card (Becker and Hickl, Berlin, Germany) as described (Becker, 2005). Parallel (I_P) and perpendicular (I_⊥) emissions were collected simultaneously into two Hamamatsu R3809U multichannel plate photomultiplier tubes (PMTs) using a polarizing beam splitter (Melles Griot, Carlsbad, CA, USA) at the non-descanned emission side. Total intensity (I=I_II+2I_⊥) and anisotropy $\left(A=\frac{I_{\text{P}}-I_{\perp }}{I_{\text{P}}+2I_{\perp }}\right)$ traces were calculated for each time point and plotted with respect to time. A_∞ was determined independently in each experiment by treating cells with saponin to remove nanoclusters (Sharma et al., 2004) and recording the resultant spread of anisotropy values obtained. These values have been indicated as a vertical line abutting the lut bar, or as a pink band in the anisotropy traces.

Image Acquisition and Anisotropy Recovery after Photobleaching

Cells were labeled with PLB^TMR and were imaged using high NA objective (63×, 1.45NA) mounted on a line-scanning LSM 5 Live Confocal system custom adapted for imaging emission anisotropy (Figure S1A). Parallel and perpendicular polarization fluorescence were collected simultaneously after resolving via a polarizing beam splitter (PBS) onto linear CCD detectors in custom-designed LSM 5 live-confocal microscope. Pixel size was adjusted to 0.1 μm. For ARAP experiments, full-field anisotropy images were taken before and after recovery of fluorescence in the bleached area (1 μm²). Bleaching was carried out by scanning the indicated area using an external laser source (543 nm He-Ne) until the fluorescence was reduced to 20% of original intensity. Fluorescence intensity images were recorded with 543 nm He-Ne laser in descanned mode before, right after, and 1 and 4 min post-bleaching to capture the recovery of intensity in the bleached area. 2 × 2 median filtering was applied to all images to reduce the noise. Image processing, analysis, and quantification were performed using Metamorph 7.0 software (Molecular Devices Corporation, CA, USA).

Comparison of Observed Statistical Distribution of Clusters with Poisson

If N molecules are scattered randomly on a lattice of L sites, the probability of a site having n molecules is given by the Poisson distribution, $P(n)=\frac{e^{-(n)}{n}^{(n)}}{n!}$, where ⟨n⟩ = N/L. We wish to compare the experimental distribution of anisotropy to one obtained when N_m monomers and N_c clusters (of coordination number c) are randomly scattered among the L pixels. We obtain an estimate of the mean intensity per pixel due to monomers and clusters, using the relations

$$\langle I_m\rangle =\frac{\left(\langle A\rangle -A_c\right)\langle I\rangle }{\left(A_m-A_c\right)}$$ (1)

$$\langle I_c\rangle =\frac{\left(\langle A\rangle -A_m\right)\langle I\rangle }{\left(A_c-A_m\right)}$$ (2)

where ⟨I⟩ and ⟨A⟩ are the mean intensity and anisotropy, respectively. We generate strings {I_m},{I_c} of intensity values due to monomers and clusters by drawing random numbers from a Poisson distribution with means given by ⟨I_m⟩ and ⟨I_c⟩. These strings are then used to generate a string of anisotropy values using

$$\left\{A\right\}=\frac{A_m\left\{I_m\right\}+A_c\left\{I_c\right\}}{\left\{I_m\right\}+\left\{I_c\right\}}.$$ (3)

A large enough string provides a well-averaged anisotropy distribution, with which we compare the experimental data. In Figure 1A, we have taken the values of A_m = 0.18 and A_c = 0.04 (Sharma et al., 2004).

Dynamical Equations for Clusters and Monomers

The dynamics of formation and breakup of the clusters is derived in terms of C_nm(t), the fraction of clusters having n proteins, m of which are unbleached, present within the confocal volume at time t (Supplemental Data). For convenience, we will assume that the GPI-APs are distributed as monomers and dimers alone; our results will hold even if we relax this assumption to include higher-order n-mers (Supplemental Data). The closed set of ordinary differential equations describing the dynamics of a mixture of dimers and monomers are

$$\begin{array}{l}\frac{d{C}_{22}}{dt}=-2b{C}_{22}-k_f{C}_{22}+\frac{k_{a}N}{2}{C}_{11}^2+\left(C_{22}(0)-C_{22}\right)d_c\\ \frac{d{C}_{21}}{dt}=-b{C}_{21}-k_f{C}_{21}+k_{a}N{C}_{10}{C}_{11}+2b{C}_{22}-d_c{C}_{21}\\ \frac{d{C}_{20}}{dt}=b{C}_{21}-k_f{C}_{20}+\frac{k_{a}N}{2}{C}_{10}^2-d_c{c}_{20}\\ \frac{d{C}_{11}}{dt}=-b{C}_{11}-k_{a}N{C}_{11}^2-k_{a}N{C}_{11}{C}_{10}+2k_f{C}_{22}+k_f{C}_{21}+\left(C_{11}(0)-C_{11}\right)d_1\\ \frac{d{C}_{10}}{dt}=b{C}_{11}-k_{a}N{C}_{10}^2-k_{a}N{C}_{11}{C}_{10}+2k_f{C}_{20}+k_f{C}_{21}-d_1{C}_{10}\end{array}$$ (4)

The bleaching rate b, the diffusion rates of monomers and clusters d₁∝D₁ and d_c∝D_c (Supplemental Data), and the rates of aggregation (k_a) and fragmentation (k_f) are parameters in the model. Implicit in the above equations are the boundary conditions (Supplemental Data). Initial conditions are provided by the values of intensity I(0)∝N (initial number of fluorophores in the confocal volume) and anisotropy A(0). Since at t = 0, the dimers and monomers are unbleached, we have, $C_{22}(0)=\frac{A(0)-A_m)}{2\left(A_c-A_m\right)},C_{11}(0)=\frac{A(0)-A_c}{A_m-A_c}$ C₂₁(0) = C₂₀(0) = C₁₀(0) = 0, where A_c and A_m (= A_∞) are the anisotropies of the cluster and monomer, respectively. These equations allow us to compute the time profiles of the intensity and anisotropy using the relations I = 2C₂₂ + C₂₁ + C₁₁ and $A=\frac{2A_c{C}_{22}+A_m{C}_{21}+A_m{C}_{11}}{2C_{22}+C_{21}+C_{11}}$.