Abstract
How do the two main types of neural dynamics, aperiodic transients and oscillations, contribute to the interactions between feedforward and feedback pathways in sensory inference and predictive processing? We discuss three theoretical perspectives: First, we critically evaluate the theory that gamma and alpha/beta rhythms play a role in Classic Hierarchical Predictive Coding (HPC) by mediating feedforward and feedback communication, respectively. Second, we outline an alternative functional model in which rapid sensory inference is mediated by aperiodic transients, while oscillations contribute to the stabilization of neural representations over time and plasticity processes. Third, we propose that the strong dependence of oscillations on predictability can be explained based on a biologically plausible alternative to Classic HPC, namely Dendritic HPC.
Theories of neural dynamics and their role in predictive processing
To construct an internal model of the environment, the brain performs inference on the statistical nature of its inputs by integrating sensory evidence with prior knowledge [1, 2]. Various theories explain how sensory inference is implemented by local recurrent networks and interactions between feedforward and feedback pathways [2, 1, 3, 4, 5]. For example, Classic Hierarchical Predictive Coding (HPC) theory posits that feedforward pathways carry sensory prediction errors, while feedback pathways convey prediction signals [2, 1]. In this Opinion article, we contrast three theoretical proposals as to how these interactions are facilitated by transient dynamics and oscillations.
First, we consider the theory that prediction errors are transmitted through gamma (see Glossary; 30-80Hz, [6, 7]) oscillations, whereas prediction signals are transmitted through alpha / beta (10-20 Hz) oscillations [8, 9, 10, 11, 12, 13, 14, 15]. We critically evaluate this theory by examining the relationship between (i) functional, structural and effective connectivity, and (ii) neural rhythms and stimulus predictability.
Glossary.
- Alpha
Alpha rhythms (8-14Hz) are found in e.g. visual, somatosensory (mu rhythm), and auditory (tau rhythm) cortex, during wakeful rest.
- Beta
A 20Hz beta rhythm is commonly observed in parietal and (pre)motor areas, mainly during the delay period of sensorimotor tasks. A distinct higher-frequency beta rhythm is found in (pre-)frontal areas and increases during the delay periods and post-trial epochs of working memory and attention tasks.
- Broadband
Refers to changes in power or functional connectivity occurring in a wide frequency range, e.g. due to the influence of firing rates.
- DAI
(directed asymmetry index) quantifies the asymmetry of LFP Granger-causal influences (as [GCout - GCin] / [GC in + GCout]). Positive DAI × SLN correlations indicate an association of structural feedforward connectivity with Granger-causal influences in that band.
- ECoG
Electrocorticography (or iEEG) refers to intracranial measures of cortical surface field potentials.
- Feedforward (FF) and Feedback (FB)
Anatomically speaking, a projection from a lower to a higher brain area (FF) or higher to lower area (FB). Hierarchy can be defined in multiple ways, e.g. through cortical gradients, anatomical connectivity, or functional response properties.
- Gamma
Gamma rhythms refer to synchronized spiking in the 30-80Hz range, and are usually associated with active processing during awake states. These rhythms are prominent in e.g. hippocampus, visual cortex, and olfactory cortex.
- Granger-causality
Measure of causal influences between stochastic signals. Granger-causality in the frequency domain is commonly defined as the fraction of explained power in a signal Y by observing X, after discounting the information that Y has about itself from the past.
- LFP (Local Field Potential)
Electrical potential differences measured extracellularly in the lower frequency range (0-200Hz). At lower frequencies, the LFP primarily measures volume return currents caused by spatially and temporally coherent transmembrane currents. At higher frequencies, the LFP also contains a direct contribution of spikes.
- Narrow-band
Refers to changes in power or functional connectivity occurring in a narrow frequency range, which may reflect a change in the amplitude of a rhythm. Narrow-band oscillations are characterized by spectral peaks and synchronization of spiking activity.
- SLN
At the anatomical level the % of supragranular labeled neurons (SLN) in area X projecting to area Y gives a good indication of hierarchical distance. These allows to place each cortical area on a hierarchy, which agrees very well with descriptions of feedforward connectivity based on projections to Layer IV.
- Variational Autoencoder
Machine learning architecture in which an input (e.g. image) x is encoded via some latent variable space z, with a density q(z|x). For static inputs, the mapping of x onto q(z|x) (i.e. inference) can be performed with a feedforward neural network. Starting from the latent space q(z|x), the posterior p(x|z) can be computed (i.e. the negative Free Energy), which requires a generative neural network.
Second, we propose an alternative functional model with dual roles for transient dynamics and oscillations. In our model, rapid sensory inference relies on communication during aperiodic transients, while rhythms are involved in stabilizing neural representations and facilitating plasticity during the feedback-dominated late phase of stimulus processing.
Third, we suggest that the emergence of rhythmic synchronization for stimuli with high spatio-temporal predictability can be explained by a biologically plausible alternative to Classic HPC, namely Dendritic HPC [3]. This proposed mechanistic model is compatible with the functional model in point (2).
Rhythms for feedforward and feedback communication?
The theory that gamma and alpha/beta rhythms underlie feedforward and feedback communication (“gamma-FF/alpha-beta-FB”) relies on three fundamental assertions: (1) Gamma and alpha/beta oscillations are widespread and observed in all brain areas [16, 17]. (2) There is a consistent relationship between gamma and alpha/beta influences and anatomical connectivity [10, 18]. (3) The functional interactions between brain areas, i.e., predictions and errors, are reliably and accurately captured by methods such as Granger-causality influences between LFP signals.
In light of contrasting evidence for the three assertions above, we propose an alternative model, referred to as “frequency-specific networks”, which is consistent with empirical studies showing that: (1) Gamma and alpha/beta rhythms are not widespread, but occur in distinct cortical networks. (2) The relationship between feed-forward/feedback anatomical connectivity and gamma-FF/alpha-beta-FB Granger-causal influences is not consistent across brain areas. (3) Granger-causal influences between LFP signals do not reflect the frequency specific transmission of predictions and errors, but rather unique power spectral signature of each cortical network.
How widespread are gamma and alpha/beta oscillations?
Understanding the ubiquity and breadth of these oscillations requires invasive electrophysiological recordings from multiple areas, ideally simultaneously, and in a manner that minimizes volume conduction.
There are limited datasets that satisfy these criteria, yet these data suggest highly localized oscillatory networks. For instance, in one set of ECoG recordings from 15 areas (occipital, parietal and frontal) in the macaque, only 4/15 areas showed strong narrow-band [19] gamma peaks in the LFP power spectra, these peaks were most prominent in areas V1 and V2 [20], and gamma-band Granger-causality influences were most prevalent between pairs of areas which included V1 or V2 [14]. These observations are supported by another dataset of 55 macaque areas, which reported that narrow-band gamma oscillations in the LFP were confined to areas V1 and V2 [21]. In addition, several studies have reported particularly strong gamma synchronization in areas V1 and V2 [22, 23, 21, 24],
Similarly, several multi-area datasets of invasive recordings in macaques have shown a localized beta-band network (a “beta-core”) [14, 20, 25, 21]. Beta-band Granger-causal influences were mainly associated with parietal regions like 7A, S1, area 5 and motor cortex [14], with LFP power spectra showing clear alpha and beta peaks in parietal and frontal but not occipital areas [20, 21]. These findings are consistent with previous reports of strong beta oscillations in the somatosensory network, which were especially prominent during the delay periods of sensorimotor tasks [21, 25, 26, 27, 15].
It has been argued that the LFP power spectral analyses might fail to reveal the presence of narrow-band rhythmic synchronization that would otherwise be evident in the spike-LFP coupling [28]. To the contrary we find that the results of spike-LFP coupling are often consistent, and agree with the LFP power spectra. For example, spike-LFP coupling in parietal cortex showed beta but not gamma synchronization, which matched the LFP power spectra [29]. Moreover, simultaneous V1 and V4 recordings have revealed locally generated gamma synchronization in V1 but not V4, which was consistent with the LFP spectra [22]. In fact, LFP power spectra may be prone to overestimate the prevalence of gamma/beta oscillatory dynamics across brain areas as a result of volume conduction [30, 31, 29].
Taken together, the evidence is more in line with the frequency-specific-network hypothesis rather than discrete gamma-FF/alpha-beta-FB communication channels. We note that the reported differences in narrow-band oscillations between areas at least suggests a major difference in oscillation strength between regions, but may also suggest a genuine absence of certain oscillations in particular areas.
The consistency of the gamma-FF/alpha-beta-FB pattern with anatomical connectivity
The gamma-FF/alpha-beta-FB hypothesis was originally motivated by the proposal that gamma and alpha/beta synchronization are generated in feedforward projecting supragranular and feedback projecting infragranular layers, respectively [10, 32]. However, later studies challenged the gamma-supra/alpha-beta-infra hypothesis, by showing that gamma and alpha/beta can be equally prominent in both infra and supra-granular layers (see Box 1).
Box 1. Gamma supragranular, alpha/beta infragranular?
It has been proposed that gamma and alpha/beta oscillations are respectively generated in supragranular and infragranular layers, the primary sources of feed-forward and feedback projections [33]. However, we argue that the evidence does not suggest a clear laminar separation between rhythms (see also [112]). Thus, we argue that the main source of variability in rhythms is the cortical area (e.g., V1 vs. S1) rather than the cortical layer.
Recordings with laminar probes and/or post-mortem histological verification indicate that both supra- and infra-granular layers of macaque V1 contain a source of gamma-band synchronization in spikes and LFPs [113, 114, 115] (Figure IA). While a recent study finds stronger LFP gamma power in supragranular as compared to infragranular layers of many macaque areas [16], the LFP spectra indicate broadband rather than narrow-band gamma oscillations (Figure IC). Laminar differences in broadband LFP power can be explained by e.g. differences in the slope of power spectra due to dendritic filtering [43, 116]. An earlier study suggested strong gamma-synchronization in supragranular layers of V1, V2 and V4, but not in infragranular layers [32]. However this study was based on inserting individual electrodes at different depths, which lacks the accuracy of laminar and histological techniques, and may have included e.g. L4 that is known to exhibit weak gamma [113, 114, 115].
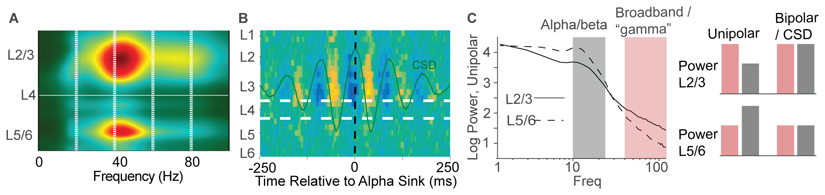
Studies have drawn different conclusions regarding the laminar distribution of alpha/beta rhythms. Earlier work found a dominant alpha source in the infragranular layers of early visual areas [117]. Yet stronger alpha power in infragranular layers may reflect the alignment of signals to infragranular alpha before computing the current source density (CSD) [118, 119]. A recent study reports a cortically widespread pattern of stronger unipolar LFP alpha/beta power [45, 16]. Yet, opposite conclusions based on the same data are reached when using bipolar derivations or CSD signals (Figure S1 in [120], Figure IC, see also [16]). Differences between unipolar LFP profiles may not reflect the strength of rhythms, but could reflect properties of passive dendritic filtering and local volume conduction [43]. An analysis of CSDs and spiking signals in laminar recordings from human cortex suggest that the alpha rhythm can be equally or more prominent in supragranular than in infragranular layers [118, 119] (Figure IB). Finally, studies suggest LFP signals show beta rhythmicity across all layers [121, 122, 123], with one study showing relatively strong beta transients in supragranular CSDs [123].
Figure I. Relationship of layers to cortical rhythms.
(A) Laminar recordings from macaque V1 during attention task. A gamma source is present both in supra- and infragranular layers [113]. (B) Unit recordings of human alpha during eye closure shows strongest spike phase locking in L3 [118]. (C) Power spectra in [45]. Note that the reported gamma effect comprises broadband fluctuations. The reversed pattern of alpha/beta and high-frequency power is specific to unipolar recordings but not found in CSD and bipolar recordings, as illustrated by the bar plot on the right that visualizes the difference between unipolar and bipolar/CSDs [120, 16, 112].
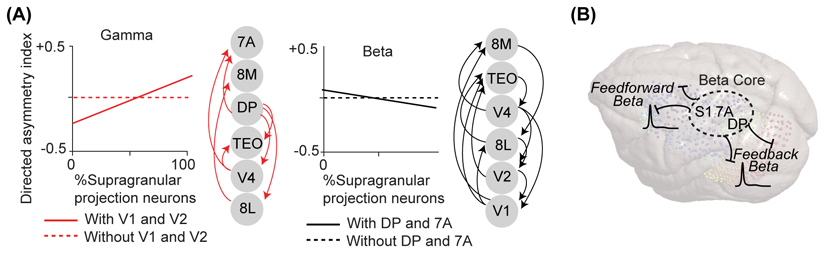
A direct test of the gamma-FF/alpha-beta-FB hypothesis requires large-scale, invasive recordings of neural activity precluding volume conduction. Only a few studies have analyzed such data. For instance, Bastos et al. [10] analyzed a unique dataset of ECoG recordings from eight macaque visual areas, and computed the correlation between the inter-areal anatomical connectivity as reflected by SLN (supragranular labeled neurons, [33]) and the LFP Granger-causual influences quantified as DAI (directed asymmetry index) (For a similar approach utilizing human magnetoencephalography data see [18]). The correlation coefficients the authors reported were in the range of -0.2 for beta (≈20 Hz) and +0.4 for the gamma range [10]. Although the Bastos et al. [10] study can be viewed as evidence for a consistent relationship between gamma-FF/alpha-beta-FB and anatomical connectivity, we note that a correlation coefficient of -0.2 and 0.4 indicate that SLN explains 4% and 16% of the beta and gamma Granger-causal influences, respectively. Moreover, further examination of these results revealed that the correlations in each band are largely driven by a few pairs of areas with particularly strong gamma or beta Granger-casual influences (i.e., V1 and V2 for gamma and posterior parietal areas for beta (see Box 2, Figure I)). Furthermore, several studies have found feedforward-beta, which challenges the assertion that beta rhythms uniquely reflect feedback communication [25, 26]. We argue that these results are not exceptions to the rule, but point to a different rule, which is consistent with frequency-specific-networks.
Box 2. Gamma feedforward, alpha/beta feedback?
The Bastos et al. [10] study is cited as key evidence for the gamma-FF/alpha-beta-FB hypothesis. Bastos et al. [10] selected 8/15 areas for analysis, and computed correlations across 56 data points (i.e., 7 × 8 area pairs; each area pair contributed two highly correlated data points). We argue that the gamma-FF/alpha-beta-FB pattern is not consistent within the set of analyzed areas: (i) Bastos et al. [10] does not provide direct statistical evidence for a consistent pattern across area pairs, because the significance of correlations is tested across subsets of trials (via bootstrapping), not area pairs. (ii) Their reported correlations are possibly inflated because each area contributes to a total of 14 (i.e., 25% of 56) area pairs, violating the assumption of statistical independent observations. Consequently, a single area can easily drive correlations. (iii) The reported SLN × DAI correlations are weak to moderate, suggesting only a loose relation between structural and functional connectivity. This is unlikely due to measurement noise, because the correlations and Granger-causality spectra were highly consistent across subsets of trials. (iv) Crucially, examination of the individual area pairs shown by Bastos et al. [10] (their Figure S3) suggests the FF-gamma/alpha-beta-FB pattern is driven by a small number of areas. In particular, the correlations between SLN and gamma DAI seem to be entirely driven by V1 and V2, which contribute to 50% (i.e., 28/56) of all area pairs. Likewise, the relation between beta DAI and anatomical connectivity seems to be driven by areas around the parietal cortex (DP and 7A) in which beta is strong (Figure IIA, [120]). Because gamma and beta are prevalent in distinct networks, only very few anatomically connected area pairs show both the gamma-FF and beta-FB pattern. (v) The selection of areas included for analysis can strongly bias the results. Bastos et al. [10] did not include parietal and frontal areas in which beta is most prominent, however other work suggests that this would have yielded many feedforward beta influences [25, 26, 33].
In sum, there appears to be no general, consistent gamma-FF/alpha-beta-FB pattern within the visual system, even though gamma oscillations may be characteristic of lower visual areas and beta oscillations of visual areas occupying intermediate hierarchical positions (e.g. DP, 7A). Furthermore, in the reviewed large-scale recording studies, gamma appears to be absent among somatosensory and motor areas [21, 20, 33], while beta appears to be associated with areas lower in the hierarchy [26, 25]. This characterization is likely premature, as much work is needed to precisely characterize the beta-network. Moreover, surface ECoG recordings, as used in Bastos et al. [10], do not necessarily reflect local spiking synchronization [29], and it remains to be tested whether beta in DP and 7A LFPs reflects intrinsic synchronization, or activity from nearby areas like area 5, 7B and S1 (e.g. via volume conduction or synaptic inputs). Furthermore, we note that some magnetoencephalography studies did report narrow-band gamma in somatosensory/motor cortex [124, 125, 23], while other studies using invasive recordings in monkey/human somatosensory and motor cortex appear to show broadband fluctuations rather than narrow-band gamma [126, 127, 128, 129, 130].
Figure I. Consistency and interpretation of gamma feedforward, alpha/beta feedback patterns.
(A) We argue that the positive correlation between gamma DAI (y-axis) and feedforward anatomical connectivity (x-axis) (observed by Bastos et al. [10]) is driven by V1 and V2, and is absent when V1 and V2 are not included. In the case of beta, we argue that the correlation is driven by DP and 7A. Significant Granger asymmetries are shown based on Figure S3 in Bastos et al. [10]. The areas are ordered hierarchically, with arrows from lower to higher nodes corresponding to feedforward connections. See also [120]. (B) We argue that strong Granger-causal influences at beta frequencies originate from regions with strong beta power, both in the feedforward [25, 26] and feedback direction[10]. (C)
Is effective communication mediated by gamma and alpha/beta synchronization?
One may counter that the gamma-FF/alpha-beta-FB pattern may still be functionally relevant for a small subset of area pairs. We contend that this argument hinges on the ability of Granger-causality to accurately capture interareal interactions. A recent computational framework (coherence-through-communication, CTCOM) challenges this assumption and suggests that the Granger-causal influence from a sender to a receiver is simply a function of the oscillatory power in the sender. That is, the Granger-causal interaction can simply be the result of the correlation of the sender with its own projected inputs to the receiver, rather than entrainment or resonance between the sender and receiver [29, 30, 34, 35, 36]. According to CTCOM, Granger-causal influences between LFPs are thus not necessarily functionally relevant but can emerge simply as a result of connectivity and differences in oscillatory power. The question that Granger-causal analysis cannot answer is the extent to which gamma and alpha/beta oscillatory inputs are effective at driving the spiking activity of neurons in postsynaptic target areas.
The dominant view on spike synchronization is that it enhances the impact on postsynaptic targets [37, 38, 7]. Importantly, however, when synchronization is confined to a narrow-frequency band, its effect necessarily depends on the resonance and filtering properties unique to each neuron type [39, 34] For example, excitatory neurons exhibit strong low-pass filtering that may render afferent, high-frequency inputs ineffective at driving these neurons [40]. Indeed, recent work suggests that gamma rhythms preferentially activate fast-spiking inhibitory interneurons rather than excitatory neurons in downstream areas [22, 40]. For instance, while robust LFP-LFP gamma coherence is observed between V1 and V4 [41, 22], gamma-rhythms in V1 are correlated with the spikes of fast-spiking interneurons in the input layer (L4) of V4, but not excitatory neurons [22]. These observations appear to be consistent across various cortical systems, including the hippocampus [42], and suggest that gamma-band feedforward communication is likely inhibitory (i.e., feedforward inhibition) rather than excitatory. A similar argument can be made with regard to beta-frequency feedback. Feedback predominantly arrives at the apical dendrites of pyramidal neurons, which show substantial low-pass filtering that can severely dampen synaptic potentials at beta frequencies [43, 44]. It is possible that top-down beta feedback may therefore predominantly drive GABAergic interneurons in lower areas.
In sum, the idea that feedforward/feedback Granger-causality influences between LFPs reflect entrainment and effective information propagation needs to be revised in light of the CTCOM model, as well as the frequency- and cell-type specific effects of oscillations on spiking activity in postsynaptic targets.
Oscillations and broadband dynamics in predictive processing
Narrow-band gamma vs. broadband fluctuations in predictive processing
Next, we discuss studies that directly tested the relationship between prediction error and gamma oscillations. Studies have reported both positive [9, 8, 11, 45, 46] and negative [47, 48, 49] relations of gamma-frequency power with prediction error. We suggest that these discrepancies reflect opposite correlations between broadband fluctuations and narrow-band gamma with stimulus predictability (Figure 1). We argue that the empirical evidence does not suggest a role for gamma oscillations in conveying sensory prediction errors, and that findings on gamma are better explained by Dendritic HPC rather than Classic HPC models (Figure 2).
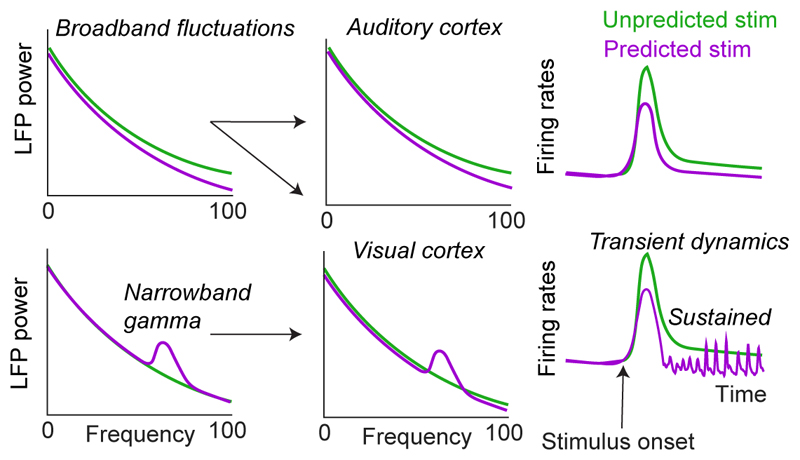
Figure 1. Broadband fluctuations vs. narrow-band gamma.
In the main text, we have argued that narrow-band gamma oscillations are typically increased for predicted stimuli, while broadband ”gamma-frequency” activity increases for unpredicted stimuli. We argue that the broadband increase is explained by concurrent increases in spiking activity. In some systems like visual cortex, narrow-band gamma oscillations are frequently observed. Differences between Local Field Potential (LFP) spectra will reflect both the broadband and narrow-band gamma effect. By contrast, in other systems like auditory cortex, differences in LFP power predominantly reflect broadband fluctuations [53].
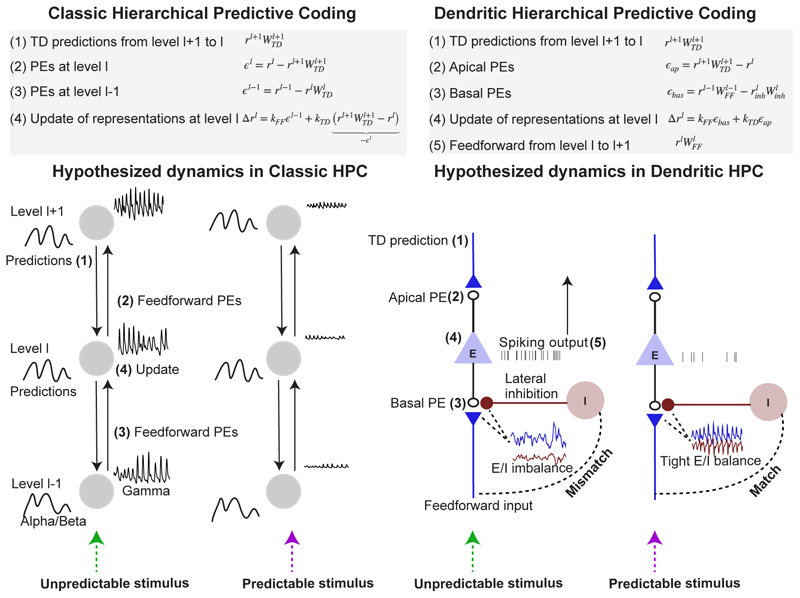
Figure 2. Emergence of rhythms in classic vs. dendritic hierarchical predictive coding.
In Classic HPC models, sensory inference results from interactions at each l-th hierarchical level between feedforward (FF) and feedback (FB) pathways that carry sensory prediction error (PE) and prediction signals, respectively [2, 1]. It was hypothesized that these feedforward error and feedback predictions signals are transmitted via 30-80Hz gamma oscillations in superficial layers, and alpha/beta oscillations in infragranular layers, respectively [8, 9, 10]. This hypothesis predicts strong gamma amplitude for unpredicted stimuli and weak amplitude for predicted stimuli, but does not entail a dependence of alpha/beta (see Main text). We argue that the emergence of gamma oscillations is better accounted for by the Dendritic HPC model, a biologically plausible PC model in which local E/I interactions play an important role [3]. The Dendritic HPC model builds on the anatomical observation that feedforward and feedback projections preferentially target basal and apical dendrites, respectively. Dendritic HPC does not contain specialized neurons (ϵl) for conveying feedforward error signals, and attributes error representation to voltage fluctuations in basal and apical dendrites. Error terms at the basal dendrites result from lateral inhibition that predicts and cancels out the feedforward inputs. Based on the Dendritic HPC model, we reason that a stimulus with high spatiotemporal predictability gives rise to tight E/I balance and sparse spiking activity, thereby promoting the emergence of fast network oscillations (as observed by [47]). We postulate that similar principles may also account for oscillations in other bands like beta and perhaps alpha.
We suggest that positive correlations between gamma-frequency power and prediction error observed in several studies reflect increased spiking activity (Figure 1). Broadband “gamma-frequency” power can be driven by aperiodic activity and spiking, and is commonly used as a proxy for spiking activity in ECoG studies [50, 19]. The reported increases in gamma-frequency power for unpredicted stimuli are typically transient, extend beyond 100Hz, and lack a narrow-band gamma peak, suggesting broadband fluctuations [51, 52, 11, 53]. Increases in gamma-frequency power for unpredicted stimuli might therefore reflect concurrent increases in spiking activity [45, 47, 8, 54] (Figure 1). To test this hypothesis, a recent study distinguished rhythmic components from broadband fluctuations using spectral decomposition techniques and multiscale-multifractal analyses. These analyses suggest that increased LFP gamma-frequency power for unpredicted stimuli reflects aperiodic processes instead of narrow-band gamma [53].
We propose that negative correlations between gamma power and prediction errors specifically involve narrow-band oscillations (Figure 1). Indeed, recent studies suggest that in area V1, gamma synchronization increases systematically with spatial predictability [48, 49, 47, 55, 23], i.e., the match between receptive-field inputs and contextual predictions [2]. Narrow-band V1 gamma also increases with temporal predictability [23]. V1 gamma-synchronization is present during regular stimulus movement and is disrupted by unpredictable motion [56, 57]. Likewise, gamma synchronization increases with stimulus repetition across trials, and decreases for novel stimuli [58, 59].
The lack of a systematic relation between gamma oscillations and top-down attention across studies [60, 61, 62, 22, 12, 38] further contradicts the hypothesis that gamma oscillations convey prediction errors that are weighted by precision (see [46]). Another finding that contradicts this hypothesis is that narrow-band V1 gamma power decreases with the bottom-up salience of natural receptive-field stimuli [47].
Alpha/beta and predictive processing
The evidence linking alpha/beta rhythms to the communication of predictions is highly indirect, and in our view, subject to multiple interpretations. Studies have reported a transient suppression of alpha/beta-band power for unpredicted as compared to predicted stimuli [45, 11, 51, 63] (but see [53, 52, 9]). Such a suppression seems expected, given that alpha/beta rhythms are suppressed by transient increases in neural activity during sensory stimulation, attention, eye movements and movement initiation [64, 18, 29, 27] (but see [65]).
Nevertheless, it has been suggested that a suppression of alpha/beta for unpredicted stimuli provides indirect evidence for a role for alpha/beta in transmitting predictions. For instance, Chao et al. [11] argued that the suppression of alpha/beta rhythms reflects the transient updating of current sensory predictions by prediction errors. And, Bastos et al. [45] argued that alpha/beta feedback exerts inhibitory effects on lower hierarchical levels, such that the suppression of top-down alpha/beta enhances sensory prediction errors in lower hierarchical levels.
We think these arguments do not make a clear case, and offer several counterarguments: (1) It is assumed that the suppression of alpha/beta rhythms causes neural activation for unpredicted stimuli, and that at the same time, increased neural activation for these stimuli leads to the suppression of alpha/beta. But this leads to a chicken-or-the-egg problem. (2) In Classic HPC, prediction errors do not result from a suppression of top-down feedback (TD). Rather, prediction errors are the difference between local representations and TD feedback [2] (Figure 2). That is, in Classic HPC, top-down feedback is required to compute stimulus prediction errors, which seems incompatible with the suppression of alpha/beta. Generally, the assumption that top-down feedback is suppressive is questionable, because feedback exerts excitatory rather than inhibitory effects on the local representational units in PC models [2, 3].
Predictability: a common principle underlying rhythmic activity?
In contrast to the gamma-FF/alpha-beta-FB hypothesis, which suggests opposing functional roles for the two bands, we propose that the emergence of gamma and alpha/beta rhythms reflects a common mechanism. For instance, both gamma and alpha-beta rhythms tend to occur during relatively stationary periods, are transiently disrupted by sensory cues or movements, and occur during periods in which firing rates are relatively low [41, 27, 29, 34]. Hence, the emergence of oscillations may in general follow a common pattern related to late stage sensory processing and may reflect the stability of sensory representations. We further argue that the emergence of oscillations is critically dependent on the spatio-temporal predictability of sensory inputs. In this framework, oscillatory states may be relatively widespread across cortex, yet allow for possibility that specific frequencies may be more, or less, prominent across cortical networks. In this view, differences in frequencies do not differentiate distinct functional roles, but rather reflect differences in area-specific circuits, intrinsic dynamics, integration, stimulus representation, or biophyical time-constants, [24, 66, 21], or input drive [67, 68].
Transients vs. oscillations in predictive processing
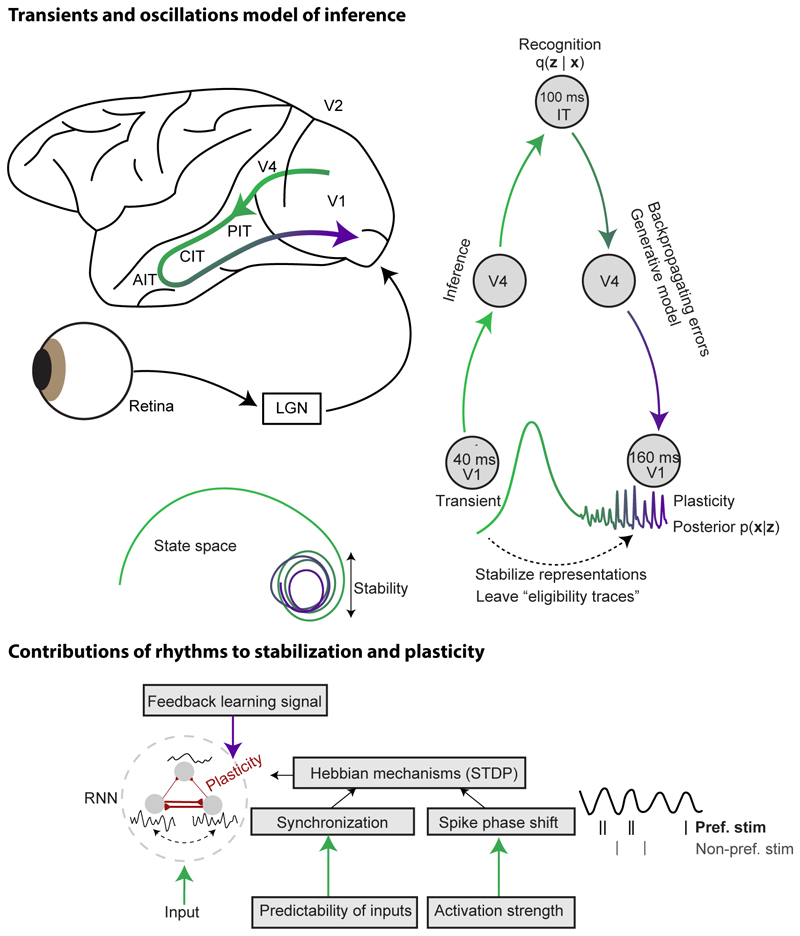
In this section, we outline a functional model contrasting the roles of transients and oscillations in sensory inference. Contrary to Classic HPC, we propose that aperiodic transients, rather than oscillations, mediate rapid sensory inference. Instead, our model posits that oscillations play a role in stabilizing neural dynamics and plasticity during the late phase of stimulus processing (Figure 3). Accordingly, we suggest that cortical circuits continuously alternate between transients and oscillatory states (i.e., states of stability and plasticity), creating two distinct sensory processing phases that are feedforward- and feedback-dominated, respectively. Notably, our model is consist with the observation that gamma oscillations are disrupted by transients (e.g., stimulus onsets and (micro)saccades) [41, 69, 70, 34], and only stabilize 100 ms or later following stimulus or (micro)saccade onset [41, 71, 34].
Figure 3. Transients vs. oscillations in sensory inference.
We posit that sensory inference predominantly relies on aperiodic transients, while rhythms play a role in stabilizing neural representations and plasticity processes during the late, feedback-dominated phase of stimulus processing. In the visual system, a stimulus onset typically leads to rapid cascade of transients across the ventral stream. Stimulus onset latencies in IT are around 100ms and the inference of object properties has been largely completed around 120ms [72]. This is noted by the inference model q(z|x), the probability distribution over the latent variable z. Learning in supervised neural networks, but also in self-supervised neural networks like Variational Autoencoders, entails that feedback from higher levels reaches early sensory areas. Here the feedback may carry back-propagating errors that interact with local eligibility traces to instruct plasticity of the local recurrent connections [86]. Furthermore, for self-supervised learning, top-down generative networks can compute the posterior probability of the inputs given the inferred latents, p(x|z), which in turn instructs plasticity. Gamma oscillations in early visual areas emerge relatively late after stimulus onset, and will be prominent when this feedback arrives. As discussed in the text, gamma oscillations can facility plasticity processes, e.g. via synchronizing neurons that receive spatiotemporally correlated inputs [47], or via activation-dependent gamma-phase shifting [87]. We also argue that gamma may stabilize the neural activity during the later stimulus phases, narrowing the region of state space that is occupied.
Transient dynamics
V1 neurons responds to visual input with latencies 30-40 ms, followed by a cascade of neural activations across the ventral stream, culminating in high-level object representations in the inferior temporal cortex (IT) by approximately 120 ms [72]. This swift processing enables non-human primates to perform object recognition for brief stimulus presentations around ≈100 ms [72, 73]. The formation of object-selective responses in IT occurs within a 60-80 ms window, suggesting a significant portion of this time is used for feedforward transmission through the visual areas V1, V2, V4, to IT [72].
Stimulus inference may therefore largely depend on the feedforward sweep [72, 74, 73], comprising a cascade of transient responses. Transients need to be distinguished from oscillations as they contain broadband energy, and have the chance to disrupt ongoing oscillations by perturbing the balance between excitation and inhibition [75]. In state space, transients correspond to a smooth and short path from one neural representation to another (i.e., from “A” to “B”), whereas oscillations comprise stochastic fluctuations in some circumscribed region of state space (e.g., around a fixed point “B”) [76] (Figure 3).
Transient inputs can be amplified via several mechanisms that do not involve rhythmic synchronization: (1) Specific input patterns can be selectively amplified dependent on the synaptic weight matrix stored in local recurrent and feedforward connections; (2) unstable recurrent excitation that is balanced by strong inhibitory feedback allows for fast, strong responses to sensory inputs [77, 75]; (3) transients contain broadband synchronized activity (resulting in large event-related potentials), which may enhance the impact on downstream receivers [78], and encode information via rapid spike sequences [74, 79].
The idea that inference relies on rapid transients is at odds with the view of inference within Classic HPC. In Classic HPC, inference relies on iterative optimization of neural representations across all hierarchical levels (Figure 2) [2]. This iterative process can be slow and result in low-frequency oscillations [65, 80]. However, such iterative optimization is not mandatory: In generative inference models like Variational Autoencoders, inference can be rapidly performed via a feedforward network. In contrast to HPC, stimulus predictions are then generated only after inference is completed. These stimulus predictions and are required for self-supervised learning, but not for inference itself [81].
Oscillations and stabilization
In sum, we argue that stimulus inference depends critically on neural transients. These transients represent transitions between different neural states, and are therefore ill-suited to stabilize and maintain neural representations. The stabilization and maintenance of neural representations may rather depend on oscillatory dynamics, which reflect the system’s movement around a fixed-point or along a limit cycle in state-space [82, 83], and can be conceived as a dynamical state that keeps the system in a specific configuration. It thus makes sense to look for functional roles of oscillations in the stabilization of neural activity, which may be played both by gamma oscillations in e.g. visual cortex, but also beta oscillations in e.g. somatosensory and motor cortex [84, 85]. The stabilization of neural activity may be important for many behaviors and cognitive functions (e.g., working memory, expectation) but also learning processes.
Gamma oscillations may stabilize neural responses by reducing their trial-by-trial variability. E/I models suggest that when neural populations engage in gamma-synchronization, neural representations exhibit less variability, and the information per spike is maximized [88]. Consistent with this model, neural variability tends to be relatively low for stimuli that induce V1 gamma oscillations [23], and gamma-synchronized spikes carry more information than non-synchronized spikes [89].
The balanced E/I interactions producing gamma oscillations may also reduce the co-variability of neural responses (i.e. noise correlations) occurring at lower frequencies [90, 89]. At the same time, the spiking correlations induced at gamma frequencies may not significantly impact downstream excitatory neurons, but rather target fast-spiking interneurons [22], and can therefore increase the signal-to-noise ratio of sensory transmission [91].
It has been argued that the highly stochastic nature of gamma oscillations, exhibiting ample variability in instantaneous cycle amplitude and duration [76, 92], may prevent a functional role for gamma in neural coding and communication [92, 71]. Yet, this stochasticity may in fact be required for a role in stabilization processes, because the variability of neural representations is minimized for stochastic, rather than regular (harmonic) oscillations [88].
Oscillations, feedback and plasticity
Both self-supervised and supervised neural network architectures typically assume separate phases for inference and plasticity/learning. For example, in deep (feedforward) neural networks, the forward pass is followed by a top-down flow of error signals, which are crucial to instruct gradient descent (Figure 3). Likewise, in generative inference models like Variational Autoencoders, the inference phase (q(z|x)) is followed by generative top-down activity that is required to approximate the surprise of the sensory input data (− ln p(x|z)), which in turn instructs gradient descent. In a biological neural network, this implies that the presentation of a stimulus first elicits a phase in which neural circuits compute and perform inference, which is then followed by a phase in which synaptic connections are fine-tuned.
It remains an open problem how biological neural networks can transition between these two phases, and what aspects of neural activity facilitate this transition [93]. We propose that transients and oscillations serve as alternating “phases” for inference and plasticity, where oscillations shift the circuit into a feedback-dominated mode and open the window for plasticity. While we focus our arguments on gamma oscillations during vision, we consider that beta oscillations may play a similar role in somatosensory processing [69].
During each stimulus presentation or eye-fixation, stimulus inference is completed in IT around 120-160ms [94]. Assuming a processing delay from IT to V1 of about 40 ms, the backward pass should arrive in V1 around 160-200 ms (i.e., towards the end of each eye fixation). During this late stimulus phase inter-areal interactions tend to be feedback rather than feedforward-dominated [95] and V1 gamma oscillations are most prominent [70]. As discussed above, gamma oscillations may dampen feedforward information flow (and thereby terminate the inference phase) by recruiting inhibitory activity in the feedforward direction. At the same time, gamma oscillations may play a role in feedback-related computations, mediated by two mechanisms:
-
1)
The feedback arriving during the backward pass needs to be integrated with activity patterns that occurred during the forward pass. Because the backward pass arrives with a large delay compared to the onset of the forward pass (Figure 3), the forward pass needs to leave a “trace”. Gamma could contribute to maintaining “traces” of the preceding transient activations, where the initial transient activation determines subsequent oscillatory wave patterns and the gamma-phase of spiking [87]. These traces can then interact with feedback signals arriving in the late stimulus phase to coordinate learning [86]. Theoretical studies suggest an advantage of oscillatory network activity for learning processes, as they mitigate both the vanishing and exploding gradient problem in recurrent neural networks [96].
-
2)
The synchronization of spiking activity can influence synaptic plasticity processes via spike-time-dependent-plasticity (STDP) mechanisms [97, 98, 99] (Figure 3). Experimental manipulations of rhythms suggest that gamma synchronization facilitates the formation of synaptic plasticity [100, 101, 99]. The precise pattern of synaptic weight changes is likely determined by the structure of the visual stimulus. The structure of the visual stimulus determines the strength of synchronization, as gamma-rhythmic synchronization occurs between neural populations that predict each other’s sensory inputs [47]. The stimulus structure also determines the phase of synchronization, because stimulus input drive is converted into a spike gamma-phase code [87]. The resulting temporal spiking patterns may recruit Hebbian mechanisms, such as STDP, which then interact with top-down learning signals to drive synaptic plasticity [86, 93].
The stochastic nature of gamma oscillations [92, 76] is compatible with a functional role in plasticity processes: First, because learning takes place on long time scales that encompass many stimulus presentations, averaging out the instantaneous fluctuations in gamma-cycle amplitude. Second, because learning algorithms require a certain degree of stochasticity. Stochasticity avoids overfitting and promotes generalization in training neural networks [102, 103]. Random sampling is also critical for the training of self-supervised algorithms like Variational Autoencoders that have an inherent probabilistic nature [81]. A recent study has shown that stochastic gamma-band oscillations are an emergent feature of E/I networks performing random sampling from a latent distribution [104].
Explaining gamma from Dendritic HPC models
We have presented several arguments against the theory that prediction errors are transmitted through gamma (30-80 Hz) oscillations, and prediction signals are transmitted through alpha/beta (10-20 Hz) oscillations. We propose that the emergence of narrow-band oscillations is well explained by dendritic HPC, a biologically realistic alternative to Classic HPC.
A key component of Dendritic HPC is the interaction between local excitatory/inhibitory (E/I) neurons [3]. The model builds on the observation that feedforward and feedback projections preferentially target basal and apical dendrites, respectively. Unlike Classic HPC, Dendritic HPC does not require specialized projection neurons for conveying feedforward error signals (ϵ), instead neurons transmit representations (r). Dendritic HPC attributes prediction error representation to voltage fluctuations in basal and apical dendrites, which are integrated at the soma and drive spiking (r) (Figure 2). At the basal dendrites, error terms result from local inhibition, which can predict and cancel out the feedforward (FF) inputs from the preceding hierarchical level (Figure 2).
The interaction between E/I neurons in Dendritic HPC model is consistent with the various conditions that are associated with prominent gamma oscillations. For instance, stimuli with high spatiotemporal predictability (e.g., surfaces of homogeneous objects) would give rise to a tight E/I balance and sparse spiking activity, which are factors associated with the emergence of gamma oscillations [23, 48, 47, 105, 106, 67, 71, 60].
In the gamma cycle, there is a substantial phase delay between balanced excitatory and inhibitory activity [107]. Such a delay between excitation and inhibition ensures that there is always some residual spiking activity [106, 60]. That is, the ”ground state” of a neural circuit in case of highly predictable stimuli may be sparse, oscillatory firing [48, 47], rather than vanishing feedforward prediction errors. Such residual firing may be important to sustain feedforward information transmission and support stimulus representations even in case of fully predictable stimuli.
Importantly, in Dendritic HPC, the E/I balance in a local circuit depends on the predictability of feedforward inputs that it receives (driving the basal prediction error), but not on the predictability of firing rate representations by top-down feedback (driving the apical prediction error; Figure 2). We therefore predict that gamma oscillations should be correlated with the predictability of feedforward inputs into a circuit. Indeed, it was recently shown that gamma oscillations in V1 are specifically (positively) correlated with the low-level predictability of sensory inputs [47], which was defined as the extent to which low-level image features can be predicted from the spatial context.
V1 firing rates, by contrast, show the strongest (negative) correlation with the predictability of high-level image features derived from neural networks for object recognition [47]. Consistently, various manipulations of object segmentation have been shown to affect V1 firing rates but not V1 gamma-synchronization [108, 109, 47]. In Dendritic HPC, the modulation of V1 activity by high-level predictability is mediated by top-down feedback arriving at the apical dendrites (Figure 2). This top-down feedback predicts local spiking activity, resulting in “apical” prediction errors that drive spiking and increased firing rates.
Concluding remarks
The dominant paradigm on oscillations is sender-focused, and portrays oscillations as causal entities, which have a functional impact on receiving areas [17]. We have instead adopted a receiver-focused perspective on oscillations, which describes oscillations in the receiver as the result of feedforward lower-level predictability. We have outlined a functional model in which rapid sensory inference is mediated by aperiodic transients, while oscillations contribute to local functions, in particular the stabilization of neural representations over time and space, as well as modulate plasticity processes.
Our discussion underscores the point that linear connectivity measures, such as Granger-causality, have limited use in studying inter-areal communication, because these measures are blind to non-linear interactions [72, 36, 34]. It is crucial to consider the non-linear and recurrent nature of stimulus inference processes [34]. Indeed, a recent study suggested that transients in lower and higher areas exhibit synergistic encoding of sensory prediction errors, reflecting such nonlinearities [110].
Causal perturbations are warranted to test the hypotheses presented here (see Outstanding Questions). For example, we hypothesize that perturbing activity during transients should have a strong impact on sensory inference, as shown by [111], while perturbation of gamma oscillations should specifically affect stabilizing neural representations over time and learning.
Outstanding Questions.
How does the dependence of oscillatory dynamics on predictability differ between different modalities (e.g., olfactory, auditory, visual) and frequency bands?
What determines the frequency of rhythms and their emergence in different networks, and to what extent are there shared mechanisms and functions between alpha, beta and gamma?
Do neural populations in visual cortex generate an intrinsic beta rhythm that is independent of the sensorimotor and frontal beta?
How does the phase locking strength of single cells vary across cortical layers, and differ between different cell types and projection neurons?
What is the functional impact of alpha and beta rhythms on spiking activity of distinct cell types and laminar compartments in receiving areas?
What are the precise circuit mechanisms, e.g., involving layers and cell types, accounting for the dependence of rhythms on temporal and spatial predictability?
Can the dendritic predictive coding model account for the emergence of rhythmic dynamics, and to what extent do aspects like recurrent excitation or resonance, which are lacking in this model, matter?
What are the respective contributions of horizontal and top-down feedback connections to the modulation of neural activity by predictability?
Do oscillatory dynamics causally contribute to the stabilization of neural representations?
Does gamma synchronization contribute causally to perception, e.g., to the stability of perception over time?
Can oscillations mediate a switch from feedforward to feedback-dominated communication between areas?
Do plasticity processes in the later phases of sensory processing causally depend on oscillations?
How do top-down learning signals precisely interact with local gamma-synchronization, and what is the role of burst spikes?
What are the distinct contributions of transients and oscillations to stimulus inference?
How do non-linear interactions measures depend on stimulus predictability, and how do these interactions differ between oscillations and transients?
To what extent do transients and oscillations provide synergistic and redundant information across cortical space?
Highlights.
We contrast the roles of two main types of neural dynamics, namely transients and oscillations, in predictive processing and sensory inference.
We propose that oscillations stabilize neural representations over time and facilitate plasticity processes during the late, feedback-dominated phase of sensory processing.
Oscillations emerge for sensory inputs with high spatio-temporal predictability, which fits better with Dendritic rather than Classic Hierarhical Predictive Coding principles.
Based on recent evidence we critically evaluate the theory that gamma and alpha/beta rhythms carry prediction error and prediction signals, respectively.
For instance, we argue that unpredicted stimuli enhanced broadband fluctuations and aperiodic transients, while predicted stimuli boost narrow-band gamma oscillations.
Finally, based on the speed of cortical processing, we argue that transient, non-oscillatory dynamics are the main conduit for inter-areal communication during sensory inference.
Acknowledgements
We thank Craig Richter, Conrado Bosman, and Wolf Singer for helpful comments on different versions of this manuscript. MV, CU and BR were supported by an ERC Starting Grant [SPATEMP, EU], a BMBF (Germany) Grant [Computational Life Sciences, project BINDA, 031L0167], DFG VI Grants (908/5-1 and 908/7-1), the NWO VIDI, and the Dutch Brain Interface Initiative. ACJ is supported by an ANID/FONDECYT Regular (1240899) research grant.
References
- [1].Friston K. The free-energy principle: a unified brain theory? Nature reviews neuroscience. 2010;11:127–138. doi: 10.1038/nrn2787. [DOI] [PubMed] [Google Scholar]
- [2].Rao RP, Ballard DH. Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat Neurosci. 1999;2:79–87. doi: 10.1038/4580. [DOI] [PubMed] [Google Scholar]
- [3].Mikulasch FA, Rudelt L, Wibral M, Priesemann V. Where is the error? hierarchical predictive coding through dendritic error computation. Trends in Neurosciences. 2023;46:45–59. doi: 10.1016/j.tins.2022.09.007. [DOI] [PubMed] [Google Scholar]
- [4].Singer W. Recurrent dynamics in the cerebral cortex: Integration of sensory evidence with stored knowledge. Proceedings of the National Academy of Sciences. 2021;118 doi: 10.1073/pnas.2101043118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Heeger DJ. Theory of cortical function. Proceedings of the National Academy of Sciences. 2017;114:1773–1782. doi: 10.1073/pnas.1619788114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Bosman CA, Lansink CS, Pennartz C. Functions of gamma-band synchronization in cognition: from single circuits to functional diversity across cortical and subcortical systems. Eur J Neurosci. 2014;39:1982–1999. doi: 10.1111/ejn.12606. [DOI] [PubMed] [Google Scholar]
- [7].Vinck M, Womelsdorf T, Fries P. In: Principles of Neural Coding. Quiroga-Quian R, Panzeri S, editors. CRC Press; 2013. Gamma-band synchronization and information transmission; p. 449. [Google Scholar]
- [8].Bastos AM, Usrey WM, Adams RA, Mangun GR, Fries P, Friston KJ. Canonical microcircuits for predictive coding. Neuron. 2012;76:695–711. doi: 10.1016/j.neuron.2012.10.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Arnal LH, Giraud AL. Cortical oscillations and sensory predictions. Trends Cogn Sci. 2012;16:390–398. doi: 10.1016/j.tics.2012.05.003. [DOI] [PubMed] [Google Scholar]
- [10].Bastos AM, Vezoli J, Bosman CA, Schoffelen J-M, Oostenveld R, Dowdall JR, De Weerd P, Kennedy H, Fries P. Visual areas exert feedforward and feedback influences through distinct frequency channels. Neuron. 2015;85:390–401. doi: 10.1016/j.neuron.2014.12.018. [DOI] [PubMed] [Google Scholar]
- [11].Chao ZC, Takaura K, Wang L, Fujii N, Dehaene S. Large-scale cortical networks for hierarchical prediction and prediction error in the primate brain. Neuron. 2018;100:1252–1266. doi: 10.1016/j.neuron.2018.10.004. [DOI] [PubMed] [Google Scholar]
- [12].van Kerkoerle T, Self MW, Dagnino B, Gariel-Mathis M-A, Poort J, van der Togt C, Roelfsema PR. Alpha and gamma oscillations characterize feedback and feedforward processing in monkey visual cortex. Proc Natl Acad Sci USA. 2014:201402773. doi: 10.1073/pnas.1402773111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Richter CG, Thompson WH, Bosman CA, Fries P. Top-down beta enhances bottom-up gamma. Journal of Neuroscience. 2017;37:6698–6711. doi: 10.1523/JNEUROSCI.3771-16.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Vezoli J, Vinck M, Bosman CA, Bastos AM, Lewis CM, Kennedy H, Fries P. Brain rhythms define distinct interaction networks with differential dependence on anatomy. Neuron. 2021;109:3862–3878. doi: 10.1016/j.neuron.2021.09.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Nougaret S, López-Galdo L, Caytan E, Poitreau J, Barthélemy FV, Kilavik BE. Low and high beta rhythms have different motor cortical sources and distinct roles in movement control and spatiotemporal attention. PLoS Biology. 2024;22:e3002670. doi: 10.1371/journal.pbio.3002670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Mendoza-Halliday D, Major AJ, Lee N, Lichtenfeld M, Carlson B, Mitchell B, Meng PD, Xiong YS, Westerberg JA, Maier A, et al. A ubiquitous spectrolaminar motif of local field potential power across the primate cortex. Nature Neuroscience. 2024 doi: 10.1038/s41593-023-01554-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Fries P. Rhythms for cognition: communication through coherence. Neuron. 2015;88:220–235. doi: 10.1016/j.neuron.2015.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Michalareas G, Vezoli J, Van Pelt S, Schoffelen J-M, Kennedy H, Fries P. Alpha-beta and gamma rhythms subserve feedback and feedforward influences among human visual cortical areas. Neuron. 2016;89:384–397. doi: 10.1016/j.neuron.2015.12.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Ray S, Maunsell JH. Different origins of gamma rhythm and high-gamma activity in macaque visual cortex. PLOS Biol. 2011;9:e1000610. doi: 10.1371/journal.pbio.1000610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Parto-Dezfouli M, Vezoli J, Bosman CA, Fries P. Enhanced behavioral performance through interareal gamma and beta synchronization. Cell reports. 2023;42 doi: 10.1016/j.celrep.2023.113249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Hoffman SJ, Dotson NM, Lima V, Gray CM. The primate cortical lfp exhibits multiple spectral and temporal gradients and widespread task-dependence during visual short-term memory. Journal of Neurophysiology. 2024 doi: 10.1152/jn.00264.2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Spyropoulos G, Schneider M, van Kempen J, Gieselmann MA, Thiele A, Vinck M. Distinct feedforward and feedback pathways for cell-type specific attention effects. Neuron. 2024 doi: 10.1016/j.neuron.2024.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Vinck M, Bosman CA. More gamma more predictions: Gamma-synchronization as a key mechanism for efficient integration of classical receptive field inputs with surround predictions. Front Syst Neurosci. 2016;10:35. doi: 10.3389/fnsys.2016.00035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Onorato I, Neuenschwander S, Hoy J, Lima B, Rocha K-S, Broggini AC, Uran C, Spyropoulos G, Klon-Lipok J, Womelsdorf T, Fries P, et al. A distinct class of bursting neurons with strong gamma synchronization and stimulus selectivity in monkey V1. Neuron. 2020;105:180–197. doi: 10.1016/j.neuron.2019.09.039. [DOI] [PubMed] [Google Scholar]
- [25].Brovelli A, Ding M, Ledberg A, Chen Y, Nakamura R, Bressler SL. Beta oscillations in a large-scale sensorimotor cortical network: directional influences revealed by granger causality. Proc Natl Acad Sci USA. 2004;101:9849–9854. doi: 10.1073/pnas.0308538101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Salazar R, Dotson N, Bressler S, Gray C. Content-specific fronto-parietal synchronization during visual working memory. Science. 2012;338:1097–1100. doi: 10.1126/science.1224000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Kilavik BE, Zaepffel M, Brovelli A, MacKay WA, Riehle A. The ups and downs of beta oscillations in sensorimotor cortex. Experimental neurology. 2013;245:15–26. doi: 10.1016/j.expneurol.2012.09.014. [DOI] [PubMed] [Google Scholar]
- [28].Brunet N, Vinck M, Bosman CA, Singer W, Fries P. Gamma or no gamma, that is the question. Trends Cogn Sci. 2014;18:507–509. doi: 10.1016/j.tics.2014.08.006. [DOI] [PubMed] [Google Scholar]
- [29].Schneider M, Broggini AC, Dann B, Tzanou A, Uran C, Sheshadri S, Scherberger H, Vinck M. A mechanism for inter-areal coherence through communication based on connectivity and oscillatory power. Neuron. 2021;109:4050–4067. doi: 10.1016/j.neuron.2021.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Pesaran B, Vinck M, Einevoll G, Sirota A, Fries P, Siegel M, Truccolo W, Schroeder C, Srinivasan R. Investigating large-scale brain dynamics using field potential recordings: analysis and interpretation. Nat Neurosci. 2018 doi: 10.1038/s41593-018-0171-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Vinck M, Bos JJ, Mourik-Donga V, Laura A, Oplaat KT, Klein GA, Jackson JC, Gentet LJ, Pennartz C. Cell-type and state-dependent synchronization among rodent somatosensory, visual, perirhinal cortex, and hippocampus CA1. Frontiers in systems neuroscience. 2016;9:187. doi: 10.3389/fnsys.2015.00187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Buffalo EA, Fries P, Landman R, Buschman TJ, Desimone R. Laminar differences in gamma and alpha coherence in the ventral stream. Proc Natl Acad Sci USA. 2011;108:11262–11267. doi: 10.1073/pnas.1011284108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Vezoli J, Magrou L, Goebel R, Wang X-J, Knoblauch K, Vinck M, Kennedy H. Cortical hierarchy, dual counterstream architecture and the importance of top-down generative networks. Neuroimage. 2021;225:117479. doi: 10.1016/j.neuroimage.2020.117479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Vinck M, Uran C, Spyropoulos G, Onorato I, Broggini AC, Schneider M, Canales-Johnson A. Principles of large-scale neural interactions. Neuron. 2023;111:987–1002. doi: 10.1016/j.neuron.2023.03.015. [DOI] [PubMed] [Google Scholar]
- [35].Dowdall JR, Schneider M, Vinck M. Attentional modulation of inter-areal coherence explained by frequency shifts. NeuroImage. 2023;277:120256. doi: 10.1016/j.neuroimage.2023.120256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Dowdall JR, Vinck M. Coherence fails to reliably capture inter-areal interactions in bidirectional neural systems with transmission delays. NeuroImage. 2023;271:119998. doi: 10.1016/j.neuroimage.2023.119998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Salinas E, Sejnowski TJ. Correlated neuronal activity and the flow of neural information. Nat Rev Neurosci. 2001;2:539–50. doi: 10.1038/35086012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Fries P, Reynolds JH, Rorie AE, Desimone R. Modulation of oscillatory neuronal synchronization by selective visual attention. Science. 2001;291:1560–1563. doi: 10.1126/science.1055465. [DOI] [PubMed] [Google Scholar]
- [39].Izhikevich EM, Desai NS, Walcott EC, Hoppensteadt FC. Bursts as a unit of neural information: selective communication via resonance. Trends in neurosciences. 2003;26:161–167. doi: 10.1016/S0166-2236(03)00034-1. [DOI] [PubMed] [Google Scholar]
- [40].Schneider M, Tzanou A, Uran C, Vinck M. Cell-type-specific propagation of visual flicker. Cell Rep. 2023;42:112492. doi: 10.1016/j.celrep.2023.112492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Bosman C, Schoffelen J, Brunet N, Oostenveld R, Bastos A, Womelsdorf T, Rubehn B, Stieglitz T, De Weerd P, Fries P. Attentional stimulus selection through selective synchronization between monkey visual areas. Neuron. 2012;75:875–888. doi: 10.1016/j.neuron.2012.06.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Schomburg EW, Fernández-Ruiz A, Mizuseki K, Berényi A, Anastassiou CA, Koch C, Buzsáki G. Theta phase segregation of input-specific gamma patterns in entorhinal-hippocampal networks. Neuron. 2014;84:470–485. doi: 10.1016/j.neuron.2014.08.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Lindén H, Pettersen KH, Einevoll GT. Intrinsic dendritic filtering gives low-pass power spectra of local field potentials. Journal of computational neuroscience. 2010;29:423–444. doi: 10.1007/s10827-010-0245-4. [DOI] [PubMed] [Google Scholar]
- [44].Vaidya SP, Johnston D. Temporal synchrony and gamma-to-theta power conversion in the dendrites of ca1 pyramidal neurons. Nature neuroscience. 2013;16:1812–1820. doi: 10.1038/nn.3562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Bastos AM, Lundqvist M, Waite AS, Kopell N, Miller EK. Layer and rhythm specificity for predictive routing. Proceedings of the National Academy of Sciences. 2020;117:31459–31469. doi: 10.1073/pnas.2014868117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Bauer M, Stenner M-P, Friston KJ, Dolan RJ. Attentional modulation of alpha/beta and gamma oscillations reflect functionally distinct processes. Journal of Neuroscience. 2014;34:16117–16125. doi: 10.1523/JNEUROSCI.3474-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Uran C, Peter A, Lazar A, Barnes W, Klon-Lipok J, Shapcott KA, Roese R, Fries P, Singer W, Vinck M. Predictive coding of natural images by v1 firing rates and rhythmic synchronization. Neuron. 2022;110:1240–1257. doi: 10.1016/j.neuron.2022.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Peter A, Uran C, Klon-Lipok J, Roese R, Van Stijn S, Barnes W, Dowdall JR, Singer W, Fries P, Vinck M. Surface color and predictability determine contextual modulation of V1 firing and gamma oscillations. eLife. 2019;8:e42101. doi: 10.7554/eLife.42101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Shirhatti V, Ravishankar P, Ray S. Gamma oscillations in primate primary visual cortex are severely attenuated by small stimulus discontinuities. PLoS biology. 2022;20:e3001666. doi: 10.1371/journal.pbio.3001666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Miller KJ, Sorensen LB, Ojemann JG, Den Nijs M. Power-law scaling in the brain surface electric potential. PLoS computational biology. 2009;5:e1000609. doi: 10.1371/journal.pcbi.1000609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Jiang Y, Komatsu M, Chen Y, Xie R, Zhang K, Xia Y, Gui P, Liang Z, Wang L. Constructing the hierarchy of predictive auditory sequences in the marmoset brain. Elife. 2022;11:e74653. doi: 10.7554/eLife.74653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Todorovic A, van Ede F, Maris E, de Lange FP. Prior Expectation Mediates Neural Adaptation to Repeated Sounds in the Auditory Cortex: An MEG Study. J Neurosci. 2011;31:9118–9123. doi: 10.1523/JNEUROSCI.1425-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Canales-Johnson A, Borges AFT, Komatsu M, Fujii N, Fahrenfort JJ, Miller KJ, Noreika V. Broadband dynamics rather than frequency-specific rhythms underlie prediction error in the primate auditory cortex. Journal of Neuroscience. 2021;41:9374–9391. doi: 10.1523/JNEUROSCI.0367-21.2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Parras GG, Nieto-Diego J, Carbajal GV, Valdés-Baizabal C, Escera C, Malmierca MS. Neurons along the auditory pathway exhibit a hierarchical organization of prediction error. Nature communications. 2017;8:1–17. doi: 10.1038/s41467-017-02038-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Hermes D, Petridou N, Kay KN, Winawer J. An image-computable model for the stimulus selectivity of gamma oscillations. Elife. 2019;8:e47035. doi: 10.7554/eLife.47035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Kruse W, Eckhorn R. Inhibition of sustained gamma oscillations (35-80 Hz) by fast transient responses in cat visual cortex. Proc Natl Acad Sci USA. 1996;93:6112–6117. doi: 10.1073/pnas.93.12.6112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Kayser C, Salazar RF, Konig P. Responses to natural scenes in cat V1. J Neurophysiol. 2003;90:1910–20. doi: 10.1152/jn.00195.2003. [DOI] [PubMed] [Google Scholar]
- [58].Brunet NM, Bosman CA, Vinck M, Roberts M, Oostenveld R, Desimone R, De Weerd P, Fries P. Stimulus repetition modulates gamma-band synchronization in primate visual cortex. Proc Natl Acad Sci USA. 2014;111:3626–3631. doi: 10.1073/pnas.1309714111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Peter A, Stauch BJ, Shapcott K, Kouroupaki K, Schmiedt JT, Klein L, Klon-Lipok J, Dowdall JR, Schölvinck ML, Vinck M, et al. Stimulus-specific plasticity of macaque v1 spike rates and gamma. Cell reports. 2021;37:110086. doi: 10.1016/j.celrep.2021.110086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Vinck M, Womelsdorf T, Buffalo EA, Desimone R, Fries P. Attentional Modulation of Cell-Class-Specific Gamma-Band Synchronization in Awake Monkey Area V4. Neuron. 2013;80:1077–1089. doi: 10.1016/j.neuron.2013.08.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Chalk M, Herrero JL, Gieselmann MA, Delicato LS, Gotthardt S, Thiele A. Attention reduces stimulus-driven gamma frequency oscillations and spike field coherence in V1. Neuron. 2010;66:114–25. doi: 10.1016/j.neuron.2010.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Das A, Ray S. Effect of stimulus contrast and visual attention on spike-gamma phase relationship in macaque primary visual cortex. Frontiers in computational neuroscience. 2018;12:66. doi: 10.3389/fncom.2018.00066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Von Stein A, Chiang C, König P. Top-down processing mediated by interareal synchronization. Proceedings of the National Academy of Sciences. 2000;97:14748–14753. doi: 10.1073/pnas.97.26.14748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Popov T, Miller GA, Rockstroh B, Jensen O, Langer N. Alpha oscillations link action to cognition: An oculomotor account of the brain’s dominant rhythm. bioRxiv. 2021 [Google Scholar]
- [65].Alamia A, VanRullen R. Alpha oscillations and traveling waves: Signatures of predictive coding? PLoS Biology. 2019;17:e3000487. doi: 10.1371/journal.pbio.3000487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Murray JD, Bernacchia A, Freedman DJ, Romo R, Wallis JD, Cai X, Padoa-Schioppa C, Pasternak T, Seo H, Lee D, et al. A hierarchy of intrinsic timescales across primate cortex. Nature neuroscience. 2014;17:1661. doi: 10.1038/nn.3862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Wang XJ. Neurophysiological and computational principles of cortical rhythms in cognition. Physiol Rev. 2010;90:1195–1268. doi: 10.1152/physrev.00035.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Roberts MJ, Lowet E, Brunet NM, Ter Wal M, Tiesinga P, Fries P, De Weerd P. Robust gamma coherence between macaque V1 and V2 by dynamic frequency matching. Neuron. 2013;78:523–536. doi: 10.1016/j.neuron.2013.03.003. [DOI] [PubMed] [Google Scholar]
- [69].Confais J, Malfait N, Brochier T, Riehle A, Kilavik BE. Is there an intrinsic relationship between lfp beta oscillation amplitude and firing rate of individual neurons in macaque motor cortex? Cerebral Cortex Communications. 2020;1:tgaa017. doi: 10.1093/texcom/tgaa017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Gieselmann MA, Thiele A. Comparison of spatial integration and surround suppression characteristics in spiking activity and the local field potential in macaque V1. Eur J Neurosci. 2008;28:447–459. doi: 10.1111/j.1460-9568.2008.06358.x. [DOI] [PubMed] [Google Scholar]
- [71].Ray S, Maunsell JH. Do gamma oscillations play a role in cerebral cortex? Trends in cognitive sciences. 2015;19:78–85. doi: 10.1016/j.tics.2014.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].DiCarlo JJ, Zoccolan D, Rust NC. How does the brain solve visual object recognition? Neuron. 2012;73:415–434. doi: 10.1016/j.neuron.2012.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Yamins DL, Hong H, Cadieu CF, Solomon EA, Seibert D, DiCarlo JJ. Performance-optimized hierarchical models predict neural responses in higher visual cortex. Proceedings of the national academy of sciences. 2014;111:8619–8624. doi: 10.1073/pnas.1403112111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74].Thorpe S, Delorme A, Van Rullen R. Spike-based strategies for rapid processing. Neural Netw. 2001;14:715–725. doi: 10.1016/s0893-6080(01)00083-1. [DOI] [PubMed] [Google Scholar]
- [75].Murphy BK, Miller KD. Balanced Amplification: A New Mechanism of Selective Amplification of Neural Activity Patterns. Neuron. 2009;61:635–648. doi: 10.1016/j.neuron.2009.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Spyropoulos G, Saponati M, Dowdall JR, Schölvinck ML, Bosman CA, Lima B, Peter A, Onorato I, Klon-Lipok J, Roese R, Neuenschwander S, et al. Spontaneous variability in gamma dynamics described by a damped harmonic oscillator driven by noise. Nature communications. 2022;13:1–18. doi: 10.1038/s41467-022-29674-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].van Vreeswijk C, Sompolinsky H. Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science. 1996;274:1724–1726. doi: 10.1126/science.274.5293.1724. [DOI] [PubMed] [Google Scholar]
- [78].Bruno RM, Sakmann B. Cortex is driven by weak but synchronously active thalamocortical synapses. Science. 2006;312:1622–7. doi: 10.1126/science.1124593. [DOI] [PubMed] [Google Scholar]
- [79].Yiling Y, Shapcott K, Peter A, Klon-Lipok J, Xuhui H, Lazar A, Singer W. Robust encoding of natural stimuli by neuronal response sequences in monkey visual cortex. Nature Communications. 2023;14:3021. doi: 10.1038/s41467-023-38587-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [80].Bogacz R. A tutorial on the free-energy framework for modelling perception and learning. Journal of mathematical psychology. 2017;76:198–211. doi: 10.1016/j.jmp.2015.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [81].Kingma DP, Mohamed S, Jimenez Rezende D, Welling M. Semi-supervised learning with deep generative models. Advances in neural information processing systems. 2014;27 [Google Scholar]
- [82].Park IM, Ságodi Á, Sokół PA. Persistent learning signals and working memory without continuous attractors. arXiv preprint. 2023:arXiv:2308.12585 [Google Scholar]
- [83].Wallace E, Benayoun M, Van Drongelen W, Cowan JD. Emergent oscillations in networks of stochastic spiking neurons. Plos one. 2011;6:e14804. doi: 10.1371/journal.pone.0014804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [84].Gelastopoulos A, Whittington MA, Kopell NJ. Parietal low beta rhythm provides a dynamical substrate for a working memory buffer. Proceedings of the National Academy of Sciences. 2019;116:16613–16620. doi: 10.1073/pnas.1902305116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85].Engel AK, Fries P. Beta-band oscillations—signalling the status quo? Current opinion in neurobiology. 2010;20:156–165. doi: 10.1016/j.conb.2010.02.015. [DOI] [PubMed] [Google Scholar]
- [86].Bellec G, Scherr F, Subramoney A, Hajek E, Salaj D, Legenstein R, Maass W. A solution to the learning dilemma for recurrent networks of spiking neurons. bioRxiv. 2020:738385. doi: 10.1038/s41467-020-17236-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [87].Vinck M, Lima B, Womelsdorf T, Oostenveld R, Singer W, Neuenschwander S, Fries P. Gamma-phase shifting in awake monkey visual cortex. J Neurosci. 2010;30:1250–1257. doi: 10.1523/JNEUROSCI.1623-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [88].Chalk M, Gutkin B, Denève S. Neural oscillations as a signature of efficient coding in the presence of synaptic delays. eLife. 2016;5 doi: 10.7554/eLife.13824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [89].Womelsdorf T, Lima B, Vinck M, Oostenveld R, Singer W, Neuenschwander S, Fries P. Orientation selectivity and noise correlation in awake monkey area V1 are modulated by the gamma cycle. Proc Natl Acad Sci USA. 2012;109:4302–4307. doi: 10.1073/pnas.1114223109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [90].Renart A, de la Rocha J, Bartho P, Hollender L, Parga N, Reyes A, Harris KD. The asynchronous state in cortical circuits. Science. 2010;327:587–590. doi: 10.1126/science.1179850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [91].Hamilton LS, Sohl-Dickstein J, Huth AG, Carels VM, Deisseroth K, Bao S. Optogenetic Activation of an Inhibitory Network Enhances Feedforward Functional Connectivity in Auditory Cortex. Neuron. 2013;80:1066–1076. doi: 10.1016/j.neuron.2013.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [92].Burns SP, Xing D, Shapley RM. Is gamma-band activity in the local field potential of V1 cortex a ”clock” or filtered noise? J Neurosci. 2011;31:9658–9664. doi: 10.1523/JNEUROSCI.0660-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [93].Payeur A, Guerguiev J, Zenke F, Richards BA, Naud R. Burst-dependent synaptic plasticity can coordinate learning in hierarchical circuits. Nature neuroscience. 2021;24:1010–1019. doi: 10.1038/s41593-021-00857-x. [DOI] [PubMed] [Google Scholar]
- [94].Kar K, Kubilius J, Schmidt K, Issa EB, DiCarlo JJ. Evidence that recurrent circuits are critical to the ventral stream’s execution of core object recognition behavior. Nature neuroscience. 2019;22:974–983. doi: 10.1038/s41593-019-0392-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [95].Semedo JD, Jasper AI, Zandvakili A, Krishna A, Aschner A, Machens CK, Kohn A, Yu BM. Feedforward and feedback interactions between visual cortical areas use different population activity patterns. Nature communications. 2022;13:1099. doi: 10.1038/s41467-022-28552-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [96].Rusch TK, Mishra S. Coupled oscillatory recurrent neural network (cornn): An accurate and (gradient) stable architecture for learning long time dependencies. arXiv preprint. 2020:arXiv:2010.00951 [Google Scholar]
- [97].Chrobak JJ, Buzsáki G. Operational dynamics in the hippocampal-entorhinal axis. Neuroscience & Biobehavioral Reviews. 1998;22:303–310. doi: 10.1016/s0149-7634(97)00016-x. [DOI] [PubMed] [Google Scholar]
- [98].Traub RD, Spruston N, Soltesz I, Konnerth A, Whittington MA, Jefferys JG. Gamma-frequency oscillations: a neuronal population phenomenon, regulated by synaptic and intrinsic cellular processes, and inducing synaptic plasticity. Progress in neurobiology. 1998;55:563–575. doi: 10.1016/s0301-0082(98)00020-3. [DOI] [PubMed] [Google Scholar]
- [99].Anisimova M, van Bommel B, Wang R, Mikhaylova M, Wiegert JS, Oertner TG, Gee CE. Spike-timing-dependent plasticity rewards synchrony rather than causality. Cerebral Cortex. 2023;33:23–34. doi: 10.1093/cercor/bhac050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [100].Galuske RA, Munk MH, Singer W. Relation between gamma oscillations and neuronal plasticity in the visual cortex. Proceedings of the National Academy of Sciences. 2019;116:23317–23325. doi: 10.1073/pnas.1901277116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [101].Wespatat V, Tennigkeit F, Singer W. Phase sensitivity of synaptic modifications in oscillating cells of rat visual cortex. Journal of Neuroscience. 2004;24:9067–9075. doi: 10.1523/JNEUROSCI.2221-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [102].Kingma DP, Ba J. Adam: A method for stochastic optimization. arXiv preprint. 2014:arXiv:1412.6980 [Google Scholar]
- [103].Schug S, Benzing F, Steger A. Presynaptic stochasticity improves energy efficiency and helps alleviate the stability-plasticity dilemma. Elife. 2021;10:e69884. doi: 10.7554/eLife.69884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [104].Echeveste R, Aitchison L, Hennequin G, Lengyel M. Cortical-like dynamics in recurrent circuits optimized for sampling-based probabilistic inference. Nature Neuroscience. 2020;23:1138–1149. doi: 10.1038/s41593-020-0671-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [105].Börgers C, Kopell NJ. Gamma oscillations and stimulus selection. Neural Comput. 2008;20:383–414. doi: 10.1162/neco.2007.07-06-289. [DOI] [PubMed] [Google Scholar]
- [106].Denève S, Machens CK. Efficient codes and balanced networks. Nature neuroscience. 2016;19:375–382. doi: 10.1038/nn.4243. [DOI] [PubMed] [Google Scholar]
- [107].Vinck M, Womelsdorf T, Buffalo EA, Desimone R, Fries P. Attentional modulation of cell-class-specific gamma-band synchronization in awake monkey area V4. Neuron. 2013;80:1077–1089. doi: 10.1016/j.neuron.2013.08.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [108].Chen G, Zhang Y, Li X, Zhao X, Ye Q, Lin Y, Tao HW, Rasch MJ, Zhang X. Distinct inhibitory circuits orchestrate cortical beta and gamma band oscillations. Neuron. 2017;96:1403–1418. doi: 10.1016/j.neuron.2017.11.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [109].Roelfsema PR, Lamme VA, Spekreijse H. Synchrony and covariation of firing rates in the primary visual cortex during contour grouping. Nat Neurosci. 2004;7:982–991. doi: 10.1038/nn1304. [DOI] [PubMed] [Google Scholar]
- [110].Gelens F, Äijälä J, Roberts L, Komatsu M, Uran C, Jensen MA, Miller KJ, Ince RAA, Garagnani M, Vinck M, Canales-Johnson A. Distributed representations of prediction error signals across the cortical hierarchy are synergistic. Nature Communications. 2024;15 doi: 10.1038/s41467-024-48329-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [111].Resulaj A, Ruediger S, Olsen SR, Scanziani M. First spikes in visual cortex enable perceptual discrimination. Elife. 2018;7:e34044. doi: 10.7554/eLife.34044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [112].Mackey C, Neymotin SA, Dura-Bernal S, Haegens S, Jones SR, Ding M, Schroeder CE. A ubiquitous spectrolaminar motif of local field potential power across the primate cortex? OSF Preprints. 2024 doi: 10.1038/s41593-023-01554-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [113].Gieselmann MA, Thiele A. Stimulus dependence of directed information exchange between cortical layers in macaque v1. Elife. 2022;11:e62949. doi: 10.7554/eLife.62949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [114].Xing D, Yeh C-I, Burns S, Shapley RM. Laminar analysis of visually evoked activity in the primary visual cortex. Proc Natl Acad Sci USA. 2012;109:13871–13876. doi: 10.1073/pnas.1201478109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [115].Livingstone MS. Oscillatory firing and interneuronal correlations in squirrel monkey striate cortex. J Neurophysiol. 1996;75:2467–2485. doi: 10.1152/jn.1996.75.6.2467. [DOI] [PubMed] [Google Scholar]
- [116].Kajikawa Y, Schroeder CE. Generation of field potentials and modulation of their dynamics through volume integration of cortical activity. Journal of neurophysiology. 2015;113:339–351. doi: 10.1152/jn.00914.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [117].Bollimunta A, Chen Y, Schroeder CE, Ding M. Neuronal Mechanisms of Cortical Alpha Oscillations in Awake-Behaving Macaques. J Neurosci. 2008;28:9976–9988. doi: 10.1523/JNEUROSCI.2699-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [118].Halgren M, Ulbert I, Bastuji H, Fabó D, Erőss L, Rey M, Devinsky O, Doyle WK, Mak-McCully R, Halgren E, et al. The generation and propagation of the human alpha rhythm. Proceedings of the National Academy of Sciences. 2019;116:23772–23782. doi: 10.1073/pnas.1913092116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [119].Haegens S, Barczak A, Musacchia G, Lipton ML, Mehta AD, Lakatos P, Schroeder CE. Laminar profile and physiology of the α rhythm in primary visual, auditory, and somatosensory regions of neocortex. Journal of Neuroscience. 2015;35:14341–14352. doi: 10.1523/JNEUROSCI.0600-15.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [120].Vinck M, Uran C, Canales-Johnson A. The neural dynamics of feedforward and feedback interactions in predictive processing. PsyArXiv. 2022 [Google Scholar]
- [121].Witham CL, Baker SN. Coding of digit displacement by cell spiking and network oscillations in the monkey sensorimotor cortex. Journal of Neurophysiology. 2012;108:3342–3352. doi: 10.1152/jn.00462.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [122].Watanabe H, Sato M-a, Suzuki T, Nambu A, Nishimura Y, Kawato M, Isa T. Reconstruction of movement-related intracortical activity from micro-electrocorticogram array signals in monkey primary motor cortex. Journal of neural engineering. 2012;9:036006. doi: 10.1088/1741-2560/9/3/036006. [DOI] [PubMed] [Google Scholar]
- [123].Sherman MA, Lee S, Law R, Haegens S, Thorn CA, Hämäläinen MS, Moore CI, Jones SR. Neural mechanisms of transient neocortical beta rhythms: Converging evidence from humans, computational modeling, monkeys, and mice. Proceedings of the National Academy of Sciences. 2016;113:E4885–E4894. doi: 10.1073/pnas.1604135113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [124].Bauer M, Oostenveld R, Peeters M, Fries P. Tactile spatial attention enhances gamma-band activity in somatosensory cortex and reduces low-frequency activity in parieto-occipital areas. J Neurosci. 2006;26:490–501. doi: 10.1523/JNEUROSCI.5228-04.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [125].Schoffelen JM, Oostenveld R, Fries P. Neuronal coherence as a mechanism of effective corticospinal interaction. Science. 2005;308:111–113. doi: 10.1126/science.1107027. [DOI] [PubMed] [Google Scholar]
- [126].Ray S, Hsiao SS, Crone NE, Franaszczuk PJ, Niebur E. Effect of stimulus intensity on the spike-local field potential relationship in the secondary somatosensory cortex. J Neurosci. 2008;28:7334–7343. doi: 10.1523/JNEUROSCI.1588-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [127].Haegens S, Nácher V, Hernández A, Luna R, Jensen O, Romo R. Beta oscillations in the monkey sensorimotor network reflect somatosensory decision making. Proc Natl Acad Sci U S A. 2011;108:10708–10713. doi: 10.1073/pnas.1107297108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [128].Miller K, Zanos S, Fetz E, Den Nijs M, Ojemann J. Decoupling the cortical power spectrum reveals real-time representation of individual finger movements in humans. J Neurosci. 2009;29:3132–3137. doi: 10.1523/JNEUROSCI.5506-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [129].Jensen MA, Huang H, Valencia GO, Klassen BT, van den Boom MA, Kaufmann TJ, Schalk G, Brunner P, Worrell GA, Hermes D, Miller KJ. A motor association area in the depths of the central sulcus. Nat Neurosci. 2023;26:1165–1169. doi: 10.1038/s41593-023-01346-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [130].Ryun S, Kim JS, Lee H, Chung CK. Tactile frequency-specific high-gamma activities in human primary and secondary somatosensory cortices. Sci Rep. 2017;7 doi: 10.1038/s41598-017-15767-x. [DOI] [PMC free article] [PubMed] [Google Scholar]