Modelling Face Memory Reveals Task-Generalizable Representations

Abstract

Current cognitive theories are cast in terms of information processing mechanisms that use mental representations [1–4]. For example, people use their mental representations to identify familiar faces under various conditions of pose, illumination and ageing, or to draw resemblance between family members. Yet, the actual information contents of these representations are rarely characterized, which hinders knowledge of the mechanisms that use them. Here, we modelled the 3D representational contents of 4 faces that were familiar to 14 participants as work colleagues. The representational contents were created by reverse correlating identity information generated on each trial with judgments of the face’s similarity to the individual participant’s memory of this face. In a second study, testing new participants, we demonstrated the validity of the modelled contents using everyday face tasks that generalize identity judgments to new viewpoints, age and sex. Our work highlights that such models of mental representations are critical to understanding generalization behavior and its underlying information processing mechanisms.

The cognitive mechanism of recognition is guided by mental representations that are stored in memory [1–4]. Personal familiarity with faces (e.g. as family members, friends or work colleagues) provides a compelling everyday illustration because the information contents representing familiar faces in memory must be sufficiently detailed to enable accurate recognition (i.e. identifying ‘Mary’ amongst other people) and sufficiently versatile to enable recognition across diverse common tasks—e.g. identifying Mary in different poses, at different ages or identifying her brother based on family resemblance [5–7]. And yet, it remains a fundamental challenge to reverse engineer the participant’s memory to model and thereby understand the detailed contents of their representations of familiar faces. This challenge is a cornerstone to understand the brain mechanisms of face identification, because they process the contents to predict the appearance of the familiar face of ‘Mary’ in the visual array and to selectively extract its identity information to generalize behavior across common tasks.

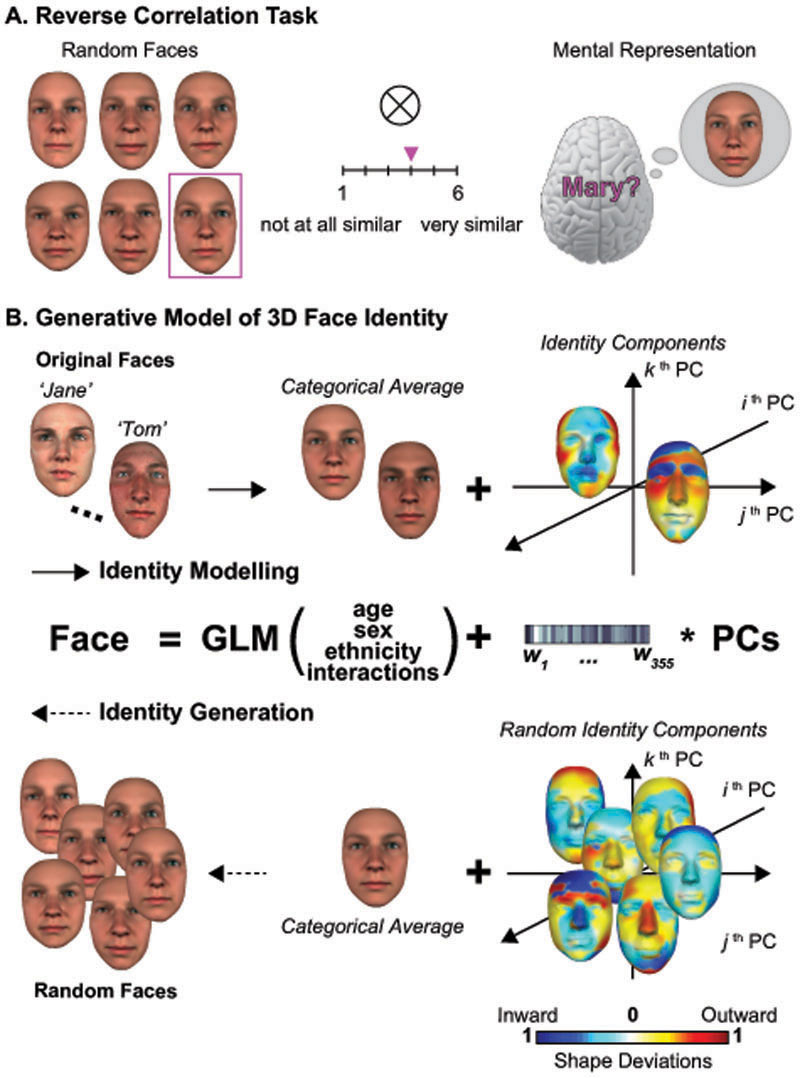
We studied how our own work colleagues recognize the faces of other colleagues from memory. The work environment provides a naturally occurring and common medium of social interactions for all participants, who had at a minimum six months of exposure with the people whose faces the study tested. To model the 3D face identity information stored in their memory, we developed a methodology based on reverse correlation (see Figure 1A, and Methods, Reverse Correlation Experiment) and a new Generative Model of 3D Face Identity (i.e. GMF, see Figure 1B, and Methods, Generative Model of Face Identity), separately for 3D shape and 2D texture information (see Supplementary Figure 1A for 3D face parameters).

Figure 1. Reverse correlating mental representations of familiar faces.

(A) Task. Illustrative experimental trial with 6 randomly generated face identities. We instructed participants to use their memory to select the face most similar to a familiar identity (here, ‘Mary’) and then to rate the similarity of the selected face (purple frame) to their memory of ‘Mary’ (purple pointer). (B) Generative Model of 3D face identity (GMF). In its forward computation flow (see identity modelling solid arrow), the General Linear Model (GLM) decomposes a 3D, textured face (e.g. ‘Jane’ or ‘Tom’) into a non-identity face shape average capturing the categorical factors of face sex, ethnicity, age and their interactions plus a separate component that defines the identity of the face (illustrated by the 3D shape decomposition; 2D texture, not illustrated, is independently and similarly decomposed). Heat maps indicate the 3D shape deviations that define ‘Jane’ and ‘Tom’ in the GMF in relation to their categorical averages. In the reverse flow (see dashed arrow of identity generation), we can randomize the 3D shape identity component (and 2D texture component, not illustrated here), add the categorical average of ‘Jane’ (or ‘Tom’) and generate random faces, each with a unique identity that share all other categorical face information with ‘Jane’ and ‘Tom.’

On each experimental trial, our GMF synthesized a set of 6 new 3D faces (see Random Faces in Figure 1A), each with a unique and randomly generated identity. Critically, each face shared other categorical face information (i.e. sex, age and ethnicity) with one of the four faces that were personally familiar to each one of our 14 participants as work colleagues—e.g. the familiar target face of ‘Mary’. To achieve this, we used a General Linear Model (GLM) to decompose the familiar target face into a categorical component (e.g., for ‘Mary’ the average of all white females faces of 30 years of age) plus a residual component that defines the specific identity of the familiar face (see Identity Modelling in Figure 1B). We then generated new random identities by keeping the categorical component of the target constant (e.g., white female, 30 years of age) and adding a random component of identity (see Identity Generation in Figure 1B, and Methods, Reverse Correlation Experiment, Random Face Identities for details). Participants saw these randomly generated faces in full frontal view and selected the one that most resembled the familiar target (e.g., ‘Mary’) and rated its similarity to the target on a 6-point Likert scale, ranging from not at all (‘1’) to highly similar (‘6’). To resolve the task, participants must compare the randomly generated faces presented on each trial with their mental representation of the familiar target in full frontal view. Therefore, each face selected comprises a match to the participant’s mental representation of the target, which is estimated by the similarity rating of that face.

After many such trials, we used reverse correlation [8] to estimate the information content of the mental representation of each target familiar face (N= 4, see Supplementary Figure 1B) in each participant (N = 14, see Methods, Reverse Correlation Experiment). Specifically, we build a statistical relationship between the information content of the faces that the participant selected on each trial with their corresponding similarity ratings. In a second stage, we tested with a new group of participants (N = 12, i.e. the validators, see Methods, Generalization Experiments) whether these modelled mental representations were sufficiently detailed to enable identification of each target familiar face and sufficiently versatile to enable resemblance judgments across diverse everyday tasks--i.e. generalization across new viewpoints, age and siblings.

To reconstruct the information contents of mental representations, we used linear regression to compute the single-trial relationship between <similarity ratings, random face identity components> for each target familiar face and participant. Specifically, we computed separate regressions between the similarity ratings and each 3D shape vertex and each RGB texture pixel that comprise the face identity components. We then used the resulting Beta coefficients to model the 3D shape and texture identity components that characterize the participant’s mental representation of each familiar face in the GMF (see Supplementary Figure 2 and Methods, Analyses, Linear Regression Model and Reconstructing Mental Representations).

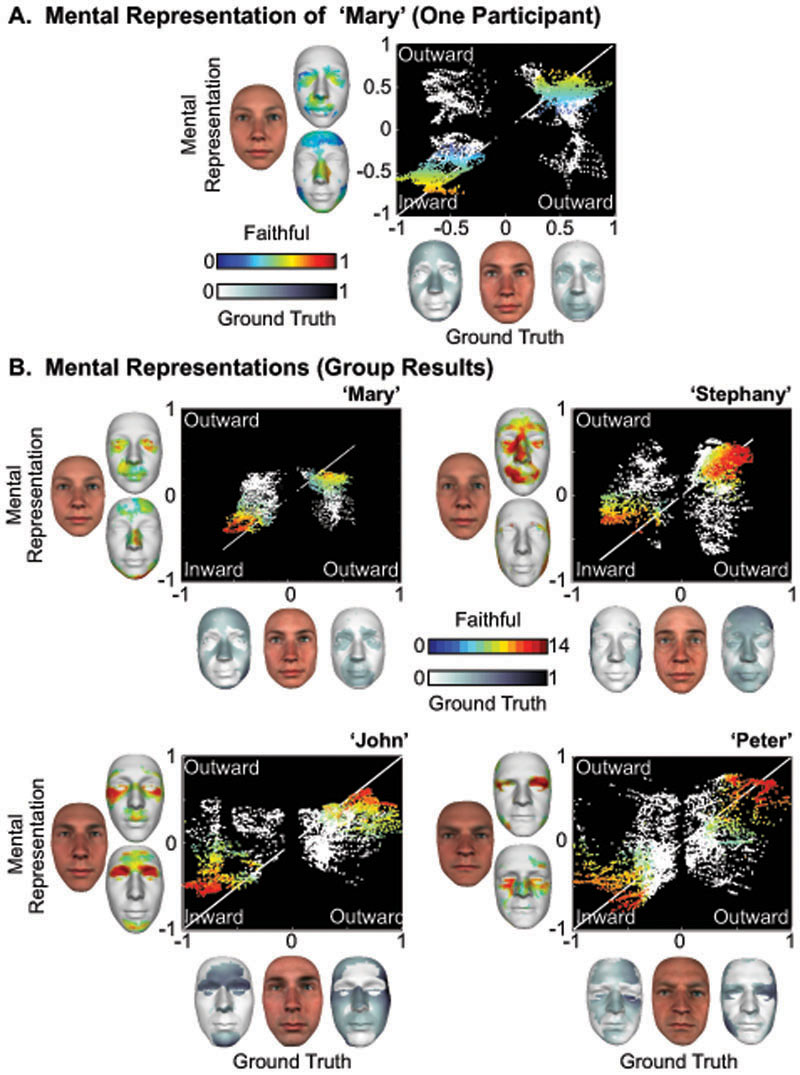
With this approach, we can formally characterize and then compare the participant’s mental representation of a familiar face with the ground truth face—i.e. the objective identity component of the scanned familiar face, see Supplementary Figure 1B. We focus only on 3D shape because there were very few and non-systematic relationships for texture (see Supplementary Figure 3). To illustrate, grey faces on the x-axis of Figure 2A show the ground truth identity component of ‘Mary’ in the GMF for Inward and Outward 3D shape deviations in relation to the categorical average (i.e., of all white females of 30 years of age, like ‘Mary’). For example, Mary’s nose is objectively thinner than the average of white females of her age, and so these vertices deviate inward (darker grey tones indicate increasing deviations). Likewise, her more pouty mouth is shown as an outward 3D shape deviation. The y-axis of Figure 2A uses the same format to show the mental representation of Mary in one typical participant, where colors indicate increasing deviations. These contents reveal faithful representations of, for example, a thinner nose and a pouty mouth (see Methods, Analyses, Vertex Contribution to Mental Representations). A scatter plot visualizes the vertex by vertex fit between the mental representation (y-axis) and the ground truth 3D face (x-axis). The white diagonal line provides a veridical reference, where the identity component in the mental representation is identical to the ground truth face, for every single 3D vertex. This is because the mental representation and ground truth faces are both registered in the same space of 3D vertices [9].

Figure 2. Contents of mental representations of familiar faces.

(A) Mental representation of ‘Mary’ (a typical participant). Ground truth: 3D vertex positions deviate both Inward (-) and Outward (+) from the categorical average to objectively define the shape of each familiar face identity. Greyscale values reported on the flanking faces color-code the normalized magnitudes of inward and outward deviations from the categorical average. Mental representation: Inward and Outward colored faces highlight the individual 3D vertices whose position faithfully deviate from the categorical average in the GMF (p < 0.05, two-sided). Blue to red colors represent the normalized magnitudes of their deviations. 2D scatter plots: Scatter plots indicate the relationship between each vertex deviation in the ground truth (normalized scale on the X-axis) and the corresponding vertex in the memory representation (normalized scale on the Y-axis). The white diagonal line provides the reference of veridical mental representation in the GMF—i.e. a hypothetical numerical correspondence between each shape vertex position in the ground truth face and in the mental representation of the same face. White dots indicate vertices that were not faithfully represented. (B) Mental Representations (group results). Same caption as Figure 2A, except that the colormap now reflects the number of participants (N = 14) who faithfully represented this particular shape vertex.

Our analyses reveal the specific vertices near the veridical line that faithfully represent ‘Mary’ in the mind of this participant as colored dots reported on the scatter and located on the y-axis faces in Figure 2A. These vertices indicate faithful representations because they are significantly closer to the ground truth faces than a null distribution of representations arising from chance (p < 0.05, two-sided, with a null distribution that iterated 1,000 times the analyses using a random permutation of the participant’s choice responses on each iteration, see details in Methods, Analyses, Vertex Contribution to Mental Representation). In contrast, white vertices away from the veridical line did not faithfully represent the identity. We repeated the analysis of represented contents for each participant (N = 14) and familiar face (N = 4). Figure 2B reports the collated group results, using the format of Figure 2A, where colors now indicate N, i.e. the number of participants who faithfully represented that identity in their mind with this particular 3D shape vertex. Figure 2B demonstrates that mental representations comprised similar information contents across the 14 individual participants. Most (10/14) faithfully represented ‘Mary’s’ thin nose, ‘John’s’ receding eyes and wider upper face (13/14), ‘Peter’s’ prominent eyebrow and jawline (13/14), ‘Stephany’s’ protruding mouth (13/14).

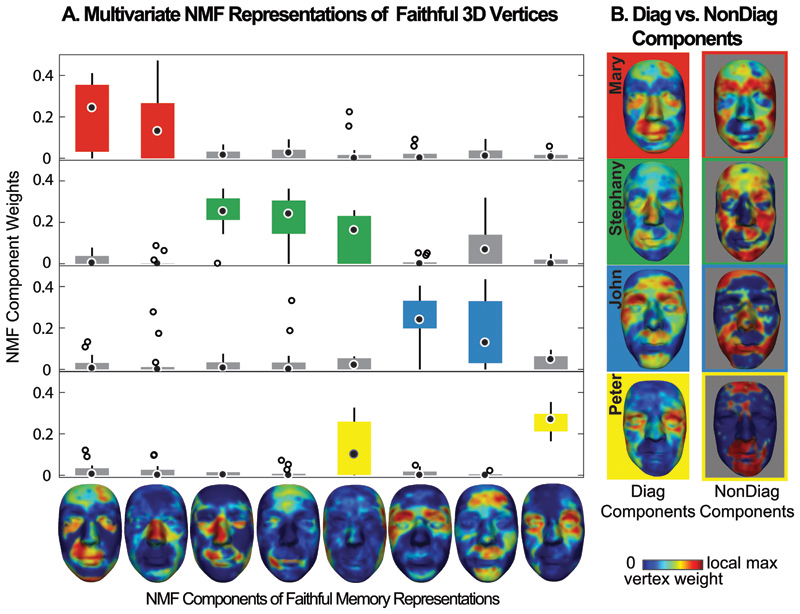
Such convergence of represented contents across participants suggests that the face representations could be multivariate (i.e. comprising contiguous surface patches rather than isolated vertices). As a final step, we extracted the main multivariate components of represented surface patches. To this end, we applied across observers (N = 14) and familiar faces (N = 4) the Non-negative Matrix Factorization (NNMF, [10]) to the faithfully represented 3D vertices (see Methods, Analyses, Components of Memory Representation). Figure 3A shows the multivariate components that faithfully represent four target identities and Figure 3B shows their combinations for the diagnostic components of each target identity (e.g. for ‘Mary,’ the red background heatmap; for ‘Stephany,’ the green one and so forth). Importantly, these diagnostic components of familiar face identity have complementary nondiagnostic components (i.e. the grey background heatmaps in Figure 3B), which capture variable face surfaces that do not comprise the participants’ mental representations.

Figure 3. NNMF multivariate and compact representations.

A. NNMF representations of faithful 3D vertices across the mental representations of participants. The x-axis heatmap presents each NNMF component, where colors indicate the relative weight of each shape vertex in the component (normalized by maximum weight across components). Boxplots on the y-axis show the loading of each NNMF component on the faithful representations (N = 14, one per participant) of each familiar identity (N = 4 familiar identities), with colored boxes indicating above 0.1 threshold loading for NNMF components. In boxplots, the bottom (vs. top) edges indicate the 25^th (vs. 75^th) percentile of the distribution; the whiskers cover the +2.7 standard deviation; the larger central circle indicates the median; the outliers are plotted in smaller circle outside the whiskers. B. Diagnostic and nondiagnostic components for each familiar identity. Heat maps in the left column show the diagnostic component for each familiar identity; heat maps in the right column show the complementary nondiagnostic components.

Here, we develop the critical demonstration that the information contents of the mental representations we modelled are valid. That is, the contents enable accurate identification of each target face and they also enable resemble tasks that preserve their identity. We asked a new group of participants (called ‘validators’) to resolve a variety of resemblance tasks that are akin to everyday tasks of face recognition. Success on these tasks would demonstrate that the diagnostic components derived from the previous experiment comprise identity information that can be used in a different generalization tasks. Therefore, although the components are extracted under one viewpoint (full-face), one age (for each identity) and one sex (that of the identity), here we tested the generalization of identification performance to new viewpoints, ages and sex.

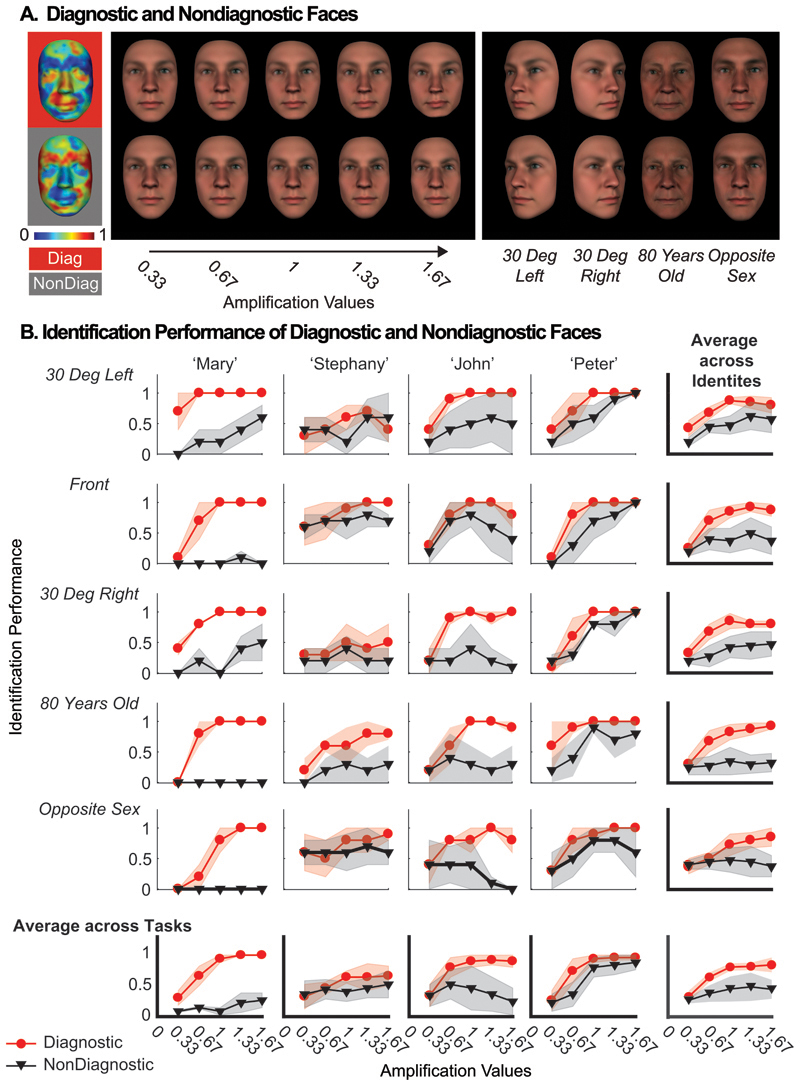
For this demonstration, we synthesized new diagnostic (vs. nondiagnostic) faces that were parametrically controlled for the relative strength of the diagnostic multivariate components of identity vs. their nondiagnostic complement (see Figure 4A and Methods, Generalization Experiments, Stimuli). It is important to emphasize that both diagnostic and nondiagnostic faces are equally faithful representations of the original ground truth. That is, their shape features are equidistant from the shared categorical average. However, whereas the diagnostic components deviate from the average with multivariate information extracted from the participants’ mental representations, the nondiagnostic components do not. We hypothesized that, though equidistant from the categorical average, only the diagnostic components will impact performance on the resemblance tasks. For all synthesized faces, we changed their viewpoint (rotation of -30 deg, 0 deg and +30 deg in depth), age (to 80 years old), and sex (to opposite) using the generative model--see Supplementary Figure 5 to 8 for each familiar target.

Figure 4. Generalization of performance across tasks.

(A) Diagnostic and nondiagnostic Faces. Left panel: The red background map shows the multivariate diagnostic components of faithful 3D shape representation of ‘Mary’; the grey background map shows the nondiagnostic complement (1 - diagnostic components). Middle panel: Faces synthesized with increasing amplification (0.33 to 1.67) of the diagnostic (top) vs. nondiagnostic (bottom) components. Right panel: For each synthesized face, we changed its viewpoint (30° left and 30° right), age (80 years old) and sex, shown here for faces synthesized at amplification = 1. (B) Task Performance. For each condition of generalization (row) and familiar identity (column), 2D plots show the median identification performance computed across 12 validators (y-axes) for faces synthesized with the diagnostic (red curves) and nondiagnostic (grey curves) faces, at different levels of amplification of the multivariate components (x-axes). Shadowed regions indicate median absolute deviations (MAD) of identification performance. Abbreviations: Diag = Diagnostic, Nondiag = Nondiagnostic.

In three independent resemblance tasks – changes of viewpoint, age and sex – we tested the identification performance of 12 validators on the diagnostic and nondiagnostic faces using a 5 Alternative Force Choice task (i.e. responding one of four familiar identities plus a ‘don’t know’ response, see Methods, Generalization Experiments, Procedure). In each task, for each identity we found a significantly higher identification performance for diagnostic faces (see Figure 4B, red curves) than for nondiagnostic faces (black curves)—i.e. a fixed effect of Face Type in a mixed effects linear model. For ‘Mary’, F (1, 12.76) = 315.49, p < 0.001, estimated slope = 0.297, 95% Confidence Intervals = [0.264, 0.33]; for ‘Stephany’, F (1, 20.62) = 25.068, p < 0.001, estimated slope = 0.058, 95% Confidence Intervals = [0.035, 0.081]; for ‘John’, F (1, 12) = 21.369, p < 0.001, estimated slope = 0.143, 95% Confidence Intervals = [0.083, 0.204]; for ‘Peter’, F (1, 12.01) = 5.76, p = 0.034, estimated slope = 0.095, 95% Confidence Intervals = [0.017, 0.173] (see Methods, Generalization Experiments, Analyses for the detailed specification and Supplementary Table 3 to 6 for the full statistical analysis of the models). Thus, the diagnostic contents of the mental representations we modelled do indeed contain the information that can resolve identity and resemblance tasks.

Mental representations stored in memory are critical to guide the information processing mechanisms of cognition. Here, with a methodology based on reverse correlation and a new 3D face information generator (i.e. our 3D GMF), we modelled the information contents of mental representations of 4 familiar faces in 14 individual participants. We showed that the contents converged across participants on a set of multivariate features (i.e. local and global surface patches) that faithfully represent 3D information that is objectively diagnostic of each familiar face. Critically, we showed that validators could identify new faces generated with these diagnostic representations across three resemblance tasks—i.e. changes of pose, age and sex—but performed much worse with equally faithful, but nondiagnostic features. Together, our results demonstrate that the modelled representational contents were both sufficiently precise to enable face identification within task and versatile enough to generalize usage of the identity contents to other resemblance tasks.

At this stage, it worth stepping away from the results and emphasize that it is remarkable that the reverse correlation methodology works at all, let alone produce robust generalization across resemblance tasks. In the experiment, we asked observers to rate the resemblance between a remembered familiar face, and randomly generated faces, that by construction are very unlike the target face (never identical, and almost never very similar). And yet, our results show that the representational contents we modelled following such a task were in fact part of the contents that objectively (i.e. faithfully) support identity recognition. This raises a number of important points that we now discuss.

There has been a recent surge of interest in modelling face representations from human memory [11–13]. These studies used 2D face images and applied dimensionality reduction (e.g. PCA [14] and multidimensional scaling) to formalize an image-based face space, where each dimension is a 2D eigenface or classification image – i.e. pixel-wised RGB (or L*A*B) values. To understand the contribution of each 2D face space dimension to memory representations (including their neural coding), researchers modelled the relationship between projected weights of the original 2D face images on each dimension and participants’ corresponding behavioral [13] (and brain [11, 12]) responses.

These studies contributed important developments in face identification research because they addressed the face identity contents that the brain uses to guide face identification mechanisms. Our aim was to model the face identity contents in the generative 3D space of faces (not the 2D space of their image projections) and to use these models to generate identification information in resemblance tasks that test the generalizability of identity information. It is important to clarify that we modelled identity information in a face space that belongs to the broad class of 3D morphable, Active Appearance Models of facial synthesis (AAMs, [15, 16]). These models contain full 3D surface and 2D texture information about faces and so with their better control superseded the former generation of 2D image-based face spaces ([14, 17] [18]). To synthesize faces, we used our GMF to decompose each face identity as a linear combination of components of 3D shape and 2D texture added to a local average (that summarizes the categorical factor of age, gender, ethnicity and their interactions, cf. Figure 1B). To model the mental representations of faces, we estimated the identity components of shape and texture from the memory of each observer. These components had generative capacity and we used them to precisely control the magnitude of identity information in new faces synthesized to demonstrate generalization across pose, age and sex. Thus, we used the same AAM framework for stimulus synthesis, mental representation estimation and generation of generalizable identities.

There is a well-known problem with using AAMs to model the psychology of face recognition. Perceptual expertise and familiarity are thought to involve representations of faces that enable the greater generalization performance that is widely reported [19–22]. However, AAMs typically adopt a brute force approach to identity representation: a veridical (i.e. totally faithful) deviation of each physical shape vertex and texture pixel from an average. Thus, as AAMs overfit identity information, they appear as a priori weak candidate models to represent perceptual expertise with faces [18]. Our approach of studying the contents of mental representations suggests a solution to this conundrum. We showed that each observer faithfully represented only a proportion of the objective identity information that defines a familiar face identity. Our key theoretical contribution to face space is to formalize the subjective 3D diagnostic information as a reduced set of multivariate face features that can be construed as dimensions of the observer’s face space. Observers develop these dimensions when they interact with the objective information that represents a new face identity in the real world. We modelled the objective information that is available to the observer for developing their face space dimensions via learning as the veridical shape and texture information of the AAM [18, 23, 24]. Key to demonstrating the psychological relevance of our psychological 3D face space dimensions is that they should comprise identity information sufficiently detailed to enable accurate face identification and sufficiently versatile to enable similarity judgments of identity in resemblance tasks. We demonstrated this potential when validators identified faces synthesized with the diagnostic dimensions in novel resemblance tasks. Thus, by introducing reduced faithful mental representations of identity information in the objective representations of AAMs we provide the means of modelling the subjective psychological dimensions of an individual’s face space.

Our work could be extended to precisely track the development of the psychological dimensions of face space if we tasked observers with learning new identities (an everyday perceptual expertise task [18, 25]). Our AAMs enable a tight control of objective face information at synthesis, such as ambient factors of illumination, pose and scale, but also categorical factors of gender, sex, age and ethnicity and components of identity. Thus, we could tightly control the statistics of exposure to faces in individual observers (even orthogonalize them across observers), and model and compare the diagnostic dimensions of the psychological face space that are learned, and finally test their efficacy as we did here. And when we understand how ambient and categorical factors influence performance as a function of differential perceptual learning, we can switch to understanding familiar face identification in the wild, by progressively introducing simulations of ambient factors (e.g. identifying the face of someone walking by a street lamp at night) and observe their specific effects on performance (e.g. ambient changes in face size, shading, and cast shadows). Otherwise, all ambient and categorical factors remain naturally mixed up, and the influence of each factor to identification performance becomes near impossible to disentangle, precluding a detailed information processing understanding of face identification mechanisms.

Our results suggest that human observers use face shape information over texture to represent familiar identities. At this stage, it is important to clarify that shape and texture have different meanings in different literatures. For example, some authors in psychology discuss shape-free faces when referring to 2D images synthesized by warping an identity-specific texture to an identical ‘face shape’ (defined as a unique and standard set of 2D coordinates that locate a few face features [26]). However, it is important to emphasize that the warped textures are not free of 3D shape information (e.g. that which can be extracted from shading [27]). In computer graphics, the generative model of a face comprises a 3D shape per identity (here, specified with 4,735 3D vertex coordinates), lighting sources (here, N = 4), and a shading model (here, Phong shading [28]). The shading model interacts with shape and texture to render the 3D face as a 2D image. To illustrate the effects of this rendering, Supplementary Figure 9 shows how applying the same 2D textures (rows) to different 3D face shapes (columns) generates 2D images with different identities. We used the better control afforded by computer graphics to generate our face images and found that shaded familiar face shape was more prevalent in the face memory of individual participants than face texture.

A general question with reverse correlation tasks is whether the resulting models represent a particular visual category (here, the visual identity of a face) or the task from which the model was reconstructed [24, 29–31]. We contributed to this debate by showing that the identity information reconstructed in one task had efficacy in other tasks that involved identity. Importantly, the tasks were designed to test two classes of factors: ambient and categorical. For example, we showed that the identity component extracted in one ambient viewpoint (full face, 0 deg) could be used to generalize identification of the same face under two new ambient viewpoints (-30 and +30 deg of rotation in depth). We also showed that the identity component extracted for identities (all < 40 years of age) generalized to older age (80 years). Furthermore, we also showed that though extracted from a given sex, the identity component would generalize to another sex, a kinship task. Hence, we found no dramatic differences due to the effect of task of extraction of the identity component. Rather, the extracted representational basis is useful for all tasks tested, whether using ambient or categorical factors of face variance. This therefore suggests that we have tapped into some essential information about familiar face representation. However, we acknowledge that the generalizations we observe might still be a function of an interaction between the nature of memory and the similarity task from which we estimated the identity component. The component could have differed had the task been more visual than memory based (e.g. identification of the same face under different orientations, or a visual matching task) and we might not have derived an identity component that enabled such effective generalization. In any case, the memorized identity components that enable task generalization reflect an interaction between memory and the input information available to represent this identity [24, 32]. Observers can compare this memory representation for that identity with a representation of the visual input for successful identification.

Our models of mental representation should be construed as the abstract information goals (i.e. the contents) that the visual system predicts when identifying familiar faces. We call them ‘abstract information goals’ because they reflect the invariant visual representations that enable the resemblance response and must be broken down into global and local constituents according to the constraints of representation and implementation at each level of the visual hierarchy—or their analogues in deep convolutional networks, where we can use a similar methodology to understand the identity contents represented in the hidden layers [33]. In norm-based coding [17, 34], face identity information is represented in reference to the average of a multi-dimensional face space. Monkey single cell responses increase their firing rate with increasing distance of a face to this average (as happens with e.g. caricaturing, [35]). As shown by Chang et al. [36], neurons selectively respond along a single axis of the face space, not to other, orthogonal axes. An interesting direction of research is to determine whether our reduced diagnostic features, as defined by our ‘abstract information goal’ (see also [37]), provide a superior fit to the neural data than the full feature sets used in the axis model used by Chang et al. [36].

Though we modelled the mental representation of a face identity in an AAM, it is important to state that we do not assume that memory really represents faces in this way (i.e. as demarcations to an average, separately for 3D shape and 2D texture). AAM is only a state-of-the-art, mathematical modelling framework. We fully acknowledge there are many possible concrete implementations into a neural, or a neurally-inspired architecture that could deliver AAM-like performance without assuming an explicit AAM representation. What is clear is that whichever implementation, in whichever architecture, the abstract information modelled under AAM framework will have to enable the performance characteristics our resemblance tasks demonstrated.

For example, we would hypothesize that the diagnostic identity components in Figure 3B are broken down, bottom to top, into the representational language of V1—i.e. as representation in multi-scale, multi-orientation Gabor-like, retinotopically mapped receptive fields [38, 39]; at intermediate levels of processing, as the sort of local surface patches [40, 41] that we reveal, and at the top level as the combinations of surface patches that enable identification and resemblance responses. Under a framework of top-down prediction [42, 43], the abstract information goal of a familiar face identity should trim, in a top-down manner, the fully-mapped but redundant information on the retina into the task-relevant features that are transferred along the occipital to ventral/dorsal visual hierarchy [37]. Tracing the construction of such a reduced memory representation of face identity in the brain should enable an accurate and detailed modelling of the processing mechanism along the visual hierarchy (see also [12, 44–46]). What our work critically provides is an estimate of the end goal of the hierarchy (i.e. the diagnostic component), which is also a prediction of what is important in the input. It is in this sense that mental representations guide task-specific information processing in the brain. Without knowing mental representations, we do not have even have an information needle to search in the fabled haystack of brain activity, let alone reconstruct the mechanisms that process its contents.

We modelled the critical mental representations of that guide the processing of visual information of familiar face identities. In several resemblance tasks that require usage of face identity, we demonstrated the efficacy of the contents we modelled. Our approach and results open new research avenues for the interplay between visual information, categorization tasks and their implementation as information processing mechanisms in the brain.

Methods

Generative Model of 3D Face Identity (GMF)

We designed a generative model to objectively characterize and control 3D face identity variance, using a database of 355 3D faces (acquired with a 4D face capture system, see Supplementary Methods, 3D Face Database) that describes each face by its shape (with 3D coordinates for each one of 4,735 vertices) and its texture (with the RGB values of 800*600 pixels, see Supplementary Figure 1A). It is critical to reiterate that the familiar faces were not part of the 3D face database.

To design the 3D GMF, we first applied a high-dimensional General Linear Model (GLM), separately to 3D vertex coordinates and 2D pixel RGB values, to model and explain away variations in face shape and texture that arise from the non-identity categorical factors of sex, age, ethnicity, and their interactions. The GLM therefore: 1) extracted as a non-identity face average the shape and texture face information explained by non-identity categorical factors; and also 2) isolated the residual information that defines the 3D shape and 2D texture identity information of each face--i.e. the identity residuals.

To further control identity information, we applied Principal Components Analysis (PCA) to the identity residuals of the 355 faces, separately for shape and texture. The PCA represented shape residuals as a 355-dimensional vector in a 355-dimensional space of multivariate components, and a separate PCA represented the texture residuals as a 355*5 (spatial frequency bands)-dimensional matrix in a space of 355*5 multivariate components. Two sets of PCA coordinates therefore represented the objective shape and texture information of each identity in the principal components space of identity residuals.

Our 3D GMF is formally expressed as follows:

$$Faces=Design Matrix \times Coefficient Matrix + weights \times PCs$$

Where Faces is the vertex (or texture) matrix of 355 faces: for vertices, it is [355 x 14,205] where 14,205 = 4,735 vertices x 3 coordinates; for texture, it is [355 x 1,440,000] where 1,440,000 = 800 x 600 pixels x 3 RBG. Design Matrix defined the non-identity categorical factors and their interactions (N = 9), i.e. constant, age, gender, white Caucasian (WC), eastern Asian (EA), black African (BA), gender x WC, gender x EA, gender x BA, for each of face (N = 355), and therefore is [355 x 9]. We estimated the linear effects of each non-identity factor and their interactions using the GLM which are represented in the Coefficient Matrix (i.e. [9 x 14,205] for shape and [9 x 1,440,000] for texture). After the GLM fit, the [355 x 14,205] shape (or [355 x 140,000] texture) residuals are further explained using the PCA analysis, resulting 355 components.

Furthermore, Supplementary Figure 1B illustrates how the generative model controlled the non-identity and identity factors using the 4 familiar faces of our experiment. First, we scanned the four familiar faces of the experiment (2^nd column). We fitted each into our 3D GMF to derive a ground truth face (the 3^rd column), with minimal distortions (shown in the 1^st column).

The model generates new 3D faces by adding the identity residuals of four familiar faces to different non-identity GLM averages, to change their age, sex or ethnicity separately, or jointly sex and ethnicity. The outcomes are older, sex swapped, ethnicity swapped and sex and ethnicity swapped versions of the same identity (the 4^th to 7^th column). We used these generative properties to derive the stimuli of the generalization experiment.

Reverse Correlation Experiment

Participants

We recruited 14 participants (all white Caucasians, 7 females, mean age = 25.86 years, SD = 2.26 years) who were personally familiar with each familiar identity as work colleagues for at least 6 months. We assessed familiarity on a 9-point Likert scale, from not at all familiar ‘1’ to highly familiar ‘9’. Supplementary Table 1 reports the familiarity ratings for each identity and participant. We chose a sample size similar to those reported elsewhere [47–49]. All participants had normal or corrected-to-normal vision, without a self-reported history or symptoms of synaesthesia, and/or any psychological, psychiatric or neurological condition that affects face processing (e.g., depression, autism spectrum disorder or prosopagnosia). They gave written informed consent and received £6 per hour for their participation. The University of Glasgow College of Science and Engineering Ethics Committee provided ethical approval.

Familiar Faces

We scanned four faces ‘Mary’ and ‘Stephany’ (white Caucasian females of 36 and 38 of age, respectively), and ‘John’ and ‘Peter’ (white Caucasian males of 31 and 38 years of age, respectively) who were familiar to all participants as work colleagues. As we will explain, we used these scanned faces to compare the objective and mentally represented identity information in each participant. Each of these four people gave informed consent for the use of their faces in published papers.

Random Face Identities

We reversed the flow of computation in the 3D GMF to synthesize new random identities while controlling their non-identity factors (see Figure 1B Identity Generation, the reverse direction is indicated by the dashed line). We proceeded in three steps: First, we fitted the familiar identity in the GLM to isolate its non-identity averages, independently for shape and texture. Second, we randomized identity information by creating random identity residuals—i.e. we generated random coefficients (shape: 355; texture: 355*5) and multiplied them by the principal components of residual variance (shape: 355; texture: 355*5). Finally, we added the random identity residuals to the GLM averages to create a total of 10,800 random faces per familiar identity in the reverse correlation experiment.

Procedure

Each experimental block started with a centrally presented frontal view of a randomly chosen familiar face (henceforth, the target). On each trial of the block, participants viewed six simultaneously presented randomly generated identities based on the target, displayed in a 2 x 3 array on a black background, with faces subtending an average of 9.5° by 6.4° of visual angle. We instructed participants to respond on one of 6 buttons to choose the face that most resembled the target. The six faces remained on the screen until response. Another screen immediately followed instructing participants to rank the similarity of their choice to the target, using a 6-point Likert scale (‘1’ = not similar, ‘6’= highly similar) with corresponding response buttons. Following the response, a new trial began. The experiment comprised 1,800 trials per target, divided into 90 blocks of 20 trials each, run over several days, for a grand total of 7,200 trials that all validators accomplished in a random order. Throughout, participants sat in a dimly lit room and used a chin rest to maintain a 76 cm viewing distance. We ran the experiment using the Psychtoolbox for MATLAB R2012a. Data collection and following analysis were not performed blind to the target faces.

Analyses

Linear Regression Model

For each participant and target face, each trial produced two outcomes: one matrix of 4,735*3 vertex (and 800*600 RGB pixel) parameters corresponding to the shape (and texture) residuals of the chosen random face on this trial, and one corresponding integer that captures the similarity between the random identity parameters and the target. Across the 1,800 trials per target, we linearly regressed (i.e. RobustFit, Matlab 2013b) the 3D residual vertices (separately for the X, Y and Z coordinates) and residual RGB pixels (separately for R, G and B color channel) with the corresponding similarity rating values. These linear regressions produced a linear model with coefficients Beta_1 and Beta_2 vectors for each residual shape vertex coordinate and residual RGB texture pixel, for each familiar face and participant. Supplementary Figure 2A illustrates the linear regression model for the 3D vertices of ‘Mary.’ Henceforth, we focus our analyses on the Beta_2 coefficients because they quantify how shape and texture identity residuals deviate from the GLM categorical average to represent the identity of each familiar face in the memory of each participant.

Reconstructing Mental Representations

Beta_2 coefficients can be amplified to control their relative presence in a newly synthesized 3D face. Supplementary Figure 2B1 illustrates such amplification for one participant’s Beta_2 coefficients of shape and texture of ‘Mary.’ Following the reverse correlation experiment, we brought each participant back to fine-tune their Beta_2 coefficients for each familiar face, using the identical display and viewing distance parameters as in the reverse correlation experiment (see Supplementary Figure 2B2 and Supplementary Methods, Fine-tuning Beta_2 Coefficients).

Vertex Contribution to Mental Representations

Vertices, whether in the ground truth face or in the participant’s mental representation can deviate inward or outward in 3D from the corresponding vertex in the common categorical average of their GLM fits (cf. Figure 1B). Thus, we can compare the respective deviations of their 3D vertices in relation to the common GLM categorical average. To evaluate this relationship, we plotted the normalized deviation of ground truth vertices from most Inward (-1) to most Outward (+1) on the X-axis of a 2D scatter plot; we also reported the normalized deviation of corresponding vertex of the mental representation on the Y-axis (as shown Figure 2A). If ground truth and mental representations were identical, their vertex-by-vertex deviations from the GLM categorical average (i.e. Euclidean distance) would be identical and would form the veridical diagonal straight white line provided as a reference in the scatter plot of Figure 2A.

Using this veridical line as a reference, for each participant and familiar face representation, we proceeded in three steps to classify each vertex as either ‘faithful’ or ‘not faithful’, and to test whether the vertices in mental representations deviated from the categorical average more than would be expected to occur by chance.

Step 1: We constructed a permutation distribution by iterating our regression analysis 1,000 times with random permutations of the choice response across the 1,800 trials. To control for multiple comparisons, we selected maximum (vs. minimum) Beta_2 coefficients across all shape vertices (and texture pixels), separately for the X, Y and Z coordinates (RGB color channels) from each iteration. We used the resulting distribution of maxima (and minima) to compute the 95% confidence interval of chance-level upper (and lower) Beta_2 value and classified each Beta_2 coefficient as significantly different from chance (p < 0.05, two-sided), or not. We consider the vertex (or pixel) as significant if the Beta_2 coefficient of any coordinate (or color channel) was significant. There were very few significant pixels, with almost no consistency across participants (see Supplementary Figure 3), so we excluded texture identity residuals from further analyses.

Step 2: We used the chance-fit Beta coefficients in Step 1 and the Beta_2 amplification value derived in Reconstructing Mental Representation to compute the equation GLM + β1 + β2 * amplifcation value (cf. Supplementary Figure 2B). As a result, we built a distribution of 1,000 chance fit faces.

Step 3: To classify whether each significant 3D vertex in the mental representation of a participant is more similar to ground truth than we would expect by chance, we computed D_chance, the mean Euclidean distance between the 1,000 chance fit faces and the veridical line, and D_memory, the distance between the same mental representation vertex and the veridical line. If D_memory < D_chance, this significant vertex is ‘faithful’ because it is significantly closer to the veridical line than chance (and we plot it with blue to red colors in Figure 2A); if D_memory > D_chance, the vertex is not faithful (and we plot it in white in Figure 2A, together with the nonsignificant vertices).

To derive group results, we counted across participants the frequency of each faithful vertex and used a Winner-Take-All scheme to determine group-level consistency. For example, if 13/14 participants represented this particular vertex as ‘faithful,’ we categorized it as such at the group level and reported the number of participants as a color indicating 13 participants. If there was no majority for a vertex, we color-coded it as white (see Figure 2B).

Components of Memory Representation

The purpose of the following analysis was to find common diagnostic components (multivariate features) that emerged in the group-level memory representation of each face identity. To do so, we factorized with Non-negative Matrix Factorization (NNMF) the total set of memory representations across familiar identities and observers.

For each participant, we recoded each vertex in the identity residuals of each familiar face as ‘faithful’ = 1, ‘not faithful’ or not significant = 0, resulting in a 4735-d binary vector. We pooled 56 such binary vectors (across 4 targets x 14 observers = 56) to create a 4735 by 56 (i.e. vertex-by-model) binary matrix to which we applied NNMF to derive 8 multivariate components that captured the main features that faithfully represent familiar faces in memory across participants (see Supplementary Methods, Non-negative Matrix Factorization). Heatmap in Figure 3A shows each NNMF component.

To determine the loading (i.e. the contribution) of each NNMF component in the group-level mental representation of each familiar face identity, we computed the median loading of this component on the 14 binary vectors representing this identity in the 14 observers. We applied a 0.1 loading threshold (> 73 percentile of all 8 components × 4 identities median loadings) to ascribe a given component to a familiar face representation. The boxplot in Figure 3A represents the loading of each NNMF component at the group-level representation, with colored boxes showing at least 2 above-threshold NNMF components represent each familiar identity.

We then constructed the diagnostic component of a familiar identity representation as follows: for each vertex we extracted the maximum loading value across the NNMF components representing it, and normalized the values to the maximum loading across all vertices. This produced a 4735-d vector V_d that weighs the respective contribution of each 3D vertex to the faithful representation of this familiar identity that we call the “diagnostic component.” The heat maps in the left column of Figure 3B represent the diagnostic component of each familiar identity. Supplementary Figure 4 shows the high accuracy of the features captured by the components.

Crucially for our validation experiment, we were then able to define a nondiagnostic component as the complement of the diagnostic component V_n = 1 – V_d. It is important to emphasize that we adjusted the total deviation magnitude of the diagnostic and nondiagnostic components from the categorical average—i.e. by equating the total sum of their deviations. This ensures that diagnostic and nondiagnostic components are both equidistant from the average face in the objective face space. The right column of Figure 3B shows the nondiagnostic component of each familiar identity representation.

Generalization Experiments

Validators

We recruited 12 further participants (7 white Caucasian and 1 East Asian females, 5 white Caucasian males, with mean age = 28.25 years and SD = 4.11 years), using the same procedure and criteria and those presiding for the selection of participants. Supplementary Table 2 reports the familiarity ratings for each identity and validator. All validators had normal or corrected-to-normal vision, without a self-reported history or symptoms of synaesthesia, and/or any psychological, psychiatric or neurological condition that affects face processing (e.g., depression, autism spectrum disorder or prosopagnosia). They gave written informed consent and received £6 per hour for their participation. The University of Glasgow College of Science and Engineering Ethics Committee provided ethical approval.

Stimuli

For each familiar identity, we synthesized new 3D faces that comprised graded levels of either the diagnostic or the nondiagnostic shape components as explained in the section Components of Memory Representation above. Specifically, we used the normalized diagnostic component V_d and its nondiagnostic complement V_n to synthesize morphed faces with shape information of each target identity as follows:

$$\begin{gathered} Diagnostic Faces = Ground Truth \times Vd \times \alpha + Categorical Average \left(1-Vd \times \alpha \right) \\ Nondiagnostic Faces = Ground Truth \times Vn \times \alpha + Categorical Average \left(1-Vn \times \alpha \right) \end{gathered}$$

with amplification factor α = 0.33, 0.67, 1, 1.33, 1.67, to control the relative intensity of diagnostic and nondiagnostic shape changes. We rendered all these morphed shapes with the same average texture. The first rows of Supplementary Figure 5 to 8 show the morphed faces for each familiar identity. We added as filler stimuli the grand average face (for both shape and texture) of the 355 database faces.

We also changed the viewpoint, age and sex of all of these synthesized faces. Specifically, we rotated them in depth by -30 deg, 0 deg and +30 deg and using the 3D GMF, we set the age factor to 80 years/swapped the sex factor, keeping all other factors constant (cf. Generative Model of 3D Face Identity in Figure 1B and Supplementary Figure 1B).

Procedure

The experiment comprised 3 sessions (viewpoint, age and sex) that all validators accomplished in a random order, with one session per day. In the Viewpoint session, validators ran 15 blocks of 41 trials (5 repetitions of 123 stimuli). Each trial started with a centrally displayed fixation for 1s, followed by a face on a black background for 500ms. We instructed validators to name the face as ‘Mary,’ ‘Stephany,’ ‘John’ or ‘Peter,’ or respond ‘other’ if they could not identify the face. Validators were required to respond as accurately and as quickly as possible. A 2s fixation separated each trial. Validators could break between blocks. In the Age and Sex sessions, validators ran 5 blocks that repeated 44 trials. They were instructed to respond “Old Mary,” “Old Stephany,” “Old John,” “Old Peter” or “Other” in the age session, and “Mary’s brother”, “Stephany’s brother,” “John’s sister,” “Peter’s sister” or “Other” in the sex session. For each session, stimuli are randomized across all trials. Across the 3 sessions, we recorded participants’ identification performance in 3 viewpoints, a change of age information and a change of sex information. Data collection and following analysis were not performed blind to the conditions of the experiments.

Analyses

For each validator and generalization condition, we computed the percent correct identification of diagnostic and nondiagnostic faces for each familiar face and at each level of feature intensity. To ensure that diagnostic and nondiagnostic faces produced the expected effect for each one of the four identities, we fitted a linear mixed effects model (i.e. fitlme, Matlab 2016b) to the data of each identity separately, using Wilkinson’s formulae:

$$Performance ~ 1 + Face Type + Task Type + Amplification + \left(Face Type + Task Type + Amplification - 1 |Subject\right)$$

The model had fixed factors of Face Type (i.e. diagnostic vs. nondiagnostic), Feature Amplification (i.e. 0.33, 0.67, 1, 1.33, 1.67) and Generalization Task (i.e. 3 views plus an age change and a sex change) as explanatory variables and participants’ response variability as random factor. From this model, we can infer whether or not the fixed factors generalized beyond the specific participant sample, separately for each identity.

We tested the specified fixed effect factor (i.e. using ANOVA, Matlab 2016b), using the Satherwither approximation to compute the approximate degrees of freedom. We found for each identity a higher identification performance with diagnostic than nondiagnostic faces (see Figure 4B), and the performance increased with amplification (an effect of Feature Amplification). The Generalization Task effect was significant for ‘Mary’ and ‘Stephany’ and not for ‘John’ and ‘Peter’. Supplementary Table 3 to 6 report the full statistics of our fixed effects, for each identity.

To further test the prediction effect of Face Type we built a null model that excludes this factor:

$$Performance ~ 1 +Task Type + Amplification + \left(Task Type + Amplification - 1 |Subject\right)$$

For each identity, we compared the original and null model with a likelihood ratio (i.e. LR). Performance was significantly better explained by the original model (with Face Type) than the null model (without Face Type). For ‘Mary’, LR statistic = 603.72.135, p < 0.001; for ‘Stephany’, LR statistic = 39.516, p < 0.001; for ‘John’, LR statistic = 205.67, p < 0.001; for ‘Peter’, LR statistic = 214.34, p < 0.001. See Supplementary Table 3 to 6 for the full statistical analysis.

We also found a significant interaction effect between Face Type and Amplification, by fitting a linear mixed effect model with this interaction included as an effect factor (see Supplementary Methods, Linear Mixed Effect Model of Face Type by Amplification Interaction, and Supplementary Table 7).