A supra-massive population of stellar-mass black holes in the globular cluster Palomar 5

Abstract

Palomar 5 is one of the sparsest star clusters in the Galactic halo and is best-known for its spectacular tidal tails, spanning over 20 degrees across the sky. With N-body simulations we show that both distinguishing features can result from a stellar-mass black hole population, comprising ~ 20% of the present-day cluster mass. In this scenario, Palomar 5 formed with a ‘normal’ black hole mass fraction of a few per cent, but stars were lost at a higher rate than black holes, such that the black hole fraction gradually increased. This inflated the cluster, enhancing tidal stripping and tail formation. A gigayear from now, the cluster will dissolve as a 100% black hole cluster. Initially denser clusters end up with lower black hole fractions, smaller sizes, and no observable tails. Black hole-dominated, extended star clusters are therefore the likely progenitors of the recently discovered thin stellar streams in the Galactic halo.

In recent years, a few dozen thin (≲ 100 pc) stellar tidal streams have been discovered in the Milky Way halo^1–4. Their elemental abundances and distribution in the Galaxy provide important constraints on the formation of the Galaxy and its dark matter distribution⁵. Their narrow widths imply that their progenitor stellar systems had a low velocity dispersion and were dark matter-free star clusters rather than dark matter-dominated dwarf galaxies. However, for none of these streams has a progenitor been found and the star cluster nature is questioned by two recent findings: firstly, the inferred mass-loss rate of the GD-1 stream is several times higher⁶ than what is found in ‘vanilla’ cluster evolution models⁷ and secondly, only mild tidal distortions and no tidal tidal tails were found⁸ for several globular clusters (GCs) with extremely radial orbits⁹ passing through the strong tidal field near the Galactic center where tidal stripping is efficient. These results raise the questions what was driving the escape rate of the streams’ progenitors and why this mechanism is not operating in all star clusters.

The metal-poor GC Palomar 5 (hereafter Pal 5) is one of the few known star clusters with extended tidal tails associated with it ¹⁰, spanning ≳ 20 degrees on the sky, making it a Rosetta stone for understanding tidal tail/stream formation. The cluster has an unusually large half-light radius of ~ 20 pc¹¹ and combined with its relatively low mass of ~ 10⁴ M_⊙, its average density is among the lowest of all Milky Way GCs: ~ 0.1 M_⊙/pc³, comparable to the stellar density in the solar neighbourhood. A low density facilitates tidal stripping and the formation of tidal tails¹², but it is not known whether this low density is the result of nature, or nurture.

It has been proposed that Pal 5 simply formed with a low density¹² and has always been a collisionless system, meaning that two-body interactions were not important in its evolution. However, some properties of Pal 5 are reminiscent of other GCs, such as a spread in sodium abundances¹³ and a flat stellar mass function¹¹. These features have been attributed to high initial densities ^14,15 and collisional evolution7 and suggest that Pal 5 in fact is, or was, a collisional stellar system, like the rest of the Milky Way GCs¹⁶. In this study we aim to reconcile the low density of Pal 5 with collisional evolution.

Since the discovery of gravitational waves¹⁷, updated metallicity-dependent stellar wind and supernova prescriptions have been implemented in GC models ^18,19. In these models, a large fraction of BHs that form from massive stars have masses above 20 M_⊙ and do not receive a natal kick, as the result of fallback of material, damping the momentum kick resulting from asymmetries in the supernova explosion^20,21. The presence of a BH population in a star cluster accelerates its relaxation driven expansion^22,23 and escape rate^24,25. Observational motivation for considering the effect of BHs on GC evolution stems from the discovery of accreting BH candidates in several GCs with deep radio observations^26,27 and a BH candidate in a detached binary in NGC 3201²⁸. Here we investigate the possibility that Pal 5 was much denser in the past and that the present-day structure and prominent tidal tails are the result of a BH population.

Results

We perform star-by-star, gravitational N-body simulations with NBODY6++GPU²⁹. All clusters are evolved for 11.5 Gyr on the orbit of Pal 5 in a three-component Milky Way (bulge, disc, halo) and the simulations include the effect of stellar and binary evolution. No primordial binaries were included. We consider two prescriptions for BH natal kicks. First we consider the most up-to-date BH recipes³⁰, in which approximately 73% of the mass of the BH population is retained after natal kicks, almost independently of the initial escape velocity of the cluster (see Methods). Then we test the collisionless hypothesis and draw BH kick velocities from a Maxwellian with the same dispersion as that of neutron stars (NSs). Because we need lower densities for these models, all BHs are ejected by the natal kicks in almost all models (in four models a single BH was retained). The latter approach is similar to that of Dehnen et al.¹², with the added effect of stellar evolution and a direct summation code to correctly include the effect of two-body interactions. We will refer to these two sets of models as wBH and noBH, respectively. The initial parameters and all results are summarised in Tables 1 and 2.

Table 1. Overview of the 17 wBH N-body simulations of Pal 5.

The different columns present: (1) initial number of stars; (2) initial half-mass density; (3) initial mass; (4) initial half-mass radius; (5) age when the cluster had the observed number of stars (N_cluster = 1550); (6) observable number of stars at 11.5 Gyr; (7) half-light radii at 11.5 Gyr; (8) bound mass at 11.5 Gyr; (9) half-mass radius of the bound stars at 11.5 Gyr; (10) BH mass fraction at an age of 11.5 Gyr; (11) fractional difference with N_cluster; (12) fractional difference with observed R_eff = l8.7±0.4 pc; (13) overall fractional difference $\delta \text{=}\sqrt{{\delta }_N^2+{\delta }_R^2}$; (14) Model ID, sorted in level of agreement with the data with wBH-1 being the closest match.

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)
No	ph0	M0	rho	T1550	Ncluster	Reff	M	rh	fBH	δN	δR	δ	Model
[103]	[M⊙/pc3]	[105M⊙]	[pc]	[Gyr]		[pc]	[104 M⊙]	[pc]	[%]	[%]	[%]	[%]
50	30	0.319	5.04	2.74	–	–	–	–	–	–	–	–	wBH-17
50	100	0.319	3.38	4.06	–	–	–	–	–	–	–	–	wBH-16
50	300	0.319	2.34	5.58	–	–	–	–	–	–	–	–	wBH-14
50	1000	0.319	1.57	8.34	1052	4.05	0.483	5.29	0.701	-32.1	-78.3	84.7	wBH-9
100	30	0.638	6.35	5.40	–	–	–	–	–	–	–	–	wBH-15
100	100	0.638	4.25	7.85	–	–	–	–	–	–	–	–	wBH-13
100	300	0.638	2.95	11.36	1448	9.8	0.732	12.8	3.09	-6.58	-47.6	48	wBH-5
100	1000	0.638	1.97	17.99	3541	6.26	1.84	9.04	0.321	+128	-66.5	145	wBH-10
200	30	1.28	7.98	8.12	–	–	–	–	–	–	–	–	wBH-12
200	100	1.28	5.34	11.43	1399	17.7	0.86	20	20.1	-9.74	-5.3	11.1	wBH-3
200	300	1.28	3.7	17.64	7210	11.1	4.05	14.9	2.75	+365	-40.8	367	wBH-11
210	80	1.34	5.85	11.47	1497	18.1	0.949	18.8	22.3	-3.42	-3.11	4.62	wBH-1
215	80	1.37	5.9	11.13	459	19.9	0.419	15.3	44.6	-70.4	+6.15	70.7	wBH-8
220	70	1.4	6.21	11.45	1411	18.5	0.953	19.8	21.9	-8.92	-0.948	8.97	wBH-2
220	80	1.4	5.94	11.31	791	20.8	0.604	19.4	33	-49	+11.5	50.3	wBH-6
225	70	1.44	6.26	11.29	1091	16.6	0.77	16.5	29.1	-29.6	-11.4	31.7	wBH-4
225	80	1.44	5.98	11.71	2372	16.8	1.45	19.8	15.1	+53.1	-10	54	wBH-7

Table 2. As in Table 1 but now for the 20 noBH models.

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)
No	ph0	M0	rho	T1550	Ncluster	Reff	M	rh	fBH	δN	δR	δ	ID
[103]	[M⊙/pc3]	[105M⊙]	[pc]	[Gyr]		[pc]	[104 M⊙]	[pc]	[%]	[%]	[%]	[%]
100	10	0.638	9.15	7.84	609	4.42	0.289	5.76	0	-60.7	-76.4	97.5	noBH-14
100	30	0.638	6.35	15.09	2682	4.71	1.49	7.24	0	+73.1	-74.8	105	noBH-15
100	100	0.638	4.25	16.71	3607	3.57	2.05	6.33	0	+133	-80.9	155	noBH-18
100	300	0.638	2.95	18.62	4219	4.05	2.16	6.65	0	+172	-78.3	189	noBH-19
200	9.5	1.28	11.7	10.79	1062	8.76	0.501	11.7	0	-31.5	-53.2	61.8	noBH-10
200	10	1.28	11.5	11.65	1675	9.03	0.812	12	0	+8.11	-51.7	52.4	noBH-6
200	30	1.28	7.98	2.35	10320	9.52	6.49	12.7	0	+566	-49.1	568	noBH-20
300	9.5	1.91	13.4	11.11	1065	13.5	0.508	17.5	0.321	-31.3	-27.7	41.8	noBH-5
300	9.625	1.91	13.3	11.38	1349	12.2	0.67	16	0.244	-13	-34.7	37.1	noBH-4
300	9.75	1.91	13.3	11.45	1500	12.2	0.736	16.1	0.222	-3.23	-35	35.1	noBH-3
300	10	1.91	13.2	12.07	2316	12.1	1.2	16.1	0.136	+49.5	-35.5	60.9	noBH-9
350	9.625	2.23	14	11.37	1136	19.6	0.583	25.3	0	-26.7	+4.84	27.1	noBH-1
350	9.75	2.23	14	11.63	1864	13.7	0.966	17.9	0	+20.3	-26.7	33.6	noBH-2
400	9.5	2.55	14.7	11.14	81	22.5	0.0436	33.5	0	-94.8	+20.2	96.9	noBH-12
400	9.625	2.55	14.7	11.40	1105	27.1	0.539	34.7	0	-28.7	+45.1	53.4	noBH-7
400	9.75	2.55	14.6	11.79	2516	14.3	1.28	19.1	0	+62.3	-23.7	66.7	noBH-11
400	10	2.55	14.5	12.16	3237	14.1	1.7	19.1	0	+109	-24.4	112	noBH-16
500	9.5	3.19	15.9	11.14	112	24	0.0573	30.8	0	-92.8	+28.2	97	noBH-13
500	9.75	3.19	15.7	11.66	2429	18.7	1.24	24.6	0	+56.7	+0.0658	56.7	noBH-8
500	10	3.19	15.6	11.92	3650	15.8	1.86	21.1	0	+136	-15.3	136	noBH-17

We vary the initial number of stars (N₀) and the initial mass density within the half-mass radius: $\rho h0\equiv 3M_0/\left(8\pi r_{h0}^3\right),$ where M₀ ≃ 0.64 M_⊙ × N₀ is the initial mass and r_h0 is the initial half-mass radius. We search for a model that best reproduces the observed number of stars of Pal 5, N_cluster = 1550, and its half-light radius, R_eff = 3.21 arcmin/18.7 pc (see Methods). R_eff is defined as the distance to the cluster center containing half the number of observed stars. We first run a coarse grid of models, followed by a finer grid close to the parameters that give the best match in the coarse grid. The best wBH model (wBH-1) has N₀ = 2.1 × 10⁵ and ρ_h0 = 80 M_⊙/pc³. This cluster lost 92% of its initial mass of l.34× 10⁵ M_⊙ by stellar evolution and escapers and the density decreased nearly three orders of magnitude because of stellar evolution and dynamical heating by BHs. We note that the half-mass radius r_h ≃ 18.8 pc, as determined from the 3-dimensional mass distribution, is similar to R_eff = 18.2 pc, which is determined from the projected distribution of observable stars. If mass follows light, R_eff ≃ 0.75r_h and for mass segregated clusters without BHs it can be as small as 0.5rh³¹. The fact that R_eff ≃ r_h for wBH-1 implies that the observable stars are less concentrated than the mass profile. This is the result of the BH population which sinks to the center via dynamical friction against the lower mass stars^{22, 23, 32}, where they remain in a quasi-equilibrium distribution³³. The surface density profile and the properties of the stream are in good agreement with the observations (Figure 1). The small-scale density variations in the tails are not reproduced by our model (see Supplementary Figure 1). This is because they are likely the result of interactions with dark matter subhalos34 or the Galactic bar and giant molecular clouds in the disc³⁵, which are not included in our model. The observed line-of-sight velocity dispersion of stars in the tails is 2.1 ± 0.4 km/s³⁶, which is well reproduced by wBH-1 (2.4 ± 0.1 km/s, for giants in the same region as the observations). The most striking property of wBH-1 is its large BH fraction at present: ƒ_BH = 22%. We define ƒ_BH as the total mass in BHs that are bound to the cluster over the total bound cluster mass, i.e. ƒ_BH = M_BH/M. The BH population is made up of 124 BHs with an average mass of 17.2 M_⊙ (i.e. M_BH = 2178 M_⊙), currently residing within R_eff (see Figure 1). This ƒ_BH is more than twice as large as what is expected from a canonical stellar initial mass function (IMF) and stellar evolution alone, and is the result of the efficient loss of stars over the tidal boundary, while the BHs were mostly retained because they are in the center.

Figure 1. Comparison between the N-body model wBH-1 and observations of Pal 5 and its stream.

(a) Density profile of observable stars in wBH-1, which provides an excellent match to the observations. There is also good agreement between the stellar stream track (b), the stream density and its gradient (c) and stream width (d) between observations and wBH-1, implying that the rate of escape of stars from Pal 5 and their velocity dispersion in the last few Gyrs are correctly reproduced by wBH-1. The blowout of the cluster shows that almost all of the 124 bound BHs are within R_eff. All error bars denote the 67% confidence interval.

In all wBH models, ƒ_BH increases in the first ~ 10 Myr because of BH formation and stellar evolution mass loss. Then, ƒ_BH decreases in the following ~ 100 Myr because of BH ejections from the core³³. This happens because binary BHs form and interact with other BHs when two-body relaxation becomes important. These binaries become more bound in these interactions, eventually ejecting BHs and themselves from the cluster. What happens next depends on ρ_h0: in dense clusters, most BHs are ejected before the cluster dissolves and these GCs have escape rates and R_eff comparable to what is found in models of clusters without BHs (Figure 2). Clusters with lower initial densities have larger relaxation times, resulting in fewer BH ejections, while tidal stripping of stars is more efficient, leading to an increasing ƒ_BH until 100%37 (Figure 2). For ƒ_BH ≳ 0.1, R_eff ~ 15 pc, comparable to what is found for about half of the GCs in the outer halo of the Milky Way³⁸, suggesting that these ‘fluffy’ GCs are BH rich and candidates to produce prominent stellar streams. This idea is further supported by the strong correlation between ƒ_BH and R_eff and the fraction of stars in the stream (Figures 3 and 4). Theory suggests33 that in idealised single-mass star clusters that fill their tidal radius there exists a critical ƒ_BH ≃ 10% at which the mass-loss rate of stars and BHs is the same and ƒ_BH remains constant at 10% while the cluster loses mass. For higher(lower) ƒ_BH, stellar mass is lost at a higher(lower) rate by tidal striping than BH mass is lost by ejections from the core. This implies that clusters can evolve to 100% BH clusters if they form with ƒ_BH ≳ 10% and can remain above it during their evolution. Our models suggest that for multimass models this critical fraction is lower: ~ 2.5%. Since for a canonical IMF the initial ƒ_BH ≃ 5 — 10%, depending on metallicity, it is possible for some GCs to remain above the critical ƒ_BH and evolve to 100% BH clusters³⁷, as we find in our wBH-1 model. Because ƒ_BH always evolves away from 10%, the distribution of ƒ_BH values of a GC population becomes bimodal. Whether cluster evolve towards BH-free clusters, or 100% BH clusters depends on their initial density relative to the tidal density. Because ƒ_BH affects the density, a unimodal initial density distribution can evolve towards a bimodal preseny-day density distribution, as is observed in the halo³⁸.

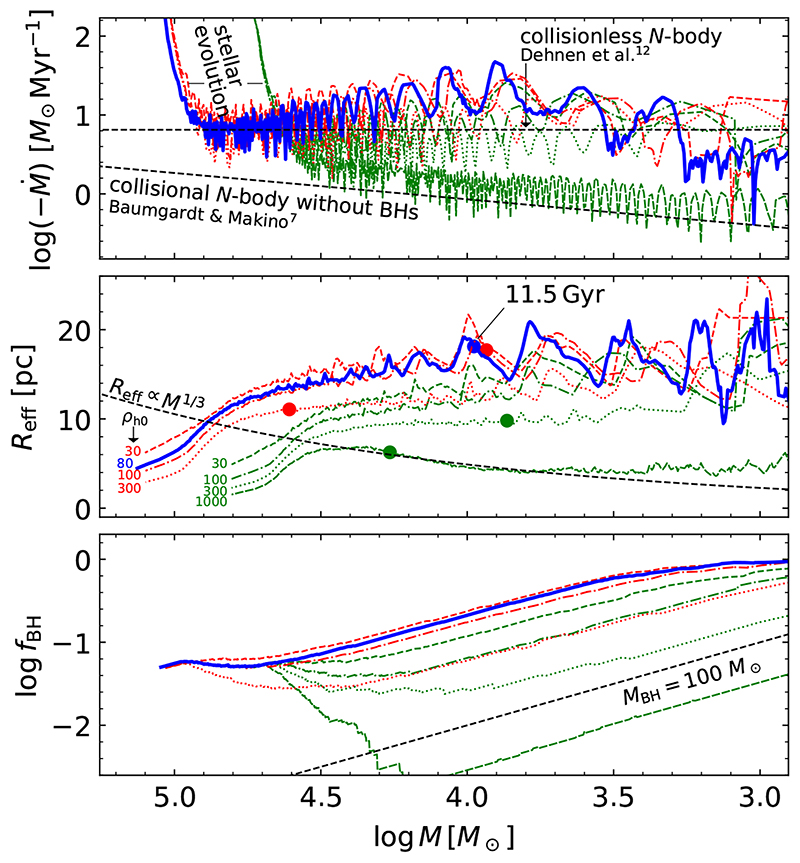
Figure 2. Results for different initial conditions for clusters with BHs.

Results of wBH-1 (blue, thick lines), compared to other wBH models with N₀ = 100k (green lines) and 200k (red lines) with different initial densities. Different panels show the variation of diagnostic quantities as a function of bound cluster mass (x-axis), which decreases in time. Top: Total (positive) mass-loss rate (–Ṁ), which is initially high as the result of stellar evolution. After about 30% of the mass is lost, Ṁ is dominated by escaping stars and BHs. The results of the collisionless N-body model of Pal 512 and that of the collisional N-body models without BHs7 are overplotted. Because of the BHs, wBH-1 loses mass at a similar rate as the lower density collisionless models. Middle: Evolution of R_eff with the age of 11.5 Gyr indicated with dots. The models do not evolve towards a constant luminosity density (i.e. R_eff ∝ M^1/3), as predicted for single-mass clusters⁵³. Instead, R_eff remains approximately constant while the cluster evolves to lower mass and there is a factor of five spread in R_eff at a given mass due to variations in ƒ_BH (bottom). Dense clusters eject all BHs, while low-density clusters lose stellar mass at a higher rate than BH mass, and evolve along tracks of nearly constant BH mass towards a 100% BH cluster.

Figure 3. Dependence of cluster and stream properties on the BH content.

Effective radius (R_eff, top) and the relative number of stars in the trailing tail (bottom) for all surviving wBH clusters when their mass is 0.95 × 10⁴ M_⊙ (the mass of wBH-1 at 11.5 Gyr) as a function of ƒ_BH. Observed values^11,34 are shown as horizontal lines with the shaded region indicating the 1σ confidence interval. Values of wBH-1 are shown with large stars. Here N_trailing is defined as the number of observable stars in the trailing tail, within 4 degree of right ascension of Pal 5, which in the model corresponds to stars that escaped in the preceding ~ 1 Gyr. Because these quantities vary along the orbit at these low masses, we plot with error bars the range within the nearest peri and apo. The strong correlation of both quantities with ƒ_BH suggests that for a given orbit and cluster mass, the BH content sets both R_eff of the cluster and the prominence of the tidal tails.

Figure 4. Dependence on stream visibility on BH content.

Density map in Galactic coordinates of unbound stars of four different wBH models with different black hole fractions at 11.5 Gyr. A density of background stars of 0.15/arcmin² was added to each model. Models with ƒ_BH ≲ 10% do not have prominent tidal tails.

We now discuss the noBH models. The best-fit model (noBH-1) has N₀ = 3.5 × 10⁵ and ρ_h0 = 9.625 M_⊙/pc³, i.e. approximately twice as massive and an order of magnitude less dense than wBH-1. The resulting observable parameters N_cluster (R_eff) are within 27%(5%) of the values of Pal 5. The resulting cluster density profile and stream properties are similar to those of wBH-1 (Supplementary Figure 1), hence based on these observables it is not possible to prefer either of the assumptions for BH kicks. The wBH-1 model predicts a higher central velocity dispersion of 580 m/s vs. 350 m/s for noBH-1 (see Methods). The inferred central dispersion from the literature compilation by Baumgardt & Hilker³⁹ is ${550}_{-110}^{+150}$ m/s, i.e. favoring the BH hypothesis. We quantified the degree of fine-tuning of N₀ and ρ_h0 that is required to obtain the best model in both cases. For the wBH models, we find that the uncertainty in the present-day properties can be covered by a relatively large range of initial densities, while for the noBH models we find that variations in the initial density are amplified by more than an order of magnitude in variations in the present-day properties (see Supplementary Information). This means that a relatively large range of initial conditions in wBH models lead to similar present-day properties, while for the noBH models a high degree of fine-tuning in the initial density is required to obtain noBH-1. In addition, noBH-1 completely dissolves at 11.8 Gyr, i.e. 300 Myr after we observe the cluster, while wBH-1 survives for another 1.4 Gyr. By assuming simple power-law distributions for the initial cluster masses and densities, we estimate that the probability of finding a cluster with the properties of Pal 5 for wBH-1(noBH-1) is 1/200(1/3.6 × 10⁵). Given that the Milky Way has ~ 150 GCs, the wBH-1 model provides the more likely explanation for Pal 5. The velocity dispersion and the fine-tuning and timing arguments all favor the BH hypothesis. The final argument in support of the BH hypothesis is that the higher initial density and the resulting collisional nature of Pal 5 make it easier to understand the flat stellar mass function, its multiple populations and its relation to the rest of the Milky Way GC population.

In the observed mass range (0.6 — 0.8 M_⊙), the mass function of Pal 5 is flatter (dN/dm ∝ m^α, with α ≃ –0.5¹¹) than what is expected from a canonical IMF (α = —2.3), suggesting that Pal 5 has preferentially lost low-mass stars. We note that this result has been questioned and the mass function slope may actually be close to the initial value (Iskren Georgiev, private communication). In Figure 5 we show the mass function of bound stars and remnants of wBH-1. For main sequence stars > 0.5 M_⊙ it has a slope of $\alpha =-{1.5}_{-0.4}^{+0.2},$ which is flatter than the IMF, but steeper than the observed slope. The noBH-1 model has a slope comparable to wBH-1, implying that in the later parts of its evolution the cluster became collisional. The similarity in mass function slope between wBH-1 and noBH-1 means that we can not use the observed mass function to distinguish between the two scenarios. However, in the noBH models the only way to reconcile the models with the observations is to start with a flatter IMF, because the alternative (i.e. reducing the initial relaxation timescale by increasing the initial density) leads to a R_eff that is too small. The BH scenario, however, leaves the possibility to increase the initial cluster density and still end up with the same present-day BH fraction, R_eff and tidal tails. For example, tidal heating by interstellar gas clouds in the early evolution is probably important in the evolution of GCs ^40,41, but this effect is not included in our models. This tidal heating leads to a decrease in the cluster mass ^42,43 and for clusters with a low central concentration the cluster density also decreases⁴⁴. BHs sink to the cluster center by dynamical friction on a fraction of a relaxation time and if this is shorter than the tidal heating timescale, then the BHs are less affected by this mechanism of tidal stripping than the stars, such that ƒ_BH increases, counteracting the reduction of ƒ_BH from BH ejections from the core due to the higher density. This would be a pathway to start with higher densities. Alternatively, something may have happened to Pal 5 at a later stage of its evolution. It is likely that Pal 5 formed in a dwarf galaxy that was accreted onto the Milky Way, which is supported by its tentative association with the Helmi streams⁴⁵. The cluster could have lost a fraction of its loosely bound stars as a result of the removal of its host galaxy⁴⁶, thereby increasing ƒ_BH. Finally, a flatter IMF at high masses would also lead to a higher ƒ_BH. This also affects the evolution, and a flatter IMF would lead to faster expansion higher mass loss rate ^24,25,47. In all these scenarios, denser initial conditions and therefore more equipartition among low-mass stars, whilst ending with the same ƒ_BH at present, is a possibility. Understanding the interplay between early mass loss, mass segregation, the (high-mass) IMF and accretion on the Milky Way to find limits on the allowed initial density is an interesting topic for a follow-up study. The initial density is a critical ingredient for our understanding of GC formation^14,15,48, evolution⁴¹, BH natal kicks21 and binary BH mergers^18,19,49.

Figure 5. Mass function of stars and remnants.

Mass function of bound stars and remnants of wBH-1 at 11.5 Gyr. The mass in each bin (M_j) is plotted for the IMF (red line), the mass function after only stellar evolution has been applied (light shaded), and for the final results of the N-body simulation (dark shaded). There is a flattening of the stellar mass function due to preferential escape of low-mass stars.

Our results have implications for our understanding of GC evolution. In ‘vanilla’ models of cluster evolution without BHs, the relaxation driven escape rate on the orbit of Pal 5 is about ~ 1 M_⊙/Myr (Figure 2). We note that our noBH models have much higher escape rates, but this is because they start with lower initial densities than what is usually done⁷. It is well-established that the mass loss rate in ‘vanilla’ models is insufficient to ‘turn-over’ a power-law initial cluster mass function with index –2, as is observed for young star clusters in the nearby Universe, into the observed peaked (logarithmic) mass distribution with a typical mass of 2 × 10⁵ M_⊙: too many low-mass GCs survive beyond ≳ 5 kpc⁵⁰. The required escape rate is about an order magnitude larger: 20 M_⊙/Myr⁵¹. From our models we can conclude that Pal 5 is currently losing mass at that rate (Figure 2), hence if a large fraction of GCs go through a similar evolutionary phase, then relaxation driven evaporation is more important in shaping the GC mass function than usually assumed, reducing the need for additional GC disruption mechanisms^40,41 or a peaked initial cluster mass function. Because variations in ƒ_BH lead to an order of magnitude variation in the escape rate (Figure 2), we conclude that the effect of BHs is of comparable importance in shaping the GC mass function as the details of the Galactic orbit.

Discussion

We now consider our results in the context of the Milky Way GC population. About 10% of the Milky Way GCs have R_eff ≳ 10 pc, which led some authors to suggest that two-body relaxation is not important and that their evolution is collisionless^12,52. These fluffy GCs are found predominantly at large Galactocentric radii and have low masses (≲ 10⁵ M_⊙). More specifically, beyond ≳ 8 kpc from the Galactic center, half of the GCs have R_eff = 10 – 20 pc³⁸. Our results suggest that these large and low-density GCs are BH rich. Their low densities, relative to the tidal densities on their orbits can be used to constrain their initial densities and masses in a similar way as we did for Pal 5. In wBH-1, about half of the observable stars are lost in the last 3 Gyr and in this period the stream became visible above the background. Combined with the remaining lifetime of ~ 1 Gyr, Pal 5 has an observable stream for 30% of its lifetime. There are 26 low-density GCs beyond 8 kpc from the Galactic center and for about half of them tidal tails or tidal features have been found (Supplementary Table 1). Of these, there are 12 that are at distances comparable to Pal 5, or closer. If we assume that the escape rate is the same for these GCs, combined with the fact the GC mass function is uniform at low masses, then about 30% of these GCs are in the final 30% of their evolution. From this we expect that ~ 4 GCs to have prominent tidal tails, providing an explanation for the rarity of Pal 5 and the low-number of known GCs with streams. We can now make an order of magnitude estimate of how many streams the MW fluffy GC population has generated in the past. The ~ 10 fluffy, nearby, GCs all have masses below 10⁵ M_⊙, hence the mass function of fluffy clusters is dN/dM ≃ 10⁻⁴ $M_{\odot }^{-1}$. If these GCs all lose mass at a constant rate of 20 M_⊙/Myr, then this mass function is constant in time and we expect that these GCs contributed 2 × 10⁻³ streams per Myr, or about 20 streams in the last 10 Gyr. This estimate supports the idea that the ~ 3^1–4 known cold streams in the halo resulted from BH-rich, extended GCs that dissolved in the Milky Way halo.

We conclude with a discussion on observational tests of the BH hypothesis. We computed the rate of microlensing events of background quasars in the field of Pal 5 and find that the event rate is too low (~ 10⁻⁸/yr). We then looked at the effect of BHs on stellar kinematics and found that it is possible to infer the BHs from the kinematics of the stars. For a BH fraction of 22%, the velocity dispersion of giant stars within R_eff is 580 m/s, which is ~ 200 m/s higher than for a cluster without BHs (Figure 6). The significance of the available velocity dispersion measurement of 550±¹⁵⁰₁₁₀ m/s³⁹ can be improved by increasing the sample of stars, and constraining the properties of binary stars, including their orbital periods. We estimate an upper limit for the periods of binaries with giant stars of P ≃ 0.5 yr, because longer period binaries were ionised by interactions with BHs. Finding a binary with a larger period would challenge our BH hypothesis, while the absence of such binaries could in combination with additional N-body model with primordial binaries be used as support for it. Finally, BHs with stellar binary companions may also exist28 and could be found from their large velocity variations. A multi-epoch observing campaign to obtain line-of-sight velocities is therefore needed to establish with high precision the central velocity dispersion and the properties of the binaries (see Methods for details). This would provide the critical test of the hypothesis that Pal 5 hosts a ≳ 2 × 10³ M_⊙ population of stellar-mass BHs.

Figure 6. Surface density profiles and velocity dispersion of models with and without BHs.

Fits of King models54 plus a constant background (green lines and shaded region representing the 1σ uncertainty) to the surface density profile of observable stars (blue circles with error bars indicating the 67% confidence interval) for wBH-1 (a) and noBH-1 (b). Panels (c) and (d) show the resulting velocity dispersion of the model fits scaled to a total mass of 5 × 10³ M_⊙ and half-mass radius of 25 pc and assuming that the total mass is due to all the stars, white dwarfs and neutron stars, i.e. no BHs. Blue points with error bars in (c) and (d) are the dispersions in the N-body models of the giants within R_eff scaled to the same mass and half-mass radius for wBH-1 and noBH-1, respectively. For noBH-1 the dispersion of the giants is 0.35 ± 0.04, consistent with the King model prediction. For wBH-1, this dispersion is 0.58 ± 0.06 km/s, or 3σ above the central dispersion prediction from the King model. With precise line-of-sight velocities and a photometric mass estimate this difference is detectable.

Methods

Milky Way model and orbit of Pal 5

We adopt a time-independent, axisymmetric Milky Way, consisting of a dark matter (DM) halo, a disc and a bulge. We derive the Milky Way parameters and the orbit of Pal 5 from a fit to the Pal 5 stream. This stream fit is nearly identical to that in Erkal et al.³⁴ which used the MWPotential2014 potential of Bovy⁵⁵, but we use updated priors based on more recent measurements of distance⁵⁶ and proper motion⁵⁷ of Pal 5 and the distance to the Galactic center⁵⁸. The fit treats Pal 5’s present-day distance, radial velocity, proper motions, the distance to the Galactic center, and the DM-halo mass and scale radius as free parameters.

The DM halo is described by a spherical NFW profile⁵⁹, with potential

$${\Phi }_{\text{halo}}\left(R_{\text{G}}\right)=-\frac{G{M}_{\text{NFW}}}{R_{\text{G}}}\text{ln}\left(1+\frac{R_{\text{G}}}{a_{\text{NFW}}}\right),$$ (1)

where R_G is the Galactocentric radius, M_NFW = 4.38713 × 10¹¹ M_⊙ is a mass scale and a_NFW = 16.043 kpc is the scale radius. For these parameters the virial mass and concentration are M_vir = 8.127 × 10¹¹ M_⊙ and c = 15.3, respectively. We note that these parameters are close to those of Bovy⁵⁵. The disc potential is that of an axisymmetric Miyamoto-Nagai disc⁶⁰

$${\Phi }_{\text{disc}}\left(R_{\text{G}}\right)=-\frac{G{M}_{\text{MN}}}{{\left[X^2+Y^2+{\left(a_{\text{MN}}+\sqrt{Z^2+b^2}\right)}^2\right]}^{1/2}},$$ (2)

where M_MN = 6.8 × 10¹⁰ M_⊙ is the mass of the disc, a_MN = 3 kpc is the disc scale length and b = 0.28 kpc is the scale height and X, Y, Z are Cartesian Galactocentric coordinates (i.e. R2 = X² + Y² + Z²). The bulge is described by a Hernquist potential⁶¹

$${\Phi }_{bulge}(R_G)=-\frac{G{M}_H}{R_G+a_H},$$ (3)

with M_H = 5 × 10⁹ M_⊙ the bulge mass and a_H = 0.5 kpc its length scale. The bulge model is slightly different from what was used by Erkal et al.³⁴, but within the orbit of Pal 5 the total enclosed mass of both bulge models is the same.

Cartesian Galactocentric phase-space coordinates of Pal 5 in the potential described above were given by the fit: [5.733,0.2069,14.34] kpc and [–41.33, –111.8, –16.85] km/s. The Sun is found to be at [–8.182, 0, 0] kpc, with a velocity of [11.1, 245.7, 7.3] km/s, which puts Pal 5 at a distance from the Sun of 19.98 kpc. To find the initial position and velocity of Pal 5’s orbit, we flipped the sign of the velocity vector and integrated the orbit backward in time. We adopt an age of 11.5 Gyr^62–64 and fix this for all models. The typical uncertainty on the age determinations is ~ 1 Gyr and varying the age would somewhat increase the uncertainty on our initial parameters, but not the parameters of our best model. The initial Galactocentric position and velocity of Pal 5 are [1.212,10.08, 2.744] kpc and [43.16, –162.6,147.0] km/s, respectively.

Cluster initial conditions and N-body code

The initial positions and velocities of the stars were sampled from an isotropic Plummer model⁶⁵, truncated at 20 scale radii. Initial stellar masses were sampled from a Kroupa IMF66 in the range 0.1 – 100 M_⊙ and a metallicity of Z = 6 × 10⁻⁴ was adopted, i.e. [Fe/H] ≃ –1.4¹³. All simulations were run with the direct (i.e. no softening) N-body code NBODY6++GPU ^29,67,68, which deploys a 4^th-order Hermite integrator with an Ahmad-Cohen neighbour scheme^69,70. It has recipes for stellar and binary evolution^71,72, with recent updates for BH masses and kicks³⁰ and it deals with close encounters with Kustaanheimo-Stiefel (KS) regularisation. We use the Graphics Processing Unit (GPU)-enabled⁷³ version and the simulations were run on a server with GeForce RTX 2080 Ti GPUs at ICCUB. A few modifications to the code were made for this project. The singular isothermal halo was replaced by the NFW halo, with the force and force derivatives derived from equation (1). Stars were stripped from the simulation when they reached a distance of 40 times the instantaneous half-mass radius of the bound particles and for each escaper the time, position and velocity in the Galactic frame was stored. The escapers were then integrated as tracer particles in the Galactic potential until 11.5 Gyr with a separate integrator to construct the tidal tails. We did not include the contribution of the cluster to the equation of motion of the tail stars. Near the end of the simulation the fractional contribution of the cluster to the total force is approximately 2 × 10⁻⁵ for stars that just left the cluster, and smaller for stars at larger distances, justifying this assumption. All models were evolved until complete dissolution, and for the models that dissolved after 11.5 Gyr, a snapshot was saved at exactly 11.5 Gyr, i.e. when the cluster is at the position of Pal 5 today.

Black hole recipes

The fast evolution codes SSE⁷¹ for stars and BSE⁷² for binaries in NBODY6++GPU were recently modified³⁰ with updated prescriptions for wind mass loss, compact object (i.e. neutron stars and BHs) formation and supernova kicks²¹. We adopt here the rapid supernova mechanism in which the explosion is assumed to occur within the first 250ms after bounce²¹, which corresponds to nsflag=3 in SSE/BSE. The BH natal kick velocities are drawn from a Maxwellian with dispersion σ = 265 km/s⁷⁴, and in the wBH models they are subsequently lowered by the amount of fallback such that momentum is conserved (i.e. kmech = 1). As a result, 63%(73%) of the number(mass) of BHs does not receive a kick for the IMF and metallicity we used. The BHs that receive a kick form from stars with ZAMS masses in the range 23 – 34 M_⊙, resulting in BH masses in the range 6 – 26 M_⊙, and because of the low escape velocities of our model clusters (10-20 km/s) they are almost all lost. As a result, the lowest mass BH in the cluster just after supernovae and kicks has a mass of 13 M_⊙ and the average BH mass is 21 M_⊙.

In natal kick models that consider the effect of fallback of mass on the BH⁷⁵, the exact fraction of BHs that do not receive a kick depends on the prescription for compact-object formation. For our IMF and metallicity we find for the STARTRACK, rapid, and delayed explosion mechanisms described in section 4 of Fryer et al.²¹, that about 83%, 73% and 56% of the total BH mass is in BHs that form without a natal kick, respectively. Our result of 73% is therefore an intermediate value. A lower(higher) initial ƒ_BH requires a lower(higher) initial cluster density to end up with the same cluster properties at the present day.

Pal 5 parameters

To find the number of observed stars (N_cluster) and half-light radius (R_eff) of Pal 5, we fit King models⁵⁴ to the density profile of figure 10 of Ibata et al.⁷⁶ using limepy⁷⁷ and the Markov Chain Monte Carlo (MCMC) code EMCEE⁷⁸. We fit for the dimensionless central potential: W_o = 4.6 ± 0.3, the number of observed stars: N_cluster = 1550 ± 40, the half-mass radius: r_h = 4.3 ± 0.1 arcmin and the background: 0.07 ± 0.01 arcmin⁻². For these parameters R_eff = 3.21 ± 0.06 arcmin, which for the adopted distance to Pal 5 of 19.98 kpc corresponds to R_eff = 18.7 ± 0.4 pc.

Data analysis

For each simulation, snapshots were saved approximately every 50 Myr. For each snapshot, we find the stars and remnants that are energetically bound to the cluster, i.e. which have a specific energy $E_i=0.5v_i^2+{\varphi }_i<0,$ where v is the velocity in the cluster’s center of mass frame and ϕ_i is the potential due to the mass of the other bound stars, which we determine iteratively. From the bound particles we determine the total cluster mass M, the mass of the BH population M_BH, the half-mass radius r_h, N_cluster and R_eff.

To compare the N-body models to observations, we use isochrones to convert masses of stars in different evolutionary phases to magnitudes. We use SDSS g-band magnitudes from MIST isochrones^79,80 for 11.5 Gyr, Z = 6 × 10⁻⁴ ([Fe/H] = −1.4), [α/Fe] = 0 and rotational velocities of 0.4 times critical. For the observations shown in Figure 1, CFHT photometry was used⁸¹ which is a slightly different photometric system than SDSS. A color transformation is provided by Ibata et al.⁸¹. For the magnitude limits we adopt here, the colors of Pal 5 stars vary between 0.3 ≲ (g – r)_CHFT ≲ 0.5 in the relevant magnitude range, resulting in corrections in the g-band between 0.07 – 0.11. We therefore adopt gsŋss = g_CFHT + 0.1 to convert between the two systems. For the observed number density profile, a magnitude range of 19 < g_CFHT < 23 was used by Ibata et al.¹¹. We apply the corresponding magnitude range 19.1 < g_SDSS < 23.1 and combined with the adopted distance (DM=16.5 mag) this implies a mass range of main sequence stars of 0.625 – 0.815 M_⊙, which is what we use to select stars in the N-body model to construct the surface density profile. For the stream we selected stars with 20.3 < g_CFHT < 23.5 mag (i.e. 20.4 < g_SDSS < 23.6) as in Ibata et al.⁸¹. This magnitude cut implies mass limits that depend on the distance of stars in the tidal tails.

Finding the best model

We varied the initial number of stars N₀ and the initial half-mass density ρ_h0 and try to reproduce N_cluster and R_eff. For the wBH models, we first ran a coarse grid of models with N₀ = [50k, 100k, 200k] and ρ_h0 = [30,100, 300,10³] M_⊙/pc³. We ran each combination of N₀ and ρ_h0, apart from N₀ = 200k and ρ_h0 = 10³ M_⊙/pc³. For each model we computed the fractional differences between the N-body results and the observations for N_cluster and R_eff at 11.5 Gyr: δ_N and δ_R, respectively, and then define the best model as the one for which $\delta \text{=}\sqrt{{\delta }_N^2+{\delta }_R^2}$ is lowest. For each model we also find the time to reach N_cluster = 1550 (i.e. T₁₅₅₀). We introduce T₁₅₅₀ to establish a goodness of fit for models that dissolve before 11.5 Gyr. Model IDs are increasing with the value of δ and for clusters that dissolved the ID is in order of increasing difference between T₁₅₅₀ and 11.5 Gyr. The model with the smallest δ in the coarse grid has N₀ = 200k, ρ_h0 = 100 M_⊙/pc³ and reproduces the two observables within 10%. From the coarse grid we estimate that a slightly larger N₀ and lower ρ_h0 would reduce the difference. We then ran a finer grid with 6 more models with N₀ in the range 210k – 225k and ρ_h0 in the range 70 – 80 M_⊙/pc³. The model with the smallest δ, wBH-1, has N₀ = 210k and ρ_h0 = 80 M_⊙/pc³. It reproduces both observables within 3% and it has a present-day mass of 9.5 × 10³ M_⊙, r_h = 18.8 pc and ƒ_BH = 0.22. For the noBH models, we first ran five models with N₀ = [100k, 200k, 300k, 400k, 500k] and ρ_h0 = 10 M_⊙/pc³, two models with N₀ = [100k, 200k] and ρ_h0 = 30 M_⊙/pc³ and two models with N₀ = 100k and ρ_h0 = [100, 300] M_⊙/pc³. Models with ρ_h0 = 10 M_⊙/pc³ gave results similar to the observations. We then ran an additional 11 models with densities ρ_h0 < 10 M_⊙/pc³ and 200k ≤ N₀ ≤ 500k and found that the model with the lowest δ has N₀ = 350k and ρ_h0 = 9.625 M_⊙/pc³. All model results are summarised in Tables 1 and 2.

Rate of growth of the tidal tails and their visibility

From the escaping stars we find that half of the observable stars in the tails of wBH-1 were ejected in the final 3 Gyr. To estimate the number of MW field stars in Figure 4 that share the same locus in color-magnitude as Pal 5, we use the CFHT data and color-magnitude selection criteria from Ibata et al.⁸¹. Additionally, we select only stars more than 0.4 deg away from the best-fit stream track from Erkal et al.³⁴ and adopt their magnitude limits of 20.0 < g_CFHT < 23.5 mag. This sample is dominated by MW field stars and has an average density of 0.142 stars/arcmin². Note that Pal 5 stream runs roughly at a constant b in the region explored in Figure 5, thus variations in the MW field density with position are negligible.

Predictions for observations

To estimate whether the BH population can be detected from the kinematics, we look at the velocity dispersion of the wBH-1 model. Within R_eff (~ 3.2 arcmin), there are 40 giant stars, with a line-of-sight velocity dispersion of 0.69 ± 0.09 km/s. Because our wBH-1 model has a steeper mass function than Pal 5, the mass of wBH-1 is likely too high. We therefore scale our model results to a conservative mass of 5 × 10³ M_⊙11 (excluding BHs) and r_h = 25 pc. This reduces the predicted dispersion of the giants to 0.58± 0.06 km/s. In the noBH-1 model we find 51 giants within R_eff, which have a (scaled) line-of-sight dispersion of 0.42±0.04 km/s. We then fit King models54 and a constant background using LIMEPY77 to the number density profile of bright main sequence stars shown in Figure 1(a). In Figure 6(a,b) we show the results. For wBH-1 we find a dimensionless central concentration of W₀ = 5.9 ± 0.2, r_h = 27.7± 0.8 pc, which results in R_eff = 20.8 ± 0.6 pc. For noBH-1 we find W₀ = 5.2 ± 0.3, r_h = 31.5 ± 1.1 pc, which results in R_eff = 23.9 ± 0.4 pc. We then derive the line-of-sight velocity dispersion of the King models by adopting a total mass (excluding the BHs) of: 5 × 10³ M_⊙ and r_h = 25 pc. The resulting velocity dispersion profiles are shown in Figure 6(c,d). The central dispersion of the King models is ~ 0.4 km/s. The dispersion of the giants in the noBH-1 model agrees with this, which means that the derived dispersion provides an accurate measure of the total mass when assuming that the surface density traces the total mass. For the wBH-1 model, however, the dispersion of the giants is about 50% (or 200 m/s) higher. A small part of this difference can be explained by the fact that wBH-1 is a factor of 1/(1 – 0.22) ≲ 1.3 more massive, because of the BHs. This higher mass increases the dispersion by a factor of $\sqrt{1.3}\simeq \mathrm{1.14.}$ The additional factor of 1.3 needed to explain the dispersion of the giants is because the BHs are centrally concentrated, inflating the central dispersion more than in the mass follows light assumption. Although it is challenging to find a 200 m/s velocity difference, it is feasible with existing high-resolution spectographs (R ~ 20 000) on 8m-class telescopes with a multi-epoch observing strategy. Baumgardt & Hilker39 present a compilation of line-of-sight velocities of Milky Way GCs. There are 32 stars in their Pal 5 sample, and the dispersion of the inner 15 stars is ${0.55}_{-0.11}^{+0.15}\text{km}/\text{s}.$ From a comparison of N-body models to the kinematics and surface brightness profiles the authors derive a central dispersion of 0.6 km/s. For such a low dispersion the orbital motions of binary stars are important. The authors have repeat observations for about half of their stars, and they reject stars with large velocity variations. Their result supports the BH hypothesis, but a more thorough analysis of the binary content is desirable. Pal 5 has approximately 50(100) stars brighter than g < 19(20) mag within 3 arcmin from the center for which (additional) line-of-sight velocities can be obtained. For individual measurement errors of 300 m/s and a velocity dispersion of 400 m/s, the estimated uncertainty in the velocity dispersion for 50(100) stars is 63(43) m/s, i.e. smaller than the difference between wBH-1 and noBH-1. Similar uncertainties can be obtained even when simultaneously fitting on the velocity dispersion and the properties of binary stars⁸².

The BH scenario also make a critical prediction for the properties of the binary stars. Soft binaries are ionised when they interact with stars83 and the binaries with the lowest binding energy are therefore indicators of the most energetic cluster members, including invisible remnants. From wBH-1 we find that the average kinetic energy of the BHs is 〈K_BH〉 = 〈0.5mv²〉 ≃ 10 M_⊙(km/s)², while for all the other stars, white dwarfs and neutron stars we find 〈K*〉 ≃ 0.3 M_⊙(km/s)². Adopting circular orbits and equal-mass binary components of 0.8 M_⊙ (i.e. the mass of giants for which we can obtain velocities) we find that the orbital period is capped at P_max ≃ 2.3× 10⁴(120) yr because of interactions with stars(BHs). However, finding no binaries with P > 120 yr does not confirm the presence of BHs, because the cluster was initially more massive and compact, such that soft binaries had shorter periods. From the initial mass and half-mass radius of wBH-1(noBH-1) we find that the initial 〈K〉 was a factor of 45(30) higher, implying that in the BH case, the maximum binary period is P_max ≃ 0.5 year, while in the noBH hypothesis the maximum period is P_max ≃ 140 yr. This suggests that the presence of binaries with 0.5 ≲ P/yr ≲ 140 would be an argument against the presence of a BH population, while the absence of such binaries combined with more detailed predictions from N-body simulations with primordial binaries could be used as support for the BH case. For P = [1,10,100] yr, the orbital velocities are [12, 5.8, 2.7] km/s, hence these binaries would be easily detectable with a baseline of weeks/months and moderate spectral resolution. In addition, multi-epoch kinematics serves to look for stars with a (detached) BH binary companion such as found in NGC3201^28,84. Although dynamical formation of BH binaries is more common, a BH with stellar companion can form in an exchange interaction⁸⁵.

We note that several studies have put forward observational signatures of BH populations in clusters by using dynamical models. These studies used either the degree of mass segregation^32,86,88 or other observational properties of GCs⁸⁹ to make predictions for the size of the BH populations in a subset of Milky Way GCs. None of these studies included Pal 5, so we can not make a comparison. We can check whether these methods would be able to infer the correct BH population given our model properties. From the scaling between ƒ_BH and the ratio of core over half-light radius (R_core/R_eff) shown in Figure 7 of Weatherford et al.88 and the ratio R_core/R_eff ≃ 0.5 in wBH-1, we would infer that Pal 5 has a BH population of (only) ƒ_BH ≃ 0.3 – 1%. The reason the inferred ƒ_BH from their relation is so different could be because R_core/R_eff saturates or goes down again for vary large ƒ_BH where they have no models, or because of a systematic difference in Rcore between the Monte Carlo and N-body methods^90,91. Using the fitted relations provided by Askar et al.⁸⁹ (see their Table A1) between the global properties of stellar-mass BHs and the observational properties of their host globular cluster, they find that about 50% of the mass in Pal 5 could be in stellar-mass BHs.

Microlensing event rate

For a BH mass of 17 M_⊙ at a distance of 20 kpc, the Einstein angle is θ_E ≃ 2.6 mas. In wBH-1 there are 124 BHs, mostly within R_eff ≃ 3 arcmin, resulting in a surface density of Σ_BH ≃ 1.2 × 10⁻⁹ mas⁻². The proper motion of Pal 5 is μ ≃ 3.2 mas/yr, such that the event rate for a single background source (i.e. an AGN) is θ_EΣ_BHμ ≃ 10⁻⁸/yr. In the recent AGN catalogue from the Gaia and WISE surveys⁹² we find 2 AGNs within R_eff of Pal 5, too low to get to a reasonable event rate. The event rate would be larger if we also consider background halo stars, but even with the estimated density of background galaxies in LSST (~ 50/arcmin²), the lensing event rate would be too low (~ 10 ⁻⁵ yr).

Data availability

A snapshot of the wBH-1 model is published on zenodo (doi:10.5281/zenodo.4739181). All N- body data are available upon request.

Code availability

NBODY6++GPU is available from https://github.com/nbodyx/Nbody6ppGPU. LIMEPY is available from https://github.com/mgieles/limepy.