Loss of neuronal network resilience precedes seizures and determines the ictogenic nature of interictal synaptic perturbations

Abstract

The mechanisms of seizure emergence, and the role of brief interictal epileptiform discharges (IEDs) in seizure generation are two of the most important unresolved issues in modern epilepsy research. Our study shows that the transition to seizure is not a sudden phenomenon, but a slow process characterized by the progressive loss of neuronal network resilience. From a dynamical perspective, the slow transition is governed by the principles of critical slowing, a robust natural phenomenon observable in systems characterized by transitions between dynamical regimes. In epilepsy, this process is modulated by the synchronous synaptic input from IEDs. IEDs are external perturbations that produce phasic changes in the slow transition process and exert opposing effects on the dynamics of a seizure-generating network, causing either anti-seizure or pro-seizure effects. We show that the multifaceted nature of IEDs is defined by the dynamical state of the network at the moment of the discharge occurrence.

Introduction

Epilepsy is the most common chronic neurological disorder affecting approximately 0.5% of the population in developed countries. It is characterized by the enduring propensity of the affected area of brain to generate spontaneous and repeated seizures¹. A seizure is a dramatic shift in brain dynamics that occurs when a large neuronal population becomes excessively active and synchronized². The seizure state is naturally inherent to the brain³. However, the dynamical route to seizure initiation varies, and several possible pathways have been proposed^{3, 4}. In a normal brain, an acute symptomatic seizure can emerge under extreme stochastic circumstances like systemic intoxication, metabolic disturbances or in association with a documented brain insult⁵. By contrast, seizures in epilepsy recur spontaneously and are unprovoked. Their seemingly unpredictable and random occurrence is the major debilitating factor. The actual mechanisms and dynamical principles responsible for seizure emergence within the epileptic brain remain an enigma. Theoretical and modeling studies have proposed several dynamical pathways governing the transition to seizure^{6, 7}. Experimental verification and identification of the neurobiological mechanisms governing their dynamics is a crucial prerequisite for our understanding of epilepsy and seizure genesis.

During interictal periods (i.e. between seizures), the presence of pathologically interconnected neurons manifests as brief and transient episodes of synchronous activity known as interictal epileptiform discharges (IEDs)⁸. The role of IEDs in the transition to seizure is still a matter of intense debate, and available theories appear mutually exclusive⁹. Studies demonstrate that IEDs can be either a seizure preventing^{10, 11} or seizure facilitating^{12, 13}. Such dichotomy is currently explained by the existence of distinct cellular, synaptic and network mechanisms that underlie the genesis of different forms of IEDs⁹.

In the current study, we aimed to address these crucial and still unresolved aspects of seizure genesis, firstly, how do seizures emerge from neural networks and what dynamical trajectories do they follow, and subsequently, what is the role of IEDs in seizure genesis? We demonstrate that the transition to seizure is associated with the progressive loss of neural network stability and a slow, but inevitable shift towards the seizure^{7, 14, 15}. This process displays features of critical slowing¹⁵, a dynamic phenomenon, which has gained increasing attention across various research fields, because it is able to capture the essence of the dynamics of a wide range of natural systems characterized by alternations between dynamical regimes (ranging from cell signaling to ecosystems and climate)¹⁶. More importantly, elucidation of the governing dynamical principles of the transition to seizure can explain the observed dichotomy of the complex role of IEDs on seizure genesis and allows unification of antagonizing theories and observations. Based on our results, we propose a new theory explaining the multifaceted nature of IED.

Results

Seizures and interictal activity in the isolated CA1 and intact hippocampi

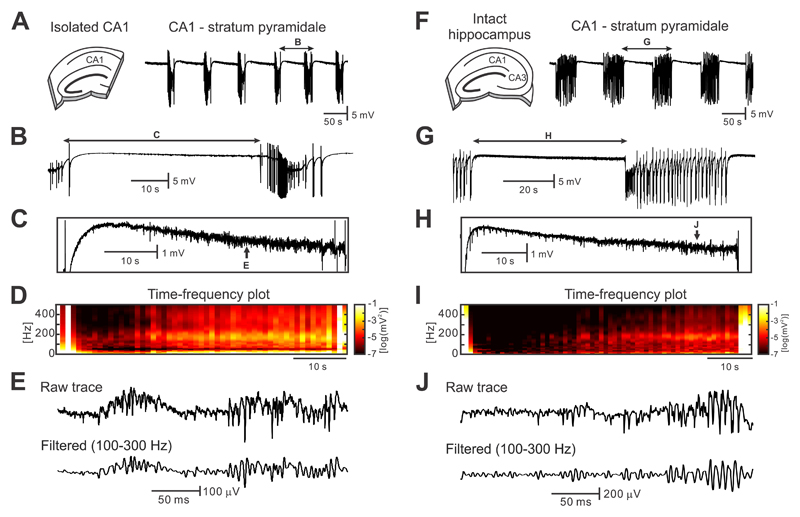
In this study, we have analyzed 67 intact hippocampal slices and 73 isolated CA1 slices in total. Perfusion of isolated CA1 slices, with the CA3 region resected, with artificial cerebral spinal fluid (ACSF) containing 8-10 mM potassium led to the occurrence of spontaneous and recurrent electrographic seizures (Fig. 1a-b). The average duration of the seizures was 14.3±0.8 s (n=114/17 seizures/slices) and the periods between seizures (i.e. the interictal periods) lasted 50.3±2.4 s (n=114/17 interictal periods/slices). Interictal periods were characterized by the presence of high-frequency activity (HFA) with an average peak frequency of 191.2±6.5 Hz (n=17 slices) and an amplitude of 82.6±4.8 μV with superimposed multiunit activity (Fig. 1c-e). HFA occurred early after perfusion of the slice with high-potassium and preceded the development of seizures.

Figure 1. Seizures and interictal activity in the high-potassium model.

(a) In the isolated CA1, perfusion of ACSF with a potassium concentration of 8-10 mM leads to the development of spontaneous and repeated seizure-like episodes (n=114/17 seizures/slices). (b,c) Periods between seizures are characterized by the presence of HFA ~190 Hz with superimposed unit activity. These electrographic phenomena are accompanied by decreasing DC shift (n=27/9 interictal periods/slices). (d) Time-frequency map demonstrates the progressive increase in power in a high-frequency band with approaching seizure (n=114/17 seizures/slices). (e) Detail of interictal HFA. (f) In intact hippocampal slices, seizures are also generated within the CA1 region (n=83/15 seizures/slices). (g-i) Interictal periods in the intact hippocampus are characterized by the increase in amplitude and power of HFA (n=83/15 interictal periods/slices), the negative shift in DC potential (n=24/8 interictal periods/slices) and also by the presence of interictal discharges. (j) Example of interictal HFA in intact hippocampal preparation.

Similar electrographic activity was observed in intact hippocampal slices with preserved CA3-CA1 connectivity (Fig. 1f-j). In this slice preparation, seizure duration was 44.4±1.3 s (n=83/15 seizures/slices) and the period between seizures lasted 69.8±2.1 s (n=83/15 interictal periods/slices; Fig. 1f). Seizures were characterized by an initial tonic phase followed by clonic discharges (Fig. 1g). Between seizures, the CA1 generated HFA, which had a frequency of 176.9±5.8 Hz and an amplitude of 167.8±40.7 μV (n=15 slices; Fig. 1h-j).

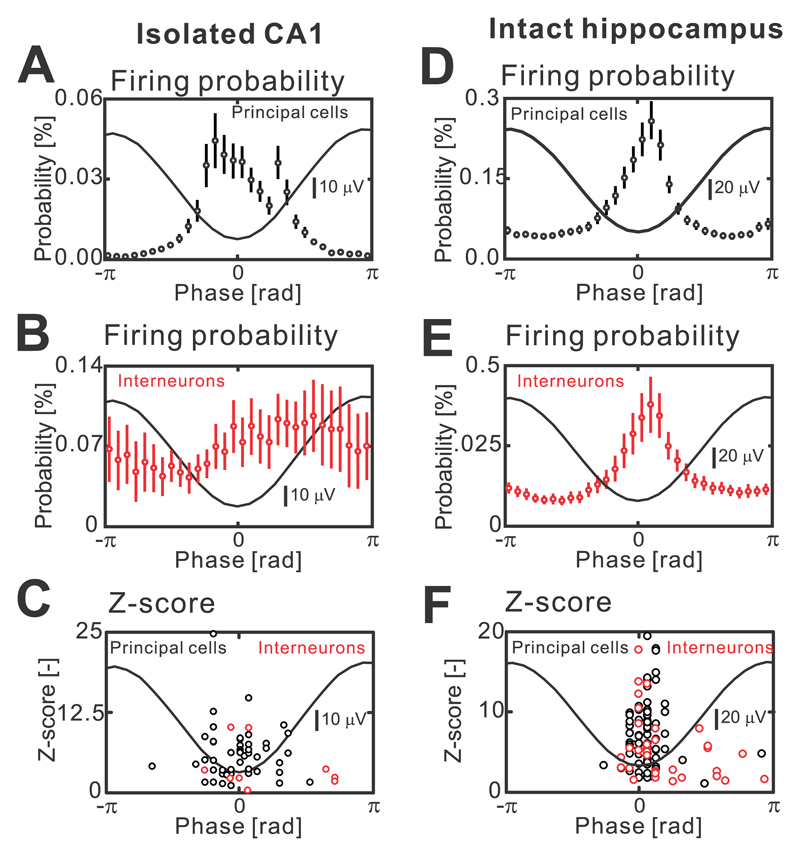
In isolated CA1, the analysis of current source density profiles has suggested that individual HFA cycles are due to action potential firing of neurons (Supplementary materials Fig. 1a-d). Tetrode recordings, phase analysis of cellular firing and estimation of the strength of firing modulation using z-score, demonstrated that the negative phase of the HFA cycle was accompanied by significant increases in the probability of all pyramidal cell firing (n=47/4 cells/slices, Kolmogorov-Smirnov test, P<0.05; Fig. 2a,c). The activity of interneurons was not uniform during the HFA cycle, and the phase relationship of individual interneurons with the HFA cycle displayed increased phase firing variability (n=9/4 cells/slices, Kolmogorov-Smirnov test, P<0.05; Fig. 2b,c). Spatially, the HFA was present across the entire CA1 region (n=50 slices; Supplementary materials Fig. 2b). Application of NMDA (APV 25 μM, n=9 slices) or non-NMDA (NBQX, 20 μM, n=10 slices) antagonists did not block the HFA. In intact hippocampus, the HFA shared a similar morphology, spatial properties (Supplementary materials Fig. 1e-h) and pharmacological profile to HFA observed in isolated CA1 preparations. The action potential firing of all principal cells displayed a significant increase during the trough of the HFA cycle (n=72/13 cells/slices, Kolmogorov-Smirnov test, P<0.05; Fig. 2d,f). However, we observed a greater trough-coupled action potential firing in a subpopulation of interneurons (n=35/13 cells/slices, Kolmogorov-Smirnov test, P<0.05; Fig. 2e,f), than in the interneuronal profiles recorded in isolated CA1 preparations.

Figure 2. Cellular properties during cycles that comprise interictal HFA.

(a) In the isolated CA1, the HFA cycle lasts around 5 ms (Supplementary Fig. 1). The cycle is characterized by an increased firing probability of principal cells during HFA troughs (n=47/4 cells/slices, Kolmogorov-Smirnov test, P<0.05). (b) An average phase histogram of interneuronal activity in the isolated CA1 (n=9/4 cells/slices, Kolmogorov-Smirnov test, P<0.05). (c) Z-value for individual neuron types and the timing of peak firing probability of individual cell. (d) The firing probability of principal cells (n=72/13 cells/slices, Kolmogorov-Smirnov test, P<0.05) and interneurons (e) (n=35/13 cells/slices, Kolmogorov-Smirnov test, P<0.05) is significantly modulated with the maximum probability around the trough of a HFA cycle. (f) Z-values of phase histogram distribution for each cell. Circles and error bars represent mean and s.e.m.

These data, supported by previous studies^{17, 18}, suggest that HFA represents low amplitude population spikes due to co-firing of a small number of pyramidal cells with a moderate interneuronal contribution.

Interictal HFA dynamics display features of early-warning signals

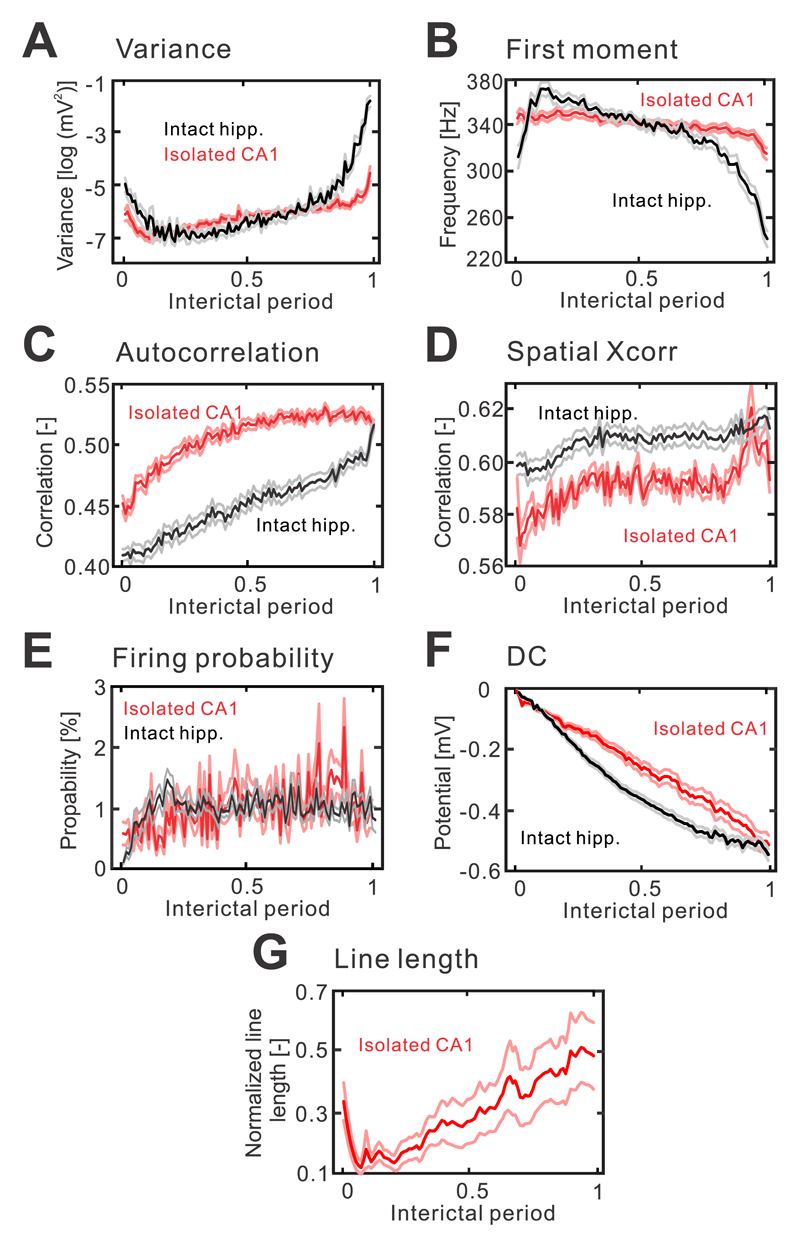
The observed HFA did not remain uniform in its properties; it displayed dynamic changes as the seizure approached (Fig. 1c,h). To describe these changes we applied several measures, which are indicative of a progressive loss of resilience and an approaching transition to a different dynamic regime ¹⁶. These measures included variance, frequency, autocorrelation and spatial correlation; in complex dynamics theory, they are called early-warning signals. In isolated CA1 preparations, the spatiotemporal profile of HFA was characterized by a progressive increase in signal variance (n=76/17 interictal periods/slices, one-way ANOVA, F_(1,7500)=154, P=0.000; Fig. 3a). Temporal evolution of the frequency profile of HFA was characterized by the progressive slowing of the first moment of power spectra in the 100-500 Hz band (n=76/17 interictal periods/slices, one-way ANOVA, F_(1,7500)=336, P=0.000; Fig. 3b) and an increase in autocorrelation (n=76/17 interictal periods/slices, one-way ANOVA, F_(1,7500)=1821, P=0.000; Fig. 3c). On the spatial scale, cross-correlation analysis demonstrated the gradual spatial expansion of HFA with the approaching seizure (n=8/2 interictal periods/slices, one-way ANOVA, F_(1,700)=206, P=0.000; Fig. 3d). At the cellular level, we observed an overall increase in neuronal firing (isolated CA1: n=56/4 cells/slices, one-way ANOVA, F_(1,3900)=51, P=0.000; Fig. 3e), which combines the increase, decrease or no change in firing of individual neurons. In intact hippocampal slices, the spatiotemporal profile of variance (n = 57/15 interictal periods/slices, one-way ANOVA, F_(1,5600)=307, P=0.000), first moment (n=57/15 interictal periods/slices, one-way ANOVA, F_(1,5600)=1830, P=0.000), autocorrelation (n=57/15 interictal periods/slices, one-way ANOVA, F_(1,5600)=1726, P=0.000), spatial correlation (n=40/11 interictal periods/slices, one-way ANOVA, F_(1,3900)=127, P=0.000) and neuronal activity (n=107/13 cells/slices, one-way ANOVA, F_(1,4100)=9, P=0.012) displayed a similar dynamical evolution as the seizure approached (Fig. 3a-e). In both slice preparations, the changes in early-warning signals were accompanied by a negative DC shift (n=24/8 interictal periods/slices, one-way ANOVA, F_(1,2399)=35, P=0.000 for intact hippocampal slice; n=27/9 interictal periods/slices, one-way ANOVA, F_(1,2699)=13, P=0.000 for isolated CA1; Fig. 3f). Apart from the early-warning signals, the loss of a system’s stability is characterized by increased sensitivity to perturbations and a delayed recovery from them. The dynamical stability can be evaluated by actively delivering the perturbation^{19, 20}. In isolated CA1 sections, we have examined the stability from the response of the system to stimulation of the Schaffer collaterals. The response was quantified using line length of the signal, which combines both measures, i.e. changes in duration and amplitude respectively (Supplementary materials Fig. 3). With the approaching seizure, the response to perturbation of constant intensity, progressively increased (n=24/8 interictal periods/slices, one-way ANOVA, F_(1,2399)=2, P=0.000; Fig. 3g),

Figure 3. Interictal changes in HFA properties display features of early-warning signals of the critical transition to seizure.

(a) In both slice preparations, seizures are preceded by a significant increase in HFA amplitude variance (isolated CA1: n=76/17 interictal periods/slices, one-way ANOVA, F_(1,7500)=154, P=0.000 for isolated CA1; intact hippocampus: n = 57/15 interictal periods/slices, one-way ANOVA, F_(1,5600)=307, P=0.000). The duration of interictal periods was normalized from 0 to 1. (b) Seizures are preceded by frequency slowing, which manifests as a progressive decrease of the first moment of power spectra (isolated CA1: n=76/17 interictal periods/slices, one-way ANOVA, F_(1,7500)=336, P=0.000 for isolated CA1; intact hippocampus: n=57/15 interictal periods/slices, one-way ANOVA, F(1,5600)=1830, P=0.000). (c) Autocorrelation (lag=5 ms; isolated CA1: n=76/17 interictal periods/slices, one-way ANOVA, F_(1,7500)=1821, P=0.000; intact hippocampus: n=57/15 interictal periods/slices, one-way ANOVA, F_(1,5600)=1726, P=0.000) and spatial correlation (d) (isolated CA1: n=8/2 interictal periods/slices, one-way ANOVA, F_(1,700)=206, P=0.000; intact hippocampus: n=40/11 interictal periods/slices, one-way ANOVA, F_(1,3900)=127, P=0.000) increase in advance of seizures. (e) At the single cell level, the seizures are predominantly preceded by an increase in cell firing (isolated CA1: n=56/4 cells/slices, one-way ANOVA, F_(1,3900)=51, P=0.000; intact hippocampus: n=107/13 cells/slices, one-way ANOVA, F_(1,4100)=9, P=0.012). (f) In both preparations, the early-warning signals are accompanied by a negative DC shift (isolated CA1: n=27/9 interictal periods/slices, one-way ANOVA, F_(1,2699)=13, P=0.000; intact hippocampus: n=24/8 interictal periods/slices, one-way ANOVA, F_(1,2399)=35, P=0.000). (g) In the isolated CA1, seizures are preceded by progressively increasing amplitude and duration of the response evoked by stimulations of Schaffer’s collaterals (n=24/8 interictal periods/slices, one-way ANOVA, F_(1,2399)=2, P=0.000). The responses were quantified using line length measurement. Lines and shaded lines represent mean and s.e.m respectively.

The presence of early-warning signals of an impending critical transition derived from the properties of HFA, suggest that with an upcoming seizure the CA1 becomes less resilient and progressively approaches the critical point (critical bifurcation) beyond which the dynamics within the CA1 enter the seizure regime. In intact hippocampal slices, however, this process of critical transition was substantially modified by the synchronous synaptic input incoming from the IEDs originating in the CA3 region.

The impact of CA3 synaptic input on the critical transition to seizure

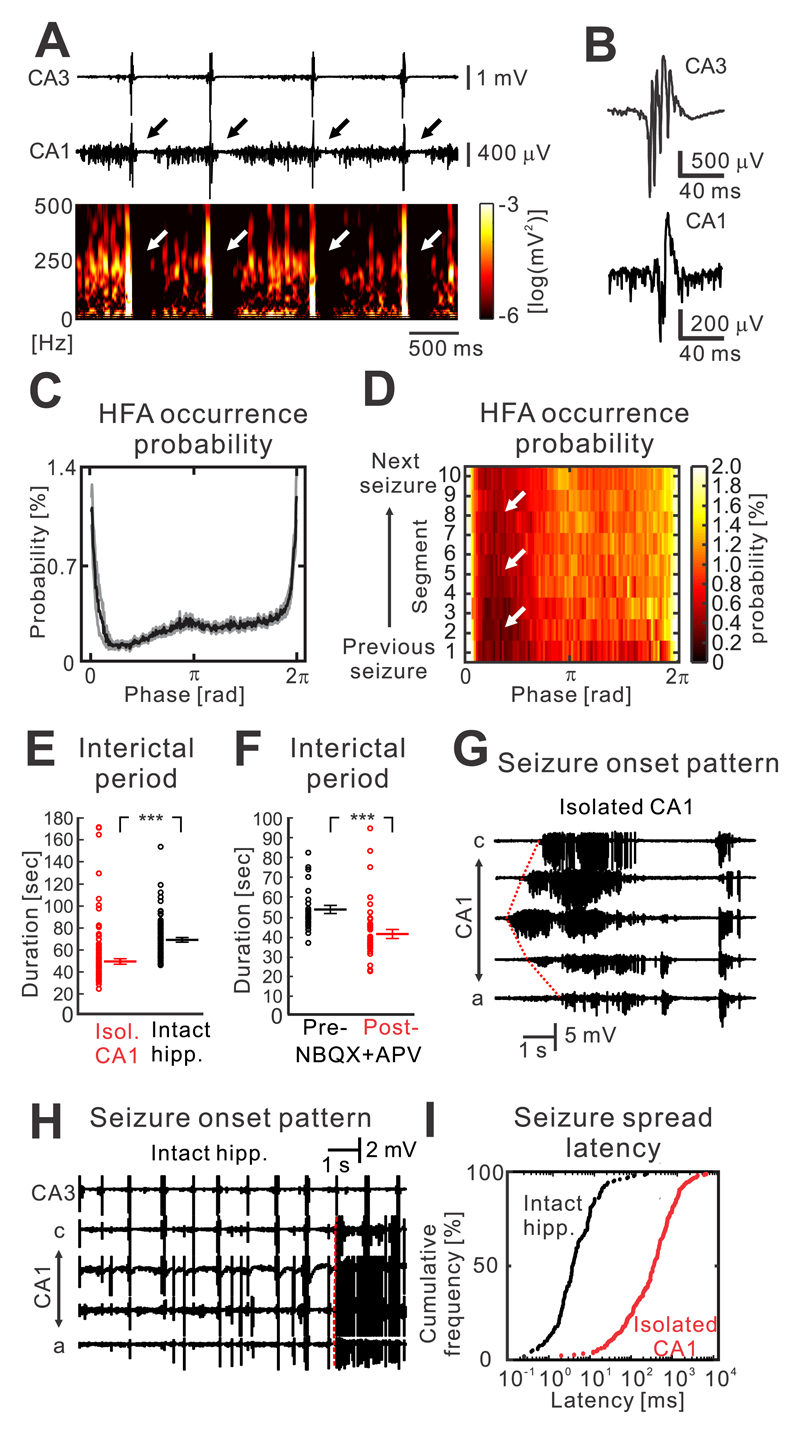
In an intact hippocampal slice, CA3 (predominantly the CA3b region) generated spontaneous and repeated IEDs with a duration of 68.9±2.6 ms and an amplitude of 1.7±0.2 mV (n=17 slices; Fig. 4a,b). IEDs occurred approximately periodically with a mean frequency of 1.2±0.1 Hz, and they were dependent on intact glutamatergic transmission (n=12 slices). Spatially, they propagated to the entire CA1 with an average propagation time of 6.4±0.5 ms (n=12 slices). In the CA1, propagated IEDs represented a population of excitatory postsynaptic potentials with an amplitude of 0.4±0.1 mV (n=17 slices; Supplementary materials Fig. 4). In the CA1, IEDs interfered in a phasic manner with the pre-seizure dynamics of HFA and the process of critical transition. During each discharge, the probability of HFA occurrence transiently increased and HFA amplitude increased to 224.5±53.2 μV (n=17 slices; Fig. 4a-c). The discharge was then followed by suppression or absence of HFA and neuronal firing for >300 ms (Fig. 4a,c). Then HFA and neuronal activity progressively increased until the next IED. In summary, the presence of discharges induced phasic changes in HFA, which were superimposed on the slow changes in the properties of HFA described in the previous section. This phasic profile of HFA was maintained during the entire interictal period (n=17 slices; Fig. 4d).

Figure 4. Impact of IEDs on the transition to seizure.

(a) IEDs interfere with the slow process of transition to seizure and HFA. Raw data and the corresponding time-frequency plot demonstrate the suppression of HFA after each discharge. (b) Details of IEDs generated in the CA3 and propagating to the CA1. (c) The average phase histogram demonstrates that the probability of HFA occurrence substantially increases during the peak of the discharge. It is then followed by transient HFA suppression and then its gradual increase until the next IED (n=15 slices). (d) Post-discharge suppression of HFA persists throughout the course of entire period between seizures. (e) Periods between seizures in intact hippocampi (n=83/15 interictal periods/slice) have longer duration than in isolated CA1 preparations, where the IEDs are absent (n=114/17 interictal periods/slice; two-sided Mann-Whitney-Wilcoxon U test, U=1577, P=0.000). (f) Block of IEDs by NBQX and APV also shortens the interictal period (baseline recording: n=27/5 interictal periods/slices; post-NBQX+APV: 42/5 interictal periods/slices, two-sided Mann-Whitney-Wilcoxon U test, U=188, P=0.000). (g) IEDs modify the seizure initiation pattern. In isolated CA1 preparations, seizures are characterized by focal initiation and slow spread of seizure activity to the rest of the CA1. (h) In intact slices, seizures initiate instantaneously across large areas or the entire CA1 due to incoming IEDs from the CA3. (i) Cumulative histogram of the seizure spread velocity in the intact hippocampus and isolated CA1 slices demonstrates that the seizure spreads by nearly two orders faster than in the intact slice. P<0.001 (***). Line and error bars represent mean and s.e.m respectively; ***P ≤ 0.001.

To explore the IED capacity to delay the onset of seizures, we examined the duration of periods between seizures in individual preparations. In the isolated CA1, the duration of the interictal period was 50.3±2.4 s (n=114/17 interictal periods/slice), while in intact slices the period between seizures lasted 69.8±2.1 s (n=83/15 interictal periods/slice, two-sided Mann-Whitney-Wilcoxon U test, U=1577, P=0.000; Fig. 4e). Pharmacological blockade of IEDs in intact slices with NBQX and APV led to shortening of the interictal period from 53.6±2.1 (n=27/5 interictal periods/slices) to 41.4±2.3 s (42/5 interictal periods/slices, two-sided Mann-Whitney-Wilcoxon U test, U=188, P=0.000; Fig. 4f).

The discharges also influenced seizure onset and its pattern. In isolated CA1 slices, the seizure onset was characterized by the spontaneous emergence of low-amplitude rhythmic activity from a single recording channel, which gradually increased in amplitude and progressively spread across the CA1 with an average time delay of 639.3±63.2 ms between adjacent electrodes (n=86/7 seizures/slices; Fig. 4g,i). In intact slices, synchronous excitatory synaptic input from CA3 was able to trigger a seizure and change its onset pattern to a high-amplitude heralding discharge occurring synchronously across the entire or large parts of the CA1 with an average delay of 10.4±2.1 ms (n=49/9 seizures/slices; Fig. 4h,i).

Our data suggest that the CA3 input perturbs the slow process of the transition to seizure within the CA1 region and that the response to this perturbation is determined by the dynamical state of the CA1 area. During the interictal period, the transient phasic suppression of HFA after IED may have a stabilizing (anti-seizure) effect and a capacity to delay the seizure onset. However, when the CA1 dynamics are close to seizure initiation (critical bifurcation), the transient fast increase in excitation or neuronal firing due to the incoming IED may have a destabilizing (pro-seizure) effect capable of prematurely shifting the CA1 dynamics into the seizure and rapidly synchronizing seizure initiation over large spatial scales.

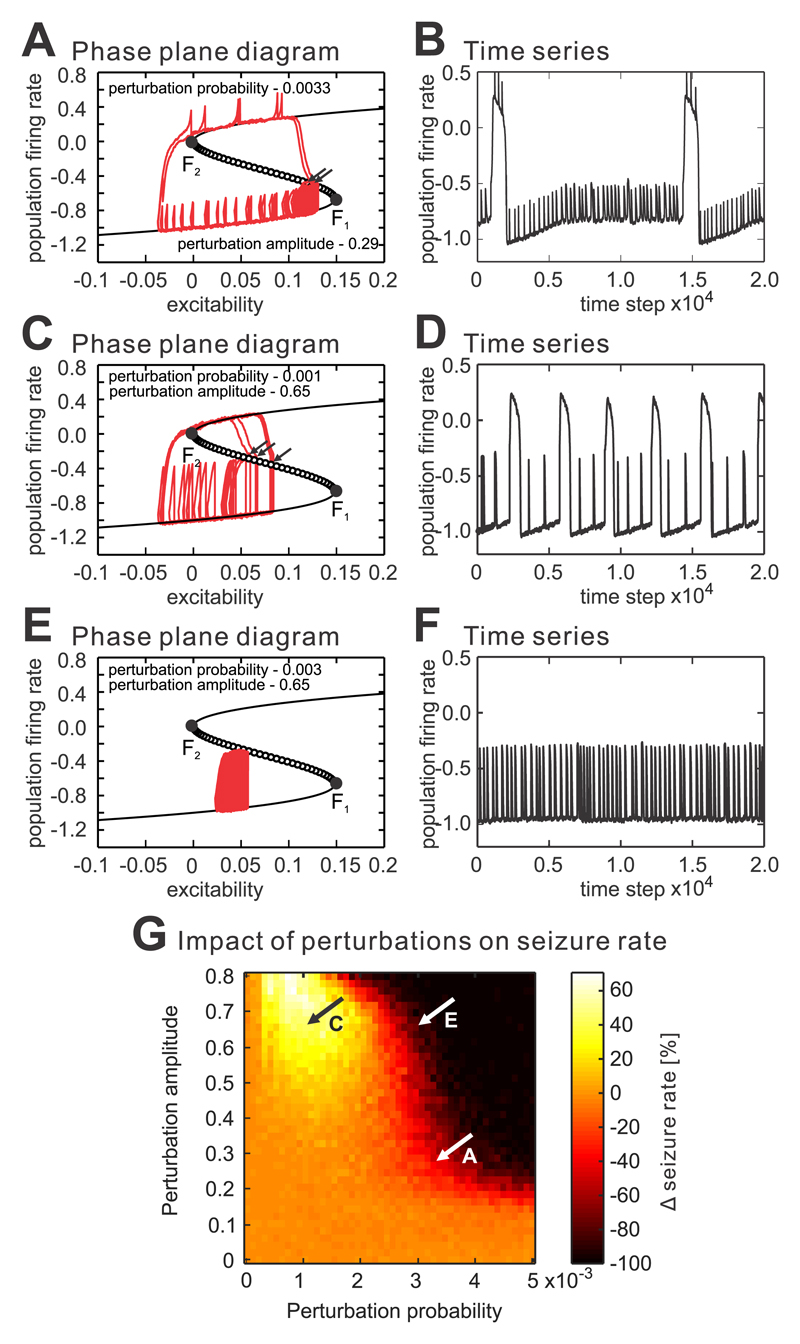
Modeling of cyclic dynamical shifts and the impact of interictal perturbations

To evaluate in detail the impact of CA3 synaptic perturbations on CA1 dynamics, we implemented a model of the slow-fast process^{14, 21}, which simulates the cyclic dynamical shifts to seizure that are characteristic of in vitro models of seizures. In this model, the excitability represents the slowly changing variable, while the population-firing rate represents the fast variable. For small values of excitability, the system has a single dynamic equilibrium (stable fixed point) corresponding to a low-firing state between seizures (Supplementary materials Fig. 5a). For high excitability values, the system has a single equilibrium at a high-firing state, i.e. seizure. For intermediate excitability values, the system is characterized by the existence of two stable states and the curve describing the response of the system to external perturbations has the feature of a fold catastrophe separated by an unstable equilibrium (unstable fixed points, Supplementary materials Fig. 5a). This system has two catastrophic fold bifurcations (F₁, F₂) when an infinitesimally small change in a control parameter induces large changes in the system dynamics by shifting it to the contrasting dynamical regime (for F₁ interictal→seizure and for F₂ seizure→interictal). If the slow-fast process is driven by dynamical changes in excitability, its dynamics have the character of a limit cycle (Supplementary materials Fig. 5b), periodically switching between seizure and interictal state (Supplementary materials Fig. 5b,c; Supplementary video 1) mimicking the dynamics observed in isolated CA1 slices. In such a scenario, the system will always slowly, but inevitably shift towards seizure.

In a dynamically changing system, we have explored the impact of IEDs on the transition to seizure. The perturbations were represented as approximately periodic transient increases in the population firing rate. Perturbation, which did not increase the firing rate beyond the unstable fixed point, shifted the system to the left, to a more stable state with lower excitability, before recovering from the perturbation (Fig. 5a,c,e; Supplementary video 2). It mimics the ‘refractory period’ observed after each IED. As a result, the IED increased the distance from the catastrophic bifurcation and slowed down the transition to seizure. If the perturbation was capable of crossing the unstable point then the dynamics of the system shifted to a seizure and the perturbation had a destabilizing pro-seizure effect (Fig. 5a-d). However, these effects were dependent on the timing of the perturbation. If the system dynamics were approaching the catastrophic bifurcation to seizure, then even weak interictal perturbations were capable of shifting the system dynamics prematurely into a seizure (Fig. 5a,b; Supplementary video 2). Large amplitude perturbations had a stronger seizure inducing capacity, and they could initiate seizures far in advance of the catastrophic bifurcation (Fig. 5c,d; ; Supplementary video 3). We performed multiple iterations where we systematically varied the most important model parameters, i.e. amplitude of the perturbation and its occurrence probability. The simulations revealed complex non-linear effects of IEDs on the transition to seizure, which emerged directly from interactions between the perturbation amplitude, frequency and the timing of the discharge occurrence, with respect to the dynamical state of the system (Fig. 5g). The seizure delaying effect increased with the increased number of perturbations and with the amplitude of perturbation and could result in the complete abolition of seizures (Fig. 5e,f,g; Supplementary video 4). However, sparse large-amplitude perturbations had the capacity to substantially increase the seizure frequency (Fig. 5c.d,g).

Figure 5. The complex effect of interictal perturbations on the transition to seizure.

(a) Approximately periodic perturbations interfere with the slow-fast process, and frequent low-amplitude perturbations have an ambiguous effect on the transition to seizure. If the perturbation occurs at the moment when the system is far from the unstable fixed point (tipping point), it will lead to a transient increase in firing followed by a shift in the system’s dynamics back towards the more stable state (less excitable state). Such a perturbation has an anti-seizure property and prolongs the interictal period. In contrast, if the system is approaching the tipping point, then even small perturbations, which increase the excitability or firing rate can shift the system over the unstable fixed point and prematurely initiate the seizure (arrow). (b) The corresponding time series. (c,d) Rare high amplitude perturbations have the capacity to cross the unstable fixed (tipping) point (arrows) far in advance of catastrophic bifurcation F₁ and substantially increase the seizure rate. The pro-seizure effect of the perturbation out-performs the anti-seizure effect and is also dependent on the instantaneous dynamical state of the system. (e,f) Frequent high-amplitude perturbations can completely abolish the seizure by locking the system dynamics far from the tipping point and preventing the system from crossing the unstable region into seizure. (g) The probability of occurrence and amplitude of perturbations were systematically varied. The results demonstrate that all of the currently known effects on the transition to seizure, i.e. no change, increase, decrease in seizure frequency or the complete abolishment of seizures can be reliably replicated. Animations of the selected transitions can be found as Supplementary Videos.

The model of the slow-fast process is able to capture the basic complexity of the transition between interictal state and seizure. However, it neglects the faster dynamics of local field potentials, i.e. seizure discharges. To determine whether the inclusion of local field potential dynamics is essential for explaining the multifaceted nature of interictal perturbation, we ran the simulations with a more biologically realistic model – the Epileptor (Supplementary materials Fig. 6)³. In the modified version of the Epileptor, we were able to replicate all the state-dependent effects of interictal perturbation on ictogenesis ranging from an increased probability of transition to seizure prevention.

State-dependent effect of interictal perturbations

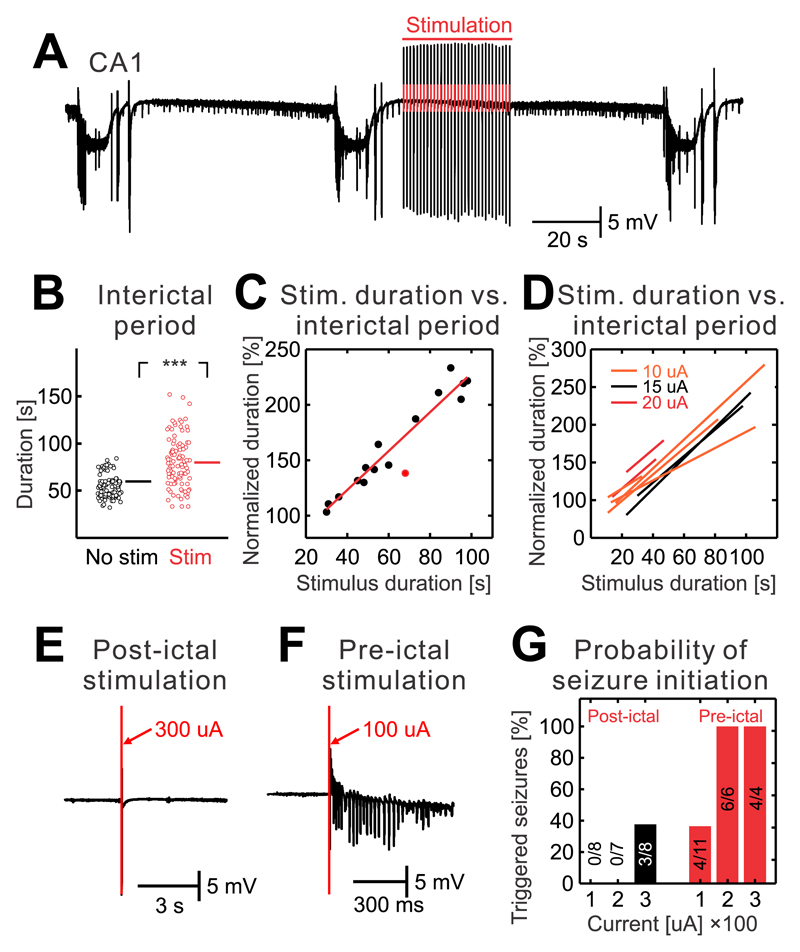
To explore theoretical predictions derived from the numerical simulations, we have performed set of experiments in which interictal perturbations were mimicked using stimulation of Schaffer collaterals in isolated CA1 preparations. First, the CA1 network was perturbed with regularly delivered stimuli with a frequency of 1 Hz. The stimulation was initiated after the end of the seizure (Fig. 6a). The duration of the interictal period with stimulation was compared with the nearest control interictal period. Results demonstrated that the early onset stimulation has the capacity to delay seizure onset by increasing the duration of the interictal period (n=213/8 stimulations/slices; Fig. 6a-d; two-sided Mann-Whitney-Wilcoxon U test, U=2180, P=0.000). Prolongation of interictal period positively correlated with the duration of the stimulation (Fig. 6c,d). To evaluate the observation, that the pro-seizure effect of IED occurs when the neural networks are unstable and close to the bifurcation point, we have delivered single stimuli early after the previous seizure (before 25 % of the time of the expected interictal period) and before the next seizure (after 75 % of the time of the expected interictal period; n=3 slices). Only 38 % of stimulations with the intensity of 300 μA were able to induce seizure (n=3/8 stimulations; Fig. 6e,g) if they were delivered during the early part of the interictal period. Meanwhile, all stimulations delivered before the seizure, were able to trigger seizures. Stimulation with the lowest intensity of 100 μA triggered a seizure in 36 % of cases (n=3/8 stimulations; Fig. 6f,g). Stimulation with an intensity of 200 μA and 300 μA induced seizure in all cases (6/6 and 4/4 stimulations respectively; Fig. 6g).

Figure 6. State-dependent effect of interictal perturbations.

(a) Seizures and interictal period without stimulation was followed by the interictal period when the train of Schaffer collateral stimulations (1 Hz) was delivered during early stages of the interictal period. The stimulation extended the duration of the interictal period. (b) The duration of interictal periods with and without early stimulations (n=213/8 stimulations/slices; two-sided Mann-Whitney-Wilcoxon U test, U=2180, P=0.000). (c) Example of an individual slice that was stimulated with an intensity of 15 μA. The results demonstrate that the duration of the interictal period increases with the duration of stimulation. Data were fitted with a regression curve. The red dot marks a stimulation, which was associated with a seizure. (d) Regression curves for individual slices and current intensities of the stimulation demonstrate the seizure-delaying effect of interictal perturbations. (e) A single stimulus of stronger intensity (300 μA) delivered during early stage of interictal period fails to induce seizures. (f) A stimulus of lower intensity (100 μA) delivered during the late phase of the interictal period has the capacity to initiate a seizure. (g) The probability of a seizure initiating effect of the stimulations delivered during the early and late stages of the interictal period (n=3 slices). During the early stages (black bars) only strong stimulations are capable of initiating seizures. During the later stage of the interictal period (red bars) both weak and strong stimulations have a higher probability to initiate seizure. Lines and error bars represent mean and s.e.m respectively; ***P ≤ 0.001.

Loss of resilience in a chronic model of temporal lobe epilepsy

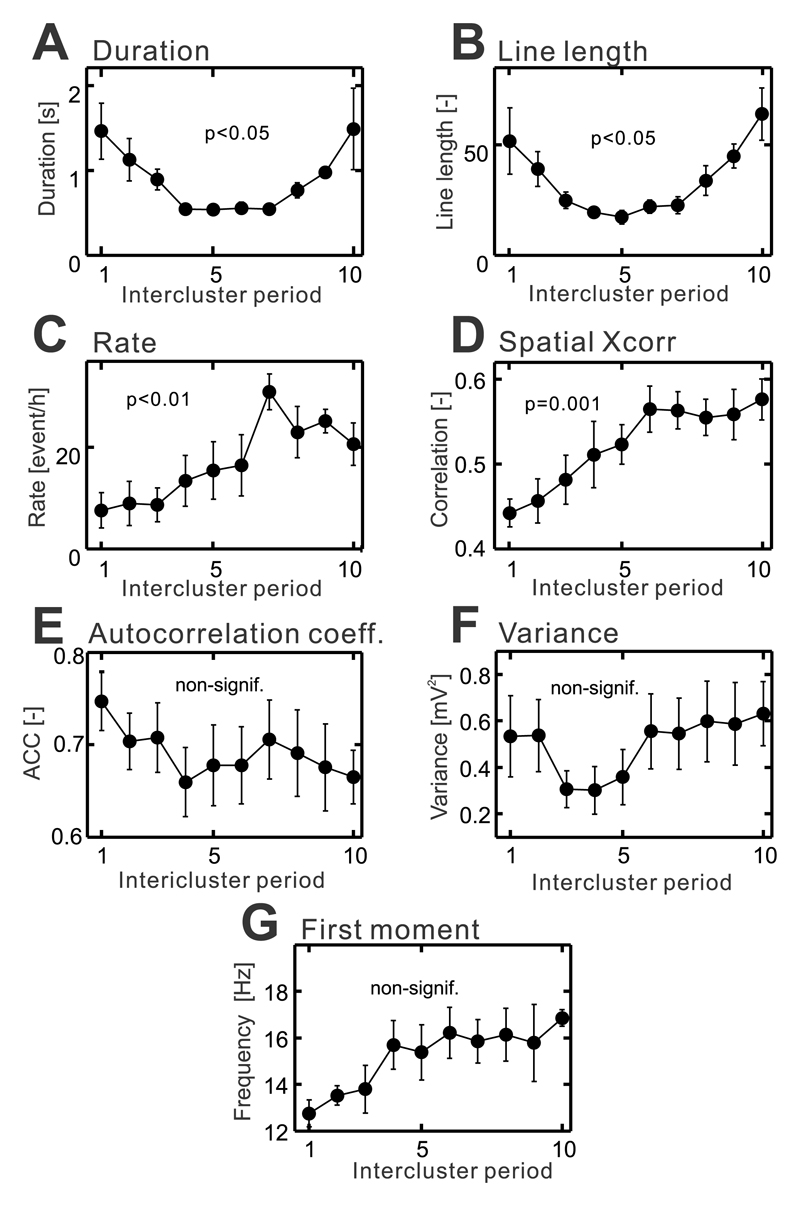
To ascertain whether the dynamical path characterized by the loss of resilience can be observed in vivo, we analyzed long-term recordings in the tetanus toxin model of temporal lobe epilepsy. In this model, we have observed changes in network stability over longer time scales. In the tetanus toxin model, seizures tend to cluster in time²² separated by seizure-free periods lasting 2.7±0.2 hours (n=6/6 intercluster periods/animal). Between seizures and clusters, a specific type of pathological activity known as epileptic bursts are present²². Bursts are characterized by an initial high-amplitude discharge followed by a burst of rhythmic activity. They have an origin in the injected hippocampus and they are distinct from IEDs (Supplementary Materials Fig. 7)^{22, 23}. The analysis of the properties of the burst (1041.3±149.2 bursts per cluster) from the perspective of critical slowing suggested that the period between clusters is characterized by a loss of the stability with the approaching cluster. The temporal profile of burst duration (n=6/6 intercluster periods/animals, one-way ANOVA, F_(1,53)=, P=0.012; Fig. 7a) and line-length (n=6/6 intercluster periods/animals, one-way ANOVA, F_(1,53)=, P=0.016; Fig. 7b) increased, which suggested that the brain displays a delayed recovery from the perturbation. Recent results from a network model demonstrated that the approaching critical transition to seizure can manifest as an increasing rate of interictal activity¹⁹, which would correspond to the observed increased rate of epileptic bursts (n=6/6 intercluster periods/animals, one-way ANOVA, F_(1,59)=, P=0.005; Fig. 7c). Spatial correlation of the bursts progressively increased (n=6/6 intercluster periods/animals, one-way ANOVA, F_(1,53)=, P=0.001; Fig. 7d) due to the enhanced propagation of bursts outside the right hippocampus to the left hippocampus and motor cortices of both hemispheres (Supplementary Materials Fig. 7b-d). We have not observed significant changes in autocorrelation (n=6/6 intercluster periods/animals, one-way ANOVA, F_(1,53)=, P=0.928; Fig. 7e), variance (n=6/6 intercluster periods/animals, one-way ANOVA, F_(1,53)=, P =0.814; Fig. 7f) or the first spectral moment of bursts (n=6/6 intercluster periods/animals, one-way ANOVA, F_(1,53)=, P =0.128; Fig. 7g).

Figure 7. Changes in the properties of epileptic bursts between clusters of seizures.

(a) With the approaching cluster the duration of the bursts increase (n=6/6 intercluster periods/animals, one-way ANOVA, F_(1,53)=, P=0.012), as well as, the line length parameter (b) (n=6/6 intercluster periods/animals, one-way ANOVA, F_(1,53)=, P=0.016). (c) The proximity to critical transition is also marked by the increasing rate of epileptic bursts (n=6/6 intercluster periods/animals, one-way ANOVA, F_(1,59)=, P=0.005). (d) Increase in spatial correlation reflects enhanced propagation of bursts to the hippocampus and motor cortex increased (n=6/6 intercluster periods/animals, one-way ANOVA, F_(1,53)=, P=0.001). (e) The autocorrelation (n=6/6 intercluster periods/animals, one-way ANOVA, F_(1,53)=, P=0.928), signal variance (f) (n=6/6 intercluster periods/animals, one-way ANOVA, F_(1,53)=, P =0.814) and the first spectral moment (g) (n=6/6 intercluster periods/animals, one-way ANOVA, F_(1,53)=, P =0.128) did not show significant changes with approaching cluster. The significance of changes in temporal profiles was analyzed using one-way ANOVA. Circles and error bars represent mean and s.e.m. respectively.

Loss of resilience and state-dependent effect of IEDs in humans

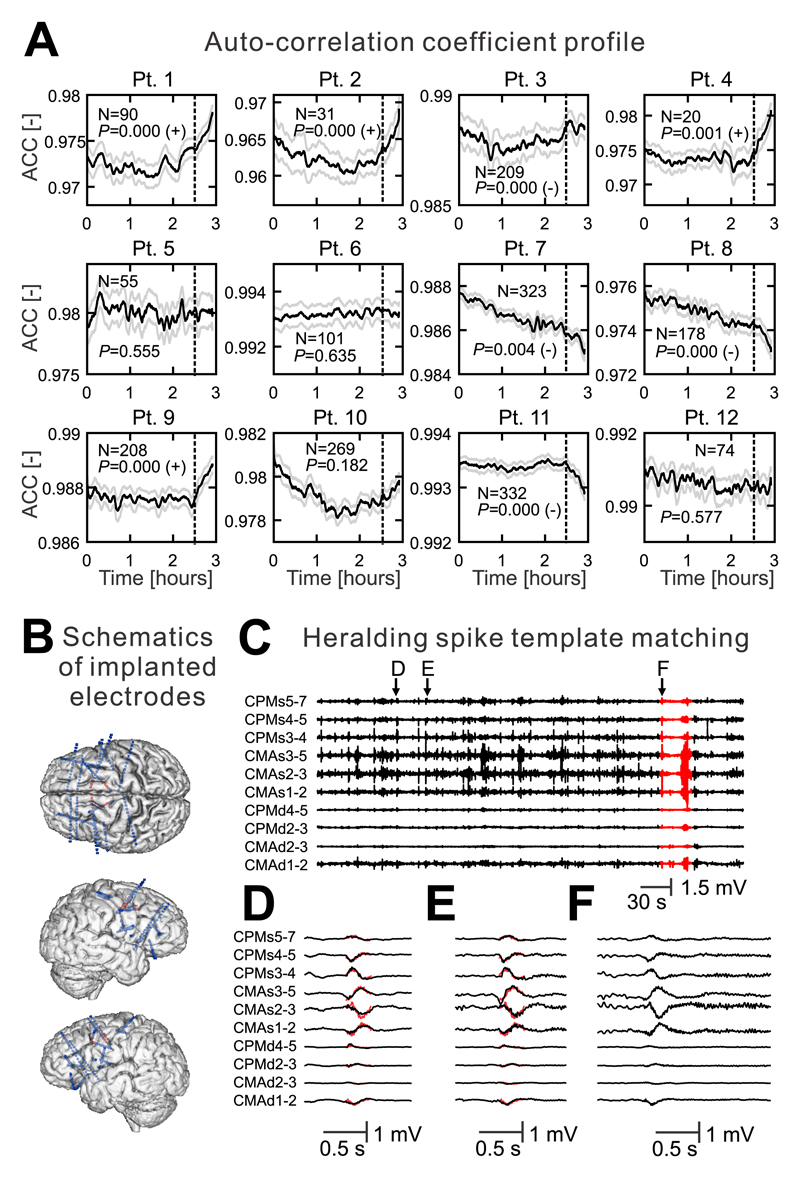
Next, we have explored whether the transition to seizure via critical slowing can be observed in humans. We have analyzed long-term intracranial recordings obtained from patients implanted with seizure prediction devices (n=12 patients)²⁴. The average number of recorded seizures per patient was 157.5±32.1 (n=12 patients). In these recordings, we have examined the temporal evolution of the lag-1 autocorrelation coefficient thirty-minutes prior to the seizure. In total, we have analyzed 1890 pre-ictal periods. In 4/12 patients, we have observed a statistically significant increase in lag-1 autocorrelation before the onset of their habitual seizures, which were consistent within each patient (Fig. 8a). In 2/12 patients we have observed a simulatenous increase in signal variance (Supplementary Materials Fig. 8). In 4/12 cases the autocorrelation and variance significantly decreased (Fig. 8a). One patient demonstrated only a decrease in variance. In 3/12 patients, the preictal changes were not significant. These results suggest that, at least for specific populations of patients, critical slowing is evident in the lead up to seizures.

Figure 8. The loss of resilience and state-dependent effect of IEDs in humans.

(a) Temporal profile of the autocorrelation coefficient (ACC) derived from intracranial recordings in 12 patients. The temporal profile three hours before a seizure is shown. The dashed line marks 30 minutes before the seizure during which the ACC profile was analyzed. In four patients, the ACC increases before the seizure. In four patients, ACC significantly decreases. N denotes the number of recorded seizures in each patient. P marks the value of Wilcoxon sign-rank test. The sign after the p-value indicates whether right-tailed (+) or left-tailed (–) Wilcoxon sign-rank test was significant. Lines and shaded lines represent mean and s.e.m. respectively. (b) Schematics of depth electrode implantation in a patient with refractory epilepsy. The signals from red contacts are shown. (c) An example of spontaneous activity recorded five minutes before and during the seizure (red) (d, e) Examples of the IEDs. Their waveforms and patterns of spatial distribution display a >98% match with the superimposed template of the heralding spike (red). (f) Heralding spike at the onset of a habitual seizure.

Next, we have explored the plausibility of the state-dependent effect of IEDs by testing the hypothesis based on in vitro and numerical observations, i.e. that the seizure-triggering spike (heralding spike) at the onset of seizure is an IED occurring during a highly unstable state of brain dynamics and capable of triggering a seizure. We compared heralding spikes to IEDs with respect to their morphology and spatial distribution using a template-matching algorithm. We have identified 37 seizures initiating with a heralding spike in 13 patients. In four patients, we found a total of eight heralding spikes that displayed a >98% morphological match to IEDs far in advance of the seizure which did not have the capacity to trigger the seizure (Fig. 8b-f).

Discussion

Seizure initiation marks the onset of a sudden and dramatic change in brain function, which represents the bifurcation of a dynamical system^{3, 6, 7}. The seizure can initiate through several bifurcation types, including Hopf, saddle-node and fold bifurcations^{25, 26}. The nature of a bifurcation can be inherent to specific seizure types (generalized tonic-clonic, absence or focal seizures with distinct seizure onset patterns), as well as reflecting the involvement of specific cellular and network mechanisms responsible for seizure initiation^{3, 25, 27}. To understand seizures and the enduring predisposition of the brain to generate seizures, it is crucial to elucidate the dynamical pathways through which the brain reaches the bifurcation point. Results from computational modeling replicating seizure dynamics have predicted the existence of specific pathways to ictal bifurcation^{7, 28}. One of the key concepts assumes the existence of bistable or multistable brain dynamics^{7, 26} where there is an initial separation between seizure and interictal state, and random perturbations do not have the capacity to reach the critical threshold to induce seizure. However, the distance between these dynamical regimes may progressively decrease due to slow changes in critical unstable parameters and manifest as a loss in the brain’s resilience as the seizure approaches^{7, 15, 19, 29}. In medicine, catastrophic transition has been shown to drive seizure termination³⁰, asthmatic attacks, cardiac arrhythmia and the onset or termination of depression^{16, 31}. In this study, we numerically, experimentally and clinically inferred that the transition to focal seizure follows this dynamical route and that the slow process displays dynamical features of critical slowing marking the progressive loss of neural network stability^{16, 21}. Early-warning signals derived from the properties of field potentials reflect the underlying discrete changes in stability of neuronal networks and the increased susceptibility to a seizure^{18, 32}. Further evidence of decreasing resilience can be derived from the response to active probing²⁰ or from the response to spontaneous perturbation¹⁹. The observed increasing probability of a pro-seizure effect of interictal synaptic perturbations with the approaching seizure, the progressively increasing sensitivity of the network to electric stimulation¹⁸ or increased rate of bursts can thus be indicative of weakening brain resilience. The idea that the brain becomes fragile in a barely visible or invisible way because of very subtle changes of a slow underlying process is the most counterintuitive aspect of critical slowing^{16, 29}. Whenever a large transition occurs, the causative event is intuitively sought in close vicinity to the transition and may result in the formulation of false causal relationships²⁹. Various cellular and network processes have been identified and postulated to play a crucial role in seizure genesis³³. However, the majority of these processes may represent only stochastic perturbations initiating a seizure in a neural network whose dynamics are already approaching the catastrophic bifurcation via critical slowing.

In this study, insights into the dynamics of seizure emergence have been the crucial prerequisite for clarifying the role of IEDs in seizure genesis – an unresolved issue that has attracted the attention of generations of epileptologists⁹. Evidence from experimental and clinical studies revealed that IEDs have both pro-seizure and anti-seizure effects^{10, 12, 13}. Disconnection of seizure-generating networks from brain regions generating IEDs or pharmacological block of IEDs leads to increased seizure frequency^{10, 34}, while electrical pacing mimicking IEDs can abolish seizures^{10, 34}. On the other hand, IEDs also have a well-documented capacity to induce seizures^{12, 13}. Studies examining changes in IED properties before seizures have described that IED frequency can increase, as well as decrease in advance of a seizure^{11, 35}. Finally, it has been claimed that IEDs have no relationship to ictogenesis at all³⁵. Such complex behaviour of IEDs is currently explained by the existence of different underlying cellular mechanisms³⁶. The first type of discharges are represented by glutamatergic ones, which can display a pro-seizure¹³ and anti-seizure effect^{10, 34}. In these types of discharges, the transient increase in excitation is usually curtailed by a subsequent suppression of the neuronal activity due to intrinsic neuronal mechanisms, inhibitory synaptic feedback, changes in the extracellular environment, etc.^{8, 37, 38}. The second class of IEDs is dependent purely on GABAergic transmission³⁹. They are accompanied by potassium transients and have been linked primarily with pro-seizure effects. IEDs in our study were of glutamatergic origin and throughout the course of the period between seizures they were always followed by a transient suppression of neuronal and network activity. These synaptic perturbations induced phasic changes, which interfered with the slow process of critical slowing and the discharges possessed both pro-seizure and anti-seizure effects, respectively. Combining experimental observations with modeling revealed that the complex effect of IEDs depends on when they occur, how often they occur and how strong the perturbations are in respect to the instantaneous dynamical state of the seizure-generating network and in respect to the character of the dynamical process that governs the slow transition to seizure. The combination of these factors could explain all the currently known effects of IEDs on seizure genesis and explain why their effects can vary in time. The anti-seizure effect is achieved via a subsequent suppression of neuronal activity, which shifts the neural network dynamics back to the more stable/resilient state. If the network is close to the tipping point, transient excitation/synchronization acts as a destabilizing perturbation, which impacts across large spatial scales. It then rapidly shifts the critical neuronal mass into a seizure in advance of the catastrophic bifurcation where the seizure would have occurred spontaneously^{18, 40}.

The implemented phenomenological model of the slow-fast process is a widely accepted model in nonlinear dynamics research^{14, 21, 29}, including applications in neuroscience and epilepsy modeling proper⁴¹. Despite being a very simplified model, it is able to capture and explain the rich and complex dynamical phenomena observed in our experimental work. The identified principles also operate in the more advanced model of the Epileptor³, which can replicate epileptiform phenomena in greater detail and which also depends on the presence of basic slow-fast dynamics of switching between seizure and non-seizure state. Other models of epileptic dynamics have been proposed to provide an explanation of the principles of seizure onset. Apart from the interictal perturbations, phenomena like, the various types of instabilities⁶, the role of network structure and network effects⁴², slow variations in global excitability⁴³, seizure spread⁴⁴ and the balance between excitation and inhibition²⁵ shape the seizure. However, experimental evidence points to the crucial role of the slowly changing variable of the slow process, which determines the dynamical trajectory of the epileptic brain, the probability of the transition to seizure and complex response to interictal perturbation. Numerical simulations and understanding the governing dynamical principles can be beneficial in the search for candidate mechanisms that underlie this slow process and for the design of dynamics-based control strategies²⁹. Also, a slowly changing process and loss of resilience have the potential to be better controlled than the random occurrence of stochastic perturbations initiating seizure. In the high-potassium model, seizures tend to occur after dozens of minutes when the CA1 network enters the bi-stable state, which suggests that ictal events depend on more complex processes than just a change in membrane potential. The transition to seizure is associated with a DC shift, which reflects slow progressive neuronal and glial membrane depolarization, which is closely but not ultimately, associated with the accumulation of potassium in the extracellular space, between seizures^{45, 46}. The slowly changing process may include a vicious circle of mutliple cellular and network changes ranging from an alteration in the KCC2 co-transporter, to increased intracellular load of chloride, erosion of inhibition, ectopic action potential generation and the involvement of non-synaptic interactions, etc.³³. The exact mechanisms underlying the slow process in humans or in vivo remain to be elucidated.

The results of this study suggest that the progressive loss of resilience of epileptic tissue may characterize the transition to both experimental and clinical seizures. In a complex system like a human or rat brain, the loss of resilience, critical slowing and the dynamical path of the transition to seizure can be substantially influenced by other parameters and processes like the progressive nature of epileptogenesis⁴⁷, long-term fluctuations in the brain’s predisposition to seize⁴⁸ and seizure clustering⁴⁷. Critical slowing will be difficult to observe if the seizure occurs prematurely due to a large external perturbation, which may be the case for some human subjects. Furthermore, critical slowing does not have to be the only dynamical pathway leading to seizure^{3, 7, 49} and trajectories leading to seizure can vary inter-individually, i.e. between patients, as well as intra-individually, within each patient^48–50. Recent theoretical work suggests that merging complex information about dynamical processes at multiple spatial and temporal scales can bring us much closer to understanding the principles of seizure emergence and initiation, and possibly to a unified theory of ictogenesis in the epileptic brain to explain the existence of the various classes of seizure type and transitions to them⁴⁹.

Online Methods

Animal and slice preparation

All experiments were performed under the Animals (Scientific Procedures) Act 1986 of the United Kingdom and Animal Care and Animal Protection Law of the Czech Republic fully compatible with the guidelines of the European Union directive 82010/63/EU. All experimental procedures were approved by the Institutional Biomedical Ethical Review Sub-Committee at the University of Birmingham and the Ethics Committee of The Czech Academy of Sciences. Animals were housed in groups under standard conditions in a room with controlled temperature (22±1°C) and 12/12 hour light/dark cycle. Animals for in vitro experiment were provided randomly by the animal facilities.

Transverse hippocampal slices (400 μm) were prepared from adult male Sprague-Dawley or Wistar rats (140-225g; 5-7 weeks of age; anaesthetized with ketamine (60 mg/kg) and medetomidine (0.25 mg/kg); killed by cervical dislocation). The slices were cut using Integraslice 7550 PSDS (Campden Instruments Ltd.) and immersed in chilled and oxygenated (95 % O₂ and 5 % CO₂) sucrose artificial cerebrospinal fluid (ACSF) containing 189 mM sucrose, 2.5 mM KCl, 26 mM NaHCO₃, 1.2 mM NaH₂PO₄·H₂O, 10 mM glucose, 5 mM MgCl₂, and 0.1 mM CaCl_2. In isolated CA1 slices, the CA3 area was cut off using a scalpel. The slices were stored, at room temperature, in a holding chamber filled with "normal" ACSF consisting of (in mM) 125 NaCl, 26 NaHCO₃, 3 KCl, 2 CaCl₂, 1 MgCl₂, 1.25 NaH₂PO₄, and 10 glucose, aerated with a humidified 95% O₂–5% CO₂ mixture. After >60 min, slices were transferred to an interface recording chamber (31-35°C) containing normal ACSF. Spontaneous seizure-like events were induced by perfusion of slices with high-potassium (8-10 mM KCl) ACSF.

In vitro electrophysiology

Extracellular field potentials were recorded using wire electrodes, which were fabricated in our laboratory from platinum/iridium wire (Advent Research Materials, Oxford, UK; diameter 25 μm, impedance <700 kΩ). Electrodes were positioned individually under visual control using a microscope and eyepiece graticule. For current source density studies electrodes were arranged along the somatodendritic axis of pyramidal cells with an interelectrode distance of 55-65 μm. To examine the spatial properties of recoded activity, electrodes were positioned along the CA1 with equal separation of 55-65 μm between electrodes. Extracellular field potentials were preamplified using a Neuralynx headstage amplifier (Neuarlynx, Inc., Tucson, USA), amplified (500x), low-pass filtered (3kHz) with Neuralynx Lynx-8 amplifiers and digitized at 5 kHz using Power 1401 analogue-digital converter and Spike2 software (Cambridge Electronic Design, Ltd., UK). Extracellular unit activity was recorded with tetrodes fabricated from tungsten wire (California Fine Wire, Grover Beach, USA; diameter 13 μm, impedance <700 kΩ). Signals from tetrodes were preamplified, 2000x amplified and filtered (high cut-off frequency 10 kHz) using Neuralynx. Data were sampled at 20 kHz. All signals were recorded in reference mode. The reference electrode was an Ag-AgCl wire (Advent Research Materials Ltd.; 0.37 mm in diameter) placed in the recording chamber outside the slice. DC recordings were performed with glass micropipettes (2–8 MΩ) filled with ACSF. Signals were amplified with an Axoclamp-1A (Axon Instruments, Union City, USA), Model 3000 AC/DC differential amplifier (A-M Systems, Seqium, USA), or Neurolog NL-106 and NL-125 amplifiers (Digitimer, Welwyn, UK). To mimic the interictal perturbations we used brief (200 μs) stimulation of Schaffer collaterals delivered using a bipolar, silver wire stimulating electrode and isolated constant current stimulator (Digitimer Ltd., Welwyn, UK).

In vitro data analyses

All data analyses were performed using Spike2 software (Cambridge Electronic Design, Cambridge, UK) and programmes written in our laboratories and running under Matlab (Mathworks Inc., USA). Only spontaneously seizing slices were included in the analysis.

Relative one-dimensional heterogeneous current source density CSD(z, t) as a function of depth z and time t was calculated using second-order differencing formula

$${\text{CSD}}_{(z,t)}={\sigma }_{(z)}\left\{\left[{\Phi }_{(z,t)}-{\Phi }_{(z-\Delta z,t)}\right]-{\sigma }_{(z+\Delta z,t)}\left[{\Phi }_{(z+\Delta z,t)}-{\Phi }_{(z,t)}\right]\right\}/{\left(\Delta z\right)}^2$$

where Φ_(z,t) is the potential value at depth z and time t and Δz is spacing between adjacent electrodes. We used known conductivity values for the CA1 region of Sprague-Dawley rats. Analysis was applied on band-pass filtered and averaged signals to determine the current source densities of specific electrographic activities.

Spike sorting was performed using Spike2 spike sorting toolbox and homemade Matlab routines. To detect spikes, recorded signals were band-pass (700-5000 Hz) filtered. The threshold for detection was set as 7SD of the background activity. To avoid false detections due to the presence of filtered IEDs, we introduced a second threshold to exclude high-amplitude events. We used a semi-automatic spike sorting approach. Spikes were sorted into clusters using an automatic template-matching algorithm, followed by manual clustering using the Spike2 graphic interface. The clustering process was based on the principle of plotting different waveform parameters and features from different electrodes. Principal component analysis was also used to extract features, usually from the first three components. Interspike interval histograms, event auto- and cross-correlograms were calculated during the clustering process to subdivide or merge clusters. If no clear refractory period (<2 ms) was detected in the autocorrelogram, the cluster was subdivided until a clear refractory period was present. Only units with clear refractory periods were included in the analysis. Then cross-correlograms between all possible pairs of units were calculated and examined for a symmetrical gap in the center bins. The presence of a gap (common refractoriness) suggested that two clusters represented the activity of the same unit, and therefore those clusters were merged. Interneurons and pyramidal cells were discriminated according to spike width and autocorrelation function¹⁸. Spikes of each unit were extracted from the original wide-band recording and averaged. The averaged spike was then resampled to 80 kHz and used to measure spike width at 25% of its amplitude.

Raw wide-band recordings were band-pass (100-300 Hz) filtered by an FIR filter. Troughs of individual oscillations with amplitudes greater than 7SD of background activity (activity with the absence of HFA) were identified. Cross-correlation functions were calculated between single unit activity and individual cycles of the fast activity, with the peak negativity of each cycle as the reference point. Auto- and cross-correlation histograms were normalized by dividing the count in each bin by the total number in all bins. To determine modulation of neuronal firing during the HFA cycle, individual cell firing phase histograms were calculated, normalized by dividing each bin by the total number of events and expressed as firing probability histograms. Using the Kolmogorov-Smirnov test we determined whether the neuronal firing was modulated (non-uniform distribution) and the strength of the modulation was determined using the z-score.

To determine the temporal profile of the several signal parameters including the early-warning parameters, the following parameters were determined: signal variance, amplitude, summated power, the first moment of power spectra, auto- and cross-correlation¹⁶. The signal was segmented into epochs lasting 0.75 s (unless otherwise stated) and for each epoch the specific parameter was calculated. The power spectrum for each epoch was estimated using the Morlet wavelet transforms¹⁸. The first moment of power spectra was determined within the range 100-500 Hz. Autocorrelation is the dynamic cross-correlations of field potentials between present period and the former period along the time domain. Field potentials were first offset by the sectional means in each 5 ms to reduce false positive correlations, and the correlations estimated between the current and the previous lags. To determine the spatial profile of the signals, cross-correlation was calculated between electrode pairs and then averaged. To allow comparison between individual slices and interictal periods, the obtained results were resampled and normalized into one hundred segments.

Tetanus toxin model of temporal epilepsy and in vivo electrophysiology

Six adult male Wistar rats weighing 350–540 g (9-17 weeks of age) were housed in groups under standard conditions in a room with controlled temperature (22±1°C) and 12/12 hour light/dark cycle. Surgical preparation was performed under isoflurane anaesthesia. Using a Hamilton microsyringe and infusion pump (KD Scientific Inc., USA) 1 μl of tetanus toxin (Quadratech Ltd., UK) solution was injected into the stratum radiatum of the right hippocampal CA3 area. The tetanus toxin solution contained 10 ng of tetanus toxin in 1 μl of 0.05 M phosphate buffered saline (PBS; Sigma-Aldrich, UK) and 2% bovine serum albumin (Sigma-Aldrich, UK). Following the injection, the animals were implanted with bipolar twisted silver electrodes (120 μm in dimeter, AM Systems, Inc, USA) bilaterally in the dorsal hippocampus and motor cortex. The two contacts of each electrode were 0.5 mm apart. The coordinates of the hippocampal and cortical electrodes with respect to bregma were AP: -4.6, L: 2.6, D: 3.3 and AP: 1.5, L: 3.0, D: 1.5 mm respectively. Ground/reference jeweller’s screws were placed over the cerebellum. Following a five-day recovery period, animals were individually video-EEG monitored for four weeks. Spontaneous electrographic activity was amplified, band-pass filtered (0.1 Hz -1.7 kHz) and digitized at 5k Hz using RHD2132 32-channel amplifier chip (Intan Technologies, USA). The signals were resampled to 100 Hz parameters. The epileptic bursts were manually labeled, extracted and analyzed using the same tools as for the in vitro studies. Early-warning signals were determined from the wide band (1-49 Hz) signal.

Human data recording and analysis

For the analysis of temporal autocorrelation as a measure of system recovery time in the lead-up to epileptic seizure, we used data recorded intracranially from 15 people with focal epilepsy. Data were obtained from a previous clinical trial (NCT01043406) for an implantable seizure prediction device²⁴. The trial was done at three clinical centres in Australia - Austin Health, the Royal Melbourne Hospital, and St. Vincent’s Hospital, all of which are part of the Melbourne University Epilepsy Group. The human research ethics committees of the participating institutes approved the study and subsequent amendments. All patients gave written informed consent before participation. We complied with all ethical regulations. ECoG was sampled continuously at 400 Hz from 16 electrodes implanted over the seizure onset zone which was determined from pre-existing medical records and neuroimaging. Dozens to hundreds of seizures were recorded for each patient, with all detections verified by expert clinicians. For the statistical analysis, only patients with >10 clinical seizures were included in the analysis (n=12). Prior to autocorrelation analysis, several pre-processing steps were performed. Due to the presence of high-frequency noise, ECoG was low-pass filtered at 150 Hz (zero-phase second-order Butterworth bandpass filter). Data contained missing segments due to telemetry dropouts. These segments were removed from analysis. In patients 1, 2 and 3, certain channels contained artifacts and were also removed from analysis.

We defined lag 1 autocorrelation r according to the following equation:

$$r(i)=\left(X_i-\mu \right)\left(X_{i-1}-\mu \right)$$

where X is the ECoG, μ is the mean (DC component) of the signal. We then calculated the mean of r in 10 s bins with 50% overlap which is denoted R(n). We also computed variance of the signal in those bins according to the equation

$$P\left(n\right)=\frac{1}{N-1}{\displaystyle \sum _{i=1}^N{\left(X_i-\mu \right)}^2}$$

where N denotes the length of the bin in samples. Finally, the autocorrelation coefficient ACC was computed for each bin

$$\text{ACC}\left(n\right)=\frac{R\left(n\right)}{P\left(n\right)}$$

Normalization by the signal power ensured that the ACC is representative of signal shape without the influence of its amplitude. To statistically evaluate the significance of visible trends in P(n) and ACC(n), we performed the following procedure. An epoch 35 to 5 minutes before the seizure of each ACC curve was fitted by a regression line and its slope determined. Then we tested whether the slopes were significantly positive or negative using one-tailed Wilcoxon sign-rank tests.

To analyze the state-dependent effect of IEDs on ictogenesis we used data recorded from patients who underwent invasive exploration with depth electrodes at Epilepsy Centre, Motol. Signals from subdural and/or depth macroelectrodes (Integra, Plainsboro, New Jersey, USA and Dixi Medical, BESANCON Cedex, France) were amplified (Schwarzer GmbH, Heilbronn, Germany), filtered using anti-aliasing filters at 1/3 of sampling frequency and sampled at a frequency of 512 or 1000 Hz (Stellate Inc., Montreal, Canada). A pair of the implanted electrodes without epileptiform abnormalities was selected as a reference electrode. To quantify the morphological similarity between IEDs and the spike triggering the seizure (heralding spike), we manually extracted heralding spikes from the ictal bipolar recordings of each patient. Then we searched for IEDs similar to the heralding spikes using the following algorithm.

Normalized sum of squared differences for two vectors x and y and for lag l was defined as

$$s_{xy}(l)=\frac{{\sum }_{i=1}^N{((x_i-\overline{x})-(y_{i+l}-\overline{y}))}^2}{{\sum }_{i=1}^N(x_i-\overline{x})(y_{i+l}-\overline{y})}$$

where i is the sample index, N is the length of x and bar denotes mean (DC component). The smaller the s_xy, the more similar the vectors are. In our case, x is the heralding spike and y is an epoch of interictal signal of given patient. To include the spatial properties of the spikes into the analysis, we analyzed the 10 channels with the highest signal power of the heralding spike, from each patient. We computed s_xy for each channel of the heralding spike moving sample by sample over the interictal ECoG of given patient. If for a given epoch of interictal signal, the mean over channels of s_xy was smaller than 0.5 and if in no channel it was higher than 1, the epoch was deemed morphologically similar to the heralding spike.

Model of the slow-fast process and cyclic regime shifts

To model the repeated transitions between seizure and interictal state, we implemented a simple model of slow-fast processes - a singular perturbation approach. This model captures the essence of repeated transitions between contrasting dynamical regimes and bistable dynamics applicable to various models of seizure including Wilson-Cowan or Epileptor models³. The transition to seizures can be modeled as an interaction between slow and fast variables, where the slow variable represents changes in population excitability and the fast variable represents the population firing rate. The model is represented by the following ordinary differential equations

$$\frac{dv}{dt}=-{\tau }_x\left(v^3+v^2-a\right)$$

where τ_x is a temporal constant of the population firing rate v and parameter a is the population excitability of the system. To introduce cyclic switching between two dynamical regimes, the model requires implementation of the dynamical changes in the excitability.

$$\frac{da}{dt}={\tau }_a\text{tanh}(c(h-v))$$

where τ_a is a temporal constant of the population excitability, c is a slope parameter of the sigmoidal shape of tanh (hyperbolic tangens), and h is a threshold. The dynamics of excitability depends on the difference between instantaneous value of the population firing rate v and a threshold parameter h. The threshold parameter defined as h=-0.44+1.6a. For values of a population firing rate above the threshold (i.e. during seizures), excitability decreases, while for values below the threshold (i.e. interictal state) the excitability increases. As long as the threshold h is between the branches corresponding to the low-firing and high-firing states, the equations give rise to a slow periodic switching between the two states. To examine the impact of IEDs on the transition to seizure, they were modeled as perturbations with a brief transient increase in the population firing rate. The occurrence of these perturbations was modeled as a random process, albeit approximately periodic, with an inter-perturbation interval drawn randomly from a normal distribution with a coefficient of variance equal to 0.2. The mean inter-perturbation interval (inverse of the discharge occurrence probability) and the amplitude of the perturbations were systematically varied to study its effect. The threshold h was kept unchanged throughout the simulations. Note that we have only systematically varied the mean and amplitude, but not the type of the inter-perturbation interval distribution. One can theoretically argue that the long-term summary effect of the perturbations on seizure frequency depends mainly on the perturbation frequency and amplitude; at least as long as the perturbations act on a shorter time-scale than the slow switching between seizure and non-seizure states.

The ordinary differential equations were solved numerically using the Euler scheme with an added white noise with zero mean and variance equal to 0.003. We used time step of 0.1 and initial conditions (v,a)=(0,0). The simulations were 19000 time units long.

Epileptor model and its modification

The Epileptor model³ is described by the following system of ordinary differential equations:

$$\frac{d{x}_1}{dt}=y_1-f_1(x_1,x_2,z)-z+I_{ex{t}_1}$$

$$\frac{d{y}_1}{dt}=c-{d{x}_1}^2-y_1$$

$$\frac{dz}{dt}=r{f}_z(s(x_1-x_0)+uz)$$

$$\frac{d{x}_2}{dt}=-y_2+x_2-{x_2}^3+I_{ex{t}_2}+0.002g-0.3(z-3.5)$$

$$\frac{d{y}_2}{dt}=\frac{1}{\tau }\left(-y_2+f_2(x_2)\right)$$

$$\frac{dg}{dt}=-0.01(g-0.1x_1),$$

where

$$f_1(x_1,x_2,z)=\{\begin{array}{cc}a{x_1}^3-b{x_1}^2& \text{if}{x}_1<0\\ -(\text{slope}-x_2+0.6(z-4^2)x_1& \text{if}{x}_1\ge 0\end{array}$$

$$f_2(x_2)=\{\begin{array}{cc}0& \text{if}{x}_2<-0.25\\ a_2(x_2+0.25)& \text{if}{x}_2\ge -0.25\end{array}$$

The five equations of the Epileptor model capture detailed features of the seizure; in particular, the pair (x₁, y₁) models the fast discharges occurring during seizure; the variable z (dynamically depending on x₁) governs the slow alternation between 'normal' and ictal periods, and the pair (x₂, y₂) allows modeling of typical spike-and-wave events. In general, the seizure onset/offset in the Epileptor is driven by the (x₁, y₁, z) subsystem which can be related to our phenomenological slow-fast process model: (x₁, y₁) ~ v, z ~ a. Similarly to the slow-fast process model, the seizure onset in the Epileptor is marked by a saddle-node bifurcation. However, instead of settling on the upper (stable) fixed point, the system escapes to a stable limit cycle enclosing the upper (unstable) fixed point. A seizure is terminated by a collision of the stable limit cycle with the middle (unstable) fixed point in a homoclinic bifurcation. For our simulations, we ran the simulations with the parameter settings adopted from the original study³, which were selected to provide a good fit to experimentally observed data. The only exception concerns the equation for the slow variable z. This variable represents the “permitivity”, with slow dynamics governed by a threshold lying between the lower and upper branches of the bifurcation diagram, corresponding to the 'normal' and ictal state. The unperturbed dynamics do not substantially depend on the particular position of this threshold (as long as it is between the branches), and thus, the specific choice of parameters in the equation for z in the original paper is relatively arbitrary. The relative height of the threshold is more relevant for modeling the effect of perturbations. Therefore, we have modified the parameters in the equation for z dynamics to qualitatively better resemble our phenomenological model. In our version of the Epileptor, the threshold was closer to the 'normal' activity branch. In such a scenario, the extreme amplitude of the perturbations is not required to bring the system transiently close or across this threshold. For the simulations, we have used specific settings of f_z=tanh (a sigmoid function providing saturation of the dependence), r=0.0024, s=0.2, u=1, and x₀=0.2. This step was sufficient to observe the dual effect of perturbations in the model. The modification did not qualitatively affect the system’s core bifurcation structure and the unperturbed dynamics of the Epileptor.

The ordinary differential equations were solved numerically using the Euler scheme. The initial conditions were set in such a way that the simulations always started inside an inter-ictal period. For the Epileptor, we used the time step of 0.01 s and the initial conditions (x₁, y₁, z, x₂, y₂) = (−2.02885, −19.5811,4.21875, −0.25,0) Perturbations were directed to minimize the "resistance" from the vector field: (∆x₁, ∆y₁, ∆z, ∆x₂, ∆y₂) = (0.04,1,0,0,0). The simulations were 10000 s long. Each input signal of a given perturbation probability 𝑝 and amplitude 𝑎 was produced by generating a periodic signal of frequency 𝑝 and amplitude 𝑎 first and then adjusting each inter-perturbation interval independently by adding a value drawn from a normal distribution (μ = 0, σ² = 0.2/𝑝). Finally, a white noise (μ = 0, σ² = 0.003) was added to the input signal.

Statistical analysis

All results and graphs are shown as mean ± s.e.m. Each in vitro experiment was replicated in multiple slices from multiple animals. The data collection was not randomized and analyses of the data were not performed in a blind fashion. No data points were excluded. Data from the repeated experiments to address specific questions were pooled together for group statistics. Statistical analysis was performed using SPSS software (SPSS Inc., Chicago, USA) and Matlab. We did not implement any statistical approach to a priori define the sample sizes. Our sample sizes correspond to sample sizes that are generally used in this field of research and based on our previous experience with similar experiments or those that have been routinely used in studies applying analogous methodological approaches and published in Nature Neuroscience. The sample size was presented as n/m, where n refers to the number of analyzed epochs or cells, and m refers to the number of slices, or only as n where the number corresponds to a number of slices. Normal distribution was tested using Kolmogorov-Smirnov test. Mann-Whitney-Wilcoxon U test was used for analysis of changes in duration of interictal periods in Fig. 4e,f and Fig. 6b. Kolmogorov-Smirnov test was used to determine the difference of phase distribution of individual cell in respect to uniform distribution (at the level of significance P<0.05). Temporal profiles and linear trends of early-warning signals and cellular behavior (Fig. 3 and Fig. 7) were analyzed using the one-way ANOVA. Wilcoxon sign-rank test was used to determine the ACC and variance temporal profile in individual patients (Fig. 8a and Supplementary materials Fig. 8). The appropriate test statistics, i.e. P values, U and Z values for Mann-Whitney-Wilcoxon U test, Wilcoxon sign-rank test and F values for one-way ANOVA test were determined.