Abstract
Structurally intact tropical forests sequestered ~50% of global terrestrial carbon uptake over the 1990s and early 2000s, removing ~15% of anthropogenic CO2 emissions1–3. Climate-driven vegetation models typically predict that this tropical forest ‘carbon sink’ will continue for decades4,5. Here, we assess trends in the carbon sink using 244 structurally intact African tropical forests spanning 11 countries, we compare them with 321 published plots from Amazonia and investigate the underlying drivers of the trends. The carbon sink in live aboveground biomass in intact African tropical forests has been stable for the three decades to 2015, at 0.66 Mg C ha-1 yr-1 (95% CI:0.53-0.79), in contrast to the long-term decline in Amazonian forests6. Thus, the carbon sink responses of Earth’s two largest expanses of tropical forest have diverged. The difference is largely driven by carbon losses from tree mortality, with no detectable multi-decadal trend in Africa and a long-term increase in Amazonia. Both continents show increasing tree growth, consistent with the expected net effect of rising atmospheric CO2 and air temperature7–9. Despite the past stability of the African carbon sink, our data suggest a post-2010 increase in carbon losses, delayed compared to Amazonia, indicating asynchronous carbon sink saturation on the two continents. A statistical model including CO2, temperature, drought and forest dynamics accounts for the observed trends and indicates a long-term future decline in the African sink, while the Amazonian sink continues to rapidly weaken. Overall, the uptake of carbon into Earth’s intact tropical forests peaked in the 1990s. Given that the global terrestrial carbon sink is increasing in size, observations indicating greater recent carbon uptake into the Northern hemisphere landmass10 reinforce our conclusion that the intact tropical forest carbon sink has already saturated. This tropical forest sink saturation and ongoing decline has consequences for policies to stabilise Earth’s climate.
Tropical forests account for approximately one-third of Earth’s terrestrial Gross Primary Productivity and one-half of Earth’s carbon stored in terrestrial vegetation11. Thus, small biome-wide changes in tree growth and mortality can have global impacts, either buffering or exacerbating the increase in atmospheric CO2. Models2,4,5,7,12, ground-based observations13–15, airborne atmospheric CO2 measurements3,16, inferences from remotely sensed data17, and synthetic approaches3,8,18 each suggest that, after accounting for land-use change, remaining structurally intact tropical forests (i.e. not impacted by direct anthropogenic impacts such as logging) are increasing in carbon stocks. This structurally intact tropical forest carbon sink is estimated at ~1.2 Pg C yr-1 over 1990-2007 using scaled inventory plot measurements1. Yet, despite its policy relevance, changes in this key carbon sink remain highly uncertain19,20.
Globally the terrestrial carbon sink is increasing2,7,8,21. Between 1990 and 2017 the land surface sequestered ~30% of all anthropogenic carbon dioxide emissions1,21. Rising CO2 concentrations are thought to have boosted photosynthesis more than rising air temperatures have enhanced respiration, resulting in an increasing global terrestrial carbon sink2,4,7,8,21. Yet, for Amazonia, recent results from repeated censuses of intact forest inventory plots show a progressive two-decade decline in sink strength primarily due to an increase of carbon losses from tree mortality6. It is unclear if this simply reflects region-specific drought impacts22,23, or potentially chronic pan-tropical impacts of either heat-related tree mortality24,25, or internal forest dynamics resulting from past increases in carbon gains leaving the system26. A more recent deceleration of the rate of increase in carbon gains from tree growth is also contributing to the declining Amazon sink6. Again, it is not known if this is a result of either pan-tropical CO2 fertilisation saturation, or rising air temperatures, or is merely a regional drought impact. To address these uncertainties, we (i) analyze an unprecedented long-term inventory dataset from Africa, (ii) pool the new African and existing Amazonian records to investigate the putative environmental drivers of changes in the tropical forest carbon sink, and (iii) project its likely future evolution.
We collected, compiled and analysed data from structurally intact old-growth forests from the African Tropical Rainforest Observation Network27 (217 plots) and other sources (27 plots) spanning the period 1968 to 2015 (Extended Data Figure 1; Supplementary Table 1). In each plot (mean size, 1.1 ha), all trees ≥100 mm in stem diameter were identified, mapped and measured at least twice using standardised methods (135,625 trees monitored). Live biomass carbon stocks were estimated for each census date, with carbon gains and losses calculated for each interval (Extended Data Figure 2).
Continental Carbon Sink Trends
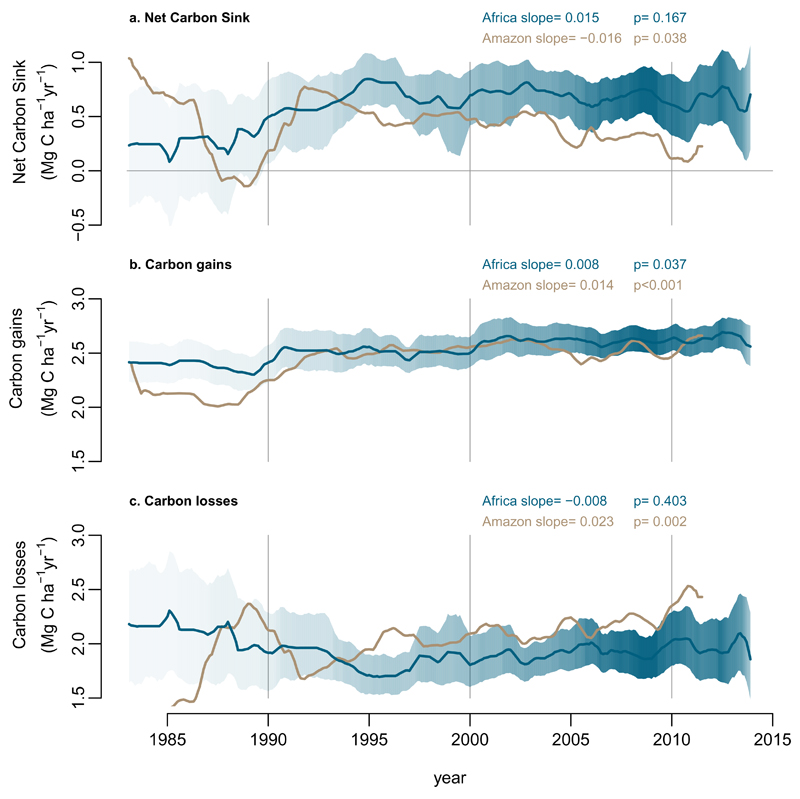
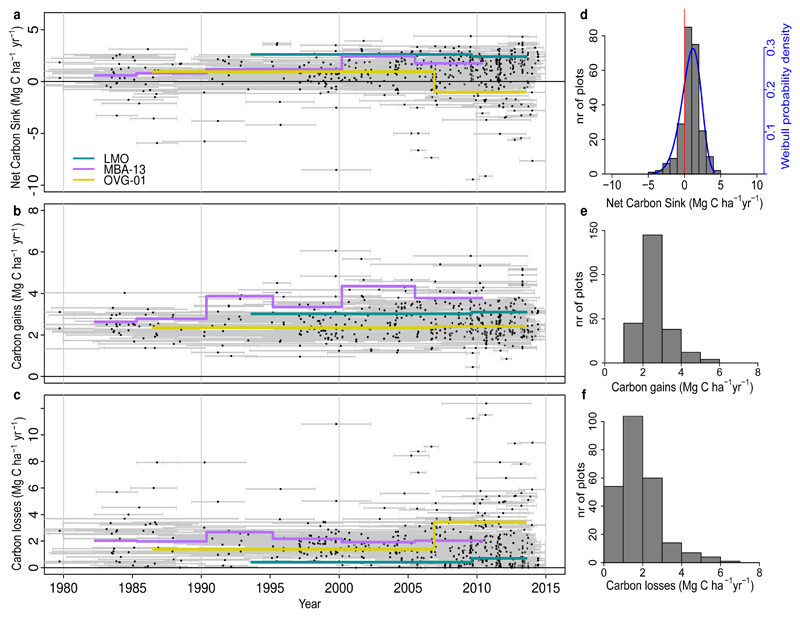
We detect no long-term trend in the per unit area African tropical forest carbon sink over three decades to 2015 (Figure 1, Table 1). The aboveground live biomass sink averaged 0.66 Mg C ha-1 yr-1 (95% CI: 0.53-0.79; n=244) and was significantly greater than zero for every year since 1990 (Figure 1). While very similar to past reports (0.63 Mg C ha-1 yr-1)13, this first estimate of the temporal trend in Africa contrasts with the declining Amazonian trend6 (Figure 1). A linear mixed effect model shows a significant difference in the slopes of the sink trends for the two continents over the common time window (pooled data from both continents, common time window, 1983-2011.5; p=0.017). Thus, the per unit area sink strength of the two largest expanses of tropical forest on Earth diverged in the 1990s and 2000s.
Figure 1. Long-term carbon dynamics of structurally intact tropical forests in Africa (blue) and Amazonia (brown).
Trends in net aboveground live biomass carbon sink (a), carbon gains to the system from wood production (b), and carbon losses from the system from tree mortality (c), measured in 244 African inventory plots (blue lines) and contrasting published6 Amazonian inventory data (brown lines; 321 plots). Shading corresponds to the 95% CI, with less transparent shading indicating a greater number of plots monitored in that year (most transparent: minimum 25 plots monitored). The CI for the Amazonian dataset is omitted for clarity, but can be seen in Figure 3. Slopes and p-values are from linear mixed effects models (see Methods).
Table 1. Carbon sink in intact forests in Africa, Amazonia and the pan-tropics: 1980-2015 and predictions to 2040.
Mean values in bold, future predictions in italics, uncertainty in parentheses, 95% bootstrapped confidence intervals for 1980-2015, and 2σ for the predictions (2010-2040).
| Period | No. | Per unit area aboveground live biomass C sink | Total C sink * | ||||||
|---|---|---|---|---|---|---|---|---|---|
| plots | (Mg C ha-1 yr-1) | (Pg C yr-1) | |||||||
|
|
|
||||||||
| Af. | Am. | Africa | Amazon | Pan-tropics† | Africa | Amazon | Pan-tropics† | ||
|
|
|
|
|||||||
| 1980-1990 | 45 | 73 | 0.33 (0.06-0.63) | 0.35 (0.06-0.59) | 0.35 (0.07-0.62) | 0.28 (0.05-0.53) | 0.49 (0.08-0.82) | 0.87 (0.16-1.52) | |
| 1990-2000 | 96 | 172 | 0.67 (0.43-0.89) | 0.53 (0.42-0.65) | 0.57 (0.39-0.74) | 0.50 (0.32-0.66) | 0.68 (0.54-0.83) | 1.26 (0.88-1.63) | |
| 2000-2010 | 194 | 291 | 0.70 (0.55-0.84) | 0.38 (0.26-0.48) | 0.50 (0.35-0.64) | 0.46 (0.37-0.56) | 0.45 (0.31-0.57) | 0.99 (0.70-1.25) | |
| 2010-2015 | 184 | 172 | 0.66 (0.40-0.91) | 0.24 (0.00-0.47) | 0.40 (0.15-0.65) | 0.40 (0.24-0.56) | 0.27 (0.00-0.52) | 0.73 (0.25-1.18) | |
| 2010-2020 ‡ | - | - | 0.63 (0.36-0.89) | 0.23 (-0.05-0.50) | 0.38 (0.11-0.65) | 0.37 (0.21-0.53) | 0.25 (-0.05-0.54) | 0.68 (0.17-1.16) | |
| 2020-2030 ‡ | - | - | 0.59 (0.24-0.93) | 0.12 (-0.29-0.51) | 0.30 (-0.08-0.67) | 0.31 (0.13-0.49) | 0.12 (-0.29-0.52) | 0.47 (-0.15-1.07) | |
| 2030-2040 ‡ | - | - | 0.55 ( 0.08-0.99) | 0.00 (-0.54-0.49) | 0.21 (-0.29-0.67) | 0.26 (0.04-0.47) | 0.00 (-0.50-0.46) | 0.29 (-0.46-0.97) | |
Total Continental C sink is the per unit area aboveground C sink multiplied by intact forest area for 1990-2010 (from ref.1, see Extended Data Table 2) and continent specific extrapolations to 2040. Total Continental C sink includes continentspecific estimates of trees <100 mm DBH, lianas and roots (see Methods).
Pan-tropical aboveground live biomass C sink is the area-weighted mean of African, Amazonian and Southeast Asian sink values. Southeast Asian values were from published per unit area carbon sink data15 (n=49 plots) for 1990-2015, with 1980-1990 assumed to be the same as 1990-2000 due very low sample sizes. Pan-tropical total C sink is the sum of African, Amazonian and Southeast Asian total continental carbon sink values. The continental sink in Southeast Asia is a modest and declining contribution to the pan-tropical sink, due to the very small area of intact forest remaining, at 0.11, 0.08, 0.07 and 0.06 Pg C yr-1 in the 1980s, 1990s, 2000s and 2010s, hence uncertainty in the Southeast Asian sink cannot reverse the pantropical declining sink trend.
Per unit area total C sink for 2010-2020, 2020-2030 and 2030-2040 was predicted using parameters from Table 2, except for the 2010-2020 sink in Africa which is the mean of the measured sink from 2010-2015 and the modelled sink from 2015-2020. For the Asian sink we assumed the parameters as for Africa, as Asian forest median CRT is 61 years, close to African median, 63 years.
The proximal cause of the divergent sink patterns is a significant increase in carbon losses (from tree mortality, i.e. the loss of carbon from the live biomass pool) in Amazonian forests, with no detectable trend over three decades in African forests (Figure 1). A linear mixed effects model using pooled data shows a significant difference in slopes of carbon losses between the two continents over the common 1983-2011.5 time window (p=0.027). Long-term trends in carbon gains (from tree growth and newly recruited trees) on both continents show significant increases (Figure 1), and we could detect no difference in slopes between the continents (p=0.348; carbon gains from tree growth alone also show no continental difference in long-term trends, p=0.322). However, an assessment of how underlying environmental drivers affect carbon gains and losses is needed to understand the ultimate causes of the divergent sink patterns.
Understanding the Carbon Sink Trends
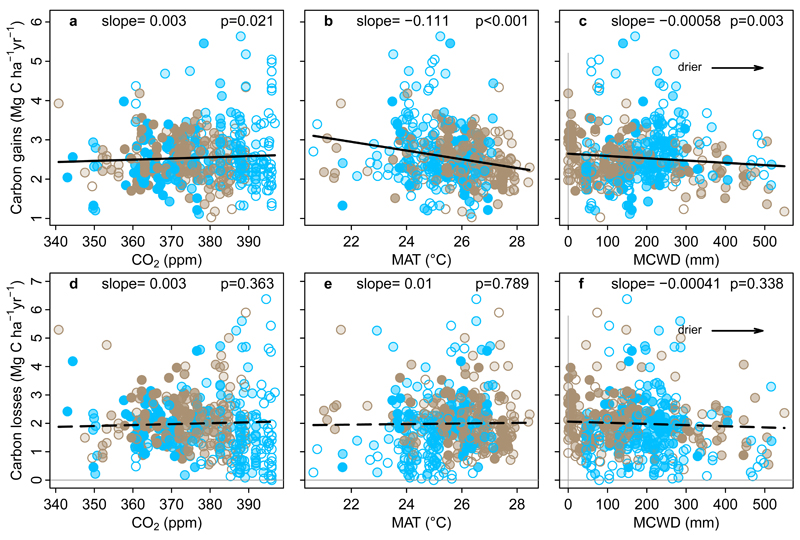
We first investigate environmental drivers exhibiting long-term change that impact theory-driven models of photosynthesis and respiration: atmospheric CO2 concentration, surface air temperature, and water availability. A linear mixed effects model of carbon gains, with censuses nested within plots, and pooling the new African and published Amazonian data, shows a significant positive relationship with CO2, and significant negative relationships with mean annual temperature (MAT) and drought (measured as the Maximum Climatological Water Deficit, MCWD14; Figure 2; Extended Data Table 1). These results are consistent with a positive CO2 fertilisation effect, and negative effects of higher temperatures and drought on tree growth, consistent with temperature-dependent increases in autotrophic respiration, and temperature- and drought-dependent reductions in carbon assimilation. By contrast, the equivalent model for carbon losses (i.e. tree mortality) shows no significant relationships with CO2, MAT or MCWD (Figure 2; Extended Data Table 1).
Figure 2. Potential environmental drivers of carbon gains and losses in structurally intact old-growth African and Amazonian tropical forests.
Aboveground carbon gains, from woody production (a-c), and aboveground carbon losses, from tree mortality (d-f), presented as time-weighted mean values for each plot, i.e. each census within a plot is weighted by its length, against the corresponding values of atmospheric carbon dioxide concentration (CO2), mean annual air temperature (MAT) and drought (as Maximum Climatological Water Deficit, MCWD), for African (blue) and Amazonian (brown) inventory plots. Each data point therefore represents an inventory plot, for visual clarity, and the level of transparency represents the total monitoring length, with empty circles corresponding to plots monitored for ≤ 5 years and solid circles for plots monitored for >20 years. Solid lines show significant trends, dashed lines non-significant trends calculated using linear mixed effect models with census intervals (n=1566) nested within plots (n=565), using an empirically derived weighting based on interval length and plot area, on the untransformed pooled Africa and Amazon dataset (see Methods). Slopes and p-values are from the same linear mixed effects models. Carbon loss data and models are presented untransformed for comparison with carbon gains, but transformation is needed to fit normality assumptions; linear mixed effects models on transformed carbon loss data does not change the significance of the results, nor does including all three parameters and transformed data in a model (see Extended Data Table 1).
We further investigate the responses of carbon gains and losses (for which the above analysis has no explanatory power) by expanding our potential explanatory variables to additionally include the change in environmental conditions (CO2-change, MAT-change, MCWD-change, see Extended Data Figure 3 for calculation details), and two attributes of forests that may influence their response to the same environmental change: plot mean wood density (which in old-growth forests correlates with below-ground resource availability28,29), and the plot carbon residence time (which measures how long fixed carbon remains in the system, hence dictates when past increases in carbon gains leave the system as elevated carbon losses30).
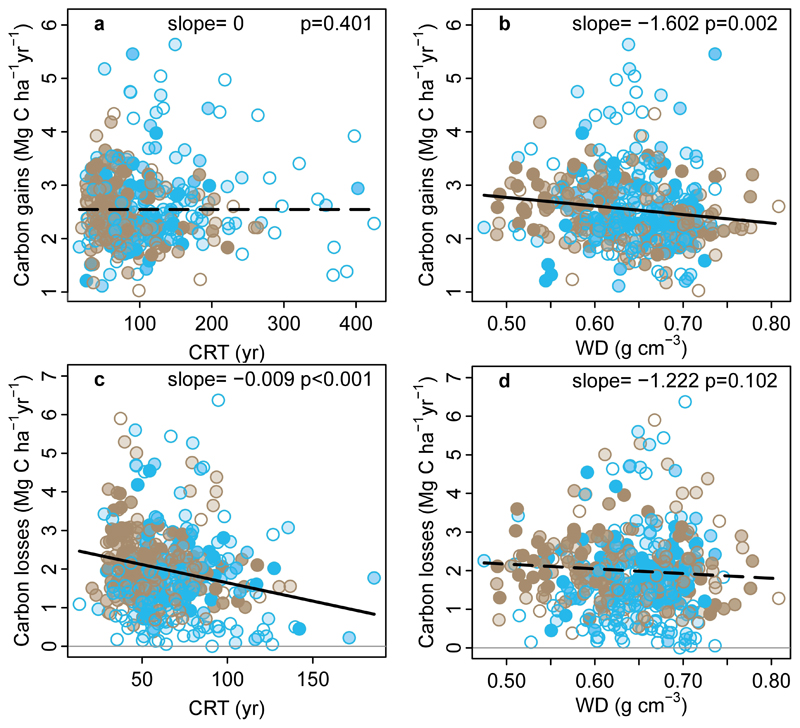
The minimum adequate carbon gain model using our expanded explanatory variables (best ranked model using multimodel inference) has a positive relationship with CO2-change, and negative relationships with MAT, MAT-change, MCWD, and wood density (Table 2; model-average results are similar, see Methods and Supplementary Tables 2-4). The retention of both MAT and MAT-change suggests that higher temperatures correspond to lower tree growth, and that trees only partially acclimate to recently rising temperatures, which further reduces growth, consistent with warming experiments31 and observations9. The inclusion of higher wood density, and it being related to lower carbon gains (Extended Data Figure 4), alongside no temporal trends in wood density (Extended Data Figure 5), suggests that old-growth forests with denser-wooded tree communities typically have fewer available below-ground resources, or such patterns may also emerge from disturbance regimes lacking large-scale exogenous events, consistent with prior studies26,28,32.
Table 2. Minimum adequate models to predict carbon gains and losses in African and Amazonian tropical forests. These are the best ranked gains and loss models.
Where continental values differ, those for Africa are reported first, followed by Amazonian values.
| Carbon gains, Mg C ha-1 yr-1 | |||||
|---|---|---|---|---|---|
|
| |||||
| Predictor variable | Parameter value | Standard Error | t-value | p-value | 2000-2015 change in gains (%) * |
|
|
|
||||
| (Intercept) | 5.255 | 5.395 | 0.603 | 0.614 | 8.7 | 8.8 | <0.001 | - |
| CO2-change (ppm yr-1) † | 0.238 | 0.096 | 2.5 | 0.013 | 3.69% | 3.71% |
| MAT (°C) | -0.083 | 0.025 | -3.3 | 0.001 | -0.67% | -1.07% |
| MAT-change (°C yr-1) ‡ | -1.243 | 0.233 | -5.3 | <0.001 | 0.58% | 0.00% § |
| MCWD (mm x1000) | -0.405 | -1.391 | 0.381 | 0.24 | -1.1 | -5.8 | 0.289 | <0.001 | -0.52% | -2.73% |
| WD (g cm-3) | -1.295 | 0.530 | -2.4 | 0.015 | 0.05% | 0.00% |
|
| |||||
| Carbon losses, Mg C ha-1 yr-1 ║ | |||||
|
| |||||
| Predictor variable | Parameter value | Standard Error | t-value | p-value | 2000-2015 change in losses (%) * |
|
|
|
||||
| (Intercept) | 1.216 | 0.086 | 14.1 | <0.001 | - |
| CO2-change (ppm yr-1) † | 0.130 | 0.059 | 2.2 | 0.026 | 11.38% | 14.81% |
| MAT-change (°C yr-1) | 0.766 | 0.162 | 4.7 | <0.001 | -1.56% | 0.00% |
| MCWD (mm x10000) ‡ | -0.232 | 0.107 | -2.2 | 0.030 | -1.21% | -2.42% |
| CRT (yr) | -0.003 | 0.001 | -6.1 | <0.001 | -0.57% | 1.39% |
The 2000-2015 change in gains/losses for each predictor variable was estimated allowing only the focal predictor to vary; this change was then expressed as a percentage of the annual gains/losses in the year 2000 allowing all predictors to vary.
Change over the past 56 years.
Change over the past 5 years.
A positive value for Africa indicates that MAT increased more slowly over 2000-2015 compared to the mean increase over 1983-2015, therefore contributing to an increase in gains; a zero value fpr Amazonia indicates that the rate of MAT increase was the same over 2000-2015 as the mean increase over 1983-2015.
Carbon loss values were normalized via power-law transformation, λ= 0.361.
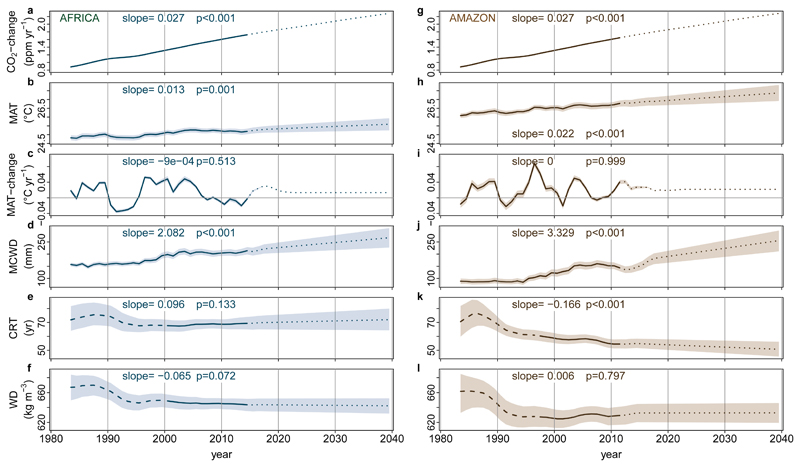
The minimum adequate carbon gain model using our expanded explanatory variables also highlights continental differences. Between 2000 and 2015 African forest carbon gains increased by 3.1% compared with a 0.1% decline in Amazonia over the same interval (Table 2). In Africa, from 2000 to 2015, the increase was composed of a 3.7% increase from CO2-change, partially offset by increasing droughts depleting gains by 0.5%, and only a slight decline in gains of 0.1% resulting from temperature increases (Table 2), because the rate of temperature change (MAT-change) decelerated over this time window (Extended Data Figure 5). For Amazonia, the same 3.7% increase due to CO2-change was seen, while increasing droughts—and these forests’ greater sensitivity to drought—reduced gains by 2.7% (five times the impact in Africa), and temperature increases at the same rate as in the past (i.e. MAT-change is zero) further reduced gains by 1.1% (ten times the impact in Africa), leaving a net change in gains slightly below zero (Table 2). Thus, the recent stalling of carbon gain increases in Amazonia6 is a response to drought and temperature and not due to an unexpected saturation of CO2 fertilisation. Overall, the larger modelled increase in gains in Africa relative to Amazonia appear to be driven by slower warming, fewer or less extreme droughts, lower forest sensitivity to droughts, and overall lower temperatures (African forests are on average ~1.1°C cooler than Amazonian forests, as they typically grow at ~200 m higher elevation). Other continental differences may also be influencing the results, including higher nitrogen deposition in African tropical forests due to the seasonal burning of nearby savannas33 and biogeographic history resulting in differing contemporary species pools and resulting functional attributes34,35.
The minimum adequate carbon loss model using our expanded explanatory variables shows higher losses with CO2-change and MAT-change, and lower losses with MCWD and the carbon residence time (CRT; Table 2). Thus, changes in carbon losses appear to be largely a function of carbon gains. First, the greater losses in forests with shorter CRT conform to a ‘high-gain high-loss’ forest dynamics pattern26. Second, wetter plots have a longer growing season and so have higher gains and correspondingly higher losses, explaining the negative relationship with MCWD. Third, as increasing CO2 levels result in additional carbon gains, after some time these additional past gains leave the system resulting in greater carbon losses, explaining the positive relationship with CO2-change. Finally, in addition to these relationships with carbon gains, the inclusion of MAT-change (p<0.001) indicates heat- or vapour pressure deficit-induced tree mortality24. Overall, our results imply that chronic long-term environmental change factors, temperature and CO2, rather than simply the direct effects of drought, underlie longer-term trends in tropical forest tree mortality, although other changes such as rising liana infestation rates seen in Amazonia36,37 cannot be excluded.
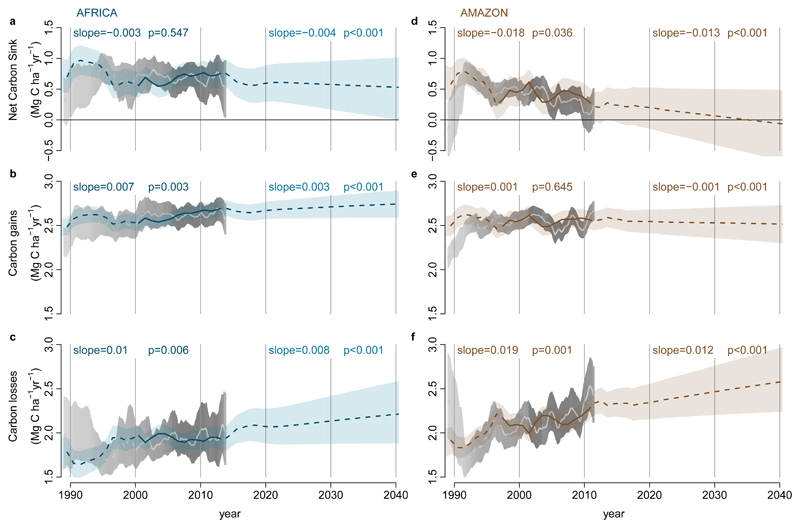
The minimum adequate carbon loss model using our expanded explanatory variables replicates the continental trends (Figure 3). The overall lower loss rates in Africa reflect their longer CRT (69 yrs, 95% CI, 66-72), compared with Amazonian forests (56 yrs, 95% CI, 54-59) while over the 2000-2015 window the much smaller increase in loss rates in Africa compared to Amazonia results from a slower increase in warming and a stable CRT in Africa compared to continued warming at previous rates and a shortening CRT in Amazonian forests (Extended Data Figure 5). Furthermore, given that losses appear to lag behind gains they should relate to the long-term CRT of plots. This is what we find: the longer the CRT the smaller the increase in carbon losses, with no increase in losses for plots with CRT ≥77 years (Extended Data Figure 6). Consequently, due to the typically longer residence times of African forests, increasing losses in Africa ought to appear 10-15 years after the increase in Amazon losses began (c.1995). Strikingly, in Africa the most intensely monitored plots suggest that losses began increasing from c.2010 (Extended Data Figure 7), and plots with shorter CRT are driving the increase (Extended Data Figure 8). Thus, a mortality-dominated African carbon sink decline appears to have begun very recently.
Figure 3. Modelled past and future carbon dynamics of structurally intact tropical forests in Africa and Amazonia.
Predictions of net aboveground live biomass carbon sink (a,d), carbon gains (b,e), and carbon losses (c,f), for African (left panels) and Amazonian (right panels) plot inventory networks, based on CO2-change, Mean Annual Temperature, Mean Annual Temperature-change, drought (as Maximum Climatological Water Deficit), plot wood density, and plot carbon residence time, using observations in Africa until 2014 and Amazonia until 2011.5, and extrapolations of prior trends to 2040. Model predictions are in blue (Africa) and brown (Amazon), with solid lines spanning the window when ≥75% of plots were monitored to show model consistency with the observed trends, and shading showing upper and lower confidence intervals accounting for uncertainties in the model (both fixed and random effects) and uncertainties in the predictor variables. Light grey lines and grey shading are the mean and 95% CI of the observations from the African and Amazonian plot networks.
Future of the Tropical Forest Carbon Sink
Our carbon gain and loss models (Table 2) can be used to make a tentative estimate of the future size of the per unit area intact forest carbon sink (Figure 3). Extrapolations of the changes in the predictor variables from 1983-2015 forward to 2040 (Extended Data Figure 5) show declines in the sink on both continents (Figure 3). By 2030 the carbon sink in aboveground live biomass in intact African tropical forest is predicted to decline by 14% from the measured 2010-15 mean, to 0.57 Mg C ha-1 yr-1 (2σ range, 0.16-0.96; Figure 3). The Amazon sink continues to decline, reaching zero in 2035 (2σ range, 2011-2089; Figure 3). Our estimated sink strength on both continents in the 2020s and 2030s is sensitive to future CO2 emissions pathways (CO2-change)38, resulting temperature increase (MAT, MAT-change) and hydrological changes (MCWD), plus changes in forest dynamics (CRT), but the sink is always lower than levels seen in the 2000s (see Methods and Supplementary Table 5). Thus, the carbon sink strength of the world’s two most extensive tropical forests have now saturated, albeit asynchronously.
Scaling Results to the Pan-tropics
Scaling our estimated mean sink strength by forest area for each continent signifies that Earth recently passed the point of peak carbon sequestration into intact tropical forests (Table 1). The continental sink in Amazonia peaked in the 1990s, followed by a decline, driven by sink strength peaking in the 1990s and a continued decline in forest area (Table 1). In Africa the per unit area sink strength peaked later in the 2000-2010 period, but the continental African sink peaked in the 1990s, due to the decline in forest area in the 2000s outpacing the small per unit area increase in sink strength. Including the modest uptake in the much smaller area of intact Asian tropical forest indicates that total pan-tropical carbon uptake peaked in the 1990s (Table 1). From peak pan-tropical intact forest uptake of 1.26 Pg C yr-1 in the 1990s, we project a continued decline reaching just 0.29 Pg C yr-1 in the 2030s (multi-decade decline of ~0.24 Pg C yr-1 decade-1), driven by (i) reduced mean pan-tropical sink strength decline of 0.1 Mg C ha-1 yr-1 decade-1 and (ii) ongoing forest area losses of ~13.5 million ha yr-1 (see Extended Data Table 2 for forest area details). Critically, climate-driven vegetation model simulations have not predicted that peak net carbon uptake into intact tropical forests has already been passed2,4,5.
Discussion
Our method of scaling to arrive at a pan-tropical sink estimate – in common with other studies using similar datasets1,6,13 – is limited. Yet, pervasive net carbon uptake is expected given that we find a strong and ongoing CO2 fertilisation effect. Using our CO2 response in Table 2, we find an increase in aboveground carbon stocks of 10.8±3.7 Mg C ha-1 100 ppm-1 CO2, or 6.5±2.2% (±SE; using an area-weighted pan-tropical mean aboveground C stock of 165 Mg C ha-1), comparable to the 5.0±1.2% increase in tropical forest C stocks 100 ppm-1 CO2 derived from a recent synthesis of CO2 fertilisation experiments, despite a lack of data from mature tropical forests39. Our result is within the range of climate-driven vegetation models2,7, although it is greater than a number of recently-published models that include potential nutrient constraints, reported as 5.9±4.7 Mg C ha-1 100 ppm-1 CO2 (Ref.40). We find that the CO2 fertilisation uptake is currently only partially offset by the negative impacts of similarly widespread rising air temperatures (-2.0±0.4 Mg C ha-1 °C-1, from Table 2), consistent with models7, limited experiments31 and independent observations9, plus negative responses to drought41,42. Long-term and extensive increases in satellite-derived greenness in tropical regions not experiencing major changes in land-use management17,43, particularly in central Africa in the past decade44, indicate increases in tropical forest net primary productivity, providing further evidence that the sink is a widespread phenomenon44.
Nonetheless, our analyses show that this pervasive tropical forest sink in live biomass is in long-term decline, first saturating in Amazonia, and more recently followed by African forests, explaining the prior Africa-Amazon carbon sink divergence as part of a longer-term pattern of asynchronous saturation and decline. From an atmospheric perspective the full impacts of the contribution to the saturation of the sink from slowing carbon gains are experienced immediately, but the contribution from rising carbon losses is delayed because dead trees do not decompose instantaneously. Decomposition of this dead tree mass is ~50% in 4 yrs, and ~85% in 10 yrs, thus rising carbon losses result in delayed carbon additions to the atmosphere45. Hence, from an atmospheric perspective the intact tropical forest biomass carbon sink likely peaked a few years later than our plot data indicate and the full impacts are not yet realised. The pan-tropical carbon sink in live biomass reduced by 0.27 Pg C yr-1 between the 1990s and 2000s (Table 1), but accounting for dead wood decomposition45 shows a smaller 0.17 Pg C yr-1 reduction from an atmospheric perspective (see Methods).
Given that the global terrestrial carbon sink is increasing, a weakening intact tropical forest sink implies that the extra-tropical carbon sink has increased over the past two decades. Independent observations of inter-hemispheric atmospheric CO2 concentration indicates that carbon uptake into the Northern hemisphere landmass has increased at a greater rate than the global terrestrial carbon sink since the 1990s, with a further disproportionate increase in the 2000s10. The inter-hemispheric analysis suggests a weakening of the tropical forest sink by ~0.2 Pg C yr-1 between the 1990s and 2000s10, which is similar to the 0.17 Pg C yr-1 weakening over the same time period that we find. This reinforces our conclusion that the intact tropical forest carbon sink has already saturated.
In summary, our results indicate that while intact tropical forests remain major stores of carbon and are key centres of biodiversity11, their ability to sequester additional carbon is waning. In the 1990s intact forests removed 17% of anthropogenic CO2 emissions. This has declined to 6% in the 2010s, because the pan-tropical weighted average per unit area sink strength declined by 33%, forest area decreased by 19%, and CO2 emissions increased by 46%. Although tropical forests are more immediately threatened by deforestation46 and degradation47, and the future carbon balance will also depend on secondary forest dynamics48 and forest restoration plans49, our analyses show that they are also impacted by atmospheric chemistry and climatic changes. Given that the intact tropical forest carbon sink is set to end sooner than even the most pessimistic climate-driven vegetation models predict4,5, our analyses suggest that climate change impacts in the tropics may become more severe than predicted. Furthermore, the carbon balance of intact tropical forests will only stabilise once CO2 concentrations and the climate stabilises.
Continued on-the-ground monitoring of the world’s remaining intact tropical forests will be required to test our prediction that the intact tropical forest carbon sink will continue to decline. Such direct ground-based measurements also provide a constraint on estimating the size and location of the terrestrial carbon sink. In addition, our conclusion that tree mortality and internal forest dynamics are important controls on the future of the tropical forest carbon sink, may assist in improving the vegetation components of future Earth System Models50 and contribute to reducing terrestrial carbon cycle feedback uncertainty19,20. Our findings also have policy implications. At the country-level: given intact tropical forests are a carbon sink, but the size is changing, national greenhouse gas reporting will require careful forest monitoring. At the international-level: given tropical forests are likely to sequester less carbon in the future than Earth System Models predict, an earlier date to reach net zero anthropogenic greenhouse gas emissions will be required to meet any given commitment to limit the global heating of Earth.
Online Methods
Plot Selection
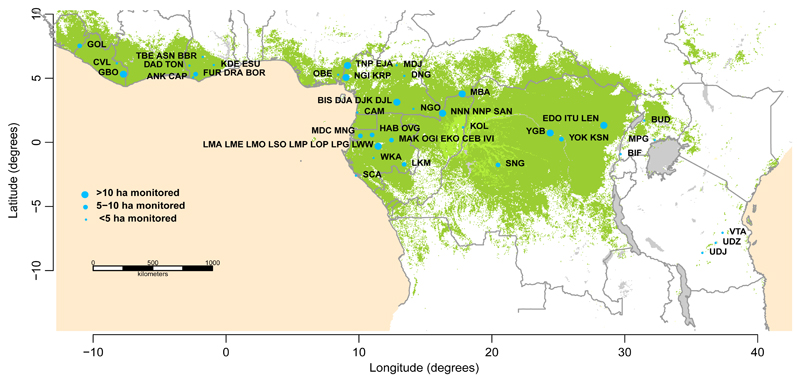
Closed canopy (i.e. not woody savanna) old-growth mixed-age forest inventory plots were selected using commonly used criteria6,13,27: free of fire and industrial logging; all trees with diameter at reference height ≥100 mm measured at least twice; ≥0.2 ha area; <1500 m.a.s.l. altitude; MAT ≥20.0°C51; annual precipitation ≥1000 mm51; located ≥50 m from anthropogenic forest edges. Of the 244 plots included in the study, 217 contribute to the African Tropical Rainforest Observatory Network (AfriTRON; www.afritron.org), with data curated at www.ForestPlots.net52,53. These include plots from Sierra Leone, Liberia, Ghana, Nigeria, Cameroon, Gabon, Republic of Congo, Democratic Republic of Congo (DRC), Uganda and Tanzania52,53 (Extended Data Figure 1). Fifteen plots are part of the TEAM network, from Cameroon, Republic of Congo, Tanzania, and Uganda54–57. Nine plots contribute to the ForestGEO network, from Cameroon and DRC58 (9 plots from DRC, codes SNG, contribute to both AfriTRON and ForestGEO networks, included above in the AfriTRON total). Finally, three plots from Central African Republic are part of the CIRAD network59,60. The large majority of plots are sited in terra firme forests and have mixed species composition, although four are in seasonally flooded forest and 14 plots are in Gilbertiodendron dewevrei monodominant forest, a locally common forest type in Africa (Supplementary Table 1). The 244 plots have a mean size of 1.1 ha (median, 1 ha), with a total plot area of 277.9 ha. The dataset comprises 391,968 diameter measurements on 135,625 stems, of which 89.9% were identified to species, 97.5% to genus and 97.8% to family. Mean total monitoring period is 11.8 years, mean census length 5.7 years, with a total of 3,214 ha years of monitoring. The 321 Amazon plots are published and were selected using the same criteria6, except in the African selection criteria we specified a minimum anthropogenic edge distance and added a minimum temperature threshold.
Plot Inventory and Tree Biomass Carbon Estimation
Tree-level aboveground biomass carbon is estimated using an allometric equation with parameters for tree diameter, tree height and wood mass density61. The calculation of each is discussed in turn. All calculations were performed using the R statistical platform, version 3.2.1 (ref.62) using the BiomasaFP R package, version 0.2.1 (ref.63).
Tree Diameter
In all plots, all woody stems with ≥100 mm diameter at 1.3 m from the base of the stem (‘diameter at breast height’, DBH), or 0.5 m above deformities or buttresses, were measured, mapped and identified using standard forest inventory methods64,65. The height of the point of measurement (POM) was marked on the trees and recorded, so that the same POM is used at the subsequent forest census. For stems developing deformities or buttresses over time that could potentially disturb the initial POM, the POM was raised approximately 500 mm above the deformity. Estimates of the diameter growth of trees with changed POM used the ratio of new and old POMs, to create a single trajectory of growth from the series of diameters at two POM heights6,13,65. We used standardised protocols to assess typographical errors and potentially erroneous diameter values (e.g. trees shrinking by >5 mm), missing values, failures to find the original POM, and other issues. Where necessary we estimated the likely value via interpolation or extrapolation from other measurements of that tree, or when this was not possible we used the median growth rate of trees in the same plot, census and size-class, defined as DBH = 100-199 mm, or 200-399 mm, or >400 mm65. We interpolated measurements for 1.3% of diameters, extrapolated 0.9%, and used median growth rates for 1.5%.
Tree height
Height of individuals from ground to the top leaf, hereafter Ht, was measured in 204 plots, using a laser hypsometer (Nikon forestry Pro) from directly below the crown (most plots), a laser or ultrasonic distance device with an electronic tilt sensor, a manual clinometer, or by direct measurement, i.e. tree climbing. Only trees where the top was visible were selected66. In most plots, tree selection was similar: the 10 largest trees were measured, together with 10 randomly selected trees per diameter from five classes: 100-199 mm, 200-299 mm, 300-399 mm, 400-499 mm, and 500+ mm trees, following standard protocols66. We measured actual height of 24,270 individual trees from 204 plots. We used these data and the local.heights function in R package BiomasaFP63 to fit 3-parameter Weibull relationships: Ht=a × (1-e((-b × (DBH/10)c)) (equation 1). We chose the Weibull model as it is known to be robust when a large number of measurements are available66,67. We parameterised separate Ht-DBH relationship for four different combinations of edaphic forest type and biogeographical region: (i) terra firme forest in West Africa, (ii) terra firme forest in Lower Guinea and Western Congo Basin, (iii) terra firme forest in Eastern Congo Basin and East Africa, (iv) seasonally flooded forest from Lower Guinea and Western Congo Basin (there were no seasonally flooded forest plots in the other biogeographical regions). The parameters are: (i) terra firme forest in West Africa, a=56.0; b=0.0401; c=0.744; (ii) terra firme forest in Lower Guinea and Western Congo Basin, a=47.6; b=0.0536; c=0.755; (iii) terra firme forest in Eastern Congo Basin and East Africa, a=50.8; b=0.0499; c=0.706; and finally (iv) seasonally flooded forest from Lower Guinea and Western Congo Basin, a=38.2; b=0.0605; c=0.760. For each of these combinations of forest type and bioregion, the local.heights function combines all height measurements from all plots belonging to that forest type/bioregion and fits the Weibull model parameters using non-linear least squares (nls function in R with default settings), with starting values of a = 25, b = 0.05 and c = 0.7 chosen as they led to regular model convergence. We fitted these models either treating each observation equally or with case weights proportional to each trees’ basal area. These weights give more importance to large trees during model fitting. We selected the best fitting of these models, determining this as the model that minimised prediction error of stand biomass when calculated with estimated heights or observed heights. The parameters were used to estimate Ht from DBH for all tree DBH measurements for input into the allometric equation. Mean measured individual total tree height is 20.5 m; the height range is 1.5 to 72.5 m. The root mean squared error (RMSE) between the full dataset of measured heights and the predicted heights, is 5.7 m, which is 8.0% of the total range. Furthermore, RMSE is 5.3 m in terra firme forest in West Africa (7.5% of the range; n=9771 trees); RMSE is 6.4 m in terra firme forest in Lower Guinea and Western Congo Basin (8.7% of the range; n=10,838 trees); RMSE is 4.8 m in terra firme forest in Eastern Congo Basin and East Africa (8.8% of the range; n=3269 trees); and RMSE is 4.1 m in seasonally flooded forest from Lower Guinea and Western Congo Basin (12.5% of the range; n=392 trees).
Wood Density
Dry wood density (ρ) measurements were compiled for 730 African species from published sources and stored in www.ForestPlots.net; most were sourced from the Global Wood Density Database on the Dryad digital repository (www.datadryad.org)68,69. Each individual in the tree inventory database was matched to a species-specific mean wood density value. Species in both the tree inventory and wood density databases were standardized for orthography and synonymy using the African Plants Database (www.ville-ge.ch/cjb/bd/africa/) to maximize matches13. For incompletely identified individuals or for individuals belonging to species not in the ρ database, we used the mean ρ value for the next higher known taxonomic category (genus or family, as appropriate). For unidentified individuals, we used the mean wood density value of all individual trees in the plot13,52.
Allometric equation
For each tree we used a published allometric equation61 to estimate aboveground biomass. We then converted this to carbon, assuming that aboveground carbon (AGC) is 45.6% of aboveground biomass70. Thus: AGC=0.456×(0.0673×(ρ×(DBH/10)2×Ht)0.976)⁄1000 (equation 2), with DBH in mm, dry wood density, ρ, in g cm-3, and total tree height, Ht, in m (ref.61).
Aboveground Carbon (AGC, in Mg C ha-1) in living biomass for each plot at each census date was estimated as the sum of the AGC of each living stem, divided by plot area (in hectares).
Carbon Gain and Carbon Loss estimation
Net Carbon Sink (in Mg C ha-1 yr-1) is estimated as carbon gains minus carbon losses. Calculation details are explained below.
Carbon Gains (in Mg C ha-1 yr-1) are the sum of the aboveground live biomass carbon additions from the growth of surviving stems and the addition of newly recruited stems, divided by the census length (in years) and plot area (in hectares). For each stem that survived a census interval, carbon additions from its growth (Mg C ha-1 yr-1) were calculated as the difference between its AGC at the end census of the interval and its AGC at the beginning census of the interval. For each stem that recruited during the census interval (i.e. reaching DBH≥100 mm), carbon additions were calculated in the same way, assuming DBH=0 mm at the start of the interval65. Carbon Losses (in Mg C ha-1 yr-1) are estimated as the sum of aboveground biomass carbon from all stems that died during a census interval, divided by the census length (in years) and plot area (in hectares). Both carbon gains and carbon losses are calculated using standard methods6, including a census interval bias correction, using the SummaryAGWP function of R-package BiomasaFP63,64,68.
As carbon gains are affected by a census interval bias, with the underestimate increasing with census length, we corrected this bias by accounting for (i) the carbon additions from trees that grew before they died within an interval (unobserved growth) and (ii) the carbon additions from trees that recruited and then died within the same interval (unobserved recruitment)65,71.
Component (i), the unobserved growth of a stem that died during a census interval, is estimated as the difference between AGC at death and AGC at the start of the census. These are calculated using equation 2, from respectively DBHdeath and DBHstart. The latter is part of the data, the first can be estimated as: DBHdeath = DBHstart × G × Ymean, where G is the plot-level median diameter growth rate (mm yr-1) of the size class the tree was in at the start of the census interval (size classes are defined as D < 200 mm, 400 mm > D ≥ 200 mm and D ≥ 400 mm) and Ymean is the mean number of years trees survived in the census interval before dying. Ymean is calculated from the number of trees that are expected to have died in each year of the census interval, which is derived from the plot-level per-capita mortality rate (ma; % dead trees yr-1) calculated following equation 5 in ref.71.
Component (ii), growth of recruits that were not observed because they died during the census interval, is estimated by calculating the number of unobserved recruits and diameter at death for each unobserved recruit. The number of unobserved recruits (stems ha-1 yr-1) is estimated as: Nu.r = Ra – Psurv × Ra, where Ra (recruited stems ha-1 yr-1) is the per area annual recruitment calculated following equation 11 in ref.71 and Psurv is the probability of each recruit surviving until the next census: Psurv = (1-ma)T, where T is the number of years remaining in the census interval. Summing Nu.r for each year in a census interval gives the total number of unobserved recruits in that census interval. We then estimate diameter at death for each unobserved recruit, which is given in mm by DBHdeath,u.r = 100 + (Gs × Ymean-rec), where Gs is the plot-level median diameter growth rate (mm yr-1) of the smallest size class (i.e. D < 200 mm) and Ymean-rec is the mean life-span of unobserved recruits calculated as the mean life-span of recruits in a given year, weighted by Nu.r. The mean life-span of recruits in a given year is calculated from the number of recruits that died in that year, which is derived from the plot-level per-capita mortality rate (ma; % dead trees yr-1). Growth of each unobserved recruit (mm yr-1) is then calculated as DBHdeath,u.r divided by Ymean-rec.
The census interval bias correction (components i and ii together) typically add <3% to plot-level carbon gains. Carbon Losses are affected by the same census interval bias, hence we corrected this bias by accounting for (i) the additional carbon losses from the trees that were recruited and then died within the same interval, and (ii) the additional carbon losses resulting from the growth of the trees that died in the interval6,15,63. These two components are calculated in the same way as for Carbon gains and typically add <3% to plot-level carbon losses.
Carbon gains include both gains from the growth of surviving stems and new recruits. Separating carbon gains from tree growth of surviving stems and newly recruited stems, shows that carbon gains from recruitment are small overall, and are significantly lower in Africa than in the Amazon, likely due to the lower stem turnover rates and longer carbon residence time (Africa: 0.17 Mg C ha-1 yr-1; CI: 0.16-0.18 versus Amazon: 0.27 Mg C ha-1 yr-1; CI: 0.25-0.28, p<0.001; two-way Wilcoxon test), but this is compensated by carbon gains from survivors being significantly larger in Africa (2.33 Mg C ha-1 yr-1; CI: 2.27-2.39) than in the Amazon (2.13 Mg C ha-1 yr-1; CI: 2.09-2.17, p=0.014). Therefore, gains overall (sum of gains from surviving stems and newly recruited stems) are indistinguishable between the continents (Africa: 2.57 Mg C ha-1 yr-1; CI: 2.51-2.67 vs Amazon: 2.46 Mg C ha-1 yr-1; CI: 2.41-2.50, p=0.460; two-way Wilcoxon test).
Long-term Gain, Loss and Net Carbon Sink Trend Estimation, 1983-2014
The estimated mean and uncertainty in carbon gains, carbon losses and the net carbon sink of the African plots from 1983-2014 (Figure 1, Extended Data Figure 7 and Extended Data Figure 8) were calculated following ref.6 to allow direct comparison with published Amazonian results. First, each census interval value was interpolated for each 0.1-yr period within the census interval. Then, for each 0.1-yr period between 1983 and 2014, we calculated a weighted mean of all plots monitored at that time, using the square root of plot area as a weighting factor6. Confidence intervals for each 0.1-yr period were bootstrapped.
Trends in carbon gains, losses and the net carbon sink over time were assessed using linear mixed effects models (lmer function in R, lme4 package72), providing the linear slopes reported in Figure 1. These models regress the mid-point of each census interval against the value of the response variable for that census interval. Plot identity was included as a random effect, i.e. assuming that the intercept can vary randomly among plots. We did not include slope as a random effect, consistent with previously published Amazon analyses6, because models did not converge due to some plots having too few census intervals. Observations were weighted by plot size and census interval length. Weightings were derived empirically, by assuming a priori that there is no significant relation between the net carbon sink and census interval length or plot size, following ref.13. The following weighting removes all pattern in the residuals: Weight= 3√lengthint + 4√plotsize -1 (equation 3), where lengthint is the length of the census interval, in years. Significance was assessed by regressing the residuals of the net carbon sink model against the weights (p=0.702).
Differences in long-term slopes between the two continents for carbon gains, carbon losses and net carbon sink, reported in the main text, were also assessed using linear mixed effects models, as described above, but performed on the combined African and Amazonian datasets and limited to their common time window, 1983 to 2011.5. For these three tests on the pooled data we included an additional interaction term between census interval date and continent, where a significant interaction would indicate that the slopes differ between continents. The statistical significance of continental differences in slope were assessed using the F-statistic (Anova function in R, car package73). Shortening the common time window to the 20 years when the continents are best-sampled, 1991.5 to 2011.5, gave very similar results, including a divergent continental sink (p=0.04).
Continental and Pan-Tropical Carbon Sink Estimates
The per unit area total net carbon sink (in Mg C ha-1 yr-1) for each time period in Table 1 (each decade between 1980 and 2010; and 2010-2015) is the sum of three components. The first component is the per unit area aboveground carbon sink from living trees and lianas with DBH≥100 mm. For Africa we use the per unit area net carbon sink values presented in this paper. For Amazonia, we use data in ref.6. For Southeast Asia, we use inventory data collected using similar standardised methods from 49 plots in ref.15. For each time window, we use all plots for which census dates overlap the period, weighted by the square root of plot area, as for the solid lines in Figure 1. The second component is the per unit area aboveground carbon sink from living trees and lianas with DBH<100 mm. This is calculated as 5.19%, 9.40% and 5.46% of the first component (i.e. aboveground carbon of large living trees) in Africa, Amazonia and Southeast Asia respectively13,74. The third component is the per unit area belowground carbon sink in live biomass, i.e. roots. This is calculated as 25%, 37% and 17% of the aboveground carbon of living trees with DBH≥100 mm in Africa13, Amazonia6 and Southeast Asia75 respectively.
For each time period in Table 1 we calculated the continental-scale total carbon sink (Pg C yr-1) by multiplying the per unit area total net carbon sink described above by the area of intact forest on each continent at that time interval (in ha) reported in Extended Data Table 2. Decades are calculated from 1990.01 to 1999.99. For comparability with previous continental-sink results, we used continental values of intact forest area for 1990, 2000 and 2010 as published in ref.1, i.e. total forest area minus forest regrowth. We used the 1990-2010 data to fit an exponential model for each continent and used this model to estimate intact forest area for 1980 and 2015.
Finally, in the main text we calculated the proportion of anthropogenic CO2 emissions removed by Earth’s intact tropical forests, as the total pan-tropical carbon sink from Table 1 divided by the total anthropogenic CO2 emissions. Total anthropogenic CO2 emissions are calculated as the sum of emissions from fossil fuel and land-use change and are estimated at 7.6 Pg C yr-1 in the 1990s, 9.0 Pg C yr-1 in the 2000s, and 11.1 Pg C yr-1 in the 2010s (ref.21, assuming 1.7% growth in fossil fuel emissions in 2018 and 2019, and mean 2010-2017 land-use change emissions for 2018 and 2019).
Carbon Sink from an Atmospheric Perspective
To estimate the evolution of the carbon sink from an atmospheric perspective, we assumed that the contribution to the atmosphere from carbon gains are experienced immediately, while the contribution to the atmosphere from carbon losses must take into account the delay in decomposition of dead trees. We did this by calculating total forest carbon loss (Mg C ha-1 yr-1) for each year between 1950-2015, using the mean 1983-2015 records from Figure 1 and assuming constant losses prior to 1983 (1.9 and 1.5 Mg C ha-1 yr-1 for Africa and Amazonia respectively). Then, for each focal year between 1950-2015, we calculated how much carbon was released to the atmosphere in the subsequent years as: yt = x0 × e-0.17× (t-1) - x0 × e-0.17× t, where x0 is the total forest carbon loss of the focal year; yt is the carbon released to the atmosphere at t years from the focal year; and -0.17 yr-1 is a constant decomposition rate calculated for tropical forests in the Amazon45. For example, carbon loss was 1.95 Mg C ha-1 in 1990 in African forests (Figure 1), from which 0.31 Mg C ha-1 was released to the atmosphere in 1991; 0.26 Mg C ha-1 in 1992; 0.22 Mg C ha-1 in 1993; 0.07 Mg C ha-1 in 2000 and 0.01 Mg C ha-1 in 2010. Hence, of the full 1.95 Mg C ha-1 dead tree biomass from 1990, ~50% was released to the atmosphere after 4 yrs, ~85% after 10 yrs, and ~97% after 20 years. Finally, for each year between 1983 and 2015, the total contribution to the atmosphere from carbon losses was calculated as the sum of all carbon contributions released at that year, from all total yearly forest carbon loss pools of the previous years. We then calculated decadal-scale mean contributions to the atmosphere from carbon losses, reported in the main text.
Predictor Variable Estimates, 1983-2014
For each census interval of each plot, we examined potential predictor variables that may explain the long-term trends in carbon gains and carbon losses, reported in Extended Data Table 1 and main text Table 2. First, the environmental conditions during the census interval; second the rate of change of these parameters; and third forest attributes that may affect how different forests respond to the same environmental change. The predictor variable estimates for each census need to avoid bias due to seasonal variation, for example the intra-annual variability in atmospheric CO2 concentration. We therefore applied the following procedure to avoid seasonal variability impacts on long-term trends: (i) the length of each focal census interval was rounded to the nearest complete year (e.g. a 1.1 year interval became a 1 year interval); (ii) we computed dates that minimised the difference between actual fieldwork dates and complete-year census dates, while ensuring that subsequent census intervals of a plot do not overlap. The resulting sequence of non-overlapping census intervals was used to calculate interval-specific means for each environmental predictor variable to remove seasonal effects. The mean difference between the actual fieldwork dates and the complete-year census dates is 0.01 decimal years.
The first group of potential predictor variables, estimated for each census interval of each plot, are theory-driven choices: atmospheric CO2 concentration (CO2), mean annual temperature (MAT), and drought intensity, which we quantified as maximum climatological water deficit (MCWD)14,20,76,77.
Atmospheric CO2 concentration (CO2, in ppm) is estimated as the mean of the monthly mean values from the Mauna Loa record78 over the census interval. While atmospheric CO2 concentration is highly correlated with time (R2=0.98), carbon gains are slightly better correlated with CO2 (Radj2=0.0027) than with time (Radj2=0.0025).
Mean Annual Temperature (MAT, in °C) was derived from the temporally resolved (1901-2015) dataset of monthly mean temperature from the Climatic Research Unit (CRU TS version 4.03; ~3025 km2 resolution; released 15 May 2019; https://crudata.uea.ac.uk/cru/data/hrg/)79. We downscaled the data to ~1 km2 resolution using the WorldClim dataset51,80, by subtracting the difference in mean monthly temperature, and applying this monthly correction to all months81. We then calculated MAT for each census interval of each plot using the downscaled monthly CRU record.
Maximum Climatological Water Deficit (MCWD, in mm) was derived from the ~3025 km2 resolution Global Precipitation Climatology Centre dataset (GPCC version 6.0) that includes many more rain gauges than CRU in tropical Africa82,83. As GPCC ends in 2013 we combined it with satellite-based Tropical Rainfall Measurement Mission data (TRMM 3B43 V7 product, ~757 km2 resolution)84. The fit for the overlapping time period (1998-2013) was used to correct the systematic difference between GPCC and TRMM: GPCC’ = a+b*GPCC, with GPCC’ the adjusted GPCC record and a and b different parameters for each month of the year and for each continent. Precipitation was then downscaled to ~1 km2 resolution using the WorldClim dataset51,80, by dividing by the ratio in mean monthly rainfall, and applying this monthly correction to all months81. For each census interval we extracted monthly precipitation values and estimated evapotranspiration (ET) to calculate monthly Climatological Water Deficit (CWD), a commonly used metric of dry season intensity for tropical forests14,76,77. Monthly CWD values were calculated for each subsequent series of 12 months (complete years)77. Monthly CWD estimation begins with the wettest month of the first year in the interval, and is calculated as 100 mm per month evapotranspiration (ET) minus monthly precipitation (P). Then, CWD values for the subsequent 11 months were calculated recursively as: CWDi= ET - Pi + CWDi-1, where negative CWDi values were set to zero77 (no drought conditions). This procedure was repeated for each subsequent complete 12 months. We then calculated the annual MCWD as the largest monthly CWD value for every complete year within the census interval, with the MCWD of a census interval being the mean of the annual MCWD values within the census interval. Larger MCWD indicates more severe water deficits.
We assume ET is 100 mm month-1 on both continents, based on measurements from Amazonia76,77, more limited measurements from West Africa summarized in ref.85, predictive skill86, and use in past studies on both continents14,87. MCWD therefore represents a precipitation-driven dry season deficit, as ET remains constant. An alternative assessment, using a data-driven ET product88,89, gave a mean ET of 95 and 98 mm month-1 for the African and Amazonian plot networks respectively. Using these values did not affect the results.
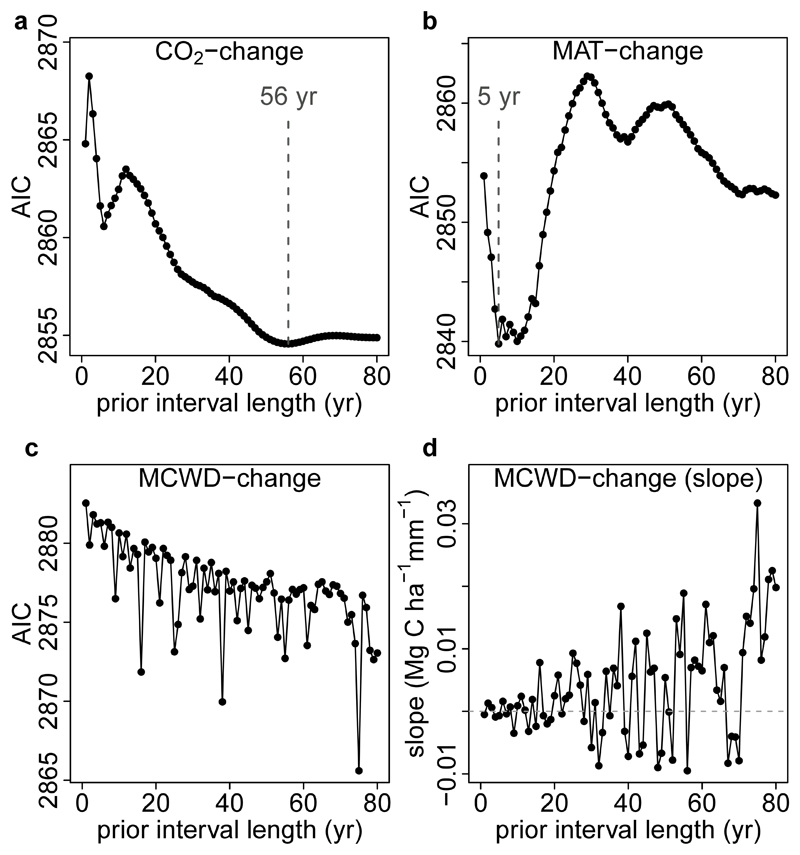
To calculate the environmental change of potential predictor variables, CO2-change (in ppm yr-1), MAT-change (in °C yr-1) and MCWD-change (in mm yr-1), we selected an optimum period over which to calculate the change, derived empirically by assessing the correlation of carbon gains (all plots, all censuses) with the change in each environmental variable, using linear mixed effects models (lmer function in R, lme4 package72). The annualised change in the environmental variable was calculated as the change between the focal interval and a prior interval (termed the baseline period) with a lengthening time window ranging from 1 year through to 80 years prior to the focal interval (i.e. 80 linear mixed effects models per variable). We calculated AIC for each model and selected the interval length with the lowest AIC. Thus, MAT-change (in °C yr-1) = (MATi-MATb)/(datei-dateb), where MATi is the MAT over the focal census interval calculated using the procedure described above, MATb is the MAT over a baseline period prior to the focal interval, datei is the mid-date of the focal census interval and dateb is the mid-date of the baseline period. The lmer results show that the baseline period for MAT-change is 5 years and for CO2-change it is 56 years, while MCWD showed no clear trend, so MCWD-change was not included in the models (see Extended Data Figure 3). All three results conform to a priori theoretical expectations. For CO2 a maximum response to an integrated 56 years of change is expected because forest stands will respond most strongly to CO2 when most individuals have grown under the new rapidly changing condition, which should be at its maximum at a time approximately equivalent to the carbon residence time of a forest stand30,90 (mean of 62 years in this dataset). For MAT, 5 years is consistent with experiments showing temperature acclimation of leaf- and plant-level photosynthetic and respiration processes over half-decadal timescales31,91. MCWD has no overall trend suggesting that once a drought ends, its impact on tree growth fades rapidly, as seen in other studies14,92. Also in the moist tropics wet-season rainfall is expected to re-charge soil water, hence lagged impacts of droughts are not expected.
We calculated estimates of two forest attributes that may alter responses to environmental change as potential predictor variables: Wood Density (WD) and Carbon Residence Time (CRT). In intact old-growth forests, mean WD (in g cm-3) is inversely related to resource availability28,93,94, as is seen in our dataset (carbon gains and plot-level mean WD are negatively correlated, Extended Data Figure 4). WD is calculated for each census interval in the dataset, as the mean WD of all trees alive at the end of the census interval, to be consistent with the previous Amazon analysis6. Carbon residence time (CRT, in yrs) is a measure of the time that fixed carbon stays in the system. CRT is a potential correlate of the impact of past carbon gains on later carbon losses30. To avoid circularity in the models, the equation used to calculate CRT differed depending on the response variable. If the response variable is carbon loss, the CRT equation is based on gains: CRT=AGC/gains, with AGC for each interval based on AGC at the end of the interval, and the gains for each interval calculated as the mean of the gains in the interval and the previous intervals (i.e. long-term gains). If the response variable is carbon gains, the CRT equation is based on losses: CRT=AGC/losses. The equation employed for use in the carbon loss model (based on gains) is the standard formula used to calculate CRT and is retained in the minimum adequate model (see below and Table 2). The non-standard CRT equation (based on losses) used in the carbon gain model is not retained in the minimum adequate model (see below).
Statistical modelling of the Carbon Gain, Loss and Sink Trends
We first constructed two models including those environmental drivers exhibiting long-term change that impact theory-driven models of photosynthesis and respiration as predictor variables: CO2, MAT, and MCWD. One model had carbon gains as the response variable, the other had carbon losses as the response variable (both in Mg C ha-1 yr-1). Models were fitted using the lme function in R, with maximum likelihood (NLME package95). All census intervals within all plots were used, weighted by plot size and census length (using equation 3 above). Plot identity was included as a random effect, i.e. assuming that the intercept can vary randomly among plots. All predictor variables in the models were scaled without centering (scale function in R, RASTER package62). Carbon gain values were normally distributed but carbon loss values required a power-law transformation (λ= 0.361) to meet normality criteria. Multi-parameter models are: carbon gains = intcp + a×CO2 + b×MAT + c×MCWD (model 1); carbon losses = intcp + a×CO2 + b×MAT + c×MCWD (model 2); where intcp is the estimated model intercept, and a, b, and c are model parameters giving the slope of relationships with environmental predictor variables. For multi-parameter model outputs see Extended Data Table 1, for single-parameter relationships, Figure 2.
The second pair of models include the same environmental predictors (CO2, MAT, MCWD), plus their rate of change (CO2-change, MAT-change, but not MCWD-change as explained above), and forest attributes that may alter how forests respond (WD, CRT), as described above. We also evaluated the possible inclusion of a differential continent effect of each variable in the full model. We first constructed models with only a single predictor variable, and allowed different slopes in each continent. Next, if removal of the continent-specific slope (using stepAIC function in R, MASS package96) decreased model Akaike Information Criterion (AIC) then the continent-specific slope was not included in the full model for that variable. Only MCWD showed a significant differential continent-specific slope. This implies that forests on both continents have common responses to CO2, CO2-change, MAT, MAT-change, WD and CRT, but respond differently to differences in MCWD. This is likely because wet-adapted species are much rarer in Africa than in Amazonia as a result of large differences in past climate variation34. Lastly, we allowed different intercepts for the two continents to potentially account for differing biogeographical or other continent-specific factors. For the carbon loss model, we applied the same continent-specific effects for slope as for the carbon gain model. Carbon loss values were transformed using a power-law transformation (λ= 0.361) to meet normality criteria.
For both carbon gains and losses we parameterized a global model including the significant continent-specific effect of MCWD, selecting the most parsimonious simplified model using all-subsets regression97,98. To do so, we first generated a set of models with all possible combinations (subsets) of fixed effect terms in the global model using the dredge function of the MuMIn package in R99. We then chose the best-ranked simplified model based on the AICc criterion, hereafter called “minimum adequate carbon gain/loss model”, reported in Table 2. The minimum adequate models are: carbon gains = intcp×continent + a×CO2-change + b×MAT + c×MAT-change + d×MCWD×continent + e×WD (model 3); carbon losses = intcp + a×CO2-change + b×MAT-change + c×MCWD + d×CRT (model 4). WD was retained in the carbon gain model, likely because growth is primarily impacted by resource availability, while CRT was retained in the carbon loss model, likely because losses are primarily impacted by how long fixed carbon is retained in the system.
Table 2 presents model coefficients of the best-ranked gain model and best-ranked loss model selected using all-subsets regression. These best-ranked gain and loss models have weights of 0.310 and 0.132 respectively, which is almost double the weight of the second ranked models (0.152 and 0.075 respectively). In Supplementary Table 2 we also used the model.avg function of the MuMIn package to calculate a weighted mean of the coefficients of the best-ranked models together representing a cumulative weight-sum of 0.95 (i.e. a 95% confidence subset). Supplementary Table 2 (model-averaged) and main text Table 2 (best-ranked) model parameters are very similar. Supplementary Tables 3 and 4 report the complete sets of carbon gains and loss models that contribute to the model average results.
The model-average results show the same continental differences in sensitivity to environmental variables as the best-ranked models. From 2000 to 2015, carbon gains increased due to CO2-change (+3.7% in both the averaged and the best-ranked models, both continents), while temperature rises led to a decline in gains, which especially had an effect in the Amazon (-1.14% and -1.07% due to MAT and MAT-change together in the averaged and best-ranked model respectively). Finally, both models result in similar predictions of the net carbon sink over the 1983-2040 period: the future net sink trend in Africa is -0.004 and -0.003 in the best-ranked and averaged models respectively; in Amazonia the future net sink trend is -0.013 and -0.011 in the best-ranked and averaged models respectively. The Amazon sink reaches zero in 2041 using model-averaged parameters compared to 2035 using the best-ranked models.
Estimating Future Predictor Variables to 2040
To calculate future modelled trends in carbon gains and losses (Figure 3), we first estimated annual records of the predictor variables (CO2-change, MAT, MAT-change, MCWD, WD and CRT) to 2040 (Extended Data Figure 5).
To do so we first calculated annual records for the period of the observed trends for each plot location (i.e. from 1983-2014 in Africa and 1983-2011.5 in Amazonia). For CO2-change, MAT, MAT-change and MCWD we extracted monthly records as described in section Predictor Variable Estimates (above). For WD and CRT we interpolated to a 0.1-yr period within each census interval (as in Figure 1). Then, we calculated the mean annual value of each predictor variable from the 244 plot locations in Africa, and separately the mean annual value of each predictor variable from the 321 plot locations in Amazonia (i.e. solid lines in ED Figure 5). For each predictor variable, we calculated annual records of upper and lower confidence intervals by respectively adding and subtracting 2σ to the mean of each annual value (shaded area in ED Figure 5).
Secondly, for each predictor variable we parameterised a linear model for each continent using the annual records for the period of the observed trends. Then for each predictor variable, the continent-specific linear regression models were used to estimate predictor variables for each plot location from 2014 to 2040 in Africa and from 2011.5 to 2040 in the Amazon (dotted lines in Extended Data Figure 5). For each predictor variable, we calculated annual records of upper and lower confidence intervals by respectively adding and subtracting 2σ to the slope of each linear model (shaded area around dotted lines in ED Figure 5).
Estimating Future Carbon Gain, Loss and Net Carbon Sink
We used the minimum adequate models (Table 2) to predict annual records of carbon gain, carbon loss and the carbon sink for the plot networks in Africa and Amazonia over the period 1983 through to 2040 (Figure 3). We extracted fitted carbon gain and loss values using the mean annual records for each predictor variable (predictSE.lme function, AICcmodavg package100). Upper and lower confidence intervals were calculated accounting for uncertainties in the model (both fixed and random effects) and predictor variables using the 2σ upper and lower confidence interval for each predictor variable (using predictSE.lme). Finally the net carbon sink was calculated by subtracting the losses from the gains. To obtain sink values in the future in Table 1, annual per unit area sink predictions, from Figure 3, were averaged over each decade and multiplied by the future forest area, as described above.
To test the sensitivity of the future predictions in Figure 3, we reran the analysis by modifying future trajectories of predictor variables one at a time, while keeping all others the same, to assess the mean C sink over 2010-15 and 2030 (averaging at 2030 is not necessary as trends in MAT-change and MCWD, which largely drive modelled inter-annual variability, are estimated as smooth trends in the future). For each predictor variable, we explored potential impacts of the likely bounds of possibility, (i) by taking the steepest slope of either continent from the extrapolated trends, doubling this slope and applying it on both continents; and (ii) by taking the steepest slope of either continent from the extrapolated trends, taking the opposite of this slope and applying it on both continents. These bounds represent deviations of >2 sigma from observed trends. Change in MAT also alters MAT-change, so we present the sensitivity of both parameters together.
Additionally, for CO2-change and MAT, we also calculated future slopes under three future Representative Concentration Pathway (RCP) scenarios38 with different radiative forcing in 2100: RCP2.6, 4.5, and 8.5. Future RCP CO2-change slopes (ppm yr-1) were calculated using RCP CO2 concentration data for the years between 2015 and 2030 inclusive. Future RCP MAT and MAT-change slopes were obtained from plot-specific MAT values extracted from downscaled 30 seconds resolution data for current80 and future51 climate from WorldClim, and averaged over 19 CMIP5 models. We subtracted the mean 2040-2060 climate MAT (i.e. 2050) from the mean 1970-2000 climate MAT (i.e. 1985), divided by 65 years to give the annual rate of change. We then calculated a mean slope over all plots per continent. Finally, to avoid mismatches between RCP-derived values of CO2 and MAT and the observed records we removed any difference in intercept between the RCP trends and observed trends, so the RCP trends were a continuation of the end-point of the observed trajectory in 2015. We did not estimate the sensitivity of MCWD under the RCP scenarios, because the CMIP5 model means do not show drought trends for our forest plot networks, unlike rain gauge data for the recent past, and thus would show little or no sensitivity to MCWD. For each modified slope, Supplementary Table 5 reports the absolute decline in the sink in each continent in 2030 compared to the 2010-15 mean sink. This shows that the future sink strength is sensitive to future environmental conditions, but within both RCP scenarios and our bounds of possibility we show a decline in the sink strength in both continents over the 2020s.
Extended Data
Extended Data Figure 1. Map showing the locations of the 244 plots included in this study.
Dark green represents all lowland closed-canopy forests, submontane forests and forest-agriculture mosaics; light green shows swamp forests and mangroves, blue circles represent plot clusters, referred to by three-letter codes (see Supplementary Table 1 for the full list of plots). Clusters <50 km apart are shown as one point for display only, with the circlesize corresponding to sampling effort in terms of hectares monitored. Land cover data is from The Land Cover Map for Africa in the Year 2000 (GLC2000 database)101,102. This map was created using the R statistical platform, version 3.2.1 (ref.62), which is under the GNU Public License.
Extended Data Figure 2. Long-term above-ground carbon dynamics of 244 African intact tropical forest inventory plots.
Points in the scatterplots indicate the mid-census interval date, with horizontal bars connecting the start and end date for each census interval for net aboveground biomass carbon change (a), carbon gains (from woody production from tree growth and newly recruited stems) (b), and carbon losses (from tree mortality) (c). Examples of time series for three individual plots are shown in purple, yellow and green. Associated histograms show the distribution of the plot-level net aboveground biomass carbon (d) (with a three-parameter Weibull probability density distribution fitted in blue, showing the carbon sink is significantly larger than zero; one-tail t-test: p<0.001), carbon gains (e), and carbon losses (f).
Extended Data Figure 3. Akaike’s Information Criterion (AIC) from correlations between the carbon gain in tropical forest inventory plots and changes in either atmospheric CO2, temperature (as MAT) or drought (as MCWD), each calculated over ever-longer prior intervals.
Panels show AIC from linear mixed effects models of carbon gains from 565 plots and corresponding, atmospheric CO2 (CO2-change) (a), Mean Annual Temperature (MAT-change) (b), and Maximum Climatological Water Deficit (MCWD-change) (c). For CO2 the AIC minimum was observed when predicting the carbon gain from the change in CO2 calculated over a 56 year long prior interval length. We use this length of time to calculate our CO2-change parameter. Such a value is expected because forest stands will respond most strongly to CO2 when most individuals have grown under the new rapidly changing condition, which should be at its maximum at a time approximately equivalent to the carbon residence time of a forest stand30,90 (mean of 62 years in this pooled African and Amazonian dataset). For MAT the AIC minimum was 5 years, which we use as the prior interval to calculate our MAT-change parameter. This length is consistent with experiments showing temperature acclimation of leaf- and plant-level photosynthetic and respiration processes over approximately half-decadal timescales31,91. For MCWD the AIC minimum is not obvious, while the slope of the correlation, shown in panel (d), shows no overall trend and oscillates between positive or negative values, meaning there is no relationship between carbon gains and the change in MCWD over intervals longer than 1 year; thus MCWD-change is not included in our models. This result suggests that once a drought ends, its impact on tree growth fades rapidly, as seen in other studies14,92. Also in the moist tropics wet-season rainfall is expected to re-charge soil water, hence lagged impacts of droughts are not expected.
Extended Data Figure 4. Potential forest dynamics-related drivers of carbon gains and losses in structurally intact African and Amazonian tropical forest inventory plots.
The aboveground carbon gains, from woody production (a-b), and aboveground carbon losses, from tree mortality (c-d), are plotted against the carbon residence time (CRT), and wood density (WD), for African (blue) and Amazonian (brown) inventory plots. Linear mixed effect models were performed with census intervals (n=1566) nested within plots (n=565) to avoid pseudo-replication, using an empirically derived weighting based on interval length and plot area (see methods). Significant regression lines for the complete dataset are shown as a solid line; non-significant regressions as a dashed line. Each dot represents a time-weighted mean plot-level value; transparency of the inner part of the dot represents total monitoring length, with empty circles corresponding to plots monitored for ≤ 5 years and solid circles for plots monitored for >20 years. Carbon loss data are presented untransformed for comparison with carbon gains; linear mixed effects models on transformed data to fit normality assumptions do not change the significance of the results. Note, CRT is calculated differently for the carbon gains and losses models (see methods).
Extended Data Figure 5. Trends in predictor variables used to estimate long-term trends in above-ground carbon gains, carbon losses and the resulting net carbon sink in African and Amazonian intact tropical forest plot networks.
Mean annual CO2-change (a), MAT (b), MAT-change (c), MCWD (d), CRT (e), and WD (f) for African plot locations in blue, and corresponding Amazon plots locations in brown (g-l). Solid lines for CO2-change, MAT, MAT-change, MCWD represent obervational data, and solid lines for CRT and WD represent plot means and a time window where >75% of the plots were monitored, long-dashed lines are plot means were <75% of plots were monitored. Dotted lines are future values estimated from linear trends on the 1983-2014 (Africa) or 1983-2011 (Amazon) data (slope and p-value reported in each panel), see methods for details. Upper and lower confidence intervals (shaded area) for the past (Africa: 1983-2014; Amazonia: 1983-2011) are calculated by respectively adding and subtracting 2σ to the mean of each annual value. Upper and lower confidence intervals for the future were estimated by adding and subtracting 2σ from the slope of the regression model.
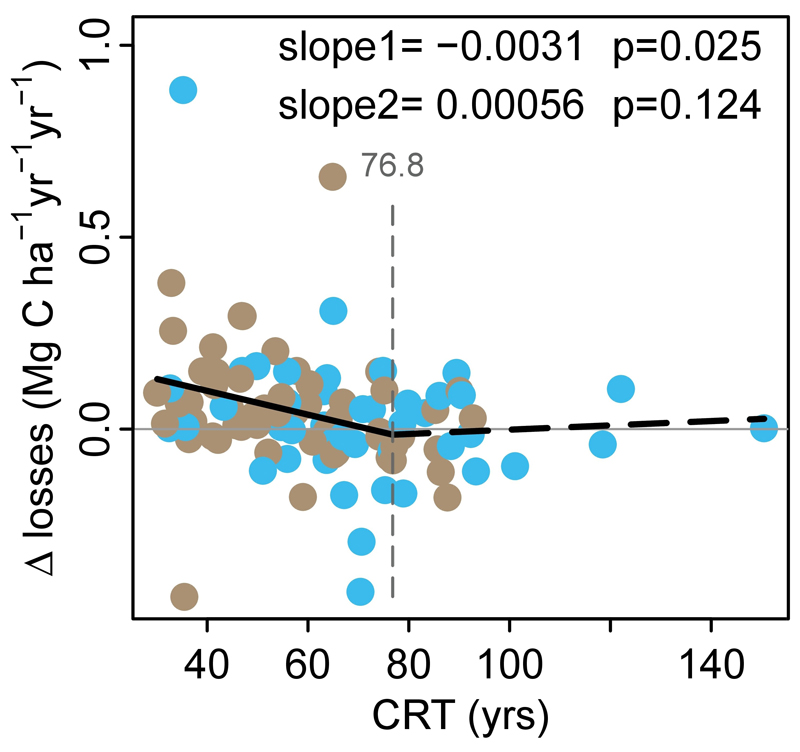
Extended Data Figure 6. The change in carbon losses versus carbon residence time (CRT) of inventory plots in Africa and Amazonia.
For plots with two census intervals, we calculated the change in carbon losses (∆losses, in Mg C ha-1 yr-1 yr-1) as the carbon losses (Mg C ha-1 yr-1) of the second interval minus the carbon losses of the first interval, divided by the difference in mid-interval dates. For plots with more than two intervals, we calculated the change in carbon losses for each pair of subsequent intervals, then calculated the plot-level mean over all pairs, weighted by the time length between mid-interval dates. This analysis includes only plots with at least two census intervals and monitored for ≥20 years (i.e. roughly one-third of the mean CRT of the pooled African and Amazon dataset; n = 116). Breakpoint regression was used to assess the CRT length below which forest carbon losses begin to increase. Plots with CRT <77 years show a recent long-term increase in carbon losses, longer CRT plots do not. Blue points are African plots, brown points are Amazonian plots.
Extended Data Figure 7. Trends in African tropical forest net aboveground live biomass carbon, carbon gains and carbon losses, calculated for the last 15 years of the twentieth century (left panels a-c) and the first 15 years of the twenty-first century (right panels d-f).
Plots were selected from the full dataset if their census intervals cover at least 50% of the respective time windows, i.e. they are intensely monitored (n=56 plots for 1985-2000, and n=134 plots for 2000-2015, respectively). Solid lines show mean values, shading corresponds to the 95% CI, as calculated in Figure 1. Dashed lines, slopes and p-values are from linear mixed effects models, as in Figure 1. The data shows a difference compared to Figure 1, notably the sink decline after ~2010 driven by rising carbon losses. This is because in Figure 1 we include all available plots over the 1983-2015 window, which includes clusters of plots monitored only in the 2010s that had low carbon loss and high carbon sink values.
Extended Data Figure 8. Twenty-first century trends in aboveground biomass carbon losses from African tropical forest inventory plots with either long (left panels) or short (right panels) carbon residence time.
Upper panels include all plots, i.e. as in Figure 1, but split into a long-CRT group (a), and a short-CRT group (b), each containing half the 244 plots. Lower panels restrict plots to those spanning >50% of the time window, i.e. intensely monitored plots, as in Extended Data Figure 7, but split into a long-CRT group (c), and a short-CRT group (d), each containing half the 134 plots. Solid lines indicate mean values, shading the 95% CI, as for Figure 1. Dashed lines, slopes and p-values are from linear mixed-effects models, as for Figure 1. Carbon losses increase at a higher rate in the short-CRT than the long-CRT group of plots, in both datasets, although this increase is not statistically significant.
Extended Data Table 1.
Models to predict carbon gains and losses in African and Amazonian tropical forests, including only environmental variables, showing long-term trends that impact theory-driven models of photosynthesis and respiration. Significant values in bold.
| Carbon gains, Mg C ha-1 yr-1 | ||||
|---|---|---|---|---|
| Predictor variable | Parameter value | Standard Error | t-value | p-value |
|
| ||||
| (Intercept) | 4.694 | 0.739 | 6.354 | 0.000 |
| CO2 (ppm) | 0.005 | 0.001 | 3.196 | 0.001 |
| MAT (°C) | -0.143 | 0.021 | -6.844 | 0.000 |
| MCWD (mm x1000) | -1.232 | 0.210 | -5.878 | 0.000 |
|
| ||||
| Carbon losses, Mg C ha-1 yr-1
* | ||||
| Predictor variable | Parameter value | Standard Error | t-value | p-value |
|
| ||||
| (Intercept) | 0.926 | 1.854 | 0.500 | 0.617 |
| CO2 (ppm) | 0.004 | 0.004 | 0.947 | 0.344 |
| MAT (°C) | -0.011 | 0.044 | -0.249 | 0.804 |
| MCWD (mm x1000) | -0.498 | 0.505 | -0.985 | 0.325 |
Carbon loss values were normalized via power-law transformation, λ= 0.361.
Extended Data Table 2.
Forest area estimates used to calculate total continental forest sink.
| Period | intact forest area (Mha)* | ||||
|---|---|---|---|---|---|
| Africa | Amazon | Southeast Asia | Pan-tropics | ||
|
|
|
||||
| 1980 | 671.5 | 958.3 | 233.6 | 1863.4 | |
| 1985 | 634.3 | 921.1 | 207.4 | 1762.8 | |
| 1990 | 600.2 | 885.2 | 190.6 | 1676.0 | |
| 1995 | 565.9 | 851.1 | 163.5 | 1580.5 | |
| 2000 | 531.8 | 817.2 | 136.9 | 1485.9 | |
| 2005 | 504.8 | 784.5 | 129.2 | 1418.5 | |
| 2010 | 477.8 | 756.3 | 118.4 | 1352.5 | |
| 2015 | 450.5 | 726.7 | 101.5 | 1278.7 | |
| 2020 | 425.5 | 698.5 | 90.1 | 1214.2 | |
| 2025 | 402.0 | 671.5 | 80.0 | 1153.4 | |
| 2030 | 379.7 | 645.4 | 71.0 | 1096.1 | |
| 2035 | 358.6 | 620.4 | 63.0 | 1042.1 | |
| 2040 | 338.8 | 596.4 | 56.0 | 991.1 | |
Intact forest area for 1990, 2000 and 2007 is published in ref.1 (i.e. the total forest area minus forest regrowth). To estimate intact forest area for the other years in this table, we fitted exponential models for each continent using the published data. intact forest area (Mha).
Supplementary Material
Supplementary Information is available online for this paper.
Acknowledgements
This paper is a product of the African Tropical Rainforest Observatory Network (AfriTRON), curated at ForestPlots.net. AfriTRON has been supported by numerous people and grants since its inception. We sincerely thank the people of the many villages and local communities who welcomed our field teams and without whose support this work would not have been possible: Sierra Leone (Barrie, Gaura, Koya, Makpele, Malema, Nomo, Tunkia, Gola Rainforest National Park), Liberia (Garley town, River Gbeh, Glaro Freetown), Ghana (Nkwanta, Asenanyo, Bonsa, Agona, Boekrom, Dadieso, Enchi, Dabiasem, Mangowase, Draw, Fure, Esuboni, Okumaninin, Kadeand Asamankese, Tinte Bepo, Tonton), Nigeria (Oban), Gabon (Ekobakoba, Mikongo, Babilone, Makokou, Leke/Moyabi Rougier Forestry Concession, Ivindo National Park, Lope National Park, Ipassa station, Kingele station, Tchimbele, Mondah, Ivindo, Ebe, Ekouk, Oveng, Sette Cama, Waka National Park), Cameroon (Campo, Nazareth, Lomié, Djomédjo, Alat-Makay, Somolomo, Deng Deng, Ejagham forest reserve, Eyumojok, Mbakaou, Myere, Nguti, Bejange, Kekpane, Basho, Mendhi, Matene, Mboh, Takamanda, Obonyi, Ngoïla), Democratic Republic of Congo (Yoko, Yangambi, Epulu, Monkoto), Republic of Congo (Bomassa, Ekolongouma, Bolembe, Makao, Mbeli, Kabo, Niangui, Ngubu, Goualaki, Essimbi), and many others.
We thank the hundreds of field assistants whose expertise and enthusiasm is indispensable to successful fieldwork: Menge Elvis Abang, Usaw Philip Achui, Francis Addai, Eyelechon Julius Agbachon, Jess Agnaka, Archaley John Akaza, Gabarie Alaman, Gregoire Alaman, Abor Enow Alexander, Kate Allen, Mobembe Amalphi, Danny Amandus, Jean Andju, Lazare Angassike Limbanga, Samuel Asamoah, Takem Martin Ashu, Moses Ashu, Joel Asse, Bangubaare Augustine, Henry Badjoko, Mayanga Balimu, Juste Baviogui-Baviogui, Solomon Benteh, Akuemo Bertrand, Akwo Bettus, Albert Bias, Andre Bikoula, Alain Bimba, Prince Bissiemou, Mensah Boateng, Etshu Bonyenga, Mopero Bosiko Ekaya, Gael Bouka, Juvenal Boussengui, Didier Bowaka Ngomo, Charles Chalange, Sylvester Chenikan, Jonathan Dabo, Emmanuel Dadize, Takyi Degraft, Joachim Dibakou, Jean-Thoussaint Dikangadissi, Pacôme Dimbonda, Edmond Dimoto, Carl Ditougou, Daniel Dorbor, Morris Dorbor, Vincent Droissart, Kwaku Duah, Edward Ebe, Osong Jerome Eji, Ekama Bertrand Ekamam, Jean-Robert Ekomindong, Essa Joseph Enow, Hiboux Entombo, Ebai Mengue Ernest, Courageux Esola, Jules Essouma, Alaman Gabriel, Nteh Genesis, Bilfanim Gideon, Afedo Godwin, Eric Grear, D. John Grear, Mokondo Ismael, Michel Iwango, Mongali Iyafo, Narcisse Kamdem, Bondele Kibinda, Alidé Kidimbu, Exaldi Kimumbu, John Kintsieri, Cisquet Kiebou Opepa, Amani Kitegile, Thérence Komo, Pokou Koué, Augustin Kouanga, Jean Jules Koumikaka, Innocent Liengola, Elias Litonga, Lisa Louvouando, Ondo Luis, Noé Madingou Mady, Felicien Mahoula, Amani Mahundu, Chris Axel Mandebet, Poungue Maurice, Karl Yannick Mayossa, Robert Mba Nkogue, Isa David Mbe, Christian Mbina, Herve Mbona, Alain Mboni, Alain Mbouni, Paulin Menzo, Michael Menge, Andah Michael, Alain Mindoumou, Joseph Minpsa, Jean Paul Mondjo, E. Mounoumoulossi, Serge Mpouam, Tofile Msigala, John Msirikale, Samuel Mtoka, Ruben Mwakisoma, Daniel Ndong-Nguema, Gilbert Ndoyame, Guy Ngongbo, Francois Ngowa, D. Nguema, Luwi Nguye, Raoul Niangadouma, Yaw Nkrumah, Seya Nshimba, Marcel Nziengui Mboumba, Francis Nzogo Obiang, Lucas Obi, Roland Obi, Eyong Louis Odjong, Félix Okon, Fabiane Olivieira, Alina Lawrence Owemicho, Leandre Oyeni-Amoni, Abia Platini, Pierre Ploton, Simon Quausah, Elasi Ramazani, Boscu Saïdou Jean, Lebienfalteur Sagang, Rosalind Salter, Adenani Seki, Deo Shirima, Murielle Simo, Igor Singono, Agboloh Eugene Tabi, Tako Gilbert Tako, Nteh Gambsi Tambe, Toha Tcho, Andrew Teah, Victor Tehtoe, Bright Joe Telephas, Marie Lesly Tonda, Angoni Tresor, Hamid Umenendo, Raymond Votere, Cyrus K. Weah, Slonean Weah, Bart Wursten, Emmanuel Yalley, Donatien Zebaze, Laurent Cerbonney, Emilien Dubiez, Hervé Moinecourt, François Lanckriet, Evina, Monazang, Engonga, Soso Samai, Mohamed Swaray, Patrick Lamboi, Mohamed Sullay, Dennis Bannah, Ibrahim Kanneh, Michael Kannah, Alhassan Kemokai, Joseph Kenneh, Morrison Lukulay.
For logistical and administrative support, we are indebted to international, national and local institutions: the Forestry Department of the Government of Sierra Leone, the Conservation Society of Sierra Leone, the Royal Society for the Protection of Birds (RSPB), The Gola Rainforest National Park, the Forestry Development Authority of the Government of Liberia (FDA), the University of Liberia, the Forestry Commission of Ghana (FC), the Forestry Research Institute of Ghana (FORIG), University of Ibadan (Nigeria), the University of Abeokuta (Nigeria), the Ministère des Eaux, Forêts, Chasse et Pêche (MEFCP, Bangui, République Centrafricaine), the Institut Centrafricain de Recherche Agronomique (ICRA), The Service de Coopération et d’Actions Culturelles (SCAC/MAE), The University of Bangui, the Société Centrafricaine de Déroulage (SCAD), the University of Yaounde I, the National Herbarium of Yaounde, the University of Buea, Biodiversity International (Cameroon), the Ministry of Forests, Seas, Environment and Climate (Gabon), the Agence Nationale des Parcs Nationaux de Gabon (ANPN), Institut de Recherche en Ecologie Tropicale du Gabon, Rougier-Gabon, the Marien Ngouabi University of Brazzaville, the Ministère des Eaux et Forêts (République du Congo), the Ministère de la Rercherche Scientifique et de l’Innovation Technologique (République du Congo), the Nouabalé-Ndoki Foundation, WCS-Congo, Salonga National Park, The Centre de Formation et de Recherche en Conservation Forestière (CEFRECOF, Epulu, D.R.Congo), the Institut National pour l’Etude et la Recherche Agronomiques en R.D.Congo (INERA), the École Régionale Postuniversitaire d’Aménagement et de Gestion intégrés des Forêts et Territoires tropicaux (ERAIFT Kinshasa), WWF-D.R.Congo, WCS-D.R.Congo, the Université de Kisangani, Université Officielle de Bukavu, Université de Mbujimayi, le Ministère de l'Environnement et Développement Durable de la R.D.C., the Lukuru Wildlife Research Foundation, Mbarara University of Science and Technology (MUST), WCS-Uganda, the Uganda Forest Department, the Commission of Central African Forests (COMIFAC), the Udzungwa Ecological Monitoring Centre (Tanzania) and the Sokoine University of Agriculture (Tanzania).
Grants that have funded the AfriTRON network including data in this paper are: a NERC grant to O.L.P., Y.M., and S.L.L. (NER/A/S/2000/01002), a Royal Society University Research Fellowship to S.L.L., a NERC New Investigators Grant to S.L.L., a Philip Leverhulme Award to S.L.L., a European Union FP7 grant to E.G. and S.L.L. (GEOCARBON; 283080), Valuing the Arc Leverhulme Program Grant to Andrew Balmford and S.L.L., a European Research Council Advanced Grant to O.L.P. and S.L.L. (T-FORCES; 291585; Tropical Forests in the Changing Earth System), a Natural Environment Research Council (NERC) Consortium Grant to Jon Lloyd and S.L.L. (TROBIT; NE/D005590/), the Gordon and Betty Moore Foundation to L.J.T.W and S.L.L., the David and Lucile Packard Foundation to L.J.T.W. and S.L.L., the Centre for International Forestry Research to T.S. and S.L.L. (CIFOR), and Gabon’s National Parks Agency (ANPN) to S.L.L. W.H. was funded by T-FORCES and the Brain program of the Belgian Federal Government (BR/132/A1/AFRIFORD and BR/143/A3/HERBAXYLAREDD grants to H.B.). O.L.P., S.L.L., M.J.P.S, A.E.-M., A.L., G.L.-G., G.P, and L.Q were supported by T-FORCES.
Additional African data were included from the consortium MEFCP-ICRA-CIRAD (Centre de Coopération Internationale en Recherche Agronomique pour le Développement), the Tropical Ecology Assessment and Monitoring Network (TEAM), and the Forest Global Earth Observatory Network (ForestGEO; formerly the Center for Tropical Forest Science CTFS). The TEAM network is a collaboration between Conservation International, the Missouri Botanical Garden, the Smithsonian Institution and the Wildlife Conservation Society, and funded by the Gordon and Betty Moore Foundation and other donors. The ForestGEO Network is a collaboration between the Smithsonian Institution, other federal agencies of the United States, the Wildlife Conservation Society (WCS) and the World Wide Fund for Nature (WWF), and funded by the U.S. National Science Foundation and other donors.
The paper was made possible by the RAINFOR network in Amazonia, with multiple funding agencies and hundreds of investigators working in Amazonia, acknowledged in Ref.6, providing comprehensive published data and code and allowing onward analysis of their data, see Ref.6. Data from AfriTRON and RAINFOR are stored and curated by ForestPlots.net, a long-term cyber-infrastructure initiative hosted at the University of Leeds that unites permanent plot records and their contributing scientists from the world’s tropical forests. The development of ForestPlots.net and curation of most data analysed here was funded by many sources, including grants to S.L.L. (Royal Society University Research Fellowship, NERC New Investigators Award, NERC NE/P008755/1), O.L.P. (principally from NERC NE/B503384/1, ERC AdG 291585 “T-FORCES”, and Gordon and Betty Moore Foundation #1656, “RAINFOR”) and E.G. (“GEOCARBON”, and NE/F005806/1 “AMAZONICA”). We acknowledge the contributions of the ForestPlots.net steering committee (T.R.B., A.L., S.L.L., O.L.P., L.Q., Euridice N. Honorio Coronado and Beatriz S. Marimon) to advising on database development and management.
Footnotes
Data and Code Availability
Source data and R-code to generate figures and tables are available from: http://dx.doi.org/10.5521/Forestplots.net/2019_1
Author Contributions
S.L.L. conceived and managed the AfriTRON forest plot recensus programme, O.L.P., T.C.H.S, L.J.T.W. and Y.M. contributed to its development. W.H., S.L.L., O.L.P., B.S. & M.J.P.S. developed the study. W.H., S.L.L., O.L.P., K.A.-B., H.B., A.C.-S., C.E.N.E., S.F., D.S., B.S., T.C.H.S., S.C.T., K.A.A., S.A.-B., C.A.A., T.R.B., L.F.B., F.Ba., S.K.B., F.Be., R.B., Y.E.B., P.Boe., P.Bou., T.B., E.C., G.B.C., C.J.C., M.C., J.A.C., D.C., A.K.D., G.C.D., T.d.H., M.D.K., J.-L.D., T.R.F., A.F., E.G.F., M.G., C.G., S.G.-F., J.S.H., A.C.H., D.J.H., T.B.H., M.B.N.H., A.H., S.A.I., K.J.J., T.J., E.K.Y., E.K., D.K., M.E.L., J.A.L., J.L., J.C.L., J.-R.M., Y.M., A.R.M., J.M., E.H.M., F.M.M., V.P.M., V.M., E.T.A.M., S.M., J.M.M., P.K.T.M., N.N.B., L.O., F.E., K.P., A.D.P., J.R.P., L.Q., J.R., F.R., M.D.S., H.T., J.Tal., J.Tap., D.M.T., D.W.T., B.T., J.T.M., D.T., P.M.U., G.V.D.H., H.V., J.V., L.J.T.W., S.W., H.W., J.T.W. and L.Z. contributed data (larger field contributions by S.L.L, W.H., A.C.-S., B.S., H.T., A.K.D., C.E.N.E, J.M.M., K.A.-B. and S.F.). O.L.P., T.R.B., S.L.L. and G.L.-G. conceived and managed forestplots.net; O.L.P., T.R.B., S.L.L., E.G., G.L.-G., G.C.P., A.L., R.J.W.B., T.R.F. and M.J.P.S. developed it. W.H., M.J.P.S., S.L.L., O.L.P., R.J.W.B., A.L., G.L.-G., A.E.-M., A.K., E.G., T.R.B., A.C.B. and G.C.P. contributed analysis tools. W.H. and S.L.L. analysed the data (with important contributions from M.J.P.S.). S.L.L. and W.H. wrote the paper. All co-authors read and approved the manuscript (with important insights provided by O.L.P., S.F., R.J.W.B., E.G., H.B., D.S., M.J.P.S., S.G.-F., P.B., H.V. and S.C.T).
Author Information
The authors declare no competing financial interests.
References
- 1.Pan Y, et al. A Large and Persistent Carbon Sink in the World’s Forests. Science. 2011;333:988–993. doi: 10.1126/science.1201609. [DOI] [PubMed] [Google Scholar]
- 2.Sitch S, et al. Recent trends and drivers of regional sources and sinks of carbon dioxide. Biogeosciences. 2015;12:653–679. doi: 10.5194/bg-12-653-2015. [DOI] [Google Scholar]
- 3.Gaubert B, et al. Global atmospheric CO2 inverse models converging on neutral tropical land exchange, but disagreeing on fossil fuel and atmospheric growth rate. Biogeosciences. 2019;16:117–134. doi: 10.5194/bg-16-117-2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Huntingford C, et al. Simulated resilience of tropical rainforests to CO2-induced climate change. Nature Geoscience. 2013;6:268–273. doi: 10.1038/ngeo1741. [DOI] [Google Scholar]
- 5.Mercado LM, et al. Large sensitivity in land carbon storage due to geographical and temporal variation in the thermal response of photosynthetic capacity. New Phytologist. 2018;218:1462–1477. doi: 10.1111/nph.15100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Brienen RJW, et al. Long-term decline of the Amazon carbon sink. Nature. 2015;519:344–348. doi: 10.1038/nature14283. [DOI] [PubMed] [Google Scholar]
- 7.Piao S, et al. Evaluation of terrestrial carbon cycle models for their response to climate variability and to CO2 trends. Global Change Biology. 2013;19:2117–2132. doi: 10.1111/gcb.12187. [DOI] [PubMed] [Google Scholar]
- 8.Schimel D, Stephens BB, Fisher JB. Effect of increasing CO2 on the terrestrial carbon cycle. Proceedings of the National Academy of Sciences. 2015;112:436–441. doi: 10.1073/pnas.1407302112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Anderegg WRL, et al. Tropical nighttime warming as a dominant driver of variability in the terrestrial carbon sink. Proceedings of the National Academy of Sciences. 2015;112:15591–15596. doi: 10.1073/pnas.1521479112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ciais P, et al. Five decades of northern land carbon uptake revealed by the interhemispheric CO2 gradient. Nature. 2019 doi: 10.1038/s41586-019-1078-6. [DOI] [PubMed] [Google Scholar]
- 11.Lewis SL, Edwards DP, Galbraith D. Increasing human dominance of tropical forests. Science. 2015;349:827–832. doi: 10.1126/science.aaa9932. [DOI] [PubMed] [Google Scholar]
- 12.Pugh TAM, et al. Role of forest regrowth in global carbon sink dynamics. Proceedings of the National Academy of Sciences. 2019;116:4382–4387. doi: 10.1073/pnas.1810512116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lewis SL, et al. Increasing carbon storage in intact African tropical forests. Nature. 2009;457:1003–1006. doi: 10.1038/nature07771. [DOI] [PubMed] [Google Scholar]
- 14.Phillips OL, et al. Drought sensitivity of the Amazon rainforest. Science. 2009;323:1344–1347. doi: 10.1126/science.1164033. [DOI] [PubMed] [Google Scholar]
- 15.Qie L, et al. Long-term carbon sink in Borneo’s forests halted by drought and vulnerable to edge effects. Nature Communications. 2017;8 doi: 10.1038/s41467-017-01997-0. 1966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gatti LV, et al. Drought sensitivity of Amazonian carbon balance revealed by atmospheric measurements. Nature. 2014;506:76–80. doi: 10.1038/nature12957. [DOI] [PubMed] [Google Scholar]
- 17.Nemani RR, et al. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science. 2003;300:1560–1563. doi: 10.1126/science.1082750. [DOI] [PubMed] [Google Scholar]
- 18.Keenan TF, et al. Recent pause in the growth rate of atmospheric CO2 due to enhanced terrestrial carbon uptake. Nature Communications. 2016;7 doi: 10.1038/ncomms13428. 13428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Booth BBB, et al. High sensitivity of future global warming to land carbon cycle processes. Environmental Research Letters. 2012;7 024002. [Google Scholar]
- 20.Lombardozzi DL, Bonan GB, Smith NG, Dukes JS, Fisher RA. Temperature acclimation of photosynthesis and respiration: A key uncertainty in the carbon cycle-climate feedback. Geophysical Research Letters. 2015;42:8624–8631. doi: 10.1002/2015GL065934. [DOI] [Google Scholar]
- 21.Le Quéré C, et al. Global Carbon Budget 2018. Earth Syst Sci Data. 2018;10:2141–2194. doi: 10.5194/essd-10-2141-2018. [DOI] [Google Scholar]
- 22.Lewis SL, Brando PM, Phillips OL, van der Heijden GMF, Nepstad D. The 2010 Amazon Drought. Science. 2011;331:554. doi: 10.1126/science.1200807. [DOI] [PubMed] [Google Scholar]
- 23.Feldpausch TR, et al. Amazon forest response to repeated droughts. Global Biogeochemical Cycles. 2016;30:964–982. doi: 10.1002/2015GB005133. [DOI] [Google Scholar]
- 24.McDowell N, et al. Drivers and mechanisms of tree mortality in moist tropical forests. New Phytologist. 2018;219:851–869. doi: 10.1111/nph.15027. [DOI] [PubMed] [Google Scholar]
- 25.Aleixo I, et al. Amazonian rainforest tree mortality driven by climate and functional traits. Nature Climate Change. 2019;9:384–388. doi: 10.1038/s41558-019-0458-0. [DOI] [Google Scholar]
- 26.Lewis SL, et al. Concerted changes in tropical forest structure and dynamics: evidence from 50 South American long-term plots. Philosophical transactions of the Royal Society of London. Series B, Biological sciences. 2004;359:421–436. doi: 10.1098/rstb.2003.1431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lewis SL, et al. Above-ground biomass and structure of 260 African tropical forests. Philosophical Transactions of the Royal Society B: Biological Sciences. 2013;368 doi: 10.1098/rstb.2012.0295. 20120295-20120295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Quesada CA, et al. Basin-wide variations in Amazon forest structure and function are mediated by both soils and climate. Biogeosciences. 2012;9:2203–2246. doi: 10.5194/bg-9-2203-2012. [DOI] [Google Scholar]
- 29.Malhi Y, et al. The above-ground coarse wood productivity of 104 Neotropical forest plots. Global Change Biology. 2004;10:563–591. [Google Scholar]
- 30.Galbraith D, et al. Residence times of woody biomass in tropical forests. Plant Ecology & Diversity. 2013;6:139–157. doi: 10.1080/17550874.2013.770578. [DOI] [Google Scholar]
- 31.Reich PB, et al. Boreal and temperate trees show strong acclimation of respiration to warming. Nature. 2016;531:633–636. doi: 10.1038/nature17142. [DOI] [PubMed] [Google Scholar]
- 32.ter Steege H, et al. Continental-scale patterns of canopy tree composition and function across Amazonia. Nature. 2006;443:444–447. doi: 10.1038/nature05134. [DOI] [PubMed] [Google Scholar]
- 33.Bauters M, et al. High fire-derived nitrogen deposition on central African forests. Proceedings Of The National Academy Of Sciences Of The United States Of America. 2018;115:549–554. doi: 10.1073/pnas.1714597115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Parmentier I, et al. The odd man out? Might climate explain the lower tree alpha-diversity of African rain forests relative to Amazonian rain forests? Journal of Ecology. 2007;95:1058–1071. [Google Scholar]
- 35.Slik JWF, et al. Phylogenetic classification of the world’s tropical forests. Proceedings of the National Academy of Sciences. 2018;115:1837–1842. doi: 10.1073/pnas.1714977115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Phillips OL, et al. Increasing dominance of large lianas in Amazonian forests. Nature. 2002;418:770–774. doi: 10.1038/nature00926. [DOI] [PubMed] [Google Scholar]
- 37.Schnitzer SA, Bongers F. Increasing liana abundance and biomass in tropical forests: emerging patterns and putative mechanisms. Ecology Letters. 2011;14:397–406. doi: 10.1111/j.1461-0248.2011.01590.x. [DOI] [PubMed] [Google Scholar]
- 38.Meinshausen M, et al. The RCP greenhouse gas concentrations and their extensions from 1765 to 2300. Climatic Change. 2011;109:213–241. doi: 10.1007/s10584-011-0156-z. [DOI] [Google Scholar]
- 39.Terrer C, et al. Nitrogen and phosphorus constrain the CO2 fertilization of global plant biomass. Nature Climate Change. 2019 doi: 10.1038/s41558-019-0545-2. [DOI] [Google Scholar]
- 40.Fleischer K, et al. Amazon forest response to CO2 fertilization dependent on plant phosphorus acquisition. Nature Geoscience. 2019;12:736–741. doi: 10.1038/s41561-019-0404-9. [DOI] [Google Scholar]
- 41.Jiang Y, et al. Widespread increase of boreal summer dry season length over the Congo rainforest. Nature Climate Change. 2019;9:617–622. doi: 10.1038/s41558-019-0512-y. [DOI] [Google Scholar]
- 42.Gloor M, et al. Recent Amazon climate as background for possible ongoing and future changes of Amazon humid forests. Global Biogeochemical Cycles. 2015;29:1384–1399. doi: 10.1002/2014gb005080. [DOI] [Google Scholar]
- 43.Kolby Smith W, et al. Large divergence of satellite and Earth system model estimates of global terrestrial CO2 fertilization. Nature Climate Change. 2015;6:306. doi: 10.1038/nclimate2879. [DOI] [Google Scholar]
- 44.Chen C, et al. China and India lead in greening of the world through land-use management. Nature Sustainability. 2019;2:122–129. doi: 10.1038/s41893-019-0220-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Chambers JQ, Higuchi N, Schimel JP, Ferreira LV, Melack JM. Decomposition and carbon cycling of dead trees in tropical forests of the central Amazon. Oecologia. 2000;122:380–388. doi: 10.1007/s004420050044. [DOI] [PubMed] [Google Scholar]
- 46.Hansen MC, et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science. 2013;342:850–853. doi: 10.1126/science.1244693. [DOI] [PubMed] [Google Scholar]
- 47.Pearson TRH, Brown S, Murray L, Sidman G. Greenhouse gas emissions from tropical forest degradation: an underestimated source. Carbon Balance and Management. 2017;12:3. doi: 10.1186/s13021-017-0072-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Schwartz NB, Uriarte M, DeFries R, Gutierrez-Velez VH, Pinedo-Vasquez MA. Land-use dynamics influence estimates of carbon sequestration potential in tropical second-growth forest. Environmental Research Letters. 2017;12 doi: 10.1088/1748-9326/aa708b. 074023. [DOI] [Google Scholar]
- 49.Lewis SL, Wheeler CE, Mitchard ETA, Koch A. Regenerate natural forests to store carbon. Nature. 2019;568:25–28. doi: 10.1038/d41586-019-01026-8. [DOI] [PubMed] [Google Scholar]
- 50.Yu K, et al. Pervasive decreases in living vegetation carbon turnover time across forest climate zones. Proceedings of the National Academy of Sciences. 2019 doi: 10.1073/pnas.1821387116. 201821387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hijmans RJ, Cameron SE, Parra JL, Jones PG, Jarvis A. Very high resolution interpolated climate surfaces for global land areas. International Journal of Climatology. 2005;25:1965–1978. doi: 10.1002/joc.1276. [DOI] [Google Scholar]
- 52.Lopez-Gonzalez G, Lewis SL, Burkitt M, Phillips OL. ForestPlots.net: a web application and research tool to manage and analyse tropical forest plot data. Journal of Vegetation Science. 2011;22:610–613. doi: 10.1111/j.1654-1103.2011.01312.x. [DOI] [Google Scholar]
- 53.Lopez-Gonzalez G, Lewis SL, Burkitt M, B TR, Phillips OL. ForestPlots.net Database. www.forestplots.net. Date of extraction [10/11/2017] 2009.
- 54.Sheil D, Bitariho R. Bwindi Impenetrable Forest TEAM Site. Data Set Identifier: TEAM-DataPackage-20151201235855_1254. 2009 [Google Scholar]
- 55.Kenfack D. Korup National Park TEAM Site. Data Set Identifier: TEAM-DataPackage-20151201235855_1254. 2011 [Google Scholar]
- 56.Rovero F, Marshall A, Martin E. Udzungwa TEAM Site. Data Set Identifier: TEAM-DataPackage-20151130235007_5069. 2009 [Google Scholar]
- 57.Hockemba MBN. Nouabalé Ndoki TEAM Site. Data Set Identifier: TEAM-DataPackage-20151201235855_1254. 2010 [Google Scholar]
- 58.Anderson-Teixeira KJ, et al. CTFS-ForestGEO: a worldwide network monitoring forests in an era of global change. Global Change Biology. 2015;21:528–549. doi: 10.1111/gcb.12712. [DOI] [PubMed] [Google Scholar]
- 59.Gourlet-Fleury S, et al. Tropical forest recovery from logging: a 24 year silvicultural experiment from Central Africa. Philosophical Transactions of the Royal Society B-Biological Sciences. 2013;368 doi: 10.1098/rstb.2012.0302. 20120302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Claeys F, et al. Climate change would lead to a sharp acceleration of Central African forests dynamics by the end of the century. Environmental Research Letters. 2019;14 doi: 10.1088/1748-9326/aafb81. 044002. [DOI] [Google Scholar]
- 61.Chave J, et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Global Change Biology. 2014;20:3177–3190. doi: 10.1111/gcb.12629. [DOI] [PubMed] [Google Scholar]
- 62.R Development Core Team. R: A Language and Environment for Statistical Computing. 2015. Available at http://www.R-project.org/
- 63.Lopez-Gonzalez G, Sullivan M, Baker T. BiomasaFP package. Tools for analysing data downloaded from ForestPlots.net. R package version 0.2.1. 2017 Available at http://www.forestplots.net/en/resources/analysis. [Google Scholar]
- 64.Phillips O, Baker T, Brienen R, Feldpausch T. RAINFOR field manual for plot establishment and remeasurement. 2016. Available at http://www.rainfor.org/upload/ManualsEnglish/RAINFOR_field_manual_version_2016.pdf.
- 65.Talbot J, et al. Methods to estimate aboveground wood productivity from long-term forest inventory plots. Forest Ecology and Management. 2014;320:30–38. doi: 10.1016/j.foreco.2014.02.021. [DOI] [Google Scholar]
- 66.Sullivan MJP, et al. Field methods for sampling tree height for tropical forest biomass estimation. Methods in Ecology and Evolution. 2018;9:1179–1189. doi: 10.1111/2041-210X.12962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Feldpausch TR, et al. Tree height integrated into pantropical forest biomass estimates. Biogeosciences. 2012;9:3381–3403. doi: 10.5194/bg-9-3381-2012. [DOI] [Google Scholar]
- 68.Chave J, et al. Towards a worldwide wood economics spectrum. Ecology Letters. 2009;12:351–366. doi: 10.1111/j.1461-0248.2009.01285.x. [DOI] [PubMed] [Google Scholar]
- 69.Zanne AE, et al. Data from: Towards a worldwide wood economics spectrum. Dryad Digital Repository; 2009. [DOI] [PubMed] [Google Scholar]
- 70.Martin AR, Doraisami M, Thomas SC. Global patterns in wood carbon concentration across the world’s trees and forests. Nature Geoscience. 2018;11:915–920. doi: 10.1038/s41561-018-0246-x. [DOI] [Google Scholar]
- 71.Kohyama TS, Kohyama TI, Sheil D, Rees M. Definition and estimation of vital rates from repeated censuses: Choices, comparisons and bias corrections focusing on trees. Methods in Ecology and Evolution. 2018;9:809–821. doi: 10.1111/2041-210x.12929. [DOI] [Google Scholar]
- 72.Bates D, Maechler M, Bolker B, Walker S. lme4: Linear mixed-effects models using Eigen and S4. Rpackage version, 1.0-4. 2013 Available at http://www.inside-r.org/packages/lme4/versions/1-0-4. [Google Scholar]
- 73.Fox J. Applied Regression Analysis and Generalized Linear Models. Second edn. Sage Publishing; 2008. [Google Scholar]
- 74.Chave J, et al. Assessing evidence for a pervasive alteration in tropical tree communities. PLoS Biology. 2008;6:0455–0462. doi: 10.1371/journal.pbio.0060045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Yuen JQ, Ziegler AD, Webb EL, Ryan CM. Uncertainty in below-ground carbon biomass for major land covers in Southeast Asia. Forest Ecology and Management. 2013;310:915–926. doi: 10.1016/j.foreco.2013.09.042. [DOI] [Google Scholar]
- 76.Aragão LEOC, et al. Spatial patterns and fire response of recent Amazonian droughts. Geophysical Research Letters. 2007;4:1–5. doi: 10.1029/2006gl028946. [DOI] [Google Scholar]
- 77.Aragão LEOC, et al. Environmental change and the carbon balance of Amazonian forests. Biological Reviews. 2014;89:913–931. doi: 10.1111/brv.12088. [DOI] [PubMed] [Google Scholar]
- 78.Tans P, Keeling R. Mauna Loa CO2 monthly mean data. 2016. Available at http://www.esrl.noaa.gov/gmd/ccgg/trends/
- 79.Harris I, Jones PD, Osborn TJ, Lister DH. Updated high-resolution grids of monthly climatic observations – the CRU TS3.10 Dataset. International Journal of Climatology. 2014;34:623–642. doi: 10.1002/joc.3711. [DOI] [Google Scholar]
- 80.Fick SE, Hijmans RJ. WorldClim 2: new 1-km spatial resolution climate surfaces for global land areas. International Journal of Climatology. 2017;37:4302–4315. doi: 10.1002/joc.5086. [DOI] [Google Scholar]
- 81.Ramirez-Villegas J, Jarvis A. Downscaling Global Circulation Model Outputs: The Delta Method. Decision and Policy Analysis Working Paper No. 1. 2010. p. 18. [Google Scholar]
- 82.Schneider U, et al. GPCC Full Data Reanalysis Version 6.0 at 0.5°: Monthly Land-Surface Precipitation from Rain-Gauges built on GTS-based and Historic Data. 2011. [DOI] [Google Scholar]
- 83.Sun Q, et al. Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Reviews of geophysics. 2017;56:79–107. doi:10.1002/ [Google Scholar]
- 84.Huffman GJ, et al. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. Journal of Hydrometeorology. 2007;8:38–55. doi: 10.1175/jhm560.1. [DOI] [Google Scholar]
- 85.Kume T, et al. Ten-year evapotranspiration estimates in a Bornean tropical rainforest. Agricultural and Forest Meteorology. 2011;151:1183–1192. doi: 10.1016/j.agrformet.2011.04.005. [DOI] [Google Scholar]
- 86.Zelazowski P, Malhi Y, Huntingford C, Sitch S, Fisher JB. Changes in the potential distribution of humid tropical forests on a warmer planet. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 2011;369:137–160. doi: 10.1098/rsta.2010.0238. [DOI] [PubMed] [Google Scholar]
- 87.James R, Washington R, Rowell DP. Implications of global warming for the climate of African rainforests. Philosophical transactions of the Royal Society of London. Series B, Biological sciences. 2013;368 doi: 10.1098/rstb.2012.0298. 20120298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Jung M, et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature. 2010;467:951–954. doi: 10.1038/nature09396. [DOI] [PubMed] [Google Scholar]
- 89.Jung M, et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. Journal of Geophysical Research. 2011;116 doi: 10.1029/2010jg001566. [DOI] [Google Scholar]
- 90.Lloyd J, Farquhar GD. The CO2 dependence of photosynthesis, plant growth responses to elevated atmospheric CO2 concentrations and their interaction with soil nutrient status. I. General principles and forest ecosystems. Functional Ecology. 1996;10:4–32. doi: 10.2307/2390258. [DOI] [Google Scholar]
- 91.Aspinwall MJ, et al. Convergent acclimation of leaf photosynthesis and respiration to prevailing ambient temperatures under current and warmer climates in Eucalyptus tereticornis. New Phytol. 2016;212:354–367. doi: 10.1111/nph.14035. [DOI] [PubMed] [Google Scholar]
- 92.Bonal D, Burban B, Stahl C, Wagner F, Hérault B. The response of tropical rainforests to drought—lessons from recent research and future prospects. Annals of Forest Science. 2016;73:27–44. doi: 10.1007/s13595-015-0522-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Quesada CA, et al. Variations in chemical and physical properties of Amazon forest soils in relation to their genesis. Biogeosciences. 2010;7:1515–1541. doi: 10.5194/bg-7-1515-2010. [DOI] [Google Scholar]
- 94.Baker TR, Swaine MD, Burslem DFRP. Variation in tropical forest growth rates: combined effects of functional group composition and resource availability. Perspectives in Plant Ecology, Evolution and Systematics. 2003;6:21–36. doi: 10.1078/1433-8319-00040. [DOI] [Google Scholar]
- 95.Pinheiro JC, Bates DM. Mixed-Effects Models in S and S-PLUS. First edn. Springer; 2000. p. 528. [Google Scholar]
- 96.Venables WN, Ripley BD. Modern Applied Statistics with S. Fourth edn. Springer; 2002. p. 498. [Google Scholar]
- 97.Olejnik S, Mills J, Keselman H. Using Wherry's Adjusted R2 and Mallow's Cp for Model Selection From All Possible Regressions. The Journal of Experimental Education. 2000;68:365–380. doi: 10.1080/00220970009600643. [DOI] [Google Scholar]
- 98.Whittingham MJ, Stephens PA, Bradbury RB, Freckleton RP. Why do we still use stepwise modelling in ecology and behaviour? Journal of Animal Ecology. 2006;75:1182–1189. doi: 10.1111/j.1365-2656.2006.01141.x. [DOI] [PubMed] [Google Scholar]
- 99.Bartoń K. MuMIn: Multi-Model Inference. Tools for performing model selection and model averaging. R package version 1.43.6. 2019. [Google Scholar]
- 100.Gelman A, Hill J. Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge University Press; New York: 2007. [Google Scholar]
- 101.Mayaux P, De Grandi G, Malingreau J-P. Central African Forest Cover Revisited: A Multisatellite Analysis. Remote Sensing of Environment. 2000;71:183–196. doi: 10.1016/S0034-4257(99)00073-5. [DOI] [Google Scholar]
- 102.Mayaux P, Bartholomé E, Cabral A, Cherlet M, Defourny P, Di Gregorio A, Diallo O, Massart M, Nonguierma A, Pekel J-F, Pretorius C, et al. The Land Cover Map for Africa in the Year 2000. GLC2000 database, European Commission Joint Research Centre. 2003. https://forobs.jrc.ec.europa.eu/products/glc2000/products.php .
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.