First Reprocessing of Southern Hemisphere ADditional OZonesondes (SHADOZ) Profile Records: 3. Uncertainty in Ozone Profile and Total Column

Abstract

Reprocessed ozonesonde data from eight SHADOZ (Southern Hemisphere ADditional OZonesondes) sites have been used to derive the first analysis of uncertainty estimates for both profile and total column ozone (TCO). The ozone uncertainty is a composite of the uncertainties of the individual terms in the ozone partial pressure (P_O3) equation, those being the ozone sensor current, background current, internal pump temperature, pump efficiency factors, conversion efficiency, and flow-rate. Overall, P_O3 uncertainties (ΔP_O3) are within 15% and peak around the tropopause (15±3km) where ozone is a minimum and ΔP_O3 approaches the measured signal. The uncertainty in the background and sensor currents dominate the overall ΔP_O3 in the troposphere including the tropopause region, while the uncertainties in the conversion efficiency and flow-rate dominate in the stratosphere. Seasonally, ΔP_O3 is generally a maximum in the March-May, with the exception of SHADOZ sites in Asia, for which the highest ΔP_O3 occurs in September-February. As a first approach, we calculate sonde TCO uncertainty (ΔTCO) by integrating the profile ΔP_O3 and adding the ozone residual uncertainty, derived from the McPeters and Labow [2012] 1-σ ozone mixing ratios. Overall, ΔTCO are within ±15 DU, representing ~5–6% of the TCO. TOMS and OMI satellite overpasses are generally within the sonde ΔTCO. However, there is a discontinuity between TOMS v8.6 (1998–2004/09) and OMI (2004/10–2016) TCO on the order of 10DU that accounts for the significant 16DU overall difference observed between sonde and TOMS. By comparison, the sonde-OMI absolute difference for the eight stations is only ~4DU.

1. Introduction

1.1. Influence of ECC Ozonesonde Measurements

The electrochemical concentration cell (ECC) ozonesonde was developed by Walter Komhyr [Komhyr, 1969] and has been flown at ~80 stations worldwide since the late 1960’s [Logan, 1985; Tiao et al., 1986; Tarasick et al., 2005; Oltmans et al., 2006; Hassler et al., 2008; Stauffer et al., 2016]. The ECC instrument consists of a gas-sampling pump connected to an ozone sensor, and an electronic interface that connects the ozone sensor to a radiosonde for data telemetry (see Figure 1 in Komhyr et al. [1995]). Measured parameters transmitted to the ground receiving station are ozone current, the ozonesonde’s pump temperature, motor voltage and current, and ambient pressure, temperature, and relative humidity (P-T-U). In recent decades, winds and GPS-enabled measurements became available. In flight, the instrument is encased in a weatherproof box that is tethered to balloon, capable of measuring ozone up to an altitude of ~35 km. The balloon ascent rate, typically around 5 m/s, and data transmission rate lead to a vertical resolution within 150 m.

Light-weight, compact, and relatively easy to prepare and launch, ozonesondes (also referred to here as sondes) fulfil an important role in providing high vertical resolution ozone (O₃) profiles from the surface to the middle stratosphere, capable of making measurements during polar night and in cloudy and rainy conditions. They are readily deployed from remote locations, such as over Antarctica, and high-latitude Europe, US and Canada. For example, during the Match campaigns over the Arctic [Von der Gathen et al., 1995; Rex et al., 1998, 2006], trajectory pathways of ozone-depleted air parcels measured from one location can be forecast and sondes launched from other sites can intercept the low-ozone filaments. The IONS series of North American campaigns collected hundreds of soundings with daily launches from 8–20 sites over 3- to 6-week periods to augment aircraft in-situ and lidar profiles [Thompson et al., 2007a, 2008, 2011]. Studies using tropical ozonesonde measurements have examined the tropical wave-one feature [Thompson et al., 2003, Sauvage et al., 2006; Thompson et al., 2017], quasi-biennial oscillations and ENSO features [Thompson et al., 2001; Logan et al., 2003; Witte et al., 2008; Lee at al., 2010; Randel and Thompson, 2011], and the tropical transition layer [Folkins et al., 1999; Gettelman and Forster, 2002; Corti et al., 2006; Fu et al., 2007; Randel et al., 2007; Thompson et al., 2012].

Ozonesonde data have become highly valued over the past 20 years as a large community is focused on O₃ trends in the upper troposphere and lower stratosphere, a region where satellite data do not provide the vertical resolution and sampling frequency that sondes typically do [Bodeker et al., 1998; Rao et al., 2003; Kivi et al., 2007; Gebhardt et al., 2014].

1.2. Reprocessing of ECC Ozonesonde Data

As popular as the sounding data have become, it is clear when long-term sonde-based O₃ records are examined in detail that changes in the ozonesonde instrument, calibration and preparation techniques, and data-processing methods lead to discontinuities and possibly artifact trends at individual sites [Witte et al. 2017]. In addition, there are station-to-station variations in satellite O₃ biases versus sondes, biases among stations, and biases within the data record of an individual station that must be corrected for if sondes are used to assess measurement uncertainties and the reliability of O₃ profile trends [Thompson et al., 2003, 2007b, 2014].

Accordingly, the ozonesonde community has worked for many years to establish quality assessment standards for ozonesondes. The first important step in this effort was the establishment in the mid-1990s of the World Calibration Center for Ozone Sondes (WCCOS) [Smit and Kley, 1998; Smit and Straeter, 2004a, 2004b]. The periodic intercomparison experiments conducted in WCCOS, called Jülich Ozonesonde Intercomparison Experiments (JOSIE), operate with a standard O₃ reference UV photometer in a chamber. In the test chamber ozone is introduced under changing temperature and pressure conditions at a rate that simulates profiles that correspond to standard high-latitude, mid-latitude, sub-tropical and tropical conditions. The first JOSIE (JOSIE-1996; Smit and Kley [1998]) included non-ECC sondes that have largely been replaced at operational stations [De Backer et al., 1998; Fujimoto et al., 2004; Stübi et al., 2008].

From subsequent JOSIE campaigns (1998, 2000) the focus of the WCCOS tests has been on ECC sondes manufactured by Science Pump Corporation (SPC) and ENSCI, and characterizing how different SST (sensing solution type) perform under the various simulations [Smit et al., 2007]. These campaigns revealed that differences in O₃, as measured among different ECC sensors, are largely due to differences in preparation procedures and SST used by participating researchers. The outcome was that two combinations of instrument type and SST were recommended as standard operating procedures (SOP) [Smit et al., 2007, Smit and ASOPOS, 2014]. The same combination emerged as the WMO (World Meteorological Organization) preferred standard during the BESOS campaign (Balloon Experiment on Standards for Ozonesondes) in 2004 that evaluated the ozone response of commonly used ECC/SST pairings following JOSIE SOP guidelines under ambient conditions [Deshler et al., 2008].

After 2010, several Ozonesonde Expert meetings and the SPARC-IO3C-IGACO-NDACC (Stratospheric Processes and their Relation to Climate, International Ozone Commission, International Gases and Aerosols Composition, Network for Detection of Atmospheric Chemical Composition Change) SI2N activities considered how to homogenize long-term datasets for trends because a number of stations had more than 30 years of ECC records, albeit with both ozonesonde and radiosonde changes. These activities and the results of JOSIE, BESOS, and further dual balloon soundings led to the creation of the O3S-DQA (Ozone Sonde Data Quality Assessment) panel report [Smit and O3S-DQA, 2012] (hereafter referred to as Smit12) the goals of which are to (1) establish guidelines for reprocessing ozonesonde data records to remove inhomogeneities due to instrumental or procedural artifacts, and (2) determine the contributions of the individual uncertainties of the different instrumental parameters to the O₃ measurement. The WMO/GAW (Global Atmospheric Watch) Report #201, referenced as Smit and ASOPOS [2014] and hereafter referred to as the WMO/GAW Report, is a comprehensive summary of the Smit12 findings. The O3S-DQA panel report has also formalized the concept of transfer functions to compensate for instrument-SST changes. Deshler et al. [2017] have recently published the set of transfer functions based on the JOSIE and BESOS experiments and on unpublished field comparisons that incorporate a total of 197 tests with the SPC and ENSCI ECC sensors.

2. SHADOZ and Data Reprocessing

Since early 2016 we have been reprocessing the Southern Hemisphere ADditional OZonesondes (SHADOZ) record [Witte et al., 2017; Thompson et al., 2017, hereafter referred to, respectively, as Witte17 and Thompson17] according to the O3S-DQA guidelines using customized software based on Skysonde (developed by Allen Jordan at NOAA/Earth Systems Research Laboratory/Global Monitoring Division (NOAA/ESRL/GMD)).

Figure 1 displays the map of the stations for which data are analyzed in detail in this study. Details of the first reprocessing of SHADOZ data from seven sites appear in Witte17. When added to data from six other SHADOZ stations, including four sets from stations reprocessed by NOAA/ESRL/GMD, 14 stations with continuous data of at least one decade have been evaluated in Thompson17. Those reprocessed SHADOZ data were compared to three BUV (backscatter UV) type satellite total column ozone (TCO) amounts spanning 1998–2016 and to co-located ground-based instruments at nine SHADOZ stations. Thompson17 showed that, compared to earlier evaluations [Thompson et al., 2003, 2007b, 2012], offsets between ozonesonde and satellite TCO are reduced due to the homogeneity of the newly reprocessed ozonesonde data records. Most stations ended up with sonde TCO, satellite and where applicable, ground-based instruments, within 2% of one another.

Figure 1.

Locations of the eight reprocessed SHADOZ sites for which uncertainty estimates are calculated. Table 1 lists the lat/lon per site.

In this paper we reprocess data for Réunion a second time and present the first reprocessed data for Costa Rica (various locations around San José) and Nairobi (refer to locations in Figure 1). However, the principal goal here is to report an uncertainty analysis of the ozonesonde measurement system, term by term, for the 8 stations we have reprocessed at NASA/GSFC, as well as uncertainties in TCO amounts. In the latter case we compare the columns to EP/TOMS (Earth Probe - Total Ozone Mapping Spectrometer) and OMI (Ozone Monitoring Instrument) satellite overpasses.

Following Witte17, this study continues the O3S-DQA goal of determining uncertainties in the ozonesonde measurement system. The treatment of uncertainty in this study closely follows the definitions described in Smit12. Section 3 describes details of the ozone measurement and the reprocessing of SHADOZ data to date. Section 4 analyzes the uncertainty relationships term by term. The profile uncertainties appear in Section 5 and column uncertainties in Section 6, followed by a Summary (Section 7).

3. Details of the Ozonesonde Measurement and Reprocessed SHADOZ Ozonesonde Data

3.1. The Ozonesonde Measurement

The ECC sensor measures O₃ using iodine/iodide electrode reactions. Two platinum electrodes are immersed in separate cathode and anode chambers of differing concentrations of potassium iodide (KI) solution. The anode cell contains a solution saturated with KI. Both cells contain an equal concentration of potassium bromide (KBr) and a phosphate buffer to maintain a neutral pH. An ion bridge connecting the two chambers allows ions to flow between the two cells but prevents mixing, thereby preserving their respective concentrations. Ambient air containing O₃ is pumped into the cathode cell and reacts with iodide (I⁻) in solution to form iodine (I₂). To maintain electrochemical equilibrium I₂ is converted back to I⁻ on the platinum electrode resulting in the release of two electrons. Thus, each O₃ molecule entering the sensor causes two electrons to flow through the ECC’s external circuit, which it measures as a current. The resulting electrical current is proportional to the amount of O₃ in the sampled air. The electrochemical technique assumes no secondary reactions take place and a 1:1 stoichiometric relationship of the O₃:I₂ is maintained. The relationship between O₃ and the electrical current is defined by the following equation:

$${\text{P}}_{\text{O}3}=4.307\times {10}^{-2}\frac{\left({\text{I}}_{\text{M}}-{\text{I}}_{\text{B}}\right){\text{T}}_{\text{P}}}{{\mathrm{\Psi }}_{\text{P}}{\text{Φ}}_{\text{P}}{\eta }_C}$$ (1)

where

P_O3 = Ozone partial pressure, mPa

I_M = Cell current, μA

I_B = Cell background current, μA

T_P = Ozonesonde pump temperature, K

Φ_P = Pump flow-rate, ml/s

Ψ_P = Pump flow efficiency, unitless

η_C = Conversion efficiency which is generally assumed to be 1.

The constant, 4.307×10⁻², is the half ratio of the ideal gas constant (8.314 JK⁻¹mole⁻¹) to Faraday’s constant (9.6487×10⁴ Cmole⁻¹). Equation 1 is similar to what is written in the WMO/GAW Report.

3.2. SHADOZ Reprocessed Data

SHADOZ is the premier archive of tropical and sub-tropical ECC ozonesonde data. Since this NASA program started in 1998, SHADOZ has archived ozonesonde profiles from up to 15 tropical sites with support from NOAA/ESRL/GMD and international partners. Data are publicly available at <https://tropo.gsfc.nasa.goc/shadoz>. Information on the eight SHADOZ sites described in this study (Figure 1) appears in Table 1; each site’s location is summarized. Launches are twice to four times per month. We use 1998–2016 data from the six sites that have been reprocessed by Witte17. Costa Rica and Nairobi were later reprocessed based on Witte17 methods that closely follow Smit12 guidelines. Evaluation of these two datasets can be found in Thompson17.

Table 1.

SHADOZ sites used in this study.

Site	Lat, Lon	Time Period	Profile Total
Ascension Is., U.K.	7.98S, 14.42W	1998 – 2010/08, 2016*	632
Costa Rica **	9.94N, 84.04W	2005/07 – 2016	510
Hanoi, Vietnam	21.02N, 105.80E	2004/09 – 2016	245
Irene, S. Africa	25.90S, 28.22E	1998/11–2007, 2012/09–2016*	337
Kuala Lumpur, Malaysia	2.73N, 101.70E	1998–2010/02, 2012/03–2016*	388
La Réunion, France	21.10S, 55.48E	1998 – 2016	618
Nairobi, Kenya	1.27S, 36.80E	1998 – 2016	827
Natal, Brazil	5.42S, 35.38W	1998–2011/05, 2014/09–2016*	595

^*Note there are data gaps.

^**Previous sites, Alajuela and Heredia, are within 0.5° of San Pedro (current site).

A transfer function based on Deshler et al. [2017] is applied to the Nairobi 1998–2010/05 data to convert O₃ measured with a non-standard ENSCI ECC/1% full buffer SST to the WMO and manufacturer recommended ENSCI/0.5% half buffer equivalent. A similar transfer function is used to homogenize 2007/08–2016 Réunion data from an ENSCI/0.5% full buffer SST to the standard ENSCI/0.5% half buffer. Both applications reduce O₃ measurements by about 4%. Witte17 applied a transfer function to 6% of the profiles in the beginning of the Réunion record where SPC/0.5% half buffer SST was adjusted to the WMO recommended ENSCI/0.5% half buffer. An overview of transfer functions applied by Witte17 and in this study to the eight SHADOZ sites is found in Table 2. Transfer functions have been applied to over half the profiles at Réunion and Nairobi, and 48% at Hanoi. Transfer functions applied at Ascension and Natal account for 10% and 17% of the datasets, respectively.

Table 2.

Summary of transfer functions applied for each SHADOZ site. Conversions applied are to WMO recommended ECC sensor/SST pairs: ENSCI/0.5% (half buffer) and SPC/1% (full buffer).

Site	Transfer Function	Dates Applied	Conversion Applied	Profiles
Ascension	Yes	1998 – 2001	ENSCI/1% -> SPC/1%	10%
Costa Rica	No	---	---	---
Hanoi	Yes	2004 – 2009/05	ENSCI/2% unbuffered -> ENSCI0.5%	48%
Irene	No	---	---	---
Kuala Lumpur	No	---	---	---
La Réunion	Yes	1998 – 2000/07,	SPC/0.5% -> ENSCI/0.5%	7%
		------------------------------------------------------------------------------------------------------------------
		8 records in 1998, 2007/08 – 2016	ENSCI/0.5% full buffer -> ENSCI/0.5%	56%
Natal	Yes	1999/03 – 2002/07	ENSCI/1% -> SPC/1%	17%
Nairobi	Yes	1998 – 2010/06	ENSCI/1% -> ENSCI/0.5%	64%

Witte17 concluded that O₃ trend assessments could not be made using original and initially reprocessed Réunion data due to the solution change after 2007/08, for which transfer functions had not yet been applied. We examine the effect of applying this additional transfer function to the reprocessed Réunion dataset by comparing time series of TCO. In this study, sonde TCO is calculated by integrating O₃ partial pressure up to 10 hPa and adding an O₃ climatology from balloon burst to the top-of-the-atmosphere, taken from the McPeters and Labow [2012] look-up table (reported in Dobson Units (DU)). From Figure 2a the reprocessed data used in Witte17 show a significant difference in mean TCO of 16.4 DU between the 1998–2006 and 2007–2016 time periods (black dashed lines). However, this difference is reduced to 6.5 DU (blue) after the additional transfer function has been applied. Thus, as of this study, the significant discontinuity found by Witte17 has almost disappeared, allowing for meaningful trend assessments. Later, we show the impact of the uncertainty of the transfer function to the total ozone uncertainty budget. Further evaluation of this newly homogenized dataset has been carried out by Thompson17.

Figure 2.

Time series of TCO at (a) Réunion and (b) Nairobi. Years are shown on the x-axis. Reprocessed data are in black and reprocessed data + transfer function are in blue. Transfer functions have been applied in (a) since 2007 and in (b) before 2010/06, marked with a vertical red line. Black dashed lines indicate the mean TCO for reprocessed data only (values included in black). The blue dashed lines shows the mean TCO for the period where transfer functions have been applied (values included in blue).

Results of applying a transfer function to the early part of the Nairobi dataset are shown in Figure 2b. As with Réunion, Nairobi retains a significant discrepancy of 9 DU, even after reprocessing, between the 1998–2010/05 and 2010/06–2016 periods (black dashed line for the reprocessed-only dataset) that disappears after transfer functions are applied (blue dashed line).

We examine more closely the impact of applying transfer functions to the Réunion and Nairobi datasets by comparing TCO values with OMI (Version 3) TCO overpass data [Levelt et al., 2006] as a reference. Results are shown in Figure 3 as histograms of the percentage difference with respect to sondes. Biases with respect to OMI at Réunion are significantly reduced after transfer functions have been applied (blue hashes, Figure 3a), where the Gaussian peak shifts from 4.3% to 0.7%. Most of the agreement falls within ±5%. The homogenized Nairobi data, in Figure 3b, show a different impact. The Gaussian peak shifts from +2.2% to −1.5%, and the sonde bias with respect to OMI changes from a mostly positive (high-bias) regime to a negative (low-bias) regime. This low-bias relationship between the Nairobi sondes and satellite data is consistent with most of the SHADOZ network datasets [Hubert et al., 2016; Thompson17]. Like Réunion, the agreement is ±5% making both these sites a stable reference for trends analysis and satellite validation.

Figure 3.

Histogram of the percentage difference in TCO between reprocessed sondes and OMI overpasses with respect to sondes for (a) 2007–2016 Réunion and (b) 1998–2010/06 Nairobi data. These are time periods for which transfer functions have been applied (blue hashed).

4. The Ozone Uncertainty Equation

To improve the ozonesonde measurement system Smit12 introduced the first instrumental uncertainty equation of the ECC type ozonesonde based on the current best knowledge of the ECC performance under lab conditions. After reprocessing to remove all known inhomogeneities, the overall uncertainty in P_O3, shown in Equation 2, is the square root of the sum of the squares of the uncertainty in each term of the ozone partial pressure equation (Eqn. 1). The uncertainties are assumed to be random and Gaussian and therefore follow the Gaussian propagation of uncertainty. In equation 2, the assumption is not only that the uncertainties are random, but also uncorrelated.

$$\frac{\mathrm{\Delta }{\text{P}}_{03}}{{\text{P}}_{03}}=\sqrt{\frac{{\left(\mathrm{\Delta }{\text{I}}_{\text{M}}\right)}^2+{\left(\mathrm{\Delta }{\text{I}}_{\text{B}}\right)}^2}{{\left({\text{I}}_{\text{M}}-{\text{I}}_{\text{B}}\right)}^2}+{\left(\frac{\mathrm{\Delta }{\eta }_C}{{\eta }_C}\right)}^2+{\left(\frac{\mathrm{\Delta }{\mathrm{\Phi }}_{\text{P}}}{{\mathrm{\Phi }}_{\text{P}}}\right)}^2+{\left(\frac{\mathrm{\Delta }{\mathrm{\Psi }}_{\text{P}}}{{\mathrm{\Psi }}_{\text{P}}}\right)}^2+{\left(\frac{\mathrm{\Delta }{\text{T}}_{\text{P}}}{{\text{T}}_{\text{P}}}\right)}^2}$$ (2)

where

ΔP_O3 = ozone partial pressure uncertainty

ΔI_M = sensor current uncertainty

ΔI_B = background current uncertainty

Δη_C = conversion efficiency uncertainty

ΔΦ_P = pump flow-rate uncertainty at the ground

Δψ_P = pump flow efficiency uncertainty below 100 hPa

ΔT_P = pump temperature uncertainty.

The individual uncertainties are defined as a relative error (Δx)/x, and can be expressed as a percentage. The value of P_O3 and its error, or uncertainty in this case, can then be expressed as the interval P_O3 ± ΔP_O3.

The first application of equation 2 was done for the McMurdo, Antarctic station dataset (reference analysis can be downloaded at: http://wwwdas.uwyo.edu/~deshler/NDACC_O3Sondes/O3s_DQA/O3S-DQAGuideline_Summary_OzUncertainty_td.pdf). Van Malderen et al. [2016] also applied Smit12 uncertainties to the ECC ozonesonde measurements at Uccle (Belgium). Sterling et al. [2017] applied the formula to two SHADOZ stations (Hilo, Hawaii and Pago Pago, American Samoa), Boulder CO, and the South Pole, and Tarasick et al. [2016] applied their own uncertainty estimates to the Canadian ozonesonde records, taking into account the uncertainty terms in equation 2. We take advantage of theses studies to compare with our methods and results.

Where applicable, based on Deshler et al. [2017] calculations, the overall uncertainty of the transfer function, ΔT_F, is 5%. We apply the Smit12 approach and add this uncertainty to the uncertainty in the conversion efficiency term.

Whereas in the Report the ΔΦ_P/Φ_P term includes Δψ_P/ψ_P, we separate the two terms for clarity. The rest of the instrumental uncertainty terms are defined in subsequent sub-sections.

Note, this study focuses only on the uncertainties of the ozonesonde instrument and does not take into account uncertainties due to radiosonde pressure offsets (offsets that lead to errors in the height registry of the computed ozone). Tarasick et al. [2016] do not correct for radiosonde errors but include a pressure offset uncertainty for the VIZ (±1 hPa) and Vaisala RS-80 (±0.5 hPa) manufacturers based on previous studies. Conversely, Sterling et al. [2017] corrects for pressure offsets but does not include the radiosonde pressure uncertainties in their ozone uncertainty calculations. The challenge of determining radiosonde errors, particularly in the non-GPS era, is still an on-going debate.

The uncertainty in the ozone current, ΔI_M, is ±0.01 μA for currents less than 1.0 μA and 1% elsewhere. This is taken as the overall resolution of the digital interface board [Smit12]. V2 and V7 interface boards have similar piecewise uncertainties [Sterling et al., 2017]. The Vaisala OIF11 and current generation OIF92 interface boards have an accuracy of 0.01 μA and 0.001 μA, respectively (taken from the Vaisala manufacturer brochure). Uncertainty analysis done for the McMurdo station dataset used ΔI_M = 0.1 μA, while this uncertainty was not taken into account by Tarasick et al. [2016]. Sterling et al., [2017] used similar ΔI_M during the digital era of the measurements that started in the 1990’s.

SHADOZ sites encompass a wide range of radiosonde/ozonesonde systems that use a variety of interface boards with varying resolutions. For example, the MODEM radiosonde used at Réunion, Lockhead-Martin-Sippican (LMS) used at Ascension and Natal, and Vaisala employed at a number of SHADOZ sites use their own interfaces, which have different AD converters and possibly different thermistors. This may impact the uncertainty estimate for the cell current and pump temperature measurement; however further investigation is needed to determine the effect, if any. In this study, we simplify ΔI_M to ±0.01 μA for currents less than 1.0 μA and 1% elsewhere, as recommended by Smit12.

Van Malderen et al. [2016] noted equation 2 does not take into account the uncertainty due to the time lag of the response of the I_M, T_P, and I_B measurements. Tarasick et al. [2016] incorporated an e-folding response time to the ozone gradient to take into account slow ECC responses to changes in ozone due to variable ascent rates.

4.1. Background Current Uncertainty, ΔI_B

The background current (I_B) is the residual current measured by the sonde when sampling ozone-free air. Conventional processing of the sonde telemetry assumes that the background current remains constant during flight. There is no statistically robust method for estimating the uncertainty of the background current, ΔI_B. JOSIE studies used small sample sizes, fewer than 14 ECC sensors, to conduct the background current experiments published in Smit et al. [2007] and recommended in the WMO/GAW Report. During JOSIE-1996, significantly high backgrounds were recorded due, in part, to the slow decay in the ozone response and not allowing enough time for the background to drop lower [Johnson et al., 2002]. Laboratory experiments by Vömel and Diaz [2010] tracked the decay of the cell current after exposure to ozone and showed that a much longer period of time (hours) can be required to approach initial values. There is also a dependence on the SST where experiments have shown a relationship between buffered KI SST and high ozone measurements due to a hysteresis effect (additional side reactions) that offset the ideal 1:1 stoichiometric ratio expected from the O₃ to I₂ reaction [Barnes et al., 1985; Davies et al., 2000; Johnson et al., 2002].

To further confound the issue, SHADOZ sites measure I_B in a number of different ways: some are based on an average value, the minimum value recorded during the conditioning process, prior to launch either in the lab or at the launch site, or set to an upper limit threshold for I_B values that exceed it. The myriad ways in which I_B is recorded are compounded by the quality of the ozone destruction filters used that does not guarantee uniformity and introduces a source of random uncertainty that cannot be easily quantified [Reid et al., 1996]. This is particularly true for ozonesondes flown in the tropics where high humidity affects the ozone removal efficiency of the filter [Newton et al., 2016]. Specific to our study that uses tropical-based sonde data, we use the 1-σ uncertainty of ±0.03 μA for sites that use the ENSCI ECC sensors and ±0.02 μA for SPC sensors based on Witte17 calculations. ΔI_B is doubled, where I_B is missing or exceeds the threshold value of 0.05 μA (based on Witte17 reprocessing criteria). Sterling et al. [2017] adopted the same strategy using ΔI_B = ±0.02 μA for ENSCI ECCs. For the McMurdo measurements, ΔI_B was higher for SPC (±0.05 μA), whereas Tarasick et al., [2016] took a different approach applying a pressure dependent correction. Table 3 summarizes the ΔI_B applied for the eight reprocessed sites based on the ECC sensor used. In general, one ECC type dominates a single site’s dataset. Included, is the percent of profiles for which I_B is missing or exceeds the 0.05 μA threshold. The large spread of these percentages illustrates the difficulty in establishing low backgrounds in tropical environments, as well as, the variation in technique. For example, Costa Rica applies a constant 0.02 μA to all profiles, and Natal recharges the cells with new solutions to determine the final background prior to launch.

Table 3.

ECC sensor and background current uncertainty (ΔI_B) applied for each SHADOZ site.

Site	ECC	ΔIB *μA+ (fraction of missing or > 0.05 μA)
Ascension Is., U.K.	SPC	0.02 (7.2%)
	ENSCI (92 records)	0.03 (7.4%)
Costa Rica	ENSCI	0.03 (0%)
Hanoi, Vietnam	ENSCI	0.03 (16.0%)
	SPC (15 records)	0.02 (1.6%)
Irene, S. Africa	SPC	0.02 (44.7%)
Kuala Lumpur, Malaysia	SPC (1998 – 11/2014)	0.02 (86.2%)
	ENSCI (12/2014 – 2016)	0.03 (14.0%)
La Réunion, France	ENSCI	0.03 (7.4%)
	SPC (40 records)	0.02 (0%)
Nairobi, Kenya	ENSCI	0.03 (74.2%)
Natal, Brazil	SPC	0.02 (0.5%)
	ENSCI (104 records)	0.03 (0.2%)

In Eqn 2 I_B is subtracted from I_m in the denominator and thus its value has a significant impact on that term, particularly in the troposphere where I_m in the tropical troposphere is typically less than 1 μA and I_B can be as high as 0.05 μA. Notably, the tropopause is a region of very low ozone, usually < 1 mPa in the tropics. Where P_O3 measures less than 1 mPa, I_m can approach I_B, thus increasing the dominance of the (ΔI_M)²+(ΔI_B)²/(I_M- I_B)² term (abbreviated to ΔI_B/ ΔI_M hereafter) in Eqn 2.

4.2. Conversion Efficiency Uncertainty, Δη_C/η_C

The conversion efficiency, η_C, comprises two parts: (1) the absorption efficiency (α_O3) from the gas to liquid phase in the sensing solution and (2) the stoichiometry of the O₃:I₂ relationship (S_O3:I2) which is assumed to be 1:1. Interferences with this one-to-one relationship can arise from the buffering of the solution [Johnson et al., 2002; Vömel and Diaz, 2010]. Setting the α_O3 equal to one applies to cases where the volume of the cathode solution is 3.0 cm³. For SHADOZ sites, such as Ascension, Natal, Irene and Réunion, that use a 2.5 cm³ cathode volume, we use the following equations in Smit12 to calculate α_O3, as a function of pressure, P: α_O3(P) = 1.0044 – (4.4×10⁻⁵)×P for 100 hPa < P < 1050 hPa, and α_O3(P) = 1.0 for P ≤ 100 hPa. In the ozone partial pressure equation (Eqn. 1), the conversion efficiency is assumed to be unity and is typically excluded from the ozone equation. However, the uncertainty of this unity assumption does contribute to the overall ozone uncertainty. These are constant unitless values for a cathode solution volume of 3.0 cm³. Thus, Δη_C/η_C can be expressed as,

$$\frac{\mathrm{\Delta }{\eta }_C}{{\eta }_C}=\sqrt{{\left(\frac{\mathrm{\Delta }{\alpha }_{03}}{{\alpha }_{03}}\right)}^2+{\left(\frac{\mathrm{\Delta }{\text{S}}_{03:\text{I}2}}{{\text{S}}_{03:\text{I}2}}\right)}^2}$$ (3)

where α_O3 = 1.0, Δα_O3 = ±0.01, S_O3:I2 = 1.0, and ΔS_O3:I2 = ±0.03. Δα_O3 is ±0.01 for both cathode volumes (Gaussian 1-σ value taken from Davies et al. [2003]). This is a simplistic approach because S_O3:I2 will increase over the course of the sonde flight due to slow side reactions involving the phosphate pH buffers [Davies et al., 2000; Johnson et al., 2002]. However, at present changes in S_O3:I2, while recognized, are poorly understood and require further research. Where a transfer function is applied, 0.05 is added to the ΔS_O3:I2 term [Smit12].

4.3. Pump Flow-rate Uncertainty at the Ground, ΔΦ_P/Φ_P

A common procedure in the ECC conditioning is the use of a soap bubble flow-meter method to measure the volumetric flow rate of the pump, Φ_P [ml/s]. However, calculating ΔΦ_P/Φ_P is not straightforward because not all quantities are known. Witte17 applied correction formulae found in section 8.4 of Smit12 that compensates for the evaporation of the soap bubble solution and rely on the saturated water vapor pressure under ambient P-T-U conditions (C_PH). There is a second correction that takes into account the temperature difference between the internal pump base temperature and the ambient room temperature, C_PL=(T_pump - T_lab)/T_lab. Our calculations reveal ΔC_PL values << 1 and thus we exclude this term which has a negligible impact on the correction of Φ_P and its uncertainty. The final equation to calculate ΔΦ_P/Φ_P can then be expressed as,

$$\frac{\text{Δ}{\text{Φ}}_{\text{P}}}{{\text{Φ}}_{\text{P}}}=\sqrt{{\left(\frac{\text{Δ}{\text{Φ}}_{\text{reprocessed}}}{{\text{Φ}}_{\text{reprocessed}}}\right)}^2+{\left(\text{Δ}{\text{C}}_{\text{PH}}\right)}^2}$$ (4)

where ΔΦ_reprocessed/Φ_reprocessed = ±0.02 and ΔC_PH is based on the minimum and maximum C_PH values in each sites dataset, i.e. ±(C_PH,High - C_PH,Low)/2 [Smit12]. Here, we assume the uncertainties in the reprocessed flow-rates are within the uncertainty of the original measured quantities. Table 4 summarizes the ΔC_PH and ΔΦ_reprocessed/Φ_reprocessed computed for the eight sites. At Irene and Kuala Lumpur, for which lab P-T-U are not documented, we double the ΔΦ_reprocessed/Φ_reprocessed term to ±0.04 and calculate ΔC_PH using the Witte17 tropical climatology of T_lab=25 ± 5°C, RH_lab=50 ± 25%, and P_sfc=mean pressure surface at launch. In the case of Costa Rica, Hanoi, and Nairobi for which a fraction of their datasets are missing lab P-T-U, we use the mean C_PH for flights with known lab conditions. ΔC_PH remains the same since the mean does not affect the min/max range of C_PH values and ΔΦreprocessed/Φreprocessed = ±0.04.

Table 4.

Values of ΔC_PH and ΔΦ_corrected/Φ_corrected for each SHADOZ site.

Site	ΔCPH	ΔΦcorrected/Φcorrected
Ascension Is., U.K.	± 0.014	± 0.02
Costa Rica	± 0.013	± 0.02 and ± 0.04*
Hanoi, Vietnam	± 0.010	± 0.02 and ± 0.04*
Irene, S. Africa	± 0.015	± 0.04	**T=25±5°C, RH=50±25%, P=850hPa
Kuala Lumpur, Malaysia	± 0.013	± 0.04	**T=25±5°C, RH=50±25%, P=1000hPa
La Réunion, France	± 0.014	± 0.02
Nairobi, Kenya	± 0.010	± 0.02 and ± 0.04*
Natal, Brazil	± 0.014	± 0.02

^*Used for profiles where Lab P-T-U is unknown.

^**Based on Witte17 tropical climatology.

4.4. Pump Flow Efficiency Uncertainty, Δψ_P/ψ_P

The pump flow rate, Ф_P, measured during the conditioning procedures is approximately constant up to 100 hPa and decreases steadily to the top of the atmosphere due to instrumental degradation at low pressures [Komhyr, 1986; Komhyr et al., 1995]. From Equation 1, the pump flow efficiency, Ψ_P, is based on empirically derived pump correction factors (PCF) that take into account the efficiency loss in Ф_P as a function of pressure. This study follows the WMO/GAW Report recommendations and applies the Komhyr [1986] PCF for sondes launched with an SPC sensor and Komhyr et al. [1995] PCF for ENSCI sensors. These PCF compensate for the effect of the buffer that creates side-reactions in the solution [Johnson et al., 2002]. The exception is at Hanoi for which almost half the dataset uses a NOAA sensing solution recipe of 2% unbuffered KI. The unique formula requires its own PCF due to the lack of the buffer in solution [Johnson et al., 2002]. These three pump flow efficiencies and their ±1-σ uncertainties (±Δψ_P) are listed in Table 5. We can interpret the effect of the buffer at low pressures as the difference in Ψ_P between the Johnson et al. [2002] and both Komhyr look-up tables: the difference ranges from 3% at 100 hPa to 15% at 5 hPa. The Deshler et al. [2017] transfer function that corrects for solution changes between the 0.5% half buffer and 1.0% full buffer solution intrinsically takes into account the effect of the buffer and therefore, its overall uncertainty of ±5% carries within it the uncertainty in the buffering.

Table 5.

Ozonesonde pump flow efficiencies, Ψ_P, with 1-σ uncertainties (± ΔΨ_P). Ψ_P are taken from the WMO/GAW Report. O3S-DQA panel revised ±ΔΨ_P values are computed to replace Komhyr, [1986] and Komhyr at al., [1995]± ΔΨ_P.

Pressure [hPa]	Komhyr, [1986] ΨP ± ΔΨP	Komhyr et al., [1995] ΨP ± ΔΨP	Johnson et al., [2002] 1 ΨP ± ΔΨP	O3S-DQA Panel ± ΔΨP
Sfc-100	1.000	1.000	1.000
100	0.993 ± 0.005	0.993 ± 0.005	0.967 ± 0.011	± 0.010
50	0.982 ± 0.006	0.982 ± 0.005	0.950 ± 0.012	± 0.012
30	0.978 ± 0.008	0.972 ± 0.008	0.935 ± 0.012	± 0.014
20	0.969 ± 0.009	0.961 ± 0.012	0.919 ± 0.014	± 0.017
10	0.948 ± 0.010	0.938 ± 0.023	0.876 ± 0.020	± 0.022
7	0.935 ± 0.012	0.920 ± 0.024	0.842 ± 0.025	± 0.028
5	0.916 ± 0.014	0.890 ± 0.025	0.803 ± 0.032	± 0.037

¹Average of ENSCI-Z model pump efficiency calibrations.

The O3S-DQA panel has recommended a revised table of PCF ±Δψ_P based on the average of combined laboratory calibration experiments conducted by NOAA/ESRL/GMD, University of Wyoming, and JMA (Japan Meteorological Agency). This study uses the revised ±Δψ_P values included in Table 5. Note these uncertainties are similar to those of Johnson et al. [2002] for a 2% unbuffered sensing solution type; thus, we expect Δψ_P/ψ_P values to be similar across the eight study sites. The revised ±Δψ_P values are considered to be a more realistic representation of the PCF uncertainties and are better quantified, being based on hundreds of profiles (refer to Table 2 in Johnson et al. [2002]). Refer to Table 3 for a summary of ECC sensor used at each site.

4.5. Pump Temperature Uncertainty, ΔT_P/T_P

All SHADOZ sites use either an ENSCI-Z or SPC-6A model that measures the pump temperature internally. These measurements are considered to be a close approximation to the ‘true’ pump temperature that is measured in the vicinity of the moving piston, T_piston [Smit12]. Witte17 reprocessing includes a correction that accounts for the temperature difference between T_piston and the internal pump temperature. For SHADOZ datasets, the ΔT_P/T_P equation is expanded to

$$\frac{\mathrm{\Delta }{\text{T}}_{\text{P}}}{{\text{T}}_{\text{P}}}=\sqrt{{\left(\frac{\mathrm{\Delta }{\text{T}}_{\text{reprocessed}}}{{\text{T}}_{\text{reprocessed}}}\right)}^2+{\left(\frac{\mathrm{\Delta }{\text{T}}_{\text{piston}}}{{\text{T}}_{\text{reprocessed}}}\right)}^2}$$ (5)

where both ΔT_reprocessed and ΔT_piston are ±0.5°K [Smit12]. As with the reprocessed flow-rates, we assume the uncertainties in the reprocessed pump temperatures are within the uncertainties of the original measured values. Witte17 replaced missing pump temperature profile data at Kuala Lumpur (1998–2005) and Irene (1998–2006) with climatological values. For these datasets the 1-σ values of the climatology (range between 3°- 4°C) are used to compute ΔT_reprocessed (see Figure A1 in Witte17).

5. Ozone Uncertainty Estimates in SHADOZ Profiles, ΔP_O3

For the eight reprocessed SHADOZ sites, we compute ΔP_O3 and the individual uncertainty terms defined in Eqn 2 for each profile. The overall profile average of the uncertainty terms for each site is also shown in Figure 4. The vertical resolution is 50 m. We show the impact of applying a 5% transfer function uncertainty to the Ascension, Natal, Nairobi, Réunion, and Hanoi datasets (Fig. 4 a-e, right panels, dashed black line). Note that the overall mean ΔP_O3 profile will lie between the solid black line, which is the dataset for which no transfer function is applied, and the dashed line. From Figure 4 (right panels) we observe:

Figure 4.

Left panels show the average profile of O₃ partial pressure (P_O3) in mPa (black) and ± uncertainty estimates (cyan) for the eight SHADOZ sites. Right panels are the individual uncertainty contributions to the total O₃ uncertainty (ΔP_O3) (black) in percent. Solid black lines in the right hand side panels for (a)-(d) are ΔP_O3 average profiles for which no transfer function was applied. Concurrently, dashed black lines are the average ΔP_O3 of profiles where a transfer function is applied. ΔI_B/Δ_M term is an abbreviation of the (ΔI_M)²+(ΔI_B)²/(I_M- I_B)² term in Eqn 2. Refer to Table 1 for each sites’ time period and total number of profiles used to calculate the averages.

• All sites show a peak in ΔP_O3 around the tropopause region (15±3km) due to I_B, as nicely illustrated in Fig. 1 in Vömel and Diaz [2010].

• The uncertainty in the background and O₃ current term (ΔI_B/ΔI_M, red) dominates the overall uncertainty of P_O3 in the troposphere. Where transfer functions have been applied (Fig. a-e), the conversion efficiency term (orange) becomes a significant contributor to the uncertainty.

• The uncertainties in the conversion efficiency (orange) and flow-rate (blue) terms dominate the overall uncertainty of P_O3 in the stratosphere.

• The application of transfer functions (Fig. 4 a-e, purple) has a significant impact on the overall uncertainty of P_O3 throughout the profile.

• The contribution of the pump temperature uncertainty term (ΔT_P/T_p, profiles in green) is minimal, accounting for only a few percent.

• Overall uncertainties are within 15%. Notable exceptions are at Hanoi (Fig. 4e, dashed line) and Kuala Lumpur (Fig. 4f) around the tropopause region.

• Costa Rica (Fig. 4g) displays a unique maximum in ΔP_O3 and ΔI_B/ΔI_M between 2–7km.

• Irene results show the smallest P_O3 uncertainties (less than 7%), relative to the other sites (Fig 5h), while Kuala Lumpur shows the largest values of ΔP_O3.

Figure 5.

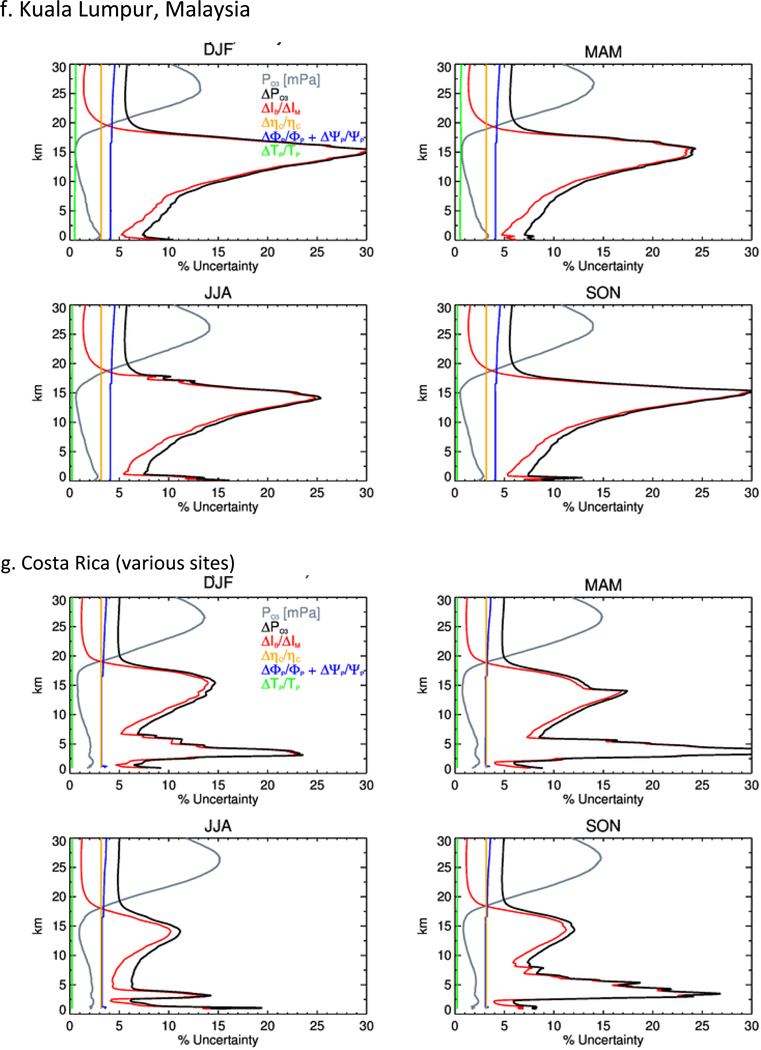
Similar to the right panels in Figure 4 but by season: DJF = December-January-February, MAM = March-April-May, JJA = June-July-August, and SON = September-October-November. Average seasonal P_O3 is shown in silver in mPa units. Dashed black lines in (a)-(e) are the average ΔP_O3 profiles for which a transfer function was applied. The solid black line denotes the average ΔP_O3 for profiles that did not apply a transfer function.

In the vicinity of the tropopause (15 ± 3 km), P_O3 is a minimum (Fig. 4, left panels). This is particularly true for Hanoi and Kuala Lumpur datasets that show the lowest mean P_O3 relative to the other sites. As the sensor current (I_M) approaches the measured background current value (I_B), the significant increase and dominance in the ΔI_B/ΔI_M term indicates that the sensor measurement is approaching its detection limit. Here, we define the detection limit where the total uncertainty is equal to the measured signal (~0.02–0.05 μA range). This is particularly true at Nairobi where the ΔI_B/ΔI_M uncertainty term matches the transfer function uncertainty between 10–18 km (Fig. 4c, right panel). Further investigation reveals a prevalence of I_B > 0.05 μA in the Nairobi metadata which contributes to a doubling of its uncertainty. In contrast, Irene (Fig. 4h) shows the highest measurements of P_O3 in the same region concurrent with the lowest values in the ΔI_B/ΔI_M and ΔP_O3. Irene is located in the very edge of the sub-tropics and can exhibit mid-latitude behavior (i.e. stratospheric fold events), as well-as southern hemisphere pollution transport [Thompson et al., 2014]. Hanoi and Kuala Lumpur are the only Asian tropical sites in the SHADOZ network and due to their geographic proximity to one another likely exhibit similar dynamics and transport features in the UT/LS (upper troposphere/lower stratosphere) region [Ogino et al., 2013]. Thompson et al. [2012] shows Hanoi and Kuala Lumpur have a similar annual cycle with almost double the O₃ amount at the Hanoi site throughout the troposphere. In fact, values of O₃ at Kuala Lumpur and Hanoi are among the lowest relative to other SHADOZ sites, corroborating the Thompson et al. [2012] result. Both sites show a higher gradient in ΔP_O3 and a larger peak > 15%, relative to the other sites.

As noted above, there is a second peak in ΔP_O3 in the lower troposphere in the Costa Rican dataset (Fig. 4g). There is a notch in P_O3 between 2–7 km (left panel) that is due to sulfur dioxide (SO₂) interference from the nearby active Turrialba volcano [Morris et al., 2010; Diaz et al., 2012]. Profiles that record near-zero I_M due to volcanic SO₂ plumes are not uncommon in a given year [Diaz et al., 2012]. This is seen in the right panel of Figure 4g where the uncertainty in the I_B/I_M term (red) increases significantly as I_M approaches I_B, and thus the detection limit of the sensor. The dataset reveals that roughly 10% of all profiles have SO₂ interference, with years 2010–2012 being particularly volcanically active. This uncertainty peak is really due to the reduction in the conversion efficiency (η_C), whereby SO₂ interference reduces η_C to zero. This is not captured in the uncertainty discussion because chemical interference is not assumed in Equations 1 and 2. The near-zero cell current measurements blow up the ΔP_O3 and ΔI_B/ΔI_M terms generating values that are much larger than they should be.

Van Malderen et al. [2016] applied corrections to the Uccle dataset for high-SO₂ interference in the Brewer-Mast ozonesondes using in-situ SO₂ measurements from a nearby site. No corrections were necessary during the ECC sonde era (1996-present) because SO₂ concentrations had diminished to levels that would not impact the ECC measurements. By filtering the obvious SO₂ layers in the Costa Rican dataset the peak would still be present but not as large or as dominant [Thompson et al., 2010].

Figure 5 presents the uncertainty terms arranged by season. P_O3 is shown in the background in silver. Similarly, we find that ΔP_O3 is a maximum around the tropopause and is dominated by the ΔI_B/ΔI_M term. In particular, in the vicinity of the tropopause region we observe in Figure 5:

• The overall uncertainty of P_O3 is the highest in DJF and MAM (with or without transfer functions) for sites in the Atlantic and Africa: Ascension, Natal, Nairobi, Réunion and Irene.

• The overall uncertainty of P_O3 is highest in DJF and SON at the two northern tropical Asian sites, Hanoi (Fig. 5e) and Kuala Lumpur (Fig. 5f), where ΔP_O3 peaks are over 20%. ΔP_O3 gradients are highest for these two sites.

• High ΔP_O3 in the Costa Rican dataset (Fig. 5g) due to volcanic SO₂ interference between 2–7 km occurs throughout the year.

• Relative to other sites, the overall uncertainty of P_O3 is smallest at Irene for all seasons (Fig. 5h). SON is a minimum (ΔP_O3 is less then 8%).

Overall, the ΔI_B/ΔI_M term dominates ΔP_O3 in the troposphere. The exception is where P_O3 measurements are high in the lowermost troposphere (silver profile), such as during the biomass burning season in SON over the Atlantic sites: Ascension (Fig. 5a), Natal (Fig. 5b), as well as Réunion (Fig. 5d) and Irene (Fig. 5h), and where the boundary layer is polluted such as at Hanoi (Fig 5e). P_O3 is elevated below 5km for all seasons in the Irene dataset (Fig. 5h), accounting for the relative minima in ΔI_B/ΔI_M (red). For all seasons, Kuala Lumpur (Fig. 5f) stands out as having the highest ΔP_O3 in the tropopause region, particularly in DJF and SON, where uncertainties peak sharply at around 30%, coincident with high ΔI_B/ΔI_M (red). Interestingly, the Nairobi dataset also shows a relative ΔP_O3 maximum in DJF (Fig. 5c). Logan at al. [2003] found that ozone concentrations at Nairobi are lowest from December to April from the tropopause to 50 hPa (~20 km). This corroborates the uncertainty results in Fig. 5c that show relatively higher ΔP_O3 during DJF and MAM where the ΔI_B/ΔI_M uncertainty term peaks at 15 ± 3 km.

Examples of applying uncertainties to profile comparisons with satellite can be found in Figure 6. We use Microwave Limb Sounder (MLS) v4.2 overpass profiles [Waters et al., 2006] at pressure levels between 261–10 hPa matched to the sonde location (within 200 km and 18 hrs). The four profile examples represent a cross-section of reprocessing techniques. Transfer functions were applied to Nairobi and Réunion profiles (Fig. 6a-b), Kuala Lumpur profiles incorporated a pump temperature climatology [Witte17] (Fig. 6c), and Costa Rica is a site that required very little reprocessing and therefore had a minor impacts to the overall dataset, relative to the original v5 dataset [Thompson2017]. One notes patterns of agreement/disagreement on a profile-by-profile basis. Applying sonde uncertainties will provide a robust metric of evaluating the accuracy of current and future generations of satellite O₃ profilers, particularly in the climate sensitive UT/LS region.

Figure 6.

Individual profiles of sonde (red) and MLS (black) for (a) Nairobi, (b) Réunion, (c) Kuala Lumpur, and (d) Costa Rica. Sonde profiles are matched to the MLS resolution. Red shading denotes the sonde ±ΔP_O3. Blue bars show the MLS precision.

How do our uncertainty estimates compare with previous studies? Smit and ASOPOS [2014] WCCOS simulation of a tropical profile estimates a similar range of ΔP_O3 values that also maximize around the tropopause (up to ~17%) due to the dominance of the ΔI_B/ΔI_M term. The main difference is that this term dominates ΔP_O3 values throughout the profile, whereas in our study, the flow-rate and conversion efficiency uncertainty dominate in the stratosphere. Sterling et al. [2017] present ΔP_O3 mean profiles for April and October at Hilo, Hawaii and American Samoa (two SHADOZ sites), which we interpret as similar to the seasonal plots shown in Figure 5. Here, we observe their range of ΔP_O3 values are similar, i.e. maxima at the tropopause (>10%) and minima else where in the profile (~5%). Sterling et al. [2017] show a relative minimum (maximum) in MAM (SON), similar to that shown for Hanoi and Kuala Lumpur (Fig. 5e-f). In comparison, mid- and high-latitude ozonesonde profiles from previous studies show that (1) the overall uncertainty is smaller, i.e. less than ~10% throughout the profile, (2) the conversion efficiency uncertainty term is a significant contributor to ΔP_O3 through-out the profile, and for some sites like Uccle be the dominant uncertainty term, (3) the impact of the ΔI_B/ΔI_M term remains an important contributor to ΔP_O3 around the tropopause [McMurdo uncertainty analysis (Terry Deshler, personal communication); Smit and ASOPOS, 2014; Tarasick et al., 2016; Van Malderen et al., 2016; Sterling et al., 2017].

6. Ozone Uncertainty Estimates in SHADOZ TCO

6.1. Calculating Total Column O₃ Uncertainty, ΔTCO

Profiles of O₃ partial pressure are integrated up to 10 hPa to generate integrated column amounts of O₃ in DU. To capture the O₃ maximum we exclude profiles that burst at pressures less than 15 hPa. We limit our column integration to 10 hPa based on the Witte17 recommendation. They found the accuracy of O₃ profile measurements below 10 hPa with respect to MLS did not improve even after reprocessing and remain highly variable and suspect. To compute the sonde TCO values the McPeters and Labow [2012] O₃ climatology is used to extract the O₃ amount from the sonde’s balloon burst to the top of the atmosphere (TOA). This is termed the ‘O₃ residual’ in this paper (P_O3residual). McPeters and Labow [2012] derived an O₃ climatology based on combining MLS (2004–2010) and ozonesonde (1988–2010) datasets. The climatology is a look-up table of monthly averaged ozone profiles from the surface to the TOA for ten-degree latitude zones. Previous studies have used the same sonde TCO formulation when analyzing SHADOZ data [Witte17; Thompson17 and references therein].

As a first approach, we compute sonde TCO uncertainties (ΔTCO) by integrating the O₃ partial pressure uncertainties (ΔP_O3) generated from Equation 2 and adding the uncertainty in the O₃ residual amount (ΔP_O3residual), i.e. ΔTCO = ΔP_O3 + ΔP_O3residual. For example, if $\text{TCO}={\int }_{sfc}^{BurstLevel}{\text{P}}_{03}(\text{z})\text{dz}+{\text{P}}_{03\text{residual}}$, then $\mathrm{\Delta }\text{TCO}={\int }_{sfc}^{BurstLevel}\mathrm{\Delta }{\text{P}}_{03}(\text{z})\text{dz}+{\int }_{BurstLevel}^{TOA}\mathrm{\Delta }{\text{P}}_{03residual}(\text{z})\text{d}z$. To generate an equivalent look-up table of ΔP_O3residual uncertainties, we use the table of monthly averaged 1-σ O₃ mixing ratios taken from McPeters and Labow [2012] and convert to DU following Ziemke et al. [2001] formulation (refer to equation 1 in that study). Thus, we can extract the ΔP_O3residual at the sonde’s lower limit altitude (15–10 hPa) in the same way. Look-up tables of ΔP_O3residual for the tropical latitude zones between 15–8 hPa are found in S1, in the supplementary material. For example, for a 10 hPa pressure burst the P_O3residual ± ΔP_O3residual range is (48–58 DU) ± (1.5–3 DU). We recognize this approach may be an oversimplified calculation and hope this study motivates future evaluation and refinement of this method.

6.2. Comparisons with TOMS and OMI overpasses

As a reference, sonde TCO ± ΔTCO are compared with satellite overpass TCO from Earth Probe Total Ozone Mapping Spectrometer (EP-TOMS V8.6 provided by the TOMS/OMI science team, McPeters et al. [1998]) and the Ozone Monitoring Instrument (OMI V3, Levelt et al. [2006]). TOMS and OMI have a local equator crossing time of 11:16 and 13:30, respectively. Sonde launch times (local) vary between 10:00 and 1500. From Figure 7 we observe that, overall, the overpasses are within the uncertainty of the sondes (red shading). Table 6 gives a summary of each site’s mean TCO ± ΔTCO, and includes the individual and combined TOMS and OMI mean overpass TCO ± 1-σ standard deviation values. Mean ±ΔTCO at the eight sites are comparable to ±1-σ from the satellite overpass data. The exception is at Kuala Lumpur where there are many cases in which TOMS and OMI are outside the uncertainty range (Fig. 7f, red shading). This amounts to a 5% offset overall. Given that there is limited metadata information for this site [Witte17], we speculate that the offset seems to be consistent with the use of a non-standard sensing solution formulae, similar to what was discovered at Réunion and Nairobi.

Figure 7.

Time series of TCO of every sonde launch (red) matched to a satellite overpass (TOMS and OMI, black). Red shading denotes the sonde TCO ± uncertainties (ΔTCO). Satellite datasets are filtered for clouds > 60% and distance from the sites location > 200km, then compared to the date of each sonde launch at the given site. The transition from TOMS to OMI overpasses occur in 2004/10 and are marked by the black triangle on the x-axis. Results are plotted in sequence, accounting for the uneven spacing of the years on the x-axis.

Table 6.

Mean Sonde TCO (TCO_sonde) and TOMS/OMI satellite overpasses for each site computed from data in Figure 7. Units are DU. ΔTCO_sonde is the mean uncertainty. The ±σ standard deviations are computed for the TOMS and OMI periods separately, and the combined TOMS/OMI period. Note that matched satellite overpasses are filtered for clouds > 60% and distance from the site location > 200 km. OMI overpasses start in 2004/10.

Satellite period	SN	$\overline{{\text{TCO}}_{\text{sonde}}}\pm \overline{\mathrm{\Delta }{\text{TCO}}_{\text{sonde}}}$	$\overline{\text{Satellite}}\pm \overline{1-\sigma }$
		Costa Rica (data since 2005)
OMI	277	255.3±12.6	255.4±14.3
		Hanoi (data since 2004/09)
OMI	147	261.7±14.7	264.5±17.6
		Ascension
TOMS/OMI	445	260.4±13.1	271.6±12.3
TOMS	220	259.1±13.4	277.7±10.9
OMI	225	261.6±12.8	265.7±10.6
		Irene
TOMS/OMI	250	272.4±15.0	269.6±16.4
TOMS	122	274.2±15.4	274.7±16.2
OMI	128	270.7±14.7	265.8±15.2
		Kuala Lumpur
TOMS/OMI	215	247.3±14.9	260.6±14.1
TOMS	86	249.7±14.9	267.4±14.5
OMI	129	245.8±14.9	256.1±11.9
		La Réunion
TOMS/OMI	454	264.9±15.8	268.5±15.7
TOMS	129	255.8±13.1	272.4±16.0
OMI	325	268.6±16.8	266.9±15.2
		Nairobi
TOMS/OMI	570	255.8±15.9	262.1±13.3
TOMS	199	257.7±17.3	270.2±12.9
OMI	371	254.7±15.1	257.7±11.3
		Natal
TOMS/OMI	436	261.1±13.4	269.2±12.7
TOMS	188	258.9±14.4	275.3±11.2
OMI	248	262.8±12.7	264.5±11.9

Ascension, Natal, Nairobi and Réunion reprocessed datasets (Fig. 7a-d) show significantly larger O₃ offsets relative to the TOMS period (1998–2004/09) compared to the OMI time series. This pattern was also noted for most of the SHADOZ stations in Thompson17. The cause for this persistent low-bias is unknown and cannot be explained by reprocessing and system differences alone. Whereas Ascension and Natal used the Lockheed Martin Sippican radiosonde/ozonesonde system during that entire period, Réunion used a Vaisala RS80 system switching to a Modem system (2007-present). The low–bias relative to TOMS is not readily apparent in the Irene reprocessed dataset (Fig. 7h) for which a Vaisala system is used and is the only sub-tropical site in this study with a data record extending back to 1998. However, Kuala Lumpur, which also used a Vaisala system during the TOMS period, show a much larger sonde-TOMS difference compared to sonde-OMI in the time series (Fig. 7f). Further investigation reveals a discontinuity between the TOMS and OMI time-series at all sites, and in particular, at Kuala Lumpur (Fig. 7f, TOMS overpasses in black). Table 6 includes the mean TCO for the individual TOMS and OMI periods at each site and reveals an almost 10 DU difference between averaged TOMS and OMI TCO with TOMS measuring higher than OMI (right column). For example, at Kuala Lumpur TOMS measures 11 DU higher TCO than OMI (TOMS=267.3 ± 14.5 DU versus OMI=256.1 ± 11.9 DU from Table 6). The Kuala Lumpur sonde dataset does not show a similarly large discontinuity in its TCO time series between the TOMS and OMI periods (249.7 ± 14.9 DU during the TOMS period versus 245.8 ± 14.9 DU during the OMI period). Interestingly, the agreement between Irene sonde TCO and TOMS is excellent; however, the agreement between TOMS and OMI is offset by 9 DU (Table 6, right column). From Table 6, excluding Irene, the average difference between sonde and TOMS is 16 DU and is significantly higher than the 4 DU difference computed for the difference between sonde and OMI. This discontinuity is likely due to a change in the TOMS processing algorithm and is currently being investigated by the TOMS/OMI science team. This TOMS to OMI TCO discontinuity is not apparent in Witte17 and Thompson17 that used an older version 8 TOMS overpass dataset taken from the AVDC (Aura Validation Data Center – https//avdc.gsfc.nasa.gov).

The sonde low-bias at Costa Rica (Fig. 7g) observed at the end of 2015 points to a change in the ENSCI instrument. Other SHADOZ sites (Samoa, Fiji, and Hilo) that use ENSCI during that period also exhibit a low-bias relative to satellite overpasses [Thompson17]. The MLS/sonde profile comparison in Fig. 6d highlights the significant underestimate in the sonde (red) observed after 2015 in Fig. 7g and in Thompson17. The sonde underestimate appears above 50 hPa and is typical of sonde/MLS profile comparisons after 2015.

7. Summary

For the first time, uncertainty estimates in profile and total column O₃ are computed using reprocessed data from eight SHADOZ sites. As a first approach, we also create a look-up table of monthly averaged O₃ residual uncertainties to compute the uncertainty in sonde TCO. Variations in reprocessing procedures at each site require a tailored approach when calculating uncertainties. For example, missing metadata such as background current and flow-rate measurements require climatological values specific to each site, and thus a doubling of the uncertainty, and not all sites require a transfer function.

A significant fraction of the Réunion and Nairobi datasets have been homogenized with the use of transfer functions; 63% and 64%, respectively. We demonstrate the efficacy and success of applying the Deshler et al. [2017] formulae to generate consistent and stable reference datasets for trends analysis and satellite validation. Biases are reduced (Réunion =0.7% and Nairobi =−1.5%) and preliminary agreement with OMI is within 5%.

Overall, O₃ profile uncertainties are less than 15% with a persistent maximum in the vicinity of the tropopause where O₃ values are low and approach the detection limits of the ECC sensor. Here, the background and sensor current uncertainties dominate, as well as in the troposphere. Stations for which transfer functions have been applied show a significant contribution from the conversion efficiency uncertainty. In the stratosphere, the conversion efficiency and flow-rate uncertainty terms dominate. We observe a unique second peak in the free-troposphere in the Costa Rican dataset due to SO₂ interference from volcanic plumes. Seasonally, uncertainties are a maximum in MAM when O₃ values are the lowest. Exceptions are at Hanoi and Kuala Lumpur, the only two northern tropical Asian sites in the SHADOZ network. Both display the highest uncertainties in DJF and SON, indicating unique meteorology relative to the other sites. The Irene dataset displays the lowest O₃ uncertainties, among the eight sites.

Overall, TCO uncertainties are less than 15 DU and represent ~5–6% of the TCO. TOMS/OMI overpass comparisons are within the sonde TCO uncertainties with the exception of Kuala Lumpur for which the sondes are low-biased by about 5%. The persistent offset mimics that found in the Réunion and Nairobi datasets for which an error in the sensing solution formulae was found. However, due to the current lack of verification in the metadata, we can only speculate on the offset. In addition, there is a discontinuity between the latest TOMS v8.6 and OMI TCO overpasses at all sites. TOMS measures higher TCO than OMI on the order of 10 DU that is not readily apparent in the older version 8 overpasses used in Witte17 and Thompson17 studies.

The advantage of doing a detailed uncertainty analysis is that it reveals areas of the measurements where we can refine operational procedures to reduce the uncertainty, and where additional research is needed to improve the basics of this measurement. 1) To improve O₃ measurements in the UT/LS in SHADOZ, we need to improve our understanding of the background current. This means that the actual measurement as done right now needs to be better quality controlled, i.e. using a high quality zero ozone air filter, time of measurement after reconditioning, and consistency of procedures. For example, the large spread of SHADOZ I_B observed in Witte17 (range is 0.01 μA - 0.12 μA) is a result of varying procedures and not a property of the sonde instrument. It also means that the definition of the background current needs to be studied in greater detail. 2) To reduce the uncertainty of the middle stratospheric measurements, i.e. region of high O₃, we need to better characterize the pump efficiency and conversion efficiency at low pressures. This is also the reason why transfer functions become pressure dependent at lower pressures. 3) Careful and complete metadata collection of lab P-T-U during preparation will reduce the uncertainty of the RH correction (ΔC_PH), and careful metadata collection of the O₃ destruct filter being used during the background measurements will help in estimating the quality of that measurement.

Key Points.

1. First analysis of ECC ozonesonde uncertainty estimates using SHADOZ data.

2. Ozone uncertainties are generally within 15% and peak around the tropopause where ozone measurements approach the uncertainty estimates.

3. Uncertainties in background and sensor current dominate the troposphere, while conversion efficiency and flowrate dominate the stratosphere.