Fast In Situ Image Reconstruction for Proton Radiography

Abstract

Objective

Proton beam therapy is an emerging modality for cancer treatment that, compared to X-ray radiation therapy, promises to provide better dose delivery to clinical targets with lower doses to normal tissues. Crucial to accurate treatment planning and dose delivery is knowledge of the water equivalent path length (WEPL) of each ray, or pencil beam, from the skin to every point in the target. For protons, this length is estimated from relative stopping power based on X-ray Hounsfield units. Unfortunately, such estimates lead to 3 to 4% uncertainties in the proton range prediction. Therefore, protons in the Bragg peak may overshoot (or undershoot) the desired stopping depth in the target causing tissue damage beyond the target volume. Recent studies indicate that tomographic imaging using protons has the potential to provide directly more accurate measurement of RSPs with significantly lower radiation dose than X-rays. We are currently working on a proton radiography system that promises to provide accurate two-dimensional (2D) images of WEPL values for protons that pass through the body. These will be suitable for positioning and range verification in daily treatments. In this study, we demonstrate that this system is capable of rapidly achieving such accurate images in clinically meaningful times.

Methods

We have developed a software platform to characterize the potential performance of the prototype proton radiography system. We use Geant4 to simulate raw data detected by the device. An especially-written software – pRad – was written to process these data as they are received and uses iterative methods to generate radiographs. The software has been designed to generate a radiograph from a few million protons in under a minute after receiving the first proton from the device. We used a head phantom with known chemical compositions that could be modelled quite accurately in Geant4 simulations of proton radiographs. The radiographs are displayed as pixelated WEPL values displayed on a 2D gray scale image of WEPL values.

Results

Rapid radiograph reconstruction of 3D phantoms using simulated proton pencil beams have been achieved with our software platform. On a modest desktop computer with a single central processing unit (CPU) and a single graphics processing unit (GPU), it takes about 11 seconds to reconstruct images using iterative linear algorithms to reconstruct a radiograph from 7.6 million protons. For the radiographic reconstructions of the head phantom described here, the mean WEPL errors, in the proton radiograph using a large majority of the pixels in the complete image were less than 1 mm when compared to images obtained without proton scattering and without detector resolution included.

Conclusion

We have demonstrated, through computer simulations of proton irradiation of a pediatric head phantom using the newly built pRad detector and image reconstruction software, that high quality proton radiographs can be generated for patient alignment and verification of water equivalent thickness of the patient before each treatment.

Introduction

Proton beam therapy provides a superior dose deposition with a relatively low dose in the entrance region (plateau) followed by a steep increase to a dose peak (Bragg peak), and an even steeper distal dose fall-off. This well-defined range, not an increased biological effectiveness, is the main advantage of proton therapy. However, the steep dose gradient and finite range can also be a profound disadvantage when its actual position in the patient is to some extent uncertain. Ignoring this uncertainty can lead to therapeutic failures. Therefore, current practice is to add distal and proximal uncertainty margins to the planning target volume in the beam direction, which increases the risk of complications by potentially placing the stopping proton beam into healthy tissue. This compromises the advantage of proton therapy. Our project aims to address this problem by improving reconstructed range accuracy in proton radiographs in the hope that doing so will enable clinicians to better realize the full potential of protons in cancer therapy.

Proton therapy has undergone a rapid technological development since the early 1990s when the first hospital-based proton therapy systems appeared. Those changes led to the development of compact accelerators and single-room installations that can be integrated into existing radiation therapy facilities. During the 2000s, technical solutions (i.e., synchrotrons or cyclotrons and gantries with conventional magnets) were still relatively large and expensive. Since then, more compact solutions have been developed and are now offered by several vendors, making single-room installations and significant cost reduction a reality. This has led to a rapid expansion of operating proton therapy installations with more than twenty-three clinical proton therapy centers in the U.S. and twenty-nine outside the U.S., with ten more under construction [1].

Another recent development in proton therapy is the appearance of image guidance systems utilizing digital X-ray radiography and X-ray cone-beam computed tomography (CT) in the treatment room for advanced pre-treatment verification and reduced planning margins [2]. The major driver of this development is its potential for reducing the margins of high-dose treatment volumes, which would lead to a reduction of complication rates and allow higher doses to the tumor. Imaging capability using X-ray technology was at first two-dimensional (2D, planar radiographs), but quickly became three-dimensional (3D, volumetric CT) with the installation of cone beam CT scanners in proton treatment rooms. However, X-ray radiographs do not provide any information on the integrated proton tissue stopping power relative to water, or relative stopping power (RSP), that could provide a range check of proton beams before treatment.

There is, however, a fundamental problem with the use of X-ray imaging for treatment planning and pre-treatment verification in proton therapy resulting in relatively large range uncertainties. Specifically, the range information it provides in the form of a map of proton RSP is imperfect due to the differences in the dependence of X-ray attenuation and proton energy loss on tissue composition (electron density and atomic number). This yields an inherently inaccurate conversion of X-ray Hounsfield units to RSP. There are additional sources of inaccuracy with X-ray CT imaging, including beam hardening and artifacts in the presence of compact bone and metal implants, the latter leading to particularly large range uncertainties when the X-ray CT scan is used for treatment planning. Accordingly, the quest for a better method of determining the stopping power is an important area of research and development [3]. Recent solutions that have been proposed include the use of dual-energy CT (DECT) for proton treatment planning [4], which allows a more accurate definition of RSP, but does not solve the problem of image artifacts nor provide an immediate check of range accuracy before treatment with the patient in treatment position. Other approaches to reduce range uncertainties in proton therapy are at various stages of development and include prompt gamma imaging [5], ionoacoustic imaging [6] during treatment, and positron emission tomography (PET) detecting proton beam-induced positron emitters post-treatment [7]. These approaches are not fully satisfactory for several reasons. First, they do not detect range inaccuracies before treatment but only during or after treatment. Thus, while range inaccuracies may be detected, they would need to be corrected after treatment. This may be problematic if the treatment is delivered in a few dose fractions or as a single fraction. Second, these techniques do not mitigate the inaccuracy of proton treatment planning inherent in using X-ray CT, including the presence of CT artifacts.

Proton imaging aims to address range inaccuracies in proton therapy. If successful, proton computed tomography (pCT) has the potential to substantially reduce the uncertainties of treatment planning by directly measuring RSP (the tissue property determining proton energy loss) without artifacts from metallic implants and much lower dose to the patient than with comparable X-ray images. Daily proton radiography (pRad) will provide the capability to verify the range of individual proton beams before treatment as well as aid in image-guidance. In summary, proton imaging with pCT and pRad has the potential to enable clinicians to fully exploit the advantages of proton radiotherapy.

Current proton imaging systems use tracking detectors to measure the transverse position of individual protons before and after the patient, and a residual range detector to determine the proton energy absorbed within the patient, as illustrated in Figure 1. pRad produces two-dimensional (2D) images with a single projection angle, directly quantifying proton range through the patient rather than integrated X-ray attenuation. pCT measures the three-dimensional (3D) RSP map of the patient by acquiring many proton histories from many projection angles and applying advanced reconstruction algorithms. In addition to the benefits of a direct measurement of proton stopping power with pCT and proton range with pRad, proton imaging deposits much less dose to the patient relative to X-ray images of comparable resolution [8].

Fig. 1.

Illustration of proton imaging, with tracking and residual range measurements for each proton. A proton radiograph would resemble the image on the right, displaying range through the patient versus transverse position.

Historically, many patients have been treated with broad proton beams passively scattered and then refined with collimators and compensators to conform to the tumor in three dimensions. In contrast, pencil beam scanning (PBS) systems use narrow beams with steering magnets programmed to rapidly scan the pencil beam across the tumor. PBS systems are becoming the standard for the delivery of proton therapy, and proton imaging systems should be designed specifically to work with PBS.

We have developed a fully functional prototype of a clinical proton radiography system that integrates a detector and imaging reconstruction software. The ProtonVDA detector design, based on well-established fast-scintillator technology, is compact, monolithic, and easily scaled to large field sizes. The individual components of the system have been tested at proton rates up to ten MHz, fast enough to acquire pRad images with a few seconds of beam time. Construction of a prototype device with a 40 × 40 cm² field size has been completed and integrated with a data acquisition system capable of sustained 10 MHz rates.

The photograph on the left side of Figure 2 shows the prototype device set up for actual radiograph imaging of a pediatric head-sized phantom. The phantom faces the beam and positioned between the upstream and downstream trackers. The right side of Figure 2 shows the radiograph of the phantom reconstructed with the software platform discussed in this paper.

Fig. 2.

Left: The prototype radiograph device set up for imaging of a pediatric head-sized phantom at Provision CARES Proton Therapy Center, Knoxville, TN. Right: Radiograph of the phantom reconstructed with the software platform discussed in this paper. Radiograph was made using proton beams with energies of 120, 160 and 180 MeV.

Our system is designed to be used with scanning pencil beams rather than broad beams. Therefore, the imaging and treatment are performed with the same beam system, streamlining operations. Imaging with pencil beams requires rapid scanning at ultra-low proton intensity. The use of such pencil beams has been demonstrated as depicted in Figure 3 and using the ProtonVDA detector shown in Figure 2 at the Northwestern Medicine Chicago Proton Center (NMCPC). The use of pencil beam scanning for imaging also streamlines quality assurance procedures. The pencil beam scanning system is calibrated to steer the beam to known positions in an isocentric coordinate system used for patient set up. Our software exploits this calibration to locate the detectors relative to isocenter, and as a result proton radiographs can directly be displayed in isocenter coordinates, enabling patient alignment checks without relying on careful detector alignment. Preliminary studies applying the NMCPC alignment procedures using simulated pRad images of adult head/neck patients suggests an alignment precision comparable to current x-ray techniques [9]. Thus, proton radiography systems could replace X-ray radiography systems in future proton therapy treatment rooms. However, any use of pRad images will require additional beam usage on top of treatment delivery. This can result in minor delays for other treatment rooms where patients are ready for beam.

Fig. 3.

Left: Three-dimensional scatter plot from test beam data with a moving low-intensity scanning pencil beam. Each point represents one proton detection in our residual range detector. The horizontal plane shows the transverse position, and the vertical axis shows the time of the detection. Right: Demonstration of a uniform proton distribution delivered to a 20 × 10 cm² area in 0.3 sec by the PBS system at the NMCPC.

As illustrated in Figure 2, NMCPC has demonstrated the ability to generate pencil beam scanning patterns for proton imaging that uniformly fill an area with the required speed. These scanning patterns will be customized for each patient. In analogy to planning the treatment, the imaging must be planned as well. Diagnostic X-ray CT scans for each patient can be used to plan the scan pattern for the imaging. The detector system can measure residual ranges up to ten cm, so the beam energy as well as the contour of the scanning area must be chosen so that protons emerge from the patient with a range less than this limit. In general, two or three energy passes will be needed to image the entire patient.

We have implemented a pRad reconstruction program on a computer equipped with a conventional multi-core central processing unit (CPU) and a separate graphical processing unit (GPU), or a CPU-GPU computer. The reconstruction program uses alignment and calibration data to reconstruct and display a pRad image within one minute of the start of data acquisition. Due to multiple Coulomb scattering, protons paths undergo random transverse scattering, potentially blurring images. The software’s iterative techniques use the information on each individual proton path to recover image sharpness.

Materials and Methods

We have developed an integrated detector-software system for the rapid reconstruction of proton radiographs using the ProtonVDA detector shown in Figure 1. The system is based on our previous experience with pCT [10,11] that uses software and hardware technologies in a multi-processor environment to reconstruct 3D RSP maps from a prototype proton-CT head scanner [12]. In pCT, proton data, in the form of detected positions and energies, are first distributed across several computers that operate in parallel, largely independently, but with some coordination. We then use GPUs at each computer to individually process in parallel each of the large number of proton histories assigned to that computer. The reconstructed RSP values from the computers are iteratively collected, collated, and distributed to all the computers using Message Passing Interface (MPI). We have demonstrated that this two-level parallelization results in significant reduction of reconstruction time in pCT.

An important difference between pCT and pRad is the manner by which data are fed into the reconstruction program. In current pCT implementations, data are collected first, followed by a preprocessing step that converts them into a format suitable for reconstruction. In pRad we have integrated the pre-processing step into the reconstruction to generate proton radiographs within a clinically meaningful time scale (i.e., within seconds of detecting the first proton). Additionally, data for pRad are only a small subset of pCT, about an order of magnitude. We have found that for pRad reconstruction, it is more beneficial to use a single multiple-core CPU computer equipped with a GPU.

We have designed and implemented our pRad reconstruction software to directly receive raw data from the data acquisition (DAQ) computer of the pRad device. The software executes on a separate and dedicated “reconstruction” CPU-GPU computer. These two computers need not be in close proximity to each other. The only requirement is for the DAQ computer to continuously stream proton data to the reconstruction computer via computer network connection in real time.

Our pRad software has two major stages. The first, preprocessing, performs all the necessary operations to convert raw data from the DAQ into a format suitable for radiograph reconstruction. Specifically, these converted data are in the form of detector coordinates and water-equivalent path length for each proton. The second stage is the actual radiograph reconstruction.

Raw data from the pRad device comprise four encoded signals from photomultipliers (PMTs) in the range detector, four sets of bitmask signals from the trackers, and a detection time-stamp for each proton. Each set of bitmask signals are encoded from multiplexed hit fibers in the x- and y-fiber planes of the upstream and downstream trackers (i.e., first and second trackers in the proton beam’s path). The PMT data are used to calculate the water-equivalent path length (WEPL). The conversion is done via look-up from a pre-calculated and pre-loaded calibration table. Likewise, the encoded fiber signals are converted to absolute detector coordinates via a two-step process. First, each event is correlated to a pre-specified distribution of beam positions – referred to as the “accelerator plan” – used in scanning an object. Then, from this correlation, the most probable strip in each x- or y- tracker plane that recorded a fiber hit is identified. This identification, called demodulation, localizes detector coordinates to within one-half of a fiber width. At the end of this pre-processing stage the DAQ data has been converted to data that are suitable for the remainder of the pRad reconstruction process.

We have also implemented a provision for the correction of potential mispositioned detector coordinates that may arise, for example, from misaligned trackers. As in the case of pCT, pRad reconstruction assumes that the trackers are perfectly aligned and parallel to each other. The hope is that the rigid construction design of the prototype device would ensure this. However, misalignment might occur due to sag from weight, or the whole setup being accidentally knocked off the beam axis.

The alignment algorithm is an outgrowth of a theorem from projective geometry that any four-point in the projective plane (any four points, including points at infinity, no three of which are collinear) can be transformed to any other four-point using a projective transformation [13]. Projective transformations preserve all straight lines and include scales, rotations and translations. 2D projective transformations include projections of 3D rotations onto 2D. In the 2D projective plane, points are represented by homogeneous 3-tuples [x y w] which are unique to a scale factor. To create a projective point from a Cartesian point, it is sufficient to set w=1. Conversion from projective points to Cartesian points is achieved (for points not at infinity) by dividing by w.

With the position of four measured points in the plane and four desired positions, it is possible to solve directly for a 3×3 matrix representing a projective transformation between the two sets [14,15]. In essence, the transformation will take all points in the measured coordinate system and transform them to the desired coordinate system, in a way that is consistent with a combination of Euclidian transformations. This approach can be sensitive to position noise. In practice, sets of many corresponding point pairs are used to robustly derive a single projective transformation through non-linear optimization, a process known as bundle adjustment in the computer vision community [16].

Currently in pRad, twenty-five well-separated spots of several thousand protons each are fired for the sake of alignment. The average spot position is calculated for each spot on both the upstream and downstream detector planes. These points are the measured points. Using the accelerator plan for the alignment along with knowledge of detector and beam geometry, positions are calculated for each theoretical spot center on the upstream and downstream detector planes. These are referred to as the ideal point positions. Then using a Levenberg-Marquardt non-linear optimization routine [17], projective transformations are calculated from the measured coordinate system to the ideal coordinate system for each of the detector planes.

The projective transformations are used in the imaging stage of pRad to take the intersections of each proton trace with the detector planes at unknown positions and orientations and convert the intersections into the corresponding coordinates with the detector planes at their ideal positions. Each coordinate transformation involves fourteen floating point operations per proton for each detector plane. This alignment-correction step is one of the pre-processing steps.

A significant design concept of the prototype radiograph device is multi-energy imaging. The range detector of the prototype device is not thick enough to stop very energetic protons. Thus, we scan different regions of an object with beams of different energies. The energies are based on the thickness of the object along the beam path. We have found that with multi-energy imaging, it is necessary to preprocess all data before proceeding with the actual reconstruction. The preprocessing stage now includes statistical-cut corrections to the data and calculation of the most-likely paths (MLP) of the protons.

In pCT, MLP calculation is done with full knowledge of a proton’s entry position and direction into, and exit position and direction out of, the object being imaged [18,19]. In conventional pCT designs, such as in [12], the entry direction is computed from the 2D positions of a proton measured by a pair of trackers (upstream) between the source of protons and the object. Likewise, positions measured by another pair of trackers (downstream) behind the object are used to compute the proton’s exit direction. Because our prototype device has only one upstream and one downstream tracker, the entry and exit directions are estimated differently. The entry direction is estimated from the measured position on the upstream tracker and the known source position. Then, the exit direction is estimated from the measured positions in the upstream and downstream trackers. For this case with unmeasured, but only estimated, exit direction, Penfold [20] has derived a suitable formulation for the calculation of the MLP.

Using these directions, the corresponding entry and exit positions of the proton in the object are obtained from intersection points on the surface of the object. This surface – the hull – is constructed in pCT directly using data from multiple proton-beam angles [21]. Because our prototype device measures radiographs at only one fixed beam angle at a time, such a hull is not readily obtained from the data, and must therefore be provided or estimated some other way. One way is to use auxiliary information such as data from other imaging modalities, or a priori known geometry of the object.

In this study, we investigate two alternative methods of using WEPL to estimate the hull. In the first method, WEPLbox, the hull is assumed to be a rectangular box whose thickness along the primary beam axis is obtained from the largest WEPL value in the data set. The width and height of the hull are equal to the lateral fields of view of the radiograph. In the second method, WEPLstick, the hull is constructed from the WEPL of each proton. The entry and exit positions are obtained from the endpoints of a stick whose length is equal to the proton’s WEPL; the stick is laid parallel to the principal beam axis, and centered at the isocenter plane.

It should be noted that there are other approaches to MLP calculation. For example, Collins-Fekete et al. have proposed an alternative maximum-likelihood method for MLP calculation [22]. In our current study, however, we have implemented Penfold’s method primarily due to our experience with his work in pCT.

In pRad, as in pCT, it is desirable to use in the reconstruction only those protons that have traversed the object via a series of small-angle, multiple Coulomb scattering interactions. This is done by examining the distributions of the exit angle relative to the principal beam axis, defined as the difference between the entry and exit angles, and WEPL of protons that pass through pre-defined areas in the radiograph. Good events used in the reconstruction are those whose relative exit angles and WEPL values fall within user-specified limits. In the pCT literature, this statistical-cut limit has been typically set to plus-or-minus three times the standard deviations with respect to the means of the relative exit angles, and plus-or-minus three times of the standard deviations with respect to the mode of the WEPL distribution. We have implemented the same “sigma” cut for WEPL in pRad. But because of the absence of measured exit-angle data, we have implemented instead the sigma cut on the lateral displacement between the entry and exit positions.

Like pCT, radiograph reconstruction can be cast as a mathematical linear problem in the form Ax=b, where b represents the measured WEPL data and x is an unknown distribution. The quantity A, referred to as the system matrix, is an operator that represents and characterizes the device’s interaction with the unknown distribution x that resulted into the measured values b. In pCT, x is a linearized version of a 3D distribution of voxels. The value in each voxel is its RSP. Each row in the system matrix A identifies the voxels in the distribution x that one proton passed through: A will have non-vanishing values for voxels that were crossed, and zero otherwise. The number of voxels (in the hundreds) touched by each proton is significantly smaller than the total number of voxels (a few millions) in the distribution x by several orders of magnitude. The number of rows in A is the number of protons in the data. As imaging applications require at least a few million protons, the system matrix is a large, sparse matrix, and the imaging equation is suitable for solution via iterative linear algorithms.

We have implemented the use of iterative linear algorithms as an intermediate step towards the reconstruction of the desired radiograph. pRad initially treats the imaging problem as one seeking a 3D solution. The solution is calculated for a 3D grid of projective voxels, such that columns of voxels follow the divergent paths of pencil-beam scanning. The resulting proton radiographs will be analogous to X-ray radiographs that similarly project along divergent X-ray paths. Projective radiographs display features projected along pencil-beam paths, which is necessary for checking the dose distribution for these features.

Each iteration in the algortihm refines the solution based on the solution of the previous iteration. After every iteration, a 2D radiograph is generated from a weighted sum of the RSPs along the projective columns of the 3D solution. The weight for each voxel is its length along the beam, with geometric correction to account for the column’s angular divergence from the primary beam axis. By default, pRad iterates up to a user-specified maximum number of iterations. We devised a stopping criterion that terminates execution before reaching said maximum (set to one hundred iterations for this study). The criterion is based on a quality index (QI) metric, which is the fraction of pixels in the radiograph where the absolute pixel-by-pixel difference between two consecutive radiographs fall below a user-specified threshold value, say 0.5 mm. Convergence to a suitable solution is deemed achieved whenever the fractional change in QI from one iteration to the next becomes smaller than another user-specified value, say 0.0001.

Currently, three iterative reconstruction algorithms are implemented in pRad: algebraic reconstruction technique (ART) [23]; diagonally relaxed orthogonal projection (DROP [24]; and component-averaged row projection (CARP) [25]. To speed up the iterative reconstruction, pRad was modified by introducing the use of threads using OpenMP [26]. With a multi-core CPU, there can be as many threads as there are cores and, in fact, through hyperthreading even more threads than cores. The linear solver task can then be distributed among several threads, where each thread operates on its own subset of the data. This approach is particularly suited for CARP. In CARP, all data subsets – or thread blocks – start with the same initial solution, and the appropriate averaging is made after all thread blocks are done to find the updated solution. When we create as many thread blocks as there are physical cores, we expect a near-linear speed up in the execution time as we increase the number of threads.

In addition to the iterative solution, pRad also has two extremely fast non-iterative methods to generate radiographs. Both methods compute the average WEPL per unit area from all protons at the isocenter plane. They only differ in the way the position crossed by each proton at the isocenter plane is calculated. In the first method, which we call straight-line projection (SLP) binning, the crossed position is simply the intersection of the line joining the entry (upstream) and exit (downstream) positions with the isocenter plane. The second method, MLP binning, uses the intersection of the proton’s non-straight most likely path with the isocenter plane.

We tested pRad using simulated data. A Geant4 [27] model of the prototype device was constructed to image a digitized version [28] of the CIRS 715-HN pediatric head phantom. The trackers were set 24 cm apart, and the 3D phantom was centered at isocenter. The primary beam axis was set to lie left-to-right. The beam parameters (distance of source to isocenter, range-energy calibration) were adapted from NMCPC. Two types of simulated proton data were generated: alignment protons, used for determining alignment correction factors for the detector coordinates; and imaging protons, used in generating the radiographs. Imaging protons were simulated at 119 and 161 MeV. The lower energy represents the highest energy that can be reliably measured by the range detector where there is no material between the tracking planes, and was used for imaging the outer parts of the object. The higher energy was chosen to pass protons through the thickest parts of the object. Thicker objects may require additional higher energies.. There were overlaps between the beam-spot positions of these two accelerator plans. A total of 7.6 million protons were simulated. Additionally, simulation of “truth” data was carried out with all stochastic events turned off. This resulted to a radiograph constructed from straight lines that run from the beam source and through both upstream and downstream detector positions.

To simulate real-time reconstruction, we converted the Geant4 simulation output into a format that mimics a continuous stream of bytes from the DAQ. In actual implementation, this stream of bytes will flow through a network socket connection between the DAQ and the reconstruction computer. The data stream comprises one or more accelerator plans, followed by the same number of proton data sets. Each accelerator plan specifies a principal beam energy, a set of beam-spot positions, the time duration at each beam-spot position, and the plan’s intended use (i.e., alignment or imaging). Because data are streamed continuously into pRad, there must be a way of determining when each data set begins and ends. This can be done via suitable time interval between two consecutive data sets, for example, one that is significantly longer than the mean time between two events when the beam is on.

The program has provisions for specification of reconstruction parameters. These parameters can be read from a pre-defined configuration file. Some of these parameters can be over-ridden by command-line options when running pRad. Important parameters are image dimensions; pixel size and slice thickness; and those for the linear solver.

In its current form, pRad does most of the preprocessing using a GPU. Even with only a single GPU, this preprocessing stage is very fast. The bulk of the reconstruction time is spent in the iterative linear solver, which is done in parallel using threads on the multi-core CPU.

Results

The main goal of pRad is the generation of a radiograph, which is the 2D distribution of proton WEPL through an object at a specified position along the primary beam axis. For the prototype device described here, that position is a plane midway between the upstream and downstream trackers. In actual software implementation, this plane is digitized into a 2D grid of square pixels. In this study, all reconstructed radiographs are 220 × 220 1-mm square pixels.

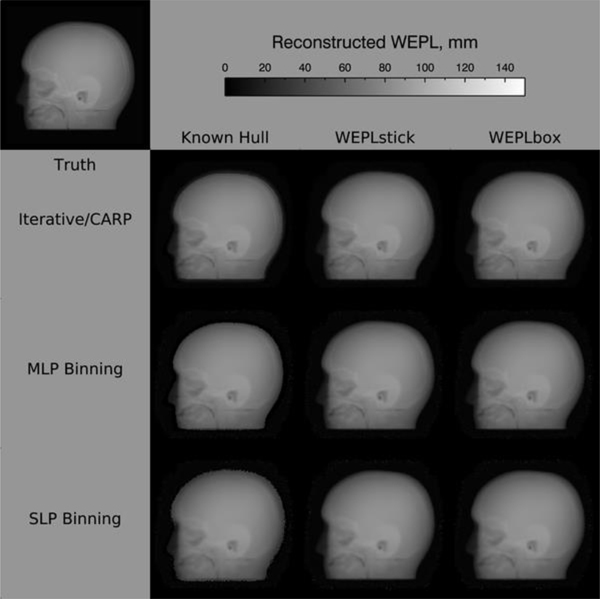
Figure 4 shows typical radiographs from pRad. The bottom three rows (top to bottom) are radiographs generated using iterative reconstruction with CARP, MLP binning, and SLP binning, respectively. The columns correspond to different hull methods used for MLP calculation. The left column shows radiographs using an a priori known hull. The middle and right columns respectively show radiographs obtained from using the WEPL-based hull methods discussed above, WEPLstick and WEPLbox. For comparison, the “truth” radiograph is the top left radiograph in the figure. Cursory inspection of the reconstructed radiographs show that most of the general features in the truth radiograph are visible. However, the radiographs reconstructed with known hull show sharper, or rather less fuzzy, outlines.

Fig. 4.

Radiograph reconstructions

Figure 5, on the other hand, shows the differences of the reconstructed radiographs from the truth. We observe that most of the departures from truth in all reconstructions occur near the outer edges of the object. Inside the object, all radiographs show smaller differences from the truth. There are some traces of larger differences, particularly in the inferior portion, where the object has more non-homogeneous structures compared to the superior region. These differences appear to be most apparent in SLP binning, and least in the iterative solution. This suggest that radiograph reconstruction must take into account the non-straight paths of protons in material media. The iterative methods do this; MLP binning also does, although to a simpler extent.

Fig. 5.

Reconstructed radiograph errors (difference from truth)

Table 1 summarizes the radiograph errors with respect to the truth. Each column shows the mean absolute difference, in millimeters, from the truth. These means were measured in three regions of interest (ROI) that all lie entirely inside the object, carefully chosen to exclude areas that vary greatly from the truth (blue and red pixels in Figure 5). The superior portion, Sup, is the mostly uniform region above what looks like the ear in Figure 4. The inferior portion, Inf, is the region below Sup, and contains most of the non-uniform structures in the object. The union of these two ROIs forms the region Total.

Table 1.

Average absolute difference from truth, in mm

	Known Hull			WEPLstick			WEPLbox
	Sup	Inf	Total	Sup	Inf	Total	Sup	Inf	Total
Iterative/CARP	0.47	0.67	0.58	0.57	0.72	0.66	0.58	0.72	0.66
MLP Binning	0.41	0.72	0.59	0.41	0.73	0.60	0.41	0.76	0.61
SLP Binning	0.41	1.04	0.77	0.41	1.04	0.78	0.41	1.04	0.78

Table 1 demonstrates more quantitatively the observation from Figure 5 that the simple straight-line projection binning gives the worst results, regardless of the hull method used. For the total internal region, the iterative method with known hull seems best. But in the absence of a priori hull data, MLP binning with either WEPLstick or WEPLbox seems to be a good choice. In any case, except for SLP binning, the mean absolute difference from truth is under one millimeter.

To assess the alignment-correction capability of pRad, additional simulations of proton imaging with known, intentional misalignment were carried out. The misalignments were in the form of lateral shifts of one tracker perpendicular to the primary beam axis; rotation of one tracker about the beam axis; rotational twist of one tracker about an axis perpendicular to the beam; and lateral shifts of both trackers along the beam axis. To test for algorithm robustness, the misalignments were larger that those expected to exist in typical clinical practice. In each case, the simulated data were reconstructed with and without alignment correction. The latter proved very illustrative of how “bad” reconstructions arise from misaligned data, while the former demonstrated the effectiveness of our alignment-correction algorithm.

Figure 6 illustrates the results for alignment correction of data where the upstream detector was shifted six mm laterally to one side. The top row shows the reconstructed radiograph without (left) and with (right) alignment correction. Visual inspection clearly shows significant discrepancies in the uncorrected radiograph. The bottom left radiograph in Figure 5 shows the difference between the alignment-corrected and uncorrected radiographs. The overall left-right asymmetry of the black (negative difference) and white (positive difference) is a good indicator for the shift direction. Finally, the bottom right image shows the difference of the alignment-corrected radiograph from the truth. This last image shows that our alignment correction does a good job of reproducing regions of nearly homogeneous WEPL, but not so well near boundaries between very dissimilar material.

Fig. 6.

Radiographs from alignment correction. See text for details.

Table 2 illustrates timing performance of pRad on our development desktop computer with the following configuration: i7–8700K CPU with 6 cores (12 hyper-threaded cores); 64GB DDR4 RAM; Nvidia GeForce GTX 1080Ti with 11GB VRAM. Input data comprise simulated protons “fired” at the pediatric head phantom. About 3.5 million imaging protons were used in two sequential sets. The first fixed the primary proton beam energy at 119 MeV; the second at 161 MeV. Additionally, about 90 thousand alignment protons were used to calculate the appropriate alignment correction factors.

Table 2.

pRad Timing Performance^a

			Linear Solver, 20 Iterations
NumThreadsb	Init	PreProcess	Non-threaded	Threaded	LinSol	Total
1	1.141	4.713	0.938	14.945	16.052	22.271
2	1.145	4.684	1.060	7.970	9.074	15.267
3	1.139	4.712	1.221	5.184	6.701	12.917
4	1.143	4.686	1.448	3.886	5.599	11.791
5	1.144	4.686	1.705	3.092	4.996	11.189
6	1.142	4.703	1.986	2.503	4.683	10.892
7	1.140	4.694	2.440	3.380	5.284	11.482
8	1.147	4.701	2.913	2.820	5.093	11.305
9	1.137	4.691	3.500	2.125	4.971	11.161
10	1.138	4.691	3.851	1.646	4.917	11.110
11	1.138	4.693	4.281	1.317	4.969	11.162
12	1.138	4.702	4.582	1.139	5.100	11.303

^aTimes in seconds.

^bRuns with 1 to 6 threads done on real cores; runs 7 to 12 done on hyper-threaded cores.

The results in Table 2 are average times, in seconds, from twenty pRad reconstructions of the test data. Except for the first column, the times in Table 2 are in seconds. The “Init” column shows the time to initialize the GPU and read auxiliary data – such as calibration tables for WEPL calculation – needed for reconstruction. The “PreProcess” column shows the time to prepare the data into a format suitable for the linear solver. As discussed above, preprocessing includes: generating alignment correction factors, correlation, demodulation, WEPL calculation, statistical cuts, and MLP computation. The bulk of preprocessing time (about 85%) is spent in MLP computation, which is done on the GPU.

A hard stop at 20 iterations was set for the linear solver. In each linear solver iteration, pRad has code that implements the CARP algorithm by looping over all the proton histories. Because these proton histories are independent of each other, such code segments are suitable for parallelization. The “Threaded” column in Table 2 shows the total time in the linear solver that was parallelized using OpenMP threading. The “Non-threaded” column, on the other hand, shows the serial component in each iteration. The “LinSol” column shows the total time spent executing the linear solver. It includes the “Threaded” and “Non-threaded” times along with some additional overhead (e.g., loop processing and collecting/redistributing from/to the threads the interim results in each iteration).

Due to multiple Coulomb scattering, protons typically scatter by 4 mm after 20 cm of water. Our simulations demonstrate path reconstruction of individual protons to better than 1 mm. Our iterative algorithm successfully produces images with 1 mm sharpness. The iterative process necessarily increases pixel noise compared to simulations neglecting multiple scattering (Fig. 7) and additional protons will be needed to achieve a given contrast. A rough of thumb is that the increase in pixel variance is proportional to the average number of column boundaries crossed by a proton. This provides further motivation to use projective voxel geometry, which results in fewer boundary crossings compared to rectangular voxel geometry.

Fig. 7.

Effect of multiple scattering on pixel noise. Ordinate is the relative variance of pixel values from simulated images of uniform water blocks, with multiple scattering of protons included or not included in the simulation.

Discussion

The linear solver is the most resource-hungry stage in pRad that is not implemented in GPU. This is because the memory needed for MLP far exceeds the RAM available in our development computer. In fact, MLP computation in the pre-processing phase is done in stages, where in each stage only a small subset of the data is used such that the MLP memory used for that subset fits in the GPU. With the use of multiple GPUs, especially more recent models with larger amounts of memory, porting the linear solver to GPU might potentially reduce radiograph reconstruction time.

Table 2 also shows that pRad reconstruction speeds up with more threads (equivalently, CARP blocks). However, speed performance appears to level off when the number of thread-blocks is equal to the number of real cores in the CPU. Therefore, there is nothing to be gained by using hyper-threaded cores. In fact, the number of iterations needed to achieve convergence is seen to increase with the number of thread-blocks used. For the reconstructions used to generate the results of Table 1, convergence was achieved after about twenty-five iterations. This represents about a 25% additional time to the “LinSol” results for six thread-blocks in Table 2, which is about 1.2 additional seconds to the total execution time.

This study highlights the importance of the hull and MLP in radiograph reconstruction. For example, from Table 1, the straight-line radiograph, which uses neither hull nor MLP informationl, exhibits the worst performance in terms of accuracy relative to truth. On the other hand, Table 1 also shows that with MLP combined with hull information – whether from known auxiliary source, or approximated by some method – decent, accurate reconstructions can be achieved. However, it should be noted that the use of known hull may not be trivial. There may be several sources for the known hull, such as imaging data from a different modality (xCT, PET, MRI, SPECT, or pCT) for the same object or patient. The challenge is to spatially align the auxiliary 3D image with the pRad data, which are essentially 2D. This is an issue that needs to be explored further.

The WEPLbox and WEPLstick hull methods presented here also have severe limitations and may only be useful under very stringent conditions. For example, they work rather well with the head phantom in this study: the phantom is more or less left-right symmetric with respect to the radiograph plane at the isocenter. Erroneous MLP calculations will result once at least one of these conditions occur: the object is not symmetric; the mid-plane of the object is not at isocenter, such that one side is closer to one tracker than the other; non-spherical symmetric object is rotated about an axis perpendicular to the beam axis.

This study has also led to new insights into the proper use of MLP in our radiograph reconstruction. Our initial implementation carried over from pCT used an “effective mean chord length” for all the voxels touched by a proton. This chord length is statistically estimated based on the dimensions of each voxel, as well as the angle at which a parallel beam of protons enters that voxel. Thus, each proton has only one chord length associated with it. This chord length is then used as the non-zero matrix elements of the system matrix A discussed earlier. Penfold [20] has shown that in pCT, the use of mean effective chord length is almost as good as using exact chord lengths, albeit at the expense of some additional noise.

In pRad, however, our early use of mean effective chord length led to reconstructions that never came near the truth, underestimating the expected values. Better, almost perfect reconstructions, as shown by the results of this study, are achieved with semi-exact chord lengths as described below. The downside to using semi-exact chord lengths are twofold: MLP memory requirement is doubled because of the need to store as many chord lengths as there are touched voxels; and the additional time required for calculating chord lengths. The addition of MLP memory alone, and the need to move between computer host and GPU, results in about 20% penalty in MLP computation time.

In the current study, we used a segmented-stepping method to calculate the variable chord length in each touched voxel. The method does not involve calculation of intersections of line segments with sides of voxels. Rather, it relies on the following stepping strategy through the reconstruction volume. First, each step is exactly one pixel along the beam direction. Second, each step along the beam direction starts and end at the centers of two adjoining voxels. These conditions ensure that each step will always span at least two voxels. Thus, unlike the half-pixel step size used in pCT, there is no need to check whether the step ends in the same or different voxel. If the step spans exactly two voxels, then the chord length assigned to each voxel is incremented by half the distance between the two end points. If the line joining the two end points spans more than two voxels, this is where the semi-exact calculation is done. The line segment is divided into a number of smaller sub-segments. We used twenty segments for each one mm step in this study. Each sub-segment is then tested to which voxel it belongs; the chord length in that voxel is then incremented with the cumulative lengths of the sub-segments that were in that voxel. If a sub-segment spans across two voxels, the chord lengths of the two voxels are each incremented with half the length of the sub-segment. As the number of sub-segments increases, the chord length approximation improves, although at the expense of more computation time. For our radiograph application, the number of steps that span exactly two voxels is significantly larger than those that spans more than two. Thus, we expect the results from our semi-exact chord-length calculation will not differ significantly from exact chord-length calculation.

While we have evaluated pRad for a pediatric-sized phantom in this study, pRad also works for adult-sized phantoms and larger objects. Although more protons are lost in nuclear interactions and increased multiple scattering will gradually degrade spatial resolution, initial studies indicate the system provides similar WEPL accuracy in thicker objects [29]. Similar precision can be achieved by increasing the number of protons to compensate for the larger range straggling in thicker patients.

Conclusion

We have described algorithms and demonstrated, through computer simulations of pencil-beam scans of a pediatric head phantom using the newly built pRad detector and image reconstruction software, that high quality proton radiographs can be generated rapidly for patient alignment and verification of water equivalent thickness of the patient before each treatment. The platform is a fully automated pipeline of data acquisition, pre-processing for event selection, WEPL calibration, and final image reconstruction. This represents a milestone towards the development of a clinically practical proton imaging system.

With this software now complete, it is possible to acquire proton data and produce images from a variety of phantoms. We note that for the results presented here, no significant efforts were spent in optimizing the parameters used for the reconstructions. Analyses of real images such as that in Fig. 2 are in progress, as well as further studies on the optimization and performance characteristics of our system platform. This will result in end-to-end testing of the system for pre-clinical evaluation.