Abstract
The new Covid-19 pandemic has left traces of suffering and devastation to individuals of almost all countries worldwide and severe impact on the global economy. Understanding the clinical characteristics, interactions with the environment, and the variables that favor or hinder its dissemination help the public authorities in the fight and prevention, leading for a rapid response in society. Using models to estimate contamination scenarios in real time plays an important role. Population compartments models based on ordinary differential equations (ODE) for a given region assume two homogeneous premises, the contact mechanisms and diffusion rates, disregarding heterogeneous factors as different contact rates for each municipality and the flow of contaminated people among them. This work considers a hybrid model for covid-19, based on local SIR models and the population flow network among municipalities, responsible for a complex lag dynamic in their contagion curves. Based on actual infection data, local contact rates () are evaluated. The epidemic evolution at each municipality depends on the local SIR parameters and on the inter-municipality transport flow. When heterogeneity of values and flow network are included, forecasts differ from those of the homogeneous ODE model. This effect is more relevant when more municipalities are considered, hinting that the latter overestimates new cases. In addition, mitigation scenarios are assessed to evaluate the effect of earlier interventions reducing the inter-municipality flux. Restricting the flow between municipalities in the initial stage of the epidemic is fundamental for flattening the contamination curve, highlighting advantages of a contamination lag between the capital curve and those of other municipalities in the territories.
Keywords: Covid-19, Sars-Cov-2, SIR model, Transport network
Highlights
-
•
Local epidemic curves resulting in unexpected behaviors at larger scales.
-
•
The effect of Inter-cities flow flattens the infected curve.
-
•
Flow interventions should be strictly implemented to obtain relevant results.
1. Introduction
The SARS-CoV-2 coronavirus pandemic, also known as Covid-19 or 2019-nCoV, emerged in the city of Wuhan, capital of Hubei province, China, in late 2019, and spread to several Chinese cities as cases of pneumonia from unknown origin. Since that moment, clinical, social and geographic characteristics of the affected patients have been recorded, providing now a better understanding of the contamination mechanism as well as of the health impacts caused by the virus.
A huge number of individuals have become infected by the SARS-CoV-2 coronavirus world wide. On January 30 2020, the World Health Organization (WHO) stated that the SARS-CoV-2 outbreak constitutes a Public Health Emergency of International Importance — the highest level of alert in the Organization, according to the International Health Regulations. On March 11, 2020, the new SARS-CoV-2 viremia was characterized by WHO as a pandemic [1].
The creation of innovative solutions to combat this pandemic, inside and outside health agencies worldwide can minimize social and economic impacts [2], [3]. Predictive models, for example, that translate numbers into future trends of growth and decrease of epidemics, can generate scenarios that serve as a basis for prior decision-making by territorial management agencies. A crucial point in the study of an epidemic phenomenon is the complexity of the causal factors that can explain its magnitude.
The Susceptible–Infected–Recovered (SIR) model is widely used to describe the spread of epidemic infectious diseases, directly transmitted through contact from one person to another. It brings up the discussion of population density and infection rate, namely, whether a population is susceptible or not to an epidemic due to its density. According to [4] one of the most important problems in epidemiology is to verify if the epidemic ends only when there are no susceptible individuals, or if the interaction of the various factors of infectivity, recovery and mortality can cause its termination, while many susceptible individuals are still present in the unaffected population. This problem has its complexity increased when non homogeneous features are included.
An important assumption made in compartmental ODE models, such as SIR, is homogeneity. This homogeneity is expressed both in the possibility of contact between individuals, everyone interacts with equal probability with everyone else, and in the dynamics of contamination, the contact rates are the same for everyone. However, it is known that in very diverse regions, as in the case of Brazil, with diverse populations, cultures and political strategies to mitigate the epidemic, the diffusion mechanisms and the possibilities of contact are much more heterogeneous than can be assumed in these models. In systems like this, the evolution of the epidemic cannot be seen as a single time series of contagion showing a complex non local spread as studied by Araújo in 2018 for dengue [5], using metapopulation approach [6], [7], [8] and a hybrid model [9].
The heterogeneity of this system causes the epidemic to appear at different times within different municipalities and with different growth patterns. Municipalities that initiated their mitigation strategies in advance will have different growth rates compared to those that do not, causing differences in the density of infected populations among municipalities, generating a complex gradient of infection that can pressure the contamination of new municipalities using the network of people flow between them [10]. Models that take this mechanism into account would estimate more realistic scenarios, in addition to allowing the testing of mitigation protocols focused on this heterogeneity. In this work, we present a hybrid diffusion model of COVID-19 with the objective of evaluating these complex dynamic scenarios and its difference from conventional homogeneous models based on ODE.
2. Materials and methods
2.1. SIR model
Most epidemiological models currently found in the literature are based on the work of Kermack and McKendrick [4], known as the Susceptible–Infected–Recovered (SIR) model. The SIR model is appropriate in studies of infectious diseases that confer permanent immunity and consider individuals within the considered region according to their disease status over time. Susceptible individuals, denoted by S, refers to those who do not have the disease at time t, but can be infected through contact with an individual in the infected state, I. The recovered state, R, are those who have recovered from the disease or are dead and can no longer transmit the disease [4], [11].
The SIR model is described by the following ordinary differential equations:
| (1) |
| (2) |
| (3) |
where S represents the population susceptible to the disease, while I and R represent the infected and recovered population. and are rates that represent the dynamics of disease spread, the disease transmission rate and the recovery rate, respectively.
Eq. (1) describes the variation in the susceptible population S(t) at time t. Since the infected population I(t) will have contact with susceptible S(t) per unit of time, the number of susceptible people will decrease by S(t)I(t) individuals and S(t)I(t) susceptible individuals will become infected at time t, Eq. (2). At the same time t, as each infected individual will recover at a rate , a total of I(t) individuals will recover, as indicated in Eqs. (2), (3).
The simplest epidemics SIR model has a high flexibility for including generalizations and has been usually used as a first step in the study of several diseases. The evolution to more complex models is the natural course in the quest to understand important characteristics of the infection progression over time. These modifications generally include heterogeneities, subdivisions of S, I and R compartments, and recovery rates for population subgroups, or even in the definition of these parameters through the social interaction network of studied individuals [12], [13].
2.2. The hybrid model
In addition to the limitations already mentioned in the standard epidemiological model, the equations that describe the dynamics of the disease consider a structure of random pair wise interactions among individuals in the studied population. However, real populations often have specific structures under which these individuals interact. This structure composed of subgroups of individuals and their connections constitute a network where infectious diseases tend to spread [11].
The information regarding the contagion dynamics between municipalities presented in this work is the result of a hybrid model composed of an epidemiological mathematical model of SIR type, which estimates the disease dynamics for each municipality, and of a flow network among municipalities that estimates the spread of cases among them. Previous studies have shown the importance of the transport flow network in the spread of viruses like dengue [14].
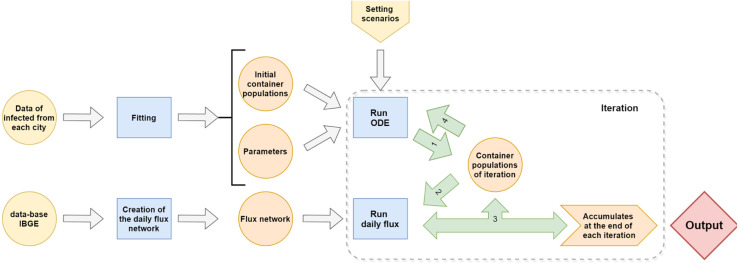
The hybrid model consists of joining two modeling techniques: a set of ordinary differential equations (ODE) and a network population diffusion model. At each time step, the model solves multiple ODE for the different municipalities within a state, considering as initial conditions the actual number of cases and recovered for each municipality. After that, the flow network is used to distribute populations of susceptible, infected and recovered among pairs of municipalities and a new population is estimated for the next step. An illustration of the algorithm is presented in Fig. 1.
Fig. 1.
A schematic view of the model algorithm. The container population block represents a set of susceptible, infected and recovered populations for each municipality.
When we include inter-municipal flow interference, Eqs. (1), (2) and (3) can be rewritten respectively by (4), (5) and (6), where compartment variations due to internal contagion, described by EDO, also depend on the variation caused by the flow of individuals.
| (4) |
| (5) |
| (6) |
where and represent the containers of the SIR model for each municipality , is the transmission rate adjusted for municipality is the set of municipalities neighboring municipality , and are the flux of susceptible and infected population from municipality j to i. In this way, the sum represents the total number of individuals in each container that is due to the flow network.
In order to illustrate the effects of heterogeneity in multiple scales we used data from Brazil, a country full of heterogeneity, with 8.516.000 km2 and multiple mitigation policies for different geographical scales. Fig. 2 shows the average weekly flow of people in Brazil, corresponding to the full set of road, air, and water transport networks were considered throughout the territory in 2016 [15].
Fig. 2.
The full set of road, waterway and air transport network in Brazil.
IBGE [15].
The values of the contact rates for each municipality () were estimated by adjusting the curves of accumulated cases of infected people in the SIR model (using Eqs. (1), (2) and (3)) to the reported data of accumulated cases for each municipality i, state s, and for the whole country, which are respectively indicated by , and . We used the gradient method to minimize the standardized error between the model and the point-to-point data. In order to find the global minimum, we start the optimization algorithm several times at different points in the parameter space and consider the result that generates the smallest standardized error. If the municipality has less than 10 days from the start of the first case and the total number of accumulated cases does not exceed 75, we use the value of the state in which the municipality is located and, if the state does not match these same criteria, we use the country value for Brazil, i.e., . The values of are computed by the sum of all cases from each municipality within the state and the value of is computed by adding the cases of all municipalities in the country. The value of used for all municipalities was 1/6 [16]. We use the municipalities as the smallest unit in the model, as they are the smallest subdivision in which case notifications were released and in which IBGE’s displacement flows are reported. The source codes for the parameter setting can be found at [17] and for the hybrid model at [18].
3. Results
Simulations were made by adjusting the cumulative case curves from the occurrence of the first case in each municipality (in Brazil, on February 24, 2020) for different periods that will be described throughout the results. The initial conditions used in the hybrid model were the number of active cases, recovered and susceptible individuals in each municipality on the last day reported in the data set and the respective contact rates i.
3.1. Comparing the hybrid model with the pure ODE model
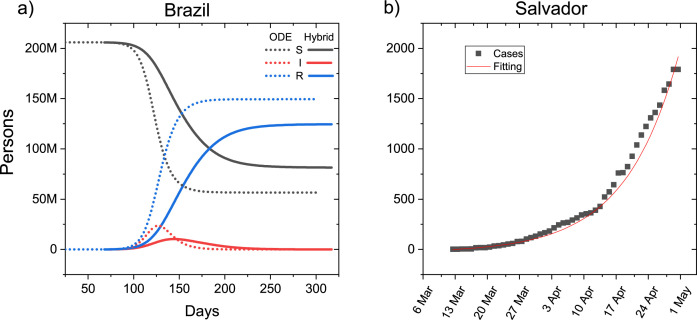
The results presented in Fig. 3(a) show the time series of the SIR compartments for Brazil resulting from the ODE and hybrid model. We notice that the hybrid model has a delay in saturation and a significant decrease in the active cases peak, showing that the heterogeneity factor acts as a mitigating mechanism in the spread of the epidemic. In Fig. 3(b) we see a comparison between the adjusted curve and the real data for the city of Salvador, explicitly a good agreement between the adjusted and the real data.
Fig. 3.
(a) Comparison of time series of susceptible (S), infected (I) and recovered (R) populations for ODE and hybrid model. (b) Fitting overlaid with real-world observations for the city of Salvador. These results were generated based on available data until May 1, 2020.
To better understand how the increase in heterogeneity affects the results, we compare the models for different territorial scales. As we increase the scales, more municipalities are included, enhancing the effect of heterogeneity in the results.
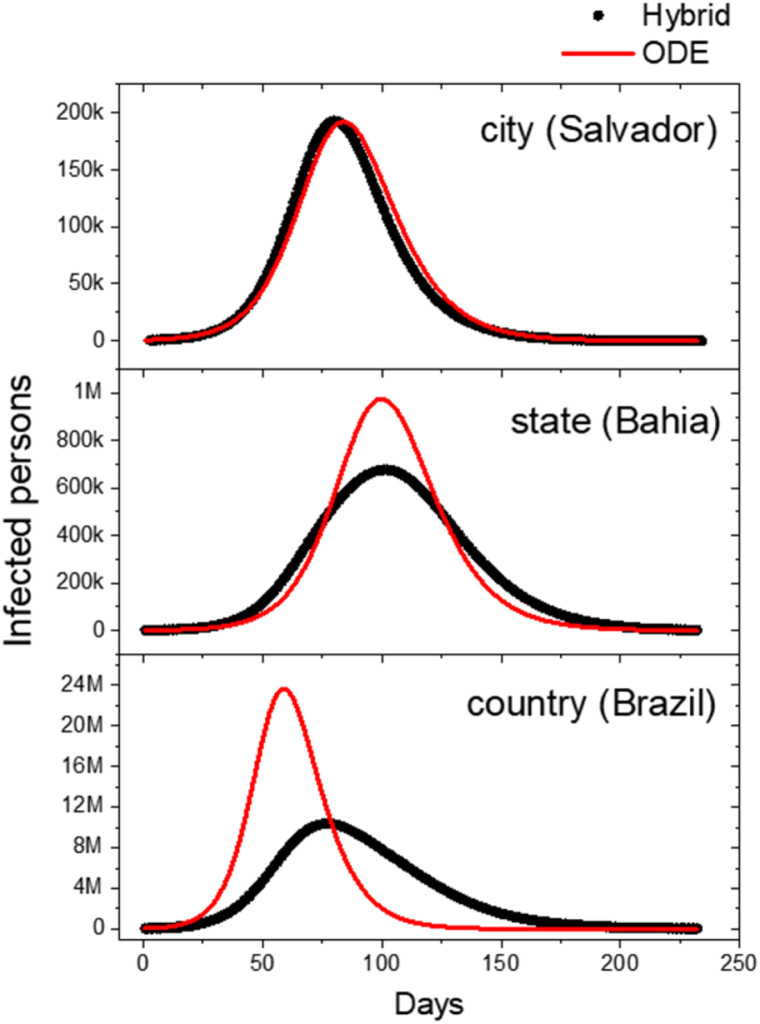
Fig. 4 shows the curves of active cases for three territorial scales: municipality scale (we consider the city of Salvador), state scale (Bahia) and country scale (Brazil). The number of municipalities in the state of Bahia and Brazil are, respectively, 417 and 5565. Note that the hybrid model departs from the ODE model as more municipalities are included, increasing the heterogeneity of the system. It can also be seen that the peak of cases decreases. This difference can be explained by the assumption that, in the ODE model, everyone interacts with everyone, while in the hybrid model the interaction is mostly restricted to each municipality. Moreover, there is a delay in the contact between the infected from one municipality with those susceptible living in other places, making the effective contact rate lower. Also, in the municipality scale for Salvador, the hybrid model has a slight earlier peak, due the importation of cases from earlier infected and larger municipalities as São Paulo and Rio de Janeiro.
Fig. 4.
Comparison of the active case curves for the ODEs and hybrid model in three territory scales: municipality scale (Salvador); state scale (Bahia) and country scale (Brazil). These results were generated based on available data until May 1, 2020.
3.2. Effect of flow network topology
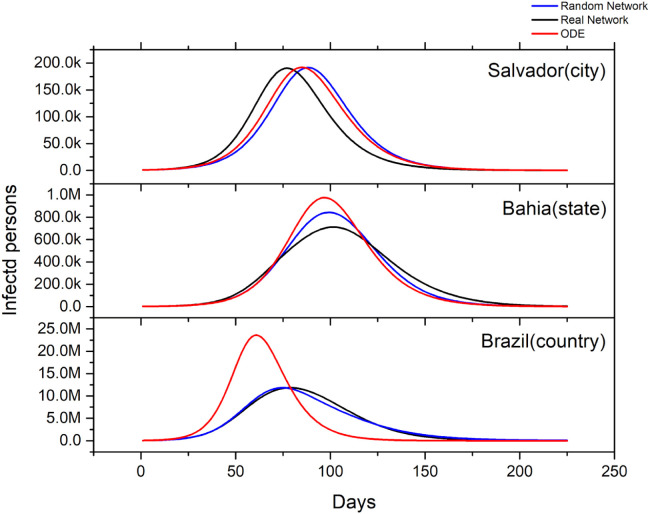
We evaluated the effect of the network topology by comparing the model results using the observed network with a random network with the same number of edges and nodes and the same weight distribution. Fig. 5 shows that randomizing the network, the infected curve presents a different behavior for each territorial scale. At the city level, the infected curve is affected similarly to Fig. 4, that is, the randomization process only seems to modify the initial configuration of the infected cities that influence the growth rate of the curve in the city of Salvador, thus changing the date of the peak. In the state curve, the results are close to those presented in the simple ODE model, that is, the randomized network that represents an intermediate topology between a completely uniform structure, assumed in the ODE model, and the real flow network of the hybrid model . On the country scale, the results of the randomized network show a significant flattening in the infected curve similar to that observed in the real flow network curve. This indicates that, on this scale, the effect on the number of cases in the real network is mainly due to the municipalities with few connections, since in the rearrangement of the edges for the random network, the municipalities that correspond to network hubs suffer most changes.
Fig. 5.
Effect of the network topology on the model results, considering the effect of the network with random topology and with the observed topology. Case curve for three scales of political separation: city scale (Salvador); state scale (Bahia) and country scale (Brazil). These results were generated based on available data until May 1, 2020.
3.3. Effect of reducing the inter municipalities flux
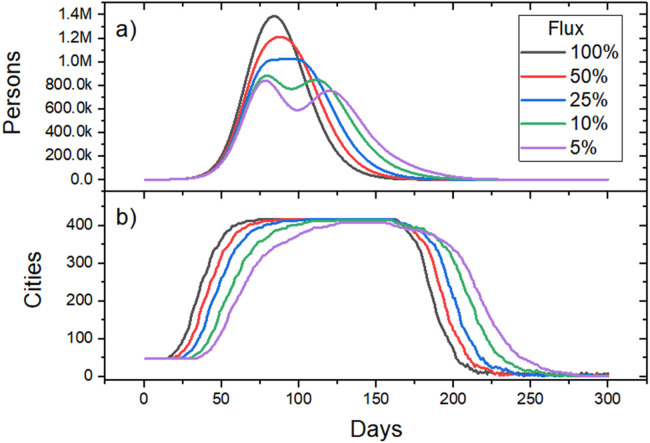
The hybrid model allows for the investigation of a wide range of scenarios. In addition to the parameters inherent to the SIR model, we can create different scenarios related to the flow patterns between the municipalities. Indeed, several decisions about mitigation strategies in the spread of epidemics in Brazil are taken at the state scale. Thus, we evaluated the effect of reducing the inter-municipal flow in the state of Bahia, as illustrated in Fig. 6. There we show the infection curves of people and municipalities for 5 inter-municipal flow scenarios.
Fig. 6.
Evaluation of the effect of reducing inter-municipal flow in the state of Bahia: (a) Effect on the curve of active cases. (b) Effect on the time series of number of municipalities with cases> 1. These results were generated based on available data until Apr 5, 2020.
The results presented in Fig. 6(a) indicate the occurrence of the flattening effect of the active case curve as the inter-municipal flow is reduced. Decreasing the flow between the municipalities causes a de-synchronization between the most populous cities, which are the first to become infected, and the other municipalities. This can even lead to a curve with two peaks, reducing the maximum number of active infected and delaying the contamination of new municipalities.
In spite of presenting a significant reduction in the number of cases, the generalized reduction in the flow of people among all pairs of municipalities can represent a high social and economic cost. However, we know that there are great differences in population size and connectivity degree of the municipalities, so that they are expected to act with greater or lesser impact in mitigating the problem. This naturally leads to investigating the effect of applying a drastic reduction in the flow of people to the most populous municipalities, which we call a flux blockage.
3.4. The flux blockage effect
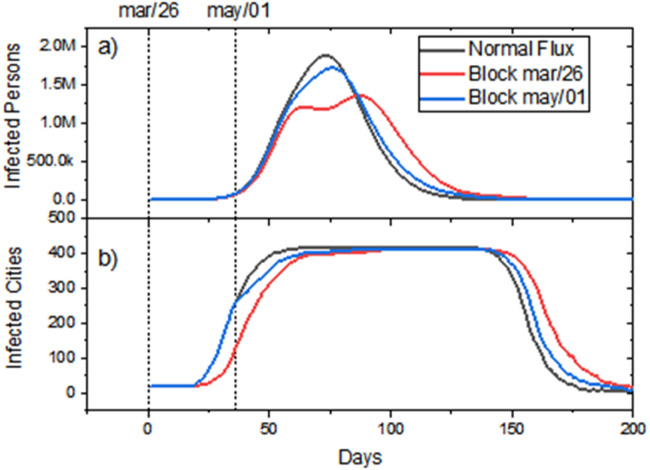
In this sub-section, we evaluated the effect of the 95% reduction in the inter-municipal flows directed to the 10% of the most populous municipalities in Bahia, maintaining the flow between the other municipalities without restrictions. We evaluated the effect of applying this strategy in the initial and advanced stages of the epidemic, corresponding to 20 days (26/Mar) and 56 days (01/May), respectively, after the first occurrence. In this analysis, we used the same contact rate values i (based on data available until Mar 26, 2020) for both scenarios, since the objective was to assess only the effect of the intervention time and not the evolution of the rates of contact that occurred due to the mitigation policies in each municipality.
In Fig. 7(a), the case curves with and without flux lockdown intervention scenarios are compared. In the initial stage (Block mar/26), we can notice a reduction of 29% of the peak in cases curve in addition to the occurrence of a second peak. When applying the same strategy at an advanced stage (56 days after, Block may/01), the second peak disappears and there is a reduction of only 9%. This effect occurs since, in the late scenario, many municipalities have already been infected and the envisaged de-synchronization between more and less populous municipalities no-longer exists, as we can see in the graphs of Fig. 7(b).
Fig. 7.
Comparison of the model projections in three scenarios: unrestricted inter-municipal flux, blockade in the initial stage of contamination (mar/26), and in an advanced stage (may/01) for (a) active cases curve and (b) number of municipalities with more than one case. Inter-municipal blocks correspond to a 95% reduction in inter-municipal flow in the 41 most populous municipalities in Bahia state. These results were generated based on available data until Mar 26, 2020.
4. Discussion
4.1. ODE x hybrid model
Our results show that the SIR hybrid model leads to important variations in the pandemic behavior predictions when compared with the SIR ODE model. This is due to three important characteristics incorporated in the model: the spatial heterogeneity for the infected populations, the different local contact rates and the network of people flow. In conventional ODE models there is no spatialization of data, that is, the population of all municipalities is treated as a single homogeneous set. In addition, the different cultural, economic, and political elements of the municipalities establish different internal mechanisms for the epidemic growth, represented by their different rates of transmission. This initially promotes a reduction in the cases growth with the spread of the infected population throughout the network.
As seen in Fig. 4, Fig. 5, the dynamics of the people flow network promotes evidence of flattening the cases curve. Considering that the smallest scale of analysis is the municipality, it was possible to verify that the hybrid model has the peak of the infected curve very similar to the ODE model with a slight advance. On the state and national scale, where heterogeneity is increasingly enhanced, there was a significant difference between the hybrid model and the ODE in terms of flattening the curve. The heterogeneity in the hybrid model acts as a temporal limiter of the interaction between the municipality populations, causing the epidemic peaks to occur in a chain, generating a pattern resulting from the unsynchronized sum of the local curves leading to the flattening of the infected curve at larger scales.
4.2. Flux blockage intervention
One of the measures adopted by official bodies worldwide was to reduce the flow of people circulating during the pandemic. Studies show that the lockdown [19] and the reduction in the flow of people have significant effects on decision making by government officials. Queiroz et al. [20] showed a significant reduction in human mobility through the monitoring of cell phones and the flow of people at the airport in the city of São Paulo (Brazil) between the months of February and March. Through our model it was possible to observe the effects of the level of flow reduction on the behavior of the curve of infected people and municipalities. The normal flow of people makes the virus spread through the municipalities more easily, causing a greater synchrony in the peaks of the different cities, causing a great peak in the epidemic curve of the states and country (which corresponds to the sum of the curve of their municipalities). Flow reduction reduces the number of infected people and promotes the double peak effect that corresponds to epidemiological peaks at different times.
The work of Chinazzi et al. [10] , assessed the effect of flow restrictions in Wuhan, China, as of January 23, 2020. Significant changes in the spread of the disease were observed only for a 90% reduction in the flow intercity flow together with a 50% increase in local social distance. In agreement with this work, our results also showed a significant reduction in the infected curve for a flow reduction greater than 90% under the same conditions of social distance. It was also observed that this result is achieved only when the restrictions occur in the first 30 days of the beginning of the epidemic. Our results showed that the anticipation of the date for reducing the flow has a great impact in the reduction of the number of infected people. Taking into account that we are analyzing a set of municipalities connected through transport network involving air, waterway and road traffic, the interruption or reduction of this flow generates a buffering effect and delays the spread of the disease. If the flow is maintained, the contamination propagules have already been disseminated and the internal dynamics of infection that will direct the pandemic’s progress has already set in. Saez et al. [21] identified a reduction in the rate of infection in Spain after different measures of physical distance, including travel flow. With the advance of the outbreak, local interventions such as lockdown, hygiene, curfew, mass examinations of the population are more efficient. Therefore, it is important to monitor human mobility to detect whether social distance policies are being implemented and adjust them in places where the population is not adhering to them.
According to our results and considering that a large proportion of coronavirus infections do not present severe symptoms or even no symptoms, blockages and reduced flow should be strictly implemented in order to obtain relevant results. This could provide a convincing explanation for the difficulty of containing the disease in countries that have implemented flexible restrictions, such as Brazil and the USA, and for the success of countries with strict flow rules, such as China and New Zealand.
When we look at the number of infected cities per day, our results are close to those found by Pujari and Shekatkar [9] for India. In this study, applying a hybrid model with time delays incorporated in its flow network, it was found that most Indian cities were infected in the first 100 days of the beginning of the epidemic. As seen in Figs. 6(b) and 7(b), in most evaluated scenarios, practically all cities in the state are already infected on the 100th day of the disease. From the management point of view, this behavior is quite interesting, first because it shows the efficiency of the intervention in controlling the pandemic and second because it allows managers to take measures that can restructure the health care system since the number of infected people is divided in two critical periods.
5. Conclusions
The application of mathematical models to describe the dynamics of infectious diseases plays an important role in policy decision-making in the field of Health Sciences. Typical mathematical models, through non-linear systems of ordinary differential equations, aim to predict and provide a guide for disease prevention and control. However, most of the outputs of these models compromise the policy making process. This is due to the fact that these methods may not properly take into account the population heterogeneity, here reflected on the spatial variability of the susceptible population.
In this work we present an innovative way to analyze data and parameterize the SIR model accommodating spatial heterogeneity to improve accuracy and prediction. Based on a hybrid model, we illustrate how the chain of epidemic peaks occur in the region, generating an unsynchronized sum of local curves and resulting in a flattening of the infected curve at larger scales. Our results demonstrated that reducing the population flow between cities affects both the number of cases and the spread of the disease through the municipalities. Moreover, the results emphasize the importance of measures of lockdown applied in advance on more dense cities, rather than on zones with a high number of cases.
CRediT authorship contribution statement
José Garcia Vivas Miranda: Conceptualization, Methodology, Software, Writing - original draft. Mateus Souza Silva: Methodology, Software. José Gabriel Bertolino: Methodology, Software. Rodrigo Nogueira Vasconcelos: Writing - review & editing, Data curation. Elaine Cristina Barbosa Cambui: Writing - review & editing, Data curation. Marcio Luis Valença Araújo: Data curation, Writing - original draft. Hugo Saba: Data curation, Writing - original draft. Diego Pereira Costa: Software. Soltan Galano Duverger: Software. Matheus Teles de Oliveira: Software. Hildebrando Simões de Araújo Neto: Resources. Washington de Jesus Sant’anna Franca-Rocha: Writing - review & editing. Daniel Cardoso Pereira Jorge: Methodology, Software. Juliane Fonseca de Oliveira: Formal analysis, Validation, Writing - review & editing. Roberto Fernandes Silva Andrade: Formal analysis, Validation, Writing - review & editing. Rafael Silva do Rosário: Supervision, Writing - review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work received financial support from the National Council of Technological and Scientific Development, CNPq, Brazil (grant numbers 310133/2016-5, 307828/2018-2, 431990/2018-2 and 313423/2019-9, 422561/2018-5 and 304257/2019-2). RFSA acknowledges the support of the National Institute of Science and Technology for Complex Systems (INCT-SC Brazil) . The authors also acknowledge the helpful suggestions from members of the CoVida Network (https://redecovida.org/), in special from contributors of the Rede CoVida Modelling Task-force: Alan A. S. Amad, Aureliano S. S. Paiva, Caio P. Castro, Gabriela L. Borges, Felipe A. C. Pereira, Gervásio F. Santos, Luciana L. Cardim, Maira L. Souza, Maria Yury Ichihara, Matheus F. Torquato, Maurício L. Barreto, Moreno S. Rodrigues, Nívea B. Silva, Pablo I. P. Ramos, Rafael V. Veiga, Rosemeire L. Fiaconne, and Suani T. R. Pinho.
Communicated by V.M. Perez-Garcia
References
- 1.WHO - World Health Organization, Coronavirus Disease 2019 (COVID-19) Situation Report 70, (n.d.). https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200409-sitrep-80-covid-19.pdf?sfvrsn=1b685d64_2.
- 2.Ferguson N.M., Laydon D., Nedjati-Gilani G., Imai N., Ainslie K., Baguelin M., Bhatia S., Boonyasiri A., Cucunubá Z., Cuomo-Dannenburg G., Dighe A., Dorigatti I., Fu H., Gaythorpe K., Green W., Hamlet A., Hinsley W., Okell L.C., van Elsland S., Thompson H., Verity R., Volz E., Wang H., Wang Y., Walker P.G.T., Walters C., Winskill P., Whittaker C., Donnelly C.A., Riley S., Ghani A.C. 2020. Report 9: Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand, imperial college COVID-19 response team. [DOI] [Google Scholar]
- 3.Fauci A.S., Lane H.C., Redfield R.R. Covid-19 - Navigating the uncharted. New England J. Med. 2020;382 doi: 10.1056/NEJMe2002387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kermack A.G., William. Ogilvy. McKendrick H.C. A contribution to the mathematical theory of epidemics. Containing Papers of a Mathematical and Physical CharacterProc. R. Soc. Lond. Ser. A. 1927;115 doi: 10.1098/rspa.1927.0118. [DOI] [Google Scholar]
- 5.Araújo M.L.V., Miranda J.G.V., Sampaio R., Moret M.A., Rosário R.S., Saba H. Nonlocal dispersal of dengue in the state of Bahia. Sci. Total Environ. 2018;631–632 doi: 10.1016/j.scitotenv.2018.02.198. [DOI] [PubMed] [Google Scholar]
- 6.Banos A., Corson N., Gaudou B., Laperrière V., Coyrehourcq S. The importance of being hybrid for spatial epidemic models:A multi-scale approach. Systems. 2015;3 doi: 10.3390/systems3040309. [DOI] [Google Scholar]
- 7.Arino J., van den Driessche P. A multi-city epidemic model. Math. Popul. Stud. 2003;10 doi: 10.1080/08898480306720. [DOI] [Google Scholar]
- 8.Pei S., Kandula S., Yang W., Shaman J. Forecasting the spatial transmission of influenza in the United States. Proc. Natl. Acad. Sci. 2018;115(11):2752–2757. doi: 10.1073/pnas.1708856115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pujari B.S., Shekatkar S.M. 2020. Multi-city modeling of epidemics using spatial networks: Application to 2019-nCov (COVID-19) coronavirus in India. [DOI] [Google Scholar]
- 10.Chinazzi M., Davis J.T., Ajelli M., Gioannini C., Litvinova M., Merler S., Pastore y Piontti A., Mu K., Rossi L., Sun K., Viboud C., Xiong X., Yu H., Elizabeth Halloran M., Longini I.M., Vespignani A. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science. 2020;368 doi: 10.1126/science.aba9757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Keeling M.J., Eames K.T.D. Networks and epidemic models. J. R. Soc. Interface. 2005;2 doi: 10.1098/rsif.2005.0051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Anderson R.M. The epidemiology of HIV infection: Variable incubation plus infectious periods and heterogeneity in sexual activity. J. R. Statist. Soc. Ser. A (Statistics in Society) 1988;151 doi: 10.2307/2982185. [DOI] [Google Scholar]
- 13.Keeling M.J., Rohani P. 2011. Modeling infectious diseases in humans and animals. [DOI] [Google Scholar]
- 14.Saba H., Moret M.A., Barreto F.R., Araújo M.L.V., Jorge E.M.F., Nascimento Filho A.S., Miranda J.G.V. Relevance of transportation to correlations among criticality, physical means of propagation, and distribution of dengue fever cases in the state of Bahia. Sci. Total Environ. 2018;618 doi: 10.1016/j.scitotenv.2017.09.047. [DOI] [PubMed] [Google Scholar]
- 15.IBGE, Instituto Brasileiro de Geografia e Estatística . 2017. Redes e fluxos do território: ligações rodoviárias e hidroviárias, 2016. (2017). https://www.ibge.gov.br/apps/ligacoes_rodoviarias/ [Google Scholar]
- 16.Weitz J.S., Beckett S.J., Coenen A.R., Demory D., Dominguez-Mirazo M., Dushoff J., Leung C.Y., Li G., Măgălie A., Park S.W., Rodriguez-Gonzalez R., Shivam S., Zhao C.Y. Modeling shield immunity to reduce COVID-19 epidemic spread. Nature Med. 2020;26 doi: 10.1038/s41591-020-0895-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.C. J.G. Bertolino de, D.C.P. Jorge, GEOCOVID/SIR-input-scripts: Paper release (Version v1.2), Zenodo. 10.5281/zenodo.4101703. [DOI]
- 18.Silva M.S., Miranda J.G.V. 2020. GEOCOVID/SIR-hybrid-model: paper release (version v1.0), Zenodo. [DOI] [Google Scholar]
- 19.Giordano G., Blanchini F., Bruno R., Colaneri P., Di Filippo A., Di Matteo A., Colaneri M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nature Med. 2020;26 doi: 10.1038/s41591-020-0883-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Queiroz L., Melo J.L., Ferraz A., Barboza G., Urbanski A.H., Gonçalves S.O., Nakaya H. 2020. Large-scale assessment of human mobility during COVID-19 outbreak, OSFPREPRINTS. [DOI] [Google Scholar]
- 21.Saez M., Tobias A., Varga D., Barceló M.A. Effectiveness of the measures to flatten the epidemic curve of COVID-19. The case of Spain. Sci. Total Environ. 2018 doi: 10.1016/j.scitotenv.2020.138761. [DOI] [PMC free article] [PubMed] [Google Scholar]