Abstract
Statistical methods are essential in medical research. They are used for data analysis and drawing appropriate conclusions. Clarity and accuracy of statistical reporting in medical journals can enhance readers’ understanding of the research conducted and the results obtained. In this manuscript, we provide guidelines for statistical reporting in medical journals for authors to consider, with a focus on the Journal of Thoracic Oncology.
Keywords: statistical results, reporting, presenting, p-value, medical journals
INTRODUCTION
High quality reporting of statistical methods and results is essential for reviewers and readers to evaluate the quality and the credibility of evidence presented in a manuscript. To help authors adhere to best practices, many journals [1–4] now provide detailed guidelines. Specific guidelines are also available, such as CONSORT statement [5] for randomized clinical trials, the STROBE statement [6] for observational studies, the STARD initiative [7] for diagnostic accuracy studies, and PRISMA statement for meta-analyses [8] (see the EQUATOR Network [9] for a comprehensive listing of study type-specific reporting guidelines). These guidelines aim to improve the clarity of presented methods and results and standardize statistical reporting to enhance comparability with similar research. Herein, we present guidelines for authors to consider when drafting manuscripts for the Journal of Thoracic Oncology (JTO).
GUIDELINES ON STATISTICAL REPORTING
In the Methods Section
The principle of writing methods section is that it should “Describe statistical methods with enough detail to enable a knowledgeable reader with access to the original data to judge its appropriateness for the study and to verify the reported results” (www.icmje.org) [10].
To achieve this goal, the statistical design of the study should be described, including objectives of the study and patient population/selection. Clinical trial design parameters, such as type I error (including choice of a one-sided or two-sided test), study power, primary endpoint effect size, and assumed accrual rate, are needed for readers to judge the validity of the sample size and/or the number of events required. Additional details on randomization scheme, planned interim analyses, primary endpoint and analysis method/populations are also necessary. For an observational study, one should mention whether the study is designed for hypothesis testing or hypothesis generating. Good practice dictates that the statistical analysis plan should be determined prior to conducting the analysis. This plan should include the level of significance that will be used in the study, meaning the threshold below which a p-value would indicate statistical significance. In addition, the plan should specify whether there will be p-value adjustment for multiple comparisons and the rationale for the decision.
Method(s) for handling missing data should also be specified. If data-driven variable selection was conducted, methods employed should be described and accompanied by sufficient details of the steps taken in the process (for example, variables initially used in the variable selection process, the threshold p-value in a step-wise selection or tuning parameter selection in a machine learning method). For Bayesian analyses or more complex statistical analyses, sufficient details should be provided in an appendix so interested readers can fully understand the methods used for the study.
Lastly, the analysis software and version should be included since they may use different optimization and numerical routines which produce slightly different results. For a clinical trial, clinical trial number should be listed accompanied by the trial protocol if required by the journal.
In the Results Section
Patient characteristic table
The first table in the results section summarizes the baseline characteristics of the study population. If there is only one group of patients in the study, this table only has a single column of summarized data. However, if the main objective is to compare across identified groups, each group should have its own column. Baseline variables measured on each patient are listed as rows. This table should include all key baseline variables that define the study population in terms of demographics, co-morbidities and history, and disease characteristics; along with prognostic variables associated with the primary outcome. Continuous variables should be summarized with mean and standard deviation. If the distribution of a value is skewed, it is recommended that the median and range (minimum and maximum values) or the interquartile range (lower quartile and upper quartile values) should be included. Categorical values should be reported as the count and percentages for each level of the variable. If there are missing observations, the number of patients with missing data should be recorded for both continuous and categorical variables. When the number of missing values are negligible, then the percentage of missing category do not need to be calculated and the denominator for percentage calculations should not include missing values.
If patients were randomized to the groups being compared, p-value should not be included in the patient characteristics table for the comparison across groups since any differences observed between the groups is random. However, if the study is an observational study, a p-value comparing the value of a specific variable across the groups (using an appropriate statistical test) should be included for each variable in the table. For data that are for a subset of randomized patients, such as quality-of-life or biomarker sub-studies that contain only patients who consented to the sub-study, the randomization no longer holds and it cannot be assumed that differences between the groups is due to chance. If the subset contains less than 90% of the originally randomized patients, it is recommended that p-values be provided in the patient characteristic table.
P-value
The p-value is the probability of obtaining a result at least as extreme as what was observed when the null hypothesis is true.[11] A small p-value usually means that the difference found in a study is unlikely due to chance alone.[12] When results are reported, the magnitude of the difference between groups should be reported along with the p-value. Differences between groups should be estimated with a point estimate (e.g. absolute differences in means or proportions, odds ratios, or hazard ratios, whichever is most appropriate for the outcomes) and confidence interval. The precise p-value should be reported rather than stating that it is less than the level of significance or that it is insignificant. Generally, it is acceptable to report p-values to two decimal places (round to the nearest hundredth) when greater than 0.01; three decimal places (round to the nearest thousandth) when less than 0.01. If a p-value is quite small, then it is acceptable to report it as p-value < 0.001. P-values arising from genome-wide association studies or other high dimensional data analyses should follow guidelines specific for those methods.[13] Two-sided p-values should be reported except when study designs explicitly assume a one-sided p-value. Recently the American Statistical Association [14] and other groups of the scientific community called for less emphasis on p-values. As a result, we recommend reporting p-values only when proper type I error controls are in place and strongly discourage p-values for secondary and subgroup analyses where point estimates and confidence intervals are preferred. Finally, if there is a pre-specified level of significance, a result is either statistically significant or not. The word “trend” should only be used in a statistical test for trends in the data and not to describe a p-value that is close to the pre-specified level of significance.
Reporting of categorical outcomes
Categorical outcomes such as response to treatment and occurrence of adverse events are common in clinical studies. Categorical outcomes are summarized by frequencies and percentages. Confidence intervals should be reported along with the point estimates. It is important to clearly state the denominator used for estimation. When the denominator is the same for all categorical outcomes being reported, it is sufficient to state the denominator once and clarify that it is used for all subsequent outcomes; otherwise, it is important to specify the denominator used in computing the estimate for each outcome. When reporting comparisons of categorical outcomes between groups of patients, specify the statistical test used, for example the Chi-square test, Fisher’s exact test, or the Z-test with/without a continuity correction. It is good practice to include the same number of decimal places for all percentages. We recommend reporting the percentage with 1 decimal place (e.g. 12.3%) when the denominator is larger than 200. [2]
Forest plots are a good way to present subgroup analysis
Forest plot is a common graphical method of showing treatment effects across all subgroups of interest at one glance.[15] It is meant as a visual aid rather than an inferential tool. An informative forest plot should include point estimates, confidence intervals and the sample sizes (including number of events when applicable) for each subgroup so the readers can judge the precision of the estimated effects. Including subgroup p-values in forest plots is strongly discouraged when trials are not powered to detect the treatment effect in subgroups. If hypothesis tests for specific subgroups are pre-specified, the trial design should be appropriately powered and should account for the number of hypothesis tests considered in the trial.
Another strongly discouraged practice is to include p-values for interaction tests in forest plots for subgroup analysis.[4] It is important to distinguish between subgroup analyses and interaction tests. An interaction test is a formal statistical test to evaluate whether the treatment effect is influenced by other patient characteristics (factor of interest). The test is conducted by a regression model that includes the treatment, the factor of interest and an interaction term between the two variables using the full patient set. This is in contrast with subgroup analysis where the treatment effect is evaluated separately for each subgroup of patients, one at a time, making it impossible to formally compare the treatment effects between subgroups of patients.
Survival analysis
Overall survival (OS) is a common outcome used in clinical studies to judge the effectiveness of a new treatment or the prognostic effect of a baseline factor. OS data consist of two components that need to be clearly defined. The first component is the time interval starting from the time of origin (the time from which OS is being measured) to the time of death or of the last follow-up. The second component is an indicator of whether the patient died or was alive at that last timepoint. OS data can be summarized in multiple ways. Kaplan-Meier curves[16] are the most common visual summary for survival data and Table 1 includes some suggestions to consider when plotting Kaplan-Meier curves with an example in Figure 1. Another quantity that is commonly reported with survival data is the median time that patients were followed in the study. The median follow-up time should be estimated using the Kaplan-Meier estimator with the event and censoring indicator reversed.[17] This method provides a more appropriate estimate of the median follow-up time than the crude median follow-up time of survivors. Additional guidelines on time-to-event analysis will be discussed in another manuscript in this special series.
Table 1.
Good practices to consider when plotting Kaplan-Meier curves.
| Domain | Recommendations |
|---|---|
| Horizontal axis | |
| ✓ The numbers of patients at risk at various time points should be included at the bottom of the plot along the horizontal axis (see ❸ in Figure 1). | |
| Summary statistics | |
| ✓ If there is interest in showing the survival probabilities at multiple time-points, this information can be included in a separate table to avoid overcrowding the plot (see ❻ in Figure 1). | |
| Others | |
| ✓ Be judicious with including p-values in the plot. If reporting results from a randomized trial comparing survival between treatment arms using the log-rank test, it is okay to include the log-rank p-value in the plot. If the survival comparison is based on other tests such as comparison of the survival probabilities at a fixed time point or a comparison based on the Cox model adjusting for other covariates, as often is the case with observational studies, clearly state the statistical test used to obtain the p-value or better yet do not include a p-value in the plot. If a p-value is included, denote whether it is one-sided or two-sided (see ❾ in Figure 1). |
Figure 1.
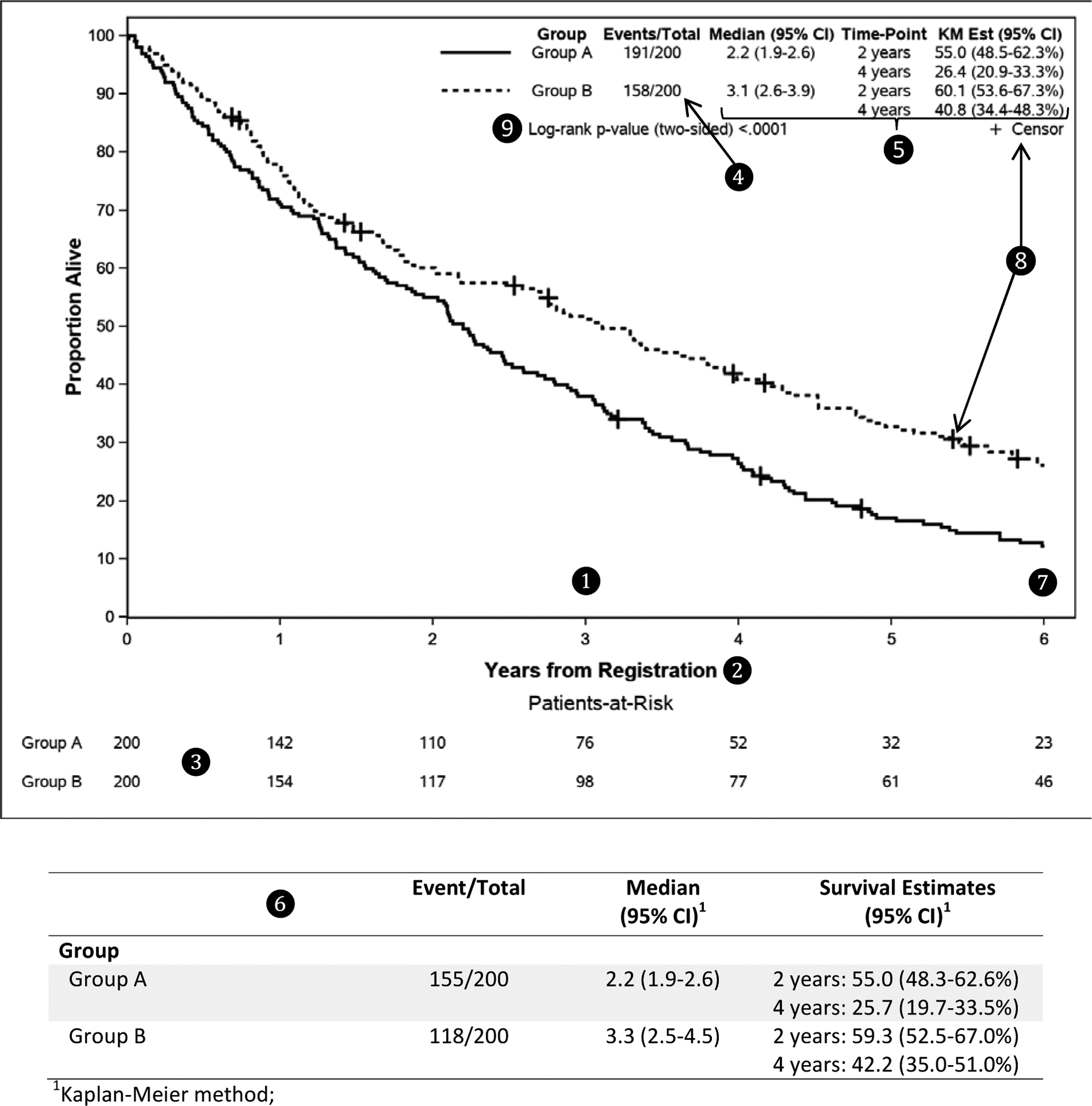
A Kaplan-Meier plot of overall survival for 2 groups of patients.
Refer to Table 1 for details about ❶ to❾.
A SAS macro is available to generate the Kaplan-Meier plot shown above (see https://communities.sas.com/t5/SAS-Communities-Library/Kaplan-Meier-Survival-Plotting-Macro-NEWSURV/ta-p/479747).
Prognostic and predictive biomarkers in oncology studies
In studies which evaluate treatment impact, goals may be to discover “prognostic” or “predictive” biomarkers. Prognostic biomarkers identify patients who have better outcomes regardless of treatment, whereas predictive biomarkers identify patients who benefit from a treatment (versus those who do not). Demonstrating there is a statistically significant association between the biomarker and outcome is sufficient to declare a biomarker as “prognostic”. On the other hand, to declare a biomarker as “predictive”, it must be shown that the biomarker status and treatment interaction term is statistically significant.[19, 20] Since the interaction between the biomarker status and treatment are required for modeling, a single-arm trial or a trial with biomarker selected patients are inappropriate for evaluation of predictive biomarkers.
In the Conclusion Section and the Interpretation of Statistical Results
P-value > 0.05 does not mean equivalence
Care must be taken to ensure that conclusions are supported by the results of the study. If a p-value is not statistically significant, it can only be concluded that no difference between the groups was observed. It cannot be concluded that the two groups are similar; this can only be concluded if the study were designed to evaluate equivalence. See the article on clinical versus statistical significance in this special series.[18]
Observational study: discuss potential bias and unmeasured confounder
Care is needed when making conclusions from observational studies. A single observational study is not sufficient to establish causation or to state that a variable impacts (influences) the outcome when the p-value for the association is statistically significant. The p-value only measures the likelihood that the differences are due to chance assuming that the groups are the same on all other factors. If there are imbalances between the groups due to biases and unmeasured confounders, this could impact the p-value; e.g. the p-value may be statistically significant because of differences between the groups that are associated with the potential confounders although the group itself is not associated with the outcome. Hence for observational study designs, an observed association or difference between groups that is statistically significant could reflect (1) a true difference/association, (2) underlying biases/unmeasured confounding, or (3) a combination of (1) and (2). The study conclusions need to properly reflect this.
CONCLUSION
In this manuscript, we provide guidelines for authors to consider when reporting statistical results in medical manuscripts. These guidelines are not exhaustive but they cover many common outcomes and statistical methods used in clinical studies. We strongly encourage authors who submit manuscripts to the JTO to use these guidelines to improve the clarity of their reported methods and results.
ACKNOWLEDGMENTS:
This work was partially supported by the National Institutes of Health Grant P30CA15083 (Mayo Comprehensive Cancer Center Grant) and U10CA180882 (Alliance for Clinical Trials in Oncology Statistics and Data Management Grant).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
CONFLICTS OF INTEREST: None
REFERENCES
- 1.Journal of Clinical Oncology. Statistical Guidelines. 2020/April/10 ]; Available from: https://ascopubs.org/jco/authors/manuscript-guidelines. [Google Scholar]
- 2.Annals of Internal Medicine. Information for Authors - General Statistical Guidance. 2020/April/10]; Available from: https://annals.org/aim/pages/author-information-statistics-only. [Google Scholar]
- 3.The Journal of the American Medical Association. Statistical Methods and Data Presentation. 2020/April/10]; Available from: https://jamanetwork.com/journals/jama/pages/instructions-for-authors#SecStatisticalMethodsandDataPresentation. [Google Scholar]
- 4.The New England Journal of Medicine. Statistical Reporting Guidelines. 2020/April/10]; Available from: https://www.nejm.org/author-center/new-manuscripts. [Google Scholar]
- 5.Schulz KF, et al. , CONSORT 2010 Statement: updated guidelines for reporting parallel group randomised trials. Trials, 2010. 11: p. 32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.von Elm E, et al. , The Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) statement: guidelines for reporting observational studies. Lancet, 2007. 370(9596): p. 1453–7. [DOI] [PubMed] [Google Scholar]
- 7.Cohen JF, et al. , STARD 2015 guidelines for reporting diagnostic accuracy studies: explanation and elaboration. BMJ Open, 2016. 6(11): p. e012799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Moher D, et al. , Preferred reporting items for systematic reviews and meta-analyses: the PRISMA statement. Ann Intern Med, 2009. 151(4): p. 264–9, W64. [DOI] [PubMed] [Google Scholar]
- 9.The EQUATOR Network. 2020/July/30]; Available from: https://www.equator-network.org/.
- 10.International Committee of Medical Journal Editors. Preparing a Manuscript for Submissio to a Medical Journal. 2020/April/10]; Available from: http://www.icmje.org/recommendations/browse/manuscript-preparation/preparing-for-submission.html.
- 11.Greenland S, et al. , Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations. Eur J Epidemiol, 2016. 31(4): p. 337–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.National Cancer Institute. Definition of p-value - NCI dictionary of cancer terms. 2020/April/15]; Available from: https://www.cancer.gov/publications/dictionaries/cancer-terms/def/p-value.
- 13.Fadista J, et al. , The (in)famous GWAS P-value threshold revisited and updated for low-frequency variants. Eur J Hum Genet, 2016. 24(8): p. 1202–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wasserstein RL and Lazar NA, The ASA Statement on p-Values: Context, Process, and Purpose. The American Statistician, 2016. 70(2): p. 129–133. [Google Scholar]
- 15.Cuzick J, Forest plots and the interpretation of subgroups. Lancet, 2005. 365(9467): p. 1308. [DOI] [PubMed] [Google Scholar]
- 16.Kaplan EL and Meier P, Nonparametric Estimation from Incomplete Observations. Journal of the American Statistical Association, 1958. 53(282): p. 457–481. [Google Scholar]
- 17.Schemper M and Smith TL, A note on quantifying follow-up in studies of failure time. Control Clin Trials, 1996. 17(4): p. 343–6. [DOI] [PubMed] [Google Scholar]
- 18.Dahlberg SE, et al. , Clinical Versus Statistical Significance in Studies of Thoracic Malignancies. J Thorac Oncol, 2020. [DOI] [PubMed] [Google Scholar]
- 19.Ballman KV, Biomarker: Predictive or Prognostic? Journal of Clinical Oncology, 2015. 33(33): p. 3968–3971. [DOI] [PubMed] [Google Scholar]
- 20.Renfro LA, et al. , Clinical trial designs incorporating predictive biomarkers. Cancer Treat Rev, 2016. 43: p. 74–82. [DOI] [PMC free article] [PubMed] [Google Scholar]


