Free Energy Landscape and Conformational Kinetics of Hoogsteen Base Pairing in DNA vs. RNA

Abstract

Genetic information is encoded in the DNA double helix, which, in its physiological milieu, is characterized by the iconical Watson-Crick nucleo-base pairing. Recent NMR relaxation experiments revealed the transient presence of an alternative, Hoogsteen (HG) base pairing pattern in naked DNA duplexes, and estimated its relative stability and lifetime. In contrast with DNA, such structures were not observed in RNA duplexes. Understanding HG base pairing is important because the underlying “breathing” motion between the two conformations can significantly modulate protein binding. However, a detailed mechanistic insight into the transition pathways and kinetics is still missing. We performed enhanced sampling simulation (with combined metadynamics and adaptive force-bias method) and Markov state modeling to obtain accurate free energy, kinetics, and the intermediates in the transition pathway between Watson-Crick and HG base pairs for both naked B-DNA and A-RNA duplexes. The Markov state model constructed from our unbiased MD simulation data revealed previously unknown complex extrahelical intermediates in the seemingly simple process of base flipping in B-DNA. Extending our calculation to A-RNA, for which HG base pairing is not observed experimentally, resulted in relatively unstable, single-hydrogen-bonded, distorted Hoogsteen-like bases. Unlike B-DNA, the transition pathway primarily involved base paired and intrahelical intermediates with transition timescales much longer than that of B-DNA. The seemingly obvious flip-over reaction coordinate (i.e., the glycosidic torsion angle) is unable to resolve the intermediates. Instead, a multidimensional picture involving backbone dihedral angles and distance between hydrogen bond donor and acceptor atoms is required to gain insight into the molecular mechanism.

Significance

Formation of unconventional Hoogsteen (HG) base pairing is an important problem in DNA biophysics because of the key role it has in facilitating the binding of DNA-repairing enzymes, proteins, and drugs to damaged DNA. X-ray crystallography and NMR relaxation experiments revealed the presence of HG base pair in naked DNA duplexes and protein-DNA complexes, but no HG base pair was observed in RNA. Molecular dynamics simulations could reproduce the experimental free energy cost of HG base pairing in DNA, but a detailed mechanistic insight was still missing. We performed enhanced sampling simulation and Markov state modeling to obtain accurate free energy, kinetics, and the intermediates in the transition pathway between the Watson-Crick and HG base pair for both B-DNA and A-RNA.

Introduction

The one-dimensional genetic information encoded in the sequence of DNA base pairs is intrinsically related to its three-dimensional structure described by the iconical Watson-Crick (WC) helix (1), with its specific hydrogen bonding pattern between purine and pyrimidine (A-T, C-G) complementary nucleobases.

Recently, a series of exciting NMR relaxation studies (2) on free DNA in solution have shown that the predominant WC base pairing pattern between A-T and G-C nucleotides is in dynamic equilibrium with a less common and transient (μs–ms lifetime) Hoogsteen (HG) form (3), in which the purine nucleotide in the base pair flips 180° around the glycosidic bond. The WC-to-HG base pair transition, a form of “DNA breathing” (4), hints to the existence of a “secondary genetic code” signaled by base pair flipping, apart from the primary encoding in the nucleotide sequence. Crystallographic experiments have reported the presence of Hoogsteen base pairs only in specific contexts, such as when DNA binds to proteins such as the p53 tumor suppressor protein (5) or integration host factor in Escherichia coli (6). Detailed biochemical studies showed that HG base pairing plays a key role in circumventing interference in DNA replication mechanism by DNA polymerase by avoiding the appearance of lesions (7,8). In the p53-binding DNA sequence, the HG conformation exposes negatively charged regions of nucleic acid to the positive arginine residue of the protein (5), leading to stability of the complex and playing a crucial role in DNA recognition (9,10). Examples of specific binding to DNA guided by HG base pairs extends beyond proteins and even includes small molecules and drugs, which in turn facilitate its recognition by proteins and enzymes (11,12). In a nutshell, HG base pairing therefore expands the structural and functional repertoire of duplex DNA beyond what can be achieved by Watson-Crick base pairing alone. For example, HG base pairs are recognized by DNA-repairing enzymes, resulting in selective binding in the damaged regions of DNA, rich in syn-anti configurations, over the anti-anti WC-rich normal DNA. Thus, apart from providing structural integrity to the damaged and deformed DNA, HG base pairs assist in the DNA repair mechanism (11).

Apart from multiple appearance of HG base pairing in damaged or distorted DNA (13, 14, 15), several studies have confirmed the presence of the HG conformation in undistorted DNA duplexes (16,17); the first x-ray crystallographic evidence of Hoogsteen base pairing in a simple stretch of DNA sequence composed exclusively of A-T base pairs was provided by Abrescia and co-workers (18). Early computational work by Gould and Kollman showed that HG base pairing between adenine and thymine nucleobases (i.e., without sugar-phosphate backbone) in vacuum was energetically more favorable (∼1 kcal/mol) than its WC counterpart (19), which was in agreement with the structure in crystalline environment (3). Subsequent ab-initio quantum chemistry calculations for gas-phase A-T base pairs have painted a more complex picture, showing that neither HG nor WC forms are the global minimum (20).

Furthermore, NMR studies have found that N-methylation of adenine favors syn HG base pairing over the anti WC form by preventing formation of a WC-specific hydrogen bond by inducing steric clash (15). NMR chemical shift perturbation, NOESY experiments, and constant pH MD simulation showed that the HG base pairing among G-C base pairs is ∼20 times less abundant than that in A-T base pairs, arguably because a protonation of cytosine is necessary for the transition to HG form (11,21). Experiments of bare DNA duplexes, such as the A-T-rich A6-DNA segment, have shown the presence of a Hoogsteen base pair in the A16-T9 position deduced from the carbon R_1ρ relaxation dispersion NMR signal (2). Similar experiments on DNA bound to base intercalating drugs, such as echinomycin and actinomycin, also showed formation of Hoogsteen base pairing (22).

Because RNA duplexes also involve WC-like base pairs, it was natural to look for the existence of Hoogsteen transitions there as well. However, HG base pairing was not observed in NMR relaxation experiments in a common A-form RNA hairpin with the same sequence as A6-DNA. In contrast to DNA, N-methylation of the RNA adenine base to induce HG base pair formation resulted in base pair melting and consequent dissociation of the RNA helical region (23). In this study, we perform a computational comparison of the free energy surface and transition paths of WC-to-HG transitions for both DNA and RNA, seeking to understand the relative stability of the HG state and the factors that modulate the dynamical equilibrium in DNA versus RNA.

The first report (2) of the NMR-measured WC-HG dynamical equilibrium also included our preliminary work on searching pathways of conformational transition using a biased molecular dynamics simulation. Further computational work from our group and others (12,22, 23, 24, 25) have since uncovered several pieces of information, including energetic details, transition pathways, and kinetics of the transition between WC and HG base pairs in naked A-T-rich DNA helical duplexes. The paths predicted in our initial study were also recently sampled by Vreede et al. (26), who have calculated the rate constants of back-and-forth transitions between WC and HG base pairs using transition path sampling (27).

Experimental estimates put the WC-HG transition in DNA on a timescale of 50–250 ms (2). Therefore, direct simulation of Hoogsteen base pair formation in explicit water for a biologically relevant system is still beyond the reach of present day computational power. In previous work, we showed that formation of the Hoogsteen base pair can be achieved in molecular dynamics simulation by applying an artificial biasing force on the the glycosidic torsion angle for free DNA (2,23) and echinomycin-bound DNA (22).

Enhanced sampling methods, such as umbrella sampling (28) and metadynamics, (29,30) can be utilized to obtain the free energy surface along slow coordinates. For example, Yang et al. have calculated the free energy landscape of DNA breathing motion for an A-T-rich duplex DNA segment from umbrella sampling (24) and multiple walker well-tempered metadynamics simulation (25). Even for a short DNA segment, it required 6 to 40 μs long enhanced sampling simulations to obtain a converged physically meaningful free energy surface.

Adaptive biasing force (ABF) (31) has recently become a good alternative to the traditional free energy sampling methods (32) for a wide range of biophysical problems, including membrane permeation (33), ion transport (34), ligand diffusion in protein (35), and binding free energy calculation (36).

Its recent variant uses metadynamics in conjunction with extended-system ABF (eABF) (37), named meta-eABF, to accelerate the sampling of the transition coordinate (38). By simultaneously depositing Gaussian bias and applying force against the potential gradient, this method has been shown to be capable of sampling configuration space and predicting reasonably accurate the free energy surface in orders of magnitude less simulation time (38). Meta-eABF sampling has been used lately to successfully model the dependence of the microenvironment on the transition between A-DNA and B-DNA (39).

We have used the meta-eABF method to calculate the potential mean force (PMF) for the WC-to-HG transition for the duplex of A6-DNA fragment and also for the A6-RNA hairpin, a synthetic construct with the same base sequence used by Zhou et al. in their experimental studies (23). Unlike A6-DNA (24,25), there is no report in the literature regarding the free energy profile of the WC-to-HG base pair transition in A6-RNA. Moreover, revisiting DNA HG base pairing with a fast-converging PMF calculation technique opens up the possibility of applying this technique in the future for a large-scale comparison of thermodynamics of HG base pairing in various protein- and drug-bound DNA complexes.

Still, in the conventional PMF calculation, the choice of reaction coordinate is relatively arbitrary because other collective variables might also contribute to the conformational transition. Apart from the torsion angles of DNA (2,24,25), H-bond donor-acceptor distances can also be considered as a viable reaction coordinate. The conformation of the thymine base is also not included in the current torsion-angle-based description. Markov state models (MSM) have shown promise in alleviating the reaction coordinate problem and found a wide range of applications, from protein conformational transitions (40,41) to ligand unbinding (42). Construction of an MSM does not require a predefined reaction coordinate, and they can include all the structural information of the molecule. Also, time-lagged independent component analysis (TICA) (43,44) can be used to construct combinations of coordinate features to capture the slowest motions of the system. Provided sufficient back and forth transition sampling between clusters, it can calculate mean first-passage times with reasonable accuracy (40). Therefore, we aimed to obtain the kinetics of HG base pairing from MSM as an added analysis. Moreover, MSM can elucidate various metastable states in between the WC and HG conformations, which modulate base pair flipping transitions. MSMs have recently been applied successfully to study the biophysical processes in nucleic acids ranging from base pair fraying (45) to large-scale conformational dynamics (46). We have constructed MSMs for both the DNA and the RNA system to identify the best collective variables to describe the process, construct a reaction-coordinate-free free energy profile, calculate the kinetics of the process, and dissect the pathways of transition by following the probability flux through various metastable states.

Methods

System preparation and equilibration

All input files were generated using the CHARMM-GUI web server (47,48) and VMD (49). All simulations were performed using the NAMD 2.12 package (50) on GPUs. The NMR structure of A6-DNA (PDB: 5UZF) (51) was used as the starting structure for the DNA. This is a 12-bp-long DNA fragment with six consecutive A-T base pairs. Experimental studies have observed the presence of Hoogsteen pairing in the A16-T9 base pair, which is one of the two G-Cs facing A-T base pairs in this DNA fragment (2). For A6-RNA, the initial structure was created using the make-na server (52). The A6-RNA is an A-form of RNA with the same sequence as A6-DNA, and at one end the two strands are stitched together with a UUCG loop (23). Both structures were solvated using TIP3P water (53) in a rectangular solvation box with 17 Å of water padding in each direction. A sufficient number of sodium ions were added to the system to neutralize the negative charge in the nucleic acid. The CHARMM36 force field (54) for nucleic acids has been successfully used in the literature to study the Hoogsteen base pairing (2,22,23), base pair opening (55,56), and conformational dynamics of DNA (57) and RNA (58,59). We used the CHARMM36 force field in this study. The starting structures for both DNA and RNA had all the base pairs in common Watson-Crick conformation. The solvated nucleic acids were energy minimized for 50,000 steps, using the conjugate gradient algorithm. The systems were gradually heated to a temperature of 298 K at a rate of 1 K/ps in the NVE ensemble with harmonic restraints of 3 kcal mol⁻¹ Å⁻² on the nucleic acid heavy atoms. Then the restraints were removed in steps of 0.5 kcal mol⁻¹ Å⁻² per 200 ps. Each system was further equilibrated for 3 ns in an NVE ensemble and 10 ns in an NPT ensemble with a small harmonic restraint on the terminal base pairs, with force constants of 0.1 and 0.05 kcal mol⁻¹ Å⁻², respectively. The terminal base pairs were continually restrained with a 0.05 kcal mol⁻¹ Å⁻² force constant for all meta-eABF and equilibrium production runs. The temperature was kept constant at 298 K using a Langevin thermostat with coupling constant 1 ps⁻¹, and the pressure was kept constant at 1 atm using the Nosé-Hoover Langevin piston with an oscillation period of 100 fs and a damping timescale of 50 fs (60,61).

Enhanced sampling simulation

We used the newly developed meta-eABF method (38) implemented in NAMD 2.12 through the colvars module (62) to obtain the potential of mean force. Theoretical details of the meta-eABF method is described in the Supporting Materials and Methods. The glycosidic angle χ and the pseudodihedral angle Θ of the A16-T9 base pair were chosen as order parameters after earlier studies (2,22,25,63). The χ angle denotes torsion of the adenine base with respect to the deoxyribose sugar (defined as the dihedral angle between O4′ – C1′–N9–C4), whereas the Θ angle captures the flip-out motion of adenine, which leads to extrahelical conformations through base pair breaking (25). The collective variable space was spanned from −180 to 180° with a 5° bin width for both the dihedral angles. For both systems, the meta-eABF simulation was started from the final structure from the NPT equilibration and continued until all the bins were sufficiently explored and the root mean-square difference of the PMF were converged. Gaussian biases of height 0.06 kcal/mol and width = 3 colvar units were deposited at every 2 ps for metadynamics. ABF bias was applied against the average local force only after 1000 samples were obtained at a given bin. We obtained a converged PMF within 0.2 μs of simulation for each system. The one-dimensional PMF along the glycosidic angle χ was obtained using Boltzmann measure integration (24)

$$A\left(\chi \right)=-k_{B}T\text{ln}\left(\int \text{exp}\left(-\frac{A\left(\chi ,\Theta \right)}{k_{B}T}\right)d\Theta \right),$$ (1)

with k_B the Boltzmann constant, T the temperature, and A(χ, Θ) the two-dimensional (2D) PMF along the χ and Θ coordinates. The PMF along Θ was computed similarly for both DNA and RNA.

Unbiased simulation and Markov state modeling

To elucidate the kinetics and the pathways of formation of Hoogsteen base pairing, we built MSM for both DNA and RNA using the PyEMMA2 package (64). A total of 45 unbiased trajectories were initiated from different starting points chosen from the biased meta-eABF trajectory. Each of them were propagated for 60 ns, resulting in 2.7 μs of total trajectory data. The first 2 ns of each of the trajectories were considered as equilibration and discarded.

A total of ∼5.2 μs of unbiased molecular dynamics data were used to generate the MSMs for both the DNA and RNA system. Trajectory snapshots were saved every 10 ps. Dimensionality reduction of the data has been performed by TICA (43,44) on the backbone and sugar dihedral angles (mentioned in the work of Zhou et al. (65)), the glycosidic dihedral angle, and the distances between hydrogen-bond-forming heavy atoms. Variational approach to Markov processes-2 (VAMP-2) scores (66) were calculated to estimate the appropriate lag time for TICA. The trajectories were projected onto the minimal number of TICA coordinates that cover 95% of the kinetic variance. For TICA analysis, a lag time of 2 ns was chosen for both systems, which produced five and six independent components (IC) for DNA and RNA, respectively. The entire simulation data were clustered into 400 clusters for DNA and 200 clusters for RNA using a k-means clustering algorithm. MSM was constructed with a lag time of 2 ns for the DNA and 7 ns for the RNA system. Implied timescale and Chapman-Kolmogorov analyses (67) were performed to check the validity of the constructed MSM (see Figs. S5–S9). The clusters were coarse grained into a few metastable states using the Perron-cluster cluster analysis algorithm (PCCA) (68). Kinetics and transition probabilities between the clusters were calculated using transition path theory (TPT) (69,70). The results were projected onto the coarse-grained space of metastable states to calculate the mean first-passage time (MFPT) and flux in between each pair of metastable states. Connections with highest probability flux were traced from the MSM network. These pathways were considered as major transition pathways and were utilized to decipher the mechanism. Three sets of clusterization were performed for the DNA and RNA system, and the mean and standard deviation of the first-passage times were calculated.

Results and Discussion

Free energy surfaces from meta-eABF

Unlike A6-DNA, the RNA hairpin with the same sequence did not show HG base pairing in NMR relaxation experiments (23). Forcing HG base pairing by methylation of adenine resulted in melting of the RNA helix both in experiment and MD simulation (23). For regular duplex RNA (unmethylated), the absence of the experimental NMR signal characteristic of HG pairing could mean either that the HG base pair is thermodynamically forbidden or that it is metastable, but the population and timescale fall outside the detection window of the NMR apparatus. A definitive answer to the question of HG stability in RNA can be addressed by computing the free energy landscape of base pairing conformational changes.

At first sight, the relevant degrees of freedom for the free energy landscape should contain a measure of flip-over and flip-out angles (i.e., χ and Θ). We obtained a converged 2D PMF along the χ and Θ torsion angles using meta-eABF simulations within 200 ns for both the DNA and RNA system. Convergence was monitored by plotting the root mean-squared deviation of the PMF at 200 ns from that at earlier times (Fig. S1). The presence of HG base pairing in DNA is reflected by the clear deep minimum at χ∼50° and Θ ∼0°. The Watson-Crick base pair is located in the deep stretched well between −180° and −50° of the glycosidic angle χ for Θ close to 0°. Meanwhile, for the RNA, the WC base pairing was observed at χ ≈ −160°. Additionally, there is a shallow minimum at χ ≈ 30° in RNA, close to that of the HG base pair in DNA (Fig. 1). Careful examination of the trajectory revealed a Hoogsteen-like structure in RNA with only one hydrogen bonding between NH₂ of adenine and the carbonyl oxygen of thymine (distance ≤3.0 Å and angle ≤30°) (Fig. 1). This HG-like structure is energetically unstable by ∼2 kcal/mol compared to the HG base pair of the DNA. This structure has previously been observed by Rangadurai et al. by computer simulation (71) using the AMBER f99 force field (72) with χ_OL3 correction (73). It is referred to as RNA HG base pair in the rest of the study. RNA also showed a higher free energy barrier between the HG and WC form.

Figure 1.

The upper panels show the structures of (a) Hoogsteen base pair in A6-DNA and (b) Hoogsteen-like base pair in A6-RNA. The χ and Θ angles have been depicted in the DNA HG base pair (a). The reader is directed to the articles by Yang et al. (24,25) for a more elaborate description of the angles. The lower panels shows a 2D PMF of (c) the A16-T9 base pair of A6-DNA and (d) the A16-U9 base pair in A6-RNA computed using meta-eABF method. To see this figure in color, go online.

It is of interest to consider the effect of N1-methylation of nucleobases, as it occurs in DNA as a form of alkylation damage and in RNA as post-transcriptional modifications. Our previous simulation work (23) showed that N1-methyladenosine has significantly different consequences. Whereas it creates Hoogsteen pairs in duplex DNA, thereby maintaining the structural integrity of the double helix, it blocks base pairing and induces local duplex melting in RNA. The experimental observation of RNA melting by methylation of adenine can be attributed to the relative instability of the RNA HG base pair, although we did not directly observe RNA helix-melting transitions in our simulations. The simulated free energy differences and barrier heights are not directly comparable with the experimental results, which are estimated based on simple assumption of Boltzmann probability and transition state theory. Still, we obtained the relative free energy of the HG base pair with respect to WC (ΔG_WC→HG) to be 4.5 kcal/mol, which is within 1 kcal/mol agreement with NMR experiments and is in quantitative agreement with multimicrosecond timescale umbrella sampling and metadynamics simulations (24,25) performed using state of the art AMBER bsc0 (74) and bsc1 force fields (75). The qualitative topology of the 2D PMF and the positions of the WC and HG minima in χ–Θ space also agree with earlier computational results (24,25). The absence of the N7(A)-N3(U) hydrogen bond can be the possible reason, which makes RNA HG unstable (71) and elusive in experiments.

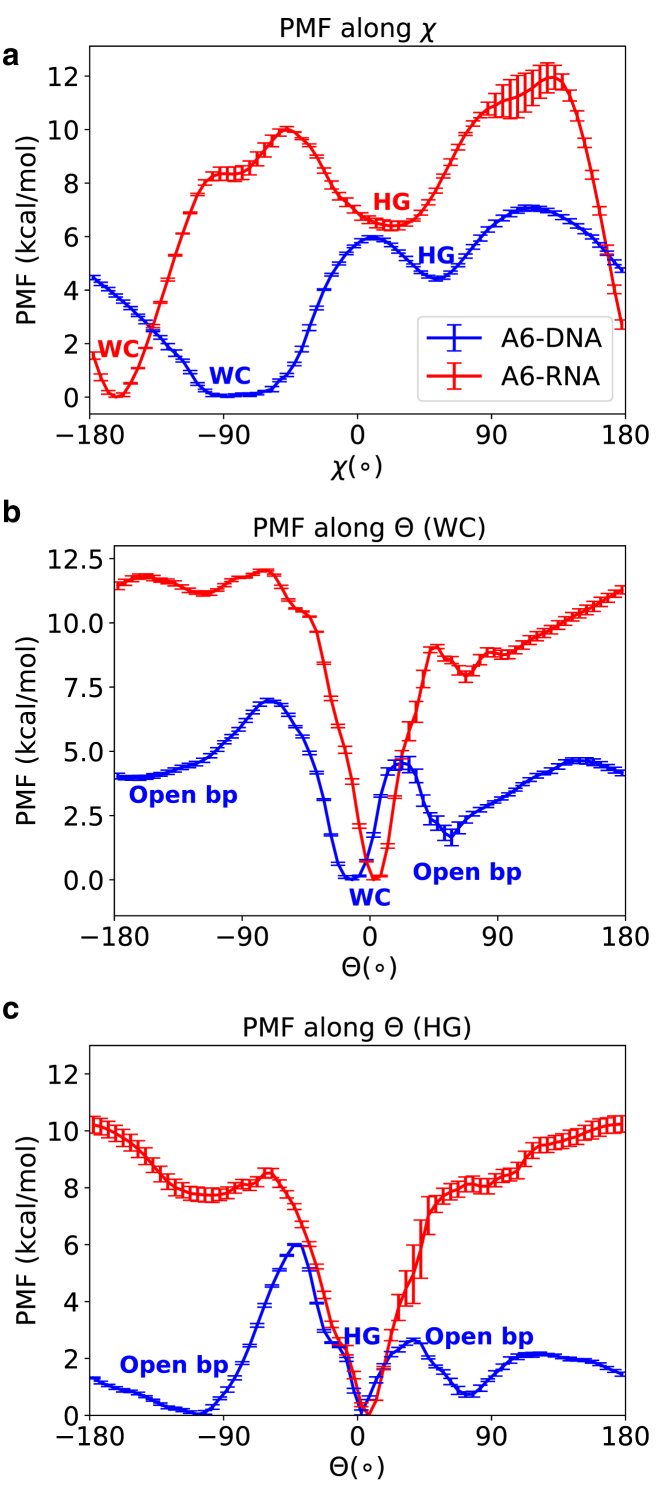
The difference of relative free energy of the HG/HG-like base pair between DNA and RNA is more apparent in the Θ−integrated one-dimensional PMF as a function of the χ angle (Fig. 2). The PMF along the base flip-out angle Θ shows a second deep minimum at Θ ∼60° connected to the WC-base paired state with a small barrier in DNA (Fig. 2). It is in agreement with the work of Lavery and co-workers (76), who obtained a similar free energy minimum for adenine base opening through the major groove via what they called a “saloon door” mechanism.

Figure 2.

Integrated one-dimensional PMF’s for both A6-DNA and A6-RNA computed using Eq. 1. (a) PMF along glycosidic angle χ is shown. (b) PMF along pseudodihedral angle Θ for WC pairing form is shown, and (c) is the same as (b) for HG base pairing form. Although calculating rigorously defined error bars for ABF-based PMFs is very expensive, we report the uncertainty estimates of the one-dimensional PMF following the method proposed by Liu et al. (90). To see this figure in color, go online.

Spontaneous base pair opening in DNA duplexes was observed in NMR experiments (77) at one order of magnitude faster rate (40–400 s⁻¹) than the formation of HG base pairing (4–20 s⁻¹) (2). We also observed a slightly lower barrier height for base pair opening in comparison to that for transition to HG conformation (Figs. 1 and 2). Consistencies with previous results bolster the conclusion that we can capture the essential physics of DNA base pair dynamics from relatively short meta-eABF simulations. Two minima corresponding to open base pair conformations are present, one toward the major and the other toward the minor groove side of the HG base pair. However, the free energy cost of base pair opening through the minor groove (ΔG_open ∼5kcal/mol) is much higher than through the major groove (ΔG_open ∼2kcal/mol). This is in agreement with the results of Giudice et al. (76) and our own results in Nikolova et al. (2), which show that the base pair opening and flipping motions take place through the major groove (positive Θ) of DNA predominantly. We do not see any such low-energy minima of open base pair conformations for RNA (Fig. 2).

However, the existence of a low-energy open base pair state near the WC basin can raise a fundamental issue of DNA stability. It can be a consequence of the force field or it can be due to the low-dimensional projection on the Θ angle used to calculate the PMF. Similar low-energy extrahelical configuration has been observed in MD simulations using both CHARMM (56) and AMBER (76) force fields. However, we show later in this article that reduced dimensional representations on two dihedral angles clearly fail to distinguish between different three-dimensional structures. Low-dimensional projection on a two-angle plane leads to an overestimation of the population and an underestimation of the free energy. MSM analysis is more reliable in this regard, albeit harder to interpret because of the use of complex high-dimensional TICA-based coordinates. Furthermore, our conclusions are limited to only a given base pair in our specific synthetic construct of DNA, and we are in no position yet to accurately predict how populations would be modulated by the cellular environment in a general DNA sequence.

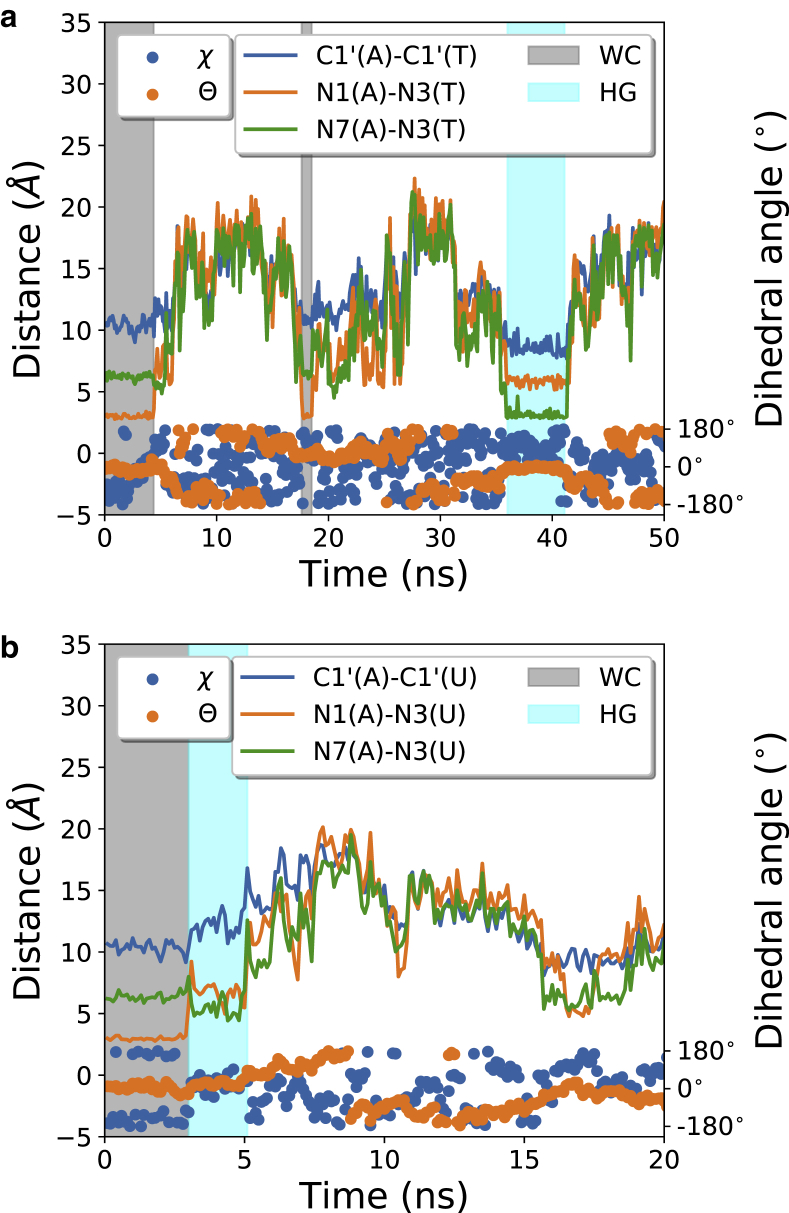
A clearer indication of base pairing can be obtained by monitoring the hydrogen bond donor-acceptor distances. In the WC pair, hydrogen bonds form between the N1 of A and N3 of U/T base, whereas for HG base pairing, N7 of A participates in hydrogen bonding instead of N1. We have plotted the N1-N3 and N7-N3 bond distances for a small stretch of the meta-eABF trajectory for both DNA and RNA (Fig. 3). Shorter distances (∼3.5Å) between N1-N3 or N7-N3 atoms correspond very well with the real WC and HG base paired conformation, respectively. The agreement of χ and Θ angles is not as good as the distances between N atoms, and there are certain structures with HG- or WC-specific χ and Θ values, although they are not base paired structures. This can be due to the fact that these angles are measured with respect to the sugar or the neighboring base pairs, whose structures also fluctuate with time. It also indicates that to get a correct picture of the transition between the WC and HG base pair, we should take hydrogen bond donor-acceptor distances into account. Fig. 3 also shows the variation of the helix diameter measured by the distance between backbone C1′ atoms of the participating nucleotide. The distance is ∼10 Å for WC-base paired forms in DNA and RNA. For HG base pairing in DNA, the helix diameter shrinks to ∼8.5 Å, in agreement with previous results (65). Interestingly, for the RNA HG-like structure, this increases to ∼12 Å, and the N7-N3 distance does not shrink as much as it does in DNA. These are the structural factors which prevent the formation of the second hydrogen bond in the RNA HG. The effects can be a result of the diameter of the A-form helix present in RNA being larger than the diameter of naturally occurring B form in DNA; so the free energy compensation for the shrinkage of the radius in the RNA helix is large. This has been deemed to be a reason for the absence of HG in RNA in a recent experimental and computational study (71).

Figure 3.

Formation of Hoogsteen base pairing in the meta-eABF simulation. The hydrogen bond donor-acceptor distance, the distance between C1′ atoms of the backbone corresponding to the adenine and thymine bases, and the χ and Θ torsion angles are shown for the first few frames of the trajectory for (a) DNA and (b) RNA. The regions of WC and HG base pairs are indicated by manual inspection of the trajectory frames. Similar behavior is also observed throughout the 200-ns trajectory, but only a small portion is shown for clarity. To see this figure in color, go online.

Markov state modeling

TICA analysis and reaction coordinate

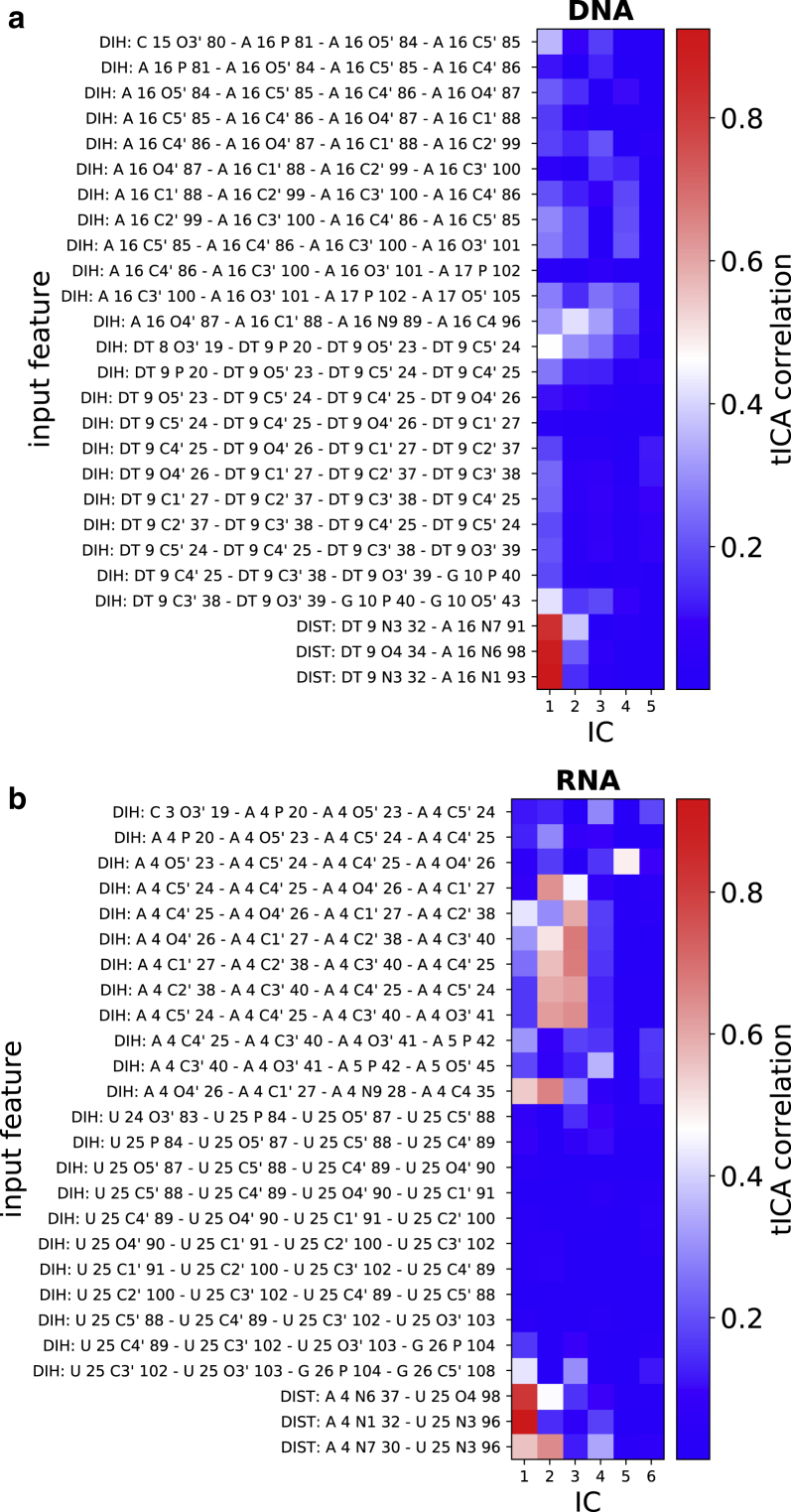
Given that the traditional torsion angles χ and Θ remain inadequate to appropriately describe the conformational transition between WC and HG base pairing forms, a multidimensional representation involving other structural features becomes necessary. TICA can be used to identify the slowest degrees of freedom in a complex conformational transition as a function of internal coordinates of the system (43,44). TICA analysis of our unbiased trajectory data predicted that the slowest IC in DNA base pair motion is strongly correlated with the hydrogen bond donor-acceptor distances (Fig. 4). The third H-bond distance between (T/U) O4-(A) N6, which is common in both WC and HG, also showed high correlation, indicating that both hydrogen bonds get broken during the slowest motions of the base pair.

Figure 4.

Absolute values of the correlation coefficients of the independent components (IC) obtained from TICA analysis with the input features (i.e, dihedral angles and possible hydrogen bond donor-acceptor distances) for (a) DNA and (b) RNA. To see this figure in color, go online.

Among features based on dihedrals, the phosphodiester bond torsion angles have the highest correlation with IC 1 in DNA, possibly indicating slow base flip-out motions. Conversely, none of the IC’s for RNA has significant correlation with the torsional angle of phosphodiester bond. In DNA the IC 2 and IC 3 shows high correlation with the glycosidic angle χ, suggesting that IC 2 is a better coordinate than IC 1 for resolving the WC-to-HG transition. Meanwhile, in RNA both IC 1 and IC 2 are strongly correlated with the χ angle. Also, IC 2 and 3 have significant contribution from the sugar pucker angles in the ribose sugar of the adenine nucleotide. None of the torsional angles in the uracil nucleotide has any contribution in the slow motions captured by our TICA analysis.

MSM structural network, free energy, and kinetics

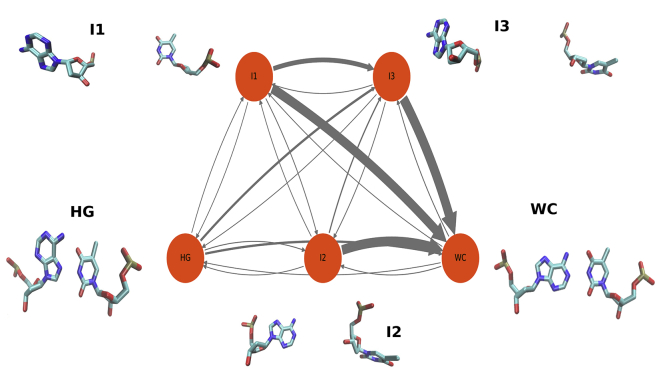
MSMs (40) decompose unbiased molecular dynamics trajectories into clusters based on structural criteria and calculates transition probabilities between them. From the transition probability data, free energy landscape, conformational kinetics, and mechanistic pathways can be elucidated (78). We constructed an MSM based on structural features using the internal coordinates (IC) obtained from TICA. The MSM was decomposed into five and four metastable states, respectively, for DNA and RNA to get an intuitive understanding of the pathway of transition. They were identified as WC, HG or intermediate (I), states by inspection of sample structures. The choice of the number of metastable states were optimum for differentiating between recognizable structural forms (e.g., WC, HG, base pair open, etc.). To analyze these states, we define a base flip-out angle for thymine/uracil (η) analogous to the Θ angle for adenine. The metastable states were then projected onto both χ–Θ and Θ–η space to understand their correspondence with the free energy landscape obtained from meta-eABF simulation (Figs. S9–S11). For DNA, the metastable states overlap each other significantly in the χ–Θ space, and many open base conformations coincide with both the WC and HG states. This result is confirmed by Θ–η plots, in which a base paired state is indicated by a cluster close to the origin. If either base is in extrahelical conformation, the corresponding pseudodihedral angle will be away from zero (Figs. S10 and S11). The I1 has at least one of the bases that is in open conformation, whereas I3 has both of them open. I2 primarily has the adenine inside the helix (Θ ∼0°), but the thymine is outside (Fig. 5). However, both I1 and I2 coincide with the base paired state in the χ–Θ space, leading to overcounting the population of WC and HG. These results indicate that conventional dihedral-angle-based representation fails to capture the true story behind the formation of HG base pairing. This limitation is, most probably, a result of not taking the conformation of the thymine base into account.

Figure 5.

A network of probability fluxes through the metastable states obtained from MSM for A6-DNA system. To see this figure in color, go online.

Unlike DNA, none of the metastable states of RNA showed extrahelical conformation. Although the interbase hydrogen bonds are broken in I, there is a new hydrogen bond between the uracil carbonyl group oxygen and the C2′-OH group in the ribose sugar of the adenine nucleotide (Fig. 7). This intermediate is further stabilized by another hydrogen bond forming between adenine (N3) and the OH group of phosphodiester bond in the backbone of uracil nucleotide. They prevent the adenine from completely flipping out of the helix. Consequently, the extrahelical conformations are unfavorable in RNA A-T base pair because of the free energy cost of breaking these additional hydrogen bonds.

Figure 7.

Same as Fig. 5 but for A6-RNA system. To see this figure in color, go online.

From the MSM, we computed the free energy landscape for the A-T/U base pair conformation as a function of the two slowest degrees of freedom obtained from TICA analysis (Fig. 6). Comparing the results with the metastable state distribution, we can get an idea of the configurations represented by different minima in the free energy surface. Clear deep minima for both WC and HG base pairing were obtained in DNA, whereas in RNA, apart from a HG-like state, we observed two different WC minima (Fig. 6). One of them has the ribose sugar in C3′-endo conformation (WC1) and the other in C2′-endo conformation (WC 2) (Fig. 7). As dictated from the involvement of sugar pucker angles in the first TICA component, the transition from C3′-endo to C2′-endo conformation is one of the slowest motion captured in our base pair dynamics model of RNA. The relative free energy of HG (ΔG_WC→HG) obtained from MSM agrees with the results of meta-eABF and with previous experimental and computational studies. However, this agreement can be a coincidence, considering that the WC and HG minima in the χ- to Θ-based PMF have contribution from nonbase paired intermediates.

Figure 6.

Free energy profile of A-T base pair conformations for (a) the DNA and (b) the RNA system as a function of the two slowest independent components (IC) obtained from TICA-based MSM. The orange dots indicate the positions of the cluster centers in the space of TICA coordinates. To see this figure in color, go online.

We utilized transition path theory (TPT) (69,70) to obtain the kinetics between the clusters. The kinetic information was projected onto the coarse-grained space to generate a flux network between various metastable states (Figs. 5 and 7). The MFPT of transition from WC-to-HG state in DNA was obtained at 1.8 ms, which is in good agreement with the experimental lifetimes of HG base pairs (0.2–2.5 ms) (79), but an order of magnitude less than the experimental first-passage times (∼50 ms) (2). Our result also agrees quite well with the recently reported rate constants of transition between WC and HG base pairing using transition path sampling (26). A simple Arrhenius-theory-based estimation yields an activation free energy of ∼14 kcal mol⁻¹ (Table 1), which matches well with such estimates made from NMR experiments (∼16 kcal mol⁻¹) (2). The majority of the flux in the DNA system is along the following two paths: HG→I3→WC (87.2%) and HG→I3→I2→WC (8.8%). It indicates that the most probable intermediate between WC and HG is the state with both base pairs flipped outside the helix. It also provides qualitative evidence that the transition between WC and HG base pairs happens through concerted outward movement of the bases, followed by movement back inside the helix, in agreement with earlier propositions (2,26).

Table 1.

MFPTs and Barrier Heights for Transition between WC and HG Base Pairing Forms Predicted from MSM for Both A6-DNA and A6-RNA

	WC→HG		HG→WC
	MFPT	Barrier Height	MFPT	Barrier Height
	(ms)	(kcal/mol)	(μs)	(kcal/mol)
DNA	1.8 ± 0.4	13.89 ± 0.14	0.85 ± 0.07	9.28 ± 0.05
RNA (WC1)	30.2 ± 10.8	15.57 ± 0.22	10.7 ± 3.85	10.76 ± 0.23
RNA (WC2)	32.0 ± 11.7	15.60 ± 0.23	567 ± 70	13.18 ± 0.07

The barrier heights corresponding to transition between WC and HG base pairing have been computed using the Arrhenius formula from the transition timescales estimated from the MSM. But the absence of any configuration with ∼14-kcal/mol energy barrier in the free energy profile computed from MSM indicates that none of the clusters actually correspond to the true transition state. It shows that the process of conformational switching is an example of a rare event in which the transition time is orders of magnitude smaller than the time spent in the energy minimum. However, an advantage of using MSM is that we could obtain the approximate barrier heights from the timescale information despite being unable to pinpoint the transition state structure.

Our MSM splits the open base pair state in Fig. 1 into intermediate states, each of which has lower probability than the open base pair state in meta-eABF PMF. Consequently, the most probable open base pair intermediate I3 has a free energy of ∼4 kcal/mol in the MSM (much higher compared with ∼2 kcal/mol in the meta-eABF PMF) and a corresponding population of ∼0.1% with respect to the WC base pair. MD simulation studies using the AMBER force field have also indicated that the DNA base can explore extrahelical conformations by spontaneous breaking of base pairs within the microsecond timescale (80). From our MSM using the CHARMM36 force field, we obtained the timescale of base pair opening to be close to a microsecond, in agreement with the above-mentioned study.

Our model predicts the transition timescale to the HG base pair from WC1 to be 30.2 ms and from WC2 to be 32.0 ms for the RNA system (Table 1), although there are no experimental data available to compare. The timescales of the NMR R_1ρ relaxation experiments are a few tens of milliseconds (81). So the transition timescale from WC to RNA HG is close to the maximal limit of this experiment and, consequently, it suggests the reason why an HG-like base pair has not been experimentally detected in the A6-RNA hairpin. The major pathways of probability flux are the following: HG→I→WC1→WC2 (84%) and HG→WC1→WC2 (16%). None of the intermediates assume open base pair conformation, which is evident from Fig. 7 and from the Θ–η distribution of the metastable states. The intermediate I could be identified as the more compact state observed at ∼17 ns of the meta-eABF trajectory of the RNA hairpin (Fig. 3). The transition between WC and HG-like base pairing in RNA takes place through an intrahelical pathway. Our 2D PMF from meta-eABF simulation also supports the claim because the free energy cost of A-U base pair opening RNA is observed to be much higher than that of A-T base pair in DNA (Fig. 2).

Conclusions

In this work, we combined the meta-eABF-enhanced sampling technique with Markov state modeling to obtain mechanistic insights into the conformational switching between WC and HG base pairing in DNA and RNA. We have constructed and compared the 2D PMF along the glycosidic and base flip-out angles, which showed presence of HG or HG-like conformation in both DNA and RNA. Markov state modeling produced a free energy landscape along the two slowest degrees of freedom, with distinct free energy minima for WC and HG base pair for DNA. It predicted the relative free energy of HG base pair within ∼1 kcal/mol accuracy of previous experimental and computational results. We also observed single-hydrogen-bonded and relatively unstable HG-like base pairing in RNA. The absence of the second hydrogen bond can be attributed to the larger diameter of the A-form helix in RNA. It does not allow for sufficient shrinkage of the helix, preventing the attainment of the optimum distance between N7(A) and N3(U) for hydrogen bonding to take place. Monitoring the distance between the backbone C1′ atoms in adenine and thymine/uracil nucleotide from the biased trajectory substantiated our conclusion about insufficient shrinkage of RNA helix diameter in HG-like base pairing. Our inference is in agreement with recent arguments made by Rangadurai et el., who showed the A-form of helix needs to perform a significant sugar-backbone rearrangement to avoid steric clash in the base in syn form present in HG (71).

A closer look at the biased trajectory revealed that the WC and HG state definitions correspond better with the hydrogen bond donor-acceptor distances than with the dihedral angles, which are traditionally chosen as collective variables. TICA analysis of multiple unbiased trajectories and dihedral angle distribution of the metastable states from MSM agree with this conclusion. The slowest dynamics of the system involve forming and breaking of the hydrogen bonds, and also conformational changes of the thymine/uracil base. The relative free energy of the RNA HG with respect to the DNA HG is ∼2 kcal/mol, which is roughly the energy of one hydrogen bond in nucleic acid base pairing (82). Although observed in protein and drug-bound DNA and synthetic DNA constructs, Hoogsteen pairing in RNA remained elusive in experimental studies. The ∼6.5 kcal/mol free energy difference with respect to WC base pairing form makes RNA HG extremely rare (<0.002% of WC, according to Boltzmann probability arguments) and unlikely to be observed with NMR relaxation dispersion techniques. The observation of RNA HG pairing is of particular significance because our enhanced sampling scheme was not directed toward any specific structure (for example, as is typically done in targeted MD (83) or other biased methods). Rangadurai et al. started their simulation from an artificially designed HG-like structure for the RNA hairpin (71). Their simulation has naturally equilibrated into an RNA HG structure. On the contrary, we started our simulation from a WC geometry and allowed the system to explore the configuration space using the meta-eABF method. Still, we observed the formation of RNA HG base pairing. This shows that there is an inherent stability of the HG-like structure in RNA, and it is not an artifact of the initial conditions of the MD simulation.

MSM constructed from TICA coordinates predicted the free energy and kinetics of transitions between WC-to-HG base pairing in A6-DNA within reasonable agreement with previous theoretical (24, 25, 26) and experimental results (2). But we also predicted that the timescales for such transition in RNA is more than 30 ms. Considering that the MSM timescale for WC-to-HG transition in DNA is one order of magnitude less than the experimental value, the true first-passage time for RNA might go well beyond the time window of the NMR R_1ρ relaxation experiment. This provides a parallel kinetic rationale for why HG-like base pairing is not observed in experimental studies. A kinetic network was constructed between a handful of structurally distinguishable metastable states obtained by decomposing the MSMs. The most probable transition pathway, traced down from the networks, indicate that the conformational switching between Watson-Crick and Hoogsteen base pair happens through an extrahelical mechanism for A6-DNA, whereas in RNA, a hairpin intrahelical mechanism is dominant. This result is explained by the much higher free energy cost of base pair opening in RNA compared with DNA obtained from the PMF using meta-eABF simulation. The analysis of pathway also resulted in the observation of a novel intermediate structure with unusual backbone-base hydrogen bonding in A6-RNA.

Application of meta-eABF method to HG pairing resulted in an accurate PMF obtained in two orders of magnitude less computational effort. This method shows promise for extensive use over a range of protein-DNA and drug-DNA complexes with HG propensity and for making comparisons between ΔG_WC→HG free energies possible within reasonable computing time in a sequence-dependent context. Pathways and timescales of HG pairing in such systems can be understood from MSMs and multidimensional path searching methods, such as those based on strings in configuration space (84, 85, 86), “traveling salesman” path searching (87), and other similar techniques (88,89). Taking additional degrees of freedom, such as H-bond donor-acceptor distances, sugar pucker angles, and the phosphodiester bond torsion angle, into consideration will provide better understanding of the molecular processes involved in HG base pair formation.

We hope our work will motivate careful experiments in both short and long timescales for the detection of HG base pairs and novel short-lived intermediates in duplexes of RNA hairpins. This work, consequently, marks the beginning of a large-scale exploration of Hoogsteen base pairing thermodynamics and kinetics in various biologically relevant nucleic acid systems through computational and subsequent experimental methods to gain detailed mechanistic understanding of the role of noncanonical base pairing in nucleic acid function and recognition.

Author Contributions

D.R. and I.A. designed research. D.R. performed simulation and analyzed data with inputs from I.A., and D.R. and I.A. wrote the study.

Editor: Christine Heitsch.