Chromosome Structural Mechanics Dictates the Local Spreading of Epigenetic Marks

Abstract

We present a theoretical model that demonstrates the integral role chromosome organization and structural mechanics play in the spreading of histone modifications involved in epigenetic regulation. Our model shows that heterogeneous nucleosome positioning, and the resulting position-dependent mechanical properties, must be included to reproduce several qualitative features of experimental data of histone methylation spreading around an artificially induced “nucleation site.” We show that our model recreates both the extent of spreading and the presence of a subdominant peak upstream of the transcription start site. Our model indicates that the spreading of epigenetic modifications is sensitive to heterogeneity in chromatin organization and the resulting variability in the chromatin’s mechanical properties, suggesting that nucleosome spacing can directly control the conferral of epigenetic marks by modifying the structural mechanics of the chromosome. It further illustrates how the physical organization of the DNA polymer may play a significant role in re-establishing the epigenetic code upon cell division.

Significance

Epigenetic regulation serves a critical role in guiding genetically identical cells to differentiate into a variety of cell types with different properties and functions. Abnormal patterns of epigenetic modifications disrupt this process and lead to a number of prevalent diseases, including diabetes, obesity, and cancers. Intervening to correct such aberrant behavior will first require an understanding of the fundamental biophysical mechanisms that govern the spreading of epigenetic modifications. To that end, we develop a theoretical model that connects DNA structure and mechanics to the formation of DNA loops and the conferral of epigenetic marks. Experimental measurements of the biological system form the basis for our model, enabling us to construct a predictive framework for local epigenetic spreading.

Introduction

Two genetically identical cells can have vastly different behavior because of chemical modifications to the chromosomal DNA and posttranslational modifications to DNA-packaging proteins. The profile of these modifications defines an epigenetic code that alters the expression of the genetic material. Acting in concert with gene regulatory proteins and transcription factors, the epigenetic code helps regulate gene expression by modulating the spatial organization of the chromosomes and differentially limiting regulatory proteins from accessing DNA within condensed chromosomal regions.

At the basepair length scale, DNA is wrapped around a set of eight histone proteins to form the nucleosome core particle, which represents the fundamental structural unit of chromatin. Chemical modifications, including acetylation and methylation, on the tails of the histone proteins control both the local and global organizational state of chromatin and modulate the accessibility of genes to transcription factors. For instance, methylation of histone proteins plays an essential role in heterochromatin formation (1) and transcriptional repression of genes (2, 3, 4). Epigenetic methyl marks on histone H3 lysine 9 (H3K9) interact with heterochromatin protein 1 (HP1), which is shown to be a necessary player in the formation of heterochromatin (5). HP1α specifically binds to methylated H3K9 (6, 7, 8) and oligomerizes with HP1α bound to adjacent nucleosomes, leading to condensation (5,9). The methyltransferase Su(var)3-9 that is responsible for the conferral of methyl marks interacts with H3K9 either directly or indirectly through the binding of HP1α (10, 11, 12).

To maintain proper cell identity and gene expression, the epigenetic code must be passed robustly from parent to daughter cells during replication. Epigenetic marks like the tri-methylation of H3K9 (H3K9me3) spread along the chromatin fiber based on biophysical mechanisms that currently are not fully understood. Chromosome capture experiments (e.g., Hi-C (high-throughput chromosome conformation capture)) that map contacts between genomically distant chromosomal loci display distinct patterns that correlate with epigenetic histone modifications, suggesting a connection between DNA looping and epigenetic regulation (13, 14, 15). Various experimental measurements investigate the transmission of epigenetic marks using in vivo assays. Hathaway et al. (16) transduce mouse embryonic stem cells and embryonic fibroblasts with a DNA-binding domain to which HP1α is fixed. Chromatin immunoprecipitation (ChIP) is used to monitor changes in the methylation profile, which exhibits a gradual enrichment in methylation over time with a peak at each side of the HP1α-modified locus. These data show that in contrast to DNA replication, which occurs on a timescale of hours, the establishment of a stable methylation profile is not an instantaneous process, but rather a slow one that takes place over 5 days.

Theoretical modeling of the spreading of methyl marks provides fundamental insight into how the kinetics of methyltransferase and nucleosome turnover can lead to stable methylation profiles (17, 18, 19, 20, 21). Previous models of the kinetics of epigenetic modifications incorporate long-range nucleosome-nucleosome interactions through distance-dependent power law distributions (17,22, 23, 24), experimental looping probabilities (18), and calculated looping probabilities from polymer models (25, 26, 27). All approaches demonstrate that local interactions between nucleosomes are not sufficient to maintain a stable epigenetic state and that cooperativity and interactions beyond the nearest neighbor are required to establish robust bistability. Modulation of the positioning of nucleosomes within chromosomal regions is likely to alter the looping behavior for such regions (28, 29, 30, 31, 32), resulting in additional contributions from heterogeneity and dynamic rearrangement.

We develop a theoretical model for the physical behavior of chromosomal DNA at length scales ranging from several nucleosomes to hundreds of nucleosomes. Our goal is to predict the local spreading of epigenetic modifications, which occurs over timescales of several days (16). Although it is widely accepted that chromosomal DNA frequently forms loops and that DNA looping serves as a mechanism for epigenetic spreading, the formation of any one particular loop is rare. Both the rarity of an individual loop forming and the long timescales associated with this problem (i.e., days in the methyl-spreading experiments) necessitate a theoretical model that captures the essential physical behavior while maintaining an analytically tractable framework.

Materials and Methods

We leverage recent results for the modeling of chromosomal DNA that account for the inhomogeneous positioning of nucleosomes along the DNA strand (33). Chromosomal DNA is organized into a structure that is dictated by DNA-associated proteins, including histones, CCCTC-binding factor (CTCF), and HP1. This organization depends on the epigenetic state of the cell and the stage in the cell cycle. Experimental measurements of methylation spreading in undifferentiated stem cells (16) serve as an inspiration and comparison for our model. Consequently, we assume that the chromosomal DNA is uncondensed and able to form looped configurations, which occur because of thermal fluctuations. Taking the simplest description of such polymer behavior, we adopt the wormlike chain model, which describes an elastic chain subjected to thermal fluctuations that offset the local deformation free energy (34,35), to represent the chromatin fiber.

The local packaging of nucleosomal DNA may be described as a fluctuating zig-zag polymer (36), and our previous work captures the mesoscale behavior of such a description based on heterogeneous localization of nucleosomes (33). Our model must account for the formation of loops that span orders of magnitude in size, from less than one persistence length to hundreds of persistence lengths, and the wormlike chain model is an appropriate choice for capturing such a range of length scales. As will be explained in more detail below, we implicitly account for the local geometry and packaging behavior of chromatin by relying on previous work (33) to inform our choice of the wormlike chain persistence length.

The space curve $\overrightarrow{r}$(s) defines the shape of the wormlike chain over the arc length parameter s, where s runs from 0 at one end to the chain length L at the opposite end. The bending deformation energy of the chain is given by the following

$$\beta E_{\text{bend}}=\frac{l_p}{2}\underset{0}{\overset{L}{\int }}ds{\left(\frac{\partial \overrightarrow{u}}{\partial s}\right)}^2,$$ (1)

where β = 1/(k_BT), l_p is the persistence length of the chain, and $\overrightarrow{u}=\left(\partial \overrightarrow{r}/\partial s\right)$ is the chain tangent vector. We enforce the assumption that the wormlike chain is inextensible (i.e., $\left|\overrightarrow{u}\right|=\left|\partial \overrightarrow{r}/\partial s\right|=1$ for all s). The end-to-end distance distribution (i.e., the Green's function for chain propagation) is formally determined as follows

$$\begin{array}{l}G\left(\overrightarrow{R};L\right)=\\ {\int }_{\overrightarrow{r}\left(0\right)=\overrightarrow{0}}^{\overrightarrow{r}\left(L\right)=\overrightarrow{R}}\mathcal{D}\left[\overrightarrow{r}\left(s\right)\right]\text{exp}\left(-\beta E_{\text{bend}}\right)\prod _s\delta \left(\left|\overrightarrow{u}\left(s\right)\right|-1\right),\end{array}$$ (2)

where $\int \mathcal{D}\left[\overrightarrow{r}\left(s\right)\right]$ indicates a path integral over all configurations $\overrightarrow{r}$(s) that begin at the origin and end at position $\overrightarrow{r}\left(L\right)=\overrightarrow{R}$. The δ-function constraint ensures that the path integration upholds inextensibility. We define a contact radius a as the end-to-end threshold for looping to determine whether the polymer chain is in an unlooped (|$\overrightarrow{R}$| > a) or looped (|$\overrightarrow{R}$| ≤ a) configuration. In this work, we set a = 5 nm to approximately correspond to the distance for nucleosome-nucleosome proximity for the H3 tail to acquire a methyl mark. Because methylation involves coordination of multiple proteins (i.e., H3, HP1α, and Su(var)3-9), the approximate scale to define contact is on the order of several nanometers, which coincides with our choice of a. We define the looping probability P_l(a, L) as the probability that two sites that are a linear distance L apart on the polymer come within a spatial distance a of each other. Using numerical approaches developed in prior work (37, 38, 39, 40), we calculate the looping probability P_l(a, L), which is given by the following

$$P_l\left(a,L\right)=4\pi {\int }_0^{a}dR{R}^{2}G\left(R;L\right),$$ (3)

for all pairs of nucleosomes.

In this treatment of the polymer chain, we do not account for volume exclusion of the nucleosomes or linker DNA. Though volume exclusion would, in principle, affect the probability of two sites coming into contact, we do not expect it to dramatically alter our results. The most significant contribution to DNA looping at short length scales is DNA mechanics, and steric effects play a much more limited role than the bending energy. At long length scales, the polymer conformational entropy dominates, and the polymer behaves like a flexible Gaussian chain. Although the difference between a random walk and a self-avoiding random walk is important at long length scales, the focus of this work is on shorter length scales at which the difference is not as pronounced. Furthermore, because it is highly unlikely that any one particular loop will form, as evidenced by looping probabilities on the order of 10⁻⁶ to 10⁻³, adjustments for volume exclusion would have a negligible numerical impact.

Experiments indicate that HP1 dimerization occurs on nearby nucleosomes in mice (41) and fission yeast (9), bringing nucleosomes closer together and facilitating the spreading of methyl marks. With the goal of comparing our model’s predictions with experimental data from undifferentiated stem cells, we assume that the chromosomal DNA is uncondensed and omit HP1 dimerization from our model. In this work, we allow for spreading between any two nucleosomes provided that HP1 is bound to at least one of them. In separate work, we incorporate the enhanced proximity that results from HP1 dimerization (42).

In the methylation-spreading experiments, HP1α is fixed to a locus near a transcription start site (TSS). Micrococcal nuclease (MNase) sequencing and chemical mapping experiments reveal the presence of a nucleosome-free region (NFR) directly upstream of a gene’s TSS (43, 44, 45). To account for the effect of the TSS and the accompanying NFR, we model the chromosome as a heterogeneous copolymer composed of three wormlike chain segments with different elasticities (i.e., persistence lengths), as illustrated in Fig. 1. With no nucleosomes to facilitate bending of the DNA fiber, the NFR is stiffer than the surrounding regions of nucleosome-containing chromatin. Accordingly, we treat the NFR as a wormlike chain with the persistence length of bare DNA, 53 nm (46,47).

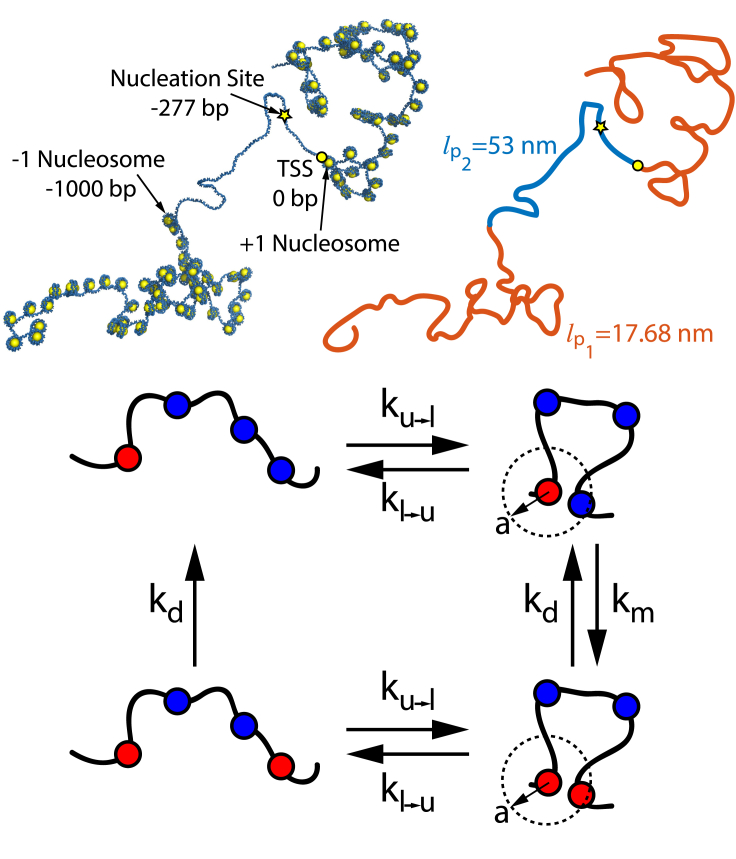
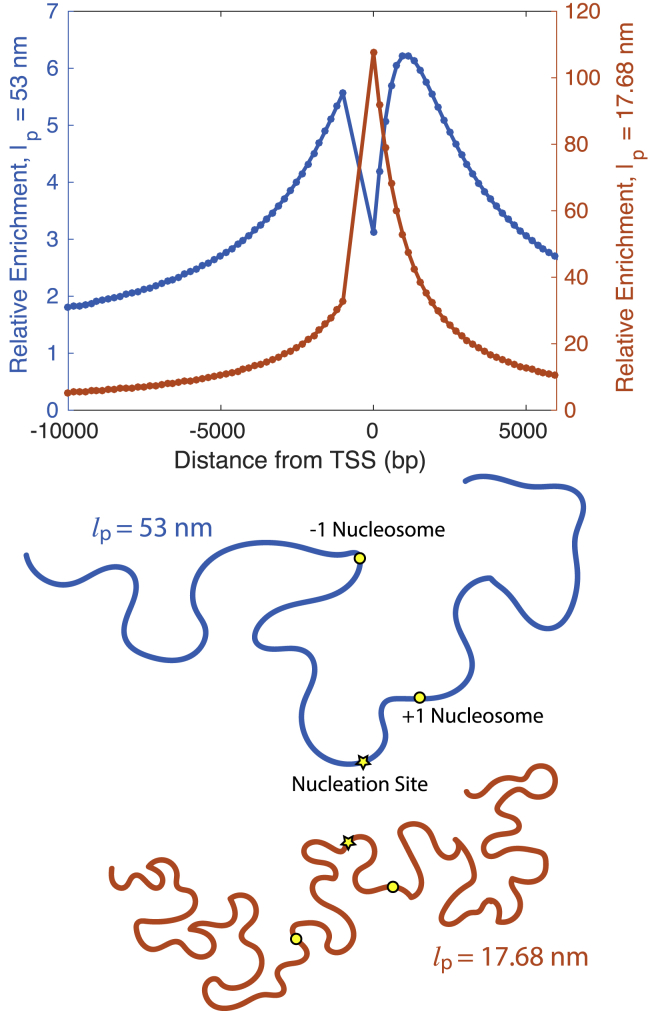
Figure 1.

The top images depict an array of nucleosomes spaced 45 bp apart with a nucleosome-free region (NFR) of 1000 bp and a nucleation site located at −277 bp. The NFR has a persistence length l_p2 = 53 nm, and the surrounding segments have a persistence length l_p1 = 17.68 nm. The top-right image shows a coarse-grained representation of the inhomogeneous polymer model that we use in this work to capture the heterogeneous structural mechanics. The bottom schematic represents the looped and unlooped configurations of the polymer and the kinetic processes that are involved in the conferral and removal of a methyl mark on a nucleosome. Each bead represents a nucleosome that is either methylated (red) or unmethylated (blue). The rate of looping k_u→l and rate of unlooping k_l→u for a chromosomal segment dictate events in which two genomically distant nucleosomes are within the contact radius a. Upon looping, a methyl mark can be conferred to the distant nucleosome with rate k_m. Demethylation of the nucleosome occurs with rate k_d whether the polymer is looped or unlooped. To see this figure in color, go online.

In the two chromosomal segments surrounding the NFR, we consider a string of heterogeneously spaced nucleosomes with an average linker length of 45 bp. Linker lengths range from ∼20 to 90 bp for different species and tissues (48,49), and even within a single genome, considerable heterogeneity in linker length can occur (50). Given this variability, we choose a moderate linker length that corresponds to the average of the experimentally measured linker length distribution in mouse embryonic stem cells (43), a reasonable value for the experimental system of interest (16). According to recent modeling work that accounts for the local geometry of chromatin and the entry and exit angles of DNA wrapped around nucleosomes, a chromatin fiber with heterogeneously spaced nucleosomes behaves like a wormlike chain with a reduced, effective persistence length, which is determined purely by the average nucleosome spacing (33). A chain with an average linker length of 45 bp is theoretically predicted to have a persistence length of 17.68 nm (33), and we use this value as the persistence length of the wormlike chain segments on either side of the NFR.

With this treatment, we implicitly account for heterogeneity in nucleosome spacing and density as well as the local bending of the DNA polymer around nucleosomes. Without explicitly modeling the exact locations and geometry of individual nucleosomes, our choice of 17.68 nm as the persistence length is based on an average linker length (45 bp in this case) and, therefore, reflects the inherent variability in linker lengths. Future work will explore how explicit heterogeneity in linker lengths might give rise to greater variation in the methylation profile.

To clarify, we note that this predicted value for the persistence length is in units of cumulative linker length, not distance along the DNA fiber. This means that with an average linker length of 45 bp, a persistence length of 17.68 nm (∼58.93 bp) corresponds to ∼1.3 linkers. Each nucleosome occupies ∼150 bp, so, together, the 1.3 linker lengths and the nucleosome they encompass amount to ∼208.93 bp (62.68 nm). In units of distance along the DNA fiber, the predicted persistence length of 62.68 nm seems reasonable.

It has been observed in yeast (51, 52, 53, 54, 55), flies (56), worms (57,58), and humans (59,60) that nucleosomes near the TSS are “statistically positioned” (61) with well-defined locations. Although such regular positioning suggests homogeneity in linker lengths in the close vicinity of a TSS, the consistent positioning decays after a few nucleosomes (54). Because we cover longer length scales (on the order of hundreds of nucleosomes) in our model, accounting explicitly for the exact positions of a few nucleosomes would have a negligible effect, and we instead treat each nucleosome-containing chromosomal segment as having heterogeneous nucleosome spacing.

Experiments that examine nucleosome occupancy along the chromatin fiber observe a wide range of NFR sizes, from as small as 200 bp to as large as 1000 bp (62). MNase data show that the nucleosome occupancy level drops significantly directly upstream of the TSS, then gradually increases until it reaches its baseline level at ∼1000 bp upstream of the TSS. MNase measurements are averaged over many cells, which may exhibit heterogeneity in nucleosome positioning. As a result, the gradual rise in occupancy in the upstream direction might indicate that nucleosomes are present in an increasing fraction of cells as the upstream distance from the TSS increases. This heterogeneity implies that although many cells might have small NFRs, some could have much larger NFRs. Additionally, the protein complex used to attach HP1 in the methyl-spreading experiments (16) is quite large and could sterically prevent nucleosomes from binding to locations close to the TSS, effectively enlarging the size of the NFR in the experimental system. The protein complex is composed of 12 zinc finger proteins (zinc finger-homeodomain 1) and five GAL4 proteins, which each have a 12- and 19-bp binding domain, respectively. Together, these proteins occupy 239 bp. Because the natural NFR at the Oct4 gene in mice embryonic stem cells is ∼250 bp (62,63), the “effective” NFR in the methyl-spreading experiments may be around 489 bp. Given the variability in biological systems, conservative estimates of the effective NFR size could have a lower bound of ∼450–500 bp and an upper bound of ∼1250 bp (i.e., a natural NFR of 1 kb with the additional ∼250-bp protein complex). With these considerations in mind, we perform our calculations over a range of NFR sizes from 500 to 1000 bp to account for the observed variability and to investigate how the size of the NFR affects the methylation profile. In the experimental system (16), HP1α is fixed 277 bp upstream of the TSS. Note that for the range of NFR sizes we consider, this so-called “nucleation site” is located within the NFR, as shown in Fig. 1.

Based on previous work (64), we employ a master equation approach that describes the average methylation profile over time. We define the probability p_i(t) as the average methylation of the ith nucleosome in the chain. As depicted in Fig. 1, we assume that a nucleosome to which HP1α is bound must loop with an unmethylated nucleosome for the methyltransferase to confer methylation to the unmethylated nucleosome. To account for the presence of a chemically linked HP1α protein in the experimental system of interest (16), we include in our model a nucleation site (numbered 0) that is always methylated and always has HP1 bound. Methyl spreading may occur through looping with either methylated or unmethylated nucleosomes along the chain, as long as HP1α is bound, or through looping with the nucleation site. We calculate the looping probability between each pair of nucleosomes and between each nucleosome and the nucleation site, and we use these values for P_l in the master equation. We include one effective rate constant for all demethylation in our model (k_d), which we assume is independent of the looped state of the nucleosome. Again, because the formation of any one particular loop is a rare event, we neglect nested loops and consider all looping events to be independent. Under these assumptions, the probability distribution p_i(t) is governed by the master equation

$$\frac{d{p}_i}{dt}=\sum _{j\ne i}{k}_m{P}_{l_{ij}}{f}_m\left(1-p_i\right)p_j+\sum _{j\ne i}{k}_m{P}_{l_{ij}}{f}_u\left(1-p_i\right)\left(1-p_j\right)+k_m{P}_{l_{0i}}\left(1-p_i\right)-k_d{p}_i,$$ (4)

where f_m and f_u are the average fractions of HP1α molecules bound to methylated nucleosomes and unmethylated nucleosomes, respectively. The values of these constants depend on the concentration of HP1 and are taken from experimental measurements of the binding isotherm of Swi6, the HP1 analog in Schizosaccharomyces pombe (9). Because the methylation spreading observed in experiments spans only ∼10 kb (16) and the looping kinetics are relatively fast at length scales this small (64), we handle the looping and unlooping processes with equilibrium looping probabilities rather than finite looping rates.

Results and Discussion

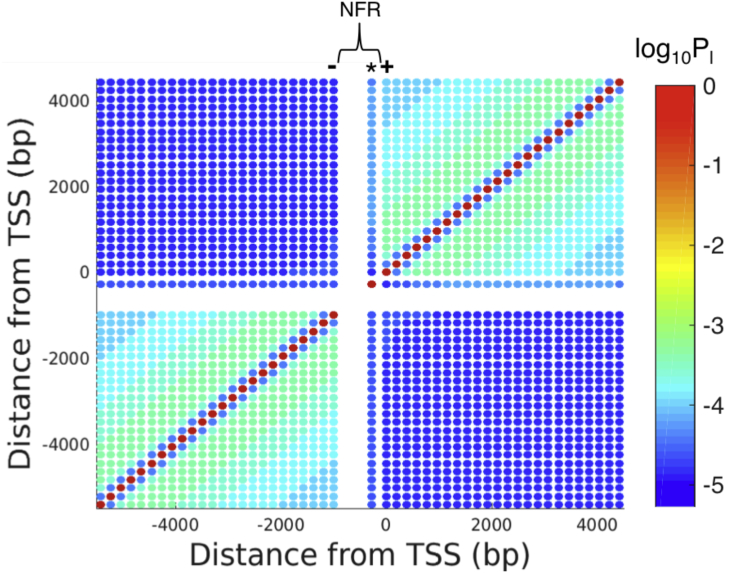
Fig. 2 shows the calculated looping probability for pairs of nucleosomes along the chromosome. We calculate these looping probabilities for locations every 45 bp along the wormlike chain, corresponding to the average linker length of the system. These locations are spaced farther apart than the contact radius of 5 nm (i.e., 16.7 bp) and are therefore not already looped. We find that the looping probability decreases nonmonotonically with loop length, as revealed by the color shift from red on the main diagonal (i.e., already looped) to dark blue on the nearest diagonal to light blue and yellow-green and back to darker blues on farther diagonals. Our model allows for loop-mediated spreading between any two nucleosomes, be they nearest neighbors or some distance apart. However, forming a loop between nearest neighbors is very unlikely because of the high cost of bending at such short length scales, as evidenced by the low (dark-blue) looping probabilities on the first diagonal in Fig. 2. As a result, spreading occurs through a trans-mechanism, rather than a cis-mechanism, that involves distal nucleosomes transiently looping. In addition, the large, dark-blue squares in the upper left and lower right indicate that looping between nucleosomes on different sides of the NFR is very unlikely. This observation suggests that the stiffness of the NFR inhibits looping contacts between the two surrounding flexible segments. Heterogeneity in the mechanics of the chromatin fiber thus directly impacts looping contacts, which in turn will influence the methylation profile.

Figure 2.

The heat map shows the log of the calculated looping probability for pairs of nucleosomes along the chromosome, with an NFR of 1000 bp. The white section from −1000 to 0 bp corresponds to the effective NFR. The dots appearing in that section correspond to looping with the nucleation site, which was inserted at −277 bp in the methylation-spreading experiments and, thus, lies within the effective NFR (16). The minus sign, star, and plus sign correspond to the −1 nucleosome, nucleation site, and +1 nucleosome, respectively. To see this figure in color, go online.

We define $p_i^{ss}$ as the steady-state, position-dependent methylation probability with a nucleation site 277 bp upstream of the TSS, the same location set in experiments (16). We also define $p_i^{ss\left(0\right)}$ as the steady-state methylation probability in the absence of a nucleation site. The steady-state profiles $p_i^{ss}$ and $p_i^{ss\left(0\right)}$ are determined by integrating Eq. 4. When obtaining $p_i^{ss\left(0\right)}$, the initial condition is set to p_i = 0 for all i. The solution $p_i^{ss\left(0\right)}$ is then used as the initial condition when obtaining $p_i^{ss}$ to mimic evolution of the experimental methyl profile from its baseline to an enriched state. At distances sufficiently far from the nucleation site, the inhomogeneous solution p_i tends to the homogeneous solution p. We integrate the governing master equation for a finite number of nucleosomes (400 total in this manuscript) and incorporate looping to nucleosomes outside of this range by approximating their methylation probability as p_i ≈ p.

The experimental methylation-spreading data are reported as relative enrichment against a known standard, so the absolute enrichment values can be considered to have arbitrary units based on the specific reference DNA (16). Our theoretical model produces predictions of the probability of methylation, which cannot be compared directly with the arbitrary units of the experimental data. To allow for a more fair comparison, we calculate the relative enrichment for our model as $p_i^{ss}/p_i^{ss\left(0\right)}$ and also rescale the experimental data by dividing the methylation profile on day 5 by the average methylation on day 0.

In fitting our theoretical predictions to the rescaled experimental data, we minimize the sum square of residuals for the location of the subdominant peak, the height of the main peak, and the ratio of peak heights (i.e., the height of the main peak divided by the height of the subdominant peak). We fix k_m/k_d = 0.042 as in (42).

The master equation describes the rate of change in methylation probability, and the equation contains a term for the change from methyl spreading arising from each other nucleosome and from the nucleation site. In examining the values of these rates of change, we note that the rate is much larger for the term corresponding to spreading from the nucleation site than for the terms corresponding to nucleosome-nucleosome spreading. This noticeable difference in magnitude indicates that the nucleation site is the main contribution to methyl spreading. As a result, the qualitative features of the methylation profile closely resemble those of the looping probability with the nucleation site, as seen in Fig. 3.

Figure 3.

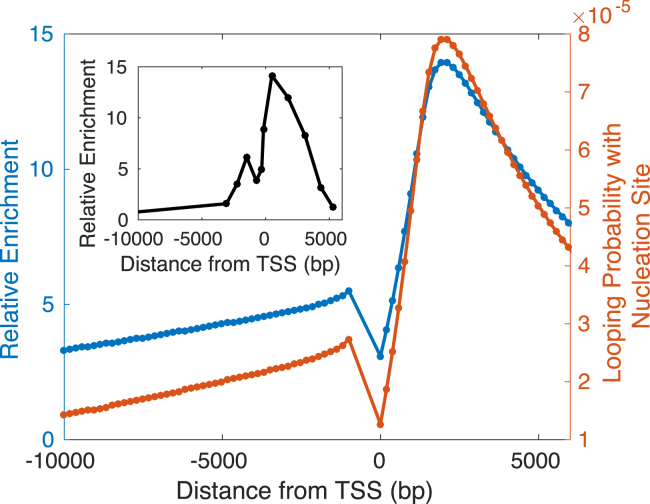
The solid blue curve (left y axis) in the main plot shows the steady-state relative enrichment of methylation, as predicted by our theoretical model. The inset shows the rescaled experimental data taken from mouse embryonic stem cells (i.e., H3K9me3 on day 5 divided by the average H3K9me3 on day 0) (16). The optimal parameters for our model are C_HP1,free = 1.37 × 10⁻⁵μM and an effective NFR of 1000 bp (fixing k_m/k_d = 0.042). The orange curve (right y axis) in the main plot shows the probability that a nucleosome forms a loop with the nucleation site as a function of genomic distance from the TSS. To see this figure in color, go online.

The orange curve in Fig. 3 shows the probability of looping with the nucleation site, which is higher for nucleosomes downstream of the TSS than for those upstream. Located at −277 bp relative to the TSS, the nucleation site is closer to the downstream nuclesomes (277 bp away from the +1 nucleosome at 0 bp) than to the upstream nucleosomes (723 bp away from the −1 nucleosome at −1000 bp). In addition, the inherent stiffness of the NFR limits its ability to bend to form loops. Together, the difference in proximity to the nucleation site coupled with the stiffness of the intervening NFR causes the nucleosome-nucleation site looping probability to be lower for upstream nucleosomes. As a result, downstream nucleosomes contact the nucleation site more often and therefore acquire a higher level of methylation than do upstream nucleosomes. Thus, the asymmetry in the methylation profile occurs because of the relative position of the nucleation site, which leads to differences in the magnitude of the nucleosome-nucleation site looping probability and, hence, the methylation level for upstream and downstream nucleosomes.

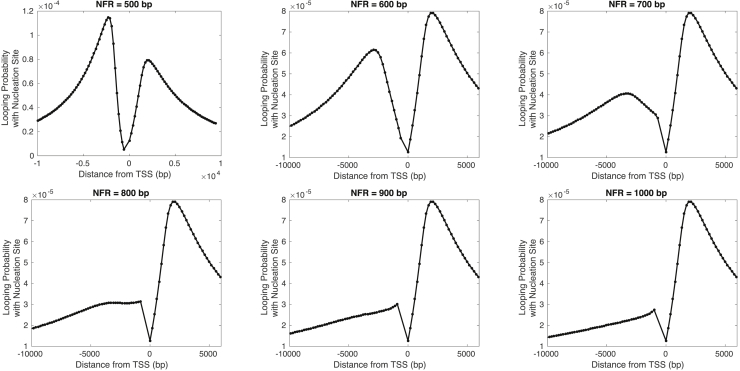
Fig. 4 shows results for the probability of looping with the nucleation site for NFR size ranging from 500 to 1000 bp. These results exhibit similar qualitative behavior for NFR ranging from 700 to 1000 bp. However, significant deviation arises for shorter NFR size, as demonstrated in the predictions for 500 and 600 bp. Therefore, our results in Fig. 3 are consistent with behavior at the intermediate and higher end of the predicted range of 450–1250 bp with considerable deviation only at the lower end (i.e., between 450 and 700 bp).

Figure 4.

Theoretical predictions for the probability that a nucleosome forms a loop with the nucleation site as a function of genomic distance from the TSS for varying sizes of NFR from 500 to 1000 bp.

The deviation in the looping probability at shorter NFR sizes can be attributed to the shorter distance between upstream nucleosomes and the nucleation site. As the NFR size decreases, upstream nucleosomes become closer to the fixed nucleation site, and their probability of looping with the nucleation site increases (we note, however, that the looping probability will not always increase with decreasing loop length because the relationship between the two quantities is nonmonotonic). Thus, as the top left plot in Fig. 4 shows, we observe that asymmetry in the looping probability (and in turn the methylation profile) can occur in the opposite direction, at least in principle, by modulating the positions of the upstream nucleosomes relative to the nucleation site.

Fig. 3 also shows a comparison of the rescaled experimental data (inset curve) and the solution to the master equation (solid blue curve) with optimal free HP1 concentration C_HP1,free = 1.37 × 10⁻⁵ μM (corresponding to total HP1 concentration C_HP1,total = 3.63 × 10⁻³ μM) and an effective NFR of 1000 bp. Our model reproduces both the magnitude of enrichment and the extent of spreading seen in experiments after 5 days from incubation (i.e., introduction of the nucleation site) (16). We find that the relative enrichment $p_i^{ss}/p_i^{ss\left(0\right)}$ is largely insensitive to k_m/k_d because k_m/k_d proportionately affects both $p_i^{ss}$ and $p_i^{ss\left(0\right)}$. Further experimental analyses that measure the absolute fraction methylation would enable a more extensive determination of model parameters, especially k_m/k_d.

Our model also replicates the presence of a smaller peak to the left of the central peak in enrichment. In our model, this peak occurs as a result of the presence of the NFR and the differential elasticities of the NFR and the surrounding nucleosome-containing chromatin. Fig. 5 shows the methylation profile for two homogeneous polymers, each composed of one wormlike chain of a single persistence length. As with the heterogeneous copolymer, we include an effective NFR of 1000 bp with no nucleosomes and assume a linker length of 45 bp between nucleosomes outside of the NFR. In this setup, all three segments (the NFR and the two surrounding, nucleosome-containing segments) have the same persistence length. Our theoretical model predicts two peaks of similar height when the persistence length of the homogeneous polymer is 53 nm (that of bare DNA), failing to capture the more pronounced asymmetry in the experimental profile. Even with a reduced persistence length of 17.68 nm for the homogeneous polymer, our model still cannot describe the asymmetrical experimental profile, predicting only one peak.

Figure 5.

The top plot shows the steady-state relative enrichment of methylation, as predicted by our theoretical model for a homogeneous polymer with a single persistence length of 53 nm (in blue, on the left y axis and depicted in the bottom schematic) and 17.68 nm (in orange, on the right y axis and depicted in the bottom schematic) for the optimal parameters C_HP1,free = 1.37 × 10⁻⁵μM and an effective NFR of 1000 bp (fixing k_m/k_d = 0.042). To see this figure in color, go online.

The stiffness that arises from the absence of nucleosomes in the NFR limits the chromosome’s ability to form loops in that region, preventing methyl spreading and causing a depletion of enrichment. The methylation profile derived from our model of a heterogeneous copolymer qualitatively reproduces the shape of the experimental profile and quantitatively matches the magnitude of the relative enrichment. This agreement demonstrates that heterogeneity in the elasticity of the chromatin fiber is a key feature that explains the asymmetry of the methylation profile.

Together, the position of the nucleation site relative to the +1 and −1 nucleosomes and the size of the NFR determine the location of the left peak as well as the relative heights of the two peaks. Changes to the position of the nucleation site and/or the size of the NFR alter the distance between the nucleation site and nucleosomes in the chain, thereby affecting the magnitude of the looping probability between each nucleosome and the nucleation site and shifting which nucleosomes are more likely to acquire a methyl mark. The asymmetry in the methylation profile thus depends on whether upstream or downstream nucleosomes have a higher probability of looping with the nucleation site, which is determined by the relative position of the nucleation site and the size of the NFR.

The concentration of HP1 determines the magnitude of the relative enrichment. Experimental measurements of the binding affinity of HP1 show that it binds to both methylated and unmethylated nucleosomes but preferentially binds to methylated ones (9). The concentration of HP1α dictates the ratio of its binding to methylated and unmethylated nucleosomes, which in turn determines the height of the main peak in the relative enrichment. The more favorable it is for HP1α to bind to the nucleation site relative to the surrounding nucleosomes, the greater the enrichment.

The location of the nucleation site relative to the downstream nucleosomes sets the position of the right peak. Because nucleosome-nucleation site looping rather than nucleosome-nucleosome looping is the primary contributor to methyl spreading, the probability of looping with the nucleation site determines which nucleosomes acquire greater enrichment of methylation. Thus, the location of the right peak coincides with the peak in the nucleosome-nucleation site looping probability, as seen in Fig. 3. In both the methyl-spreading experiments (16) and our model, the location of the nucleation site is fixed. As a result, the distance between each downstream nucleosome and the nucleation site, and hence each nucleosome-nucleation site looping probability, is also fixed and unaffected by the choice of the parameters C_HP1,free and k_m/k_d. Under our model, the location of the right peak would only shift if the location of the nucleation site shifted, thus changing the nucleosome-nucleation site distances and looping probabilities.

We note that our model overestimates the relative enrichment at the left and right tails of the methylation profile. This difference might be attributed to our treatment of the ends of the chromosomal segment and the influence of unspecified biological factors that are not present in our model. To avoid an artificial end effect and account for the continuation of the chromosome past the local section of interest, we include in our master equation approach looping with an infinite array of nucleosomes beyond the range of the experimental data shown in Fig. 3. This inclusion ensures that our model’s predictions are not sensitive to the size of the system, but it may also not fully reflect the biological features of the extended regions. Beyond the local region, we assume continuity of the persistence length of 17.68 nm and thus homogeneity in chromatin elasticity. However, it is possible that there are other genes nearby with their own TSSs that cause heterogeneity in the fiber’s stiffness and limit looping contacts, thereby reducing the relative enrichment below the values we predict. There may also be additional proteins that bind to the chromatin fiber at specific locations and in turn alter its mechanical properties and looping behavior. Without precise knowledge of such factors, we omit them from our model to avoid unknown or uncertain parameters, with the understanding that doing so might cause a quantitative difference in relative enrichment at the tails. Despite this difference, the success of our model in recapitulating the overall shape of the methylation profile and the magnitude of the two peaks highlights the significant impact of chromatin structural mechanics on methyl spreading.

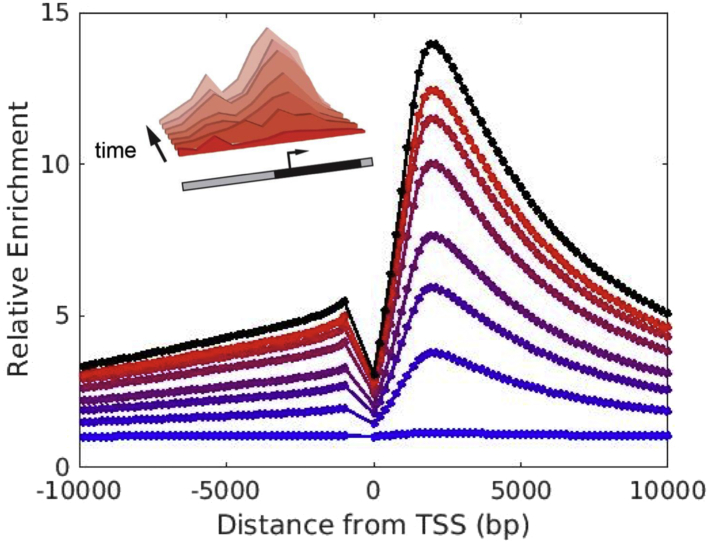
Based on our model, we predict the dynamics of the relative enrichment after the introduction of the nucleation site. Fig. 6 shows numerical integration of our master equation (Eq. 4) for model parameters k_m/k_d = 0.042 and C_HP1,free = 1.37 × 10⁻⁵ μM and an effective NFR of 1000 bp. We define the dimensionless time τ = k_dt, which gives the time relative to the nucleosome turnover time 1/k_d. Fig. 6 shows relative enrichment p_i(t)/$p_i^{ss\left(0\right)}$ for time running from τ = k_dt = 0.05 (blue) to τ = k_dt = 0.90 (red) for a system that begins at p_i(t = 0) = $p_i^{ss\left(0\right)}$. The black curve shows the steady-state relative enrichment $p_i^{ss}/p_i^{ss\left(0\right)}$, which is the solution as τ → ∞. The inset shows the raw (i.e., not rescaled) experimental ChIP sequencing data (16) for times running from 0 to 5 days after incubation. For our predictions, the onset of the spreading occurs on timescales comparable to 1/k_d, suggesting that the demethylation rate (dictated by nucleosome turnover) sets the time scale of local enrichment. Upon removal of the nucleation site, the methylated domain will dissipate. As stated earlier, we assume in our treatment that the chromosomal DNA is uncondensed, lacking higher order structure. Without structural components in our model to create positive feedback between the three-dimensional organization and the one-dimensional methylation sequence, there is no epigenetic memory of the methylated domain. The long time associated with the experimental enrichment in H3K9 marks necessitates a theoretical treatment that can accommodate such timescales.

Figure 6.

Dynamics of the relative enrichment p_i(t)/$p_i^{ss\left(0\right)}$ for time running from τ = k_dt = 0.05 (blue) to τ = k_dt = 0.90 (red) for k_m/k_d = 0.042, C_HP1,free = 1.37 × 10⁻⁵μM, and an effective NFR of 1000 bp. The black curve shows the steady-state relative enrichment $p_i^{ss}/p_i^{ss\left(0\right)}$. The inset shows the ChIP sequencing data presented in (16) for 0 time to 5 days after incubation. To see this figure in color, go online.

Conclusions

In this work, we address the effect of chromosome structure and mechanics on the local, loop-mediated spreading of methylation around a nucleation site. We propose a physical mechanism that explains how the elasticity of the chromosome determines which segments can come into spatial proximity and participate in methyl mark conferral. Differential stiffness along the chromatin fiber facilitates some chromosomal contacts and inhibits others, thereby laying the basis for the resulting methylation profile. Thus, our model shows that chromatin structural mechanics plays an important role in dictating the local spreading of methyl marks and also provides a plausible explanation of how asymmetrical spreading behavior arises because of the heterogeneity in the elasticity of the chromatin fiber.

Because heterogeneity in chromatin organization and its mechanics affects the spreading of epigenetic modifications, the cell could use nucleosome positioning as a way to control the conferral of epigenetic marks and, consequently, gene regulation. By altering the spacing between nucleosomes, the cell could drive changes in the chromatin’s mechanical properties, which in turn would impact the epigenetic profile to cause gene activation or repression. The cell could similarly rely on nucleosome positioning to ensure that specific regions of the chromosome contain the appropriate epigenetic modifications and thereby robustly re-establish the epigenetic sequence after replication.

The predictions from our model are consistent with the degree of spreading and the asymmetrical profile observed experimentally. The fact that a relatively simple structural description of the chromatin fiber (a heterogeneous copolymer) captures the qualitative features of the experimental methyl profile reinforces that structural mechanics is a fundamental feature governing methyl spreading. Our work suggests that the inherent dynamics of DNA as a polymer, coupled with its structure and mechanics, could serve as a built-in physical mechanism to prevent unrestrained spreading. The results from our theoretical model may help explain how localized regions of epigenetic marks arise without the need for DNA-associated proteins to demarcate domain boundaries because stiffer regions of DNA would serve as natural barriers to epigenetic spreading. Furthermore, our model could be extended to apply to other epigenetic marks and/or experimental systems. Given the knowledge of the relevant biological details, such as binding affinities and the interactions between proteins that control organization and those that facilitate mark spreading, aspects of our model could be adjusted to reflect different biological or experimental conditions. In particular, the length of the NFR, the persistence length of the surrounding chromatin segments, the average linker length between nucleosomes, the binding affinity of HP1 (or an HP1 analog), and the relative rate of mark transfer could all be tuned appropriately. Thus, although the results of this study describe one specific epigenetic mark and experimental setup, our model framework is flexible enough to be adapted to apply more broadly.

With a basic understanding of the influence of chromosomal mechanical properties on local spreading, future work will investigate the physical components and conditions required for gene silencing. Our model will be used to determine the features (perhaps the location and strength of additional nucleation sites) necessary to increase the methylation level past the requisite threshold to render the gene inactive. In this work, we assume that the protein complex attached at the nucleation site remains bound for the duration of the experiment. Follow-up work will address the extent to which a finite on or off binding rate for the protein complex affects the flexibility of the NFR and in turn the looping behavior and methylation profile.

Author Contributions

S.H.S. designed the research, conducted the research, and wrote the article. D.K. designed and conducted the research. B.G.B. designed the research. A.J.S. designed the research and wrote the article.

Editor: Anatoly Kolomeisky.