The Location and Rate of the Phosphate Release Step in the Muscle Cross-Bridge Cycle

Abstract

It is controversial whether the phosphate (Pi) release step in the cross-bridge cycle occurs before or after the first tension-generating step and whether it is fast or slow. We have therefore modified our previous model of the frog cross-bridge cycle by including a Pi release step either before (model A) or after (model B) the first tension-generating step and refined the two models by downhill simplex runs against experimental data for the force-velocity relation and the tension transients after length steps. Pi release step was initially made slow (70 s⁻¹), but after refinement, it became fast (∼500 s⁻¹ for model A and ∼6000 s⁻¹ for model B). The two models gave similar fits to the experimental tension transients after length steps, but model A gave a better fit to the lengthening limb of the force-velocity relation than model B. 50 mM Pi inhibited the isometric tension of model A by ∼50% but that of model B by only ∼25%. The half-inhibition was at 6.0 mM Pi for model A and at 1.6 mM Pi for model B. The values for model A were consistent with experimental data. We also simulated the effect Pi jump as in caged Pi experiments. For model A, a Pi jump induced a tension fall at a rate similar to the experimental phase II. There was then a small rise in tension to the steady state mimicking the experimental phase III. The initial tension fall was caused by detachment of M⋅ADP⋅Pi myosin heads from actin and reversal of the first tension-generating step. For model B, the fall in tension was more rapid and due to reversal of the first tension-generating step, and phase III was not observed. We conclude that, as in model A, the Pi release step is before the first tension-generating step and is moderately fast.

Significance

Our day-to-day activities—walking, talking, breathing, etc.—are dependent on muscle, a motor that produces movement. At a subcellular, molecular level, it is the interaction of two proteins, myosin heads (cross-bridges) and actin filaments; a cross-bridge attaches to actin, generates force and power, and then detaches. This mechanics cycle is coupled to an enzymic reaction, hydrolysis of ATP by actomyosin ATPase, so that energy liberated during release of phosphate (Pi) and ADP is converted into work (and heat): an active muscle is a “machine converting chemical to mechanical energy.” Exactly how these two cyclic processes, chemical and mechanical, are coupled remains unclear. Our modeling of Pi effects on the cross-bridge cycle provides important insight and shows inadequacies.

Introduction

In each turn of the muscle cross-bridge cycle, the products of ATP hydrolysis, phosphate (Pi) and ADP, are released in that order (1,2). Pi release occurs close to the first tension-generating step, but it is controversial whether it occurs before or after this step and how fast it is (3). This is hampering the attainment of a complete description of the kinetic pathway of the cycle.

Information about the Pi release step has been obtained by altering the [Pi] of permeabilized mammalian muscle fibers or of myofibrils. Raising the [Pi] decreases the isometric tension (4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14). The dependence of the isometric tension on the added [Pi] is approximately hyperbolic (13). Pi reduces the stiffness of fibers but to a smaller extent than the isometric tension (7,9,15,16). However, if filament compliance is taken into account, the stiffness of the cross-bridge array declines in proportion to the tension, suggesting that the force per cross-bridge remains constant (17) and a common process causes loss of both stiffness and tension. The ATPase and unloaded shortening velocity are little affected by altering [Pi] (18,19). A rise in [Pi] is a major cause of muscle fatigue (5,20, 21, 22, 23, 24), so understanding the molecular basis of the inhibition of tension by Pi is an important goal.

Perturbation of the cross-bridge cycle by rapid changes in length, tension, temperature, pressure, or Pi concentration has added substantially to our understanding of the cycle. But, unlike the other perturbants, Pi jumps should target only one step in the cycle, the Pi release step, and so examining their effect should be especially instructive. By photolysis of caged Pi, it is possible to cause very rapid (0.04 ms) increases in the [Pi] bathing rabbit psoas fibers (9,25). In the first phase (I) of the response to the raised [Pi], an appreciable lag (1–4 ms at 10°C) appeared to be present before a second phase (II), in which there was a rapid near-exponential fall in tension whose average rate at 10°C increased from 30 to 70 s⁻¹ as [Pi] increased from 2 to 12 mM. This tension fall was accompanied by a slightly smaller fall in stiffness. This was followed by a third phase (III), characterized by a small slow late rise in tension to the final steady-state level. It was concluded that the Pi release step was an immediate neighbor of the first tension-generating step in a two-step process. It has usually been supposed that the drop in tension was caused by a reversal of the first tension-generating step and that the Pi release step occurred after this step (9,11,25, 26, 27, 28, 29, 30, 31). But a minority view was that the release step occurred before the tensing step (32, 33, 34, 35, 36, 37, 38). Also, there have been a few studies in which, using different techniques, Pi release has been considered not directly coupled to force generation in the cross-bridge cycle in muscle (39,40). In different interpretations, the Pi release step in muscle has been taken to be fast or relatively slow (9,11,25, 26, 27, 28, 29, 30, 31, 32,34,35,37,38). It is relevant to note also that the Pi sensitivity and reversibility seen in muscle are in stark contrast to the difficulty of binding Pi to the A⋅M⋅ADP state prepared by binding M⋅ADP to actin in solution (41). Such considerations led Sleep and Hutton (40) to propose the existence of a precursor state (A⋅M⋅ADP) on the pathway of the cross-bridge cycle.

Until recently, the notion that the tension fall is due to the reversal of the tensing step has not been questioned, probably because pre-tensing states have in the past been assumed not to bear force (9). If that were so, detachment of M⋅ADP⋅Pi from actin would reduce stiffness, but not tension. Smith (35) challenged this common interpretation by pointing out that the tension fall (∼100 s⁻¹) after a Pi jump was too slow to be compatible with the rapid tension changes (up to 5000 s⁻¹) observed after rapid length steps (42). He instead proposed that the relatively slow fall in tension when Pi was raised was largely due to the slow detachment of M⋅ADP⋅Pi from actin. This required the Pi release step to occur before the first tensing step. This gave a simple and satisfying explanation of why the time courses of tension fall in phase II and stiffness decrease were so similar. His model gave a good account of the effect of Pi on tension and stiffness and of the phase II tension response after a Pi jump. This basic idea that Pi release occurred before the first force-generating step in the cross-bridge cycle has received support from a number of later experimental and modeling studies (36,43,44).

Modeling of the effect of Pi on the cross-bridge cycle can give important insights. In particular, the properties of muscle can be examined over a wider range of [Pi] that cannot be achieved experimentally. Also, important insights on the molecular processes responsible for tension changes can be gained by studying the effect of [Pi] on the occupancies of the states of the cycle. We previously developed a model of the cross-bridge cycle in frog muscle that was able to give a good account of the force-velocity relation and the tension transients after rapid length steps (45). Additionally, this basic model could be used to account for temperature jumps and the temperature dependence of isometric tension and the force-velocity relation (46) in mammalian muscle. Analyses indicated that mammalian muscle is adapted to operate at ∼10°C higher temperature, so that mammalian muscle data at 10–15°C were comparable to frog muscle data at 0–5°C (see (46)). Hence, although the ideal would be to examine the effects of Pi on a model specific for mammalian muscle, we have found that our frog model can give important insights into the mechanism by which Pi affects the cross-bridge cycle by studying the effect of [Pi] on isometric tension and the force-velocity relation and by simulating Pi jumps.

Our main aims were 1) to examine whether the Pi release step occurs before or after the first tensing step and 2) to consider whether the Pi release step is fast or slow.

Methods

Kinetic schemes

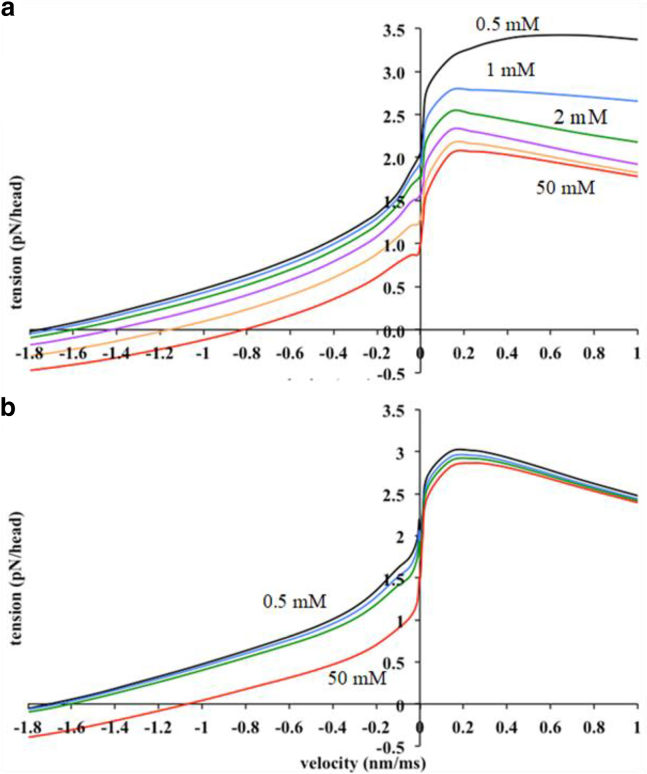
Model A

Our kinetic scheme for model A, in which the Pi release occurs before the first tensing step, is shown in Fig. 1. After attachment of M⋅ADP⋅Pi to actin, Pi is released with no change in strain. The first tensing step that follows generates tension by a conformational change in the myosin head (symbolized in the diagram by showing a myosin head as M′). This is followed by a second tensing step (the myosin head after the conformational being symbolized by M″). The cycle is completed by a sequence of a slow release of ADP, followed immediately by rapid binding of ATP and detachment of M⋅ATP. To avoid the build-up of highly strained intermediates during lengthening if the Pi release step were slow, the scheme allows the reversible strain-sensitive detachment of M⋅ADP from actin. So, if during lengthening, an AM⋅ADP intermediate became highly positively strained and therefore contributed a substantial positive tension, the M⋅ADP head would rapidly detach with the loss of this tension and then reattach with near-zero strain.

Figure 1.

Kinetic scheme for model A.

This model has 19 parameters, three more than our earlier model with two tensing steps that assumed that Pi release was very fast and closely coupled to the first tensing step (45). The additional parameters required were K_p, the second-order equilibrium constant of the Pi release step; k_p, the forward rate constant of this step; and a factor d₁ by which the rate constant of detachment of M⋅ADP (k_det2) is reduced compared with that of M⋅ADP⋅Pi (k_det1). It was assumed that the rate constants of attachment (k_att) were identical for M⋅ADP and M⋅ADP⋅Pi. The parameters are given in Table 1.

Table 1.

Comparison of Parameters and Scores for Models A and B at the Start and After Refinement

Model	A		B
	Start	After	Start	After
kaAM′ (s−1)	266	323	266	254
kdAM (s−1)	0.857	2.37	0.857	0.996
kkyd (s−1)	100	127	100	129
k−hyd (s−1)	10	12.7	10	12.9
Ktens1AM	234	221	234	48.4
Ktens2AM	173	176	173	37.8
ktens1AM (s−1)	2060	3210	2060	1398
ktens2AM (s−1)	7670	13,080	7670	2340
kiAM (s−1)	332	570	332	265
ΔD (nm)	0.698	0.561	0.698	1.22
κ (pΝ/nm)	1.7	1.7	1.7	1.71
l1 (nm)	5.6	5.9	5.6	6.75
l2 (nm)	4.55	4.47	4.55	4.98
d (nm)	2.16	2.76	2.16	2.3
f1	0.402	0.531	0.402	0.4
f2	0.851	0.555	0.851	0.581
c	0.546	0.482	0.546	0.458
kp (s−1)	70	493	70	6620
Kp (mM)	10	1.33	10	3.14
d1	0.01	0.0005	0.01	0.0026
d2	–	–	0.01	0.000069
P0 (pN/Head)	2.47	2.03	2.66	1.91
Isometric occupancy attached	0.546	0.482	0.546	0.458
Isometric ATPase (s−1)	0.189	0.477	0.236	0.012
% efficiency	30.2	31.7	34.9	40.7
P0 score	0.546	0.271	0.662	0.193
Efficiency score	0.123	0.104	0.064	0.009
pv score	14.13	1.014	13.38	1.312
κ score	0	0	0	0
T1 score	0.852	0.342	1.709	0.26
Transient score	4.962	1.965	12.52	1.873
Pi score	1.285	0.048	1.04	0.592
Total score	21.9	3.74	29.4	4.24

Model B

The kinetic scheme for the case in which the Pi release occurs after the first tensing step is shown in Fig. 2. After attachment of M⋅ADP⋅Pi to actin, the first tensing step generates tension, and it is only after this step that Pi is released. This is followed by a second tensing step. The cycle is completed by a slow release of ADP, followed immediately by binding of ATP and detachment of M⋅ATP. To avoid the build-up of highly strained intermediates during both shortening or lengthening, the scheme allows the reversible strain-sensitive detachment of both M′⋅ADP⋅Pi and M′⋅ADP from actin. So, if the Pi release step were slow, then during shortening, an AM′⋅ADP⋅Pi intermediate would tend to become highly negatively strained and thus contribute a substantial negative tension. However, if the M′⋅ADP⋅Pi head could rapidly detach with the loss of this negative tension and then reattach with near-zero strain, this problem is removed.

Figure 2.

Kinetic scheme for model B.

This model has 20 parameters (see Table 1), four more than our earlier model (40). As with model A, the additional parameters required included K_p and k_p. But now, two additional factors, d₁ and d₂, by which the rate constants of detachment of M′⋅ADP⋅Pi (k_det2) and M′⋅ADP (k_det3) were changed compared with that of M⋅ADP⋅Pi (k_det1) were included. It was again assumed that the rate constants of attachment (k_att) were identical for all three nucleotide complexes. The rate constants of very rapid steps were capped at 10⁵ s⁻¹.

For both types of model, the starting value of K_p at the beginning of refinement of the initial model was 10 mM and that of k_p was 70 s⁻¹, a value similar to the rate constant of Pi release for actomyosin in solution (37). The starting values of d₁ and d₂ were both 0.01. The initial values of the other parameters were the same as those found for our earlier model with no kinetically separate Pi release (45) and are given in Table 1. It was assumed that the Pi concentration in muscle with no added Pi was 0.5 mM (13).

To convert these two schemes into mechanokinetic models, in addition to specifying the rate constants of the steps in solution, it is necessary to define how strain affects those rate constants. This requires the cross-bridge stiffness to be specified together with the relative contributions of cross-bridges and filaments to the compliance of the sarcomere in an isometric contraction and the strain sensitivity of tensing steps. The starting values of these parameters were as obtained or used previously (45).

The refinements each consisted of five successive downhill simplex runs. The refined model after each of these runs became the starting model for the subsequent run. Each model was scored for several properties. As listed below, these included the same criteria as previously used (45). Thus, scores for each model included the fits to the isometric tension, to the force-velocity relation, to the time courses of tension transients, to the tension (T₁) at the end of a range of length steps, to the thermodynamic efficiency, and to the value of the cross-bridge stiffness.

The transient score: tension responses to length steps

The experimental tension-time traces (of (42)) were digitized and tension values intrapolated at 0.1 ms intervals after normalization with respect to the isometric tension (Po). The root mean-square (rms) deviation of the normalized tensions of the model from the experimental values was calculated in three time periods: 1) at 0.1 ms intervals from the end of the length step up to 4 ms, 2) at 0.1 ms intervals from 4 to 8 ms, and 3) at 0.2 ms intervals from 8 to 200 ms. The goodness-of-fit value for a model (the “transient score”) was taken as the sum of twice the rms deviation for (1) plus the rms deviations for (2) and (3).

T₁ score

To obtain the T₁- and T₂-values of the model for each length step, the tension-time curves were analyzed as described (42). The goodness-of-fit value for the normalized T₁ tension (the “T₁ score”) was taken to be the rms deviation between the model and the experimental normalized T₁ tensions for the five length steps from −6 to +1.5 nm/hs. The subsequent tension recovery was then examined to get the maximum (for a release) or minimum (for a stretch) corresponding to the T₂ tension.

pv score: force-velocity relation

The steady-state force-velocity relation of our models is compared with the data of Edman (47). The goodness-of-fit value of a model (the “pv score”) was taken as the rms deviation of the normalized tensions of the model from those of experiment for 21 velocities.

P₀ score

The goodness-of-fit for the isometric tension (the “P₀ score”) was given by the modulus of the fractional deviation of the isometric tension from the experimental value of 1.6 pN/head (7).

Efficiency score

The goodness-of-fit for the optimum thermodynamic efficiency (the “efficiency score”) was given by the modulus of the fractional deviation of the efficiency of the model from an experimental value of 40% (see (45)).

k score

The stiffness, k, of cross-bridges was 1.7 pN/nm. Any model with a cross-bridge stiffness less than 1.7 pN/nm was penalized by calculating a goodness-of-fit value (the “k score”) equal to the fractional difference between this and the model stiffness. Models with a cross-bridge stiffness greater than 1.7 pN/nm were not penalized.

The total score for each model was obtained by summing the individual goodness-of-fit values for the characteristics described above, each multiplied by a weighting factor (the weighting factors were 100 for the force-velocity relation, 50 for T₁ tension, 10 for the transient tension responses, 1 for the isometric tension, 0.5 for the efficiency, and 2 for the cross-bridge stiffness).

With the aim of achieving a global search of parameters, models were refined by minimizing the total score using simulated annealing (see (45)), followed by repeated downhill simplex runs. The starting simplex was created by incrementing or decrementing in turn each of the starting parameters by a fraction 0.2. Programs written in C were converted for parallel programming with OpenMP protocols and calculations performed on the Bristol University high performance computer BlueCrystal phase 3.

For simulating the Pi jumps, the [Pi] for each refined model was changed linearly over 0.04 ms. The time courses of the tension changes after Pi jumps were fitted with a biexponential function of the form P + A(1 − exp[−at]) + B(1 − exp[−bt]), where t is the time, P is the initial isometric tension, A and B are the amplitudes (positive for a tension rise, negative for a tension fall), and a and b are the rates of the fast and slow phases. The fit was refined by repeated downhill simplex runs, using as a score the rms deviation between the tension and the biexponential function calculated at equal time intervals. We also calculated the average initial rate of tension fall from the time for half the tension fall by multiplying the reciprocal half time by ln2.

Results

Refinement of models

We refined two types of model: in model A, the Pi release step preceded the first tensing step, whereas in model B, it followed the first tensing step. Table 1 shows the parameters and scores of the starting models and after the end of their refinements. Notable changes during the refinement included the very large increase in k_p, the rate constant of Pi release, a decrease in K_p, the equilibrium constant of Pi release, and the decrease in parameters d₁ and d₂. The score for the fit to the time course of tension transients was slightly lower (i.e., better) for model B than for model A, but the score for the fit to the force-velocity relation was appreciably better for model A. The total score for model A was lower than that for model B.

Comparison of the force-velocity relation for models A and B

Fig. 3 a shows the steady-state force-velocity relation for the refined models A and B at the endogenous [Pi] of 0.5 mM. Both gave reasonable fits to the experimental data of Edman (47). In the shortening limb, there is little difference between models A and B with regard to their fit to the Edman data, but the model plots were slightly less curved than the experimental plot. Both models gave a value of the unloaded shortening velocity (v_max) similar to the experimental value. At the small lengthening velocities studied by Edman (47), model A gave a better fit to the experimental. At larger lengthening velocities, which were not studied by Edman (47), model A approached a plateau, whereas model B showed a substantial decline with increasing velocity. Such a decline has not been observed in other studies of lengthening muscle (e.g., (48)).

Figure 3.

Dependence on sliding velocity of tension (a), ATPase (b), and power (c) of the models (model A, solid circles; model B, solid triangles). (a) Force-velocity relation for models (compared with the experimental data from Edman (42), shown as open squares) is given. (The two models show data similar to experimental on the shortening side, but the lengthening side is different; model B shows decrease of force). (b) Dependence on velocity of the ATPase rate is shown. (c) Dependence on the shortening velocity of the power output is shown. (ATPase and power (and efficiency) are basically similar for the two models.)

Fig. 3 b compares the dependence on velocity of the ATPase for the two models. Both show a near-hyperbolic relation of the ATPase with shortening velocity with the ATPase nearly reaching a plateau at velocities approaching v_max. Model A gave a slightly higher ATPase than model B. The ATPase for both models was very low for lengthening velocities.

As expected from the similarity of their force-velocity relations, the power-velocity relations for models A and B were very similar, with a maximal power of 508 zW/head at a shortening velocity of −0.74 nm/ms (Fig. 3 c). The efficiency-velocity relations of the two models were also similar, but model A gave a maximal efficiency of ∼32%, and model B gave a higher maximal efficiency of ∼41%.

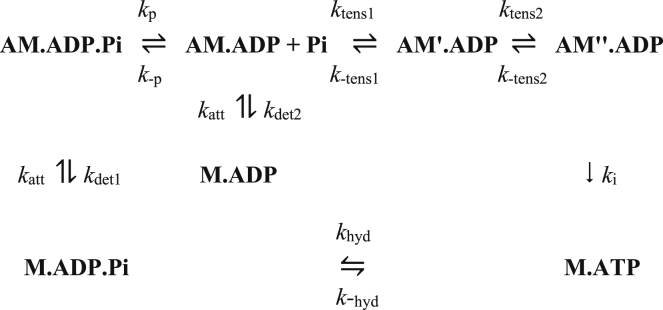
Dependence of the occupancies of cross-bridge states on the velocity

Fig. 4 a shows for model A the dependence on sliding velocity of the occupancies of both attached and detached states. The occupancy of all states changed substantially on either side of zero velocity. The occupancies of AM⋅ADP⋅Pi and AM⋅ADP were higher for lengthening velocities than for shortening velocities, whereas the occupancy of AM′⋅ADP was higher on the shortening side and that of AM″⋅ADP was negligible on the lengthening side and only became significant during shortening. So, on the lengthening side, only the AM⋅ADP⋅Pi and AM⋅ADP states and, to a minor extent, AM′⋅ADP contributed. Lengthening would cause the first tensing step in model A to shut down, but the Pi release step would be unaffected. This explains why in lengthening, the occupancy of AM⋅ADP is high. The total occupancy of attached states was highest at zero velocity (isometric state) but decreased on either side.

Figure 4.

Dependence on velocity of occupancies of cross-bridge states. (a) For model A: occupancy of AM⋅ADP⋅Pi, blue; AM⋅ADP, green; AM′⋅ADP, red; AM″⋅ADP, purple; M⋅ADP⋅Pi, orange; M⋅ATP, brown; total occupancy of attached states, black. (b) For model B: occupancy of AM⋅ADP ⋅Pi, blue; AM′⋅ADP⋅Pi, pink; AM′⋅ADP, red; AM″⋅ADP, purple; M⋅ADP⋅Pi, orange; M⋅ATP, brown; total occupancy of attached states, black.

The dependence on velocity of the occupancies of the states in model B was broadly similar to that of model A (Fig. 4 b). However, on the lengthening side, AM⋅ADP⋅Pi is dominant, and the occupancy of AM′⋅ADP⋅Pi was low.

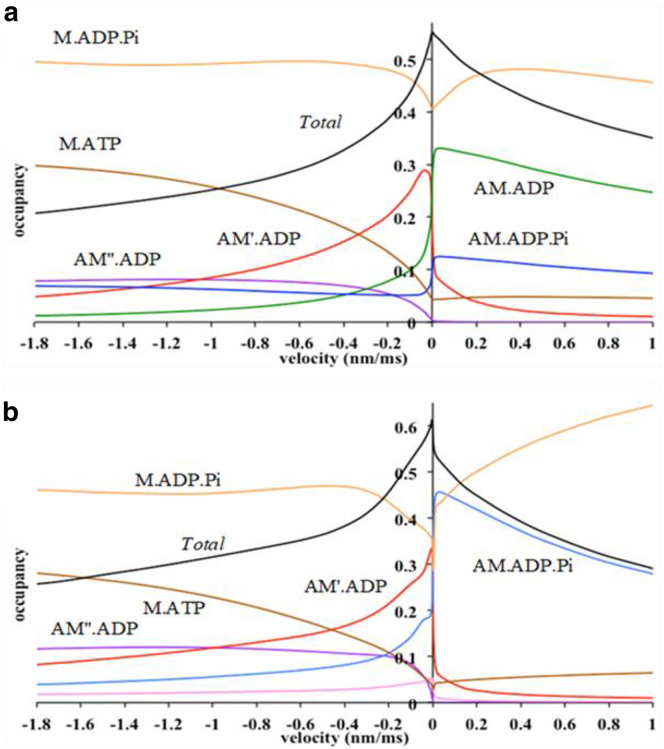
Dependence of isometric tension on [Pi]

Fig. 5 compares the dependence on [Pi] of the isometric tension of models A and B over the experimental range of 0–50 mM. Pi inhibits the isometric tension of model A substantially; at 50 mM Pi, the inhibition was 51%. The plot is not perfectly hyperbolic because even at 100 mM, the inhibition was not saturated. This is understandable because at very high [Pi], the equilibrium of the Pi release step would lie strongly in favor of AM⋅ADP⋅Pi, so the tensing steps would barely occur. The [Pi] giving half the inhibition of that at 50 mM Pi was 6.0 mM, not very different from the value of 9 mM found by Coupland et al. (13) for rabbit fibers at 10°C.

Figure 5.

Inhibition of isometric tension by [Pi]. Tension inhibition with Pi added is plotted as a percentage of control isometric tension (Po). Model A, solid lines; model B, dashed lines. (Note that tension inhibition is greater with model A.)

The inhibition by Pi of the isometric tension of model B was much smaller; at 50 mM Pi, the inhibition was only 25.6%. Notably, substantial inhibition occurred at low [Pi]; the [Pi] giving half the inhibition of that obtained with 50 mM Pi was only 1.5 mM. Thus, the inhibition of isometric tension by Pi of model A was closer to the experimental data on rabbit fibers.

Further analyses of the isometric state showed that for model A, the total fraction of heads attached to actin declined with increase of [Pi] from 0.5 at 0.5 mM Pi to 0.36 at 100 mM Pi; this is consistent with the reduction in fiber stiffness caused by addition of Pi as shown in experimental studies (9,10,15, 16, 17). For model B, the total occupancy of attached states increased slightly with [Pi].

Pi had only a small effect on the rate of ATPase in an isometric state. For model A, the ATPase rate with 0.5 mM Pi was 0.48 s⁻¹. For model B, the isometric ATPase was lower than for model A and also much lower than experimental measurements of the ATPase in fibers by Ferenczi et al. (49). Cooke et al. (18) found that increasing [Pi] from 3 to 20 mM caused a small decrease (9–17%) in the ATPase of rabbit psoas fibers at 10°C. Over this range in [Pi], model A had an ATPase of 0.52 s⁻¹ at 3 mM and 0.53 s⁻¹ at 20 mM Pi, an insignificant increase. For model B, the ATPase was 0.0103 s⁻¹ at 3 mM Pi and 0.0062 s⁻¹ at 20 mM Pi, a much larger reduction than found by Cooke et al. (18).

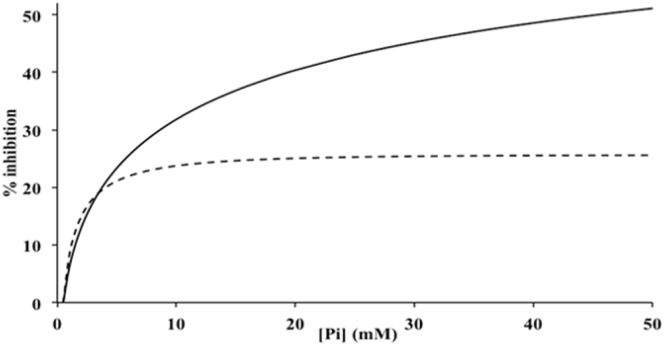
Effect of [Pi] on the force-velocity relation of models A and B

For model A, the lengthening tension was very sensitive to increase in [Pi] (Fig. 6 a). At a lengthening velocity of 0.24 nm/ms, an increase in [Pi] from 0.5 to 2 mM inhibited the lengthening tension 23.4%, 15 mM Pi inhibited 34%, and 50 mM Pi inhibited 36.7%. Thus, the inhibition of the lengthening tension approached saturation. The shortening tension of model A was also substantially inhibited by Pi, but higher concentrations were needed. At a shortening velocity of −0.34 nm/ms, the inhibition by 2 mM Pi was only 11.6%, that at 15 mM Pi was 40.1%, and that at 50 mM Pi 62.8%. 15 mM Pi inhibited isometric tension by 26.8%. These results were similar to experimental data of Stienen et al. (19) in permeabilized rabbit fibers at 15°C; 15 mM Pi inhibited lengthening tension at a velocity of 0.25 nm/ms by ∼24%, isometric tension by ∼34%, and shortening tension at a velocity of −0.4 nm/ms by ∼36%.

Figure 6.

The force-velocity relation at different [Pi] (a) for model A and (b) for model B. Pi concentration: 0.5 mM, black; 1 mM, blue; 2 mM, green; 5 mM, purple; 15 mM, orange; 50 mM, red. (Basically, with model A, tension is depressed with added Pi in both shortening and lengthening, whereas with model B, tension during steady shortening tension is depressed by Pi, but tension during lengthening is much less sensitive to Pi.)

In contrast, for model B, the lengthening tension was much less sensitive to Pi. 2 mM Pi inhibited lengthening tension only slightly (by 3.2%) at a velocity of 0.24 nm/ms and 50 mM Pi by 5.8%. 15 mM inhibited isometric tension by 26% and shortening tension at a velocity of −0.4 nm/ms by 35% (Fig. 6 b). The insensitivity to Pi of lengthening tension in model B, compared with the marked sensitivity exhibited by model A, again favors model A.

For model A, 15 mM Pi decreased v_max by 32%. This was similar to the finding from modeling of Smith (35) that 25 mM Pi decreased v_max by 20%. For model B, the inhibition was smaller. Experimentally, Cooke and Pate (5) found no difference in v_max between 1 and 12 mM, whereas Cooke et al. (18) found no significant change between 3 and 20 mM Pi.

Pi jump experiments

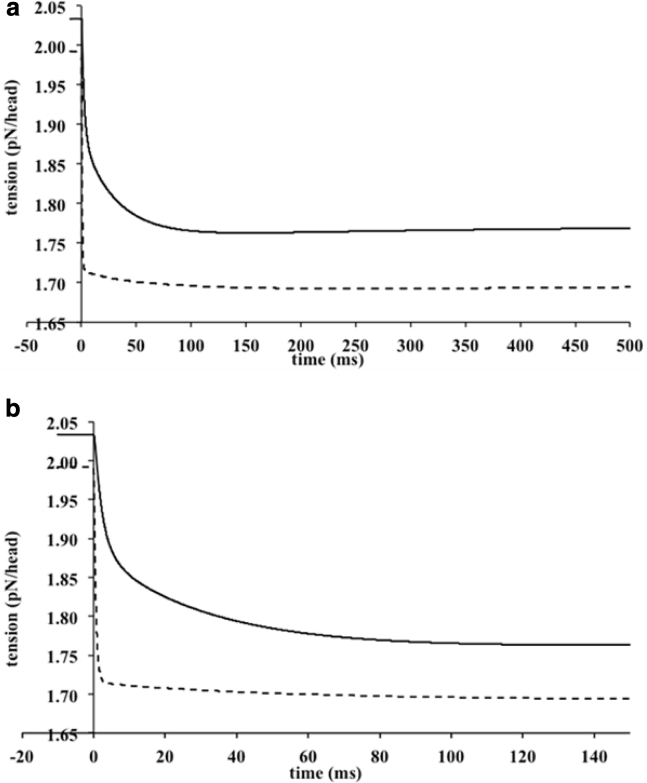
To simulate the caged Pi experiments on rabbit fibers of Dantzig et al. (9), [Pi] was increased from a background level of 0.5–2 mM in 40 μs. Fig. 7 shows the time course of tension for both models after such a Pi jump. For both models, the increased [Pi] caused a fall in tension. A lag was observed before the fall in tension, but it was much smaller than that seen experimentally (9,28). For model A, the lag was 0.20 ms, and for model B, it was 0.077 ms. This is understandable because the rate of re-equilibration of the Pi release step after the Pi jump is the sum of the forward and reverse rate constants at the final [Pi] of 2 mM. For model A, the rate would be 1230 s⁻¹, and for model B, it would be 10,800 s⁻¹.

Figure 7.

Time course of tension after a Pi jump from 0.5 to 2 mM Pi (Pi jump made at 0 ms). (a) shows long time course, 500 ms; (b) shows short time course, 100 ms. Model A, solid lines; model B, dashed lines (tension decreases in both models, but their time courses are different, being much faster in model B.)

For model A, an initial very fast fall in tension was accompanied by a slower fall (Fig. 7 a). The time course of the change in tension over the first 150 ms was well fitted by a biexponential function (Fig. 8 a). The rates of the fast and slow phases were 386 and 33.5 s⁻¹, and their amplitudes were 0.146 and 0.123 pN/head, respectively. Thus, the ratio of the contribution to the tension fall due to the fast phase to that due to the slow phase was 1.19. The rate of the slow component (33.5 s⁻¹) is similar to the experimental rate (35 s⁻¹) of the single exponential fitted to the experimental tension fall for rabbit fibers at 10°C (9). The average rate of the tension fall in the first 100 ms calculated from the time for half the tension fall was 88.2 s⁻¹ comparable to the experimental rate. The tension reached a minimum at ∼150 ms and was followed by a small late rise in tension (Fig. 5) resembling the phase III response observed by Dantzig et al. (9).

Figure 8.

Biexponential fit to tension fall after Pi jump from 0.5 to 2 mM Pi. (a) shows model A, and (b) shows model B. Tension fall, solid lines; fit to tension, short dashed lines; fast phase, long dashed lines; slow phase, dotted lines. (Note that in speed and amplitude, the tension fall for model A (a) resembles that of experimental more closely than for model B (b).)

For model B, the fast fall of tension after the Pi jump was larger and the slower fall much smaller than for model A (see Fig. 8), so most of the tension fall occurred much earlier than in model A (Fig. 7, a and b). The tension response over the first 150 ms could also be well fitted by a biexponential function (see Fig. 8). The rates of the fast and slow phases were 1570 and 17.7 s⁻¹, and their amplitudes were 0.278 and 0.0220 pN/head. So, for model B, the amplitude of the fast component was over 10 times greater than that of the slow component, whereas for model A, the amplitudes for the fast and slow components were similar. The average rate for the first 100 ms calculated from the half time was very much larger than the experimental values (132 and 114 s⁻¹) for similar Pi jumps. The minimal tension was reached at ∼250 ms. After this minimum, the tension rose only very slightly, i.e., the phase III response was minimal.

The rate of tension fall after the Pi jump for model A resembled that found experimentally more closely than found for model B.

Fig. 9 shows for models A and B the time course of the occupancy of all states after a Pi jump from 0.5 to 2 mM. The occupancy of the AM″⋅ADP state in these near-isometric conditions remained very low for both models. For model A, the immediate effect of the Pi jump is a very fast increase in the occupancy of AM⋅ADP⋅Pi and a similar fall in that of AM⋅ADP due to the fast reversal of the Pi release step (Fig. 8 a). By a mass action effect, this fall in AM⋅ADP caused a small reduction of the occupancy of AM′⋅ADP over the first 20 ms due to reversal of the first tensing step. The occupancy of AM′⋅ADP then slowly rose again in the long approach to the final steady state, accompanied by a decrease in the occupancy of AM⋅ADP caused by the forward operation of the first tensing step. This would account for the late phase III small rise in tension. Importantly, in the first 70 ms, there was an appreciable increase in the occupancy of the detached M⋅ADP⋅Pi state caused by enhanced detachment of M⋅ADP⋅Pi from actin. This was associated with a fall in the total occupancy of attached states as suggested by Smith (35).

Figure 9.

Time course of occupancies of cross-bridge states after Pi jump from 0.5 to 2 mM Pi. (a) Model A occupancy: AM⋅ADP ⋅Pi, blue; AM⋅ADP, green; AM′⋅ADP, red; M⋅ADP⋅Pi, orange; M⋅ATP, brown; total attached states, black. (b) Model B occupancy: AM⋅ADP⋅Pi, blue; AM′⋅ADP⋅Pi, pink; AM′⋅ADP, red; M⋅ADP⋅Pi, orange; M⋅ATP, brown; total attached states, black. (The occupancy of AM″⋅ADP in the isometric state is negligible and not shown.)

For model B, the immediate effect of the Pi jump was a very fast fall in the occupancy of AM′⋅ADP accompanied by a rise in AM′⋅ADP⋅Pi due to the fast reversal of the Pi release step (Fig. 9 b). This is followed more slowly by a rise in AM⋅ADP⋅Pi due to the reversal of the first tensing step. The occupancy of detached M⋅ADP⋅Pi only very slightly increased, so the total occupancy of attached heads scarcely changed.

The analyses show that with the Pi release step before the first tensing step (model A), the tension fall after a Pi jump was the result of two, not one, processes. One of these processes was the detachment of M⋅ADP⋅Pi from actin resulting in a fall in the occupancy of attached heads. The other process was the reversal of the first tensing step. The fall in occupancy of attached heads would account for the decrease in fiber stiffness (2,7,15, 16, 17). In contrast, for model B, the major cause of tension fall was the reversal of the first tensing step, with very little change in the total occupancy of attached heads. This would not explain the experimentally observed reduction in fiber stiffness. These results therefore favor model A, the mechanism advocated by Smith (35), in which the Pi release step precedes the first tensing step.

Discussion

The location of the Pi release step

One of the main aims of this work was to use modeling to examine whether the Pi release step is located before or after the first tensing step in the cross-bridge cycle. We modified our previous model of the frog cross-bridge cycle (45), which had been refined to fit both the experimental force-velocity relation and the transient tension responses to length steps, by including a kinetically separate Pi release step either before (model A) or after (model B) the first tensing step. Our simulations on the models after refinement showed that the response of the cross-bridge cycle to changes in [Pi] differed depending on which of these models was studied. In brief, our main results bearing on this problem were the following.

• 1)An increase in [Pi] results in a decrease in isometric tension for both model A and model B. The tension inhibition with 50 mM Pi was ∼50% for model A, as seen experimentally (see (13)); for model B, it was low, ∼25% (see Fig. 5).
• 2)The steady-state force-velocity relation for both models (see Fig. 3) gave reasonable fits to the experimental data in the shortening limb. With increase of lengthening velocity, tension in model A approached a plateau (as seen experiments of Roots et al. (48)). Tension in model B showed a substantial decline that has not been reported in experiments.
• 3)Examining the effect of Pi on the force-velocity relation (see Fig. 6), with model A, an increase in [Pi] caused a reduction in lengthening (and shortening) tension as found experimentally (19). With model B, an increase in [Pi] reduced the lengthening tension very much less.
• 4)After a Pi jump, the amplitude and the average rate of the tension fall for model A were comparable to that of phase II observed experimentally by Dantzig et al. (9), but not for model B. Also, after tension fall in phase II, a small late rise of tension was seen with model A that mimicked the phase III observed in experiments (9). This late rise was not seen with model B (see Fig. 7).
• 5)With model A, raising [Pi] caused a drop in stiffness associated with the fall in tension, as experimentally observed (see (9)). With model B, raising [Pi] showed no drop in stiffness (Fig. 9).

From the findings listed above, although not statistically analyzed and established beyond doubt (as mentioned below in Conclusions), model A seems to fit in better with the experimental observations on the Pi effects on muscle force. This leads us to conclude, in agreement with Smith (35) and Månsson (44), that the Pi release step occurs before, not after, the first tensing step. So, Pi can be thought of as triggering, i.e., gating, the first tensing step.

Smith (35) pointed out that a scheme in which the Pi is released before the first tensing step explains why the speed of tension recovery after a quick stretch increases with [Pi] but the speed of tension recovery after a quick release is [Pi] insensitive (see (16)). This is because after a stretch, the reversal of the tensing step is promoted by the binding of Pi to AM⋅ADP.

This conclusion from our modeling of the kinetics of the cross-bridge cycle fits in well with some recent structural studies. In the prestroke state, the presence of ADP, switch 1, and switch 2 at the active site of the myosin head would prevent Pi leaving the way it entered, suggesting that Pi must escape by an alternative “back door” exit route (50). Llinas et al. (36) have obtained a new crystal structure of a fragment of myosin VI complexed with ADP that helps to define the structural nature of this exit route. They propose that Pi can leave through a tunnel created when actin binds more strongly and stereospecifically to the myosin head. This involved limited closure of the outer cleft causing switch 2 to move by 4 Å, thus opening the tunnel. Only after this Pi release can the lever arm swing to generate force and full cleft closure to occur. When crystals of this new structure were allowed to bind Pi and then rapidly frozen, the Pi was found either at the exit of the tunnel or near ADP. If the freezing was delayed, the prestroke structure was reformed, thus retrapping the bound Pi. This demonstrated the reversibility of Pi binding, as in the study by Reubold et al. (51).

In a recent experimental study, using an ultra-high-speed optical trap technique, Woody et al. (52) have examined actin binding by β-cardiac myosin. The initial actomyosin state can proceed directly to the stroke or detach before releasing Pi; they conclude, using other findings as well, that the stroke precedes phosphate release, and after P_i release, P_i can rebind enabling reversal of the working stroke. Whether this would apply to other myosins remains to be seen, but the conclusion supports the notion held in several previous studies (9,11,25,27,53).

The speed of the Pi release step in muscle and in solution

The rate constant for the release of Pi from actomyosin in solution was found by rapidly mixing an equilibrium mixture of rabbit M⋅ADP⋅Pi and M⋅ATP with a high concentration of actin (37). The rate of Pi release with the phosphate-binding protein was measured to be 75 s⁻¹, much slower than that found by our modeling of the cross-bridge cycle in intact muscle. Muretta et al. (30,31) extended this analysis by comparing the rate of Pi release with that of the power stroke by Förster resonance energy transfer analysis of the bending of the relay helix in the myosin head in both rabbit and dictyostelium actomyosin. They showed that Pi release was irreversible with a rate constant of only 37 s⁻¹, whereas that of the power stroke was much faster. They therefore concluded that Pi release followed the tensing step.

In our modeling of active muscle at the beginning of the refinements of our two models, the initial value of k_p, the rate constant for Pi release, was therefore taken to be slow (70 s⁻¹). However, this value rose dramatically during refinement of these muscle models to 493 s⁻¹ for model A and 6620 s⁻¹ for model B. At first sight, there therefore appears to be a serious conflict between the rates of the Pi release step in our modeling and in solution.

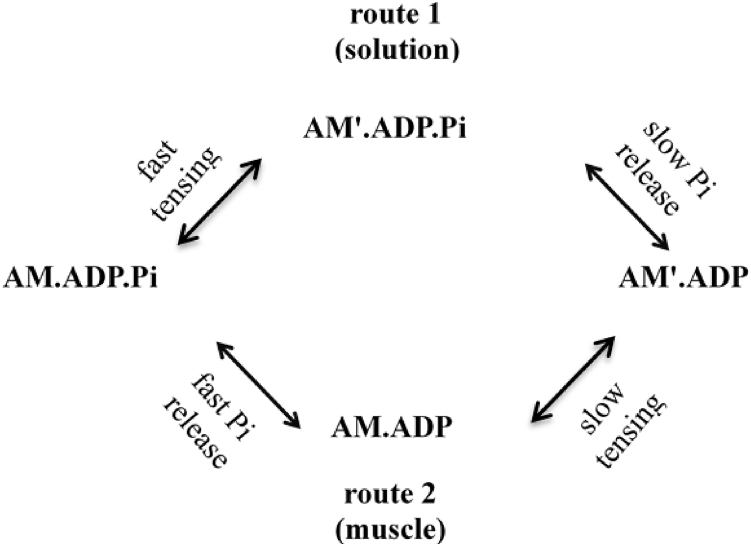
One way of explaining this difference is prompted by the demonstration of Rohde et al. (54) that the drug omecamtiv mecarbil slowed the power stroke of cardiac actomyosin but speeded up Pi release. The result was that in the presence of this drug, Pi release occurs before, not after, the power stroke. They therefore suggested that the order of the Pi release step and the first tensing step is not fixed, but Pi may be released either before or after the tensing step depending on conditions. It therefore seems reasonable to suggest that the order of these steps could be different in active muscle and in solution because the mechanics are so very different in these two scenarios. If the tensing step is fast enough, it will lead; if slow enough, it will follow the Pi release step. If the tensing step leads, the state from which Pi is released is AM′⋅ADP⋅Pi. If it follows, the state from which Pi is released is AM⋅ADP⋅Pi. There is no reason why the rate constant of Pi release should be the same for these two cases.

Fig. 10 shows a scheme of two routes differing in the order of the steps. In the upper route (route 1), the first tensing step is fast and the Pi release step that follows is slow and irreversible (as in (41)). In the lower route (route 2), the Pi release step is fast and is followed by a slow first tensing step. Which of the two routes dominates will depend on the mechanical situation. In solution, the AM⋅ADP⋅Pi heads carry no strain because they are not attached to a thick filament backbone. Consequently, when these heads undergo the conformational change equivalent to the first tensing step, they will encounter no mechanical resistance to the change. Hence, in solution, the first tensing step will be very fast and hence occur before the slow Pi release, i.e., they will follow route 1. This is consistent with the results of Muretta et al. (30,31), who showed that in actomyosin in solution, the tensing step preceded a slow (∼37 s⁻¹) Pi release.

Figure 10.

A two-route scheme.

In active muscle, the situation is very different. When heads execute the tensing step in muscle, they have to perform work against the cross-bridge compliant element. Hence, the tensing step will be substantially slower than in solution, and the Pi release step may have the opportunity to take place before the tensing step, i.e., the pathway will follow route 2. This will be particularly the case in isometrically contracting or lengthening muscle, in which the strain on the AM⋅ADP⋅Pi heads will on average be either near zero or positive so the work done in executing the first tensing step is large.

In rapidly shortening muscle, newly formed AM⋅ADP⋅Pi heads will initially have low strain and will therefore start to follow route 2. Those that have yet to undergo the first tensing step will of course be dragged to negative strains, causing the first tensing step to become more favorable and more rapid. Nevertheless, it is only when the negative strain reaches half the stroke distance (i.e., ∼−3 nm) that the equilibrium constant of the tensing step starts to exceed that in solution (45). At a shortening velocity of −0.8 nm/ms (about half the unloaded shortening velocity), that would take ∼4 ms, and by that time, those heads would have completed route 2. Our modeling studies that employ only one route suggest that the Pi release step is very fast and precedes the first tensing step, i.e., they follow route 2.

The fact that the Pi release step in solution is irreversible (30,31,41), but in muscle, the Pi release step in muscle is reversible (9) adds weight to the hypothesis that they are different in nature.

An alternative explanation for the difference in the rate of Pi release found in solution and in modeling active muscle is that the phosphate-binding protein can detect Pi only when it is released into the solvent, and if Pi moved away from ADP but remained in the tunnel near its exit, this would not be detected, and the rate of the Pi release would be underestimated (35,36).

Conclusions

• 1)Considerable progress has been made in the last ∼50 years or so in our understanding of the molecular processes of muscle contraction both from experimental findings and from modeling based on such work ((27,55,56); for more information, see (3,35), and references therein).
• 2)Developing a model to simulate the force-velocity data, length-step force transients, cross-bridge stiffness, and energetics in active frog muscle, we found that two force-generation steps were adequate in a simple five-state unbranched cross-bridge cycle (see (45)). This study basically introduced the Pi release step into that model cycle before or after the first force-generating step. On the basis of the model fittings to Pi effects on force in experimental data, it does seem that the Pi release step precedes the first force-generation step rather than following it. This is similar to the conclusion reached by Smith (35) and Månsson (44) from analyses of experimental data and modeling.
• 3)Considering the published experimental data of Woody et al. (52) on single cardiac myosin molecules showing Pi release in the cross-bridge cycle is after force generation, further work is necessary to elucidate whether Pi release may be different in myosin types (muscle types, species, etc.). Also, there have been claims from experiments that working stroke in muscle is independent and not coupled to Pi release (39) and also that Pi effects on force may work along a different kinetic pathway to force generation (57).
• 4)It can be argued that to fully map the sensitivity of a model to perturbations in parameter space, one should ideally perform “all-parameter” optimization and error surface testing, beginning with randomized starting conditions to avoid local minimum. As described by Johnson (58), using the software package KinTek Explorer can provide a robust evaluation of the degree to which a model fits the experimental data most succinctly.
• 5)Clearly, it would be important to examine this topic in the future by further modeling, experimentation, and better analyses to account for the exact underlying basis of the Pi sensitivity of muscle force and force generation in the cross-bridge cycle under varied conditions.

Author Contributions

G.O. and K.W.R. contributed to the conception and design of the research and wrote the manuscript. G.O. wrote the programs and carried out the computer simulations. Additionally, it is relevant to mention that cross-bridge modeling work reported here is the fourth in the series. The first modeling work was published in Biophysical Journal in 2013, and that study set the basic thinking; cross-bridge cycle parameters were adjusted to account for experimental muscle mechanics, and the model required two force-generation steps (see (45)). The second one (The Journal of Physiology, 2015) examined the temperature effects on muscle contraction using the same basic model (see (46)). The third model study using the same basic thinking was published in Biophysical Journal in 2016 (59), and it dealt with a process that had been neglected in previous studies (see (54)). The work reported here was in progress at that time and completed in mid-2019. It is with great sadness that I (K.W.R.) have to say that some short time after we agreed and decided on the version of this manuscript on the modeling of Pi effects on the cross-bridge cycle, Gerald became ill and passed away (see (60)); hence, I felt obliged to request this be published in Biophysical Journal.

Editor: Samantha Harris.