Abstract
Migratory cells are known to adapt to environments that contain wide-ranging levels of chemoattractant. Although biochemical models of adaptation have been previously proposed, here, we discuss a different mechanism based on mechanosensing, in which the interaction between biochemical signaling and cell tension facilitates adaptation. We describe and analyze a model of mechanochemical-based adaptation coupling a mechanics-based physical model of cell tension coupled with the wave-pinning reaction-diffusion model for Rac GTPase activity. The mathematical analysis of this model, simulations of a simplified one-dimensional cell geometry, and two-dimensional finite element simulations of deforming cells reveal that as a cell protrudes under the influence of high stimulation levels, tension-mediated inhibition of Rac signaling causes the cell to polarize even when initially overstimulated. Specifically, tension-mediated inhibition of Rac activation, which has been experimentally observed in recent years, facilitates this adaptation by countering the high levels of environmental stimulation. These results demonstrate how tension-related mechanosensing may provide an alternative (and potentially complementary) mechanism for cell adaptation.
Significance
Migratory cells, such as human neutrophils, encounter environments that contain wide-ranging levels of chemoattractant. To move, these cells must maintain an organized front-rear signaling polarity despite this wide variation in environmental stimuli. Past research has demonstrated a number of biochemical-based mechanisms by which cells adapt to variable signal levels. Here, we demonstrate that the interplay between Rho-family GTPase signaling and tension-mediated feedback loops may provide an alternative mechanochemical mechanism for adaptation to high levels of signaling.
Introduction
Human neutrophils and other migratory cells are able adapt to environments that contain wide-ranging levels of chemoattractant to maintain polarity. How does this adaptation occur? Models of adaptation based on biochemical processes such as receptor occupancy or receptor arrangement (1) have long been proposed. Here, we demonstrate that well-established mechanochemical interactions between Rac signaling and protrusion-related changes in cell tension can facilitate adaptation to maintain polarity when cells are exposed to wide-ranging levels of chemoattractant.
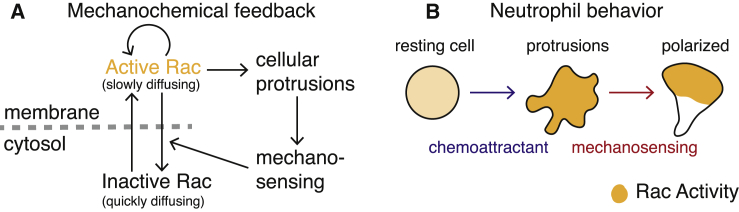
In the context of cell signaling, adaptation refers to the ability of cells to adjust to high levels of signaling or stimulation. Most signal response systems have a range of inputs over which they are sensitive to differences. When stimulus levels are sufficiently high to saturate the underlying regulatory system, the system loses its ability to distinguish signaling levels. For migration, cells must be able to adapt to higher stimulus levels as they proceed closer to the attractant source. In neutrophil migration, the Rho-family GTPase Rac rapidly polarizes to orient the cell in the direction of the stimulus (2,3). Interestingly, when these cells are subjected to high levels of stimulation, Rac first becomes highly activated throughout the cell and subsequently polarizes (3). Thus, in response to high levels of stimulation, these cells first adapt and then subsequently polarize. It has been previously demonstrated that feedback from cell tension to GTPase activation causes competition between multiple cellular protrusions (Fig. 1 B; (4,5)), ensuring that the cell protrudes in only one direction at a time. Here, we demonstrate that this feedback could also provide the cell with a form of mechanochemical adaptation to high, saturating levels of stimulation.
Figure 1.
Overview of the mechanochemical feedback model and observed neutrophil behavior. (A) Schematic of mechanochemical feedback. Active (respectively inactive) Rac GTPases are assumed to be bound (respectively unbound) to the membrane and, therefore, slow (respectively fast) diffusing. Active Rac is autoactivated and causes cellular protrusions by activating downstream effectors. Cellular protrusions increase mechanosensing, which increases the deactivation rate of Rac. (B) Shown is a cartoon of the observed neutrophil behavior in a chemoattractive environment. A resting neutrophil is washed in chemoattractant, causing multiple sites of protrusive activity (within 20 s after stimulation). Subsequently, the cell adapts to the high signaling environment and polarizes to form a single leading front (∼60 s after stimulation). (B) is adapted from Fig. 3 B of (5) and the timescales are estimated from Fig. 2 A of (3). To see this figure in color, go online.
Our model mechanisms and results incorporate ideas related to adaptation, polarity, and tension regulation, each of which is well-studied in its own right. Adaptation has been primarily studied from a biochemical perspective. Models traditionally devised to explain the run-and-tumble behavior of bacterial chemotaxis (6) typically incorporate either negative feedback loops (7) or incoherent feed-forward loops (8) to achieve perfect adaptation to step changes in stimulus magnitude (9). These ideas were later combined with Meinhardt’s concept of lateral inhibition for biological pattern formation (10) to explain how cells could adapt to environments and polarize in response to chemoattractant if the stimulus simultaneously triggered both a local excitatory activator and global inhibitor (11,12). This mechanism, known as LEGI (local excitation global inhibition), and variants have been extensively studied experimentally and theoretically (13, 14, 15, 16, 17, 18, 19). However, not all forms of adaptation are biochemical in nature. Cells can adapt to sustained mechanical stresses (20), for example, and large-scale cytoskeletal structures are known to lead to adaptive responses in cell migration to stiffness gradients in the environment (21).
Similarly, polarity regulation itself has seen sustained interest for multiple decades (22). Much (though not all) of this study has been dedicated to understanding the role of Rho GTPases, which regulate cytoskeletal remodeling, in polarity generation (23). The wave-pinning model of polarity (24, 25, 26), which we will build on here, demonstrated that the conservative activation and inactivation dynamics of these proteins are sufficient to explain the broad characteristics of the polarization process. The cell polarity and cell adaptation literature have been bridged by coupled models that exhibit both adaptive and polarity characteristics (19); however, such models are still biochemical in nature. More recently, models that couple single-cell mechanics and cytoskeletal mechanobiology with biochemistry have begun to explore the role of mechanochemical feedback loops on cell dynamics (3,4,27,28). However, the possible impact of cytoskeletal mechanics on adaptation during migration has yet to be explored.
Here, we build on the well-studied wave-pinning model of Rho GTPase dynamics (24, 25, 26, 27,29, 30, 31, 32, 33) to analyze the consequences of feedback between signaling, cell protrusion (which affects tension), and tension. We include three critical assumptions into this model. First, Rac signaling (which is modeled using wave-pinning dynamics) promotes protrusion of the cell membrane through downstream activation of actin polymerization (23). Second, protrusion-related changes in cell surface area result in an increase or decrease in membrane tension. Third, membrane tension inhibits GTPase signaling (4,5,34, 35, 36, 37, 38, 39, 40, 41). We combine these assumptions into a moving-boundary mechanochemical model (Fig. 1 A) that incorporates reaction-diffusion partial differential equations (PDEs) for Rac activity in a moving domain and a continuum-based description of cellular mechanics that affect the domain.
To understand the resulting model, we first use local perturbation analysis (LPA) (42,43) and numerical bifurcation analysis to analyze how tension changes resulting from changes in cell size influence GTPase signaling. Results indicate that increases in tension cause the cell to transit from an overstimulated to a polarizable regime of the GTPase signaling model. To test whether this adaptive response induces polarization, we use one-dimensional (1D) and two-dimensional (2D) minimal models to describe cellular physics and simulate the reaction-diffusion Rac signaling model in fully moving cells. Our purpose here is not to develop a high-fidelity model of cellular biophysics (see (44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55) for such models) or to propose an adaptation mechanism to replace biochemical models such as LEGI. Instead, our purpose is to use these models to assess how cell protrusions, tension, and GTPase signaling interact to provide an adaptive response that may act in parallel to other biochemical adaptation mechanisms. Both 1D and 2D simulations demonstrate that the feedback between signaling and tension does lead to adaptation in which the cell initially protrudes everywhere in response to a high stimulus but subsequently polarizes, as predicted. These results demonstrate that the feedback for establishment of polarity via membrane tension can be described using a wave-pinning model of Rac signaling and, more importantly, that mechanosensing may (in addition to biochemical forms of adaptation) facilitate adaptation of migratory cells to high signaling levels.
Materials and Methods
We will develop and analyze a model of the feedback between Rac signaling, cell size change, and tension changes. The purpose here is to use this model to study how these feedback loops may influence a cell’s response to large stimuli. More specifically, we use this model to explore the hypothesis that these feedback loops provide a mechanochemical form of adaptation.
Here, we briefly outline the core elements of the model and analysis approach. We provide further details in subsequent sections. The model (illustrated in Fig. 1 A) builds on the well-studied wave-pinning model of Rho GTPase dynamics (24, 25, 26, 27,29, 30, 31, 32, 33) to integrate tension effects resulting from changes in cell surface area. At a broad level, this model incorporates the cycling of Rac between activated (membrane-bound) and inactivated (cytosolic) states, Rac-mediated tension production (via cell protrusion), and tension-mediated inhibition of Rac activation (see below for further detail), all of which are well-established in neutrophil cells (4,5,34, 35, 36, 37, 38, 39, 40, 41).
Because addressing the questions of interest here involves nonlinear interactions between signaling, shape change, and mechanics, we take several steps to analyze the dynamics of this system, with each building in additional complexity. First, we use the LPA (a form of spatio-temporal bifurcation analysis) to approximately map out the parametric dynamics of the system. Second, we study the effects of tension and cell size changes over time using 1D fixed domain simulations of the spatial PDE model in which tension and length are treated as parameters that we manually vary over time. This allows us to manually simulate tension to understand its potential effect on signaling dynamics. Third, we simulate a 1D moving-boundary version of the model in which Rac promotes protrusion, leading to cell size changes and tension effects. Finally, we simulate a 2D moving-boundary version of this model, coupling continuum mechanics with Rac signaling.
Reaction-diffusion Rac GTPase signaling model
We first describe the core model of Rac signaling that will be responsible for regulating protrusion in this model. We adopt the well-studied wave-pinning model (24, 25, 26, 27,29, 30, 31, 32, 33) of GTPase activity. We consider Rac activity in a 1D or 2D domain with no-flux boundary conditions at the cell periphery and model the activity of both membrane-bound active Rac (R(x,t)) and freely-diffusing cytosolic inactive Rac (Ri(x,t)) forms as illustrated in the left part of Fig. 1 A. The nondimensionalized PDEs describing these dynamics in a stationary domain are as follows:
| (1a) |
| (1b) |
The term in parentheses is a standard Hill function representation of autoactivation kinetics, with b representing a basal-activation rate and c the magnitude of autoactivation (i.e., positive feedback). The parameter δ is the deactivation rate, and D and Di are the diffusion coefficients of the active and inactive forms, respectively. The ratio D/Di is small because membrane-bound diffusion is slower than cytoplasmic diffusion. Because Rac cycles between inactive and active forms with no-flux boundary conditions, the total amount is conserved as a function of time: ʃR(x,t) + Ri(x,t)dx = RT. Full model and nondimensionalization details are in Supporting Materials and Methods.
External chemoattractant stimulation and feedback from tension
The two critical parameters of this model that we will focus on are the basal-activation rate b and the deactivation rate δ. The basal-activation rate will be used to encode the level of external stimulation applied to the cell. For example, application of a uniform stimulus will be modeled as an increase in the parameter b as the Rac signaling pathway becomes activated upon external stimulation. The δ parameter will be used to describe tension (T)-mediated inhibition of signaling:
| (2) |
In cases in which we are not explicitly modeling tension, we will describe the effects of tension through changes in the parameter δ. For example, an increase in tension will be assumed to increase δ. Other functional forms (e.g., Hill functions) of δ(T) could, of course, be used. We use a linear function here for simplicity and to reduce the number of extraneous parameters in the model.
LPA, bifurcation analysis, and steady-state behavior
To approximately determine how stimulus level (b) and tension strength (δ) jointly affect the spatial dynamics of this system, we used LPA to analyze the behavior of the PDE model in the bδ plane. The LPA is an approximate asymptotic analysis that predicts whether the model ((1a), (1b)) will respond to a spatial perturbation (either small or large) and give rise to a spatial pattern formation. More specifically, it helps identify regions of parameter space associated with both linear instabilities (i.e., Turing regions) and stimulus-induced patterning (in which large stimuli are required for a response). The LPA has been demonstrated to be an effective analysis tool for studying GTPase and other systems (29,31,33,56, 57, 58, 59, 60). An explanation of the LPA method and a detailed step-by-step guide can be found in the “Computational Tools” article by Holmes et al. (43) and the references therein.
In practice, this method reduces the PDE system ((1a), (1b)) to an ordinary differential equation (ODE) system that approximately describes the dynamics of an asymptotically localized perturbation. By mathematically analyzing how the model system responds to this type of mathematically convenient perturbation, we can efficiently assess whether the model will give rise to spatial pattern formation and map its parameter space. This is carried out by studying the reduced LPA ODE system with numerical bifurcation software XPPAUT to determine the perturbed system’s behavior in different parameter regimes (Fig. 2 A). Full details of the bifurcation analysis of the LPA ODE system can be found in Supporting Materials and Methods, including a corresponding one-parameter bifurcation diagram (Fig. S1).
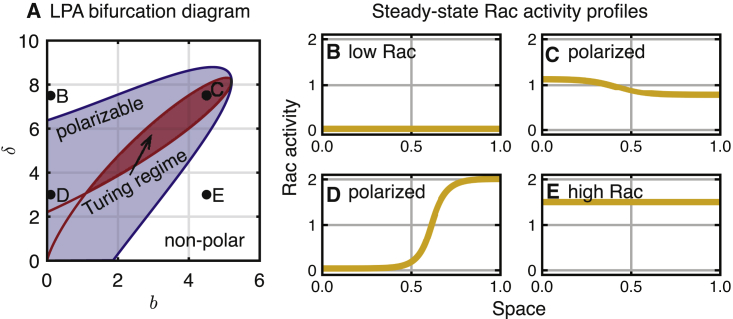
Figure 2.
Parameter regimes of polar and nonpolar behavior and steady-state PDE solutions on a stationary domain. (A) The local perturbation analysis (LPA) reveals regimes of nonpolar (unshaded), stimulus-induced polarizable (blue shaded), and Turing unstable steady state, i.e., polarizable (red shaded), cell behavior in the bδ plane. The dots correspond to the parameters for steady-state Rac activity profiles in (B)–(E). (B–E) Shown are steady-state-simulated solutions to the PDEs. Initial conditions R(x, 0) = 0 except R(x, 0) = 5 for x > 0.9 are used in (B), (D), and (E). For (C), R(x, 0) = 1 + sin(4πx)/10 is used. Spatially homogeneous initial conditions were used for the inactive amount to ensure the total Rac (RT) is preserved: . (B) Shown is the low Rac activity, b = 0.1 and δ = 7.5. (C) Shown is the polarized Rac activity, b = 0.1 and δ = 3. (D) Shown is the polarized Rac activity in the Turing regime, b = 4.5 and δ = 7.5. (E) Shown is the high Rac activity, b = 4.5 and δ = 3. The other parameters are D = 0.01, Di = 10, c = 5, n = 6, and RT = 2. To see this figure in color, go online.
1D mechanochemical model
Before moving to a full 2D changing domain model of the cell, we first develop a simpler 1D changing domain model to provide a preliminary analysis of the effects of tension and signaling feedback. To interrogate the mechanosensing-adaptation hypothesis in a moving, 1D cell, we couple the wave-pinning model for Rac activity to a simple spring-like mechanical model of the deforming cell. The underlying assumption here is that our simulated cells in 1D and 2D models capture the cell’s substrate contact length or area that changes as the cytoskeleton is remodeled. We do not explicitly model cell volume because the three-dimensional aspect is negligible in crawling cells on a 2D substrate, and the predominant dynamics occur on the 2D substrate contact area.
This minimal 1D deforming cell model consists of two components: 1) an overdamped, elastic spring model of the cell and 2) an adapted version of the Rac model to appropriately account for the changing domain. These are coupled with two conditions. First, we assume that active Rac at the cell ends can exert a protrusive force on the cell that opposes the restoring linear elastic spring force. This protrusive force depends sigmoidally on Rac activity at the end points. Second, the deactivation rate δ increases linearly with tension according to Eq. 2. Here, we define tension to be the difference between the cell length L(t) and rest length 0: T = L(t) − 0. Together, these assumptions result in a moving-boundary problem in which the Rac activity is transported within a time-dependent domain Ω(t) = [x−(t), x+(t)]:
| (3a) |
| (3b) |
with no-flux boundary conditions. We can determine the velocity field a(x,t) throughout the cell body from the forces imposed at the cell ends because we assume that the cell changes length isotropically (as in (61, 62, 63, 64)). This assumption means that as the cell length, L(t) = x+(t) − x−(t), changes, each Lagrangian volume element will change proportionally to the total length change (this is a simplifying approximation that will be relaxed in the 2D model to follow). This relation specifies the flow a so that Rac is transported in the domain accordingly. Full model details can be found in Supporting Materials and Methods.
We assume that the movement of the cell’s end points depends on a linear elastic restoring force and protrusive forces determined by Rac activity at the end points:
| (4a) |
| (4b) |
Here, γ is the viscosity, k is the spring constant, 0 is the rest length of the spring, and the functions F± describe the protrusive forces oriented outward from the cell from R. Note that inertial effects are ignored as appropriate for modeling cell motion. We use a smoothed Heaviside function for the Rac-dependent force function F±(R):
| (5) |
The parameters s1 and s0 control the sharpness and location of the switch, respectively, and fR > 0 is the magnitude of the force due to Rac activity.
2D mechanochemical model
We use a 2D continuum mechanics model coupled to reaction-diffusion PDEs for Rac activity to simulate 2D moving cells. The domain can freely deform in response to Rac activity and mechanics (these changes are no longer uniform as in 1D) because we assume that Rac activity leads to expansion in the normal direction. For Rac activity within the domain, we assume that the diffusion of active and inactive Rac is isotropic and leave the reactions ((1a), (1b)) unchanged.
To describe the mechanical model of the cell, we use the conservation of linear momentum from continuum mechanics. The inertial terms are neglected, leading to an approximation of first-order dynamics. This dynamical model relates the Cauchy stress σ and displacement u fields:
| (6) |
where γ is the Stokes damping coefficient that represents the viscous forces in the extracellular environment that resist cell motion and denotes the time derivative of displacement. We assume that intracellular strains are captured by the standard linear Kelvin-Voigt viscoelastic constitutive relation and, therefore, decompose σ = σe +σv into the elastic stress σe and viscous stress σv. The elastic and viscous stresses are related to the strain ε through linear isotropic constitutive models, respectively:
| (7) |
Here, is the identity tensor, λ and μ are the Lamé coefficients that are related to the Young’s modulus E and Poisson’s ratio ν, and β is a viscous parameter related to the first and second coefficients of viscosity βλ and βμ (see Supporting Materials and Methods for full details). We also use the 2D plane stress conditions by assuming the z-directional thickness of the cell is small relative to the expanding area and contains no z-directional stresses. Last, we use the infinitesimal, small-strain approximation for the kinematic relationship between the strain and displacement:
| (8) |
The mechanical model is coupled to Rac activity through the same conditions as in the 1D context but with three modifications. First, we assume the protrusive force from active Rac acts normal to the membrane boundary at any given point. Second, the deactivation rate now depends on a proxy for 2D tension, T = A(t) − A0, the difference between the area A(t) and rest area A0. Third, we account for the deforming mechanical domain in the solution of the reaction-diffusion system as follows. The kinematic relationship between an initial and deformed geometry in the mechanical model is described by the deformation gradient tensor F = I + and its determinant J = det(F). This relationship can be used to map the spatial and temporal differential operators, and allows the reaction-diffusion equations to be solved on a stationary reference domain with fixed coordinates :
| (9a) |
| (9b) |
where the function f describes the wave-pinning reaction kinetics as before: f(R,Ri) =Ri. Full model details can be found in the Supporting Materials and Methods.
Numerical methods
For the 1D model, we used a method of lines discretization with centered differences in space and the Python function odeint from SciPy (65) to integrate the resulting ODE system in time (odeint solves a system of ODEs using LSODA from the FORTRAN library odepack that automatically switches between stiff and nonstiff methods (66,67)) and Matplotlib (68) for visualization. We generated the steady-state Rac activity profiles in Fig. 2, B–E with this method using N = 1000 spatial grid points and integrated until time t = 100. We used the same method for all 1D PDE numerics; however, we adapted the scheme for time-dependent parameters and to simulate the mechanochemical model. To do so, we first transformed the moving-boundary problem to a stationary domain. Next, we solved the stationary-domain problem while simultaneously solving additional ODEs for the location of the cell’s end points. By reversing the transformation, we can obtain the full moving-boundary solution. This method is similar to that used in other investigations of pattern formation on time-dependent domains (61, 62, 63, 64).
We used the finite element method to solve the 2D mechanochemical model on the stationary reference domain (a circle of area 1) using the Python interface of the open source finite element modeling package FEniCS (69). We used standard linear Lagrange elements for the reaction-diffusion PDE and standard quadratic Lagrange elements for the mechanics equations with a mesh containing 4438 elements and 2325 nodes. In each time-step, we first solved the mechanics equations to obtain the displacement. Second, we calculate the deformation gradient tensor F and Jacobian J = det(F). Last, using these values, we solved the reaction-diffusion PDE ((9a), (9b)) using a first-order backward Euler time-stepping scheme with Δt = 0.1 and FEniCS solve command with default parameters (FEniCS automatically solves the linear mechanics problem and uses Newton’s method for the nonlinear reaction-diffusion problem). Finally, we transform the solution to the moving cell by displacing the stationary domain according to the displacements obtained from solving the mechanics equation.
We validated the numerical methods in both 1D and 2D by checking for Rac mass conservation over time for each simulation and by checking that the mass conservation error decreases as the spatial resolution increases (Figs. S2 and S3). Polarity is assessed in two ways. First, we calculate the difference between maximal and minimal Rac activity throughout the domain. If this difference is sufficiently high (>0.1) we consider the cell polarized. Second, we plot and calculate the interquartile range (IQR) of the distribution of Rac activity throughout the cell at a given time. Polarized cells have relatively large IQR and bimodal Rac activity distributions, whereas nonpolar cells have smaller IQR and unimodal Rac activity. See Supporting Materials and Methods for full details.
Parameters
We nondimensionalized the Rac signaling PDEs (see Supporting Materials and Methods for details) because quantitative estimates of these parameters are not available. The Rac signaling parameters (RT = 2, n = 6, and c = 5, respectively) were chosen to be consistent with prior studies (31) of the wave-pinning motif that ensure a large polarizable region in the bδ plane (basal-activation rate b and deactivation rate δ). We set D = 0.01 and Di =10 for our simulations because we are working with a unit length cell, and it is known that the active and inactive forms have diffusion length scales much smaller and larger, respectively, than the cell size (26). These reaction-diffusion parameters are used in both 1D and 2D simulations.
For the 1D mechanical model, we chose damping coefficient γ and spring constant k so that viscous drag dominates the elastic restoring force with γ = 1 and k = 0.01 consistent with estimates that friction dominates elastic forces by several orders of magnitude (64). Finally, we chose the force magnitude from Rac, fR = 0.001, and switch parameters, s0 = 1 and s1 = 10, so that changes in the cell length are smaller and slower compared with Rac activity and such that the cell length changes are less than 10% of the original length when Rac is uniformly highly activated throughout the domain. This relatively small but significant area change is similar to that observed in experiments (3).
For the 2D mechanical model, we used E = 0.3 kPa for the Young’s modulus as estimated for HL-60 cells (70) that serve as a valid model system for human neutrophils (71) and ν = 0.45 for the Poisson’s ratio (ν = 0.499 represents incompressibility). The viscous parameter β = 10 s is the ratio of the viscosity of the internal actin cytoskeleton βμ = 1 kPa⋅s (72) and shear modulus μ ≈ 0.1 kPa (calculated from E and ν). To determine the magnitude of the force due to Rac activity fR, we started with the maximal force due to actin polymerization of 0.8 nN/μm (73), and subsequently, we chose fR = 0.3 nN/μm along with switch parameters s0 = 1 and s1 = 10 so that the cell area changes are around or less than 30% of the original area when Rac is uniform and highly activated throughout the domain as in Fig. 6 A. This ensures that dilution effects (as the cell expands, conserved Rac becomes more dilute) to Rac signaling dynamics are minimized. Finally, we estimated the Stokes damping coefficient γ = 20 kPa⋅s/μm2 so that our simulated cells in Fig. 6 B move with velocity ≈0.17 μm/s (1 spatial unit in 60 s ≈ 10 μm in 60 s) that is within the velocity range of migrating neutrophils in experiments 0.1–0.2 μm/s (71,74).
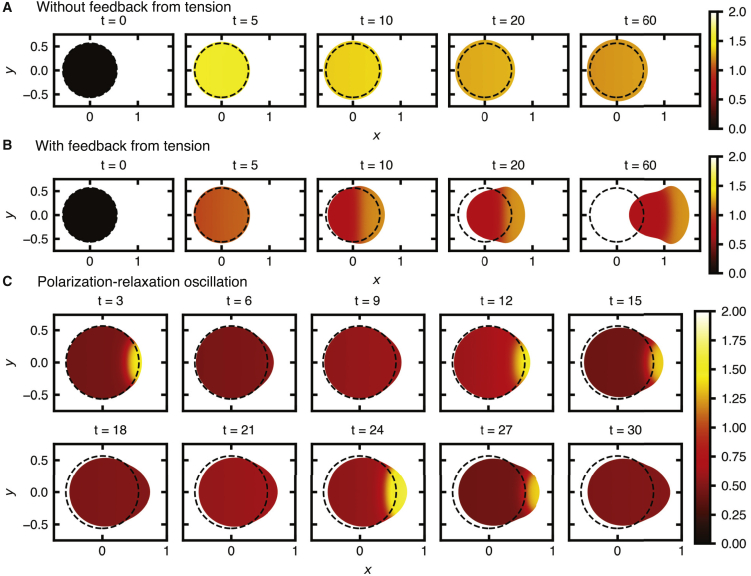
Figure 6.
Cell polarization in the 2D mechanochemical model. (A) Uniform stimulation leads to cell expansion without feedback from tension δ1 = 0. The dashed line indicates the cell’s initial position, and color corresponds to Rac activity. Here, δ depends on T as before: δ(T) = δ0 + δ1T; but tension is defined as the difference between this area and the rest area: T = A(t) − A0 with δ0 = 2 and A0 = 1. We apply a small internal chemoattractant gradient in the reference domain (i.e., in -coordinates) to ensure polarization along the x-axis according to b() = b0 + b1, with b0 = 4 and b1 = 0.1. The mechanical parameters are fR = 0.3 nN/μm, E = 0.3 kPa, ν = 0.45, γ = 20 kPa⋅s/μm2, and β = 10 s. The initial conditions are R(x, t) = 0, Ri(x, 0) = 2, with the mechanical system at rest (no displacement). See Video S5. (B) The cell is resting when exposed to chemoattractant at t = 0; it first expands uniformly and subsequently polarizes and migrates because of increased feedback from tension δ1 = 30. Other parameters are as in (A). See Video S6. (C) Shown is the predicted oscillatory behavior when not oversaturated with b0 = 2.0 and δ1 = 160. Other parameters are as in (A). See Video S7. See Fig. S5 for plots of cell area and polarity over time. To see this figure in color, go online.
Results
LPA and steady-state behavior of the Rac signaling model
We first use the LPA to approximately map the dynamics of the signaling system in the bδ plane. Results show that the bδ plane can be divided into three regions (Fig. 2 A): 1) a nonpolar regime in which the only stable solutions to the PDE are homogeneous steady states that correspond to a uniform Rac activity level across the cell; 2) a polarizable regime in which a sufficiently large spatially heterogeneous stimulus can result in the formation of a polarized pattern; and 3) a Turing regime in which the homogeneous steady states are linearly unstable, leading to polarization. Numerical simulations of the full PDE system verify the presence of these different regimes. Fig. 2, B–E illustrates the stable steady-state Rac distributions at the four marked points in Fig. 2 A. In the case of point C, random noise from the homogeneous steady state is sufficient to generate patterning (here, we used a small amplitude sine function). For D, a large heterogeneous perturbation is required, consistent with the LPA prediction. Neither B nor E is capable of polarizing.
Proof of concept: fixed domain, 1D model with manually varied tension
The bifurcation structure in Fig. 2 A suggests a possible mechanism for adaptation in the presence of high levels of signaling. Consider a high level of chemoattractant that over-stimulates a cell, leading to uniform Rac activation and protrusions across the periphery. In modeling terms, this would correspond to an increase in the basal-activation parameter (b), as illustrated in Fig. 3 A. This broad protrusion would lead to an increase in tension (and the parameter δ), moving the model cell back into the polarization regime. In this way, uniform high levels of stimulation would initially lead to cell wide protrusion that later gives way to polarization as observed experimentally. In the coming sections, we explore this idea in more detail.
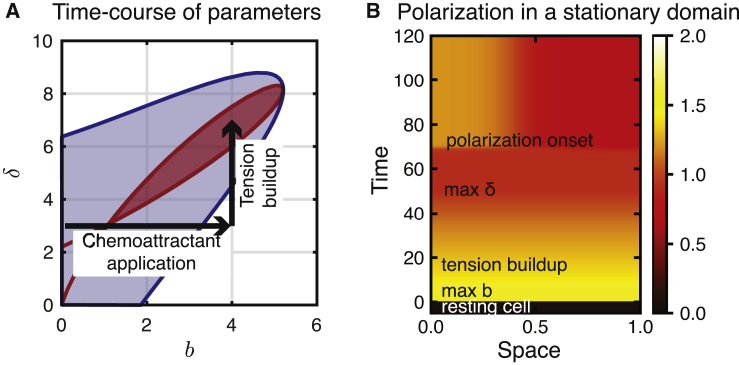
Figure 3.
Time-dependent parameters on a stationary domain mimic observed neutrophil behavior. (A) Shown is the trajectory of time-dependent parameters in the bδ plane mimicking uniform activation followed by increased tension-mediated inactivation. The shaded blue and red regions are the same as in Fig. 2A. Note that for a wide-range of parameter values, a change in δ (moving vertically across the bifurcation diagram) can push the cell into the polarizable or Turing regime in response to a change in chemoattractant levels, which modulate the activation of Rac through the parameter b (moving horizontally). (B) Shown is the kymograph of Rac activity in a stationary-domain simulation for these time-dependent parameters. The cell is at rest for t < 0 with b = 0.1 and δ = 3 (other parameters as in Fig. 2). For 0 < t < 5 (“max b”), the cell is stimulated with uniform chemoattractant b = 4 and jumps to the high Rac homogeneous steady state. For 5 < t < 50 (“tension buildup”), δ increases linearly in time: δ(t) = 3 + 4/45(t − 5) to reach a maximum of 7 at t = 50 (“max δ”). As a result of the increasing δ, the system re-polarizesdue to numerical error because the homogeneous steady state is linearly unstable with parameters in the Turing regime (“polarization onset”). See Video S1. To see this figure in color, go online.
To begin, we first simulate the 1D spatial version of this model on a fixed domain. Because the domain is fixed, we do not model cell size change and tension changes explicitly but rather temporally change parameters to account for those effects. To mimic uniform stimulation followed by tension build up, we temporally vary the model parameters in two phases. First, b is increased to mimic stimulation, as indicated by the horizontal arrow on Fig. 3 A. Second, we gradually increase δ after the vertical arrow. Fig. 3 B shows the results of this simulation. The initial resting cell becomes highly uniformly stimulated upon onset of stimulation. As tension builds up, uniform Rac activation levels decrease. Finally, without the application of any further perturbation, the model cell polarizes. This suggests that the mechanism of expansion followed by tension build up may facilitate adaptation to high signaling levels. This modeling experiment acts as a proof of concept of the mechanosensing-adaptation hypothesis.
1D mechanochemical moving-boundary model demonstrates tension-mediated adaptation
Using the 1D mechanochemical model, we mimicked the simulation depicted by the arrows in Fig. 3 A. A cell at rest (uniform Rac activity and stable length) is stimulated by suddenly increasing b. From this point on, all cellular changes are driven by the mechanochemical model. Fig. 4, B–D demonstrates the results of three simulations that yield distinct results after an initial period of uniform expansion. In Fig. 4 B, there is no tension-mediated deactivation (δ1 = 0), and the cell expands approximately by 10% but does not polarize. In Fig. 4 C, there is feedback from tension (δ1 = 80), and as predicted by prior simulations, after the cell has sufficiently expanded, tension increases lead to polarization. This confirms the plausibility of this mechanosensing-adaptation hypothesis in a 1D deforming cell model.
Figure 4.
1D mechanochemical model and tension-mediated cell polarization. (A) The cell is modeled as a 1D elastic spring (spring constant k) and viscous damping (damping constant γ). The PDEs are solved in the domain Ω(t) = [x−(t), x+(t)], which varies over time because of forces F± that depend on Rac activity at the cell ends (x±(t)). (B) Uniform stimulation leads to cell expansion without feedback from tension δ1 = 0. Black lines show x−(t) and x+(t), and color shows Rac activity. For this simulation, the cell is initialized at rest at time t = −5. The basal-activation rate parameter jumps from b = 0.1 to b = 4 at time t ≥ 0. Tension feeds back onto inactivation according to δ(T) = δ0 + δ1T, T = L(t) − 0, δ0 = 3, and 0 = 1. Other parameters are fR = 0.001, s1 = 10, s0 = 1, γ = 1, k = 0.01, c = 5, n = 6, RT = 2, D = 0.01, and Dii = 10. The initial conditions are R(x, 0) = 0.05645 and Ri(x, 0) = RT − 0.05645. See Video S2. (C) Uniform stimulation leads to cell expansion and polarization with feedback from tension δ1 = 80. Other parameters are as in (B). See Video S3. (D) With b = 2, uniform stimulation leads to indicate cyclical phases of polarization and relaxation. Other parameters and initial conditions are as in (C). See Video S4. To see this figure in color, go online.
The third simulation (Fig. 4 D) illustrates a different type of dynamic that occurs at lower levels of stimulation. Here, the cell undergoes oscillatory phases of polarized protrusion followed by loss of polarity and relaxation. In this case, the levels of stimulation are not sufficiently high to maintain polarization when tension-mediated inactivation increases. We note that this polarization-relaxation oscillation may be a consequence of the lack of explicit contractile signaling along with the simplified nature of cellular mechanics used in this model and is not observed in neutrophil stimulation experiments (to our knowledge). However, such length oscillations are observed in amoeboid cells during stepping motility (75). Thus, although we include it here for completeness, it is not the focus of this study.
Bifurcation and parameter space analysis
To supplement our proof of concept example simulations in Figs. 3 and 4, we next sought to understand the relationship between cell length changes, chemoattractant levels in the environment (modeled by the parameter b), and the resulting cell behaviors: polarized, polarization-relaxation oscillation, and nonpolarized. First, we used LPA on this system in which length is itself a parameter. In this approach, length affects the model in two ways: 1) it controls tension and 2) leads concentration or dilution effects resulting from a fixed total amount of GTPase being distributed on a smaller or larger cell surface area.
We used LPA to map the cell behavior in the bL plane (Fig. 5 A). Results demonstrate that the cell can exist in either a nonpolar state, stimulus-induced polarized state, or in a linearly unstable regime in which polarization results from noise (Turing regime), depending on this cell length, L, and the given basal-activation rate, b. Using this result, we can now map the dynamics of the deforming 1D model in terms of length rather than δ.
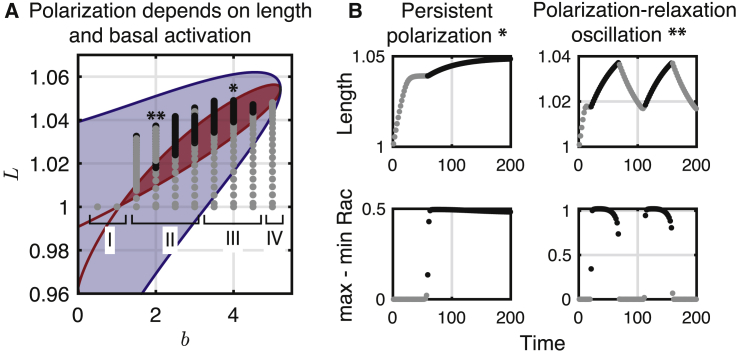
Figure 5.
Analysis of length dependence of dynamics. (A) LPA of the fixed domain system (L is thus a parameter, not a variable) reveals regimes of nonpolar (unshaded), stimulus-induced polarization (blue shaded region), and Turing instability (i.e., polarizable; inside the red shaded region) in the bL plane. Gray and black points illustrate length L trajectories from PDE simulations for various b-values. As the length changes because of Rac activity (dependent on mechanical parameters), the cell can be in a polarized (black) or nonpolar (gray) state. Once the cell’s length is in the Turing regime, polarization may occur. Regions I–IV denote the characteristic behavior for a range of b-values: I nonpolar, resting cells; II polarization-relaxation oscillation; III persistent polarization; and IV nonpolar, expanded cells. (B) Given are the plots of cell length (top row) and polarity strength (bottom row) for two example simulations of the coupled model in regimes III (b = 4; left column, labeled ∗ in A) and II (b = 2; right column, labeled ∗∗ in A), respectively. Top row: shown is the length as a function of time. Bottom row: shown is the difference between maximal and minimal Rac activity as a function of time (a proxy for polarization). Color indicates polar (black) or nonpolar (gray) Rac activity. To see this figure in color, go online.
In Fig. 5 A, we superimpose the length variations of the simulated 1D cell onto the bifurcation diagram in the bL plane. We simulated several 1D deforming cells with different values of b (exactly as in Fig. 4, B and C). Fig. 5 A illustrates the trajectories of these in length-space as gray and black trajectories. Gray indicates that the cell is apolar at that point in the trajectory, whereas black indicates polarity. For small b-values (region I), the Rac activity remains sufficiently low that the cell’s length does not change, and the cell remains nonpolar. For intermediate b-values (region II), the Rac activity is sufficient to induce length changes, resulting in Rac polarization. However, there is sufficient Rac activity to increase the cell length beyond the Turing regime, and polarization is lost so that the cell relaxes. When the length returns to the Turing regime, spontaneous polarization reoccurs, and the cell again lengthens, inducing a polarization-relaxation oscillation (as shown in Fig. 4 C). Quantification of cell length and level of polarity (top and bottom panels, respectively, of Fig. 5 B) further illustrate the link between polarized growth and apolar relaxation. For larger intermediate values of b (region III), the cell lengthens, and polarization persists. In this case, the length increases monotonically before approaching a constant value, with a persistent polarity. Finally, for large b-values (region IV), stimulation is too strong for polarity to occur. Cells in this region remain nonpolar and expanded. We do note that receptor saturation or other factors could limit the maximal level of b because Rac activation is downstream of a receptor-mediated signaling cascade. Thus, if the maximal level of receptor signaling is limited, it is possible that no level of external stimulation would perpetually overstimulate the cell.
Verification of the mechanosensing-adaptation hypothesis in a 2D continuum mechanics model
Using the 2D mechanochemical model, we repeated the simulation depicted by the arrows in Fig. 3 A and shown using the 1D model in Fig. 4. In Fig. 6, we perform the same simulation experiment in which an initially at rest, circular cell is uniformly stimulated with high levels of chemoattractant. As in the 1D model, if there is no feedback from tension (δ1 = 0; Fig. 6 A), the cell simply expands because of the uniformly increased Rac activity (dashed line indicates the cell’s initial position). Note that there is slight movement in the positive x-direction because we apply a small gradient of the parameter b to each cell to ensure the cells consistently polarize in the same direction. With feedback from tension (δ1 = 30; Fig. 6 B), the cell initially expands isotropically to a point, polarizes, and then migrates. In Fig. S5, we illustrate that polarization occurs because of an increase in area to about A ≈ 1.1 caused by increased Rac activity. We also observe the polarization-relaxation oscillation found in the 1D model for lower basal-activation rate b = 2 (Fig. 6 C); however, in 2D, we used δ1 = 160 instead of δ1 = 80 as in the 1D model. For these parameters, the polarization-relaxation oscillation is transiently present but not stable. As the cell elongates, polarization persists but oscillates in magnitude (see Video S7). These results confirm that tension-signaling feedback still leads to adaptive polarization when embedded in a 2D geometry.
Mechanosensing adaptation in a chemoattractant gradient
Thus far, we have demonstrated that tension-mediated inhibition can facilitate polarization at higher, uniform stimulation levels than are possible without it. Based on this, we hypothesize that tension will allow cells to migrate further up a stimulus gradient because they are exposed to higher and higher signaling as they migrate up a gradient.
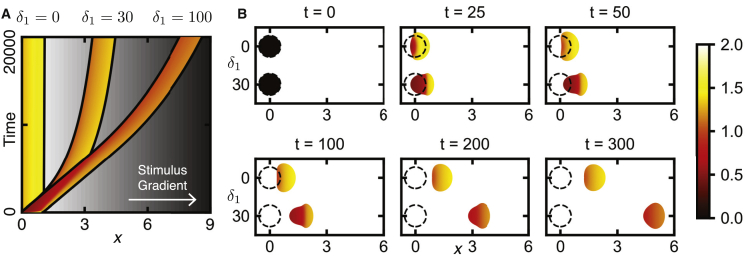
To test this, we simulated the 1D and 2D mechanochemical models in a chemoattractant gradient encoded in a spatial gradient of the activation parameter b. We simulated 1D cells with the same parameters as in Fig. 4 for a range of feedback strengths δ1. Each cell is subjected to a chemoattractant gradient encoded in a spatially varying basal-activation rate b(x) = b0 + b2x. 1D simulation results show that feedback from tension (δ1 > 0) enables cells to migrate further up this gradient (Figs. 7 A and Video S5. Uniform Stimulation Leads to Cell Expansion without Feedback from Tension in the Two-Dimensional Model, Document S2. Article plus Supporting Material). We simulated 2D cells in the same gradient as in 1D with parameters as in Fig. 6. The cell with feedback from tension (δ1 = 30; Figs. 7 B and S5 B) migrates further as expected based on the 1D results. Together, these results suggest that feedback from tension does enable further migration and that the cell’s with stronger feedback from tension (larger δ1) migrate further than cells without feedback. In cells with stronger feedback, we observe that polarized Rac activity persists for longer than in those with weaker or without feedback (Figs. S5–S7). We do note that this is not a form of “perfect” adaptation. Eventually, all cells with this mechanism saturate their signaling and halt migration. Thus, although this form of adaptation is a natural consequence of tension inhibition, we are not proposing it as a replacement for known forms of biochemical adaptation.
Figure 7.
Mechanosensing adaptation enables persistent migration in a chemoattractant gradient. Cells migrate up a chemoattractant gradient encoded in the basal-activation rate b(x) = b0 + b2x with b0 = 2.5 and b2 = 1. (A) 1D cells with feedback from tension (δ1 > 0) are able to migrate further up the chemoattractant gradient than those without feedback from tension (δ1 = 0) before becoming overstimulated and losing polarity (see also Figs. S5A and S6). (B) Snapshots over time of migrating cells in 2D without (top cell; δ1 = 0) and with (bottom cell; δ1 = 30) feedback from tension reveal the same behavior as in 1D (see also Fig. S7B). Shown are parameters as in Fig. 6, A and B except there is no longer an internal gradient applied to the interior of the cell in the stationary domain (b1 = 0). The dashed circle shows the initial position. See Videos S8 and S9. Color shows Rac activity in all panels. To see this figure in color, go online.
Discussion
In this study, we coupled a reaction-diffusion model of Rac dynamics to a minimal model of cell mechanics to illustrate that the two-way feedback from membrane tension to Rac activity allows cells such as human neutrophils to adapt to saturating levels of chemoattractive environment and maintain cell polarity. We first used the LPA to map the parameter regimes of behavior of the wave-pinning model with respect to the basal activation (b, which is altered by stimulation) and deactivation rates (δ, which is altered by tension). Given the shape of polarizable region in the bδ plane, we hypothesized that an increase in the basal activation that pushes the cell into an overactivated state can be counterbalanced by a commensurate increase in the deactivation rate δ arising from increases in cell tension resulting from protrusion. We then simulated the cell’s response to stimulation from uniformly high levels and a gradient of chemoattractant using 1D and 2D deformable cell models in which signaling influences cell size and tension and vice versa. Results confirmed that the interaction between tension and signaling can lead to polarization adaptation to high signaling levels and that cells with feedback from tension can migrate further up a chemoattractant gradient before becoming oversaturated and losing polarity. We coupled the LPA with these full model simulations to demonstrate that the adaptive polarity that arises after uniform stimulation is the result of the cell passing through a bifurcation in the GTPase system. Thus, cell area changes that result from overstimulation force the cell back into a polarizable state by counterbalancing that stimulation. These results broadly support the hypothesis that mechanosensing can act as an adaptive response to maintain polarity in migrating cells. Further, they are consistent with the conclusions of experimental observations connecting cell mechanics and cell signaling (3, 4, 5).
Our study makes several testable predictions. First, our model predicts a relationship between polarity, tension, and cell area. Measurements of cell polarity, tension, and cell area during neutrophil stimulation experiments could be jointly plotted to test the presence of such a relationship. Fluorescent probes or downstream readouts can be used to assess Rac activity levels during neutrophil stimulation experiments (3,41), whereas the optical trap force measurements can measure tension (76). Second, to test whether tension plays a role in the adaptive response, the neutrophil stimulation experiment could be performed on cells with inhibited actin-based protrusion. If tension is responsible for the adaptive response, the hypothesis would be that in the absence of protrusion, uniform signaling activation would occur and persist instead of polarization (though it is possible the formation of blebs (41) or some other unintended effect could complicate matters). Such cells (with and without feedback from tension) could also be exposed to chemoattractant gradients as in Fig. 7 to assess whether tension enables persistent migration. Third, at lower levels of chemoattractant stimulation, the simulated cells oscillate between a polarized and relaxed state. Although such length oscillations are observed during stepping motility in amoeboid cells (75), to our knowledge, they are not observed in uniformly stimulated neutrophils.
Numerous studies have used differing computational approaches to study the consequences of mechanics, geometry, and tension on cell dynamics, such as explicitly modeling the competition between separate front and rear cellular compartments (77,78), phase-field simulations incorporating feedback from tension, and other physical parameters (46,47,49,51,54,55), cellular Potts model simulations (53,79,80), level-set methods (81, 82, 83), immersed-boundary models (45,84,85), free-boundary models (48,86), or stochastic methods (50,87). Our work differs from these numerous prior studies in that we study how the interplay between mechanics and signaling facilitates adaptation. In this sense, our work is most similar to that of Buttenschön et al. (64), who considered the wave-pinning model coupled to a similar 1D mechanical model. Their work did not, however, incorporate feedback from mechanics to signaling. Zmurchok et al. (88) investigated the consequences of this feedback. However, because this study was primarily concerned with collective, multicellular dynamics, each cell was treated as a well-mixed point entity (i.e., polarity was not possible), and adaptation was not studied. Kopfer et al. (89) coupled a model of GTPase kinetics with actin and myosin dynamics along with a viscous active gel model for cellular physics (opposite our continuum mechanics model). Their results, however, primarily focused on demonstrating the ability of tension to limit protrusion to a single front and resolve conflicting stimuli. Thus, although our mechanochemical modeling fits into this larger body of literature, the intent and results, namely to demonstrate the adaptive nature of tension-mediated mechanochemical feedback, are distinct.
This study does have limitations. We chose to allow cell mechanics to affect the deactivation rate (δ). This is likely an oversimplification. It is possible that tension could influence activation in an inverse way, though this would likely lead to similar qualitative results. We also chose to study the simplest model for Rac signaling and did not explore more complicated variants that include multiple GTPases (26,31,33) or additional feedback networks (80). This was motivated by both simplicity and the fact that the interaction between Rac and tension has been well studied experimentally (3, 4, 5). We also defined cell tension as a global quantity despite evidence suggesting that membrane tension is more localized than previously thought (76) and that cells such as keratocytes generate tension gradients (90,91). In our study, however, we are concerned primarily with how cells respond to uniformly high stimulation that would be expected to, broadly speaking, lead to global increases in tension due to protrusion. Lastly, we used the simplest mechanical models appropriate for cell mechanics (an overdamped elastic spring in 1D and linear viscoelasticity in 2D) and approximate estimates of biochemical and biophysical parameters. Although this is sufficient for our purpose, a more detailed model of cell mechanics and/or precisely measured or estimated biophysical parameter values would be required to study 2D migration itself (as has been done by many others (44, 45, 46, 47, 48, 49, 50, 51, 52, 53,55)).
Despite these limitations, this study demonstrates that mechanosensing can act as an adaptive response to maintain polarity in environments with high levels of chemoattractant. We confirm that the feedback for establishment of polarity via membrane tension can be described using a wave-pinning model of Rac signaling. Although we have assumed that membrane tension is a global quantity that feeds back into Rac signaling dynamics, we note that the underlying signaling network is responsible for the adaptive response. Any signal that acts on Rac dynamics in a similar way could induce a similar response (calcium influx, for example, as suggested by Shi et al. (76)). This type of mechano-chemical adaptation is a potential alternative that may work in parallel to biochemical mechanisms of adaptation.
Data availability
The code used to produce the 1D simulations is available as an archived GitHub repository at https://doi.org/10.6084/m9.figshare.11916495. The code for the 2D simulations can be made available upon request.
Author Contributions
C.Z. and W.R.H. designed the research. C.Z. and J.C. performed the research and analyzed the data. All authors wrote the article.
Acknowledgments
The authors acknowledge Christopher Bradley for helpful discussions on numerical implementation of the coupled mechanics and reaction-diffusion simulations and Andreas Buttenschön for helpful discussions of the 1D model.
This work was supported by a National Science Foundation, United States, grant DMS1562078 (to W.R.H.) and a Natural Sciences and Engineering Research Council of Canada Postdoctoral Fellowship Award (to C.Z.).
Editor: Padmini Rangamani.
Footnotes
Cole Zmurchok and Jared Collette contributed equally to this work.
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.08.035.
Supporting Citations
Reference (92) appears in the Supporting Material.
Supporting Material
References
- 1.Zigmond S.H. Mechanisms of sensing chemical gradients by polymorphonuclear leukocytes. Nature. 1974;249:450–452. doi: 10.1038/249450a0. [DOI] [PubMed] [Google Scholar]
- 2.Gardiner E.M., Pestonjamasp K.N., Bokoch G.M. Spatial and temporal analysis of Rac activation during live neutrophil chemotaxis. Curr. Biol. 2002;12:2029–2034. doi: 10.1016/s0960-9822(02)01334-9. [DOI] [PubMed] [Google Scholar]
- 3.Weiner O.D., Marganski W.A., Kirschner M.W. An actin-based wave generator organizes cell motility. PLoS Biol. 2007;5:e221. doi: 10.1371/journal.pbio.0050221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Houk A.R., Jilkine A., Weiner O.D. Membrane tension maintains cell polarity by confining signals to the leading edge during neutrophil migration. Cell. 2012;148:175–188. doi: 10.1016/j.cell.2011.10.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Saha S., Nagy T.L., Weiner O.D. Joining forces: crosstalk between biochemical signalling and physical forces orchestrates cellular polarity and dynamics. Philos. Trans. R Soc. Lond. B Biol. Sci. 2018;373:20170145. doi: 10.1098/rstb.2017.0145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Spiro P.A., Parkinson J.S., Othmer H.G. A model of excitation and adaptation in bacterial chemotaxis. Proc. Natl. Acad. Sci. USA. 1997;94:7263–7268. doi: 10.1073/pnas.94.14.7263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Barkai N., Leibler S. Robustness in simple biochemical networks. Nature. 1997;387:913–917. doi: 10.1038/43199. [DOI] [PubMed] [Google Scholar]
- 8.Koshland D.E., Jr. A response regulator model in a simple sensory system. Science. 1977;196:1055–1063. doi: 10.1126/science.870969. [DOI] [PubMed] [Google Scholar]
- 9.Iglesias P.A., Shi C. Comparison of adaptation motifs: temporal, stochastic and spatial responses. IET Syst. Biol. 2014;8:268–281. doi: 10.1049/iet-syb.2014.0026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Meinhardt H. Orientation of chemotactic cells and growth cones: models and mechanisms. J. Cell Sci. 1999;112:2867–2874. doi: 10.1242/jcs.112.17.2867. [DOI] [PubMed] [Google Scholar]
- 11.Parent C.A., Devreotes P.N. A cell’s sense of direction. Science. 1999;284:765–770. doi: 10.1126/science.284.5415.765. [DOI] [PubMed] [Google Scholar]
- 12.Levchenko A., Iglesias P.A. Models of eukaryotic gradient sensing: application to chemotaxis of amoebae and neutrophils. Biophys. J. 2002;82:50–63. doi: 10.1016/S0006-3495(02)75373-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ma L., Janetopoulos C., Iglesias P.A. Two complementary, local excitation, global inhibition mechanisms acting in parallel can explain the chemoattractant-induced regulation of PI(3,4,5)P3 response in dictyostelium cells. Biophys. J. 2004;87:3764–3774. doi: 10.1529/biophysj.104.045484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Levine H., Kessler D.A., Rappel W.J. Directional sensing in eukaryotic chemotaxis: a balanced inactivation model. Proc. Natl. Acad. Sci. USA. 2006;103:9761–9766. doi: 10.1073/pnas.0601302103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Iglesias P.A., Devreotes P.N. Navigating through models of chemotaxis. Curr. Opin. Cell Biol. 2008;20:35–40. doi: 10.1016/j.ceb.2007.11.011. [DOI] [PubMed] [Google Scholar]
- 16.Xiong Y., Huang C.H., Devreotes P.N. Cells navigate with a local-excitation, global-inhibition-biased excitable network. Proc. Natl. Acad. Sci. USA. 2010;107:17079–17086. doi: 10.1073/pnas.1011271107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Iglesias P.A., Devreotes P.N. Biased excitable networks: how cells direct motion in response to gradients. Curr. Opin. Cell Biol. 2012;24:245–253. doi: 10.1016/j.ceb.2011.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang M.J., Artemenko Y., Devreotes P.N. The directional response of chemotactic cells depends on a balance between cytoskeletal architecture and the external gradient. Cell Rep. 2014;9:1110–1121. doi: 10.1016/j.celrep.2014.09.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Devreotes P.N., Bhattacharya S., Miao Y. Excitable signal transduction networks in directed cell migration. Annu. Rev. Cell Dev. Biol. 2017;33:103–125. doi: 10.1146/annurev-cellbio-100616-060739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Matthews B.D., Overby D.R., Ingber D.E. Cellular adaptation to mechanical stress: role of integrins, Rho, cytoskeletal tension and mechanosensitive ion channels. J. Cell Sci. 2006;119:508–518. doi: 10.1242/jcs.02760. [DOI] [PubMed] [Google Scholar]
- 21.Trichet L., Le Digabel J., Ladoux B. Evidence of a large-scale mechanosensing mechanism for cellular adaptation to substrate stiffness. Proc. Natl. Acad. Sci. USA. 2012;109:6933–6938. doi: 10.1073/pnas.1117810109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Rappel W.J., Edelstein-Keshet L. Mechanisms of cell polarization. Curr. Opin. Syst. Biol. 2017;3:43–53. doi: 10.1016/j.coisb.2017.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ridley A.J. Rho GTPase signalling in cell migration. Curr. Opin. Cell Biol. 2015;36:103–112. doi: 10.1016/j.ceb.2015.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mori Y., Jilkine A., Edelstein-Keshet L. Wave-pinning and cell polarity from a bistable reaction-diffusion system. Biophys. J. 2008;94:3684–3697. doi: 10.1529/biophysj.107.120824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mori Y., Jilkine A., Edelstein-Keshet L. Asymptotic and bifurcation analysis of wave-pinning in a reaction-diffusion model for cell polarization. SIAM J. Appl. Math. 2011;71:1401–1427. doi: 10.1137/10079118X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jilkine A., Marée A.F.M., Edelstein-Keshet L. Mathematical model for spatial segregation of the Rho-family GTPases based on inhibitory crosstalk. Bull. Math. Biol. 2007;69:1943–1978. doi: 10.1007/s11538-007-9200-6. [DOI] [PubMed] [Google Scholar]
- 27.Holmes W.R., Carlsson A.E., Edelstein-Keshet L. Regimes of wave type patterning driven by refractory actin feedback: transition from static polarization to dynamic wave behaviour. Phys. Biol. 2012;9:046005. doi: 10.1088/1478-3975/9/4/046005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rajagopal V., Holmes W.R., Lee P.V.S. Computational modeling of single-cell mechanics and cytoskeletal mechanobiology. Wiley Interdiscip. Rev. Syst. Biol. Med. 2018;10:e1407. doi: 10.1002/wsbm.1407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Edelstein-Keshet L., Holmes W.R., Dutot M. From simple to detailed models for cell polarization. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2013;368:20130003. doi: 10.1098/rstb.2013.0003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Holmes W.R., Liao L., Edelstein-Keshet L. Modeling the roles of protein kinase Cβ and η in single-cell wound repair. Mol. Biol. Cell. 2015;26:4100–4108. doi: 10.1091/mbc.E15-06-0383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Holmes W.R., Edelstein-Keshet L. Analysis of a minimal Rho-GTPase circuit regulating cell shape. Phys. Biol. 2016;13:046001. doi: 10.1088/1478-3975/13/4/046001. [DOI] [PubMed] [Google Scholar]
- 32.Holmes W.R., Golding A.E., Edelstein-Keshet L. A mathematical model of GTPase pattern formation during single-cell wound repair. Interface Focus. 2016;6:20160032. doi: 10.1098/rsfs.2016.0032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zmurchok C., Holmes W.R. Simple rho GTPase dynamics generate a complex regulatory landscape associated with cell shape. Biophys. J. 2020;118:1438–1454. doi: 10.1016/j.bpj.2020.01.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Katsumi A., Milanini J., Schwartz M.A. Effects of cell tension on the small GTPase Rac. J. Cell Biol. 2002;158:153–164. doi: 10.1083/jcb.200201105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gauthier N.C., Masters T.A., Sheetz M.P. Mechanical feedback between membrane tension and dynamics. Trends Cell Biol. 2012;22:527–535. doi: 10.1016/j.tcb.2012.07.005. [DOI] [PubMed] [Google Scholar]
- 36.Lessey E.C., Guilluy C., Burridge K. From mechanical force to RhoA activation. Biochemistry. 2012;51:7420–7432. doi: 10.1021/bi300758e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Masters T.A., Pontes B., Gauthier N.C. Plasma membrane tension orchestrates membrane trafficking, cytoskeletal remodeling, and biochemical signaling during phagocytosis. Proc. Natl. Acad. Sci. USA. 2013;110:11875–11880. doi: 10.1073/pnas.1301766110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tao J., Sun S.X. Active biochemical regulation of cell volume and a simple model of cell tension response. Biophys. J. 2015;109:1541–1550. doi: 10.1016/j.bpj.2015.08.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Scott D.W., Tolbert C.E., Burridge K. Tension on JAM-A activates RhoA via GEF-H1 and p115 RhoGEF. Mol. Biol. Cell. 2016;27:1420–1430. doi: 10.1091/mbc.E15-12-0833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.He L., Tao J., Sun S.X. Role of membrane-tension gated Ca2+ flux in cell mechanosensation. J. Cell Sci. 2018;131:jcs208470. doi: 10.1242/jcs.208470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Graziano B.R., Town J.P., Weiner O.D. Cell confinement reveals a branched-actin independent circuit for neutrophil polarity. PLoS Biol. 2019;17:e3000457. doi: 10.1371/journal.pbio.3000457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Holmes W.R. An efficient, nonlinear stability analysis for detecting pattern formation in reaction diffusion systems. Bull. Math. Biol. 2014;76:157–183. doi: 10.1007/s11538-013-9914-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Holmes W.R., Mata M.A., Edelstein-Keshet L. Local perturbation analysis: a computational tool for biophysical reaction-diffusion models. Biophys. J. 2015;108:230–236. doi: 10.1016/j.bpj.2014.11.3457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Holmes W.R., Edelstein-Keshet L. A comparison of computational models for eukaryotic cell shape and motility. PLoS Comput. Biol. 2012;8:e1002793. doi: 10.1371/journal.pcbi.1002793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Wu T., Feng J.J. Modeling the mechanosensitivity of neutrophils passing through a narrow channel. Biophys. J. 2015;109:2235–2245. doi: 10.1016/j.bpj.2015.10.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Winkler B., Aranson I.S., Ziebert F. Membrane tension feedback on shape and motility of eukaryotic cells. Physica D. 2016;318–319:26–33. [Google Scholar]
- 47.Camley B.A., Zhao Y., Rappel W.J. Crawling and turning in a minimal reaction-diffusion cell motility model: coupling cell shape and biochemistry. Phys. Rev. E. 2017;95:012401. doi: 10.1103/PhysRevE.95.012401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Nickaeen M., Novak I.L., Slepchenko B.M. A free-boundary model of a motile cell explains turning behavior. PLoS Comput. Biol. 2017;13:e1005862. doi: 10.1371/journal.pcbi.1005862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wang W., Tao K., Liu F. Exploring the inhibitory effect of membrane tension on cell polarization. PLoS Comput. Biol. 2017;13:e1005354. doi: 10.1371/journal.pcbi.1005354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Trogdon M., Drawert B., Petzold L.R. The effect of cell geometry on polarization in budding yeast. PLoS Comput. Biol. 2018;14:e1006241. doi: 10.1371/journal.pcbi.1006241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Cao Y., Ghabache E., Rappel W.J. Plasticity of cell migration resulting from mechanochemical coupling. eLife. 2019;8:e48478. doi: 10.7554/eLife.48478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Marzban B., Kang J., Yuan H. A contraction–reaction–diffusion model: integrating biomechanics and biochemistry in cell migration. Extreme Mech. Lett. 2019;32:100566. [Google Scholar]
- 53.Rens E.G., Edelstein-Keshet L. From energy to cellular forces in the Cellular Potts Model: an algorithmic approach. PLoS Comput. Biol. 2019;15:e1007459. doi: 10.1371/journal.pcbi.1007459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Cao Y., Ghabache E., Rappel W.J. A minimal computational model for three-dimensional cell migration. J. R. Soc. Interface. 2019;16:20190619. doi: 10.1098/rsif.2019.0619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Tao K., Wang J., Zhang L. Tuning cell motility via cell tension with a mechanochemical cell migration model. Biophys. J. 2020;118:2894–2904. doi: 10.1016/j.bpj.2020.04.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Walther G.R., Marée A.F.M., Grieneisen V.A. Deterministic versus stochastic cell polarisation through wave-pinning. Bull. Math. Biol. 2012;74:2570–2599. doi: 10.1007/s11538-012-9766-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Mata M.A., Dutot M., Holmes W.R. A model for intracellular actin waves explored by nonlinear local perturbation analysis. J. Theor. Biol. 2013;334:149–161. doi: 10.1016/j.jtbi.2013.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Nakamura N., Shibata T. Bifurcation analysis of a self-organizing signaling system for eukaryotic chemotaxis. Jpn. J. Ind. Appl. Math. 2015;32:807–828. [Google Scholar]
- 59.Jacobs B., Molenaar J., Deinum E.E. Small GTPase patterning: how to stabilise cluster coexistence. PLoS One. 2019;14:e0213188. doi: 10.1371/journal.pone.0213188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Liu Y., Rens E.G., Edelstein-Keshet L. Spots, strips, and spiral waves in models for static and motile cells. arXiv. 2019 doi: 10.1007/s00285-021-01550-0. arXiv:1909.10504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Crampin E.J., Gaffney E.A., Maini P.K. Reaction and diffusion on growing domains: scenarios for robust pattern formation. Bull. Math. Biol. 1999;61:1093–1120. doi: 10.1006/bulm.1999.0131. [DOI] [PubMed] [Google Scholar]
- 62.Crampin E.J., Hackborn W.W., Maini P.K. Pattern formation in reaction-diffusion models with nonuniform domain growth. Bull. Math. Biol. 2002;64:747–769. doi: 10.1006/bulm.2002.0295. [DOI] [PubMed] [Google Scholar]
- 63.Baker R.E., Maini P.K. A mechanism for morphogen-controlled domain growth. J. Math. Biol. 2007;54:597–622. doi: 10.1007/s00285-006-0060-8. [DOI] [PubMed] [Google Scholar]
- 64.Buttenschön A., Liu Y., Edelstein-Keshet L. Cell size, mechanical tension, and GTPase signaling in the single cell. Bull. Math. Biol. 2020;82:28. doi: 10.1007/s11538-020-00702-5. [DOI] [PubMed] [Google Scholar]
- 65.Jones E., Oliphant T., Peterson P. SciPy: open source scientific tools for Python. SciPy. 2001 http://www.scipy.org/ [Google Scholar]
- 66.Hindmarsh A.C. ODEPACK, a systematized collection of ODE solvers. In: Stepleman R.S., Carver M., Peskin R., Ames W.F., Vichnevetsky R., editors. Scientific Computing. North-Holland Publishing Company; 1983. [Google Scholar]
- 67.Petzold L. Automatic selection of methods for solving stiff and nonstiff systems of ordinary differential equations. SIAM J. Sci. Statist. Comput. 1983;4:136–148. [Google Scholar]
- 68.Hunter J.D. Matplotlib: a 2D graphics environment. Comput. Sci. Eng. 2007;9:90–95. [Google Scholar]
- 69.Alnæs M., Blechta J., Logg A. 2015. The FEniCS project version 1.5. Archive of Numerical Software. [DOI] [Google Scholar]
- 70.Armistead F.J., Gala De Pablo J., Evans S.D. Cells under stress: an inertial-shear microfluidic determination of cell behavior. Biophys. J. 2019;116:1127–1135. doi: 10.1016/j.bpj.2019.01.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Hauert A.B., Martinelli S., Niggli V. Differentiated HL-60 cells are a valid model system for the analysis of human neutrophil migration and chemotaxis. Int. J. Biochem. Cell Biol. 2002;34:838–854. doi: 10.1016/s1357-2725(02)00010-9. [DOI] [PubMed] [Google Scholar]
- 72.Bausch A.R., Ziemann F., Sackmann E. Local measurements of viscoelastic parameters of adherent cell surfaces by magnetic bead microrheometry. Biophys. J. 1998;75:2038–2049. doi: 10.1016/S0006-3495(98)77646-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Mogilner A., Oster G. Force generation by actin polymerization II: the elastic ratchet and tethered filaments. Biophys. J. 2003;84:1591–1605. doi: 10.1016/S0006-3495(03)74969-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Hoang A.N., Jones C.N., Irimia D. Measuring neutrophil speed and directionality during chemotaxis, directly from a droplet of whole blood. Technology (Singap World Sci) 2013;1:49–57. doi: 10.1142/S2339547813500040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Copos C.A., Walcott S., Guy R.D. Mechanosensitive adhesion explains stepping motility in amoeboid cells. Biophys. J. 2017;112:2672–2682. doi: 10.1016/j.bpj.2017.04.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Shi Z., Graber Z.T., Cohen A.E. Cell membranes resist flow. Cell. 2018;175:1769–1779.e13. doi: 10.1016/j.cell.2018.09.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Holmes W.R., Park J., Edelstein-Keshet L. A mathematical model coupling polarity signaling to cell adhesion explains diverse cell migration patterns. PLoS Comput. Biol. 2017;13:e1005524. doi: 10.1371/journal.pcbi.1005524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Park J., Holmes W.R., Levchenko A. Mechanochemical feedback underlies coexistence of qualitatively distinct cell polarity patterns within diverse cell populations. Proc. Natl. Acad. Sci. USA. 2017;114:E5750–E5759. doi: 10.1073/pnas.1700054114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Marée A.F.M., Jilkine A., Edelstein-Keshet L. Polarization and movement of keratocytes: a multiscale modelling approach. Bull. Math. Biol. 2006;68:1169–1211. doi: 10.1007/s11538-006-9131-7. [DOI] [PubMed] [Google Scholar]
- 80.Marée A.F.M., Grieneisen V.A., Edelstein-Keshet L. How cells integrate complex stimuli: the effect of feedback from phosphoinositides and cell shape on cell polarization and motility. PLoS Comput. Biol. 2012;8:e1002402. doi: 10.1371/journal.pcbi.1002402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Wolgemuth C.W., Zajac M. The Moving Boundary Node Method: a level set-based, finite volume algorithm with applications to cell motility. J. Comput. Phys. 2010;229:7287–7308. doi: 10.1016/j.jcp.2010.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Neilson M.P., Veltman D.M., Insall R.H. Chemotaxis: a feedback-based computational model robustly predicts multiple aspects of real cell behaviour. PLoS Biol. 2011;9:e1000618. doi: 10.1371/journal.pbio.1000618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Shi C., Huang C.H., Iglesias P.A. Interaction of motility, directional sensing, and polarity modules recreates the behaviors of chemotaxing cells. PLoS Comput. Biol. 2013;9:e1003122. doi: 10.1371/journal.pcbi.1003122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Vanderlei B., Feng J.J., Edelstein-Keshet L. A computational model of cell polarization and motility coupling mechanics and biochemistry. Multiscale Model. Simul. 2011;9:1420–1443. doi: 10.1137/100815335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Strychalski W., Copos C.A., Guy R.D. A poroelastic immersed boundary method with applications to cell biology. J. Comput. Phys. 2015;282:77–97. [Google Scholar]
- 86.Rubinstein B., Jacobson K., Mogilner A. Multiscale two-dimensional modeling of a motile simple-shaped cell. Multiscale Model. Simul. 2005;3:413–439. doi: 10.1137/04060370X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Copos C., Mogilner A. A hybrid stochastic-deterministic mechanochemical model of cell polarization. Mol. Biol. Cell. 2020;31:1637–1649. doi: 10.1091/mbc.E19-09-0549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Zmurchok C., Bhaskar D., Edelstein-Keshet L. Coupling mechanical tension and GTPase signaling to generate cell and tissue dynamics. Phys. Biol. 2018;15:046004. doi: 10.1088/1478-3975/aab1c0. [DOI] [PubMed] [Google Scholar]
- 89.Kopfer K.H., Jäger W., Matthäus F. A mechanochemical model for rho GTPase mediated cell polarization. J. Theor. Biol. 2020;504:110386. doi: 10.1016/j.jtbi.2020.110386. [DOI] [PubMed] [Google Scholar]
- 90.Lieber A.D., Schweitzer Y., Keren K. Front-to-rear membrane tension gradient in rapidly moving cells. Biophys. J. 2015;108:1599–1603. doi: 10.1016/j.bpj.2015.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Fogelson B., Mogilner A. Computational estimates of membrane flow and tension gradient in motile cells. PLoS One. 2014;9:e84524. doi: 10.1371/journal.pone.0084524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Simon C.M., Vaughan E.M., Edelstein-Keshet L. Pattern formation of Rho GTPases in single cell wound healing. Mol. Biol. Cell. 2013;24:421–432. doi: 10.1091/mbc.E12-08-0634. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The code used to produce the 1D simulations is available as an archived GitHub repository at https://doi.org/10.6084/m9.figshare.11916495. The code for the 2D simulations can be made available upon request.