Skip to main content
PMC home page
IUCrJ logoLink to IUCrJ
. 2020 Sep 9;7(Pt 6):965–975. doi: 10.1107/S2052252520011379

Advances in long-wavelength native phasing at X-ray free-electron lasers

Karol Nass a,*,‡, Robert Cheng b,‡, Laura Vera a,‡, Aldo Mozzanica a, Sophie Redford a, Dmitry Ozerov c, Shibom Basu a, Daniel James d, Gregor Knopp a, Claudio Cirelli a, Isabelle Martiel a, Cecilia Casadei a, Tobias Weinert d, Przemyslaw Nogly e, Petr Skopintsev d,f, Ivan Usov c, Filip Leonarski a, Tian Geng g, Mathieu Rappas g, Andrew S Doré g, Robert Cooke g, Shahrooz Nasrollahi Shirazi b, Florian Dworkowski a, May Sharpe a, Natacha Olieric d, Camila Bacellar a, Rok Bohinc a, Michel O Steinmetz d,h, Gebhard Schertler d,f, Rafael Abela b, Luc Patthey a, Bernd Schmitt a, Michael Hennig b, Jörg Standfuss d, Meitian Wang a,*, Christopher J Milne a,*
PMCID: PMC7642782  PMID: 33209311

Significant improvements to the current state-of-the-art in phasing strategies in serial femtosecond crystallography are presented and quantified.

Keywords: serial femtosecond crystallography, X-ray free-electron lasers, single-wavelength anomalous diffraction, de novo protein structure determination, anomalous data-quality indicators

Abstract

Long-wavelength pulses from the Swiss X-ray free-electron laser (XFEL) have been used for de novo protein structure determination by native single-wavelength anomalous diffraction (native-SAD) phasing of serial femtosecond crystallography (SFX) data. In this work, sensitive anomalous data-quality indicators and model proteins were used to quantify improvements in native-SAD at XFELs such as utilization of longer wavelengths, careful experimental geometry optimization, and better post-refinement and partiality correction. Compared with studies using shorter wavelengths at other XFELs and older software versions, up to one order of magnitude reduction in the required number of indexed images for native-SAD was achieved, hence lowering sample consumption and beam-time requirements significantly. Improved data quality and higher anomalous signal facilitate so-far underutilized de novo structure determination of challenging proteins at XFELs. Improvements presented in this work can be used in other types of SFX experiments that require accurate measurements of weak signals, for example time-resolved studies.

1. Introduction  

Serial femtosecond crystallography (SFX) is a unique method for macromolecular structure determination from small, weakly diffracting and radiation-sensitive crystals (Schlichting, 2015 ▸; Spence, 2017 ▸). The ultra bright and ultra short X-ray free-electron laser (XFEL) pulses allow most radiation-damage effects to be avoided in comparison with structure determination at synchrotrons (Nass, 2019 ▸). The XFEL pulses also enable time-resolved crystallography at room temperature with sub-picosecond time resolution (Barends et al., 2015 ▸). Compared with synchrotron sources, ∼1 000 000 000 times higher peak brilliance of these pulses destroys the exposed microcrystal after the diffraction signal is obtained (Barty et al., 2012 ▸; Lomb et al., 2011 ▸). Consequently, each diffraction pattern typically originates from a different microcrystal in a random orientation. Additionally, the femtosecond duration of XFEL pulses precludes rotation of the crystal during exposure, yielding still diffraction patterns with partial Bragg reflection intensities. Retrieval of a complete data set with full reflection intensities can be achieved by assembling several thousand diffraction images (Kirian et al., 2011 ▸).

The ability to obtain diffraction data from small crystals while avoiding radiation damage is particularly attractive for de novo phasing of difficult protein targets. However, the XFEL radiation is generated by a stochastic self-amplified spontaneous-emission process that can introduce fluctuations in the intensity, pointing direction and spectral properties of the pulses. These instabilities, combined with variations in crystal size and quality in addition to challenges in processing still diffraction patterns, introduce noise in the SFX data analysis, which complicates accurate measurement of the weak anomalous signals needed for de novo phasing, particularly for native single-wavelength anomalous diffraction (native-SAD) (Rose et al., 2015 ▸). To decrease random errors and improve the accuracy of SFX data to a level sufficient for de novo phasing, an exceedingly high redundancy of measurements is mandatory (Barends et al., 2014 ▸; Kirian et al., 2011 ▸). While this approach has worked at XFELs, it is inefficient in terms of sample consumption and beam-time usage. Results from previous studies demonstrating de novo phasing using SFX data were mostly acquired from crystals diffracting strongly to high resolution (Barends et al., 2014 ▸; Fukuda et al., 2016 ▸; Gorel et al., 2017 ▸; Hunter et al., 2016 ▸; Nakane et al., 2016 ▸; Yamashita et al., 2017 ▸), including native-SAD phasing studies (Batyuk et al., 2016 ▸; Nakane et al., 2015 ▸; Nass et al., 2016 ▸), which still required ≥150 000 indexed images to succeed (Table 1 ▸).

Table 1. A summary of de novo phasing SFX studies and selected de novo phasing serial crystallography studies at synchrotron sources.

Sample Element Bijvoet ratio (%) Phasing method Minimal number of images Resolution (Å) Photon energy (keV) Facility Publication
A2A S 2.5 SAD 50000 2.65 4.57 SwissFEL This work
A2A S 1.5 SAD 500000 2.5 6.0 LCLS Batyuk et al. (2016 ▸)
A2A S 1.5 SAD 243537 2.67 6.0 SLS Weinert et al. (2017 ▸)
Thaumatin S 3.2 SAD 20000 2.65 4.57 SwissFEL This work
Thaumatin S 2.0 SAD 50000 1.95 6.06 SwissFEL This work
Thaumatin S 2.0 SAD 150000 2.1 6.0 LCLS Nass et al. (2016 ▸)
Lysozyme S + Cl 1.9 SAD 150000 2.1 7.0 SACLA Nakane et al. (2015 ▸)
Se-B SA Se 1.2 SAD 481079 1.9 12.8 LCLS Hunter et al. (2016 ▸)
Stem Se 3.7 SAD 13000 1.4 13.0 SACLA Yamashita et al. (2017 ▸)
ACG Se 2.2 SAD 60000 1.5 13.0 SACLA Yamashita et al. (2017 ▸)
CuNiR Cu 1.6 SAD 155588 1.6 10.8 SACLA Fukuda et al. (2016 ▸)
LRE Hg 4.2 SAD 11000 1.5 12.6 SACLA Yamashita et al. (2017 ▸)
LRE Hg 4.2 SIRAS 18000 1.7 12.6 SACLA Yamashita et al. (2015 ▸)
BinAB Hg, Gd, I – MIRAS 357765 2.4, 2.35, 2.6 8.8 LCLS Colletier et al. (2016 ▸)
bR I 10.5 SAD 23347 2.1 7.0 SALCA Nakane et al. (2016 ▸)
Lysozyme Gd 10.2 SAD 5000 1.9 9.0 SACLA Gorel et al. (2017 ▸)
Lysozyme Gd 10.2 MAD 5000 1.9, 2.0 9.0 + 7.0 SACLA Gorel et al. (2017 ▸)
Lysozyme Gd 11.0 SAD 60000 2.1 8.5 LCLS Barends et al. (2014 ▸)
Proteinase K Pr 4.8 SAD 3000 1.5 10 SACLA Sugahara et al. (2017 ▸)
Proteinase K Pr 4.8 SIRAS 2000 1.5 10 SACLA Sugahara et al. (2017 ▸)
Open in a new tab

Long-wavelength X-rays can be utilized to increase the anomalous signal from naturally occurring heavy elements in proteins such as sulfur and phospho­rus (Aurelius et al., 2017 ▸). This increased signal can be employed in native-SAD phasing and, in the specific case of SFX, may reduce the required number of indexed images, and thus reduce sample consumption and beam time. Additionally, the strong absorption of long-wavelength X-rays by air and large protein crystals, typically problematic at standard synchrotron macromolecular crystallography beamlines, are mitigated in SFX experiments as these are often carried out in a vacuum or helium environment with microcrystals delivered in a liquid jet or high-viscosity stream of limited diameter or on a solid support of limited thickness.

Here, we present an improvement in native-SAD phasing in SFX experiments by using longer wavelength X-rays and improved data processing. We demonstrate an up-to-tenfold reduction in the required number of indexed images for both model proteins and more challenging targets. In addition to an increased anomalous signal at longer wavelengths, we attribute this significant reduction to advances in data-analysis methods which reduced the negative impact on data quality from partial intensities and inaccurate experimental geometry in SFX data sets. This achievement can facilitate de novo structure determination of small and weakly diffracting protein crystals at XFELs, a potential that remains heavily underexploited.

2. Methods  

2.1. Preparation of A2A receptor microcrystals  

The expression, purification and crystallization of human A2A adenosine receptor (A2A) microcrystals were performed as previously described (Weinert et al., 2017 ▸). The A2A microcrystals had a plate-like shape and their average size was ∼35 × 35 × 5 µm (see Fig. S1 in the Supporting information). They were loaded into a lipidic cubic phase (LCP) injector prior to the measurements at SwissFEL directly from the Hamilton syringes in which they were grown.

2.2. Preparation of thaumatin microcrystals  

Thaumatin from Thaumatococcus danielii was purchased from Sigma–Aldrich GmbH (Buchs, Switzerland). Crystals were grown at 20°C using the vapour-diffusion method in sitting-drop CrysChem plates (Hampton Research, USA). Drops were composed of 2 µl of thaumatin solution (50 mg ml−1 dissolved in water) and 2 µl of reservoir solution (24% potassium sodium tartrate tetrahydrate, 100 mM bis-Tris propane pH 6.5) and were set up over wells containing 500 µl of reservoir solution. Crystals appeared overnight and grew over three to five days to a final size of 800 × 400 µm. The crystals were crushed in order to produce a seed stock, which was used to nucleate the growth of microcrystals as described below.

Micrometre-sized crystals were obtained by gently mixing 400 µl of thaumatin dissolved in 100 mM Na HEPES pH 7.0 at 88 mg ml−1 with 400 µl of the precipitant (1.6 M potassium sodium tartrate tetrahydrate, 100 mM Na HEPES pH 7.0) supplemented with 20 µl of the seed stock. Microcrystals grew overnight to a size of ∼20 µm in length and 10 µm in width. The microcrystalline slurry was then centrifuged at 8000g for two minutes and washed twice with the washing solution (0.8 M potassium sodium tartrate, 100 mM Na HEPES pH 6.8).

2.3. Embedding of thaumatin microcrystals in LCP  

To prepare the crystals for injection, LCP was obtained in a 100 µl Hamilton syringe by mixing 30 µl of monoolein with 20 µl of the washing solution. LCP was then mixed with 10 µl of the batch-grown microcrystals. An additional 15 µl of monoolein was added in order to keep the phase cubic.

2.4. Diffraction data collection  

SFX data from A2A and thaumatin microcrystals were collected in August 2018 during the very first SFX experiment at SwissFEL. The high-viscosity injector designed at the Arizona State University (Weierstall et al., 2014 ▸) and manufactured at the Paul Scherrer Institute (PSI) was used to deliver protein microcrystals grown or embedded in LCP to the interaction region with X-ray pulses. The injector was installed in the Prime chamber of the Alvra experimental hutch in a vertical configuration, with a distance of ∼95 mm between the nozzle tip and the detector surface. The injector was equipped with nozzles of 50 and 75 µm inner diameter for the A2A and thaumatin samples, respectively. Pressure to drive the injector was supplied by a high-performance liquid chromatography (HPLC) system (Shimadzu) remotely controlled through software. The flow rate set on the HPLC pump ranged from 0.002 to 0.003 ml min−1 resulting in a sample consumption rate of 0.15 to 0.22 µl min−1. The downstream displacement of the LCP stream between two consecutive X-ray pulses was 50–75 µm and 20–30 µm (calculated) for the capillary diameters of 50 and 75 µm, respectively.

After each injector exchange and prior to the measurements the pressure in the Alvra Prime chamber was reduced to 100 mbar, then the chamber was filled with He gas to 800 mbar and reduced again to 100 mbar. The temperature in the hutch was kept constant at 24°C. An X-ray beam transmission of 2% was used for all data sets. This value was chosen to minimize disruption of the LCP column caused by interaction with X-ray pulses, to reduce the number of saturated Bragg spots and to reduce the noise originating from the background scattering while preserving high-resolution Bragg spots. Single-shot diffraction patterns were recorded using the JUNGFRAU 16M detector (Fig. S2) (Mozzanica et al., 2016 ▸), with a hole in the middle for the direct beam, and saved to disk as HDF5 files containing images in the raw format as read out directly by the detector without any modifications. The data-acquisition system was operated at 25 Hz matching the repetition rate of the X-ray laser. A Kapton foil of 75 µm thickness was installed ∼20 mm from the detector surface to separate the detector compartment filled with N2 gas from He gas in the main experimental chamber. The pressure in these chambers was regulated to maintain equilibrium between the two sections. A detailed description of online data monitoring and offline data conversion can be found in the Supporting information.

2.5. Data processing, geometry optimization, phasing and refinement  

Diffraction images after applying pedestal and gain corrections were processed using CrystFEL version 0.7.0 (White et al., 2012 ▸). Peak finding was performed on every diffraction image using the peakfinder8 method with threshold and signal-to-noise ratio (SNR) parameters set to 50 and 5, respectively. Every diffraction image containing ten or more found Bragg peaks was identified as a ‘crystal hit’. Indexing of all data sets was performed using the asdf indexing algorithm method. We tested two other indexing methods available in CrystFEL 0.7.0: DirAx (Duisenberg, 1992 ▸) and MOSFLM (Battye et al., 2011 ▸). We used the number of indexed patterns as a benchmark. We found that the number of indexed patterns was the highest for asdf when other parameters such as peak-finding threshold, SNR and integration radius were kept the same. We used the default values of bandwidth and divergence and the profile radius parameters automatically determined by CrystFEL 0.7.0 for every indexed diffraction image. The fixed geometry of the multi-segment JUNGFRAU 16M detector was refined using geoptimizer (Yefanov et al., 2015 ▸) from the CrystFEL software suite. The beam centre location was optimized using peak-prediction refinement and detector-shift Python script from the CrystFEL suite.

The distance between the interaction region with X-ray pulses and the detector surface was optimized by indexing each data set separately with different detector distances and measuring the standard deviation of the distribution of the unit-cell parameters. The increment of the detector distance used in this analysis was 20 µm. The smallest standard deviation of the unit-cell parameters indicated the most optimal sample-to-detector distance as described by Nass et al. (2016 ▸).

Peak integration was performed using the rings-grad method for all data sets. Integrated reflection intensities were scaled and averaged in a Monte Carlo manner (Kirian et al., 2011 ▸) using partialator from the CrystFEL software suite versions 0.8.0 and 0.7.0 with and without partiality refinement to compare the effect of post-refinement and partiality correction between different CrystFEL versions. The following parameters were used for merging in partialator with partiality and post-refinement, --model = xsphere --iterations = 1 --no-deltacchalf --push-res = 0.5; and without partiality refinement, --model = unity --iterations = 1 --no-deltacchalf --push-res = 0.5. We optimized the number of iterations (1, 2 or 3) and push-res values [infinity (the default) or 0.5] with and without the no-deltacchalf parameter, and determined the set of parameters that led to the best structural solution with the least indexed patterns for our samples and experimental conditions. The --overpredict parameter was not used. The resulting set of merged reflections was then converted to the XDS_ASCII format, passed through XSCALE for outlier rejection and converted to structure-factor amplitudes using XDSCONV from the XDS software package (Kabsch, 2010 ▸). The progress of the partiality refinement was monitored using the plot-pr and plot-contourmap scripts from CrystFEL 0.8.0 (Fig. S3).

Structure determination of the thaumatin and A2A data sets was performed using the automated pipeline for substructure identification with SHELXD (Sheldrick, 2010 ▸), with refinement, phasing and model building implemented in the Crank2 pipeline (Skubák & Pannu, 2013 ▸). Additionally, iterative cycles of manual model rebuilding using Coot (Emsley & Cowtan, 2004 ▸) and refinement using Phenix (Adams et al., 2010 ▸) were performed to obtain final models of the A2A and thaumatin molecules. The model quality was assessed using MolProbity (Chen et al., 2010 ▸).

The peak heights from sulfur atoms in the phased anomalous difference Fourier maps of thaumatin used for the estimation of the anomalous signal strength (S ano) were calculated using the program ANODE (Thorn & Sheldrick, 2011 ▸), with phases from the refined model of thaumatin and reflection intensities from the whole resolution range (Table 2 ▸).

Table 2. SFX data-collection and refinement statistics.

Data set A2A Thaumatin Thaumatin
  All 50000 All 50000 All 20000
Wavelength, photon energy (Å, keV) 2.713, 4.57 2.046, 6.06 2.713, 4.57
Temperature (K) 297 297 297
Space group C2221 P41212 P41212
Unit-cell dimensions a, b, c (Å) 40.34 ± 0.08, 180.66 ± 0.37, 143.05 ± 0.33 58.32 ± 0.13, 58.32 ± 0.11, 150.90 ± 0.24 58.50 ± 0.14, 58.50 ± 0.14, 151.25 ± 0.24
No. of collected patterns 2251787 — 1169996 — 1476000 —
No. of indexed patterns (% of collected) 199136 (8.8) 50000 271609 (23.2) 50000 242578 (16.4) 20000
No. of unique reflections 29351 29281 36568 33828 15488 15488
Resolution (Å)† 35.71–2.65 (2.71–2.65) 35.71–2.65 (2.71–2.65) 24.39–1.95 (2.00–1.95) 24.39–2.00 (2.05–2.00) 35.71–2.65 (2.71–2.65) 35.71–2.65 (2.71–2.65)
Completeness (%) 100 (100) 100 (100) 100 (100) 100 (100) 100 (100) 100 (100)
Average redundancy 858 (293) 193 (13) 1149 (280) 188 (13) 1292 (384) 125 (37)
CC1/2 0.999 (0.707) 0.997 (0.453) 0.999 (0.732) 0.998 (0.451) 0.999 (0.864) 0.995 (0.856)
CC† 0.999 (0.910) 0.999 (0.790) 0.999 (0.919) 0.999 (0.788) 0.999 (0.963) 0.999 (0.961)
CCano 0.568 (0.086) 0.318 (0.073) 0.640 (0.279) 0.296 (−0.009) 0.877 (0.207) 0.387 (0.049)
Overall 〈I/σ(I)〉 23.29 (0.70) 12.70 (0.97) 23.96 (0.65) 11.81 (1.17) 34.97 (0.99) 11.14 (0.79)
R split (%)‡ 2.26 (135.73) 4.61 (109.68) 1.97 (134.86) 4.81 (95.33) 1.72 (75.81) 5.93 (111.57)
Refinement            
Resolution (Å) 34.50–2.65 34.50–2.65 23.15–1.95 23.15–2.00 31.98–2.65 31.98–2..65
Number of reflections used in refinement 29238 29312 36026 33556 14496 14552
R work/R free 0.1974/0.2203 0.1939/0.2210 0.1441/0.1681 0.1393/0.1692 0.1503/0.1870 0.1529/0.1962
Number of atoms 3286 3286 1622 1656 1563 1563
Protein 2998 2998 1558 1558 1553 1553
Ligand 288 288 10 10 10 10
Water 0 0 54 79 0 0
Overall B factor (Å2) 117.6 96.6 56.0 44.6 85.9 86.2
R.m.s. deviations            
Bond lengths (Å) 0.011 0.010 0.007 0.008 0.008 0.008
Bond angles (°) 1.664 1.593 0.817 0.978 0.932 0.931
Ramachandran plot (%)            
Most favoured 97.66 97.66 98.54 97.56 96.59 96.59
Additionally allowed 2.34 2.34 1.46 2.44 3.41 3.41
Disallowed 0 0 0 0 0 0
Open in a new tab
†

Numbers in parentheses refer to the highest resolution shell.

‡

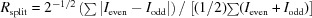
Inline graphic

2.6. XFEL parameters at SwissFEL  

The pulse parameters at SwissFEL were as follows: a repetition rate of 25 Hz; a pulse-duration upper limit of 130 fs full width at half-maximum (FWHM) (estimated from a measured electron-bunch length of 130 fs FWHM); photon energies of 4.57 keV (2.713 Å) and 6.06 keV (2.046 Å) measured by monochromator scans; energy bandwidths of 0.87% (FWHM) (40 eV/4570 eV) and 0.66% (FWHM) (40 eV/6060 eV) estimated from the monochromator scans using FWHM; beam sizes of ∼8 × 8 µm at 6.06 keV and ∼10 × 10 µm at 4.57 keV focused by a pair of Kirkpatrick–Baez mirrors, measured by knife-edge scans; and pulse intensities of 5.5 × 1015 W cm−2 corresponding to 5.93 × 1011 photons pulse−1 at 4.57 keV [calculated from the 435 ± 11 µJ average pulse-energy value measured by the pulse-intensity monitor (Juranić et al., 2018 ▸)] and 8 × 1015 W cm−2 corresponding to 4.15 × 1011 photons pulse−1 at 6.06 keV (402 ± 43 µJ). A beamline transmission of ∼50% and an attenuation factor of 98%, used deliberately to avoid jet instabilities and to reduce background scattering as described earlier, were not included in the above calculations.

2.7. Data and materials availability  

We deposited all diffraction data that contained crystal hits reported in this study in the Coherent X-ray Imaging Data Bank (CXIDB) with the accession codes ID 103, ID 104 and ID 105 (Maia, 2012 ▸). The atomic coordinates and the structure-factor amplitudes have also been deposited in the Protein Data Bank (PDB) under the accession codes highlighted in this article.

3. Results  

3.1. Experimental setup and data-collection parameters  

SFX data sets from microcrystals of thaumatin and human A2A adenosine receptor (A2A) were measured using X-ray wavelengths of 2.046 Å (6.06 keV) and 2.713 Å (4.57 keV) at the SwissFEL (Milne et al., 2017 ▸), and recorded with the new JUNGFRAU 2D X-ray detector that allows the acquisition of excellent quality data (Mozzanica et al., 2016 ▸). The microcrystals were grown (A2A) or embedded (thaumatin) in LCP and injected into the interaction region with focused X-ray pulses in the Alvra Prime experimental chamber at SwissFEL using an LCP injector (see Methods ). We collected 271 609 indexable diffraction images from thaumatin crystals at 6.06 keV and 242 578 images at 4.57 keV, and 199 136 images from A2A crystals at 4.57 keV at a repetition rate of 25 Hz (Table 2 ▸). We evaluated the data quality while systematically decreasing the number of images and determined the minimum for native-SAD phasing and automatic model building (see Methods and the Supporting information).

3.2. De novo structure determination of thaumatin at 6.06 keV  

We first performed native-SAD phasing of thaumatin data collected at 6.06 keV with all the images. To find the minimum number of images for successful and fully automatic structure determination, we systematically decreased the size of our data set, leading to 50 000 patterns required. The overall and split into resolution bins data-quality indicators from CrystFEL of the whole and minimal thaumatin 6.06 keV data sets are given in Tables S1–S3 in the Supporting information. The sub-structure determination, phasing and automatic model building were accomplished using the Crank2 pipeline and resulted in 97% of the model being built automatically (see Methods and Figs. S4–S7). The resolution of our data set extended to 1.95 Å; however, data to 2.8 Å were sufficient for de novo structure determination.

3.3. De novo structure determination of thaumatin at 4.57 keV  

In an identical setup, we carried out a native-SAD experiment using thaumatin microcrystals at 4.57 keV to exploit the enhanced imaginary part of the anomalous scattering factor of sulfur atoms (f′′ = 1.51 e− at 4.57 keV versus f′′ = 0.95 e− at 6.06 keV). Here, 20 000 indexed diffraction patterns were already sufficient for de novo structure determination at 2.65 Å resolution and model building using Crank2, with 92% of the model built automatically (see Methods , Tables S4–S6 and Figs. S8–S11). The maximal attainable resolution of this data set was limited to 2.65 Å because of geometrical constraints of the experimental setup and wavelength.

3.4. Comparison of anomalous signal strength from thaumatin at 6.06 and 4.57 keV  

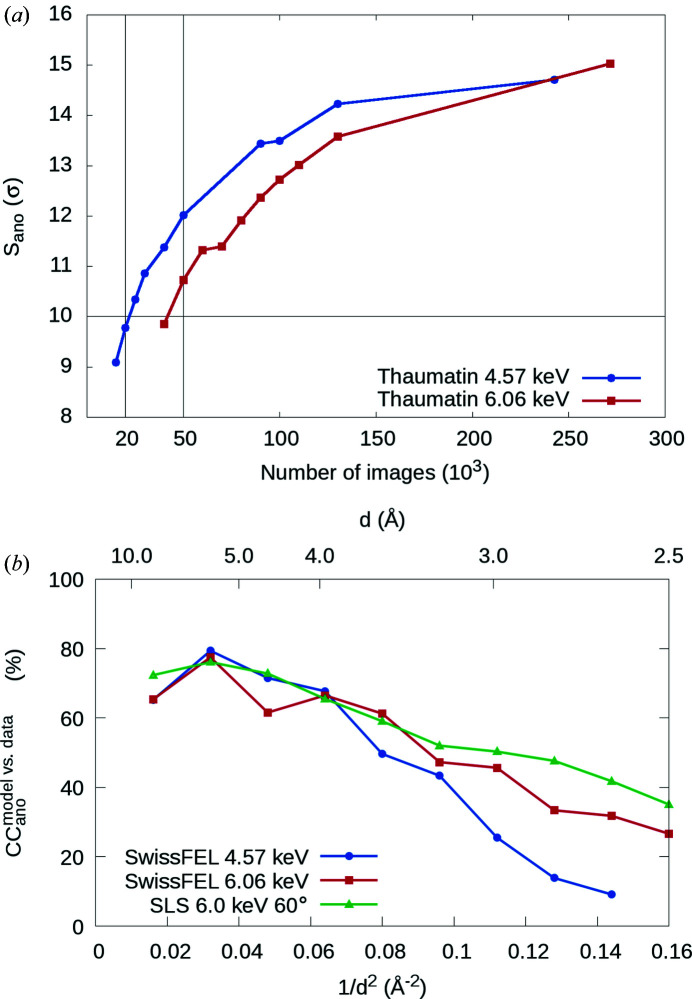
To quantify the effect of lower photon energy on the anomalous signal in SFX, we estimated the magnitude of the anomalous signal contained in our thaumatin data sets. We calculated the average peak heights of the phased anomalous Fourier difference maps (S ano) for different numbers of indexed diffraction images at two photon energies, 6.06 and 4.57 keV [Fig. 1 ▸(a)]. S ano is an unbiased data-quality indicator that allows direct comparison of the quality and accuracy of the measured data sets that contain anomalous signal. An S ano value of 10 or higher typically indicates whether the structure can be determined using SAD phasing (Terwilliger et al., 2016 ▸). In accordance with the expected 2.5-fold enhancement of f′′ [(1.51/0.95)2 = 2.5] at lower photon energy, the anomalous signal strength (S ano) from sulfur atoms in thaumatin at 4.57 keV is higher than at 6.06 keV for data sets with the same number of indexed images. Consequently, 2.5 times fewer diffraction images were required to determine the structure using native-SAD phasing at 4.57 keV. At both photon energies, the thaumatin data sets with the minimum number of indexed images required to solve the structure had S ano values of ∼10 [Fig. 1 ▸(a), horizontal and vertical lines].

Figure 1.

Figure 1

Open in a new tab

Anomalous data-quality indicators. (a) Anomalous signal strength (S ano) of thaumatin 4.57 and 6.06 keV data sets for different numbers of indexed diffraction images. The horizontal line indicates an S ano value of 10, below which SAD phasing is difficult. The two vertical lines indicate the minimal numbers of indexed images required for structure determination using native-SAD in this study. (b) Correlation coefficient between the measured and calculated anomalous difference structure-factor amplitudes (CCano model versus data) for thaumatin data sets with minimal amount of data necessary for successful structure solution using native-SAD at the SwissFEL and the Swiss Light Source (SLS) (Leonarski et al., 2018 ▸).

3.5. Comparison of anomalous data-quality indicators for thaumatin data sets with minimal number of indexed images required to determine the structure  

To further investigate the anomalous data-quality indicators, we calculated the correlation coefficients between the observed (|ΔF obs|) and the expected (|ΔFcalc|) anomalous difference structure-factor amplitudes (CCano model versus data) from data sets with the minimal number of images. We compared it with the CCano model versus data obtained from a synchrotron-rotation data set from a thaumatin crystal collected at 6 keV photon energy with a JUNGFRAU detector (Leonarski et al., 2018 ▸) [Fig. 1 ▸(b)]. The CCano model versus data values were calculated using a custom script that is available upon request. The synchrotron data set contains the minimum amount of data necessary for successful native-SAD phasing (60°) (Leonarski et al., 2018 ▸). Indeed, the 6.06 keV SwissFEL data set with 50 000 patterns has a similar CCano model versus data to the synchrotron data, indicating that the anomalous signal has been accurately extracted from our SFX data set. The 4.57 keV SFX data has comparable anomalous signal strength to 3.5 Å resolution, from which point on it gradually deteriorates toward higher resolution. The decrease of the CCano model versus data of the 4.57 keV thaumatin SFX data set at resolutions higher than 3.5 Å was primarily caused by excessive absorption of X-rays (up to 50%) at high diffraction angles by the 75 µm Kapton window mounted in front of the JUNGFRAU 16M detector. The Kapton window was used to separate the detector from the He atmosphere in the chamber. Nevertheless, high-resolution data were not required for sub-structure determination and data up to 2.8 Å were sufficient for density modification and automatic model building in Crank2.

3.6. Optimization of the sample-to-detector distance  

The indexing success rate and accuracy largely depend on the precise knowledge of the experimental geometry. Systematic errors introduced during data collection, such as slightly different detector distances between sample changes, can negatively affect the final data quality (Nass et al., 2016 ▸). Reduction of such errors is especially important in cases where high accuracy in the measurement is necessary, e.g. in de novo phasing and time-resolved SFX experiments. In order to reduce the negative influence of systematic errors in our data sets, we optimized the positions of the individual detector modules, determined the optimal beam-centre position using peak-prediction refinement protocol implemented in CrystFEL and optimized the sample-to-detector distance (see Methods ).

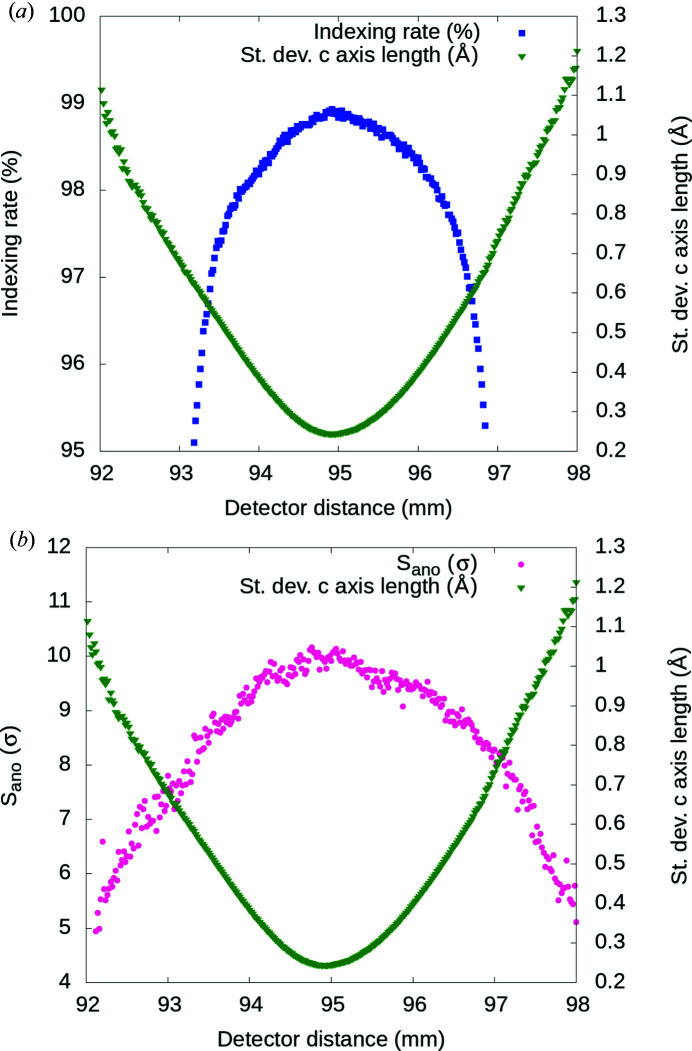
In order to find the optimal detector distance, we calculated the standard deviation of the distribution of the unit-cell parameters for each sample change at different detector distances. Fig. 2 ▸(a) shows the standard deviation of unit-cell length c and the indexing rate for different detector distances for one of the thaumatin 4.57 keV samples. This batch contained 25 821 selected diffraction images with crystal hits, up to 98.9% of which could be indexed at the optimal detector distance. The optimal detector distance, which corresponds to the minimum of the standard deviation of the distribution of the unit-cell length c, was 94.9 mm. Analysis of other unit-cell parameters yielded the same results. The optimal detector distance also corresponded to the highest indexing rate. We observed that the quality of the indexing solution directly relates to the accuracy of the measured structure-factor amplitudes, and hence to the strength of the anomalous signal (S ano), which in this sample batch was highest for the optimized detector distance of 94.9 mm [Fig. 2 ▸(b)]. Data sets for all sample batches indexed using optimized sample-to-detector distances were merged together to create final data sets with all indexed images.

Figure 2.

Figure 2

Open in a new tab

Detector-distance optimization using thaumatin crystals. (a) The smallest standard deviation of the distribution of the unit-cell parameters (green triangles) indicates the optimal sample-to-detector distance 94.9 mm. The indexing rate (blue squares) is highest at the optimal detector distance. (b) Average peak height of the anomalous Fourier difference map (S ano) from thaumatin at 4.57 keV (pink circles) calculated at different detector distances. S ano is highest at the optimal detector distance which corresponds to the smallest standard deviation of c axis length (green triangles).

3.7. Comparison of post-refinement and partiality correction procedures in different CrystFEL versions  

Partially recorded Bragg spot intensities are intrinsic to every SFX data set. In most SFX experiments performed to date, full reflection intensities were determined by averaging a large enough number of partial measurements of the same reflection from different crystals (Kirian et al., 2010 ▸, 2011 ▸). An estimation of the partiality of each such reflection in the presence of random and systematic errors has been notoriously difficult, although various partiality refinement protocols have been developed (Ginn et al., 2015 ▸; Kabsch, 2014 ▸; Sauter, 2015 ▸; White, 2014 ▸). One of the pre-requisites for accurate partiality estimation is precise knowledge of the experimental geometry (White, 2014 ▸). After optimizing the geometrical parameters of our experimental setup as described above, we investigated whether we could improve data quality with the recent developments in the CrystFEL post-refinement procedures, such as advanced scaling and partiality correction (White et al., 2016 ▸).

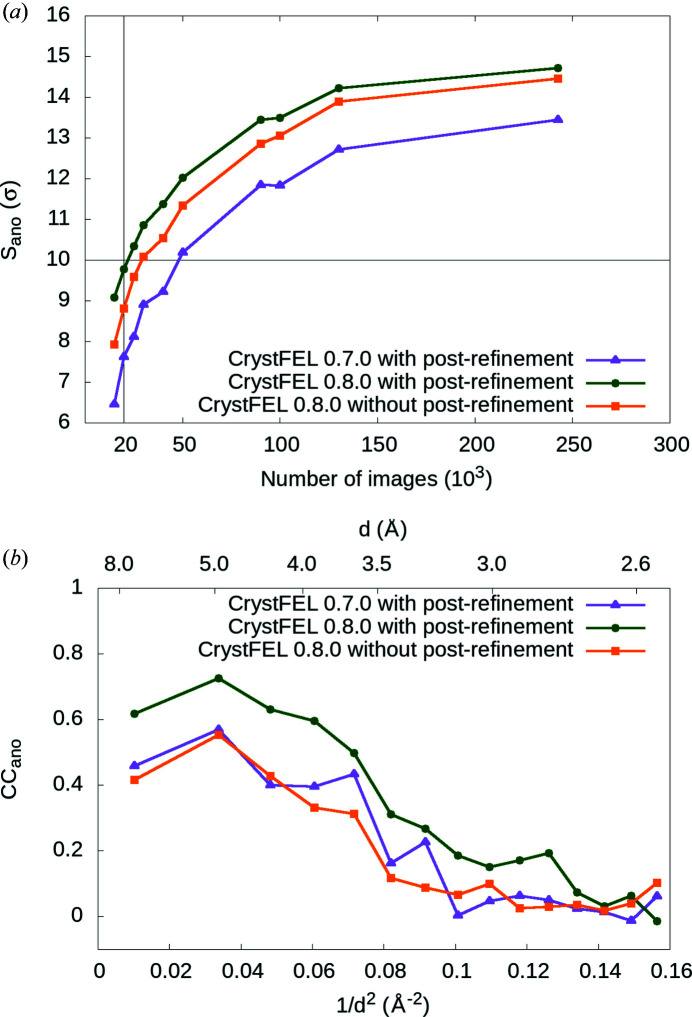
We used data-quality indicators sensitive to the overall accuracy of the data set, anomalous signal strength (S ano) and anomalous correlation coefficient (CCano) to quantify whether the improvements in the post-refinement protocols implemented in CrystFEL version 0.8.0 with respect to the previous CrystFEL version 0.7.0 have an influence on the accuracy of the structure factors in our final data sets. We calculated S ano values for thaumatin 4.57 keV data sets with different numbers of indexed images using CrystFEL versions 0.7.0 and 0.8.0 with scaling, post-refinement and partiality correction and using CrystFEL 0.8.0 without post-refinement and partiality correction but with scaling [Fig. 3 ▸(a)]. We observed that S ano values were higher for the same number of images when the newer CrystFEL version was used to merge partial reflections into the final data set. Within the newer CrystFEL version, we also observed that the post-refinement with partiality correction further improved the quality of the data sets as indicated by the highest S ano values (Table S7).

Figure 3.

Figure 3

Open in a new tab

Comparison of the anomalous signal strength (S ano) and anomalous correlation coefficient (CCano) for thaumatin at 4.57 keV. (a) Data sets with different numbers of images were processed using old and new versions of partialator from the CrystFEL software suite, with and without post-refinement and partiality correction. S ano is significantly larger when the newer version of post-refinement and partiality correction is used (green circles), as compared with the older version (purple triangles) and the newer version with only scaling (orange squares). (b) Similarly, CCano from 50 000 randomly selected thaumatin 4.57 keV diffraction images is higher when the newer version of CrystFEL with post-refinement and partiality correction is used on the same data set (green circles).

To quantify whether CCano also improved when using the newer CrystFEL version, we used 50 000 randomly selected indexed diffraction images from the thaumatin 4.57 keV data set and calculated CCano values as a function of the resolution [Fig. 3 ▸(b)]. Here, we observed that CrystFEL 0.8.0 with post-refinement and partiality correction resulted in higher CCano values indicating that the improvements implemented in CrystFEL 0.8.0 have a positive effect on the accuracy of the data set.

3.8. De novo structure determination of A2A at 4.57 keV  

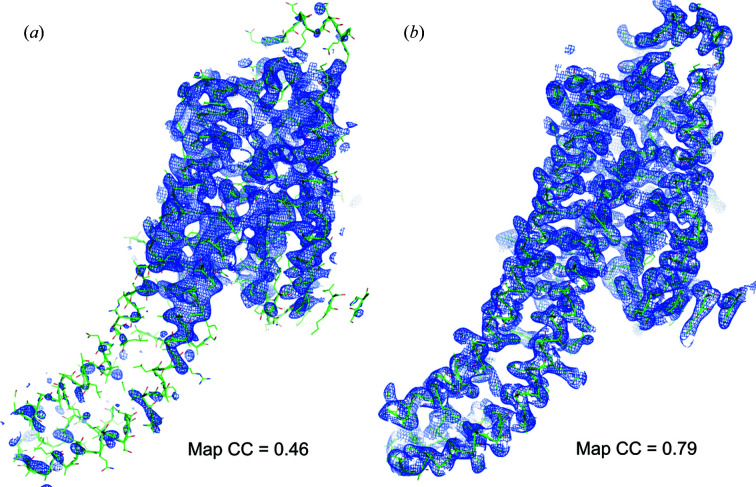
After establishing the improvements in native-SAD phasing with the thaumatin SFX data sets, we applied native-SAD at 4.57 keV to a membrane-protein target, the human A2A adenosine receptor, as a control with qualities closer to a more realistic sample. Although the A2A crystals diffracted strongly beyond the geometrically imposed resolution limit (2.65 Å), they have a higher overall B factor than thaumatin crystals, therefore representing a more difficult test case. Using all available indexed diffraction patterns (199 136), the structure of A2A was determined readily. With only 50 000 indexed images of A2A processed with individual crystal-dependent resolution cut-offs to suppress noise at high resolution from weak data, the positions of sulfur atoms were identified by SHELXD, and the iterative density modification and model building in Crank2 built an almost complete model (403 of 433 residues) (see Fig. 4 ▸, Methods , Tables S8–S11 and Figs. S12–S15).

Figure 4.

Figure 4

Open in a new tab

Phasing and automatic model building. (a) The experimental electron-density map (contoured at 1.0σ) after phasing and density modification obtained from the A2A data set with a minimal number of indexed images (50 000) at 4.57 keV superposed with the A2A molecule after automatic model building and refinement. (b) The 2mF o − DF c electron-density map after automatic model building and refinement. The MapCC values indicate the correlation coefficient between the map shown in the figure and the final refined map.

4. Discussion  

Here, we have applied long-wavelength XFEL pulses from SwissFEL and advances in data analysis to determine the structures of thaumatin and the A2A adenosine receptor using native-SAD phasing. Moreover, we provide a comprehensive analysis of factors that improved these native-SAD results. While a direct comparison of SAD phasing results obtained at different facilities using different detectors, machine properties and experimental setups may be constrained by the many differences, a careful comparison can still be informative.

The improvements presented in this work are primarily caused by a combination of the following factors: (i) an increased anomalous signal from sulfur atoms at a longer X-ray wavelength, (ii) a careful optimization of the experimental geometry that decreased systematic errors, (iii) an improved post-refinement and partiality correction in the CrystFEL 0.8.0 software suite and (iv) an accurate measurement of the diffraction signals using the low-noise high-dynamic range JUNGFRAU 16M detector (Mozzanica et al., 2016 ▸). We addressed the first three contributing factors using thaumatin data sets.

First, we compared the effect of a longer wavelength on the anomalous signal strength (S ano) and the effectiveness of automatic structure determination of thaumatin for different numbers of patterns collected at 4.57 and 6.06 keV at SwissFEL (Fig. 1 ▸). We needed only 20 000 diffraction images at 4.57 keV compared with 50 000 at 6.06 keV to determine the structure using fully the automatic native-SAD pipeline from Crank2, despite the fact that the resolution of the 4.57 keV data set was geometrically limited to 2.65 Å. This result suggests that using a longer XFEL wavelength for native-SAD phasing results in lower sample consumption and beam-time usage, by a factor of 2.5 in our case.

Next, we investigated whether systematic errors such as incorrect detector distance and geometry have a negative impact on the anomalous signal strength and the quality of indexing. We found that S ano and the indexing rate is maximized when the spread of the unit-cell parameters is smallest, indicating that the detector distance should be optimized for each sample batch to reduce systematic errors and to improve the accuracy of the final data set (Fig. 2 ▸). A similar approach to improve the integrated structure-factor intensity and heavy-atom anomalous peak heights from XFEL data by refining the experimental-geometry parameters was successfully applied in other studies (Brewster et al., 2018 ▸; Nass et al., 2016 ▸). Other sources of random error that negatively influence the precision of SFX data are shot-to-shot fluctuations of the X-ray pulses (e.g. pulse intensity, wavelength spread, spiky spectra, pulse duration) and crystal-to-crystal differences (e.g. size distribution, non-isomorphism). Most of the SFX studies to date have relied on averaging enough measurements of the same reflection in a Monte Carlo manner to minimize these errors. The same approach was applied to overcome the difficulty of retrieving full Bragg spot intensities from partially recorded reflections in still diffraction patterns from crystals in random orientations. Thirdly, we identified that the upgraded post-refinement and partiality corrections introduced in the CrystFEL version 0.8.0 software suite improved the accuracy of the final structure-factor intensities when compared with the previous version. In particular, the S ano and CCano values were higher in thaumatin data sets when the newer software version was used, which allowed us to determine the structures de novo using fewer images (Fig. 3 ▸).

Finally, we applied the improved methods in native-SAD phasing at XFELs identified at SwissFEL using the model system thaumatin to a more challenging target, the A2A human adenosine receptor. This system represents a class of membrane proteins, G-protein-coupled receptors (GPCRs), which, in general, pose a challenge for structure determination because they are characterized by a higher flexibility (temperature factor) and thus higher crystal disorder. In this case, we used up to one order of magnitude fewer images of the A2A adenosine receptor for native-SAD phasing compared with what was needed previously at an XFEL (Batyuk et al., 2016 ▸). Importantly, in both studies the resolution of the data sets was similar because of geometrical limitations imposed by the experimental setup and wavelength, which excludes the impact of different high-resolution limits on the performance of structure determination (Yamashita et al., 2017 ▸). This significant improvement opens up an opportunity for native-SAD phasing of small and radiation-sensitive membrane protein crystals with significantly reduced sample consumption and beam time.

In the case of thaumatin, we achieved a 2.5-fold improvement of the number of patterns required for structure determination at 4.57 keV compared with 6.06 keV using the same experimental setup at SwissFEL, and a threefold improvement when compared with a thaumatin native-SAD phasing study at 6 keV, compared with previous XFEL measurements (Nass et al., 2016 ▸). This is also the lowest number of indexed diffraction patterns needed for native-SAD in SFX to date, which is approaching those required for de novo phasing using seleno­methio­nine incorporation or heavy-metal derivatization in previously reported SFX studies (Table 1 ▸).

We attribute this remarkable achievement to the collective technological improvements enabling the use of longer-wavelength XFEL pulses for SFX and better data-analysis methods. Native-SAD phasing using long-wavelength XFEL pulses provides a compelling strategy to obtain unbiased experimental phases when structure determination is difficult because of inaccurate molecular-replacement models, particularly with low-resolution data. This work suggests that long-wavelength native-SAD experiments at XFELs have the potential to extend the scope of attainable novel structures in cases where radiation damage or poor phase quality is limiting the structure determination at synchrotrons. This is particularly important for membrane proteins that do not crystallize readily to a size sufficient for synchrotron studies. Several other XFEL facilities worldwide are capable of reaching X-ray beam parameters including the tender X-ray energy regime (2–5 keV), providing excellent opportunities for long-wavelength native-SAD phasing of difficult targets. Recent developments, such as the multivariate Bayesian model for estimating anomalous differences (Garcia-Bonete & Katona, 2019 ▸) and improvements to the error estimates of XFEL data (Brewster et al., 2019 ▸), could potentially improve the SAD phasing of XFEL data further. Moreover, the improved data-analysis methods implemented in CrystFEL version 0.8.0 and detector-distance optimization protocols can be applied to all types of SFX studies, not only to SAD phasing.

Supplementary Material

Supporting information. DOI: 10.1107/S2052252520011379/zf5013sup1.pdf

m-07-00965-sup1.pdf (1.4MB, pdf)

PDB reference: A2A, 4.57 keV, all diffraction images, 6s0l

PDB reference: A2A, 4.57 keV, 50 000 diffraction images, 6s0q

PDB reference: thaumatin, 4.57 keV, all diffraction images, 6s19

PDB reference: thaumatin, 4.57 keV, 20 000 diffraction images, 6s1d

PDB reference: thaumatin, 6.06 keV, all diffraction images, 6s1e

PDB reference: thaumatin, 6.06 keV, 50 000 diffraction images, 6s1g

Acknowledgments

MH, GS and RA are co-founders of LeadXpro AG, a company employing serial crystallography for structure-based drug design. RC and SNS are employees of LeadXpro. ASD, MR, RCo and TG are employees of Sosei Heptares. The remaining authors declare no competing financial interests.

Funding Statement

This work was funded by Schweizerischer Nationalfonds zur Förderung der Wissenschaftlichen Forschung grants PZ00P3_174169, 31003A_159558 , and 31003A_166608.

References

  1. Adams, P. D., Afonine, P. V., Bunkóczi, G., Chen, V. B., Davis, I. W., Echols, N., Headd, J. J., Hung, L.-W., Kapral, G. J., Grosse-Kunstleve, R. W., McCoy, A. J., Moriarty, N. W., Oeffner, R., Read, R. J., Richardson, D. C., Richardson, J. S., Terwilliger, T. C. & Zwart, P. H. (2010). Acta Cryst. D66, 213–221. [DOI] [PMC free article] [PubMed]
  2. Aurelius, O., Duman, R., El Omari, K., Mykhaylyk, V. & Wagner, A. (2017). Nucl. Instrum. Methods Phys. Res. B, 411, 12–16. [DOI] [PMC free article] [PubMed]
  3. Barends, T. R., Foucar, L., Ardevol, A., Nass, K., Aquila, A., Botha, S., Doak, R. B., Falahati, K., Hartmann, E., Hilpert, M., Heinz, M., Hoffmann, M. C., Kofinger, J., Koglin, J. E., Kovacsova, G., Liang, M., Milathianaki, D., Lemke, H. T., Reinstein, J., Roome, C. M., Shoeman, R. L., Williams, G. J., Burghardt, I., Hummer, G., Boutet, S. & Schlichting, I. (2015). Science, 350, 445–450. [DOI] [PubMed]
  4. Barends, T. R., Foucar, L., Botha, S., Doak, R. B., Shoeman, R. L., Nass, K., Koglin, J. E., Williams, G. J., Boutet, S., Messerschmidt, M. & Schlichting, I. (2014). Nature, 505, 244–247. [DOI] [PubMed]
  5. Barty, A., Caleman, C., Aquila, A., Timneanu, N., Lomb, L., White, T. A., Andreasson, J., Arnlund, D., Bajt, S., Barends, T. R., Barthelmess, M., Bogan, M. J., Bostedt, C., Bozek, J. D., Coffee, R., Coppola, N., Davidsson, J., Deponte, D. P., Doak, R. B., Ekeberg, T., Elser, V., Epp, S. W., Erk, B., Fleckenstein, H., Foucar, L., Fromme, P., Graafsma, H., Gumprecht, L., Hajdu, J., Hampton, C. Y., Hartmann, R., Hartmann, A., Hauser, G., Hirsemann, H., Holl, P., Hunter, M. S., Johansson, L., Kassemeyer, S., Kimmel, N., Kirian, R. A., Liang, M., Maia, F. R., Malmerberg, E., Marchesini, S., Martin, A. V., Nass, K., Neutze, R., Reich, C., Rolles, D., Rudek, B., Rudenko, A., Scott, H., Schlichting, I., Schulz, J., Seibert, M. M., Shoeman, R. L., Sierra, R. G., Soltau, H., Spence, J. C., Stellato, F., Stern, S., Struder, L., Ullrich, J., Wang, X., Weidenspointner, G., Weierstall, U., Wunderer, C. B. & Chapman, H. N. (2012). Nat. Photonics, 6, 35–40.
  6. Battye, T. G. G., Kontogiannis, L., Johnson, O., Powell, H. R. & Leslie, A. G. W. (2011). Acta Cryst. D67, 271–281. [DOI] [PMC free article] [PubMed]
  7. Batyuk, A., Galli, L., Ishchenko, A., Han, G. W., Gati, C., Popov, P. A., Lee, M.-Y., Stauch, B., White, T. A., Barty, A., Aquila, A., Hunter, M. S., Liang, M., Boutet, S., Pu, M., Liu, Z., Nelson, G., James, D., Li, C., Zhao, Y., Spence, J. C., Liu, W., Fromme, P., Katritch, V., Weierstall, U., Stevens, R. C. & Cherezov, V. (2016). Sci. Adv. 2, e1600292. [DOI] [PMC free article] [PubMed]
  8. Brewster, A. S., Bhowmick, A., Bolotovsky, R., Mendez, D., Zwart, P. H. & Sauter, N. K. (2019). Acta Cryst. D75, 959–968. [DOI] [PMC free article] [PubMed]
  9. Brewster, A. S., Waterman, D. G., Parkhurst, J. M., Gildea, R. J., Young, I. D., O’Riordan, L. J., Yano, J., Winter, G., Evans, G. & Sauter, N. K. (2018). Acta Cryst. D74, 877–894. [DOI] [PMC free article] [PubMed]
  10. Chen, V. B., Arendall, W. B., Headd, J. J., Keedy, D. A., Immormino, R. M., Kapral, G. J., Murray, L. W., Richardson, J. S. & Richardson, D. C. (2010). Acta Cryst. D66, 12–21. [DOI] [PMC free article] [PubMed]
  11. Colletier, J. P., Sawaya, M. R., Gingery, M., Rodriguez, J. A., Cascio, D., Brewster, A. S., Michels-Clark, T., Hice, R. H., Coquelle, N., Boutet, S., Williams, G. J., Messerschmidt, M., DePonte, D. P., Sierra, R. G., Laksmono, H., Koglin, J. E., Hunter, M. S., Park, H. W., Uervirojnangkoorn, M., Bideshi, D. K., Brunger, A. T., Federici, B. A., Sauter, N. K. & Eisenberg, D. S. (2016). Nature, 539, 43–47. [DOI] [PMC free article] [PubMed]
  12. Duisenberg, A. J. M. (1992). J. Appl. Cryst. 25, 92–96.
  13. Emsley, P. & Cowtan, K. (2004). Acta Cryst. D60, 2126–2132. [DOI] [PubMed]
  14. Fukuda, Y., Tse, K. M., Nakane, T., Nakatsu, T., Suzuki, M., Sugahara, M., Inoue, S., Masuda, T., Yumoto, F., Matsugaki, N., Nango, E., Tono, K., Joti, Y., Kameshima, T., Song, C., Hatsui, T., Yabashi, M., Nureki, O., Murphy, M. E., Inoue, T., Iwata, S. & Mizohata, E. (2016). Proc. Natl Acad. Sci. USA, 113, 2928–2933. [DOI] [PMC free article] [PubMed]
  15. Garcia-Bonete, M.-J. & Katona, G. (2019). Acta Cryst. A75, 851–860. [DOI] [PMC free article] [PubMed]
  16. Ginn, H. M., Brewster, A. S., Hattne, J., Evans, G., Wagner, A., Grimes, J. M., Sauter, N. K., Sutton, G. & Stuart, D. I. (2015). Acta Cryst. D71, 1400–1410. [DOI] [PMC free article] [PubMed]
  17. Gorel, A., Motomura, K., Fukuzawa, H., Doak, R. B., Grünbein, M. L., Hilpert, M., Inoue, I., Kloos, M., Kovácsová, G., Nango, E., Nass, K., Roome, C. M., Shoeman, R. L., Tanaka, R., Tono, K., Joti, Y., Yabashi, M., Iwata, S., Foucar, L., Ueda, K., Barends, T. R. M. & Schlichting, I. (2017). Nat. Commun. 8, 1170. [DOI] [PMC free article] [PubMed]
  18. Hunter, M. S., Yoon, C. H., DeMirci, H., Sierra, R. G., Dao, E. H., Ahmadi, R., Aksit, F., Aquila, A. L., Ciftci, H., Guillet, S., Hayes, M. J., Lane, T. J., Liang, M., Lundström, U., Koglin, J. E., Mgbam, P., Rao, Y., Zhang, L., Wakatsuki, S., Holton, J. M. & Boutet, S. (2016). Nat. Commun. 7, 13388. [DOI] [PMC free article] [PubMed]
  19. Juranić, P., Rehanek, J., Arrell, C. A., Pradervand, C., Ischebeck, R., Erny, C., Heimgartner, P., Gorgisyan, I., Thominet, V., Tiedtke, K., Sorokin, A., Follath, R., Makita, M., Seniutinas, G., David, C., Milne, C. J., Lemke, H., Radovic, M., Hauri, C. P. & Patthey, L. (2018). J. Synchrotron Rad. 25, 1238–1248. [DOI] [PMC free article] [PubMed]
  20. Kabsch, W. (2010). Acta Cryst. D66, 125–132. [DOI] [PMC free article] [PubMed]
  21. Kabsch, W. (2014). Acta Cryst. D70, 2204–2216. [DOI] [PMC free article] [PubMed]
  22. Kirian, R. A., Wang, X., Weierstall, U., Schmidt, K. E., Spence, J. C., Hunter, M., Fromme, P., White, T., Chapman, H. N. & Holton, J. (2010). Opt. Express, 18, 5713–5723. [DOI] [PMC free article] [PubMed]
  23. Kirian, R. A., White, T. A., Holton, J. M., Chapman, H. N., Fromme, P., Barty, A., Lomb, L., Aquila, A., Maia, F. R. N. C., Martin, A. V., Fromme, R., Wang, X., Hunter, M. S., Schmidt, K. E. & Spence, J. C. H. (2011). Acta Cryst. A67, 131–140. [DOI] [PMC free article] [PubMed]
  24. Leonarski, F., Redford, S., Mozzanica, A., Lopez-Cuenca, C., Panepucci, E., Nass, K., Ozerov, D., Vera, L., Olieric, V., Buntschu, D., Schneider, R., Tinti, G., Froejdh, E., Diederichs, K., Bunk, O., Schmitt, B. & Wang, M. (2018). Nat. Methods, 15, 799–804. [DOI] [PubMed]
  25. Lomb, L., Barends, T. R., Kassemeyer, S., Aquila, A., Epp, S. W., Erk, B., Foucar, L., Hartmann, R., Rudek, B., Rolles, D., Rudenko, A., Shoeman, R. L., Andreasson, J., Bajt, S., Barthelmess, M., Barty, A., Bogan, M. J., Bostedt, C., Bozek, J. D., Caleman, C., Coffee, R., Coppola, N., DePonte, D. P., Doak, R. B., Ekeberg, T., Fleckenstein, H., Fromme, P., Gebhardt, M., Graafsma, H., Gumprecht, L., Hampton, C. Y., Hartmann, A., Hauser, G., Hirsemann, H., Holl, P., Holton, J. M., Hunter, M. S., Kabsch, W., Kimmel, N., Kirian, R. A., Liang, M., Maia, F. R., Meinhart, A., Marchesini, S., Martin, A. V., Nass, K., Reich, C., Schulz, J., Seibert, M. M., Sierra, R., Soltau, H., Spence, J. C., Steinbrener, J., Stellato, F., Stern, S., Timneanu, N., Wang, X., Weidenspointner, G., Weierstall, U., White, T. A., Wunderer, C., Chapman, H. N., Ullrich, J., Strüder, L. & Schlichting, I. (2011). Phys. Rev. B, 84, 214111.
  26. Maia, F. R. (2012). Nat. Methods, 9, 854–855. [DOI] [PubMed]
  27. Milne, C. J., Schietinger, T., Aiba, M., Alarcon, A., Alex, J., Anghel, A., Arsov, V., Beard, C., Beaud, P., Bettoni, S., Bopp, M., Brands, H., Brönnimann, M., Brunnenkant, I., Calvi, M., Citterio, A., Craievich, P., Csatari Divall, M., Dällenbach, M., D’Amico, M., Dax, A., Deng, Y. P., Dietrich, A., Dinapoli, R., Divall, E., Dordevic, S., Ebner, S., Erny, C., Fitze, H., Flechsig, U., Follath, R., Frei, F., Gärtner, F., Ganter, R., Garvey, T., Geng, Z., Gorgisyan, I., Gough, C., Hauff, A., Hauri, C. P., Hiller, N., Humar, T., Hunziker, S., Ingold, G., Ischebeck, R., Janousch, M., Juranić, P., Jurcevic, M., Kaiser, M., Kalantari, B., Kalt, R., Keil, B., Kittel, C., Knopp, G., Koprek, W., Lemke, H. T., Lippuner, T., Llorente Sancho, D., Löhl, F., Lopez-Cuenca, C., Märki, F., Marcellini, F., Marinkovic, G., Martiel, I., Menzel, R., Mozzanica, A., Nass, K., Orlandi, G. L., Ozkan Loch, C., Panepucci, E., Paraliev, M., Patterson, B., Pedrini, B., Pedrozzi, M., Pollet, P., Pradervand, C., Prat, E., Radi, P., Raguin, J. Y., Redford, S., Rehanek, J., Réhault, J., Reiche, S., Ringele, M., Rittmann, J., Rivkin, L., Romann, A., Ruat, M., Ruder, C., Sala, L., Schebacher, L., Schilcher, T., Schlott, V., Schmidt, T., Schmitt, B., Shi, X., Stadler, M., Stingelin, L., Sturzenegger, W., Szlachetko, J., Thattil, D., Treyer, D. M., Trisorio, A., Tron, W., Vetter, S., Vicario, C., Voulot, D., Wang, M., Zamofing, T., Zellweger, C., Zennaro, R., Zimoch, E., Abela, R., Patthey, L. & Braun, H. H. (2017). Appl. Sci. 7, 720.
  28. Mozzanica, A., Bergamaschi, A., Brueckner, M., Cartier, S., Dinapoli, R., Greiffenberg, D., Jungmann-Smith, J., Maliakal, D., Mezza, D., Ramilli, M., Ruder, C., Schaedler, L., Schmitt, B., Shi, X. & Tinti, G. (2016). J. Instrum. 11, C02047–C02047.
  29. Nakane, T., Hanashima, S., Suzuki, M., Saiki, H., Hayashi, T., Kakinouchi, K., Sugiyama, S., Kawatake, S., Matsuoka, S., Matsumori, N., Nango, E., Kobayashi, J., Shimamura, T., Kimura, K., Mori, C., Kunishima, N., Sugahara, M., Takakyu, Y., Inoue, S., Masuda, T., Hosaka, T., Tono, K., Joti, Y., Kameshima, T., Hatsui, T., Yabashi, M., Inoue, T., Nureki, O., Iwata, S., Murata, M. & Mizohata, E. (2016). Proc. Natl Acad. Sci. USA, 113, 13039–13044. [DOI] [PMC free article] [PubMed]
  30. Nakane, T., Song, C., Suzuki, M., Nango, E., Kobayashi, J., Masuda, T., Inoue, S., Mizohata, E., Nakatsu, T., Tanaka, T., Tanaka, R., Shimamura, T., Tono, K., Joti, Y., Kameshima, T., Hatsui, T., Yabashi, M., Nureki, O., Iwata, S. & Sugahara, M. (2015). Acta Cryst. D71, 2519–2525. [DOI] [PMC free article] [PubMed]
  31. Nass, K. (2019). Acta Cryst. D75, 211–218. [DOI] [PMC free article] [PubMed]
  32. Nass, K., Meinhart, A., Barends, T. R. M., Foucar, L., Gorel, A., Aquila, A., Botha, S., Doak, R. B., Koglin, J., Liang, M., Shoeman, R. L., Williams, G., Boutet, S. & Schlichting, I. (2016). IUCrJ, 3, 180–191. [DOI] [PMC free article] [PubMed]
  33. Rose, J. P., Wang, B.-C. & Weiss, M. S. (2015). IUCrJ, 2, 431–440. [DOI] [PMC free article] [PubMed]
  34. Sauter, N. K. (2015). J. Synchrotron Rad. 22, 239–248. [DOI] [PMC free article] [PubMed]
  35. Schlichting, I. (2015). IUCrJ, 2, 246–255. [DOI] [PMC free article] [PubMed]
  36. Sheldrick, G. M. (2010). Acta Cryst. D66, 479–485. [DOI] [PMC free article] [PubMed]
  37. Skubák, P. & Pannu, N. S. (2013). Nat. Commun. 4, 2777. [DOI] [PMC free article] [PubMed]
  38. Spence, J. C. H. (2017). IUCrJ, 4, 322–339. [DOI] [PMC free article] [PubMed]
  39. Sugahara, M., Nakane, T., Masuda, T., Suzuki, M., Inoue, S., Song, C., Tanaka, R., Nakatsu, T., Mizohata, E., Yumoto, F., Tono, K., Joti, Y., Kameshima, T., Hatsui, T., Yabashi, M., Nureki, O., Numata, K., Nango, E. & Iwata, S. (2017). Sci. Rep. 7, 703. [DOI] [PMC free article] [PubMed]
  40. Terwilliger, T. C., Bunkóczi, G., Hung, L.-W., Zwart, P. H., Smith, J. L., Akey, D. L. & Adams, P. D. (2016). Acta Cryst. D72, 346–358. [DOI] [PMC free article] [PubMed]
  41. Thorn, A. & Sheldrick, G. M. (2011). J. Appl. Cryst. 44, 1285–1287. [DOI] [PMC free article] [PubMed]
  42. Weierstall, U., James, D., Wang, C., White, T. A., Wang, D., Liu, W., Spence, J. C., Bruce Doak, R., Nelson, G., Fromme, P., Fromme, R., Grotjohann, I., Kupitz, C., Zatsepin, N. A., Liu, H., Basu, S., Wacker, D., Won Han, G., Katritch, V., Boutet, S., Messerschmidt, M., Williams, G. J., Koglin, J. E., Marvin Seibert, M., Klinker, M., Gati, C., Shoeman, R. L., Barty, A., Chapman, H. N., Kirian, R. A., Beyerlein, K. R., Stevens, R. C., Li, D., Shah, S. T., Howe, N., Caffrey, M. & Cherezov, V. (2014). Nat. Commun. 5, 3309. [DOI] [PMC free article] [PubMed]
  43. Weinert, T., Olieric, N., Cheng, R., Brünle, S., James, D., Ozerov, D., Gashi, D., Vera, L., Marsh, M., Jaeger, K., Dworkowski, F., Panepucci, E., Basu, S., Skopintsev, P., Doré, A. S., Geng, T., Cooke, R. M., Liang, M., Prota, A. E., Panneels, V., Nogly, P., Ermler, U., Schertler, G., Hennig, M., Steinmetz, M. O., Wang, M. & Standfuss, J. (2017). Nat. Commun. 8, 542. [DOI] [PMC free article] [PubMed]
  44. White, T. A. (2014). Philos. Trans. R. Soc. B, 369, 20130330. [DOI] [PMC free article] [PubMed]
  45. White, T. A., Kirian, R. A., Martin, A. V., Aquila, A., Nass, K., Barty, A. & Chapman, H. N. (2012). J. Appl. Cryst. 45, 335–341.
  46. White, T. A., Mariani, V., Brehm, W., Yefanov, O., Barty, A., Beyerlein, K. R., Chervinskii, F., Galli, L., Gati, C., Nakane, T., Tolstikova, A., Yamashita, K., Yoon, C. H., Diederichs, K. & Chapman, H. N. (2016). J. Appl. Cryst. 49, 680–689. [DOI] [PMC free article] [PubMed]
  47. Yamashita, K., Kuwabara, N., Nakane, T., Murai, T., Mizohata, E., Sugahara, M., Pan, D., Masuda, T., Suzuki, M., Sato, T., Kodan, A., Yamaguchi, T., Nango, E., Tanaka, T., Tono, K., Joti, Y., Kameshima, T., Hatsui, T., Yabashi, M., Manya, H., Endo, T., Kato, R., Senda, T., Kato, H., Iwata, S., Ago, H., Yamamoto, M., Yumoto, F. & Nakatsu, T. (2017). IUCrJ, 4, 639–647. [DOI] [PMC free article] [PubMed]
  48. Yamashita, K., Pan, D., Okuda, T., Sugahara, M., Kodan, A., Yamaguchi, T., Murai, T., Gomi, K., Kajiyama, N., Mizohata, E., Suzuki, M., Nango, E., Tono, K., Joti, Y., Kameshima, T., Park, J., Song, C., Hatsui, T., Yabashi, M., Iwata, S., Kato, H., Ago, H., Yamamoto, M. & Nakatsu, T. (2015). Sci. Rep. 5, 14017. [DOI] [PMC free article] [PubMed]
  49. Yefanov, O., Mariani, V., Gati, C., White, T. A., Chapman, H. N. & Barty, A. (2015). Opt. Express, 23, 28459–28470. [DOI] [PMC free article] [PubMed]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting information. DOI: 10.1107/S2052252520011379/zf5013sup1.pdf

m-07-00965-sup1.pdf (1.4MB, pdf)

PDB reference: A2A, 4.57 keV, all diffraction images, 6s0l

PDB reference: A2A, 4.57 keV, 50 000 diffraction images, 6s0q

PDB reference: thaumatin, 4.57 keV, all diffraction images, 6s19

PDB reference: thaumatin, 4.57 keV, 20 000 diffraction images, 6s1d

PDB reference: thaumatin, 6.06 keV, all diffraction images, 6s1e

PDB reference: thaumatin, 6.06 keV, 50 000 diffraction images, 6s1g

Articles from IUCrJ are provided here courtesy of International Union of Crystallography

RESOURCES