Superensemble forecast of respiratory syncytial virus outbreaks at national, regional, and state levels in the United States

Abstract

Respiratory syncytial virus (RSV) infections peak during the winter months in the United States, yet the timing, intensity, and onset of these outbreaks vary each year. An RSV vaccine is on the cusp of being released; precise models and accurate forecasts of RSV epidemics may prove vital for planning where and when the vaccine should be deployed. Accurate forecasts with sufficient spatial and temporal resolution could also be used to support the prevention or treatment of RSV infections. Previously, we developed and validated an RSV forecast system at the regional scale in the United States. This model-inference system had considerable forecast skill, relative to the historical expectance, for outbreak peak intensity, total outbreak size, and onset, but only marginal skill for predicting the timing of the outbreak peak. Here, we use a superensemble approach to combine three forecasting methods for RSV prediction in the US at three different spatial resolutions: national, regional, and state. At the regional and state levels, we find a substantial improvement of forecast skill, relative to historical expectance, for peak intensity, timing, and onset outbreak up to two months in advance of the predicted outbreak peak. Moreover, due to the greater variability of RSV outbreaks at finer spatial scales, we find that improvement of forecast skill at the state level exceeds that at the regional and national levels. Such finer scale superensemble forecasts may be more relevant for effecting local-scale interventions, particularly in communities with a high burden of RSV infection.

1. Introduction

Models of infectious diseases can help elucidate transmission dynamics, estimate epidemiological parameters, evaluate hypothetical containment or transmission events, and forecast epidemics. Depending on the modeling objectives, mathematical models can be composed of compartments classified by stage of infection (Shaman et al., 2013; Shaman and Karspeck, 2012; Yang et al., 2015), based on individual agents operating within a stochastic framework (Ferguson et al., 2005; Willem et al., 2015), or defined by statistical associations with environmental or sociological factors (Darrow et al., 2014; Ségala et al., 2008). Forecasts generated using different modeling methodologies can be highly discrepant; however, statistical approaches can be used to reconcile and combine different forecast products into a more accurate weighted average forecast. Such superensemble forecasting is well-established in weather and climate forecasting (Krishnamurti et al., 2001; Yun et al., 2003), and has been applied recently to the forecast of infectious disease outbreaks (Ray and Reich, 2018; Yamana et al., 2017, 2016). In particular, Bayesian Model Averaging (BMA) is a multi-model averaging method that quantifies model uncertainty and combines different conceptual models based on their uncertainty and robustness. The resulting multi-model averages or superensembles have been shown to improve overall forecast accuracy compared to forecasts generated from a single model (Xu et al., 2017; Yamana et al., 2016).

Respiratory syncytial virus (RSV) has been modeled statistically to identify associations with meteorological parameters (du Prel et al., 2009; Onozuka, 2014; Ségala et al., 2008; Sloan et al., 2011), and simulated using a variety of compartmental model forms to investigate epidemiological dynamics (Pitzer et al., 2015; Reis and Shaman, 2016; Velasco-Hernández et al., 2015; Weber et al., 2001; White et al., 2007). Our previous work developed an RSV simulation and epidemic forecasting system that used a susceptible-infected-recovered (SIR) compartmental model, the ensemble adjustment Kalman filter (EAKF), and Census Division and Health and Human Services (HHS) regional data in the United States (Reis and Shaman, 2016). This model-inference system produced forecasts of peak intensity and epidemic onset with greater accuracy, or skill, than historical expectance at leads of up to four weeks, long enough to provide additional planning time for administration of prophylactic treatment to at-risk individuals. However, the forecasts of peak epidemic timing were only marginally more accurate than historical expectance, largely due to the regularity of RSV epidemics at the regional scale.

In this study, we simulate and forecast RSV using three distinct forecasting systems, and combine these component forecasts into a superensemble, using a BMA algorithm. We apply this prediction system to RSV observations at the national, regional, and state levels, with the objective of identifying the efficacy and utility of forecast systems of varying complexity at different spatial scales. We hypothesized that with ample data, the simplest historical models could compete with complex models at large spatial scales, particularly early in an outbreak. Conversely, we expected increasing accuracy for the superensemble forecasting system, relative to historical expectance, at more localized geographic scales where RSV outbreaks exhibit greater variability.

2. Materials

For each spatial scale, we used specimen laboratory RSV tests collected through the National Respiratory and Enteric Virus Surveillance System (NREVSS) and disseminated by the Centers for Disease Control and Prevention (CDC) (Centers for Disease Control and Prevention, 2017). We summed the positive specimens identified through antigen detection, viral isolation, and PCR testing and divided by the number of total tests administered. Antigen detection has been the most common method of RSV testing since at least 1997. PCR tests became widespread around 2010, and are slowly replacing both antigen detection and viral culture as the dominant test for RSV. To account for changing testing patterns and utilize a broader RSV signal, we summed the positive specimens identified through antigen detection, viral isolation, and PCR testing and divided by the number of total tests administered. Data were provided from 1997 to 2014, allowing for 17 seasons of RSV outbreaks at the national level. At the regional level, a sufficient volume of tests (≥20 samples per region) did not become available until 2004, allowing for simulation and forecast of 10 seasons of RSV outbreaks, sub-divided in the 19 overlapping Census Division and Health and Human Services divisions. At the state level, we summed the number of positive antigen and PCR detected RSV tests and divided by the total number of these tests, which were provided online as a three-week backward-looking moving average (Centers for Disease Control and Prevention, 2017). Our state data time series commences 2013–2014 and continues through the 2016–2017 season, with 26 states reporting three seasons with at least 30 observations. Time series of all three data aggregations are shown in Fig. 1.

Fig. 1.

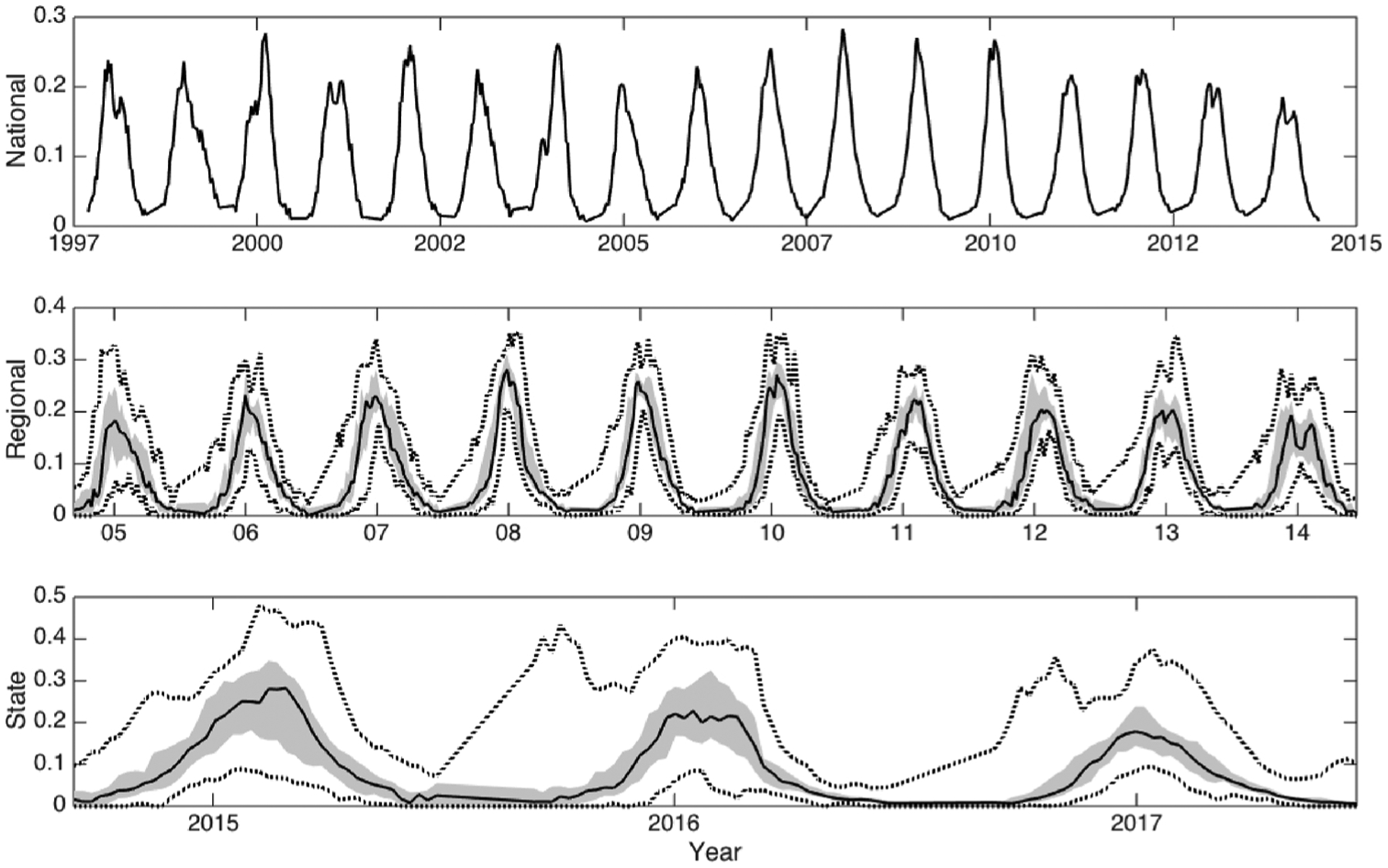
MedianRSV percent positive specimen data across each spatial resolution over the 42-weekRSV season, with the bounded region from the 25^th to 75^th percentiles of region-specific incidence shaded. Dotted lines indicate the minimum and maximum values.

For all three data forms, we simulated 42-week single-season RSV epidemics starting week 37, in mid-September, and ending on week 26, in early July. For each data stream, we generated retrospective forecasts of RSV epidemics using three independent forecast models (F1–F3). As described below, F1 and F2 employ Bayesian inference approaches, and F3 uses the historical expectance and serves as a simple null model. Forecast skill is evaluated based on superensemble performance relative to the null model.

3. Methods

We used three methods to generate retrospective forecasts of RSV outbreaks for four separate epidemic characteristics: 1) peak intensity, the maximum value in the 42-week RSV epidemic; 2) peak timing, the week of peak intensity; 3) mean cases, the mean percent of samples that were positive during the 42-week cycle; and 4) epidemic onset, defined as the first of two consecutive weeks in a season for which RSV incidence meets or exceeds a threshold of 10% positive, as specified by the CDC. Weekly forecasts were generated beginning on week 40 of each season and continuing for 37 weeks (through mid-June).

3.1. F1. Bayesian weighted outbreaks

For the first forecast method, Bayesian Weighted Outbreaks (BWO), we simulated each measure of RSV incidence using multi-model averaging. As described in (Yamana et al., 2016), we use the Bayesian Model Averaging (BMA) algorithm to model the future progression of a disease outbreak as a weighted sum of historical epidemic trajectories. Trajectory weights are determined based on the likelihood of the observed data being correct, given the historical trajectories over a training period, which in this case is the four weeks leading up to the week of the forecast, t. The BMA weighting scheme is determined by optimizing the following equation:

$$p\left(y_{(t-4):t}\mid f_{1,(t-4):t},\dots ,f_{k,(t-4):t}\right)=\sum _{k=1}^K{w}_k{g}_k\left(y_{(t-4):t}\mid f_{k,(t-4):t}\right)$$ (1)

where y is the observed incidence over the training period, w_kis the weight assigned to each historical trajectory f_k (i.e. an array of historically observed weekly incidence), and g_k (y| f_k) is the conditional probability density function (PDF) associated with each trajectory. K is the number of historical trajectories being considered. Each conditional PDF for y is assumed to be normal with mean f_kand standard deviation σ. We determine w_k and σ by applying a log-likelihood optimization algortihm using the expectation-maximization algorithm (Raftery et al., 2005), in effect, minimizing the difference between observations and the BMA-generated forecasts. Optimization tolerance was set to 10⁻⁴, with a maximum of 600 iterations.

The optimized weights, which sum to one, are multiplied by f_k and summed to obtain the forecast trajectory for all future weeks (t +1 through 42):

$$E\left(y_{(t+1):42}{f}_{1,(t+1):42},\dots ,f_{k,(t+1):42}\right)=\sum _{k=1}^K{w}_k{f}_{k,(t+1):42}$$ (2)

In other words, the BWO forecast is the expected value from the posterior model probability, or weights w_k, multiplied by the historical trajectories f_k.

3.2. F2. SIR-EAKF

For the second approach, and as described previously (Reis and Shaman, 2018, 2016), we simulated and forecast RSV outbreaks using the ensemble adjusted Kalman filter (EAKF) combined with a dynamical susceptible-infected-recovered (SIR) model:

$$\frac{dS}{dt}=-\frac{R_{0}IS}{DN}$$ (3)

$$\frac{dI}{dt}=\frac{R_{0}IS}{DN}-\frac{I}{D}$$ (4)

with S as the susceptible population, I as the number of infected, R₀ as the basic reproductive number, D as the mean infection period, and N as the size of the population. N was held constant at an arbitrary size of 500,000 people.

The model-filter structure employs an ensemble of simulations. Here, 300 ensemble members are integrated per modeling run, which provide a mean and variance associated with each forecast. All ensemble simulations were initiated at the beginning of a season, with a random selection of state variable and parameter distributions, which are listed in Table 1.

Table 1.

The initial parameters used in the SIR-EAKF are described by their range, mean, or standard deviation, and distribution type. All simulations were initialized with these values.

Variable or parameter	Initialized Range	Distribution
Susceptible, S	1.4 × 105 – 4.9 × 105 people; μ = 29.5 × 104; σ =7.1 × 104	Normal
Infectious, I	One to 1.5 × 103 people; μ = 14.8	Exponential
Duration of Infection, D	4–9 days	Uniform
Reproductive number, R0	1.3–4.0 new cases per infection	Uniform

We repeated each 300-member ensemble simulation five times to account for stochastic effects stemming from the random initialization. The EAKF, which is described in depth in Anderson (2001), is used to adjust the observed state variable, RSV incidence, with each new observational estimate of RSV incidence. This adjustment accounts for observation-ascribed uncertainty, here called the observed error variance (OEV), as well as model estimated uncertainty, derived from the ensemble prior variance. Following update of the observed state variable, the unobserved state variable and parameter estimates are then adjusted based on their co-variability with the new posterior observed state variable. OEV is defined as:

$$OEV=OE{V}_0+\frac{{\overline{OBS}}^2}{a}$$ (5)

where OEV₀ is the minimum OEV, and a is a constant. With this form [E5], OEV increases with observation magnitude, as measured by a simple three-week moving average $\overline{OBS}$. Following sensitivity analysis, we set OEV₀ as 10⁵ and a as 50. We mapped our observations to the incidence of population I with a scalar γ, set to 0.05, which accounts for the passive rather than active sampling scheme of the NREVSS data that tests only symptomatic individuals. SIR-EAKF forecasts (F2) were generated by integrating the posterior, following EAKF update, through to the end of the season without further adjustment. The mean trajectory from the 300 ensemble members is used as the SIR-EAKF forecast.

3.3. F3. Historical expectance or null

Our third forecast method, called the null model, used historical expectance (Reis and Shaman, 2016), which was defined as the mean epidemic trajectory or time-series from each location s, leaving out the current year. The historical expectance is akin to the RSV epidemic that a health expert might expect based on their prior experience with patient demand at the beginning of the season.

3.4. Superensemble

Following Yamana et al. (Yamana et al., 2016), our superensemble merges predictions from different forecasting methods. This weighted average accounts for model uncertainty and offsets the biases of each individual forecast. To generate our superensemble forecasts, we combined the three prediction methods (F1 to F3) using the same BMA algorithm described in Eqs. (1) and (2). Rather than assigning weights based on the observed epidemic trajectory, as was done for the F1 forecast, training data for the superensemble are the observed and predicted values of each of the four epidemic characteristics over a training forecast period (here termed TF1 to TF3). We again leave out the current year, so that the set of training forecasts consists of data from all regions for all years except the year being forecast.

To prevent superensemble forecast of a given year that included BWO (F1) or null (F3) forecasts generated using training data from the year being forecast, we generated ‘parallel’ forecasts for use in the superensembles each year; e.g., a superensemble for year 3 would weigh F1 – F3 that were generated excluding training data from year 3. For simplicity, we term this approach advanced leave-one-out (ALOO).

Because the relative accuracy of the three individual forecasting methods varies based on the stage of the epidemic, weights are calculated separately for each calendar week, as in (Ray and Reich, 2018; Yamana et al., 2016). For example, a superensemble forecast for a given location during week 10 uses training forecasts for week 10 from the other years for all regions. Similarly, previous work has demonstrated that ensemble compartmental model-filter forecasts can be calibrated based on ensemble variance; i.e. forecast accuracy can be predicted based on ensemble spread (Reis and Shaman, 2016; Shaman et al., 2013; Shaman and Karspeck, 2012). To incorporate this a posteriori information about the accuracy of the SIR-EAKF forecasts (F2) when generating the superensemble, we stratify forecasts into two categories: those with above-median F2 ensemble variance and those with below-median F2 ensemble variance. As high-variance SIR-EAKFs (F2) are known to be unreliable, we exclude such forecasts from the superensemble, and instead use TF1 and TF3 to obtain weights for F1 and F3. Conversely, for below-median F2 ensemble variance forecasts, we use TF2 with below-median variance and the corresponding TF1 and TF3 forecasts to obtain weights for F1–F3. In sum, we adapted the BMA algorithm (E1–E2) to combine forecasts F1 to F3, and stratified the weighting based on the SIR-EAKF forecast variance and week of forecast t:

$$p(yTF1,TF2,TF3)=\sum _{k=1}^3{w}_k{g}_k\left(y\mid T{F}_k,t,v\right)$$ (6)

The superensemble forecasts are the sum of weights w_k multiplied by forecasts F_k, which are each associated with a PDF g_k (yTF_k, t, v) that is optimized by the BMA algorithm using the log-likelihood function, thus generating a forecast per E2.

When evaluating the superensemble retrospective forecast accuracy, we grouped forecasts based on observed standard deviation of epidemic characteristics, superensemble variance, and lead week, which is defined as the current week minus the week of predicted peak intensity. We used the historical expectance as a benchmark for judging the utility of the other forecast methods; in particular, superensemble forecast accuracy must exceed historical expectance to justify its utilization. We define relative skill as the mean absolute error (MAE) of historical expectance minus the MAE of the superensemble.

4. Results

The superensemble RSV forecasts at each spatial scale were generally more accurate than each of the individual forecasting methods in predicting outbreak peak intensity, peak timing, mean cases, and onset. Fig. 2 shows the forecast mean absolute error (MAE) as a function of actual lead week (current week minus observed epidemic peak) for the superensemble and three individual forecasting approaches for data at the regional spatial grouping. The superensemble predictions exceeded historical expectance for leads of 0–7 weeks (i.e. 0 to −7) or longer for each characteristic. The mean error of each forecast type and each spatial aggregation is plotted in S1 Fig. Generally the predicted value is lower than the observed early in the outbreak, and vice versa after the actual peak. SIR-EAKF forecasts underestimate the mean cases characteristic throughout the outbreak, albeit by less than 5% at leads of eight weeks or fewer. Note that here we used actual lead week (current week minus actual peak timing) to compare concurrent forecasts from F1–F3, but unless otherwise specified, all other plots use predicted lead week as defined in the Methods.

Fig. 2.

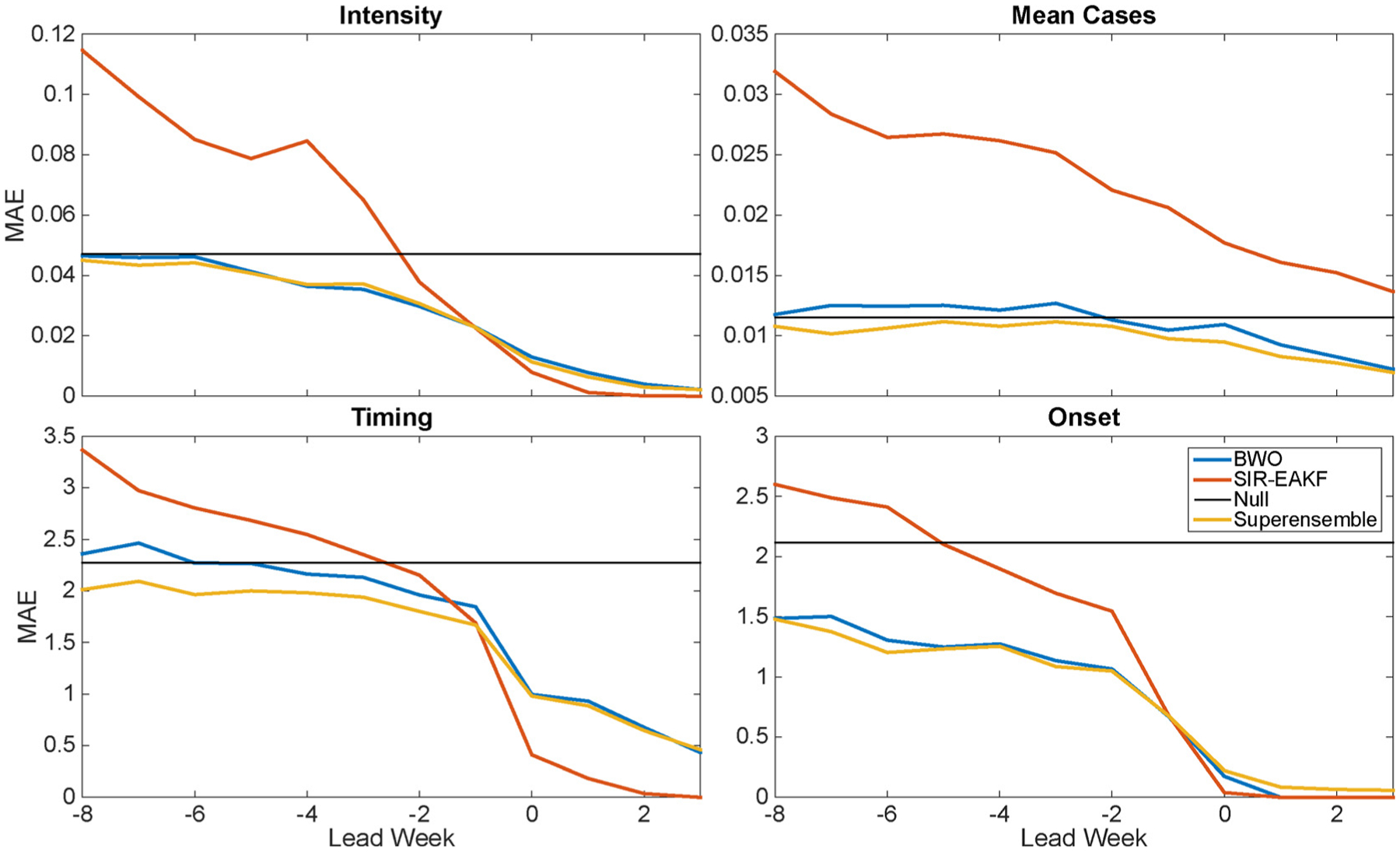
Mean absolute error (MAE) of RSV forecasts at the regional scale plotted as a function of actual lead week (forecast initiation week minus observed peak week for intensity, timing and total cases; forecast initiation week minus observed onset week for onset). The three models used to generate the superensemble are shown.

The mean weights optimized for F1–F3 to create the superensemble for all spatial groupings are shown in Fig. 3. The left column of Fig. 3 shows weights assigned only based on F1 and F3 for which the SIR-EAKF forecasts (F2) with above-median variance were omitted from the superensemble calculation. The right column of Fig. 3 shows the weights assigned to all three forecasts for SIR-EAKF forecasts with below-median variance. Early in an outbreak, the null model was given the greatest weight for the intensity, mean cases, and timing characteristics. Little weight is allocated to the SIR-EAKF forecasts for the outbreak characteristics measuring magnitude, intensity and mean cases, until about week 4 (late January). Likewise, the BWO, a weighted average of past epidemics, was assigned little weight in superensemble forecasts of intensity early in the epidemic, suggesting that RSV epidemic peak intensity does not strongly correlate with the magnitude of incidence early in the RSV season. As the epidemic developed, more weight was applied to the BWO and SIR-EAKF systems, which more explicitly use recent observations to adjust their predictions of future outcomes. Although the null model nearly matches superensemble forecasts at the state scale for timing (Fig. 2), the superensemble assigned the null very little weight when forecasting epidemic onset.

Fig. 3.

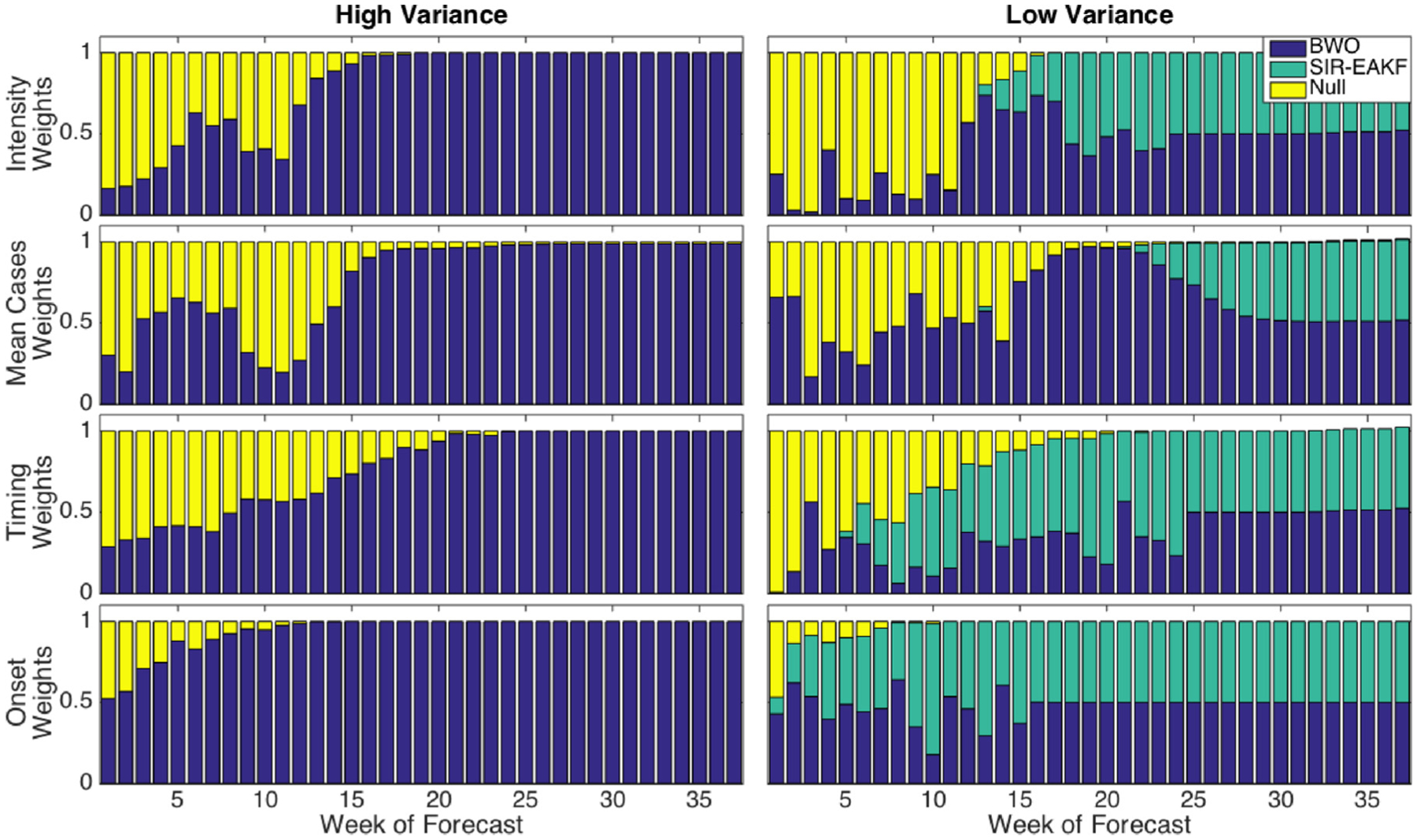
RSV superensemble weights, averaged over all spatial groupings, as a function of week of forecast. Left column: Superensemble weights calculated without SIR-EAKF training data, from SIR-EAKF forecasts with above-median variance. Right column: superensemble weights calculated with SIR-EAKF forecasts, from SIR-EAKF forecasts with below-median variance.

Fig. 4 shows the superensemble skill relative to historical expectance (superensemble MAE minus null MAE) versus predicted lead week, with the superensemble skill as a centered running mean, binned at 2-week intervals; MAE at one-week intervals is plotted with a dotted line. At the regional level, the MAE of intensity, timing, and onset for the superensemble forecasts were lower than historical expectance for leads of more than ten weeks (Fig. 4). At the state level, superensemble MAE of these characteristics were lower than historical expectance at leads of six or more weeks, depending on the forecast metric (Fig. 4). For mean cases, the superensemble at the 3 spatial scales, national, regional and state, matched or underperformed historical expectance, due to a relatively stable overall RSV mean annual burden, as measured by percent positivity. Similarly, national level outbreaks of RSV were similar in timing, intensity, and mean cases from year to year, such that the superensemble forecast MAE for these characteristics was lower only at shorter leads of about 2 weeks. At all levels, the superensemble outperforms the null for the onset by 0.5 weeks starting at a lead of eight weeks.

Fig. 4.

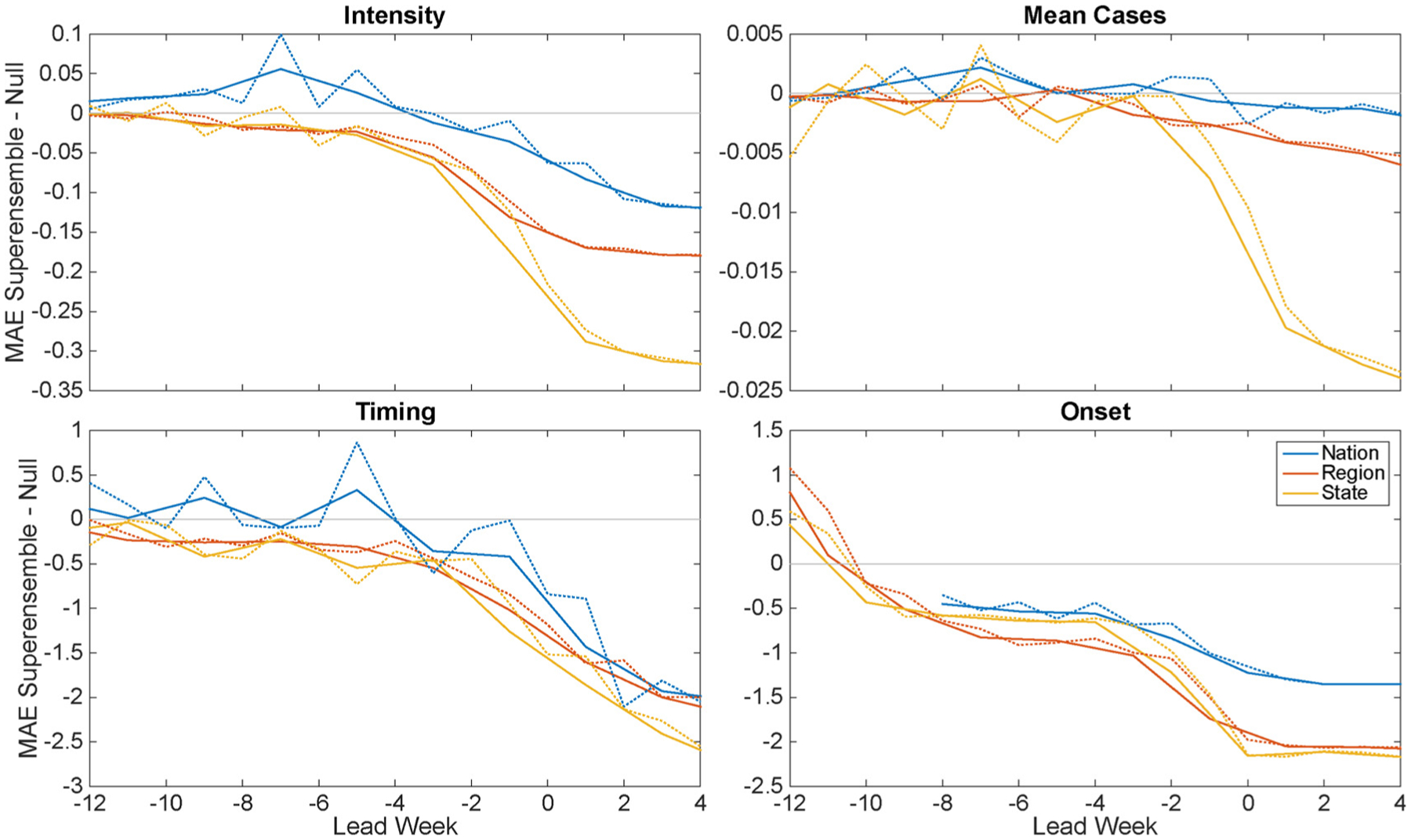
The mean absolute error (MAE) of the superensemble minus the MAE of the null model plotted as a function of predicted lead week (forecast initiation week minus predicted peak week for intensity, timing, and total cases; forecast initiation week minus predicted onset week for onset). MAE at one-week intervals is plotted with a dotted line and MAE aggregated at two-week intervals is plotted with a solid line.

The difference in MAE between the superensemble and historical expectance is plotted in Fig. 5 as a function of the observed standard deviation of each outbreak characteristic. As a reference, the observed standard deviation of the four epidemic characteristics for each spatial grouping is shown in S2 Fig. The observed standard deviation significantly correlates with the superensemble skill, with the slope p-value shown, for lead week groupings beginning eight weeks before the predicted peak for peak timing and onset, and beginning four and six weeks for intensity and mean cases, respectively. Fig. 5 plots each region and state in the lead week interval groupings, as well as the overall mean for each spatial grouping (shown with a larger marker outlined in black). As the variability of observed RSV outbreak metrics increases, the MAE of the superensemble forecast decreases. This negative association between epidemic variability and forecast error, which is particularly pronounced for the timing and onset characteristics, indicates that RSV forecasts have particular utility in areas where RSV outcomes are less regular.

Fig. 5.

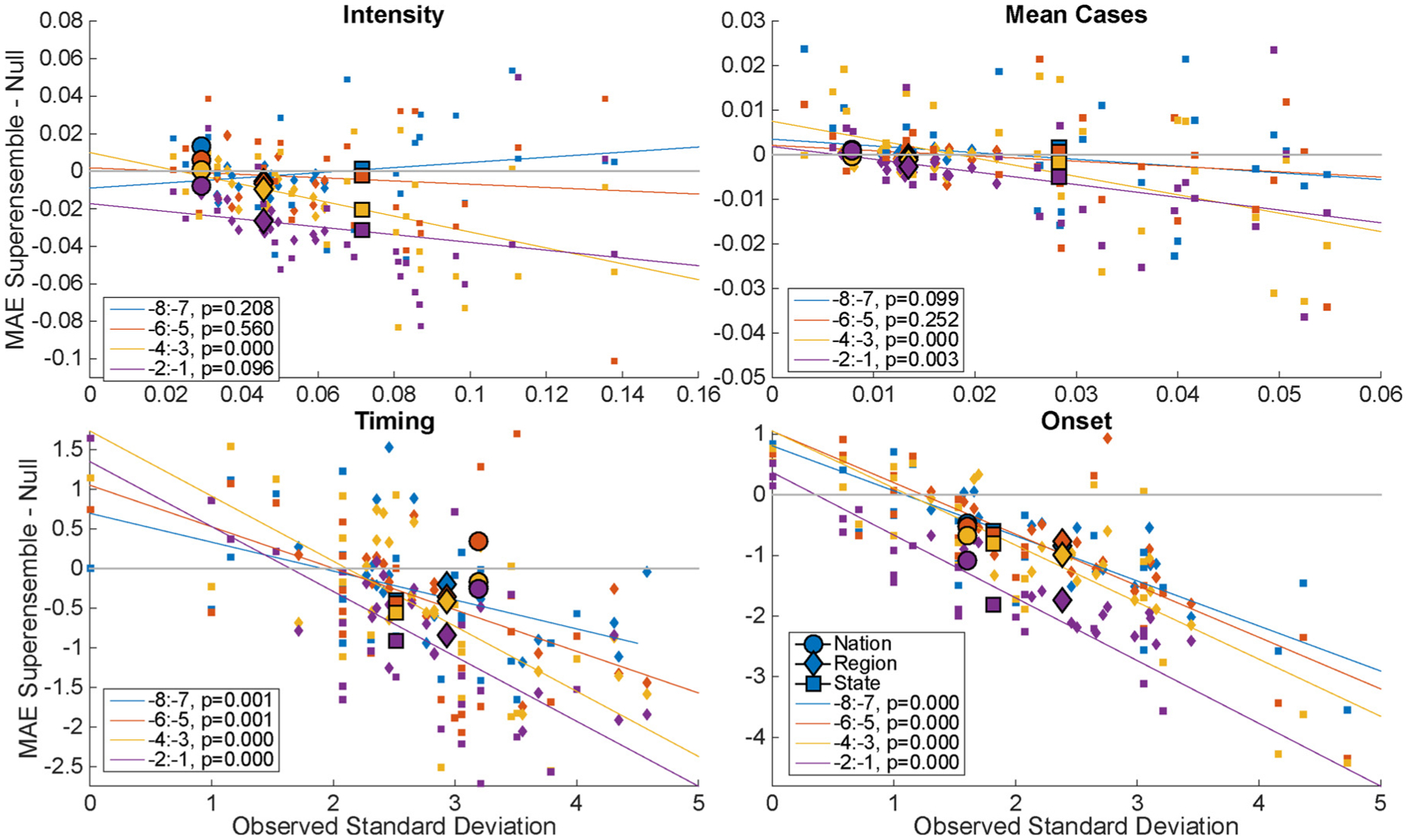
Relative skill, i.e. the MAE of the superensemble minus historical expectance (null) compared to the standard deviation of the observed metric. Colors indicate lead week increments. Trend line includes all spatial groupings. Circle: nation, diamond: region, square: state. Larger markers indicate mean of spatial grouping. The p-values indicate the significance of a linear model of the relative skill and observed standard deviation.

5. Discussion

Healthcare officials could use accurate, calibrated RSV forecasts to help plan for the distribution of expensive RSV prophylaxis or future vaccines, and increase medical preparedness by anticipating patient demand, which may decrease emergency department wait times. Here, we demonstrated a robust, flexible, and accurate RSV epidemic forecast system. We significantly improved upon our previous SIR-EAKF model-filter RSV forecasts (Reis and Shaman, 2016) by using a superensemble approach that combines three model methodologies. Previously our forecasts of regional RSV peak timing exceeded historical expectance just two weeks before the predicted peak; here the superensemble forecast skill exceeds historical expectance for timing with a lead of more than ten weeks in the regional and state groupings. Peak intensity was better predicted with a lead of six weeks at the state level and 10 weeks at the regional level. Prediction of mean cases was limited to two lead weeks, perhaps a reflection of the limited interannual variability exhibited by percent positivity data. Prediction of outbreak onset out-performed historical expectance at lead times of more than ten weeks at regional and state groupings.

Generally, the superensemble capitalizes on the strength of each forecast method. Early in the epidemic, the F3 null model was assigned more weight within the superensemble, particularly for peak intensity (Fig. 3). Later in the epidemic season, the BWO and SIR-EAKF forecasts, which are updated with each new observation, were assigned greater weight. The SIR-EAKF forecasts were assigned less weight than the BWO forecasts for characteristics that reflect outbreak magnitude, peak intensity and mean cases, and conversely, more weight for the peak timing and onset characteristics.

We showed that forecast error can be predicted using a combination of forecast lead (Fig. 4) and the observed standard deviation of each epidemic characteristic (Fig. 5). Calibration of the forecast allows quantification of expected accuracy of a forecast in real time (Shaman et al., 2014; Yang et al., 2014), and thus provides a measure of confidence in choosing between the superensemble forecast and historical expectance. We expected to find greater variability among epidemics at finer spatial resolution, and a corresponding increase in forecast accuracy over historical expectance, such that forecasts at more local scales would be more skillful relative to the null model. Indeed, state forecasts usually had the highest skill for each of the four metrics, although at times it was surpassed by the regional forecasts (Fig. 4). Conversely, the national RSV epidemics have lower observed variability in intensity and mean cases (S2 Fig.), and this outbreak regularity is reflected in the high accuracy of the historical expectance forecast. As a result, the benefits of using a superensemble approach were smaller than at the region and state levels (Figs. 4 and 5). Overall, we found a consistent negative association between observed standard deviation of epidemic characteristics and forecast MAE (Fig. 5). Thus, the forecasts appear to have greater utility in areas with high year-to-year variability.

For our superensemble, we selected one statistical model based on historical outbreaks (BWO), one process-based model (SIR-EAKF), and a simple null model. While an SIR model forecast is similar to that of other dynamical systems (e.g. including an exposed category in an SEIR model, as shown in S3 Fig), additional models might have generated distinct outbreak structures that could have informed the superensemble. Indeed, a larger superensemble comprised of more competing models with more potentially offsetting biases might produce still more accurate weighted-average predictions. Further, it would be interesting to see whether outbreaks at each spatial scale could inform forecasts at other spatial scales.

In this work, we combined antigen, viral, and PCR testing results to capture a larger sample of RSV infections and in doing so incorporate changing testing practices over time. Both viral and PCR tests generally have a lower percent positive rate than antigen tests, because they may be conducted on patients with a wide variety of respiratory symptoms, in comparison to antigen detection tests which are only administered on suspected RSV patients. These differences may shift biases in the combined test signal, as rates of utilization of a particular test can change.

While the retrospective superensemble forecasts developed here are encouraging, real-time, operational RSV forecasting still has yet to be generated and validated. The RSV data we present are generally available with a 1–2 week delay, so, in practice, a forecast lead of less than two weeks would only estimate the real-time incidence of RSV. While this information could still inform health care decision-making, a longer lead time (e.g. that observed at the region or state level) would be required to allow public health officials time to implement responses. Further, RSV data as initially released by the CDC is often subject to revision, which will further increase the error of real-time forecasts.Nowcast estimates of RSV for the most recent weeks could be developed to bridge the gap between the present and the most recent available data. A separate study is needed to develop such nowcast estimates using statistical approaches combined with real-time proxy data, such as online search and twitter activity.

Smoothing the model weights across weeks, or another covariate, may also improve superensemble performance (e.g. Ray and Reich, 2018). As Fig. 5 demonstrates, with sufficient variability in outbreak characteristics, the superensemble outperforms the null model. Future work could test whether stratifying by observed standard deviation, or other characteristics, improves superensemble performance. One limitation of this work was that superensemble variance output from the BMA algorithm was not well correlated with forecast performance, so we do not present probability estimates associated with the superensemble forecasts. However, forecast accuracy can be computed for each spatial aggregation to show the expected accuracy of a forecast by lead week (e.g. S4 Fig for the regional scale).

The improved skill of superensemble RSV epidemic forecasts relative to historical expectance could help medical professionals prepare for RSV patient demand. Although RSV outbreaks vary less than other infectious outbreaks (e.g. influenza), an accurate quantitative expectation of RSV patients could help health care facilities plan during the busy winter season, when morbidity spikes in a variety of infectious and non-infectious diseases. Increasing awareness of RSV as a threat to a growing elderly population as well as vulnerable infants (Openshaw et al., 2017), increasing access to rapid PCR testing of RSV infection, and rapid development in RSV vaccine availability (Giersing et al., 2017; Moscona, 2015) make accurate and calibrated forecasts of RSV more relevant than ever. Infants at risk for severe RSV-induced bronchiolitis, whether due to their prematurity or other risk factors, are usually recommended to receive five doses of expensive prophylaxis, which are not available to all at-risk infants (Committee on Infectious Diseases et al., 2014; Resch, 2014). As others have noted, any changes to the recommended prophylactic dosing would require rigorous additional study by physicians (Panozzo and Hampp, 2015), particularly given the vulnerability of the population at risk for severe RSV-induced bronchiolitis; yet as a theoretical exercise, if accurate, calibrated RSV epidemic forecasts could reduce the required prophylactic from five to four doses per month by anticipating the RSV epidemic timing two months earlier, an additional 20% of children could be covered by prophylaxis. Assuming an optimistic 96% reduction in hospitalization from prophylaxis (Banerji et al., 2014; Homaira et al., 2014; Paes et al., 2012), a 20% increase in prophylaxes coverage could prevent over 400,000 outpatient visits of children under five years old per year in the United States, including over 100,000 emergency department cases (Hall et al., 2009). This simple calculation indicates the potential value of RSV forecasts in terms of both illnesses averted and saved hospital resources.