Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2020 Oct 21;5(43):28285–28295. doi: 10.1021/acsomega.0c04243

Refined Force Field for Liquid Sulfolane with Particular Emphasis to Its Transport Characteristics

Srimayee Mukherji 1, Nikhil V S Avula 1, Sundaram Balasubramanian 1,*
PMCID: PMC7643274  PMID: 33163812

Abstract

graphic file with name ao0c04243_0012.jpg

An all-atom force field dedicated to capturing the properties of multifunctional sulfolane is necessary. In addition to being an excellent solvent and extractor, sulfolane is also a frequently investigated component for battery electrolytes in recent times. Given this, theoretically capturing its transport properties is essential. However, given the rather high shear viscosity of liquid sulfolane and its polar aprotic nature, formulating an appropriate non-polarizable force field for this compound remains a challenge. Starting from a generic force field, we report a refined force field for sulfolane which quantitatively captures its bulk properties, resulting in significantly improved estimates for self-diffusion constant and shear viscosity of sulfolane in comparison to force fields reported hitherto. Density, self-diffusion constant, and shear viscosity were determined between temperatures (303 and 398) K and at 1 bar pressure. All properties determined from the refined force field are in good agreement with experiments. The refined model employs atomic site charges obtained from the density-derived electrostatic and chemical (DDEC6) method for liquid sulfolane modeled using quantum density functional theory. Lennard-Jones parameters were refined using quantum potential energy scans. Despite possessing a large dipole moment, the large molecular size of sulfolane partially disrupts intermolecular dipolar ordering in liquid sulfolane. Molecular dipoles of near neighbor sulfolane, however, retain a partial preference for antiparallel orientation even at the highest temperatures investigated here.

Introduction

Sulfolane (IUPAC: thiolane 1,1-dioxide, CAS: 126-33-0) is an indispensable industrial solvent. Since sulfolane is a member of the sulfone class of molecules, it is also commonly referred to as tetramethylene sulfone. Liquid sulfolane has high thermal stability and a wide liquidus range, making it a very useful solvent for several high-temperature reactions even in the presence of strong acids and bases.1 Sulfolane is particularly useful in the separation of aromatic hydrocarbons from a mixture of hydrocarbons and in the sulfinol process of purifying natural gas through the removal of carbon dioxide, hydrosulfuric acid, and a few other sulfur-containing compounds.1 In recent times, however, liquid sulfolane is also being studied for its benefits as a solvent in lithium (Li)-ion and sodium (Na)-ion batteries.2−7 High oxidative stability, thermal stability, and relative permittivity (43.38) of sulfolane make it a strong prospective solvent candidate for electrolytes in highly stable, high-voltage batteries.2−4 Certain high salt concentration electrolytes formed with sulfolane in Li–S batteries have proven particularly promising. In these batteries, sulfolane behaves as a sparingly soluble solvent for Li2SX. These batteries are stable with better cycling, high-durability, and high energy density.5 Sulfolane combined with hydrofluoroethers has the added advantage of enhancing the diffusivity and rate capability in these Li–S batteries.5

Active research in the use of high concentrations of a lithium (or sodium) salts in sulfolane as battery electrolytes is in progress since these super-concentrated electrolytes address both increased energy and safety requirements for next-generation rechargeable batteries.2,5 However, it is also important to note that sulfone-based electrolytes have certain disadvantages in being used as a battery component. Some of these are their high melting point (except sulfolane with melting point Tm = 301.55 K),1 high viscosity (of liquid-sulfolane—10.35 mPa·s at 303.15 K1), inferior wettability of electrodes and separators, and formation of unstable solid–electrolyte interface materials.9 These challenges can be overcome, however. For example, sulfolane in combination with non-solvating fluorinating ether overcomes these challenges in addition to providing high-efficiency cycling of Li metal even at high Li salt concentrations.10

The broad applicability of sulfolane partially finds its footing in its “two-in-one”structure, a predominantly carbon atom-composed ring and a SO2 crown. Although aprotic, the SO2 group of sulfolane is the source of its significant dipole moment (5.65 debye from MP2 level calculations carried out in this work). The massive dipole moment contributes to its high relative permittivity of 43.3,8 when compared to other dipolar aprotic solvents. Sulfolane’s ring of carbon atoms and its large dielectric constant come with a twin benefit. Sulfolane is miscible in several polar organic compounds, and at the same time, as a solvent, it solvates many inorganic compounds.1,11 Examining its SO2 group more closely, the vibrational spectrum of SO2 in sulfolane is very typical of most sulfones and is therefore also of wide interest in understanding this class of compounds.12 Keeping the aforementioned in mind, a comprehensive understanding of sulfolane’s physicochemical nature and exploring the full utility of this promising multipurpose solvent are important. Apart from experiments, this necessity can also be met through computational studies on sulfolane by providing molecular level insights into its properties, which may serve as new directions for future experimental studies.

In the past, molecular simulations, molecular dynamics (MD) simulations, and configurational-bias Monte Carlo simulations have used general and refined force fields to accurately capture several, if not all, experimentally reported thermophysical and thermochemical properties of substances.13−23 However, a force field that accurately captures the transport properties of sulfolane and whose potential energy surface (PES) is in good agreement with the quantum mechanical PES is currently absent. The availability of such a force field is of paramount importance to realize the utility of sulfolane-based battery electrolytes. The simulations of Aparicio and co-workers in ref (24) on sulfolane reproduce the density, heat of vaporization, and self-diffusion constant in fair comparison with experiments; however, the shear viscosity predicted by the model is half of that of the experimental value, which is somewhat surprising as the self-diffusion coefficient predicted by the model too is 23% lesser than the experimental value. Furthermore, the electric dipole moment of a single molecule of sulfolane calculated from the model is just 3.9 debye when compared to the value calculated from MP2 level quantum calculations of 5.65 debye (vide infra). Thus, our continued search for a more physicochemically meaningful and quantitatively reliable force field for sulfolane is not out of place.

While general, all-purpose force fields capture relatively simpler physical properties such as the density of such solvents, quantitatively accurate force fields for transport properties of sulfolane are required, which can enable molecular simulations to provide insights and directions to experimental research on a near-equal footing. The current manuscript is aimed in that direction.

In this study, we aim to arrive at effective force field parameters for sulfolane with particular emphasis on selecting appropriate non-bonded descriptors such as site charges and Lennard-Jones (LJ) parameters, for use in molecular simulations. The atomic-site charges in a liquid can, in principle, be considerably different from those obtained through quantum gas-phase calculations.21 To derive liquid-phase atomic-site charges for our MD simulations of bulk sulfolane, quantum density functional theory (DFT) optimizations of independent snapshots obtained from the liquid phase of sulfolane were carried out. These snaphshots were selected from MD simulations using a generic force field and gas-phase DDEC625 charges (see computational methods). Later, this electron density was partitioned to atomic site charges through the well-established density-derived electrostatic and chemical (DDEC6) charge partitioning method.25 Correspondingly, we have also modified the LJ interaction parameters to improve the match to quantum PES scans between a pair of molecules. In addition to refining the non-bonding parameters, we have derived the equilibrium values for bond lengths and bond angles through single-molecule quantum geometry optimizations at the MP2 level of theory. The dihedral parameters used in ref (2) were retained in the current study. We find that our force field parameters, while being the closest in reproducing quantum potential energy scans, predict properties such as density and heat of vaporization nearly at par with force fields such as the optimized potentials for liquid simulation (OPLS) force field.15 This refined force field predicts diffusivity, viscosity, and interfacial properties of sulfolane in better agreement with experiments than other force fields. As a test of the applicability of the refined parameters, in the Results and Discussion section, we provide the comparison between the values of several experimentally determined properties against those predicted by our force field and two other general force fields. We also calculate the various properties of sulfolane as a function of temperature and compare them against values reported from experiments.

Computational Methods

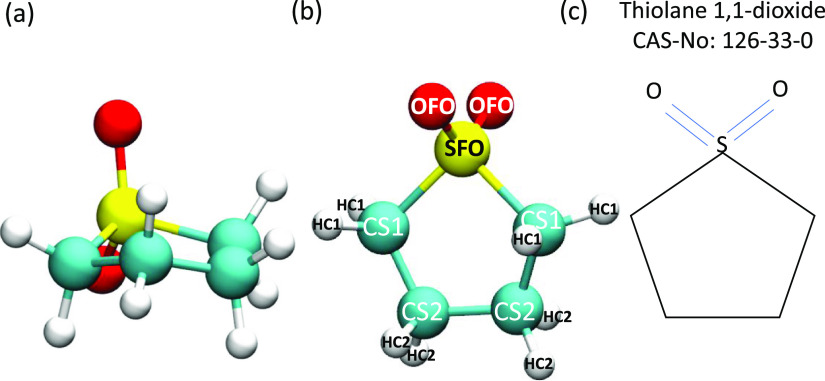
The non-planar nature of a sulfolane molecule is illustrated in Figure 1 which also provides atom labels which will be later used in the manuscript.

Figure 1.

Figure 1

Open in a new tab

(a) Molecular structure of sulfolane. (b) Atom types of sulfolane. (c) Chemical identifiers of compound sulfolane.

Liquid sulfolane modeled at 303 K and 1 bar using the force field described in ref (2) yielded a reasonably accurate density of 1284 kg·m–3. However, the self-diffusion coefficient of sulfolane using the force field of ref (2) (DRef 2 was calculated to be 6.0 × 10–13 m2·s–1) was more than two orders of magnitude lesser than the experimental value of Dexp,extrapolated = 14.72 × 10–11 m2·s–1 obtained from extrapolation from experimental data in ref (2). As a consequence of the underestimation of diffusivity, the viscosity of sulfolane was inestimable from molecular simulations even when calculated through a long MD trajectory of 25 ns duration.

To investigate the applicability of the OPLS force field of sulfolane, we first obtained its parameters from the LigPArGen server.26−28 Although we found that the OPLS force field with the 1.14*CM1A-LBCC charges27 estimates many physical properties of liquid sulfolane well, the viscosity calculated using this force field was around twice the experimentally reported value of 10.284 mPa·s.54 Hence, a refined force field for sulfolane capturing its transport properties accurately remained a necessity.

We started the force field refinement of sulfolane using the parameters used in ref (2) as our initial guess.

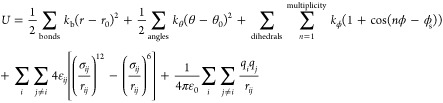graphic file with name ao0c04243_m001.jpg 1

The total potential energy of the system is a sum total of energies from non-bonded contributions such as the Coulombic and the LJ interactions and those from the bonded contributions of bond, angle, and dihedral-angle excitations (eq 1). We refine the Coulombic and LJ interactions and bond and angle equilibrium values to arrive at the refined set of parameters reported here. r0 is equilibrium bond length, kb is bond force constant, θ0 is equilibrium bond angle, kθ is angle force constant, and ϕ, kϕ, and ϕs are dihedral parameters. σij and ϵij are LJ parameters, and rij is the distance between the centers of the ith and jth atoms. ϵ0 is the permittivity of free space, and qi is the atomic site charge of the ith atom.

Non-bonded Parameters

Deriving Atomic-Site Charges

The method of refining atomic site charges (DDEC) used here has earlier been employed to refine parameters for imidazolium cation-based ionic liquids. Refined for the imidazolium cation–PF6– anion pair, these parameters were found to be transferable across a family of imidazolium-based ionic liquids.21,30,31 The fact that this procedure, when systematically applied to two very different kinds of liquids, has yielded reliable parameters (property predictions are comparable to experimentally measured values) prompts us to believe that this procedure can now be used to refine force field parameters for many different classes of liquids. It is also possible that the refined force field for sulfolane reported here is extendable with minor modifications to the entire class of sulfone compounds.

In order to derive atomic site charges from DFT calculations of liquid sulfolane, seven independent snapshots were chosen from a NVT MD run. This MD run used the force field of ref (2) barring the atomic site charges. Atomic site charges used were obtained for a single sulfolane molecule from DDEC625 calculations (Table S1). This MD run contained 26 sulfolane molecules in the liquid phase at 303 K. The linear dimension of the NPT equilibrated box was 16.3 Å. These snapshots were then geometry optimized within quantum DFT using CP2K software (version 6.1)32 with the Perdew, Burke, and Ernzerhof (PBE) exchange–correlation functional33 and Grimme’s D3 empirical van der Waals corrections.34 A convergence criteria of 10–6 a.u. for the gradient of electronic wave functions and 5 × 10–3 a.u. for the force on the nuclei were employed. The core electrons and nuclei were accounted for using the Geodecker–Teter–Hutter pseudopotentials.35,36 All valence electrons were represented by triple-ζ double-polarized basis sets with an energy cutoff of 320 Ry. The coordinates obtained from this minimization were used to obtain valence electron density at the same level of theory. This density was stored in a cube file and was used to obtain DDEC6 liquid-phase atomic charges using Chargemol software (Version 3.5).37 The atomic site charge distributions over seven snapshots were fairly narrow (see Supporting Information Figure S1), and hence, their means were utilizable. More detailed discussions on the applicability of this procedure followed in deriving condensed-phase charges can be found in ref (30). Site charges were averaged over all the molecules of a snapshot as well as over all the seven snapshots to arrive at the final liquid-phase DDEC6 charges employed in the refined force field simulations. These charges are presented in Table 1. Charges from ref (2) and those from OPLS27 are also provided for the sake of completeness.

Table 1. Atomic Site Charges q (e) of Sulfolane Derived from Quantum Calculations of Bulk Liquid and Used in the Simulations Reported Herea.
atom type ref (2) OPLS This work
SFO 1.56000 1.22980 1.067020
OFO –0.78000 –0.57030 –0.562630
CS1 –0.12000 –0.46675 –0.324400
CS2 –0.12000 –0.16105 –0.135542
HC1 0.06000 0.16740 0.142387
HC2 0.06000 0.12420 0.102144
Open in a new tab
a

Charges from ref (2) and of the OPLS force field26−28 are provided for the sake of completeness.

Refinement of LJ Parameters

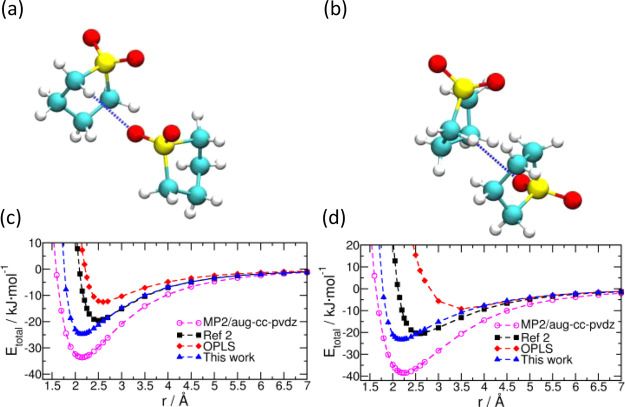
The LJ parameters were obtained by conducting several trials to fit quantum chemical rigid PES scans of a pair of sulfolane molecules as a function of distance between them. The PES scans were performed using Gaussian 16 software.38 These scans were performed in the gas phase along two different directions of approach of the molecules (shown in Figure 2a,b). The two initial configurations for gas-phase calculations were created in GaussView software (version 5.0.9.39). Subsequently, the LJ parameters employed in ref (2) were suitably modified through several trials so that the total potential energy calculated with the force field matches the quantum chemical PES as closely as possible (shown in Figure 2c,d). Since the PES calculations were carried out in the gas phase, the gas-phase DDEC6 site charges presented in Table S1 were used to arrive at the refined LJ parameters. The LJ parameters of ref (2), OPLS, and our refined force field (used henceforth in this work) are provided in Table 2. The PESs of both OPLS and of ref (2) are much shallower when compared to the MP2 result.

Figure 2.

Figure 2

Open in a new tab

(a,b) Directions along which a pair of sulfolane molecules are made to approach each other during the PES scan. (c,d) Corresponding PE surfaces.

Table 2. LJ Parameters for all the Force Fields Studied—σii (Å) and ϵii (kJ·mol–1) of Eq 1a.
  σ
 ϵ
atom type ref (2) OPLS this work ref (2) OPLS this work
SFO 3.55 3.55 3.80 1.046 1.046 2.000
OFO 2.96 2.96 2.90 0.879 0.711 0.711
CS1 3.50 3.50 3.55 0.276 0.276 0.100
CS2 3.50 3.50 3.50 0.276 0.276 0.100
HC1 2.50 2.50 2.00 0.126 0.126 0.050
HC2 2.50 2.50 2.50 0.126 0.126 0.067
Open in a new tab
a

Those of ref (2) and of OPLS26−28 are provided for the sake of completeness.

The bonded parameters (bond stretch and angle bending) used in the current manuscript are provided in the Supporting Information Tables S2 and S3. Sulfolane, being a cyclic molecule, was anticipated to have large dihedral energy barriers compared to kBT, where kB is the Boltzmann constant and T, temperature (303 to 398) K. Hence, we do not expect that at these temperatures, the dihedral angles deviate much from the equilibrium structure. Therefore, any refinement to dihedral parameters was anticipated to have a negligible effect on transport properties. Hence, dihedral parameters were adopted as such from ref (2) without any refinement.

MD Simulations of Liquid Sulfolane

Liquid sulfolane was modeled using these refined parameters. Classical MD simulations were performed using GROningen MAchine for Chemical Simulations, that is, GROMACS package.40−42 (version 2018.3). The particle–particle mesh Ewald solver was used to calculate the long-range electrostatic interactions.43 A precision of 10–5 was used for the same. The leap-frog algorithm, with a time step of 1 fs, was used to evolve the system in time. Atom coordinates were dumped at an interval of 1 ps. C–H covalent bonds were held constrained with the LINCS (Linear Constraint Solver) algorithm present in GROMACS.44 The Verlet algorithm used by GROMACS was employed for neighbor lists.45 Van der Waals and Coulomb cutoff distances were both taken to be 12 Å, with a neighbor list up to 14 Å. Interactions between different atom types were defined using the geometric mean, that is, σij = (σiiσjj)1/2 and ϵij = (ϵiiϵjj)1/2. The same combining rules are used by OPLS and our calculations using the force field in ref (2). 1–2 and 1–3 pairs interact via bond stretch and bending interactions only. For the non-bonding interaction involving 1–4 pairs, a scale factor of 0.5 is applied to both the LJ and Coulomb interactions. For all remaining atom pairs, the scale factor for non-bonding interactions is 1.0. Long-range energy and pressure dispersion corrections were applied. The Nosé–Hoover thermostat46 was employed with a coupling time constant of 0.5 ps. NVT production trajectories were used for a majority of the analyses. Berendsen47 and Parrinello–Rahman barostats48,49 were used for constant temperature and constant pressure NPT equilibration and NPT production runs, respectively. In either case, a coupling time constant of 2 ps was used. The barostat was coupled to the system every 10 steps when using the Berendsen barostat and every step with the Parrinello–Rahman barostat. All algorithms mentioned are as implemented by GROMACS.42An initial configuration of 800 sulfolane molecules was generated using the packing optimization for the automated generation of starting configurations for MD simulation (Packmol-Version 18.002) software.50 Minimization using the steepest gradient method was followed by constant NPT equilibration of the system for 10 ns, following constant NPT production runs of 25 ns. After that, constant NVT equilibration for 10 ns was performed. In the OPLS force field framework and that of the refined force field reported here, the NVT productions runs at 303 K were of duration 50 ns each. Only in the case of the simulations carried out using the force field of ref (2) at 303 K, owing to its sluggishness, an NVT production of 1 μs was required to reach the diffusive regime.

Liquid sulfolane was simulated at several temperatures in the range 303–398 K using the refined force field. NVT production runs of 50 ns were conducted for simulations at 303 K, 25 ns at 323 and 348 K, and over 12 ns at 373 and 398 K. Other details for these runs remain the same as those for the one performed at 303 K.

Periodic boundary conditions were applied along all three directions. The NPT equilibrated box lengths to accommodate 800 sulfolane molecules for various force fields studied here and for the various temperatures at which the refined force field was studied are given in the Supporting Information Table S4. Visualization was carried out in Visual MD (VMD) software.51

Results and Discussion

All percentage deviations mentioned are calculated from the corresponding experimental value, unless stated otherwise. All expanded uncertainties (U) are those calculated on the average value of the property reported.

Density

The average density for each force field studied was calculated by considering 25 ns of the NPT production run (after NPT equilibration). The data was divided into five blocks of 5 ns duration each. The method of calculating the expanded uncertainty (U) on the mean is provided in the Supporting Information. The NPT equilibrated box lengths are provided in Table S4. As shown in Table 3, percentage errors in density (Δρ) with respect to the experimental density, defined as 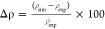Inline graphic for all force fields, are within 3%.

Table 3. Density ρsim (kg·m–3) of Liquid Sulfolane Estimated by all Force Fields at Temperature T = 303 K and Pressure p = 1 bara.

force field ρsimb Δρ (%)
force field of ref (2) 1297.15 ± 1.8 2.71
OPLS 1250.00 ± 0.3 –1.02
this work 1292.28 ± 0.4 2.33
literature 1262,53 1262.329  
  1261.9,54 1260.455  
  1260.4,56 1260.8057  
Open in a new tab
a

Experimental density at the same state point is ρexp = 1262.9 kg·m–3 (ref (52)).

b

The expanded uncertainty (U) is reported at 95% level of confidence.

The force field also predicts the temperature dependence of the density of liquid sulfolane rather well. These values are provided in Table 4 and Figure 3.

Table 4. Comparison between Density of Liquid Sulfolane from This Work ρthiswork (kg·m–3) with the Density of Sulfolane from Experiments ρexp (kg·m–3) in the Temperature Range T = (303–398) K and at Pressure p = 1 bara.

temperature/K ρThisworkb,c ρexp Δρ (%)
303 1292.28 ± 0.4 1262.952 2.33
313 1280.66 ± 0.4 1254.152 2.12
323 1268.89 ± 0.5 1245.252 1.90
348 1239.15 ± 0.7 1222.954 1.33
373 1208.09 ± 0.4 1200.954 0.60
398 1177.21 ± 0.4 1178.954 –0.14
Open in a new tab
a

Δρ is calculated with respect to the corresponding experimental value.

b

The expanded uncertainty (U) is reported at 95% level of confidence.

c

Density data follows a linear fit, y = mx + c, with m = −1.21 kg·m–3·K–1, and c = 1660.18 kg·m–3.

Figure 3.

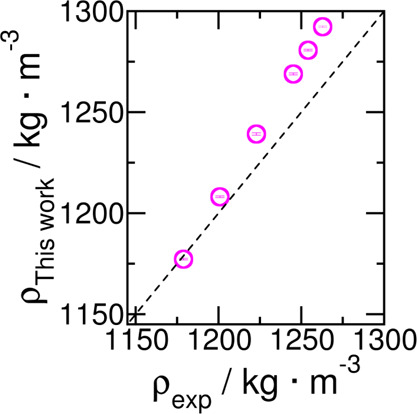
Figure 3

Open in a new tab

Comparison between densities predicted from this work with those from experiments in the temperature range T = 303–398 K and at pressure p = 1 bar.

Intermolecular Structure: Radial Distribution Functions

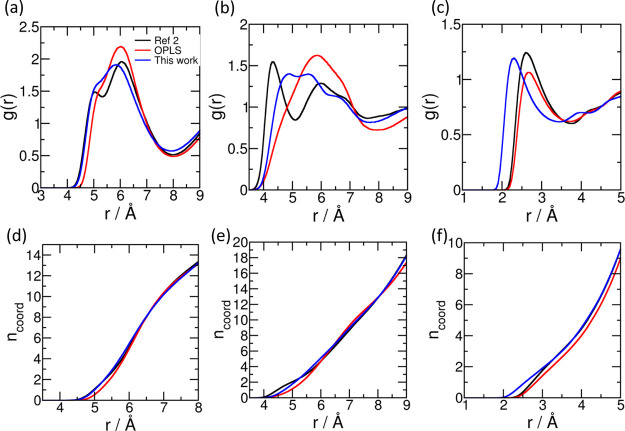
The intermolecular radial distribution functions (RDFs) between select pairs of sites calculated from all the three force fields at 303 K are presented in Figure 4. The center of mass (COM)–COM RDF (Figure 4a) and SFO-SFO RDF (Figure 4b) suggest that the first coordination shell of sulfolane ends a little short of 8 Å. Also, reminiscent of liquid argon, the first coordination shell contains 13 molecules on an average. From Figure 4c, we see that the HC1 hydrogens can be found closer to the OFO oxygen in simulations using the force field reported here in comparison to the remaining two. This may be a consequence of the fact that the refined force field reported here justifiably identifies two types of hydrogens (HC1 and HC2), depending on the electronegativity of the carbon atoms (CS1 or CS2) they are attached to. Although the OPLS force field also considers sulfolane to have two hydrogen and carbon atom types in terms of their charges, its LJ parameters do not distinguish between these two types. The position of the first peak of the OFO–HC1 RDF obtained using the force field of ref (2) and that from OPLS match with each other and are at slightly larger distance than the one obtained from the refined force field; this observation is consistent with the respective PES presented in Figure 2. RDFs for other atom pairs are reported in Figure S3.

Figure 4.

Figure 4

Open in a new tab

RDF between the following pairs of atoms at 303 K—(a) COM–COM, (b) SFO–SFO, and (c) OFO–HC1 (intermolecular). (d–f) coordination numbers corresponding to (a–c), respectively. Black—force field of ref (2), red—OPLS, and blue—this work.

Molecular Dipole Moment and Intermolecular Dipole Correlations

The dipole moment from each force field of a single sulfolane molecule was calculated using the geometry optimized structure obtained from the MP2 level of theory but with charges as prescribed by the respective force field. These values are tabulated in Table 5. The magnitude of the dipole moment from the OPLS force field and that from our force field are within 5% of the MP2 value, while that described in ref (2) is within 10% of the same.

Table 5. Dipole Moment p (debye) of a Sulfolane Molecule in the Gas Phase Obtained By All Force Fields and Quantum Chemical Calculationa.

description p/debye Δp (%)
MP2/aug-cc-pvdz 5.646  
force field of ref (2) 6.178 9.42
OPLS 5.425 –3.91
this work 5.922 4.89
Open in a new tab
a

The dipole moment predicted from the refined force field (this work) uses the derived DDEC6 liquid phase charges reported under “This work”in Table 1. The experimentally determined gas-phase dipole moment is 4.69 debye.1 The deviation Δp has been calculated with respect to the MP2/aug-cc-pvdz value.

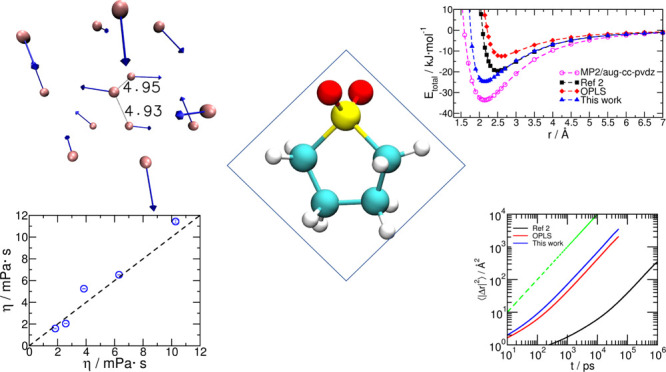
One can expect the significantly large electric dipole moment (Figure 4a) of sulfolane to influence the intermolecular structure and orientation in its liquid phase. As mentioned earlier, MP2 calculations of the single molecule yield a dipole moment value of 5.65 debye (Figure 5a). Despite the fact that sulfolane possesses a gas-phase dipole moment which is significantly higher than that of water (1.85 debye58), its static dielectric constant is much lesser (43.38) than that of liquid water (76.55 at 303 K59) and is comparable to that of dimethyl sulfoxide (DMSO) (4660 at 298 K). The molecular size (volume) of a sulfolane molecule is approximately 101.04 cm3/mol (167.8 Å3 per molecule) from a single-molecule gas phase from quantum calculations using Gaussian 16 software.38 Details for this calculation are provided in the Supporting Information.

Figure 5.

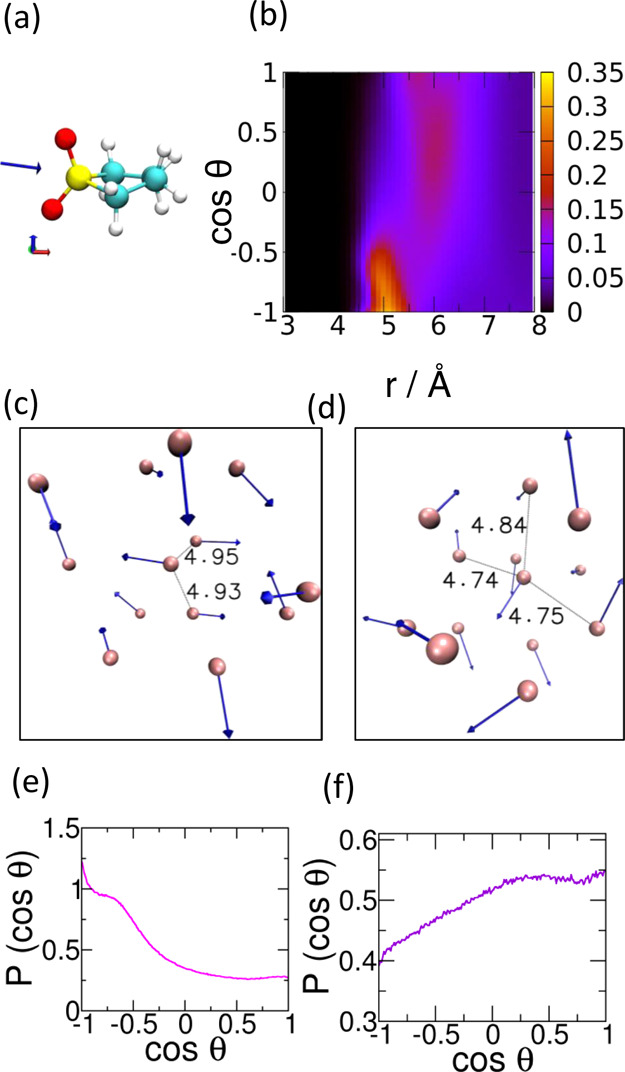
Figure 5

Open in a new tab

(a) Orientation of the dipole moment vector of the sulfolane molecule obtained from MP2 level calculations. (b) Combined intermolecular interdipole orientational (cos θ) and radial distance (r) PDF, illustrating the distance dependence of dipole orientation around any central sulfolane dipole. Among the sulfolane dipoles within the first solvation shell (8 Å) of a central molecule, the ones closest (within 5 Å) show an orientational preference of close to 180° as in (c) and close to 130° as in (d). Pink spheres in panels (c,d) are molecular COMs, and the blue arrows are molecular dipole moment vectors. Distances marked are in Angstrom. Snapshots (c,d) have been chosen randomly among those sulfolane molecules with 12 neighbors in the first solvation shell. The PDF of the cosine of the angles between dipoles for a range of distances, (e) from 4.5 to 5.5 Å, and (f) from 5.5 to 6.0 Å.

This large molecular volume and hence large intermolecular distances even to the first solvation shell (see the COM–COM pair-correlation function in Figure 4a) limit the extent of intermolecular orientational preferences that can potentially arise from its large dipole moment; the large molecular volume of sulfolane results in smaller dielectric constant in comparison to DMSO1 and water. However, the large dipole moment of sulfolane may possibly be a part of the reason behind its higher dielectric constant in comparison to other polar aprotic solvents.1

Figure 5b shows the combined probability density function (PDF), P(r,cos θ), representing orientational preference and spatial distribution of dipoles of sulfolane molecules around a central sulfolane dipole. Here, r is the radial distance from the central sulfolane dipole, and θ is the angle made between the central dipole and the dipole at r. P(r,cos θ) is averaged over all sulfolane dipoles over a 5 ns trajectory. Figure 5b–d suggests that the orientational effect of a central dipole on its neighboring dipoles is limited; however, a certain degree of antiparallel or near-antiparallel alignment of near neighbor sulfolane molecules is seen. The PDF of dipole orientations for dipoles present between 4.5 and 5.5 Å from a central sulfolane molecule is shown in Figure 5e. Once again, a preference for antiparallel orientations is noticed. The increased intensity between 5.5 and 6 Å in Figure 5b (corresponding to Figure 5f) coincides with the first peak position of the COM–COM pair correlation function presented in Figure 4a. A weak preference for a parallel orientation with the central sulfolane dipole is seen at these distances. This feature is due to a weak competition in the dipole–dipole interactions of molecules in this region with the central molecule and with molecules in the 4.5 to 5.5 Å region.

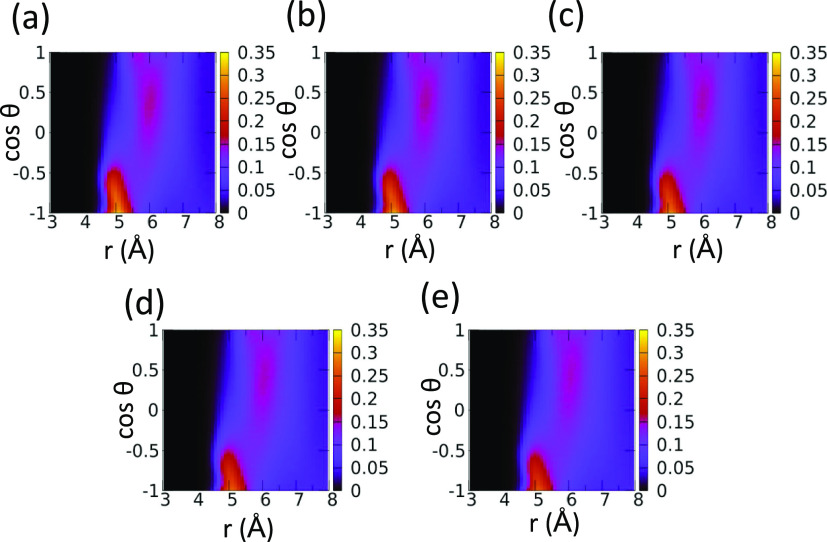
We also study P(r,cos θ) as a function of temperature (Figure 6). We find that temperature does not have a significant effect on P(r,cos θ) over the temperature range studied here. This, we speculate, is due to the large dipole moment of sulfolane. However, we see some decrease in the number of sulfolane molecules whose dipoles align antiparallelly to the central sulfolane dipole. Also, the various regions of P(r,cos θ) shift marginally to larger distances as a result of the decrease in density with an increase in temperature.

Figure 6.

Figure 6

Open in a new tab

Temperature dependence of a combined intermolecular interdipole orientational and radial distance PDF. (a) 303, (b) 323, (c) 348, (d) 373, and (e) 398 K.

Heat of Vaporization

The heat of vaporization provides a good estimate of the strength of intermolecular interactions present in any liquid. Assuming ideality in the gas phase, it is defined as ΔHvap = Egas – Eliq + RT,61 where ΔHvap is the heat of vaporization, Egas is the average total energy of a sulfolane molecule in the gas phase, Eliq is the average total energy per molecule in the liquid phase, R is the universal gas constant, and T is temperature. The mean heat of vaporization of liquid sulfolane at 303 K was calculated from three independent single-molecule gas phase NVT calculations (Egas) (Nsample = 3) and from a common single realization of Eliq for each force field. Details are provided in the Supporting Information.

All the force fields yield heat of vaporization within 11% of the experiment (Table 6).

Table 6. Heat of Vaporization ΔH (kJ·mol–1) Obtained Using Force Fields at Temperature T = 303 K and Pressure p = 1 bara.

force field ΔHvap,sim/kJ·mol–1b Δ(ΔHvap) (%)
force field of ref (2) 67.05 ± 0.17 0.48
OPLS 60.71 ± 0.24 –9.02
this work 59.43 ± 0.27 –10.94
Open in a new tab
a

The experimental value using the Clapeyron and Cox equations is 66.73 kJ·mol–1.62

b

The expanded uncertainty (U) is reported at 95% level of confidence.

Surface Tension

Details of calculation of surface tension are provided in the Supporting Information. The surface tension data estimated from all the force fields, including the one presented here, are presented in Table 7. Surface tension data in the literature seems to vary greatly from one experimental report to another. Thus, we desisted from calculating it as a function of temperature and limited ourselves to ambient conditions.

Table 7. Surface Tension γ (mN·m–1) of Liquid Sulfolane at Temperature T = 303 K and Pressure p = 1 bar Calculated Using Different Force Fieldsa.

force field γ/mN·m–1b Δγ (%)
force field of ref (2) 53.43 ± 4.6 50.51
OPLS 45.50 ± 1.6 28.17
this work 34.62 ± 0.5 –2.48
literature 35.564  
  35.5c  
  47.9529  
Open in a new tab
a

Experimentally determined value is ηexp = 35.50.63

b

The expanded uncertainty (U) is reported at 95% level of confidence.

Shear Viscosity

Another crucial transport property to validate the transport properties obtained through the force field is shear viscosity. We calculate it from the off-diagonal components of the pressure tensor from equilibrium MD simulations. The stress–stress time correlation function and the shear viscosity derived therefrom are calculated according to the Green–Kubo method in a manner similar to ref (65). The Green–Kubo expression used for viscosity calculation is provided in the Supporting Information eq S1. An example for the pressure tensor correlation function in time is shown in Figure S4. Further details of the calculation are provided in the Supporting Information.

The viscosity predicted by the current force field compares very well with the experimental value. The calculation of uncertainty U on the reported viscosity (Table 8 and Figure 7) obtained from block averaging was obtained in a manner very similar to that of density.

Table 8. Shear Viscosity η (mPa·s) Estimated by All Force Fields at Temperature T = 303 K, and Pressure p = 1 bara.

force field η/mPa·sb Δη (%)
force field of ref (2) not estimable within 25 ns run not estimable
OPLS 20.47 ± 0.04 99.05
this work 11.43 ± 0.15 10.02
literature 10.228,56 10.0529  
  10.30,53 10.07457  
  10.401052  
Open in a new tab
a

Experimentally determined value of shear viscosity is 10.284 mPa·s.54

b

The expanded uncertainty (U) is reported at 95% level of confidence.

Figure 7.

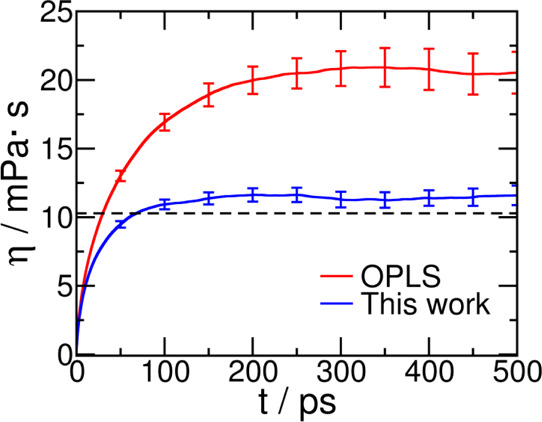
Figure 7

Open in a new tab

Running integral for shear viscosity of liquid sulfolane estimated from the OPLS force field and from the current work at temperature T = 303 K and pressure p = 1 bar. The dashed line is drawn at an experimental value of 10.284 mPa·s54 for comparison.

We have also calculated the shear viscosity of liquid sulfolane at different temperatures and find that the calculated values using the refined force field are in good agreement with the experiments (see Table 9 and Figure 8). The running integral of the pressure time correlation function as a function of temperature is shown in the Supporting Information Figure S5.

Table 9. Comparison between the Shear Viscosity of Liquid Sulfolane Calculated Using the Force Field Reported Here, ηthiswork (mPa·s), with That Reported in Experiments ηexp(mPa·s) in the Temperature Range T = (303–398) K, and at Pressure p = 1 bara.

temperature/K ηthisworkb,c ηexp Δη (%)
303 11.43 ± 0.15 10.28454 10.02
323 6.53 ± 0.03 6.31254 3.45
348 5.25 ± 0.03 3.84654 36.50
373 2.05 ± 0.02 2.5754 –20.23
398 1.59 ± 0.04 1.83554 –13.35
Open in a new tab
a

Δη is calculated with respect to the experimental value.

b

The expanded uncertainty (U) is reported at 95% level of confidence.

c

The data follows the Vogel–Fulcher–Tammann (VTF) equation,66 η = η0 eB/T–TVF, where η0 = 0.0026 mPa·s, B = 2554.6092 K, and TVF = 0.0 K. Since, in the present case, the VTF equation reduces to the Arrhenius equation, the activation energy obtained from an Arrhenius fit is 21.24 kJ·mol–1.

Figure 8.

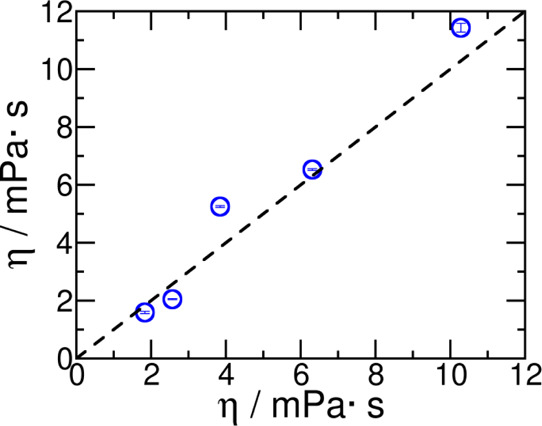
Figure 8

Open in a new tab

Comparison between shear viscosity predicted from this work with those reported in experiments in the temperature range T = (303–398) K and at pressure p = 1 bar.

Self-Diffusion Coefficient

The self-diffusion coefficient of sulfolane was calculated from the mean squared displacement (MSD). Reliable measurements of the experimental diffusion coefficient were not found in the literature. Thus, we estimated it by a linear extrapolation of the experimentally reported diffusivity of sulfolane in solutions of varying concentrations of LiBF42 to zero concentration of LiBF4 at 303 K. The diffusion constant obtained through this procedure is 14.72 × 10–11 m2·s–1 and is herein considered as the experimental diffusion constant, against which values from different force fields are compared. Constant NVT simulations of duration 50 ns at the equilibrated density were used to calculate the MSD for the OPLS force field and for the refined force field (see Figure 9). The smallest time interval for which MSD was calculated was 1 ps. The diffusive regime was determined from the time point, and the exponent β(t) defined in the Supporting Information eq S2 reaches unity (2 to 26 ns). Further details of the calculation are provided in the Supporting Information.

Figure 9.

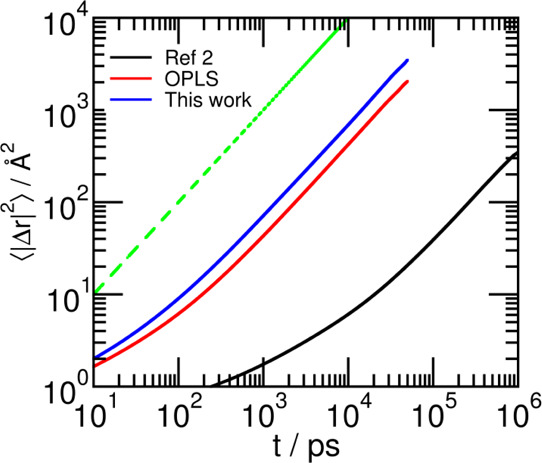
Figure 9

Open in a new tab

MSD of sulfolane of the COM as a function of time for all force fields studied in this work. The dashed green line represents the y = x line, provided here for the sake of comparison.

⟨|Δr|2⟩ (MSD) as a function of time interval t is shown in Figure 9. β(t) for sulfolane in each force field considered is shown in the Supporting Information Figure S6. The self-diffusion coefficients (D) calculated are provided in Table 10. The diffusion constant from the refined force field developed herein is closest to the experimental value.

Table 10. Self Diffusion Coefficient D (m2·s–1) of Liquid Sulfolane Estimated From Simulations Using the Three Force Fields, at Temperature T = 303 K and Pressure p = 1 bara.

force field D/10–11·m2·s–1b ΔD (%)
force field of ref (2) 0.06 ± 0.001 –99.59
OPLS 7.12 ± 0.08 –51.63
this work 11.89 ± 0.4 –19.16
Open in a new tab
a

Experimentally determined value of diffusion constant obtained through extrapolation from data in ref (2) is 14.72 × 10–11 m2·s–1.

b

The expanded uncertainty (U) is reported at 95% level of confidence.

We also calculated the self-diffusion coefficient of sulfolane as a function of temperature. The results are provided in Table 11 and Figure 10. Experimental self-diffusion constants were not found in the literature for comparison.

Table 11. Self-Diffusion Coefficient of Liquid Sulfolane as a Function of Temperature as Predicted from This Work, D.

temperature/K D/10–11·m2·s–1a,b
303 11.89 ± 0.4
323 22.33 ± 0.5
348 40.83 ± 0.7
373 65.77 ± 1.2
398 103.38 ± 1.3
Open in a new tab
a

The expanded uncertainty (U) is reported at 95% level of confidence.

b

The data follows an exponential fit of the form: D = A e–Ea/kBT. Where activation energy Ea = 22.60 kJ·mol–1 and A = 97372.59 × 10–11·m2·s–1.

Figure 10.

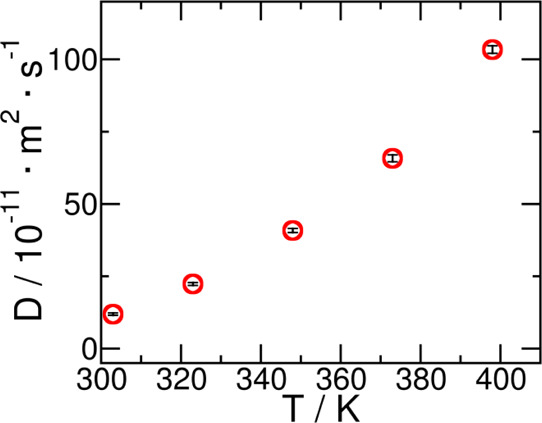
Figure 10

Open in a new tab

Self-diffusion coefficients of liquid sulfolane as a function of temperature in the range T = (303–398) K.

Conclusions

In this work, the need for a force field that quantitatively captures the transport properties of liquid sulfolane has been met. In order to achieve this, average atomic site charges were derived for the liquid phase of sulfolane using periodic DFT calculations and the DDEC6 method for partitioning the electronic density into atomic site charges. Narrow atomic site charge distributions in the liquid allowed for obtaining site charges through DFT geometry optimizations of independent snapshots chosen from a MD trajectory.

A modification of charges necessitates a refinement of LJ parameters as well. Thus, chemically different atom types were identified, and their LJ-parameters were tuned so that the total potential energy of a pair of sulfolane molecules as a function of their intermolecular distance calculated within the refined force field matches that obtained from reference quantum chemical calculations as closely as possible. Lastly, we also modified the equilibrium bond length and bond angles to those obtained from gas-phase quantum chemical optimization of a sulfolane molecule.

Although our force field is a non-polarizable one, the values predicted by our force field for several physical and chemical properties such as molecular dipole moment, liquid density, viscosity, self-diffusion coefficient, and surface tension quantitatively matching the experimental data to a fair extent with the benefit of having computed them with much lesser computational cost as compared to simulations using ab-initio MD methods or with polarizable force fields. In particular, we stress on the remarkable agreement of self-diffusion coefficient and shear viscosity of this refined force field with experiments since reproducing transport quantities from non-polarizable force fields has always posed a challenge.65 We notice that the match of density and heat of vaporization from the refined force field with experiments is not as good as that for transport properties and surface tension. However, among other force fields studied here, the refined force field parameters reported here yield the closest match to the quantum PES scans. Also, the rigorous method used for derivation of atomic site charges within the liquid phase of sulfolane reinforces our faith in the reliability of the refined force field, particularly for transport properties. A temperature-dependent study of several physical quantities yielded results in quantitative agreement with experiments. This increased the reliability of this refined force field. The near-neighbor structure in liquid sulfolane is characterized by antiparallel arrangement of molecular dipoles.

Several quantitative predictions regarding sulfolane-assisted reactions and its viability as an emerging battery electrolyte component can now be made with fair certainty. It is also interesting to note that the refined force field for sulfolane may be applicable to the entire class of sulfone compounds with minor modifications. To investigate along these various lines using this refined force field is our future objective.

Acknowledgments

The Authors thank the International Bilateral Cooperation Division of the Department of Science and Technology, for Project Funds. S.M. thanks Rahul Kumar for fruitful interactions on quantum potential energy scans.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c04243.

  • Determination of gas-phase DDEC6 charges; charge distribution obtained in liquid-phase DDEC6 charge calculation; bonded parameters; additional MD details; example of block average calculation: illustrated via density; additional RDF plots; details for single-molecule volume calculation; uncertainty calculation for heat of vaporization; calculation of surface tension; shear viscosity Green–Kubo relation; pressure tensor time correlation function; calculation of mean shear viscosity and uncertainty on the mean, defining the diffusive regime; calculation of the mean diffusion constant and uncertainty on the mean (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao0c04243_si_001.pdf (1.1MB, pdf)

References

  1. Tilstam U. Sulfolane: a versatile dipolar aprotic solvent. Org. Process Res. Dev. 2012, 16, 1273–1278. 10.1021/op300108w. [DOI] [Google Scholar]
  2. Dokko K.; Watanabe D.; Ugata Y.; Thomas M. L.; Tsuzuki S.; Shinoda W.; Hashimoto K.; Ueno K.; Umebayashi Y.; Watanabe M. Direct Evidence for Li Ion Hopping Conduction in Highly Concentrated Sulfolane-Based Liquid Electrolytes. J. Phys. Chem. B 2018, 122, 10736–10745. 10.1021/acs.jpcb.8b09439. [DOI] [PubMed] [Google Scholar]
  3. Sedlarikova M.; Vondrak J.; Maca J.; Bartusek K. Sulfolane as Solvent for Lithium Battery Electrolytes. J. New Mater. Electrochem. Syst. 2013, 16, 65–71. 10.14447/jnmes.v16i2.10. [DOI] [Google Scholar]
  4. Maca J.; Frk M.; Rozsivalova Z.; Sedlarikova M. Properties of Sulfolane Based Aprotic Electrolytes. Port. Electrochim. Acta 2013, 31, 321–330. 10.4152/pea.201306321. [DOI] [Google Scholar]
  5. Nakanishi A.; Ueno K.; Watanabe D.; Ugata Y.; Matsumae Y.; Liu J.; Thomas M. L.; Dokko K.; Watanabe M. Sulfolane-Based Highly Concentrated Electrolytes of Lithium Bis(trifluoromethanesulfonyl)amide: Ionic Transport, Li-Ion Coordination, and Li-S Battery Performance. J. Phys. Chem. C 2019, 123, 14229–14238. 10.1021/acs.jpcc.9b02625. [DOI] [Google Scholar]
  6. Seita T.; Matsumae Y.; Liu J.; Tatara R.; Ueno K.; Dokko K.; Watanabe M. Graphite-Lithium Sulfide Battery with a Single-Phase Sparingly Solvating Electrolyte. ACS Energy Lett. 2019, 5, 1–7. 10.1021/acsenergylett.9b02347. [DOI] [Google Scholar]
  7. Okamoto Y.; Tsuzuki S.; Tatara R.; Ueno K.; Dokko K.; Watanabe M. High Transference Number of Na Ion in Liquid-State Sulfolane Solvates of Sodium Bis(fluorosulfonyl)amide. J. Phys. Chem. C 2020, 124, 4459–4469. 10.1021/acs.jpcc.9b11458. [DOI] [Google Scholar]
  8. Vaughn J. W.; Hawkins C. F. Physical Properties of Tetrahydrothiophene-1, 1-Dioxide and 3-Methyltetrahydrothiophene-1, 1-Dioxide. J. Chem. Eng. Data 1964, 9, 140–142. 10.1021/je60020a047. [DOI] [Google Scholar]
  9. Xu K. Nonaqueous liquid electrolytes for lithium-based rechargeable batteries. Chem. Rev. 2004, 104, 4303–4418. 10.1021/cr030203g. [DOI] [PubMed] [Google Scholar]
  10. Ren X.; Chen S.; Lee H.; Mei D.; Engelhard M. H.; Burton S. D.; Zhao W.; Zheng J.; Li Q.; Ding M. S.; Schroeder M.; Alvarado J.; Xu K.; Meng Y. S.; Liu J.; Zhang J.-G.; Xu W. Localized high-concentration sulfone electrolytes for high-efficiency lithium-metal batteries. Chem 2018, 4, 1877–1892. 10.1016/j.chempr.2018.05.002. [DOI] [Google Scholar]
  11. Domańska U.; Moollan W. C.; Letcher T. M. Solubility of sulfolane in selected organic solvents. J. Chem. Eng. Data 1996, 41, 261–265. 10.1021/je950236w. [DOI] [Google Scholar]
  12. Katon J. E.; Feairheller W. R. Jr. The vibrational spectra and molecular configuration of sulfolane. Spectrochim. Acta 1965, 21, 199–201. 10.1016/0371-1951(65)80117-5. [DOI] [Google Scholar]
  13. Berweger C. D.; van Gunsteren W. F.; Müller-Plathe F. Force field parametrization by weak coupling. Re-engineering SPC water. Chem. Phys. Lett. 1995, 232, 429–436. 10.1016/0009-2614(94)01391-8. [DOI] [Google Scholar]
  14. Liu H.; Mueller-Plathe F.; van Gunsteren W. F. A force field for liquid dimethyl sulfoxide and physical properties of liquid dimethyl sulfoxide calculated using molecular dynamics simulation. J. Chem. Eng. Data 1995, 117, 4363–4366. 10.1021/ja00120a018. [DOI] [Google Scholar]
  15. Jorgensen W. L.; Maxwell D. S.; Tirado-Rives J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. 10.1021/ja9621760. [DOI] [Google Scholar]
  16. Zhao W.; Eslami H.; Cavalcanti W. L.; Müller-Plathe F. A Refined All-Atom Model for the Ionic Liquid 1-n-Butyl 3-Methylimidazolium bis(Trifluoromethylsulfonyl)imide [bmim][Tf2N]. Z. Phys. Chem. 2007, 221, 1647–1662. 10.1524/zpch.2007.221.11-12.1647. [DOI] [Google Scholar]
  17. Rai N.; Rafferty J. L.; Maiti A.; Siepmann J. I. Prediction of the bubble point pressure for the binary mixture of ethanol and 1,1,1,2,3,3,3-heptafluoropropane from Gibbs ensemble Monte Carlo simulations using the TraPPE force field. Fluid Phase Equilib. 2007, 260, 199–211. 10.1016/j.fluid.2007.06.034. [DOI] [Google Scholar]
  18. Rai N.; Wagner A. J.; Ross R. B.; Siepmann J. I. Application of the TraPPE force field for predicting the Hildebrand solubility parameters of organic solvents and monomer units. J. Chem. Theory Comput. 2008, 4, 136–144. 10.1021/ct700135j. [DOI] [PubMed] [Google Scholar]
  19. Zhao W.; Leroy F.; Heggen B.; Zahn S.; Kirchner B.; Balasubramanian S.; Müller-Plathe F. Are there stable ion-pairs in room-temperature ionic liquids? Molecular dynamics simulations of 1-n-butyl-3-methylimidazolium hexafluorophosphate. J. Am. Chem. Soc. 2009, 131, 15825–15833. 10.1021/ja906337p. [DOI] [PubMed] [Google Scholar]
  20. Rai N.; Tiwari S. P.; Maginn E. J. Force field development for actinyl ions via quantum mechanical calculations: an approach to account for many body solvation effects. J. Phys. Chem. B 2012, 116, 10885–10897. 10.1021/jp3028275. [DOI] [PubMed] [Google Scholar]
  21. Mondal A.; Balasubramanian S. A molecular dynamics study of collective transport properties of imidazolium-based room-temperature ionic liquids. J. Chem. Eng. Data 2014, 59, 3061–3068. 10.1021/je500132u. [DOI] [Google Scholar]
  22. Eggimann B. L.; Sun Y.; DeJaco R. F.; Singh R.; Ahsan M.; Josephson T. R.; Siepmann J. I. Assessing the Quality of Molecular Simulations for Vapor-Liquid Equilibria: An Analysis of the TraPPE Database. J. Chem. Eng. Data 2019, 65, 1330–1344. 10.1021/acs.jced.9b00756. [DOI] [Google Scholar]
  23. Chen J. L.; Xue B.; Mahesh K.; Siepmann J. I. Molecular simulations probing the thermophysical properties of homogeneously stretched and bubbly water systems. J. Chem. Eng. Data 2019, 64, 3755–3771. 10.1021/acs.jced.9b00284. [DOI] [Google Scholar]
  24. Gutiérrez A.; Atilhan M.; Aparicio S. Microscopic Characterization of CO2 and H2S Removal by Sulfolane. Energy Fuels 2017, 31, 9800–9813. 10.1021/acs.energyfuels.7b01577. [DOI] [Google Scholar]
  25. Manz T. A.; Limas N. G. Introducing DDEC6 atomic population analysis: part 1. Charge partitioning theory and methodology. RSC Adv. 2016, 6, 47771–47801. 10.1039/c6ra04656h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Jorgensen W. L.; Tirado-Rives J. Potential energy functions for atomic-level simulations of water and organic and biomolecular systems. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 6665–6670. 10.1073/pnas.0408037102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Dodda L. S.; Vilseck J. Z.; Tirado-Rives J.; Jorgensen W. L. 1.14*CM1A-LBCC: Localized Bond-Charge Corrected CM1A Charges for Condensed-Phase Simulations. J. Phys. Chem. B 2017, 121, 3864–3870. 10.1021/acs.jpcb.7b00272. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Dodda L. S.; de Vaca I. C.; Tirado-Rives J.; Jorgensen W. L. LigParGen web server: an automatic OPLS-AA parameter generator for organic ligands. Nucleic Acids Res. 2017, 45, W331–W336. 10.1093/nar/gkx312. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Kelayeh S. A.; Jalili A. H.; Ghotbi C.; Hosseini-Jenab M.; Taghikhani V. Densities, Viscosities, and Surface Tensions of Aqueous Mixtures of Sulfolane + Triethanolamine and Sulfolane + Diisopropanolamine. J. Chem. Eng. Data 2011, 56, 4317–4324. 10.1021/je200124h. [DOI] [Google Scholar]
  30. Mondal A.; Balasubramanian S. Quantitative prediction of physical properties of imidazolium based room temperature ionic liquids through determination of condensed phase site charges: A refined force field. J. Phys. Chem. B 2014, 118, 3409–3422. 10.1021/jp500296x. [DOI] [PubMed] [Google Scholar]
  31. Avula N. V. S.; Mondal A.; Balasubramanian S. Charge Environment and Hydrogen Bond Dynamics in Binary Ionic Liquid Mixtures: A Computational Study. J. Phys. Chem. Lett. 2018, 9, 3511–3516. 10.1021/acs.jpclett.8b01481. [DOI] [PubMed] [Google Scholar]
  32. Hutter J.; Iannuzzi M.; Schiffmann F.; VandeVondele J. cp2k: atomistic simulations of condensed matter systems. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2014, 4, 15–25. 10.1002/wcms.1159. [DOI] [Google Scholar]
  33. Perdew J. P.; Burke K.; Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. 10.1103/physrevlett.77.3865. [DOI] [PubMed] [Google Scholar]
  34. Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
  35. Goedecker S.; Teter M.; Hutter J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 1703. 10.1103/physrevb.54.1703. [DOI] [PubMed] [Google Scholar]
  36. Hartwigsen C.; Goedecker S.; Hutter J. Relativistic separable dual-space Gaussian pseudopotentials from H to Rn. Phys. Rev. B: Condens. Matter Mater. Phys. 1998, 58, 3641. 10.1103/physrevb.58.3641. [DOI] [PubMed] [Google Scholar]
  37. Limas N. G.; Manz T. A. Introducing DDEC6 atomic population analysis: part 4. Efficient parallel computation of net atomic charges, atomic spin moments, bond orders, and more. RSC Adv. 2018, 8, 2678–2707. 10.1039/c7ra11829e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Frisch M.; Trucks G.; Schlegel H.; Scuseria G.; Robb M.; Cheeseman J.; Scalmani G.; Barone V.; Petersson G.; Nakatsuji H.; et al. Gaussian 16 revision a. 03. 2016; Gaussian Inc: Wallingford CT, 2016, 2.
  39. Dennington R.; Keith T.; Millam J.. GaussView, version 5, 2009.
  40. Bekker H.; Berendsen H.; Dijkstra E.; Achterop S.; Van Drunen R.; Van der Spoel D.; Sijbers A.; Keegstra H.; Reitsma B.; Renardus M.. Gromacs: A parallel computer for molecular dynamics simulations. Physics Computing; World Scientific Publishing, 1993; pp 252–256. [Google Scholar]
  41. Hess B.; Kutzner C.; Van Der Spoel D.; Lindahl E. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
  42. Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
  43. Darden T.; York D.; Pedersen L. Particle mesh Ewald: AnN·log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
  44. Hess B.; Bekker H.; Berendsen H. J. C.; Fraaije J. G. E. M. LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. . [DOI] [Google Scholar]
  45. Páll S.; Hess B. A flexible algorithm for calculating pair interactions on SIMD architectures. Comput. Phys. Commun. 2013, 184, 2641–2650. 10.1016/j.cpc.2013.06.003. [DOI] [Google Scholar]
  46. Nosé S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. 10.1080/00268978400101201. [DOI] [Google Scholar]
  47. Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; DiNola A.; Haak J. R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
  48. Parrinello M.; Rahman A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
  49. Nosé S.; Klein M. L. Constant pressure molecular dynamics for molecular systems. Mol. Phys. 1983, 50, 1055–1076. 10.1080/00268978300102851. [DOI] [Google Scholar]
  50. Martínez L.; Andrade R.; Birgin E. G.; Martínez J. M. PACKMOL: a package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
  51. Humphrey W.; Dalke A.; Schulten K. VMD—Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  52. Mesquita F. M. R.; Feitosa F. X.; Aznar M.; de Sant’Ana H. B.; Santiago-Aguiar R. S. Density, Viscosities, and Excess Properties for Binary Mixtures of Sulfolane + Alcohols and Sulfolane + Glycols at Different Temperatures. J. Chem. Eng. Data 2014, 59, 2196–2206. 10.1021/je500153g. [DOI] [Google Scholar]
  53. Jalili A. H.; Shokouhi M.; Samani F.; Hosseini-Jenab M. Measuring the solubility of CO2 and H2S in sulfolane and the density and viscosity of saturated liquid binary mixtures of (sulfolane + CO2) and (sulfolane + H2S). J. Chem. Thermodyn. 2015, 85, 13–25. 10.1016/j.jct.2015.01.001. [DOI] [Google Scholar]
  54. Casteel J. F.; Sears P. G. Dielectric constants, viscosities, and related physical properties of 10 liquid sulfoxides and sulfones at several temperatures. J. Chem. Eng. Data 1974, 19, 196–200. 10.1021/je60062a001. [DOI] [Google Scholar]
  55. Murrieta-Guevara F.; Rebolledo-Libreros E.; Trejo A. Gas solubility of carbon dioxide and hydrogen sulfide in mixtures of sulfolane with monoethanolamine. Fluid Phase Equilib. 1993, 86, 225–231. 10.1016/0378-3812(93)87178-4. [DOI] [Google Scholar]
  56. Águila-Hernández J.; Trejo A.; García-Flores B. E.; Molnar R. Viscometric and volumetric behaviour of binary mixtures of sulfolane and N-methylpyrrolidone with monoethanolamine and diethanolamine in the range 303-373K. Fluid Phase Equilib. 2008, 267, 172–180. 10.1016/j.fluid.2008.02.023. [DOI] [Google Scholar]
  57. Yang C.; Yu W.; Ma P. Densities and Viscosities of Binary Mixtures of Ethylbenzene +N-Methyl-2-pyrrolidone, Ethylbenzene + Sulfolane, and Styrene + Octane from (303.15 to 353.15) K and Atmospheric Pressure. J. Chem. Eng. Data 2005, 50, 1197–1203. 10.1021/je049572f. [DOI] [Google Scholar]
  58. Clough S. A.; Beers Y.; Klein G. P.; Rothman L. S. Dipole moment of water from Stark measurements of H2O, HDO, and D2O. J. Chem. Phys. 1973, 59, 2254–2259. 10.1063/1.1680328. [DOI] [Google Scholar]
  59. Malmberg C. G.; Maryott A. A. Dielectric constant of water from 0 to 100 C. J. Res. Natl. Bur. Stand. 1956, 56, 1. 10.6028/jres.056.001. [DOI] [Google Scholar]
  60. Prestbo E. W.; McHale J. L. Static dielectric constants and Kirkwood correlation factors of dimethyl sulfoxide/carbon tetrachloride solutions. J. Chem. Eng. Data 1984, 29, 387–389. 10.1021/je00038a006. [DOI] [Google Scholar]
  61. Krekeler C.; Dommert F.; Schmidt J.; Zhao Y. Y.; Holm C.; Berger R.; Delle Site L. Electrostatic properties of liquid 1,3-dimethylimidazolium chloride: role of local polarization and effect of the bulk. Phys. Chem. Chem. Phys. 2010, 12, 1817–1821. 10.1039/b917803c. [DOI] [PubMed] [Google Scholar]
  62. Fulem M.; Ružička K.; Ružička M. Recommended vapor pressures for thiophene, sulfolane, and dimethyl sulfoxide. Fluid Phase Equilib. 2011, 303, 205–216. 10.1016/j.fluid.2011.02.002. [DOI] [Google Scholar]
  63. Kirk R. E.; Othmer D. F.; Grayson M.; Eckroth D.. Encyclopedia of Chemical Technology; Interscience Publishers, 1978, [Google Scholar]
  64. Dean J. A.Langes Handbook of Chemistry 15th ed.; McGraw-Hill: New York, 1999. [Google Scholar]
  65. Zhang Y.; Otani A.; Maginn E. J. Reliable viscosity calculation from equilibrium molecular dynamics simulations: A time decomposition method. J. Chem. Theory Comput. 2015, 11, 3537–3546. 10.1021/acs.jctc.5b00351. [DOI] [PubMed] [Google Scholar]
  66. Stachurski Z. H.Fundamentals of Amorphous Solids: Structure and Properties; John Wiley & Sons, 2015. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c04243_si_001.pdf (1.1MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES