Hippocampal Network Reorganization Underlies the Formation of a Temporal Association Memory

SUMMARY

Episodic memory requires linking events in time, a function dependent on the hippocampus. In “trace” fear conditioning, animals learn to associate a neutral cue with an aversive stimulus despite their separation in time by a delay period on the order of tens of seconds. But how this temporal association forms remains unclear. Here we use two-photon calcium imaging of neural population dynamics throughout the course of learning and show that, in contrast to previous theories, hippocampal CA1 does not generate persistent activity to bridge the delay. Instead, learning is concomitant with broad changes in the active neural population. Although neural responses were stochastic in time, cue identity could be read out from population activity over longer timescales after learning. These results question the ubiquity of seconds-long neural sequences during temporal association learning and suggest that trace fear conditioning relies on mechanisms that differ from persistent activity accounts of working memory.

INTRODUCTION

Episodic memory recapitulates the sequential structure of events that unfold in space and time (Eichenbaum, 2017). In the brain, the hippocampus is critical for binding the representations of discontiguous events (Kitamura et al., 2015; Eichenbaum, 2017), corroborated by recent observations of sequential neural activity in CA1 that bridges the gap between sensory experiences (Pastalkova et al., 2008; MacDonald et al., 2011) to support memory (Wang et al., 2015; Robinson et al., 2017). However, it remains a long-standing challenge to track how hippocampal coding is modified as animals learn to associate events separated in time.

Pavlovian fear conditioning provides a framework to study the neuronal correlates and mechanisms of associative learning in the brain (Letzkus et al., 2015; Gründemann and Lüthi, 2015; Maddox et al., 2019; Grewe et al., 2017). Classical “trace” fear conditioning (tFC) has long been used as a model behavior for studying temporal association learning (Raybuck and Lattal, 2014; Kitamura et al., 2015). Subjects learn that a neutral conditioned stimulus (CS) predicts an aversive, unconditioned stimulus (US), which follows the CS by a considerable time delay (“trace” period). Circuitry within the dorsal hippocampus is required for forming these memories at trace intervals on the scale of tens of seconds (Raybuck and Lattal, 2014; Huerta et al., 2000; Quinn et al., 2005; Fendt et al., 2005; Chowdhury et al., 2005; Sellami et al., 2017). Furthermore, silencing activity in CA1 during the trace period itself is sufficient to disrupt temporal binding of the CS and US in memory (Sellami et al., 2017). Although these experiments pinpoint a role for hippocampal activity in forming trace fear memories, the underlying neural dynamics remain unresolved. Importantly, tFC precludes a simple Hebbian association of CS and US selective neural assemblies, because of the non-overlapping presentation of the stimuli.

Previous work has proposed that persistent activity enables the hippocampus to connect representations of events in time, bridging time gaps on the order of tens of seconds. Theories suggest that representation of the neutral CS and aversive US are linked through the generation of stereotyped, sequential activity in CA1 (Kitamura et al., 2015; Sellami et al., 2017). Alternatively, hippocampal activity could generate a sustained response to the CS that maintains a static coding of the sensory cue in working memory over the trace interval, as in attractor models of neocortical activity (Amit and Brunel, 1997; Barak and Tsodyks, 2014; Takehara-Nishiuchi and McNaughton, 2008) and as recently observed in the human hippocampus (Kamiński et al., 2017). However, these hypotheses of persistent activity remain to be tested during trace fear learning.

Here we leveraged two-photon microscopy and functional calcium imaging to record the dynamics of CA1 neural populations longitudinally as animals underwent trace fear learning, in order to resolve the underlying patterns of network activity and their modifications with learning. Our findings show that persistent activity does not manifest strongly during this paradigm, incongruous with sequence or attractor models of temporal association learning. Instead, learning instigated broad changes in network activity and the emergence of a sparse and temporally stochastic code for CS identities that was absent prior to conditioning. These findings suggest that the role of the hippocampus in trace conditioning may be fundamentally different from learning that requires continual maintenance of sensory information in neuronal firing rates.

RESULTS

We previously developed a head-fixed variant of an auditory tFC paradigm (Kaifosh et al., 2013) conducive to two-photon microscopy. Water-deprived mice were head-fixed and immobilized in a stationary chamber (Guo et al., 2014) to prevent locomotion from confounding learning strategy (MacDonald et al., 2013) (Figure 1A). Mice were presented with a 20 s auditory cue (CS), followed by a 15 s temporal delay (“trace”), after which the animals received aversive air puffs to the snout (US). A water port was accessible throughout each trial, and we used animals’ lick suppression as a readout of learned fear (Kaifosh et al., 2013; Lovett-Barron et al., 2014; Rajasethupathy et al., 2015). We first verified that learning in auditory head-fixed tFC was dependent on activity in the dorsal hippocampus. Optogenetic inhibition of CA1 activity resulted in a significant reduction in lick suppression (Figure S1), indicating that, as in freely moving conditions (Raybuck and Lattal, 2014; Huerta et al., 2000; Fendt et al., 2005; Chowdhury et al., 2005), head-fixed tFC is dependent on the dorsal hippocampus.

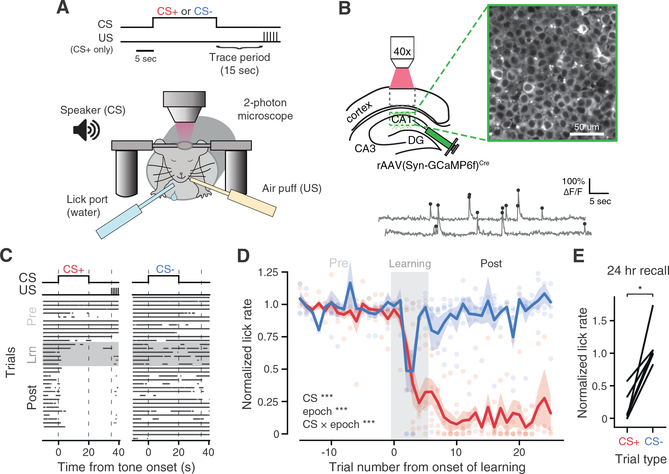
Figure 1. Two-Photon Functional Imaging of CA1 Pyramidal Neurons during Differential tFC.

(A) Schematic of experimental paradigm. A head-fixed mouse is immobilized and on each trial exposed to an auditory cue (CS+ or CS−) for 20 s, followed by a 15 s stimulus-free “trace” period, after which the US is triggered (CS+ trials). Air puffs are used as the US and lick suppression as a measure of learned fear. Operant water rewards are available throughout all trials.

(B) Top, schematic of in vivo imaging with two-photon field of view in dorsal CA1. Bottom: calcium traces (gray) and inferred event times (black) from an example neuron.

(C) Behavioral data for an example mouse over the complete paradigm. Each row is a trial, where dots indicate licks.

(D) Summary of behavioral dataset. We compute a normalized lick rate for each trial by dividing the lick rate during the tone (0–20 s) by the rate in the pre-CS (−10 to 0 s) period (mean ± SEM; n = 6 mice; linear mixed-effects model with fixed effects of CS and learning epoch, with mouse as random effect; main effect significance shown in inset; post hoc models fit to each epoch separately with fixed effects of CS and trial number; Pre-Learning: no significant effects; Learning: effect of trial number [***] and CS × trial number [**]; Post-Learning: effect of CS [***]; Wald χ² test). Scatter shows data from individual mice.

(E) Mean 24 h recall licking responses to first CS cue presentations of each day in the Post-Learning period for each mouse (n = 6 mice; Wilcoxon signed-rank test).

*p < 0.05, **p < 0.01, and ***p < 0.001.

In order to investigate the underlying network dynamics during tFC, we selectively expressed the fluorescent calcium indicator GCaMP6f in CA1 pyramidal neurons (Figure 1B) via injection of an adeno-associated virus (AAV) containing Cre-dependent GCaMP6f in CaMKIIα-Cre mice (Dragatsis and Zeitlin, 2000). The head fixation apparatus was mounted beneath the two-photon microscope objective, and mice were again water-restricted and trained to lick for water rewards while immobilized in the chamber (Guo et al., 2014). Once mice licked reliably, we began neural recordings during a differential tFC paradigm (Figure 1A), in which on each trial mice were exposed to one of two auditory cues (CS+ and CS−; either constant 10 kHz or pulsed 2 kHz, randomized across mice). After collecting 10–15 “PreLearning” trials per CS cue with exposure to the cue alone, we conditioned mice by selectively pairing CS+ trials with the US. Mice quickly acquired the trace association in the first 6 trials of CS+/US pairings (“Learning” trials). We recorded subsequent trials with continued US reinforcement, to prevent extinction; behavioral responses maintained a steady asymptote during these 20–25 “Post-Learning” trials (Figures 1C and 1D). Mice readily discriminated between the two cues throughout Post-Learning, as they suppressed licking consistently on CS+ trials but not CS− trials, in which the air puff was never presented (Figures 1C and 1D). Mice consistently discriminated between cues on the first trial of each day in the Post-Learning period, prior to receiving US reinforcement on that day, indicating retention (24 h recall) of the memory (Figure 1E).

Imaging data from each trial were motion corrected (Kaifosh et al., 2014; Pachitariu et al., 2017), and region of interest (ROI) spatial masks and activity traces were extracted using the Suite2p software package (Pachitariu et al., 2017). All traces were deconvolved (Friedrich et al., 2017) to estimate underlying spike event times. After registering ROIs across sessions, we identified 1,991 CA1 pyramidal neurons from six mice (158–500 neurons per mouse) that were each active on at least four trials, which were used for subsequent analyses (Figure 2A). Neural activity spanned all trial periods during the task, with a large population response to the US (Figure 2A). We also noted a transient increase in activity prior to CS onset (−10 s), which may reflect neural responses to a mixture of salient events at the beginning of each trial (e.g., lick port access, reward onset, shutter, and scanning mirror sounds).

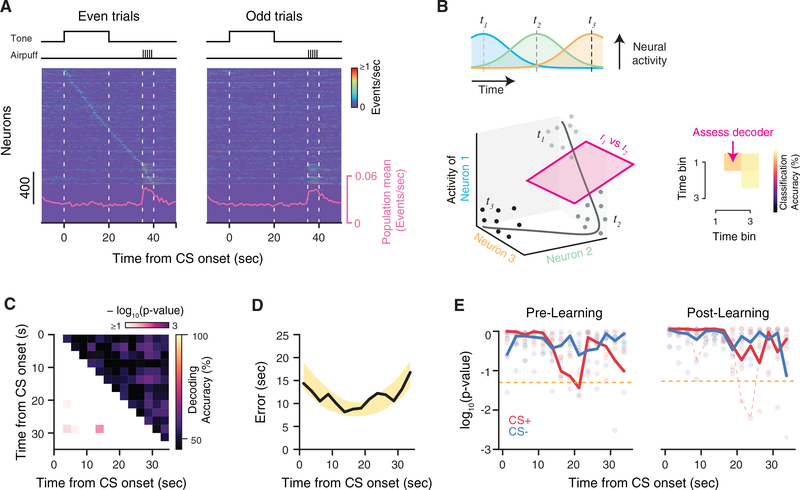
Figure 2. Temporal Dynamics of CA1 Activity during tFC.

(A) Summary of neural activity during Post-Learning CS+ trials, shown separately for even- and odd-numbered trials. Activity is trial averaged and sorted byneurons’ peak firing rate latency during 0–40 s in even trials. The population average event rate is overlaid.

(B) Schematic of time decoding analysis. Top: trial-averaged tuning curves of a hypothetical sequence of time cells. Bottom: state space representation of theneural data. Dots indicate the neural state on single trials at three time points in the task. Right: a separate support vector machine (SVM) was trained to discriminate between population activity from every pair of time points in the task.

(C) Matrix of classifiers for an example mouse during Post-Learning CS+ trials. Each square is the classifier result for comparing the pair of time bins corresponding to the x- and y-axis positions. The upper triangle reports the cross-validated accuracy, while the lower triangle reports the p value relative to a shuffle distribution. Most pairwise classifiers perform at chance level.

(D) Time prediction performance for the example shown in (C). For each time bin in a test trial, all classifiers vote to determine the decoded time. Decodingaccuracy is the absolute error between real and predicted time. Black, cross-validated average of time decoding error. Yellow shading, 95% bounds of the null distribution. Decoding error is within chance levels throughout the trial.

(E) Summary of decoding significance relative to the null distribution during Pre-Learning and Post-Learning trials. Bold lines are combined p values across micevia Fisher’s method. Red dashed line is the example shown in (C) and (D). Scatter shows individual p values across mice. Gold dashed line indicates p = 0.05.

We first asked whether the hippocampus generated a consistent temporal code during each trial to connect the CS and US representations (Sellami et al., 2017; Kitamura et al., 2015). After ordering trial-averaged population activity by the latency of neurons’ peak firing rates, a sequence naturally appears to span the trial period (Figure 2A, left), but this activity is not necessarily consistent across trials (compare with Figure 2A, right). We used decoding to probe for evidence of sequential activity in the neural data that was consistent across trials, as the presence of sequential dynamics such as “time cells” (MacDonald et al., 2011) should allow us to decode the passage of time from the neural data (Bakhurin et al., 2017; Robinson et al., 2017; Cueva et al., 2019).

We used an ensemble of linear classifiers trained to discriminate the population activity between every pair of time points (Bakhurin et al., 2017; Cueva et al., 2019) in the tone and trace periods of the trial (0–35 s, 2.5 s bins) to decode elapsed time from the neural data (Figure 2B; see also STAR Methods). As the ability to decode time is not an exclusive feature of neural sequences but a signature of any consistent dynamical trajectory whereby the neural states become sufficiently decorrelated in time (e.g., consider monotonically “ramping” cells [Cueva et al., 2019] or chaotic dynamics [Buonomano and Maass, 2009]), our analysis addresses the broader question of whether any temporal coding arises during the task, without a priori assumptions on its form.

We assessed whether neural activity was linearly separable between each pair of time points in the tone and trace periods of the task (Figure 2C). Decoding accuracy was no better than chance for most pairwise classifiers, suggesting that either the pattern of neural activity remains relatively constant, or the dynamics are not consistent across trials. As an additional test of temporal coding, we can combine the output of the classifier ensemble to predict the time bin label of individual activity vectors (Bakhurin et al., 2017; Cueva et al., 2019). For each time bin in a test trial, the neural activity is given to all pairwise classifiers, whose binary decisions are combined to determine the predicted time bin label of the data. Despite combining the information learned by all classifiers, decoding accuracy did not exceed chance-level performance (Figure 2D). We did not find consistent evidence of temporal coding during either Pre- or Post-Learning trials (Figure 2E). We obtained similar results using a nonlinear decoder and using data binned at a coarser time resolution (Figure S2A). In other tasks, hippocampal time cells were previously identified in simultaneously recorded populations of just tens of neurons (Pastalkova et al., 2008; MacDonald et al., 2011, 2013), an order of magnitude smaller than the recordings we analyzed here, suggesting that CA1 time cell sequences are not a prominent phenomenon during this trace fear memory paradigm.

One caveat of the time decoding analysis is that it is sensitive mainly to temporal dynamics that have consistent onset timing and scaling; any variation in these parameters across trials could degrade our ability to detect sequences. We alternatively analyzed the order of each cell’s peak firing time across trials, but the order consistency was within chance levels for both CS cues, during Pre- and Post-Learning (Figures S2B–S2E). Here we also assessed whether any sequential dynamics might have rapidly and transiently emerged during the initial “Learning” trials but did not find evidence for reliable temporal patterns (Figures S2B–S2E). We finally tested the hypothesis that the neural population might transition between different patterns of activity during each trial in a way that was not time locked to specific sensory or behavioral events but via neural sequences occurring at different times in each trial. We fit hidden Markov models (HMMs) to the data to identify these network motifs (Mazzucato et al., 2019; Maboudi et al., 2018), but despite considering a range of model parameters, we could not find evidence for sequential activity during any task phase (Figures S3A–S3F). These results indicate that temporal coding is not a dominant network phenomenon during tFC, so sequential activity is unlikely to bridge the gap between CS and US presentations even during the initial Learning phase.

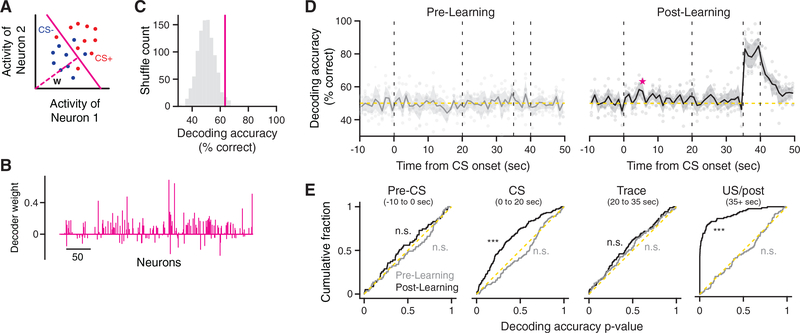
Our time decoding analyses indicated that most periods in time during the task were not consistently separable, which suggests that the network state during each trial may be relatively static. We considered an alternative hypothesis consistent with static activity, in which CS information is maintained by persistent activation of a subgroup of neurons (Kamiński et al., 2017), as in attractor models of working memory (Amit and Brunel, 1997; Barak and Tsodyks, 2014; Takehara-Nishiuchi and McNaughton, 2008). Under this scenario, the population dynamics would not evolve in time but discretely shift to a static state according to the trial’s CS cue, permitting the identity of the cue to be decoded throughout the duration of the trial.

To test this, we trained a separate linear decoder at each time bin during the task to predict the identity of the CS cue (Figures 3A–3C). Our choice of linear classifiers also allowed us to measure the importance of each neuron to the decoder’s decisions, by examining the weights of each neuron along a vector orthogonal to the separating hyperplane (Figures 3A and 3B). Examining these results across time bins, we found that we were unable to decode the CS identity with high accuracy during Pre-Learning or Post-Learning trials at any point prior to the delivery of the US (Figure 3D), indicating that information about the CS identity does not appear to be maintained in the moment-to-moment activity of CA1 pyramidal cell populations. Relatedly, activity was not robustly tied to instantaneous licking behavior, which differed markedly between cues during Post-Learning trials (Figures 1C and 1D). CS decoding accuracy was generally high during US delivery in Post-Learning trials, consistent with the reliable population response to the air puff (Figure 2A). We note that similar analyses applied to appetitive trace conditioning paradigms in monkeys allowed CS identity to be decoded from activity in amygdala and prefrontal cortex (Saez et al., 2015), though the trace period was an order of magnitude shorter than in our paradigm. We did notice an increase in the accuracy of classifiers’ performance during the tone delivery in Post-Learning trials, such that across the distribution of decoders, performance exceeded chance levels (Figure 3E). This suggested to us that there may be cue-selective responses in the population that appeared with variable timing across trials, so they could not be reliably decoded at more granular time resolutions.

Figure 3. CS Identity Is Not Persistently Encoded in the Moment-to-Moment Activity of CA1.

(A) Schematic of CS decoding analysis. A separate classifier was trained to discriminate between CS+ and CS− trials using population activity at each time point during the task (1 s bins).

(B) Neuron weights for an example population decoder learned from Post-Learning data (averaged over cross-validation folds).

(C) Accuracy of the decoder shown in (B). Purple line, average cross-validated decoding accuracy. Gray histogram, accuracy distribution obtained under surrogate datasets with shuffled trial labels.

(D) CS decoding accuracy during Pre-Learning (left) and Post-Learning (right) trials. Data are presented as mean ± SEM across mice. Scatter shows average cross-validated decoding accuracy of individual mice at each time point. The example shown in (B) and (C) is marked in purple.

(E) Cumulative distribution of decoding p values (calculated relative to shuffled data), shown separately for each trial time period. Dashed yellow line indicates the uniform distribution (chance, one-sample Kolmogorov-Smirnov test against the uniform distribution). *p < 0.05, **p < 0.01, and ***p < 0.001.

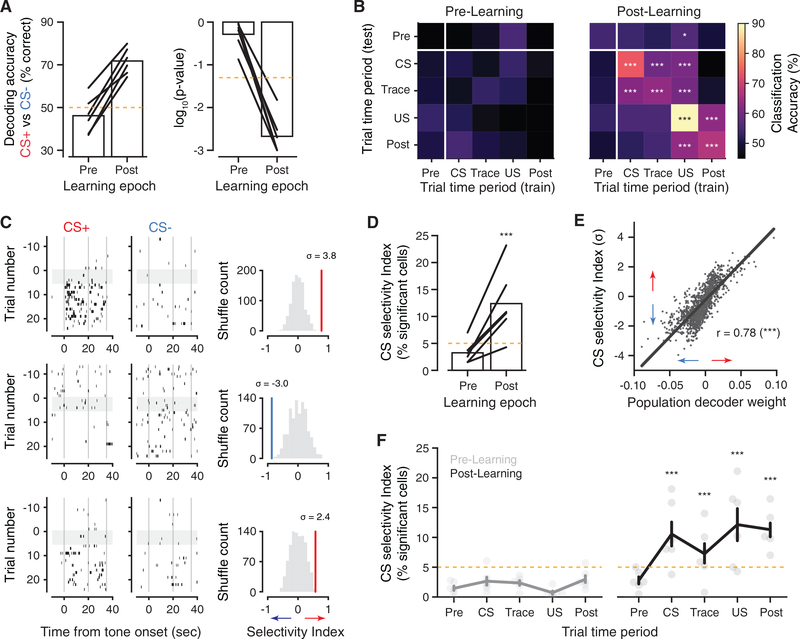
We tested the hypothesis that neural activity levels were predictive at longer timescales, first by attempting to decode the CS identity from the average activity rate across the CS and trace periods of each trial (0–35 s; Figure 4A). Surprisingly, we found that at this timescale, we could significantly decode the CS identity from the population activity rates in all mice. Decoding accuracy exceeded chance only during Post-Learning trials, congruent with a change in network organization following learning. As external sensory information about the stimulus is available only during the CS period, we next asked whether average activity rates during other trial periods were still predictive of the cue identity and how those activity patterns compared with CS-period activity. To address this, we constructed a cross-time period decoding matrix (Figure 4B). Values along the diagonal of the matrix gauge how reliably activity during each time block predicts the cue, while off-diagonal entries assess how decoders generalize to other trial periods. Decoding during Pre-Learning trials was at chance level for all conditions, but during Post-Learning, significant decoding accuracy was observed in all time blocks starting from the tone onset (Figure 4B). Additionally, decoders showed significant generalization between the CS and trace periods, suggesting that a representation of the tone is maintained in the stimulus-free trace interval, and that this representation is similar to activity during the CS. Decoders trained or tested on the trace period performed worse than those trained and tested on the CS period, indicating that activity during the trace was less stable than in the CS period. Decoders trained on the US period showed significant generalization to all other times, though accuracy was low and the reverse relationships were not significant. It follows that representation of the CS and US were largely distinct following trace learning, unlike observations in the basolateral amygdala during delayed conditioning (Grewe et al., 2017).

Figure 4. CS Identity Is Predicted by CA1 Activity Rates on Longer Timescales.

(A) CS decoding accuracy for classifiers trained on the average activity within each trial’s CS and trace period. Left: percentage accuracy; right: p value from nulldistributions calculated as in Figure 3. Each line is the average cross-validated result from one mouse.

(B) Decoding CS identity from average activity in each trial time period. Decoders are trained and tested across each possible pair of time periods. Accuracy isaveraged across mice, and p values are combined via Fisher’s method, with Bonferroni correction.

(C) Raster plots of three simultaneously recorded CS-selective neurons (from average activity across CS and trace period). Right: Post-Learning CS selectivity index for each neuron, compared with null distributions generated by recomputing the index on data with shuffled trial labels.

(D) Percentage of active cells with significant CS selectivity, computed from average activity across CS and trace periods.

(E) Regression of Post-Learning CS selectivity index for each neuron with its population decoder weight from (A) (Pearson’s correlation).

(F) Fraction of selective neurons, computed separately in each trial time period. Data are presented as mean ± SEM across mice. Scatter show values of individualmice. p values indicate significant binomial test against the null hypothesis of ≤5%, pooled across mice. *p < 0.05, **p < 0.01, and ***p < 0.001.

Our analysis established that stimulus identity could be read out from the population activity during the tone and trace period in a learning-dependent manner, so we sought to connect these findings to changes in neural activity at the level of individual neurons. Although some neurons exhibited robust cue preferences following learning (Figure 4C, top), these were rare, and most cells showed graded firing rate changes (Figure 4C, bottom). We quantified neuronal tuning with a selectivity index and measured the fraction of significantly CS-tuned neurons. Selectivity mirrored the population decoding results when computed over the tone and trace periods (Figure 4D) and was tightly correlated with neurons’ weights in the population decoder (Figure 4E), demonstrating that the decoding analysis relied on neurons in the population with strong tuning to CS identity. Similar to decoding accuracy measured during the trace (Figure 4B), the fraction of tuned neurons was lower during the trace than the CS period (Figure 4F) but above chance levels, consistent with some maintenance of cue information during the trace period.

Finally, we sought to characterize how network structure changed during learning on a trial-to-trial basis. Specifically, we asked how the set of active neurons compared across trials by measuring the overlap between the set of neurons active during the CS and trace periods, between each pair of trials (Figure S4A). Activity patterns shifted from Pre- to Post-Learning, demonstrating that learning is accompanied by a large modification in the active neuronal population (Figures S4B and S4C). Across all epochs, the active ensemble between CS+ and CS− trials largely overlapped, although this tended to decrease in Post-Learning (Figure S4D). Given the established role of hippocampal circuits in contextual memory (Maren et al., 2013; Urcelay and Miller, 2014; Fanselow, 2010), this overlap may reflect a representation of the broader context, in addition to or independent of the encoding of the individual CS cues.

DISCUSSION

Here we show that network dynamics during tFC are inconsistent with hypotheses of sequential (Kitamura et al., 2015; Sellami et al., 2017) or static (Kamiński et al., 2017 ) activity in CA1. Rather we find that learning is underpinned by the emergence of a subset of cue-selective neurons in CA1 with stochastic dynamics across trials. These units encode cue information in a learning-dependent manner and may relate to descriptions of hippocampal memory “engram cells,” identified via immediate-early gene (IEG) products (Liu et al., 2012; Vetere et al., 2017; Tanaka et al., 2018; Rao-Ruiz et al., 2019).

Consistent with this notion, CS-selective cells that emerge with learning fall within the range of the 10%–20% of CA1 pyramidal neurons recruited in engrams supporting hippocampal-dependent memory (Tayler et al., 2013; Tanaka et al., 2018; Rao-Ruiz et al., 2019). If the sparse subset of cells we identified do represent engram cells, then this would further support the notion that gating mechanisms exist to ensure sparsity of engrams, as the engram size does not vary with behavioral paradigms, such as tFC used here compared with contextual learning in freely moving animals (Rao-Ruiz et al., 2019). We also speculate that neuromodulatory circuits may play an important role in regulating engram recruitment. For example, cholinergic inputs can have long-lasting effects on neuronal excitability (Letzkus et al., 2011, 2015) and may contribute to the emergence of CS-selective cells in CA1 through mechanisms similar to that recently reported in auditory cortex (Guo et al., 2019), in which there is also an absence of persistent principal cell activity in a 5 s “trace” learning paradigm. It is important to note, however, that in our data, CS selectivity manifested along a continuum of firing rate differences between conditions (Figures 4C and 4E), and it is unclear how coding differences at these scales would be resolved with IEG-based engram analysis.

Our data show that cue information is not actively transmitted by principal neurons’ moment-to-moment firing rates. Neural activity is instead relatively sparse across time and conditions. The lack of reliable CS coding during the Pre-Learning epoch is consistent with prior evidence that few CA1 pyramidal neurons respond to passive playback of auditory stimuli (Aronov et al., 2017). It is possible that these dynamics also differ according to sensory modality and behavioral states, such as locomotion. In previous studies that report neural sequences in CA1 during delay periods (Pastalkova et al., 2008; MacDonald et al., 2011; Wang et al., 2015; Robinson et al., 2017), the hippocampal network state was in a regime dominated by frequent burst firing by pyramidal neurons (Buzsáki and Moser, 2013) reminiscent of activity during active behaviors such as spatial exploration. Indeed, in these experiments the animals were trained to run during the delay period (Pastalkova et al., 2008; Wang et al., 2015; Robinson et al., 2017) or could freely move in the delay area (MacDonald et al., 2011). Delay sequences in immobility are less stable with lower firing rates (MacDonald et al., 2013), and in freely moving animals, they are absent at time intervals longer than a few seconds (Sabariego et al., 2019). The dynamics we observe resemble more closely the activity often seen during immobility and awake quiescence, where pyramidal neurons fire only sparsely (Buzsáki, 2015).

We observe sparse and temporally variable activity that nevertheless is predictive of task information when averaged over longer time periods. It is possible, then, that these dynamics may arise from stochastic reactivation of memory traces (Mongillo et al., 2008; Barak and Tsodyks, 2014). We attempted to identify patterns of neural co-activity in our data (Figures S3G and S3H) but did not find strong evidence for cue-selective, reliably synchronous events, at least at fine timescales. Given the general sparsity of activity during the task and the unreliability of single spike detection with calcium imaging, it is likely that we have underestimated the task-related activity here. Co-active neurons may be more readily apparent with faster imaging speeds and with denser sampling of CA1 populations (Malvache et al., 2016).

Sparse reactivation of neural assemblies may also suggest a fundamentally different mode of propagating information over time delays during trace fear learning, for example, by storing information transiently in synaptic weights (Mongillo et al., 2008; Barak and Tsodyks, 2014). Such a method could confer a considerable metabolic advantage for maintaining memory traces over long time delays. Previous theoretical work to this end has focused on short-term plasticity in networks with pre-existing attractor architectures, where pre-synaptic facilitation among the neurons in a selected attractor drives its reactivation in response to spontaneous input (Mongillo et al., 2008) by outcompeting the other attractors. The time constant of facilitation limits the lifetime of these memory traces to around the order of a second, which is much shorter than the trace period we considered here. Instead, we speculate that coding assemblies may develop through continual Hebbian potentiation over trials and that plasticity induced by the most recently presented cue biases reactivated network states by increasing the depth of the corresponding basins of attraction. A similar scheme has been explicitly modeled in the case of visuo-motor associations (Fusi et al., 2007), and it is known to require synaptic modifications on multiple timescales (Benna and Fusi, 2016). However, it has never been considered in the case of fear learning and long time intervals and will be an important direction for future work.

We observed an overall marked turnover in the set of active neurons from Pre- to Post-Learning trials and a high degree of overlap in the active population between CS+ and CS− trials (Figure S4). It is possible that this broader change in representation associates the context with the US itself or reflects an association with more abstract knowledge of the cue-outcome rules (Maren et al., 2013; Urcelay and Miller, 2014; Fanselow, 2010). Relatedly, memories experienced closely in time may be encoded by overlapping populations of neurons (Cai et al., 2016), consistent with a shared neural ensemble between CS trial types in Post-Learning. This linking of distinct but related memories may occur as a result of transient increases in the excitability of neural subpopulations, which bias engram allocation (Yiu et al., 2014; Cai et al., 2016; Rashid et al., 2016).

Our findings highlight a hippocampal-dependent learning process that associates events separated in time in the absence of persistent activity. Given that associations in real-world scenarios are often dissociated from emotionally valent outcomes by appreciable time delays (Raybuck and Lattal, 2014), our findings have broad implications for models of temporal association learning and circuit dynamics underlying the dysregulation of anxiety and fear in neuropsychiatric disorders.

STAR*METHODS

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources and reagents should be directed to the Lead Contact, Attila Losonczy (al2856@columbia.edu).

Materials Availability

All unique resources generated in this study are available from the Lead Contact with a completed Materials Transfer Agreement.

Data and Code Availability

The data and analysis code generated in this study are available upon reasonable request to the corresponding authors.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All experiments were conducted in accordance with the NIH guidelines and with the approval of the Columbia University Institutional Animal Care and Use Committee. Experiments were performed with adult (8–16 weeks) male and female C57BL/6 mice (Jackson Laboratory) and transgenic CaMKIIα-Cre mice on a C57BL/6 background, where Cre is predominantly expressed in pyramidal neurons (R4Ag11 line, Dragatsis and Zeitlin (2000); Jackson Laboratory, Stock No: 027400).

METHOD DETAILS

Behavior and Imaging

Viruses

Optogenetic experiments were performed by bilaterally injecting (see below) either recombinant adeno-associated virus (rAAV) expressing ArchT (rAAV2/1-Syn-ArchT) or tdTomato control protein (rAAV2/1-Syn-tdTom), under the Synapsin promoter, into male and female C57BL/6 mice. These viruses were the generous gift of Dr. Boris Zemelman. Imaging experiments were performed by injecting Cre-dependent recombinant adeno-associated virus (rAAV) expressing GCaMP6f (rAAV1-Syn-Flex-GCaMP6f-WPRE-SV40, Addgene/Penn Vector Core) into male and female transgenic CaMKIIα-Cre mice (Dragatsis and Zeitlin, 2000) to label pyramidal neurons.

Surgical procedure

Viral delivery to hippocampal area CA1 and implantation of headposts, optical fibers, and imaging cannulae were as described previously (Kaifosh et al., 2013; Kheirbek et al., 2013; Lovett-Barron et al., 2014). Briefly, mice were anesthetized under isofluorane and viruses were delivered to dorsal CA1 by stereotactically injecting 50 nL (10 nL pulses) of rAAVs at three dorsoventral locations using a Nanoject syringe (−2.3 mm AP; −1.5 mm ML; −0.9, −1.05 and −1.2 mm DV relative to bregma). For head-fixed optogenetic experiments, mice were chronically implanted with bilateral optical fiber cannulae above the CA1 injection sites immediately after virus delivery (Lovett-Barron et al., 2014; Kheirbek et al., 2013). A stainless steel headpost was then fixed to the skull (Kaifosh et al., 2013). The cannula, headpost, and any exposed skull were secured and covered with black grip cement to block light from the implanted optical fibers. For imaging experiments, mice were allowed to recover in their home cage for 3 days following virus delivery procedures. They were then surgically implanted with a custom metal headpost (stainless steel or titanium) along with an imaging window (diameter, 3.0 mm; height, 1.5 mm or 2.3 mm) over the left dorsal hippocampus. Imaging cannulae were constructed by adhering (Narland optical adhesive) a 3 mm glass coverslip (64–0720, Warner) to a cylindrical steel cannula. The imaging window surgical procedure was performed as detailed previously (Kaifosh et al., 2013; Lovett-Barron et al., 2014). Briefly, mice were anesthetized and the skull was exposed. A 3 mm hole was made in the skull over the virus injection site. Dura and cortical layers were gently removed under visual guidance while flushing with ice-cold cortex buffer. The imaging cannula was inserted through the surgical opening in the skull and secured so that external capsule fibers were visible through the cannula glass. Finally, the metal headpost was affixed to the skull with dental cement. For all surgeries, monitoring and analgesia (buprenorphine or meloxicam as needed) was continued for 3 days postoperatively.

Behavioral apparatus

We adopted our previously described (Kaifosh et al., 2013; Lovett-Barron et al., 2014) head-fixed system for combining 2-photon imaging with microcontroller-driven (Arduino) stimulus presentation and behavioral readout. To maintain immobility and constrain neural activity related to locomotion (MacDonald et al., 2013), mice were head-fixed in a body tube chamber (Guo et al., 2014). The chamber was lined with textured fabric that was interchanged between trials to control for mouse excretions and prevent contextual conditioning. Tones were presented via nearby speakers and air-puffs delivered by actuating a solenoid valve, which gated airflow from a compressed air tank to a pipette tip pointed at the mouse’s snout. Water reward delivery during licking behavior was gated by another solenoid valve in response to tongue contact with a metal water port coupled to a capacitive sensor. Electrical signals encoding mouse behavior and stimulus presentation were collected with an analog-to-digital converter, which was synchronized with either optogenetic laser delivery or 2-photon image acquisition by a common trigger pulse.

Head-fixed trace fear conditioning

Starting 3–7 days after surgical implantation, mice were habituated to handling and head-fixation as previously described (Kaifosh et al., 2013; Lovett-Barron et al., 2014; Guo et al., 2014). Within 3 days, mice could undergo up to an hour of head-fixation on the behavioral apparatus while remaining calm and alert. They were then water deprived to 85%–90% of their starting body weight and trained to lick operantly for small-volume water rewards (~500 nL/lick) while head-fixed. Before undergoing experimental paradigms, mice were required to maintain consistent licking for multiple (6–12) 60 s trials per day while maintaining their body weight between 85%–90% of starting weight.

For optogenetic experiments, we utilized our previously described head-fixed ‘trace’ fear conditioning paradigm (Kaifosh et al., 2013). Briefly, we paired a 20 s auditory conditioned stimulus (CS, either 10 kHz constant tone or 2 kHz tone pulsed at 1Hz) with air-puffs (unconditioned stimulus, US; 200 ms, 5 puffs at 1 Hz), separated by a 15 s stimulus-free ‘trace’ period. During each conditioning trial, we recorded licking from mice over a 50 s period: 10 s pre-CS, 20 s CS, 15 s trace, and 5 s US. Mice were conditioned across trials spaced throughout three consecutive days. On each trial, we used suppression of licking during the tone, normalized to licking during the 10 s pre-CS period, as a measure of conditioned fear. We changed the fabric material in the behavioral chamber between every trial to prevent contextual fear conditioning (Kaifosh et al., 2013; Lovett-Barron et al., 2014).

For 2-photon imaging experiments, we expanded our behavioral paradigm to a differential learning assay using the 2 different auditory cues above as either a CS+ or CS− (where only CS+ is paired with the aversive US). We randomized the assignment of CS+ and CS− tones across mice. Prior to the introduction of US-paired conditioning trials, we obtained multiple trials of behavioral responses (10–15 trials; “Pre-Learning”) to each CS cue presented alone in pseudorandom order over 2–3 days. Mice underwent blocks of 4–6 trials with 1–5 min inter-trial intervals each day (¿1 hour between trial blocks). We then subjected mice to our 3-day conditioning protocol with US-pairing as above, but with alternation between CS+ and CS− trials (“Learning”). Finally, over another 2–3 days, we collected additional trials beyond where behavioral responses plateaued (~20–25 of each CS presented in pseudo-random order, with trial blocks of 4–6 trials as above, “Post-Learning”) with continued US reinforcement on CS+ trials (to avoid extinction). During Pre-Learning and Post-Learning trials, contextual cues, consisting of the chamber fabric material and a background odor of either 70% ethanol or 2% acetic acid, were randomly changed across trials.

Head-fixed optogenetics

200 μm core, 0.37 numerical aperture (NA) multimode optical fibers were constructed as previously detailed (Kheirbek et al., 2013). A splitter patch cable (Thorlabs) was used to couple bilaterally implanted optical fibers to a 532 nm laser (50 mW, OptoEngine) for ArchT activation while mice were head-fixed. All cables/connections were shielded to prevent light leak from laser stimuli and matching-color ambient LED illumination was continuously provided in the behavioral apparatus so as to prevent the laser activation from serving as a visual cue. After the 10 s pre-CS period on each trace fear conditioning trial, 10 mW of laser light was continuously delivered through each optical fiber for the entire CS-trace-US sequence. Experimenters were blinded to subject viral injections. After data collection, mice were processed for histology and recovery of optical fibers. Subjects were excluded from the study if the implant entered the hippocampus, if viral infection was not complete in dorsal CA1, or if there were signs of damage to the optical fiber that could have compromised intracranial light delivery.

2-photon microscopy

For imaging experiments, mice were habituated to the imaging apparatus (e.g., microscope/objective, laser, sounds of resonant scanner and shutters) during the training period. All imaging was conducted using a 2-photon 8 kHz resonant scanner (Bruker) and 40× NIR water immersion objective (Nikon, 0.8 NA, 3.5mm working distance). Images were acquired as either single plane (n = 3 mice) or dual-plane (n = 3 mice) data. For dual-plane acquisitions, we coupled a piezoelectric crystal to the objective as described in Danielson et al. (2016), allowing for rapid displacement of the imaging plane in the z dimension, which permitted simultaneous data collection from CA1 neurons in 2 different optical sections. To align the CA1 pyramidal layer with the horizontal two-photon imaging plane, we adjusted the angle of the mouse’s head using two goniometers (±10° range, Edmund Optics). For excitation, we used a 920 nm laser (50–100 mW at objective back aperture, Coherent). Green (GCaMP6f) fluorescence was collected through an emission cube filter set (HQ525/70 m-2p) to a GaAsP photomultiplier tube detector (Hamamatsu, 7422P-40). A custom dual stage preamp (1.4 × 105 dB, Bruker) was used to amplify signals prior to digitization. All experiments were performed at 1–2× digital zoom, covering ~166–332 mm × 166–332 mm per imaging plane. Dual-plane images (512 × 512 pixels each) were separated by 20 μm in the optical axis and acquired at ~8 Hz given a 30ms settling time of the piezo z-device. Single-plane data (512 × 512 pixels each) was collected at 30 Hz in the absence of the piezo z-device.

QUANTIFICATION AND STATISTICAL ANALYSIS

Image preprocessing

All imaging data were pre-processed using the SIMA software package (Kaifosh et al., 2014). For dual-plane acquired data, motion correction was performed separately on individual trials using a modified 2D hidden Markov model (Dombeck et al., 2007; Kaifosh et al., 2013) in which the model was re-initialized on each plane in order to account for the settling time of the piezo. For motion correction of single-plane acquired data, trials were registered (non-rigid registration) using the Suite2p software package (Pachitariu et al., 2017). All recordings were visually assessed for residual motion. In cases where motion artifacts were not adequately corrected, the affected data were discarded from further analysis. We then used the Suite2p software package (Pachitariu et al., 2017) to identify spatial masks corresponding to neural region of interest (ROIs) and extract associated fluorescence signal within these spatial footprints, correcting for neuropil contamination. Identified ROIs were curated post hoc using the Suite2p graphical interface to exclude non-somatic components.

For each session, we detected only a subset of neurons that were physically present in the FOV. Once signals were extracted for all sessions, we registered ROIs across each session as follows. We first chose the session with the largest number of detected neurons as the reference session, and then computed an affine transform between the time-averaged FOV of all other sessions to the reference. Transforms were visually inspected to verify accuracy. Using these transforms, we processed each session serially to register ROIs to a common neural pool across sessions. For a given session (referred to now as the current session), the calculated FOV transform was applied to all ROI masks to map them to the reference session coordinates. We calculated a distance matrix (using Jaccard similarity) that quantified the spatial overlap between all pairs of reference and current session ROIs. We then applied the Hungarian algorithm (Kuhn, 1955) to identify the optimal pairs of reference and current ROIs. All pairs with a Jaccard distance below 0.5 were automatically accepted as the same ROI. For the remaining unpaired current ROIs, pairs were manually curated via an IPython notebook, which allowed the user to select the appropriate reference ROI to pair or enter the current ROI as a new ROI (i.e., not in the reference pool). Any current ROIs whose centroids were more than 50 pixels away from an unpaired reference ROI were automatically entered as new ROIs, to accelerate the curation. Once all ROIs for the current session were processed (either paired with a reference ROI or labeled as new), the new ROIs were appended to the reference list. The remaining sessions were then processed serially in the same fashion, where the reference ROI list is augmented on each step to include additional ROIs that were not presented in any previously processed session. Once all sessions were processed, this process yielded a complete list of reference ROIs and their identity in each individual session. As a final step, the reference ROIs were warped back to the FOVs of each individual session via affine transform and ROIs that fell outside the boundaries of any session FOV were discarded, so that all analyzed neurons were physically in view for all sessions. Inbound reference ROIs that were not functionally detected in any individual session were assumed to be silent in that session for subsequent analysis.

Neural data analysis

Event detection

All fluorescence traces were deconvolved to detect putative spike events, using the OASIS implementation of the fast non-negative deconvolution algorithm (Friedrich et al., 2017). Following spike inferencing, we discarded any events whose energy was below 4 median absolute deviations of the raw trace. This avoided including small events within the range of the noise, which could artificially inflate activity rates and correlations between neurons.

Given the dominant sparsity of activity, we then discretized each ROI trace to indicate whether an event was present in each frame. Trials for each experiment were collected over the span of several days. Consequently, we found that discretization was necessary to prevent variations in imaging system parameters from exerting undue influences on the analysis, as this could introduce arbitrary variance in the scale of calcium events across sessions.

Decoding

All classifiers in the main text were support vector machines (SVM) with a linear kernel, using the implementation in scikit-learn (Pedregosa et al., 2011). For cross-validation, data were randomly divided into two non-overlapping groups of trials, used for training and testing the classifiers (75/25% split). This procedure was repeated 100 times for each classifier with random training/test subdivisions and reported as the average across cross-validation folds. Trials were balanced by subsampling the overrepresented class, and all decoding results were compared against a null distribution built by repeating the analyses on appropriately shuffled surrogate data, which controlled for the effects of finite sampling. This is particularly important for fear learning paradigms such as ours, where trial counts are very limited.

Decoding elapsed time

We designed a decoder to predict the elapsed time during each trial, in order to assess whether there were consistent temporal dynamics in the neural data during the experiment, such as sequences of time cells. To illustrate the idea behind this analysis (see Figure 2B schematic), we can summarize the activity of the network at each point in time as a point in a high dimensional neural state space, where the axes in this space corresponds to the activity rate of each neuron. The state of the network at each point in time during a trial traces out a path of points in neural state space. If the neural dynamics continually evolve in time (e.g., time cell sequences), then the neural state at one point in time (t) should be different from the states that occur at points further away in time (t + Δt), reflecting the recruitment of different neurons at each point in the sequence. If these dynamics are reliable across many trials, we should be able to train a linear decoder to accurately classify whether data came from one time point or the other, by finding the hyperplane that maximally separates data from time t and t + Δt in the neural state space. By extending this analysis to compare all possible pairs of time points (i.e., for all possible Dts), we can identify moments during the task that exhibit reliable temporal dynamics across trials (Bakhurin et al., 2017; Cueva et al., 2019).

Time decoding was done separately for CS+ and CS− trials, and for Pre- and Post-Learning trial blocks, to assess differences between cues and over learning. We analyzed data during both the tone and trace period, for a total of 35 s on each trial. We averaged each neuron’s activity in non-overlapping 2.5 s bins, so that each trial was described by a sequence of 14 population vectors of activity in time.

Our time decoder uses a 1 versus 1 approach through an ensemble of linear classifiers. For each pair of time bins in the experiment, we train a separate classifier to distinguish between population vectors of activity that came from those two time bins. For comparing 14 time bins, this results in a set of 91 binary classifiers trained on all unique time comparisons (Bakhurin et al., 2017; Cueva et al., 2019). We first evaluated the performance of the individual classifiers by testing their ability to correctly label time bins from held out test trials, where in this analysis each classifier is tested only on time bins from the trial times that it was trained to discriminate. This result is presented as a matrix in Figure 2C, and demonstrates the linear separability of any two points in time during the task. We then used the decoder to perform a multi-class time prediction analysis. Here each population vector in a held-out test trial is presented to all pairwise classifiers, which “vote” on what time bin the data came from (i.e., for each possible time bin, we tabulate the number of classifiers that decided the population activity came from that time). We take the decoded time to be the time bin with the plurality of votes, and repeat this procedure across all sample population vectors in each test trial to decode the passage of time.

For all time decoding analyses, we compare the classification accuracy or prediction error to a null distribution, which we calculate by repeating these analyses on 1000 surrogate datasets, where for each trial independently, we randomly permute the order of the time bins. This destroys any consistent temporal information across trials, while preserving the average firing rates and correlations between neurons within each trial.

We repeated the above analyses at a coarser time resolution (5 s, yielding a sequence of 7 population vectors in each trial), as well as repeated the analysis for both fine and coarse time resolutions using a nonlinear SVM (RBF kernel via scikit-learn, Pedregosa et al. [2011]), all of which produced similar results to those reported in the main text (see Figure S2A).

Decoding stimulus identity from instantaneous firing rates

We also used a population decoding approach to assess the times in the experiment during which there was significant information about the stimulus identity in the neural data. This analysis can be schematized similar to that above, where the different CS cues are associated with different network states that can be reliably segregated in state space by a hyperplane (Figure 3A). On each trial, we averaged the activity of each neuron in non-overlapping 1 s bins. We then trained a separate linear classifier on each time bin to predict whether the population vector came from a CS+ or CS− trial. Classifiers were cross-validated as above on held-out test data. We similarly compared the classification accuracy for trial information to a null distribution, where here we repeated the decoding analysis on 1000 surrogate datasets where the CS trial label was randomly shuffled.

Decoding from average firing rates

We similarly assessed our ability to decode stimulus identity from the average firing rates of the neurons within a set trial period on each trial. This procedure is identical to the one outlined above, and we used it to assess our ability to decode the CS identity during the Pre-CS (−10 to 0 s), CS (0 to 20 s), Trace (20 to 35 s), US (35 to 40 s), and Post-US (40 to 170 s) periods of the trial (Figure 4B), as well as during the CS and trace periods combined (0 to 35 s, Figure 4A).

We additionally assessed how decoders learned at one time period in the task generalize to activity observed in other time periods, by constructing a cross-time period decoding analysis. Here on each cross-validation fold, we trained different decoders to predict CS identity from the activity during each trial period separately. Then on the held-out test data, we tested each decoder not only on the activity from the time period on which it was trained, but on the activity of all other time periods as well (e.g., train on CS, test on trace). The result is a matrix of pairwise trial period comparisons, where the columns indicate the time period used for training the classifier and the row indicate the time period for testing. These comparisons are not necessarily symmetric (e.g., we find that CS period decoders can be used to predict the cue when tested on trace-period activity better than the reverse).

Selectivity index analysis

To assess CS-selectivity at the level of single neurons, we computed a selectivity index as:

$$SI=\frac{f_{+}-f_{-}}{f_{+}+f_{-}}$$

where f₊ and f₋ are the average activity of the neuron in the examined trial time period on CS+ and CS− trials, respectively. This yields an index bounded between +1 (all activity during CS+ trials) and −1 (all activity during CS trial). Similar to the decoding analysis, we compared this selectivity index to those calculated from 1000 surrogate datasets where the trial type labels were randomly shuffled, which controlled for spurious firing rate differences attributable to small numbers of trials. We computed these scores separately for Pre- and Post-Learning trials, and quantified the fraction of cells active during that trial type which showed significant CS-selectivity, determined by calculating a p value from the observed SI relative to its shuffle distribution. For the regression to population decoder weights shown in Figure 4E, we z-scored each SI (computed from average activity over CS and trace periods; 0–35 s) relative to its shuffle distribution’s mean and standard deviation.

Sequence score

For analysis of neural sequences using cell firing orders, we detected the latency to peak firing rate for each neuron during the CS and trace periods (0 to 35 s) that was active on at least one trial. We compared this firing order between all trial pairs via Spearman’s rank correlation, and assigned a sequence score as the average pairwise rank correlation between trials. This analysis was done separately for CS+ and CS− trials. To assess significance, sequence scores were compared to those calculated from 1000 surrogate datasets, where for each neuron, its activity trace was randomly permuted on each trial independently to randomize the temporal ordering between cells’ activity events.

Hidden Markov model

We used hidden Markov models (HMMs) as an additional, more flexible probe for sequential dynamics in the neural data (Mazzucato et al., 2019; Maboudi et al., 2018). The HMM identifies a set of latent neural states, which can be thought of as a recurring pattern of population activity: each state dictates a probability for each neuron that it will be active when the network is in that state. The HMM is simultaneously a clustering algorithm which identifies periods of similar neural activity, and a model of neural sequences, as it models the transitions between latent states over time. We use this framework to analyze both the temporal and covariance structure of neural population activity.

Formally, we model the neural states as evolving in time under first order Markovian dynamics. Let q denote the discrete state variable and {S₁…S_K} be the set of possible states. Then the probability of transitioning from one state q(t) = S_i to the next q(t + 1) = S_j depends only on the current state, and these “transition” probabilities are described by a K × K matrix A with elements a_ij:

$$P(q(t+1)=S_j)=P(q(t+1)=S_j|q(t)=S_i)=a_{ij}$$

The state variable q is never observed directly, but rather exerts an influence on the observed neural activity. Since we are working with binarized calcium events, it is natural to describe each neuron as an independent Bernoulli process, whose activation probability depends on the current neural state. Letting n_i(t) be the activation of the ith neuron at time t which can take values ∈˛{0,1}, and {n₁(t)…n_N(t)} = n(t):

$$P(n_i(t)|q(t)=s_j{)}^{\sim }\mathrm{Bernoulli}[b_{ij}]$$

$$P(\mathbf{n}(t)|q(t)=s_j)=\prod _{i=1}^N{b}_{ij}^{n_i(t)}{(1-b_{ij})}^{1-n_i(t)}$$

Here the b_ij are elements of the “observation” matrix B, which summarizes the firing rates (activation probability) of the ith neuron when the network is in the jth state. In sum, the columns of B give us the pattern of activity observed when the network is in each neural state, and A describes how the network moves dynamically between states over time. Together with the vector π which describes the probability of starting in each state, the model is completely specified by these parameters {A,B,π} (Rabiner, 1989).

The HMM parameters {A,B,π} are not known a priori and must be fit to the observed neural data. We used the standard Baum-Welch expectation-maximization algorithm to iteratively update the model parameters in order to maximize the likelihood of the data (Rabiner, 1989), treating each trial as an observation sequence. During each M-step of the procedure, we enforced a minimum activity rate of 0.001 Hz to regularize the model (Maboudi et al., 2018). The optimization is non-convex and prone to local minima, which we combated by first initializing B using a modified K-means clustering of the neural data. The hyperparameter K, which specifies the number of latent neural states in the model, is not learned and must be set manually. We fit 12 models to the dataset for each value of K ∈ {5…50}, using randomized initial conditions, and for each K we retained the model that maximized the likelihood of the data. We trained a separate set of models for Pre-Learning and Post-Learning trials, for each mouse.

HMM transition analysis

After fitting the model, we estimated the most likely sequence of states on each trial via the Viterbi algorithm (Rabiner, 1989). From this sequence, we constructed single trial transition matrices by counting state transitions along the Viterbi path. Similar to the rank sequence analysis described previously, we computed the correlation between these transition matrices for all pairs of trials, as a measure of the similarity of trial activity sequences. For this calculation, we set the diagonal of each transition matrix to zero, so that the correlations focused on which state transitions appeared on a given trial, rather than the state duration implicit in self-transition probabilities. To determine significance, we compared this averaged sequence correlation to a distribution of correlations generated by randomly shuffling the order of time bins independently on each trial prior to calculation (Recanatesi et al., 2020). This procedure was repeated for all model complexities, separately for CS+ and CS− trials.

Decoding CS using HMM states

For each trial, we calculated the posterior probability of each state at each point in time, given the model parameters and the observed neural data. From this, we estimated the frequency that each state appeared in the trial as the average of the state posterior probability over time (Rabiner, 1989). Similar to our decoding analysis using mean firing rates described previously, we trained a linear SVM to decode the identity of the CS cue using the state frequencies on each trial, calculated from 0–35 s relative to the cue onset (i.e., CS and trace period).

We gauged how much each state reflected strongly co-active neurons by counting the number of neurons whose observation probabilities exceeded 75%. We also assigned each state a CS selectivity ranking based on the absolute value of its weight in the decoder trained on state frequencies. We then plotted the average number of strongly co-active neurons in each state, separately for each selectivity rank (Figure S3).

Ensemble overlap analysis

We measured the similarity in the active set of neurons between a pair of trials by computing the Jaccard similarity index, which for two sets is given by the size of the set intersection divided by the size of the set union (Figure S4). Intuitively, if the sets of active neurons overlap completely, the set intersection and union are equal and the index is 1, while if trials recruit orthogonal sets of neurons, the intersection and thus the index are 0. This metric is biased by the fraction of active neurons on a given trial; if two trials randomly recruit 50% of neurons, the Jaccard similarity will tend to be higher than if they randomly recruited 10% of neurons, as the former will tend to have more overlapping elements purely by chance. To control for differences in activity rates across trials, we generated 1000 surrogate scores for each trial pair where we recomputed the index between two binary vectors whose elements were randomly assigned as active or inactive to match the fraction of active neurons in the real trials. The observed index was then z-normalized relative to this distribution, to quantify the population similarity beyond that expected from random recruitment of the same number of neurons.

Statistics

Statistical details of experiments can be found in the figure legends. Statistical details of analysis methods are described in the corresponding sections above. No statistical methods were used to predetermine sample sizes, but our sample sizes are similar to those reported in previous publications.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and Virus Strains
rAAV1.Syn.Flex.GCaMP6f.WPRE.SV40	Addgene	Addgene virus 100833-AAV1
rAAV2/1.Syn.ArchT	Boris Zemelman	N/A
rAAV2/1.Syn.tdTom	Boris Zemelman	N/A
Deposited Data
Analyzed data	This paper	N/A
Experimental Models: Organisms/Strains
Mouse: R4Ag11: B6.Cg-Tg(CamKIIα-Cre)3Szi/J	Bina Santoro (Dragatsis and Zeitlin, 2000)	Jackson Laboratory Strain 027400
Software and Algorithms
Python 3.6.8	https://www.python.org	N/A
SIMA	Kaifosh et al., 2014	https://github.com/losonczylab/sima
Suite2p	Pachitariu et al., 2017	https://github.com/MouseLand/suite2p
OASIS	Friedrich et al., 2017	https://github.com/j-friedrich/OASIS
Custom data processing and analysis code	This paper	N/A

Highlights.

• Population activity in hippocampal CA1 was studied during trace fear conditioning

• CA1 does not generate persistent activity to bridge the “trace” delay period

• Neurons encoding the CS during cue and trace periods emerge with learning

• Neural activity is temporally variable but predicts CS identity over longer periods