Accurate reconstructions of pelvic defects and discontinuities using statistical shape models

Abstract

Treatment of large acetabular defects and discontinuities remains challenging and relies on the accurate restoration of the native anatomy of the patient. This study introduces and validates a statistical shape model for the reconstruction of acetabular discontinuities with severe bone loss through a two-sided Markov Chain Monte Carlo reconstruction method. The performance of the reconstruction algorithm was evaluated using leave-one-out cross-validation in three defect types with varying severity as well as severe defects with discontinuities. The two-sided reconstruction method was compared to a one-sided methodology. Although, reconstruction errors increased with defect size and this increase was most pronounced for pelvic discontinuities, the two-sided reconstruction method was able to reconstruct the native anatomy with higher accuracy than the one-sided reconstruction method. These findings can improve the preoperative planning and custom implant design in patients with large pelvic defects, both with and without discontinuities.

Introduction

Treatment of large acetabular defects and discontinuities remains one of the most challenging procedures in revision hip arthroplasty (Buckup et al. 2013). High post-operative complication rates of 25% to 80% have been reported following surgical treatment of pelvic discontinuities (Christie et al. 2001; Holt & Dennis 2004; Villanueva et al. 2008; Blumenfeld 2016; Hasenauer et al. 2018). Successful surgical outcome relies on the accurate restoration of the native anatomy of the patient, including restoration of the hip joint centre (Villanueva et al. 2008; Sporer 2011; Blumenfeld 2012; Amenabar et al. 2016), but is impeded by the lacking bone support and limited fixation possibilities in these patients with acetabular defects (Paprosky et al. 2005; DeBoer et al. 2007). In patients where pelvic discontinuities occur, the detachment of the inferior hemipelvis and consequent mobility of the inferior aspect makes this even more challenging (Martin et al. 2016). Indeed, multiple studies have found that patients with pelvic discontinuities have higher complication rates than patients with less severe acetabular defects (Berry et al. 1999). In recent years, custom triflange acetabular components (CTAC) have been introduced to successfully treat patients with pelvic defects (Berasi et al. 2015), although several authors reported issues related to implant fitment, especially in cases of pelvic discontinuities, and consequentially incidence of dislocations remained high (Barlow et al. 2016; Myncke et al. 2017; De Martino et al. 2019).

In any case, an accurate source for the patient’s native anatomy is required for successful preoperative planning and implant design. Multiple studies have shown that the contra-lateral hemi-pelvis can be used as a reliable template (Gelaude et al. 2007; Paul et al. 2010). However, the contra-lateral hemi-pelvis is not available in patients with bilateral hip degeneration (Vanden Berghe et al. 2017). As a solution, statistical shape models have been used to reconstruct the native anatomy of moderate to severe acetabular defects, with good, or better, accuracy compared to contra-lateral methods (Krol et al. 2013; Vanden Berghe et al. 2017; Hettich et al. 2019). However, to the author’s knowledge, none of the methods used in these studies are able to reconstruct pelvic discontinuities where the relative position of the superior and inferior aspects can be altered compared to the native anatomy (Sporer et al. 2012). Although only one of the aspects can be used for the reconstruction method, the reconstruction accuracy of these methods would be hampered, hereby affecting planning accuracy or CTAC’s design decisions.

Therefore, the objective of this study is to develop and validate a statistical shape model for the reconstruction of pelvic discontinuities with severe acetabular bone loss, using a method which reconstructs the separated pelvic aspects independent of their relative position. Hereby, we aim to further improve the reconstruction of pelvic discontinuities using statistical shape models.

Methods:

The training dataset used to construct the statistical shape model consisted of 90 clinically available unilateral CT scans of patients (45 males, 45 females) without any bony abnormalities, as rated by an experienced orthopaedic hip surgeon (M.M.). This study was approved by the ethical committee of the university hospitals Leuven (S61746). The CT scans were segmented and converted to watertight 3D models using Mimics Innovation Suite (v21.0, Materialise, Leuven, Belgium). The resulting 3D models were smoothed taking care that significant anatomical details were preserved in the 3D models upon visual inspection. The smoothed models served as input for an iterative registration procedure in MATLAB (2019b, The Mathworks Inc., Natick, Massachusetts, USA) to establish accurate point-to-point correspondences between all these models: First, a single model from the training dataset was randomly chosen as a template for registration with all other training models. Secondly, the position of the template is initiated using manually annotated landmarks (crude rigid registration step), after which a rigid iterative closest point (R-ICP) algorithm was used to rigidly align the template with each of the training shapes (fine rigid registration step). Thirdly, point-to-point correspondences were established using an open-source non-rigid surface registration algorithm available in the MeshMonk toolbox for MATLAB (White et al. 2019) (fine non-rigid registration step). Finally, to remove the possible bias induced by the randomly chosen template, we uniformly remeshed the calculated mean shape and repeated the R-ICP and non-rigid registration steps. The resulting correspondences were then used to construct a Gaussian process morphable model using principal component analysis (Lüthi et al. 2018). The model’s performance was characterized using the generalization and compactness metrics (Davies 2002).

The reconstruction algorithm seeks to synthesize pre-diseased bone morphology based on the healthy parts of a given pathologic bone using the shape model’s modes of variation. The algorithm was implemented using the open-source shape modelling library Scalismo in Scala (Lüthi et al. 2018). The Gaussian process model was limited to the first 30 modes of variation based on the observed improvement in cross-validation results. To improve the model’s ability to conform to unlearned data, the Gaussian process model was augmented with additional variation through a Gaussian kernel. The reconstruction procedure starts with a rough alignment of the shape model to the defect shape, after which a Metropolis-Hastings algorithm is used to generate Markov chain Monte Carlo (MCMC) samples for shape and pose (translation and rotation) parameters simultaneously (Schönborn et al. 2017). The parameters which corresponds to the best fitting sample, using the average distance to the goal surface as a metric, is chosen for the virtual reconstruction.

To reconstruct discontinuous pelvic bones, a novel method was implemented where MCMC samples are generated for the poses of both aspects simultaneously. One set of the pose parameters is used to optimise the shape model position of the superior aspect, the other set is used for the inferior aspect. Only one set of shape parameters is optimized. Thus, the result of this procedure is a continuous, reconstructed pelvis which is fitted to the shape of both aspects but is independent of their relative position.

Reconstruction performance was evaluated by leave-one-out cross-validation. Artificial defects of four different severities were created for each available dataset, while its original shape was excluded from the training of the shape model. Each of the artificial defects was first annotated on the template shape and then automatically transferred to each of the validation shapes using the earlier established point-to-point correspondences. As shown on figure 1, three different defects were defined based on the Paprosky classification ranging from IIA-IIB to IIIB defects, similar to Vanden Berghe et al. (Vanden Berghe et al. 2017). Additionally, one defect was defined simulating pelvic discontinuity with severe bone loss, corresponding to a type IV defect according to the American Academy of Orthopaedic Surgeons (AAOS) Classification of Acetabular Bone Loss (D’antonio et al. 1989). In this defect, the inferior part was rotated and translated relative to the superior part in the range of 0–20 degrees and 0–20 mm respectively. Rotation and translation axes, as well as, rotation and translation magnitude were selected randomly. The pose of each validation shape was altered, so that its position is different than in the model’s training dataset.

Figure 1.

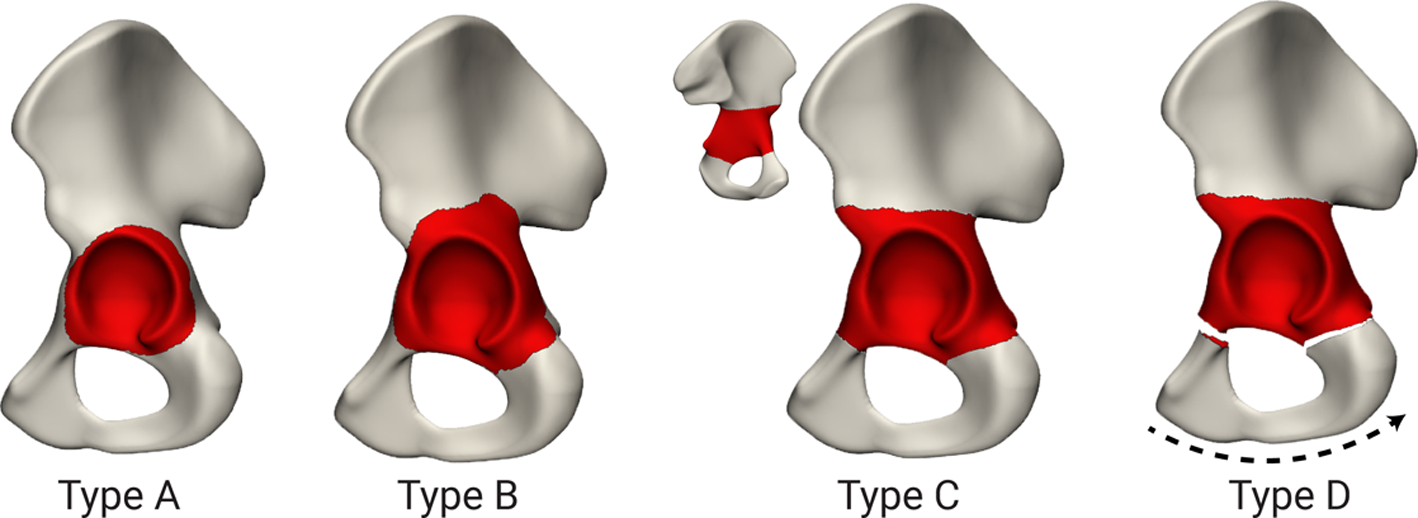
Cross-validation was performed using synthetic defects. Type A, B and C were based on the Paprosky defects ranging from IIA-IIIB. Type D is based on a type IV pelvic discontinuity according to the AAOS classification.

The same point-to-point correspondences were also used to automatically perform anatomical reference measurements on the training dataset in MATLAB. These measurements included acetabular parameters typically used during preoperative planning: acetabular radius, hip joint centre (HJC) position and acetabular direction. As shown on figure 2, the acetabular hip joint surface was used to calculate a fitted sphere, with the centre point and radius of this sphere defined as the HJC and acetabular radius, respectively. The acetabular direction was defined as the orthogonal to a plane fitted through the points of the acetabular rim, through the HJC. For the most severe, discontinued defect two types of reconstructions were performed. (1) The one-sided reconstruction method, where only the superior aspect was used for the reconstruction, omitting the rotated inferior aspect from the reconstruction. (2) The two-sided reconstruction method where both the superior and inferior aspects were used to reconstruct the original shape.

Figure 2.

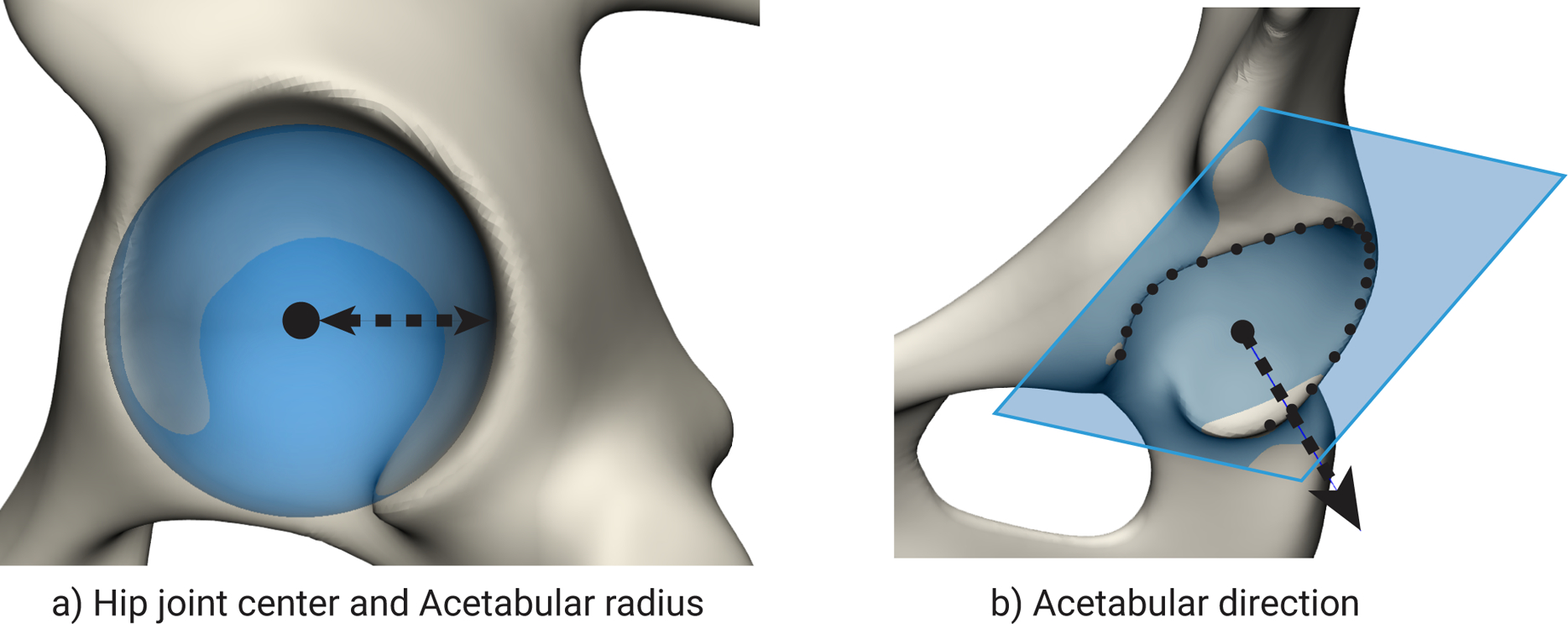
a) A sphere fitted to the acetabular hip joint surface to determine the hip joint centre and acetabular radius. b) The normal fitted to the acetabular rim points is used to determine the acetabular direction.

The anatomical reconstruction errors for each validation shape were defined as the difference between the anatomical measurements on the original and the reconstructed bone. The HJC misalignment was calculated using the Euclidean distance between the native and reconstructed centre point positions. The error in terms of acetabular direction was defined as the angle between the native and reconstructed directions. To quantify the overall accuracy of the reconstructed surface, a reconstruction error was defined as the root-mean-square error (RMSE) of the Euclidean distance between the reconstructed shape and unknown defect surface. A fit error was defined as the RMSE of the Euclidean distance between the reconstructed shape and the known parts of the bone. The significance of differences between the one-sided and two-sided reconstruction method results was statistically tested using the non-parametric Wilcoxon Signed-rank test in SPSS (v26.0, IBM Corp., Armonk, N.Y, USA). A visual representation of the methods used in this study is provided as a supplementary material.

Results:

The performance of the model is visualized in figure 3, the compactness measurements indicate that the first mode of variation explains 50% of the total variation. The first five modes explain approximately 75% of the variation in the training data set. In order to explain 95% of the total shape variations 25 modes are required. The generalization measurement shows that the shape model has the ability to represent new shape instances with an average error of 0.62 mm if all modes of variation are used. The generalization ability decreases to 0.82 mm when 30 modes are used.

Figure 3.

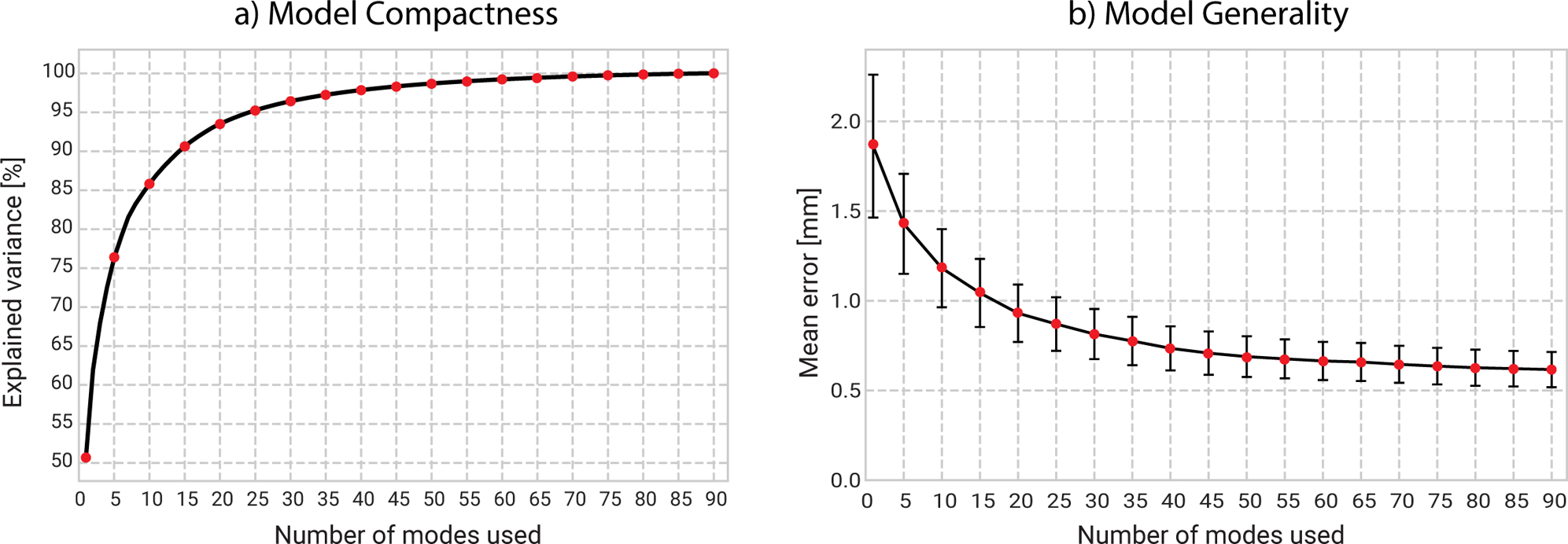
Model performance is evaluated using its compactness (a) and generality (b) measurements. The first five modes account for approximately 75 % of the total variation. The generality graph snows that unlearned samples are able to be explained with an average error of 0.62 mm.

The results of the reconstruction method are shown in figure 4. From here on, one-sided and two-sided reconstruction methods are labelled D and D*, respectively. Due to their skewness, error measurements were found to be non-normally distributed, therefore errors are expressed using the median and 25–75% percentiles.

Figure 4.

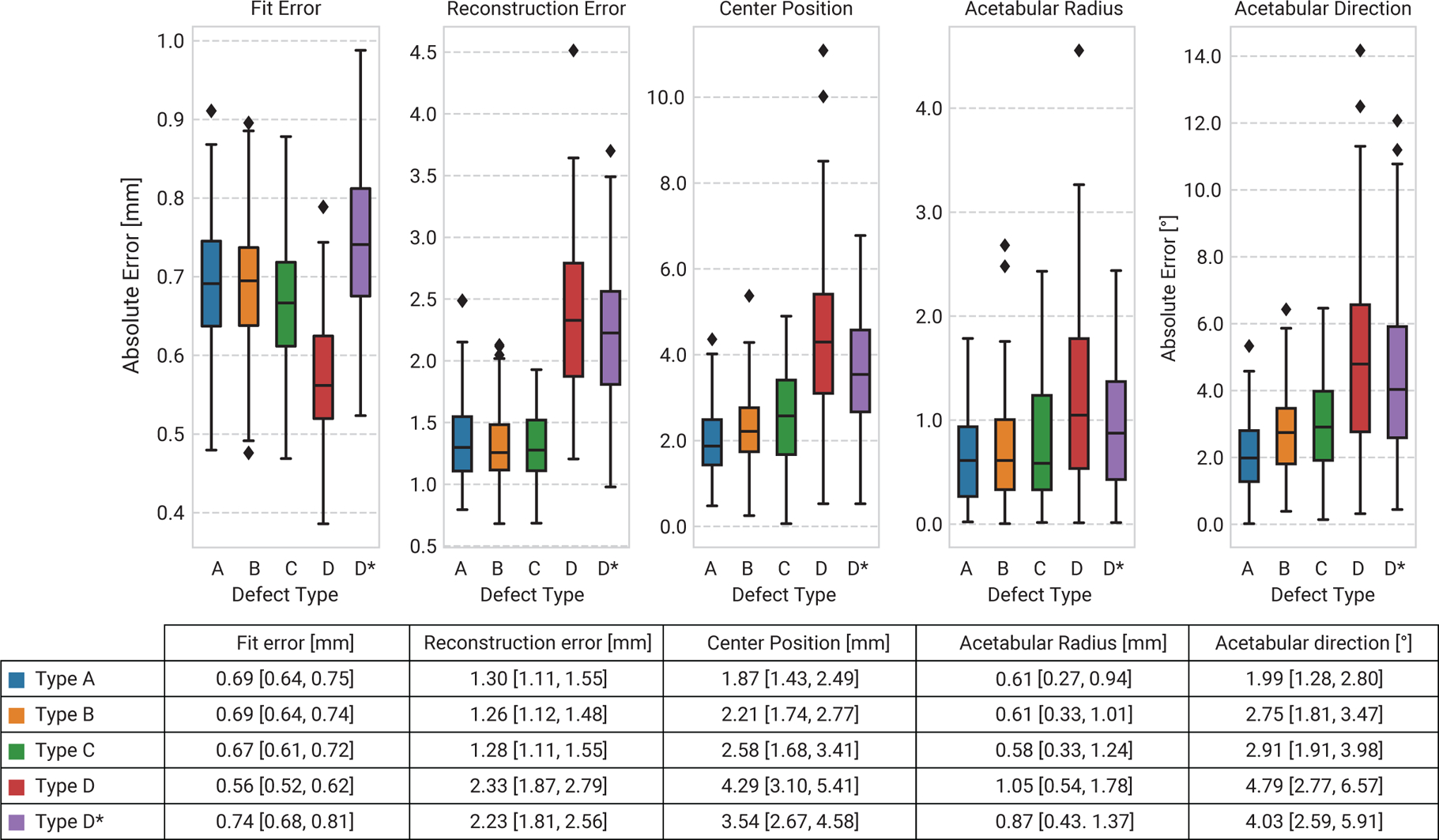
The cross-validation results show that reconstruction errors and uncertainties increase with increasing defect size. A significant increase is found for reconstruction of pelvic discontinuities. Two-sided reconstructions (D*) can obtain better reconstruction accuracies than one-sided reconstructions (D). Reconstruction errors in the results table are shown as median, [25% – 75%] confidence intervals.

The fit error was found to be approximately equal for type A to C defects, with median errors ranging from 0.69 mm to 0.67mm, whereas it was smallest for the one-sided reconstructions of type D defects (0.56 mm) and largest for two-sided reconstructions (0.74 mm). The median error between the original defect surface and the reconstructed surface, expressed as the reconstruction error, does not increase for the reconstruction of defect types A to C. However, the reconstruction errors significantly increased if pelvic bone discontinuities were present. In these cases, the reconstruction surface error was found to be significantly lower using the two-sided reconstruction method compared to the one-sided reconstruction method (P=0.005,R=0.21).

The accuracy of the reconstructed hip joint centre worsens with increasing defect sizes. The HJC in the smallest defect types can be predicted with a median error of 1.87 mm, whereas for type B and C these errors increase to 2.21 and 2.58 mm, respectively. For reconstructions of pelvic discontinuities, this error increases to 4.29 mm using the one-sided method but significantly improves again to 3.54 mm when using the two-sided reconstruction method (P<0.0001,R=0.30). Reconstructions of type A through C do not show any differences in reconstruction accuracy of the acetabular radii, with median reconstruction errors of 0.61, 0.61 and 0.58 mm respectively. Again, the two-sided reconstruction method is able to achieve significantly higher accuracy compared to the one-sided method (P=0.04,R=0.15). Defect size influences the reconstruction accuracy of the acetabular direction throughout all defect sizes, for the smallest defects the associated median error equals 1.99°, for type B defects 2.75° and for type C defects to 2.91°. Acetabular direction predictions worsened for pelvic discontinuities for both reconstruction methods. The one-sided reconstruction reconstructed the acetabular direction with a median accuracy of 4.79°, whereas the two-sided method predicted the direction with a accuracy of 4.03° (not significant).

Also, the maximum errors reduced for all measurements when a two-sided instead of one-side reconstruction approach was used, as shown in figure 4. The HJC reconstruction error was reduced from 11.09 mm to 6.78 mm, acetabular radius error from 4.56 to 2.44 and acetabular direction error from 14.17 ° to 12.07 °.

Discussion

A method for the virtual reconstruction of acetabular defects capable of handling discontinuities was implemented and evaluated using artificial bone defects in a leave-one-out cross-validation procedure. These artificial bone defects were applied to each of the 90 training dataset shapes and based on the Paprosky and AAOS classifications for acetabular bone loss (D’antonio et al. 1989; Paprosky et al. 1994). Defect types A, B and C represent continuous pelvises, while type D represents pelvic discontinuities with inclusion of relative movement between the superior and the inferior aspect. The study motivation is similar to the study of Vanden Berghe, Hettich and Krol et al. but takes into account the additional difficulties associated with large acetabular defects for which accurate preoperative planning and subject-specific implants are especially beneficial (Wyatt 2015).

The training dataset consisted of 90 unique unilateral pelvic shapes, which exceeds the recommended number of shapes to capture the non-pathologic shape variations of the pelvis (Chintalapani et al. 2007). The model compactness indicates that 25 modes are required to model 95% of the shape variation in the training dataset, the model used by Vanden Berghe et al. only required 23 modes to reach this variability number, which might indicate that additional variation is present in our training dataset. This is further supported by the generality metric which indicates our model is able to account for the variation in new shapes with higher accuracy, compared to theirs. To the best of our knowledge, no other studies reported shape model performance that allow further comparison of these measures.

The anatomical measurements, namely the error on the centre position, acetabular radius and direction, indicate that reconstruction errors increase with increased defect sizes. Interestingly, this error increases significantly for pelvic discontinuities. Although the reconstruction error does not increase for type A through C defects, further investigations show that this error does increase when only evaluating the acetabular surface. The additional surface to reconstruct in type B and C defects is easier to predict and less complex than the acetabular fossa, hereby compensating for the larger error in the acetabular area and reducing the average error. For detailed information, see the supplementary data.

Again, our validation results can be compared to the results of Vanden Berghe et al. due to the similarity in defect sizes of type A, B and C and the use of the same anatomical measurements in both studies (Vanden Berghe et al. 2017). Our results show an average improvement for all anatomical measurements of 18%, these improvements are largest for the smallest defects of type A (28%, 13% and 34% for HJC, radius and direction respectively), whereas improvement is somewhat less for the larger defects of type C (19%, 16% and 9% for HJC, radius and direction respectively). Also Hettich et al. performed a similar study using bilateral pelvises with artificial defects comparable to our type C defects (Hettich et al. 2019) and apparently identical definitions of HJC position and radius measurement methods as in our study. They reported a HJC error of 3.5 mm and radius error of 1.0 mm. Our results show an improvement of 26% and 40%, for these measurements, respectively. We believe the above improvements can be attributed to our use of the MCMC reconstruction algorithm and its ability to optimize shape and pose simultaneously, hereby decreasing the likelihood of reaching a local optimum. Other studies used an iterative approach where pose and shape parameters are instead optimized separately. Furthermore, we found improvements in reconstruction accuracies when augmenting the shape model with additional variation to improve the fit errors to the healthy bone parts.

The reconstruction error for pelvic discontinuities (Defect type D) specifically has, to the best of our knowledge, not yet been reported in the literature. Therefore, we chose to perform reconstructions of these severe defects using a one-sided and a two-sided method and found significantly higher error outcomes for both methods when compared to non-discontinued defects. However, as intended, the two-sided reconstruction method performed better for all reconstruction accuracy measurements, with significant differences in favour of the two-sided reconstruction method for the reconstruction error, HJC position and acetabular radius errors. These results indicate that reconstructing the native relative position is challenging even when using both the superior and inferior aspects of the discontinued pelvis. The presence of a large acetabular defect increases the distance between the known parts of the pelvis, increasing the level of uncertainty for the reconstruction method. Using a two-sided method significantly improves the reconstruction accuracy obtained compared to one-sided method. These improvements are advantageous in patients with severe pelvic defects and discontinuities as they benefit most from patient-specific implants which require these reconstructions (Wyatt 2015).

The maximum reconstruction errors are not a statistically robust measurement to differentiate the reconstruction accuracy of both methods. There are however large improvements for all measurements between the two-sided and one-sided reconstruction methods indicating that two-sided reconstructions are less likely to produce outliers than the one-sided reconstruction method. This is further supported by the narrower confidence intervals displayed in figure 4.

These improvements in reconstruction accuracy can improve the accuracy of surgical planning and subject-specific implant design. Accurate restoration of the HJC has been shown to reduce wear-rate, occurrence of dislocations and aseptic loosening (Karachalios et al. 1993; Bicanic et al. 2009; Baghdadi et al. 2013). The increased robustness of the presented method is especially important when these reconstructions are used in the design process of CTACs. Here, it is impossible to make design changes intra-operatively and large reconstruction errors could lead to fitment issues, as has been mentioned in the literature (Myncke et al. 2017).

This study evaluated the reconstruction of severe acetabular defects with more bio-fidelity than other studies on this subject, as they typically do not consider the relative displacements occurring between the aspects of the pelvis. A strength of the implementation is the use of open-source tools and flexibility of the implementation. This implementation can easily be transferred to unstable fractures of different bones, such as pelvic fractures or clavicle fractures, where reconstruction surgery can be challenging and requires patient-specific solutions (Vancleef et al. 2019). Finally, we believe that the used method is highly robust and repeatable due to the use of automated measurements instead of manual measurements. A weakness of the implemented method is the need for manual annotations and segmentations of the defect pelvis, which can be challenging in real cases due to the presence of metal artefacts and requires good knowledge of pelvic anatomies. Automated segmentation is a very actively researched topic, where for example deep convolutional neural networks have recently been introduced for automated volumetric CT scan segmentations of complex anatomical structures (Dou et al. 2017). However, to our knowledge, no studies have explored the use of AI-based segmentations in revision arthroplasty, specifically. Herein, specific challenges arise from the large inter-patient shape variation and the occurrence of metal artefacts in CT scans caused by the presence of voluminous metallic implants. With regards to the subsequent annotation step, Plessers et al. recently proposed an automated method to reconstruct the glenoid in shoulder joint arthropathy which eliminated the manual annotation of the defect region (Plessers et al. 2020). This method could also be applied in the pelvic bone anatomy, but still relies on accurate segmentation of the defect shape.

Conclusion

This study developed a pelvic statistical shape model for the reconstruction of acetabular defects, including associated pelvic discontinuities. A two-sided reconstruction method was implemented for the reconstruction of pelvic discontinuities and compared to current state-of-the-art one-sided reconstruction method. Its reconstruction performance was evaluated using leave-one-out cross-validation. Reconstruction errors increased with defect size and more significantly for pelvic discontinuities. The two-sided reconstruction method was able to reconstruct the native anatomy of pelvic discontinuities with higher accuracy than the one-sided method. These improvements can be used in the preoperative planning of patients with severe pelvic defects and can be applied in the design of subject-specific implants.