Abstract
Control strategies can be optimized to attain air quality standards at minimal cost through selecting optimal combinations of controls on various pollutants and regional sources. In this study, we developed a module for least-cost control strategy optimization based on a real-time prediction system of the responses of pollution concentrations to emissions changes and marginal cost curves of pollutant controls. Different from other method, in this study the relationship between pollution concentrations to and precursor emissions was derived from multiple air quality simulations in which the nonlinear interactions among different precursor emissions can be well addressed. Hypothetical control pathways were designed to attain certain air quality goals for particulate matter (PM2.5) and ozone (O3) in the Beijing–Tianjin–Hebei region under the 2014 baseline emission level. Results suggest that reducing local primary PM emissions was the most cost-efficient method to attain the ambient PM2.5 standard, whereas for O3 attainment, reducing regional emission sources of gaseous pollutants (i.e., SO2, NOx, and volatile organic compounds (VOCs)) exhibited greater effectiveness. NH3 controls may be cost-efficient in achieving strengthened PM2.5 targets; however, they might not help in reducing O3. To achieve both PM2.5 (< 35 μg m−3) and O3 (daily 1-hour maxima concentration < 100 ppb) targets in Beijing, the reduced rates in BTH regions of NOx, SO2, NH3, VOCs and primary PM are 75%, 75%, 5%, 55%, and 85%, respectively from the emission levels in the year of 2014. Local reduction is the most effective method of attaining moderate PM2.5 and O3 targets; however, to achieve more aggressive air quality goals, the same level of reductions must be conducted across the whole Beijing–Tianjin–Hebei region.
Keywords: air pollution, control strategy, least-cost optimization, air quality attainment, ozone, fine particles
1. Introduction
Airborne fine particles (PM2.5) are responsible for the haze and severely impaired visibility in cities across China. Since late 2000s, substantial measures have been taken to reduce SO2, NOx, and primary particulate matter (PM) emissions. Particularly, since the Action Plan on Prevention and Control of Air Pollution was implemented in 2013, noticeable improvements have been observed in ambient PM2.5 concentrations, which have exhibited declining trends in three key regions in China. PM2.5 levels in the Beijing–Tianjin–Hebei (BTH), Yangtze–River–Delta (YRD) and Pearl–River–Delta (PRD) regions decreased from 110, 70, and 48 μg m−3 in 2013 to 85, 55 and 34 μg m−3 respectively in 2015 (Wang et al., 2017). However, 75.1% of China’s 338 cities at the prefecture or higher level still exceeded the national annual averaged PM2.5 standard of 35 μg m−3 in 2016 (Environment Bulletin of China). With further plans to strengthen abatement of SO2, NOx, and primary PM emissions, ambitious control policies for VOC and NH3 must be enforced to further reduce ambient PM2.5 concentrations in China (Huang et al., 2014; Fu et al., 2017). NH3 emission controls can be a cost-efficient strategy to reduce PM2.5 (Pinder et al., 2007; Winiwarter and Klimont, 2011); however, few NH3 emission control measures have been implemented in China to date (Wang et al., 2017). Relevant modeling studies have demonstrated the importance of VOC controls in reducing PM2.5 with improved secondary organic aerosols (SOA) simulation modules (Zhao et al., 2015; Zhao et al., 2017). VOC emission controls have also been suggested for their control effectiveness in reducing O3, which tends to be slightly enhanced in urban areas where NOx is abundant (VOC–limited regime). For example, some cities in the PRD regions present an increasing O3 trend accompanied by effective controls on PM2.5 through reducing NOx (Li et al., 2014). Optimizing the control ratios for all pollutants is a major policy challenge in attaining the objectives for both PM2.5 and O3.
Most relevant studies in China have adopted the concept of atmospheric environmental capacity to calculate the maximum permissible pollutant emissions when the air pollution concentration reaches the national ambient air quality standard (Xue et al., 2014; An et al., 2007; Li et al., 2013; Zhou and Zhou, 2017; Liu et al., 2017). However, the calculation of atmospheric environmental capacity is not straightforward if the concentration of pollutants (e.g., PM2.5 and O3) is contributed by various emission sources through nonlinear behavior (Cohan et al., 2005; Tsimpidi et al., 2008). In particular, regional sources play a critical role in PM2.5 and O3 concentrations in receptor region, suggesting the importance of joint regional controls (Wu et al., 2015; Xing et al., 2017a). With multiple factors involved, the atmospheric environmental capacity can only be calculated in an economically efficient manner, which is to be performed with optimization techniques (e.g., linear programming) based on receptor-oriented models and marginal cost curves. The optimized control strategy is supposed to select the best combination of controls to attain the air quality standard at minimal cost (Cass and McRae, 1981; Harley et al., 1989; Cohan et al., 2006).
Studies on least-cost control strategy optimization have been conducted for O3 (Heyes et al., 1997; Cohan et al., 2006; Fu et al., 2006) and PM2.5 (Harley et al., 1989; Amann et al., 2001; Carnevale et al., 2012), mostly in the United States and Europe. Cost–benefit analysis has become an essential module in integrated assessment modeling, such as in the Greenhouse gas Air pollution Interactions and Synergies model (GAINS; Amann et al., 2011a) developed by the International Institute for Applied Systems Analysis. In GAINS, the source–receptor relationships are based on reduced-form approximations derived from the unified European Monitoring and Evaluation Programme (EMEP) Eulerian model (Heyes et al., 1996). The GAINS model has been applied in Europe (Amann et al., 2011b), China (Amann et al., 2008), and India (Purohit et al., 2010). However, limitations were also recognized, such as the SOA and nonlinearity in the joint controls of pollutants not being addressed well (Amman et al., 2011a). Since 2012, a new policy-oriented integrated scientific assessment system, the Air Benefit and Cost and Attainment Assessment System (ABaCAS), has been continually developing by an international team of scientists from the United States and China, aims to provide the cost-efficient control strategy for policy makers (Xing et al., 2017b). In ABaCAS, the response surface model (RSM), an advanced statistical interpolation technique based on meta-simulation scenarios, has the ability to represent a nonlinear air quality response to emission perturbations, and thus make real-time predictions of the responses of pollution concentrations to emission changes (Xing et al., 2011; Wang et al., 2011; Zhao et al., 2015). Since the RSM was built on multiple air quality simulations, the advantage of this system is that the nonlinear interactions among different precursor emissions can be well addressed without involving additional assumptions. The costs associated with certain control strategies were estimated by the International Cost Estimate Tool (ICET; previously Cost, the China Multi-Pollutant Control Cost Model) based on cost information of control technologies and was successfully applied in the YRD region (Sun et al., 2014). However, the optimization of control strategies between the ICET and RSM has not yet been developed. The design of a cost-efficient control strategy is expected to be straightforward after the application of the RSM with polynomial function (pf-RSM) developed recently which largely improves the computational efficiency in estimating the air quality response to the emission change (Xing et al., 2017c).
In this study, the module of LEast-COst control strategy optimization (LE-CO) was developed based on a pf-RSM with marginal cost curves. The LE-CO was further implemented in the ABaCAS system and applied to a case study in China’s BTH region.
2. Method
2.1. Framework design of LE-CO
The LE-CO module was designed to select the optimal combination of controls that can not only meet air quality standards but are also the most cost-efficient control strategy among all candidates. Generally, the air quality criteria represent the air quality standards. In this study, we selected the thresholds of annual mean of PM2.5 and daily 1-hour maxima of O3 to be 35 μg m−3 and 100 ppb respectively, which correspond to Class II of the National Ambient Air Quality Standard in China. Beijing city was chosen as the target region to represent the BTH, considering it is located in the center of the BTH region.
The real-time responses of PM2.5 and O3 to emission reduction ratios were calculated using a RSM that quantified the nonlinear relationship between PM2.5 and O3 concentrations to emissions of five pollutants including NOx, SO2, NH3, volatile organic compounds (VOCs; i.e., VOC and intermediate VOC), and primary PM (including primary organic aerosol (POA) and other primary PM) in five regions over BTH, which included Beijing, Tianjin, northern Hebei (denoted as HebeiN), eastern Hebei (denoted as HebeiE), and southern Hebei (denoted as HebeiS). The reduction ratios of different pollutants and regions were calculated using LE-CO through optimization with the following nonlinear programming procedure:
Minimize
| (E1) |
Subject to
| (E2) |
| (E3) |
| (E4) |
Where CostT is the total cost; is the cost for pollutant p (i.e., NOx, SO2, NH3, VOCs, and primary PM) at region r (i.e., Beijing, Tianjin, HebeiN, HebeiE, and HebeiS); is the control ratio of pollutant p at region r; is the cost control ratio function of pollutant p at region r; is the function of concentration of pollutant sp (i.e., PM2.5 and O3) to based on RSM; and obj_Concsp is the air quality criteria of pollutant sp (i.e., PM2.5 and O3).
The framework of LE-CO is displayed in Figure 1. Since RSM has high efficiency in predicting the air quality responses under various emission reductions, the optimized can be determined through the grid searching method to select the strategy that meets the environmental targets with minimal cost. First, the high-dimension sampling space was divided into grids with ten steps from 5% to 95% reductions for each pollutant, resulting in 10000 grid cells (control scenarios) with the combination of different reduction ratios of five pollutants. Second, the concentration responses for all control scenarios were estimated based on the RSM. Third, the total control costs associated with each control scenario were estimated based on the ICET. At last, the optimized control scenario will be selected from the candidate control scenarios which meets the ambient target with least control cost. One thing should be noted that the control scenarios are hypothetical, since the controls in reality cannot be implemented immediately. This study aims to conduct a counterfactual analysis to estimate what if we had better emission controls today and what would they cost.
Figure 1.
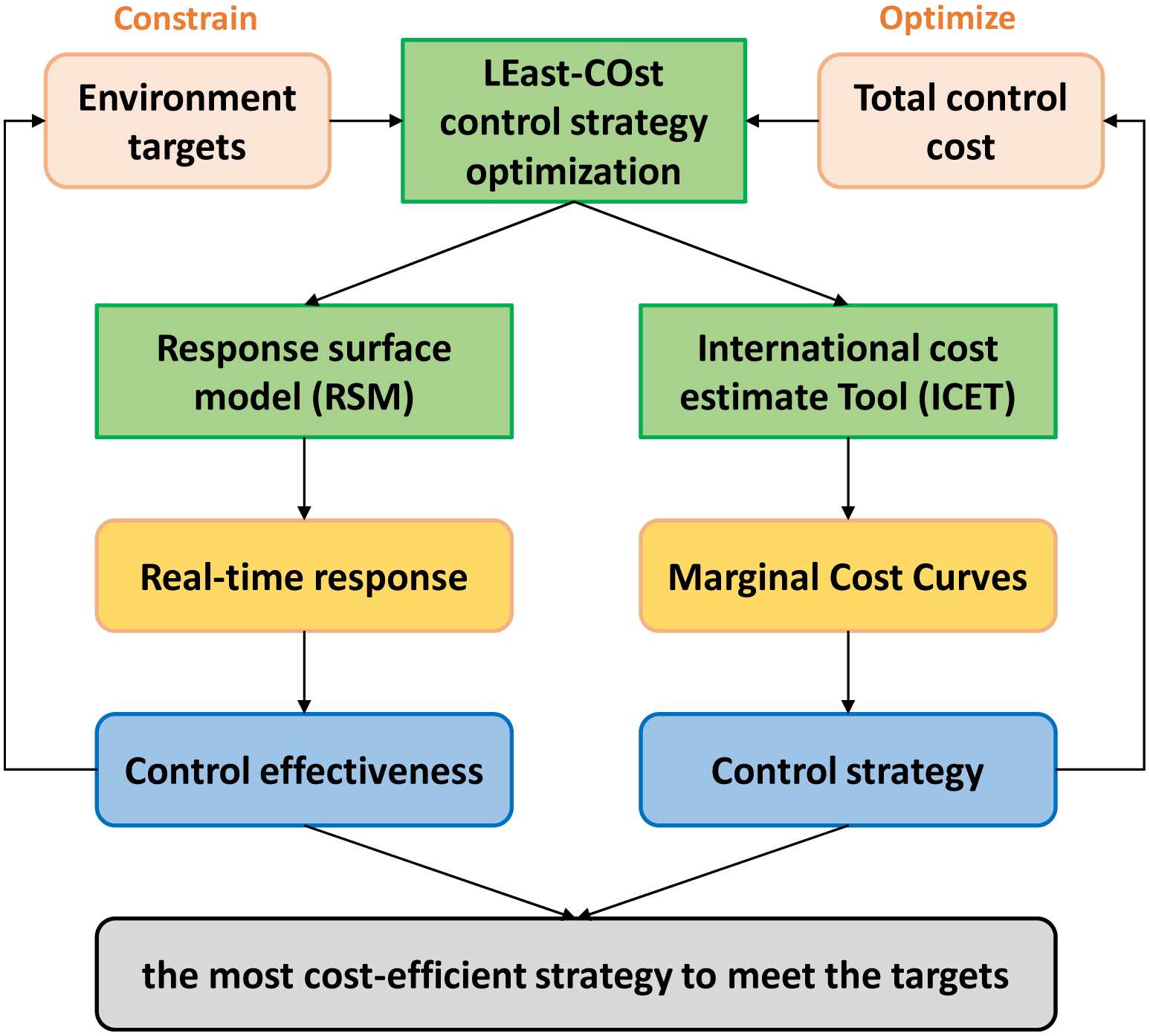
Conceptual framework of the least-cost control stratege optimization (LE-CO) module
2.2. Marginal abatement cost curves
The marginal abatement cost curves for pollutant emissions were established based on the ICET module in the ABaCAS system. The cost estimated in ICET refers to the cost associated with control technology application, while the social cost (e.g., subsidy to promote the control policy) was not considered in ICET in this study. For each pollutant in each region, the total cost under certain abatement targets was calculated using the linear programming model based on the unabated emissions and current control applications, as well as unit cost, potential application rate, and emission control efficiency of various control technologies (Sun et al., 2014), as follows:
Minimize
| (E5) |
Subject to
| (E6) |
| (E7) |
| (E8) |
| (E9) |
| (E10) |
Where is the cost of technology i for pollutant p (i.e., NOx, SO2, NH3, VOCs, and primary PM) at region r (i.e., Beijing, Tianjin, HebeiE, HebeiN, and HebeiS); UCp,i is the unit cost of technology i for pollutant p; is the emission reduction by the technology i for pollutant p at region r; CEp,i is the control efficiency of technology i for pollutant p; is the control application rate of technology i for pollutant p at region r; is the current control application rate of technology i for pollutant p at region r; is the unabated emissions of pollutant p at region r in sector s where control technology i is applied; is the baseline emissions of pollutant p at region r in sector s where control technology i is applied; and max_AppRp,i is the maxima application rate of technology i.
In this study, the data of , , and CEp,i were derived from the study of the bottom-up emission inventory of the BTH region (Zhao et al., 2017). The parameters of UCp,i and max_AppRp,i basically referred to the ICET and GAINS-Asia models with some updates for power plants and key industries from references, as summarized in a separated paper (Zhang et al., in preparation).
In Figure 2, the marginal abatement cost curses represents the optimized combinations of control technologies for each pollutants individually. Clearly, the cost increases sharply with the growth of the pollutant reduction ratio because the most cost-efficient control technologies will be first selected (Zhang et al., in preparation). The SO2 and primary PM emission controls cost significantly less compared with other pollutants, and thus were prioritized for selection of control choices. The cost of NH3 emission controls is slightly lower than NOx and VOCs. Although not receiving much attention in current policy, NH3 emission controls have the potential to be selected under higher reduction requirements when the cost of reducing NOx and VOCs become much higher than NH3. The pollutants cannot be fully controlled because of the limitations of control technologies. The maxima reduction ratio of NOx, SO2, NH3, VOCs and primary PM was set to be about 85%, 75%, 75%, 65% and 95% respectively after considering all potential controls.
Figure 2.
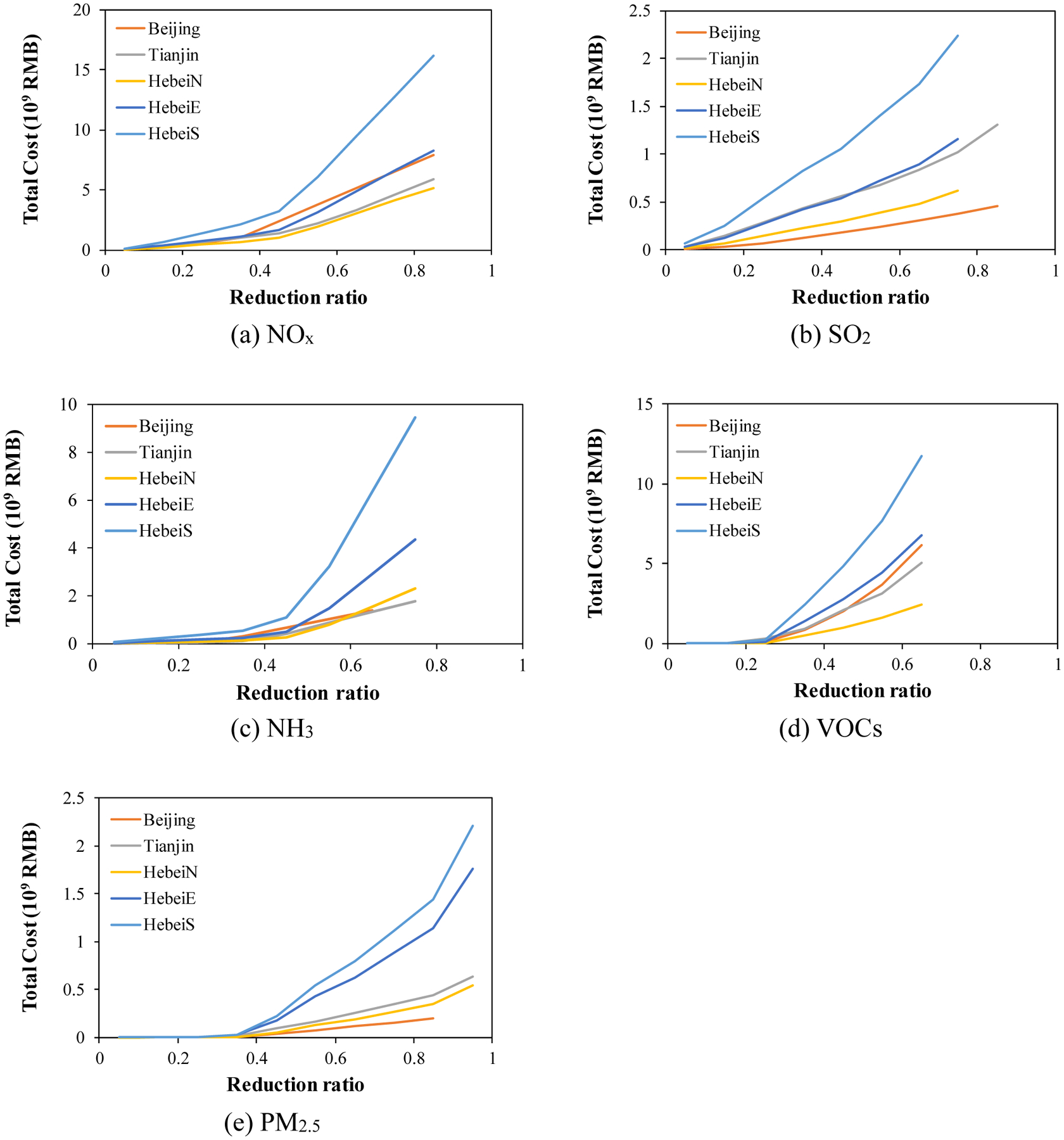
Marginal abatement cost curves of five pollutants in Beijing-Tianjin-Hebei region
The marginal abatement cost curves for all pollutants were further input into the LE-CO to optimize the combination of pollutants. One thing should be noted that the marginal abatement cost curves for each pollutants were calculated individually. Some control technologies can simultaneously reduce multiple pollutants; for instant, vehicles technologies can reduce NOx, VOCs, and primary PM. To avoid double counting issue, the cost for such multiple-pollutant control technology will be included only for the pollutant with the highest application rate (i.e., its cost for other pollutants will be set as zero) in the calculation of total cost with the combination of pollutant controls. To simplify the optimization process in this study, we assumed that the control technologies could be applied in each region independently. Such assumption might lead to an uncertainty when only applying strengthened local controls, since some technology applications need be ensured with corresponding agreement across provinces (e.g., improvement of fuel quality, vehicle standard). However, the uncertainty becomes negligible when regional joint control is applied.
2.3. Response of air quality to emission controls
This study adopted the pf-RSM method, which quantifies the responses of air quality to emission controls with a set of polynomial functions (Xing et al., 2017c). The responses of PM2.5 and O3 concentrations to primary PM emissions exhibits linear behaviors that can be represented through linear regression (Zhao et al., 2017). Thus, the following linear term was added into the pf-RSM to represent the response to primary PM emissions:
| (E11) |
Where ΔConc is the response of O3 and PM2.5 concentrations to changes in individual emissions; EP1 and EP2 are the change ratios of two precursor (P1 and P2 can represent any two of NOx, SO2, NH3, VOCs, or POA) emission related to baseline; EPM is the change ratio of PM emission related to baseline; Ai, , Bi, Ci are the coefficients of terms; the superscript i, j is the degree of precursor; and are the degrees of precursors P1 and P2, respectively; and the superscript b is the total number of interaction terms between P1 and P2 (i.e., multiplied by ).
The term selections for pollutants in pf-RSM were determined in the previous paper (Xing et al., 2017c), and the coefficients of Ai, , Bi, Ci were fitted for daily concentrations of PM2.5 and O3, as well as precursor concentrations of NOx, SO2, NH3, VOCs, and POA required for the five regions of BTH (Beijing, Tianjin, HebeiN, HebeiE, and HebeiS). The selected terms in E11 for PM2.5 and O3 in single-regional RSM are the same as Xing et al (2017c), as summarized in Table 1. Then the single-regional RSMs in five regions was combined together based on the latest extended RSM technique by which the multi-regional interactions are estimated as the sum of three components: 1) local chemistry formation of the pollutant associated with the change in its precursor levels at receptor region; 2) regional transport of the pollutant from source region to receptor region; 3) interregional effects among multiple regions (Xing et al., 2017a). January and July in 2014 were selected to represent winter and summer, respectively. The annual mean of PM2.5 was roughly estimated through averaging these two months. The simulated PM2.5 and O3 concentrations in the pf-RSM were adjusted to be consistent with observations for the purpose of attainment analysis.
Table 1.
The selected terms in the pf-RSM for PM2.5 and O3
| Term | O3 | PM2.5 |
|---|---|---|
| 1 | NOx5 | VOC |
| 2 | NOx4 | NH3 |
| 3 | NOx3 | NH32 |
| 4 | NOx2 | NH33 |
| 5 | NOx | SO2 |
| 6 | VOC | VOC2 |
| 7 | VOC2 | NOxVOC |
| 8 | VOC3 | NOx2VOC |
| 9 | NOxVOC | NOx4VOC |
| 10 | NOxVOC3 | NOxNH3 |
| 11 | NOx5VOC | NOx |
| 12 | NOx2VOC | NOx2 |
| 13 | SO2 | NOx3 |
| 14 | NH3 | NOx4 |
| 15 | Primary PM | Primary PM |
3. Results
3.1. Control pathway design to attain certain air quality goals
The ambient O3 and PM2.5 concentrations are contributed by multiple pollutants, therefore various combinations of pollutant controls can achieve the O3 and PM2.5 target, as list in Table 1. All of the scenarios can be one candidate to attain the air quality goals as PM2.5 less than 35 μg/m3 and O3 less than 100 ppb in Beijing. The emission reduction rate varies largely for all pollutants as NOx, SO2 and NH3 from 5% to 95%, VOCs from 15% to 85%, primary PM from 55% to 95%, suggesting that there are multiple choices to attain certain air quality goals without consideration of control cost. For example, small reduction of NOx (5%) can be compensated by large VOCs reduction (85%) for O3 target as shown in Scenario 1, while part of VOCs reduction (70%) can also be replaced by substantial reduction of NOx (95%) as shown in Scenario 16. Moderate primary PM controls (55%) requires large reductions in SO2 (85%) and NH3 (95%) in Scenario 2, while more aggressive controls of primary PM (95%) can loosen the controls on SO2 (5%) and NH3 (65%) as shown in Scenario 11. However, the control over 95% is unrealistic since it either exceeds the maxima reduction potentials or has extremely large cost. Optimization of the pollutant control combinations is necessary for maker more achievable policy.
Through the LE-CO, we defined and compared four types of optimized control combinations of pollutants to attain the ambient air quality targets. Beijing was selected as one example in Figure 3. The four types are as follows: (1) To only meet the PM2.5 target with no NH3 control (Figure 3a); (2) to only meet the PM2.5 target but with NH3 control (Figure 3b); and (3) to meet both PM2.5 and O3 targets with NH3 controls (Figure 3c). Moderate to strengthened PM2.5 targets were selected from 60 to 35 μg m−3, whereas only one O3 target was selected and set to 100 ppb. The controls were designed to be measured across the whole BTH region (i.e., the reduction in other regions of BTH was assumed to be the same as the target region).
Figure 3.

Selected control pathways and their effectiveness to achieve certain PM2.5 and O3 targets in Beijing (a: only PM2.5 target with no NH3 control; b: only PM2.5 target but with NH3 control; c: both PM2.5 and O3 targets)
In Figure 3a–b, where only the PM2.5 target was considered, the controls on primary PM and SO2 emissions were the dominant selection (greater than 50% reduction) to achieve moderate PM2.5 targets (i.e., greater than 40 μg m−3) because of their lower control costs compared with other pollutants. Under strengthened targets (i.e., PM2.5 lower than 40 μg m−3), controls on other pollutants including VOCs, NOx, and NH3 could be partially considered. The difference between Figure 3a and Figure 3b is the choice on NH3 controls; NH3 can be observed to be a candidate for achieving PM2.5 targets through replacing substantial reductions in NOx and VOCs. Considering NH3 controls might be a cost-efficient method of achieving PM2.5 targets because the cost in Figure 3a is lower than in Figure 3b. However, they might not be helpful in reducing O3, which is shown in the control on O3 in Figure 3b not being as effective as in Figure 3a. In Figure 3a, the O3 and PM2.5 are simultaneously reduced because of substantial controls on their common precursors (i.e., NOx and VOCs). However, in Figure 3b, the NH3 control replaces NOx and partial VOCs controls, leading to a comparatively lower reduction in O3.
In Figure 3c, where the O3 target (< 100 ppb) is also considered, the NOx and VOCs controls are critical even at a moderate level of PM2.5 targets. The O3 target can be achieved through reducing NOx by 85% and VOCs by 55%, which also benefits PM2.5 target attainment. The control on primary PM (approximately 55%) is smaller than in Figure 3a–b because it was partially replaced with the controls on NOx and VOCs, but also results significantly affect cost; the control cost of NOx and VOCs is much higher than for primary PM and SO2. Meanwhile, although NH3 control is a cost-efficient method of achieving stricter PM2.5 targets, the NH3 control is not selected because of strengthened controls of NOx and VOC for O3 attainment in Figure 3c. Interesting finding is that, when PM2.5 target becomes stricter from 40 μg m−3 to 35 μg m−3, the least-cost optimization process leads to an enhanced reduction in SO2 from 35% to 75% and VOCs from 25% to 55%, but a loosen reduction in NOx control which is reduced from 85% to 75%. That indicates the control rate of certain pollutant may not be monotonously increasing along with the strengthening of air quality target due to the nonlinearities of the cost and air quality response.
3.2. Apportionment of control cost and effectiveness
Achieving PM2.5 and O3 targets in Beijing requires joint controls on multiple pollutants across the BTH region. To explore the control efficiency of certain pollutants and regional sources, we apportioned cost and control effectiveness. Figure 4 estimates and displays the share of cost and effectiveness for the suggested control strategy for achieving both PM2.5 and O3 targets in Beijing. The reduced rates of NOx, SO2, NH3, VOCs, and primary PM are 75%, 75%, 5%, 55%, and 85%, respectively in all regions. Combined with the marginal cost curves, the cost of reductions in individual sources are compared in Figure 4a. The total cost is largely dominated by the NOx and VOCs controls, even though their reduction rates are no greater than SO2 and primary PM. The cost of reductions in HebeiS is the highest of all regions because HebeiS is responsible for the most emissions (Zhao et al., 2017). Although the target region is Beijing, the shared costs in Beijing are lower than the shared costs outside.
Figure 4.
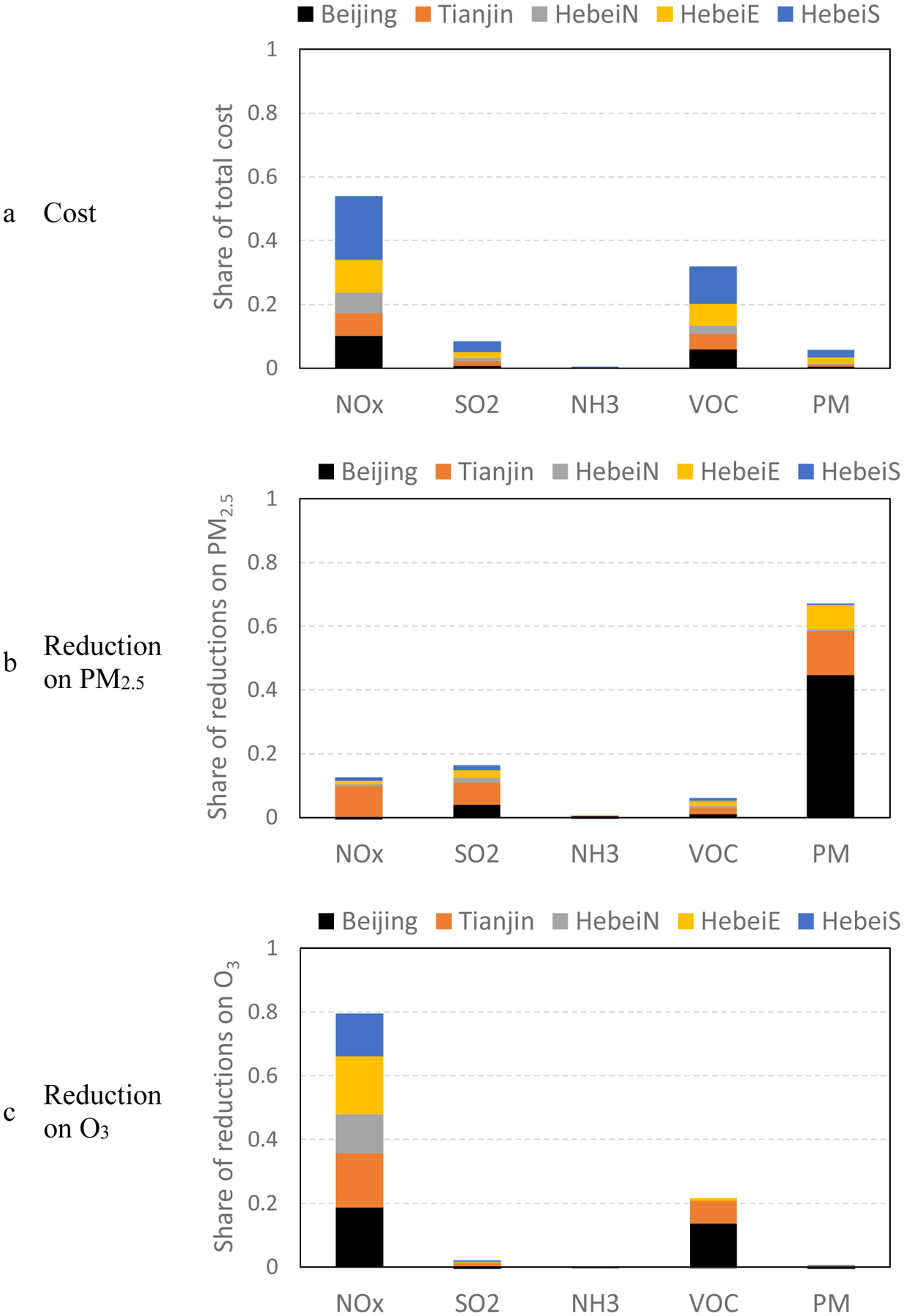
Share of cost and effectiveness for the control strategy (the reduced rates of NOx, SO2, NH3, VOCs, and PM are 75%, 75%, 5%, 55%, and 85%, respectively) to achieve both PM2.5 (monthly averaged concentration less than 35 μg m−3) and O3 targets (daily maxima hourly concentration less than 100 ppb) in Beijing
The primary PM control accounts for the largest share of reductions in PM2.5, followed by SO2, VOCs, and NOx (see Figure 4b). Considering its smaller share of cost, primary PM control is the most cost-efficient method of reducing PM2.5. The primary PM controls are mostly through local reduction; whereas for gaseous pollutants (SO2, NOx, and VOCs), greater effectiveness is displayed in regional controls, particularly in Tianjin.
The reduction in O3 was because of NOx and VOCs controls (see Figure 4c). The share of contributions from controls on regional sources (70%) is larger than the share from local controls (30%), which indicates the importance of joint controls on regional sources, particularly for NOx. Moreover, controls on emission sources from Tianjin (25%) and HebeiE (20%) contribute considerable shares of effectiveness in O3 reduction in Beijing.
3.3. Atmospheric environmental capacity and overloading rate
In this study, the atmospheric environmental capacity is defined as the maxima emission allowance reaching the ambient air quality standards of PM2.5 and O3, which corresponds to the 24-hour mean PM2.5 and 1-hour maxima O3 being 35 μg m−3 and 100 ppb, respectively. From our previous discussion, we estimated that the optimized control pathway to achieve the PM2.5 and O3 targets in Beijing is to reduce NOx, SO2, NH3, VOCs, and primary PM by 75%, 75%, 5%, 55%, and 85%, respectively, across the whole BTH region (i.e., each region benefits from the joint controls). The emissions of NOx, SO2, NH3, VOCs, and primary PM in Beijing are 197.0, 78.0, 52.2, 357.7, and 47.8 kt yr−1. Thus, the emissions of NOx, SO2, NH3, VOCs, and primary PM after reductions required to meet the PM2.5 and O3 targets (i.e., atmospheric environmental capacity) were calaulated to be 49.3, 19.5, 49.6, 161.0 and 7.2 kt yr−1, respectively, in Beijing. The current overloading rates of NOx, SO2, NH3, VOCs and primary PM are the ratios of atmospheric environmental capacity to current emissions, which are 4.0, 4.0, 1.1, 2.2, and 6.7, respectively.
The largest overloaded pollutant is primary PM considering its greater control effectiveness and lower cost, which suggests substantial potential in reducing primary PM emissions. NH3 presents a small overloaded rate because its less effectiveness in reducing O3; however, NH3 controls could help to achieve stricter PM2.5 targets when controls of NOx and VOC are limited and their costs become exteremly high.
3.4. Optimized combination between local and regional controls
To further investigate the combination of local and regional controls, the cost curves to achieve different PM2.5 and O3 targets were estimated from the LE-CO. In Beijing, as shown in Figure 5, large variations in cost exist among five types of combined local and regional controls based on the ratios of local to regional reduction: (1) local to regional control is 1:1 (L:R = 1:1), representing that the same reduction rate is applied to local and regional sources; (2) local to regional control is 1:0.75 (L:R = 1:0.75), representing that the regional reduction rate is 75% of the local reduction rate; (3) local to regional control is 1:0.5 (L:R = 1:0.5), representing that the regional reduction rate is half of the local reduction rate; (4) local to regional control is 0.5:1 (L:R = 0.5:1), representing that the regional reduction rate is twice the local reduction rate; and (5) local to regional control is 1:0 (L:R = 1:0), representing that only local reductions are considered.
Figure 5.

Combination of multi-regional controls to achieve PM2.5 and O3 targets separately in Beijing (black line (L:R = 1:1) represents that the same reduction rate is applied in local and regional sources; dark blue line (L:R = 1:0.75) represents that the regional reduction rate is 75% of the local reduction rate; green line (L:R = 1:0.5) represents that the regional reduction rate is half of the local reduction rate; light blue line (L:R = 0.5:1) represents that the regional reduction rate is twice the local reduction rate; red line (L:R = 1:0) represents that only local reductions are considered, the secondary X-axis indicates the share of cost in GDP in 2014 GDP of Beijing–Tianjin–Hebei region)
As the PM2.5 target is strengthened, the cost increases in all cases (Figure 5a). Under moderate PM2.5 targets (i.e., 45–80 μg m−3), the cases with higher ratio of local controls (i.e., L:R = 1:0.5 and 1:0.75) cost less than the case with a higher ratio of regional controls (i.e., L:R = 0.5:1). This is because local reduction is more effective at reducing local pollution than regional reduction, presenting a cost–efficient method of reducing certain amount of pollution. However, when the PM2.5 target becomes stricter (i.e., <45 μg m−3), the case with an equal rate of local and regional controls (i.e., L:R = 1:1) costs less than the others. This is because the marginal cost of further reducing local pollution becomes equal or even higher than reducing regional sources. In addition, the cases with no or limited regional controls cannot achieve the most strengthened PM2.5 target (i.e., L:R = 1:0).
Similar to PM2.5, the local controls for O3 (Figure 5b) tend to be more cost–efficient under mild and moderate O3 targets (i.e., > 104ppb). When the O3 target is strengthened (< 100 ppb), the cases with an equal rate of local and regional controls (i.e., L:R = 1:1) cost less than the others and also can achieve more strengthened O3 target (i.e., <95 ppb). The cost for reducing O3 is much higher than reducing PM2.5 due to the high cost associated with NOx and VOC controls, and it will take more than 1% of the GDP in BTH to achieve strengthened O3 target (i.e., <90ppb).
We found similar results for the other four regions in BTH (Supplementary Information), except for the case with a higher ratio of regional controls (i.e., L:R = 0.5:1) in HeibeiE which tends to be slightly more effective in reducing O3 due to greater effectiveness in regional controls than local controls. Our findings indicate that local reduction has priorities for attaining moderate PM2.5 and O3 targets. However, to achieve more aggressive targets, the same level of reductions must be conducted across the whole BTH region.
3.5. Sensitivities of optimization to the variation of control costs
The cost of controls largely determines the shares of reductions among the five pollutants. The sensitivity of optimization to control cost was analyzed to understand the robustness of the optimization to variations in control cost, which is likely to happen in the future because of the evolution of control technologies as well as the changes in the economic structure and air control policy. With LE-CO, we calculated the responses of the optimized control strategy to achieve both PM2.5 (less than 35 μg m−3) and O3 (less than 100 ppb) targets in Beijing to a wide range of perturbations of cost from 10−10 to 1010 times as much as the current cost level. Optimization based on current cost estimation suggested that the reduced rates of NOx, SO2, NH3, VOCs and PM should be 75%, 75%, 5%, 55%, and 85%, respectively. When the cost of certain pollutants changed from 10−10 to 1010 times the current level, its reduced rate increases or decreases, as displayed in Figure 6.
Figure 6.
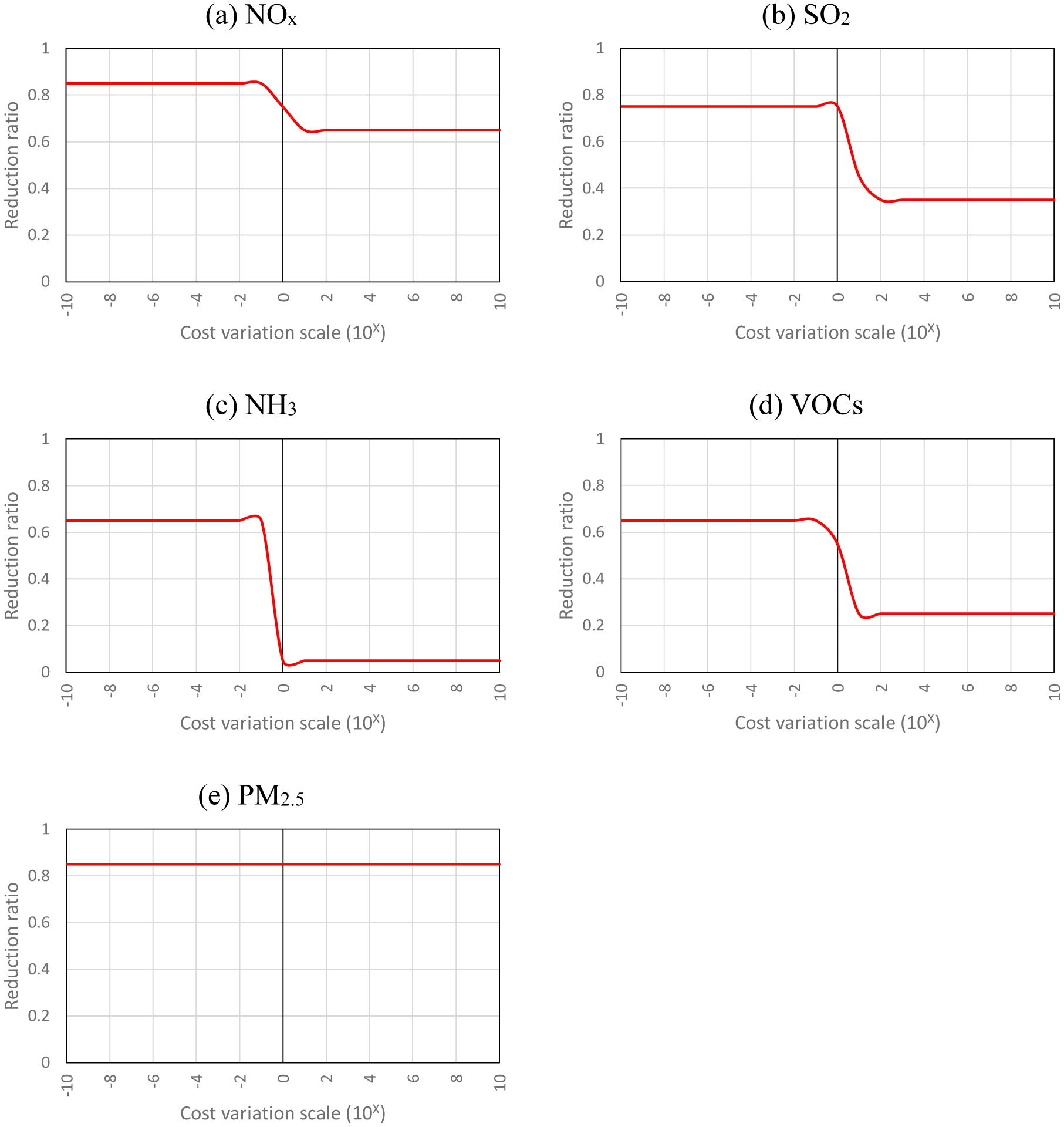
Sensitivities of reduction ratios of five pollutants to the variation of control costs to attain air quality targets of both PM2.5 (less than 35 μg m−3) and O3 (less than 100 ppb) in Beijing
For NOx, when the perturbation of cost is within the range of 0.1 to 10 times the current level, it remains at the current optimized rate of 75%. The share of NOx controls increases to the maxima reduction ratio of 85% when the cost becomes lower than 0.01 times the current level. In contrast, when the cost varies to larger than 100, it will be replaced by reducing other pollutants. The share of NOx controls is at least 65% for O3 target achievement.
VOCs exhibit similar result to NOx. It remains at the current optimized rate of 55% when the perturbation of cost is within the range of 0.1 to 10 times the current level. When the cost varies to larger than 100, the share of VOCs controls reduced to the least as 25%.
For SO2, the current optimized reduction rate remains at 75% when the cost becomes lower than the current level. If the cost of SO2 increases in the future, the reduced rate of SO2 will decrease to 35%.
The current cost of NH3 seems too high for application, and thus its control is currently limited. However, if the cost of NH3 control reduces to 0.1 time the current level, the reduction rate will increase to 65%.
The current cost level of PM2.5 is low, and thus the current optimized reduced rate of PM2.5 is 85%. Even though the cost of PM2.5 increased by 1010, it still maintains 85% reduction rate, indicating the importance of control on primary PM emissions.
Noteworthily, we only considered the variation in control cost for each pollutant individually. The simultaneous change of cost (i.e., the relative value of control cost of all pollutants kept the same) does not affect the order of priorities in the pollutant control selection.
4. Conclusion
This study developed a module for least-cost control strategy optimization and designed control pathways to attain certain air quality goals for PM2.5 and O3 in the BTH region. The optimization of combined controls is determined using the marginal abatement cost curves for each pollutant in each region and the response of air quality to certain emission control strategies. The results suggest that local primary PM control was the most cost-efficient method of reducing PM2.5.NH3 controls may be cost-efficient in achieving strengthened PM2.5 target but may not be helpful in reducing O3. In addition, the NH3 controls require targeting completely different sectors (i.e., agriculture and livestock) from other pollutants that mostly related to energy consumptions, thus increasing the complexity in control actions or stakeholder engagement in implementing the regulation. Regional controls exhibit greater effectiveness for O3 attainment, while same level of reductions in local and regional sources are recommended to achieve more aggressive air quality goals. Besides, the regional joint control becomes more important in the consideration of some control technologies that can only be implemented nationwide.
Uncertainties associated with the cost and air quality response to emissions will influence on the results of optimization. For cost estimations, uncertainties exist in this study because of the lack of local information about control cost and efficiency. Future investigation into the detailed costs are necessary to obtain an accurate estimation of control costs. The response of air quality to emission controls in this study was developed based on the Community Multi-scale Air Quality (CMAQ) Modeling System (version 5.0.1). To improve the simulation of SOA, we replaced the treatment of organic aerosols in the AERO6 aerosol module with the two-dimensional volatility basis set framework. This significantly increased the transition rate of VOCs to SOA, resulting in an increased contribution to PM2.5 from VOCs emissions, which tends to be underestimated in the basic version of CMAQ v5.0.1. However, uncertainties in modeling PM2.5 remain substantial enough to effect the response of air quality to emission reduction, and thus influence the optimization of control strategy. For example, recent studies have suggested that NO2 and NH3 plays a critical role in sulfate aerosol formation (He et al., 2014; Cheng et al., 2016; Wang et al., 2016), which has not been addressed well in current modeling work. Further improvements in the atmospheric modeling of secondary aerosols are crucial for improving the accuracy of control policy design.
Supplementary Material
Table 2.
Potential candidates to meet the PM2.5 and O3 target achievement* in Beijing
| Scenario | NOx | SO2 | NH3 | VOCs | Primary PM |
|---|---|---|---|---|---|
| 1 | 5% | 85% | 95% | 85% | 55% |
| 2 | 5% | 65% | 25% | 75% | 85% |
| 3 | 65% | 45% | 65% | 65% | 85% |
| 4 | 65% | 25% | 75% | 65% | 85% |
| 5 | 65% | 75% | 95% | 65% | 65% |
| 6 | 85% | 95% | 5% | 25% | 85% |
| 7 | 75% | 55% | 65% | 55% | 85% |
| 8 | 85% | 65% | 65% | 35% | 85% |
| 9 | 85% | 35% | 65% | 65% | 85% |
| 10 | 85% | 15% | 75% | 65% | 85% |
| 11 | 85% | 5% | 65% | 35% | 95% |
| 12 | 85% | 75% | 75% | 65% | 75% |
| 13 | 85% | 75% | 5% | 45% | 85% |
| 14 | 85% | 75% | 55% | 35% | 85% |
| 15 | 85% | 75% | 65% | 25% | 85% |
| 16 | 95% | 55% | 5% | 15% | 85% |
based on LE-CO; PM2.5 -target: monthly averaged concentration less than 35 μg m−3; O3-target: daily maxima hourly concentration less than 100 ppb
Highlights.
A module of least-cost control strategy optimization was developed for air quality attainment
Local primary PM control was the most cost-efficient method of reducing PM2.5
NH3 controls may be cost-efficient in achieving strengthened PM2.5 target
Regional controls exhibit greater effectiveness for O3 attainment
Same level of reductions in local and regional sources are recommended to achieve more aggressive air quality goals
Acknowledgements
This work was supported in part by National Science Foundation of China (51861135102), National Research Program for Key Issues in Air Pollution Control (DQGG0301), Strategic Pilot Project of Chinese Academy of Sciences (XDB05030401) and National Key Technology R&D Program (2014BAC06B05, 2016YFC0207601). This work was completed on the “Explorer 100” cluster system of Tsinghua National Laboratory for Information Science and Technology.
Footnotes
Supporting Information Available
Combination of multi-regional controls to achieve PM2.5 and O3 targets in 5 regions are shown in supplementary information.
Reference
- Amann M, Bertok I, Borken-Kleefeld J, Cofala J, Heyes C, Höglund-Isaksson L, Klimont Z, Nguyen B, Posch M, Rafaj P and Sandler R, 2011a. Cost-effective control of air quality and greenhouse gases in Europe: Modeling and policy applications. Environmental Modelling & Software, 26(12), pp.1489–1501. [Google Scholar]
- Amann M, Bertok I, Borken-Kleefeld J, Cofala J, Heyes C, Höglund-Isaksson L, Klimont Z, Rafaj P, Schöpp W and Wagner F, 2011b. Cost-effective emission reductions to improve air quality in Europe in 2020: Analysis of policy options for the EU for the revision of the Gothenburg Protocol.
- Amann M, Johansson M, Lükewille A, Schöpp W, ApSimon H, Warren R, Gonzales T, Tarrason L and Tsyro S, 2001. An integrated assessment model for fine particulate matter in Europe. Water, Air, and Soil Pollution, 130(1–4), pp.223–228. [Google Scholar]
- Amann M, Kejun J, Jiming HAO, Wang S, Xing Z, Xiang DY, Hong L, Xing J, Zhang C, Bertok I and Borken-Kleefeld J, 2008. GAINS Asia. Scenarios for cost-effective control of air pollution and greenhouse gases in China.
- An X, Zuo H and Chen L, 2007. Atmospheric environmental capacity of SO 2 in winter over Lanzhou in China: a case study. Advances in Atmospheric Sciences, 24(4), pp.688–699. [Google Scholar]
- Carnevale C, Finzi G, Pisoni E, Volta M, Guariso G, Gianfreda R, Maffeis G, Thunis P, White L and Triacchini G, 2012. An integrated assessment tool to define effective air quality policies at regional scale. Environmental Modelling & Software, 38, pp.306–315. [Google Scholar]
- Cass GR and McRae GJ, 1981. Minimizing the cost of air pollution control. Environmental Science & Technology, 15(7), pp.748–757. [DOI] [PubMed] [Google Scholar]
- Cheng Y, Zheng G, Wei C, Mu Q, Zheng B, Wang Z, Gao M, Zhang Q, He K, Carmichael G and Pöschl U, 2016. Reactive nitrogen chemistry in aerosol water as a source of sulfate during haze events in China. Science advances, 2(12), p.e1601530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohan DS, et al. Nonlinear response of ozone to emissions: source apportionment and sensitivity analysis. Environ. Sci. Technol 39, 2005, 6739–6748. [DOI] [PubMed] [Google Scholar]
- Cohan DS, Tian D, Hu Y and Russell AG, 2006. Control strategy optimization for attainment and exposure mitigation: Case study for ozone in Macon, Georgia. Environmental management, 38(3), pp.451–462. [DOI] [PubMed] [Google Scholar]
- Fu JS, Brill DE Jr and Ranjithan RS, 2006. Conjunctive use of models to design cost-effective ozone control strategies. Journal of the Air & Waste Management Association, 56(6), pp.800–809. [DOI] [PubMed] [Google Scholar]
- Fu X, Wang S, Xing J, Zhang X, Wang T and Hao J, 2017. Increasing Ammonia Concentrations Reduce the Effectiveness of Particle Pollution Control Achieved via SO2 and NO X Emissions Reduction in East China. Environmental Science & Technology Letters.
- Harley RA, Hunts SE and Cass GR, 1989. Strategies for the control of particulate air quality: Least-cost solutions based on receptor-oriented models. Environmental science & technology, 23(8), pp.1007–1014. [Google Scholar]
- He H, Wang Y, Ma Q, Ma J, Chu B, Ji D, Tang G, Liu C, Zhang H and Hao J, 2014. Mineral dust and NOx promote the conversion of SO2 to sulfate in heavy pollution days. Scientific reports, 4, p.4172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heyes C, et al. A model for optimizing strategies for controlling ground-level ozone in Europe. Interim Report IR-97–002; 1997.
- Huang RJ, Zhang Y, Bozzetti C, Ho KF, Cao JJ, Han Y, Daellenbach KR, Slowik JG, Platt SM, Canonaco F and Zotter P, 2014. High secondary aerosol contribution to particulate pollution during haze events in China. Nature, 514(7521), p.218. [DOI] [PubMed] [Google Scholar]
- Li J, Lu K, Lv W, Li J, Zhong L, Ou Y, Chen D, Huang X and Zhang Y, 2014. Fast increasing of surface ozone concentrations in Pearl River Delta characterized by a regional air quality monitoring network during 2006–2011. Journal of Environmental Sciences, 26(1), pp.23–36. [DOI] [PubMed] [Google Scholar]
- LI WH, CHEN J, WANG FQ and MAO MC, 2013. Estimation of the Atmospheric Environmental Capacity and Remaining Capacity in Xi’an City Based on Amending A-value Method [J]. Safety and Environmental Engineering, 4, p.017. [Google Scholar]
- Nianlei LIU, Yaling LU, Hongqiang JIANG and Xi CHENG, 2017. Environmental carrying capacity evaluation methods and application based on environmental quality standards. PROGRESS IN GEOGRAPHY, 36(3), pp.296–305. [Google Scholar]
- Pinder RW, Adams PJ and Pandis SN, 2007. Ammonia emission controls as a cost-effective strategy for reducing atmospheric particulate matter in the eastern United States. [DOI] [PubMed]
- Purohit P, Amann M, Mathur R, Gupta I, Marwah S, Verma V, Bertok I, Borken-Kleefeld J, Chambers A, Cofala J and Heyes C, 2010. Gains Asia: Scenarios for cost-effective control of air pollution and greenhouse gases in India.
- Sun J, Schreifels J, Wang J, Fu JS and Wang S, 2014. Cost estimate of multi-pollutant abatement from the power sector in the Yangtze River Delta region of China. energy policy, 69, pp.478–488. [Google Scholar]
- Tsimpidi AP, et al. Response of Fine Particulate Matter to Emission Changes of Oxides of Nitrogen and Anthropogenic Volatile Organic Compounds in the Eastern United States, J. Air & Waste Manage. Assoc 2008, 58:1463–1473, DOI: 10.3155/1047-3289.58.11.1463 [DOI] [PubMed] [Google Scholar]
- Wang G, Zhang R, Gomez ME, Yang L, Zamora ML, Hu M, Lin Y, Peng J, Guo S, Meng J and Li J, 2016. Persistent sulfate formation from London Fog to Chinese haze. Proceedings of the National Academy of Sciences, 113(48), pp.13630–13635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Zhao B, Wang S, Yang F, Xing J, Morawska L, Ding A, Kulmala M, Kerminen VM, Kujansuu J and Wang Z, 2017. Particulate matter pollution over China and the effects of control policies. Science of the Total Environment. [DOI] [PubMed]
- Wang SX, Xing J, Jang C, Zhu Y, Fu JS, Hao J Impact assessment of ammonia emissions on inorganic aerosols in east China using response surface modeling technique. Environ. Sci. Technol 2011, 45, 9293–9300. [DOI] [PubMed] [Google Scholar]
- Winiwarter W and Klimont Z, 2011. The role of N-gases (N 2 O, NO x, NH 3) in cost-effective strategies to reduce greenhouse gas emissions and air pollution in Europe. Current opinion in environmental sustainability, 3(5), pp.438–445. [Google Scholar]
- Wu D, Xu Y and Zhang S, 2015. Will joint regional air pollution control be more cost-effective? An empirical study of China’s Beijing–Tianjin–Hebei region. Journal of environmental management, 149, pp.27–36. [DOI] [PubMed] [Google Scholar]
- Xing J, Wang SX, Jang C, Zhu Y, Hao JM Nonlinear response of ozone to precursor emission changes in China: a modeling study using response surface methodology. Atmos. Chem. Phys 2011, 11, 5027–5044. [Google Scholar]
- Xing J, Wang S, Zhao B, Wu W, Ding D, Jang C, Zhu Y, Hao J Quantifying Nonlinear Multiregional Contributions to Ozone and Fine Particles Using an Updated Response Surface Modeling Technique. Environmental science & technology, 51(20), 11788–11798., 2017a. [DOI] [PubMed] [Google Scholar]
- Xing J, Wang S, Jang C, Zhu Y, Zhao B, Ding D, Wang J, Zhao L, Xie H, Hao J ABaCAS: an overview of the air pollution control cost-benefit and attainment assessment system and its application in China. The Magazine for Environmental Managers - Air & Waste Management Association 2017b, April. [Google Scholar]
- Xing J, Ding D, Wang S, Zhao B, Jang C, Wu W, Zhang F, Zhu Y, and Hao J: Quantification of the enhanced effectiveness of NOx control from simultaneous reductions of VOC and NH3 for reducing air pollution in the Beijing–Tianjin–Hebei region, China, Atmos. Chem. Phys, 18, 7799–7814, 10.5194/acp-18-7799-2018, 2018. [DOI] [Google Scholar]
- Xue WB, Fu F, Wang JN, He KB, Lei Y, Yang JT, et al. Modeling study on atmospheric environmental capacity of major pollutants constrained by PM2.5 compliance of Chinese cities. China Environmental Science. 2014; 34(10): 2490–2496. (in Chinese) [Google Scholar]
- Zhang F, Xing J, Zhou Y, Wang S, Jang C, Zhu Y, Hao J: Estimation of air pollution emission abatement potential and cost curves in China, in preparation
- Zhao B; Wang S; Donahue NM; Chuang W; Hildebrandt Ruiz L; Ng NL; Wang Y; Hao J Evaluation of one-dimensional and two-dimensional volatility basis sets in simulating the aging of secondary organic aerosols with smog-chamber experiments, Environ. Sci. Technol 49, 2245–2254, DOI 10.1021/es5048914, 2015. [DOI] [PubMed] [Google Scholar]
- Zhao B; Wang SX; Xing J; Fu K; Fu JS; Jang C; Zhu Y; Dong XY; Gao Y; Wu WJ; Wang JD Assessing the nonlinear response of fine particles to precursor emissions: development and application of an extended response surface modeling technique v1.0. Geosci. Model Dev 2015, 8, 115–128. [Google Scholar]
- Zhao B; Wu W; Wang S; Xing J; Chang X; Liou K-N; Jiang JH; Gu Y; Jang C; Fu JS; Zhu Y; Wang J; Hao J A modeling study of the nonlinear response of fine particles to air pollutant emissions in the Beijing-Tianjin-Hebei region, Atmos. Chem. Phys. Discuss, 10.5194/acp-2017-428, in press, 2017. [DOI]
- Zhao B; Wu W; Wang S; Xing J; Chang X; Liou K-N; Jiang JH; Gu Y; Jang C; Fu JS; Zhu Y; Wang J; Hao J A modeling study of the nonlinear response of fine particles to air pollutant emissions in the Beijing-Tianjin-Hebei region, Atmos. Chem. Phys, 2017.
- Zhou Y and Zhou J, 2017. Urban atmospheric environmental capacity and atmospheric environmental carrying capacity constrained by GDP–PM 2.5. Ecological Indicators, 73, pp.637–652 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


