Learning a Gradient Guidance for Spatially Isotropic MRI Super-Resolution Reconstruction

Abstract

In MRI practice, it is inevitable to appropriately balance between image resolution, signal-to-noise ratio (SNR), and scan time. It has been shown that super-resolution reconstruction (SRR) is effective to achieve such a balance, and has obtained better results than direct high-resolution (HR) acquisition, for certain contrasts and sequences. The focus of this work was on constructing images with spatial resolution higher than can be practically obtained by direct Fourier encoding. A novel learning approach was developed, which was able to provide an estimate of the spatial gradient prior from the low-resolution (LR) inputs for the HR reconstruction. By incorporating the anisotropic acquisition schemes, the learning model was trained over the LR images themselves only. The learned gradients were integrated as prior knowledge into a gradient-guided SRR model. A closed-form solution to the SRR model was developed to obtain the HR reconstruction. Our approach was assessed on the simulated data as well as the data acquired on a Siemens 3T MRI scanner containing 45 MRI scans from 15 subjects. The experimental results demonstrated that our approach led to superior SRR over state-of-the-art methods, and obtained better images at lower or the same cost in scan time than direct HR acquisition.

1. Introduction

It is inevitable to deal with the trade-off between image resolution, signal-to-noise ratio (SNR), and scan time, in magnetic resonance imaging (MRI) practice [1]. Images of higher resolution provide more details, and correspondingly increase the scan time. Higher SNR renders the signals of interest better from noise contamination. According to MRI physics, SNR is proportional to slice thickness and scan time. In pursuit of higher SNR, however, thick slices lower image resolution, while long scans discomfort subjects and potentially lead to subject motion during the acquisition, which adversely affects image quality. Literature has shown many effective methods to acquire images of high resolution, high SNR, and low scan time, such as parallel imaging [15] and robust K-space sampling [12]. Among these methods, super-resolution reconstruction (SRR) has recently been demonstrated to be capable of obtaining better images than direct high-resolution (HR) acquisition, for certain image contrasts and sequences, such as T₂ weighted images [13]. As a result, SRR has become one of the most widely used methods that acquire MR images of high quality.

The idea of SRR originated in [19] for natural images where multiple low-resolution (LR) images were combined into an HR reconstruction. Extensive methods expanded this idea and achieved various SRR schemes in MRI [14,16]. Recently, deep learning-based methods have achieved impressive results for 2D natural images [5]. These 2D learning models were directly applied to 3D MRI volumes by means of slice-by-slice processing [8,23]. However, by the nature that MRI volumes reveal anatomical structures in 3D space, it is straightforward to learn 3D models for capturing richer knowledge. It has been shown that 3D models outperformed their 2D counterparts in MRI [3,11]. To this end, extensive 3D learning models were developed [2–4,11,20]. Unfortunately, these 3D models required large-scale training datasets, that contain HR labels that are practically difficult to obtain at excellent SNR due to subject motion, to learn the patterns mapping from LR to HR images. Although few datasets are publicly available, there is no known theory that indicates a satisfactory amount of training data has been incorporated in the training process. Furthermore, since the LR inputs were manually generated as blurred images, the learned function may be brittle when faced with data from a different scanner or with different intensity properties.

In this work, we aimed at developing the learning model that is not subject to the above limitations. Instead of learning end-to-end mappings from LR to HR images, we turned to learn the inherent structure of the HR reconstruction, and then as prior knowledge the learned structure was incorporated in a forward model-based SRR framework. To this end, we targeted the spatial image gradients in the learning, since they can be equivalently decomposed from 3D space onto 2D space, and correspondingly the required amount of training data was substantially reduced. More importantly, by incorporating the anisotropic acquisition schemes, our learning model was trained over the LR images themselves only, as the training data consisted of the pairs of an in-plane HR slice of an LR image and a through-plane LR slice of another LR image. A gradient-guided SRR framework [17] was leveraged to incorporate the learned gradients for the HR reconstruction.

The SRR method [17] used the gradients of LR images as HR gradient estimates. An LR image containing n_s slices can provide n_s accurate HR gradients for the HR reconstruction containing N_s slices, as the n_s slices are in-plane HR. Since the upscale factor N_s/n_s is often 4 or 5 in practice, 75–80% gradients in [17] had to be estimated from interpolated slices. The interpolation led to blurry or displaced image edges, and thus resulted in less accurate gradient localization. In this work, we aimed at improving the localization accuracy of those 75–80% gradients. We used a CNN to learn over the n_s in-plane HR slices the patterns mapping from LR slices to HR gradients, enabled by a strategy that is able to decompose a 3D gradient onto 2D space. The learned patterns were used to infer the HR gradients over the rest N_s −n_s slices. As high frequencies were gained in the inference, improved gradient localization was achieved, compared to [17], and thus increased the quality of deblurring done in the SRR. In addition, a closed-form solution to the SRR model was developed, instead of an iterative optimization algorithm used in [17] that may be stuck in local optima.

2. Methods

2.1. Gradient-Guided Framework

Given n LR images ${\left\{{\mathcal{Y}}_k\right\}}_{k=1}^n$, acquired from n scans with arbitrary orientations and displacements, the forward model over the HR image $\mathcal{X}$, which describes the MRI acquisition process, is formulated as

$$y_k=D_k{H}_k{T}_{k}x+{\mu }_k,$$ (1)

where x and y_k are the column vectors of their volumetric forms $\mathcal{X}$ and ${\mathcal{Y}}_k$ in a lexicographical order of voxels; T_k denotes a rigid transform that characterizes subject motion between scans; H_k denotes a point spread function (PSF); D_k denotes a downsampling operator; μ_k denotes the noise in the acquisition. According to [7], μ_k can be assumed to be additive and Gaussian when SNR > 3. As the problem defined by the forward model is ill-posed, prior knowledge is commonly used, known as the regularization, to restrict the HR estimate. By incorporating the gradient guidance regularization [17], the SRR is achieved by

$$\underset{\mathbf{x}}{\text{min}}\sum _{k=1}^n{\Vert D_k{H}_k{T}_{k}x-y_k\Vert }_2^2+\lambda \sigma (\nabla x-g),$$ (2)

where g denotes the gradient guidance for the HR estimate x, ∇ computes the spatial gradient, σ (·) penalizes the difference between the actual gradient and the guidance, and λ > 0 balances between the data fidelity and the regularization.

2.2. Gradient Guidance Learning

As shown in Eq. (2), the accuracy of the gradient guidance estimate g is critically important to the quality of the HR reconstruction x. Thanks to the fact that a 3D gradient can be decomposed onto 2D space, we are able to compute the gradient of a volume slice by slice. Specifically, the 3D gradient ${\nabla }_d^{s}x$ at a scale s in direction d ∈ {x, y, z,−x,−y,−z} is computed from

$${\nabla }_d^{s}x=\left(I-{\mathbf{\Psi }}_d^s\right)x=\prod _{k=1}^N\left(I-S_d^{s,k}\right)x,$$ (3)

where I denotes an identity matrix, ${\Psi }_d^s$ shifts a volume circularly by s voxels in direction d, and $S_d^{s,k}$ shifts the k-th slice circularly by s pixels in direction d.

Architecture of the Learning Model.

By the above decomposition, the gradient guidance is learned over slices by a convolutional neural network (CNN). The overview of our proposed learning model is shown in Fig. 1. The CNN takes as input 2D LR image patches, and outputs the 2D gradients of HR image patches. ℓ₂-loss is used to minimize the difference between the gradient of k-th HR patch $p_H^k$ and the CNN’s output for the k-th inputted LR patch $p_L^k$:

$$\underset{\theta }{\text{min}}\sum _k{\Vert \nabla p_H^k-f_{\theta }\left(p_L^k\right)\Vert }_2^2,$$ (4)

where f_θ (·) is the function defined by the CNN, and θ denotes the hyperparameters. The CNN has 3 layers: a layer with 64 filters of size 9 × 9 × 1; a layer with 32 filters of size 1 × 1 × 64; and a with 2 filters of size 5 × 5 × 32. A ReLU is imposed on the outputs of the first 2 layers. Since a slice contains 2D information, the CNN outputs two gradients in two in-plane perpendicular directions.

Fig. 1.

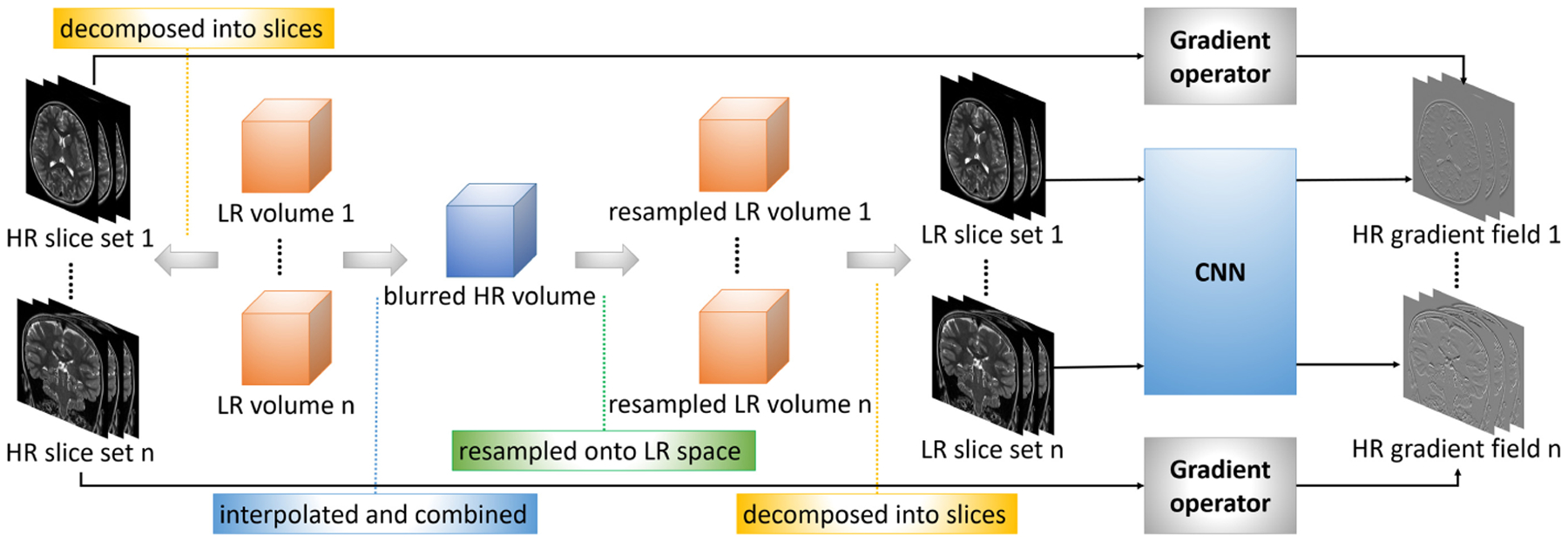
Overview of our proposed approach to learning the gradient guidance.

Pairing LR Inputs and HR Labels for Training Data.

The LR images are of in-plane HR, through-plane LR, and different orientations. Therefore, the gradients of the in-plane HR slices are directly used as the HR labels. The corresponding LR inputs are found in the following steps. First, all the LR images are aligned and interpolated by a third-order B-spline method to the size and resolution the same as the HR reconstruction. These interpolated LR images are combined into a mean image by averaging them out over their voxels. This mean image is then resampled according to the geometric properties of each original LR image, respectively. The slices of the resampled images are HR (small voxel size) but blurry due to the averaging, and are used as the LR inputs. The training dataset is thus constructed from the pairs of the LR inputs and the HR labels.

Training.

The LR-HR pairs in the training are of size 33 × 33 pixels. By adjusting the strides, about 20,000 data pairs are sampled uniformly with overlap from the slices to form the training dataset. The CNN is trained for 2000 epochs on an NVIDIA Quadro P5000 GPU with TensorFlow. Stochastic gradient descent with a learning rate of 1e⁻⁴ is used to optimize the hyperparameters θ in Eq. (4).

2.3. Super-Resolution Reconstruction

In the SRR, the CNN is first trained over the LR-HR pairs. The mean image is calculated following the steps mentioned above. The slices from each plane of the mean image are inputted to the trained CNN. The outputted gradients that are in the same direction are averaged into a single gradient. All the gradients form a gradient guidance g for the SRR.

As the gradient guidance is highly accurate due to the learning, a squared error is incorporated in the regularization. Therefore, the SRR is achieved by

$$\underset{x}{\text{min}}\sum _{k=1}^n{\Vert D_k{H}_k{T}_{k}x-y_k\Vert }_2^2+\lambda \sum _{g\in \mathcal{G}}{\Vert {\nabla }_{g}x-g\Vert }_2^2,$$ (5)

where all the gradients at different scales in different directions are organized in a set $\mathcal{G}$, and ∇_g computes the gradient at the same scale and in the same direction as g. H_k is designed as a sinc function in the slice selection direction of y_k (corresponding a boxcar in Fourier domain) convolved with a Gaussian kernel. In this work, the gradient guidance is computed at a scale of 1 in 3 directions of x, y, and z. λ is fixed at 0.5 according to the empirical results.

A closed-form solution to Eq. (5) is developed to obtain the HR reconstruction x from

$$\widehat{\text{x}}=\frac{{\sum }_{k=1}^n{\widehat{H}}_k^{*}°{\widehat{\tilde{y}}}_k+\lambda {\sum }_{\mathbf{\text{g}}\in \mathcal{G}}{\widehat{\nabla }}_{\mathbf{\text{g}}}^{*}°\widehat{\mathbf{\text{g}}}}{{\sum }_{k=1}^n{\widehat{H}}_k^{*}°{\widehat{H}}_k+\lambda {\sum }_{\mathbf{\text{g}}\in \mathcal{G}}{\widehat{\nabla }}_{\mathbf{\text{g}}}^{*}°{\widehat{\nabla }}_{\mathbf{\text{g}}}},$$ (6)

where ${\tilde{y}}_k=T_k^T{D}_k^T{y}_k$ denotes the interpolated and aligned form of the LR image y_k, $\widehat{\cdot }$ denotes 3D discrete Fourier transform, ·* computes complex conjugate, ○ denotes Hardamard product, and the fraction denotes element-wise division.

2.4. Experimental Setup

Simulated Data.

We simulated a dataset by using the MPRAGE data from the Dryad package [10]. We downsampled the original image of isotropic 0.25 mm to the image of isotropic 0.5 mm, and used it as the ground truth. We then downsampled the ground truth by factors of {2, 3, 4, 5, 6, 8} in the directions of x, y, and z, respectively, to form an axial, an coronal, and a sagittal LR image at each factor. Simulated motion with maximum magnitudes of 10 mm for translation and 10% for rotation was randomly generated and applied to each LR image. Gaussian noise was also randomly generated with a power of 10% of mean voxel intensities and added to each LR image. We assessed the quality of the HR reconstruction on this dataset in terms of peak signal-to-noise ratio (PSNR), structural similarity (SSIM) [21], and root square mean error (RMSE).

Real Data.

We acquired 45 MRI scans from 15 subjects with various acquisition schemes on a Siemens 3T MRI scanner. All scans were performed in accordance with the local institutional review board protocol.

Origin-Shifted Axial LR Acquisitions (OSA).

We acquired two axial LR T₂ weighted images with their origins shifted by a distance of half slice thickness. The in-plane resolution is 1 mm × 1 mm and the slice thickness is 2 mm. We also acquired an HR image of isotropic 1 mm as the ground truth. The HR reconstruction was evaluated in terms of PSNR, SSIM, and sharpness [6].

Axial and Coronal LR Acquisitions (AC).

We acquired 42 images from 14 subjects. With each subject, an axial and a coronal LR T₂-TSE image were acquired with in-plane resolution of 0.4 mm × 0.4 mm and slice thickness of 2 mm. It took about 2 min in acquiring a T₂-TSE image. A 3D T₂-SPACE image of isotropic 0.9 mm was acquired as the reference. The HR reconstruction was of isotropic 0.4 mm. Since the T₂-TSE has different contrast from the 3D T₂-SPACE image, we evaluated the HR reconstruction in terms of the blind assessment metrics that focus on image contrast and sharpness, including average edge strength (AES) [22], gradient entropy (GRENT) [9], and diagonal XSML (LAPD) [18]. As the HR reconstructions were assessed blindly on this dataset, we reported the normalized metrics that were computed from $\rho (x)/\rho \left(x^{\prime }\right)$, where ρ (·) denotes a metric function, x denotes a reconstruction, and x′ denotes a reference · image. Higher metric values produce better image quality for all metrics. We also investigated the accuracy of the gradient guidance estimate in terms of edge localization error that was computed from ${\Vert g-g^{\prime }\Vert }_1/{\Vert g^{\prime }\Vert }_1$, where g is the gradient guidance, and g^′ is the gradients computed from the reference image.

Baseline Methods.

We employed a CNN-based learning model as a baseline, which is similar to [8], trained on the same data, with the same network architecture as our model except that the output is the HR slice. The HR reconstruction was obtained from the fusion over the HR slice stacks estimated in different planes. We denoted this baseline by deepSlice. We compared our approach to deepSlice to demonstrate that learning a gradient guidance is superior to learning an end-to-end mapping for HR slices in volumetric SRR. We also compared our approach to the plain gradient guidance regularization method [17], denoted by GGR, to demonstrate that our approach led to a more accurate gradient guidance estimate, and in turn resulted in better HR reconstruction. We denoted our approach by deepGG, that stands for deep gradient guidance.

3. Results

We compared the accuracy of the gradient guidance estimates obtained from GGR and deepGG on the AC dataset in terms of edge localization errors. As shown in Fig. 2(a), deepGG yielded much smaller errors than GGR on all 14 HR reconstructions. The representative slices of the learned gradient guidance obtained from deepGG are shown in Fig. 2(b).

Fig. 2.

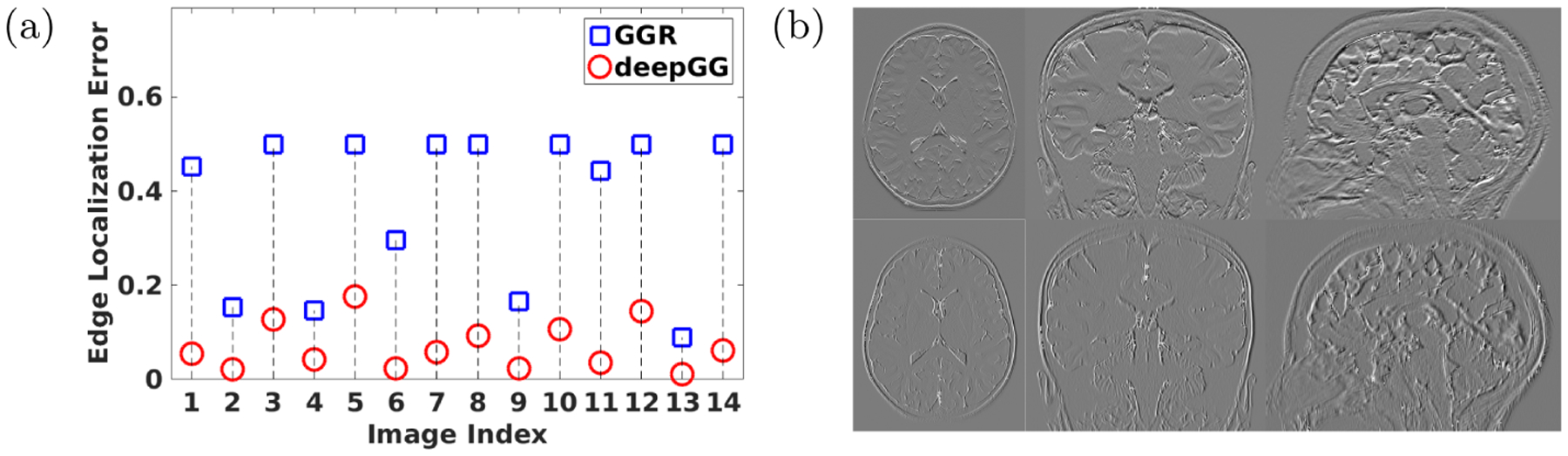
Evaluation results of the gradient guidance estimation on the AC dataset. (a) Comparisons between GGR and deepGG in the edge localization errors. (b) Representative slices of the learned gradient guidance obtained from deepGG.

Figure 3 shows the evaluation results of deepSlice, GGR, and deepGG on the simulated dataset. It is evident that deepGG consistently outperformed the two baselines by large margins at all upscale factors in terms of all metrics.

Fig. 3.

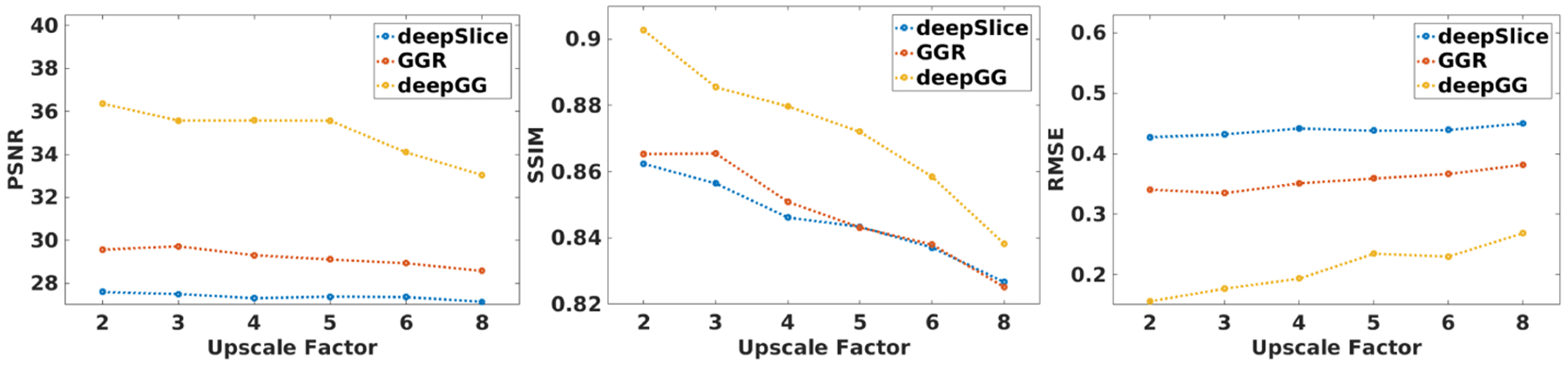
Evaluation results obtained from the three methods on the simulated dataset.

On the OSA dataset, the quantitative evaluation results were in terms of 1) PSNR: deepSlice = 35.01, GGR = 34.45, deepGG = 35.71; 2) SSIM: deepSlice = 0.912, GGR = 0.910, deepGG = 0.921; and 3) sharpness: deepSlice = 0.75, GGR = 0.78, deepGG = 0.86. Figure 4 shows the representative slices of an LR image and the reconstructed images obtained from deepSlice, GGR, and deepGG. The deepGG method achieved the sharpest images and the best contrast, which was consistent with the quantitative assessments, in particular with the sharpness metric.

Fig. 4.

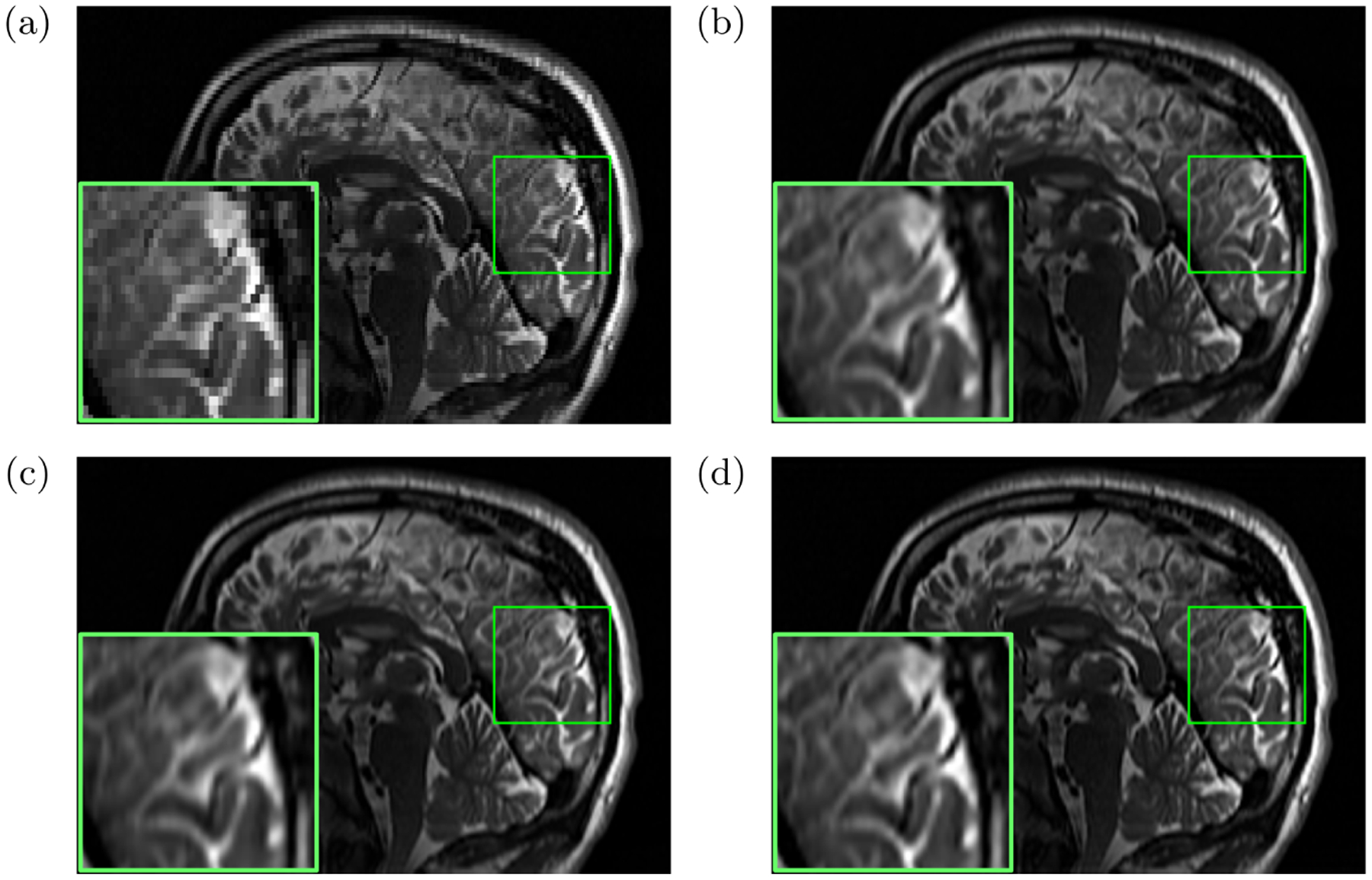
Representative slices of (a) an LR image and the reconstructed images obtained from (b) deepSlice, (c) GGR, and (d) deepGG (ours), respectively, on the OSA dataset.

Figure 5 plots the evaluation results of the three methods on the AC dataset. It is evident that deepGG considerably outperformed the two baselines. Figure 6 shows the representative slices of an LR image, and the HR images reconstructed by the three methods. It is shown that deepGG achieved more image details than the two baselines, and obtained the best contrast and the sharpest images.

Fig. 5.

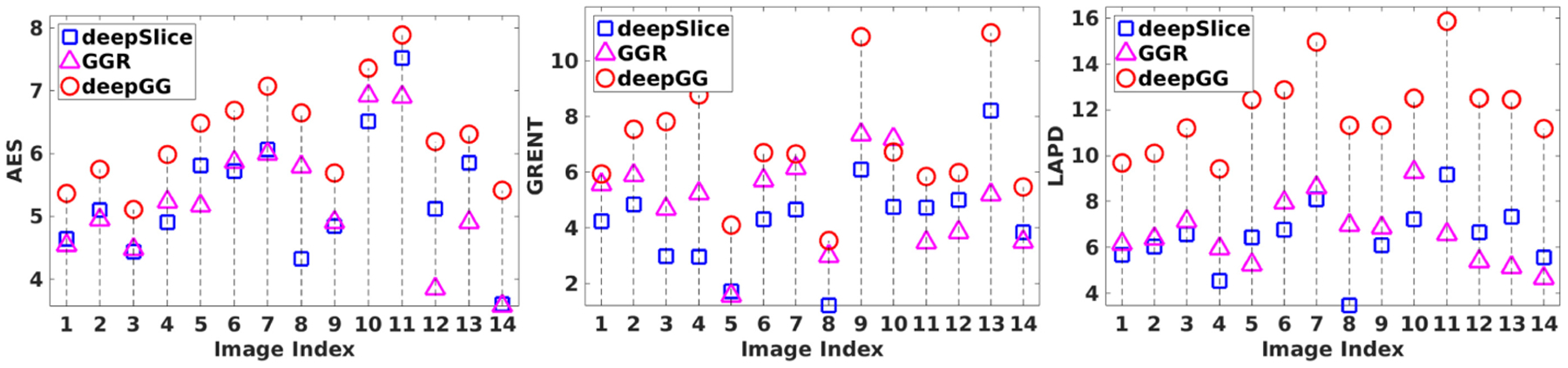
Evaluation results on the AC datasets in terms of average edge strength (AES), gradient entropy (GRENT), and diagonal XSML (LAPD), respectively.

Fig. 6.

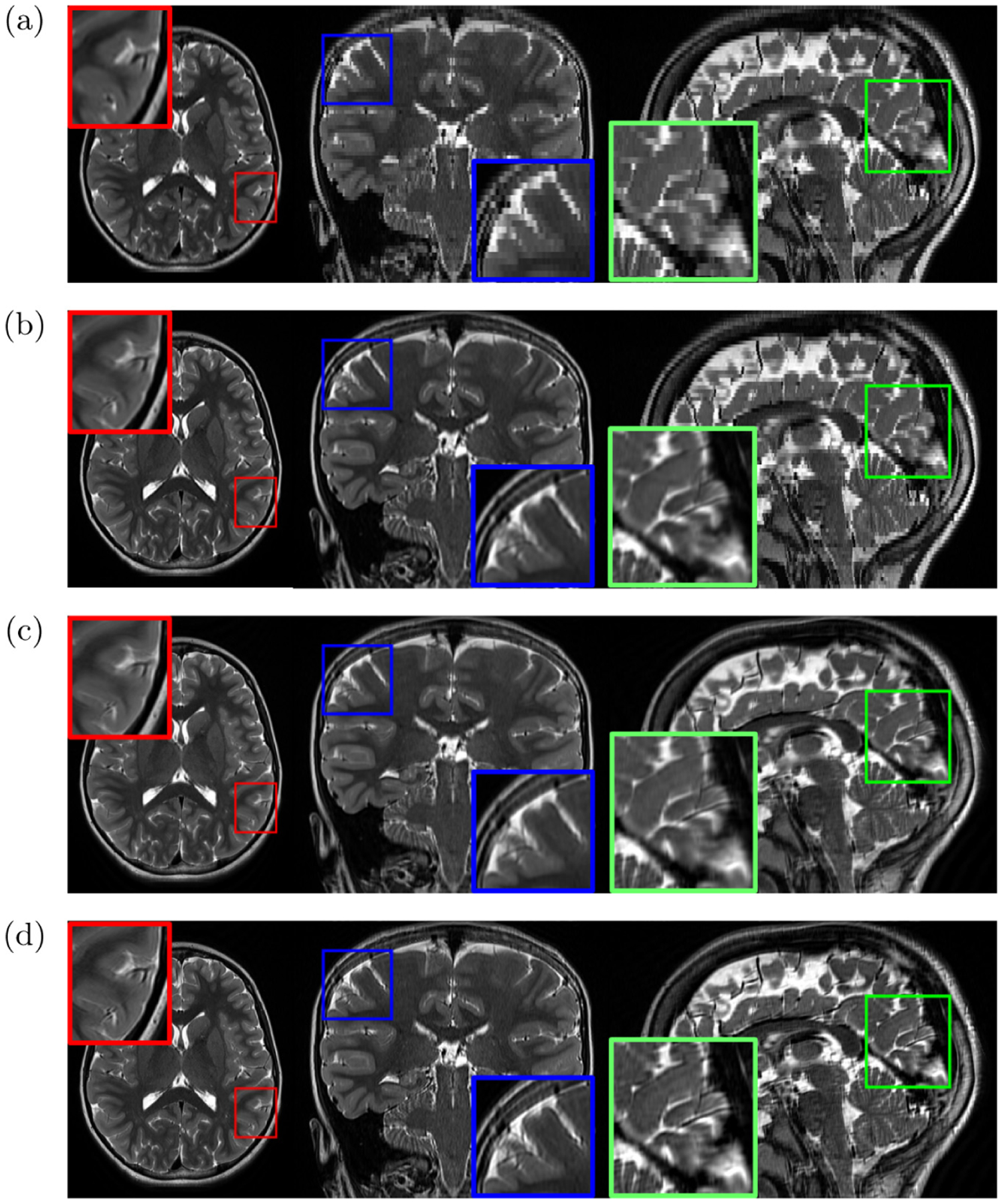
Representative slices of (a) an LR image, and the reconstructed images obtained from (b) deepSlice, (c) GGR, and (d) deepGG (ours), respectively, on the AC dataset.

4. Conclusions

We have developed a learning-based method to estimate the gradient guidance prior for MRI SRR. The learning tasks have been decomposed from 3D volumes onto 2D slices. The training dataset was constructed by exploiting the correspondences of in-plane HR and through-plane LR slices when incorporating the anisotropic acquisition schemes. Therefore, the learning model has been trained over the LR images themselves only. The learned gradient guidance, as prior knowledge, has been integrated into a forward model-based SRR framework. A closed-form solution to the SRR model, which is globally optimal, has been developed for obtaining the HR reconstruction. Extensive experimental results on both simulated and real data have demonstrated that our approach led to superior SRR over state-of-the-art methods, and obtained better images at lower or the same cost in scan time than direct HR acquisition.