Ensemble-Based Deep Learning for Estimating PM_2.5 over California with Multisource Big Data Including Wildfire Smoke

Abstract

Introduction:

Estimating PM_2.5 concentrations and their prediction uncertainties at a high spatiotemporal resolution is important for air pollution health effect studies. This is particularly challenging for California, which has high variability in natural (e.g, wildfires, dust) and anthropogenic emissions, meteorology, topography (e.g. desert surfaces, mountains, snow cover) and land use.

Methods:

Using ensemble-based deep learning with big data fused from multiple sources we developed a PM_2.5 prediction model with uncertainty estimates at a high spatial (1km × 1km) and temporal (weekly) resolution for a 10-year time span (2008–2017). We leveraged autoencoder-based full residual deep networks to model complex nonlinear interrelationships among PM_2.5 emission, transport and dispersion factors and other influential features. These included remote sensing data (MAIAC aerosol optical depth (AOD), normalized difference vegetation index, impervious surface), MERRA-2 GMI Replay Simulation (M2GMI) output, wildfire smoke plume dispersion, meteorology, land cover, traffic, elevation, and spatiotemporal trends (geo-coordinates, temporal basis functions, time index). As one of the primary predictors of interest with substantial missing data in California related to bright surfaces, cloud cover and other known interferences, missing MAIAC AOD observations were imputed and adjusted for relative humidity and vertical distribution. Wildfire smoke contribution to PM_2.5 was also calculated through HYSPLIT dispersion modeling of smoke emissions derived from MODIS fire radiative power using the Fire Energetics and Emissions Research version 1.0 model.

Results:

Ensemble deep learning to predict PM_2.5 achieved an overall mean training RMSE of 1.54 μg/m³ (R²: 0.94) and test RMSE of 2.29 μg/m³ (R²: 0.87). The top predictors included M2GMI carbon monoxide mixing ratio in the bottom layer, temporal basis functions, spatial location, air temperature, MAIAC AOD, and PM_2.5 sea salt mass concentration. In an independent test using three long-term AQS sites and one short-term non-AQS site, our model achieved a high correlation (>0.8) and a low RMSE (<3 μg/m³). Statewide predictions indicated that our model can capture the spatial distribution and temporal peaks in wildfire-related PM_2.5. The coefficient of variation indicated highest uncertainty over deciduous and mixed forests and open water land covers.

Conclusion:

Our method can be generalized to other regions, including those having a mix of major urban areas, deserts, intensive smoke events, snow cover and complex terrains, where PM_2.5 has previously been challenging to predict. Prediction uncertainty estimates can also inform further model development and measurement error evaluations in exposure and health studies.

1. Introduction

Exposure to fine particulate matter with aerodynamic diameter smaller than 2.5μm (PM_2.5) is associated with a range of acute and chronic adverse health effects (EPA 2017; WHO 2013a, b) including mortality (Atkinson et al. 2014) and morbidity (Lu et al. 2015). Studies have documented PM_2.5 effects on multiple organ systems and health outcomes including cardiovascular (Liang et al. 2014; Lippmann 2014), respiratory (Xing et al. 2016), atherosclerosis (Allen et al. 2012; Kunzli et al. 2010), birth outcomes (Yuan et al. 2019; Zhu et al. 2015), neurodevelopment and cognitive functions (Fu et al. 2019; Zheng et al. 2019). Accurate estimation of PM_2.5 exposures at a high spatiotemporal resolution is important for evaluating its health effects, particularly at small temporal (days to weeks) and spatial (neighborhood) scales. Although many countries have a substantial network of regulatory PM_2.5 monitoring stations, their spatial coverage is still very limited in terms of accurately representing population exposures, especially in regions of the world that have complex spatiotemporal variability in emissions, topography, meteorology, land-use and population density, such as the state of California (CA) in the United States (US) (Lee 2019; Li et al. 2015; Liu et al. 2009; Monn 2001).

The Moderate Resolution Imaging Spectroradiometer (MODIS) instruments onboard the polar-orbiting TERRA and AQUA satellites, launched in in 2000 and 2002, respectively, provide daily aerosol optical depth (AOD) data which have been widely used to increase spatial coverage for estimating ground-level PM_2.5 concentrations. AOD is a column-integrated sum of total ambient particle extinction and is significantly correlated with ground/surface PM_2.5 (Toth et al. 2014). MODIS AOD products generated using the early Dark Target (DT) and Deep Blue (DB) algorithms (spatial resolution: 3–10 km), and the recent Multiangle Implementation of Atmospheric Correction (MAIAC) algorithm (spatial resolution: 1 km) have been used as reliable predictors of PM_2.5 concentrations (Chu et al. 2016). For example, the addition of satellite AOD improved the Pearson’s correlation between estimated and observed PM_2.5 in the US by 0.3–0.6 (Chu et al. 2016; van Donkelaar et al. 2006) and over Massachusetts increased the model adjusted R² by 0.31 (Liu et al. 2009).

MODIS AOD can also provide information on wildfires (Ichoku and Ellison 2014), an increasingly important area of study in California due to their increasing frequency, environmental damage and associated health impacts, particularly in terms of exacerbations of asthma and chronic obstructive pulmonary disease (Reid et al. 2016). However, MODIS AOD retrievals are unreliable in the presence of thick smoke plumes as they can be misclassified as cloud (Ichoku and Ellison 2014; Livingston et al. 2014). Retrievals are also difficult over bright reflective surfaces such as deserts and in the presence of snow, cloud cover or glint. The MAIAC algorithm was developed to overcome some of these retrieval data quality issues (Lyapustin et al. 2011), yet in complex terrains such as California, issues remain. For example we found 41% of daily MAIAC AOD were missing over California during 2000–2016 (Li et al. 2020), which can have considerable impact on applications of satellite AOD in PM_2.5 estimation especially in the Western US (Chu et al. 2016). We recently developed a method using residual deep learning to reliably impute missing MAIAC AOD at a high spatial (1 km × 1 km) and temporal (weekly) resolution in California (Li et al. 2020) based on Modern-Era Retrospective analysis for Research and Applications Global Modeling Initiative Replay Simulation (M2GMI) AOD (Strode et al. 2019), meteorology, elevation and geographic coordinates with improved performance (mean test R² 0.94; independent test R² with AErosol RObotic NETwork (AERONET) AOD: 0.69), compared with the existing imputation methods of MODIS AOD (Di et al. 2016; Kloog 2016; Lv et al. 2016; Xiao et al. 2017).

Early studies using satellite AOD to estimate PM_2.5 established the AOD-PM_2.5 relationship using empirical statistical correlation (Gupta et al. 2006; Kloog et al. 2011), two stage generalized additive models (Liu et al. 2009) and land-use regression (LUR) plus Bayesian maximum entropy (BME) (Beckerman et al. 2013) with cross validation (CV) R² of approximately 0.60–0.81 at a coarse spatial resolution (8.9–12 km). Later, mixed effects models (Just et al. 2015; Lee et al. 2009; Lee et al. 2015; Xie et al. 2015) and geographically weighted regressions (GWR) (Bai et al. 2016; Guo et al. 2017; Hu et al. 2014) were widely used due to flexibility of allowing the AOD-PM_2.5 relationship to vary in space and/or time. Recently, machine learning (ML) methods including random forests (Brokamp et al. 2017; Huang et al. 2018; Wei et al. 2019), feed-forward neural network (Biancofiore et al. 2017; Di et al. 2016; Feng et al. 2015) and ensemble learning (Di et al. 2019; Li et al. 2018) have been increasingly used in estimation of PM_2.5 with improved performances (CV or test R² generally > 0.8). Although these existing methods achieved competent performance, compared with modern deep learning methods, LUR, generalized additive model (GAM) and mixed models have limitations in flexibility and learning capacity. Deep learning leverages multiple layers of artificial neural networks to progressively extract advanced features or representations from the model inputs. Due to the flexibility (unlimited hidden layers with their numbers of nodes) of network structure, a deep neural network has strong learning capacity to model non-linear associations and interactions among variables that can automatically extract advanced representations compared with many traditional ML algorithms, including GAM, support vector machine and Gaussian process regression (Goodfellow et al. 2016). Compared with random forests or other decision tree-based algorithms, deep neural networks do not require discretization of the input features, maintaining their full value ranges. Such discretization may lead to abrupt spatial variation in the predictions for the tree-based algorithms if limited training samples were used. On the other hand, the feed-forward neural network with deep hidden layers may have the issue of gradient vanishing during learning. Thus, residual learning may be employed to improve the learning (He et al. 2016a).

Although recent PM_2.5 modeling efforts that have incorporated satellite AOD data with other variables achieved a high CV R² of 0.80–0.86 (root mean square error (RMSE): 2.79–2.94 μg/m³) for the contiguous US (Di et al. 2019; Di et al. 2016; Hu et al. 2017), considerable regional differences in model performance remain. Particularly, the southwestern or Pacific regions of US where CA is located had lower R² (0.74–0.80) and higher RMSE (2.85–4.05 μg/m³) than national averages or eastern regions of US. In California, PM_2.5 concentrations are generally elevated in winter compared to summer due to high emissions of aerosol precursors, topography, and low mixing height (Toth et al. 2014; van Donkelaar et al. 2006). In winter, the surface PM_2.5-satellite relationship is further complicated by aerosol vertical distribution, high relative humidity (Li et al. 2015) and high cloud and snow cover leading to a greater proportion of missing data. Throughout the year, the impact of wildfire smoke also presents challenges to the use of satellite observations for prediction of ground-level PM_2.5 in CA. Satellite AOD retrievals over smoke plumes are masked as cloud and discarded in some AOD products. For locations where AOD retrievals are not masked, there is difficulty in representing the vertical distribution of the smoke, as smoke may be present aloft and detected by satellite while having no impact on surface pollution. Therefore, accurate estimation of ground-level PM_2.5 is particularly challenging for CA. Previous studies have overcome some challenges by omitting periods of high PM_2.5 (Larsen et al. 2020), which is likely to exclude peak PM_2.5 concentrations due to wildfire smoke. Given recent increases in wildfire event frequency (Dennison et al. 2014) and magnitude along with the substantial contribution of these events to enhanced PM_2.5 (Larsen et al. 2020; Larsen et al. 2018), there is a need to ensure that PM_2.5 models used in exposure studies adequately represent wildfire smoke while also addressing the other challenges of air quality modeling that impact CA. In addition, there are no outputs of uncertainty for the estimated PM_2.5 in most existing studies using ML methods (Chu et al. 2016) even though such uncertainty can inform the user on areas for model improvement, confidence in and variability of PM_2.5 predictions, and can be used in downstream analyses of health effects to decrease the potential bias (Girguis et al. 2019, 2020).

In this study we developed an ensemble-based deep learning model to estimate PM_2.5 over CA by fusing multisource big data, including modeled dispersion of wildfire smoke. In ensemble learning, the autoencoder-based full residual deep network was used as a base model to model non-linear associations and complex interactions among the variables with the state-of-the-art performance, as demonstrated in our previous study (Li et al. 2020). In order to account for high variability of PM_2.5 in CA, we used the imputed MAIAC AOD with the full spatial coverage, MERRA-2 GMI Replay Simulation (M2GMI) data, land use data, traffic variables, and modeled wildfire smoke plume dispersion. Based on MERRA2, M2GMI improves the representation of transport and chemistry with higher spatial and temporal resolution, compared with previous MERRA-2 simulations (Strode et al. 2019). In addition, meteorological variables were extracted from the high-resolution gridMET dataset (e.g., air temperature, surface shortwave radiation, specific humidity, precipitation, wind speed) (Abatzoglou 2011) and the background-scale M2GMI (e.g., planetary boundary layer height (PBLH), wind speeds at different altitudes, evaporation land) (Brauer et al. 2016; Randles et al. 2017). Other remotely sensed data (normalized difference vegetation index (NDVI), impervious surface and land cover) were also used. Geo-coordinates, temporal basis functions and time index were used to capture spatiotemporal trends in PM_2.5 concentration. Using the big data from multiple sources in a parallel computing environment, we conducted preprocessing, downscaling of various parameters to the target spatial scale (1km × 1km) aggregating daily into weekly data, training of the models and outputting gridded PM_2.5 concentration and uncertainty estimates. By validation and comparison with PM_2.5 contributed by wildfires smoke, this study shows the importance of a robust deep learning method and sufficient features (including wildfire smoke plumes) to capture spatiotemporal variability of PM_2.5 for a large region with diverse aerosol emission sources, including wildfires, topography and meteorology. Our proposed method can be also applied to other similarly heterogeneous and complex regions.

Supplementary Table S1 provides a list and brief description of all acronyms used in this paper.

2. Materials

2.1. Study Domain

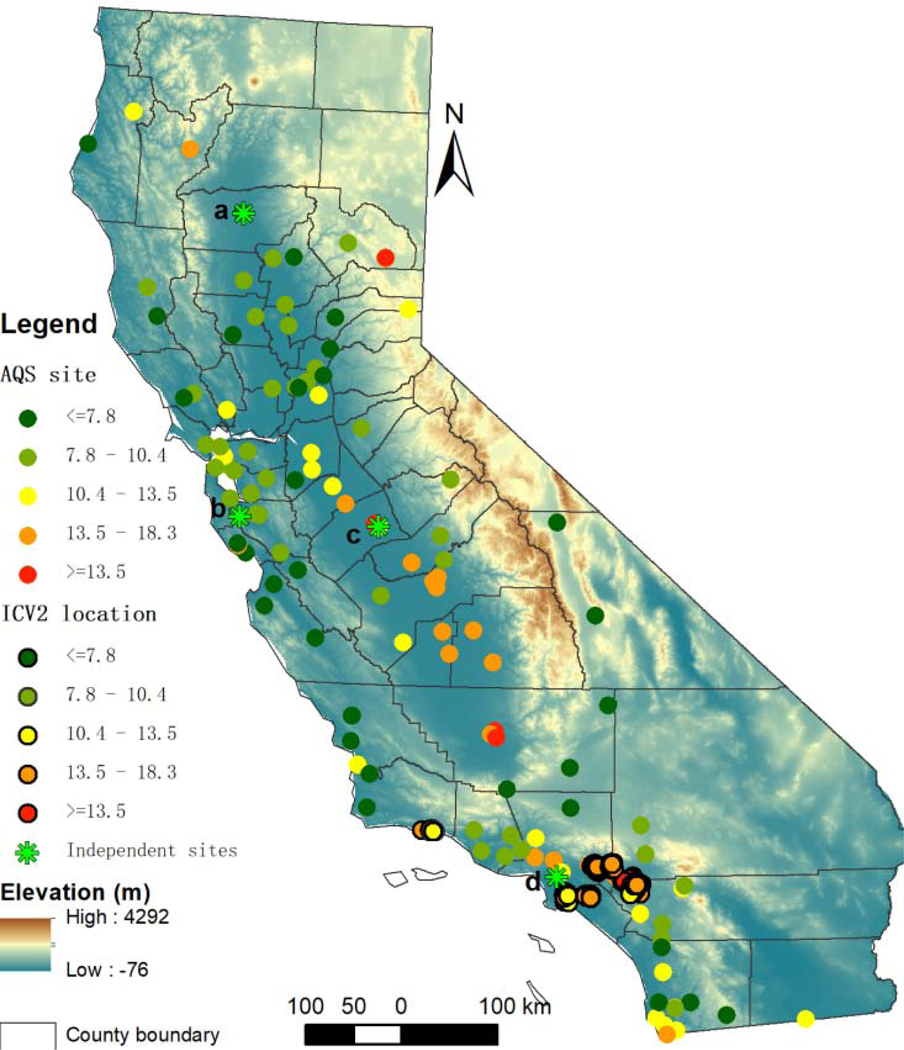
Our study domain (Fig. 1) is the state of California located between approximately −124°65’ and −114°13’ west to east longitude and between 32°51’ to 42°01’ north to south latitude. With an area of 423,970 km², CA has heterogenous topography (desert surfaces, mountains, snow cover), aerosol emission sources (e.g., natural sources: wildfires and dust; anthropogenic sources: fossil fuel exhaust, agriculture, and biomass burning) and meteorological processes (Fast et al. 2014). This subsequently results in differences in AOD (more reflective surfaces), the chemical composition of PM_2.5 (more contribution of nitrate (Tolocka et al. 2001)) and seasonal variation in aerosol vertical distribution, compared to eastern states of the US (Fast et al. 2014; Li et al. 2015).

Fig 1.

California study region showing sampling period PM_2.5 averages at AQS and ICV2 monitoring sites and four independent test sites (a, b, c and d)

2.2. PM_2.5 Measurements

We obtained daily PM_2.5 measurements (2008–2017) from the United States Environmental Protection Agency (EPA) Air Quality System (AQS) (https://www.epa.gov/aqs) that were collected by state, local, and tribal air pollution control agencies. We also obtained spatially dense (267 locations) biweekly PM_2.5 samples (2008–2009) from the University of Southern California Intra-Community Variability study 2 (ICV2). These samples were collected in 8 southern California communities from Santa Barbara south to Riverside (Figure 1) using Harvard Cascade Impactors described in more detail in (Fruin et al. 2014). To temporally downscale biweekly ICV2 samples to weekly values, we derived a scaling ratio of weekly to biweekly means based on the AQS stations closest to the ICV sites. We chose to develop a PM_2.5 model with weekly temporal resolution because this was the shortest exposure window needed for anticipated epidemiologic analyses of pregnancy outcomes. The AQS PM_2.5 network includes both continuous monitoring and 24-hour sampling on a 1-in-6 day, 1-in-3 day and everyday schedule. The 2008–2017 database provides daily PM_2.5 measurements for about half of days at the sites that measured PM_2.5 for at least one year. Measurements alone would provide only 43% valid weekly values using EPA’s 75% completeness criteria at these sites. Linear regression models were developed to fill in missing daily values at most sites by using daily data from nearby sites (within 50 km) with significant data availability (more than 1 year of data). The median R² was 0.74 (IQR=0.63 to 0.83) for all regression models; two-thirds of daily estimates were made using “two-nearby sites” regression models (median R²=0.77). Weekly values for model training and evaluation were developed using at least 5 daily measurements (allowing up to maximum of 2 daily values estimated from the regression models). The fill in procedures increase the availability of complete weekly samples from 43% to 79% in the 2008–2017 period, with a trend of increasing completeness in the later years because of increased deployment of continuous monitors.

For weekly PM_2.5 predictions we generated a fixed spatial grid of 1 km × 1 km over California using the Universal Transverse Mercator (UTM) zone 11N coordinate system (ellipsoid: World Geodetic System 1984, unit: meter).

2.3. Features

2.3.1. MAIAC AOD

As an advanced algorithm, MAIAC leverages a spatial and temporal algorithm to simultaneously retrieve atmospheric aerosols and bidirectional reflectance from MODIS data. Compared with the DT and DB algorithms, MAIAC further detects clouds and corrects atmospheric effects over both dark vegetated surfaces and bright desert targets to obtain better daily AOD values at a higher spatial resolution (1 km × 1 km) (Lyapustin et al. 2018). The algorithm is also tuned to reduce masking of wildfire smoke as clouds (Lyapustin et al. 2012). We acquired MAIAC AOD (at 550 nm with quality assurance flags) covering California for 9 years (01/01/2008 to 12/31/2016) from MODIS TERRA and AQUA satellites that had equatorial crossing at about 10:30 AM and 1:30 PM local time, respectively, from a NASA ftp site (ftp://maiac@dataportal.nccs.nasa.gov/DataRelease; the website is inaccessible now). We obtained 2017 MAIAC AOD from the updated NASA website (https://lpdaac.usgs.gov/products/mcd19a2v006/) which had a change in the projection used from Alberts to the global Sinusoidal projection. Therefore, all the MAIAC AOD images were converted into the target projection of UTM Zone 11. The evaluation with AERONET measurements using co-located samples (Supplementary Table S2) showed consistency in MAIAC AOD between 2008–2016 and 2017 with a very small difference (Pearson’s correlation>0.91 with p-value<0.01). We used autoencoder-based residual deep network to impute missing MAIAC AOD with a high performance as described in our earlier work (Li et al. 2020).

2.3.2. Meteorology

Meteorological factors play very important roles in forming, dispersion and transport of PM_2.5 at regional and local scales (Chu et al. 2016). We extracted meteorological parameters from daily high spatial resolution (~4 km, 1/24th degree) surface meteorological data for the gridMET of the contiguous US (http://www.climatologylab.org/gridmet.html) (Abatzoglou 2011). These parameters include daily minimum air temperature (°C), maximum air temperature (°C), wind speed (meters/second, m/s), specific humidity (grams of vapor per kilogram of air, g/kg), daily mean downward shortwave radiation (watt/meter², w/m²) and accumulated precipitation (millimeters of rain per meter² in 1 h, mm/m²). Weekly averages of the meteorological features were generated from daily values. Bilinear resampling was used to transform the meteorological data into the target UTM Zone 11 projection.

2.3.3. MERRA-2 Global Modeling Initiative Replay Simulation

The MERRA-2 Global Modeling Initiative output (publicly available from https://portal.nccs.nasa.gov/datashare/merra2_gmi) is generated through the simulation for the atmospheric composition coupling MERRA2 meteorological fields (winds, temperature and pressure) with the Global Modeling Initiative (GMI)’s stratosphere-troposphere chemical mechanism. The simulation is interactively coupled to the Goddard Chemistry Aerosol Radiation and Transport module and includes similar emissions to what was used for MERRA-2 (NASA 2018; Strode et al. 2019). From M2GMI bottom layer, we extracted 30 modeled gaseous air pollutants and particulate matter source contributions in the PM_2.5 size fraction (including carbon monoxide, nitrogen dioxide and oxide, ozone, and mass concentrations of sea salt, nitrate, sulfur dioxide, ammonia, sulfate, organic carbon, dust, and black carbon), 12 meteorological parameters (including PBLH, air temperature, specific humidity, precipitation, wind speed) and 24 other parameters at ~50km spatial resolution. From 66 M2GMI variables, we selected 18 as predictors based either on their correlations (absolute value >= 0.05) with weekly PM_2.5 concentration or plausible physical interpretation for their influence on PM_2.5 concentrations. Based on M2GMI wind speeds at 10 m and 50 m altitudes, we derived indicators of vertical stagnation and wind sheer/mechanical mixing as follows:

$$w_{\text{stag}}=\left(\sqrt{u_{50}^2+v_{50}^2}-\sqrt{u_{10}^2+v_{10}^2}\right)$$ (1)

$$w_{\text{mix}}=\left(\sqrt{u_{10}^2+v_{10}^2}-\sqrt{u_2^2+v_2^2}\right)$$ (2)

where w_stag is the indicator of stagnation, w_mix is wind sheer/mechanical mixing, u₁₀ is 10-meter eastward wind speed, v₁₀ is 10-meter northward wind speed, u₂ is 2-meter eastward wind speed, v₂ is 2-meter northward wind speed, u₁₀ is 50-meter eastward wind speed, and v₅₀ is 50-meter northward wind speed.

2.3.4. Wildfire Smoke Plume Dispersion Modeling

Wildfire smoke plumes can result in peak PM_2.5 concentrations and considerably affect spatiotemporal variability of PM_2.5 in California. We calculated ground-level PM_2.5 from smoke using dispersion modeling of primary emissions of PM_2.5 from wildfires, where emissions were determined from the Fire Energetics and Emissions Research version 1.0 (FEER.v1) model (Ichoku and Ellison 2014) with MODIS Aqua and Terra fire radiative power retrievals. To capture local impacts and long-range smoke transport, we estimated emissions from all fires in California and all large fires (>1000 acres) throughout the western U.S. and portions of Canada and Mexico. Fire area was calculated using ecoregion-specific per-detect area estimates, as in the 2014 National Emissions Inventory (EPA 2018). To reduce computational requirements, we clustered all hotspots within 0.05° using the density-based DBSCAN methodology (Ester et al. 1996) and summed the emissions of clustered hotspots.

We modeled smoke dispersion using the Hybrid Single-Particle Lagrangian Integrated Trajectory (HYSPLIT) model (Stein et al. 2015) and calculated smoke injection height using the Sofiev et al. (2013) model. We distributed daily emissions totals using the hourly emissions profile using the WRAP time profile (Western Regional Air Partnership 2005), which estimates minimal emissions (<0.01%) between 8 PM and 9 AM, with peak emissions at 4 PM (17% of total emissions). Dispersion was driven using North American Mesoscale Forecasting System (NAM) 12 km gridded meteorological data, which was obtained from NOAA Air Resources Laboratory (https://www.ready.noaa.gov/archives.php). PM_2.5 from smoke was carried over for up to 5 days from smoke release. The HYSPLIT model’s 100m surface layer concentrations were used as ground-level PM_2.5 from smoke. We estimated resulting concentrations on the NAM 12km grid on an hourly time step. To prepare the data for subsequent modeling, we averaged the hourly data to weekly concentrations and further downscaled the weekly values from 12-km to 1-km resolution using bilinear interpolation.

2.3.5. Land Cover Variables

Land use parameters can capture PM_2.5 emission sources and sinks and have been used in many studies. The National Land Cover Database (NLCD) (https://www.mrlc.gov) provides nationwide data on land cover and its change at a 30m resolution. From the NLCD, we generated annual percent cover of each land cover class on the target modeling grid of 1 km (Yang et al. 2018). For each of 16 land cover classes (e.g., open water, developed with low intensity, developed with high intensity, barren land, grassland and cultivated crops etc.), we calculated the proportion of cover between 0 and 1 of each class within 1km grid cells for each available year (2001, 2003, 2006, 2008, 2011, 2013, and 2016), and linearly interpolated to annual values for unavailable years of 2001–2016. We used 2016 land cover data for 2017. For the PM_2.5 modeling, we excluded the land cover types that were not as frequently observed in CA (<1%).

From the NLCD, we also extracted the surface imperviousness layer that represents urban impervious surfaces as a percentage of developed surface over every 30-meter pixel in the US for the years 2001, 2006, 2011, and 2016. We used similar linear interpolation to derive impervious surface percentage in missing years (also assuming no change for 2017).

We calculated monthly average NDVI using 16-day MODIS NDVI average values from NASA’s Aqua and Terra satellite (MOD13A2 V6 and MCD13A2 V6). The 16-day NDVI product was obtained on a 1km resolution grid, and we resampled the final monthly averages to the standard 1 km modeling grid described above.

2.3.6. Temporal Basis Functions

Using iterative singular value decomposition, we extracted four temporal basis functions (Finkenstadt et al. 2007) from the AQS PM_2.5 measurements of 10 years (2008–2017). As shown in our previous study (Li et al. 2019), four temporal basis functions represented the major temporal trend of PM_2.5 concentrations from 2008 to 2017 for CA, and can be used in the models to capture long- and short-term temporal variability of PM_2.5 over a complex and large region like CA.

2.3.7. Elevation, Geographic Coordinates and Time Index

We obtained 30 m resolution elevation from GoogleMaps API and calculated its average within each 1 km MAIAC grid cell. The central x and y coordinates of the target resolution of 1 × 1 km² with the target projection were used to account for spatial variability. The day of year was used to account for seasonal variability and the year index was used to account for annual variability.

3. Methods

In order to model the non-linear associations and complex interactions among the features and PM_2.5 concentration, an autoencoder-based full residual deep network was used in three phases: downscaling, imputation of missing AOD, and base model and ensemble learning.

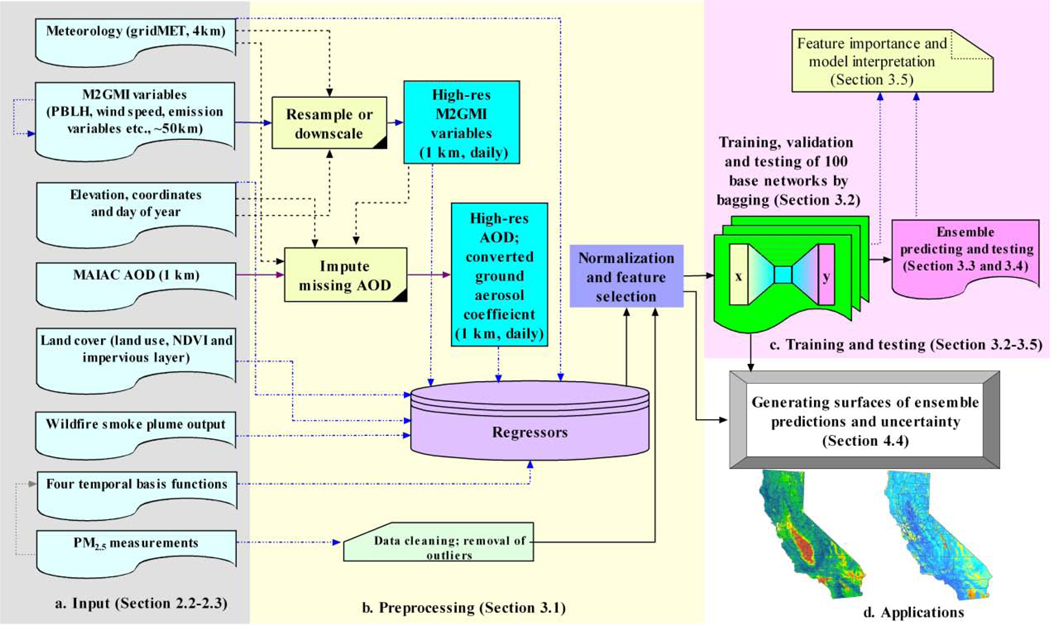
Fig. 2 shows the flowchart of our PM_2.5 modeling process in California. The model inputs include multisource heterogeneous data (Fig. 2-a). From one input (M2GMI variables) we derived vertical stagnation and wind sheer, and from the PM_2.5 measurements we extracted four temporal basis functions (Sections 2.2-2.3). In order to have all regressors with the same projection and spatiotemporal resolution (1 km), preprocessing including resampling or downscaling, and imputation was performed for M2GMI variables and MAIAC AOD (Fig. 2-b, Section 3.1). Data cleaning, outlier filtering, AOD conversion and feature selection were also performed in preprocessing. With all data prepared, 100 residual deep network models were trained and validated (Section 3.2), ensemble predictions were made (Section 3.3) and evaluated (Section 3.4), and feature importance quantification and model interpretation were conducted (Section 3.5) (Fig. 2-c). After the optimal models were obtained, 1 km resolution gridded daily surfaces of PM_2.5 estimates with complete spatiotemporal coverage over California were generated (Fig. 2-d; Section 4.4 for the results).

Fig 2.

Flowchart of the PM_2.5 modeling process in California

3.1. Preprocessing

Preprocessing includes data cleaning, removal of outliers, downscaling, imputing missing AOD, conversion of column MAIAC AOD to ground aerosol extinction coefficient, normalization and feature selection. In data cleaning, data quality flags (e.g., valid value range: (0, 3) for MAIAC AOD; (−1, 1) for NDVI; (0, 1) for land-use area proportion) were used to remove invalid values among each feature. The outer fence (NIST/SEMATECH 2016) was used to filter outliers. The downscaling algorithm based on residual deep network (Li et al. 2020) was used to downscale M2GMI variables (~50km spatial resolution) to the target resolution (1 km). In our downscaling, spatial coordinates, elevation and gridMET variables were used as the features at the target resolution. In addition, missing MAIAC AODs were imputed using residual deep network (Li et al. 2020). Normalization by standardization was performed to ensure all the variables to be on a consistent scale, and to stabilize model training (Bhandari 2020). For feature selection, the features with a low, non-statistically significant correlation (absolute value <0.02) with weekly PM_2.5 concentrations were removed from the list of potential predictors. Physical interpretability and redundancy were then considered to filter out remaining features. For example, M2GMI variables in the PM_2.5 size fraction or in the bottom surface layer were retained. M2GMI gases or other parameters were retained based on a priori knowledge of their physical or chemical relationship to PM_2.5 formation or dispersion, or interpretability.

In addition, an empirical formula was used to convert satellite column AOD to surface aerosol extinction coefficient (Wang et al. 2010) adjusting for vertical distribution and effects of relative humidity as follows:

$$k_g=\frac{{\tau }_c\cdot {(1-h/100)}^g}{H_A}$$ (3)

where k_g is the converted surface-level aerosol extinction coefficient hypothesized to correlate more closely with ground measured PM_2.5 than column AOD, τ_c is column satellite AOD (MAIAC AOD), H_A is the scale height of aerosol, approximated by M2GMI PBLH (Koelemeijer et al. 2006), h is relative humidity (unit:%), and g is the empirical parameter to be optimized.

3.2. Base Model of Full Residual Deep Network

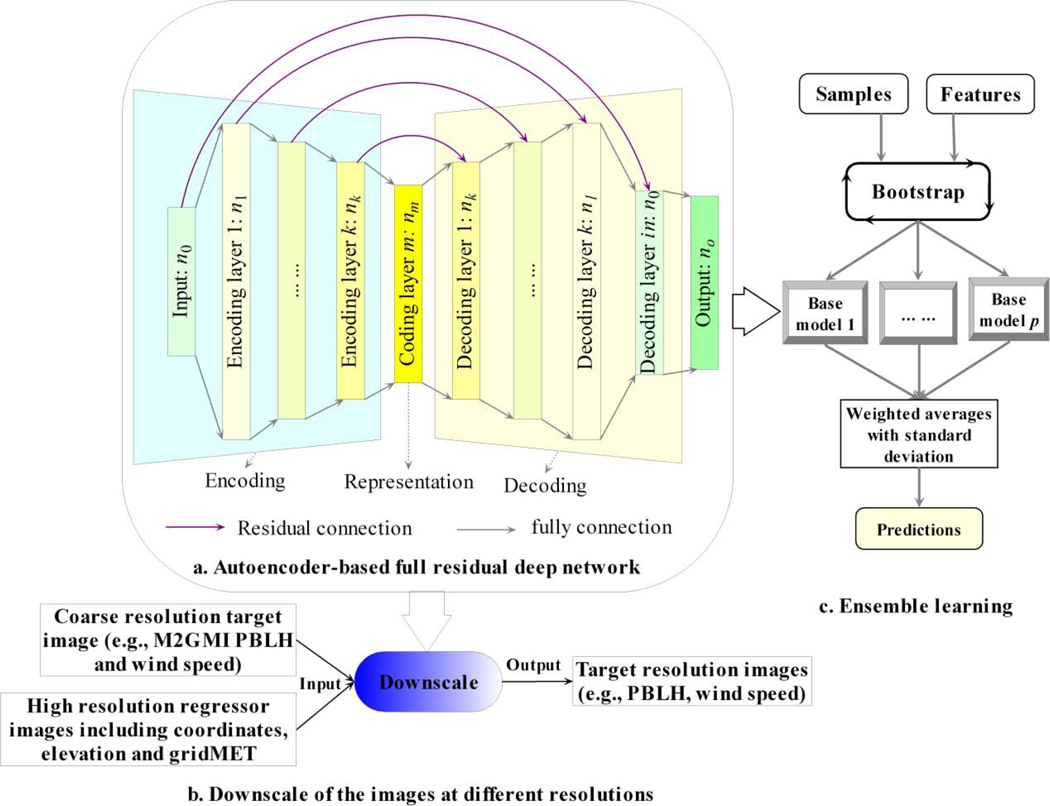
Full residual deep network was developed as the base model, which consists of the encoding layers (including the input layer and hidden layers with a decreasing number of nodes), the latent (coding) representation layer, the decoding layers, and the output layer (Fig. 3-a) (Li et al. 2020). In the autoencoder, the coding/latent layer is used to extract the representation from the input; each decoding layer has the same number of nodes corresponding to its symmetrical encoding layer. The latent layer has a compressed dimension to have a powerful representation for the input layer and help with efficient model training. Full residual connections in the autoencoder were introduced: each of the encoding layers has a shortcut of identity mapping (residual connection) to its corresponding decoding layer to improve training and error back-propagation. Residual learning is an efficient method to appropriately increase the depth of the hidden layers without reduction in the performance. Inspired by the pyramidal cells in the cerebral cortex (Thomson 2010), residual learning utilizes shortcuts to jump over some layers, and thus reuse activations from a previous layer to reduce or avoid the problem of vanishing gradients (He et al. 2016b). Based on the encoding-decoding structure of autoencoder, full residual connections for all encoding layers and their corresponding decoding layers can be constructed in a nested way (Fig. 3-a) to considerably boost robustness in training and improve the generalization of the trained models, as demonstrated in our previous study (Li et al. 2020).

Fig. 3.

Autoencoder-based full residual deep network (a), downscaling (b) and ensemble learning (c).

Given powerful capability to model the non-linear associations among the predictive features and the target variables, full residual deep network was used in three phases of this study: downscaling in preprocessing (Fig. 3-b), imputation of massive missing MAIAC AOD, and spatiotemporal estimation of PM_2.5 concentrations. Our previous study (Li et al. 2020) describes the downscaling algorithm in detail (also used to downscale the M2GMI variables in this study) and imputation of missing MAIAC AOD of 2000–2016 over CA (validation with AERONET AOD: correlation = 0.83; R² = 0.69). The same method was also used to impute missing MAIAC AOD of 2017 over CA.

For the output layer of PM_2.5 spatiotemporal estimation, we used the following loss function of a single output (estimate of PM_2.5 concentration):

$$\mathcal{l}\left({\theta }_{\text{w},\text{b}}\right)={\mathcal{l}}_{\text{y}}\left(y,f_{{\theta }_{\text{W},\text{b}}}^{\text{y}}(X)\right)+\mathrm{\text{Ω}}\left({\theta }_{\text{w},\text{b}}\right)$$ (4)

where ly is the loss function of PM_2.5 without regularization, ℓ(θ_W,b) is the final loss function with regularizer, W is the weight matrix, b is bias vector, θ_W,b are the parameters for W and b, y is the ground truth of the target variable (PM_2.5 concentration), $f_{{\theta }_{\text{W},\text{b}}}^{\text{y}}(X)$ is the estimate of y by the trained model for the input matrix X, Ω(θ_W,b) is the regularizer of elastic net (Zou and Hastie 2005) that is defined as:

$$\mathrm{\Omega }\left({\theta }_{w,b}\right)={\lambda }_1\left|\sum _{p\in {\theta }_{\text{w},\text{b}}}p\right|+{\lambda }_2\sum _{p\in {\theta }_{\text{w},\text{b}}}{p}^2$$ (5)

where |·| is the absolute value operator, p is the parameter to be learned within θ_W,b, λ₁ and λ₂ are the weights assigned as the hyper-parameters for lasso and ridge regularizers. Their optimal solution can be retrieved using grid search (Chicco 2017).

Due to the relatively small sample size of the PM_2.5 dataset in comparison with the satellite AOD dataset, the output of single parameter has a lower training bias and a better test performance than that of multiple parameters used in imputation of the MAIAC AOD (Li et al. 2020). An optimal network structure (the number of encoding layers and the number of nodes for each layer) was obtained using grid search.

3.3. Bagging and Ensemble Predictions

Using the full residual deep network as the base model, bootstrap aggregating (bagging) was conducted to obtain ensemble predictions (Fig. 3-c). Bootstrap sampling was conducted for the data samples and partially for the features. By bootstrap, we used approximately 63.3% of the samples for training and the remaining 36.7% of the samples for testing. In total, we had 59 predictive features available for modeling. Of these features, 28 had statistically significant correlation (absolute value >0.1) with PM_2.5 and were used as fixed predictors to keep the performance of the trained model above a certain level, and the remaining 31 features were sampled with replacement (see Supplementary Table S3). On average, approximately 50 predictive features in total were used in a base model. The ensemble predictions were obtained using the weighted averages of all the predictions of all the trained base models:

$${\widehat{x}}_w=\frac{\sum _{i=1}^N{w}_i{\widehat{x}}_i}{\sum _{i=1}^n{w}_i}$$ (6)

$$\widehat{\sigma }\left({\widehat{x}}_w\right)=\sqrt{\frac{\sum _{i=1}^N{w}_i{\left({\widehat{x}}_i-{\widehat{x}}_w\right)}^2}{\frac{\left(N^{\prime }-1\right)\sum _{i=1}^N{w}_i}{N^{\prime }}}}$$ (7)

where w_i is the weight assigned to model i (e.g., w_i=1/RMSE_i in our study), $\widehat{x}$ is the weighed sum, N is the number of samples, N′ is the number of non-zero weights, ${\widehat{x}}_w$ is the ensemble weighted estimate and $\widehat{\sigma }\left({\widehat{x}}_w\right)$ is the estimate of standard deviation as an uncertainty metric for ${\widehat{x}}_w$. From the estimated standard deviation, we derived the coefficient of variation through normalization by the predicted mean.

The bootstrap for the samples and the features was used to reduce the correlations among the trained models. In addition, we also introduced a small variation by sampling in a small interval ([−10, 10]) for the number of nodes for each hidden layer based on the optimal base model to reduce the correlation between the trained models. Theoretically, ensemble predictions with less standard error can be obtained by aggregating the outputs of the less correlated models. Assuming that 𝜀_𝑖 is the error contained in each model’s predictions with the errors drawn from a zero-mean multivariate normal distribution ($\mathbb{E}\left[{\epsilon }^2\right]=\nu$ and $\mathbb{E}{\left[{\epsilon }_i{\epsilon }_j\right]}_{i\ne j}=c$), the expected squared error of the ensemble predictor is:

$$\mathbb{E}\left[{\left(\frac{1}{m}{\Sigma }_i{\epsilon }_i\right)}^2\right]=\frac{1}{m^2}\mathbb{E}\left[\sum _i\left({\epsilon }_i^2+\sum _{j\ne i}{\epsilon }_i{\epsilon }_j\right)\right]=\frac{v}{m}+\frac{(m-1)c}{m}$$ (8)

where m is the number of models, c represents the correlation in the errors between different models. If c=0 (no correlation), the squared error is just $\frac{1}{m}\nu$, indicating a linear decrease with the ensemble size. But if c=v (perfectly correlated, Pearson’s correlation=1), the ensemble error does not change (still v). Thus, the smaller the Pearson’s correlation, the smaller are the expected squared errors in the ensemble predictions.

In ensemble learning, we have several hyper-parameters, ϑ(m,λ₁,λ₂,l_r,n_b) (m: the number of trained models; λ₁ and λ₂: the weight for lasso and ridge regularizers; l_r: initial learning rate; n_b: the sample size of a mini batch in training) to be solved. In our method, due to the high learning efficiency the mini-batch gradient descent was used to find an optimal solution. In this optimization the training samples are split into small batches, where each batch of samples is iteratively used to calculate model error and update model coefficients. The sample size (n_b) of a mini batch is one of the important hyper-parameters for model training (Goodfellow et al. 2016). We used grid search to find an optimal solution for these parameters. We used the Spark big data platform for parallel data processing, ensemble training and grid search.

Another advantage of using ensemble learning to predict PM_2.5 is that we can derive the coefficient of variation for the predicted PM_2.5 as an uncertainty metric to inform the confidence degree of the predicted values.

In order to reduce the dependence between samples in each bootstrap, we used an effective stratification strategy. In this strategy, the samples were first divided into different groups based on the spatiotemporal factor of county id and month index; random shuffling and bootstrap were then conducted between different strata, and within each selected stratum. By merging all of the selected samples, we obtained the training samples for each bootstrap (the rest of the samples were used as the validation and test samples). As an improved version of non-overlapping simple block bootstrap that is generally used to bootstrap the samples in the time series data (Carlstein 1986), our method performed additional bootstrap sampling within each stratum. With the spatiotemporal stratification based on both county and month index, each stratum corresponded to a block, and the stratification method substantially reduced spatiotemporal dependence between blocks (strata). Compared with the original data, we obtained the training samples with less dependence between them. Sensitivity analyses were conducted to compare our stratification strategy and simple block bootstrap. In the simple block bootstrap, we first used K-Means to group the samples based on the coordinates and time index (week index) into 500 clusters (similar to the number of strata in our strategy), and then performed bootstrap at the block level and retrained the models.

3.4. Validation and Independent Test

By bootstrap between strata and within each stratum, we selected approximately 63.3% of the samples for training and validation, and the remaining 36.7% for independent test. Of the selected 63.3% of the samples, 80% were used in training and the remaining 20% were used in validation. The 36.7% of the total samples were used as the independent test.

In addition, we collected the time-series of PM_2.5 measurements from four monitoring sites for independent tests (Fig. 1). Data from three AQS routine sites were used for site-based independent testing (i.e., excluded from model training and validation). The three AQS sites were selected to represent northern, eastern and central populated sub-regions of CA (compared the less populated western sub-region). For the southern sub-region, we used data from the University of Southern California (USC) Particle Instrumentation Unit monitoring site in Los Angeles (Shirmohammadi et al. 2016) as a third-party independent test. This data was collected as part of a fine particle characterization study described in more detail in Shirmohammadi et al. (2016) and was not used in model training and validation. Briefly, the USC site is located about 3 km south of downtown Los Angeles, CA. Five-day integrated samples were collected every week from Monday to Friday, between July 2012 and February 2013, using Micro-Orifice Deposit Impactors (MOUDIs, Model 110 MSP Corporation). Collocated AQS data at three other nearby sites from the same study were used in a generalized additive model to adjust the bias in the PM_2.5 measurements caused by the different instruments at the AQS sites and the USC monitoring site.

3.5. Feature Importance and Model Interpretation

In order to interpret the influence of key features in the trained models on performance, we used the Shapley Additive exPlanations (SHAP) tool (Lundberg and Lee 2017) to measure each predictor’s average contribution (feature significance) to our trained model. In addition, we used the individual conditional expectation (ICE) plot (Goldstein et al. 2015) with partial dependence plot (PDP) (Friedman 2001) to visualize the relationship between each predictive feature and the target variable (PM_2.5 concentration). The PDP shows the marginal effect of one feature on the outcome of a trained model, and it can show whether the relationship between the target and a feature is linear, monotonic or more complex (non-linear). ICE plots can visualize the dependence of the prediction on a feature for each instance separately, resulting in one dependence line per instance, compared to one line overall in PDP.

4. Results

4.1. Summary and Correlation

In total, we included 34,812 weekly PM_2.5 samples among which, 34,005 routine samples were from 133 AQS sites, and 807 field samples were from 267 ICV2 locations (Fig. 1). The mean PM_2.5 concentration over the study region was 10.41 μg/m³ (standard deviation: 6.21 μg/m³) with higher values in winter than in summer (12.05 vs. 10.26 μg/m³) and higher values in southern California than in northern California (10.95 vs. 9.49 μg/m³) (Supplementary Fig. S1 for the boxplots and histograms of observed PM_2.5 and MAIAC AOD). Unlike the eastern US, California has a seasonal variation of higher AOD in summer than in winter (0.10 vs. 0.06), opposite to that of PM_2.5. Using Eq. (3) to convert MAIAC AOD to surface aerosol extinction coefficient with empirical parameter g=0.21, the correlation of MAIAC AOD with PM_2.5 improved from 0.25 to 0.47.

In total, we had 59 predictive features (MAIAC AOD, 20 M2GMI variables, 16 land-use variables, 6 meteorological variables, wildfire smoke, 2 traffic variables, 5 coordinates, NDVI, elevation, year, day of year, 4 temporal basis functions) and selected about 50 features for modeling in each bootstrap. The first 4 temporal basis functions were extracted from 133 AQS routine stations (Supplementary Fig. S2). Table 1 shows descriptive statistics for the feature in each category with an absolute correlation>0.1 with weekly PM_2.5 and Supplementary Fig. S3 shows the bar plot for the correlation of these selected features.

Table 1.

Summary of the predictive features with a high or moderate correlation with PM_2.5 concentration

Category	Name	Unit	Range	IQR	Mean	Median	Correlation
Satellite AOD	MAIAC AOD		0 to 1.55	0.05	0.07	0.06	0.47*
M2GMI or derived feature	Nitrate surface mass concentration-PM2.5	kg/m3	1.25E-13 to 5.13E-09	6.22E-10	5.28E-10	3.64E-10	0.37*
	Carbon monoxide	mol/mol	5.67E-08 to 9.27E-07	3.18E-08	1.17E-07	1.14E-07	0.35*
	Wind sheer/ mechanical mixing	m/s	0.08 to 2.46	0.43	0.9	0.88	−0.3*
	Dry deposition of Ox	kg/m2/s	3.38E-11 to 2.84E-10	5.50E-11	1.30E-10	1.25E-10	−0.24*
	Sea salt surface mass concentration-PM2.5	kg/m3	3.38E-11 to 2.84E-10	2.35E-09	2.24E-09	1.72E-09	−0.2*
	SO4 surface mass concentration	kg/m3	5.32E-12 to 1.38E-08	9.33E-10	1.65E-09	1.39E-09	0.2*
	Black carbon surface mass concentration	kg/m3	1.31E-10 to 6.97E-09	4.13E-10	6.59E-10	5.04E-10	0.2*
	Evaporation land	Kg/m2/s	1.98E-11 to 5.04E-08	1.37E-05	1.15E-05	8.22E-06	−0.19*
	Indicator of stagnation	m/s	−0.48 to 2.7	0.63	0.7	0.72	−0.18*
	Mean planetary boundary layer height	m	121.58 to 3589.42	526.72	920.07	845.35	−0.12*
Meteorology	Wind speed	m/s	0.58 to 10.97	1.27	3.27	3.07	−0.33*
	Daily mean downward shortwave radiation	watt/meter2	40.25 to 377.54	166.52	228.44	235.24	−0.14*
	Precipitation	mm/m2	0 to 85.4	0.74	1.13	0	−0.12*
Temporal basis functions	Temporal basis function 1		−1.51 to 2.42	1.03	−0.22	−0.38	0.35*
	Temporal basis function 3		−1.23 to 2.39	1.01	0.79	0.85	−0.19*
Coordinates	Longitude	○	−124.2 to −115.48	3.46	−119.92	−120.1	0.18*
Remote sensing	Normalized difference vegetation index		723.8 to 7843.4	1465.3	3127.29	3073.6	−0.16*
	Impervious layer		0.03 to 87.79	43.74	41.29	44.34	0.15*
Land-use	Shrub/scrub		0 to 0.86	0.03	0.05	0	−0.14*
Wildfire	Wildfire smoke	μg/m3	0 to 264.83	0.29	0.78	0.06	0.14*
Time index	Year		2008 to 2017	5	2013.33	2014	−0.15*

^*: indicates statistical significance (p-value<0.01).

4.2. Optimal Base Model and Ensemble Learning

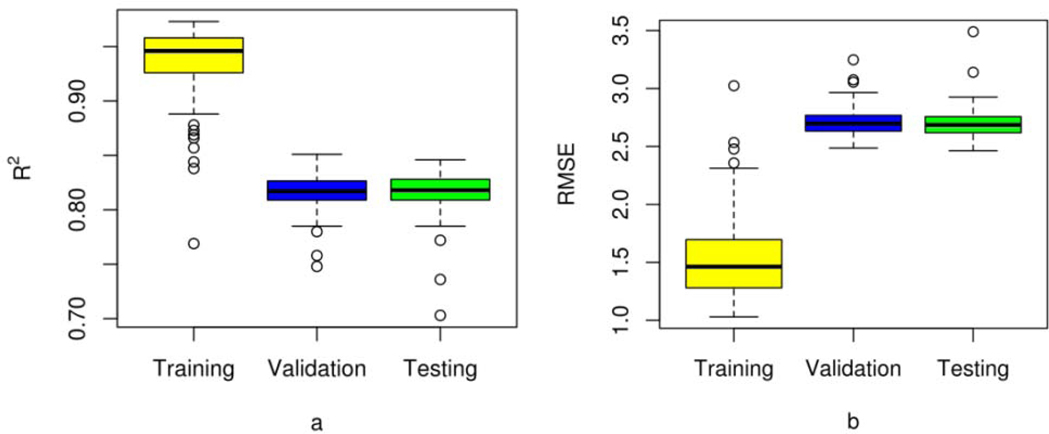
Through grid search we obtained an optimal benchmark structure with the encoding and latent layers having the numbers ([50, 128, 64, 32, 16]) of nodes for PM_2.5 estimation. Correspondingly, we had eleven layers in total with one input layer, four encoding layers, one latent layer, four decoding layers, and one output layer. For the hyper-parameters ϑ(m,λ₁,λ₂,l_r,n_b) in our optimal solution, we obtained an optimal number (m=100) of trained models, an initial learning rate (l_r=0.01), weights for elastic net (λ₁=0.5 and λ₂=0.5), and a mini batch size (n_b=512). In total, we trained 100 base models with each having a change in the number of nodes for each hidden layer based on the benchmark network structure. In summary (Table 2), we obtained mean training R² of 0.94 (range: 0.77 to 0.97) (mean training RMSE: 1.54 μg/m³, range: 1.03–3.02 μg/m³), and mean testing R² of 0.82 (range: 0.70 to 0.85) (mean testing RMSE: 2.70 μg/m³, range: 2.46–3.49 μg/m³) (Fig. 4).

Table 2.

Performance statistics of 100 trained models in ensemble learning

	Training		Validationa		Testingb
	Mean	Range	Mean	Range	Mean	Range
Sample size	17,629		4,407		12,776
R2 (range)	0.94	(0.77, 0.97)	0.82	(0.75, 0.85)	0.82	(0.70, 0.85)
RMSE (μg/m3)	1.54	(1.03, 3.02)	2.70	(2.49, 3.24)	2.70	(2.46, 3.49)

^a: the samples not used to train the models but used to validate the model (adjusting the hyper-parameters to get an optimal effect);

^b: the samples used to test the trained models (not used in training and validation).

Fig. 4.

Boxplots of training, validation and testing R² (a) and RMSE in μg/m³ (b).

Sensitivity analysis (Table 2 vs. Supplementary Table S4; Fig. 4 vs. Supplementary Fig. S4) showed better performance (mean test R²: 0.82 vs. 0.72; by an improvement of 10%) for our stratified sampling, compared with simple block bootstrap. For ensemble predictions (Supplementary Fig. S5) of simple block bootstrap, we obtained test R² of 0.79, compared with the test R² of 0.87 in our stratification method (an improvement of 8%).

The ICE and PDP results (Supplementary Fig. S6-S7) illustrate marginal associations or/and interactions of MAIAC AOD, carbon monoxide, wildfire smoke, black carbon surface mass concentration, coordinates, wind speed, and air temperature etc. with PM_2.5. Plots are shown here for a single model (Model 1) and selected features that generally ranked among the highest predictive features across all 100 models.

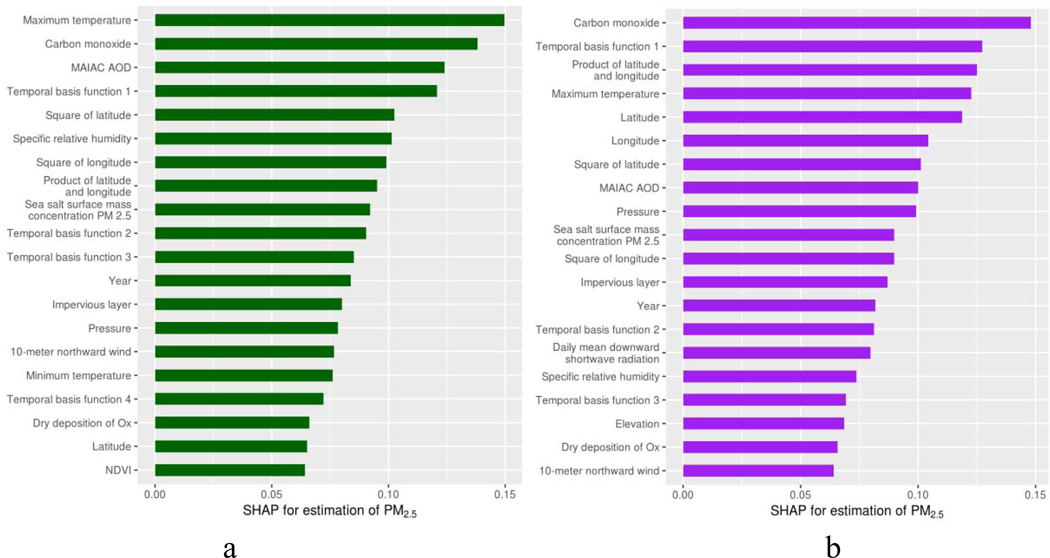
For each single base model, we ranked the contribution of each predictor by calculating its SHAP value (Fig. 5-a for the top 20 features and Supplementary Fig. S8 for all the features). SHAP contributions were averaged over the 100 trained models (Fig. 5-b for the top 20 features and Supplementary Fig. S9 for all the features). As shown in these figures, the top 10 features across the 100 trained models included carbon monoxide, temporal basis function, coordinates (latitude, longitude, and their products), maximum temperature, MAIAC AOD, pressure, and sea salt surface PM_2.5.

Fig. 5.

Bar plots of the feature importance of the top 20 features by SHAP (a. a single trained base model; b. averages of 100 trained models).

4.3. Evaluation

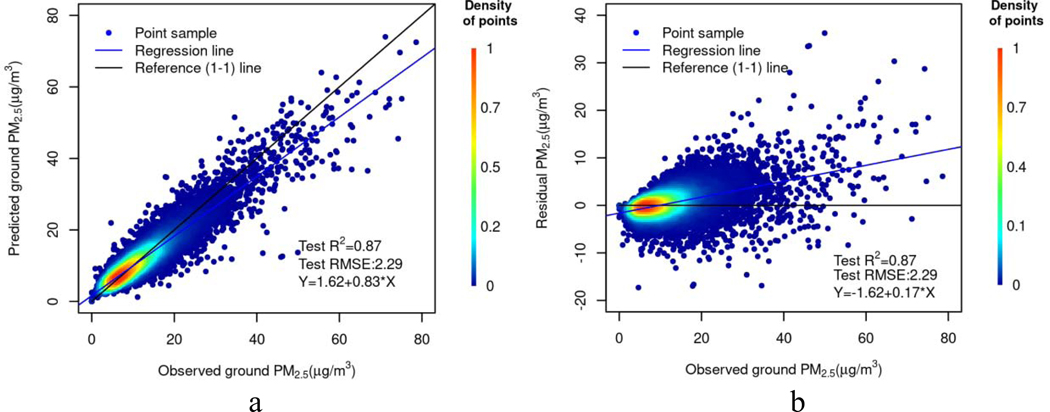
In ensemble learning, the ensemble predictions by 100 trained models had an improvement of approximately 5% over the average performance of the single base model based on the test R² (0.87 vs. 0.82) (RMSE: 2.29 vs. 2.70 μg/m³) (Table 3). Increasing the number of models beyond 100 only improved model performance very slightly, but added training time substantially. Compared with a single base model, the ensemble predictions had few extreme values and outliers (Fig. 6 for the scatter plots of observed vs. predicted (a) or residual (b) PM_2.5). The observed PM_2.5 and ensemble predicted PM_2.5 also presented very similar distributions (Supplementary Fig. S10 and S11 for their histograms and boxplots). The residuals of the ensemble predictions presented a normal distribution with mean close to zero and a small standard deviation (Supplementary Fig. S12). The autocorrelation was very low (mostly <0.08) between the residuals for most of lags (Supplementary Fig. S13), indicating that spatiotemporal variability of PM_2.5 in this study region was well captured by our models.

Table 3.

Performance of ensemble predictions in the independent test

	All samples	AQS samples	USC ICV2 samples
Sample size	12,776	12,266	510
R2 (range)	0.87	0.87	0.82
RMSE (μg/m3)	2.29	2.30	2.70

Fig. 6.

Scatter plots of observed vs. predicted PM_2.5 (a) and observed vs. residual PM_2.5 (b).

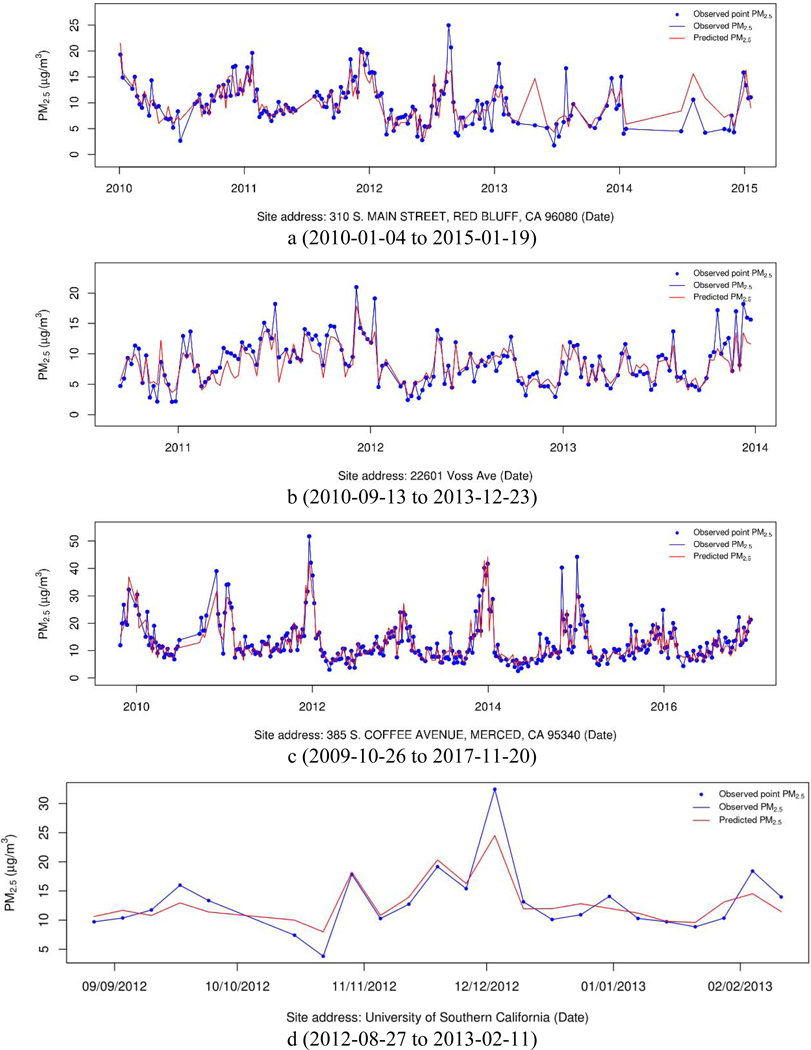
The times series of predicted PM_2.5 for four sites (three routine AQS site and one USC site) in the independent test were shown in Fig. 7, and their R² and RMSE were shown in Table 4 (their locations shown in a, b, c and d of Fig. 1). The results show that the temporal (seasonal and yearly) trends and variations were well captured in the ensemble models (R²: 0.67–0.87; RMSE: 1.80–2.81 μg/m³).

Fig. 7.

Time series of observed vs. predicted PM_2.5 in the independent test.

Table 4.

Performance for the time series in independent test

Site address	Source	#Time slices	Correlation	Mean PM2.5 (μg/m3)	R2	RMSE (μg/m3)
a. 310 S. Main St., Red Bluff, CA	AQS	171	0.82	9.88	0.67	2.36
b. 22601, Voss Av., Cupertino, CA	AQS	162	0.90	8.70	0.76	1.80
c. 385 S. Coffee Av., Merced, CA	AQS	329	0.93	13.32	0.87	2.81
d. University of Southern California	Shirmohammadi et al. (2016)	34	0.92	13.04	0.78	2.55

4.4. Surfaces of Predicted PM_2.5 and Wildfires

The 1×1 km² surfaces of weekly PM_2.5 averages of ensemble predictions and their uncertainty (coefficient of variation) from 2008 to 2017 were generated based on bagging of the 100 trained models. The surfaces of four weeks in different seasons from 2008 to 2017 were shown in Fig. 8 (a and b: a spring week of April 21–27, 2008; c and d: a summer week of July 16–22, 2012; e and f: an autumn week of September 14–20, 2015; g and h: a winter week of December 25–31, 2017). The predicted surfaces show reasonable variation of PM_2.5 concentration across different seasons and across CA. The coefficient of variation (Fig. 8 –b, d, f, and h) showed higher uncertainty (mean: 0.57, standard deviation: 0.39) over deciduous forest, mixed forest and water bodies (e.g., lakes) (Supplementary Fig. S14) or high altitude. This might be indirectly caused by false high AOD due to water, snow in winter (higher uncertainty in winter than in summer), cloud or other high reflectance. These uncertainty estimates provide a quantitative estimate of variability or confidence in predicted PM_2.5 and can be incorporated into analyses examining measurement error in these predictions and its subsequent impact on health effect estimates in downstream (Girguis et al. 2019, 2020).

Fig. 8.

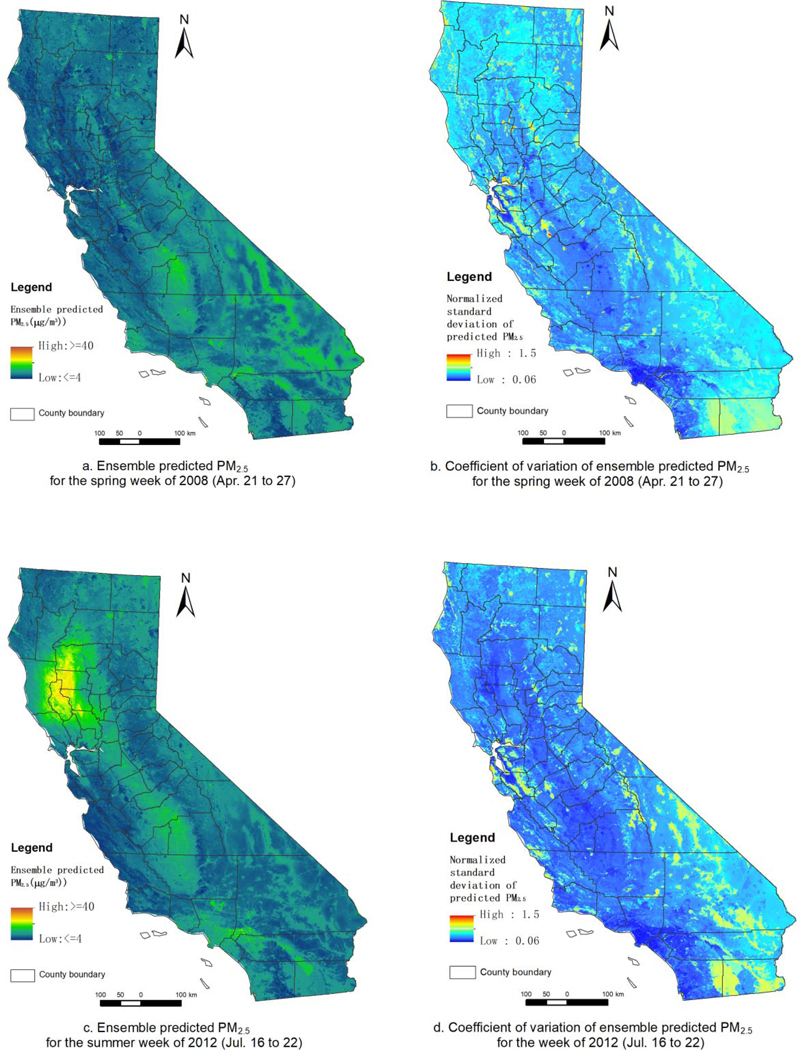
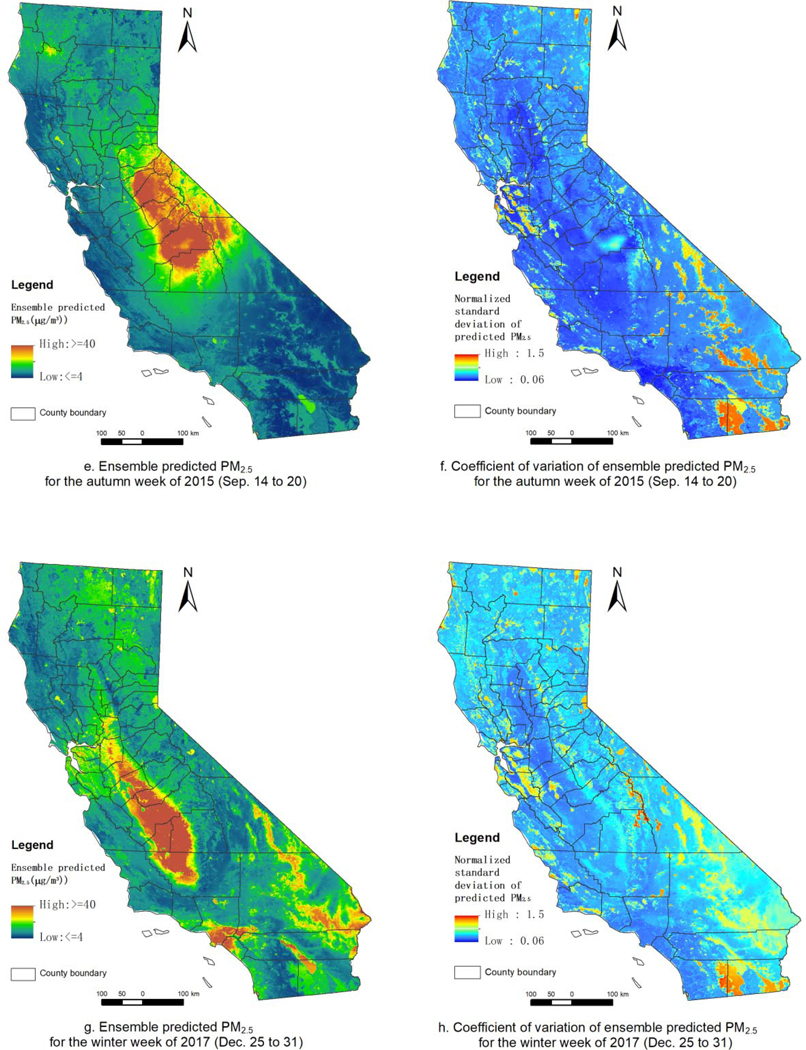
Surfaces of ensemble predicted PM_2.5 (a, c, e and g) and their the coefficient of variation (b, d, f and h) for four typical seasonal weeks in different years (a and b for spring week of 2008; c and d for summer week of 2015; e and f for autumn week of 2015; g and h for winter week of 2017).

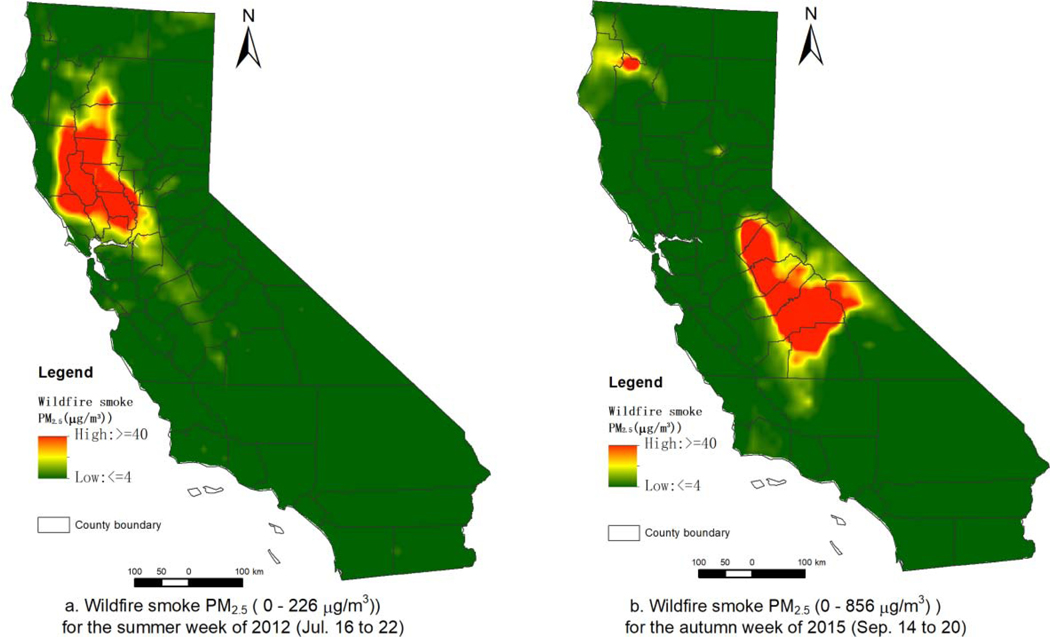
Historically wildfires in CA most frequently occur in summer and autumn. Fig. 8- c and e presents predicted surfaces of PM_2.5 for two weeks impacted by wildfires (in summer and autumn with higher smoke PM_2.5 concentrations in autumn) which presented different spatial distributions (summer: higher PM_2.5 concentrations in the northeastern to mid sub-region; autumn: higher PM_2.5 concentrations in the mid-eastern sub-region). The spatial distribution of average ensemble predicted PM_2.5 during these two wildfire weeks closely matched that of HYSPLIT-generated wildfire smoke PM_2.5 (Fig. 8-c vs. Fig. 9-a; Fig. 8-e vs. Fig. 9-b). Also, see Supplementary Fig. S15 and S16 for the comparison between total predicted PM_2.5 and wildfire smoke PM_2.5 (HYSPLIT) for the weeks before and after the wildfire weeks. We observed similar patterns during wildfire impacted weeks in other years. We also compared the time series of observed (at smoke impacted sites), ensemble model predicted and HYSPLIT-derived PM_2.5 for these two wildfire weeks and found that our model was able to sufficiently capture the PM_2.5 temporal peaks caused by wildfires (Supplementary Fig. S17 and S18). These results demonstrated that our method can capture spatial distribution and temporal peaks of PM_2.5 during wildfire smoke events.

Fig. 9.

Distributions of HYSPLIT modeled wildfire smoke PM_2.5 for two wildfire season weeks in 2012 and 2015.

5. Discussion

Spatiotemporal prediction of PM_2.5 over a large heterogeneous region such as California with high variability in emission sources, land-use, topography, meteorology and population is challenging. Using multisource data integrated into an ensemble deep learning framework we were able to capture temporal and spatial trends over the region, including weeks where wildfires were present. As far as we know, this study is one of the first to leverage a variety of big data sources including M2GMI variables and wildfire smoke PM_2.5, and to use a residual deep learning to account for variability and improve estimation of PM_2.5 in California. Comparatively, in a statewide mixed model (Lee et al. 2016) and two recent national models (Di et al. 2016; Hu et al. 2017), California obtained R² of 0.66 to 0.80 (RMSE: 2.85–5.69 μg/m³), lower than that of the eastern states of US. Our California-specific models generally had improved performance with greater R² (>7%) and lower RMSE (0.55–3.39 μg/m³).

Particular matter (PM) contains both primary PM directly emitted into the air and secondary PM formed in the air by chemical reactions and other mechanisms from precursors emitted by fuel combustion and other sources (EPA 2014). Regarding composition, fine particles are made up of multiple chemical components, including carbon, sulfate and nitrate compounds as well as crustal materials (e.g., soil, dust and ash). California has a mixture of major urban areas with dense traffic network and industrial facilities, rural areas with agriculture, deserts and intensive smoke events (e.g., wildfires), which results in multiple emission sources and complexity in constituents for PM_2.5. In addition to observed and imputed MAIAC AOD (Li et al. 2020), we used traffic and/or land-use variables to account for the emission influence, as done in many studies (Beckerman et al. 2013; Di et al. 2019; Hu et al. 2017; Huang et al. 2018; Zhai et al. 2018). But land-use variables lack temporal variation and only indirectly reflect the emission influence, thus making limited contribution to estimation of PM_2.5. Several variables from the M2GMI dataset, not normally used in previous studies, made important contributions to explain the variability of PM_2.5, as measured by the SHAP values. Carbon monoxide concentrations and O₃ dry deposition were important predictors presumably because they broadly indicated the location and intensity of primary combustion sources and correlated with secondary formation of particles, respectively. Sea salt aerosol concentrations contributed perhaps because they distinguished coastal and inland aerosol characteristics. These variables were included along with variables like PM_2.5 black carbon concentrations which were strongly suspected of explaining PM_2.5 variability. Different from the MAIAC AOD, traffic and land-use variables, these M2GMI variables compensated the insufficiency in the data of emissions and constituents of PM_2.5 for California and can be used as important predictors for estimation of PM_2.5.

Meteorology also plays an important role in the formation and variability of particle matter (Tai et al. 2010). For example, air temperature, sunlight, water vapor and humidity can affect shifting between solid/liquid and gaseous phases; wind can transport fine particle over long distances; and planetary boundary layer (PBL) can play an important role in the turbulent mixing and vertical distribution of pollutants in the lower troposphere (Wang et al. 2019). The PBL height determines the volume available for pollution dispersion and transport, and significantly affects vertical structure and turbulent mixing that is responsible for variability of ground air quality. Undoubtedly, as a key input, PBLH is a critical variable that influences ground concentration of air pollutants including PM_2.5 (Knote et al. 2015; Su et al. 2018). In our study, the gridMET dataset provided high-resolution meteorological parameters (air temperature, wind speed, humidity, shortwave radiation and precipitation) but lacked other important parameters such as PBLH and wind speed at different altitudes. Therefore, we extracted the PBLH variable from M2GMI that was critically used in the conversion of column satellite AOD to ground aerosol extinction coefficient (improving the correlation between AOD and PM_2.5 by 0.22), and estimation of PM_2.5. In addition, we derived the indicator of stagnation and wind sheer/mechanical mixing from wind speeds at the altitudes of 2m, 10m and 50m. Wind sheer/mixing presented high correlation with PM_2.5 compared with many other features. This study shows the important roles of the critical meteorological parameters, especially vertical ones, and pollutant concentrations from the M2GMI dataset in spatiotemporal estimation of PM_2.5. The M2GMI dataset is available globally from 1980 to 2018 and can be effectively used to obtain important parameters for estimation of PM_2.5.

California has extensive wildfires each year that can result in peak PM_2.5 concentration of smoke well beyond the typical range concentrations otherwise observed. Variability in spread and intensity of wildfire plumes can result in variability of spatial distribution of PM_2.5 during the wildfire seasons (Thompson and Calkin 2011), as illustrated in the results. In this study, we incorporated wildfire smoke PM_2.5 as a predictive feature to account for influence of wildfire events. Wildfire smoke PM_2.5 was generated using a top down approach for emissions and then a bottom up approach for the HYSPLIT dispersion modeling, with coincident measurements of fire radiative power (FRP) and AOD of MODIS (Ichoku and Ellison 2014). The results show the consistency between our predicted PM_2.5 surfaces and smoke PM_2.5 during the wildfire seasons. Few studies used the wildfire-related smoke feature to account for the influence of wildfire events, as ours (Chu et al. 2016). For California, wildfires are an important factor for spatiotemporal variability of PM_2.5 and an important public health concern, and the direct inclusion of PM_2.5 wildfire smoke in our model supports the representation of peak PM_2.5 concentrations that can typically be missed by similar modeling approaches.

Given the big and heterogeneous data from multiple sources, we leveraged ensemble deep learning, i.e. bagging of the base residual deep network to model the complex non-linear associations and interactions among features and PM_2.5. Residual learning was used in our models to boost the learning and improve the generalization. The autoencoder-based full residual deep network was demonstrated to be robust in non-linear modeling and our spatiotemporal imputation of MAIAC AOD (Li et al. 2020), and also used in downscaling of the M2GMI variables at a coarse spatial resolution to the target resolution of 1×1 km² in this study. For spatiotemporal estimation of PM_2.5, sensitivity analysis (Supplementary Table S5) shows that the base residual deep network improved testing R² over GAM by 21% and over feed-forward neural network by 5%. Bootstrapping using stratification by a spatiotemporal factor (county id and month) to de-correlate the training samples was important for the improvement of the test performance of our method compared to a simple block bootstrap. In simple block bootstrapping, the samples in each block were interdependent, which resulted in poorer test performance. Further, bagging of 100 base residual deep networks improved the testing R² over a single base model by 5% on average. The regular feed-forward neural network has been commonly used in estimation of PM_2.5 (Di et al. 2019; Di et al. 2016; Feng et al. 2015). Our ensemble method also generated the coefficient of variation of ensemble predictions as an uncertainty metric to inform error evaluation in exposure and health studies. Compared with recent existing methods, our method improved R² for 2008–2017 estimation (with the coefficient of variation) of PM_2.5 by at least 7%, which shows that our method well accounted for spatiotemporal variability of PM_2.5 for California with high variability of PM_2.5.

This study has several limitations. First, multisource data at different resolutions (e.g., M2GMI variables and MAIAC AOD) were fused to obtain estimation of PM_2.5 at the spatial resolution of 1 km. This inconsistency among spatial resolutions might introduce bias in estimation. We used the autoencoder-based residual deep network to downscale coarse-resolution images to fine-resolution ones with the features of elevation and coordinates to capture spatial variability. With high test accuracy in downscaling, we could reduce the bias. Second, the uncertainty analysis showed high uncertainty (the coefficient of variation) over the land-use of deciduous and mixed forests, and water body (e.g., lakes, rivers) for predicted PM_2.5. Since such predictions with high uncertainty made up a small proportion of all the pixel-level predictions in California and most subject locations for exposure estimation are likely located in more urbanized areas, away from the rural areas, we do not expect this pattern in uncertainties to introduce significant bias into the assessment of downstream population health effects. Third, our method generated weekly, not daily PM_2.5 at a spatial resolution of 1×1 km² to ultimately support epidemiological studies of pregnancy outcomes; however, we are encouraged by its performance and expect that it can be adapted and generalized to daily resolution.

6. Conclusion

This study presents an ensemble deep learning method to fuse multisource heterogeneous big data to estimate PM_2.5 over California, a large region with high variability in emissions, topography, meteorology, and wildfire events. To account for high spatiotemporal variability and complexity of PM_2.5 across California and across 10 years from 2008 to 2017, we imputed massive missing MAIAC AOD, extracted factors related with the emissions and constituents, included critical meteorological factors (e.g., PBLH and wind speeds at different altitudes) from M2GMI, fused wildfire smoke, and included traffic and land-use variables as well as temporal basis functions. Elevation and the coordinates were also used to account for spatial variability. In this study, the full autoencoder residual deep network was used in downscaling to reduce the bias by the difference in spatial resolutions from multiple sources of data, imputation of massive missing MAIAC AOD due to cloud, snow and high surface reflectance, and as base models in ensemble deep learning to model the non-linear associations and complex interactions among the variables. Compared with the existing models for the California region, our method improved test R² to 0.87 and reduced test RMSE to 2.29μg/m³. Prediction uncertainty estimates were derived, which can inform error assessment and model development in downstream evaluation of exposure and health effects of PM_2.5. Regarding the multisource features and the non-linear modeling method of deep learning, this study has important implications for improving spatiotemporal PM_2.5 estimation over a large, heterogeneous region.

Highlights.

• California has high variability in PM_2.5 sources, meteorology and topography

• We used ensemble deep learning with multisource big data to improve PM_2.5 estimates

• We reliably imputed missing satellite AOD and fused wildfire dispersion estimates

• Our model achieved high PM_2.5 prediction performance with uncertainty estimates