Impact of Using Uniform Attenuation Coefficients for Heterogeneously Dense Breasts in a Dedicated Breast PET/X-ray Scanner

Abstract

We investigated PET image quantification when using a uniform attenuation coefficient (μ) for attenuation correction (AC) of anthropomorphic density phantoms derived from high-resolution breast CT scans. A breast PET system was modeled with perfect data corrections except for AC. Using uniform μ for AC resulted in quantitative errors roughly proportional to the difference between μ used in AC (μ_AC) and local μ, yielding approximately ± 5% bias, corresponding to the variation of μ for 511 keV photons in breast tissue. Global bias was lowest when uniform μ_AC was equal to the phantom mean μ (μ_mean). Local bias in 10-mm spheres increased as the sphere μ deviated from μ_mean, but remained only 2–3% when the μ_sphere was 6.5% higher than μ_mean. Bias varied linearly with and was roughly proportional to local μ mismatch. Minimizing local bias, e.g., in a small sphere, required the use of a uniform μ value between the local μ and the μ_mean. Thus, biases from using uniform-μ AC are low when local μ_sphere is close to μ_mean. As the μ_sphere increasingly differs from the phantom μ_mean, bias increases, and the optimal uniform μ is less predictable, having a value between μ_sphere and the phantom μ_mean.

I. Introduction

PET/X is a rectangular breast PET scanner designed to mount onto a mammography machine and acquire registered PET/x-ray mammography images [1–4]. Fig. 1 shows the geometry used in this work and a photograph of the prototype PET/X scanner. There is interest in investigating correlations between response to breast cancer therapies as measured by changes in PET image biomarkers and conventional clinical response measures [5–13]. The goal is to use PET imaging in the neo-adjuvant setting for prognostic information, or as an early predictor of therapy efficacy. Understanding the quantitative bias and variance of biomarkers derived from PET/X images is needed to determine confidence limits on the biomarker results, statistical correlations with other biomarkers or outcome measures, and for powering clinical studies that use image biomarkers.

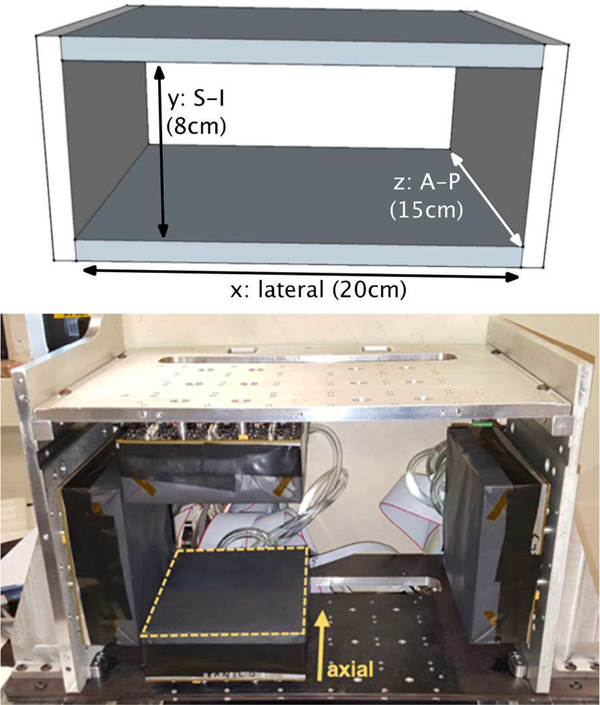
Fig. 1.

Top: Dimensions and coordinates of the four-sided rectangular PETX scanner used for this work. S-I: superior-inferior, A-P: anterior-posterior. Bottom: Photograph of the PETX scanner that consists of six flat detector panels, two of which are removed in the photo. This is a frame for benchtop testing only, not the mechanism that mounts to a mammography machine. Photos of a prototype mechanism for mounting the PET detectors on a mammography machine are shown in a separate publication [4].

Correcting for attenuated 511 keV photons is required for quantitatively accurate PET images. On clinical whole-body PET scanners this is done using a transmission image (e.g., an x-ray CT image on PET/CT scanners) that provides a map of linear attenuation coefficients (μ) within the subject being imaged. An accurate μ -map is critical for whole-body imaging because of the wide range of μ values within the body (soft-tissues, bone, lungs, and air). For dedicated breast PET imaging there is much less variation in μ of the object. In this simulation study we investigated the errors introduced when using a constant, uniform μ value to perform attenuation correction (AC) of emission data from an anthropomorphic, heterogeneously dense breast phantom object.

A variety of breast PET scanners have been developed and tested [14–22]. Certain designs are coupled to dedicated breast CT systems [17, 20], others are PET-only scanners, and so lack a registered anatomical image from which to derive AC maps. The breast PET scanner with perhaps the most reported clinical experience is the PEM Flex Solo II scanner (CMR Naviscan Corporation) [16, 23–28]. The PEM Flex does not use AC in the image reconstruction process. In acknowledging this lack of quantitative correction, the PEM Flex manufacturer recommended using a target-to-background ratio (TBR) measured from images in place of the conventional standardized uptake value (SUV) commonly used in whole-body PET imaging. Both SUV and TBR represent a ratio of target uptake to ‘background’ uptake: the SUV uses the ‘whole-body background’ represented by the injected activity divided by a patient volume surrogate (frequently patient mass); for the TBR, the background is taken as the mean value of a disease-free region within the image of the breast. In using the TBR, one hopes that the bias in measured uptake due to the lack of quantitative corrections will be roughly equal for the target and the background region, and thus will cancel in the TBR metric.

More recently, the MAMMI dedicated breast PET scanner has been made commercially available (OncoVision SE, [19]). The MAMMI scanner is a fully tomographic scanner in ring format, but, like the PEM Flex, it is PET-only without means to directly measure attenuation in breast tissue. MAMMI uses the approach that we aim to test in this study, namely, it uses a uniform attenuation correction to perform AC [29]. Note that this approach relies on having an estimate of the breast boundary based on the PET emission data, which is a subject that is not studied in the present work.

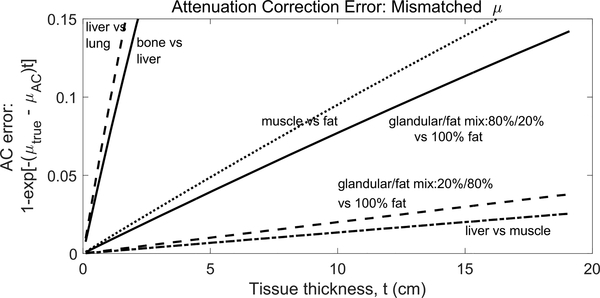
In this study we investigated the bias in PET image activity recovery when a uniform linear attenuation coefficient is used to correct attenuation from heterogeneously dense breasts. Fig. 2 shows the quantitative bias introduced to line-of-response (LOR) data when using an inaccurate linear attenuation coefficient in the AC process. The figure shows biases from attenuation coefficient mis-matches expected in dedicated breast PET imaging and in whole-body PET. It is known from prior studies that errors in local radiotracer uptake measures are proportional to errors in the AC map for that region [30]. Here we focused on two issues: errors introduced when using a uniform μ for AC when the object has non-uniform density and the relationship between those errors and the selected value of uniform μ. We compared quantitative accuracy in small spheres and background regions from images reconstructed with different AC maps. This provides fundamental comparisons based on anticipated attenuation coefficients in dedicated breast PET imaging.

Fig. 2.

Percent error when attenuation coefficients (μ) used for correction are not matched to the attenuation coefficient of the medium being imaged. Different coincidence lines-of-response will experience different errors depending on the tissue thickness they traverse. This is a simple one-dimensional calculation using attenuation coefficients from SimSET tables. Table I gives μ values of mixed breast tissue used in this work.

II. Materials and Methods

A. PET/X Scanner Model

We simulated the PET/X scanner using the SimSET simulation package [1, 3, 31]. The scanner model consisted of four monolithic panels of perfect absorber material forming a rectangle field of view (FOV) as shown in Fig. 1. The two larger panels were 20 cm in the patient lateral dimension; the two smaller panels were 10 cm in the superior-inferior dimension. All panels were 15 cm in the anterior-posterior dimension, corresponding to the axis of the scanner. The larger panels were separated by 8 cm (Fig. 1), creating a 20 cm × 8 cm × 15 cm FOV.

B. Digital Breast Phantoms

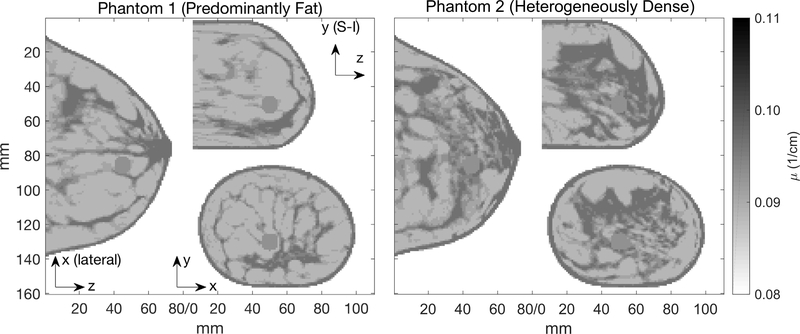
Anthropomorphic digital breast phantoms were created from high-resolution dedicated breast CT scans of disease-free breasts [32], and segmented into 5 tissue densities representing a range of adipose/glandular mixtures. A finite-element application was used to compress each phantom to a 78 mm thickness [33]. Fig. 3 shows the two phantoms used here, one with ‘predominantly fat’ tissue density, and another with ‘extremely dense’ density.

Fig. 3.

Breast phantoms shown here and used in simulations have 1.0 mm voxels and attenuation coefficients given in Table I. They were down-sampled from 0.5 mm high-resolution dedicated breast CT scans with indexed density values [32]. The 3-D outline of each breast phantom #1 and #2 is the same. A third phantom with uniform μ was also created with the same outline. The image slices shown here contain sphere #2.

Breast tissue linear attenuation coefficients for use in SimSET were estimated by comparing breast tissue Hounsfield units (HU) to other tissue HUs in several clinical CT scans. The SimSET package contains tables of attenuation coefficients for several materials, but not for breast fibroglandular tissue. Using a utility within SimSET, attenuation tables for mixed-tissue materials were created as surrogates for the mixed adipose-glandular tissues of the breast. The HU values observed in the breast tissue on CT scans ranged from that of adipose tissue at the low density end to a maximum density somewhat lower than muscle. Based on these observations, five adipose-muscle mixed-tissue linear attenuation coefficients were created to represent different mixtures of adipose and glandular tissue (Table I). The material with 20% adipose and 80% muscle was the highest density tissue in the phantoms.

TABLE I.

Linear Attenuation Coefficients (μ) in the Breast Phantom Object

% adipose	% muscle	μ(511keV) (10−3/cm)
0	0	0.11 (Air)	μair
100	0	88.65	μ100
80	20	90.67	μ80
60	40	92.69	μ60
40	60	94.68	μ40
20	80	96.67	μ20
Mean μ Phantom 1		90.756	μmean1
Mean μ Phantom 2		91.946	μmean2

Two spheres with uniform μ and 10 mm diameter (543 voxels) were inserted into the phantoms with locations given below. Image activity quantification was studied using these spheres as the regions of interest. The sphere μ value was set to μ₂₀, μ₆₀, and μ₁₀₀ in separate simulations. The relative activity level of the spheres is described below.

The sphere locations within the 200 mm (x) by 80 mm (y) by 150 mm (z) FOV were: sphere #1 at (x, y, z) = (90, 50, 20); sphere #2 at (x, y, z) = (110, 30, 50). For presentation purposes, images shown in figures 3, 5, and 6 truncate empty space, e.g., only 160 mm and 100 mm of the 200 mm x-dimention are shown in the x-z and x-y planes, respectively. Thus, sphere locations in the figures can appear offset with respect to the full FOV coordinates.

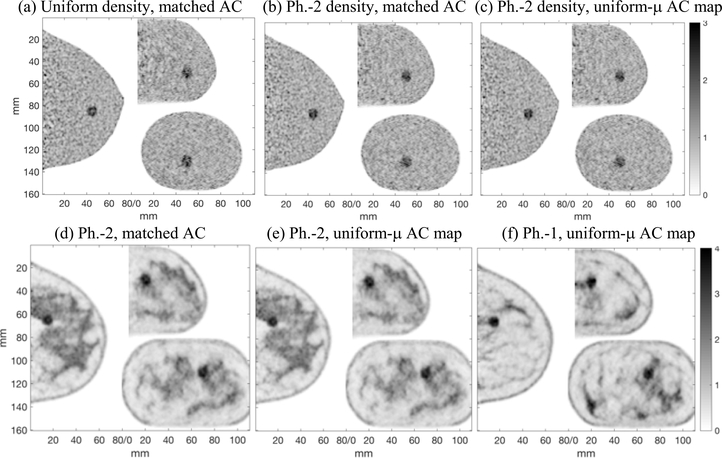
Fig. 5.

Top row: Images of the phantom with uniform background activity, 10mm sphere #2 with TBR=2, and (a) uniform density, reconstructed with matched AC, (b) anthropomorphic density (Phantom-2), reconstructed with matched AC, (c) anthropomorphic density (Phantom-2), reconstructed with a uniform-μ AC map (μ_AC = μ_mean2). The top row images are shown with no post-reconstruction smoothing to illustrate the noise level. Bottom row: Images of the phantoms with non-uniform activity distribution, sphere #1, and anthropomorphic density: (d) Phantom-2 reconstructed with matched AC, (e) Phantom-2 reconstructed with uniform-μ AC map, (f) Phantom-1 reconstructed with uniform-μ AC map. A 3D Gaussian post-reconstruction smoothing (sigma = 0.75mm) was applied to the images in the bottom row. Single 1mm thick slices are shown in all cases. Artifacts from mis-matched AC are not observed.

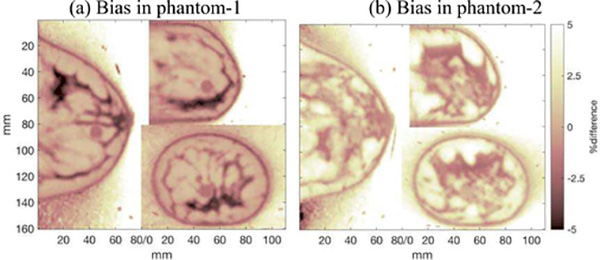
Fig. 6.

Voxel-by-voxel bias images: (100%)(V_uniAC - V_matchAC) / (V_matchAC), where V_uniAC and VmatchAC are the image volumes reconstructed with uniform AC (μ_AC = μ_mean) and matched AC, respectively. A single slice of the difference images are shown here for the phantoms with uniform background activity, TBR = 4, and (a) Phantom-1, and (b) Phantom-2 attenuation distributions. The difference images were very similar for the corresponding cases of images of the phantoms with heterogeneous activity distribution. Outside of the breast object (air), activity image voxel values are nominally zero; image reconstruction yielded small finite values in these voxels, resulting in finite bias for these voxels.

C. Data Simulation and Image Reconstruction

In order to support the PET/X FOV geometry in SimSET, it was necessary to use a custom user function. First, annihilation photons from the object were tracked through the attenuating phantom to an over-sized SimSET object cylinder (larger than the PET/X FOV). Then, the photon paths were re-projected back to the surface of the PET/X scanner using a custom user function. In the present work these photon positions were the final detected positions due to the perfect absorber modeled here. In general, the SimSET detector module can be used at this point to subsequently track the photons through the PET/X detector material [3].

Fifty million positron decays were simulated from the phantoms. Positron range and photon acolinearity were not modeled, and scattered photons were rejected.

Coincidence data between all possible detector panel pairs were binned into planograms using 2 mm bins. Image reconstruction was performed using a 3D MLEM algorithm with a system matrix derived from distance-driven projectors. The image voxels were 1 mm cubes. The algorithm was developed by Qian et al. specifically for PET/X [2]. The algorithm includes geometric corrections and attenuation correction, but uses no regularization and has yet to be optimized. Post-reconstruction smoothing was applied in certain cases as described in the Results section, but given the idealized simulation conditions and focus on the effects of AC in this work, systematic post-reconstruction smoothing was not investigated; most results were calculated without smoothing.

D. Phantom Configurations and Attenuation Correction (AC)

Different combinations of uniform and anthropomorphic activity and attenuation distributions were simulated. Some of the combinations were unrealistic or idealized but useful for the purposes of studying the quantitative accuracy of radiotracer activity recovery in images. For example, phantoms were simulated using an anthropomorphic distribution of attenuating material (Fig. 3) but with a uniform activity distribution. The simulated emission data were corrected for attenuation using an AC map that matched the heterogeneous object and with AC maps derived for phantoms of uniform μ.

The combinations of simulated attenuation and activity distributions are given in Table II. Simulated emission data from phantoms with anthropomorphic density distribution were reconstructed using a series of AC maps derived for a uniform attenuation coefficient phantom; each of the linear attenuation coefficient values listed in Table I were used for AC (the mean μ was used only for its corresponding phantom and μ of air was not used).

TABLE II.

Combinations of uniform and heterogeneous objects and AC maps

Phantom background activity	Phantom density distribution	AC μ-map	Object-to-AC correspondence	Objective
Uniform	Uniform	Uniform	Matched μ value	Establish baseline quantitative accuracy for 10 mm diameter hot spheres.
Uniform	Anthropomorphic	Anthropomorphic	Matched	Baseline quantitative accuracy in presence of non-uniform attenuating medium.
Uniform	Anthropomorphic	Uniform	Mis-matched	Evaluate impact of using uniform μ AC to correct data from non-uniform attenuating medium.
Anthropomorphic	Anthropomorphic	Anthropomorphic	Matched	Investigate additional impact of non-uniform activity distribution on above results.
Anthropomorphic	Anthropomorphic	Uniform	Mis-matched

In all cases, the 3D outline shape of the breast object was perfectly matched by the AC-map.

Small spheres with elevated activity concentration were used to simulate lesions in which activity recovery was studied (Fig. 3). The spheres had either twice (TBR=2) or four-times (TBR=4) higher activity concentration than the uniform background activity.

Anthropomorphic activity distribution was also used in the simulations to simulate more realistic conditions. The simulated activity distribution followed the attenuation distribution, with higher activity assigned to higher density (μ) areas. The contrast of the hot spheres is less well-defined for these phantoms because the background surrounding the sphere was not uniform.

A 40 mm diameter hot sphere in the uniform phantom was simulated separately and reconstructed using a matched AC map in order to examine baseline results for a case where partial volume errors are minimized or eliminated.

E. Image Metrics

The primary aim of this work was to compare image quantification between images reconstructed with a matched AC map and images reconstructed with mis-matched AC maps derived from a uniform μ throughout the object. We studied this using the activity in small hot spheres and the root mean square error between the full image volumes. TBR and relative recovery coefficients were also investigated.

Quantitative Bias

The bias in the sphere activity was calculated as the percent difference between sphere volume of interest (VOI) values extracted from images reconstructed with matched AC and images reconstructed with uniform AC factors:

$$Bias=(100\%)(S_{uniAC}-S_{matchAC})/\left(S_{matchAC}\right)$$ Eqn. 1

where S_uniAC and S_matchAC are the sphere VOI values from the images reconstructed using a uniform-μ AC and matched-AC, respectively.

VOIs used to calculate activity from the 10 mm spheres consisted of the sphere voxels defined in the phantom with a single layer of voxels removed from the perimeter of the sphere, resulting in 8 mm diameter VOIs (309 voxels).

TBR

Image TBR was calculated from images reconstructed with different AC methods to observe quantitative bias in this metric for different AC maps. Calculation of the background VOI values used in the TBR metric is described below.

Sphere bias and TBR were studied as a function of the μ value used in the uniform-μ AC maps. Results are presented as a function of Δμ, where Δμ is the percent difference between the constant attenuation coefficient used for image reconstruction (μ_AC) and the mean attenuation coefficient of the anthropomorphic phantom (μ_mean):

$$\mathrm{\Delta }\mu =(100\%)({\mu }_{\mathrm{AC}}-{\mu }_{\mathrm{mean}})/\left({\mu }_{\mathrm{mean}}\right)$$ Eqn. 2

RMSE

The root mean square error (RMSE) was calculated between images reconstructed with different AC methods and between images and phantoms. The 10 image slices closest to the chest wall were removed from image volumes when calculating the RMSE. These image slices are at the edge of the PETX ring and experience higher random noise due to lower geometric sampling than slices closer to the FOV center.

Relative Activity Recovery and Image Background Noise

Relative activity recovery and image noise were used to assess the baseline performance of the simulated system and to select reconstruction iteration number used for the analyses. The relative activity recovery, C_R, was defined as the TBR measured from images divided by the true TBR in the phantom object:

$$C_R=\frac{S_{img}/B_{img}}{S_{ph}/B_{ph}}$$ Eqn. 3

where S_img, B_img, S_ph, B_ph are the activities taken from the sphere and background VOIs of the image and phantom.

Image noise was calculated using the Background Variability (BV) metric defined in the NEMA Image Quality Phantom testing report [34]. For the breast phantom used in this work, BV was calculated using 32 VOIs within the phantom background: the VOIs were the same shape and size as the spheres with 8 each distributed (away from the hot spheres) on 4 image slices separated by 1 cm. For TBR calculations, data from the 8 background spheres on the image slice nearest to the hot sphere were averaged to obtain B_img. The same was done for non-uniform activity images; in this case, B_img was not from a uniform region but it serves for comparing images reconstructed with matched-AC to those reconstructed with uniform- AC because they have the same underlying phantom voxel values.

III. Results

Results are presented beginning with baseline performance of the modeled system using matched AC maps. These results were then used as the standard against which local errors (bias) and global errors (RMSE) were measured in subsequent sections that present data from images reconstructed with uniform- μ AC maps.

A. Baseline Performance: Matched AC

Approximately 12M (24%) of the simulated decays were detected in the idealized scanner with perfect absorber detector material.

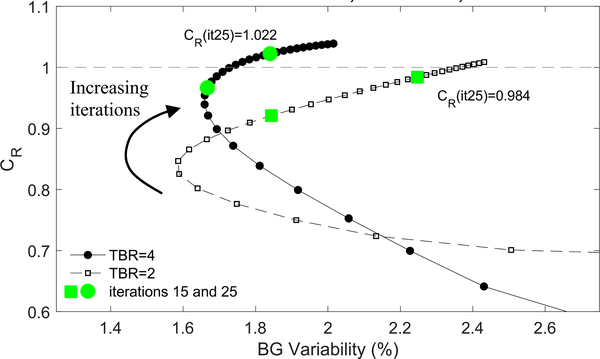
The BV noise metric reached a minimum of 1.6%-to-1.7% after 10-to-15 iterations of the reconstruction algorithm and increased slowly for higher iterations (Fig. 4).

Fig. 4.

C_R in the 10-mm diameter sphere-2 vs. BG-Variability in images of the phantom with uniform activity and uniform attenuating background reconstructed with matched AC μ-map.

Activity recovery in the 40 mm sphere converged to C_R = 0.99 at iteration 7 (iteration 11) for phantom TBR=4 (TBR=2).

Relative activity recovery in the 10 mm diameter spheres is shown in Fig. 4 as a function of BG Variability for increasing iterations of image reconstruction. Fig. 5 shows results from images of the phantom with uniform activity and uniform attenuation that were reconstructed with matched AC.

Except as noted, images and activity recovery data presented in the following sections are taken from the iteration 25 images with no post-reconstruct smoothing. In Table III the sphere maximum values were taken from image iteration 25 with a 3D Gaussian smoothing (σ = 0.75mm) applied to mitigate noise in the VOI maximum metric. Performing post-reconstruction 3D Gaussian smoothing reduced the C_R mean values, but did not change the relative findings of this work.

TABLE III.

Activity Recovery in Images (iteration=25) with uniform back ground activity and matched AC

Phantom density distribution	Sphere Contrast in the Phantom (TBR)	Sphere Number	Image CR Matched AC
			mean	max*
Uniform	2	1	0.90	1.12
		2	0.98	1.15
	4	1	0.98	1.16
		2	1.02	1.15
Anthropomorphic Phantom 1 (‘predominantly fatty’)	2	1	0.92	1.10
		2	0.98	1.15
	4	1	0.97	1.17
		2	1.02	1.18
Anthropomorphic Phantom 2 (‘heterogeneously dense’)	2	1	0.94	1.38
		2	1.02	1.28
	4	1	0.98	1.30
		2	1.05	1.22

^*VOI max values were taken from smoothed images; see text.

B. Images with 10 mm Diameter Spheres

Images of the phantoms with 10 mm diameter spheres are shown in Fig. 5. Examples are shown with different combinations of uniform and anthropomorphic activity, attenuation, and attenuation correction. There are no obvious artifacts from the use of a uniform-μ AC map; the images generated with mis-matched AC maps are visually almost indistinguishable from the images reconstructed with matched AC maps.

C. Activity Bias Images

Fig. 6 shows the activity bias in images reconstructed with uniform-μ AC relative to matched-AC. The displayed image slices contain one of the 10 mm spheres with elevated activity. The mean μ of each phantom was used for the uniform-μ AC map in these difference images (μ_AC = μ_mean). The bias within the images reconstructed using uniform-μ AC maps mimics the mis-match between attenuation coefficients in the object and reconstruction process. This can be seen by comparing the bias images in Fig. 6 to the phantoms shown in Fig. 3; regions of the bias images where the phantom μ is high have negative bias corresponding to under-correction, and vice-versa.

The biases in images of phantoms with non-uniform activity distribution were similar qualitatively and quantitatively.

D. Image RMSE, Sphere Bias, and TBR

Image metrics were compared between images reconstructed with matched AC maps (baseline) and images reconstructed with uniform AC maps using six μ values listed in Table I (excluding air μ, including the corresponding phantom mean μ).

Table IV contains the RMSE between images and phantoms for images reconstructed with matched and mis-matched AC for different phantom configurations and the case of μ_AC = μ_mean. The aim here is to compare the ‘Matched AC’ and ‘Uniform μ-AC’ columns; the absolute RMSE values between images and phantoms are not the focus of this work but provide context for the comparison across different phantom configurations for the case of a single uniform μ_AC.

TABLE IV.

RMSE

Object			RMSE: Image vs. Phantom (arbitrary voxel units)
Phantom		TBR	Matched AC	Uniform-μ AC
Activity	Attenuation
Uniform		2	64.81
Uniform		4	65.76
Uniform	Anthro.1	2	64.76	64.78
Uniform	Anthro.1	4	65.75	65.76
Uniform	Anthro.2	2	64.89	64.79
Uniform	Anthro.2	4	65.88	65.77
Anthro.1		N/A	73.88	73.44
Anthro.2		N/A	74.28	73.70

Anthro.1/2: Anthropomorphic activity distribution in phantom 1/2 (TBR: N/A for anthro. activity distribution). Uniform-μ AC: μ_AC = μ_mean

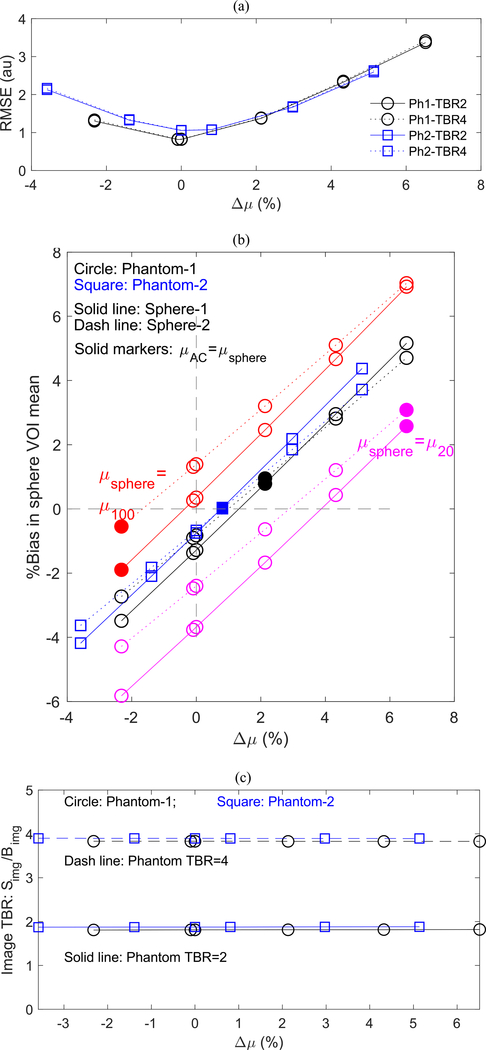
Fig. 7 shows the impact of uniform-μ AC for varying μ_AC values on (a) global RMSE between images reconstructed with matched and uniform-μ AC, (b) bias in 10 mm diameter hot sphere VOI mean, and (c) TBR: S_img/B_img. Each metric is shown as a function of Δμ, the difference between the constant μ value used in the AC (μ_AC) and the mean phantom μ (μ_mean). Results in Fig. 7 are from simulations in which μ_sphere = μ₆₀(Table I). Fig. 7(b) includes results from separate simulations in which μ_sphere was equal to μ₂₀ and μ₁₀₀. The solid markers in Fig. 7(b) indicate, via Δμ (Eqn. 2), where μ_AC matched μ_sphere. Only the sphere voxel μ values were modified in these separate simulations (i.e., the anthropomorphic phantoms were otherwise the same across all simulations).

Fig. 7.

As a function of Δμ: (a) Global RMSE between image volumes reconstructed with matched and uniform AC maps. (b) Bias in 10mm diameter sphere VOI mean for TBR = 2. The sphere VOI maximum values followed similar linear relationships. Solid markers indicate the case where μ_AC = μ_sphere. Simulations used μ_sphere = μ₁₀₀, μ₆₀, and μ₂₀. Results were equivalent for TBR = 4 images. (c) S_img/B_img for sphere VOI mean. S_img/B_img for sphere VOI max was similarly constant with varying Δμ. These results were independent of the μ of the sphere.

For images of phantoms with non-uniform activity distribution, the RMSE, sphere bias, and TBR vs. Δμ relationships were similar to those shown above for uniform activity phantoms.

IV. Discussion

This study compared activity recovery in simulated breast PET images that were reconstructed using AC maps ideally matched to the phantom object and using AC maps with a uniform-μ. Three digital breast phantoms were used, one with uniform attenuation and two others derived from high-resolution breast CT scans; one characterized as having predominantly fatty tissue distribution and the other was heterogeneously dense. Breast PET detector properties and other data corrections were idealized to examine the effect of AC alone.

The variability in attenuation coefficient for 511 keV photons in breast tissue is less than for other parts of the body. Fig. 2 shows an estimate of errors introduced in LORs when the wrong μ is used for the AC process. The errors for breast tissues are considerably less than worst-case scenarios found in whole-body PET scanning, but LOR errors in the 5%-15% range could occur in the worst-case scenario of μ mis-match for breast (i.e., μ of adipose tissue vs. μ of glandular tissues).

AC error artifacts were not observable in images of the anthropomorphic phantoms reconstructed with uniform AC (Fig. 5). Also, there was no substantial difference in the RMSE of the images reconstructed using matched or uniform AC map with respect to the phantom (Table IV ‘Matched AC’ column vs. ‘Uniform-μ AC’ column).

Globally, reconstructed activity bias was minimized when the μ value used in uniform-μ AC maps was equal to the mean μ value of the phantom, as demonstrated by the image-wide RMSE (Fig. 7a). Bias was measured against the image reconstructed with matched AC maps.

Closer inspection of the image quantification showed a bias in activity recovery proportional to the mis-match in μ between the phantom and the uniform μ AC map, as seen in the activity bias images in Fig. 6. The first impression is that quantitative errors in sphere activity recovery would be proportional to the difference between sphere μ and the μ used in the uniform AC map. Indeed, bias in the 10mm spheres varied linearly with μ value used for uniform-μ AC (Fig. 7b). However, using the sphere μ as the constant μ value for uniform- μ AC did not clearly outperform the case of using the phantom mean μ for uniform-μ AC. Results were consistent for each phantom and each TBR value, and varied somewhat for the two spheres that were placed in different local surroundings and FOV position. Quantification of sphere VOI maximum values followed the same trends but suffered higher bias and variability compared to the sphere VOI mean values. Generally, the bias in the spheres would be minimized for an AC map with constant μ value somewhere between the sphere μ and the phantom mean μ. Thus, if the mean phantom μ or the sphere μ are used in a uniform-μ AC map, the biases will be largest when the sphere μ value is at the extremes of the range of object μ (Fig. 7b). Since even ‘heterogeneously dense’ breast tissue contains substantial amounts of adipose tissue, mean μ values (at 511keV) for breast tissue will tend to be closer to the low density (adipose) values than to that of glandular tissue (Table I). This means that spheres/lesions embedded in tissue with μ value at the high extreme (glandular) will suffer larger biases than those embedded in the low density extreme (adipose) when using mean phantom μ or sphere/lesion μ for uniform-μ AC.

Absolute quantification, as discussed above for the hot sphere VOIs, represents the metric most used in clinical WB PET imaging in the form of the SUV. Alternatively, local contrast in the hot spheres, TBR, measures local activity normalized to surrounding non-target tissue activity. The consistency in activity bias between background regions and hot spheres resulted in TBR independent of the μ value used in uniform- μ AC (Fig. 7c). Using a relative uptake measure requires selection of a representative background region and introduces the uncertainty of the background VOI into the uptake metric. In practice, selection of a consistent background region could be challenging, depending on the radiotracer. For example, FDG is taken up non-uniformly in the breast and thus finding a consistent background region could be challenging. Other highly specific radiotracers may have little or no background uptake to use in a relative measure. On the other hand, it can be argued that for the application of measuring response to therapy, where two scans are relatively close in time and can be acquired and reconstructed under very similar conditions, the background conditions should remain sufficiently consistent for use in normalizing target uptake.

The mean attenuation coefficient for 511 keV photons within a patient breast is not known in practice. The attenuation factors used in this work were based on the surrogates described in section II.B. X-ray-based imaging (mammography, tomosynthesis, CT) is typically performed for breast cancer patients and holds potential for estimating μ values for use in breast PET AC. Methods for estimating μ values from these forms of x-ray imaging could follow methods used for estimating PET μ values from clinical CT, with appropriate measures taken to account for the energy difference between clinical CT and breast x-ray imaging modalities. Methods for quantitative measures of breast density have been the subject of considerable research in recent years (e.g., [35]), although they do not address converting the density to 511 keV linear attenuation coefficients.

The PET/X image reconstruction process has not been fully optimized and lacks corrections other than AC and geometric sensitivity. The image quantification capabilities of this preliminary reconstruction process were studied in this work and in a prior study [3]. For ‘baseline’ performance, i.e., using matched AC, the activity recovery readily converged in the 40 mm sphere (section 3.1). Fig. 4 shows the activity recovery trend in the 10 mm spheres, where partial volume effects and dependence on reconstruction iteration number are seen. Variations in sphere quantification due to position within the PETX FOV may contribute to the observed different results for the two spheres in this study. These baseline results were included for reference to illustrate the level of quantitative accuracy achieved by the current image reconstruction process. However, the emphasis of this study was not absolute quantification of baseline images, but rather on comparing image quantification between baseline images and those reconstructed with uniform-μ AC maps.

The simulated emission data analyzed in this work were generated under idealized conditions. We chose these conditions to focus on the errors due to the attenuation correction process. Hot spheres mimicking lesions were sized for expected clinical relevance where some degradation from the partial-volume effect is experienced. More realistic detector and scanning parameters based on estimations or preliminary results from the prototype PETX scanner could have been used. However, data corrections such as normalizations and the reconstruction process are not yet optimized, thus, we did not see the benefits of introducing estimated scanner performance metrics that would have added uncertainty and potentially occluded the impact of AC errors.

The ultimate impact of using a uniform-μ AC map for quantitative breast PET, and the clinical acceptability, must be determined with an operating scanner and by the goals of clinical applications. The preferred method will be to use a reliable measured AC map. The PET/X scanner is designed to operate on a clinical mammography system. We have initiated studies into the use of a (2D planar) mammogram to estimate an AC map for correcting PET/X emission data [36]. The dependence of lesion quantification accuracy on attenuation properties of the breast presented in this work may be applied in the development and use of 3D attenuation correction methods derived from 2D attenuation images (2D mammography), e.g., by guiding image-specific priorities for the derived AC map to best improve image quantification accuracy depending on the local attenuation environment of the lesion of interest. Other methods under development include coupling breast PET to breast CT and (pseudo-3D) tomosynthesis are other approaches under development [17–18].

While the adaptation of x-ray based breast imaging for breast PET AC was not investigated here, we believe the present work establishes performance to which future AC methods can be compared, and could be applicable to breast PET systems currently in use: PEM Flex Solo II (which uses the TBR metric) and MAMMI (which uses the uniform-mu AC method).

V. Conclusions

For 511 keV photons, the variability of attenuation coefficients of breast tissues is relatively small, and the use of a uniform μ AC-map that ignores this variability leads to activity recovery inaccuracies in PET images that are correspondingly small. Quantitative inaccuracies scaled linearly with the μ value used for constant- μ AC. Globally they were minimized when the μ value used for constant- μ AC was equal to the mean μ of the heterogeneously dense object whereas the bias in localized hot spheres was minimized for an AC μ between that of the local sphere and the overall phantom mean μ. Quantitative bias in the image background and in the hot spheres was equivalent, leading to locally calculated sphere contrast quantification that was independent of the μ used in uniform μ AC.