Effects of TOF Resolution Models on Edge Artifacts in PET Reconstruction from Limited-Angle Data

Abstract

Limited-angle data, such as data obtained from a dual-panel Breast-PET scanner, result in substantial image blur in directions coinciding with the missing cone of the image spectrum. On systems with time-of-flight (TOF) capabilities, this blur is reduced as given by the TOF uncertainty, with the image spectrum being correspondingly expanded into the missing spectral cone. Modeling of the TOF uncertainty in the reconstruction is expected to deconvolve this residual TOF blurring. We have however observed that, as a tradeoff, this TOF de-blurring process also introduces ringing artifacts at the edges, analogous to the edge effects observed with line-of-response (LOR) resolution modeling, which attempts to deconvolve the blur due to detector resolution effects. However, in the former case, the ringing artifacts are much wider due to the spatial extent of the TOF uncertainty as compared to the width of typical LOR resolution blur. We illustrate and investigate the effects of using matched, as well as under-modeled and over-modeled, TOF kernels on edge artifacts in reconstruction from limited-angle data, and compare them with TOF reconstructions of complete data. Although for the conventional data with full angular coverage the reconstruction is fairly insensitive to the exact size of the TOF kernel and TOF modeling does not produce ringing artifacts, it is not the case for the limited-angle data. We show that it is important to use some form of regularization of the TOF uncertainty deconvolution process within reconstruction of the limited-angle data, such as decreasing the TOF kernel size.

I. INTRODUCTION

POSITRON emission tomography (PET) data acquired on a system with time-of-flight (TOF) capabilities are typically reconstructed with a TOF kernel matched to the TOF resolution of the PET system. Although it was shown that such kernel provides optimum signal-to-noise (SNR) performance, the SNR value changes very slowly with the TOF kernel size, and moderate under- or over-modeling of the kernel show only small impact on the image quality for the PET systems with complete data [1]. Unlike resolution modeling of the point spread function (PSF) which causes ringing (Gibbs-like) artifacts even when reconstructed with a matched resolution kernel [2, 3], matched TOF kernel does not suffer from this issue for the conventional full-ring systems (as illustrated in Fig. 1-first column).

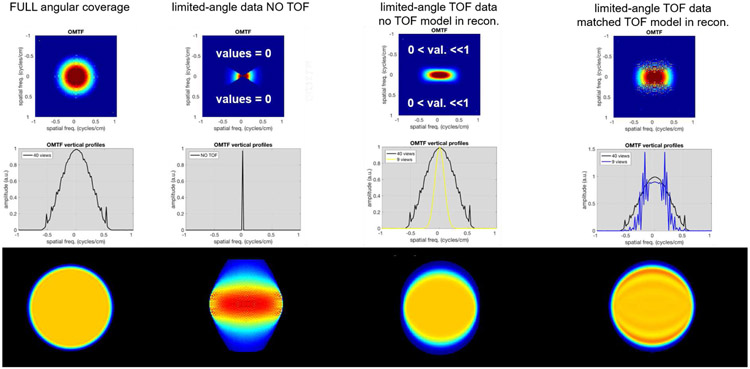
Fig. 1.

Illustrations of reconstructed images and their spectral content for the full angular coverage and limited-angle systems. Top row: Object-specific modulation transfer functions (OMTF, [2]) of the reconstructed images slightly smoothed to focus on the shape. Middle row: Central vertical profiles through the OMTFs. Bottom row: Corresponding reconstructed images. 1^st column: Full angular coverage reconstruction (the small ripples are due to discretization). 2^nd column: Limited-angle reconstruction from non-TOF data (i.e. for data acquired on a system without TOF capabilities). 3^rd column: Limited-angle reconstruction from TOF data, but without TOF modeling (i.e. for data acquired on a system with TOF capabilities, but reconstructed without modeling the TOF uncertainty). 4^th column: Limited-angle TOF reconstruction using matched TOF kernel.

For systems with limited angular data, such as a dual panel Breast-PET (B-PET) system [4, 5, 6, 7] or a dual-panel PET system for radiation deposit imaging during proton therapy [8, 9], substantial image blur is inherent in the directions coinciding with the missing cone of the image spectrum (Fig. 1-second column). Adding TOF capabilities to the scanner makes it possible to estimate the approximate location of each annihilation event along the line-of-response (LOR) based on the measured arrival time difference of the generated photon pairs. This in turn allows to reduce the limited-angle related blur along LORs to the extent given by the TOF measurement uncertainty, with the image spectral data being correspondingly expanded into the missing spectral cone (Fig. 1-third column). For limited-angle data, the TOF can thus provide new information by reducing the missing cone region in frequency domain [10]. This TOF uncertainty can be further modeled within TOF reconstruction in order to attempt to deconvolve this blur and recover the suppressed information in the corresponding spectral cone. However, due to the values in this region being very small and susceptible to noise, the inverse problem of deconvolution becomes ill-posed. Consequently, when modeling the uncertainties at matched TOF kernel (as conventionally performed with a full ring system), the corresponding suppressed frequencies are not properly recovered which results in oscillations and Gibbs-like artifact in the reconstructed image (Fig. 1-fourth column).

In our previous research, using limited-angle data from a realistic GATE simulation of a dual-panel B-PET system with TOF capabilities (currently being developed by our group [4]), we have proposed and investigated spatially-variant image-based resolution models to reduce the effects of strong PSF deformations caused by the limited-angle and depth-of-interaction inherent of this system [5, 6]. Although application of the spatially-variant PSF models led to better and more uniform quantification of small lesions across the field-of-view (FOV), efficacy of such an approach is limited to small objects, such as point-sources and small lesions. On the other hand, large object deformations caused by the limited-angle reconstruction cannot be corrected with PSF modeling alone. Although using the TOF information in reconstruction is of crucial benefits here, as discussed above, we have observed that using accurate TOF kernels for the limited-angle data reconstruction produced ringing artifacts, propagating from the edges of the deconvolved object, with their amplitude and spatial extent being quite large due to the size of the TOF resolution kernel (which is typically about an order of magnitude longer as compared to the LOR resolution width for current TOF systems with about 300ps timing resolution).

To get a better understanding of these artifacts, in this work we investigate and demonstrate the effects of TOF models on edge artifacts by using idealized limited-angle and full ring system data, for which the reconstruction model is perfectly matched to the generated data in order to avoid any possible effects caused by an imperfect reconstruction model. We propose and investigate a simple regularization method to reduce the edge artifacts by reducing the TOF kernel width applied within reconstruction, analogous to reducing the width of the conventional LOR resolution model [2, 3]. We further compare those results with an approach using post-smoothing, in the direction of the missing data, for the limited angle case (that is, in the direction of the Gibbs-like oscillations from the reconstruction using the matched TOF kernel). Finally, we demonstrate the studied effects and approaches using more realistic simulated data for our dual-panel B-PET scanner.

II. METHODS

A. Idealized simulations of complete and limited-angle data

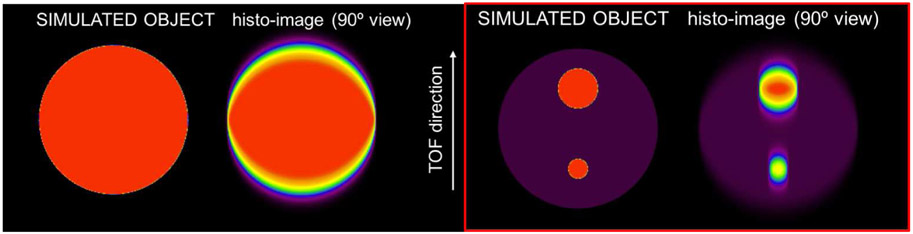
We simulated data for a 2D full-ring system with a timing resolution of 300ps at full-width at half-maximum (FWHM) TOF kernel (emulating the TOF FWHM of our developed B-PET system), corresponding to ~45mm FWHM in the spatial domain. The first simulated object consisted of a large 35cm diameter uniform disk (Fig. 2-left). The object size was made large enough to avoid interaction of oscillations from opposing edges (with the extent of the oscillations being related to the TOF kernel size) and focus on the edge effects only. Then, in order to investigate the effects of potential oscillation interactions inside the object, we simulated a second object which consisted of the large uniform disk with a 45mm diameter insert (matching the simulated timing resolution width of ~45mm) and an insert twice that size (90mm). Both inserts were simulated with an 8:1 activity to background ratio (Fig. 2-right).

Fig. 2.

Simulated 2D objects with corresponding histo-image at 90°. Left: Uniform 35cm diameter object. Right: Uniform 35cm diameter object with two inserts (45mm and 90mm in diameters) with an 8:1 activity to background ratio.

To simulate the 300ps timing resolution, each object was forward-projected with a 300ps FWHM TOF kernel. The forward projection was performed using the Direct Image REConstruction for TOF (DIRECT) approach [11] with 60 transaxial views over 180°, with 3° angular steps. To focus our analysis on the effects of using different TOF kernel size in reconstruction, and avoid confounding the results with noise, no noise was introduced into these idealized simulated data.

B. 3D GATE simulation of dual-panel B-PET data

To verify the observations made using idealized 2D data and their implications for realistic 3D limited-angle data, a GATE simulation [12] of our B-PET system was performed for a breast phantom, with realistic attenuation structures, with and without lesions.

As presented in our previous work [6], the simulated B-PET system, which has a timing resolution of 300ps ¹. consisted of two flat detector panels 9cm apart, each with dimensions of 20cm×10cm and with 1.5mm×1.5mm×15mm LYSO crystals, giving the maximum transaxial angular range of ±66° in the center of the FOV (i.e. maximum 73% angular coverage in the center and gradually decreasing out of the center) and maximum axial angular range of ±48° (Fig. 3).

Fig. 3.

Diagram of the simulated B-PET system including the uniform breast (left and center), with the illustrated maximum angular coverage at the center of the FOV (right) (note that the angular coverage decreases for the out-of-the-center locations).

The uniform phantom (without lesions) consisted of an anthropomorphic compressed breast phantom with dimensions of 12.60cm×6.80cm×6.15cm [13], while the lesion phantom additionally contained a set of thirty-five simulated lesions, i.e. 5mm diameter spheres (7 spheres in x and 5 spheres in y, spaced every 12.5mm on each side of the center) with an 8:1 activity to background ratio. To reduce the impact of noise and focus our analysis on the edge effects while using different TOF kernel sizes in reconstruction, a high-count simulation (~100 million counts collected over a 100 minutes imaging time) was performed.

C. Reconstruction parameters

For the idealized simulations, we used all 60 simulated transaxial views for reconstruction of the complete angular coverage data. For the limited-angle case, we limited the number of views to 9 central transaxial views (from 60), which corresponds to ±13.5° angular range (giving a 15% uniform angular coverage throughout the FOV for the idealized data). For these idealized data, we dramatically restricted the angular coverage to focus on the limited-angle effects. Nevertheless, these results are related to, and confirmed by, the more realistic simulation of our B-PET system which has larger (but spatially variant) angular coverage. The reconstructed image consisted of a grid of 576×576×1 voxels with a size of 1mm³. In this study, the same (matched) forward-projector used to create the simulated data was also used for the reconstruction. Reconstruction was performed using DIRECT [11] with the row-action maximum likelihood algorithm (RAMLA) [14] for a total of 600 iterations with a relaxation parameter of 0.1. Four different TOF kernels were applied separately during reconstruction: two narrower TOF kernels (FWHM = 250ps, 275ps), and a wider kernel (FWHM = 350ps) to observe the effect of under- and over-modeling the simulated timing resolution of 300ps, as well as a matched 300ps TOF kernel.

For the GATE simulations of our dual-panel B-PET system, only the limited-angle case was considered, since the dual-panel detector scanner is intrinsically a limited-angle system. The simulated list data were deposited into histo-images with a set of 39 transverse views (with 3° angular steps within ±58.5°) and 15 axial tilts (with 4.7° angular steps). The histo-images for angles other than those perpendicular to the detector panels contained missing data regions within the object FOV due to the limited size of the detector panels; these data truncations within the histo-images are properly modeled through the normalizations and geometric sensitivity file in the DIRECT reconstruction [6, 11]. The histo-images have isotropic voxels of size 1mm³ on a 221×221×101 grid. Attenuation and system sensitivity (i.e. normalization) were considered within the simulation and modeled in the reconstruction. Reconstruction was performed, with the same TOF reconstruction kernels used for the idealized simulations above, using DIRECT with RAMLA including spatially-variant image-based resolution modeling [6], with a relaxation parameter of 0.1, and run for a total of 60 iterations. The relaxation parameter for RAMLA was selected based on our experience from whole-body applications for which the attenuation is relatively large along the LORs (which efficiently relaxes the RAMLA update) and for which this parameter is thus set to 1.0. Consequently, since our breast sized objects have about 10-times lower attenuation, the relaxation parameter has therefore been decreased to 0.1. Nevertheless, if kept within a reasonable range, the relaxation parameter controls mostly the rate of convergence.

D. Comparison with post-smoothing

As an alternative to the regularization approach via the narrowing of the TOF kernel size within reconstruction, we also investigated an approach involving a post-smoothing of the images which were reconstructed with matched TOF (i.e. 300ps). For this case, a post-smoothing using a 1D-Gaussian kernel was applied in the direction perpendicular to the detectors, i.e. conservatively limiting the smoothing only to the direction in which the oscillations are observed in the limited-angle reconstruction using matched TOF kernel. The width of each post-reconstruction smoothing kernel (FWHM_POST) was determined in order to obtain an effective deconvolution kernel width corresponding to the above decreased TOF kernel sizes (FWHM_{TOF_under}) with respect to the matched TOF kernel size (FWHM_{TOF_matched}) used in the reconstruction, i.e.:

$${\text{FWHM}}_{\text{TOF}\_\text{under}}=\sqrt{({\text{FWHM}}_{\text{TOF}\_\text{matched}}{)}^2-({\text{FWHM}}_{\text{POST}}{)}^2},$$ (1)

where FWHM_{TOF_matched} = 300ps (45mm in space), and FWHM_{TOF_under} = 250ps and 275ps (37.5mm and 41.25mm) for this work, which corresponds to an FWHM_POST of about 166ps (~25mm) and 120ps (~18mm), respectively.

III. RESULTS

A. Simulated idealized data

1). Uniform Disk

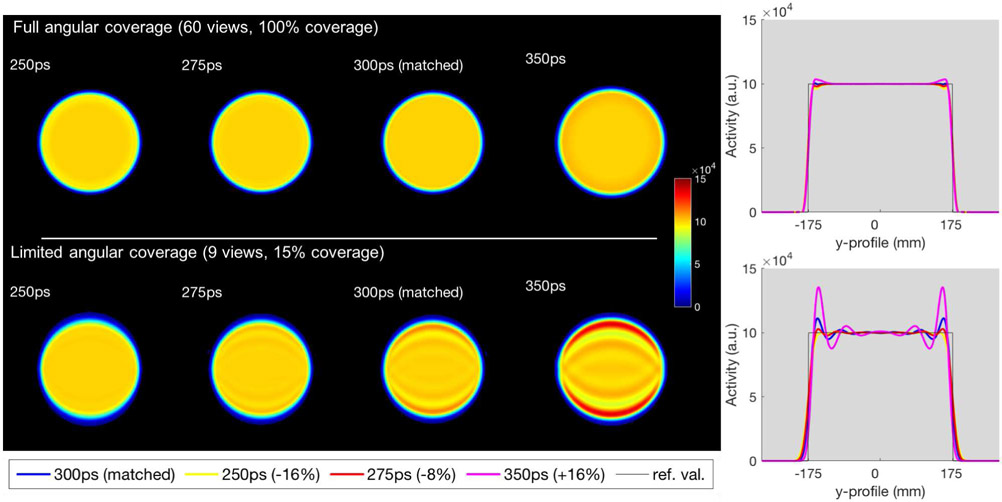
Fig. 4 shows the reconstructed images of the uniform object for the full angular coverage using all 60 views and 10 iterations, and the limited-angle case using only 9 central views and 60 iterations (giving similar number of updates to the full coverage case), reconstructed using TOF kernels of 250ps (−16%), FWHM, 275ps (−8%), matched 300ps FWHM, and 350ps (+16%) FWHM, with their corresponding profiles (center of the images in the TOF direction on the y-axis).

Fig. 4.

Simulated uniform disk reconstructions with different TOF kernel widths using all projection angles (top) and a limited set of angles (bottom). 1^st column: TOF FWHM = 250ps (−16%). 2^nd column: TOF FWHM = 275ps (−8%). 3^rd column: matched TOF FWHM = 300ps. 4^th column: TOF FWHM = 350ps (+16%). Right: corresponding central vertical profiles.

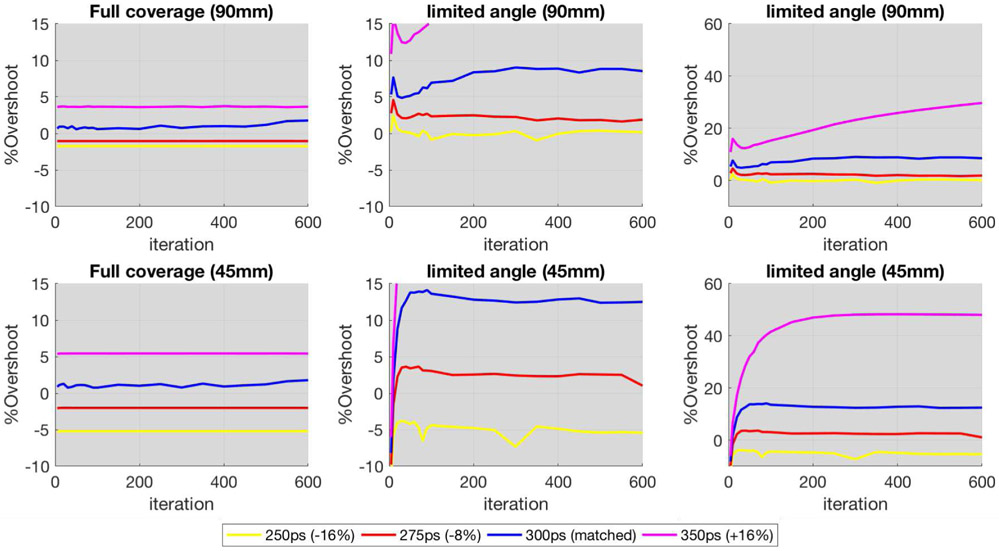
The plots in Fig. 5 display the %Overshoot between the maximum value of the overshoot of the ringing artifacts for the reconstructed images with different TOF kernel widths, as compared to the simulated reference, as a function of iteration (up to 600 iterations). The results for the full ring system are on the left, and the corresponding results for limited-angle data (9 views) are on the right.

Fig. 5.

%Overshoot vs iteration number (from 1 to 600), for the reconstructed simulated uniform disk with different TOF kernel widths. Left: All 60 views. Center: Only 9 views (limited-angle) zoomed to the same y-range. Right: Only 9 views (limited-angle) without zoom for full picture. Note that under- or over- modeling the TOF kernel width has minimal impact on the overshoots for the full angular coverage, while the impact is clearly more considerable for the limited-angle case with under-modeling reducing the overshoots. For the full angular coverage, it takes a TOF kernel of 500ps (~67% wider) to reach a similar level of Gibbs oscillations as observed for the limited-angle reconstruction using matched (300ps) TOF kernel.

It is clear that using matched TOF kernel in the reconstruction for the limited-angle case leads to overshoots, and more so when over-modeling, while decreasing the TOF kernel size does mitigate these overshoots, by providing a more uniform profile, albeit a slight departure from the true object at the edges due to this TOF kernel not being able to fully deconvolve the blurring. On the other hand, the impact of modestly varying the width of the TOF kernels for the full angular case is minimal, as seen in the images and plots. Based on these observations, we have further increased the kernel width, for the full angular coverage, to see at which point the level of Gibbs-like oscillations was comparable to those observed for the limited-angle case at matched TOF kernel. As a matter of fact, it takes about a 67% wider TOF kernel with full angular coverage to reach a similar level of Gibbs oscillations (with about 10% overshoot) as observed with limited-angle reconstruction using matched TOF kernel (illustrated by the dashed cyan line in the %Overshoot plot of Fig.5-left representing the full angular reconstruction using 500ps kernel).

2). Uniform disk with inserts

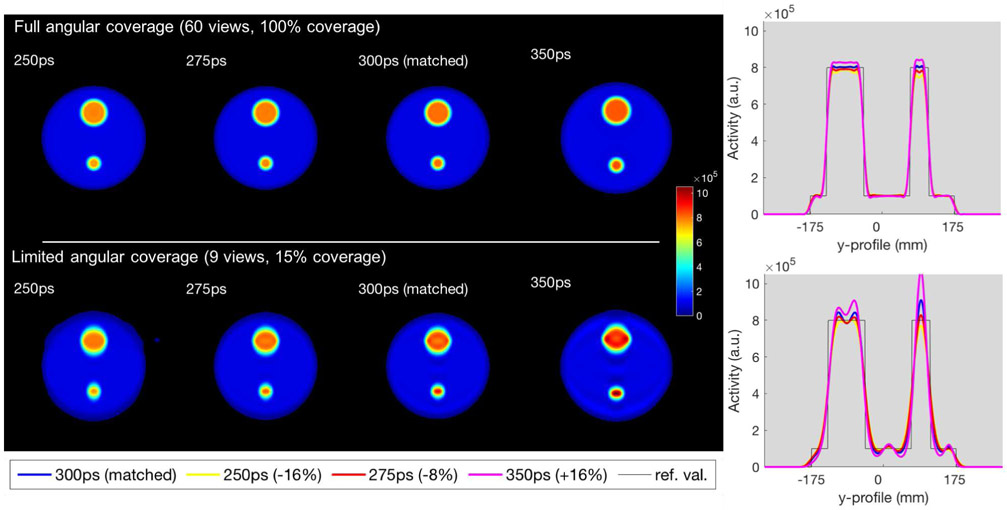
The results for the simulated object with inserts are displayed in Fig. 6 and Fig. 7, with Fig. 6 showing the reconstructed images with their profiles, and Fig. 7 the %Overshoot of the ringing artifacts for the 90mm insert (top) and the 45mm insert (bottom).

Fig. 6.

Simulated 2D uniform disk, including hot inserts, reconstructed data with different TOF kernel width using all projection angles (top) and a limited set of angles (bottom). 1^st column: TOF FWHM = 250ps (−16%). 2^nd column: TOF FWHM = 275ps (−8%). 3^rd column: matched TOF FWHM = 300ps. 4^th column: TOF FWHM = 350ps (+16%). 5^th column: corresponding central vertical profiles.

Fig. 7.

%Overshoot vs iteration (from 1 to 600), for the reconstructed simulated uniform disk including hot inserts (90mm top and 45mm bottom) with different TOF kernel width. Left: All 60 views. Center: Only 9 views (limited-angle) zoomed to the same y-range. Right: Only 9 views (limited-angle) without zoom for full picture. Similar to the uniform disk, under- or over- modeling of the TOF kernel width has minimal impact on the overshoots (albeit more noticeable) for the full angular coverage, while the impact is clearly more considerable for the limited-angle case with under-modeling reducing the overshoot. Interestingly, for the small 45mm lesion, at matched and over-modeled kernels the %Overshoot is higher than for the larger 90mm lesion because the oscillations overlap in the middle which amplifies the overshoots.

As observed for the uniform disk, it is clear that matched TOF kernel for the limited-angle case leads to overshoots at the edges of the larger 90mm insert. Interestingly, for the smaller 45mm insert (approximately equal to the simulated system timing resolution), due to the oscillations being related to the TOF kernel size, there is an overlap of the oscillations within the insert which causes the %Overshoot to be higher compared to the situation when no interaction occurs such as in the larger insert. Nevertheless, it can be seen that the oscillations start to overlap even in the larger object, shown by the reduced dip in the middle of its profile, when using a wider TOF kernel of 350ps. For the full angular coverage case, the impact of modeling different TOF kernels is still minimal.

B. Simulated dual-panel B-PET data

Fig. 8 shows the reconstructed images for the uniform breast phantom (top) using TOF kernels, from left to right, of 250ps, 275ps, 300ps (matched kernel), and 350ps respectively, with their corresponding profiles (bottom). For clarity, the images were smoothed with an isotropic 3D Gaussian kernel with 2mm FWHM, and the profiles in the direction normal to the panels (y-direction) were averaged across slices in x and z.

Fig. 8.

Uniform breast images reconstructed (iteration 60) using different TOF kernel widths. Top row: reconstructed images (white lines denote the object boundaries). Bottom row: profiles averaged across slices in x and z (black line denotes true object). 1^st column: 250ps (−16%) TOF kernel, 2^nd column: 275ps (−8%) TOF kernel, 3^rdcolumn: matched 300ps TOF kernel, 4^th column: 350ps (+16%) TOF kernel. The matched TOF kernel of 300ps clearly leads to overshoots, while decreasing the kernel size delivers more uniform images, but with a slight departure for the object edges. For clarity, images have been smoothed with a 2mm FWHM isotropic 3D Gaussian kernel.

The observations made for the simpler idealized 2D simulation are clearly confirmed for this more realistic 3D GATE simulation, for which using matched TOF kernel in the reconstruction also leads to overshoots, and over-modeling leads to much stronger overshoots, as expected. Narrowing the TOF kernel does mitigate these overshoots by providing a more uniform profile, but with a slight departure from the true object at the edges due to this TOF kernel not being able to fully deconvolve the blurring.

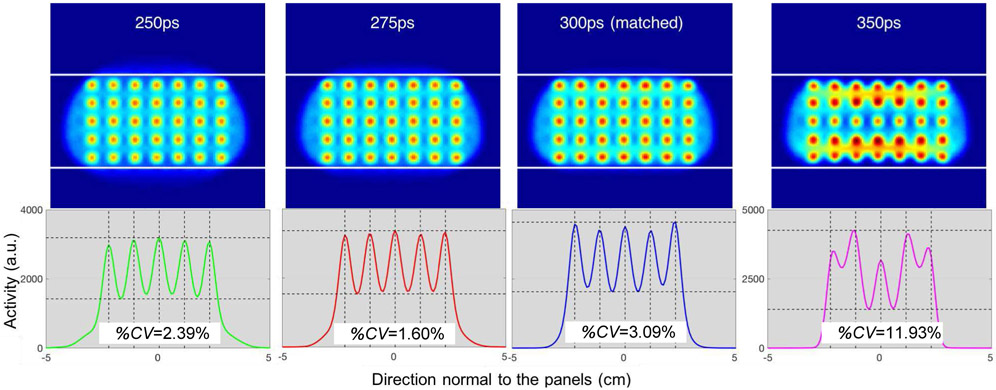
Fig. 9 shows the reconstructed images for the breast phantom with lesions (top) using TOF kernels, from left to right, of 250ps, 275ps, 300ps (matched kernel), and 350ps respectively, with their corresponding profiles (across the five lesions located at the center) in the direction normal to the panels (bottom). For clarity, the images were smoothed with a 5mm FWHM isotropic 3D Gaussian kernel which corresponds to the diameter of the spherical lesions.

Fig. 9.

Breast images with lesions reconstructed (iteration 60) using different TOF kernel widths. Top row: reconstructed images (white lines denote the object boundaries). Bottom row: corresponding vertical profiles across the five lesions located at the center of the breast with the %CV as the measure of uniformity across the lesion peak values (vertical dashed lines mark the true centers of each simulated lesion and horizontal dashed lines delineate the maximum peak and minimum valley for each case.). 1^st column: 250ps (−16%) TOF kernel, 2^nd column: 275ps (−8%) TOF kernel, 3^rd column: matched 300ps TOF kernel, 4^th column: 350ps (+16%) TOF kernel. Narrowing the TOF kernel size to 275ps delivers more consistent lesion activity recovery than the matched kernel of 300ps. For clarity, images have been smoothed with a 5mm FWHM isotropic 3D Gaussian kernel, which corresponds to the diameter of the lesion.

It can be seen that using a TOF kernel of 275ps delivers better consistency in lesion activity recovery compared to the matched kernel of 300ps, which is confirmed by a measure of the uniformity across the lesion peak values expressed as their %CV. However, for 250ps, although the activity recovered for the three lesions at the center is quite consistent, the lesions located at the edges are not as well recovered due to this TOF kernel not being able to fully deconvolve the blurring at the edges of the object, as observed with the profiles for the uniform breast phantom (Fig. 8).

Finally, over-modelling with a kernel of 350ps delivers inconsistent and severely corrupted images, which can be expected when comparing with the profile of the uniform breast phantom (Fig. 8), whereas the overshoots are much wider and farther from the true object edges, and an undershoot exists in the middle. This translates to the row of lesions in the middle of the breast being underestimated, and the rows on the bottom and top edges getting high and inconsistent values (Fig. 9-top-right).

C. Comparison with post-smoothing

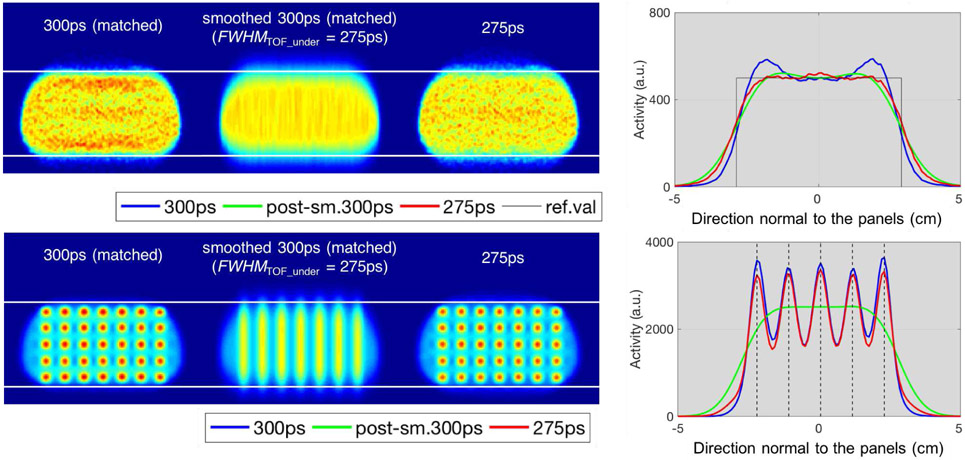
Fig. 10 shows the comparisons between images reconstructed with a matched TOF kernel of 300ps (first column), their post-smoothed versions, as an alternative simple regularization approach (second column), and images reconstructed using a narrowed TOF kernel of 275ps (third column), for the uniform breast phantom (top) and the breast phantom with lesions (bottom) simulated for the dual-panel B-PET system. The post-smoothed images involved 1D Gaussian filter (in the direction of the Gibbs-like oscillations) with FWHM_POST = 120ps (~18mm) to obtain an effective deconvolution effect (as defined in (1)) corresponding to the narrowed TOF kernel of size 275ps. Plots on the right, show the corresponding profiles, with the top figure containing the profiles in the direction normal to the panels (y-direction) averaged across slices in x and z of the uniform phantom, and the bottom plot showing the profiles across the five lesions located at the center of the breast phantom.

Fig. 10.

Impact of post-smoothing of images reconstructed at matched TOF kernel vs narrowing of the TOF kernel within reconstruction, for the simulated uniform breast phantom (top), and the breast phantom with lesions (bottom). 1^st column: reconstructed images with a matched TOF kernel (i.e. 300ps). 2^nd column: corresponding image smoothed after reconstruction with FWHM_POST in (1) of about 120ps (~18mm). 3^rd column: corresponding reconstructed images regularized with a narrower TOF kernel (i.e. 275ps). 4^th column: profiles in the direction normal to the panels (y-direction), for the uniform phantom, averaged across slices in x and z (top); profiles across the five lesions located at the center of the breast phantom (bottom). For clarity, images for the uniform phantom have been smoothed with a 2mm FWHM isotropic 3D Gaussian kernel, and images for the lesion phantom have been smoothed with a 5mm FWHM isotropic 3D Gaussian kernel, which corresponds to the diameter of the lesions.

For the uniform breast phantom (top), the post-smoothing based on (1) (green line in plot) provides a similar level of uniformity (oscillations suppression) to the profiles of the reconstruction with the correspondingly narrowed TOF kernel (red line), but also leads to a slightly more blurred object edges. Although for the uniform breast phantom, the profiles between regularization with a narrower TOF kernel within reconstruction (red line) and by post-smoothing (green line) are not too different, this is clearly not the case for the phantom with lesions (bottom), where the post-smoothing blurs out features (e.g. lesions) narrower than the smoothing kernel, thus making the 5mm lesions not distinguishable. On the other hand, narrowing the post-smoothing kernel to reduce this blurring of lesions leads to insufficient oscillations suppression (not shown).

IV. DISCUSSION

It is well known that for full angular data reconstruction, the TOF information brings improvement to the reconstructed image in terms of improved SNR, but only if the reconstructed object is at least a few times larger in its extent than the TOF resolution kernel width (FWHM). In that case, the improvement is proportional to the square-root of the ratio of the reconstructed object size over the TOF resolution kernel size [15]. However, the situation is diametrically different in the limited-angle TOF case, where TOF provides extra information, which would not be otherwise available due to the missing spectral cone data. In this case, the TOF reconstruction brings definite improvement (over the non-TOF reconstruction) even for small objects, such as a compressed breast (to 8-9 cm extent) on a B-PET system with 300ps resolution (giving 4.5 cm FWHM kernel). As a matter of fact, since the limited-angle data do not satisfy the Orlov’s condition [16] (or Tuy’s complete data sampling condition), the exact reconstruction from limited-angle data is not possible. Theoretical modulation transfer function (MTF) of an idealized non-TOF reconstruction will be given by a bow-tie shaped region for the 2D case, as illustrated in Fig. 1 (column 2) (for the 3D case, see, e.g. Fig. 3 of [10]). Of course, the particular effect of this truncated MTF on the reconstructed image will strongly depend on the Fourier spectrum of an object, e.g. on how much of the object spectrum is being truncated due to the missing region in the MTF. For example, for an ideal object with no vertical spectral components, e.g. an object comprised of only vertical lines, the reconstruction will be perfect, while an object comprised of purely horizontal lines cannot be recovered at all from limited-angle data. For TOF data, this missing region in Fourier domain will be (vertically) reduced (as illustrated in Fig. 1, column 3) due to the additional information provided by TOF, as discussed in details in [10].

Since the limited-angle data case is less compliant with the data sampling condition, which is usually required by analytical reconstruction methods, we have, in this work, concentrated on statistical iterative reconstruction attempting to recover this decayed information via TOF modeling. Although slightly under- or over-modeling the TOF kernel FWHM has minimal impact when using full angular coverage (as also demonstrated in [17]), the results presented herein clearly show that it is not the case for the limited-angle data. In fact, for the limited-angle data, reconstructing images with a TOF kernel matched to the scanner TOF resolution leads to overshoots at the edges of the reconstructed objects. This is because the MTF of limited-angle system decays to very low values in the "missing region." Consequently, the reconstruction is unstable and a full restoration is not possible and leads to Gibbs-like artifacts due to the relatively sharp and unstable transition between the possibly recovered and not recovered spectral regions (as illustrated in Fig. 1, column 4). For large objects, the amplitude of the overshoots and oscillations at the edges is directly related to the contrast (amplitude) of the object edges. However, for small objects, these edge related oscillations will interact depending on the edge shapes and edge distances in a complicated way. These observations are confirmed in our studies with a uniform disk (Fig. 4), a disk with inserts of two different sizes (Fig. 6), a uniform breast phantom (of elongated shape) (Fig. 8), and a breast phantom with lesions (Fig. 9), where the artifacts are appearing at the edges of each object including the inserts. Furthermore, for smaller objects (with size in the vicinity of the TOF kernel FWHM), the artifacts will interact within the object and create potentially higher overshoots (as illustrated in Fig. 6 bottom).

As a simple regularization, we have explored using a modest narrowing of the TOF kernel, which delivers more uniform images (Fig. 4, Fig. 6, and Fig. 8), as well as more consistent lesion recovery (Fig. 9), albeit with slightly blurred object edges. This is confirmed by the overshoots being closer to zero with narrowing of the TOF kernel compared to the matched TOF kernel for which the %Overshoot can be as high as 10%, and considerably more when over-modeling (Fig. 5 and Fig. 7). Interestingly, for the small 45mm lesion, the %Overshoot becomes even higher compared to the larger 90mm lesion, due to the oscillations overlapping in the center and thus amplifying the overshoot.

Although decreasing the TOF kernel size maybe counterintuitive from the physics point of view, from the reconstruction point of view this is similar to reducing the LOR resolution kernel size for (PSF) resolution modeling to minimize the Gibbs-like artifacts, but in this case the TOF kernel width is an order of magnitude wider (~45mm) than a typical PSF kernel (width ~3-8mm, depending on the PET system). These effects are usually modeled in the system matrix. In general, the tomographic reconstruction with TOF information is a well-posed problem. However, for the limited angle case, restoration of the quickly decreasing information in the limited angle data spectral region is an ill-posed problem. The problem becomes more ill-posed with larger TOF kernel size and less ill-posed with narrower TOF kernel size. The narrowing of the TOF kernel size can be considered as a form of regularization, from the point of view of improving the conditioning of the system matrix.

As an alternative to reducing the TOF kernel size within the reconstruction, we tested applying a post-reconstruction smoothing on the image reconstructed with the matched 300ps TOF kernel. For the uniform breast phantom (top row of Fig. 10) the post-reconstruction smoothing delivered similar suppression of the oscillations, but at slightly wider edge tails in the profiles, than the corresponding reconstructed image with a narrower TOF kernel. However, the similarity is clearly not observed for the lesion phantom (bottom row of Fig. 10) whereas post-smoothing eliminates the separation between the lesions and blends them all together as a result of the post-smoothing kernel being considerably larger (~18mm) than the diameter of the lesion size (5mm). As a compromise, we have also investigated reducing the post-smoothing kernel size (results not shown), but no reasonable edge-related oscillations suppression could be reached without overly smoothing the image.

The main objective of this work was to demonstrate that image reconstruction with a TOF kernel matched to the scanner TOF resolution leads to Gibbs-like artifacts for limited-angle data. A simple regularization of the reconstruction, by modest narrowing of the TOF kernel, provides good compromise between the suppression of these edge-related oscillations and resolution loss. Nevertheless, other more advanced regularization techniques (such as alternative optimized TOF kernel shapes) might provide better trade-offs and are open for further investigations. Moreover, practical TOF kernel size reduction and/or parameters will depend on, and will have to be optimized for the practical system and data characteristics (such as, acceptance angle, system resolution, and data counts), reconstructed objects (such as, object and lesion sizes as well as activity), as well as on the given imaging task at hand (such as lesion SUV quantitation, lesion detectability, or lesion localization).

V. CONCLUSION

In this work, we investigated and demonstrated the effects of TOF models on edge artifacts using an idealized limited-angle and full ring system data, as well as using the more realistic case of a dual-panel B-PET system for which limited-angle data is inherent. We also proposed and investigated a regularization approach by simply reducing the TOF kernel size applied within reconstruction, analogous to the conventional approach applied for resolution modeling of the PSF, and compared the results with conventional smoothing applied after reconstruction.

For the full angular data, the reconstruction is not sensitive to variation (within reason) of the TOF kernel size. However, for limited-angle data, it is clear that image reconstruction with a TOF kernel matched to the scanner timing resolution leads to overshoots at the edges of the reconstructed objects, and regularization using a modestly narrower TOF kernel delivers more uniform images albeit with slightly blurred object edges. On the other hand, applying smoothing after reconstruction to decrease the overshoots, is clearly worse compared to the use of a narrower TOF kernel within reconstruction, especially if the object contains small lesions.