Metal-Tolerant Noncircular Orbit Design and Implementation on Robotic C-Arm Systems

Abstract

Metal artifacts are a major confounding factor for image quality in CT, especially in image-guided surgery scenarios where surgical tools and implants frequently occur in the field-of-view. Traditional metal artifact correction methods typically use algorithmic solutions to interpolate over the highly attenuated projection measurements where metal is present but cannot recover the missing information obstructed by the metal. In this work, we treat metal artifacts as a missing data problem and employ noncircular orbits to maximize data completeness in the presence of metal. We first implement a local data completeness metric based on Tuy’s condition as the percentage of great circles sampled by a particular orbit and accounted for the presence of metal by discounting any rays that pass through metal. We then compute the metric over many locations and many possible metal locations to reflect data completeness for arbitrary metal placements within a volume of interest. We used this metric to evaluate the effectiveness of sinusoidal orbits of different magnitudes and frequencies in metal artifact reduction. We also evaluated noncircular orbits in two imaging systems for phantoms with different metal objects and metal arrangements. Among a circular, tilted circular, and a sinusoidal orbit of two cycles per rotation, the latter is shown to most effectively remove metal artifacts. The noncircular orbit not only reduce the extent of streaks, but allows better visualization of spatial frequencies that cannot be recovered by metal artifact correction algorithms. These results illustrate the potential of relatively simple noncircular orbits to be robust against metal implants which ordinarily present significant challenges in interventional imaging.

I. Introduction

Cone-beam computed tomography (CBCT) acquisitions have traditionally followed a circular source-detector orbit. Despite well-known cone-beam artifacts as a result of insufficient sampling away from the central slice (i.e., the null cone), a circular orbit can be achieved with relatively simple mechanical designs and therefore has remained the dominant scan geometry on CBCT systems. The advent of modern robotic c-arms has enabled greater flexibility in source-detector placements around the patient. This capability has primarily been used for intra-operative fluoroscopy guidance, but it has also provided opportunity to realize a host of noncircular orbits designs for CT acquisition. Many designs have been proposed to combat cone-beam artifacts - e.g., circle-and-line,[1] saddle orbits,[2] circle-plus-arc,[3] etc. These designs often aim to improve or satisfy cone-beam data completeness conditions first proposed by Tuy.[4] Customized noncircular orbits for particular objects or patient anatomy have also been designed for specific image quality objectives, including task-based detectability.[5], [6]

In this work, we investigate noncircular orbits for metal artifact minimization. Metal artifacts are especially relevant in image-guided surgery scenarios where surgical tools and implants frequently appear in the field-of-view. The traditional solution to metal artifacts is to apply any number of data correction approaches. Projection measurements where x-rays have passed through metal are highly attenuated - often to the point where they can be consider “missing data”. Algorithms therefore seek to replace these measurements via interpolation schemes based on neighboring projection data, prior information from previous or other patient scans, or other in-painting approaches.[7], [8] These methods can reduce the apparent severity of the artifacts, but are typically not able to “fill in” the true missing information. That is, these algorithms do not improve the completeness of the data, and anatomical details not sampled in the acquisition will remain missing in the reconstruction. In this work, we aim to address the root cause of metal artifacts by designing orbits that are metal-tolerant by maximizing data completeness in the presence of metal.

II. Theoretical Methods

A. Local Completeness Metric

We adapt Tuy’s condition to a local context where data sufficiency is quantified for a single point in the object. A specific “probe” point is completely sampled if all planes passing through it intersects the orbit. We denote points in the object as l with subscript i and discrete source locations on the orbit as S with subscript j. As shown in Fig.1, for each l_i, we define a local spherical coordinate system, (θ_li, ϕ_li). Each plane passing through l_i intersects a great circles on the unit sphere. We sample an ensemble of great circles (denoted as c with subscript k) at regular intervals of θ_li and ϕ_li, which can be equally represented by their unit normals, $\overrightarrow{v_{c_k}}$.

Fig. 1:

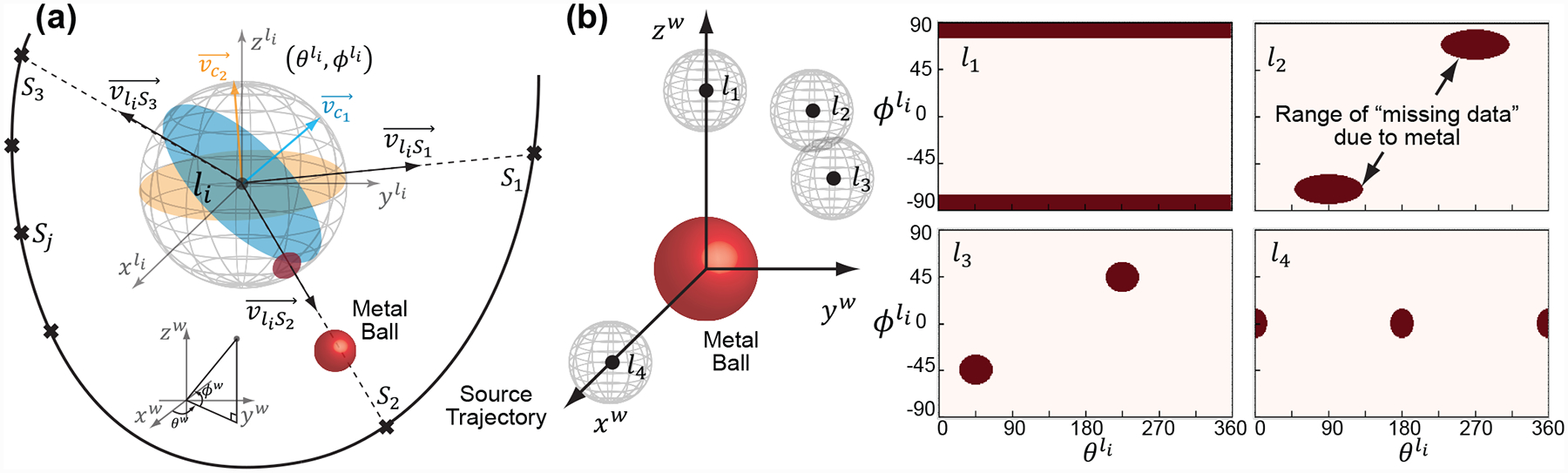
(a) Local Tuy completeness metric at a specific “probe” point, l_i, as the percentage of great circles intersected by the source trajectory. The presence of metal projects a “missing data” (red) space onto the unit sphere around l_i that no longer contributes to sampling. (b) The “missing data” space in dependent on the size of the metal and the relative location of the metal and the location of interest, illustrated here for four locations around a metal ball.

We then calculate whether a particular source location intersects any great circles by finding the angle between $\overrightarrow{v_{c_k}}$ and the vector connecting the source location to the location of interest, $\overrightarrow{v_{l_i}{S}_j}$. If the angle falls within 90° ± ϵ, the great circle c_k has been sampled by the orbit. For example, in Fig.1, S₁ intersects c₂ and S₂ intersects c₁ (as well as many others, not shown). We repeat the calculation for all source locations S_j and all great circles c_k. The local completeness metric is defined as the percentage of great circles that have been intersected by the orbit.

In the presence of metal, rays intersecting the metal are highly attenuated - often to the point they provide no useful information. Therefore, we no longer count great circles sampled by such source locations (e.g., S₂ and c₁) towards the completeness metric. Instead, these great circles need to be sampled by an alternative source location (e.g., S₃) that circumvents the metal. In other words, the presence of metal results in a range of (θ_li, ϕ_li) that represent “missing data” due to high attenuation. When the metal can be approximated as a sphere, this range of (θ_li, ϕ_li) can be computed as the equirectangular projection of the metal sphere onto the unit sphere around l_i based on the size and relative location of the metal to l_i. Fig.1(b) illustrates the range of (θ_li, ϕ_li) to avoid for four example l_i around a metal ball.

B. Noncircular Orbit Design

An orbit that can circumvent metal and achieve a 100% completeness at all probe locations within an object can theoretically eliminate metal (and cone-beam) artifact. We therefore use the completeness metric to identify orbits that are robust against metal artifacts in the presence of metal at arbitrary locations. In this work, we assume the metal object to be a sphere of radius 18 mm, and sampled metal locations within a cylindrical field of view with radius of 16 cm and height of 20 cm. For each metal location, we evaluated the local completeness metric over 50 probe locations distributed over a spherical shell that is 10 mm away from the surface of the metal. We only evaluated locations close to the metal because they suffer from the most severe metal artifacts, i.e., lowest percentage completeness. We can then compute a scalar metric, e.g., the mean, the minimum, etc. to quantify data completeness over the volume at arbitrary metal locations. The metal locations and probe locations around each metal ball used in this work are illustrated in Fig.2.

Fig. 2:

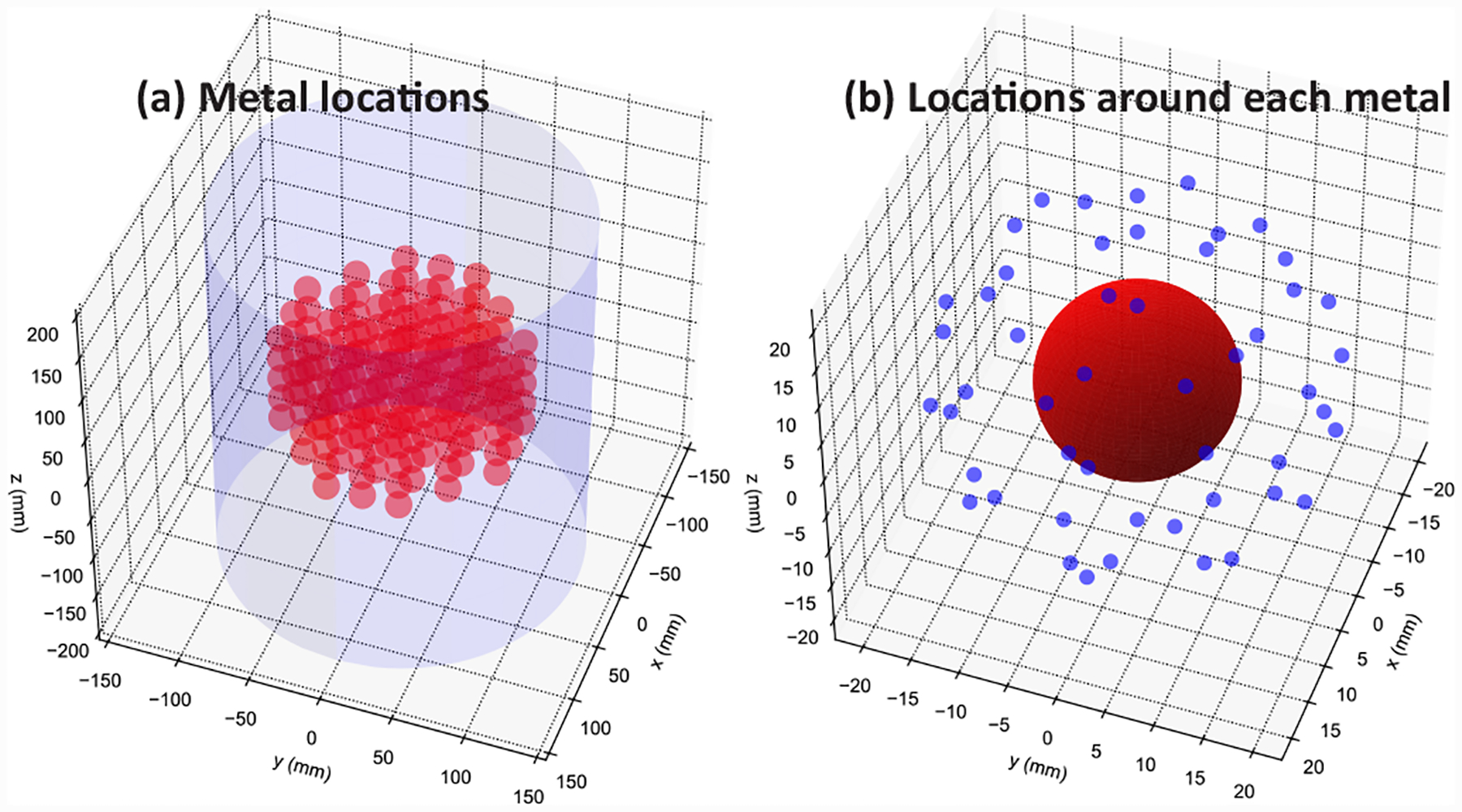
Sampling locations for (a) metal and (b) probe locations around each metal.

In previous work,[9] we performed an orbit optimization using the maximum of the minimum local percentages as the objective function. We found that many noncircular orbits can achieve similar levels of completeness. Thus, additional constraints need to be used to select among similar near-complete orbits. In this work, we focus on simple sinusoidal orbits and apply the completeness metric to evaluate the effectiveness of a range of sinusoids of different frequencies, f, and magnitude, ϕ_max. In the spherical world coordinates, (θ_w, ϕ_w), the sinusoidal orbits are expressed as:

$${\varphi }_w={\varphi }_{max}cos(f{\theta }_w)$$ (1)

where θ_w is the traditional gantry rotation angle, ranging from 0° to 360°, and ϕ_w is the gantry tilt angle [see Fig.1(a) for world coordinate definitions]. The maximum achievable tilt on the imaging system (e.g. due to mechanical constraints, patient positioning, table, etc.) is denoted by ϕ_max. Special cases of this definition include ϕ_max = 0° for a circular orbit and f = 1 for a tilted circular orbit.

We computed the completeness metric for sinusoidal orbits of frequencies ranging from 0.25 to 8 at 0.25 increment, and of ϕ_max ranging from 0° to 50°.

III. Experimental Methods

A. Imaging phantoms and Imaging Systems

We illustrated the robustness of the noncircular orbits in two phantoms shown in Fig.3(a). Both phantoms are constructed with a cluttered background by mixing plastic balls of different sizes and materials. In this first phantom, on the central axial slice, we inserted three stainless steel balls of 18 mm diameter and surrounded by 3D-printed radial line pairs. These radial line pairs are designed specifically to challenge CT imaging around metal. According to the Fourier slice theorem, the frequencies that will be missed by an in-plane circular orbit are those perpendicular to the metal ball. Thus, line pairs directed to the center of the metal balls would present a significant challenge for interpolation-based correction methods. Two smaller stainless steel balls were also inserted 2.5cm above and below the central axial plane. A second phantom was constructed with the same background clutter but with a spinal fusion hardware complex. Specifically, three pairs of stainless steel pedicle screws were placed in the phantom. Each set of three screws are joined by a stainless steel rod.

Fig. 3:

(a) Imaging phantoms consisting of a cluttered background. We inserted two sets of metal objects: 1) stainless steel balls surrounded by 3D printed radial line pairs, and 2) spine fusion hardware consisting of three pairs of pedicle screws. (b) Noncircular orbits were realized on a CBCT test bench and a Zeego C-arm system.

Noncircular orbits were realized on two physical systems. First, experiments were conducted on a CBCT test bench comprised of a Varex 4343CB flat-panel detector, Varex Rad-94 x-ray tube and an Alio Industries “hybrid hexapod” system capable of six degree-of-freedom motion, which served as an object stage. This system can emulate a robotic C-arm system with arbitrary orbits. In these studies, source-detector distance was fixed and source, detector, and hexapod motion was used to emulate sinusoidal orbits with tilts up to approximately 24°. The second system used for investigation was a modified Siemens Zeego robotic C-arm system. This research system was adapted to permit specification of largely arbitrary orbits in a step-and-shoot fashion.[10] This system in shown in Fig.3(b) and also has a maximum tilt limitation of approximately 24°.

B. Geometry calibration using 2D-3D registration

The noncircular orbit was calibrated using a self-calibration routine described in Ref [11]. Briefly, a reconstruction of the phantom from a circular geometry was used as a known model of the object. Projections of the known model was then registered to each view of the noncircular acquisition to identify the projection matrix. The ensemble of projection matrices were then used to reconstruct data from the noncircular acquisition.

C. Reconstruction

For reconstruction, we chose a model-based algorithm due to its ability to accommodate arbitrary acquisition geometries. We adopted a a penalized weighted least squares objective with a Huber penalty and used a separable footprint projector. No metal artifact correction methods were applied to highlight the extent of metal artifact as a result of orbit alone.

IV. Results

The results of the completeness metric evaluation is summarized in Fig.4 as the minimum over all metal and probe locations. A number of features are important. The percentage completeness is the lowest for circular (ϕ_max = 0) and tilted circular orbit (f = 1). In general, the degree of completeness improves with larger ϕ_max and increased frequency.

Fig. 4:

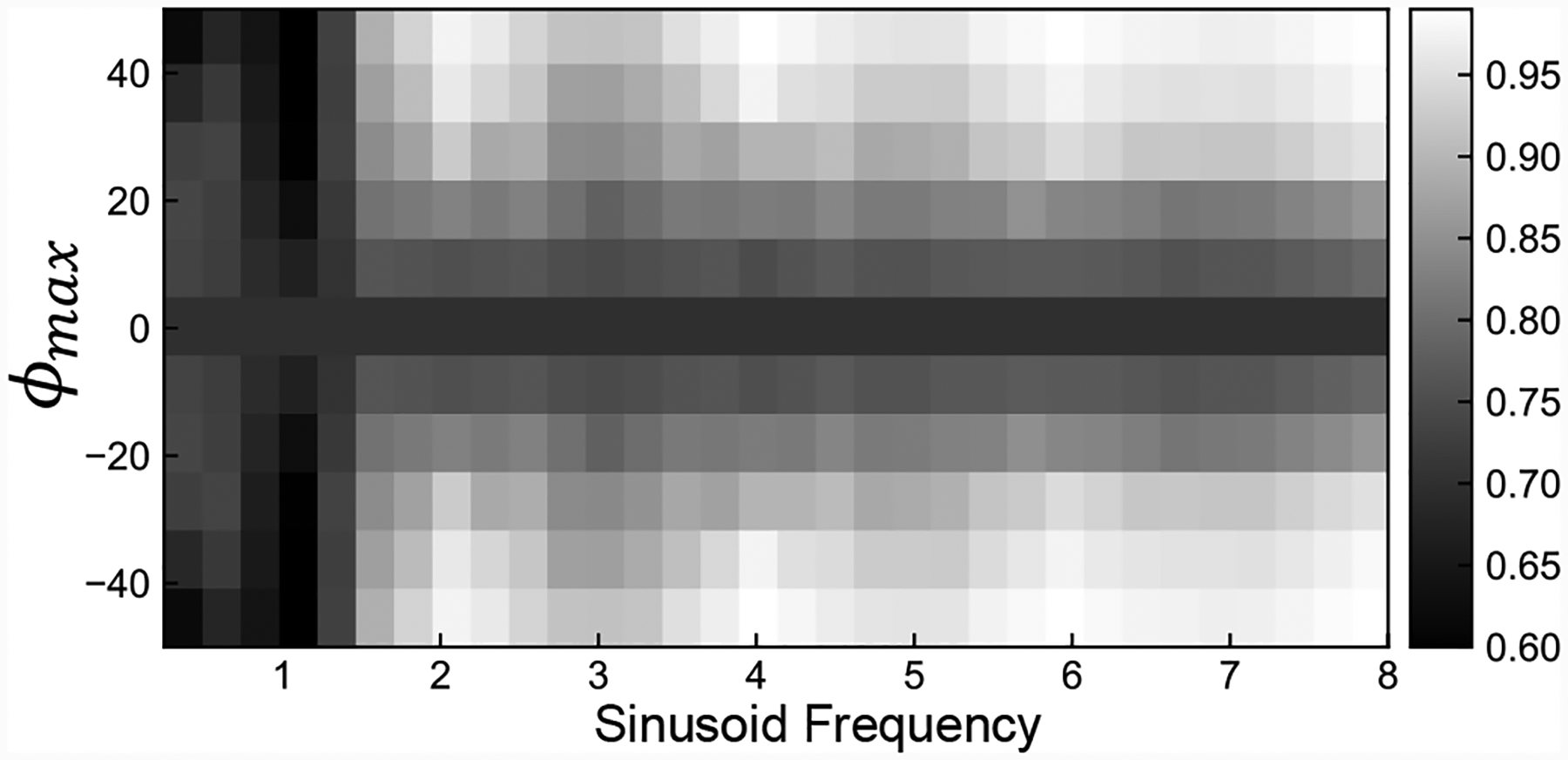
The minimum percentage complete over all metal and probe locations for sinusoidal orbits of different frequencies and magnitudes.

We observe some periodicity where odd frequencies perform worse than even frequencies. This is due to odd frequencies not taking advantage of redundancy in θ to sample different ϕ. That is, the rays (lines of response) that are collected at θ and θ + 180° are simlar (for small fan angles). Even orbits, on the other hand, leverage inherent redundancy of a 360° orbit to provide rays sampled at different ϕ and are therefore more robust against metal artifacts. At high frequencies, the space is densely sampled and therefore the periodicity is not as pronounced.

Reconstructions for the two phantoms in Fig.3 are shown in Fig.5 for a circular, tilted circular, and a sinusoid acquisition at f = 2. Reconstructions following circular orbits have severe streaking as a result of multiple in-plane metal objects. Moreover, the radial line pairs cannot be faithfully reproduced in-plane since those frequencies were never sampled. The tilted circular orbit improves in-plane visualization but displaces the metal artifacts to outof-plane, evident in the saggital slices. The f = 2 sinusoid exhibits the least metal artifacts both in-plane, and out-of-plane. The reduction in metal artifact is not only reflected in the reduced streak artifacts, but also in the ability to see sphere details between metals which would not be visible had a metal artifact reduction algorithm been used.

Fig. 5:

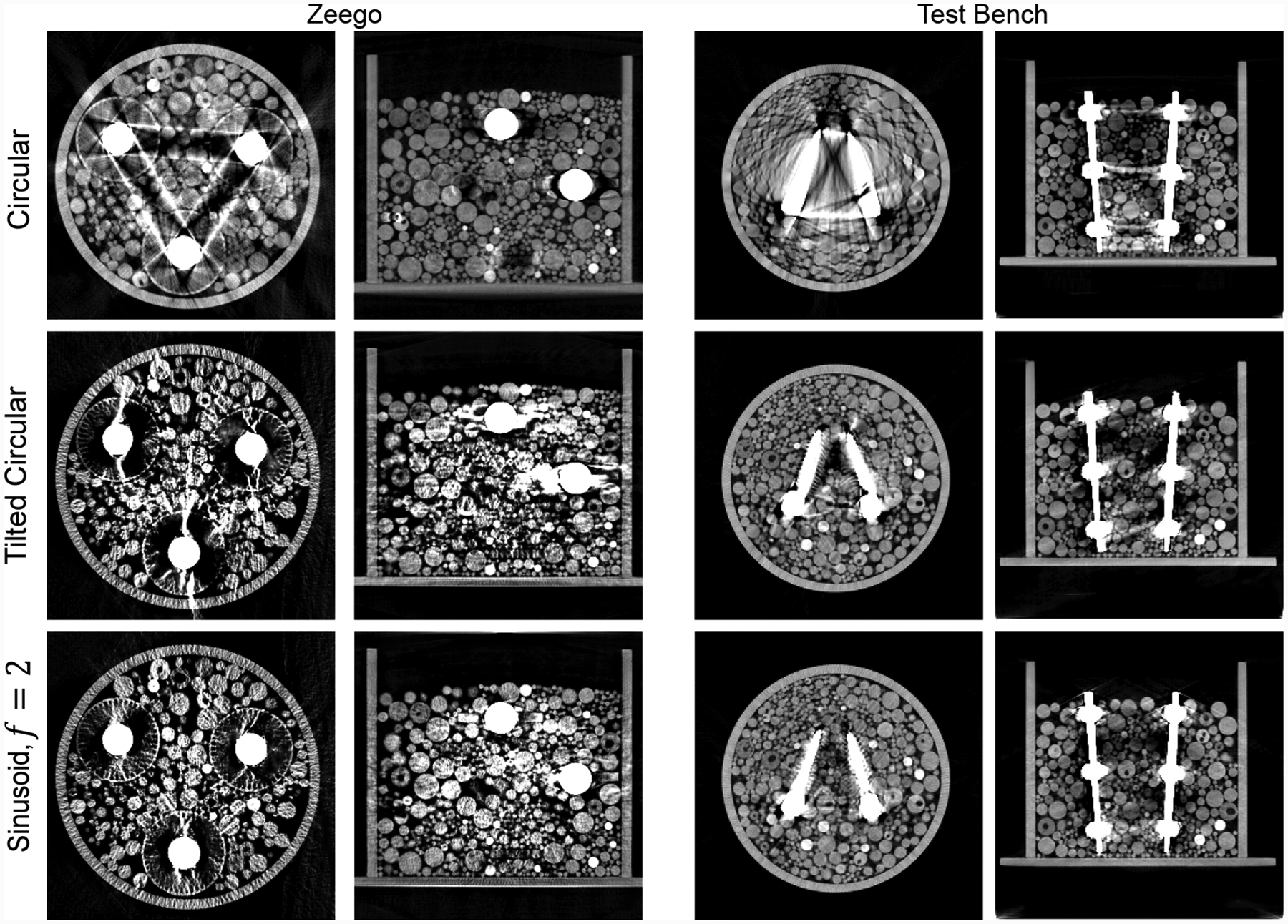
Reconstructions for the two phantom configurations using a circular orbit, a tilted circular orbit, and a sinusoidal orbit of f = 2

V. Discussions and Conclusions

This works presents noncircular orbit design and implementation for metal artifact minimization. We used a local Tuy completeness metric to quantify the extent of sampling in the presence of metal and investigated the robustness of sinusoidal orbits of different frequencies and magnitudes. The orbits were realized on an experimental CBCT test bench and a Zeego system for two phantoms with metal balls and pedicle screws. We observed that a sinusoidal orbit of frequency equals 2 effectively removes metal artifacts by improving sampling and reducing the missing data effects as a result of metal implants.

Ongoing work is seeking to extend orbital designs for patients with hip implants and to implement such metal-tolerant orbits on other clinical systems including mobile C-arms. Similarly, quantitative comparisons with traditional metal artifact correction approaches are underway. Future work will include new orbital design that seek solutions within the class of complete orbits using additional image quality measures. For example, image quality is also driven by patient anatomy (habitus and bone) that can be used to select from metal-tolerant complete orbits.

This work has illustrated the basic feasibility for using noncircular orbits to significantly reduce metal artifacts by addressing the source of the problem - missing data. Complete orbits as simple as sinusoids can provide sufficiently redundant data to eliminate metal artifacts - providing a potential clinical solution for interventional CT to a longstanding problem for surgical tools and metal implants.