Prospective Prediction and Control of Image Properties in Model-based Material Decomposition for Spectral CT

Abstract

Model-based material decomposition (MBMD) directly estimates the material densities from the spectral CT data and has found opportunities for dose reduction via physical and statistical modeling and advanced regularization. However, image properties such as spatial resolution, noise, and cross-basis response in the context of material decomposition are dependent on regularization, and high-dimensional exhaustive sweeping of regularization parameters is suboptimal. In this work, we proposed a set of prediction tools for generalized local impulse response (LIR) that characterizes both in-basis spatial resolution and cross-basis response, and noise correlation prospectively. The accuracy of noise predictor was validated in a simulation study, comparing predicted and measured in- and cross-basis noise correlations. Employing these predictors, we composed a specialized regularization for cross-talk reduction and showed that such prediction tools are promising for task-based optimization in spectral CT applications.

1. INTRODUCTION

Spectral CT is finding increasing application in a number of areas due to its ability to estimate material density distributions using energy-dependent measurements. Traditionally, material decomposition and reconstruction are sequentially processed. In image domain decomposition, spectral channels are reconstructed separately, followed by a decomposition of the image volumes. This often requires additional correction for beam-hardening effects since the reconstruction uses a monoenergetic model. In projection-domain decomposition, spectral measurements are decomposed into material line integral estimates followed by reconstruction. Projection-domain methods require matched system geometry between channels, which is not always available (e.g., in kVp-switching or split-filter approaches). More recently, model-based material decomposition (MBMD) permits estimation of material density directly from spectral measurements without an intermediate step. MBMD merges a polychromatic forward model and statistical model into a nonlinear objective function that can be solved iteratively like “standard” model-based iterative reconstruction (MBIR). Such direct MBMD has does not require matched geometries between spectral channels, can handle arbitrary sampling patterns, and explicitly models (and eliminates) beam-hardening effects. Moreover, like MBIR, direct estimation results benefits from statistical weighting and flexible regularization design. However, (also like MBIR) the relationship between image properties and regularization and object-dependence can be complicated. Improper regularization parameters may result in over blurry or noisy images; and, specific to spectral CT, artifacts due to cross-talk between material bases. Traditional parameter tuning that uses exhaustive evaluation is particularly time-consuming and may not generalize due to the inherent object- and data-dependence of MBMD.

In recent work ¹, we presented a mathematical framework for prediction of a generalized local impulse response (LIR) in MBMD. This generalized LIR specifies both the local resolution properties but also the cross-talk between material channels due to coupling in the objective function. We extend this prediction tool to noise analysis with a closed-form expression for local covariance (or, equivalently noise power spectrum), which also include the noise cross-talk. The combined performance prediction framework permits prospective regularization design for specific imaging goals. We show an example use of the prediction framework to minimize cross-talk between reconstructed material bases using generalized LIR predictions.

2. METHODS

2.1. Model-based material decomposition

The polychromatic forward model that relates material density volumes ρ to mean spectral CT measurements $\overline{y}$ is:

$$\overline{y}=\mathbf{\text{GS}}\hspace{0.17em}\text{exp}\left\{-\text{QA}\rho \right\}.$$ (1)

The CT system is characterized by the system matrix A, a material mass attenuation coefficient matrix Q (containing discretized energy bins and over each material basis), a spectral combination matrix S (quantifying the system spectral response including incident photon spectrum, detector energy sensitivity, etc.) and a diagonal gain matrix G (overall fluence, detector gains, etc.). Note that this forward model is general and S (and A) can model various Spectral CT approaches including kV-switching, photon counting detectors, dual-layer detectors, dual-source systems, etc.

Presuming the measurements follow a multivariate Gaussian distribution with covariance K_y, we can estimate ρ by minimizing the following objective function, which includes a data fidelity term L(ρ, y) and a penalty term R(ρ). In this work, we focus on a quadratic penalty of pairwise difference in 4 nearest neighborhood.

$$\Phi \left(\rho ;y\right)={\mathbf{\text{K}}}_y+R\left(\rho \right)=\frac{1}{2}{\left(y-\overline{y}\right)}^T{K}_y^{-1}\left(y-\overline{y}\right)+R\left(\rho \right),R\left(\rho \right)=\frac{1}{4}\sum _j{\beta }_k\sum _j\sum _{l\in {\mathbf{\text{N}}}_{\mathbf{\text{j}}}}{\left({\rho }_k^j-{\rho }_k^l\right)}^2$$ (2)

2.2. Mathematical Derivations of MBMD Image Properties

2.1.1. Derivation of generalized local impulse response

To quantify the mean imaging properties, we will consider a generalized local impulse response – defined as the relative change of density estimates to a small local perturbation. This can be represented using a derivative of the estimates with respect to truth. Applying the chain rule, the response to a local impulse at the j^th voxel in the k^th material basis is

$$l_k^j=\frac{\partial \widehat{\rho }\left(\overline{y}\right)}{\partial {\rho }_k^j}={\nabla }_{\overline{y}}\widehat{\rho }\left(\overline{y}\right)\frac{\partial \overline{y}}{\partial {\rho }_k^j}.$$ (3)

We decompose the system response into two steps, the measurements acquisition step $\left(\rho \to y\right){\nabla }_{\overline{y}}\widehat{\rho }\left(\overline{y}\right)$ and the decomposition step $\left(y\to \widehat{\rho }\right)$:

$$\frac{\partial \overline{y}}{\partial {\rho }_k^j}=-\mathbf{\text{GS}}D\left\{\text{exp}\left\{-\mathbf{\text{QA}}\rho \right\}\right\}\mathbf{\text{QA}}{e}_k^j=-\mathbf{\text{WQA}}{e}_k^j,$$ (4)

$${\nabla }_{\overline{y}}\widehat{\rho }\left(\overline{y}\right)=-{\left[{\mathbf{\text{A}}}^T{\mathbf{\text{Q}}}^T{\mathbf{\text{W}}}^T{\mathbf{\text{K}}}_y^{-1}\mathbf{\text{WQA}}+\mathbf{\text{R}}\right]}^{-1}{\mathbf{\text{A}}}^T{\mathbf{\text{Q}}}^T{\mathbf{\text{W}}}^T{\mathbf{\text{K}}}_y^{-1}$$ (5)

where $e_k^j$ is a Kronecker delta vector that has the same shape as ρ with unity at the j^th voxel in the k^th material basis, R is the Hessian of the penalty term R(ρ), and $\mathbf{\text{W}}=\mathbf{\text{GS}}D\left\{\text{exp}\left\{-\mathbf{\text{QA}}\rho \right\}\right\}$ is the spectral channel-wise weights which can be estimated without a complete decomposition. Substituting (4) and (5) into (3), the closed-form expression of LIR is

$$l_k^j={\left[{\mathbf{\text{A}}}^T{\mathbf{\text{Q}}}^T{\mathbf{\text{W}}}^T{\mathbf{\text{K}}}_y^{-1}\mathbf{\text{WQA}}+\mathbf{\text{R}}\right]}^{-1}{\mathbf{\text{A}}}^T{\mathbf{\text{Q}}}^T{\mathbf{\text{W}}}^T{\mathbf{\text{K}}}_y^{-1}\mathbf{\text{WQA}}{e}_k^j$$ (6)

Note that the LIR carries all the dependencies one would expect from an MBIR approach including location-dependence (j), object/data-dependence (via W, and regularization-dependence (R).

2.2.2. Derivation of covariance

The covariance of the estimator $\widehat{\rho }$ is approximated as:

$$\text{Cov}\left\{\widehat{\rho }\right\}\approx {\nabla }_{\overline{y}}\widehat{\rho }\left(\overline{y}\right)\text{Cov}\left\{y\right\}{\left[{\nabla }_{\overline{y}}\widehat{\rho }\left(\overline{y}\right)\right]}^T$$ (7)

Substituting K_y and (5) into (7), the closed-form expression of covariance is

$$\text{Cov}\left\{\widehat{\rho }\right\}={\left[{\mathbf{\text{A}}}^T{\mathbf{\text{Q}}}^T{\mathbf{\text{W}}}^T{\mathbf{\text{K}}}_y^{-1}\mathbf{\text{WQA}}+\mathbf{\text{R}}\right]}^{-1}{\mathbf{\text{A}}}^T{\mathbf{\text{Q}}}^T{\mathbf{\text{W}}}^T{\mathbf{\text{K}}}_y^{-1}\mathbf{\text{WQA}}{\left[{\mathbf{\text{A}}}^T{\mathbf{\text{Q}}}^T{\mathbf{\text{W}}}^T{\mathbf{\text{K}}}_y^{-1}\mathbf{\text{WQA}}+\mathbf{\text{R}}\right]}^{-1}.$$ (8)

2.2.3. Fast Fourier approximation

The closed-form expressions (6) and (8) involve matrix inversion, which can be solved using iterative methods (e.g. conjugate gradients) but with significant computation time. We propose a fast circulant approximation in a local region of interest (ROI) around the impulse and solve the matrix inversion using Fourier methods. For compactness, we denote the 2D Fourier transform of the ROI of ${\mathbf{\text{A}}}^T{\mathbf{\text{Q}}}^T{\mathbf{\text{W}}}^T{\mathbf{\text{K}}}_y^{-1}\mathbf{\text{WQA}}{e}_k^j$ in the k′^th material basis with ${\mathcal{F}}_{k^{\prime },k}^j$. Similarly, we denote the 2D Fourier transform of the ROI of $\left[{\mathbf{\text{A}}}^T{\mathbf{\text{Q}}}^T{\mathbf{\text{W}}}^T{\mathbf{\text{K}}}_y^{-1}\mathbf{\text{WQA}}+\mathbf{\text{R}}\right]e_k^j$ in the k′^th material basis as ${\mathcal{R}}_{k^{\prime },k}^j$. Thus, for a dual-material decomposition, the circulant approximation of LIR and noise power spectrum (NPS, Fourier transform of covariance) are

$$l_{1,1}^j={\mathcal{F}}^{-1}\left\{\frac{{\mathcal{F}}_{1,1}^j\odot {\mathcal{R}}_{2,2}^j-{\mathcal{F}}_{2,1}^j\odot {\mathcal{R}}_{1,2}^j}{{\mathcal{R}}_{1,1}^j\odot {\mathcal{R}}_{2,2}^j-{\mathcal{R}}_{2,1}^j\odot {\mathcal{R}}_{1,2}^j}\right\};l_{2,1}^j={\mathcal{F}}^{-1}\left\{\frac{{\mathcal{F}}_{2,1}^j\odot {\mathcal{R}}_{1,1}^j-{\mathcal{F}}_{1,1}^j\odot {\mathcal{R}}_{2,1}^j}{{\mathcal{R}}_{1,1}^j\odot {\mathcal{R}}_{2,2}^j-{\mathcal{R}}_{2,1}^j\odot {\mathcal{R}}_{1,2}^j}\right\}$$ (9)

$${\mathbf{\text{NPS}}}_{1,1}^j=\frac{\left({\mathcal{F}}_{1,1}^j\odot {\mathcal{R}}_{2,2}^j-{\mathcal{F}}_{1,2}^j\odot {\mathcal{R}}_{1,2}^j\right)\odot {\mathcal{R}}_{2,2}^j-\left({\mathcal{F}}_{2,1}^j\odot {\mathcal{R}}_{2,2}^j-{\mathcal{F}}_{2,2}^j\odot {\mathcal{R}}_{1,2}^j\right)\odot {\mathcal{R}}_{2,1}^j}{{\left[{\mathcal{R}}_{1,1}^j\odot {\mathcal{R}}_{2,2}^j-{\mathcal{R}}_{2,1}^j\odot {\mathcal{R}}_{1,2}^j\right]}^2}$$

$${\mathbf{\text{NPS}}}_{2,1}^j=\frac{-\left({\mathcal{F}}_{1,1}^j\odot {\mathcal{R}}_{2,2}^j-{\mathcal{F}}_{1,2}^j\odot {\mathcal{R}}_{1,2}^j\right)\odot {\mathcal{R}}_{1,2}^j+\left({\mathcal{F}}_{2,1}^j\odot {\mathcal{R}}_{2,2}^j-{\mathcal{F}}_{2,2}^j\odot {\mathcal{R}}_{1,2}^j\right)\odot {\mathcal{R}}_{1,1}^j}{{\left[{\mathcal{R}}_{1,1}^j\odot {\mathcal{R}}_{2,2}^j-{\mathcal{R}}_{2,1}^j\odot {\mathcal{R}}_{1,2}^j\right]}^2}$$ (10)

where ${\mathcal{F}}^{-1}$ denotes the discrete Fourier transform. Here $\odot$, /, and ${[\cdot ]}^2$ denote the element-wise multiplication, division, and squaring respectively. The predictor provides prospective quantification of both the in-basis response and noise correlations ($l_{1,1}^j$, ${\text{NPS}}_{1,1}^j$– quantifying in-basis resolution and noise) as well as cross-basis properties ($l_{1,1}^j$,${\text{NPS}}_{1,1}^j$ – quantifying cross-talk and noise correlations between material bases).

2.3. Validation of noise predictors in simulation experiments

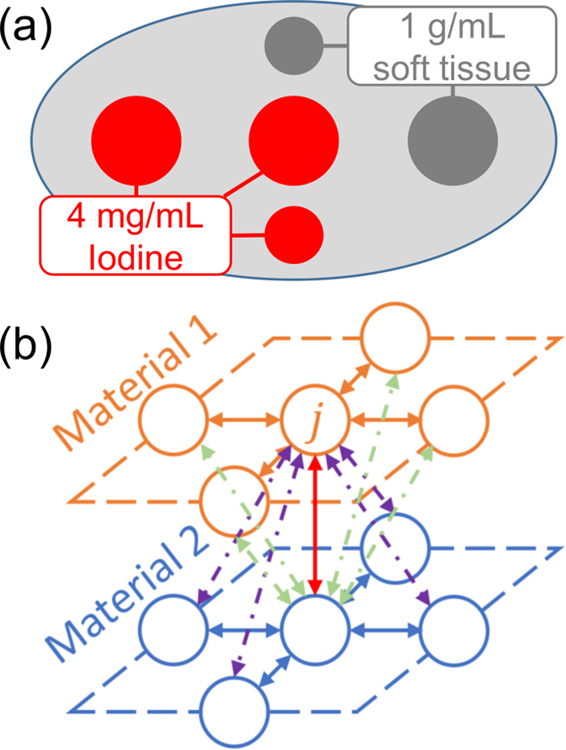
For numerical validation of prediction accuracy, a water/iodine material phantom (Figure 1) was emulated for spectral measurements in an 80/120 kVp switching dual-energy CT system. The source-to-axis distance was 600 mm with a magnification of 2. We emulated 360 angles × 512 bins and reconstructed 2 material bases, each consisting of 128 × 256 0.5 mm cubic voxels. 4000 iterations of an MBMD algorithm (Tilley et al 2019 ²) were applied to guarantee convergence. We added Poisson noise to the mean measurements with a bare-beam fluence level at 5 × 10⁵ photons/pixel and generated 10 realizations. A 1D sweep over regularization strengths was performed in the soft tissue and water basis, (β_s and β_I), between (3 × 10⁷,1 × 10¹⁰) and (3 × 10⁹,1 × 10¹²). 9 noise-only image volumes were computed as the difference of the consecutive realizations. The in-basis and cross-basis NPS were computed as follows:

$${\text{NPS}}_{\text{k}}=\frac{a_x{a}_y}{2n_x{n}_y}\langle {\left|\text{DFT}\left[\Delta {\text{ROI}}_{\text{I}}\right]\right|}^2\rangle ;\hspace{0.17em}{\text{NPS}}_{\text{k},{\text{k}}^{\prime }}=\frac{a_x{a}_y}{2n_x{n}_y}\langle {\left|\text{DFT}\left[\Delta {\text{ROI}}_{\text{k}}\right]\right|}^2\odot \left|\text{DFT}\left[\Delta {\text{ROI}}_{{\text{k}}^{\prime }}\right]\right|\rangle$$ (11)

where $\text{DFT}\left[\Delta {\text{ROI}}_{\text{k}}\right]$ denotes the discrete Fourier transform of a 2D ROI (16 × 16 voxels) at the center, a_x/a_y and n_x/n_y are voxel size and number of voxels in ROI in x/y directions, respectively. $\langle \cdot \rangle$ and $|\cdot |$ are averaging and absolute value calculation. The predictions were computed using the Fourier method of Equation (10).

Figure 1:

(a) Dual-material digital phantom with cylindrical soft tissue and iodine on top of a water ellipse. (b) Illustration of the 4-nearest neighborhood cross-basis regularization.

2.4. Regularization design for cross-talk reduction

The cross terms such as $l_{2,1}^j$ in (9) describe the influence, for example, of a perturbation of material 1 on the material 2 estimate permitting prediction (as a function of regularization, data, etc.) and control. That is, theoretically, one can design cross-basis penalties to eliminate the cross-talk: specifically when ${\mathbf{\text{R}}}_{21}={\mathcal{F}}^{-1}\left\{\left({\mathcal{R}}_{11}-{\mathcal{F}}_{11}\right)\odot {\mathcal{F}}_{21}/{\mathcal{F}}_{11}\right\}$. Cross-basis penalty design is promising for cross-talk elimination; however, theoretical penalty design solutions are not necessarily local. To maintain a reasonable computational cost, we designed a 4-neighborhood mask that captures the principle components of the theoretical solution. Specifically, we adopt the following penalty form (shown in Fig. 1b):

$$R\left(\rho \right)=\frac{1}{4}\sum _j\sum _{l\in {\mathbf{\text{N}}}_{\mathbf{\text{j}}}}\sum _{k=1,2}{\beta }_k{\left({\rho }_k^j-{\rho }_k^l\right)}^2+\frac{1}{4}\sum _j\sum _{l\in {\mathbf{\text{N}}}_{\mathbf{\text{j}}}}2{\gamma }^j\sqrt{{\beta }_1{\beta }_2}\left({\rho }_1^j-{\rho }_1^l\right)\left({\rho }_2^j-{\rho }_2^l\right),{\gamma }^j\le 1$$ (12)

We may then find the coefficients of this cross penalty (γ^j) via an optimization than minimizes the cross LIR terms (e.g., minimizing the cross-talk). Specifically, the cost function for cross-talk reduction is simply the ℓ₂ norm of the combined cross-talk:${\Vert l_{1,2}^j\left({\gamma }^j\right)\Vert }_2^2+\omega {\Vert l_{2,1}^j\left({\gamma }^j\right)\Vert }_2^2$. We adopted the Nelder-Mead simplex direct search algorithm to find the optimized γ_j locally. A constant γ was estimated at the central location for a shift-invariant cross-basis penalty, while a γ^j map was estimated as interpolation of optimized γ^j on a coarse grid for shift-variant cross-basis penalty. These cross-basis penalized MBMD images were compared with in-basis penalized MBMD results. The same overall regularization strengths were applied for a fair comparison.

3. RESULTS

3.1. Noise predictor accuracy validation

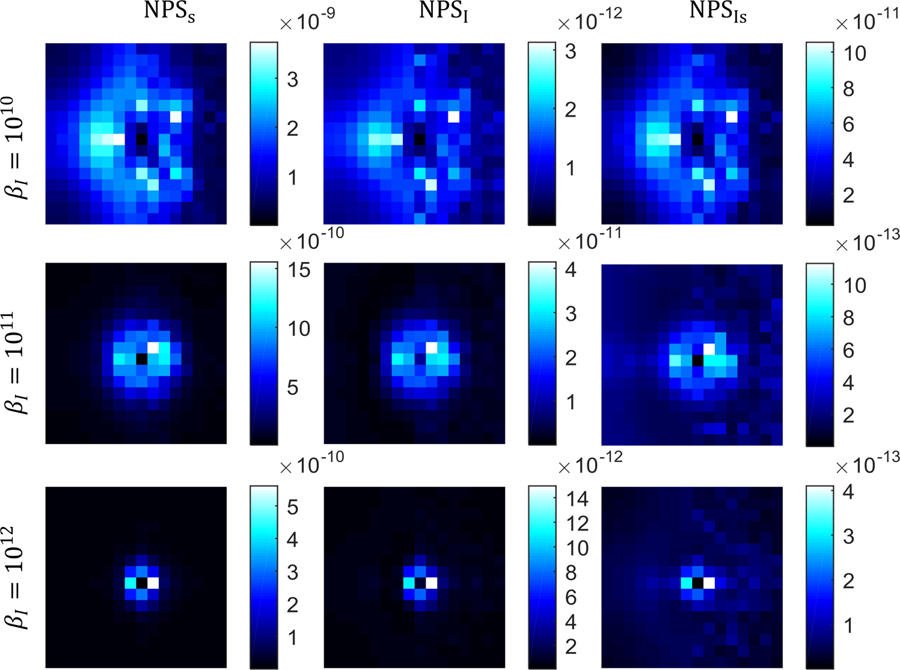
Figure 2 shows the predicted NPS on the left half of each subplot and measured NPS on the right with 3 different in-basis regularization strengths. NPS_s, NPS_I, and NPS_Is denote the noise properties in the soft tissue basis, the iodine basis, and between the two material bases, respectively. Due to small number of samples, the measured NPS is somewhat noisy, especially for low regularization cases. However, we see good agreement of magnitude and extent between the prediction and the estimation. With higher regularization strength, the high-frequency noise and overall noise magnitude is reduced. This trend is observed in simulation experiments, and revealed with predictors.

Figure 2:

Predicted and estimated NPS in soft tissue basis, iodine basis, and between two material bases. The unit is mg² m² L⁻².

3.2. Regularization design for cross-talk reduction

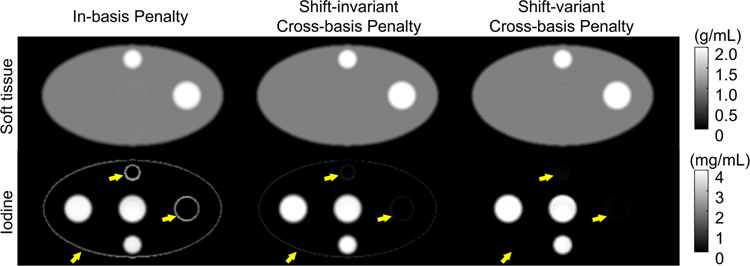
Figure 3 shows the optimized γ map used in shift-variant cross-basis regularization design. The constant γ is 0.485 in shift-invariant cross-basis regularization design. Figure 4 shows the material density maps decomposed with different penalty design. Due to the coupling between two material bases, the cross-talk leads to artifacts at the soft tissue edges in the iodine basis indicated with the yellow arrows, with the in-basis penalty. Such artifacts are mostly reduced with the shift-invariant cross-basis penalty, and nearly perfectly eliminated with the shift-invariant cross-basis penalty design.

Figure 3:

Cross-basis regularization γ map for cross-talk reduction.

Figure 4:

From left to right: MBMD results using in-basis penalty, shift-invariant cross-basis penalty, and shift-variant penalty.

4. CONCLUSIONS

Following previous work of LIR analysis ¹, we presented a closed-form expression of both LIR and noise correlation in MBMD. The predictors provide prospective quantification of in-basis resolution, cross-talk between material bases, and noise correlations in- and cross-basis. Such predictors account for all the expected dependencies on spectral system configuration (geometry, spectrum separation between channels, and fluence modulation), patient anatomy, and the decomposition processing including regularization. Thus, these prediction tools are potentially important for system optimization and regularization control in MBMD for specific imaging task. In this work, we proposed a cross-basis regularization scheme for cross-talk reduction. This is just one simple example of the control of imaging properties in MBMD and spectral imaging using the prediction tools. In ongoing work, we will investigate more sophisticated image quality criteria with task-based metrics that balance the importance of noise and resolution for specific goals.