Doubly robust inference when combining probability and non-probability samples with high dimensional data

Summary.

We consider integrating a non-probability sample with a probability sample which provides high dimensional representative covariate information of the target population. We propose a two-step approach for variable selection and finite population inference. In the first step, we use penalized estimating equations with folded concave penalties to select important variables and show selection consistency for general samples. In the second step, we focus on a doubly robust estimator of the finite population mean and re-estimate the nuisance model parameters by minimizing the asymptotic squared bias of the doubly robust estimator. This estimating strategy mitigates the possible first-step selection error and renders the doubly robust estimator root n consistent if either the sampling probability or the outcome model is correctly specified.

1. Introduction

Probability sampling is regarded as the gold standard in survey statistics for finite population inference. Fundamentally, probability samples are selected under known sampling designs and therefore are representative of the target population. However, many practical challenges arise in collecting and analysing probability sample data such as data collection costs and increasing non-response rates (Keiding and Louis, 2016). With advances of technology, non-probability samples become increasingly available for research purposes, such as remote sensing data and web-based volunteer samples. Non-probability samples provide rich information about the target population and can be potentially helpful for finite population inference. These complementary features of probability samples and non-probability samples raise the question of whether it is possible to develop data integration methods that leverage the advantages of both sources of data.

Existing methods for data integration can be categorized into three types. The first type is the so-called propensity score adjustment (Rosenbaum and Rubin, 1983). In this approach, the probability of a unit being selected into the non-probability sample, which is referred to as the propensity or sampling score, is modelled and estimated for all units in the non-probability sample. The subsequent adjustments, such as propensity score weighting or stratification, can then be used to adjust for selection biases; see, for example, Lee and Valliant (2009), Valliant and Dever (2011), Elliott and Valliant (2017) and Chen, Li and Wu (2018). Stuart et al. (2011, 2015) and Buchanan et al. (2018) used propensity score weighting to generalize results from randomized trials to a target population. O’Muircheartaigh and Hedges (2014) proposed propensity score stratification for analysing a non-randomized social experiment. One notable disadvantage of propensity score methods is that they rely on an explicit propensity score model and may be biased and highly variable if the model is misspecified (Kang and Schafer, 2007). The second type uses calibration weighting (Deville and Särndal, 1992; Kott, 2006; Chen, Valliant and Elliott, 2018; Chen et al., 2019). This technique forces the moments or the empirical distribution of auxiliary variables to be the same between the probability sample and the non-probability sample, so that after calibration the weighted distribution in the non-probability sample appears similar to that in the target population (DiSogra et al., 2011). The third type is mass imputation, which imputes the missing values for all units in the probability sample. In the usual imputation for missing data analysis, the respondents in the sample constitute a training data set for developing an imputation model. In the mass imputation, the non-probability sample is used as a training data set, and imputation is applied to all units in the probability sample; see, for example, Breidt et al. (1996), Rivers (2007), Kim and Rao (2012), Chipperfield et al. (2012) and Yang and Kim (2018).

Let $X\in {ℝ}^p$ be a vector of auxiliary variables (including an intercept) that are available from two sources of data, and let Y be a general-type study variable of interest. We consider combining a probability sample observing X, referred to as sample A, and a non-probability sample observing (X, Y), referred to as sample B, to estimate μ the population mean of Y. Because the sampling mechanism of a non-probability sample is unknown, the target population quantity is not identifiable in general. Researchers rely on an identification strategy that uses the non-informative sampling assumption imposed on the non-probability sample. To ensure that this assumption holds, researchers try to control for all covariates that are predictors of both sampling and the outcome variable. In practice, subject matter experts recommend a rich set of potentially useful variables but typically will not identify the set of variables to adjust for. In the presence of a large number of auxiliary variables, variable selection is important, because existing methods may become unstable or even infeasible, and irrelevant auxiliary variables can introduce a large variability in estimation. There is a large literature on variable-selection methods for prediction, but little work on variable selection for data integration that can successfully recognize the strengths and the limitations of each source of data and utilize all information captured for finite population inference. Gao and Carroll (2017) proposed a pseudolikelihood approach to combining multiple non-survey data with high dimensionality; this approach requires that all likelihoods are correctly specified and therefore is sensitive to model misspecification. Chen, Valliant and Elliott (2018) proposed a model-based calibration approach using lasso regression; this approach relies on a correctly specified outcome model. To our knowledge, robust inference has not been addressed in the context of data integration with high dimensional data.

We propose a doubly robust variable-selection and estimation strategy that harnesses the representativeness of the probability sample and the outcome information in the non-probability sample. The double robustness entails that the final estimator is consistent for the true value if either the probability of selection into the non-probability sample, which is referred to as the sampling score, or the outcome model is correctly specified, but not necessarily both (a double-robustness condition); see, for example, Bang and Robins (2005), Tsiatis (2006), Cao et al. (2009) and Han and Wang (2013). To handle high dimensional covariates, our strategy separates the variable selection step and the estimation step for the finite population mean to achieve two different goals.

In the first step, we select a set of variables that are important predictors of either the sampling score or the outcome model using penalized estimating equations. We assume that the sampling score follows a logistic regression model with unknown parameter $\alpha \in {ℝ}^p$ and the outcome follows a generalized linear model with unknown parameter $\beta \in {ℝ}^p$. Importantly, we separate the estimating equations for α and β to achieve stability in variable selection under the double-robustness condition. Specifically, we construct the estimating equation for α by calibrating the weighted average of X from sample B, weighted by the inverse of the sampling score, to the weighted average of X from sample A (i.e. a design-unbiased estimate of population mean of X). We construct the estimating equation for β by minimizing the standard least squared error loss under the outcome model. To establish the selection properties, we consider the ‘large n, diverging p’ framework. The major technical challenge is that, under the finite population framework, the selection indicators of sample A are not independent in general. To overcome this challenge, we construct martingale random variables with a weak dependence that enables the application of the Bernstein inequality. This construction is used in establishing our selection consistency result.

In the second step, we re-estimate (α, β) on the basis of the joint set of covariates selected from the first step and consider a doubly robust estimator of μ, ${\widehat{\mu }}_{\text{dr}}\left(\widehat{\alpha },\widehat{\beta }\right)$.We propose to use different estimating equations for (α, β), derived by minimizing the asymptotic squared bias of ${\widehat{\mu }}_{\text{dr}}\left(\widehat{\alpha },\widehat{\beta }\right)$. This estimation strategy is not new; see, for example, Kim and Haziza (2014) for missing data analyses in low dimensional data; here, we demonstrate its new role in high dimensional data to mitigate the possible selection error in the first step. In essence, our strategy for estimating (α, β) renders the first-order term in the Taylor series expansion of ${\widehat{\mu }}_{\text{dr}}\left(\widehat{\alpha },\widehat{\beta }\right)$ with respect to (α, β) to be exactly zero, and the remaining terms are negligible under regularity conditions. This estimating strategy makes the doubly robust estimator root n consistent if either the sampling probability or the outcome model is correctly specified. This also enables us to construct a simple and consistent variance estimator allowing for doubly robust inferences. Importantly, the estimator proposed enables model misspecification of either the sampling score or the outcome model. In the existing high dimensional causal inference literature, the doubly robust estimators have been shown to be robust to selection errors by using penalization (Farrell, 2015) or approximation errors by using machine learning (Chernozhukov et al., 2018). However, this double-robustness feature requires both nuisance models to be correctly specified. We relax this requirement by allowing one of the nuisance models to be misspecified. We clarify that, even though the set of variables for estimation may include the variables that are solely related to the sampling score but not the outcome and therefore may harm efficiency of estimating μ (De Luna et al., 2011; Patrick et al., 2011), it is important to include these variables for ${\widehat{\mu }}_{\text{dr}}\left(\widehat{\alpha },\widehat{\beta }\right)$ to achieve consistency in the case when the outcome model is misspecified and the sampling score model is correctly specified; see Section 6.

The paper proceeds as follows. Section 2 provides the basic set-up of the problem. Section 3 presents the proposed two-step procedure for variable selection and doubly robust estimation of the finite population mean. Section 4 describes the computation algorithm for solving penalized estimating equations. Section 5 presents the theoretical properties for variable selection and doubly robust estimation. Section 6 reports simulation results that illustrate the finite sample performance of the method. In Section 7, we present an application to analyse a non-probability sample collected by the Pew Research Center (PRC). We relegate all proofs to the on-line supplementary material.

2. Basic set-up

2.1. Notation: two samples

Let $\mathcal{U}=\left\{1,\dots ,N\right\}$ be the index set of N units for the finite population with N known. The finite population consists of ${\mathcal{F}}_N=\left\{\left(X_i,Y_i\right):i\in \mathcal{U}\right\}$. The parameter of interest is the finite population mean $\mu =N^{-1}{\Sigma }_{i=1}^N{Y}_i$. We consider two sources of data: a probability sample, referred to as sample A, and a non-probability sample, referred to as sample B. Table 1 illustrates the observed data structure. Sample A consists of observations ${\mathcal{O}}_{\text{A}}=\left\{\left(d_{\text{A},i}={\pi }_{\text{A},i}^{-1},X_i\right):i\in \mathcal{A}\right\}$ with sample size n_A, where ${\pi }_{\text{A},i}=P\left(i\in \mathcal{A}\right)$ is known in sample A. Sample B consists of observations ${\mathcal{O}}_{\text{B}}=\left\{\left(X_i,Y_i\right):i\in \mathcal{B}\right\}$ with sample size n_B. We define I_A,i and I_B,i to be the selection indicators corresponding to sample A and sample B respectively. Although the non-probability sample contains rich information on (X, Y), the sampling mechanism is unknown, and therefore we cannot compute the first-order inclusion probability for Horvitz-Thompson estimation. The naive estimators applied to sample B without adjusting for the sampling process are subject to selection biases (Meng, 2018).

Table 1.

Two sources of data^†

Sample		Sampling weight π−1	Covariate X	Study variable Y
Probability sample	1	✓	✓	?
	⋮	⋮	⋮	⋮
	nA	✓	✓	?
Non-probability sample	nA + 1	?	✓	✓
	⋮	⋮	⋮	⋮
	nA + nB	?	✓	✓

^†Sample A is a probability sample, and sample B is a non-probability sample. ‘✓’ and ‘?’ indicate observed and unobserved data respectively.

2.2. An identification assumption

Before presenting the proposed methodology for integrating the two sources of data, we first discuss the identification assumption. Let f(Y|X) be the conditional distribution of Y given X in the superpopulation model ζ that generates the finite population. We make the following assumption.

Assumption 1.

1. The selection indicator I_B of sample B and the response variable Y are independent given X, i.e. P(I_B = 1|X, Y) = P(I_B = 1|X), which is referred to as the sampling score π_B(X), and

2. π_B(X) > N^γ−1δ_B > 0 for all X, where $\gamma \in (\frac{2}{3},1]$.

Assumption 1(a) implies that m(X) = E(Y|X) = E(Y|X, I_B = 1) can be estimated solely on the basis of sample B. Assumption 1(b) specifies a lower bound of π_B(X). A standard condition in the literature imposes a strict positivity in the sense that π_B(X) > δ_B > 0; however, it implies that $n_{\text{B}}^{-1}=O\left(N^{-1}\right)$, which may be restrictive in survey practice. Here, we relax this condition and allow $n_{\text{B}}^{-1}=O\left(N^{-\gamma }\right)$, where γ can be strictly less than 1.

Assumption 1 is a key assumption for identification. Under assumption 1, E(μ) is identifiable on the basis of sample A by E{I_Am(X)} or sample B by E{I_BY/π_B(X)}. However, this assumption is not verifiable from the observed data. To ensure that this assumption holds, researchers often consider many possible predictors for the selection indicator I_B or the outcome Y, resulting in a rich set of variables in X.

2.3. Existing estimators

In practice, the sampling score function π_B(X) and the outcome mean function m(X) are unknown and need to be estimated from the data. Let π_B(X^Tα) and m(X^Tβ) be the postulated models for π_B(X) and m(X) respectively, where α and β are unknown parameters. Various estimators of μ have been proposed in the literature, each requiring different model assumptions and estimation strategies. We provide examples below and discuss their properties and limitations.

2.3.1. Example 1 (inverse probability of sampling score weighting)

Given an estimator $\widehat{\alpha }$, the inverse probability of sampling score weighting estimator is

$${\widehat{\mu }}_{\text{IPW}}={\widehat{\mu }}_{\text{IPW}}\left(\widehat{\alpha }\right)=\frac{1}{N}\sum _{i=1}^N\frac{I_{\text{B},i}}{{\pi }_{\text{B}}\left(X_i^{\text{T}}\widehat{\alpha }\right)}{Y}_i.$$ (1)

The justification for ${\widehat{\mu }}_{\text{IPW}}$ relies on a correct specification of π_B(X) and the consistency of $\widehat{\alpha }$. There are different approaches to obtain $\widehat{\alpha }$. Following Valliant and Dever (2011), we can obtain $\widehat{\alpha }$ by fitting the sampling score model on the basis of the combined data ${\mathcal{O}}_{\text{A}}\cup {\mathcal{O}}_{\text{B}}=\left\{\left({\omega }_i=d_{\text{A},i},X_i,I_i=0\right):i\in \mathcal{A}\right\}\cup \left\{\left({\omega }_i=1,X_i,I_i=1\right):i\in \mathcal{B}\right\}$, weighted by ω_i. The resulting estimator $\widehat{\alpha }$ is valid n_B is relatively small (Valliant and Dever, 2011). Elliott and Valliant (2017) proposed an alternative strategy based on the Bayes rule: π_B(X) ∝ P(I_A = 1|X)O_B(X), where $O_{\text{B}}\left(X\right)=P\left(I_{\text{B}}=1\mid X,{\mathcal{O}}_{\text{A}}\cup {\mathcal{O}}_{\text{B}}\right)/P\left(I_{\text{B}}=0\mid X,{\mathcal{O}}_{\text{A}}\cup {\mathcal{O}}_{\text{B}}\right)$ is the odds of selection into sample B among the combined sample. This approach does not require n_B to be small; however, if X does not correspond to the design variables for sample A, it requires postulating an additional model for P(I_A = 1|X). Moreover, variable selection based on this approach is not straightforward with a high dimensional X. To obtain $\widehat{\alpha }$, we use the following estimating equation for α:

$$\sum _{i=1}^N\left\{\frac{I_{\text{B},i}}{\pi \left(X_i^{\text{T}}\alpha \right)}-\frac{I_{\text{A},i}}{{\pi }_{\text{A},i}}\right\}h\left(X_i;\alpha \right)=0,$$ (2)

for some h(X_i; α) such that equation (2) has a unique solution. Kott and Liao (2017) advocated the use of h(X; α) = X and Chen, Li and Wu (2018) advocated the use of h(X; α) = π(X^T; α)X.

2.3.2. Example 2 (outcome regression based on sample A)

The outcome regression estimator is

$${\widehat{\mu }}_{\text{reg}}={\widehat{\mu }}_{\text{reg}}\left(\widehat{\beta }\right)=\frac{1}{N}\sum _{i=1}^N{I}_{\text{A},i}{d}_{\text{A},i}m\left(X_i^{\text{T}}\widehat{\beta }\right),$$ (3)

where $\widehat{\beta }$ is obtained by fitting the outcome model based solely on ${\mathcal{O}}_{\text{B}}$ under assumption 1.

The justification for ${\widehat{\mu }}_{\text{reg}}$ relies on a correct specification of m(X^Tβ) and the consistency of $\widehat{\beta }$. If m(X^Tβ) is misspecified or $\widehat{\beta }$ is inconsistent, ${\widehat{\mu }}_{\text{reg}}$ can be biased.

2.3.3. Example 3 (calibration weighting)

The calibration weighting estimator is

$${\widehat{\mu }}_{\text{cal}}={\widehat{\mu }}_{\text{cal}}=\frac{1}{N}\sum _{i=1}^N{\omega }_i{I}_{\text{B},i}{Y}_i,$$ (4)

where $\left\{{\omega }_i:i\in \mathcal{B}\right\}$ satisfies constraint (i) ${\Sigma }_{i\in {\mathcal{S}}_{\text{B}}}{\omega }_i{X}_i={\Sigma }_{i\in {\mathcal{S}}_{\text{A}}}{d}_{\text{A},i}{X}_i$ or constraint (ii) ${\Sigma }_{i\in {\mathcal{S}}_{\text{B}}}{\omega }_{i}m\left(X_i;\widehat{\beta }\right)={\Sigma }_{i\in \mathcal{A}}{d}_{\text{A},i}m\left(X_i;\widehat{\beta }\right)$ (McConville et al., 2017; Chen, Valliant and Elliott, 2018; Chen et al., 2019).

The justification for ${\widehat{\mu }}_{\text{cal}}$ subject to constraint (i) relies on the linearity of the outcome model, i.e. m(X) = X^Tβ* for some β*, or the linearity of the inverse probability of sampling weight, i.e. π_B(X)⁻¹ = X^Tα* for some α* (Fuller (2009), theorem 5.1). The linearity conditions are unlikely to hold for non-continuous variables. In these cases, ${\widehat{\mu }}_{\text{cal}}$ may be biased. The justification for ${\widehat{\mu }}_{\text{cal}}$ subject to constraint (ii) relies on a correct specification of m(X; β).

2.3.4. Example 4 (doubly robust estimator)

The doubly robust estimator is

$${\widehat{\mu }}_{\text{dr}}={\widehat{\mu }}_{\text{dr}}\left(\widehat{\alpha },\widehat{\beta }\right)=\frac{1}{N}\sum _{i=1}^N\left[\frac{I_{\text{B},i}}{{\widehat{\pi }}_{\text{B}}\left(X_i^{\text{T}}\widehat{\alpha }\right)}\left\{Y_i-m\left(X_i^{\text{T}}\widehat{\beta }\right)\right\}+I_{\text{A},i}{d}_{\text{A},i}m\left(X_i^{\text{T}}\widehat{\beta }\right)\right].$$ (5)

The estimator ${\widehat{\mu }}_{\text{dr}}$ is doubly robust with fixed dimensional X (Chen, Li and Wu, 2018), in the sense that it achieves consistency if either π_B(X^Tα) or m(X^Tβ) is correctly specified, but not necessarily both. The double robustness is attractive; therefore, we shall investigate the potential of ${\widehat{\mu }}_{\text{dr}}$ in a high dimensional set-up.

3. Methodology in high dimensional data

In the presence of a large number of covariates, not all of them are relevant for making inference of the population mean of the outcome. Including unnecessary covariates in the model makes the computation unstable and increases estimation errors. Variable selection is required to handle high dimensional covariates. For any vector $\alpha \in {ℝ}^p$, denote the number of non-zero elements in α as ${\Vert \alpha \Vert }_0={\Sigma }_{j=1}^{p}I\left({\alpha }_j\ne 0\right)$, the L₁-norm as ${\Vert \alpha \Vert }_1={\Sigma }_{j=1}^p|{\alpha }_j|$, the L₂-norm as ${\Vert \alpha \Vert }_2=\surd {\sum }_{j=1}^p{\alpha }_j^2$ and the L_∞-norm as ${\Vert \alpha \Vert }_{\infty }={\text{max}}_{1⩽j⩽p}|{\alpha }_j|$. For any $\mathcal{J}\subseteq \left\{1,\dots ,p\right\}$, let ${\alpha }_{\mathcal{J}}$ be the subvector of α formed by elements of α whose indices are in $\mathcal{J}$. Let ${\mathcal{J}}^{\text{c}}$ be the complement of $\mathcal{J}$. For ${\mathcal{J}}_1$, ${\mathcal{J}}_2\subseteq \left\{1,\dots ,p\right\}$ and matrix $\Sigma \in {ℝ}^{p\times p}$, let ${\Sigma }_{{\mathcal{J}}_1,{\mathcal{J}}_2}$ be the submatrix of Σ formed by rows in ${\mathcal{J}}_1$ and columns in ${\mathcal{J}}_2$. Following the literature on variable selection, we first standardize the covariates so that they have variances approximately equal to 1, which makes the variable-selection procedure more stable. We make the following modelling assumptions.

Assumption 2 (sampling score model).

The sampling mechanism of sample B, π_B(X), follows a logistic regression model π_B(X^Tα), i.e. logit{π_B(X^Tα)} = X^Tα for $\alpha \in {ℝ}^p$.

Assumption 3 (outcome model).

The outcome mean function m(X) follows a generalized linear regression model, i.e. m(X) = m(X^Tβ) for $\beta \in {ℝ}^p$, where m(·) denotes the link function.

Define α* to be the p-dimensional parameter that minimizes the Kullback-Leibler divergence,

$${\alpha }^{*}=\text{arg}\underset{\alpha \in {ℝ}^p}{\text{min}}E\left[{\pi }_{\text{B}}\left(X\right)\text{log}\left\{\frac{{\pi }_{\text{B}}\left(X\right)}{{\pi }_{\text{B}}\left(X^{\text{T}}\alpha \right)}\right\}+\left\{1-{\pi }_{\text{B}}\left(X\right)\right\}\text{log}\left\{\frac{1-{\pi }_{\text{B}}\left(X\right)}{1-{\pi }_{\text{B}}\left(X^{\text{T}}\alpha \right)}\right\}\right],$$

and ${\beta }^{*}=\text{arg}{\text{min}}_{\beta \in {ℝ}^p}E\left[{\left\{Y-m\left(X^{\text{T}}\beta \right)\right\}}^2\right]$.

In assumption 2, we adopt the logistic regression model for the sampling score following most of the empirical literature; but our framework can be extended to the case of other models such as the probit model. The models π_B(X^Tα) and m(X^Tβ) are working models, which may be misspecified. If the sampling score model is correctly specified, we have π_B(X) = π_B(X^Tα*). If the outcome model is correctly specified, we have m(X) = m(X^Tβ*).

The procedure proposed consists of two steps: the first step selects important variables in the sampling score model and the outcome model, and the second step focuses on doubly robust estimation of the population mean.

In the first step, we propose to solve penalized estimating equations for variable selection. Using equation (2) with h(X; α) = X, we define the estimating function for α as

$$U_1\left(\alpha \right)=\frac{1}{N}\sum _{i=1}^N\left\{\frac{I_{\text{B},i}}{{\pi }_{\text{B}}\left(X_i^{\text{T}}\alpha \right)}-\frac{I_{\text{A},i}}{{\pi }_{\text{A},i}}\right\}{X}_i.$$

To select important variables in m(X^Tβ), we define the estimating function for β as

$$U_2\left(\beta \right)=\frac{1}{N}\sum _{i=1}^N{I}_{\text{B},i}\left\{Y_i-m\left(X_i^{\text{T}}\beta \right)\right\}{X}_i.$$

Let U(θ) = (U₁(α)^T, U₂(β)^T)^T be the joint estimating function for θ = (α^T, β^T)^T. When p is large, following Johnson et al. (2008), we consider the penalized estimating function for (α, β) as

$$U^{\text{p}}\left(\alpha ,\beta \right)=U\left(\alpha ,\beta \right)-\left(\begin{array}{c}{q}_{{\lambda }_{\alpha }}\left(|\alpha |\right)\text{sgn}\left(\alpha \right)\\ q_{{\lambda }_{\beta }}\left(|\beta |\right)\text{sgn}\left(\beta \right)\end{array}\right),$$ (6)

where $q_{{\lambda }_{\alpha }}\left(\alpha \right)={\left(q_{{\lambda }_{\alpha }}\left(|{\alpha }_0|\right),\dots ,q_{{\lambda }_{\alpha }}\left(|{\alpha }_p|\right)\right)}^{\text{T}}$ and $q_{{\lambda }_{\beta }}\left(\beta \right)={\left(q_{{\lambda }_{\beta }}\left(|{\beta }_0|\right),\dots ,q_{{\lambda }_{\beta }}\left(|{\beta }_p|\right)\right)}^{\text{T}}$ are some continuous functions, $q_{{\lambda }_{\alpha }}\left(|\alpha |\right)\text{sgn}\left(\alpha \right)$ is the elementwise product of $q_{{\lambda }_{\alpha }}\left(\alpha \right)$ and sgn(α), and $q_{{\lambda }_{\beta }}\left(|\beta |\right)\text{sgn}\left(\beta \right)$ is the elementwise product of $q_{{\lambda }_{\beta }}\left(\beta \right)$ and sgn(β). We let q_λ(x) = dp_λ(x)/dx, where p_λ(x) is some penalization function. Although the same discussion applies to different non-concave penalty functions, we specify p_λ(x) to be a folded concave smoothly clipped absolute deviation penalty function (Fan and Lv, 2011). Accordingly, we have

$$q_{\lambda }\left(|\theta |\right)=\lambda \left\{I\left(|\theta |<\lambda \right)+\frac{{\left(a\lambda -|\theta |\right)}_{+}}{\left(a-1\right)\lambda }I\left(|\theta |⩾\lambda \right)\right\},$$ (7)

for a > 0, where (·)₊ is the truncated linear function, i.e., if x ⩾ 0, (x)₊ = x and, if x < 0, (x)₊ = 0. We use a = 3.7 following the suggestion of Fan and Li (2001). We select the variables if the corresponding estimates of coefficients are non-zero in either the sampling score or the outcome model, indexed by $\mathcal{C}$.

Remark 1.

To help to understand function (6) we discuss two scenarios. If |α_j| is large, then $q_{{\lambda }_{\alpha }}\left(|{\alpha }_j|\right)$ is 0, and therefore U_1,j(α) is not penalized. In contrast, if |α_j| is small but non-zero, then $q_{{\lambda }_{\alpha }}\left(|{\alpha }_j|\right)$ is large, and U_1,j(α) is penalized with a penalty term. The penalty term then forces ${\widehat{\alpha }}_j$ to be 0 and excludes the jth element of X from the final selected set of variables. The same discussion applies to U₂(β) and $q_{{\lambda }_{\beta }}\left(|\beta |\right)$.

In the second step, we consider the doubly robust estimator ${\widehat{\mu }}_{\text{dr}}\left(\widehat{\alpha },\widehat{\beta }\right)$ in equation (5) with $\left(\widehat{\alpha },\widehat{\beta }\right)$ re-estimated on the basis of $X_{\mathcal{C}}$. As we shall show in Section 5, the set $\mathcal{C}$ contains the true important variables in either the sampling score model or the outcome model with probability approaching 1 (the oracle property). Therefore, if either the sampling score model or the outcome model is correctly specified, the asymptotic bias of ${\widehat{\mu }}_{\text{dr}}\left({\alpha }^{*},{\beta }^{*}\right)$ is 0; however, if both models are misspecified, the asymptotic bias of ${\widehat{\mu }}_{\text{dr}}\left({\alpha }^{*},{\beta }^{*}\right)$ is

$$\begin{gathered} \text{a}.\text{bias}\left({\alpha }^{*},{\beta }^{*}\right)=E\left\{{\widehat{\mu }}_{\text{dr}}\left({\alpha }^{*},{\beta }^{*}\right)-\mu \right\} \\ =E\left[\frac{1}{N}\sum _{i=1}^N\left\{\frac{I_{\text{B},i}}{{\pi }_{\text{B}}\left(X_i^{\text{T}}{\alpha }^{*}\right)}-1\right\}\left\{Y_i-m\left(X_i^{\text{T}}{\beta }^{*}\right)\right\}\right] \\ +E\left\{\frac{1}{N}\sum _{i=1}^N\left(I_{\text{A},i}{d}_{\text{A},i}-1\right)m\left(X_i^{\text{T}}{\beta }^{*}\right)\right\}. \end{gathered}$$

To minimize a.bias(α, β)², we consider the estimating function

$$\frac{\partial \text{a}.\text{bias}{(\alpha ,\beta )}^2}{\partial {\left({\alpha }_{\mathcal{C}}^{\text{T}},{\beta }_{\mathcal{C}}^{\text{T}}\right)}^{\text{T}}}=2\text{a}.\text{bias}\left(\alpha ,\beta \right)\left(\begin{array}{c}{I}_{\text{B}}\left\{\frac{1}{{\pi }_{\text{B}}\left(X^{\text{T}}\alpha \right)}-1\right\}\left\{Y-m\left(X^{\text{T}}\beta \right)\right\}{X}_{\mathcal{C}}\\ \left\{\frac{I_{\text{B}}}{{\pi }_{\text{B}}\left(X^{\text{T}}\alpha \right)}-d_{\text{A}}{I}_{\text{A}}\right\}\partial m\left(X^{\text{T}}\beta \right)/\partial {\beta }_{\mathcal{C}}\end{array}\right)$$ (8)

and the corresponding empirical estimating function

$$J\left(\alpha ,\beta \right)=\left(\begin{array}{l}{J}_1\left(\alpha ,\beta \right)\hfill \\ J_2\left(\alpha ,\beta \right)\hfill \end{array}\right)=\left(\begin{array}{c}\frac{1}{N}\sum _{i=1}^N{I}_{\text{B},i}\left\{\frac{1}{{\pi }_{\text{B}}\left(X_i^{\text{T}}\alpha \right)}-1\right\}\left\{Y_i-m\left(X_i^{\text{T}}\beta \right)\right\}{X}_{iC}\\ \frac{1}{N}\sum _{i=1}^N\left\{\frac{I_{\text{B},i}}{{\pi }_{\text{B}}\left(X_i^{\text{T}}\alpha \right)}-d_{\text{A},i}{I}_{\text{A},i}\right\}\frac{\partial m\left(X_i^{\text{T}}\beta \right)}{\partial {\beta }_{\mathcal{C}}}\end{array}\right)$$ (9)

for estimating (α, β), constrained on $\left\{{\left({\alpha }^{\text{T}},{\beta }^{\text{T}}\right)}^{\text{T}}\in {ℝ}^{2p}:{\alpha }_{{\mathcal{C}}^{\text{c}}}=0,{\beta }_{{\mathcal{C}}^{\text{c}}}=0\right\}$.

To summarize, our two-step procedure is as follows.

• Step 1: solve the penalized joint estimating equation U^p(α, β) = 0, denoted by $\left(\tilde{\alpha },\tilde{\beta }\right)$. Let ${\widehat{\mathcal{M}}}_{\alpha }=\left\{j:{\tilde{\alpha }}_j\ne 0\right\}$, ${\widehat{\mathcal{M}}}_{\beta }=\left\{j:{\tilde{\beta }}_j\ne 0\right\}$ and $\mathcal{C}={\widehat{\mathcal{M}}}_{\alpha }\cup {\widehat{\mathcal{M}}}_{\beta }$.

• Step 2: obtain the proposed estimator as

  $${\widehat{\mu }}_{\text{p}-\text{dr}}={\widehat{\mu }}_{\text{p}-\text{dr}}\left(\widehat{\alpha },\widehat{\beta }\right)=\frac{1}{N}\sum _{i=1}^N\left\{I_{\text{B},i}\frac{Y_i-m\left(X_i^{\text{T}}\widehat{\beta }\right)}{{\pi }_{\text{B}}\left(X_i^{\text{T}}\widehat{\alpha }\right)}+I_{\text{A},i}{d}_{\text{A},i}m\left(X_i^{\text{T}}\widehat{\beta }\right)\right\},$$ (10)

  where $\widehat{\alpha }$ and $\widehat{\beta }$ are obtained by solving J(α, β) = 0 for α and β with ${\alpha }_{{\mathcal{C}}^{\text{c}}}=0$ and ${\beta }_{{\mathcal{C}}^{\text{c}}}=0$.

Remark 2.

The two steps use different estimating functions (6) and (9) for selection and estimation with the following advantages. First, function (6) separates the selection for α and β in U₁(α) and U₂(β), so it stabilizes the selection procedure if either the sampling score model or the outcome model is misspecified. Second, using equation (9) for estimation leads to an attractive feature for inference about μ. We point out that, although the joint estimating function (9) is motivated by minimizing the asymptotic bias of ${\widehat{\mu }}_{\text{dr}}\left({\alpha }^{*},{\beta }^{*}\right)$ when both nuisance models are misspecified, we do not expect the proposed estimator for μ to be unbiased in this case. Instead, using function (9) has the advantage in the case when either the sampling score or the outcome model is correctly specified. It is well known that post-selection inference is notoriously difficult even when both models are correctly specified because the estimation step is based on a random set of variables being selected. We show that our estimation strategy based on function (9) mitigates the possible first-step selection error and makes ${\widehat{\mu }}_{\text{dr}}\left(\widehat{\alpha },\widehat{\beta }\right)$ root n consistent if either the sampling probability or the outcome model is correctly specified in high dimensional data. Heuristically this is achieved because the first Taylor series expansion term is set to be 0 because of function (8). We relegate the details to Section 5.

Remark 3.

Variable selection circumvents the instability or infeasibility of direct estimation of (α, β) with high dimensional X. Moreover, in step 2, we consider the union of covariates $X_{\mathcal{C}}$, where $\mathcal{C}={\widehat{\mathcal{M}}}_{\alpha }\cup {\widehat{\mathcal{M}}}_{\beta }$. It is worth comparing this choice with two other common choices in the literature. The first considers separate sets of variables for the two models, i.e. the sampling score is fitted on the basis of ${\widehat{\mathcal{M}}}_{\alpha }$, and the outcome model is fitted on the basis of ${\widehat{\mathcal{M}}}_{\beta }$. However, we note that in the joint estimating equations J₁(α, β) and J₂(α, β) should have the same dimension; otherwise, a solution to J(α, β) = 0 may not exist. Moreover, Brookhart et al. (2006) and Shortreed and Ertefaie (2017) have shown that including outcome predictors in the propensity score model will increase the precision of the estimated average treatment effect without increasing bias. This implies that an efficient variable-selection and estimation method should take into account both sampling-covariate and outcome-covariate relationships. As a result, ${\widehat{\mu }}_{\text{dr}}\left(\widehat{\alpha },\widehat{\beta }\right)$ may have a better performance than the oracle estimator that uses the true important variables separately in the sampling score and the outcome model. Second, many researchers have suggested that including predictors that are solely related to the sampling score but not the outcome may harm estimation efficiency (De Luna et al., 2011; Patrick et al., 2011). However, this strategy is effective when both the sampling score and the outcome models are correctly specified. When the sampling score model is correctly specified but the outcome model is misspecified, restricting the variables to be the outcome predictors may make the sampling score misspecified by using the wrong set of variables. The simulation study suggests that ${\widehat{\mu }}_{\text{p}-\text{dr}}$ restricted to the set of variables in ${\widehat{\mathcal{M}}}_{\beta }$ is not doubly robust.

4. Computation

In this section, we discuss the computation for solving the penalized estimating equation (6). Following Johnson et al. (2008), we use an iterative algorithm that combines the Newton-Raphson algorithm for solving estimating equations and the minorization-maximization algorithm for the non-convex penalty of Hunter and Li (2005).

First, by the minorization-maximization algorithm, the penalized estimator $\tilde{\theta }=\left(\tilde{\alpha },\tilde{\beta }\right)$ solving equation (6) satisfies

$$U^{\text{p}}\left(\tilde{\theta }\right)=U\left(\tilde{\theta }\right)-\left(\begin{array}{c}{q}_{{\lambda }_{\tilde{\alpha }}}\left(|\tilde{\alpha }|\right)\text{sgn}\left(\tilde{\alpha }\right)\frac{|\tilde{\alpha }|}{ϵ+|\tilde{\alpha }|}\\ q_{{\lambda }_{\tilde{\beta }}}\left(|\tilde{\beta }|\right)\text{sgn}\left(\tilde{\beta }\right)\frac{|\tilde{\beta }|}{ϵ+|\tilde{\beta }|}\end{array}\right)=0,$$ (11)

where ϵ is a predefined small number. In our implementation, we choose ϵ to be 10⁻⁶.

Second, we solve equation (11) using the Newton-Raphson algorithm. It may be challenging to implement the Newton-Raphson algorithm directly, because it involves inverting a large matrix. For computational stability, we use a co-ordinate decent algorithm (Friedman et al., 2007) by cycling through and updating each of the co-ordinates. Define m^(k)(t) = d^km(t)/d^kt for k ⩾ 1:

$$\begin{gathered} \nabla \left(\theta \right)=\frac{\partial U\left(\theta \right)}{\partial {\theta }^{\text{T}}}=\text{diag}\left\{\frac{\partial U_1\left(\alpha \right)}{\partial {\alpha }^{\text{T}}},\frac{\partial U_2\left(\beta \right)}{\partial {\beta }^{\text{T}}}\right\}, \\ \frac{\partial U_1\left(\alpha \right)}{\partial {\alpha }^{\text{T}}}=-\frac{1}{N}\sum _{i=1}^N{I}_{\text{B},i}\frac{1-{\pi }_{\text{B}}\left(X_i^{\text{T}}\alpha \right)}{{\pi }_{\text{B}}\left(X_i^{\text{T}}\alpha \right)}{X}_i{X}_i^{\text{T}}, \\ \frac{\partial U_2\left(\beta \right)}{\partial {\beta }^{\text{T}}}=-\frac{1}{N}\sum _{i=1}^N{I}_{\text{B},i}{m}^{\left(1\right)}{\left(X_i^{\text{T}}\beta \right)}^2{X}_i{X}_i^{\text{T}}, \end{gathered}$$ (12)

and

$$\Lambda \left(\theta \right)=\left(\begin{array}{ccc}{q}_{\lambda 1}\left(|{\theta }_1|\right)& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & q_{{\lambda }_{2p}}\left(|{\theta }_{2p}|\right)\end{array}\right).$$

Let θ start at an initial value ${\tilde{\theta }}^{\left[0\right]}$. With the other co-ordinates fixed, the kth Newton-Raphson update for θ_j is

$${\tilde{\theta }}_j^{\left[k\right]}={\tilde{\theta }}_j^{\left[k-1\right]}+{\left\{{\nabla }_{jj}\left({\tilde{\theta }}^{\left[k-1\right]}\right)+N{\Lambda }_{jj}\left({\tilde{\theta }}^{\left[k-1\right]}\right)\right\}}^{-1}\left\{U_j\left({\tilde{\theta }}^{\left[k-1\right]}\right)-N{\Lambda }_{jj}\left({\tilde{\theta }}^{\left[k-1\right]}\right){\tilde{\theta }}_j^{\left[k-1\right]}\right\},$$ (13)

where ∇_jj(θ) and Λ_jj(θ) are the jth diagonal elements in ∇(θ) and Λ(θ) respectively. The procedure cycles through all the 2p elements of θ and is repeated until convergence.

We use K-fold cross-validation to select tuning parameters (λ_α, λ_β). More specifically, we partition both samples into approximately K equal sized subsets and pair subsets of sample A and subsets of sample B randomly. Of the K pairs, we retain one single pair as the validation data and the remaining K − 1 pairs as the training data. We fit the models on the basis of the training data and estimate the loss function on the basis of the validation data. We repeat the process K times, with each of the K pairs used exactly once as the validation data. Finally, we aggregate the K estimated loss function. We select the tuning parameter as the parameter that minimizes the aggregated loss function over a prespecified grid.

Because the weighting estimator uses the sampling score π_B(X) to calibrate the distribution of $X_{\mathcal{C}}$ between sample B and the target population, we use the following loss function for selecting λ_α:

$$\text{Loss}\left({\lambda }_{\alpha }\right)=\sum _{j=1}^p{\left(\sum _{i=1}^N\left[\frac{I_{\text{B},i}}{{\pi }_{\text{B}}\left\{X_i^{\text{T}}\tilde{\alpha }\left({\lambda }_{\alpha }\right)\right\}}-\frac{I_{\text{A},i}}{{\pi }_{\text{A},i}}\right]X_{i,j}\right)}^2,$$

where $\tilde{\alpha }\left({\lambda }_{\alpha }\right)$ is the penalized estimator $\tilde{\alpha }$ with tuning parameter λ_α.We use the prediction error loss function for selecting λ_β:

$$\text{Loss}\left({\lambda }_{\beta }\right)=\sum _{i=1}^N{I}_{\text{B},i}{\left[Y_i-m\left\{X_i^{\text{T}}\tilde{\beta }\left({\lambda }_{\beta }\right)\right\}\right]}^2,$$

where $\tilde{\beta }\left({\lambda }_{\beta }\right)$ is the penalized estimator $\tilde{\beta }$ with tuning parameter λ_β.

5. Asymptotic results for variable selection and estimation

We establish the asymptotic properties for the proposed double variable-selection and doubly robust estimation method. We assume that sample A is collected by simple random sampling or Poisson sampling with the following regularity conditions. Although it appears restrictive, our results extend to high entropy sampling designs; see remark 4.

Assumption 4.

For all 1 ⩽ i ⩽ N, π_A,i ⩾ N^γ−1δ_A > 0, where $\gamma \in (\frac{2}{3},1]$.

Similarly to assumption 1(b), we relax the strict positivity on π_A,i and assume n_A = O(N^γ) for γ possibly strictly less than 1. Let n = min(n_A, n_B), which is O(N^γ) under assumptions 1 and 4.

Remark 4.

We discuss the applicability of our asymptotic framework to sample A with high entropy sampling designs. Examples of high entropy sampling designs include simple random sampling, correlated Poisson sampling designs, normalized conditional Poisson sampling designs, Rao-Sampford sampling, the Chao design and the stratified design; see Berger (1998a,b), Brewer and Donadio (2003) and Grafström (2010). The asymptotic properties for high entropy sampling designs are determined solely by their first-order inclusion probabilities. Therefore, for two high entropy sampling designs with the same first-order inclusion probabilities, their asymptotic behaviours are the same. In particular, we can consider the conditional Poisson sampling design (Hájek, 1964; Tillé, 2011), which appears when conditioning the Poisson design on a fixed sample size n_A. Let p_A = {p_A,i: i = 1, … , N} with ${\Sigma }_{i=1}^N{p}_{\text{A},i}=n_{\text{A}}$ be the inclusion probabilities for the conditional Poisson sampling design. Given p_A, it is possible to find π_A = {π_A,i: i = 1, … , N} with ${\Sigma }_{i=1}^N{\pi }_{\text{A},i}=n_{\text{A}}$ such that the conditional Poisson sampling design with p_A is asymptotically equivalent to the Poisson sampling design with the inclusion probabilities π_A (Hájek, 1964; Conti, 2014). Therefore, for a high entropy design, to apply our theoretical results, we check the conditions for the corresponding inclusion probability π_A under Poisson sampling.

Let ${\mathcal{M}}_{\alpha }=\left\{1⩽j⩽p:{\alpha }_j^{*}\ne 0\right\}$, ${\mathcal{M}}_{\beta }=\left\{1⩽j⩽p:{\beta }_j^{*}\ne 0\right\}$ and ${\mathcal{M}}_{\theta }={\mathcal{M}}_{\alpha }\cup \left\{p+{\mathcal{M}}_{\beta }\right\}$. Define s_α = ∥α*∥₀, s_β = ∥β*∥₀, s_θ = s_α + s_β and λ_θ = min(λ_α, λ_β).

Assumption 5.

The following regularity conditions hold.

• Condition 1. The parameter θ belongs to a compact subset in ${ℝ}^{2p}$, and θ* lies in the interior of the compact subset.

• Condition 2. $\left\{X_i:i\in \mathcal{U}\right\}$ are fixed and uniformly bounded.

• Condition 3. There are constants c₁ and c₂ such that

  $$0<c_1⩽{\lambda }_{\text{min}}\left(\frac{1}{N}\sum _{i=1}^N{X}_i^{\text{T}}{X}_i\right)⩽{\lambda }_{\text{max}}\left(\frac{1}{N}\sum _{i=1}^N{X}_i^{\text{T}}{X}_i\right)⩽c_2<\infty ,$$

  where λ_min(·) and λ_max(·) are the minimum and the maximum eigenvalue of a matrix respectively.

• Condition 4. Let ${ϵ}_i(\beta )=Y_i-m\left(X_i^{\text{T}}\beta \right)$ be the ith residual. There is a constant c₃ such that E{|ϵ_i(β*)|^2+δ} ⩽ c₃ for all 1 ⩽ i ⩽ N and some δ > 0. There are constants c₄ and c₅ such that E[exp{c₄|ϵ_i(β*)|}|X_i] ⩽ c₅ for all 1 ⩽ i ⩽ N.

• Condition 5. $m^{\left(1\right)}\left(X_i^{\text{T}}\beta \right)$, $m^{\left(2\right)}\left(X_i^{\text{T}}\beta \right)$ and $m^{\left(3\right)}\left(X_i^{\text{T}}\beta \right)$ are uniformly bounded away from ∞ on ${\mathcal{N}}_{\theta ,\tau }=\{\theta \in {ℝ}^{2p}:\Vert {\theta }_{{\mathcal{M}}_{\theta }}-{\theta }_{{\mathcal{M}}_{\theta }}^{*}\Vert ⩽\tau \surd \left(s_{\theta }/n\right),{\theta }_{{\mathcal{M}}_{\theta }^{\text{c}}}=0\}$ for some τ > 0.

• Condition 6. ${\text{min}}_{j\in {\mathcal{M}}_{\alpha }}|{\alpha }_j^{*}|/{\lambda }_{\alpha }\to \infty$ and ${\text{min}}_{k\in {\mathcal{M}}_{\beta }}|{\beta }_k^{*}|/{\lambda }_{\beta }\to \infty$, as n → ∞.

• Condition 7. s_θ = o(n^1/3), λ_α, λ_β → 0, $\text{log}{(n)}^2=o\left(n{\lambda }_{\theta }^2\right)$, $\text{log}(p)=o\left\{n{\lambda }_{\theta }^2/\text{log}{(n)}^2\right\}$, $p{s}_{\theta }^4\text{log}{(n)}^6=o\left(n^3{\lambda }_{\theta }^2\right)$ and $p{s}_{\theta }^4\text{log}{(n)}^8=o\left(n^4{\lambda }_{\theta }^4\right)$, as n → ∞.

These assumptions are typical in the literature on penalization methods. Condition 2 specifies a fixed design which is well suited under the finite population inference framework. Condition 4 holds for Gaussian distributions, sub-Gaussian distributions, and so on. Condition 5 holds for common models. Condition 7 specifies the restrictions on the dimension of covariates p and the dimension of the true non-zero coefficients s_θ. To gain insight, when the true model size s_θ is fixed, condition 7 holds for p = O(n), i.e. p can be the same size as n.

We establish the asymptotic properties of the penalized estimating equation procedure.

Theorem 1.

Under assumptions 1–5, there is an approximate penalized solution $\tilde{\theta }$, which satisfies the selection consistency properties:

$$P\left\{|U_j^{\text{p}}\left(\tilde{\theta }\right)|=0,j\in {\mathcal{M}}_{\theta }\right\}\to 1,$$ (14)

$$P\left\{|U_j^{\text{p}}\left(\tilde{\theta }\right)|⩽\frac{{\lambda }_{\theta }}{\text{log}\left(n\right)},j\in {\mathcal{M}}_{\theta }^{\text{c}}\right\}\to 1,$$ (15)

$$P\left({\tilde{\theta }}_{{\mathcal{M}}_{\theta }^{\text{c}}}=0\right)\to 1$$ (16)

and

$${\tilde{\theta }}_{{\mathcal{M}}_{\theta }}-{\theta }_{{\mathcal{M}}_{\theta }}^{*}=O_P\left\{\surd \left(s_{\theta }/n\right)\right\},$$ (17)

as n → ∞:

Results (14) and (15) imply that $U(\tilde{\theta })=o_P\left\{{\lambda }_{\theta }/\text{log}(n)\right\}$. Results (16) and (17) imply that, with probability approaching 1, the penalized estimating equation procedure would not overselect irrelevant variables and estimate the true non-zero coefficients at the ✓(s_θ/n) convergence rate, which is the so-called oracle property of variable selection.

We now establish the asymptotic properties of ${\widehat{\mu }}_{\text{p}-\text{dr}}(\widehat{\alpha },\widehat{\beta })$. Define a sequence of events ${\mathcal{D}}_n=\left\{{\mathcal{M}}_{\theta }\subset \mathcal{C}\right\}$, where we emphasize that ${\mathcal{D}}_n$ depends on n but we suppress the dependence of ${\mathcal{M}}_{\theta }$ and $\mathcal{C}$ on n. Following the same argument as for equation (17), given the event ${\mathcal{D}}_n$, we have $\left\{{\left(\widehat{\alpha }-{\alpha }^{*}\right)}^{\text{T}},{\left(\widehat{\beta }-{\beta }^{*}\right)}^{\text{T}}\right\}=O_p\left\{\surd \left(s_{\theta }/n\right)\right\}$. Combining with $P\left({\mathcal{D}}_n\right)\to 1$, we have

$$\left\{{\left(\widehat{\alpha }-{\alpha }^{*}\right)}^{\text{T}},{\left(\widehat{\beta }-{\beta }^{*}\right)}^{\text{T}}\right\}=O_p\left\{\surd \left(s_{\theta }/n\right)\right\}.$$ (18)

By Taylor series expansion,

$$\begin{gathered} n^{1/2}\left\{{\widehat{\mu }}_{\text{p}-\text{dr}}\left(\widehat{\alpha },\widehat{\beta }\right)-\mu \right\}=n^{1/2}\left\{{\widehat{\mu }}_{\text{p}-\text{dr}}\left({\alpha }^{*},{\beta }^{*}\right)-\mu \right\}+n^{1/2}\frac{{\widehat{\mu }}_{\text{p}-\text{dr}}\left(\widehat{\alpha },\widehat{\beta }\right)}{\partial \left({\alpha }^{\text{T}},{\beta }^{\text{T}}\right)}\left(\begin{array}{c}\widehat{\alpha }-{\alpha }^{*}\\ \widehat{\beta }-{\beta }^{*}\end{array}\right) \\ +O_P\left\{n^{1/2}{\Vert \left(\begin{array}{l}\widehat{\alpha }-{\alpha }^{*}\hfill \\ \widehat{\beta }-{\beta }^{*}\hfill \end{array}\right)\Vert }_2^2\right\} \\ =n^{1/2}\left\{{\widehat{\mu }}_{\text{p}-\text{dr}}\left({\alpha }^{*},{\beta }^{*}\right)-\mu \right\}+O_P\left\{n^{1/2}{\Vert \left(\begin{array}{c}\widehat{\alpha }-{\alpha }^{*}\\ \widehat{\beta }-{\beta }^{*}\end{array}\right)\Vert }_2^2\right\} \end{gathered}$$ (19)

$$=n^{1/2}\left\{{\widehat{\mu }}_{\text{p}-\text{dr}}\left({\alpha }^{*},{\beta }^{*}\right)-\mu \right\}+o_p\left(1\right),$$ (20)

where ${\widehat{\mu }}_{\text{p}-\text{dr}}(\alpha ,\beta )$ is defined in equation (10). Equation (19) follows because we solve equation (9) for (α, β). Equation (20) follows because of equation (18) and assumption 5. As a result, the way for estimating (α, β) leads to asymptotic equivalence between ${\widehat{\mu }}_{\text{p}-\text{dr}}(\widehat{\alpha },\widehat{\beta })$ and ${\widehat{\mu }}_{\text{p}-\text{dr}}\left({\alpha }^{*},{\beta }^{*}\right)$.

We now show that ${\widehat{\mu }}_{\text{p}-\text{dr}}\left({\alpha }^{*},{\beta }^{*}\right)$ is asymptotically unbiased for μ if either π_B(X^Tα) or m(X^Tβ) is correctly specified. We note that

$$n^{1/2}E\left[\left\{{\widehat{\mu }}_{\text{p}-\text{dr}}\left({\alpha }^{*},{\beta }^{*}\right)-\mu \right\}\right]=\frac{n^{1/2}}{N}\sum _{i=1}^{N}E\left[E\left\{\frac{I_{\text{B},i}}{{\pi }_{\text{B}}\left(X_i^{\text{T}}{\alpha }^{*}\right)}-1\mid X_i\right\}E\left\{Y_i-m\left(X_i^{\text{T}}{\beta }^{*}\right)\mid X_i\right\}\right].$$ (21)

If π_B(X^Tα) is correctly specified, then π_B(X^Tα*) = π_B(X) and therefore equation (21) is 0; if $m\left(X_i^{\text{T}}\beta \right)$ is correctly specified, then $m\left(X_i^{\text{T}}{\beta }^{*}\right)=m\left(X_i\right)$ and therefore equation (21) is 0.

Following the variance decomposition of Shao and Steel (1999), the asymptotic variance of the linearized term is

$$V\left[n^{1/2}\left\{{\widehat{\mu }}_{\text{p}-\text{dr}}\left({\alpha }^{*},{\beta }^{*}\right)-\mu \right\}\right]=n^{1/2}E\left[V\left\{{\widehat{\mu }}_{\text{p}-\text{dr}}\left({\alpha }^{*},{\beta }^{*}\right)-\mu \mid I_{\text{B}},X,Y\right\}\right]+n^{1/2}V\left[E\left\{{\widehat{\mu }}_{\text{p}-\text{dr}}\left({\alpha }^{*},{\beta }^{*}\right)-\mu \mid I_{\text{B}},X,Y\right\}\right]:=V_1+V_2,$$

where the conditional distribution in E(·|I_B, X, Y) and V(·|I_B, X, Y) is the sampling distribution for sample A. The first term V₁ is the sampling variance of the Horvitz-Thompson estimator. Thus,

$$V_1=E\left\{\frac{n}{N^2}\sum _{i=1}^N\sum _{j=1}^N\left({\pi }_{\text{A},ij}-{\pi }_{\text{A},i}{\pi }_{\text{A},j}\right)\frac{m\left(X_i^{\text{T}}{\beta }^{*}\right)}{{\pi }_{\text{A},i}}\frac{m\left(X_j^{\text{T}}{\beta }^{*}\right)}{{\pi }_{\text{A},j}}\right\}.$$ (22)

For the second term V₂, note that

$$E\left\{{\widehat{\mu }}_{\text{p}-\text{dr}}\left({\alpha }^{*},{\beta }^{*}\right)-\mu \mid I_{\text{B}},X,Y\right\}=\frac{1}{N}\sum _{i=1}^N\left\{\frac{I_{\text{B},i}}{{\pi }_{\text{B},i}\left(X_i^{\text{T}}{\alpha }^{*}\right)}-1\right\}\left\{Y_i-m\left(X_i^{\text{T}}{\beta }^{*}\right)\right\}.$$

Thus,

$$V_2=\frac{n}{N^2}\sum _{i=1}^{N}E\left[{\left\{\frac{I_{\text{B},i}}{{\pi }_{\text{B},i}\left(X_i^{\text{T}}{\alpha }^{*}\right)}-1\right\}}^2{\left\{Y_i-m\left(X_i^{\text{T}}{\beta }^{*}\right)\right\}}^2\right].$$ (23)

Theorem 2 summarizes the asymptotic properties of ${\widehat{\mu }}_{\text{p}-\text{dr}}(\widehat{\alpha },\widehat{\beta })$.

Theorem 2.

Under assumptions 1–5, if either π_B(X^Tα) or m(X^Tβ) is correctly specified,

$$n^{1/2}\left\{{\widehat{\mu }}_{\text{p}-\text{dr}}\left(\widehat{\alpha },\widehat{\beta }\right)-\mu \right\}\to \mathcal{N}\left(0,V\right),$$

as n→∞, where V = lim_n→∞(V₁ + V₂), and V₁ and V₂ are defined in equations (22)) and (23) respectively.

To estimate V₁, we can use the design-based variance estimator applied to $m\left(X_i^{\text{T}}\widehat{\beta }\right)$ as

$${\widehat{V}}_1=\frac{n}{N^2}\sum _{i\in {\mathcal{S}}_{\text{A}}}\sum _{j\in {\mathcal{S}}_{\text{A}}}\frac{{\pi }_{\text{A},ij}-{\pi }_{\text{A},i}{\pi }_{\text{A},j}}{{\pi }_{\text{A},ij}}\frac{m\left(X_i^{\text{T}}\widehat{\beta }\right)}{{\pi }_{\text{A},i}}\frac{m\left(X_j^{\text{T}}\widehat{\beta }\right)}{{\pi }_{\text{A},j}}.$$ (24)

To estimate V₂, we further express V₂ as

$$V_2=\frac{n}{N^2}\sum _{i=1}^{N}E\left[\left\{\frac{I_{\text{B},i}}{{\pi }_{\text{B},i}{\left(X_i^{\text{T}}{\alpha }^{*}\right)}^2}-\frac{2I_{\text{B},i}}{{\pi }_{\text{B},i}\left(X_i^{\text{T}}{\alpha }^{*}\right)}\right\}{\left\{Y_i-m\left(X_i^{\text{T}}{\beta }^{*}\right)\right\}}^2+{\left\{Y_i-m\left(X_i^{\text{T}}{\beta }^{*}\right)\right\}}^2\right].$$ (25)

Let ${\sigma }^2\left(X_i^{\text{T}}{\beta }^{*}\right)=E\left[{\left\{Y_i-m\left(X_i^{\text{T}}{\beta }^{*}\right)\right\}}^2\right]$, and let ${\widehat{\sigma }}^2\left(X_i\right)$ be a consistent estimator of ${\sigma }^2\left(X_i^{\text{T}}{\beta }^{*}\right)$. We can then estimate V₂ by

$${\widehat{V}}_2=\frac{n}{N^2}\sum _{i=1}^N\left[\left\{\frac{I_{\text{B},i}}{{\pi }_{\text{B}}{\left(X_i^{\text{T}}\widehat{\alpha }\right)}^2}-\frac{2I_{\text{B},i}}{{\pi }_{\text{B}}\left(X_i^{\text{T}}\widehat{\alpha }\right)}\right\}{\left\{Y_i-m\left(X_i^{\text{T}}\widehat{\beta }\right)\right\}}^2+I_{\text{A},i}{d}_{\text{A},i}{\widehat{\sigma }}^2\left(X_i\right)\right].$$

By the law of large numbers, ${\widehat{V}}_2$ is consistent for V₂ regardless of whether one of ${\pi }_{\text{B},i}\left(X_i^{\text{T}}\alpha \right)$ or ${\pi }_{\text{B},i}\left(X_i^{\text{T}}\beta \right)$ is misspecificed, and therefore it is doubly robust.

Theorem 3 (double robustness of $\widehat{V}$).

Under assumptions 1–5, if either π_B(X^Tα) or m(X^Tβ) is correctly specified, $\widehat{V}={\widehat{V}}_1+{\widehat{V}}_2$ is consistent for V.

Remark 5.

It is worth discussing the relationship of our proposed method to existing variable-selection methods in the survey literature. On the basis of a single probability sample source, McConville et al. (2017) proposed a model-assisted survey regression estimator of finite population totals using the lasso (the least absolute shrinkage and selection operator) to improve the efficiency. Chen, Valliant and Elliott (2018) and Chen et al. (2019) proposed model-based calibration estimators using the lasso based on non-probability samples integrating with auxiliary known totals or probability samples respectively. However, their methods require that the working outcome model includes sufficient population information and therefore are not doubly robust. To the best of our knowledge, our paper is the first to propose doubly robust inference of finite population means after variable selection.

6. Simulation study

6.1. Set-up

In this section, we evaluate the finite sample performance of the procedure proposed. We first generate a finite population ${\mathcal{F}}_N=\left\{\left(X_i,Y_i\right):i=1,\dots ,N\right\}$ with N = 10000, where Y_i is a continuous or binary outcome variable, and X_i = (1, X_1,i, …, X_p−1,i)^T is a p-dimensional vector of covariates with the first component being 1 and other components independently generated from the standard normal distribution. We set p = 50. From the finite population, we select a non-probability sample $\mathcal{B}$ of size n_B ≈ 2000, according to the selection indicator I_B,i ~ Ber(π_B,i). We select a probability sample $\mathcal{A}$ of the average size n_A = 500 under Poisson sampling with π_A,i ∝ (0.25 + |X_1i| + 0.03|Y_i|). The parameter of interest is the population mean $\mu =N^{-1}{\Sigma }_{i=1}^N{Y}_i$.

For the non-probability sampling probability, we consider both linear and non-linear sampling score models:

1. $\text{logit}\left({\pi }_{\text{B},i}\right)={\alpha }_0^{\text{T}}{X}_i$, where α₀ = (−2, 1, 1, 1, 1, 0, 0, 0, … , 0) (model PSM I);

2. $\text{logit}\left({\pi }_{\text{B},i}\right)=3.5+{\alpha }_0^{\text{T}}\text{log}\left(X_i^2\right)-\text{sin}\left(X_{3,i}+X_{4,i}\right)-X_{5,i}-X_{6,i}$, where α₀ = (0, 0, 0, 3, 3, 3, 3, 0, … , 0)^T (model PSM II).

For generating a continuous outcome variable Y_i, we consider both linear and non-linear outcome models with β₀ = (1, 0, 0, 1, 1, 1, 1, 0, … , 0)^T:

1. $Y_i={\beta }_0^{\text{T}}{X}_i+{ϵ}_i,{ϵ}_i~\mathcal{N}(0,1)$ (model OM I);

2. $Y_i=1+\text{exp}\left\{3\text{sin}\left({\beta }_0^{\text{T}}{X}_i\right)\right\}+X_{5,i}+X_{6,i}+{ϵ}_i,{ϵ}_i~\mathcal{N}(0,1)$ (model OM II).

For generating a binary outcome variable Y_i, we consider both linear and non-linear outcome models with β₀ = (1, 0, 0, 3, 3, 3, 3, 0, … , 0)^T,

1. Y ~ Ber{π_Y(X)} with $\text{logit}\left\{{\pi }_Y(X)\right\}={\beta }_0^{\text{T}}X$ (model OM III);

2. Y ~ Ber{π_Y(X)} with $\text{logit}\left\{{\pi }_Y(X)\right\}=2-\text{log}\left\{{\left({\beta }_0^{\text{T}}X\right)}^2\right\}+2X_{5,i}+2X_{6,i}$ (model OM IV).

We consider the following estimators:

1. naive, ${\widehat{\mu }}_{\text{naive}}$, the naive estimator using the simple average of Y_i from sample B, which provides the degree of the selection bias of sample B;

2. oracle, ${\widehat{\mu }}_{\text{ora}}$, the doubly robust estimator ${\widehat{\mu }}_{\text{dr}}\left({\widehat{\alpha }}_{\text{ora}},{\widehat{\beta }}_{\text{ora}}\right)$, where ${\widehat{\alpha }}_{\text{ora}}$ and ${\widehat{\beta }}_{\text{ora}}$ are based on the joint estimator restricting to the known important covariates for comparison;

3. p-ipw, ${\widehat{\mu }}_{\text{p}-\text{ipw}}$, the penalized inverse probability of sampling weighting estimator ${\widehat{\mu }}_{\text{IPW}}=N^{-1}{\Sigma }_{i\in \mathcal{B}}{\widehat{\pi }}_{\text{B},i}^{-1}{Y}_i$, where $\text{logit}\left({\widehat{\pi }}_{\text{B},i}\right)=X_i^{\text{T}}\widehat{\alpha }$ using a logistic regression model, and $\widehat{\alpha }$ is obtained by a weighted penalized regression of I_B,i on X_i based on the combined data from sample A and sample B, with the units in sample A weighted by the known sampling weights and the units in sample B weighted by 1.

4. p-reg, ${\widehat{\mu }}_{\text{p}-\text{reg}}$, the penalized regression estimator ${\widehat{\mu }}_{\text{p}-\text{reg}}=N^{-1}{\Sigma }_{i\in \mathcal{A}}{d}_{\text{A},i}m(X;\widehat{\beta })$, where $\widehat{\beta }$ is obtained by a penalized regression of Y_i on X_i based on sample B;

5. p-dr0, ${\widehat{\mu }}_{\text{p}-\text{dr}0}$, the penalized double estimating equation estimator based on the set of outcome predictors ${\widehat{\mathcal{M}}}_{\beta }$;

6. p-dr, ${\widehat{\mu }}_{\text{p}-\text{dr}}$, the proposed penalized double estimating equation estimator based on the union of sampling and outcome predictors ${\widehat{\mathcal{M}}}_{\alpha }\cup {\widehat{\mathcal{M}}}_{\beta }$.

We also note that ${\widehat{\mu }}_{\text{dr}}$ without variable selection is severely biased and unstable and therefore is excluded for comparison.

6.2. Simulation results

All simulation results are based on 500 Monte Carlo runs. Table 2 reports the selection performance of the proposed penalization procedure in terms of the proportion of underselecting (‘Under’) or overselecting (‘Over’), the average false negative results, FN (the average number of selected covariates that have the true 0 coefficients), and the average false positive results, FP (the average number of selected covariates that have the true 0 coefficients). The procedure proposed selects all covariates with non-zero coefficients in both the outcome model and the sampling score model under the true model specification. Moreover, the number of false positive results is small under the true model specification.

Table 2.

Simulation results for selection performance for the proposed double-penalized estimating equation procedure under four scenarios^†

Scenario	β*				α*
	Under (×102)	Over (×102)	FN	FP	Under (×102)	Over (×102)	FN	FP
Continuous outcome
(i) OM I and PSM I	0.0	31.8	0.0	1.4	0.0	0.0	0.0	0.0
(ii) OM II and PSM I	70.6	15.0	0.9	0.2	0.0	0.0	0.0	0.0
(iii) OM I and PSM II	0.0	32.8	0.0	1.4	100.0	100.0	4.0	1.0
(iv) OM II and PSM II	0.0	0.4	0.0	0.4	100.0	100.0	3.5	4.3
Binary outcome
(i) OM III and PSM I	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
(ii) OM IV and PSM I	100.0	0.0	2.1	0.0	0.0	0.0	0.0	0.0
(iii) OM III and PSM II	0.0	0.0	0.0	0.0	100.0	100.0	4.0	1.0
(iv) OM IV and PSM II	100.0	0.0	4.0	0.0	100.0	96.0	4.0	1.0

^†Under OMI and OMII, or OMIII and OMIV, the outcome model is respectively correctly specified and misspecified, and, under PSM I and PSM II, the probability of sampling score model is respectively correctly specified or misspecified.

Fig. 1 displays the simulation results for the continuous outcome. The naive estimator ${\widehat{\mu }}_{\text{naive}}$ shows large biases across all scenarios. The oracle estimator ${\widehat{\mu }}_{\text{ora}}$ is doubly robust, in the sense that, if either the outcome or the sampling score is correctly specified, it is unbiased. The penalized inverse probability of sampling weighting estimator ${\widehat{\mu }}_{\text{p}-\text{ipw}}$ shows largest biases except for scenario (ii). This approach is justifiable only if the sampling rate of sample B is relatively small compared with the population size. The penalized regression estimator ${\widehat{\mu }}_{\text{p}-\text{reg}}$ is only singly robust. When the outcome model is misspecified as in scenarios (ii) and (iv), it shows large biases. The proposed estimator ${\widehat{\mu }}_{\text{p}-\text{dr}}$ based on ${\widehat{\mathcal{M}}}_{\alpha }\cup {\widehat{\mathcal{M}}}_{\beta }$ is doubly robust, and its performance is comparable with the oracle estimator that requires knowing the true important variables. Moreover, ${\widehat{\mu }}_{\text{p}-\text{dr}}$ is slightly more efficient than ${\widehat{\mu }}_{\text{ora}}$. This efficiency gain is due to using the union of covariates selected for the sampling score model and the outcome model. This is consistent with the findings in Brookhart et al. (2006) and Shortreed and Ertefaie (2017). The proposed penalized double estimating equation estimator ${\widehat{\mu }}_{\text{p}-\text{dr}0}$ based on ${\widehat{\mathcal{M}}}_{\beta }$ is slightly more efficient than ${\widehat{\mu }}_{\text{p}-\text{dr}}$ based on ${\widehat{\mathcal{M}}}_{\alpha }\cup {\widehat{\mathcal{M}}}_{\beta }$ in scenario (i) when both the outcome and the sampling score models are correctly specified; however, ${\widehat{\mu }}_{\text{p}-\text{dr}0}$ has a large bias in scenario (ii) when the outcome model is misspecified and therefore is not doubly robust anymore; see remark 3.

Fig. 1.

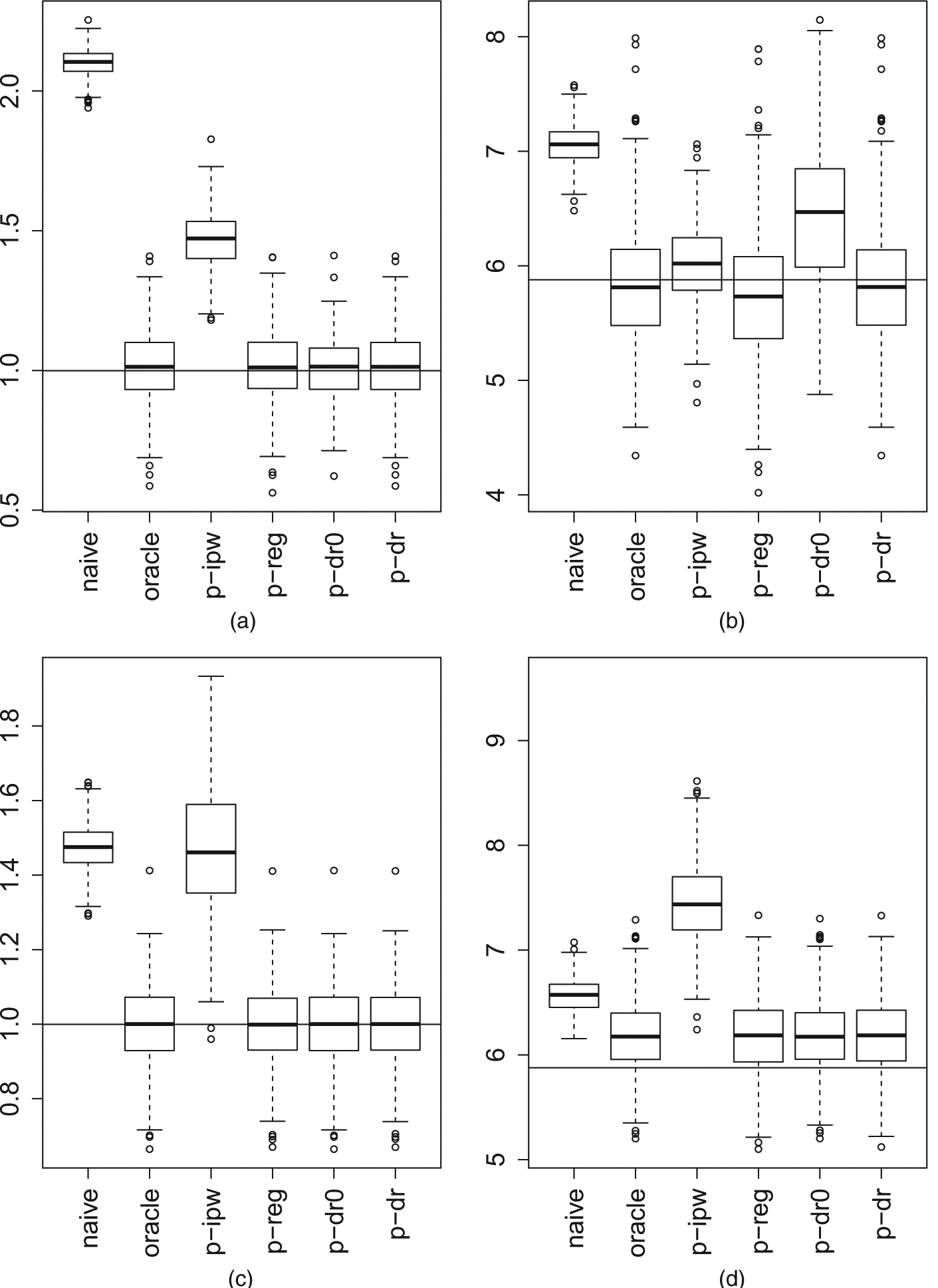
Estimation results for the continuous outcome under four scenarios (under OM I and OM II, the outcome model is respectively correctly specified and misspecified, and, under PSM I and PSM II, the probability of sampling score model is respectively correctly specified and misspecified): (a) scenario (i),OMI and PSM I; (b) scenario (ii), OM II and PSM I; (c) scenario (iii), OM I and PSM II; (d) scenario (iv), OM II and PSM II

Fig. 2 displays the estimation results for the binary outcome. The same discussion above applies here. Moreover, when the outcome model is incorrectly specified, the oracle estimator has a large variability. In this case, the estimator proposed outperforms the oracle estimator, because the variable selection step helps to stabilize the estimation performance.

Fig. 2.

Estimation results for the binary outcome under four scenarios (under OMIII and OMIV, the outcome model is respectively correctly specified and misspecified, and, under PSM I and PSM II, the probability of sampling score model is respectively correctly specified and misspecified): (a) scenario (i), OM III and PSM I; (b) scenario (ii), OM IV and PSM I; (c) scenario (iii), OM III and PSM II; (d) scenario (iv), OM IV and PSM II

Table 3 reports the simulation results for the coverage properties for the continuous outcome and binary outcome. Under the double-robustness condition (i.e. if either the outcome model or the sampling score model is correctly specified), the coverage rates are close to the nominal coverage, whereas, if both models are misspecified, the coverage rates are off the nominal coverage.

Table 3.

Simulation results for the coverage properties for the continuous and binary outcomes: empirical coverage rate and empirical coverage rate ±2×Monte Carlo standard error

Scenario	Results for continuous outcome	Results for binary outcome
(i) OM I or OM III and PSM I	95.2 (93.3, 97.1)	95.7 (93.9, 97.6)
(ii) OM II or OM IV and PSM I	94.6 (92.6, 96.6)	95.5 (93.6, 97.4)
(iii) OM I or OM III and PSM II	96.2 (94.2, 97.8)	95.6 (93.8, 97.5)
(iv) OM II or OM IV and PSM II	88.2 (85.3, 91.1)	42.9 (38.3, 47.6)

7. An application

We analyse two data sets from the 2005 PRC (http://www.pewresearch.org/) and the 2005 behavioural risk factor surveillance system (BRFSS). The goal of the PRC study was to evaluate the relationship between individuals and community (Chen, Li and Wu, 2018; Kim et al., 2018). The 2005 PRC data set is from a non-probability sample provided by eight vendors, which consists of n_B = 9301 subjects. We focus on two study variables: a continuous Y₁ (days had at least one drink last month) and a binary Y₂ (an indicator of voted in local elections). In contrast, the 2005 BRFSS sample is a probability sample, which consists of n_A = 441456 subjects with survey weights. This data set does not have measurements on the study variables of interest; however, it contains a rich set of common covariates with the PRC data set listed in Fig. 3. To illustrate the heterogeneity in the study populations, Fig. 3 contrasts the covariate means from the PRC data and the design-weighted covariate means (i.e. the estimated population covariate means) from the BRFSS data set. The covariate distributions from the PRC sample and the BRFSS sample are considerably different, e.g. age, education (high school or less), financial status (no money to see doctors; own house), retirement rate and health (smoking). Therefore, the naive analyses of the study variables based on the PRC data set are subject to selection biases.

Fig. 3.

Covariate means by two samples (age is divided by 100): ● sample A; ▲ sample B

We compute the naive and proposed estimators. To apply the method proposed, we assume that the sampling score is a logistic regression model, the continuous outcome follows a linear regression model and that the binary outcome follows a logistic regression model. Using fivefold cross-validation, the double-selection procedure identifies 18 important covariates (all available covariates except for the north-east region) in the sampling score and the binary outcome model, and it identifies 15 important covariates (all available covariates except for black, an indicator of smoking every day, the north-east region and the south region) in the continuous outcome model.

Table 4 presents the point estimates, the standard errors and the 95% Wald confidence intervals. For estimating the standard error, because the second-order inclusion probabilities are unknown, following the survey literature, we compute the variance estimator in equation (24) by assuming that the survey design is single-stage Poisson sampling. We find significant differences in the results between the naive estimator and the proposed estimator. As demonstrated by the simulation study in Section 6, the naive estimator may be biased because of selection biases, and the estimator proposed utilizes a probability sample to correct for such biases. From the results, on average, the target population had at least one drink for 4.84 days over the last month, and 71.8% of the target population voted in local elections.

Table 4.

Point estimate, standard error and 95% Wald confidence interval CI

Method	Y1 (days had at least 1 drink last month)			Y2 (whether voted in local elections)
	Estimate	Standard error	CI	Estimate ×102	Standard error ×102	CI×102
Naive	5.36	0.90	(5.17, 5.54)	75.3	0.5	(74.4, 76.3)
Proposed	4.84	0.15	(4.81, 4.87)	71.8	0.2	(71.3, 72.2)