Abstract
Photoswitchable molecules are employed for many applications, from the development of active materials to the design of stimuli-responsive molecular systems and light-powered molecular machines. To fully exploit their potential, we must learn ways to control the mechanism and kinetics of their photoinduced isomerization. One possible strategy involves confinement of photoresponsive switches such as azobenzenes or spiropyrans within crowded molecular environments, which may allow control over their light-induced conversion. However, the molecular factors that influence and control the switching process under realistic conditions and within dynamic molecular regimes often remain difficult to ascertain. As a case study, here we have employed molecular models to probe the isomerization of azobenzene guests within a Pd(II)-based coordination cage host in water. Atomistic molecular dynamics and metadynamics simulations allow us to characterize the flexibility of the cage in the solvent, the (rare) guest encapsulation and release events, and the relative probability/kinetics of light-induced isomerization of azobenzene analogues in these host–guest systems. In this way, we can reconstruct the mechanism of azobenzene switching inside the cage cavity and explore key molecular factors that may control this event. We obtain a molecular-level insight on the effects of crowding and host–guest interactions on azobenzene isomerization. The detailed picture elucidated by this study may enable the rational design of photoswitchable systems whose reactivity can be controlled via host–guest interactions.
Introduction
Photochromic molecular switches such as azobenzene,1 spiropyran,2,3 or arylazopyrazole4,5 are responsive molecules that isomerize upon irradiation with light. Achieving fine control of these compounds’ isomerization kinetics is important since they represent crucial components for the development of functional photoresponsive materials,3,6−9 light-powered molecular machines,10−15 and in photopharmacology,16,17 where spatiotemporal control of molecular transitions/reactions is needed. In nature, a widely employed strategy for controlling chemical reactions involves accommodating the reactants in a confined space, where encapsulation may influence and control reaction mechanism and kinetics. Enzymes, for example, can catalyze and control reactions with exquisite efficiency and fidelity by exploiting principles of molecular confinement and selective molecular/supramolecular host–guest interactions.18−21
In the attempt to mimic natural catalytic systems, chemists have designed synthetic cavities that exploit specific and nonspecific interactions to accommodate reactants with high selectivity in a confined space.22 Notable examples of synthetic confined spaces are nanopores within metal–organic frameworks,23−25 surfaces of nanoparticles26−28 and nanopores within their aggregates,29 microemulsion droplets,30,31 and cavities within molecular capsules.32 Alternatively, cavities can be found within self-assembled cages33−38 that can encapsulate reactants in solution.39,40 Confinement inside such cavities has been shown to be crucial in accelerating chemical reactions29,41−43 or stabilizing otherwise unstable species.44−48 Notable studies have reported that the photoisomerization of molecular switches can be accelerated,49 slowed down,50 or even completely inhibited within crowded molecular environments.51,52 In some cases, the isomerization of photoresponsive guests may also result in expulsion of the guest53,54 and even in disassembly of the cage.55 A key role is attributed to the structural rigidity of synthetic host cavities, which are not capable of accommodating the large conformational changes associated with the photoisomerization of the guest.1,3,56,57 For this reason, much interest has recently been directed toward the design of flexible molecular cages.58−61
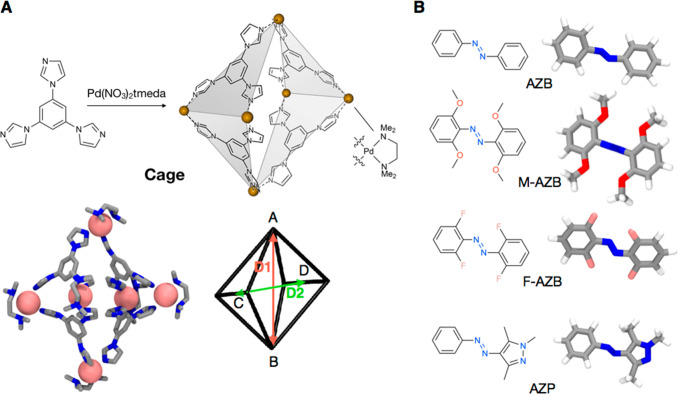
In this sense, an interesting example is self-assembled metal–organic cage shown in Figure 1A.61 This cage has been observed to encapsulate and allow for water solubilization of several different molecular switches, including azobenzene (AZB), methoxylated azobenzene (M-AZB), fluorinated azobenzene (F-AZB), various spiropyrans, as well as arylazopyrazole (AZP) (Figure 1B).62−64 NMR and UV/vis absorption studies provided useful information about the guest encapsulation and the host−guest stoichiometry in these systems.62−64 X-ray crystallography provided additional experimental insight on the conformations of the crystallized complexes.62,64 Qualitatively, these efforts indicated that encapsulation and switching of the guests are enabled by large distortions within the cage structure, while confinement alters the isomerization behavior of the guests.63
Figure 1.
Model host–guest systems. (A, top) Structure of the supramolecular cage studied herein, formed via the self-assembly of triimidazole-based donors and cis-blocked Pd acceptors. (A, bottom) Atomistic model of the supramolecular host cage, along with a schematic representation of its octahedral structure, which can be described by the axial and equatorial distances, D1 (red) and D2 (green). (B) Structural formulas and atomistic models of the guests studied herein: azobenzene (AZB), methoxylated azobenzene (M-AZB), fluorinated azobenzene (F-AZB), and arylazopyrazole (AZP) (here shown as trans isomers).
These findings suggest that the flexibility of the cage enables adaptation of its cavity in response to the isomerization of encapsulated guests. However, a clear understanding of the flexibility exhibited by such cages in solution is difficult to obtain experimentally. In particular, correlating such effects with isomerization events that occur on very fast time scales52 (the trans → cis isomerization of excited azobenzene occurs on the order of picoseconds in the absence of confinement) and studying the mechanisms that control photoswitching under confinement are prohibitive tasks. In these cases, however, molecular simulations are extremely useful. Quantum mechanics/molecular mechanics (QM/MM), all-atom (AA), and coarse-grained (CG) simulations have been used to investigate azobenzenes and their isomerization within dense monolayers, nanocavities, supramolecular tubules, nanoparticles, and vesicles,6,8,29,49,50,52,65−68 to name a few. Molecular models can provide detailed insight on the isomerization process49,52 as well as on the effect of these molecular transitions on the stability8,66,69 and out-of-equilibrium behavior of the system.50
Here we used AA molecular simulations to obtain an exhaustive characterization of the host–guest systems involving azo compounds AZB, M-AZB, F-AZB, and AZP (Figure 1B) as the guests and cage shown in Figure 1A as the host. Combining molecular dynamics (MD) and metadynamics (MetaD) simulations, our approach allows a thorough exploration of the flexibility of the cage in solution and of the mechanisms of guest encapsulation and release under realistic conditions. Coupled with a kinetic study of the isomerization of the excited guests within the cage, these simulations allow us to reconstruct the role of confinement on guest switching and to study the molecular factors that may allow control over this process. We found structure–reactivity relationships having a general character, which may have a profound impact on the rational design of molecular systems with programmable photoswitching properties.
Results and Discussion
Characterization of Cage Flexibility in Solution
The first step to understanding the behavior of the system is to determine the most favorable conformation(s) assumed by the cage, and how flexible this is in solution under realistic conditions (solvent, temperature, etc.). We started by considering the native cage, without incorporated guests. We developed an atomistic model of the cage (Figure 1A, bottom), starting from the crystal structure for the same cage containing two trans-F-AZB guests (which have been manually deleted).62 Starting from this extended conformation of the cage, we ran a classical MD simulation in explicit water molecules at 297 K and 1 atm (see SI Methods section for details). During this MD run, we analyzed the structural rearrangements of the cage by monitoring two variables describing the geometry of the cage: D1, the axial distance between the “top” and “bottom” Pd atoms (Figure 1A, bottom; points A and B), and D2, the distance between the midpoints of the two opposite equatorial edges of the octahedral cage (points C and D). In agreement with previous studies,63 this preliminary MD simulation showed a significant flexibility within the cage. As seen in Figure S1, D1 and D2 have been found to undergo large structural fluctuations, which, however, are observed rarely during 1 μs of a MD simulation.
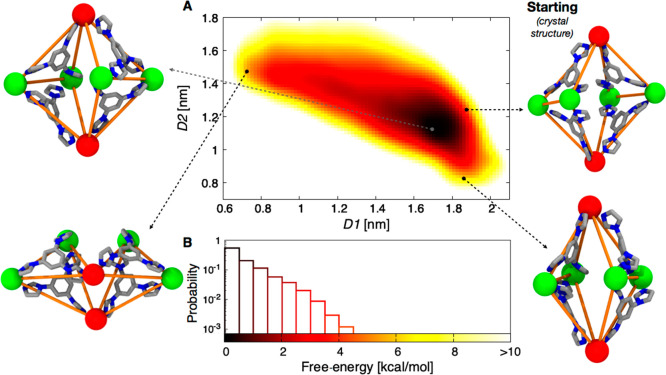
To better characterize the conformational landscape and the slow structural dynamics of the cage, we turned to MetaD,70 which allows a more exhaustive exploration of the conformational space of the cage in solution. Using the same operative conditions, we ran a MetaD simulation exploring the possible structural conformations that the cage can dynamically assume in the solvent. In the MetaD run, we used D1 and D2 as the collective variables, descriptors of the cage conformations (see SI Methods for details). From this simulation, we could reconstruct the free-energy surface (FES) for the system as a function of D1 and D2. Shown in Figure 2, the FES shows the conformational landscape of the cage (i.e., all the possible conformations that the cage can assume) associated with its relative free-energy. Dark regions in the FES identify the minimum energy (most favorable) configurations for the cage, while red, orange, yellow regions identify conformations that are increasingly higher in free-energy. We can observe a single free-energy minimum (the black region in figure) in which the cage is mildly elongated along the D1 axis (top left snapshot in Figure 2), and is generally less extended than the initial crystal structure for the cage, which is found ∼4–5 kcal/mol higher in free-energy (Figure 2, top right snapshot). Exploiting the rotation of the 12 imidazole-rings with respect to the central benzene ring,62 the MetaD allows the system to explore a wide range of conformations (including very elongated shapes), a selection of which are shown in Figure 2. In most cases, these configurations are considerably higher in free-energy and are thus unlikely to be observed in solution. Furthermore, we calculated the probability associated with the different colored regions of the FES (see SI Methods). The result of this analysis (Figure 2B) shows that, from a statistical point of view, only the cage configurations lying within 1.5 kcal/mol of the global minimum are really accessible by the cage (dark regions on the FES and first three bins of Figure 2B). This means that the cage will most likely assume configurations within D1 ∼ 1.4–1.9 nm and D2 ∼ 0.9–1.3 nm (dark FES region). Under these conditions, these conformations will constitute ∼90% of the global population of cages in the system. It is worth adding that the shape of the FES minimum also provides important information about the flexibility of the cage in solution. In this case, the FES minimum is quite broad, which is in agreement with the experimentally observed63 high flexibility of the cage. Altogether, this analysis provides interesting information not only on the level of flexibility of the cage under experimentally relevant conditions, but also on what we could reasonably/statistically expect to find in terms of the structural diversity of the cage in a realistic solution.
Figure 2.
Conformational free-energy landscape of the empty cage. (A) Free-energy surface (FES) as a function of D1 (distance between the axial/red Pd atoms) and D2 (distance between the midpoints of opposite edges of the cage identified by the equatorial/green Pd atoms). The color scale in the FES indicates the free-energy associated with cage conformations on the D1–D2 plane (scale and legend shown in B). Four representative snapshots are shown: the starting, extended configuration (top right) corresponding to the crystal structure of the cage,62 the energetic minimum of the FES (top left), a D1-elongated structure (bottom right), and a D2-elongated structure (bottom left). Axial and equatorial Pd atoms are colored in red and green, respectively, while the connectivity scheme is colored in orange to facilitate interpretation of the structures. (B) Probability associated with all cage conformations as a function of the relative free-energy (bin width, 0.5 kcal/mol).
Effects of Guest Encapsulation on Cage Flexibility
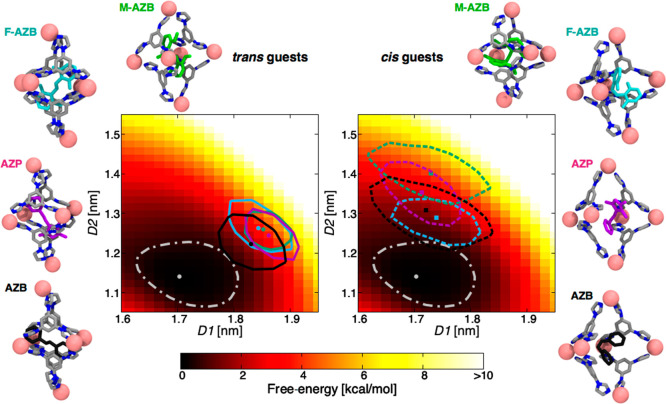
The flexibility of the cage influences its ability to encapsulate guest molecules. Conversely, guest encapsulation itself may have an effect on the flexibility of the cage. For our next step, we thus studied the effect of guest encapsulation on the cage. Starting again from the crystal structure of the cage containing two trans-F-AZB guests,62 we deleted one guest and replaced the remaining one, where necessary, in order to obtain starting models for the cage encapsulating one F-AZB, M-AZB, AZP, or AZB guest (Figure 1B). These starting host–guest complex models were then equilibrated via 1 μs of MD simulation (see SI Methods for details). In particular, we compared the effect of incorporating either trans or cis conformers of all guests, analogous to the states of the cage before and after the isomerization. In all cases, we monitored the equilibrium conformations of the cage in terms of D1 and D2. We could observe that all guests remained steadily bound within the cage during the whole MD simulation time. Figure 3 shows the equilibrium configuration for the cage in terms of D1 and D2 in all cases (colored points) on the FES of the empty cage. The colored isolines in Figure 3 identify the associated free-energy regions within 0.5 kcal/mol of the global minima for each case (the same isoline for the empty cage is shown in white).
Figure 3.
Free-energy cost of guest encapsulation. Representative equilibrium conformations (in the D1–D2 plane) of the cage encapsulating different trans (left) or cis (right) guests. For each host–guest system, we report the position of the minimum-energy conformation (colored points) and the associated isolines (same colors) enclosing all conformations within 0.5 kcal/mol from the minimum of each system. The data are projected onto the FES of the empty cage (same as Figure 2), for which we also indicate the global minimum and associated 0.5 kcal/mol isoline (in white).
On the basis of the data in Figure 3, we can draw the following conclusions. In order to incorporate a guest, the cage must undergo structural rearrangements, specifically to open up, which is accompanied by a free-energy cost. The FES data in Figure 3 allows us to assess the free-energy penalty associated with encapsulation of each guest. This value can be calculated as the difference in free-energy between the white point (empty cage) and the colored points (a higher free-energy configuration that the cage has to reach to encapsulate the guest). We have found values for ΔG in the range ∼3–5 kcal/mol, depending on the guest. Such a free-energy penalty can be seen as an entropic cost (i.e., unfavorable) for the encapsulation, as the cage elongates both axially and equatorially upon encapsulating the guest. From the data in Figure 3 we can also observe how guest encapsulation affects the flexibility of the cage. In general, the colored isolines encompass a smaller area than the white isoline associated with the empty cage. This observation suggests that the cage loses flexibility upon encapsulating a guest, the effect being more pronounced for trans (left panel) than for cis guests (right panel). Moreover, by comparing the regions occupied by the cage when hosting trans or cis guests, we note that they enclose similar free-energy values. This result suggests that isomerization of the encapsulated guest would not require a consistent free-energy cost in terms of host deformation, thus demonstrating the energetic accessibility of the process. These results are consistent with the evidence that the trans → cis isomerization of the guests occurs inside the cage, and the resulting cis complexes remain stable also after isomerization.62−64
Experiments have shown that our cage can often accommodate two trans guest molecules at the same time.62,64 On the basis of these observations, we have modeled two additional systems wherein the cage encapsulates two trans-AZBs or two trans-F-AZBs, and have obtained equilibrated configurations for these complexes via 1 μs of MD simulation. In these cases, we observed that the cage undergoes considerable deformations compared to when only one encapsulated trans guest is present in the cavity of the model cage (see Figure S2). However, the stability observed for two-guest complexes suggests that the affinity between the encapsulated guests and the cage is significant. We anticipate that this competition between the free-energy penalty associated with the crowding inside the cage cavity and the host–guest affinity represents a crucial factor that can regulate the reactivity of these host–guest complexes.
Trans–Cis Isomerization of Azobenzenes Inside the Cage
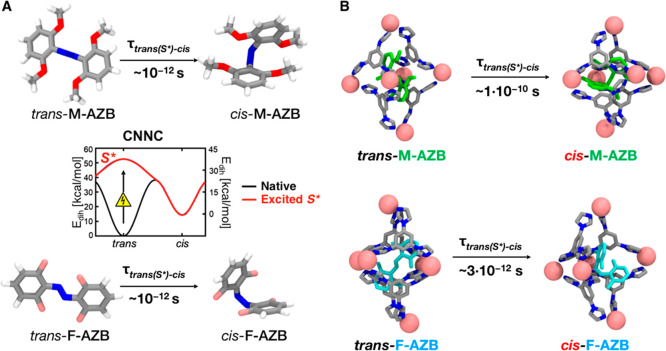
An interesting question is how, and to what extent, the switching of excited azobenzenes is affected by encapsulation inside the cage. The trans → cis isomerization of azobenzenes occurs mainly via a rotational mechanism involving the torsion of the central N–N bond, which produces the out-of-plane rotation of one end of the molecule71,72 (see snapshots in Figure 4A). To simulate the trans → cis transition of the guests within the cage, we use a model for excited trans-azobenzenes (S*) that has been recently employed to study azobenzene switching inside self-assembled tubules via atomistic and coarse-grained simulations.50 In this atomistic model, the central CNNC dihedral potential term for the azobenzene unit is modified from the black curve (unperturbed trans-azobenzene) into the blue curve in the inset of Figure 4. In this model, the trans-azobenzene guest, which is assumed to reach the excited state (S*), undergoes spontaneous trans → cis switching according to the correct transition pathway and kinetics during classical MD runs.50 Starting from the equilibrated models for the cage encapsulating single molecules of each trans guest (Figure 3, left), we studied the kinetics of their switching inside and outside the cage by means of MD simulations.
Figure 4.
Trans → cis transitions of azo-switches inside and outside the cage. (A) Kinetics of trans → cis isomerization of the excited M-AZB (top) and F-AZB (bottom) outside the cage (in solution) reported as examples. The measured transition times, reported below the isomerization arrows, are obtained from MD simulations using an atomistic model where the CNNC dihedral potential term for the trans-azobenzene derivatives (Edih, reported in the plot as a function of the dihedral angle), is changed from the black curve (native/unperturbed state) to the blue curve (excited trans-azobenzene, S*).50 (B) Kinetics of trans → cis isomerization of excited M-AZB (top) and F-AZB (bottom) switches confined inside the cage. Transition times for all the guests in the cage are reported in Table 1.
As shown in Figure 4A, the isomerization of all excited unbound trans-azobenzenes studied here occurs on the time scale of picoseconds, consistent with the kinetics of isomerization for free azobenzenes (unconstrained conditions).52 However, the process can become significantly slower as a result of encapsulation within the cage (see Figure 4B) (i.e., molecular crowding).50 The trans → cis isomerization times for the guests studied herein are reported in Table 1. Interestingly, the slowing of the transition can be negligible or different by of orders of magnitude, depending on the encapsulated guest. For example, in the case of AZB and AZP, the transition kinetics is not significantly affected by the confinement in the cage. On the other hand, the switching is ∼3 or even up to ∼100 times slower for confined F-AZB and M-AZB, respectively (Figure 4B). Moreover, it is worth noting that such a considerable switching deceleration is obtained using a model where the excited trans guests cannot de-excite back.50 Considering that the lifetime of the excited state S* of trans-azobenzene is on the order of picoseconds,52 however, de-excitation of S* to the ground state is a non-negligible event in real systems. This suggests that the considerable deceleration in transition rates associated with encapsulated F-AZB and M-AZB could actually be, at worst, underestimated by our model. Such a difference is interesting, especially considering that cases have been reported in which azobenzene isomerization may become rare (as in highly ordered self-assembled tubules50) or impossible (such as within dense azobiphenyl monolayers52).
Table 1. Thermodynamic and Kinetic Data for trans Guest Binding and Isomerization Inside the Cage.
| guest | ΔG [kcal/mol] | τoff [s] | Kb [M–1] | koff [s–1] | kona [M–1 s–1] | τtrans–cis [s] |
|---|---|---|---|---|---|---|
| AZB | –5.3 ± 0.3 | (3.9 ± 0.2) × 10–4 | 7.87 × 103 | 2.65 × 103 | 2.1 × 107 | (1.05 ± 0.05) × 10–12 |
| M-AZB | –7.9 ± 1.3 | (1.2 ± 0.1) × 10–2 | 6.41 × 105 | 8.3 × 101 | 5.32 × 107 | (1.00 ± 0.05) × 10–10 |
| F-AZB | –5.3 ± 0.9 | (3.8 ± 0.1) × 10–3 | 7.87 × 103 | 2.63 × 102 | 2.1 × 106 | (3.0 ± 0.1) × 10–12 |
| AZP | –5.7 ± 0.8 | (4.2 ± 0.1) × 10–4 | 1.55 × 104 | 2.38 × 103 | 3.7 × 107 | (1.25 ± 0.05) × 10–12 |
Guest concentration in the model systems is ∼11.4 mM; to obtain the effective kon values in [s–1], the values in the table should be multiplied by 11.4 mM.
In our specific systems, guest isomerization may even result in an unstable complex. This is the case when the cage incorporates two trans-F-AZB guests at the same time. Right after isomerization is triggered in this system, one of the two encapsulated guests is expelled from the cage.62 Interestingly, we found the same behavior in our simulations (Figure S3). Co-encapsulation of one trans- and one cis-F-AZB guest inside the cage leads to a highly unstable species, leading to the release of one of the two guests within short time scales (∼10–100 ns). The molecular factors that may affect the switching process inside the cage cavity will be discussed more in detail in the last section. Nonetheless, these results indicate that in order to fully understand and characterize the transitions in these systems, it is first necessary to study the intrinsic dynamics of the host–guest complexes and the kinetics of guest encapsulation and release.
Mechanisms of Guest Encapsulation/Release and Switching
The results discussed in the previous section provide information about the kinetics of trans → cis switching of excited guests inside the cage. However, this information is not sufficient to draw conclusions about whether the isomerization occurs inside or outside the cage, or about the stability of the guest encapsulation inside the host before and after the transition. To obtain a complete picture of the transition mechanism, we have studied the thermodynamics and kinetics of the guest encapsulation and expulsion in/out the cage. In fact, the ΔG for guest encapsulation (and the related kon vs koff) determines the effective probability of finding the guests inside/outside the cage and their residence time inside the cage.
Since guest encapsulation and release are, in general, rare events in these systems, it is difficult to study them via classical MD simulations. Consequently, we used MetaD simulations to investigate the thermodynamics and kinetics of guest binding/release. Starting from the equilibrated trans complexes, we conducted MetaD simulations during which the guests exchange multiple times in and out of the cage, allowing for a thorough exploration of the bound and unbound states and of the transition between them. These simulations allowed us to retrieve the free-energy difference, ΔG, between the encapsulated and free states and to calculate the corresponding Kb values (see Figure 5 and Table 1 for the data for all trans guests; the complete series including cis guests is listed in Tables S1 and S2). These data offer an exhaustive picture of the thermodynamics governing guest encapsulation, which is crucial to uncovering the probability of guest binding/release. We found that formation of the host–guest complex is energetically favored in all the tested cases, with a free-energy gain ranging from ∼3.6 kcal/mol for cis-F-AZB up to ∼8 kcal/mol for trans-M-AZB.
Figure 5.
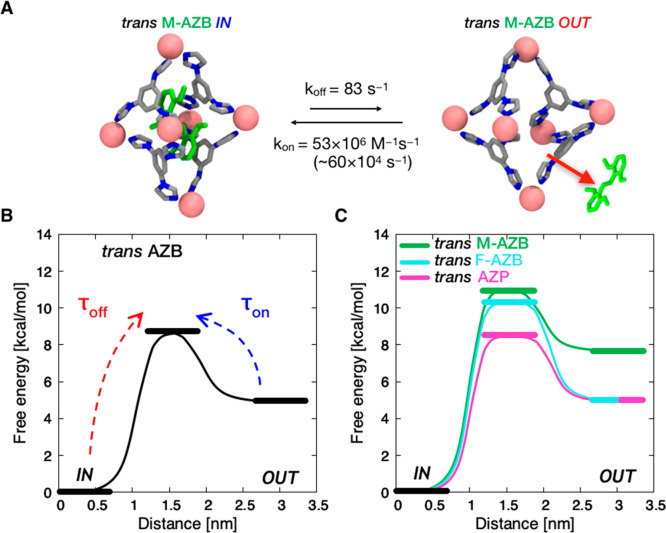
Thermodynamics and kinetics of trans guest binding/release. (A) Representative MetaD snapshots of the reversible binding and release of trans-M-AZB inside the cage; koff and kon denote the kinetic constants for the expulsion and encapsulation processes (the kon value inside the brackets is explicitly calculated, accounting for the guest concentration used in the model ∼11.4 mM, providing the actual rate). (B) Thermodynamic and kinetic scheme representing the expulsion and encapsulation mechanisms for trans-AZB in/out the cage as a function of the distance between the guests’ and the cage’s centers of mass (identifying IN and OUT states). (C) Thermodynamic schemes representing the expulsion/encapsulation of the trans isomers of M-AZB (green), F-AZB (cyan), and AZP (violet) guests. All ΔG differences between IN vs OUT states were computed from converged MetaD simulations, while the transition barriers were more accurately estimated from multiple infrequent MetaD runs (see the SI Methods section for further details).
As recently done to study the kinetics of monomer exchange in supramolecular polymers,73 we then studied the kinetics of guest binding/release by means of infrequent MetaD simulations74 (see SI Methods for details). From multiple infrequent MetaD runs activating/biasing guest release out from the cage, we could reconstruct unbiased kinetics for the event and estimate residence times for the encapsulated guest, τoff. The kinetic constant for guest release can be calculated as koff = 1/τoff. The kinetic constant for guest encapsulation (kon) can be then derived as follows: Kb = kon/koff. In this way we can obtain the complete thermodynamic and dynamic characterization of these host–guest systems, as represented in the thermodynamic schemes in Figure 5 and in the data collected in Tables 1, S1, and S2. These results reveal some subtle aspects of the binding/release processes. For example, we found that the cis conformers on average exhibit shorter residence times inside the cage with respect to the corresponding trans isomers, including more weakly binding trans isomers such as trans-AZB and trans-AZP. This effect is attributed to the lower free-energy barrier that the cis guest has to overcome to leave the cage as compared to the trans guest (see Table S2), which could be correlated with the relatively high flexibility of the host cage while accommodating cis guests (see Figure 3). Most importantly, we can observe from Table 1 that the characteristic transition times for trans → cis isomerization (τtrans–cis) are orders of magnitude shorter than the characteristic time for the release of trans guests from the cage (τoff). This indicates that isomerization in these systems occurs most probably inside the cage.
We also conducted MetaD simulations to study the encapsulation of a second trans guest in the case where one trans guest is already encapsulated inside the cage. We know from the experimental results62 and from the plain MD simulations (see previous sections), that the cage can often incorporate two trans guests (e.g., F-AZB or AZB). Conversely, other molecules, such as M-AZB, can only form complexes incorporating one guest molecule.62 The FESs obtained from MetaD simulations with two M-AZB vs two F-AZB or two AZB guests are consistent with this picture (Figure S4). In particular, these results clearly demonstrate that while incorporation of a second F-AZB, or AZB, guest in the cage is an energetically favored event (Figure S4, center and right), in the case of M-AZB, this process is highly unfavorable and unlikely (Figure S4, left). This is consistent, for example, with the available crystal structures, showing that two trans-F-AZB and two trans-AZB guests can be encapsulated within one cage, while the same cage accommodates only one trans-M-AZB at a time.62 Moreover, while quantities such as the ΔG, Kb, kon, and koff of guest encapsulation/expulsion can be difficult to determine experimentally, the overall binding constant governing encapsulation of two trans-AZB guests within the cage could be estimated from NMR experiments, giving a value in the range of ∼109 M–2.62 We could also estimate such overall binding constant (Kb(tot)) from the MetaD simulations using the Kb values associated with the first and the second trans-AZB guests (i.e., as Kb(tot) = Kb(guest-1) × Kb(guest-2)). The calculated value for Kb(tot) is ∼0.3 × 109 M–2 (see Table S3), which is consistent with the value obtained experimentally. The results of our simulations are also qualitatively consistent with the experimental evidence available for the other systems, for which experimental Kb values could not be obtained. We conducted infrequent MetaD simulations to compare the residence times of two F-AZB guests inside the cage before and after trans → cis isomerization of one guest. We found that while the switching similarly occurs within the cage, one of the two guests is then expelled promptly, within very fast time scales (nanoseconds)—orders of magnitude shorter than in the two-trans case (see Figure S3). In particular, the expulsion of cis-F-AZB is ten times more likely (or faster) than that of the trans isomer (residence times inside the cage of ∼10 ns and ∼100 ns, respectively; see also Figure S5). This finding is consistent with the experimental results62 demonstrating that the (trans+cis)-cage ternary complex is unstable and that the isomerization of trans-F-AZB produced the rapid expulsion from the cage of one out of the two guests (most likely the cis isomer). Together, these results support the reliability of our models and provide a comprehensive characterization of the system both from thermodynamic and kinetic points of view. They also show how, in order to characterize the transition kinetics inside the cage, it is also necessary to characterize the binding and release of the guests in/out the cage.
Molecular Determinants of Guest Transitions in the Cage
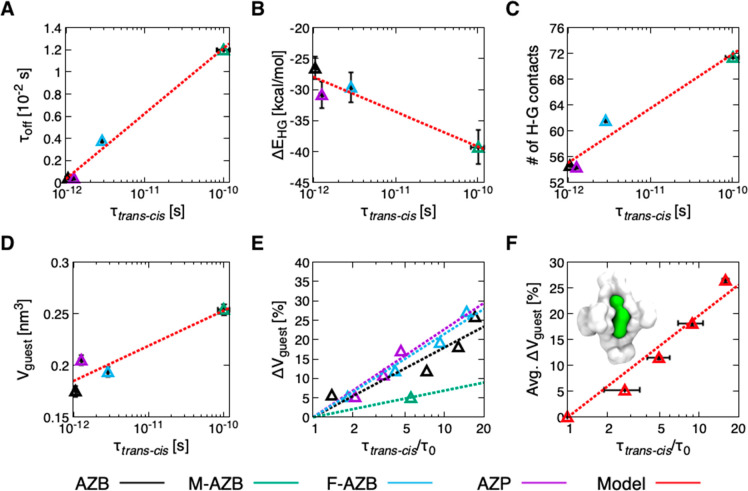
In the final step, we analyzed the results from our simulations to investigate the molecular determinants that control in-cavity isomerization of the guests in these systems. Table 1 lists data describing dynamic host–guest binding in the systems and the kinetics of isomerization inside the cage cavity. Interestingly, by comparing the τtrans–cis with the τoff data, we obtain a nontrivial relationship between the residence time of the guests inside the host and the characteristic time scale needed for guest switching. In particular, we can observe that longer residence times in the cavity correspond to slower transitions (Figure 6A), suggesting that the same molecular factors regulating the stability of host–guest binding have an impact on the switching rates of the guests.
Figure 6.
Molecular determinants of isomerization under confinement. (A) Relationship between isomerization rate (τtrans–cis) and residence times (τoff) of the guests inside the cage. (B) Relationship between τtrans–cis and potential energy of host–guest interactions, ΔEHG. (C) Relationship between τtrans–cis and the number of contacts between the cage and the guest. (D) Relationship between τtrans–cis and the volume (V) of guest molecules (see the SI Methods section for details on guest volume estimation). (E) Switching deceleration, τtrans–cis/τ0, as a function of the increase in guest volume (%ΔVguest), in which τ0 denotes isomerization time measured at the original volume of each guest. In plots A–E, the points correspond to guests AZB (black), M-AZB (green), F-AZB (cyan), and AZP (violet). (F) Average τtrans–cis/τ0 as a function of the average increase in guest volume (%ΔVguest), obtained by averaging all data from plot E between systems with similar %ΔVguest. The error bars indicate the standard deviation of %ΔVguest and τtrans–cis/τ0 values. Inset: cartoon showing the volume of encapsulated M-AZB (green) inside the cage (white). The dashed lines in all plots are the logarithmic fit of the data.
In general, the energy of the host–guest interaction ΔEHG correlates with τoff. When this interaction is stronger, guest release from the cage is slower, meaning that the guest spends more time in the cage. Molecular crowding in the cavity has a similar effect. When there is a higher number of contacts between the host and the guest, τoff is longer, and guest release is less probable. We can clearly observe this effect for all simulated systems, both with trans and cis guests (see Figure S6A,B). This result is reasonable, as the interactions and the number of contacts between the host and the guest are intimately correlated to one another (see Figure S6C). This correlation is especially relevant when considering flexible hosts: stronger affinity between the host and guest leads to larger deformation of the host, as a flexible cage can structurally adapt to enhance contacts with the guest. At the same time, the relationship obtained in Figure 6A indicates that both host–guest affinity and molecular crowding impact the transition rate (τtrans–cis). This relationship between τtrans–cis and ΔEHG, and between τtrans–cis and the number of contacts, is demonstrated by the trends in Figure 6B and C, respectively. These results suggest that both host–guest affinity and molecular crowding can in principle be used to control the transition rates in the system.
Because extrapolating design principles from these plots is not trivial, we chose a more elegant strategy. We started from the simplistic consideration that, for a given impact of host–guest contacts on the switching process, the ratio between the volume occupied by the guest and the volume accessible in the cage (e.g., Vguest/Vcavity) constitutes a discriminant parameter governing transitions in the system. Given that the cage is the same in all systems, and assuming that the variations in Vcavity are negligible when comparing between the various systems (simplification), we plotted Vguest against τtrans–cis (Figure 6D) and obtained a trend similar to those described above. Even considering the approximations required to make this observation, this qualitative trend reveals a molecular-level relationship between the volume of the guest and the transition rate under confinement.
Recently, we demonstrated how reliable chemically relevant molecular models can be used as “toy models” to obtain pseudomolecular, yet useful information. By “playing” with these flexible models, we can then learn about the factors that control the system.50,73 Having observed that guest volume has a strong impact on transition rate within the cage, we developed a computational strategy to increase the number of available data points in this trend. Starting from equilibrated models of the cage encapsulating one trans guest of each type, we artificially increased the radii of guests’ atoms in the models to increase Vguest. In all cases, the atomic radii have been increased to achieve a global increase of ∼5, 10, 20, or 30% for Vguest. Repeating the isomerization simulations for all these cases then allowed us to monitor transition deceleration as a function of the increase in guest volume (%ΔVguest). In this way, we obtained the trends shown in Figure 6E for the various guests.
These results show that transition rate generally slows down as %ΔVguest increases. Some variability between the different guests can be expected (e.g., M-AZB in green), as other features of the guest, such as chemical structure and shape, can also impact isomerization. These results are in agreement with our observation that host–guest affinity also has an impact on the rate of isomerization (Figure 6B). We also note that for some guests (M-AZB and AZP), the series is incomplete because isomerization does not occur inside the cage over a certain %ΔVguest (∼20% for AZP and ∼5–10% for M-AZB). In these cases, isomerization is either impeded by the cage or results in the release of the isomerizing guest. This observation is consistent with experimental results and with the simulations for two-guest systems. In fact, encapsulating two guests inside the cage can be assumed to be comparable to a %ΔVguest of ∼100%, well over the maximum %ΔVguest for which isomerization occurs inside the cage. As previously shown, isomerization of one guest produces rapid expulsion of one guest from two-guest systems (see Figure S3).
Finally, if we average the rate deceleration data at different values of %ΔVguest for the various systems (Figure 6E), we obtain the plot shown in Figure 6F, which shows a clear general trend between the average increase in guest volume and the deceleration of guest transitions. This trend is clearly qualitative, as other variables may also be important in controlling guest isomerization under confinement. Nevertheless, this result demonstrates a direct correlation between guest volume, crowding within the cage, and the guest transition rates. This observation helps rationalize experimental62,75 and computational results,50,52,76 showing that azobenzene isomerization may be hindered in highly crowded molecular systems. The generality of the computational approach presented herein offers a context for developing the idea that molecular environments can be, in principle, rationally designed to control molecular switching processes.
Conclusions
Learning how to control chemical reactions inside confined spaces will unlock many applications. Here we used atomistic simulations to investigate the mechanisms and molecular factors that control trans → cis isomerization of various azo compounds within a coordination cage. Classical molecular dynamics and metadynamics simulations allowed us to characterize these host–guest systems from thermodynamic and kinetic points of view. In this way, we obtained an exhaustive mechanistic understanding of guest encapsulation, reversible guest uptake/release dynamics and guest switching transitions, and results in agreement with experimental observations.
To elucidate the kinetics of molecular transitions under confinement, we show that it is necessary to understand the intrinsic dynamics of guest binding and release processes. We demonstrate how this equilibrium is influenced by the free-energy cost associated with host reconfiguration upon guest encapsulation, and by the energy gain due to host–guest interactions. This competition determines the residence time of encapsulated azobenzene guests inside the cage and the slowing rate of their isomerization. We identify molecular crowding and host–guest affinity as two key factors governing isomerization rate/probability in these systems. Our results demonstrate that, in principle, tuning the volume of the guest may have a direct impact on the transition rate inside the cage, or even dictate whether the transition will occur inside or outside the cage.
Overall, the advantages of the approach employed herein are many. Our approach enables a thorough characterization of (i) the flexibility and conformations accessible by the cage under given conditions of solvent and temperature, (ii) the isomerization rates for encapsulated guests, and (iii) the effect of guest encapsulation and isomerization on the flexibility and conformational distortion of the cage. The metadynamics simulations allow us to obtain molecular-level information on the thermodynamics and kinetics of the host–guest encapsulation, providing values for, e.g., kon, koff, ΔG, free-energy barriers, etc., which can be challenging to determine experimentally. From a holistic point of view, this reveals the synergies between structure, thermodynamics, and dynamics within these complex molecular systems, which concur to determine the behavior of these host−guest molecular systems. In principle, the molecular simulations approaches described herein are versatile and can be applied to investigate not only other cages but also stimuli-responsive host–guest systems in general. Our approach can provide clearer insight into the molecular factors that control structure, host–guest affinity, and dynamics, thus guiding the rational design, or customization, of systems with controllable reactivity. We envisage that this approach will find application in fields ranging from the rational design of photoresponsive host–guest systems and artificial enzymes to the control of chemical reactions in confined spaces.
Acknowledgments
GMP acknowledges the funding received by the Swiss National Science Foundation (SNSF grant number 200021_175735) and by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement no. 818776 – DYNAPOL). The authors also acknowledge the computational resources provided by the Swiss National Supercomputing Center (CSCS). RK acknowledges funding from the Minerva Foundation. ABG acknowledges funding from the Zuckerman STEM Leadership Program.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c03444.
Details on the creation and parametrization of the molecular systems, simulation setup, and analysis of molecular dynamics and metadynamics simulations; additional data and figures from the simulations (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Bandara H. M. D.; Burdette S. C. Photoisomerization in Different Classes of Azobenzene. Chem. Soc. Rev. 2012, 41, 1809–1825. 10.1039/C1CS15179G. [DOI] [PubMed] [Google Scholar]
- Shi Z.; Peng P.; Strohecker D.; Liao Y. Long-Lived Photoacid Based upon a Photochromic Reaction. J. Am. Chem. Soc. 2011, 133, 14699–14703. 10.1021/ja203851c. [DOI] [PubMed] [Google Scholar]
- Klajn R. Spiropyran-Based Dynamic Materials. Chem. Soc. Rev. 2014, 43, 148–184. 10.1039/C3CS60181A. [DOI] [PubMed] [Google Scholar]
- Weston C. E.; Richardson R. D.; Haycock P. R.; White A. J. P.; Fuchter M. J. Arylazopyrazoles: Azoheteroarene Photoswitches Offering Quantitative Isomerization and Long Thermal Half-Lives. J. Am. Chem. Soc. 2014, 136, 11878–11881. 10.1021/ja505444d. [DOI] [PubMed] [Google Scholar]
- Wang Y.-T.; Liu X.-Y.; Cui G.; Fang W.-H.; Thiel W. Photoisomerization of Arylazopyrazole Photoswitches: Stereospecific Excited-State Relaxation. Angew. Chem., Int. Ed. 2016, 55, 14009–14013. 10.1002/anie.201607373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fredy J. W.; Méndez-Ardoy A.; Kwangmettatam S.; Bochicchio D.; Matt B.; Stuart M. C. A.; Huskens J.; Katsonis N.; Pavan G. M.; Kudernac T. Molecular Photoswitches Mediating the Strain-Driven Disassembly of Supramolecular Tubules. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 11850–11855. 10.1073/pnas.1711184114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yagai S.; Iwai K.; Yamauchi M.; Karatsu T.; Kitamura A.; Uemura S.; Morimoto M.; Wang H.; Würthner F. Photocontrol Over Self-Assembled Nanostructures of π-π Stacked Dyes Supported by the Parallel Conformer of Diarylethene. Angew. Chem., Int. Ed. 2014, 53, 2602–2606. 10.1002/anie.201310773. [DOI] [PubMed] [Google Scholar]
- Molla M. R.; Rangadurai P.; Antony L.; Swaminathan S.; de Pablo J. J.; Thayumanavan S. Dynamic Actuation of Glassy Polymersomes through Isomerization of a Single Azobenzene Unit at the Block Copolymer Interface. Nat. Chem. 2018, 10, 659–666. 10.1038/s41557-018-0027-6. [DOI] [PubMed] [Google Scholar]
- Pianowski Z. L. Recent Implementations of Molecular Photoswitches into Smart Materials and Biological Systems. Chem. - Eur. J. 2019, 25, 5128–5144. 10.1002/chem.201805814. [DOI] [PubMed] [Google Scholar]
- Feringa B. L. The Art of Building Small: From Molecular Switches to Motors (Nobel Lecture). Angew. Chem., Int. Ed. 2017, 56, 11060–11078. 10.1002/anie.201702979. [DOI] [PubMed] [Google Scholar]
- Sauvage J.-P. From Chemical Topology to Molecular Machines (Nobel Lecture). Angew. Chem., Int. Ed. 2017, 56, 11080–11093. 10.1002/anie.201702992. [DOI] [PubMed] [Google Scholar]
- Stoddart J. F. Mechanically Interlocked Molecules (MIMs)—Molecular Shuttles, Switches, and Machines (Nobel Lecture). Angew. Chem., Int. Ed. 2017, 56, 11094–11125. 10.1002/anie.201703216. [DOI] [PubMed] [Google Scholar]
- Dri C.; Peters M. V.; Schwarz J.; Hecht S.; Grill L. Spatial Periodicity in Molecular Switching. Nat. Nanotechnol. 2008, 3, 649–653. 10.1038/nnano.2008.269. [DOI] [PubMed] [Google Scholar]
- Kassem S.; Lee A. T. L.; Leigh D. A.; Marcos V.; Palmer L. I.; Pisano S. Stereodivergent Synthesis with a Programmable Molecular Machine. Nature 2017, 549, 374–378. 10.1038/nature23677. [DOI] [PubMed] [Google Scholar]
- Katsonis N.; Lubomska M.; Pollard M. M.; Feringa B. L.; Rudolf P. Synthetic Light-Activated Molecular Switches and Motors on Surfaces. Prog. Surf. Sci. 2007, 82, 407–434. 10.1016/j.progsurf.2007.03.011. [DOI] [Google Scholar]
- Broichhagen J.; Frank J. A.; Trauner D. A Roadmap to Success in Photopharmacology. Acc. Chem. Res. 2015, 48, 1947–1960. 10.1021/acs.accounts.5b00129. [DOI] [PubMed] [Google Scholar]
- Weston C. E.; Krämer A.; Colin F.; Yildiz Ö.; Baud M. G. J.; Meyer-Almes F.-J.; Fuchter M. J. Toward Photopharmacological Antimicrobial Chemotherapy Using Photoswitchable Amidohydrolase Inhibitors. ACS Infect. Dis. 2017, 3, 152–161. 10.1021/acsinfecdis.6b00148. [DOI] [PubMed] [Google Scholar]
- Fiedler D.; Leung D.; Bergman R.; Raymond K. Selective Molecular Recognition, C-H Bond Activation, and Catalysis in Nanoscale Reaction Vessels. Acc. Chem. Res. 2005, 38, 349–358. 10.1021/ar040152p. [DOI] [PubMed] [Google Scholar]
- Tripp B. C.; Smith K.; Ferry J. G. Carbonic Anhydrase: New Insights for an Ancient Enzyme. J. Biol. Chem. 2001, 276, 48615–48618. 10.1074/jbc.R100045200. [DOI] [PubMed] [Google Scholar]
- Zhang X.; Houk K. N. Why Enzymes Are Proficient Catalysts: Beyond the Pauling Paradigm. Acc. Chem. Res. 2005, 38, 379–385. 10.1021/ar040257s. [DOI] [PubMed] [Google Scholar]
- Whicher J. R.; Dutta S.; Hansen D. A.; Hale W. A.; Chemler J. A.; Dosey A. M.; Narayan A. R. H.; Håkansson K.; Sherman D. H.; Smith J. L.; Skiniotis G. Structural Rearrangements of a Polyketide Synthase Module during Its Catalytic Cycle. Nature 2014, 510, 560–564. 10.1038/nature13409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grommet A. B.; Feller M.; Klajn R. Chemical Reactivity under Nanoconfinement. Nat. Nanotechnol. 2020, 15, 256–271. 10.1038/s41565-020-0652-2. [DOI] [PubMed] [Google Scholar]
- Janiak C.; Vieth J. K. MOFs, MILs and More: Concepts, Properties and Applications for Porous Coordination Networks (PCNs). New J. Chem. 2010, 34, 2366–2388. 10.1039/c0nj00275e. [DOI] [Google Scholar]
- Goettmann F.; Sanchez C. How Does Confinement Affect the Catalytic Activity of Mesoporous Materials?. J. Mater. Chem. 2007, 17, 24–30. 10.1039/B608748P. [DOI] [Google Scholar]
- Boyd P. G.; Chidambaram A.; García-Díez E.; Ireland C. P.; Daff T. D.; Bounds R.; Gładysiak A.; Schouwink P.; Moosavi S. M.; Maroto-Valer M. M.; Reimer J. A.; Navarro J. A. R.; Woo T. K.; Garcia S.; Stylianou K. C.; Smit B. Data-Driven Design of Metal–Organic Frameworks for Wet Flue Gas CO2 Capture. Nature 2019, 576, 253–256. 10.1038/s41586-019-1798-7. [DOI] [PubMed] [Google Scholar]
- Chu Z.; Han Y.; Bian T.; De S.; Král P.; Klajn R. Supramolecular Control of Azobenzene Switching on Nanoparticles. J. Am. Chem. Soc. 2019, 141, 1949–1960. 10.1021/jacs.8b09638. [DOI] [PubMed] [Google Scholar]
- Ahrens J.; Bian T.; Vexler T.; Klajn R. Irreversible Bleaching of Donor–Acceptor Stenhouse Adducts on the Surfaces of Magnetite Nanoparticles. ChemPhotoChem. 2017, 1, 230–236. 10.1002/cptc.201700009. [DOI] [Google Scholar]
- Zdobinsky T.; Sankar Maiti P.; Klajn R. Support Curvature and Conformational Freedom Control Chemical Reactivity of Immobilized Species. J. Am. Chem. Soc. 2014, 136, 2711–2714. 10.1021/ja411573a. [DOI] [PubMed] [Google Scholar]
- Zhao H.; Sen S.; Udayabhaskararao T.; Sawczyk M.; Kučanda K.; Manna D.; Kundu P. K.; Lee J.-W.; Král P.; Klajn R. Reversible Trapping and Reaction Acceleration within Dynamically Self-Assembling Nanoflasks. Nat. Nanotechnol. 2016, 11, 82–88. 10.1038/nnano.2015.256. [DOI] [PubMed] [Google Scholar]
- Fallah-Araghi A.; Meguellati K.; Baret J.-C.; Harrak A. E.; Mangeat T.; Karplus M.; Ladame S.; Marques C. M.; Griffiths A. D. Enhanced Chemical Synthesis at Soft Interfaces: A Universal Reaction-Adsorption Mechanism in Microcompartments. Phys. Rev. Lett. 2014, 112, 028301 10.1103/PhysRevLett.112.028301. [DOI] [PubMed] [Google Scholar]
- Franco C.; Rodríguez-San-Miguel D.; Sorrenti A.; Sevim S.; Pons R.; Platero-Prats A. E.; Pavlovic M.; Szilágyi I.; Ruiz Gonzalez M. L.; González-Calbet J. M.; Bochicchio D.; Pesce L.; Pavan G. M.; Imaz I.; Cano-Sarabia M.; Maspoch D.; Pané S.; de Mello A. J.; Zamora F.; Puigmartí-Luis J. Biomimetic Synthesis of Sub-20 nm Covalent Organic Frameworks in Water. J. Am. Chem. Soc. 2020, 142, 3540–3547. 10.1021/jacs.9b12389. [DOI] [PubMed] [Google Scholar]
- Zhang G.; Mastalerz M. Organic Cage Compounds – from Shape-Persistency to Function. Chem. Soc. Rev. 2014, 43, 1934–1947. 10.1039/C3CS60358J. [DOI] [PubMed] [Google Scholar]
- Kang J.; Rebek J. Acceleration of a Diels–Alder Reaction by a Self-Assembled Molecular Capsule. Nature 1997, 385, 50–52. 10.1038/385050a0. [DOI] [PubMed] [Google Scholar]
- Yoshizawa M.; Klosterman J. K.; Fujita M. Functional Molecular Flasks: New Properties and Reactions within Discrete, Self-Assembled Hosts. Angew. Chem., Int. Ed. 2009, 48, 3418–3438. 10.1002/anie.200805340. [DOI] [PubMed] [Google Scholar]
- Roy B.; Ghosh A. K.; Srivastava S.; D’Silva P.; Mukherjee P. S. A Pd8 Tetrafacial Molecular Barrel as Carrier for Water Insoluble Fluorophore. J. Am. Chem. Soc. 2015, 137, 11916–11919. 10.1021/jacs.5b08008. [DOI] [PubMed] [Google Scholar]
- Wang K.; Cai X.; Yao W.; Tang D.; Kataria R.; Ashbaugh H. S.; Byers L. D.; Gibb B. C. Electrostatic Control of Macrocyclization Reactions within Nanospaces. J. Am. Chem. Soc. 2019, 141, 6740–6747. 10.1021/jacs.9b02287. [DOI] [PubMed] [Google Scholar]
- Cook T. R.; Stang P. J. Recent Developments in the Preparation and Chemistry of Metallacycles and Metallacages via Coordination. Chem. Rev. 2015, 115, 7001–7045. 10.1021/cr5005666. [DOI] [PubMed] [Google Scholar]
- Sepehrpour H.; Fu W.; Sun Y.; Stang P. J. Biomedically Relevant Self-Assembled Metallacycles and Metallacages. J. Am. Chem. Soc. 2019, 141, 14005–14020. 10.1021/jacs.9b06222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu M.; Zhang L.; Little M. A.; Kapil V.; Ceriotti M.; Yang S.; Ding L.; Holden D. L.; Balderas-Xicohténcatl R.; He D.; Clowes R.; Chong S. Y.; Schütz G.; Chen L.; Hirscher M.; Cooper A. I. Barely Porous Organic Cages for Hydrogen Isotope Separation. Science 2019, 366, 613–620. 10.1126/science.aax7427. [DOI] [PubMed] [Google Scholar]
- Merget S.; Catti L.; Piccini G.; Tiefenbacher K. Requirements for Terpene Cyclizations inside the Supramolecular Resorcinarene Capsule: Bound Water and Its Protonation Determine the Catalytic Activity. J. Am. Chem. Soc. 2020, 142, 4400–4410. 10.1021/jacs.9b13239. [DOI] [PubMed] [Google Scholar]
- Yoshizawa M.; Tamura M.; Fujita M. Diels-Alder in Aqueous Molecular Hosts: Unusual Regioselectivity and Efficient Catalysis. Science 2006, 312, 251–254. 10.1126/science.1124985. [DOI] [PubMed] [Google Scholar]
- Ueda Y.; Ito H.; Fujita D.; Fujita M. Permeable Self-Assembled Molecular Containers for Catalyst Isolation Enabling Two-Step Cascade Reactions. J. Am. Chem. Soc. 2017, 139, 6090–6093. 10.1021/jacs.7b02745. [DOI] [PubMed] [Google Scholar]
- Maestri M.; Iglesia E. First-Principles Theoretical Assessment of Catalysis by Confinement: NO–O2 Reactions within Voids of Molecular Dimensions in Siliceous Crystalline Frameworks. Phys. Chem. Chem. Phys. 2018, 20, 15725–15735. 10.1039/C8CP01615A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mal P.; Breiner B.; Rissanen K.; Nitschke J. R. White Phosphorus Is Air-Stable Within a Self-Assembled Tetrahedral Capsule. Science 2009, 324, 1697. 10.1126/science.1175313. [DOI] [PubMed] [Google Scholar]
- Yamashina M.; Sei Y.; Akita M.; Yoshizawa M. Safe Storage of Radical Initiators within a Polyaromatic Nanocapsule. Nat. Commun. 2014, 5, 4662. 10.1038/ncomms5662. [DOI] [PubMed] [Google Scholar]
- Galan A.; Ballester P. Stabilization of Reactive Species by Supramolecular Encapsulation. Chem. Soc. Rev. 2016, 45, 1720–1737. 10.1039/C5CS00861A. [DOI] [PubMed] [Google Scholar]
- Qiu Y.; Antony L. W.; Torkelson J. M.; de Pablo J. J.; Ediger M. D. Tenfold Increase in the Photostability of an Azobenzene Guest in Vapor-Deposited Glass Mixtures. J. Chem. Phys. 2018, 149, 204503. 10.1063/1.5052003. [DOI] [PubMed] [Google Scholar]
- Qiu Y.; Antony L. W.; de Pablo J. J.; Ediger M. D. Photostability Can Be Significantly Modulated by Molecular Packing in Glasses. J. Am. Chem. Soc. 2016, 138, 11282–11289. 10.1021/jacs.6b06372. [DOI] [PubMed] [Google Scholar]
- Fregoni J.; Granucci G.; Persico M.; Corni S. Strong Coupling with Light Enhances the Photoisomerization Quantum Yield of Azobenzene. Chem. 2020, 6, 250–265. 10.1016/j.chempr.2019.11.001. [DOI] [Google Scholar]
- Bochicchio D.; Kwangmettatam S.; Kudernac T.; Pavan G. M. How Defects Control the Out-of-Equilibrium Dissipative Evolution of a Supramolecular Tubule. ACS Nano 2019, 13, 4322–4334. 10.1021/acsnano.8b09523. [DOI] [PubMed] [Google Scholar]
- Kusukawa T.; Fujita M. Ship-in-a-Bottle” Formation of Stable Hydrophobic Dimers of Cis-Azobenzene and -Stilbene Derivatives in a Self-Assembled Coordination Nanocage. J. Am. Chem. Soc. 1999, 121, 1397–1398. 10.1021/ja9837295. [DOI] [Google Scholar]
- Cantatore V.; Granucci G.; Rousseau G.; Padula G.; Persico M. Photoisomerization of Self-Assembled Monolayers of Azobiphenyls: Simulations Highlight the Role of Packing and Defects. J. Phys. Chem. Lett. 2016, 7, 4027–4031. 10.1021/acs.jpclett.6b02018. [DOI] [PubMed] [Google Scholar]
- Clever G. H.; Tashiro S.; Shionoya M. Light-Triggered Crystallization of a Molecular Host-Guest Complex. J. Am. Chem. Soc. 2010, 132, 9973–9975. 10.1021/ja103620z. [DOI] [PubMed] [Google Scholar]
- Dube H.; Ajami D.; Rebek J. Photochemical Control of Reversible Encapsulation. Angew. Chem., Int. Ed. 2010, 49, 3192–3195. 10.1002/anie.201000876. [DOI] [PubMed] [Google Scholar]
- Mohan Raj A.; Raymo F. M.; Ramamurthy V. Reversible Disassembly–Assembly of Octa Acid–Guest Capsule in Water Triggered by a Photochromic Process. Org. Lett. 2016, 18, 1566–1569. 10.1021/acs.orglett.6b00405. [DOI] [PubMed] [Google Scholar]
- Yang Y.; Hughes R. P.; Aprahamian I. Visible Light Switching of a BF2-Coordinated Azo Compound. J. Am. Chem. Soc. 2012, 134, 15221–15224. 10.1021/ja306030d. [DOI] [PubMed] [Google Scholar]
- Helmy S.; Leibfarth F. A.; Oh S.; Poelma J. E.; Hawker C. J.; Read de Alaniz J. Photoswitching Using Visible Light: A New Class of Organic Photochromic Molecules. J. Am. Chem. Soc. 2014, 136, 8169–8172. 10.1021/ja503016b. [DOI] [PubMed] [Google Scholar]
- Zhang D.; Ronson T. K.; Mosquera J.; Martinez A.; Guy L.; Nitschke J. R. Anion Binding in Water Drives Structural Adaptation in an Azaphosphatrane-Functionalized FeII4L4 Tetrahedron. J. Am. Chem. Soc. 2017, 139, 6574–6577. 10.1021/jacs.7b02950. [DOI] [PubMed] [Google Scholar]
- Rizzuto F. J.; Nitschke J. R. Stereochemical Plasticity Modulates Cooperative Binding in a CoII12L6 Cuboctahedron. Nat. Chem. 2017, 9, 903–908. 10.1038/nchem.2758. [DOI] [PubMed] [Google Scholar]
- Mondal P.; Sarkar S.; Rath S. P. Cyclic Bis-Porphyrin-Based Flexible Molecular Containers: Controlling Guest Arrangements and Supramolecular Catalysis by Tuning Cavity Size. Chem. - Eur. J. 2017, 23, 7093–7103. 10.1002/chem.201700577. [DOI] [PubMed] [Google Scholar]
- Samanta D.; Mukherjee S.; Patil Y. P.; Mukherjee P. S. Self-Assembled Pd6 Open Cage with Triimidazole Walls and the Use of Its Confined Nanospace for Catalytic Knoevenagel- and Diels–Alder Reactions in Aqueous Medium. Chem. - Eur. J. 2012, 18, 12322–12329. 10.1002/chem.201201679. [DOI] [PubMed] [Google Scholar]
- Samanta D.; Gemen J.; Chu Z.; Diskin-Posner Y.; Shimon L. J. W.; Klajn R. Reversible Photoswitching of Encapsulated Azobenzenes in Water. Proc. Natl. Acad. Sci. U. S. A. 2018, 115, 9379–9384. 10.1073/pnas.1712787115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samanta D.; Galaktionova D.; Gemen J.; Shimon L. J. W.; Diskin-Posner Y.; Avram L.; Král P.; Klajn R. Reversible Chromism of Spiropyran in the Cavity of a Flexible Coordination Cage. Nat. Commun. 2018, 9, 641. 10.1038/s41467-017-02715-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanopolskyi A. I.; De S.; Białek M. J.; Diskin-Posner Y.; Avram L.; Feller M.; Klajn R. Reversible Switching of Arylazopyrazole within a Metal–Organic Cage. Beilstein J. Org. Chem. 2019, 15, 2398–2407. 10.3762/bjoc.15.232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Böckmann M.; Peter C.; Site L. D.; Doltsinis N. L.; Kremer K.; Marx D. Atomistic Force Field for Azobenzene Compounds Adapted for QM/MM Simulations with Applications to Liquids and Liquid Crystals. J. Chem. Theory Comput. 2007, 3, 1789–1802. 10.1021/ct7000733. [DOI] [PubMed] [Google Scholar]
- Peter C.; Site L. D.; Kremer K. Classical Simulations from the Atomistic to the Mesoscale and Back: Coarse Graining an Azobenzene Liquid Crystal. Soft Matter 2008, 4, 859–869. 10.1039/b717324e. [DOI] [PubMed] [Google Scholar]
- Ilnytskyi J. M.; Slyusarchuk A.; Saphiannikova M. Photocontrollable Self-Assembly of Azobenzene-Decorated Nanoparticles in Bulk: Computer Simulation Study. Macromolecules 2016, 49, 9272–9282. 10.1021/acs.macromol.6b01871. [DOI] [Google Scholar]
- Osella S.; Minoia A.; Beljonne D. Combined Molecular Dynamics and Density Functional Theory Study of Azobenzene–Graphene Interfaces. J. Phys. Chem. C 2016, 120, 6651–6658. 10.1021/acs.jpcc.6b00393. [DOI] [Google Scholar]
- Döbbelin M.; Ciesielski A.; Haar S.; Osella S.; Bruna M.; Minoia A.; Grisanti L.; Mosciatti T.; Richard F.; Prasetyanto E. A.; De Cola L.; Palermo V.; Mazzaro R.; Morandi V.; Lazzaroni R.; Ferrari A. C.; Beljonne D.; Samorì P. Light-Enhanced Liquid-Phase Exfoliation and Current Photoswitching in Graphene–Azobenzene Composites. Nat. Commun. 2016, 7, 11090. 10.1038/ncomms11090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laio A.; Parrinello M. Escaping Free-Energy Minima. Proc. Natl. Acad. Sci. U. S. A. 2002, 99, 12562–12566. 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pederzoli M.; Pittner J.; Barbatti M.; Lischka H. Nonadiabatic Molecular Dynamics Study of the Cis–Trans Photoisomerization of Azobenzene Excited to the S1 State. J. Phys. Chem. A 2011, 115, 11136–11143. 10.1021/jp2013094. [DOI] [PubMed] [Google Scholar]
- Tiago M. L.; Ismail-Beigi S.; Louie S. G. Photoisomerization of Azobenzene from First-Principles Constrained Density-Functional Calculations. J. Chem. Phys. 2005, 122, 094311 10.1063/1.1861873. [DOI] [PubMed] [Google Scholar]
- Bochicchio D.; Salvalaglio M.; Pavan G. M. Into the Dynamics of a Supramolecular Polymer at Submolecular Resolution. Nat. Commun. 2017, 8, 147. 10.1038/s41467-017-00189-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tiwary P.; Parrinello M. From Metadynamics to Dynamics. Phys. Rev. Lett. 2013, 111, 230602. 10.1103/PhysRevLett.111.230602. [DOI] [PubMed] [Google Scholar]
- Pace G.; Ferri V.; Grave C.; Elbing M.; von Hänisch C.; Zharnikov M.; Mayor M.; Rampi M. A.; Samorì P. Cooperative Light-Induced Molecular Movements of Highly Ordered Azobenzene Self-Assembled Monolayers. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 9937. 10.1073/pnas.0703748104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Titov E.; Granucci G.; Götze J. P.; Persico M.; Saalfrank P. Dynamics of Azobenzene Dimer Photoisomerization: Electronic and Steric Effects. J. Phys. Chem. Lett. 2016, 7, 3591–3596. 10.1021/acs.jpclett.6b01401. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.