Abstract
FLASH radiotherapy delivers a high dose (≥10 Gy) at a high rate (≥40 Gy/s). In this way, particles are delivered in pulses as short as a few nanoseconds. At that rate, intertrack reactions between chemical species produced within the same pulse may affect the heterogeneous chemistry stage of water radiolysis. This stochastic process suits the capabilities of the Monte Carlo method, which can model intertrack effects to aid in radiobiology research, including the design and interpretation of experiments. In this work, the TOPAS-nBio Monte Carlo track-structure code was expanded to allow simulations of intertrack effects in the chemical stage of water radiolysis. Simulation of the behavior of radiolytic yields over a long period of time (up to 50 s) was verified by simulating radiolysis in a Fricke dosimeter irradiated by 60Co γ rays. In addition, LET-dependent G values of protons delivered in single squared pulses of widths, 1 ns, 1 μs and 10 μs, were obtained and compared to simulations using no intertrack considerations. The Fricke simulation for the calculated G value of Fe3+ ion at 50 s was within 0.4% of the accepted value from ICRU Report 34. For LET-dependent G values at the end of the chemical stage, intertrack effects were significant at LET values below 2 keV/μm. Above 2 keV/μm the reaction kinetics remained limited locally within each track and thus, effects of intertrack reactions remained low. Therefore, when track structure simulations are used to investigate the biological damage of FLASH irradiation, these intertrack reactions should be considered. The TOPAS-nBio framework with the expansion to intertrack chemistry simulation provides a useful tool to assist in this task.
INTRODUCTION
Monte Carlo simulations for particle transport typically follow one particle at a time as it traverses the material along its trajectory. The shower induced by each initial particle is a computationally independent event or history. This approach is reasonable when the physical interactions of one history do not impact another. In conventional radiotherapy this assumption even holds for individual particles belonging to the same history, studied with biophysical simulations on a step-by-step basis (following all ionizations) at the nanometer scale. In this scenario, for typical clinical dose rates, several particles may interact in close spatial proximity within a single cell nucleus without impacting each other, in part due to the separation of particles in time. Radiation treatments are spread out over minutes, while physics events occur within femtoseconds, preserving the independence of each simulated particle track. When chemical reactions of reactive oxygen species (ROS) induced by radiolysis are considered, the assumption of independence still applies because the time lapse of the non-homogeneous chemical stage of each history (10−7–10−6 s) (1) is much shorter than the time delay between subsequent histories (conventional dose rates are ≤0.03 Gy/s). The likelihood of the ROS created by one history reacting with the ROS created by another is negligible in clinical or environmental exposures. ROS are scavenged within nanosecond (ns) in cells (2), and the heterogeneous chemistry of radiolysis ends within the first microsecond after the initiating radiation interaction.
This all changes with FLASH radiotherapy (FLASH-RT). This technique delivers a relatively high dose (10 Gy or more) at a very high dose rate (> 40 Gy/s) (3, 4). FLASH-RT, in some cases, has shown greatly reduced normal tissue toxicities without affecting tumor control in animal systems (3, 5–7). However, comparison between tumor control probability for FLASH and conventional radiotherapy has not been published, since assays in animal systems are typically terminated within days whereas at least one year of follow-up is recommended (7). Studies initially done decades ago suggest that the tissue-sparing effect is caused by radiochemical depletion of oxygen (8–10). A key contender to explain this effect is that at FLASH dose rates the available oxygen is depleted as considerably more electrons are liberated per unit time, resulting in substantially more ionization than that produced at conventional dose rates (4). The potential to increase the therapeutic ratio with FLASH has led to significant interest, yet many questions remain. For example, more work is needed to determine exactly what dose, linear energy transfer (LET) and dose rate are required to achieve the FLASH effect, how the FLASH effect is influenced by fractionation, and what mechanisms are responsible for the FLASH effect.
Analytical and phenomenological models have been developed to investigate the physical parameters involved in the beam delivery, depletion and repletion of oxygen in tissue and the effects of dose and dose rate in the oxygen enhancement ratio, and to predict survival fractions of cells irradiated at ultra-high dose rates (11–13). Nevertheless, the effects of radiolysis, including potential oxygen depletion, can be modeled using the Monte Carlo method. In particular, Monte Carlo track structure has been used in the past in studies on the effect of oxygenation on the chemical yields (12, 13), and for the quantification of oxygen enhancement ratio for different radiation qualities and oxygen concentrations (14, 15). FLASH dose rates are typically delivered in short pulses of radiation, with pulses spread over a short time (a few ms between pulses) or even delivered in a single pulse (5). At such high dose rates, the assumption of independent histories can be maintained for physics interactions. For the chemical stage, where ROS can migrate distances comparable to the spatial separation between histories (several hundred nm) in the time taken to deliver a FLASH dose, which may be comparable to the chemical stage duration, the intertrack interactions have to be considered. The effect on chemical yields from the physical aspects of the time pulse, e.g., width, shape and radiation quality, can be studied using Monte Carlo track-structure simulations. In (16), the biophysical Monte Carlo code PARTRAC (17) was used to study the intertrack effect at the chemical stage between ion histories close in space and time, and its effect in DNA strand-break induction. The authors reported that the yield of chemical species (produced by protons of 20 MeV, alpha particles of 1 MeV and 20 MeV, and carbon ions of 60 MeV) can be affected when sufficient particle histories overlap (intertrack effect) and depends on both the spatial and time separation between histories; i.e., dose and dose rate. The intertrack effect in DNA damage is expected after several tens of Gray dose; according to Kreipl et al. (16), 50 Gy of deposited dose delivered simultaneously led to a reduction of approximately 8% in DNA clustered lesions with respect to no-intertrack for 20 MeV protons. However, in Kreipl et al. (16), the motivation for a comprehensive study for further radiation qualities appeared to be curtailed by the lack of the availability of clinical accelerators capable of delivering doses and dose rates higher than the typically used 2–5 Gy per fraction at ≤0.03 Gy/s. The current high interest in FLASH therapy, coupled with the ongoing development of treatment machines to reach FLASH dose rates covering a range of radiation qualities (18), clinical studies using microsecond (ms) pulses (19) and preclinical studies of treatment with ns and ms width pulses (5, 19, 20), further motivate the study of intertrack effects with particle pulses below ms width and for a wide variety of radiation qualities.
In this work, we present the method implemented for Monte Carlo track-structure simulations to include intertrack chemical reactions after radiolysis at pulsed, high dose rates. The calculation engine for the heterogeneous chemistry relies on the independent reaction time (IRT) method that was implemented in the TOPAS-nBio framework (21). The IRT implementation in TOPAS-nBio provides a computationally more efficient algorithm (by two orders of magnitude) than the step-by-step approach implemented in Geant4-DNA (22), which is similar to the method used by Kreipl et al. (16). The TOPAS-nBio IRT method was extended to allow the simulation of radiation pulses within the sub-millisecond (sub-ms) range. Squared pulses of several widths were simulated: 1 ns, 1 μs and 10 μs. The implementation was tested through verification of the behavior of radiolytic yields over a long time period (50 s), through the simulation of radiolysis in a Fricke dosimeter with comparison to published measured data. Finally, time-dependent and LET-dependent yields of •OH radicals and e−aq from protons delivered in time pulses of different sub-ms widths were calculated using IRT. The selection of these chemical species of high interest is justified since it has been shown that the •OH radical is responsible for the indirect damage to the DNA (2). On the other hand, e−aq is a highly reactive species with dissolved oxygen and is expected to contribute significantly to its depletion at early stages after the ionizing radiation interaction (8, 15).
MATERIALS AND METHODS
TOPAS-nBio Monte Carlo Tool
The TOPAS Monte Carlo tool (23) was specifically designed to provide a means for the medical physics community to harness the power of the general-purpose Monte Carlo toolkit Geant4 (24). The tool facilitates the use of Monte Carlo simulations of radiotherapy employing a text-based parameter control system, removing the barrier of requiring programming expertise. TOPAS-nBio (21) extends TOPAS to the nanometer scale, providing the same user-friendly parameter control system. Physics processes down to vibrational energies are provided via the Geant4-DNA Monte Carlo track-structure code (25–27). Variance reduction techniques are provided specifically for nanodosimetric applications (28). Multiple cells and sub-cellular geometries (29) can be combined to obtain DNA damage patterns that can be propagated using repair kinetic models to simulate the expected biological outcome (30, 31). TOPAS-nBio can be used with and without tracking of chemical species (32). Recently, the ability to follow chemical species using the IRT method was added, as described below.
In the study presented here, we used TOPAS-nBio version 1.0, with TOPAS version 3.2.p02, which is based on Geant4/Geant4-DNA version 10.5.p01. Unless otherwise indicated, the default TsEmDNAPhysics list was used for electron interactions. This physics module combines the following interaction models described in Incerti et al. (26) that have provided the more accurate comparison with experimental radiolytic yields among the provided Geant4-DNA models (21, 32, 33). For electrons, inelastic interactions are handled via the Born models (G4DNABornExcitationModel and G4DNABornIonisationModel), attachment and vibrational excitations are handled by Melton (G4DNAMeltonAttachmentModel) and Sanche (G4DNASancheExcitationModel), respectively; for elastic scattering the CPA100 approach is used (G4DNACPA100ElasticModel). Electrons are followed down to 11 eV where a one-step thermalization model using the Ritchie model is applied. The ionization process for protons is modeled using the Rudd method (G4DNARuddIonisationModel) up to 1 MeV and then the Born approximation (G4DNABornIonisationModel). For excitation events of protons, the Miller-Green formulation (G4DNAMillerGreenExcitationModel) is used up to 500 keV, followed by Born excitations above this value (G4DNABornExcitationModel). After the physical stage (occurring within the first 10−15 s after irradiation), the pre-chemical stage (occurring at 10−15–10−12 s after irradiation) is simulated using the same water dissociation channels and probabilities used by Geant4-DNA and reported elsewhere (22, 27, 33).
For simulations where the condensed history approach was employed, we used the Livermore physics list constructor (G4EmLivermorePhysics), which provides electromagnetic physics interactions in the range of 100 eV to 100 GeV for electrons.
IRT for Radiolysis Simulations
The IRT method (34–38) is an elegant Monte Carlo technique that allows the calculation of time-dependent radiolytic yields while avoiding the burden of following the step-by-step trajectory of the diffusive chemical species. Thus, this technique provides a much more efficient simulation compared to the step-by-step method. The IRT method relies on the independent pair approximation to perform the simulation of the reaction times between the chemical species created at the end of the pre-chemical stage. The reaction times are sampled from probability distribution functions that represent the solution to the interparticle diffusion equation (35, 37, 38). The sampled reaction times, between all possible pairs of reactive diffusive species, are assembled along with the pairs in an array following a combinatorial process. Subsequently, the array is sorted in ascending order, and the realization of reactions is sequentially performed by removing pairs with the shortest reaction times from the array. Any other remaining pairs in the array involving species belonging to an already removed pair is discarded. If reactive species are produced in a reaction, then, for each product, reaction times with the remaining unreacted species are sampled and merged into the array; after this process, the array is again sorted in ascending order (34). The IRT method is finished after all possible reactions are exhausted or when reaching a defined upper time cut, typically 1 μs, the end of the heterogeneous chemical stage. The accuracy of this technique to reproduce experimental radiolysis yields of radiation tracks interacting in liquid water has been studied extensively (39–46).
The IRT method was implemented in TOPAS-nBio using the molecules, reactions, reaction rate coefficients, and diffusion coefficients used by the RITRACKS software. These values are shown in Tables 1 to 6 described by Plante and Devroye (38).
TABLE 1.
Percentage Differences Caused by Intertrack in Pulses of Width Different from Zero
| Species | 1 ns | 1 μs | 10 μs |
|---|---|---|---|
| 1 MeV | |||
| •OH | 14.5% ± 0.6% | 11.3% ± 1.1% | 5.7% ± 0.9% |
| e−aq | 6.2% ± 0.3% | 22.3% ± 1.7% | 15.4% ± 1.2% |
| 100 MeV | |||
| •OH | 5.6% ± 0.3% | −8.6% ± 0.4% | −12.0% ± 0.4% |
| e−aq | 2.3% ± 0.2% | −6.1% ± 0.3% | −10.1% ± 0.4% |
Notes. G values of •OH and e−aq were obtained at t = W for both 1 MeV and 100 MeV protons. Errors are combined statistical uncertainty, one standard deviation.
Verification of Long Time-Scale Calculations: Electron Radiolysis of the Fricke Dosimeter
Given the width of the time pulses used in this work (discussed below in the section, Intertrack Considerations for the IRT Method to Simulate G Values from Particles Delivered in Sub-ms Time Pulses), the chemical stage needed to be simulated for long times, up to 1 ms. Beyond the end of the spur expansion at 0.1–1 μs (47), reactions between diffusive species and the background take over the primary role. To simulate reactions with the background, the continuum approach using time-independent rate coefficients (37) and the set of reactions from Table 6 in Plante and Devroye (38) were implemented. In this approach, species that comprise the background are assumed to be distributed uniformly with a given concentration. Then, diffusive species are assumed to react with the background species at time t with a probability of 1 – exp(–k[B] t), where k is the reaction rate coefficient and [B] is the concentration. The product k[B] is the scavenging capacity of the solution.
Validation of the TOPAS-nBio IRT implementation to perform long time-scale scenarios was performed by simulating the radiolysis occurring in the Fricke dosimeter (48). This dosimeter consists of an aerated solution of ferrous sulfate (FeSO4), and sulfuric acid (H2SO4) diluted in water. In the Fricke dosimeter, the rate of oxidation of ferrous ions (Fe2+) is proportional to the absorbed energy, fluence and radiation quality (49). It has been shown that sub-percentage dosimetric accuracy can be achieved under low-LET irradiation (50–52), making the Fricke dosimeter a suitable application to validate a Monte Carlo tool. When simulating this type of dosimeter, the effect of acidity introduced by H2SO4, which affects the ionic strength in all the reactions between ions, must be considered, especially at high concentrations of H3O+. These considerations were implemented in TOPAS-nBio following the detailed procedure reported elsewhere (45, 46, 53). The reactions and reaction rate coefficients, original and corrected values, added to TOPAS-nBio are shown in Appendix Tables A1, A2 and A3. The concentrations of the added compounds were 0.4 M of H2SO4 (pH 0.46), 5 mM of FeSO4, and 0.25 mM of O2. The standard Fricke dosimeter consists of 1 mM instead of 5 mM of FeSO4; however, to compare the time evolution of G(Fe3+) with data from Plante (46), 5 mM was selected. The Fenton-type reaction that was also included (last row in Appendix Table A1) required the simulation of the chemical stage up to 50 s (45, 46).
The simulation setup consisted of a homogenous cubic water phantom containing the Fricke solution with 100-μm sides irradiated with electrons. The source was an isotropic point source of electrons positioned at the center of the water phantom. In total, 5,000 histories were simulated, delivered at time zero but independent of each other. The energy spectrum of the source was obtained in a separate simulation with TOPAS using the condensed history Monte Carlo method. For that purpose, an isotropic 60Co point source, consisting of equal numbers of 1.17 and 1.33 MeV γ rays, was placed at the center of a water cube of 20-cm side. In total, 108 histories were simulated. The energy spectrum of secondary electrons set in motion by the gamma rays was obtained from a phase space file scored on a 5-cm radius sphere centered on the source. The sampled spectrum included a low proportion (<1 %) of energy values above 1 MeV, which is the upper limit of the Geant4-DNA models. If an electron with a primary energy higher than 1 MeV was sampled, the energy was set to 1 MeV. It has been previously shown that for electrons with initial energies above 100 keV, the change in radiation chemistry yields as a function of the energy is negligible (54).
In the Fricke dosimeter setup, given the range of primary electron energies and phantom dimensions, short-track segments are produced. Previously published studies have shown that the approach of using track-segments of monoenergetic electrons or protons, instead of 60Co γ rays, produced very good agreement with measured G values (32, 33, 39, 45, 46, 55).
Intertrack Considerations for the IRT Method to Simulate G Values from Particles Delivered in Sub-ms Time Pulses
In this work, the TOPAS-nBio IRT implementation was enhanced to allow the realization of reactions between chemical species initially created in different histories at different times. A history was defined as all the chemical species created at the end of the pre-chemical stage, triggered by the interaction of a primary charged particle and all its descendants with the media. Thus, an initial time tH was assigned to each new history. The time tH could be obtained in a random or deterministic fashion. If random, tH values were sampled from a uniform distribution function of a given width W, with values sampled within the range [1 ps, W + 1 ps). If deterministic, user-defined tH values were assigned to each history. The IRT method was then run after a specific number of histories was simulated, or after a prescribed dose was accumulated in a sensitive region from multiple histories. Subsequently, the G value (number of chemical species produced or lost per 100 eV of deposited energy) was obtained as a function of the time. For that, the number of all chemical species was normalized by the accumulated energy deposited from multiple histories at the corresponding sample time tH.
Intertrack interactions from different particle histories at the physical stage can be neglected because the subsequent histories were delayed by time lapses much larger than the duration of the physical stage (10−15 s), which was also pointed out by Kreipl et al. (16). On the other hand, multiple ionizations of the same water molecule (44) were not simulated because the cross section for that process was not available in Geant4-DNA. We previously showed that this affects the accuracy of H2O2 yields by 20–40% at LET values above 10 keV/μm for simulations based on Geant4-DNA, but does not significantly affect the accuracy for other chemical species (32).
The simulation setup consisted of two concentric cubic water phantoms of 20-μm and 5-μm sides, respectively, uniformly irradiated by protons. The smaller cube was the scoring region, and the larger cube ensured a contribution of backscattered electrons near the boundaries of the smaller cube. A monoenergetic proton source was uniformly distributed on the surface of the smaller cube. The initial energies ranged from 1–100 MeV, and the initial directions were randomly directed to the inner region of the smaller cube. This irradiation setting resembles the random directions of incidence on a cell nucleus (56). The chemical species created at the end of the pre-chemical stage within the scoring region were used as input of the IRT method, with the initial time of each history randomly sampled from a uniform distribution and assigned, as described above. The widths, W, of the time distributions were: 1 ns, 1 μs and 10 μs. The IRT method was initiated after a prescribed dose of 50 cGy was accumulated from multiple histories in the sensitive region. Finally, G values were obtained by averaging the results from 130 batches, the number of available CPUs, with independent random seeds. Point-to-point ratios with respect to reference simulations, i.e., simulations performed with independent histories, were obtained at times t1 = 1 μs and t2 =W + 10 μs. At the time t1, the end of the chemical stage for reference simulations was achieved. At the time t2, the end of the chemical stage for simulations using multiple histories was already ended.
RESULTS
Verification of Long-Time-Scale Simulations through the Fricke Dosimeter
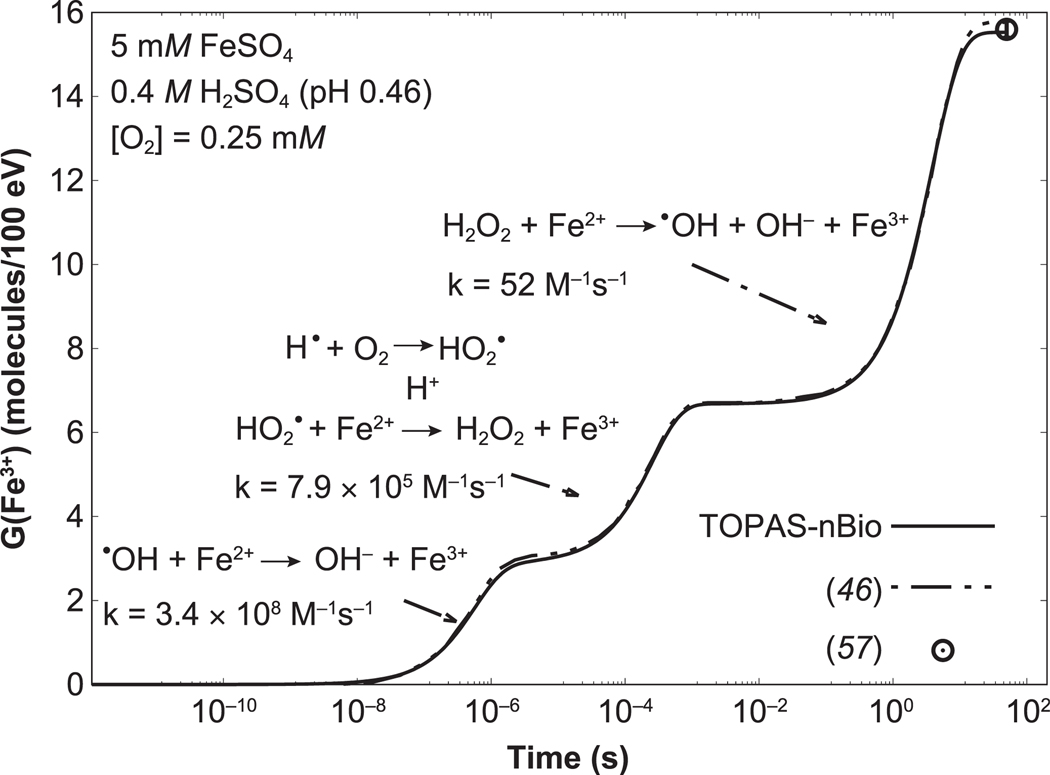
The time evolution of the G value of Fe3+ is shown in Fig. 1. The time evolution of the G value calculated with TOPAS-nBio is in reasonable agreement with published data (46), with a maximum difference of 0.2 molecules/100 eV at 50 s. At 50 s, the G value calculated with TOPAS-nBio was 15.5 ± 0.1 molecules/100 eV, which agrees with the accepted value for 60Co from ICRU Report 34 of 15.5 ± 0.2 molecules/100 eV (57).
FIG. 1.
Time evolution of the G value of Fe3+ from 60Co irradiation of a Fricke solution, calculated using TOPAS-nBio (solid line). The reactions between •OH, HO2•, and H2O2 with Fe2+ that leads to Fe3+, and their reaction rate coefficients, are also shown. The arrows indicate the time stages when these reactions contribute to the G value. Simulated data from Plante (46) and accepted measured value from ICRU Report 34 (57) for 60Co are shown as the dot-dashed line and the open circle, respectively.
Time-Dependent G Values from Particles Delivered in Time Pulses of Sub-ms Width
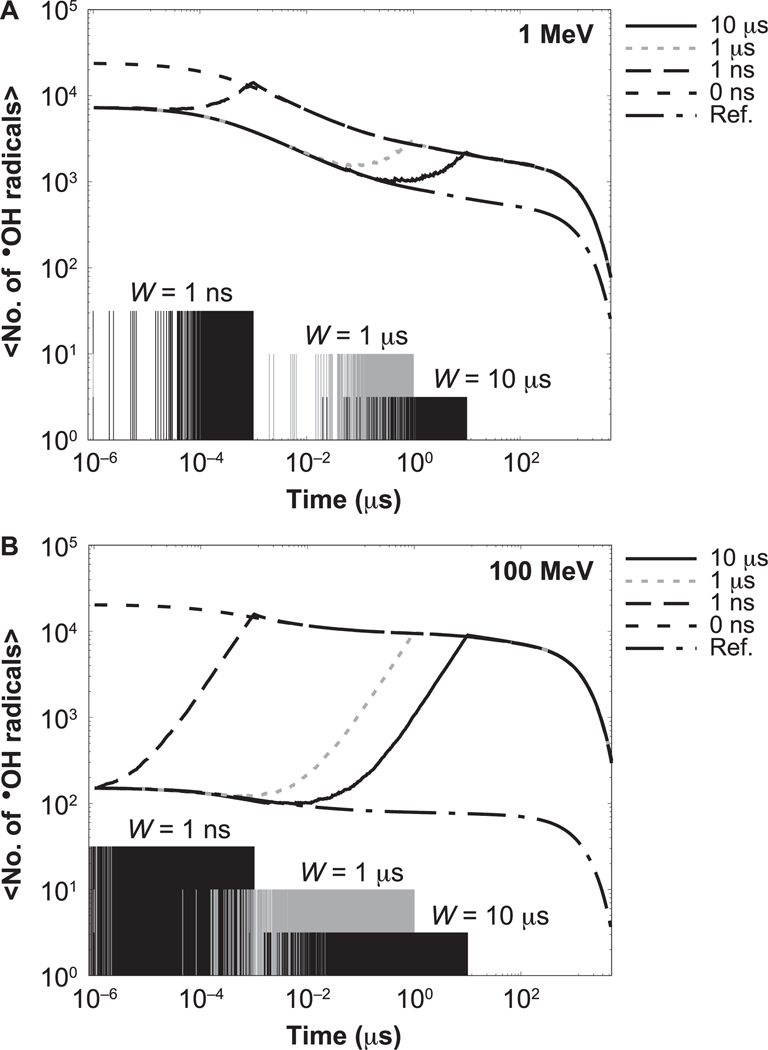
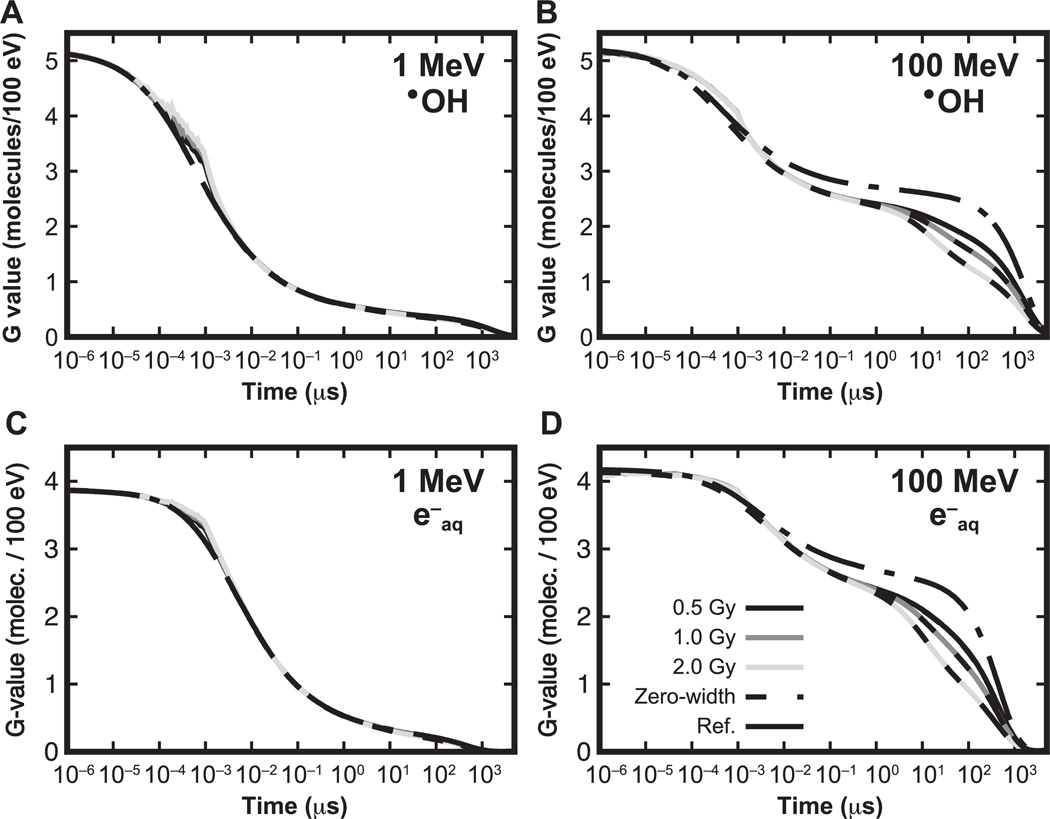
For the behavior of time-dependent yields, i.e., the number of chemical species existing at time t, results for the •OH radical from the highest-LET proton (1 MeV) and lowest-LET proton (100 MeV) are shown in Fig. 2. The behavior is similar for e−aq. Figure 2 shows the time evolution of the mean number of •OH radicals produced by a dose of 50 cGy. Results are shown for histories delivered randomly spaced in time, in pulses of different widths. Reference results from simulations using independent histories (with no intertrack chemistry) are also shown. The IRT simulations start at the beginning of the chemical stage of the first history at 1 ps. The distributions present the time evolution of the •OH radical yields after 1 ps. As shown, the time evolution of the number of existing •OH radicals increases over time from the initial reference value until coinciding with the number of •OH radicals produced with protons delivered in a zero-width pulse, due to the interaction of reactive molecules formed from subsequent histories delayed in time. The time each history is initiated is shown in the figure with vertical impulse lines. For intermediate LET values, the difference between reference simulations and zero-width pulse simulations varies in increasing order, increasing with the proton energy.
FIG. 2.
Time evolution of the mean number of •OH radicals for irradiations with 1 MeV (left) and 100 MeV (right) protons for a dose of 50 cGy. Results for different pulse widths are shown: 0 ns (dashed), 1 ns (long dashed), 1 μs (dotted) and 10 μs (solid). Reference results calculated with protons delivered independently of each other are indicated by dashed-dotted lines. The times when a new history was generated are shown with impulse lines at the bottom; different amplitudes are shown to distinguish each option.
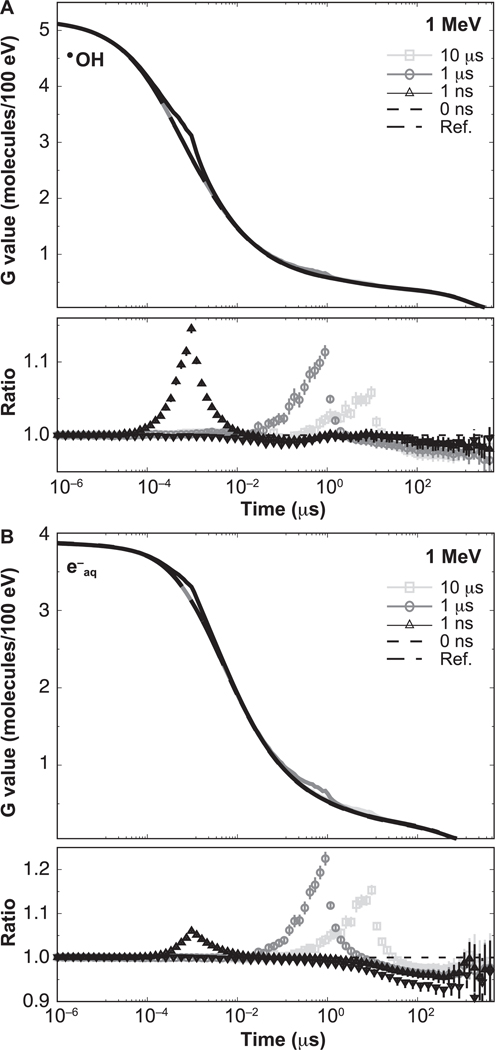
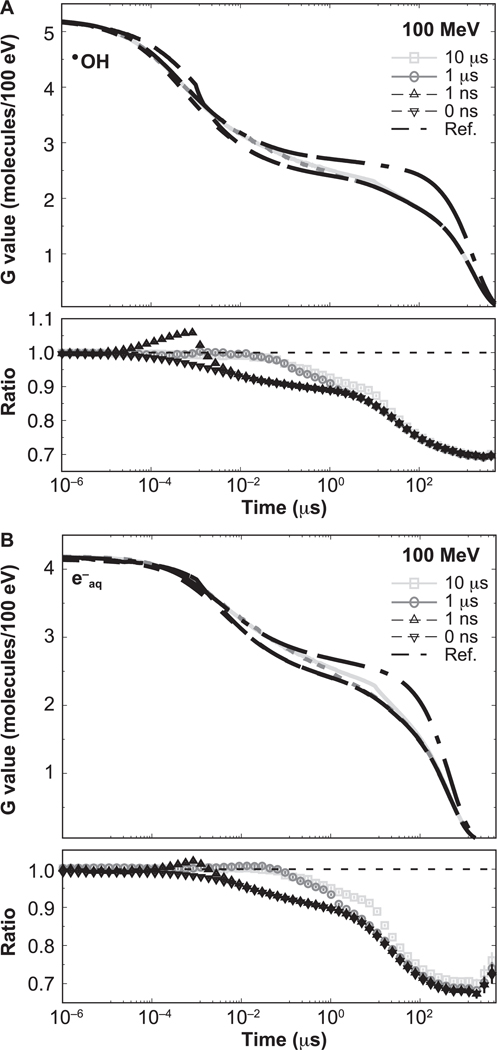
The time-dependent G values for •OH and e−aq produced by 1 MeV and 100 MeV protons are shown in Figs. 3 and 4, respectively, illustrating the effect on the G values at the ms scale for type VI reactions, as classified in (36): e−aq + H3O+ → H• and •OH + •OH− → O• − + H2O. For both figures, differences caused by the intertrack reactions are notable. The lower section of each figure panel shows the ratio with respect to the reference simulations (no intertrack reactions considered). For 1 MeV, the G values from zero-width pulse simulations were lower than the reference simulations by 1% in the entire time range. For pulses of non-zero width, the G values are increased by the contribution of delayed proton tracks until they reach a maximum at t = W, and eventually converge to the zero-width pulse results. At t = W, differences were significant, as shown in Table 1. For 100 MeV, there was an increasing difference between results from the zero-width pulse and the reference simulation. This difference reached −11.1% ± 0.4 % at 1 μs. For pulses with non-zero width, differences were significant but lower than for the zero-width pulse result; these are shown in Table 1.
FIG. 3.
Time-dependent G values from proton tracks of 1 MeV delivering a dose of 50 cGy with different pulse widths: 0 ns, 1 ns, 1 μs and 10 μs. Reference results are indicated by the dashed-dotted lines. Ratios with respect to the reference simulations are shown in the lower section of each panel. Error bars represent one standard deviation of the combined statistical uncertainty.
FIG. 4.
Time-dependent G values from proton tracks of 100 MeV delivering a dose of 50 cGy with different pulse widths: 0 ns, 1 ns, 1 μs and 10 μs. Reference results are indicated by the dashed-dotted lines. Ratios with respect to the reference simulations are shown in the lower section of each panel. Error bars represent one standard deviation of the combined statistical uncertainty.
LET-Dependent G Values from Particles Delivered in Time Pulses of Sub-ms Width
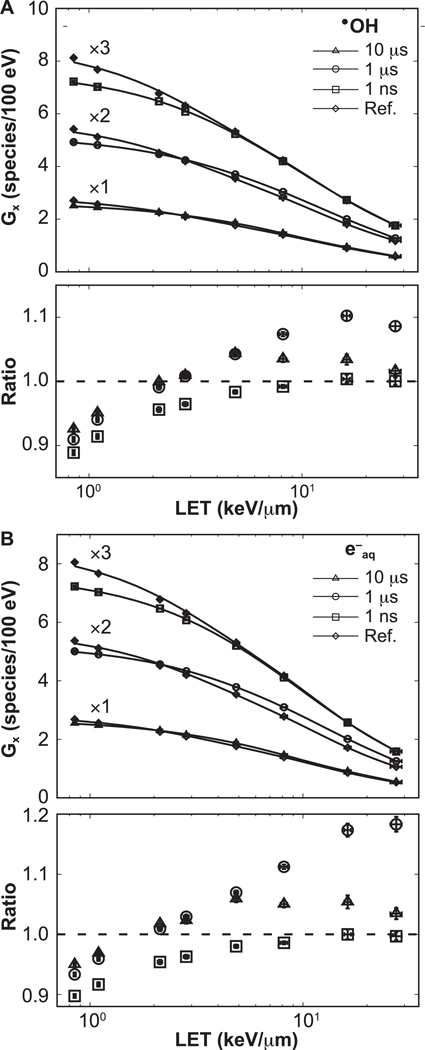
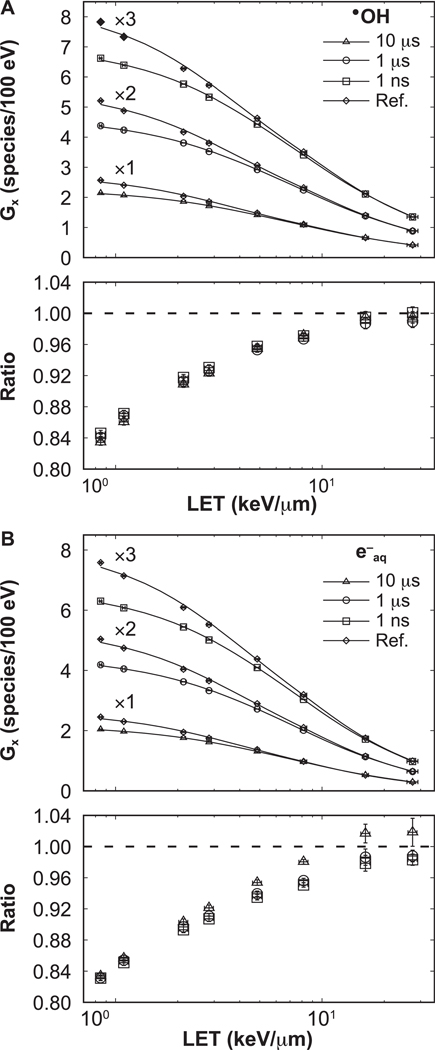
The LET-dependent G values obtained at t1 = 1 μs and at t2 = W + 10 μs are shown in Figs. 5 and 6, respectively. Statistical uncertainties were less than 1.2%, 1 standard deviation. The G values reproduce the expected behavior with increasing LET (32, 36, 46, 58). In the lower section of each panel, the ratios with respect to reference simulations are shown, with error bars representing the combined statistical uncertainties. Results for the 0-ns pulse width agreed within statistical uncertainty (1 standard deviation) to the 1-ns pulse width.
FIG. 5.
LET-dependent G values at t1 = 1 μs. The data for each option were scaled by factors of 1, 2, 3, as shown, for clarity. Connecting lines are added to guide the eye. Ratios with respect to the reference results are shown in the lower section of each panel. Ratios corresponding to 0 ns pulse width (not shown) agreed within statistical uncertainty with results from 1 ns pulse width. Error bars represent one standard deviation of the combined statistical uncertainties.
FIG. 6.
LET-dependent G values at t2 = W + 10 μs. The data for each option was scaled by factors of 1, 2, 3, as shown, for clarity. Connecting lines are added to guide the eye. Ratios with respect to the reference results are shown in the lower section of each panel. Ratios corresponding to 0 ns pulse width agreed within statistical uncertainty with results from 1 ns pulse width and, for clarity, are not displayed. Error bars represent one standard deviation of the combined statistical uncertainties.
At t1, the ratios for both 0-ns and 1-ns pulse widths gradually decrease with increasing proton energy, down to a ratio of 0.89 ± 0.01 and 0.90 ± 0.01, respectively. For the 1-μs pulse width, a transition point around 2 keV/μm exits where e−aq and •OH swap from being less than the reference simulations by 0.90 ± 0.01 and 0.93 ± 0.01 for •OH and e−aq, respectively, to exceed the reference simulations by 1.10 ± 0.01 and 1.18 ± 0.01 for •OH and e−aq, respectively. A similar behavior to that of the 1-μs pulse is seen for 10-μs pulses. There, ratios were down to 0.93 ± 0.01 and 0.95 ± 0.01 for •OH and e−aq below 2 keV/μm, respectively, and up to 1.04 ± 0.01 and 1.06 ± 0.01 above 2 keV/μm for •OH and e−aq, respectively.
At t2, the ratios increase monotonically with the LET for all pulse widths considered in this work. The ratios were increasing from 0.84 ± 0.01 and 0.83 ± 0.01 to reach unity within one statistical uncertainty (1.2%), for •OH and e−aq, respectively.
DISCUSSION
In this work, the TOPAS-nBio tool was extended to allow the simulation of intertrack effects and then demonstrated for proton tracks delivered in pulses of sub-ms width. Our focus on protons was due to our current interest in proton FLASH therapy. TOPAS-nBio may be just as easily used to simulate other particles in the future, including electrons and X rays.
Verification studies of the long-time behavior, up to 50 s, of G values were performed using the Fricke dosimeter simulation. By using the electron spectrum from 60Co γ rays in water, an agreement with the ICRU recommended value was found within the experimental error. Our simulation results had a statistical precision better than 0.7%. The calculated spectrum of secondary electrons set in motion by 60Co γ rays (1.17 and 1.33 MeV) in water had a mean energy of 0.43 MeV (root-mean-square of 0.25 MeV). Clinical linear accelerator (linac) X rays produce secondary electron energy spectra with higher mean energies. We used the 6-MV X rays of a Siemens Oncor™ linac (59) to calculate the electron spectrum in a 10 cm × 10 cm beam on water at 100 cm SSD in a 1 cm wide cubic voxel at 10 cm depth. The mean energy was 1.29 MeV (root-mean-square of 1.02 MeV). Pimblott and LaVerne (54) demonstrated that increasing the initial electron energy above 0.1 MeV had negligible effect on the decay kinetics of e−aq, •OH, and the formation of products. Thus, the calculation of G(Fe3+) presented in this work for 60Co irradiation is expected to be comparable to megavoltage photon irradiation.
G values were calculated as a function of time from 1 ps to 10 ms for a range of proton energies with pulse widths of 10 μs or less. The time-dependent yields evolve from the initial yield at 1 ps that is independent of particle flux, to eventually converge to results from simulations using particle tracks delivered simultaneously, i.e., pulses of zero width. Thus, the maximum change in the G value caused by intertrack effects is that induced by particles delivered in a pulse of zero width. This behavior was also seen in idealistic simulations in Kreipl et al. (16) using pairs of ions (protons, alpha or carbon ions) traveling simultaneously in a parallel direction and separated by a few nanometers. In this work, we extended that study to a scenario with a more realistic separation between proton tracks in space and time. Our study includes pulse widths larger than the 100-ns limit reported by Kriepl et al. (16). We have shown that the intertrack effect produces significant effects in the G values for a full range of pulse widths of 1 ns, 1 μs and 10 μs. These pulse widths are all clinically relevant. The 1-ns width has been reported in preclinical studies of FLASH proton treatment (20). The 1-μs width covers the reaction kinetics that occur within and beyond the duration of the chemical stage for a single track; the first patient treated with FLASH radiotherapy received 5.6 MeV electrons (~0.2 keV/μm) delivered in pulses of 1-μs width (19), and preclinical studies have reported pulses about 1.8-μs width (5). Finally, the 10-μs width covers times well beyond the chemical stage.
The effect of intertrack contributions on the time evolution of the G value is more prominent for particles of low LET. This can be explained as follows. Approximately 40-fold more tracks were needed in the simulations with 100-MeV protons (low LET) compared to 1-MeV protons (high LET) to deliver the same dose. This caused more proton histories in close proximity: for 50 cGy, the planar fluences were 0.13 protons/μm2 for 1 MeV and 5.34 protons/μm2 for 100 MeV protons. For low LET, the species from each individual history were sufficiently spread out to travel long distances without reacting. In contrast, for high-LET tracks the high density of chemical species created around the track core resulted in more local reactions, and then less reactants were available for intertrack reactions. Therefore, intertrack reactions were more likely to occur for low-LET irradiation, as shown in Fig. 6.
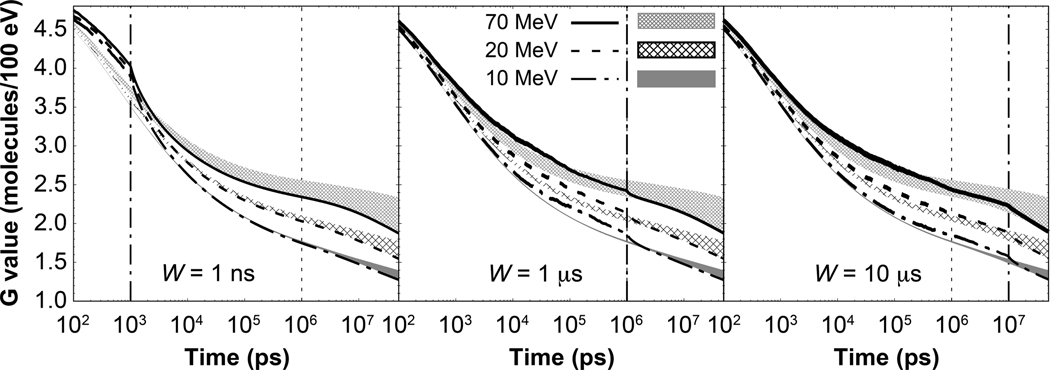
For pulse widths of 1 μs or more, the selection of t1 = 1 μs to report the LET-dependent G values led to a decrease in the G value when including intertrack effects at low LET, and an increase at high LET (Fig. 5). The selection of t1 follows the common practice of reporting G values at 1 μs. The behavior from Fig. 5 is explained as follows. Contrary to the results from G values produced by pulses of 1-ns width, for wider pulses, histories are still arriving and reactions are ongoing at 1 μs. This increases the G value, extending its convergence to the G value from a pulse of zero width to longer times (Fig. 7). Furthermore, the G value from a pulse of zero width equals the G value from the reference simulation at the highest LET values (see results for 10 MeV protons in Fig. 7). Therefore, at 1 μs, the ongoing reactions and arriving histories increase the G value, exceeding the G value from reference simulations at the highest LET values. Therefore, it is preferable to report the G value at longer times than 1 μs when proton pulses are considered.
FIG. 7.
Time-dependent G value for •OH radical for protons delivered in pulses of 1 ns, 1 μs and 10 μs widths at three energies, as shown. The shaded gap regions represent the gap between results from protons delivered in pulses of zero width (lower bound of the gap), and the reference results (upper bound of the gap). The vertical dotted-dashed lines show the time duration of the proton pulses, whereas the dotted line shows the time commonly used to report the G value at the end of the chemical stage in independent particle histories. Line width represents 1 standard deviation of statistical uncertainty.
Increasing the dose rate affects the G value for low-LET protons. FLASH dose rates delivered in a single pulse vary from 109 Gy/s of laser-accelerated protons used in preclinical studies (20), to 106 – 107 Gy/s used in clinical machines under investigation for clinical treatment (4, 19, 60) when delivering doses between 10–30 Gy (60). In the current study, we investigated the effect of dose rates delivered instantaneously (zero-width pulse), and at 5 × 108 Gy/s, 5 × 105 Gy/s, and 5 × 104 Gy/s. Figure 8 shows the effect between instantaneous pulses and pulses of 1-ns width when increasing the dose and, accordingly, the dose rate by a factor of two and four for the highest dose rate for 1 MeV and 100 MeV. The dose rate in this case exceeds that reported for clinical machines currently used in patient treatment (19). As shown, for each dose the G values match the results of the corresponding zero-width pulses (dotted lines) at longer times. At the highest dose rate used in this study, a higher dose may well result in reduced G values for •OH and e−aq at 100 MeV, the lowest LET, due to an increased number of intertrack contributions. However, for 1 MeV (highest LET), the fluence is too low to produce intertrack effects, as increasing the dose by a factor of four only represents a reduction in the proton track separation by a factor of two. The effect of increasing the dose, however, is negligible if the G values are reported at 1 μs.
FIG. 8.
G values as a function of the time for •OH and produced by 1 MeV and 100 MeV. A dose of 0.5 Gy, 1.0 Gy and 2.0 Gy was simulated within a pulse of 1 ns. For each dose, the corresponding zero-width pulse simulations are indicated by dashed lines. Reference simulations at 0.5 Gy, with no intertrack effects, are indicated by dotted-dashed lines.
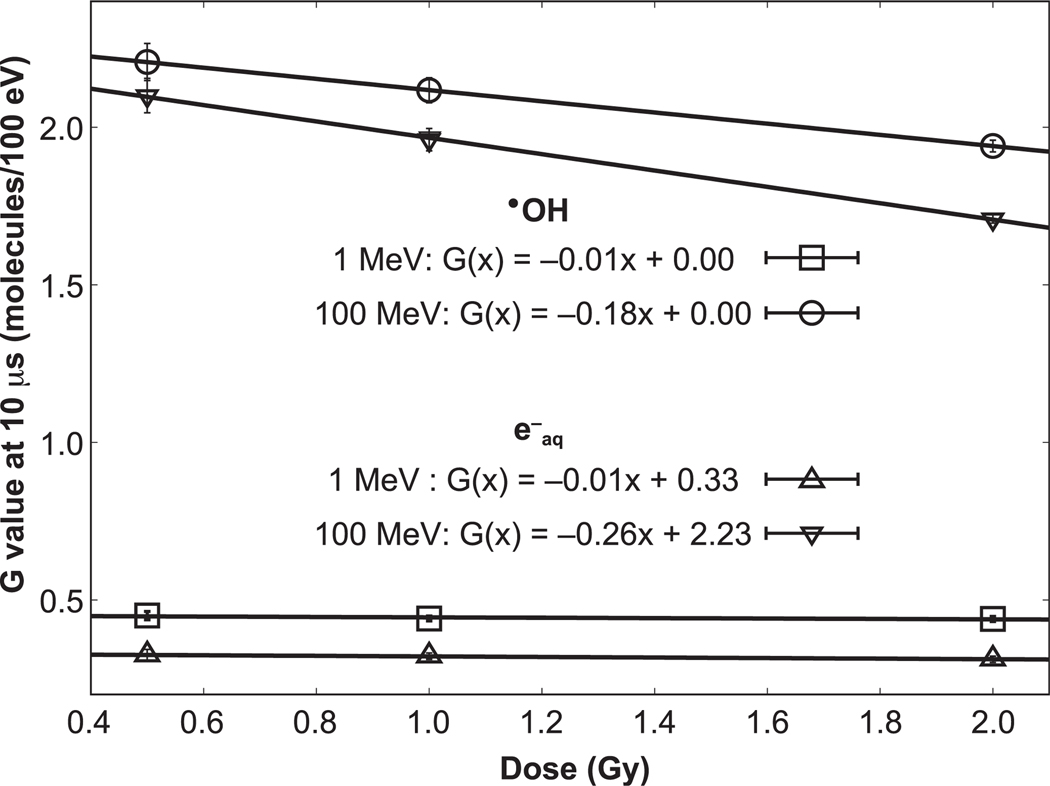
Most reported FLASH experiments have been conducted using doses above 10 Gy (60). If the FLASH effect is due to oxygen depletion in irradiated cells, the currently dominant theory in the field, then doses above ~8 Gy in low-oxygen cells are necessary to sufficiently deplete the oxygen (7). Figure 9 shows the linear interpolation between the G values at 10 μs for three doses/dose rates we simulated for •OH and e−aq. The figure clearly shows the importance of LET. For high-LET protons, intertrack reactions will likely also become relevant with sufficiently high doses, but as can be seen, the potential size of the effect is much smaller than for low-LET protons (or photons). This may become significant in FLASH proton therapy where the distal end of the treatment fields, which features high LET, is typically outside the target volume, potentially requiring a new strategy in treatment design, considering dose, dose rate and LET.
FIG. 9.
Linear fit to the change in G values at 10 μs for 100 MeV and 1 MeV protons for instantaneous dose delivery.
The results presented in this work correspond to the contribution of the intertrack events occurring in liquid water to the G values. Thus, their application to a biological environment should be taken with care. In a biological cell, the scavenging capacity has been estimated as approximately 3.4 × 108 s−1 (61). At such scavenging capacities, solvated electrons and hydroxyl radicals are consumed at times shorter than the duration of the FLASH pulses (62). A more detailed mechanistic simulation that takes into account the cellular environment entails incorporation of diffusion coefficients in the cell, reactions with organic radicals, and the reaction rate coefficients. The difficulty in collecting such parameters may be mitigated by establishing a limited time scale, which in turn, will permit a practical determination of the capabilities of tools that utilize the Monte Carlo method. In addition, Monte Carlo tools that include such parameters should be capable of performing intertrack reactions to provide a more realistic model, oriented to extend our knowledge of the FLASH effect from first principles.
CONCLUSIONS
We extended TOPAS-nBio to allow the simulation of the chemical stage considering intertrack contributions from different particle histories and the simulation of Fricke dosimetry. Our results show that intertrack reactions affect the G value of •OH and e−aq. The size of the effect depends on the particle LET, being more significant in the low-LET region. This was shown for setups considering protons delivered in realistic pulses of nanosecond, and microsecond widths. These results encourage the quantification of the intertrack effect on the biological damage when ultrashort pulses are used. Here we provide a tool to assist in this task in the TOPAS-nBio framework.
ACKNOWLEDGMENTS
Support for this work has been provided by UCSF School of Medicine bridge funding and, in part, by the National Institutes of Health/National Cancer Institute (NIH/NCI grant no. R01 CA187003: “TOPAS-nBio: A Monte Carlo tool for radiation biology research”), and the Damon Runyon-Rachleff Innovation Award (no. DRR 57-19). Additional support was provided by Consejo Nacional de Ciencia y Tecnología (CONACyT; for NDK).
APPENDIX
Tables A1–A3 show the reactions and reaction rates, original and corrected due to the presence of H2SO4 solutions for Fricke dosimeter simulations. Original values were obtained from Autosavapromporn et al. (45), and Plante and Devroye (38). Corrected values were automatically calculated using TOPAS-nBio by following the methodology detailed in this work.
TABLE A1.
Reactions, and Reaction Rate Constants Added to TOPAS-nBio to Simulate the Radiolysis in the Fricke Dosimeter
| Reaction | Reaction rate constant (M−1 s−1) |
|---|---|
| •OH + → H2O + | 1.5 × 105 |
| H + → | 1.0 × 1010 |
| H2O2 + → HO2 + | 1.2 × 107 |
| OH− + → •OH + | 8.3 × 107 |
| + → | 4.4 × 108 |
| + Fe2+ → Fe3+ + | 2.79 × 108 |
| + → + | 1.2 × 1010 |
| H + → + | 2.5 × 107 |
| Fe2+ + •OH → Fe3+ + •OH− | 3.4 × 108 |
| Fe2+ + HO2 → Fe3+ + | 7.9 × 105 |
| Fe2+ + H2O2 → Fe3+ + •OH + OH− | 52 |
TABLE A2.
Reactions from TOPAS-nBio with Corrected Reaction Rate Constant for Ionic Strength Given 0.4 M H2SO4 Solution and 5 mM FeSO4 Solution
| Reaction | Original reaction rate constant (M−1 s−1) | Corrected reaction rate constant (M−1 s−1) |
|---|---|---|
| + H+ → H | 2.11 × 1010 | 1.12 × 1010 |
| O− + OH− + OH− | 2.31 × 1010 | 4.35 × 1010 |
| + O− → H2O2 + OH− + OH− | 1.29 × 1010 | 2.43 × 1010 |
| + → O− + OH− | 3.51 × 109 | 6.61 × 109 |
| + → + | 1.2 × 1010 | 4.25 × 1010 |
| H+ + + H2O2 | 5 × 1010 | 2.65 × 1010 |
| H+ + OH− → H2O | 1.18 × 1010 | 6.26 × 1010 |
| H+ + O− → •OH | 4.78 × 1010 | 2.53 × 1010 |
| H+ + → OH + O2 | 9 × 1010 | 4.77 × 1010 |
| H+ + → HO2 | 4.78 × 1010 | 2.53 × 1010 |
| + O− → O2 + OH− + OH− | 6 × 108 | 1.13 × 109 |
| + O− → + OH− | 3.5 × 108 | 6.59 × 108 |
| O− + O− → H2O2 + OH− + OH− | 1 × 108 | 1.88 × 108 |
| O− + → + | 7 × 108 | 1.31 × 109 |
| OH− + → OH + | 8.3 × 107 | 1.56 × 108 |
| + → | 4.4 × 108 | 8.28 × 108 |
TABLE A3.
Reactions from TOPAS-nBio with corrected scavenging capacity for 0.4 M H2SO4 and 5 mM FeSO4 solution.
| Reaction | Original scavenging capacity (s−1) | Corrected scavenging capacity (s−1) |
|---|---|---|
| •OH + OH− → O− + H2O | 624 | 1.52 × 10−4 |
| H2O2 + OH− → + H2O | 46.6 | 1.15 × 10−5 |
| HO2 + OH− → + H2O | 624 | 1.52 × 10−4 |
| + H+ → H | 2.09 × 103 | 4.54 × 109 |
| + H+ → H2O2 + H2O | 4.98 × 103 | 1.08 × 1010 |
| OH− + H+ → H2O | 1.11 × 104 | 2.41 × 1010 |
| O− + H+ → OH• | 4.73 × 103 | 1.02 × 1010 |
| + H+ → HO2 | 4.73 × 103 | 1.02 × 1010 |
| + H+ → OH + O2 | 8.91 × 103 | 1.93 × 1010 |
| OH + → + H2O | 1.5 × 105 | 5.85 × 104 |
| + OH− → OH + | 8.3 | 3.81 × 10−6 |
| + Fe2+ → Fe3+ + | 2.79 × 105 | 7.85 × 104 |
REFERENCES
- 1.Sanguanmith S, Muroya Y, Meesungnoen J, Lin M, Katsumura Y, Mirsaleh Kohan L, et al. Low-linear energy transfer radiolysis of liquid water at elevated temperatures up to 350°C: Monte-Carlo simulations. Chem Phys Lett 2011; 508:224–30. [Google Scholar]
- 2.von Sonntag C. Free-radical-induced DNA damage and its repair. Berlin, Heidelberg, Germany: Springer-Verlag; 2006. [Google Scholar]
- 3.Favaudon V, Fouillade C, Vozenin M-C. Ultrahigh dose-rate, “flash” irradiation minimizes the side-effects of radiotherapy. (Article in French) Cancer Radiother 2015; 19:526–31. [DOI] [PubMed] [Google Scholar]
- 4.Vozenin M-C, Hendry JH, Limoli CL. Biological benefits of ultra-high dose rate FLASH radiotherapy: Sleeping Beauty awoken. Clin Oncol 2019; 31:407–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Montay-Gruel P, Petersson K, Jaccard M, Boivin G, Germond JF, Petit B, et al. Irradiation in a flash: Unique sparing of memory in mice after whole brain irradiation with dose rates above 100 Gy/s. Radiother Oncol 2017; 124:365–9. [DOI] [PubMed] [Google Scholar]
- 6.Vozenin MC, De Fornel P, Petersson K, Favaudon V, Jaccard M, Germond JF, et al. The advantage of FLASH radiotherapy confirmed in mini-pig and cat-cancer patients. Clin Cancer Res 2019; 25:35–42. [DOI] [PubMed] [Google Scholar]
- 7.Hendry J. Taking care with FLASH radiation therapy. Int J Radiat Oncol 2020; 107:239–42. [DOI] [PubMed] [Google Scholar]
- 8.Spitz DR, Buettner GR, Petronek MS, St-Aubin JJ, Flynn RT, Waldron TJ, et al. An integrated physico-chemical approach for explaining the differential impact of FLASH versus conventional dose rate irradiation on cancer and normal tissue responses. Radiother Oncol 2019; 139:23–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kozin S V, Zolotov VA, Ponomareva NA. Hypoxic proton radiotherapy of solid Ehrlich tumors with different dose magnitudes. (Article in Russian) Med Radiol (Mosk) 1984; 29:27–33. [PubMed] [Google Scholar]
- 10.Hornsey S, Alper T. Unexpected dose-rate effect in the killing of mice by radiation. Nature 1966; 210:212–3. [DOI] [PubMed] [Google Scholar]
- 11.Weiss H. An equation for predicting the surviving fraction of cells irradiated with single pulses delivered at ultra-high dose rates. Radiat Res 1972; 50:441. [PubMed] [Google Scholar]
- 12.Pratx G, Kapp DS. A computational model of radiolytic oxygen depletion during FLASH irradiation and its effect on the oxygen enhancement ratio. Phys Med Biol 2019; 64:185005. [DOI] [PubMed] [Google Scholar]
- 13.Petersson K, Adrian G, Butterworth K, McMahon SJ. A quantitative analysis of the role of oxygen tension in FLASH radiation therapy. Int J Radiat Oncol 2020; 107:539–47. [DOI] [PubMed] [Google Scholar]
- 14.Colliaux A, Gervais B, Rodriguez-Lafrasse C, Beuve M. Simulation of ion-induced water radiolysis in different conditions of oxygenation. Nucl Instrum Methods Phys Res B 2015; 365:596–605. [Google Scholar]
- 15.Boscolo D, Krämer M, Fuss MC, Durante M, Scifoni E. Impact of target oxygenation on the chemical track evolution of ion and electron radiation. Int J Mol Sci 2020; 21:424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kreipl MS, Friedland W, Paretzke HG. Interaction of ion tracks in spatial and temporal proximity. Radiat Environ Biophys 2009; 48:349–59. [DOI] [PubMed] [Google Scholar]
- 17.Dingfelder M, Hantke D, Inokuti M, Paretzke HG. Electron inelastic-scattering cross sections in liquid water. Radiat Phys Chem 1999; 53:1–18. [Google Scholar]
- 18.van de Water S, Safai S, Schippers JM, Weber DC, Lomax AJ. Towards FLASH proton therapy: the impact of treatment planning and machine characteristics on achievable dose rates. Acta Oncol 2019; 58:1463–9. [DOI] [PubMed] [Google Scholar]
- 19.Bourhis J, Sozzi WJ, Jorge PG, Gaide O, Bailat C, Duclos F, et al. Treatment of a first patient with FLASH-radiotherapy. Radiother Oncol 2019; 139:18–22. [DOI] [PubMed] [Google Scholar]
- 20.Zlobinskaya O, Siebenwirth C, Greubel C, Hable V, Hertenberger R, Humble N, et al. The effects of ultra-high dose rate proton irradiation on growth delay in the treatment of human tumor xenografts in nude mice. Radiat Res 2014; 181:177–83. [DOI] [PubMed] [Google Scholar]
- 21.Schuemann J, McNamara AL, Ramos-Mendez J, Perl J, Held KD, Paganetti H, et al. TOPAS-nBio: An extension to the TOPAS Simulation Toolkit for cellular and sub-cellular radiobiology. Radiat Res 2018; 191:125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Karamitros M, Mantero A, Incerti S, Friedland W, Baldacchino G, Barberet P, et al. Modeling radiation chemistry in the Geant4 Toolkit. Prog Nucl Sci Technol 2011; 2:503–8. [Google Scholar]
- 23.Perl J, Shin J, Schumann J, Faddegon B, Paganetti H. TOPAS: An innovative proton Monte Carlo platform for research and clinical applications. Med Phys 2012; 39:6818–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Agostinelli S, Allison J, Amako K, Apostolakis J, Araujo H, Arce P, et al. GEANT4 – A simulation toolkit. Nucl Instrum Methods Phys Res A 2003; 506:250–303. [Google Scholar]
- 25.Incerti S, Ivanchenko A, Karamitros M, Mantero A, Moretto P, Tran HN, et al. Comparison of GEANT4 very low energy cross section models with experimental data in water. Med Phys 2010; 37:4692–708. [DOI] [PubMed] [Google Scholar]
- 26.Incerti S, Kyriakou I, Bernal MA, Bordage MC, Francis Z, Guatelli S, et al. Geant4-DNA example applications for track structure simulations in liquid water: A report from the Geant4-DNA Project. Med Phys 2018; 45:e722–39. [DOI] [PubMed] [Google Scholar]
- 27.Bernal MA, Bordage MC, Brown JMC, Davídkova M, Delage E, El Bitar Z, et al. Track structure modeling in liquid water: A review of the Geant4-DNA very low energy extension of the Geant4 Monte Carlo simulation toolkit. Phys Med 2015; 31:861–74. [DOI] [PubMed] [Google Scholar]
- 28.Ramos-Mendez J, Schuemann J, Incerti S, Paganetti H, Schulte R, Faddegon B. Flagged uniform particle splitting for variance reduction in proton and carbon ion track-structure simulations. Phys Med Biol 2017; 62:5908–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.McNamara AL, Ramos-Méndez J, Perl J, Held K, Dominguez N, Moreno E, et al. Geometrical structures for radiation biology research as implemented in the TOPAS-nBio toolkit. Phys Med Biol 2018; 63:175018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.McMahon SJ, McNamara AL, Schuemann J, Paganetti H, Prise KM. A general mechanistic model enables predictions of the biological effectiveness of different qualities of radiation. Sci Rep 2017; 7:1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Henthorn NT, Warmenhoven JW, Sotiropoulos M, Mackay RI, Kirkby NF, Kirkby KJ, et al. In silico non-homologous end joining following ion induced DNA double strand breaks predicts that repair fidelity depends on break density. Sci Rep 2018; 8:1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ramos-Mendez J, Perl J, Schuemann J, McNamara A, Paganetti H, Faddegon B. Monte Carlo simulation of chemistry following radiolysis with TOPAS-nBio. Phys Med Biol 2018; 63:105014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shin W-G, Ramos-Mendez J, Faddegon B, Tran HN, Villagrasa C, Perrot Y, et al. Evaluation of the influence of physical and chemical parameters on water radiolysis simulations under MeV electron irradiation using Geant4-DNA. J Appl Phys 2019; 126:114301. [Google Scholar]
- 34.Clifford P, Green NJB, Oldfield MJ, Pilling MJ, Pimblott SM. Stochastic models of multi-species kinetics in radiation-induced spurs. J Chem Soc, Faraday Trans 1. 1986; 82:2673–89. [Google Scholar]
- 35.Green NJB, Pilling MJ, Pimblott SM, Clifford P. Stochastic modeling of fast kinetics in a radiation track. J Phys Chem 1990; 94:251–8. [Google Scholar]
- 36.Frongillo Y, Goulet T, Fraser M-J, Cobut V, Patau JP, Jay-Gerin J-P. Monte Carlo simulation of fast electron and proton tracks in liquid water. II. Nonhomogeneous chemistry. Radiat Phys Chem 1998; 51:245–54. [Google Scholar]
- 37.Pimblott SM, Pilling MJ, Green NJB. Stochastic models of spur kinetics in water. Int J Radiat Appl Instrument Part C. 1991; 37:377–88. [Google Scholar]
- 38.Plante I, Devroye L. Considerations for the independent reaction times and step-by-step methods for radiation chemistry simulations. Radiat Phys Chem 2017;139(September 2016):157–72. [Google Scholar]
- 39.Pimblott SM, LaVerne JA, Bartels DM, Jonah CD. Reconciliation of Transient Absorption and Chemically Scavenged Yields of the Hydrated Electron in Radiolysis. J Phys Chem 1996; 100:9412–5. [Google Scholar]
- 40.Pimblott SM, Laverne JA. Stochastic simulation of the electron radiolysis of water and aqueous solutions. J Phys Chem 1997; 101:5828–38. [Google Scholar]
- 41.Goulet T, Fraser M-J, Frongillo Y, Jay-Gerin J-P. On the validity of the independent reaction times approximation for the description of the nonhomogeneous kinetics of liquid water radiolysis. Radiat Phys Chem 1998; 51:85–91. [Google Scholar]
- 42.Herve du Penhoat M-A, Meesungnoen J, Goulet T, Filali-Mouhim A, Mankhetkorn S, Jay-Gerin J-P. Linear-energy-transfer effects on the radiolysis of liquid water at temperatures up to 300°C – a Monte-Carlo study. Chem Phys Lett 2001; 341:135–43. [Google Scholar]
- 43.LaVerne JA, Stefanic I, Pimblott SM. Hydrated electron yields in the heavy ion radiolysis of water. J Phys Chem A 2005; 109:9393–401. [DOI] [PubMed] [Google Scholar]
- 44.Meesungnoen J, Jay-Gerin J-P. Effect of multiple ionization on the yield of H2O2 produced in the radiolysis of aqueous 0.4 M H2SO4 solutions by high-LET 12C6+ and 20Ne9+ ions. Radiat Res 2005; 164:688–94. [DOI] [PubMed] [Google Scholar]
- 45.Autsavapromporn N, Meesungnoen J, Plante I, Jay-Gerin J-P. Monte Carlo simulation study of the effects of acidity and LET on the primary free-radical and molecular yields of water radiolysis – Application to the Fricke dosimeter. Can J Chem 2007; 85:214–29. [Google Scholar]
- 46.Plante I. A Monte-Carlo step-by-step simulation code of the non-homogeneous chemistry of the radiolysis of water and aqueous solutions-Part II: Calculation of radiolytic yields under different conditions of LET, pH, and temperature. Radiat Environ Biophys 2011; 50:405–15. [DOI] [PubMed] [Google Scholar]
- 47.Sanguanmith S, Meesungnoen J, Muroya Y, Lin M, Katsumura Y, Jay-Gerin JP. On the spur lifetime and its temperature dependence in the low linear energy transfer radiolysis of water. Phys Chem Chem Phys 2012; 14:16731–6. [DOI] [PubMed] [Google Scholar]
- 48.Fricke H, Morse S. The chemical action of roentgen rays on dilute ferrous sulfate solutions as a meausre of dose. Am J Roetgenol Radium Ther 1927; 18:430–2. [Google Scholar]
- 49.Allen AO. Hugo Fricke and the development of radiation chemistry: A perspective view. Radiat Res 1962; 17:254. [Google Scholar]
- 50.Shortt KR. The temperature dependence of G(Fe3+) for the Fricke dosemeter. Phys Med Biol 1989; 34:1923–6. [Google Scholar]
- 51.Ross CK, Klassen NV, Shortt KR, Smith GD. A direct comparison of water calorimetry and Fricke dosimetry. Phys Med Biol 1989; 34:23–42. [DOI] [PubMed] [Google Scholar]
- 52.Klassen NV, Shortt KR, Seuntjens J, Ross CK. Fricke dosimetry: the difference between G (Fe 3+) for 60 Co gamma-rays and high-energy x-rays. Phys Med Biol 1999; 44:1609–24. [DOI] [PubMed] [Google Scholar]
- 53.Meesat R, Sanguanmith S, Meesungnoen J, Lepage M, Khalil A, Jay-Gerin J-P. Utilization of the ferrous sulfate (Fricke) dosimeter for evaluating the radioprotective potential of cystamine: Experiment and Monte Carlo simulation. Radiat Res 2012; 177:813–26. [DOI] [PubMed] [Google Scholar]
- 54.Pimblott SM, LaVerne JA. Effect of electron energy on the radiation chemistry of liquid water. Radiat Res 1998; 150:159–69. [PubMed] [Google Scholar]
- 55.Uehara S, Nikjoo H. Monte Carlo simulation of water radiolysis for low-energy charged particles. J Radiat Res 2006; 47:69–81. [DOI] [PubMed] [Google Scholar]
- 56.Zhu H, McNamara AL, McMahon SJ, Ramos-Mendez J, Henthorn NT, Faddegon B, et al. Cellular response to proton irradiation: A simulation study with TOPAS-nBio. Radiat Res 2020; 194:9–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Boag JW, Epp E, Fielden EM, Parker RP. ICRU Report 34. The dosimetry of pulsed radiation. J Int Comm Radiat Units Meas 1982; os18. [Google Scholar]
- 58.Kreipl MS, Friedland W, Paretzke HG. Time- and space-resolved Monte Carlo study of water radiolysis for photon, electron and ion irradiation. Radiat Environ Biophys 2009; 48:11–20. [DOI] [PubMed] [Google Scholar]
- 59.Sawkey D, Faddegon BA. Simulation of large x-ray fields using independently measured source and geometry details. Med Phys 2009; 36:5622–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Wilson JD, Hammond EM, Higgins GS, Petersson K. Ultra-high dose rate (FLASH) radiotherapy: Silver bullet or fool’s gold? Front Oncol 2020; 9:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Michaels HB, Hunt JW. A model for radiation damage in cells by direct effect and by indirect effect: A radiation chemistry approach. Radiat Res 1978; 74:23–24. [PubMed] [Google Scholar]
- 62.Wardman P. Radiotherapy using high-intensity pulsed radiation beams (FLASH): A radiation-chemical perspective. Radiat Res 2020; Epub ahead of print. [DOI] [PubMed] [Google Scholar]