Enhancer Predictions and Genome-Wide Regulatory Circuits

Abstract

Spatiotemporal control of gene expression during development requires orchestrated activities of numerous enhancers, which are cis-regulatory DNA sequences that, when bound by transcription factors (TFs), support selective activation or repression of associated genes. Proper activation of enhancers is critical during embryonic development, adult tissue homeostasis, and regeneration; and inappropriate enhancer activity is often associated with pathological conditions such as cancer. Multiple Consortia (e.g., ENCODE, Roadmap) and independent investigators have mapped putative regulatory regions in a large number of cell types and tissues, but the sequence determinants of cell specific enhancers are not yet fully understood. Machine learning approaches trained on large sets of these regulatory regions can identify core TF binding sites and generate quantitative predictions of enhancer activity and the impact of sequence variants on activity. Here, we review these computational methods in the context of enhancer prediction and gene regulatory network models specifying cell fate.

Enhancers in Development and Human Disease

Most of our understanding of the function of enhancers comes from developmental biology or studies of the genetics of human disease. Human traits typically have a hereditary component, but demonstrate complex patterns of inheritance. Genome wide association studies (GWAS) have been widely used to identify complex trait loci and have identified more than 25,000 single nucleotide polymorphisms (SNPs) that are significantly associated with variation in >700 traits and diseases(70). Although GWAS can still only explain a small fraction of the phenotypic variance(47), the list of validated regulatory mutations responsible for heritable susceptibility to diseases is growing at a steady rate. The significant role of regulatory variation in complex trait heritability is underscored by the finding that the vast majority of the trait associated SNPs are non-exonic(46) and occur within putative regulatory elements far more often than expected by chance(28, 48). This suggests that disruption of regulatory function is a common mechanism by which noncoding sequence variants contribute to human disease. When a regulatory variant is identified, it is often hypothesized that the variant disrupts a TF binding site, creates a new binding site, or both. In a recently elucidated example, the common SNP rs339331 was shown by GWAS to increase prostate cancer risk(64) (odds ratio=1.22, p=1.6x10⁻¹²). Taipale and Wei et al. dissected this locus and showed that the risk SNP allele TTTTATGAG is bound by HOXB13, while the protective allele TTTCATGAG is not bound by HOXB13. This particular TF, in combination with FOXA1 and AR, activates RFX6 and promotes cell migration and metastatic disease(30). Since typically ~50 SNPs are in tight LD with each GWAS associated variant, similar detailed experimentation will be required to identify causal variants within disease associated loci, but only a small number of these loci have yet been studied in detail. A long standing problem encountered when attempting to generalize known binding site disruptions is that the biological consequences of variation in a specific binding site is strongly dependent on both cell type and the neighboring local sequence context, which defines the combinatorial TF interactions with cell-specific cofactors. Because most TF binding sites are short and degenerate, there are usually thousands of what appear to be very good binding sites in the genome, yet only a fraction of these are occupied in a given cell type.(7) Mutation of a binding site will only have a functional consequence in an occupied site. Therefore, the combinatorial code which determines cell-specific TF occupancy will determine which variants can alter regulatory element activity. Several computational methods have shown promise in detecting and quantitatively assessing the impact of variants in enhancers, by training on uniformly processed genome wide epigenomic datasets generated by ENCODE and Roadmap consortia. (18, 58, 73)

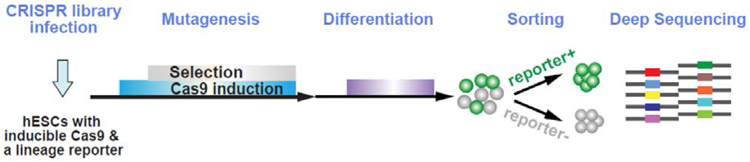
In the context of embryonic development, multicellular organisms require cells to make fate decisions by integrating extracellular cues ranging from biochemical to mechanical signals. We now have a sophisticated understanding of how extracellular inputs, especially signaling molecules such as SHH or TGFβ, are transduced intracellularly, and ultimately activate a relatively small set of TFs that play pivotal roles in cell fate determination. For instance, Nodal/TGFβ signaling is required for specifying definitive endoderm (DE) differentiation in gastrulating mouse and zebrafish embryos (2, 13, 19, 59), a process that has been recapitulated using human and mouse embryonic stem cells (hESCs, mESCs) through directed differentiation (16, 36). Nodal/TGFβ signaling activates the SMAD2/3/4 TFs, which then cooperate with key lineage TFs including FOXH1, EOMES, MIXL1, and GATA6 to activate the DE transcriptional program (43, 45, 54, 65, 68). Indeed, all of these core TF genes (FOXH1, EOMES, MIXL1, GATA6, SMAD2 and SMAD4), along with additional new regulators, were uncovered in our pooled, genome-scale CRISPR/Cas loss-of-function screens for genes that are required for DE differentiation from hESCs, as shown in Fig 1(43). We used the ESC-DE differentiation system to interrogate DNA elements in the regulatory network which controls induction of hESCs into endoderm (definitive endoderm, DE), induced in our system by TGF-β and Wnt signaling. DE differentiation is triggered when hESCs are treated with CHIR-99021 and Activin A (Fig. 1). A SOX17/GFP transgene reports the DE fate(33), assessed by flow cytometry. To detect regulators of this process, we infected iCas9 SOX17/GFP+ cells with the human GeCKO v2 gRNA library.

Figure 1. Overview of the in situ perturbation screening strategy to uncover core regulators based on lineage reporters.

After selection for cells with viral integration and induction of Cas9 expression, DE differentiation was performed and SOX17/GFP+ DE and SOX17/GFP− non-DE cells were isolated by FACS. The abundance of individual gRNAs in each population was determined by high-throughput sequencing: gRNAs that target positive or negative regulators of endoderm specification should be depleted or enriched, respectively, in SOX17/GFP+ compared to SOX17/GFP− cells. A Z-score was calculated for each gRNA based on the ratio of gRNA reads in the populations. The top 20 hits included almost all non-redundant, cell-autonomous required genes in the Nodal pathway (ACVR1B, SMAD2, and FOXH1)(59), as well as established DE TFs EOMES and MIXL1(76). TFs required to maintain the ESC state can also be screened by sequencing the pool of gRNAs enriched in self-renewing conditions.

However, there is a major gap in our knowledge about how TFs control the gene regulatory networks that dictate cell fate decisions. We often know which TF(s) are required for the acquisition or maintenance of a cell state during development, but the exact cascade of molecular events that either drives the cell state transition or stabilizes the cell state is unclear. Genomic data such as ChIP-seq can provide rich information regarding the chromatin association of a TF, and knockout studies can identify genes with altered expression levels when the TF is deleted. However, these experiments may not indicate direct transcriptional consequences. There are two challenges to establish causality of the TF binding and gene expression changes relevant to cell fate determination. First, a TF (e.g. TF-A) usually has multiple binding sites near a gene of interest (e.g. gene-X). Thus, even if the deletion of TF-A causes a change of gene-X expression, the impact (if any) of individual TF-A binding site on the control of gene-X expression is typically unknown. Second, differentiation involves a cascade of molecular events, so it is conceivable that TF-A regulates TF-B expression, which then directly regulates the expression of gene-X, even though TF-A may also bind to genomic regions near gene-X. In fact, multiple TFs often bind to the same region, but they may or may not directly contribute to transcriptional regulation, and some of the TFs may have overlapping, additive, synergistic or buffering effects. Globally, it is challenging to determine from the genomic occupancy pattern alone which TFs are required for the cell to make a specific cell fate decision.

Therefore, in order to establish a predictive gene regulatory network for cell fate control, it is necessary to build upon our knowledge of the TFs required for fate specification. This will allow us to identify cognate functional enhancer regions and measure the local and global consequences of perturbing these enhancers. For this purpose, we have been focusing on enhancers that mediate ESC-DE transition because of their importance to the development of endoderm-derived organs including the pancreas and liver. We expect that the identification of functional noncoding regulatory elements will establish edges in the gene regulatory networks. Furthermore, the measurements will form the basis for building quantitative models that describe how combinatorial TF genomic occupancy at multiple enhancers controls lineage-specific gene expression in embryonic development, tissue homeostasis, regeneration and aging.

Core Regulatory Genomic Circuits

We believe it is useful to develop a conceptual framework to address the issues raised above. We reason that instead of characterizing/identifying enhancers solely based on their ability to drive gene expression, it would be more productive to devise targeted strategies to interrogate enhancers that play distinct roles in the gene regulatory network. In particular, some enhancers, by virtue of their ability to regulate the expression of fate-determining genes, may play central roles in development. For this purpose, we define two classes of developmental enhancers based on their endogenous activity. The first class of enhancers are “core” enhancers that have a global impact in terms of cell fate maintenance or transition. The second class of enhancers are “peripheral” enhancers that regulate the expression of one or sometimes multiple adjacent gene(s) in cis, but have no or little global (developmental) impact. From the viewpoint of the gene regulatory networks that control developmental lineage decisions, the core enhancers are likely to regulate the expression of lineage-determining TFs that connect them into nonlinear networks that produce bifurcations between stable cell states. The peripheral enhancers are downstream targets that have an impact on specific gene expression levels, for example of differentiated cells, but don’t feedback into the control circuit. This separation of peripheral and core regulators has been particularly useful in the interpretation of the heritability of complex traits.(10, 44)

Identifying separate core and peripheral genes and enhancers in the regulatory network has implications for how to model regulatory networks using computational genomics and machine learning, and how to interrogate these classes of enhancers using distinct experimental methods. Computational machine learning and statistical methods rely on the existence of many examples which contain patterns that represent likely predictive causal mechanisms. In the case of enhancer prediction, the biological structure of these circuits provides the redundant examples from which these patterns can be learned. Each peripheral gene is driven by a small set of enhancers (at least one, sometimes just one), each containing binding sites for the core TFs. The fact that core genes are greatly outnumbered by peripheral genes has two key consequences. First, the set of core TFs in each cell type (the TF vocabulary) is small enough so that the TF vocabulary of a given cell type is of limited complexity and is learnable, and second, that the large number of peripheral genes (say 5000-15000) active in any cell type requires a large set of peripheral gene enhancers which can be used as examples to train the computational model.

Based on our studies of the ESC-DE transition (43), and many previous works, we can summarize a schematic gene regulatory network model of the core regulators controlling the ESC-DE transition in Fig 2. The features of this model are built upon and consistent with the observations listed in Fig 2b from our computational sequence analysis of cell specific distal enhancers in many cell types, as described in more detail below. The fact that the sequence based modeling can accurately predict a held out test set, and that the features required to make this classification map to a relative small set of TFs, implies that the set of core regulatory TFs is small (5-20), and the much larger set of enhancers containing these binding sites map to peripheral target genes which don’t typically affect the activity of the core regulator TFs directly. Additionally, each target enhancer typically contains TFBS for multiple core regulator genes.

Figure 2. Cell specific gene regulatory network model.

A model of the ESC and DE cell states (a) consistent with observations (b) from our sequence based computational analysis, perturbative studies, and functional studies of the ESC-DE transition, where the activity of a small set of core regulators interact through local enhancers and target a large number peripheral gene enhancers. (c) Functional studies show that these core TFs and bind cooperatively at enhancers specific to ESC or DE states, and that shared cofactors shuttle between binding cooperatively with different sets of the core factors active in each state across the transition.

By classifying enhancers into core and peripheral groups, they can be interrogated separately using different methods. For the core enhancers, we only need to focus on perturbing putative enhancers regulating a relatively small number of core TF genes. Because core enhancers regulate core lineage-determining TFs, their perturbation would have a global impact on cell fate decisions. It is therefore possible to use a downstream cell fate specific reporter (e.g. OCT4-GFP for hESC state, or SOX17-GFP for the DE state, and use large-scale, pooled CRISPR perturbation screens to determine the impact of perturbation on the cell fate. The regulation of hESC self-renewal and hESC-DE transition may involve both overlapping and distinct cis-regulatory sequences. It should be feasible to identify cis-regulatory elements that regulate the reporter gene expression (OCT4 or SOX17). On the other hand, there are obvious risks for identifying enhancers that regulate an upstream lineage-determining TF, which in turn regulates the cell fate decision. This would require the enhancer to not only have a relatively large effect on the transcription of the target gene, but also have secondary, tertiary or even relatively indirect effects which would ultimately impact on the cell fate.

DNA Sequence-based Machine Learning Enhancer Models

Computational machine learning and statistical methods rely on the existence of many examples from which to extract patterns that represent likely predictive causal mechanisms. In the case of enhancer prediction, the biological structure of these circuits provides the redundant examples from which these patterns can be learned.

Enhancer activity is associated with both increased chromatin accessibility and histone modifications to chromatin state which contribute to the establishment and maintenance of activity.(4, 8, 15, 29, 56, 57) Many epigenomic functional assays interrogate this active state and generate peaks of activity which can be used to define putative enhancer sets to train enhancer models, including ATAC-seq,(11) DNase-seq,(9, 14, 60, 61, 66) histone ChIP-seq for H3K27ac, H3K4me1, or TF ChIP-seq(69) when core TFs are known. H3K4me3 marks are typically specific to promoters. ATAC-seq and DNase-seq reflect chromatin accessibility, which does not necessarily indicate enhancer activity, but does have the advantage of higher spatial resolution relative to histone marks, which tend to flank the core TF binding sites. In addition, ATAC-seq and DNase-seq do not require the complete set of relevant TFs to be known, as is usually the case. For a complete set of TF ChIP-seq experiments in a cell-type, the full complement of TFs must be known, and good antibodies must exist, a tall order. Once a set of appropriate marks are chosen, there are two common approaches to defining the training set. Many methods train on a limited positive set of 10000-20000 cell specific peaks (1, 3, 5, 20, 23, 27, 39-41, 49, 62, 74) spanning 100bp-1000bp centered on the peak, and usually an equal sized or larger negative set. This has the advantage of focusing on identifying the core TF binding sites in a specific cell type. Other methods (34, 75) bin the genome in regularly spaced fixed length (1000bp) bins that are not necessarily centered on an activity peak, but have a multi-class label reflecting the epigenomic state of that bin for the full set of training datasets (n=919 for DeepSea). This regular training bin approach has the advantage of generating a very large set of sequences required for DNN’s to obtain strong class label accuracy, but may miss the subtleties in the differences in TF vocabulary between specific biologically relevant cell states. This may especially be a concern for the less well covered cell types in ENCODE, and such models should be retrained for these cases. In particular, the RFX6 SNP example in the introduction is missed by training on all ENCODE datasets, even though the prostate cancer cell line LNCaP is included in the training set(6).

Support Vector Machines (SVMs) and Deep Neural Networks (DNNs) are two of the main classes of machine learning methods which have been successful for enhancer prediction. These methods differ in the way the classifier score function is specified and how the parameters of this function are determined. They also differ in how the DNA sequence is converted into a mathematical input vector of features for each sequence element to be classified. In gkm-SVM (23) for example, each sequence is converted to a normalized vector of integer gapped-kmer counts. The parameters of this kmer vocabulary are specified before training, we use the full list of gapped-kmers of length L with k informative positions and L-k free positions (gaps or wildcards), we typically use (L,k)=(10,6) or (11,7). (11,7) is slightly more accurate and ~2x slower. In the DNN, the input feature later is usually converted into a 4xL binary integer matrix with each nucleotide represented by a permutation of (1,0,0,0).

The training sequence set will determine the features detected, and should be designed to most clearly reflect the specific biological processes one aims to model. For example, when building a sequence model to predict SNPs which affect chromatin accessibility (caQTLs or dsQTLs) in a cell line or primary cells, it is important to include examples of all accessible regions which may be altered by genomic variants in the experiment. Thus, in order to predict dsQTLs in lymphoblasts (17, 40) or atacQTLs in T-cells (22), we trained gkm-SVM on a positive set of a large number (~23000) of peaks of length L=300bp centered on the peak signal vs. an equal size GC and repeat matched negative sequence set. For sets of this size, the gkm-SVM R package(25) is most convenient, but for larger training sets ls-gkm(38) is recommended. Training the SVM yields a gkm-SVM score function S(x_j) = Σ_i α_i K(x_i, x_j) specified by the set of support vector coefficients α_i which optimally separate the sequence elements x_j in the positive and negative training sets.(23) The gkm-weight distribution is constructed from the gapped-kmer counts x_j in the support vectors, w_j = Σ_i α_i K(x_i, x_j). We often map the gapped-kmer weights to full kmer-weights for ease of interpretability, which produce an equivalent scoring function after training.(24) The tails of these weight distributions, shown in Fig 3ab, encode the features required to distinguish the positive and negative training sets cell specific enhancer activity. In this case these weights encode the TFBS required to predict chromatin accessibility in lymphoblasts, and the long positive tail of the weight distribution from 1 to 6 in Fig 3b all map to binding sites for the 10 TFBS shown in Fig 3c. In this case there are 3 classes of features: CTCF, promoter specific TFBS (NRF1, SP1, NFY, ELK4), and lymphoblast distal enhancer specific TFBS (IRF2, BATF, RUNX1, NFkB, PU.1). Lymphoblast dsQTL SNPs disrupt all of these TFs and accurate prediction of lymphoblast dsQTLs requires resolution of all three classes of features. In DNNs these important features are encoded in the first PWM layer of convolution filters (typically 360 filters of length 8bp are used).

Figure 3. gkm-SVM gapped kmer weight distribution quantifies contribution of TF binding to cell-specific chromatin accessibility.

(a) Gapped kmer weights for gkm-SVM trained on lymphoblast DHS. (b) Mapping to full 10-mers produces an equivalent SVM scoring function. (14) (c) The long positive tail of this weight distribution specifies relative rank of binding site strength for a set of active TFs in lymphoblasts. Highlighted in red: (a) gapped kmers (b) top 10-mer GGAAATCCCC, and (c) PWM for NFkB.

Alternative training set design can be used to detect more specific regulatory signals. For instance, to detect the TFs controlling the ESC-DE transition, instead of training vs. inaccessible genomic negative sequence and comparing the weight vectors, we can isolate the differentially active TFs by choosing as a positive set the most differentially accessible peaks. In Figure 4a, we show the ATAC-seq signal from Ref (43) in ESC and DE at the union of all peaks from each state. Training a gkm-SVM model using the 5000 most differentially accessible peaks in DE as a positive set (blue in Fig 4a) and the 5000 most differentially accessible peaks in ESC as a negative set (red in Fig 4a) yields a classifier with AUROC=0.92. The tails of this gkm-weight vector contain binding sites for the core TF regulators of the DE (TCF, EOMES, SMAD2/3, GATA, AP1, and FOXH1) and ESC states (OCT4, NANOG, SOX2, EBOX, CTCF), whose PWMs and top weights are listed in Fig 4b and 4c. Training on ATAC-seq data from human tissue derived cells or stem cell derived often detects very similar regulatory programs, as shown for human islet and pancreatic progenitor cells in Figure 5. These islet specific enhancers form islet specific DNA looping interactions in a Type 2 diabetes associated locus as shown in Fig 5a, as measured by promoter capture Hi-C (PCHi-C).(51) Although some computational models have been proposed to predict the gene targets of these enhancers(71), the predictive power of these methods is much lower than initially reported,(12, 72) and additional higher resolution enhancer-promoter interaction data is needed to develop improved models.

Figure 4. Detecting ESC and DE TF regulators.

TFBS mapping to the tail of the gkm-SVM weight distribution trained on differentially active ATAC-seq regions (AUROC=.92) (a) Here gkm-SVM is trained on DE d1 open (blue) vs. ESC open (red) ATAC-seq regions and (b) detects the core DE d1 specific TFs (blue) and ESC specific TFs (red). Each dot in (b) is a distinct kmer. From the two ATAC-seq experiments a set of core regulators for the ESC and DE states can be found.

Figure 5. Similar TF vocabulary identified in human islets and stem cell derived pancreatic progenitors.

a) ATAC-seq data from Human Islets(51, 67) and our ATAC-seq data generated in PP1 pancreatic progenitors(42) in the KCNJ11-ABCC8 T2D associated locus detect peaks with islet specific PCHI-C interactions(51). (b) gkm-SVM detects overlapping regulatory programs in ATAC peaks from PP1 and islets and detects known islet regulators.

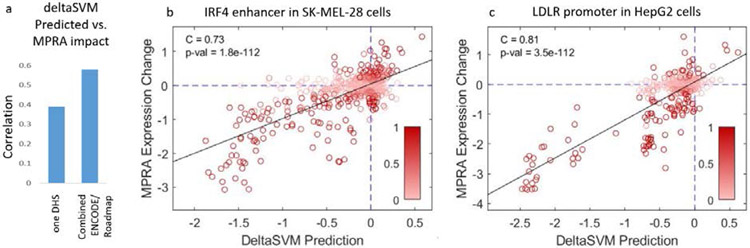
These sequence based enhancer prediction models have been tested with luciferase and Massively Parallel Reporter Assays (MRPA) in a wide cell types (mouse liver, retina, neurons, melanocytes; human T-cells, lymphoblasts, GM12878, K562, HepG2, SK-N-SH).(6, 22, 32, 35, 37, 39, 49, 52, 55) Most recently, in a prediction assessment of MPRA data, five enhancers and nine promoters were tested by saturation mutagenesis in disease relevant cell types, where we found that the best models combined sequence features derived from enhancer prediction models that were trained on different ENCODE/Roadmap datasets.(63) Using our previous approach,(23, 39) we trained gkm-SVM on only the single cell type relevant DHS/ATAC-seq dataset, which produced an average overall correlation with expression output of (C=.39), as shown in Fig. 6a. Performance improved to C=.58 when training on multiple datasets and combining the deltaSVM scores with random forest regression, as described in (63). This method also improves correlations at individual enhancer and promoter loci, as shown in Fig 6bc.

Fig 6. Comparisons of deltaSVM predictions and MPRA expression change.

(a) Overall correlation across 15 tested elements improves from C=.39 to C=.58 when trained on multiple ENCODE datasets(46). (b) IRF4 enhancer, C=.73 (c) and LDLR promoter, C=.81.

Regulatory Network Models of Cell Fate Transitions

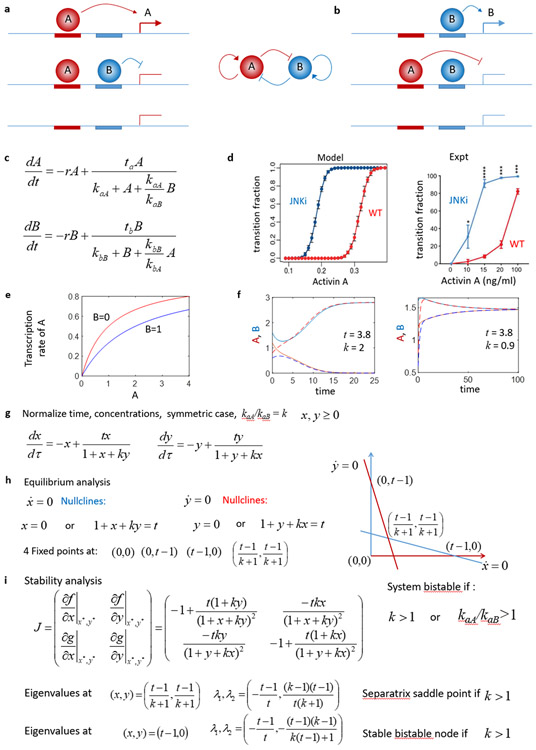
We introduced a very simple continuum model of a gene regulatory network for a bistable genetic switch which described some features of the ESC-DE transition in Ref (43), using reaction rate equation models similar to those previously used to model cell state transitions.(21, 31, 53) It is reasonable to question the form of these reaction rate equation models on theoretical grounds in the small molecule limit relevant to some low expressed TFs, and a more technically rigorous and computationally much more challenging approach would utilize stochastic Langevin(26) or chemical master equations(50). Nevertheless, properly modelled reaction rate equations yield much clearer interpretations that lead to more facile biological insights. Also, the agreement between the experimental perturbations and our initial modelling(43), in addition to the precision and robustness of embryonic developmental cell state transitions, and the stability of cell states critical to multicellular life, suggests that a more theoretically rigorous model would lead to qualitatively similar conclusions. In our model, shown in Figure 7ab, TFs A and B activate their own transcription by each binding to an enhancer near their gene (red and blue boxes near a or b) and negatively regulate the other TF. We will use lower case to describe the genes (a,b) and upper-case for the protein products (A,B). Gene a is only transcribed (Fig 7a) when TF A is bound but B is not: when B is bound at the gene a locus, gene a is in a non-productive transcriptional state, thus the transcription rate of gene a is given by the bound concentration of A (in the absence of B) at its own gene, [aA]. We assume that equilibrium occupancy of regulators A and B at genes a and b is established rapidly relative to rates of protein production, so the equilibrium of A and B at their binding sites are given by Michaelis-Menten kinetics: [aA]=[a][A]/k_aA = [a₀][A]/(k_aA+[A]+(k_aA/k_aB)[B]), where k_aA is the dissociation constant for A at its gene-a binding site, k_aB is the dissociation constant for B at its gene-a binding site, and [a₀] is total DNA concentration that we will absorb into the transcription rate t_a. Similarly, [bB]=[b₀][B]/(k_bB+[B]+(k_bB/k_bA)[A]). Both [A] and [B] are degraded at rate r, and the transcription of each is proportional to t_a[aA] and t_b[bB], yielding the model in Fig 7c. Stochastic simulations of induced cell state transitions can be modeled by adding a time dependent impulse of Activin increasing the transcription of one TF (here B is a DE specific TF), and weakening auto-activation models the effect of JNK inhibition (JNKi) and allows transition to DE at lower Activin concentrations, in agreement with experiment (Fig 4d).(43) The transcription rate for A is reduced by increased B, as shown in Fig. 7d. For parameters t=3.8, k=k_aA/k_aB=2, this system equilibrates at either a high A-low B or high B-low A state, depending on initial conditions as shown in Fig. 7e. The full stability of this model can be worked out simply when parameters for A and B are symmetric as in Fig 7f. In this case there are 4 fixed points as shown in Fig 7g, and both high-x low-y and low-x high-y are stable if k= k_aA/k_aB > 1, in the usual case where t>1. The fixed point at x=y is an unstable saddle for k>1, so for k>1 this system exhibits bistability, and can transition from one state to another with a significant perturbation, as shown in Fig 7d and Ref. (43). However, this stability analysis shows that this system is somewhat sensitive to parameter choices. Since k_aA and k_aB are the dissociation constants for A and B at gene a, k>1 requires that the repressive TF B binds at gene a with stronger affinity than the activating TF A, and vice versa at the gene b locus. While understandable in the context of this mathematical model, this seems to be a rather difficult and unnatural requirement to satisfy for all mammalian cellular circuits.

Figure 7. Analysis of a simple non-cooperative model of cell-state bifurcation transitions driven by autoregulation and negative feedback.

a,b) Bistable genetic circuit where genes A and B auto-activate their own transcription by binding an enhancer driving their own expression but interfere with or repress the transcription of the other TF. c) Rate equations describing the evolution of concentrations of TF A and B under this model. d) Stochastic simulations of this simple circuit show how transitions from the high A to high B state can be induced by external simulation and qualitatively agree with experimentally observed transition rates.(43) e) Concentration dependence of transcription rate of gene A according to this model. f) Bistable solutions and cell-state transitions exist for some parameter choices (t=3.8, k=2) but not others (t=3.8, k=0.9). g) Normalized system of equations for stability analysis. h) Fixed points of this system. i) Stability analysis shows that system is only bistable for k>1, which requires possibly unrealistically strong negative feedback.

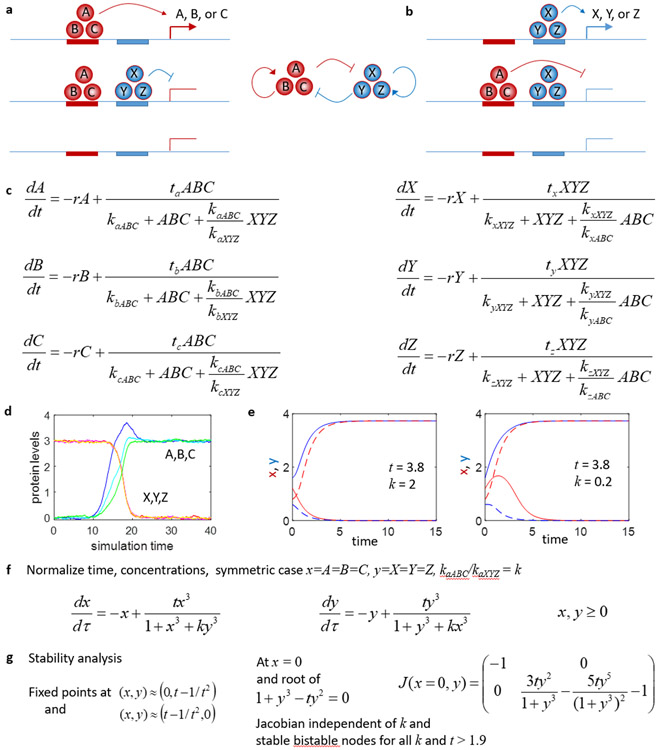
A more realistic model is shown in Fig 8, which now incorporates the observations from Fig 2 that there are multiple core TFs active in each cell state which bind cooperatively at activating and repressive regulatory DNA elements. Here, the TFs A, B, and C bind cooperatively at their cognate enhancers with binding sites for A, B, and C at gene a, b, c, and x, y, z. However, at gene a, b, c the complex binding produces a transcriptionally productive DNA looping conformation, while at gene x, y, z they produce a transcriptionally inactive conformation. Similarly, X, Y, and Z bind cooperatively, activate gene x, y, and z, and produce a transcriptionally inactive DNA conformation when they bind at a, b, or c. Now the relevant kinetic parameters are the dissociation constants for the ABC and XYZ complexes at the relevant gene enhancers, e.g. k_aABC and k_aXYZ, etc. The model equations for this situation are shown in Fig 8c, and when simulated can produce a transition from the high X, Y, Z, state to the high A, B, C state as shown in Fig 8d, with a sufficiently large perturbation. This system can also be studied with phase-plane analysis techniques if we assume x=A=B=C and y=X=Y=Z, essentially modeling the complex concentrations, as in Fig 8f, and the system is now bistable for all k, as shown in Fig 8e. Stability analysis shows that when t>1.9, there are two fixed points at $(x,y)=(0,t-\frac{1}{t^2}+a\left(\frac{1}{t^3}\right))$ and $(x,y)=(t-\frac{1}{t^2}+a\left(\frac{1}{t^3}\right),0)$, and since the Jacobian here is independent of k these are stable nodes for all k, as shown in Fig 8g. Thus, this cooperative model produces multiple stable states over a much wider range of kinetic parameter choices. It is possible that the ubiquity of cooperative binding by multiple TFs at mammalian developmental enhancers may have evolved because the state switching dynamics of these cooperative circuits are more robust to binding site strength parameters than less cooperative gene regulatory networks involving single TFs.

Figure 8. Analysis of cooperative model of cell-state bifurcation transitions.

a,b) Bistable genetic circuit where genes A,B,C and X,Y,Z cooperatively auto-activate their own transcription by binding an enhancer driving their own expression, but interfere with or repress the transcription of the other three TFs. c) Rate equations describing the evolution of concentrations of TF A,B,C and X,Y,Z under this model. d) Stochastic simulations of this simple circuit show how transitions from the high ABC to high XYZ state can be induced by external stimulation of A. e) For the cooperative model, bistable solutions and cell-state transitions exist for a much broader range of parameter choices; now both (t=3.8, k=2) and (t=3.8, k=0.2) support bistable behavior. f) Normalized system of equations for stability analysis. g) Stability analysis shows that the cooperative system is bistable for all choices of k, as long as transcription is not weak (t>1.9).

Summary Points.

1. DNA sequence based enhancer prediction and perturbative and functional studies detect consistent features of genetic regulatory networks controlling cell states and transitions.

2. Predictive sequence features map to a relatively small set of core TF regulators.

3. Cell-specific enhancers contain binding sites for multiple core TF regulators.

4. Machine learning based models trained as discriminative classifiers yield quantitative accuracy when predicting the impact of a mutation in reporter assays.

5. Continuum dynamical models can yield insight into the features of genetic networks and the types of nonlinear interactions which support the stability and transitions between differentiated cellular states.

Future Issues.

1. Linear and nonlinear classifiers currently often yield comparable overall accuracy. Improved models in reduced feature spaces may allow models to learn nonlinear interactions between TFs and regulatory elements with existing amounts of training data.

2. Methods of training on integrated large data sets can provide targeted training sequence data to detect more subtle regulatory events and should yield improved models.

3. Higher resolution 3D chromatin looping measurements will likely be required to more fully understand and model the regulatory element interactions mediating promoter activation and repression.