Evaluating riboswitch optimality

Abstract

Riboswitches are RNA elements that recognize diverse chemical and biomolecular inputs, and transduce this recognition process to genetic, fluorescent, and other engineered outputs using RNA conformational changes. These systems are pervasive in cellular biology and are a promising biotechnology with applications in genetic regulation and biosensing. Here, we derive a simple expression bounding the activation ratio—the proportion of RNA in the active vs. inactive states—for both ON and OFF riboswitches that operate near thermodynamic equilibrium: $1+[I]/K_d^I$, where [I] is the input ligand concentration and $K_d^I$ is the intrinsic dissociation constant of the aptamer module toward the input ligand. A survey of published studies of natural and synthetic riboswitches confirms that the vast majority of empirically measured activation ratios have remained well below this thermodynamic limit. A few natural and synthetic riboswitches achieve activation ratios close to the limit, and these molecules highlight important principles for achieving high riboswitch performance. For several applications, including “light-up” fluorescent sensors and chemically-controlled CRISPR/Cas complexes, the thermodynamic limit has not yet been achieved, suggesting that current tools are operating at suboptimal efficiencies. Future riboswitch studies will benefit from comparing observed activation ratios to this simple expression for the optimal activation ratio. We present experimental and computational suggestions for how to make these quantitative comparisons and suggest new molecular mechanisms that may allow non-equilibrium riboswitches to surpass the derived limit.

1. Introduction

Riboswitches are sophisticated sensors that make use of RNA’s ability to bind and recognize a wide variety of substrates. They offer promise as genetic regulators (Sherwood & Henkin, 2016; Vazquez-Anderson & Contreras, 2013), as control elements for precise genetic editing systems via CRISPR/Cas9 (Liu et al., 2016; Tang, Hu, & Liu, 2017), as biosensors (Hallberg, Su, Kitto, & Hammond, 2017; Mehdizadeh Aghdam, Hejazi, & Barzegar, 2016), as devices for disease monitoring and diagnostics (Kellenberger et al., 2015; Seetharaman, Zivarts, Sudarsan, & Breaker, 2001), as metal ion detectors (Wedekind, Dutta, Belashov, & Jenkins, 2017), and as targets for future antibiotic therapies (Deigan & Ferré-D’Amaré, 2011; Lee, Han, & Lee, 2016). As sensors, riboswitches offer many benefits over proteins with comparable functions: RNA molecules can be simpler to synthesize in living systems than proteins (Berens & Suess, 2015) and offer the possibility of modular regulatory platforms that can be readily incorporated into new genes or readouts of interest (Berens, Groher, & Suess, 2015; Ceres, Trausch, & Batey, 2013).

A riboswitch can be defined as an RNA molecule that undergoes a conformational change upon binding a specific “input” ligand by an internal recognition module, or aptamer (blue, Fig. 1). This conformational change affects some form of output, such as altered transcription or translation rates (Suess, Fink, Berens, Stentz, & Hillen, 2004), ribozyme (RNA enzyme) activity (Tang & Breaker, 1997a, 1997b), or fluorescence by controlled capture of a fluorogenic ligand (Kellenberger, Wilson, Sales-Lee, & Hammond, 2013) or labeled protein (Kennedy, Vowles, d’Espaux, & Smolke, 2014). Control of these outputs requires a second RNA segment (red, Fig. 1) that recruits a separate ligand or biomolecule to the riboswitch whose role is to affect the downstream output. If the formation of the input module reduces correct formation and binding by the output segment, the riboswitch is typically called an OFF switch (Fig. 1A). Conversely, if binding of the input ligand promotes formation of the active output segment, it is typically called an ON switch (Fig. 1B).

Fig. 1.

Schematics for how an RNA conformational change can induce anticooperativity or cooperativity in binding an input and output ligand, corresponding to (A) an OFF-switch and (B) an ON-switch, respectively.

There has been remarkable progress in riboswitch discovery in recent years, and the field appears poised to create numerous real-world applications. To appreciate this progress, a common figure-of-merit for riboswitches is the “activation ratio” (AR)—the ratio of the output signal in the presence vs. absence of input ligand. While ARs for most natural and synthetic riboswitches have remained around 10-fold or lower, ARs exceeding 10,000 have been reported for riboswitches discovered through in vitro selection (Seetharaman, Zivarts, Sudarsan, & Breaker, 2001). Despite these successes, several questions remain. In studies seeking to design riboswitches that couple new inputs and outputs, AR values of 2- to 10-fold are widespread and often considered satisfactory—with better design, could these values go as high as the AR values in the best riboswitches (>10,000), or are there fundamental laws that limit their performance? To address these questions, biophysical modeling of riboswitches is important but can often become complicated and tied to assumptions particular to the system (Beisel & Smolke, 2009; Espah Borujeni, Mishler, Wang, Huso, & Salis, 2015; Findeiβ et al., 2018). Here, inspired by simple analyses of switches in other areas of biophysics (Bintu et al., 2005), we present a thermodynamic model that reveals a simple expression for the maximum activation ratio of a riboswitch. The final expression depends on only two factors: the concentration of the input ligand and the intrinsic dissociation constant of the riboswitch’s aptamer module for binding the input ligand. This limit is independent of fine details of the output event, and the limit holds for some systems that are out of thermodynamic equilibrium, including riboswitches deployed in complex biological contexts. Applying the derived expression for the thermodynamic optimum to previously described riboswitch systems helps define limits on the maximal performance achievable by these systems, and we outline a methodology that future studies can take to understand, achieve, and surpass the activation ratios set by the formula.

2. A thermodynamic bound for riboswitch performance

This section derives a simple and quite general expression for the optimal activation ratio of ON and OFF riboswitches that depends only on properties of the riboswitch aptamer, i.e., the RNA’s recognition module for the input ligand (blue, Fig. 1). Our derivation follows standard approaches to modeling thermodynamics of biological systems; the reader is referred to an excellent chapter in a previous volume of Methods in Enzymology for an introduction (Garcia, Kondev, Orme, Theriot, & Phillips, 2011).

2.1. Optimal activation ratio for a minimal model

We start where the derivation is simplest, with an OFF switch whose output signal is reduced by reversible binding of an input ligand and effected by reversible recruitment of an output ligand. Fig. 1A shows an example of this mechanism (Kellenberger et al., 2013), in which an RNA conformational change is toggled by the presence of cyclic di-GMP as the input ligand (blue symbol). Binding of this small molecule input to the riboswitch’s c-di-GMP aptamer segment (blue line) favors a structure that disrupts the formation of the Spinach aptamer (red line), an aptamer that would otherwise recruit the small molecule 3,5-difluoro-4-hydroxybenzylidene imidazolinone (DFHBI, red shape) and induce its fluorescence, generating the output in the ligand-free state. Following (Garcia et al., 2011), we write out the states of the thermodynamic model and their respective weights in Fig. 2A. This model can be expanded to consider the entire set of possible states of an RNA engaging with two ligands; Appendix A gives this complete model and derivation, but, for simplicity, we stick to minimal models, which lead to the same expression.

Fig. 2.

Minimal thermodynamic model for riboswitch function. Depicted are states and associated Boltzmann weights for (A) an OFF-switch and (B) an ON-switch.

In any riboswitch, the set of RNA conformations can be partitioned into those that present the input-binding aptamer in the correct secondary structure (abbreviated B, for binding) and those unable to bind the input (abbreviated F, for free). We note that while we show a single structure for each of these states in Fig. 2, each state can involve a panoply of secondary and tertiary structures, and such structural heterogeneity appears to be present for some systems like adenine riboswitches (Tian, Kladwang, & Das, 2018; Warhaut et al., 2017).

In our minimal model, only one state is able to bind the output and thus directly modulate the downstream signal of interest (e.g., binding of the DFHBI fluorophore). Since we are considering an OFF switch, only the F state binds the output ligand O. Similarly, for OFF switches, only the B state is able to bind the input molecule I. These considerations result in two additional states with the different ligands bound, which we call FO and BI. The resulting four-state model is shown in Fig. 2A. We note that unlike typical “short-hand” schematics shown in the literature (e.g., Fig. 1A), it is important to recognize that any RNA conformation that binds a ligand must also exist in the absence of the ligand, and the equilibrium ratio between the two is $[L]/K_d^L$, where [L] is the free concentration of the input ligand and $K_d^L$ is the intrinsic dissociation constant of the riboswitch ligand aptamer (Garcia et al., 2011). It is the presence of these states that are able to bind input ligand, yet remain unbound, that set a useful limit on the activation ratio.

Now, we use the Boltzmann weights for each state (Fig. 2A) to compute the fraction signal observed via the output molecule (O),

$$signal=\frac{e^{-\beta {ϵ}_{FO}}}{e^{-\beta {ϵ}_F}+e^{-\beta {ϵ}_B}+e^{-\beta {ϵ}_{BI}}+e^{-\beta {ϵ}_{FO}}}=\frac{\frac{[O]}{K_d^O}}{1+K_{fold}+\frac{[I]}{K_d^{\text{I}}}{K}_{fold}+\frac{[O]}{K_d^O}}$$ (1)

Here, β is 1/k_BT, where k_B is the Boltzmann constant and T is the temperature. The second expression is rewritten in terms of equilibrium constants: $K_{fold}=e^{-\beta {ϵ}_B}/e^{-\beta {ϵ}_F}$ is the equilibrium constant between the riboswitch conformations that can bind the input ligand vs. those that cannot. [I] is the input molecule concentration, [O] is the output molecule concentration, and $K_d^I$ and $K_d^O$ are the intrinsic dissociation constants for the correctly folded aptamers toward the input and output ligands, respectively. Rearranging Eq. (1) shows that the signal depends on the concentration of the output ligand, but in a simple form that mimics a standard ligand-binding isotherm with an observed dissociation constant $K_d^{obs}$:

$$\begin{gathered} signal=\frac{[O]}{[O]+K_d^{obs}}, \\ {K}_d^{obs}=K_d^O\left[1+K_{fold}\left(1+\frac{[I]}{K_d^I}\right)\right] \end{gathered}$$ (2)

That is, the riboswitch has an apparent binding affinity to the output “activator” ligand that becomes weaker (i.e., $K_d^{obs}$ increases) when the input ligand concentration [I] is increased. How much can this signal change with input ligand concentration? The activation ratio is the ratio of the signal in the OFF state (for an OFF riboswitch, the state triggered by ligand) and the ON state (for an OFF riboswitch, the ligand-free state):

$$AR=\frac{\mathrm{signal}\text{ON}}{\mathrm{signal}\text{OFF}}=\frac{\frac{[O]}{[O]+K_d^{ON}}}{\frac{[O]}{[O]+K_d^{OFF}}}=\frac{[O]+{\text{K}}_d^{OFF}}{[O]+K_d^{ON}}$$ (3)

Here, $K_d^{OFF}$ and $K_d^{ON}$ are apparent dissociation constants for the output ligand given by the expression in Eq. (2) evaluated at [I] = 0 and at the input ligand concentration used to toggle the switch, respectively. When there is a high concentration of output ligand [O], the AR decreases, as described in Eq. (3). At very large [O], the activation ratio approaches unity, corresponding to no observed switching. The presence of the output ligand pulls the equilibrium of the riboswitch toward the activated state, and high [O] saturates the riboswitch in the active state. So there is a necessary tradeoff here: the best case scenario (maximal AR) involves using minimal amounts of output ligand, which decreases the magnitude of signal observed. Fig. 3A plots the output signal of the riboswitch as a function of [O], both without and with input ligand. At high [O] the signal saturates as the output ligand “loads” the switch. The maximum activation ratio is attained at lower output concentrations (marked with arrow).

Fig. 3.

Modelling illustrates tradeoffs in riboswitch behavior. (A) As the output ligand concentration [O] is changed, there is a tradeoff between achieving high activation ratio and low K_ds to the output, i.e., high activity. (B) The relationship between the achievable $K_d^{OFF}$ and $K_d^{ON}$ is strongly dependent on the ratio of input concentration to input K_d. Within each of these curves, there is another tradeoff between achieving high activation ratio $\frac{K_d^{OFF}}{K_d^{ON}}$ and low K_ds to the output, i.e., high activity.

Taking the limit of the activation ratio in Eq. (3) at low [O], we obtain

$$AR<\underset{[O]\to 0}{\lim }AR=\frac{K_d^{OFF}}{K_d^{ON}}=\frac{1+K_{\text{f}old}\left(1+\frac{[I]}{K_d^I}\right)}{1+K_{fold}}$$ (4)

The right-hand side expression is maximized at high K_fold. Taking this limit, we have

$$AR<\underset{{\mathrm{K}}_{\text{fold}}\to large}{\lim }AR=A{R}_{max}=1+\frac{[I]}{K_d^I}$$ (5)

Thus, we set a bound on the activation ratio of AR_max that depends only on the input ligand concentration [I] and the intrinsic dissociation constant of the riboswitch aptamer segment $K_d^I$.

Optimal riboswitch performance is achieved in the limit where K_fold is large. This corresponds to a situation that, at first glance, may be counterintuitive. The “perfect” OFF riboswitch is achieved when the riboswitch only weakly binds the output ligand in the absence of input and this association becomes even weaker when input ligand is present. Because maximal performance requires minimal [O] (Eq. 3), this additional consideration presents a second tradeoff in which having a large activation ratio necessitates preventing saturated output even in the ligand-free state of the riboswitch.

To illustrate this tradeoff, Fig. 3B shows how the binding of the riboswitch to the output ligand (parameterized by its $K_d^{obs}$) is toggled at different ligand concentrations, for a wide sweep of the K_fold variable. The best possible activation ratio $\frac{K_d^{OFF}}{K_d^{ON}}$ is achieved when K_fold is set to give poorer (higher) values of $K_d^{ON}$—this optimal region corresponds to the part of the curves in Fig. 3B near the top-right of the plot. It is important to note that this observed binding dissociation constant $K_d^{ON}$ is necessarily worse (higher) than the intrinsic dissociation constant of the riboswitch’s output-recruiting segment to the output ligand $K_d^O$ (red in Figs. 1 and 2). Indeed, to achieve the best activation ratios, $K_d^{ON}$ may be much worse than the intrinsic dissociation constant for the output $K_d^O$.

2.2. Optimal activation ratio for an ON switch

The derivation above applies to OFF switches. A minimal thermodynamic model of ON switches is illustrated in Fig. 2B and yields the following expression for the activation ratio,

$$AR<\frac{K_d^{OFF}}{K_d^{ON}}=\frac{\left(1+K_{fold}\right)\left(1+\frac{[I]}{K_d^I}\right)}{1+K_{fold}\left(1+\frac{[I]}{K_d^I}\right)}$$ (6)

This equation is maximized at low K_fold,

$$AR<A{R}_{max}=1+\frac{[I]}{K_d^I}$$ (7)

This AR_max for ON switches is the same expression as for OFF switches. Here again, the best activation ratio for an ON switch corresponds to a situation (here, small K_fold) in which the riboswitch has highly suppressed activity in the absence of input ligand and then, in the presence of input ligand, gives improved—but not saturating—output activity.

2.3. Generality of the thermodynamic bound

The above analyses of minimal thermodynamic models of OFF and ON riboswitches both lead to the same upper bound on the activation ratio: $A{R}_{max}=1+\frac{[I]}{K_d^I}$ (compare Eqs. 5 and 7). This bound applies even if we relax some assumptions of the analysis. The expressions above have ignored some states; for example, a poorly designed OFF switch may form “leaky” structures that are not bound to input ligand but nonetheless can still bind the output molecule. As described in Appendix A, such states will produce ARs that are even lower than the expressions given above, and the bound $A{R}_{max}=1+\frac{[I]}{K_d^I}$ still holds.

The analyses above involve the free input ligand concentration [I]. In typical cases, experimenters set the total ligand concentration and not the free concentration, which can be reduced if, for example, the input ligand is sequestered by binding the riboswitch or to other macromolecules in the system (especially in vivo). In those cases, the free ligand concentration will be reduced compared to the input, and the $A{R}_{max}=1+\frac{[I]}{K_d^I}$ bound still holds if [I] refers to the total input ligand concentration. Tighter bounds on the activation ratio can be set in models that account for RNA sequestration of input ligand, which can reduce the free concentration relative to total concentration (see, e.g., Espah Borujeni et al., 2015).

Another assumption in the analyses above is that the input aptamer region and the output ligand-recruiting region bind their targets with K_d values that are independent of one another; that is, the riboswitch function is mediated solely through an allosteric RNA conformational change. This assumption appears to hold for the majority of natural and synthetic riboswitches. However, there are notable exceptions, such as a natural ribozyme that binds a glucosamine-6-phosphate input and uses this bound metabolite to help catalyze RNA cleavage. This glmS ribozyme is not well described by the models of Fig. 2 and is not considered here.

Many riboswitches create an output through an irreversible event rather than reversible recruitment of an output ligand (red symbols in Fig. 2), but such systems still have limits in which the derived activation ratio should still hold. For example, some synthetic riboswitches effect their output through cleavage of the RNA by an embedded ribozyme (see, e.g., Koizumi, Soukup, Kerr, & Breaker, 1999; Soukup & Breaker, 1999b; Win & Smolke, 2007). If the cleavage rate is slower than RNA conformational changes, the model in Fig. 2 holds with a minor update: the equilibrium constant for recruiting an output $[O]/K_d^O$ to the ON state (red line) needs to change to the rate of cleavage of the ribozyme. The same bound on activation ratio $A{R}_{max}=1+\frac{[I]}{K_d^I}$ still holds as long as the RNA input ligand binding and conformational rearrangements reach equilibrium before cleavage (which has a timescale on the order of minutes). As a more common example of a distinct “output” mechanism, many natural and synthetic riboswitches act during transcription of the riboswitch by bacterial RNA polymerase. These systems effect their output through display of a special terminator hairpin, which signals the RNA polymerase to terminate transcription. In these cases, the RNA polymerase can be considered the output “ligand,” and replacing the expression $[O]/K_d^O$ with k_termination, a rate constant for the terminator hairpin interacting with RNA polymerase, allows derivation of the same bound of $A{R}_{max}=1+\frac{[I]}{K_d^I}$, as long as RNA conformational changes equilibrate faster than the termination event and synthesis of the RNA by polymerase.

As a final note, we emphasize that our expression is based on a thermodynamic model for riboswitch function, but in several riboswitch mechanisms, attaining thermodynamic equilibrium is not guaranteed. Indeed, various riboswitch classes have been experimentally verified to function in the kinetic regime and, among other features, shown to require ligand concentrations significantly above their dissociation constants for activation (Furtig, Nozinovic, Reining, & Schwalbe, 2015; Greenleaf, Frieda, Foster, Woodside, & Block, 2008; Lin, Yoon, Hyeon, & Thirumalai, 2015; Ottink et al., 2007; Sun, Zhao, & Chen, 2018; Wickiser, Cheah, Breaker, & Crothers, 2005). These reports imply that the riboswitch activation process is often a delicate balance between ligand concentration, binding and folding kinetics, and the processing speed of RNA transcription and translation machinery. Modeling and predicting kinetic regulation of riboswitches through cotranscriptional folding and other mechanisms remains an active area of research and discussion. Nevertheless, most out-of-equilibrium effects in riboswitch studies actually work to reduce the activation ratio. For example, if a riboswitch is transcribed so quickly that it does not have time to bind its input ligand before facing the task of activating its output (e.g., transcription termination), its activation ratio will be poor (see, e.g., Ceres, Garst, Marcano-Velazquez, & Batey, 2013; Ceres, Trausch, et al., 2013; Endoh & Sugimoto, 2018; Wickiser et al., 2005). Kinetic mechanisms that might instead boost the activation ratio above the thermodynamic bound of $A{R}_{max}=1+\frac{[I]}{K_d^I}$ are discussed in Section 4.

3. How close are current riboswitches to the thermodynamic optimum?

The bound on the activation ratio $A{R}_{max}=1+\frac{[I]}{K_d^I}$ provides an easily computed metric that the best performing riboswitches should achieve. Do any natural or engineered riboswitches meet this bound? Do any riboswitches surpass it? In this section, we compare observed activation ratios to optimal activation ratios for riboswitch molecules from across literature, harnessing a wide variety of input ligands to a wide variety of outputs. We tabulated experimentally measured AR (AR_exp) from these studies and, where possible, we compute the riboswitch’s optimality, defined as

$$optimality=A{R}_{exp}/A{R}_{max}$$ (8)

These calculations were not always possible. On one hand, for experimentally observed activation ratios AR_exp, most prior studies of riboswitches directly report—or provide enough information to compute—these values. The output signals (fluorescence of translated GFP, cleavage or transcription termination rate of RNAs, etc.) are expected to be directly proportional to the fraction of the studied riboswitch displaying a correctly folded output-recruiting region (red in Figs. 1 and 2). Other performance measures, such as dynamic range (Ceres, Garst, et al., 2013; Reining et al., 2013), can typically be converted to activation ratio with appropriate additional measurements on, e.g., the maximum output signal of the riboswitch.

On the other hand, for computing the optimal activation ratios AR_max, we need the input ligand concentrations [I] and the intrinsic dissociation constant of the aptamer segment for the input ligand $K_d^I$. Total input ligand concentrations [I] used to toggle the riboswitches are widely reported, although, for in vivo settings, there is uncertainty in what the ligand concentrations are inside cells compared to the concentrations set outside cells. An intracellular concentration higher than the growth media concentration, which can arise due to active transport of metabolites, would result in a higher optimal AR than estimated from the growth media concentration.

Estimating $K_d^I$ can be more challenging. This dissociation constant for the input ligand is not the same as the observed midpoint of the riboswitch output signal as the input ligand concentration is varied; in general that midpoint value is higher than the intrinsic dissociation constant for the input ligand $K_d^I$ by a large factor, reflecting the energetic cost of coupling input ligand binding to the riboswitch conformational change. For example, for the OFF switch in Fig. 2A, this inflation factor for the observed dissociation constant for input ligand is 1+K_fold, with K_fold being large; see Eq. (2). Measuring the intrinsic dissociation constant for the input ligand $K_d^I$ requires separate measurements on RNA molecules that have been stabilized in a state capable of binding the input ligand via site-directed mutation or careful minimization of the ligand-binding region (state B in Fig. 2). Since these stabilized molecules no longer toggle binding of the output ligand, measurement of $K_d^I$ necessarily requires using some other readout of ligand binding, e.g., nucleotide-resolution chemical mapping of RNA reactivity in the ligand-binding pocket, dialysis of radiolabeled ligand, or competition with fluorophore-labeled ligand analogs. In our survey, these ligand $K_d^I$ values, if not reported in the work itself, were located through referenced works or elsewhere (see Table S1 in the online version at https://doi.org/10.1016/bs.mie.2019.05.028 for sources). Table 1 depicts a sample of collected data from a variety of synthetic riboswitches. In some cases, the solution conditions for these $K_d^I$ determinations were different than in the riboswitch activation ratio measurements, and some of these cases are noted below. We note that riboswitches that bind oligonucleotide ligands through Watson-Crick base pairing are often expected to have intrinsic $K_d^I$ values that are extraordinarily tight (sub-fM) and nucleic acid dissociation rates may be extremely slow (weeks or centuries) compared to other timescales, breaking our assumption of thermodynamic equilibrium; for these reasons, natural and synthetic riboswitches that respond to RNA or DNA (Chappell, Westbrook, Verosloff, & Lucks, 2017; Penchovsky & Breaker, 2005) are not discussed in detail here.

Table 1.

Example theoretical maximum AR (AR_max) and estimated optimality from values reported in literature, including necessary information needed to perform calculation.

Source	Ligand	Switch direction	${\mathit{K}}_{\mathit{d}}^{\mathit{I}}$ (μM)	ARexp	Source of ARexp estimate	[I] at ARmax(μM)	$\mathit{A}{\mathit{R}}_{\mathit{m}\mathit{a}\mathit{x}}:\mathbf{1}+[\mathit{I}]/{\mathit{K}}_{\mathit{d}}^{\mathit{I}}$	Optimality: ARexp/ARmax
Tang and Breaker (1997b)	ATP	OFF	10a	180	Ribozyme cleavage products on gel	1000	101	1.78
Soukup and Breaker (1999a)	FMN	ON	0.5b	33	Ribozyme cleavage products on gel	20	40	0.83
Suess et al. (2004)	Theophylline	OFF	0.3c	8	Beta-galactosidase activity in B. subtilis	6000	17,650	0.0005
Wieland, Benz, Klauser, and Hartig (2009)	TPP	ON	0.32d	7.5	GFP fluorescence in E. coli	100	313	0.02
Kellenberger et al. (2013)	c-AMP-GMP	ON	4.2e	6.4	Spinach-DFHBI fluorescence in E. coli	100	25	0.26

$K_d^I$ estimates sourced from

^aSassanfar and Szostak (1993)

^bBurgstaller and Famulok (1994)

^cJenison, Gill, Pardi, and Polisky (1994)

^dLang, Rieder, and Micura (2007)

^eKellenberger et al. (2013)

^fBraselmann et al. (2018).

Full data for the optimality estimates presented in Figs. 4 and 5 may be found in Table S1 in the online version at https://doi.org/10.1016/bs.mie.2019.05.028.

3.1. Optimality of natural riboswitches

Fig. 4 presents the observed activation ratios AR_exp and the estimated maximal activation ratios AR_max for a range of natural riboswitches, with studies presented in order of appearance in the literature. Fig. 4A depicts the experimental AR in dark bars, and the theoretical maximum AR in light bars; Fig. 4B depicts the optimality of each construct, defined as the ratio of the experimental AR to the theoretical maximum AR (Eq. 8). Each of these natural riboswitches has a clearly defined input and output module in its RNA sequence and therefore should be described well by the modeling of Section 2, at least when operating in the thermodynamic regime. The input ligands span a wide variety of natural metabolites, from the large coenzyme B12 to the small amino acid glycine. In each of the cases described in Fig. 4A, studies isolated and characterized an aptamer from the riboswitch that binds the input ligand. The output mechanisms involve presentation of other segments of the riboswitch in conformations able to recruit other molecular machines. The release of a Shine-Dalgarno region enables recruitment of the bacterial ribosome; the formation of a terminator hairpin trailed by multiple uridine bases initiates termination of the bacterial RNA polymerase. In a few eukaryotic cases, folding or presentation of appropriate pre-mRNA elements toggle recognition by the spliceosome. Data for these respective output mechanisms are colored blue, gray, and orange in Fig. 4. In all of these cases, if ligand-dependent riboswitch RNA rearrangements are fast compared to recruitment of the output, we expect the limit on activation ratio given by $A{R}_{max}=1+\frac{[I]}{K_d^I}$ to hold.

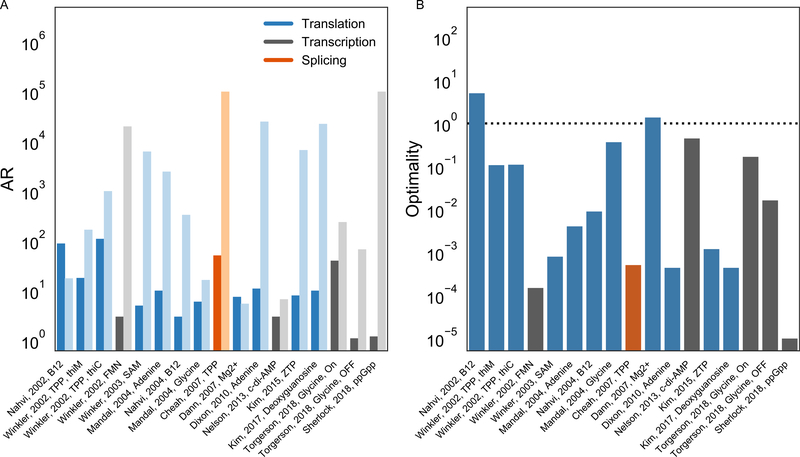
Fig. 4.

(A) Comparison of experimental (dark bars) and theoretically optimal ARs (light bars) of natural riboswitches in literature to date, as computed using the thermodynamic model presented here, presented in order of appearance in the literature. (B) Optimalities of natural riboswitches, computed as experimental AR/theoretical AR.

(C) Scatter plot of experimental and theoretical ARs. Values are only shown for cases where previous literature provide enough information to estimate both experimental and theoretically optimal ARs, see main text for caveats.

The vast majority of the natural riboswitches we surveyed did give activation ratios less than the optimum set by the input ligand concentration (15 of 17 cases). Indeed, for most of these riboswitches, AR_exp was lower than AR_max by more than an order of magnitude (13 of 17 cases). In these seemingly sub-optimal cases, the reporter systems used to experimentally characterize activation ratios may have perturbed the riboswitch from achieving peak performance, e.g., by saturating the output (see Eq. 3). For in vivo experiments, the intracellular input ligand concentrations may be smaller than the externally set total ligand concentrations, as noted above. Furthermore, these riboswitches are likely tuned through evolution to achieve the precise activation ratio necessary for their functional roles in natural systems. Indeed, the median AR_exp of these switches is 9.0 and is considered respectable for designed synthetic riboswitches (see next section), and natural riboswitches may make a tradeoff to ensure strong activation in their ON states.

For two of the cases we surveyed, the experimentally observed activation ratio exceeded the AR_max bound set from thermodynamic considerations. In one of these “super-optimal” cases, a Mg²⁺ sensor (Dann 3rd et al., 2007), both AR_exp and AR_max values were close to 5.0, and the values of intrinsic dissociation constant and activation ratios came from distinct studies by different groups, so it is unclear if the apparent super-optimality of this riboswitch is significant. The other super-optimal case came from a seminal study by Breaker and colleagues describing the first adenosylcobalamin riboswitch (abbreviated as B12 in Fig. 4), a btuB leader element in E. coli that toggles translation of a gene for a cobalamin transporter. All numbers needed for the optimality comparison were measured in the same study, using E. coli reporter measurements and in vitro equilibrium dialysis as appropriate. The AR_exp of this btuB leader element was 88.7 with adenosylcobalamin concentration [I] of 5μM. This experimentally observed activation ratio is higher by five-fold than the estimated AR_max value of 18, based on dissociation constant $K_d^I$ for the isolated riboswitch aptamer of 0.3 μM. It is possible that the apparent super-optimality of this riboswitch might be due to deviations of the intracellular ligand concentrations due to, e.g., active transport of extracellular adenosylcobalamin into E. coli, though it is worth considering possible mechanisms by which a translational riboswitch might surpass the thermodynamic limit (see Section 4).

3.2. Optimality of synthetic riboswitches

Fig. 5 presents observed and estimated maximal activation ratios for synthetic riboswitches, again with studies listed in order of appearance in the literature. As with natural riboswitches, each of these riboswitches contains a readily identifiable aptamer region for the input ligand and a separate region that recruits a separate ligand or molecular machine to activate an output. In terms of input ligands, synthetic riboswitches include aptamer segments for metabolites like thiamine pyrophosphate (abbreviated TPP in Fig. 5), reused from natural riboswitches described above. Synthetic riboswitches also make use of in vitro selected aptamers for a wide variety of small molecules that are not widespread in nature, such as tetracycline. In terms of output mechanisms, synthetic riboswitches have been designed to use the same translational, transcriptional, and splicing output as seen in natural riboswitches (blue, gray, and orange, respectively, in Fig. 5), but also illustrate novel applications that have not yet been seen in Nature. Output mechanisms including the activation of RNA self-cleavage through a hammerhead ribozyme module, binding of fluorescently labeled proteins such as the MS2 bacteriophage coat protein, or small molecules that become fluorescent when bound to RNA, and activation of CRISPR complexes by rearrangement or hammerhead-ribozyme processing of the guide RNA (brown, purple, red, green, and pink, respectively, in Fig. 5) have enabled control of metabolic pathways, visualization of tagged RNAs or cellular metabolites, and chemical control of CRISPR-mediated gene expression (see, e.g., Kellenberger et al., 2015, 2013; Liu et al., 2016; Win & Smolke, 2007).

Fig. 5.

(A) Comparison of experimental (dark bars) and theoretical ARs (light bars) of synthetic riboswitches in literature to date, presented in order of appearance in the literature. (B) Optimalities of synthetic riboswitches, computed as experimental AR/theoretical AR.

(C) Scatter plot depiction of optimal vs. experimental ARs. Values are only shown for cases where previous literature provide enough information to estimate both experimental and theoretically optimal ARs, see main text for caveats.

As with natural riboswitches, a majority of synthetic riboswitches give experimental activation ratios AR_exp that are significantly less than the AR_max bound set by $1+\frac{[I]}{K_d^I}$: 52 of 87 have optimalities below 10%, and 31 of 87 have optimalities below 1%.

It is again instructive to review the riboswitches that did obtain high optimality to try to understand how their mechanisms allow such performance or how caveats in the measurement and prediction of activation ratios might artifactually give rise to such high super-optimality. Synthetic riboswitches with stand-out activation ratios, when compared to their theoretical thermodynamic optimum values, include switches that couple binding of theophylline, flavin mononucleotide (FMN), and ATP to in vitro selected aptamers to hammerhead ribozyme (HHR) cleavage, discovered by Breaker and colleagues (Koizumi et al., 1999; Soukup & Breaker, 1999a, 1999b; Soukup, Emilsson, & Breaker, 2000); the c-AMP-GMP ON switch from (Kellenberger et al., 2013); S-adenosyl methionine (SAM), theophylline, 2-aminopyridine (2-AP), and other switches from (Ceres, Garst, et al., 2013; Ceres, Trausch, et al., 2013); the thyroxine OFF-switch from (Espah Borujeni et al., 2015); and a TPP-TAR riboswitch from (Endoh & Sugimoto, 2018). For most of these near-optimal or super-optimal cases, the optimal and experimental activation ratios were each 10-fold or lower and similar in value, and typically inferred from different studies (Endoh & Sugimoto, 2018; Espah Borujeni et al., 2015; Kellenberger et al., 2013); the actual optimality may be somewhat higher or lower depending on experimental uncertainties and it is difficult to comment further. For the HHR-coupled riboswitches reported in Koizumi et al. (1999), plotted with open symbols in Fig. 5, the aptamer segments were selected from random libraries concurrently with selection for ligand-dependent cleavage. It is possible that efforts to characterize the aptamer segment in isolation remain incomplete, or that the actual ligand binding sites involve segments of the hammerhead ribozyme that cannot be cleanly separated from the aptamer (Soukup, DeRose, Koizumi, & Breaker, 2001).

However, the other riboswitches appear exceptional. The general success of Ceres et al.’s modular incorporation of a variety of aptamers into transcription terminator riboswitches (Ceres, Garst, et al., 2013; Ceres, Trausch, et al., 2013), with high optimality for nearly all of their constructs, speaks to the effectiveness of their design principle for mixing and matching natural riboswitch transcriptional units to synthesize new switches. The types of riboswitch that exhibited the highest optimality were hammerhead-based ribozymes designed by Breaker and colleagues. Their success may be tied to the kinetic mechanism of HHR cleavage. Due to the tradeoffs described in Section 2, riboswitches that achieve optimality are unlikely to give strong output signals even under ON conditions, so most riboswitch design studies sacrifice activation ratio in order to yield an observable signal. Use of the hammerhead ribozyme cleavage readout, however, allows for direct characterization of riboswitch output even as cleavage rates change by >10,000-fold, and permits development and in vitro selection of extraordinary riboswitches. Due to the tradeoffs described in Section 2, these switches’ active states are not as efficient as constitutive hammerhead ribozymes. Nevertheless, the cleavage rates are still sufficiently fast such that total cleavage is attained in tens of minutes.

Despite these successes—which include several cases from early in the history of in vitro riboswitch engineering—this survey of activation ratios of synthetic riboswitches highlights the general difficulty of achieving optimality. For entire classes of riboswitches, including those that effect changes in pre-mRNA splicing and newer molecules that seek to couple binding of small molecules to binding of fluorophores or toggling of CRISPR-guided gene expression, activation ratios typically remain under 10-fold, and no switches have convincingly achieved the thermodynamic bound in activation ratio derived in Section 2.

4. Going beyond thermodynamic optimality

Deriving the bound on riboswitch activation ratio (Section 2) suggests ways in which the maximum activation ratio $A{R}_{max}=1+\frac{[I]}{K_d^I}$ might be consistently surpassed. These mechanisms might be worth searching for and establishing in natural riboswitches and might also be useful strategies for future studies designing synthetic riboswitches. We describe three mechanisms to go beyond the thermodynamic optimum, each involving riboswitch behaviors beyond the assumptions of our thermodynamic model.

First, the introduction of multiple instances of the aptamer within the target structure, enabling multiple ligands to bind simultaneously, effectively increases the ligand-binding energy. In this case, n copies of the aptamer results in an n-fold increased maximum activation achievable:

$$A{R}_{max}=1+{\left(\frac{[I]}{K_d^I}\right)}^n$$ (9)

Interestingly, some natural riboswitches for glycine, tetrahydrofolate, and cyclic di-AMP bind two copies of their target ligand. Thermodynamic analyses of intrinsic ligand binding to isolated riboswitch aptamers remains incomplete (see, e.g., Kladwang, Chou, & Das, 2012; Sherman et al., 2014), especially because, for some of these cases, the presence of two ligand binding sites only became evident after crystallographic studies that followed biochemical characterizations. However, it may be worthwhile to test if these riboswitches are surpassing the optimal activation ratios achieved with single ligands and to find out how close they get to the higher multiple-ligand AR_max bound in Eq. (9). For synthetic riboswitches, metal ion responsive hammerhead ribozymes discovered through in vitro selection give remarkable AR_exp values, higher than 10,000 (Seetharaman et al., 2001); biochemical characterization suggests that these RNAs also respond to multiple metal ions, but isolation of the metal ion binding aptamer regions and determination of intrinsic dissociation constants $K_d^I$ has not yet been carried out.

Another way to increase the energy introduced upon ligand binding and, thereby, the activation ratio is to design a riboswitch that utilizes multiple distinct binding sites to coordinate a single input ligand. Such extra contacts beyond the ligand aptamer, potentially including nucleotides in the output region, could increase the affinity of the riboswitch to its ligand, resulting in higher activation ratios than those predicted by the models herein. We predict that such extra contacts may be at play for some of the most effective synthetic riboswitches discovered in the literature, including the cyclic dinucleotide responsive and metal-ion responsive hammerhead ribozymes described by Koizumi et al. (1999) and Seetharaman et al. (2001). 3D structural approaches have not yet been brought to bear on those systems but might reveal contacts of the metal-ion binding regions to the hammerhead ribozyme “output” segment.

A final strategy for increasing activation ratios beyond $A{R}_{max}=1+\frac{[I]}{K_d^I}$ is suggested by natural systems that use out-of-equilibrium kinetic mechanisms to amplify specificities beyond the bounds set by equilibrium thermodynamics. The most famous examples are the kinetic proofreading mechanisms proposed by Ninio and Hopfield and applied to understand numerous molecular biological processes, including translation by the ribosome (Hopfield, 1974; Ninio, 1975). The ribosome is able to achieve extremely low error rates despite the small energy difference between a tRNA binding a correct vs. mismatched codon in the RNA message for a protein. This specificity is realized by requiring multiple pseudo-irreversible steps during the readout mechanism; passing each of these steps requires binding of the correct tRNA. This mechanism can increase optimal activation ratio by the power of n, given an n-step process to reach the downstream readout, as long as each step is separated by an irreversible process. Interestingly, similar to our discussion in Section 2, such mechanisms typically trade output optimality for enhanced specificity. Enforcing such irreversibility requires energy expenditure, and in the case of riboswitches, kinetic amplification of activation ratios can be instantiated through the polymerization of RNA by RNA polymerase or by the translation of ribosomes (R. Das, unpublished results). The riboswitch literature has already pointed out such out-of-equilibrium effects are likely occurring in natural and synthetic riboswitches with potentially positive consequences (see, e.g., Badelt, Hammer, Flamm, & Hofacker, 2015; Espah Borujeni & Salis, 2016; Sun et al., 2018; Wickiser et al., 2005). Establishing and designing “super-optimal” activation ratios in these out-of-equilibrium systems will be important milestones for upcoming riboswitch research.

5. How to evaluate riboswitch optimality

As riboswitch design and discovery efforts become more sophisticated, we propose that future studies should establish the efficacy of new riboswitches by comparing their experimentally observed performance to their maximum expected values. A useful first step in such comparisons is the one carried out herein: comparing experimental observed activation ratios to the best possible value for a riboswitch responding to its input ligand at thermodynamic equilibrium. Comparing the most useful data and experiments that we encountered across previous publications suggests six steps that could help ensure accurate evaluation of riboswitch optimality in future studies:

1. Measure the observed activation ratio AR_exp over a wide variety of input and output ligand concentrations.

A large source of uncertainty in our literature survey of AR_exp values involves incomplete characterization in the experimentally measured output signals, which are often presented without estimates of background signal rates (which require negative controls), maximal signal rates (which would require positive controls of ON-stabilized riboswitches), or error estimates. In addition to acquiring this information, riboswitch experiments would benefit from input ligand titrations, rather than a single choice of input ligand concentration. This helps test for saturation of the riboswitch output, and could provide insights into the mechanisms governing the system. Ceres, Garst, et al. (2013) and Truong, Hsieh, Truong, Jia, and Hammond (2018) provide excellent illustrations of these characterizations. For riboswitches that involve reversible recruitment of output molecules, e.g., small molecule biosensors that bind light-up fluorophores, the concentration of the output ligand ideally would also be varied. Fitting the resulting data to a standard binding isotherm (Eq. 2) would give more precise ARs than current procedures which typically choose a single output ligand concentration.

2. Estimate input ligand concentrations.

For in vitro applications, the input ligand concentrations ([I] in Section 2) are typically set by the experimentalist and are unambiguous. For in vivo applications, however, intracellular concentrations of the ligand may be different from extracellular concentrations and are typically not well characterized. We believe that an important methodological step in future studies should be to actually measure the total intracellular concentrations of the ligands as a function of extracellular ligand concentration, using quantitative mass spectrometry (Bennett, Yuan, Kimball, & Rabinowitz, 2008).

3. Estimate $K_d^I$.

For many synthetic riboswitch design studies, the input aptamer is sourced from previous in vitro selection or biochemical characterization studies, and the intrinsic dissociation constant $K_d^I$ is known, although it is worthwhile repeating that measurement under temperature and solution conditions that match the conditions used to characterize the full riboswitch. For studies of natural riboswitches, mutations or truncations must be introduced that stabilize the natural RNA in the conformation ready to bind the ligand; for riboswitches whose aptamers have been crystallized, such stabilized constructs have already been developed. There are several available methods to estimate dissociation constants of ligands to RNA in vitro in nearly arbitrary solution conditions; perhaps the most general approach involves chemical probing of the aptamer RNA as the ligand concentration is changed (Regulski & Breaker, 2008). Extensions of these chemical mapping approaches to in vivo characterization of dissociation constants would be powerful but have not been established.

4. Estimate AR_max.

Authors should compute $A{R}_{max}=1+\frac{[I]}{K_d^I}$ of their riboswitch system at each input ligand concentration. If the observed activation ratio AR_exp is lower than AR_max, it is worth considering what factors might cause this, and, if necessary, how to modulate the riboswitches optimality. Possible factors are alternative conformational states that do not properly couple input to output (see Appendix A), saturation of output, and errors in experimental estimates. If the observed activation ratio AR_exp is higher than AR_max, the thermodynamic bound has been surpassed, and it is important to understand how that has happened. Section 4 outlines possible scenarios.

5. Computational prediction of activation ratios.

There are few cases in the literature that computationally predict the activation ratio of a riboswitch given its sequence and the known structures of its input aptamer and output-recruiting module. Sophisticated computational methods have existed for a long time to model riboswitch conformational ensembles and energetics but have typically required software “hacks” to get the information needed to estimate activation ratios. The recent availability of user-defined ligand binding sites and energetic bonuses in the Vienna 2.0 RNA folding package (Findeiβ et al., 2018) is therefore strongly welcomed. In Appendix B, we include an example calculation for the activation ratio of a riboswitch that toggles translation with theophylline using this latest Vienna package and find reasonable agreement of the calculation with the experiments.

6. More detailed modeling.

While we believe that measuring activation ratios and comparing to theoretical optima is a first step in understanding how a riboswitch works, a deeper understanding comes from modeling the complete ligand dependence of the systems, the kinetics of the process, and perhaps idiosyncratic events in how any recruited molecular machines eventually give rise to outputs. For example, some riboswitch studies already provide detailed data sweeping the input ligand concentrations over very wide ranges (e.g., Ceres, Garst, et al., 2013; Ceres, Trausch, et al., 2013). These data strongly constrain models of the riboswitch behavior; for example the K_fold parameter in Section 2 can be set based on the midpoint of these input ligand titrations and the known intrinsic aptamer $K_d^I$. Additional data from these experiments can rigorously test predictions—such as how the maximal activation ratio seen at high input ligand concentrations is set by K_fold—and check that mutations of the sequences in switch and aptamer regions behave as predicted from prospective computational methods such as Vienna 2.0. Such quantitative biophysical modeling will be particularly critical for riboswitches designed or discovered to surpass the thermodynamic optimum (Section 4).

In summary, riboswitches are promising genetic regulation elements that can render the exquisite specificity of RNA recognition into a variety of important biological processes, but thus far the optimality of the majority of designed riboswitches has been low. This chapter has presented a method to compute the theoretical maximum activation ratio of a riboswitch operating at thermodynamic equilibrium and highlights existing natural and synthetic riboswitches that have obtained the highest efficiencies. With the method presented here to estimate riboswitch optimality, we hope that researchers will be able to better characterize what factors are currently dampening riboswitch performance and that this will lead to improvements in general riboswitch design.

Supplementary Material

Table S1

Full dataset of riboswitch constructs displayed in in Fig. 4, Fig. 5. Data include literature citations, riboswitch types, experimental conditions, reported ligand concentrations, reported experimental activation ratios (ARs), ligand-aptamer dissociation constants used for estimating theoretically optimal AR and the source of the dissociation constant, and computed theoretically optimal ARs.

Appendix A. Optimal activation ratio for a general model

We here present the fully generalized nine-state model for riboswitch function. We assume a riboswitch contains two distinct sequence motifs, or aptamers, one of which binds an input molecule (I), and one of which binds an output molecule (O), which may be a ribosome, a fluorogenic molecule, etc. To write an expression for the partition function of the system, we begin by defining the set of states that the riboswitch can adopt. We group all of the possible RNA structures based on the presence of zero, one, or both aptamers. The conversion of each aptamer from a conformation unable to bind a ligand to a conformation that is able to bind a ligand has an associated free energy penalty. Each of these states can bind zero, one, or two molecules (I or O), limited by the presence of the required aptamer motif. There are nine possible states (Fig. A1). Thus, the partition function for our system contains nine terms,

$$\begin{array}{l}Z=\exp \left(-\frac{\Delta G_{fold}^{init}}{k_{B}T}\right)+\exp \left(-\frac{\Delta G_{fold}^O}{k_{B}T}\right)+\exp \left(-\frac{\Delta G_{fold}^O+\mathrm{\Delta }{G}_{bind}^O}{k_{B}T}\right)\\ +\exp \left(-\frac{\Delta G_{fold}^I}{k_{B}T}\right)+\exp \left(-\frac{\Delta G_{fold}^I+\mathrm{\Delta }{G}_{bind}^I}{k_{B}T}\right)+\exp \left(-\frac{\Delta G_{fold}^{I,O}}{k_{B}T}\right)\\ +\exp \left(-\frac{\Delta G_{fold}^{I,O}+\mathrm{\Delta }{G}_{bind}^I}{k_{B}T}\right)+\exp \left(-\frac{\Delta G_{fold}^{I,O}+\mathrm{\Delta }{G}_{bind}^O}{k_{B}T}\right)\\ +\exp \left(-\frac{\Delta G_{fold}^{I,O}+\mathrm{\Delta }{G}_{bind}^I+\mathrm{\Delta }{G}_{bind}^O}{k_{B}T}\right)\end{array},$$

Fig. A1.

A depiction of states and weights for a generalized nine-state model of riboswitch function.

where ΔG_fold is the Gibbs free energy cost of folding (superscript I and O indicate the presence and absence of the respective aptamer motif in the RNA structure), and ΔG_bind is the Gibbs free energy contribution of binding the input or output as indicated (depicted in Fig. A1).

We set the state where neither aptamer has formed, in the absence of ligands I and O, to have an energy of zero, $\Delta G_{fold}^{init}=0$. We substitute $\exp \left(-\frac{\Delta G_{fold}}{k_{B}T}\right)=S$ for clarity. For both aptamers, we make the substitution

$$\exp \left(-\frac{\Delta \Delta G_{bind}}{k_{B}T}\right)=\frac{[T]}{K_d^T},$$

where $K_d^T$ is the dissociation constant of the aptamer with molecule T, and [T] is the concentration of the molecule. The partition function above becomes

$$Z=1+S_O\left(1+\frac{[O]}{K_d^O}\right)+S_I\left(1+\frac{[I]}{K_d^I}\right)+S_{IO}\left(1+\frac{[O]}{K_d^O}+\frac{[I]}{K_d^I}+\frac{[O]}{K_d^O}\frac{[I]}{K_d^I}\right).$$

We wish to determine the fraction of RNA that exists in the output-bound state (f_OB), as this represents the downstream signal generated by the riboswitch. This can be determined as

$$\begin{gathered} f_{OB}=\frac{S_O\frac{[O]}{K_d^O}+S_{IO}\left(\frac{[O]}{K_d^O}+\frac{[O]}{K_d^O}\frac{[I]}{K_d^I}\right)}{Z}Z=\frac{[O]\left(\frac{[O]}{K_d^O}+\frac{S_{IO}}{K_d^O}+\frac{S_{IO}}{K_d^O}\frac{[I]}{K_d^I}\right)}{Z} \\ =\frac{[O]\left(\frac{K_d^I{S}_O+K_d^I{S}_{IO}+S_{IO}[I]}{K_d^I{K}_d^O}\right)}{Z} \end{gathered}$$

Substituting in the full partition function and simplifying further, we obtain

$$f_{OB}=\frac{[O]}{[O]+K_d^O\left(\frac{K_d^I\left(1+S_O+S_I+S_{IO}\right)+[I]\left(S_I+S_{IO}\right)}{K_d^I\left(S_O+S_{IO}\right)+[I]S_{IO}}\right)}.$$

This equation thus describes the magnitude of the riboswitch signal as it relates to the concentrations of reporter and ligand, the binding affinities of the aptamers, and the folding free energies of the different aptamer-containing structures.

We define the activation ratio of a riboswitch as the signal difference in the absence vs. presence of the target ligand. The background signal of the riboswitch is simply f_OB evaluated at [I] = 0,

$$f_{OB}^{[I]=0}=\frac{[O]}{[O]+K_d^O\left(\frac{1+S_O+S_I+S_{IO}}{S_O+S_{IO}}\right)}$$

The activation ratio for an ON-switch can then computed as

$$AR=\frac{f_{OB}}{f_{OB}^{[I]=0}}=\frac{[O]+K_d^O\left(\frac{1+S_O+S_I+S_{IO}}{S_O+S_{IO}}\right)}{[O]+K_d^O\left(\frac{K_d^I\left(1+S_O+S_I+S_{IO}\right)+[I]\left(S_I+S_{IO}\right)}{K_d^I\left(S_O+S_{IO}\right)+[I]S_{IO}}\right)}$$

For an OFF-switch, the AR is defined as $\frac{f_{OB}^{[I]=0}}{f_{OB}}$ and gives the same equation. From here, we can identify the properties and conditions of an ideal riboswitch that maximize the activation ratio. First, this ratio is maximized as the concentration of reporter becomes very small (i.e., [O]→0):

$${AR}^{[O]\to 0}=\frac{\frac{1+S_O+S_I+S_{IO}}{S_O+S_{IO}}}{\frac{K_d^I\left(1+S_O+S_I+S_{IO}\right)+[I]\left(S_I+S_{IO}\right)}{K_d^I\left(S_O+S_{IO}\right)+[I]S_{IO}}}=\frac{1+\frac{[I]}{K_d^I}\left(\frac{S_{IO}}{S_O+S_{IO}}\right)}{1+\frac{[I]}{K_d^I}\frac{S_I+S_{IO}}{1+S_O+S_I+S_{IO}}}$$

Thus, an optimal riboswitch has very costly transitions into the input and output aptamer-containing structures (described by S_I and S_O, respectively); so S_O, S_I≪1, and a relatively more favorable (but still costly) transition into the state containing both aptamers (S_IO); that is, S_O+S_I+S_IO≈S_IO≪1. Under these conditions, the riboswitch obtains its maximum activation ratio:

$$A{R}_{max}=1+\frac{[I]}{K_d^I}$$

Appendix B. Computational prediction of activation ratios

As an example, we walk through the calculation of error rates for a theophylline riboswitch described by Lynch, Desai, Sajja, and Gallivan (2007) (clone 8.1). We assume that translation will be activated proportionally to the prevalence of structures that have the RBS and start codon exposed.

First, we calculate the probability that the sequence will adopt an exposed conformation in the absence of theophylline. We use ViennaRNA 2.4.4 (Lorenz et al., 2011) to compute the ensemble free energies with and without a constraint specifying that the RBS and start codon are unpaired.

   $ echo −e
   “GGUGAUACCAGCAUCGUCUUGAUGCCCUUGGCAGCACCCCGCUGCAAGACAACAAGAUG\n.....
   .......................................xxxxxxxxxxxxx” | RNAfold −p −C
      GGUGAUACCAGCAUCGUCUUGAUGCCCUUGGCAGCACCCCGCUGCAAGACAACAAGAUG
(((...))).(((((.....))))).....(((((.....)))))............. (−15.30)
(((...})).(((((,...,))))).....(((((.....)))))............. [−15.88]
(((...))).(((((.....))))).....(((((.....))))).............{−15.30
      d=1.98}
       frequency of mfe structure in ensemble 0.389169; ensemble diversity
      3.22

The value −15.88 is the ΔG_constrained, the free energy of the RNA in kcal/mol, summed over all structures with the constraint that the RBS and start codon are unpaired.

 $  echo  “GGUGAUACCAGCAUCGUCUUGAUGCCCUUGGCAGCACCCCGCUGCAAGACAACAA
GAUG” | RNAfold −p
GGUGAUACCAGCAUCGUCUUGAUGCCCUUGGCAGCACCCCGCUGCAAGACAACAAGAUG
(((...))).....(((((((.((..((((.((((.....)))))))).)).)))))))
(−18.40)
(((,..,,)..,..(((((((.((..(((,{((((.....)))))))).)).)))))))
[−19.75]
..............(((((((.((..(((.(((((.....)))))))).)).))))))) {−17.10
d=5.39}
  frequency of mfe structure in ensemble 0.112679; ensemble diver-
sity 7.67

The value −19.75 is the ΔG_{unconstrained}, the free energy of the RNA in kcal/mol, summed over all structures with no constraints. We then calculate the probability as

$$signa{l}_{OFF}=\frac{\exp \left(-\mathrm{\Delta }{G}_{constrained}/k_{B}T\right)}{\exp \left(-\mathrm{\Delta }{G}_{unconstrained}/k_{B}T\right)}=1.87\times {10}^{-3}$$

Here, we used k_BT=0.616 kcal/mol.

We perform a similar calculation for signal in the presence of ligand, but with an energetic bonus for the formation of the theophylline aptamer. We compute the energetic bonus as

$$E=-k_{B}T\ln \frac{[theo]}{K_d^{theo}}=-4.91\text{kcal}/\text{mol}.$$

where we used [theo] of 1 mM and $K_d^{theo}$ of 340 nM. We then use ViennaRNA to obtain the constrained and unconstrained ensemble free energies, with this ligand bonus.

$ echo −e
“GGUGAUACCAGCAUCGUCUUGAUGCCCUUGGCAGCACCCCGCUGCAAGACAACAAGAUG\n...
...........................................xxxxxxxxxxxxx” | RNAfold –
motif=“GAUACCAG&CCCUUGGCAGC,(...((.(&)....))...),−4.9” −p −C
GGUGAUACCAGCAUCGUCUUGAUGCCCUUGGCAGCACCCCGCUGCAAGACAACAAGAUG
((((...((.(((((.....)))))....))...))))..................... (−16.39)
((((...((.(((((,...,)))))....))...))))..................... [−16.84]
((((...((.(((((.....)))))....))...))))..................... {−11.50
d=3.10}
  frequency of mfe structure in ensemble 0.48021; ensemble diver-
sity 4.89
$    echo    “GGUGAUACCAGCAUCGUCUUGAUGCCCUUGGCAGCACCCCGCUGCAAGACAACA
AGAUG”| RNAfold –motif=“GAUACCAG&CCCUUGGCAGC,(...((.(&)....))...),−
4.9” −p
GGUGAUACCAGCAUCGUCUUGAUGCCCUUGGCAGCACCCCGCUGCAAGACAACAAGAUG
(((...))).....(((((((.((..((((.((((.....)))))))).)).))))))) (−18.40)
(((,..,,)..,..(((((((.((..(((,{((((.....)))))))).)).))))))) [−19.75]
..............(((((((.((..(((.(((((.....)))))))).)).))))))) {−17.10
d=5.63}
  frequency of mfe structure in ensemble 0.111545; ensemble diver-
sity 8.13

This unconstrained free energy is very similar to that without theophylline, due to the relatively low prevalence of the theophylline-aptamer-forming structures in the overall ensemble. We calculate the probability of adopting a translation-compatible conformation as

$$signa{l}_{ON}=\frac{\exp \left(-\mathrm{\Delta }{G}_{constrained}/k_{B}T\right)}{\exp \left(-\mathrm{\Delta }{G}_{unconstrained}/k_{B}T\right)}=8.88\times {10}^{-3}.$$

Finally, we compute the predicted activation ratio,

$$A{R}_{predicted}=signa{l}_{ON}/signa{l}_{OFF}=\mathrm{4.75.}$$

This predicts the correct direction of switching. Though the experimentally measured activation ratio (36) is substantially higher than the value above, these calculations suggest that this riboswitch is mostly off, even in the presence of theophylline. This is aligned with the observation that there is a tradeoff between high fold ratio and high signal level (see main text in Section 2).