Age-dependent cut-offs for pathological deep gray matter and thalamic volume loss using Jacobian integration

Highlights

• •Longitudinal MRI data of 189 healthy controls and 127 MS patients were analyzed.
• •Deep gray matter (deep GMVL) thalamic volume loss (ThalaVL) was assessed.
• •Magnitude of measurement error was estimated by means of 162 MRI scan-rescans.
• •Age-dependent cut-offs for pathological deep GMVL and ThalaVL are provided.
• •Result help interpreting deep GMVL and ThalaVL measurements in individual MS patients.

Abstract

Introduction

Several recent studies indicate that deep gray matter or thalamic volume loss (VL) might be promising surrogate markers of disease activity in multiple sclerosis (MS) patients. To allow applying these markers to individual MS patients in clinical routine, age-dependent cut-offs distinguishing physiological from pathological VL and an estimation of the measurement error, which provides the confidence of the result, are to be defined.

Methods

Longitudinal MRI scans of the following cohorts were analyzed in this study: 189 healthy controls (HC) (mean age 54 years, 22% female), 98 MS patients from Zurich university hospital (mean age 34 years, 62% female), 33 MS patients from Dresden university hospital (mean age 38 years, 60% female), and publicly available reliability data sets consisting of 162 short-term MRI scan-rescan pairs with scan intervals of days or few weeks. Percentage annualized whole brain volume loss (BVL), gray matter (GM) volume loss (GMVL), deep gray matter volume loss (deep GMVL), and thalamic volume loss (ThalaVL) were computed deploying the Jacobian integration (JI) method. BVL was additionally computed using Siena, an established method used in many Phase III drug trials. A linear mixed effect model was used to estimate the measurement error as the standard deviation (SD) of model residuals of all 162 scan-rescan pairs For estimation of age-dependent cut-offs, a quadratic regression function between age and the corresponding annualized VL values of the HC was computed. The 5th percentile was defined as the threshold for pathological VL per year since 95% of HC subjects exhibit a less pronounced VL for a given age. For the MS patients BVL, GMVL, deep GMVL, and ThalaVL were mutually compared and a paired t-test was used to test whether there are systematic differences in VL between these brain regions.

Results

Siena and JI showed a high agreement for BVL measures, with a median absolute difference of 0.1% and a correlation coefficient of r = 0.78. Siena and GMVL showed a similar standard deviation (SD) of the scan-rescan error of 0.28% and 0.29%, respectively. For deep GMVL, ThalaVL the SD of the scan-rescan error was slightly higher (0.43% and 0.5%, respectively). Among the HC the thalamus showed the highest mean VL (−0.16%, −0.39%, and −0.59% at ages 35, 55, and 75, respectively). Corresponding cut-offs for a pathological VL/year were −0.68%, −0.91%, and −1.11%. The MS cohorts did not differ in BVL and GMVL. However, both MS cohorts showed a significantly (p = 0.05) stronger deep GMVL than BVL per year.

Conclusion

It might be methodologically feasible to assess deep GMVL using JI in individual MS patients. However, age and the measurement error need to be taken into account. Furthermore, deep GMVL may be used as a complementary marker to BVL since MS patients exhibit a significantly stronger deep GMVL than BVL.

1. Introduction

Magnetic resonance imaging (MRI)-derived whole brain volume loss (BVL) is increasingly recognized as an important imaging marker of neurodegeneration in multiple sclerosis (MS), and has recently been recommended to be included into the “no evidence of disease activity” (NEDA) criteria (Giovannoni, et al., 2015). However, measurement of BVL in individual MS patients is a matter of controversy (Barkhof, 2016, Zivadinov et al., 2016). Individual measures appear impacted by short-term biological noise (De Stefano et al., 2017, Hagemann et al., 2011), such as hydration status (Duning, et al., 2005) and the difficulty that with increasing age also BVL increases, even in the absence of pathological processes (Hedman, et al., 2012). Several recent publications addressed these issues. Age dependent cut-offs for annual BVL (BVL per year) have been suggested to help distinguishing physiological from pathological BVL (Battaglini et al., 2019, Opfer et al., 2018a). Furthermore, the measurement error and magnitude of potential short-term biological confounders such as hydration status have been determined (Narayanan et al., 2020, Opfer et al., 2018b).

A number of these studies showed that BVL in MS is not homogeneous but rather has a more focal distribution (for review see (Lansley, et al., 2013)). Most studies found patterns of gray matter (GM) volume loss (GMVL) in relapsing remitting MS (RRMS) patients involving deep GM structures such as the thalamus and basal ganglia (Lansley, et al., 2013). The MAGNIMS study group proved deep GM volume loss (deep GMVL) a driver of disability worsening (Eshaghi, et al., 2018). Furthermore, in recent phase III MS drug trials thalamic volume loss (ThalaVL) and GMVL were included as an exploratory (Cohen et al., 2010, Kappos et al., 2010) or even a secondary endpoint (Cohen et al., 2019, Comi et al., 2019).

As is the case in BVL, it is important to determine age dependent cut-off values and the magnitude of the measurement error in order to allow for a solid interpretation of deep GMVL in individual MS patients. Due to the mentioned more focal distribution of BVL it is not possible to apply results established for BVL to measurements of regional VL (Azevedo, et al., 2019).

In this study Jacobian integration (JI) (Ashburner, 2007, Nakamura et al., 2014) was used to determine GMVL, deep GMVL, and ThalaVL. Siena (Smith, 2002) is an established method used in many phase III drug trials to quantify BVL. However, since Siena critically depends on brain surface changes, it is not a suitable methodology to determine regional VL. JI uses elastic registration between a baseline and follow-up image. The volume change is derived from the transformation between these two images (more precisely from the Jacobian determinant of the transformation field). Therefore, JI can be used to compute BVL (like Siena) but regional VL in addition. The JI method has previously been validated (Nakamura, et al., 2014) and is widely accepted as a tool to assess regional VL in structural MRI (Steenwijk, et al., 2017). However, there are different implementations of JI available. Depending on the deployed underlying registration algorithms, results derived from JI can differ significantly (Beadnall, et al., 2019).

The aim of this paper is to define age-dependent cut-off values for GMVL, deep GMVL, and ThalaVL. For these measures an estimation of the measurement error shall be determined, which provides an estimation of the confidence in a measurement of an individual patient. A cohort of MS patients with longitudinal MRI data was used to determine the fraction of patients showing pathological VL taking the patient’s age into account.

2. Methods and materials

2.1. Longitudinal cohort of healthy controls (HC)

A cohort of 189 individuals with no history of or currently ongoing neurological or psychiatric condition, with at least two MRI scans of the same scanner and same acquisition protocol and no structural abnormalities on these brain MRIs according to visual inspection by an experienced radiologist (C.G.) was consecutively extracted from a group of asymptomatic, healthy subjects undergoing a brain MRI scan as part of an extensive medical prevention program at the Conradia Medical Prevention Center in Hamburg, Germany. All subjects gave written informed consent. The study was approved by the Ethics Committee of the Board of Physicians in Hamburg, Germany. Eligible subjects received two or more MRI examinations on the same 1.5 Tesla (T) Magnetom Avanto scanner (Siemens Medical Solutions, Erlangen, Germany) using identical sequence settings. The sequence was obtained before contrast agent administration. Scanner, protocol settings, head coil, and software version were kept unchanged for all subjects enrolled into this study. Mean age of the 189 individuals was 53.9 years with a standard deviation (SD) of 10.6 years. Mean interval between first and last MRI scan was 3.5 years. An average of 2.4 scans was available for each patient with a mean time interval between two consecutive scans of 2.5 years. Detailed protocol settings as well as a clinical characterization of all cohorts are provided in Table 1.

Table 1.

Patient characteristics and MRI protocol details.

	Healthy controls	MS patients		Reliability datasets
Cohorts		Zurich	Dresden	Maclaren	OASIS	Biberacher
sample size	189	94	33	3	20	2
healthy	189	NA	NA	3	20	NA
MS type at BL (CIS/RRMS/SPMS/PPMS)	NA	33/54/0/3	0/33/0/0	NA	NA	0/2/0/0
female	43 (22%)	58 (62%)	20 (60%)	1 (33%)	12 (60%)	2 (100%)
age (years)	53.9 (±10.6)	34.2 (±8.8)	38.2 (±10.1)	26, 31 and 30	22 (20–25)	29 and 24
disease duration (years)	NA	2.7 (±4.5)	5.2 (±4.8)	NA	NA	5 and 5.5
EDSS	NA	1.3 (±1.3)	2.7 (±1.6)	NA	NA	1 and 2
mean no. of scans per patient	2.4	3.5	3.9	40	2	5 or 6
mean interval between two consecutive scans	2.5 years	1.1 years	1.1 years	1 (max 3) days	11 (3–31) days	3 (3–4) days
mean scan interval first and last scan	3.5 (±1.9) years	2.8 (±1.3) years	3.0 (±0.4) years	30 days	11 (3–31) days	2–3 weeks
MRI scanner	1.5 T Siemens Avanto	3 T Philips Ingenia	3 T Siemens Verio	3 T GE Discovery	1.5 T Siemens Vision	3 T GE Signa
						3 T Philips Achiva
						3 T Siemens Verio
voxel size in mm	1	0.7	1.25	1	1	0.9, 1, 1
slice thickness (mm)	1	0.9	1.5	1.2	1.25	1
flip angle (°)	15	8	9
TR (ms)	980	8.9	2000	7.3	9.7	8.2, 9, <9
TE (ms)	2.95	4.07	2.8	3	4	3.2, 4, 2.45
TI (ms)	600	NA	900	400	20	450, 1000, 900

2.2. Longitudinal cohort of MS patients

2.2.1. Zurich MS cohort

This data set of 94 MS patients is part of an observational study carried out at the University Hospital of Zurich, Switzerland. All images were acquired with a 3.0 T Philips Ingenia scanner (Philips, Eindhoven, Netherlands). Mean age was 34.2 years (SD 8.8 years). Mean interval between first and last MRI scan was 2.8 years. For each patient an average of 3.5 scans were available with a mean time interval between two consecutive scan of 1.1 years. All subjects gave written informed consent. The study was approved by the local ethics committee.

2.2.2. Dresden MS cohort

MRIs from 33 MS patients were included, acquired at Institute of Diagnostic and Interventional Neuroradiology, University Hospital Carl Gustav Carus, with a 3.0 T Siemens Verio scanner. Mean age was 38.2 years (SD 10.1 years). 32 patients had 4 scans each with a mean time interval between two consecutive scans of 1.1 years. For one patient only two scans were available. Mean interval between first and last MRI scan for all patients was 3.9 years. All subjects gave written informed consent. The study was approved by the local ethics committee.

2.3. Reliability datasets

As in a previous study (Opfer, et al., 2018b) three publicly available MRI datasets were used to estimate the magnitude of the measurement error.

2.3.1. Maclaren dataset

This freely available MRI dataset contains data from three healthy subjects (2 males, 1 female; 26, 31 and 30 years old) (Maclaren, et al., 2014). For each subject, 20 MRI examinations were performed within a 31-day period on a 3.0 T General Electric (GE) MRI scanner. In each scanning session, every subject was scanned twice with repositioning of the subject between scans.

2.3.2. OASIS reliability dataset

The OASIS reliability dataset is part of the cross-sectional Open Access Series of Imaging Studies (OASIS (Marcus, et al., 2007), http://oasis-brains.org/) and contains data from 20 healthy controls who received two MRI examinations on a 1.5 T Siemens scanner. Median age is 22 (interquartile range (IQR) 20–25) years and median interval between the two scans 11 (IQR 3–31) days.

2.3.3. Biberacher dataset

The freely available MRI dataset from Biberacher and colleagues (Biberacher, et al., 2016) provides data from two relapsing-remitting MS patients (both female; 29 and 24 years old). Within three weeks, patients received five or six MRI examinations, each time on three different 3.0 T scanners (Philips, Siemens and GE) with an interval of several days between scans.

2.4. Lesion filling

To mitigate the effect of mis-registration between baseline (BL) and follow-up (FU) scan due to appearance of new or enlarged lesions a lesion filling procedure was performed as a first processing step for all images (BL and FU) belonging to the longitudinal MS cohorts. For both MS cohorts a 3D FLAIR MRI sequence was acquired in the same imaging session the corresponding T1 weighted sequence (Table 1) was acquired. Hyperintense lesions were contoured on the corresponding FLAIR images with a semiautomatic procedure. The resulting lesion maps were rigidly registered to the corresponding T1 image and the lesion map was used to replace the voxel intensities of lesion voxels in the T1-weighted MRI image with estimated “healthy” white matter intensity using the algorithm by Valverde and colleagues (Valverde, et al., 2017). The Statistical Parameter Mapping (SPM version 12, Oxford, UK) software package (short SPM12) toolbox “SLF_lesion_filling” as provided by this author was deployed. For the MS cohorts the lesion filled images were used for further computations in Section 2.5 (Siena) and 2.6 (Jacobian integration).

2.5. BVL loss with Siena

BVL between two time points was quantified using the Structural Image Evaluation using Normalisation of Atrophy (Siena, version 5.06) method (Smith, 2002), which is part of the FMRIB Software Library (FSL; http://www.fmrib.ox.ac.uk/fsl). It is well known that the performance of Siena can differ greatly depending on parameter settings and preprocessing steps (Cover, et al., 2014) (Popescu, et al., 2013). As in (Opfer et al., 2018a, Opfer et al., 2018b) we applied the FSL script “fslreorient2std” to match the orientation of all images to that of the standard template image (Montreal Neurological Institute). In addition a neck removal as recommended in (Popescu, et al., 2012) was performed. As recommended in the mentioned papers Siena settings “-B -f 0.2 -m” were used, which differ from the default settings. The parameter “-B -f 0.2” means that the default option for the brain extraction tool (BET) is changed from default 0.5 to 0.2 and “-m” enforces a standard-space masking in addition to BET. With the configuration described, BVL (in %) was calculated for all MRI data pairs.

2.6. Regional VL with Jacobian integration (JI) method

Regional VL was computed by a number of processing steps as described in the following. The processing was performed using SPM12 under MATLAB 2014a. For the statistical analysis the Statistics and Machine Learning Toolbox by MATLAB was used.

2.6.1. Image registration and JI

For longitudinal assessment of regional VL the “longitudinal pairwise registration” toolbox as provided by SPM12 was used. The longitudinal registration technique is based on a pairwise inverse-consistent highly elastic diffeomorphic alignment of the BL and the FU scan to a halfway space of the subject. The approach incorporates rigid registration into a halfway space (a space between BL and FU image) and correction for intensity inhomogeneities (Ashburner, 2007, Ashburner and Ridgway, 2012). The tool provides the Jacobian determinant (short, the Jacobian) of the transformation field as an output image in the same space as the halfway image space. The output Jacobian is the composition of two Jacobians: the Jacobian of the transformation field from the halfway space image to the FU scan and the negative Jacobian from the halfway image to the BL scan. Each voxel of the Jacobian therefore describes the percentage volumetric change between BL and FU image for that particular voxel location. In order to obtain volumetric change of certain subregions of the brain the signal of the Jacobian needs to be integrated over a region of interest. Region of interests are defined by image segmentation of the halfway image space.

2.6.2. Segmentation of gray and white matter

For each subject the halfway T1 MRI image (lesions were filled for the MS patients) was segmented into gray matter (GM) and white matter (WM) using a previously described and validated atlas-based volumetry approach implemented in SPM12 (Huppertz et al., 2010, Opfer et al., 2016). The resulting GM and WM maps are probability maps in the halfway image space of the subject with values between 0 and 1.

2.6.3. Segmentation of deep gray matter structures

Deep GM structures in the halfway image space of each subject were segmented using the FIRST module from the FMRIB’s Software Library (FSL; version 5.0; http://fsl.fmrib.ox.ac.uk/fsl). The FIRST module provides binary segmentation masks of the thalamus, caudate, putamen, pallidum, hippocampus, amygdala and accumbens.

2.6.4. Computing regional VL

Regional VL was computed as the weighted sum over the Jacobian for the following regions

• •whole brain volume loss: $\mathrm{B}\mathrm{V}\mathrm{L}\mathrm{J}\mathrm{I}=\sum {\mathrm{J}\mathrm{a}\mathrm{c}\mathrm{o}\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{n}}_i·\left(g{m}_i+w{m}_i\right)/\sum (g{m}_i+w{m}_i)$,
• •gray matter volume loss: $\mathrm{G}\mathrm{M}\mathrm{V}\mathrm{L}\mathrm{J}\mathrm{I}=\sum {\mathrm{J}\mathrm{a}\mathrm{c}\mathrm{o}\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{n}}_i·g{m}_i/\sum g{m}_i$,
• •deep gray matter volume loss: deep GMVL JI = $\sum {\mathrm{J}\mathrm{a}\mathrm{c}\mathrm{o}\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{n}}_i·deepg{m}_i/\sum deepg{m}_i$,
• •thalamic volume loss: ThalaVL JI = $\sum {\mathrm{J}\mathrm{a}\mathrm{c}\mathrm{o}\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{n}}_i·tha{l}_i/\sum tha{l}_i$,

with the sum over all image voxels i. Deep GM was defined as the sum of the thalamus, caudate, putamen, amygdala, and the pallidum. The same definition was used in the recent study by the MAGNIMS study group (Eshaghi, et al., 2018).

2.6.5. Regularization

The JI approach is based on an elastic, highly non-linear registration between two longitudinal images. To co-register the images, an optimization problem is solved. The optimization minimizes a weighted sum of two terms. The first term describes the similarity between the deformed image and the target image and the second regularization term describes the complexity of the applied non-linear transformation. This regularization term is introduced to prevent sharp discontinuities in the resulting transformation fields and to achieve anatomically consistent and meaningful results. In general a higher weight on the regularization term will result in a more rigid transformation field. In (Ashburner and Ridgway, 2012) the influence of the 5 regularization parameters is described. The default regularization parameter provided by the toolbox (the values [0 0 100 25 100]) were used. The SPM12 longitudinal pairwise registration toolbox allows specifying a time interval in years between the scans. In the default implementation the values [0 0 100 25 100] are divided by the scan interval in years, resulting in a lower regularization. This approach is based on the assumption that healthy individuals exhibit approximately −0.2% BVL per year. Since BVL depends on the age and since MS patient can have significantly higher BVL per year than healthy individuals this approach was modified. The regularization was chosen to be inversely proportional to the BVL measured by the Siena method (see above). The regularization parameters [0 0 100 25 100] were divided by the factor abs(measured BVL Siena)/0.2 and the time interval was set to 1 year regardless of the true scanning interval. The interval was set to 1 year in order to prevent the built-in scaling of the regularization parameter with the scan interval. The resulting BVL was annualized by dividing the measured BVL with the true scan interval in years (BVL per year or short BVL/year). For an individual with a BVL of 0.2% per year this would result in the default setting for a one-year interval. For higher BVL the regularization is relaxed and allows the transformation field to be more flexible regardless of the time interval.

2.6.6. VL for more than two time points

For many individuals more than two MRI scans were available. In these cases, VL was calculated for each pair of two consecutive MRI scans. Annualized VL was calculated for each subject from the regression line fitted to all VL measurements for that subject. More precisely, if $\mathit{bv}{l}_i$denotes the percentage VL between the age of the patient $\mathit{ag}{e}_i$ and $\mathit{ag}{e}_{i+1}$, then the participant’s brain volume $\mathit{vo}{l}_{i+1}$at age $\mathit{ag}{e}_{i+1}$, will change according to the formula $\mathit{vo}{l}_{i+1}=vo{l}_i·(1+bv{l}_i/100)$. Example: $\mathit{vo}{l}_0=1000\mathrm{m}\mathrm{l},ag{e}_0=50\mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s},ag{e}_1=52\mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s},bv{l}_0=-0.2\%$ then the brain volume at age 52 years will be $\mathit{vo}{l}_1=998$ ml. A linear regression function $f$fitting the data$(ag{e}_i,vo{l}_i)$ was computed. The final annualized percentage BVL for each study participant was then determined by $100·\frac{f(ag{e}_0)-f(ag{e}_n)}{f\left(ag{e}_0\right)\left(ag{e}_n-ag{e}_0\right)}$ where $\mathit{ag}{e}_0$ is the age at baseline and $\mathit{ag}{e}_n$ is the age at the last follow-up scan. The VL/year computed with the formula above is independent from the brain volume $\mathit{vo}{l}_0$ at baseline (since this value is unknown it was set to 100 in our computation). In the case there are only two MRI scans available (and thus only one VL measurement) the above procedure boils down to the known formula for annualized VL: $100·\frac{f(ag{e}_0)-f(ag{e}_1)}{f\left(ag{e}_0\right)\left(ag{e}_1-ag{e}_0\right)}=\frac{\mathit{bv}{l}_1}{{\mathrm{a}\mathrm{g}\mathrm{e}}_1-{\mathrm{a}\mathrm{g}\mathrm{e}}_0}$.

2.7. Manual quality control

As described above, the BVL was computed with Siena and with JI. All timely consecutive image pairs with an absolute difference between the Siena and the JI measurement of more than 2% where subjected to a manual quality control. The data pair was excluded from the original cohort if an objective reason for the large deviation between the two measurements (Siena and JI) was found. In addition all MRI images were reviewed to check whether they met the minimum image quality standard. Objective reasons for exclusion were

• •strong motion artefacts in one of the two images,
• •gadolinium contrast in one of the two images, or
• •strong distortions in one of the two images.

2.8. Comparison of BVL with Siena and JI

For all the remaining data pairs BVL was computed with Siena and with JI and annualized as described in the section above. The two methods were compared for the HC and for the two MS cohorts. The Pearson correlation coefficient was used to compute the level of agreement between the two methods. In addition the mean difference between Siena and JI was computed. A paired t-test was used to test whether there are systematic differences between the two methods. Finally, the 25th, the median, and the 75th of the absolute percentages differences were computed.

2.9. Estimation of measurement error

The measurement errors were estimated by means of the three reliability datasets with scan intervals of days to weeks for BVL with Siena and JI, GMVL, deep GMVL and ThalaVL. Since no VL is expected in that short time period VL measurements comprise the intrinsic measurement error of the method and the potential short-term (days/weeks) biological fluctuations of the brain volume (Opfer, et al., 2018b). For each pair of consecutive MRI scans VL was computed for each of the three reliability datasets. For the Maclaren dataset for each of the three subjects 20 MRI examinations were performed. In each session each subject was scanned twice with repositioning of the subject between scans. Since in each session two MRIs were acquired for each pair of timely consecutive MRI sessions there are 4 possible pairs of MRIs. However, VL was only computed between the first of the two scan-rescans and between the second scans (e.g. between scan1_timepoint1 vs. scan1_timepoint2 and between scan2_timepoint1 vs. scan2_timepoint2). Therefore, for each subject we obtained (2*19 = ) 38 VL measurements and hence altogether (3*38 = ) 114 VL measurements. For the OASIS dataset 20 VL measurements were obtained (20 subjects with 2 scans within 1 to 31 days). The Biberacher dataset resulted in 13 (5 times GE, 4 times Philips, and 4 times Siemens) BVL measurements for patient# 1 and 15 (5 times GE, 5 times Philips, and 5 times Siemens) VL measurements for patient# 2. All data were pooled into one single data set. As subjects contributed a varying number of scans, we performed an analysis using a linear mixed effect model. The 25 subjects as well as the 5 different scanners involved were used as random effects (model was ‘BVL ~ 1 + (1 | Subject) + (1 | Scanner)’). The full covariance matrix was used in the mixed effect model. Despite the large number of VL measurements analyzed, our cohort contains only 25 subjects, with an age range between 20 and 31 years. Therefore an adjustment for age, sex or baseline brain volume was not possible with the chosen cohorts and beyond the scope of this manuscript. The standard deviation (SD) of the model residuals is a suitable measure for the SD of the pooled VL measurements since it takes repeated measurements into account. In addition the median and the 95th percentile of the absolute VL measurements were computed for the pooled data and for each cohort individually.

2.10. BVL, GMVL, deep GMVL, and ThalaVL in healthy aging

For the HC cohort a quadratic regression function between age and the corresponding VL measurements (BVL, GMVL, deep GMVL and ThalaVL) per year was computed. Since regression can be distorted by outliers the regression was performed in an iterative fashion. After the first regression the standard deviation (SD) of the residuals was determined. Points with a distance to the regression function higher than 3.5 times the SD were removed from the second regression computation. Points on the second and final regression line can be interpreted as mean VL per year for a particular age. The 5th and 20th percentile of the residuals of the second regression function were computed. The regression function was shifted down by the magnitude of the 5th and 20th percentile, respectively. For each age we can expect 95% of the measurements to exceed the 5th percentile and 80% to exceed the 20th percentile line. Therefore, the 5th percentile can be used as a cut-off for pathological VL per year with an error probability of 5% and the 20th percentile can be used as a cut-off with an error probability of 20%.

2.11. BVL, GMVL, deep GMVL, and ThalaVL for MS patients

The mean VL and SD of VL were computed for the HC cohort as well as for both MS cohorts. Since VL increases with age and subjects of the HC cohort are significantly older than MS patients it is not possible to directly compare VL of HC subjects and MS patients. We therefore adjusted all VL measurements by computing the residuals to the quadratic regression function as described above. All adjusted VL/year values were tested for differences between males and females with a two-sample t-test (p = 0.05). In order to understand better which brain region is best suited to discriminate between HC and MS patients a receiver operating characteristic (ROC) curve was computed. The ROC was computed for varying percentiles of the age adjusted VL measures for the HC cohort ranging from 0 to 100. Each percentile was used as potential cut-off value to discriminate between normal and pathological VL. For the 20th percentile, for example, 20% of the HC cohort would be wrongly classified as pathological. The sensitivity for a particular cut-off was determined as of being the ratio of MS patients below that threshold (e.g. correctly classified as pathological).

2.12. Comparison of VL for different brain regions

We compared VL adjusted for age between the investigated brain regions by computing the mean difference between these regions for the Zurich and the Dresden MS cohorts. A paired t-test was used to test whether there are systematic differences in VL.

3. Results

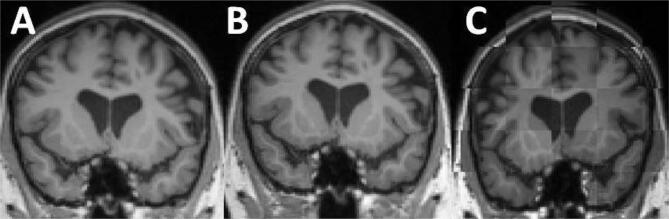
For the HC cohort no MRI was excluded for reasons of image quality issues. Three MRIs were excluded belonging to three different patients from the Zurich MS cohort due to Gadolinium contrast (which was not indicated in the DICOM header). Since for these three patients more than 2 MRIs were originally available, no patient had to be removed from the study. For the Dresden MS cohort 9 MRIs were not included into the study. All 9 MRIs were the last ones of the 4 MRI scans. Consequently, for 9 patients only 3 instead of 4 MRIs were used for the analyses. The reason in all 9 cases was a distortion in the last MRI scan. This is illustrated in Fig. 1. Images A and B show time points 3 and 4 of one of the excluded cases. For illustration, both images were rigidly registered into the halfway image space of the two images. Subplot C shows a tile plot of images A and B. The images are superimposed showing alternating image A and B. The upper part of the skull seems to be distorted. The Jacobian would provide wrong information on the superior part of the brain.

Fig. 1.

One of the 9 excluded MRIs from the Dresden MS cohort. The images A and B show time points 3 and 4 of one of the 33 MS patients. Both images are rigidly registered into the halfway image space of the two images. Subplot C shows a tile plot of images A and B. The images are superimposed showing alternating image A and B. The upper part of the skull seems to be distorted.

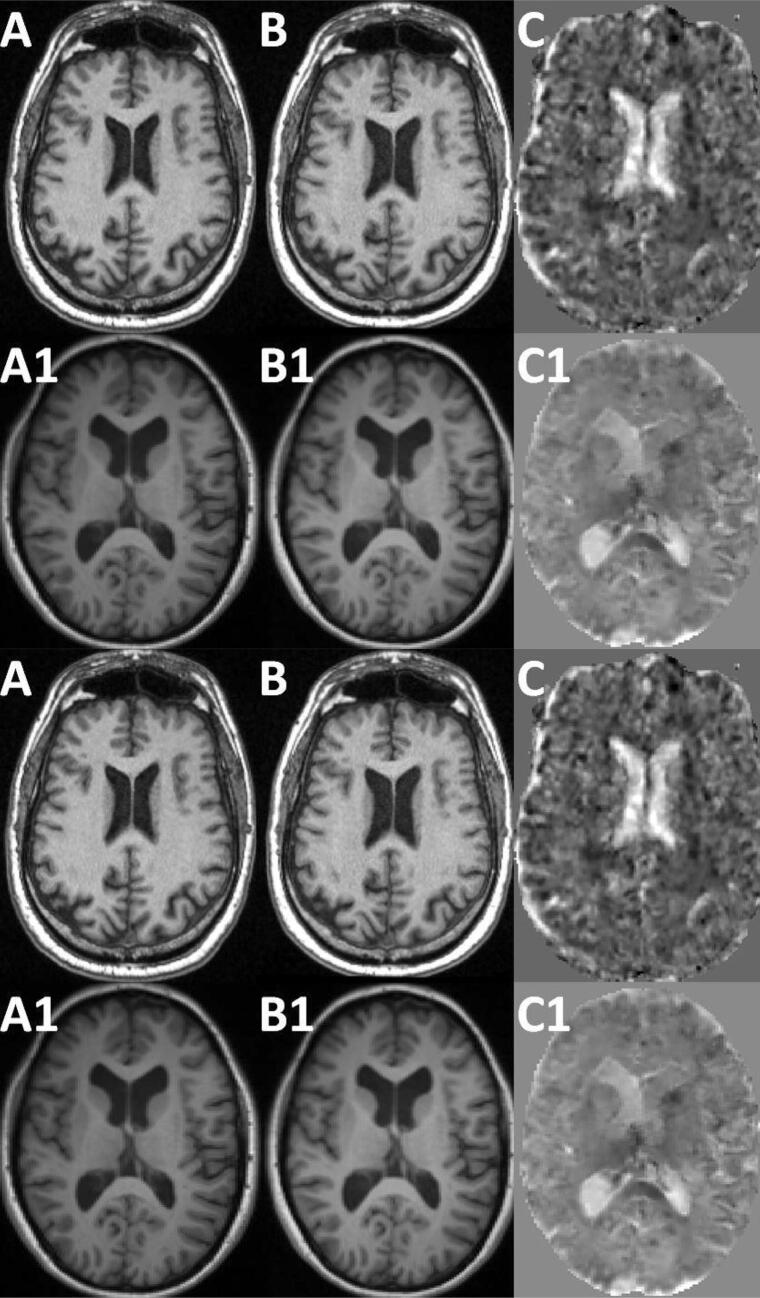
Fig. 7 shows the Jacobians for two sample cases. Image A and B of Fig. 7 show a male subject from the HC cohort at 69.2 and 75.1 years, respectively. Plot C shows the corresponding Jacobian. This HC case features a BVL JI of −0.52% per year. Image A1 and B1 show an MS patient of the Dresden cohort at 32.7 and 34.0 years, respectively. Plot C1 shows the corresponding Jacobian. The MS patient features a BVL JI of −1.21% per year and a ThalaVL of −2.11% per year.

Fig. 7.

Jacobian for two examples. Image A and B show a male HC subject at 69.2 and 75.1 years, respectively. Plot C shows the corresponding Jacobian. This HC case features a BVL JI of −0.52% per year. Image A1 and B1 show a MS patients of the Dresden cohort at 32.7 and 34.0 years, respectively. As above plot C is the corresponding Jacobian. The MS patient case features a BVL JI of −1.21% per year and a ThalaVL of 2.11% per year.

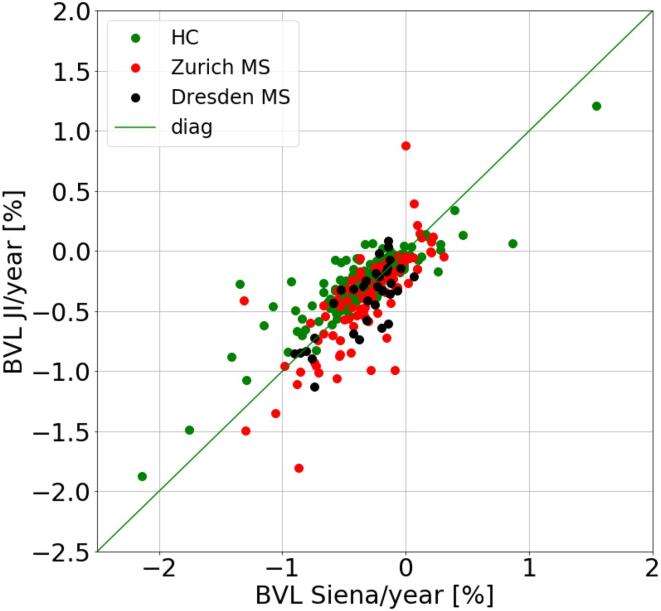
Table 2 and Fig. 2 demonstrate the comparison between BVL per year in % measured with Siena and JI for HC subjects and for the two MS patient cohorts. There is a quantitative agreement between the two methods for all three cohorts with a correlation coefficient of r = 0.88 (HC), r = 0.76 (Zurich MS), and r = 0.77 (Dresden MS). The median absolute difference between the two methods was 0.09% (HC), 0.12% (Zurich MS), and 0.14% (Dresden MS). For the HC cohort Siena measured slightly stronger BVL per year than the JI method (mean difference −0.07% per year, p = 0.02). There was no significant difference between the methods for the Zurich and Dresden MS cohorts.

Table 2.

Comparison between BVL per year in % measured with Siena and JI for the cohort of healthy controls (HC) and for the two MS patient cohorts (Zurich and Dresden).

	Correlation BVL/year (Siena vs. JI)		BVL/year (Siena – JI) [%]		BVL/year abs(Siena – JI) [%]
	r	p	Mean	p	25th	median	75th
HC	0.88	<0.001	−0.07	0.0248	0.03	0.09	0.15
Zurich MS	0.77	<0.001	0.00	0.1787	0.06	0.13	0.23
Dresden MS	0.75	<0.001	0.07	0.3488	0.07	0.15	0.24
All	0.78	<0.001	−0.02	0.3488	0.04	0.10	0.19

Fig. 2.

Scatter plot for BVL per year in % measured with Siena against JI for the cohort of healthy controls (HC) and the two MS patient cohorts (Zurich and Dresden).

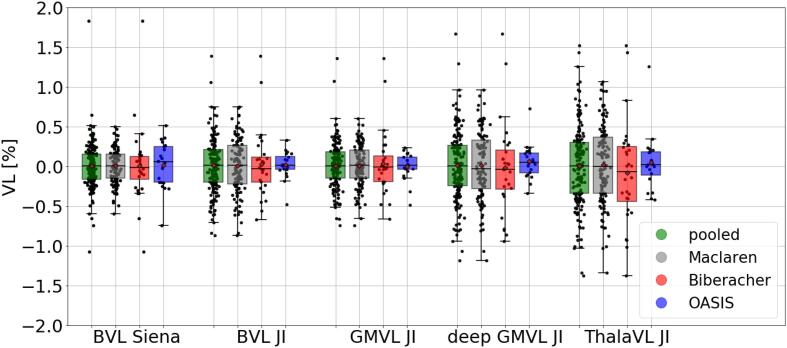
In Table 3 and Fig. 3 the measurement error for Siena as well as JI (for the different brain regions) is shown. Estimate of the SD of the model residuals were smallest for Siena (0.28%). Deep GMVL JI and ThalaVL JI featured the largest error of 0.43% and 0.50%, respectively. The intercept of the model was not statistically different from zero for all brain regions.

Table 3.

Measurement error of the three reliability datasets for Siena and for JI. Table shows standard deviations (SD) of the model residuals of the pooled reliability datasets (column 2). The other columns show the median and the 95th percentile of the absolute (unsigned) VL measurements of the pooled data and for each cohort individually.

	pooled			Maclaren		Biberacher		OASIS
	SD	median	95%	median	95%	median	95%	median	95%
BVL Siena	0.28	0.16	0.49	0.15	0.43	0.13	0.93	0.23	0.53
BVL JI	0.34	0.21	0.65	0.23	0.64	0.18	0.92	0.09	0.34
GMVL JI	0.29	0.16	0.51	0.19	0.49	0.19	0.93	0.10	0.33
deep GMVL JI	0.43	0.26	0.81	0.30	0.79	0.27	1.17	0.13	0.36
ThalaVL JI	0.50	0.33	1.02	0.35	0.96	0.34	1.41	0.18	0.46

Fig. 3.

VL measurement error for Siena and for JI for different brain regions. The bar plots show the signed VL measurements of the three reliability datasets.

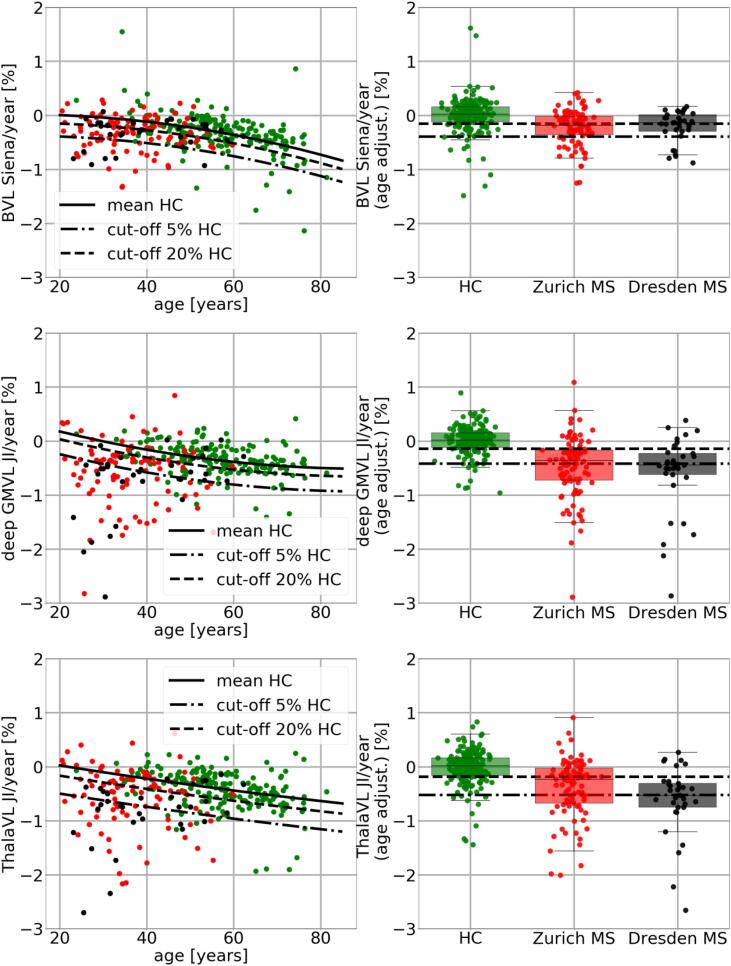
In Table 4 the age-dependent cut-offs for pathological VL for all anatomical structures are presented. As explained above, the cut-off values are derived from the HC cohort. Mean BVL per year for Siena and JI was −0.08% vs. −0.07%, −0.29% vs. −0.23%, and −0.63% vs. −0.44% at ages 35, 55, and 75, respectively. The thalamus featured the highest mean volume loss per year namely −0.16%, −0.39%, and −0.59% at ages 35, 55, and 75, respectively. The cut-offs for a pathological ThalaVL per year (with an error probability of 5%) were 0.68%, 0.91%, and 1.11% at ages 35, 55, and 75, respectively (see last two columns per block in Table 4).

Table 4.

Mean, the 80th percentile, and 95th percentile for VL per year in the age range between 35 and 75 years for Siena and JI and different brain regions. The values in the last two columns per block can be used as age-dependent cut-offs for pathological VL with an error probability of 20% and 5%, respectively.

	BVL Siena			BVL JI			GMVL JI			deep GMVL JI			ThalaVL JI
age	mean	20%	5%	mean	20%	5%	mean	20%	5%	mean	20%	5%	mean	20%	5%
35	−0.08	−0.23	−0.47	−0.07	−0.19	−0.40	−0.11	−0.22	−0.46	−0.09	−0.23	−0.51	−0.16	−0.35	−0.68
40	−0.12	−0.28	−0.51	−0.11	−0.23	−0.43	−0.13	−0.24	−0.48	−0.16	−0.31	−0.58	−0.22	−0.41	−0.74
45	−0.17	−0.32	−0.56	−0.14	−0.26	−0.47	−0.15	−0.26	−0.50	−0.23	−0.37	−0.65	−0.28	−0.47	−0.80
50	−0.23	−0.38	−0.62	−0.18	−0.30	−0.51	−0.18	−0.28	−0.52	−0.29	−0.43	−0.71	−0.34	−0.52	−0.86
55	−0.29	−0.45	−0.69	−0.23	−0.35	−0.55	−0.21	−0.32	−0.55	−0.34	−0.49	−0.76	−0.39	−0.58	−0.91
60	−0.36	−0.52	−0.76	−0.27	−0.40	−0.60	−0.25	−0.35	−0.59	−0.39	−0.53	−0.81	−0.44	−0.63	−0.96
65	−0.44	−0.60	−0.84	−0.32	−0.45	−0.65	−0.29	−0.40	−0.64	−0.43	−0.57	−0.85	−0.49	−0.68	−1.01
70	−0.53	−0.69	−0.93	−0.38	−0.50	−0.71	−0.34	−0.45	−0.68	−0.46	−0.60	−0.88	−0.54	−0.73	−1.06
75	−0.63	−0.78	−1.02	−0.44	−0.56	−0.76	−0.39	−0.50	−0.74	−0.48	−0.63	−0.90	−0.59	−0.78	−1.11

In both MS cohorts and for all brain regions there was no statistically significant difference in VL between male and female.

In Table 5 VL between HC and MS patients is compared. Column 2 and 4 of Table 5 summarize VL for the HC and for the two MS cohorts for all anatomical structures under consideration. Column 5, 6, and 7 list the same values but adjusted for age. For BVL Siena, Zurich MS patients showed 0.22% more BVL per year and Dresden MS patients showed 0.21% more BVL than the HC. In the thalamus MS patients featured 0.47% for Zurich and for Dresden 0.60% more VL per year than the HC.

Table 5.

Columns 2 and 3 summarize VL for HC subjects and for MS patients for all anatomical structures under consideration. Columns 4 and 5 list the same values but adjusted for age. Columns 6 and 7 show ratios of the pooled MS patients which are below the 5th and 20th percentile.

	mean (SD) regional VL per year in %			mean (SD) regional VL per year (%) adjusted for age			sensitivities (%) for the pooled MS data for error probability of
	HC	Zurich MS	Dresden MS	HC	Zurich MS	Dresden MS	5%	20%
BVL (Siena)	−0.33 (0.37)	−0.32 (0.32)	−0.35 (0.26)	0.00 (0.32)	−0.22 (0.32)	−0.21 (0.29)	22.05	51.97
BVL JI	−0.26 (0.27)	−0.39 (0.40)	−0.41 (0.29)	−0.01 (0.23)	−0.31 (0.40)	−0.30 (0.33)	40.16	66.14
GMVL JI	−0.24 (0.26)	−0.44 (0.4)	−0.35 (0.27)	0.00 (0.24)	−0.31 (0.4)	−0.21 (0.29)	36.22	67.72
deep GMVL JI	−0.33 (0.33)	−0.57 (0.57)	−0.75 (0.63)	0.01 (0.31)	−0.47 (0.57)	−0.60 (0.72)	48.03	77.17
ThalaVL JI	−0.42 (0.40)	−0.59 (0.66)	−0.92 (0.75)	−0.01 (0.36)	−0.42 (0.66)	−0.70 (0.81)	37.80	62.20

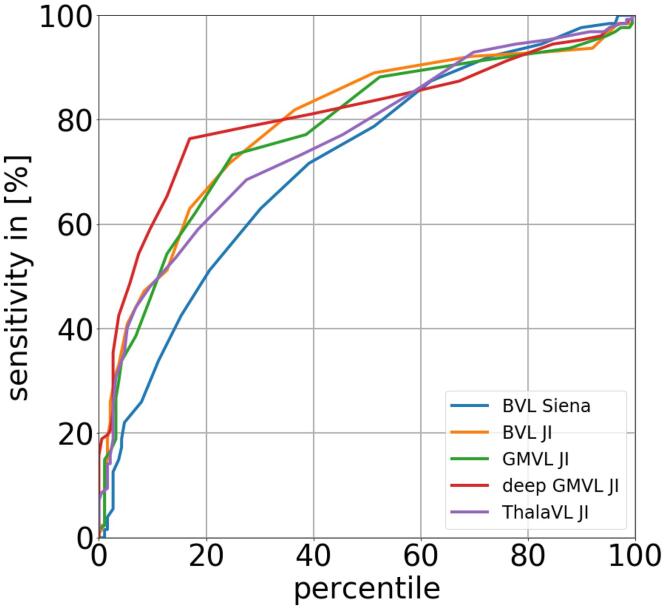
In Fig. 4 VL measurements are plotted against age (left column). The plot shows the quadratic regression function as well as the 5th and 20th percentile lines fitting the HC data. In the right column of Fig. 4 the VL measurements are adjusted for age and shown as box plots for the HC as well as for the MS patients. In Column 8 and 9 of Table 5 for each brain region the ratio of MS patients which are below the 5th and 20th percentile line is determined. For instance for BVL measured with JI 66.1% of all MS patients are below the 20th percentile line which means that these patients have a lower BVL than 80% of the HC. For deep GMVL there are 77.17% below that 20th percentile line. In Fig. 5 ROC curves for the different brain regions is shown. The curve for the deep GMVL is steepest in the range between the 0 and 40 percentile.

Fig. 4.

VL measurements are plotted against age (left column). The plot shows the regression line as well as the 5th and 20th percentile lines fitting the HC data. In the right column the VL measurements are adjusted for age and shown as box plots for the HC subjects as well as for the MS patients.

Fig. 5.

ROC curves discriminating HC from MS patients for the different brain regions.

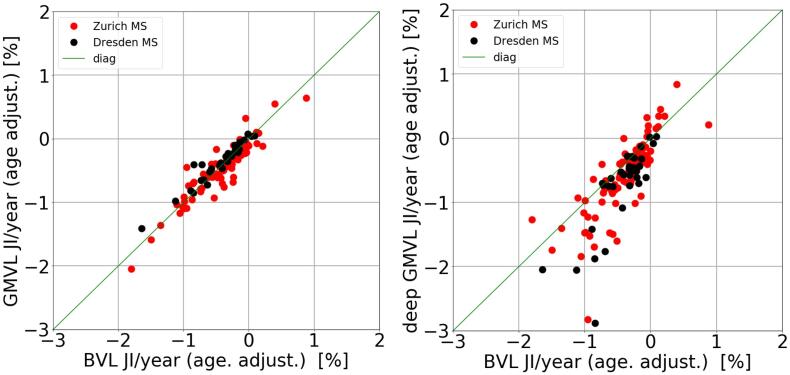
In Fig. 6 and Table 6 the comparison between brain regions for both MS cohorts is shown. For both cohorts there is no significant difference between BVL JI and GMVL JI. However, the Zurich MS patients show on average 0.16% more deep GMVL JI than BVL JI (p = 0.02) and the Dresden MS patients show 0.30% more deep GMVL JI than BVL JI (p = 0.03). For both MS cohorts there was no significant difference between deep GMVL JI and ThalaVL JI.

Fig. 6.

Scatter plot between BVL JI and GMVL JI (left) and between BVL JI and deep GMVL (right).

Table 6.

Mean differences and p-values between BVL JI and GMVL JI as well as between BVL JI and deep GMVL for the Zurich and the Dresden MS cohorts. Asterisks mark significant volume differences.

	Zurich MS		Dresden MS
	mean	p	mean	p
BVL JI - GMVL JI [%]	0.01	0.9919	−0.09	0.2580
BVL JI - deep GMVL JI [%]	0.16	0.0271*	0.30	0.0342*
BVL JI - ThalaVL JI [%]	0.11	0.1701	0.40	0.0131*
GMVL JI - deep GMVL JI [%]	0.16	0.0281*	0.39	0.0062*
GMVL JI - ThalaVL JI [%]	0.11	0.1735	0.49	0.0026*
deep GMVL JI - ThalaVL JI [%]	−0.05	0.5702	0.10	0.6121

4. Discussion

In this study JI was used to determine age-dependent cut-offs to distinguish physiological from pathological VL for various brain regions. Stability of the method and the implementation was investigated by deploying reliability data sets consisting of short term repeated scans with scan intervals between days and a few weeks. In addition the method was used to analyze two longitudinal cohorts of MS patients. The ratio of MS patients showing pathological volume loss in the investigated brain regions was determined. Finally, the BVL, GMVL, deep GMVL, and ThalaVL were mutually compared for the two MS patient cohorts.

In this study the JI method is based on the longitudinal pairwise registration toolbox as provided by Statistical Parameter Mapping (SPM12). The toolbox is based on an algorithm by Ashburner and colleagues (Ashburner, 2007). The default parameter setting provided by the toolbox was deployed. However, the regularization approach was changed slightly. It is important to understand the effect of the regularization in JI since the choice of that parameter can greatly impact the result. In Ashburner and Ridgway the effect of different regularization parameters is explained in detail (Ashburner and Ridgway, 2012). In general the regularization term is introduced to prevent sharp discontinuities in the resulting transformation fields and to achieve anatomically consistent and meaningful results. A higher weight on the regularization term will result in a more rigid transformation field. A too high regularization will result in a too rigid transformation which might not capture the true biological changes between the images. In the original SPM12 implementation the regularization was inversely proportional to the time interval. The rationale behind this choice (as described in the user manual) is that bigger changes between the two images are expected for longer time intervals and therefore regularization needs to be relaxed in order to allow the algorithm to capture these changes. For short time intervals smaller changes are expected and therefore in order to improve the stability a higher regularization is applied. This approach might be suitable for healthy individuals. However, MS patients can feature a volume loss far exceeding ranges of what can be expected due to physiological aging despite of a relatively short time interval between scans. We therefore adjusted this approach in our study. The regularization was chosen to be inversely proportional to the BVL measured by Siena. In a recent study from the MAGNIMS study group (Storelli, et al., 2018) different implementation for the JI method were compared. The authors compared the SPM12 implementation of the JI method with other available tools. The authors used the default regularization. From the four methods compared in Storelli et al. the SPM12 implementation turned out to be the most stable one. Stability was assessed in that paper by scan-rescan data with only few weeks between the scans. As explained above for the default SPM12 implementation short intervals result in a high regularization and therefore stable results by default. The results on the reliability data presented in this study (Fig. 3 and Table 3) show a much higher variability. The 95th percentile of the error in BVL JI was 0.65% (Table 3) in our study whereas in the discussed study it was lower than 0.2% (Fig. 7 in (Storelli, et al., 2018)). This can be explained by the different regularization approaches. The reverse side of the different regularization approach is that in (Storelli, et al., 2018) the SPM12 implementation was stable but lacked sensitivity to capture effects. The GMVL for the MS patient cohort alternated in that study around zero with a mean of + 0.1% (Fig. 6 in (Storelli, et al., 2018)) whereas in our study the mean GMVL was −0.44% and −0.35% for the MS patient cohorts which seems to be more reasonable. A similar effect using the default SPM12 pipeline was observed in the study by Battaglini et al. (Battaglini, et al., 2018).

Ideally BVL Siena and BVL JI should provide identical results since both methods attempt to measure the same effect. However, since both methods follow a very different algorithmic approach this cannot be expected in practice. Nevertheless, there was a high agreement of BVL measurement between the Siena method and the JI method. This indicates that the regularization approach as discussed above works properly. In all three cohorts (HC, and the two MS cohorts) the median absolute difference in BVL per year between Siena and JI was less than 0.14% (Table 1). The proposed regularization approach therefore seems to provide a good balance between stability and accuracy. This difference between the methods was smaller than the corresponding measurement errors (0.16% for BVL Siena, 0.21% for BVL JI, see Table 3). For the HC cohort, the Siena method measured slightly stronger BVL per year than the JI method (mean −0.07, p = 0.02). A reason might be the longer scan intervals in that cohort. The mean scan interval for two consecutive scans in the HC cohort was 2.5 years whereas the MS patients had a yearly MRI.

In a recent study by Beadnall et al. (Beadnall, et al., 2019) the Siena method was compared to a different implementation of the JI method provided by Icometrix, Leuven, Belgium. The authors found a correlation coefficient of r = 0.80 between Siena and JI in a cohort of 102 MS patients. A similar result was shown in an earlier study (Smeets, et al., 2016). This is consistent with the correlation between Siena and the JI method found in this study (r = 0.88 HC, r = 0.76 Zurich MS, r = 0.77 Dresden MS).

In Table 4 mean BVL per year for the HC cohort representing BVL in physiological aging for the different GM brain regions and ages are presented. To our knowledge this is the first paper presenting age-dependent cut-offs to distinguish physiological from pathological BVL for different brain regions. For BVL with Siena the results are similar to those recently presented in Opfer et al. (Opfer, et al., 2018a). This is understandable since the applied method (Siena) is the same and the HC cohort in our study is an extended cohort used in Opfer et al. ThalaVL and deep GMVL seem to have a different dynamic in HC cohort than BVL. For 35 year old individuals a mean BVL of −0.08 (-0.07% for JI) was found whereas ThalaVL was −0.16% per year at the same age. These results are consistent with other studies (Azevedo, et al., 2019),(Schippling, et al., 2017). In Azevedo et al. HC subjects at the age of 30 showed a BVL per year of + 0.01% and annual ThalaVL was −0.15% (Azevedo, et al., 2019). In Schippling et al. (Schippling, et al., 2017) regional mean BVL per year was determined from a cross-sectional cohort of HC subjects (which is possible as explained in that paper). Mean ThalaVL at the age of 35 was −0.25% (vs. −0.16% in our study) and −0.40% at the age of 60 years (vs. −0.44% in this study). However, at age of 60 a slightly higher ThalaVL per year (-0.62%) was determined (Azevedo, et al., 2019). Reasons for the difference could be the cohort itself, the method used to determine the VL (Freesurfer vs. JI in this study), or the statistical analysis. In this study quadratic regression whereas in (Azevedo, et al., 2019) linear mixed effect model was used.

As shown in Table 5 the Dresden cohort has a more pronounced ThalaVL and deep GMVL than the Zurich cohort. A reason for this might be the different cohort characteristics. The Zurich cohort has a mean EDDS of 1.3 and a mean disease duration of 2.7 years whereas the Dresden cohort has a mean EDDS of 2.7 and a mean disease duration of 5.2 years. The Dresden cohort was originally assembled to validate an automatic lesion activity detection algorithm (Krüger, et al., 2020). Therefore, many patients were included with disease activity and a severe cause of the MS. Consequently, MS patient selection was biased towards a pronounced disease activity and a severe course of MS.

In Fig. 6 and Table 6 BVL and GMVL was compared for the two MS cohorts. In both cohorts there was a high agreement and no significant difference between BVL and GMVL. This indicates that BVL might appear uniquely distributed between GM and WM. Another explanation is that the applied JI method cannot distinguish between GMVL and WMVL. The registration is controlled by areas of contrast, such as the cortex or ventricles. Since the T1 scan has little contrast within the WM to control the registration, it might happen that the deformation from areas with more contrast is smoothly extrapolated into the WM.

However, the GMVL measurement showed less error compared to BVL (Fig. 3) and GMVL might therefore be better suited to measure VL in individual patients than BVL. In both MS cohorts deep GMVL was significantly more pronounced than GMVL. This is consistent with a recent longitudinal study of the MAGNIMS group (Eshaghi, et al., 2018). In that study deep GMVL was also associated with disability worsening. It might therefore be an interesting approach to use deep GMVL as a surrogate for disability progression in individual patients. A larger than normal deep GMVL was also found in two recent cross-sectional studies on ThalaVL in MS patients (Hänninen et al., 2019, Raji et al., 2018).

To use the provided information for decision making in an individual patient the age dependent cut-offs of Table 4 as well as the magnitude of the measurement error provided in Table 3 should be taken into account. We explain how to aggregate that information by a hypothetical example. For instance, we assume that for a 35 years old MS patient deep GMVL is −2.1% with a scan interval between baseline and follow-up of two years. The SD of the deep GMVL measurement error is 0.43% (second column of Table 3). That means that the true VL lies within the interval −2.1 ± 1.96*0.43 with an error probability of 5%. Assuming the most optimistic case the patient features a VL of −2.1 + 1.96*0.43% =-1.25%. Since the scan interval is 2 years, the annualized most optimistic VL per year would be −1.25/2 = -0.625%. This is still lower than the 5% cut-off of −0.51%. So this patient exhibits a VL in deep GM which is pathological with an error probability of 5% at most. More generally, if x is the measured VL with a certain scan interval length between baseline and follow-up the value (x + 1.96*SD)/interval length should be below the cut-off thresholds provided in Table 4 in order to be pathological.

A limitation of this study is that subjects in the HC cohort (mean 53.9 years) are older than the MS patients in the Zurich and Dresden cohort (mean 34.2. and 38.2 years, respectively). Subjects of the HC cohort were acquired in a prevention center as part of a health screening program. Hence, there are only a few asymptomatic individuals younger than 35 years who underwent repeated MRI scans. Moreover most publically available datasets containing repeated MRI scans of HC subjects (such as ADNI, OASIS, MIRIAD, etc.) do not contain individuals younger than 35 years. In order to compare the MS patients with the HC cohort a regression function was computed and the residuals to the regression function were compared. However, since there were few HC subjects younger than 35 years the regression might be inaccurate due to insufficient data in that range. The HC cohort is still growing and it will be an interesting task for future work to repeat the analysis with more HC subjects younger than 35 years once being available.

Overall, our results suggest that it might be methodologically feasible to assess deep GMVL in MS patients. When using this measurement for individual MS patients, the patient’s age and the level of measurement error need to be taken into account. Deep GMVL may be used as a complementary marker to BVL since MS patients exhibit a significant stronger deep GMVL loss than BVL, which may increase sensitivity in interventional trials.

CRediT authorship contribution statement

Roland Opfer: Conceptualization, Methodology, Software, Writing - original draft, Visualization, Formal analysis. Julia Krüger: Software, Writing - original draft. Lothar Spies: Writing - original draft. Marco Hamann: Data curation. Carla A. Wicki: Data curation. Hagen H. Kitzler: Data curation. Carola Gocke: Data curation. Diego Silva: Data curation. Sven Schippling: Supervision, Data curation.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.