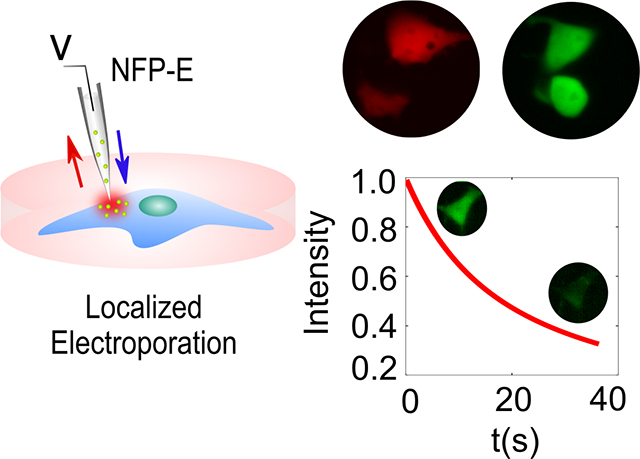
Abstract
Introducing exogenous molecules into cells with high efficiency and dosage control is a crucial step in basic research as well as clinical applications. Here we report the capability of the nanofountain probe electroporation (NFP-E) system to deliver proteins and plasmids in a variety of continuous and primary cell types with appropriate dosage control. We show that the NFP-E can achieve fine control over the relative expression of two cotransfected plasmids. Lastly, we investigate the dynamics of electro-pore closure after the pulsing ends with the NFP-E. Localized electroporation has recently been utilized to demonstrate the converse process of delivery (sampling), in which a small volume of the cytosol is retrieved during electroporation without causing cell lysis. Single-cell temporal sampling confers the benefit of monitoring the same cell over time and could provide valuable insights into the mechanisms underlying processes such as stem-cell differentiation and disease progression. We identify NFP-E parameters that maximize the membrane resealing time, which is essential for increasing the sampled volume and in meeting the challenge of monitoring low copy number biomarkers. We envision its application in CRISPR/Cas9 gene editing, stem cell reprogramming, and single-cell sampling studies.
Keywords: Nano-pipette, single cell, sampling, electroporation, plasmid delivery
Graphical Abstract
Versatility of molecular cargo delivery into different immortalized cell lines and primary cells using the Nanofountain Probe Electroporation (NFP-E) technique is demonstrated. Ratiometric control over delivery of co-transfected plasmids is achieved. Fundamental insight into post pulse dynamics of electro-pores is provided by time-lapse imaging of NFP-E mediated loss of calcein from cells.
1. Introduction
Intracellular delivery of biomolecules is an essential aspect of biomedical research and its translation to clinical applications. Delivery is required for gene editing,[1, 2] the study of disease pathology[3] and cellular engineering.[4] For example, human induced pluripotent stem cells (hiPSCs) are employed in studies related to personalized drug development, disease modeling, and tissue and organ transplantation.[5–7] Efficient induction of hiPSCs from somatic cells requires control over the relative concentrations of the reprogramming factors that are delivered to cells.[8] Similarly, the specificity of CRISPR-based editing methods depends on appropriate dosage control of Cas9/gRNA ribonucleoprotein (RNP).[4, 9] Hence, there is a need for a versatile technology that can deliver precise quantities of bioactive cargo molecules to different cell types.
Delivery of exogenous biomolecules into cells can be achieved by a variety of methods including viral vectors,[10] chemical carriers such as cell-penetrating peptides and polymer nano-capsules,[11, 12] mechanical perturbation of the plasma membrane,[13] and bulk electroporation.[14, 15] Each method has advantages and limitations. For example, methods that employ chemical carriers have the disadvantage of delayed unpacking and excessive toxicity,[16, 17] and viral vectors can cause immune responses and insertional genotoxicity.[18] Techniques like cell squeezing that involve mechanical perturbation can damage intracellular components including the nucleus, cytoskeleton, and genome.[18] Methods that rely on mechanical perturbation can also initiate signaling cascades that induce cells to enter a quiescent‐like state characterized by temporary cessation of protein synthesis.[19] Lastly, bulk electroporation reduces cell viability due to the high voltages applied and provides low precision over dosage.[20]
During the last decade, we[21–24] and others[25, 26] have shown that disadvantages associated with bulk electroporation can be overcome by focusing an electric field on a small region of the plasma membrane. Localized electroporation—owing to the confined electric field—also benefits from strong electro-kinetic effects that can confer improved delivery.[27] More recently, the reverse process (sampling) has been demonstrated, whereby a small volumetric fraction of the cytosol is extracted without incurring cell lysis.[22, 28] Certain methods for analyzing cytosolic material such as RNA sequencing involve a lysis step[29] and thus provide information only for one time point. Moreover, bulk analyses of cell populations can mask cell heterogeneity.[30] Therefore, quantitative analysis of cytosolic material sampled from single cells at multiple time points could improve our understanding of disease pathology,[31] stem cell reprogramming[32], and cell differentiation.[33, 34] However, the limited sensitivity of existing assays such as qPCR or mass spectrometry, in combination with the fact that the volume of cytosol sampled is less than 1–7% of the total cell volume, restricts the application of localized electroporation-based sampling to a small number of cells, typically 15–100.[28]
Localized electroporation-based delivery has been demonstrated in microfabricated formats such as microfabricated chips containing arrays of cantilever probes with embedded microchannels and a sub-micron aperture, [21, 35] arrays of single nanochannels,[25, 35] track-etched membranes, and nanostraws.[28, 36] Here, we employ a commercially available NFP-E system based on glass nanopipette tips, in lieu of sub-micron probes that would need to be custom-made, to transfect cells using localized electroporation (Figure 1a,b). We highlight the versatility of the NFP-E system by delivering a variety of molecular cargo to commonly employed continuous cell lines and to primary cells that are difficult to transfect. We show that the NFP-E can simultaneously deliver two plasmids in different concentration ratios, resulting in different ratios of co-expression of the proteins. Lastly, we study the temporal characteristics of post-pulse electro-pore evolution by utilizing time-lapse fluorescence imaging of intracellular calcein in single cells. We find that the membrane resealing time scales nonlinearly with the pulse voltage and the number of electroporation pulses, reaching a maximum at intermediate values. Thus, long pulsing times or extremely high voltages appear not to be necessary for efficient molecular transport across cell membranes, which could enable us to achieve high transport efficiency while keeping cell toxicity to a minimum. This study can serve as a guideline towards the judicious design of pulse profiles in localized electroporation.
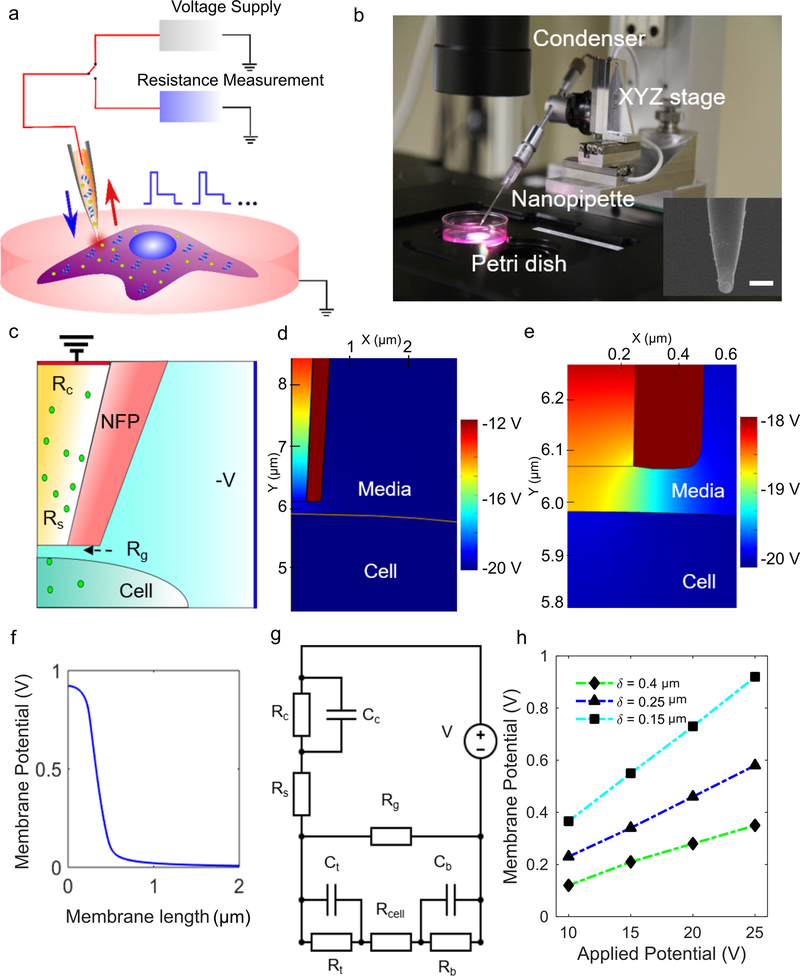
Figure 1.
NFP-E setup and prediction of transmembrane potential from the lumped model. a) The schematic shows the NFP-E engaged on a cell with voltage supply and resistance measurement systems. b) Setup of the NFP-E with XYZ piezo control. Inset: scanning electron microscope image of the nanopipette. Scale bar: 1 μm. c) Schematic of the NFP-E nanopipette used in the FEA simulation. d) Potential map from FEA simulation. e) Contour plot showing high transmembrane potential developed in the part of the membrane directly underneath the NFP-E nanopipette tip, compared to rest of the membrane. f) Transmembrane potential along the upper boundary of the cell from the FEA model for an input voltage of 20 V and cell-nanopipette tip gap of 0.3 μm. g) Lumped electric circuit model of the NFP-E system. h) Steady-state membrane potentials vs. applied potentials for different gap distances between the cell and the NFP-E nanopipette tip (obtained from the lumped circuit model).
2. Results
2.1. Modeling of NFP-E
Electroporation of the cell membrane and subsequent transport of molecules across it are governed by a three-step process: charging of the cell membrane, formation and evolution of electro-pores, and transport of molecules across the electro-pores.[37] The second step depends on the transmembrane potential (the potential difference across the cell membrane).
To compute the transmembrane potential of a cell in the NFP-E system, we calculated the spatial distribution of the electric potential by modelling the cell and the NFP-E nanopipette using COMSOL Multiphysics software. The simulation geometry is diagrammed in Figure 1c. The governing equations and the boundary conditions are:
| #(1) |
| #(2) |
where σ is the conductivity (S m–1), V is the potential [V], ε is the permittivity of the relevant domain, n is the surface unit normal vector, and J is the electric flux vector (V m; parameter values in Table 1). The boundary condition in equation (2) applies to the nanopipette walls. We modeled the cell membrane in equation (3) as a thin resistive material with an effective contact impedance:
| #(3) |
where Vm is the transmembrane potential (V) and d is the thickness of the cell membrane [m].
Table 1:
Parameter values used in the finite element simulation (nd: non-dimensional)
| PARAMETER | VALUE |
|---|---|
| σc, conductivity of the cytoplasm | 0.3 [S m−1] |
| σb, conductivity of the media | 1.5 [S m−1] |
| σm, conductivity of the cell membrane | 5E–7 [S m−1] |
| εmr, relative permittivity of the cell membrane | 5 [nd] |
| εcr, relative permittivity of the cytoplasm | 72 [nd] |
| εer, relative permittivity of the media | 72 [nd] |
Based on the contour plots of the potential in Figure 1d–f, a rise (>200 mV) in transmembrane potential is localized only to the region of the cell directly underneath the NFP-E. Hence, we can model the electrical behavior of the cell membrane as a combination of two pairs of resistors and capacitors, where one pair (Rt, Ct) represents the region of the membrane experiencing a rise in transmembrane potential and the other pair (Rb, Cb) represents the rest of the membrane.[21, 25] This system can be represented by a lumped model (Figure 1g; values of resistors and capacitors are in Table S1, Supporting Information). Rg denotes the gap resistance between the probe and the cell membrane which we estimated from multiple resistance measurements (Figure S1a,b, Supporting Information). Rc and Cc are the contact resistance and capacitance, respectively, between the electrode and the media. Rs is the resistance of the fluid in the probe which we derived analytically (Figure S2, Supporting Information). Rcell is the resistance of the cytoplasm.
The lumped model consists of a system of three ordinary differential equations (Equations 4–6) that are obtained by applying voltage and current conservation laws at different nodes of the circuit (Figure 1g). The model input is the applied far-field voltage (V). We solve for the resulting potential difference across the cell membrane:
| #(4) |
| #(5) |
| #(6) |
In Eqs. 4–6, V1 is the potential drop across the electrode due to its contact impedance, V2 is the potential difference across the cell membrane directly underneath the NFP-E, and V3 is the potential difference across the rest of the cell membrane. Coefficients in the lumped model are in Table S2 (Supporting Information). The distance between the cell’s surface and the nanopipette tip determines the value of the gap resistance (Rg); a decrease in the cell-nanopipette-tip distance (δ) increases Rg. We computed the transmembrane potential for a range of applied voltages and cell-nanopipette tip distances (δ) (Figure 1h).
2.2. Delivery of a large protein to continuous and primary cells
We examined whether the far-field voltage parameters obtained using the lumped model would yield successful delivery of a large protein to various cell types. Bovine serum albumin (BSA, ~66.5 kDa) tagged with a fluorescent marker (Alexa Fluor 488) was delivered to continuous cell lines and primary cells. Unlike small molecules such as propidium iodide that can be readily delivered using a variety of electroporation parameters, large molecules like bovine serum albumin tagged with Alexa Fluor 488 (BSA-AF488) require a specific range of pulse parameters for delivery. Owing to its larger size, BSA-AF488 is a useful construct for optimizing conditions that are expected to work for biological cargo such as plasmids. We electroporated HeLa cells on the NFP-E system using a bilevel waveform (15 V peak amplitude and 100 pulses; Figure S3, Supporting Information) and observed delivery of BSA-AF488, as evident from the green fluorescence in targeted cells (Figure 2a, Figure S4, Supporting Information). In a typical experiment, we prescribed a resistance change of ~ 1% before applying electroporation pulses. The ground electrode is connected to the nanopipette while the positive reference electrode is submerged in the media containing the cells. This electrode arrangement was chosen to take advantage of electrophoretic effects for the delivery of proteins and plasmids, which are negatively charged in physiological buffers (1× PBS in this case). Although the amount of cargo delivered could be increased by prescribing a greater change of resistance (by reducing the gap between the cell and nanopipette), we chose the aforementioned value to minimize pickup of cell membrane elements that could potentially clog the tip. By employing the same voltage parameters, we were able to deliver BSA-AF488 to other continuous cell lines including MDA-MB-231 cells (Figure 2b) and HEK 293FT cells (Figure 2c).
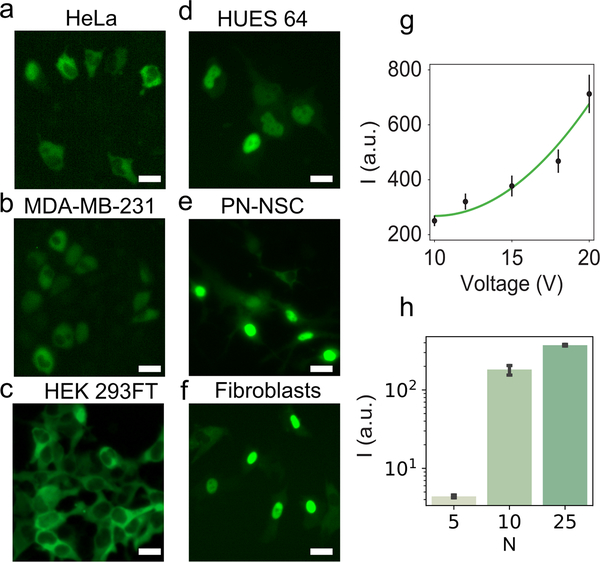
Figure 2.
BSA-AF488 delivery to continuous and primary cells using NFP-E. (a–f) Representative fluorescence images for a) HeLa, b) MDA-MB-231, c) HEK 293FT, d) HUES 64, e) PN-NSCs, and f) fibroblasts. Scale bar: 20 μm. g) Mean fluorescence intensity of HeLa cells after BSA-AF488 delivery using five different pulse voltages. A quadratic function (a(x-10)2 + c) was fit to the data; a = 4.08, c = 268. The equation was fitted with the constraint to be monotonically increasing above 10 V and is intended to model voltages ≥ 10 V. Each voltage condition included at least 15 cell measurements. h) Mean fluorescence intensity of MDA-MB-231 cells after BSA-AF488 delivery using three different numbers of pulse trains (N: number of trains; 1 train = 50 pulses). Each condition included at least three cell measurements. Error bars indicate the standard error of the mean.
Primary cells generally are difficult to transfect using bulk electroporation and require extensive testing of electroporation buffers and voltage parameters.[38] Hence, we evaluated the ability of NFP-E to deliver BSA-AF488 into a panel of primary cells—human embryonic stem cells (HUES 64), differentiating post-natal neural stem cells (PN-NSCs), and fibroblasts—employing the same electroporation parameters as those used for the continuous cell lines. Fluorescence microscopy confirmed the delivery of BSA-AF488 into each cell type (Figure 2d–f). Furthermore, live-dead staining of electroporated HUES 64 and HEK 293FT cells confirmed that they remained viable at 4 h post-electroporation (Figure S5a–c, Supporting Information). The 4-hour time point was chosen to check for early onset of apoptosis. Data for cell viability at 15 hours post-electroporation are shown in Figure S5d,e (Supporting Information).
Next, we examined whether delivery dosage could be modulated by varying the peak voltage amplitude and/or number of pulses. We used the NFP-E to deliver BSA-AF488 into HeLa cells under different pulse conditions. We employed five different values for the peak voltage amplitude (10, 12, 15, 18, and 20 V) with the number of pulses constant at 100. The fluorescence intensity of the delivered BSA-AF488 was averaged for the five voltage cases (Figure 2g). In agreement with the lumped model predictions, we observed that electroporation occurred for all five voltage values, and the amount delivered increased monotonically with the applied voltage. The molecular influx due to electroporation is composed of two components: an electrophoretic component and a diffusive component. By assuming that the number of electro-pores created during electroporation depends linearly on the applied voltage, the transported amount has been shown to have a quadratic dependence on the applied voltage.[27] Our experimental data were well-described by a quadratic function (Figure 2g). We also investigated how the delivered amount of an exogenous protein varied with number of electroporation pulses. For these experiments, we used MDA-MB-231 cells and BSA-AF488 (Figure 2h). Signal intensity increased monotonically up to 500 pulses. In addition, we observed substantial blebbing (Figure S6, Supporting Information) in experiments with 500 pulses and 1,250 pulses, suggesting that these conditions should be avoided.
2.3. Plasmid delivery and ratiometric expression
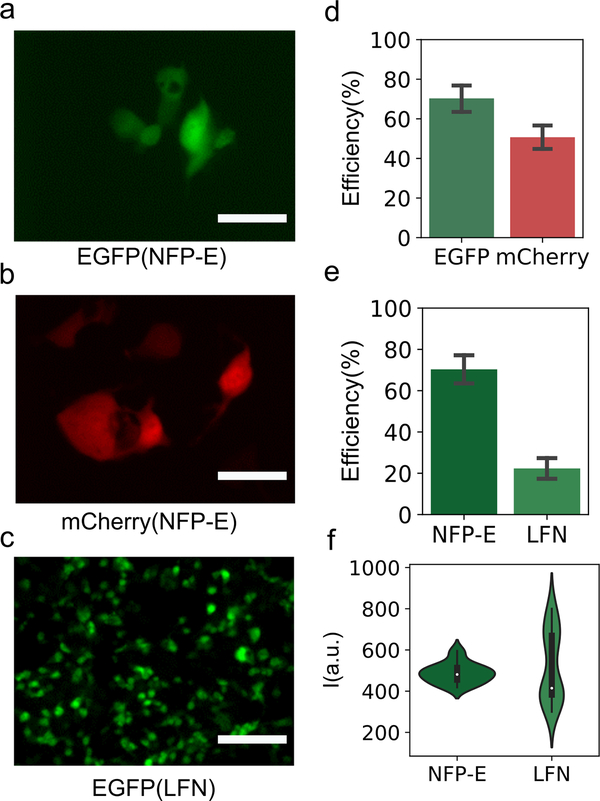
Efficient plasmid transfection is important in applications ranging from stem cell reprogramming to gene editing. We investigated the use of NFP-E for transfection using plasmids for expression of EGFP and mCherry. Transfection was achieved with each plasmid in HEK 293FT cells (Figure 3a,b, Figure S7a,b, Supporting Information). The mean transfection efficiency with EGFP plasmid was 70.3% (n = 126 cells) with a standard deviation (SD) of 18.0%, and for mCherry plasmid it was 50.7% (n = 110 cells) with a SD of 13.9%. The HEK 293FT cell line is transformed with an SV40 large T antigen, which drives replication of plasmid vectors containing the SV40 origin of replication. This cell line also has a better transfection efficiency with Lipofectamine than cancerous cell lines (such as HeLa or MDA-MB-231). These attributes make it appropriate for comparison of the transfection efficiencies with the NFP-E and Lipofectamine. All the transfection experiments (NFP-E and Lipofectamine) were carried out in standard culture medium (DMEM). The mean efficiency of EGFP plasmid transfection with Lipofectamine was 22.3% (SD = 11.2%) compared to the 70.3% for NFP-E–mediated transfection (Figure 3e). Here, the efficiency of Lipofectamine-mediated transfection is likely low because the cells were retained in DMEM rather switched to Opti-MEM (as the manufacturer protocol recommends). The choice of maintaining the buffer was to do a one-to-one comparison with the NFP-E. We note that one benefit of NFP-E–based transfection is that specialized transfection media or buffers are not required to attain a high transfection efficiency. The distribution of the EGFP fluorescence intensity for the cells transfected via NFP-E had a much lower spread relative to that observed in the case of transfection with Lipofectamine (Figure 3f). The SDs of the fluorescence intensities of the NFP-E–transfected and Lipofectamine-transfected cells were 9.98% and 32.5% of their corresponding mean intensity values, respectively. Thus, when compared to Lipofectamine, NFP-E conferred tighter control over plasmid delivery and subsequent transgene expression. Potential contributing factors to the observed difference in spread might include: 1) variation in the number of plasmids per lipoplex is greater than variation in the number of plasmids delivered by NFP-E, and 2) delivery by lipoplex might depend more on certain sources of heterogeneity, such as cell cycle, than does delivery by NFP-E. Plasmid delivery was also attempted in hard to transfect cells like HUES 64 and post-natal neural stem cells (Figure S8, Supporting Information).
Figure 3.
Comparison of plasmid delivery using NFP-E and Lipofectamine (LFN). (a–c) Representative fluorescence images. a) HEK 293FT cells expressing EGFP after plasmid delivery with NFP-E, and b) HEK 293FT cells expressing mCherry after plasmid delivery with NFP-E. Scale bar: 20 μm. c) HEK 293FT cells expressing EGFP after plasmid delivery with LFN. Scale bar: 100 μm. d) Transfection efficiency for EGFP plasmid and mCherry plasmid with NFP-E. 126 cells were targeted with EGFP plasmid, and 110 cells were targeted with mCherry plasmid. e) Transfection efficiency with EGFP plasmid for NFP-E and LFN. Error bars indicate the standard error of the mean. f) Distribution of fluorescence intensity for EGFP-expressing cells transfected using NFP-E or LFN. In the violin plots, dots are the median, bars are the interquartile range, and lines are the ±1.5 interquartile range.
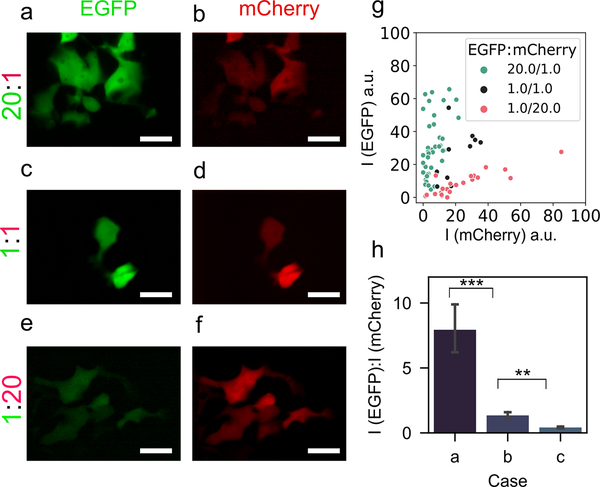
Next, we examined whether two plasmids could be delivered at a desired ratio to control their relative expression. We tested three cases: (a) co-transfection of 200 ng μl–1 EGFP plasmid and 10 ng μl–1 mCherry plasmid (20:1); (b) co-transfection of both at 100 ng μl–1 each (1:1); and (c) co-transfection of 10 ng μl–1 EGFP plasmid and 200 ng μl–1 mCherry plasmid (1:20). As expected, compared to the equal concentration base case b (1:1), in case a, the relative fluorescence intensity of EGFP was much higher than that of mCherry (Figure 4a,b), and the converse was true for case c (Figure 4e,f). Figure 4g shows the fluorescence intensities in each channel for transfected cells across the three cases. The average values of the ratio of EGFP and mCherry fluorescence intensities (from multiple cells within each case) are in Figure 4h. We observed significantly higher relative expression of EGFP than mCherry for case a vs. b (p < 0.001), and significantly lower relative expression of EGFP for case c vs. b (p < 0.01). We also compared the ratiometric delivery of the NFP-E with that of calcium phosphate transfection for the plasmid concentration ratios (Figure S9, Supporting Information); we conclude that NFP-E can be used to co-deliver cargo at different ratios, and that one may need to prepare a higher plasmid concentration ratio to achieve the intended protein expression ratio.
Figure 4.
Ratiometric delivery of EGFP plasmid and mCherry plasmid using NFP-E. Representative fluorescence micrographs showing the expression of EGFP (a, c, e) and mCherry (b, d, e) in HEK 293FT cells corresponding to 20:1, 1:1, and 1:20 EGFP-to-mCherry plasmid concentration ratios. Scale bar: 20 μm. g) EGFP and mCherry fluorescence intensities (in distinct arbitrary units) for the three different plasmid concentration ratios. Each data point represents a transfected cell. h) Relative fluorescence intensity ratios of EGFP and mCherry for the three cases a (20:1), b (1:1), and c (1:20). Each condition includes more than 10 cell measurements. *** (p < 0.001), ** (p < 0.01).
2.4. Dynamics of post-pulse molecular transport during sampling
To understand the dynamics of disease mechanisms and differentiation, intracellular contents might need to be assayed across time points with single-cell resolution; this is often done by lysing parallel cell cultures.[39, 40] However, lysis-based methods preclude the analysis of the same cells over time, which could be important in addressing single-cell heterogeneity. Recent reports have demonstrated viable extraction of cellular contents from a small population of cells via electroporation by exploiting the transient permeability of the cell membrane.[22, 24, 28] However, little knowledge exists on the effective design of voltage pulses for electroporation-based sampling. This gap in knowledge could be overcome in part by examining the dynamics of post-pulse molecular transport and the timescales involved in this process. It would be useful to provide an estimate of the membrane resealing time post-electroporation, and thus potentially aid in optimizing the extraction of intracellular contents. This information is particularly relevant for the design of voltage profiles for implementing multiple time-point sampling from the same cells without compromising cell function. The process of electro-pore creation is commonly assumed to involve nucleation of hydrophilic toroidal pores in the plasma membrane. The electro-pores nucleate and evolve during the pulse and then start to close post-pulse application. The nucleation, evolution and disappearance of these toroidal electro-pores depends nonlinearly on the transmembrane potential and is governed by the Smoluchowski advection-diffusion equation.[41] Based on prior modeling analysis, it is known that the post-pulse distribution of such electro-pores is initially centered on a radius of ~1 nm for millisecond pulses, and it subsequently diffuses towards a critical pore radius of 0.65 nm, which is the minimum radius allowable for a hydrophilic pore.[42, 43] We reasoned that as calcein’s hydrodynamic radius (0.74 nm)[44] is less than the average hydrophilic nanopore radius (1 nm) and close to the critical pore radius, calcein would be a well-suited test case for probing the dynamics of post-pulse transport.
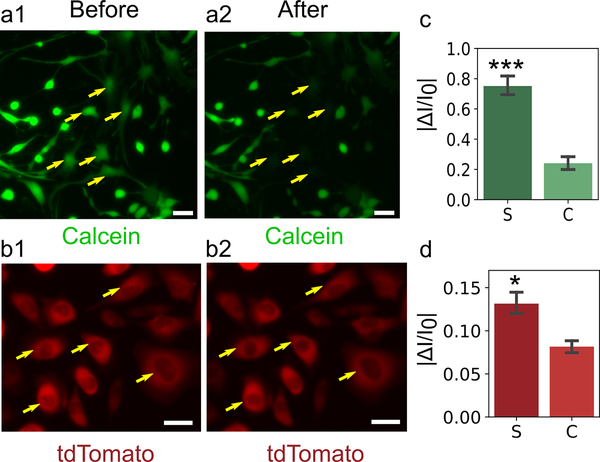
First, we examined whether the NFP-E system with standard electroporation parameters would allow the sampling of calcein as well as an exogenous protein. Figure 5a1 and Figure S10a,c (Supporting Information) show post-natal neural stem cells (PN-NSCs) that were subjected to a differentiation protocol and stained with calcein-AM before electroporation pulses were applied. Figure 5a2 and Figure S10b,d (Supporting Information) show lower fluorescence intensity in the same cells due to electroporation-mediated removal of calcein. The change in fluorescence intensity of the electroporated cells was averaged, and the normalized data are presented in Figure 5c. To confirm that the reduction in intensity was due to electroporation and not to artifacts such as photobleaching, the change in the fluorescence intensity of several non-electroporated control cells was determined. The reduction in fluorescence intensity of electroporated cells was significantly different (p < 0.001) than that of control cells. We also engineered an MDA-MB-231 cell line to constitutively express tdTomato under a CMV promoter and subjected these cells to the same protocol (Figure 5b1,b2). The normalized change in fluorescence intensity of tdTomato for the electroporated cells is presented along with that for a control population in Figure 5d. The data show a significant change (p < 0.05) in the intensity of the electroporated cells compared to that of the control group. However, the intensity changes here are less discernible when compared to the case of calcein. tdTomato (54.2 kDa) is a much larger molecule than calcein (0.6 kDa) and hence by the Stoke-Einstein’s relation for diffusivity, tdTomato would have a much lower diffusion coefficient than does calcein. This difference could potentially explain the much lower outflow of tdTomato when compared to that of calcein.
Figure 5.
Intracellular sampling of calcein and tdTomato using NFP-E. a) Representative images of calcein-containing PN-NSCs before (a1) and after (a2) pulse application. Yellow arrows indicate electroporated cells, and the cells undergo loss of calcein (a small molecule, radius < 1 nm). b) MDA-MB-231 cells before (b1) and after (b2) pulse application. The cells undergo loss of tdTomato protein (a relatively large molecule, radius > 1 nm). Scale bar: 30 μm. c) Absolute value of the fractional change in fluorescence intensity of sampled and control PN-NSCs for the case of calcein outflow. Eleven sampled cells (S) and 10 control cells (C) were analyzed. d) Absolute value of the fractional change in fluorescence intensity of sampled and control MDA-MB-231 cells for the case of tdTomato outflow. Five sampled cells and five control cells were analyzed. *** (p < 0.001), * (p < 0.05). Error bars indicate the standard error of the mean.
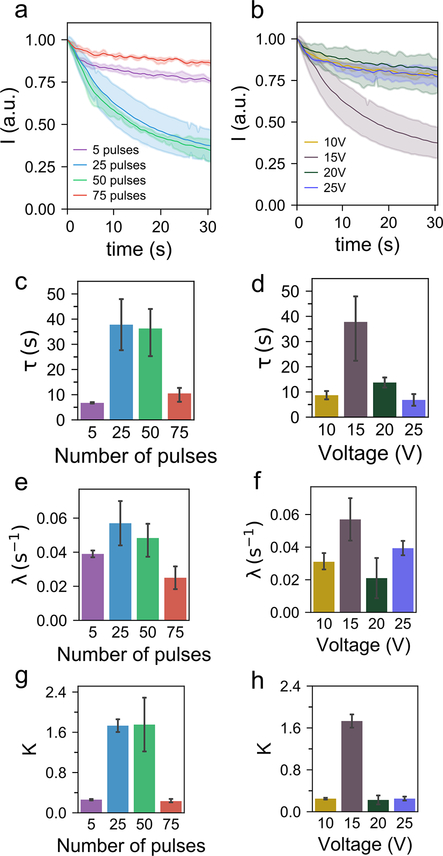
Next, we briefly describe the protocol involved in a typical time-lapse imaging experiment. HeLa cells were stained with calcein-AM, and electroporation pulses were then applied. We varied either the peak voltage or the number of pulses in these experiments, while keeping the frequency and duration of each individual pulse constant at 50 Hz and 3 ms respectively. The pulse generator in the NFP-E system has the flexibility to synchronize with other data acquisition modules: a 5 V TTL signal is sent to the sCMOS camera (Andor Zyla) which triggers a time-lapse image acquisition session in μManager.[45] The decay of calcein fluorescence intensity over time in electroporated cells was obtained from the images using a custom MATLAB script. Figure 6a,b shows the time traces of mean (n = 3) fluorescence intensities corresponding to the cases of electroporation with different number of pulses and pulse voltages respectively.
Figure 6.
Post pulse electro-pore dynamics. a) Decay in fluorescence intensity of calcein-containing HeLa cells after electroporation with different numbers of pulses, keeping the pulse voltage at 15 V. b) Decay in fluorescence intensity of calcein-containing HeLa cells after electroporation with different pulse voltages, keeping number of pulses at 25. Shading indicates the 95% confidence interval. (c–h) Variation of the model parameters with different numbers of pulses (c, e, g) and different voltages (d, f, h). For each experimental condition, 3 samples were analyzed. Error bars indicate the standard error of the mean for three samples.
To model the experimental observations, we assumed the post-pulse transport of calcein across the cell membrane to be purely diffusive. This assumption is valid as the time scale of the observation (~30 s) is much longer than the maximum total pulsing duration (~0.225 s). With these assumptions and by utilizing Fick’s law of diffusion, we show (Supporting Information) that the intracellular concentration over time can be expressed as indicated below (see also Wang, et al.[46] for a similar analysis):
| #(7) |
where ci is the initial concentration (a.u.), τ [s] is the time constant for membrane resealing and λ [s–1] is a parameter that is proportional to the initial permeabilized fractional area of the membrane (Supporting Information). We assumed that the fluorescence intensity of calcein scales linearly with its concentration, as previously reported.[47] Using equation (7) we also arrived at a quantitative estimate of the fraction of calcein sampled (Supporting Information).
| #(8) |
We fitted the model in Eq. 7 to the experimental data (Figure 6a,b). We investigated the dependence of τ, λ and K on pulse voltage and number of pulses (Figure 6c–h). We note that the time constant (τ) does not scale linearly with either the pulse voltage or number of pulses (Figure 6c,d); it reaches a maximum for intermediate values of pulse parameters. A nonlinear trend is also observed for the parameter λ (Figure 6e,f). The time constant for membrane resealing (τ) is an estimate of the rate at which the membrane permeability reduces over time after pulse application. Therefore, to maximize the sampled volume, τ needs to be increased so that pores remain open for a sufficient period of time. Moreover, since λ is a measure of the initial fraction of permeabilized area, a higher λ would also contribute towards more sampling. As expected, we observe that K which is a logarithmic measure of the loss of calcein (Supporting Information) is high for the cases that have high values of both τ and λ (Figure 6c–h).
3. Discussion
The lumped model for electroporation presented here predicts that for a range of applied voltages the transmembrane potential align with the well accepted threshold (0.2–1 V) for successful electroporation and cargo delivery.[20, 48] Indeed, we observed delivery of a variety of molecular cargo in experiments with these far-field voltages (Figures 2, 3). Since the lumped model substantially decreases the computational time, it might enable the modeling of electroporation-based experiments, which are usually on the several-second timescale.
For protein and plasmid delivery experiments, the same pulsation protocol was effective across different cell types, which speaks to the generality of the method. The direct delivery of protein complexes is advantageous in situations where other strategies such as viral vectors or plasmid DNA can lead to cytotoxicity, off-target effects, or low control over protein expression.[49, 50] Gene-editing studies employing CRISPR/Cas9 systems,[51, 52] induction of pluripotency for tissue engineering,[53] and stimulation of immune cells for therapeutic purposes are avenues where direct protein delivery using the NFP-E might prove beneficial. We have also shown that the NFP-E approach can attain relatively high transfection efficiency in normal cell culture medium without requiring a media change. This may be convenient for some applications because growing cells in low serum media (which is recommended for transfection by lipofection) can decrease cell viability and protein expression.[54]
Recent studies indicate that ratiometric control of Cas9 and sgRNA is important in CRISPR/Cas9 gene editing.[55] Hence, establishing a universal transfection method that exploits delivery mechanisms in which dosage control can be achieved, at the single-cell level, is a high priority. Previous studies have shown that the stoichiometry of the genetic factors is an important variable in stem cell reprogramming. For instance, the induction efficiency of iPSCs from somatic cells is sensitive to the dosage of Oct4, and higher expression of Oct4 and Klf4, relative to Sox2 and c-Myc, correlates with greater reprogramming efficiency.[32] Furthermore, the relative concentration of reprogramming factors affects not only induction efficiency but can also result in chromatin modifications.[56] The cotransfection experiments reported here with the NFP-E highlight its utility for investigating stoichiometries that could be useful for stem cell engineering.
From the temporal studies of electroporation-mediated loss of calcein, we can conclude that the post-pulse transport of molecules across the cell membrane depends on two parameters: τ and λ, where τ is the rate of membrane resealing and λ is a measure of the initial fraction of the permeabilized area. The maximum transport of calcein molecules across the cell membrane occurs at intermediate values of the pulse parameters. A similar trend was also demonstrated previously,[22, 24, 57] where the maximum transfection efficiency of a plasmid occurred for an intermediate value of the pulse voltage amplitude in multiple cell types.
Several advances have been made in improving the sensitivity of bioanalytical assays at the single-cell level (digital PCR, RNA-Seq, etc.), but many of these analyses involve cell lysis and are thus limited to a single time point. Methods that overcome this limitation often depend on measuring a limited subset of secreted markers or on building a pseudo-time profile by lysing different cells at different times. A contrasting approach to temporal analysis is to extract a minute portion of the cytosol using localized electroporation and to assay the retrieved biomarkers.[22, 28] Such an approach provides the potential to monitor a single cell over time and to improve our understanding of cell behaviors. Here, the electroporation-mediated loss of calcein and tdTomato with the NFP-E provides a proof of concept for extracting small molecules and cytosolic proteins. Moreover, the nanopipette of the NFP-E can be tuned to collect intracellular samples, which could then be used in downstream analyses like RNA-Seq. For example, electro-wetting within the nanopipette can be used to extract cellular material from live cells in culture, and such samples may be analyzed by sequencing.[58] We emphasize that the mechanism of the NFP-E is distinct from other probe-based sampling methods.[58–61] The latter methods rely on micro-injection and consequently puncture a large areal fraction of the cell membrane, whereas localized electroporation with the NFP-E perturbs only a miniscule portion of the membrane underneath the probe tip. A thorough analysis, however, of transcriptomic and chromatin changes induced by different delivery and sampling methods is still needed.[24]
A major impediment to single-cell temporal sampling is the trace amount of cytosol extracted that makes downstream assays challenging. For perspective, in microinjection-based sampling methods,[58, 59] the extraction efficiency was approximately 70–85% for an exogenous mRNA in HeLa cells, with even lower values for housekeeping genes such as β-actin. The problem compounds in the case of biologically relevant mRNA that have lower copy numbers, e.g., neural stem cells have less than 20 copies of the differentiation-relevant mRNA tyrosine hydroxylase, per cell[62]—an order of magnitude less than typical housekeeping mRNAs. Thus, there is a need to understand the transport mechanisms involved in localized electroporation-based sampling, with the goal of finding ways to increase the sampled amount without adversely affecting the cell. The results presented here on the scaling of membrane resealing time as function of various electroporation parameters begin to address this need. To overcome throughput limitations with the serial nature of the NFP-E, future efforts will be focused on automating the process of cell detection with image processing and machine learning methods An additional goal would be to extend NFP-E based delivery to suspended cells. Cell trapping methods could be used in conjunction with the NFP-E to facilitate delivery into suspended cells.[63] Alternatively, cells in suspension can be centrifuged so that they settle down and do not tremble, thus enabling contact between the nanopipette and cell membrane required for the NFP-E methodology. [57]
4. Conclusion
In summary, we demonstrate a versatile method for delivering large proteins and plasmids in various cell types with fine control over dosage. Further, we investigated the dynamics of molecular transport after the pulsing and established scaling laws for the membrane resealing time with respect to the pulse voltage and the number of pulses. In a previous report, we showed that coupling the model for predicting transmembrane potential with the Smoluchowski equation (which governs the nucleation, diffusion, and destruction of pores) provided qualitative insights into the observed experimental trends.[22] Hence, combining the Smoluchowski equation-based pore evolution model with the lumped model might explain the basis of the scaling laws and could be investigated in future studies. We anticipate that integration of low-loss sample retrieval methods such as electrowetting[58] or oil-droplet based[59] within the nanopipette of the NFP-E should allow downstream assaying with existing methods (RT-PCR, ELISA etc.).
5. Experimental section
5.1. Cell culture
5.1.1. MDA-MB-231, HEK 293FT and HeLa cells
Cell lines were cultured in Dulbecco’s Modified Eagle Medium (DMEM) supplemented with 10% fetal bovine serum (FBS) and 1% penicillin-streptomycin. Cells were grown in an incubator at 37°C with 5% CO2 and passaged every 3–5 days upon reaching 80–90% confluency using 0.25% trypsin. Reagents were purchased from Life Technologies and used per the manufacturer-provided specifications. Experiments were performed on cells that had been passaged fewer than ten times.
5.1.2. Human fibroblasts
Primary dermal fibroblasts were procured from ATCC (PCS-201–012) and cultured using fibroblast basal medium supplemented with a low-serum growth kit (ATCC PCS-201–041). Cells were passaged upon reaching confluency using 0.05% trypsin-EDTA and trypsin inhibitor solution (Life Technologies). Experiments were performed on cells that had been passaged fewer than ten times.
5.1.3. Postnatal murine neurospheres
All procedures involving animals were approved in advance by the Northwestern University Institutional Animal Care and Use Committee. Neural stem cells (NSCs) were isolated from the subventricular zone in postnatal day 1 mice and cultured as neurospheres in DMEM: F12 medium supplemented with B27, N2, and EGF (20 ng mL–1). In electroporation experiments, NSCs were plated in 35 mm petri dishes using medium with lower EGF concentration (0.5 ng mL–1). To promote adhesion, petri dishes were pre-coated with poly-D-lysine (50 μg mL−1) overnight. Cells were allowed to adhere for at least 24 hours prior to electroporation. All experiments were performed on cells that had been passaged (using 0.05% trypsin) at most three times.
5.1.4. Human embryonic stem cells (HUES 64)
HUES 64 cells were cultured in Essential 8™ Medium (basal medium and supplements, Thermo Fisher Scientific) on Matrigel-coated 6-well plates (Corning). The medium was replaced every 24 hours. Cells were passaged by dissociating in 0.5 mM EDTA (Thermo Fisher Scientific) in PBS every 4–5 days before reaching full confluency. ROCK inhibitor (Tocris Y-27632) was added at a final concentration of 10 μM to the medium after passaging. Cells were transferred to ROCK inhibitor-free medium after 24 hours.
5.2. General protocol for electroporation using the NFP-E
Infinitesimal’s point-click-transfect NFP-E system was employed in all experiments. Glass nanopipette tips (Eppendorf) with an inside diameter of 500 nm (Figure 1b) were employed in the transfection experiments. Nanopipette tips were first loaded with the desired solution using a micro-loader (Eppendorf) and subsequently mounted on Infinitesimal’s NFP-E system with XYZ motion control achieved via three linear piezo actuators (closed loop, resolution < 10 nm). Infinitesimal’s software and electronic circuit were used to measure the resistance across the nanopipette tip (150 Hz sampling rate) and to automatically apply bi-level electroporation pulses. The movement of the nanopipette tip was observed under an inverted microscope (Nikon Eclipse) coupled to a CCD camera (Andor Zyla). When the resistance between the tip and the cell increased by approximately 1%, bilevel electroporation pulses (15 V 0.5 ms, 10 V 2.5 ms typical; Figure S2, Supplementary Information) were applied at a frequency of 50 Hz. Each train consisted of 50 such bilevel pulses, and typically 1 or 2 trains were used in the delivery experiments.
5.3. Delivery of bovine serum albumin (BSA)
Bovine serum albumin (BSA) tagged to Alexa Fluor 488 (Life Technologies) was resuspended in 1× PBS and used in electroporation experiments at a final concentration of 2.5 mg mL–1.
5.4. Ratiometric delivery of plasmids in HEK 293FT cells
The two plasmids pEGFP and pmCherry (each ~4.7 kb) contain a pcDNA plasmid backbone of ~4 kb with an SV40 origin of replication, a neomycin/kanamycin resistance gene, and an insert of ~0.7 kb that encodes a fluorescent reporter gene (EGFP and mCherry, respectively) driven by a CMV promoter. Plasmids were stored at 4°C at a concentration of 1 μg mL–1 and diluted in 1× PBS to the desired concentration (0.1–200 ng mL–1) before electroporation.
5.5. Plasmid Delivery using Lipofectamine 2000
Cells were plated in a 24-well plate and allowed to reach a confluency of 70–90% before transfection with Lipofectamine 2000 (Thermo Fisher Scientific). 50 μL of serum-free DMEM was combined with varying volumes (2–5 μL) of Lipofectamine and 0.5 μg of plasmid (in 25 μL DMEM) to identify conditions for maximal transfection efficiency. 50 μL of this cocktail was added to cell culture. Cells were incubated for 48 hours, after which fluorescent protein expression was examined by fluorescence microscopy.
5.6. Calcein sampling in differentiating post-natal neural stem cells (PN-NSCs)
PN-NSCs were subjected to differentiation conditions for at least 5 days leading up to experiments. Calcein-AM (1 mg mL–1, Life Technologies) was diluted 100-fold in 1× PBS, and cells were stained for 10 minutes at 37°C and 5% CO2. Cells were washed twice with 1× PBS, and sampling experiments were performed immediately with the NFP-E.
5.7. tdTomato sampling in MDA-MB 231 cells
MDA-MB-231 cells (< 10 passages) were plated in a petri dish and incubated for at least a day, by which time they had adhered. Cells were washed twice with 1× PBS, and sampling experiments were performed immediately with the NFP-E.
5.8. Image Analysis
To compute the normalized change in fluorescence intensity in calcein and tdTomato sampling experiments, we utilized the open source software FIJI (version 2.0.0). Briefly, a region of interest (ROI) was first drawn around the central region of the cell of interest; then the measurement tool was used to obtain the mean fluorescence intensity of the pixels within the ROI. The size of the ROI was kept constant across the images analyzed. For time-lapse experiments, the stack file consisting of all of the frames acquired during the experiment was first saved as individual image sequences using ImageJ. The individual frames were then processed in MATLAB 2016. The first image of the sequence was used to create a mask encompassing all of the pixels in the area of interest, which was either a cell exposed to localized electroporation or a control cell. The process of creating the mask involved converting the raw greyscale image into a binary image by applying the method of adaptive thresholding. Then, a series of erosions and dilations were applied to the first binary image in order to reflect the ROI as accurately as possible. The binary image obtained after this processing step was used as the mask used for all further calculations. In the mask, all pixels in the ROI had intensity = 1 while the other pixels had intensity = 0. The time-lapse data (Figure 6a,b) represent the mean fluorescence intensity of the ROI in all of the frames in a stack. This value was obtained by calculating the mean fluorescence intensity of the non-zero pixels in the mask for all of the frames in the stack. For every case, the final values of intensity were obtained after background subtraction.
5.9. Modelling of the NFP-E
We used COMSOL Multiphysics to compute the transmembrane potential in the NFP-E system. Finite element simulations were performed using the Electrical Currents module, and the system of ODEs in the lumped model was solved using the Global ODEs and DAE Interfaces module.
5.10. Calcium phosphate transfection
HEK 293FT cells were plated in 24-well plates (1.5×105 cells in 0.5 ml DMEM per well) and transfected after having adhered to the plates. Plasmids were mixed together in defined amounts, CaCl2 (2 M, 15% v/v) was added, and the solution was pipetted dropwise into an equal volume of 2× HEPES-buffered saline (500 mM HEPES, 280 mM NaCl, 1.5 mM Na2HPO4). This solution was pipetted gently four times, and three minutes later it is pipetted vigorously 20 times and added dropwise onto cells (0.1 ml per well). A consistent total mass of DNA per well was maintained by including in the transfection mix an “empty vector” (pcDNA backbone) that does not encode a fluorescent protein. A mixture 200 ng of EGFP and 10 ng of mCherry was used for the 20:1 plasmid concentration ratio case, 100 ng of both was used for the 1:1 case and 10 ng of EGFP and 200 ng of mCherry was used for the 1:20 case. At one day after plating, the medium was aspirated and replaced with fresh medium.
5.11. Flow cytometry and data analysis
Samples were prepared for flow cytometry two days after transfection. Medium was aspirated, several drops of PBS were added and then aspirated, and two drops of trypsin-EDTA (Gibco) were added. Cells were incubated (37°C, 5 min), plates were tapped to detach cells, and several drops of DMEM were added to quench the trypsinization. The contents of each well were pipetted to detach cells and pipetted into FACS tubes containing FACS buffer (2 ml; PBS pH 7.4, 5 mM EDTA, 0.1% w/v BSA). Tubes were centrifuged (150×g, 5 min), liquid was decanted, and a couple of drops of FACS buffer were added. Samples were kept on ice and wrapped in foil, and run on a BD LSR Fortessa special order research product using the FITC channel (488 nm excitation laser, 505LP 530/30 nm filter) for EGFP and the PE-Texas Red channel (552 nm excitation laser, 600LP 610/20 nm filter) for mCherry. Approximately 104 live single-cell events were measured per sample. Data were analyzed using FlowJo software to gate on single-cell (FSC-A vs. FSC-H) and live-cell (FSC-A vs. SSC-A) bases. Compensation was performed using compensation control samples. The mean fluorescent signal was obtained for each sample. The mean and the standard error of the mean for the three biological replicates were calculated.
Statistical Analysis
Statistical comparisons were performed using two-tailed Student’s t-tests.
Supplementary Material
Acknowledgements:
Research reported in this publication was supported by the National Cancer Institute of the National Institutes of Health under award number U54CA199091; NIH SBIR Phase 1 award number 1R43GM128500-01 and NIH R21 award number 1R21GM132709-01. We thank Patrick Donahue, Taylor Dolberg, Hailey Edelstein, and Kelly Sarnese for providing reagents.
Footnotes
Conflict of Interest: HDE declares majority ownership of iNfinitesimal LLC, a company commercializing bio-tools for cell manipulation and analysis.
Contributor Information
S. Shiva P. Nathamgari, Department of Mechanical Engineering, Northwestern University, Evanston, IL 60208, USA Theoretical and Applied Mechanics Program, Northwestern University, Evanston, IL 60208, USA.
Nibir Pathak, Department of Mechanical Engineering, Northwestern University, Evanston, IL 60208, USA; Theoretical and Applied Mechanics Program, Northwestern University, Evanston, IL 60208, USA.
Vincent Lemaitre, iNfinitesimal LLC, Skokie, Illinois 60077, United States.
Prithvijit Mukherjee, Department of Mechanical Engineering, Northwestern University, Evanston, IL 60208, USA; Theoretical and Applied Mechanics Program, Northwestern University, Evanston, IL 60208, USA.
Joseph J. Muldoon, Department of Chemical and Biological Engineering and Interdisciplinary Biological Sciences Program, Northwestern University, Evanston, IL 60208, USA
Chian-Yu Peng, Department of Neurology, Northwestern University Feinberg School of Medicine, Chicago, IL 60611, USA.
Tammy McGuire, Department of Neurology, Northwestern University Feinberg School of Medicine, Chicago, IL 60611, USA.
Joshua N. Leonard, Department of Chemical and Biological Engineering and Interdisciplinary Biological Sciences Program, Northwestern University, Evanston, IL 60208, USA Center for Synthetic Biology, Northwestern University, Evanston, Illinois 60208, USA.
John A. Kessler, Department of Neurology, Northwestern University Feinberg School of Medicine, Chicago, IL 60611, USA
Horacio D. Espinosa, Department of Mechanical Engineering, Northwestern University, Evanston, IL 60208, USA Theoretical and Applied Mechanics Program, Northwestern University, Evanston, IL 60208, USA.
References
- [1].Hendel A, Bak RO, Clark JT, Kennedy AB, Ryan DE, Roy S, Steinfeld I, Lunstad BD, Kaiser RJ, Wilkens AB, Bacchetta R, Tsalenko A, Dellinger D, Bruhn L, Porteus MH, Nat. Biotechnol. 2015, 33, 985–989. DOI 10.1038/nbt.3290 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Liu J, Gaj T, Yang Y, Wang N, Shui S; Kim S, Kanchiswamy CN, Kim JS, Barbas III CF, Nat. Protoc. 2015, 10, 1842–1859. DOI 10.1038/nprot.2015.117. [DOI] [PubMed] [Google Scholar]
- [3].Hultquist JF, Schumann K, Woo JM, Manganaro L, McGregor MJ, Doudna J, Simon V, Krogan NJ, Marson A, Cell Rep. 2016, 17 (5), 1438–1452. DOI [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Liang X, Potter J, Kumar S, Zou Y, Quintanilla R, Sridharan M, Carte J, Chen W, Roark N, Ranganathan S, Ravinder N, Chesnut JD, Biotechnol J. 2015, 208, 44–53. DOI 10.1016/j.jbiotec.2015.04.024. [DOI] [PubMed] [Google Scholar]
- [5].Ebert AD, Yu J, Rose FF Jr, Mattis VB, Lorson CL, Thomson JA, Svendsen CN, Nature 2008, 457, 277–280. DOI 10.1038/nature07677 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Spence JR, Mayhew CN, Rankin SA, Kuhar MF, Vallance JE, Tolle K, Hoskins EE, Kalinichenko VV, Wells SI, Zorn AM, Shroyer NF, Wells JM, Nature 2010, 470, 105–109. DOI 10.1038/nature09691 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Inoue H, Yamanaka S, Clin. Pharmacol. Ther. 2011, 89 (5), 655–661. DOI 10.1038/clpt.2011.38. [DOI] [PubMed] [Google Scholar]
- [8].Papapetrou EP, Tomishima MJ, Chambers SM, Mica Y, Reed E, Menon J, Tabar V, Mo Q, Studer L, Sadelain M, Proc. Natl. Acad. Sci. U. S. A. 2009, 106 (31), 12759–12764. DOI 10.1073/pnas.0904825106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Mali P, Esvelt KM, Church GM, Nat. Methods 2013, 10 (10), 957–963. DOI 10.1038/nmeth.2649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Roth CM, Sundaram S, Annu. Rev. Biomed. Eng. 2004, 6 (1), 397–426. DOI 10.1146/annurev.bioeng.6.040803.140203. [DOI] [PubMed] [Google Scholar]
- [11].Gros E, Deshayes S, Morris MC, Aldrian-Herrada G; Depollier J, Heitz F, Divita G, Biochim Biophys Acta Biomembr 2006, 1758 (3), 384–393. DOI 10.1016/j.bbamem.2006.02.006. [DOI] [PubMed] [Google Scholar]
- [12].Li J, Zhang L, Liu Y, Wen J, Wu D, Xu D, Segura T, Jin J, Lu Y, Wang H, Chem. Commun. (London) 2016, 52 (93), 13608–13611. DOI 10.1039/C6CC05099A. [DOI] [PubMed] [Google Scholar]
- [13].Chow YT, Chen S, Wang R, Liu C, Kong C.-w., Li RA, Cheng SH, Sun D, Sci. Rep. 2016, 6, 24127 DOI 10.1038/srep24127 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Costa M, Dottori M, Sourris K; Jamshidi P, Hatzistavrou T, Davis R, Azzola L, Jackson S, Lim SM, Pera M, Elefanty AG, Stanley EG, Nat. Protoc. 2007, 2, 792–796. DOI 10.1038/nprot.2007.105. [DOI] [PubMed] [Google Scholar]
- [15].Golzio M, Teissié J, Rols MP, Proc. Natl. Acad. Sci. U. S. A. 2002, 99 (3), 1292–1297. DOI 10.1073/pnas.022646499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Schaffer DV, Fidelman NA, Dan N, Lauffenburger DA, Biotechnol. Bioeng. 2000, 67 (5), 598–606. DOI . [DOI] [PubMed] [Google Scholar]
- [17].Lv H, Zhang S, Wang B, Cui S, Yan J, J. Controlled Release 2006, 114 (1), 100–109. DOI 10.1016/j.jconrel.2006.04.014. [DOI] [PubMed] [Google Scholar]
- [18].Stewart MP, Langer R, Jensen KF, Chem. Rev. 2018, 118 (16), 7409–7531. DOI 10.1021/acs.chemrev.7b00678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Gonzalez MR, Bischofberger M, Frêche B, Ho S, Parton RG,, van der Goot FG, Cell. Microbiol. 2011, 13 (7), 1026–1043. DOI 10.1111/j.1462-5822.2011.01600.x. [DOI] [PubMed] [Google Scholar]
- [20].Wang M, Orwar O, Olofsson J, Weber SG, Anal. Bioanal. Chem. 2010, 397 (8), 3235–3248. DOI 10.1007/s00216-010-3744-2. [DOI] [PubMed] [Google Scholar]
- [21].Kang W, Yavari F, Minary-Jolandan M, Giraldo-Vela JP, Safi A, McNaughton RL, Parpoil V, Espinosa HD, Nano Lett. 2013, 13 (6), 2448–2457. DOI 10.1021/nl400423c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Mukherjee P, Nathamgari SSP, Kessler JA, Espinosa HD, ACS Nano 2018, 12 (12), 12118–12128. DOI 10.1021/acsnano.8b05473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Kang W, Giraldo-Vela JP, Nathamgari SSP, McGuire T, McNaughton RL, Kessler JA, Espinosa HD, Lab Chip 2014, 14 (23), 4486–4495. DOI 10.1039/c4lc00721b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Nathamgari SSP, Mukherjee P, Kessler JA, Espinosa HD, Proc. Natl. Acad. Sci. U. S. A. 2019, 116 (46), 22909 DOI 10.1073/pnas.1911718116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Boukany PE, Morss A, Liao WC, Henslee B, Jung HC, Zhang XL, Yu B, Wang X, Wu Y, Li L, Gao K, Hu X, Zhao X, Hemminger O, Lu W, Lafyatis GP, Lee LJ, Nat. Nanotechnol. 2011, 6 (11), 747–754. DOI 10.1038/Nnano.2011.164. [DOI] [PubMed] [Google Scholar]
- [26].Xie X, Xu AM, Leal-Ortiz S, Cao Y, Garner CC, Melosh NA, ACS Nano 2013, 7 (5), 4351–4358. DOI 10.1021/nn400874a. [DOI] [PubMed] [Google Scholar]
- [27].Cao Y, Chen H, Qiu R, Hanna M, Ma E, Hjort M, Zhang A, Lewis RS, Wu JC, Melosh NA, Sci. Adv. 2018, 4 (10), eaat8131 DOI 10.1126/sciadv.aat8131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Cao Y, Hjort M, Chen H, Birey F, Leal-Ortiz SA, Han CM, Santiago JG, Paşca SP, Wu JC, Melosh NA, Proc. Natl. Acad. Sci. U. S. A. 2017, 114 (10), E1866–E1874. DOI 10.1073/pnas.1615375114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Svensson V, Vento-Tormo R, Teichmann SA, Nat. Protoc. 2018, 13 (4), 599–604. DOI 10.1038/nprot.2017.149. [DOI] [PubMed] [Google Scholar]
- [30].Papalexi E, Satija R, Nat. Rev. Immunol. 2018, 18 (1), 35–45. DOI 10.1038/nri.2017.76. [DOI] [PubMed] [Google Scholar]
- [31].Baruch K, Rosenzweig N, Kertser A, Deczkowska A, Sharif AM, Spinrad A, Tsitsou-Kampeli A, Sarel A, Cahalon L, Schwartz M, Nat. Commun. 2015, 6, 7967 DOI 10.1038/ncomms8967 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Carey BW, Markoulaki S, Hanna JH, Faddah DA, Buganim Y, Kim J, Ganz K, Steine EJ, Cassady JP, Creyghton MP, Welstead GG, Gao Q, Jaenisch R, Cell Stem Cell 2011, 9 (6), 588–598. DOI 10.1016/j.stem.2011.11.003. [DOI] [PubMed] [Google Scholar]
- [33].Kang W, McNaughton RL, Espinosa HD, Trends Biotechnol 2016, 34 (8), 665–678. DOI 10.1016/j.tibtech.2016.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Meyers EA, Kessler JA, Cold Spring Harbor Perspect. Biol. 2017, 9 (8), a022244 DOI 10.1101/cshperspect.a022244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Kim KH, Moldovan N, Espinosa HD, Small 2005, 1 (6), 632–635. (Page numbers). DOI 10.1002/smll.200500027. [DOI] [PubMed] [Google Scholar]
- [36].Kang W, Nathamgari SSP, Giraldo-Vela JP, McNaughton RL, Kessler JA, Espinosa HD, In Optimization of a microfluidic device for localized electroporation of cells, 14th IEEE Int. Conf. Nanotechnol., 14th, 18–21 Aug. 2014; 2014; pp 1–3. [Google Scholar]
- [37].Weaver JC, Chizmadzhev YA, Bioelectrochem. Bioenerg. 1996, 41 (2), 135–160. DOI 10.1016/S0302-4598(96)05062-3. [DOI] [Google Scholar]
- [38].Gresch O, Altrogge L, Methods Mol Biol. 2012; pp 65–74. [DOI] [PubMed] [Google Scholar]
- [39].Duan L, Bhattacharyya BJ, Belmadani A, Pan L, Miller RJ, Kessler JA, Mol. Neurodegener. 2014, 9 (1), 3 DOI 10.1186/1750-1326-9-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Tsankov AM, Akopian V, Pop R, Chetty S, Gifford CA, Daheron L, Tsankova NM, Meissner A, Nat. Biotechnol. 2015, 33 (11), 1182–1192. DOI 10.1038/nbt.3387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Vasilkoski Z, Esser AT, Gowrishankar TR, Weaver JC, Phys. Rev. E 2006, 74 (2), 021904 DOI 10.1103/PhysRevE.74.021904. [DOI] [PubMed] [Google Scholar]
- [42].Saulis G, Saulė R, Biochim Biophys Acta Biomembr 2012, 1818 (12), 3032–3039. DOI 10.1016/j.bbamem.2012.06.018. [DOI] [PubMed] [Google Scholar]
- [43].Son RS, Smith KC, Gowrishankar TR, Vernier PT, Weaver JC, J Membr Biol 2014, 247 (12), 1209–1228. DOI 10.1007/s00232-014-9699-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Chenyakin Y, Ullmann DA, Evoy E, Renbaum-Wolff L, Kamal S, Bertram AK, Atmos. Chem. Phys. 2017, 17 (3), 2423–2435. DOI 10.5194/acp-17-2423-2017. [DOI] [Google Scholar]
- [45].Edelstein A, Amodaj N, Hoover K, Vale R, Stuurman N, Curr. Protoc. Mol. Biol. 2010, 92 (1), 14.20.1–14.20.17. DOI 10.1002/0471142727.mb1420s92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Wang M, Orwar O, Weber SG, Anal. Chem. 2009, 81 (10), 4060–4067. DOI 10.1021/ac900265f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Imamura R, Murata N, Shimanouchi T, Yamashita K, Fukuzawa M, Noda M, Sensors (Basel) 2017, 17 (7), 1630 DOI 10.3390/s17071630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Teissié J, Rols MP, Biophys. J. 1993, 65 (1), 409–413. DOI 10.1016/S0006-3495(93)81052-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Lee Y-W, Luther DC, Kretzmann JA, Burden A, Jeon T, Zhai S, Rotello VM, Theranostics 2019, 9 (11), 3280–3292. DOI 10.7150/thno.34412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Fu A, Tang R, Hardie J, Farkas ME, Rotello VM, Bioconjugate Chem. 2014, 25 (9), 1602–1608. DOI 10.1021/bc500320j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Kim S, Kim D, Cho SW, Kim J, Kim J-S, Genome Res. 2014, 24 (6), 1012–1019. DOI 10.1101/gr.171322.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Yang R, Lemaître V, Huang C, Haddadi A, McNaughton R, Espinosa HD, Small 2018, 14 (12), 1702495 DOI 10.1002/smll.201702495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Kim D, Kim C-H, Moon J-I, Chung Y-G, Chang M-Y, Han B-S, Ko S, Yang E, Cha KY, Lanza R, Kim K-S, Cell stem cell 2009, 4 (6), 472–476. DOI 10.1016/j.stem.2009.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Rashid M-U, Coombs KM, J. Cell. Physiol. 2019, 234 (6), 7718–7724. DOI 10.1002/jcp.27890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Hsu PD, Scott DA, Weinstein JA, Ran FA, Konermann S, Agarwala V, Li Y, Fine EJ, Wu X, Shalem O, Cradick TJ, Marraffini LA, Bao G, Zhang F, Nat. Biotechnol. 2013, 31 (9), 827–832. DOI 10.1038/nbt.2647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Nishimura K, Kato T, Chen C, Oinam L, Shiomitsu E, Ayakawa D, Ohtaka M, Fukuda A, Nakanishi M, Hisatake K, Stem Cell Rep 2014, 3 (5), 915–929. DOI 10.1016/j.stemcr.2014.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Cao Y, Ma E, Cestellos-Blanco S, Zhang B, Qiu R, Su Y, Doudna JA, Yang P, Proc. Natl. Acad. Sci. U. S. A. 2019, 116 (16), 7899–7904. DOI 10.1073/pnas.1818553116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Actis P, Maalouf MM, Kim HJ, Lohith A, Vilozny B, Seger RA, Pourmand N, ACS Nano 2014, 8 (1), 546–553. DOI 10.1021/nn405097u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Guillaume-Gentil O, Grindberg RV, Kooger R, Dorwling-Carter L, Martinez V, Ossola D, Pilhofer M, Zambelli T, Vorholt JA, Cell 2016, 166 (2), 506–516. DOI 10.1016/j.cell.2016.06.025. [DOI] [PubMed] [Google Scholar]
- [60].Shekaramiz E, Doshi R, Wickramasinghe HK, J. Nanobiotechnol. 2018, 16 (1), 67 DOI 10.1186/s12951-018-0395-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Li X, Tao Y, Lee DH, Wickramasinghe HK, Lee AP, Lab Chip 2017, 17 (9), 1635–1644. DOI 10.1039/c7lc00133a. [DOI] [PubMed] [Google Scholar]
- [62].Chovancova P, Merk V, Marx A, Leist M, Kranaster R, Biol. Methods Protoc. 2017, 2 (1), (bpx008). DOI 10.1093/biomethods/bpx008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Hammarström B, Evander M, Barbeau H, Bruzelius M, Larsson J, Laurell T, Nilsson J, Lab Chip 2010, 10 (17), 2251–2257. DOI 10.1039/C004504G. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.