DeepDTI: High-fidelity six-direction diffusion tensor imaging using deep learning

Abstract

Diffusion tensor magnetic resonance imaging (DTI) is unsurpassed in its ability to map tissue microstructure and structural connectivity in the living human brain. Nonetheless, the angular sampling requirement for DTI leads to long scan times and poses a critical barrier to performing high-quality DTI in routine clinical practice and large-scale research studies. In this work we present a new processing framework for DTI entitled DeepDTI that minimizes the data requirement of DTI to six diffusion-weighted images (DWIs) required by conventional voxel-wise fitting methods for deriving the six unique unknowns in a diffusion tensor using data-driven supervised deep learning. DeepDTI maps the input non-diffusion-weighted (b = 0) image and six DWI volumes sampled along optimized diffusion-encoding directions, along with T₁-weighted and T₂-weighted image volumes, to the residuals between the input and high-quality output b = 0 image and DWI volumes using a 10-layer three-dimensional convolutional neural network (CNN). The inputs and outputs of DeepDTI are uniquely formulated, which not only enables residual learning to boost CNN performance but also enables tensor fitting of resultant high-quality DWIs to generate orientational DTI metrics for tractography. The very deep CNN used by DeepDTI leverages the redundancy in local and non-local spatial information and across diffusion-encoding directions and image contrasts in the data. The performance of DeepDTI was systematically quantified in terms of the quality of the output images, DTI metrics, DTI-based tractography and tract-specific analysis results. We demonstrate rotationally-invariant and robust estimation of DTI metrics from DeepDTI that are comparable to those obtained with two b = 0 images and 21 DWIs for the primary eigenvector derived from DTI and two b = 0 images and 26–30 DWIs for various scalar metrics derived from DTI, achieving 3.3–4.6 × acceleration, and twice as good as those of a state-of-the-art denoising algorithm at the group level. The twenty major white-matter tracts can be accurately identified from the tractography of DeepDTI results. The mean distance between the core of the major white-matter tracts identified from DeepDTI results and those from the ground-truth results using 18 b = 0 images and 90 DWIs measures around 1–1.5 mm. DeepDTI leverages domain knowledge of diffusion MRI physics and power of deep learning to render DTI, DTI-based tractography, major white-matter tracts identification and tract-specific analysis more feasible for a wider range of neuroscientific and clinical studies.

1. Introduction

Noninvasive mapping of tissue microstructure and structural connectivity in the living human brain by diffusion magnetic resonance imaging (MRI) offers a unique window into the neural basis of human cognition, behavior and mental health. Diffusion MRI sensitizes the MR signal to the Brownian motion of water (Hahn, 1950; Carr and Purcell, 1954; Torrey, 1956; Stejskal and Tanner, 1965) and is unsurpassed in its ability to infer white-matter tissue properties noninvasively at the micron level, which is far below the spatial resolution of the MR image. It is the most sensitive and reliable diagnòstic imaging modality for early detection of cerebral ischemia (Moseley et al., 1990a, 1990b). Beyond clinical applications, the biophysical modeling of diffusion MRI data enables the mapping of axonal orientation (Basser et al., 1994; Behrens et al., 2003; Tournier et al., 2004; Wedeen et al., 2005; Yeh et al., 2010; Tian et al., 2019), density (Zhang et al., 2012), dispersion (Zhang et al., 2012), diameter (Assaf and Basser, 2005; Assaf et al., 2008; Huang et al., 2020; Fan et al., 2019), myelination (Fujiyoshi et al., 2016) and g-ratio (Yu et al., 2019). Diffusion MRI coupled with tractography is currently the only method for in vivo mapping of human white-matter fascicles (Mori et al., 1999; Conturo et al., 1999; Tian et al., 2018; Cartmell et al., 2019).

Diffusion tensor MRI (DTI) is the most widely used diffusion MRI method for extracting white-matter tissue properties and identifying the major white-matter tracts in vivo. The metrics from DTI have great specificity in mapping the microstructural changes caused by normal aging (Salat et al., 2005), neurodegeneration (Nir et al., 2013) and a number of neurological (Roosendaal et al., 2009; Zheng et al., 2014) and psychiatric (Kubicki et al., 2005; Cullen et al., 2010) disorders. DTI-based tractography provides crucial information regarding white-matter tract infiltration and displacement due to brain tumors and is routinely used for presurgical planning of tumor resection. DTI-based tractography has also been used to locate thalamic nuclei by measuring the relative location relative to the white-matter tracts that run in close proximity but do not intersect the target for functional neurosurgery (Anthofer et al., 2014; Sammartino et al., 2016). Recent advances have further integrated DTI-based tractography and microstructural imaging to enable the quantification of voxel-wise white-matter tissue properties along the length of white-matter tracts with high sensitivity for capturing the along-tract variations in tissue properties within individuals and across groups (Smith et al., 2006; Colby et al., 2012; Yeatman et al., 2012, 2018). Tract-specific analysis of DTI-mapped tissue properties has proven to be a valuable tool for elucidating changes in white-matter microstructure across the lifespan (Yeatman et al., 2014) and white-matter plasticity in response to experience (Huber et al., 2018) and neurosurgical intervention (Pineda-Pardo et al., 2019).

Nonetheless, this simple yet elegant method is fundamentally limited in the need to perform directional encoding many times in order to sample the diffusive motion of water within white-matter tracts of arbitrary orientation in the brain, leading to long acquisition times that pose a critical barrier to performing high-quality DTI in routine clinical practice and large-scale research studies. Despite only six unique unknown elements in the diffusion tensor model, it has been shown that at least 30 measurements (5–10 s per measurement) along uniformly distributed directions are needed to achieve statistically rotational invariance, such that the precision of the estimated DTI metrics are independent of the orientation of the underlying tracts (Jones, 2004; Jones et al., 2013). The presence of thermal noise and spatially and temporally varying artifacts induced by subject motion and cardiac pulsation in the diffusion measurements adds to the demand for more data to enable robust tensor model fitting and high accuracy in estimating DTI metrics. For very noisy diffusion measurements such as those from high spatial resolution imaging data (McNab et al., 2013; Setsompop et al., 2018; Liao et al., 2019, 2020), the required number of measurements can be far more than 30.

The angular sampling requirement represents the bottleneck to further reduce the acquisition time of a DTI scan. Since the invention of DTI in the mid-1990s, numerous imaging advances, including faster and stronger gradient systems for shortened imaging readout and diffusion encoding, highly-parallelized phased-array radiofrequency receiver for reduced data sampling requirement of each imaging plane and simultaneous acquisition of multiple imaging planes, have emerged to dramatically reduce the acquisition time of a diffusion-weighted measurement of the whole human brain from about 10 minutes to just a few seconds. The angular sampling efficiency for DTI, however, has remained largely unaddressed because of the unevolved processing techniques. The diffusion tensor model fitting has always been performed per voxel using a least-squares fit or more advanced methods since the invention of DTI (Basser et al., 1994; Chang et al., 2005; Kingsley, 2006; Koay et al., 2006), which neglects the spatial redundancy of information in neighboring voxels and between non-local spatial regions, as well as the redundancy across diffusion-encoding directions and image contrasts. On the other hand, previous studies have successfully utilized the data redundancy in image space (Hu et al., 2019), diffusion space (Bilgic et al., 2012; Menzel et al., 2011) and the joint image-diffusion space (Hu et al., 2020; Shi et al., 2015; Wu et al., 2019) for improving diffusion MR image formation and utilized the data redundancy in the joint image-diffusion space for accelerating high angular resolution diffusion MRI (Cheng et al., 2015; Pesce et al., 2017, 2018; Chen et al., 2018) via techniques such as compressed sensing and convex optimization. Nonetheless, it is unclear how to fully utilize the data redundancy in the joint image-diffusion space for reducing the data requirement to obtain high-fidelity diffusion tensors.

Advances in high-performance computing hardware and deep learning offer a powerful tool set for exploiting the data redundancy for DTI processing techniques. The seminal work of Golkov et al. introduced the deep learning concept to diffusion MRI and established the q-space deep learning (q-DL) framework, which has greatly benefited the subsequent work in this field. The q-DL method proposed to synthesize an increased number of q-space samples from a small number of acquired q-space samples without imposing any diffusion models using a multilayer perceptron (Golkov et al., 2015, 2016). The large number of synthesized q-space samples could then be used to fit any preferred diffusion model for improved results. q-DL and other subsequent studies have also demonstrated the promise of deep learning in using a small amount of diffusion data to predict high-quality scalar diffusion metrics from DTI (Li et al., 2018, 2019; Gong et al., 2018; Aliotta et al., 2019) and more advanced diffusion analysis methods, such as diffusion kurtosis imaging (Golkov et al., 2016; Gong et al., 2018), diffusion spectrum imaging (Gibbons et al., 2018) and neurite orientation dispersion and density imaging (Golkov et al., 2016; Gibbons et al., 2018) obtained from a large amount of diffusion data, as well as mapping voxel-wise axonal orientations (Lin et al., 2019) and long-range fascicles (Poulin et al., 2017). In these works, artificial neural networks were trained to directly predict output diffusion metrics from the input diffusion-weighted images (DWIs). These works used multilayer perceptrons (Golkov et al., 2015, 2016; Aliotta et al., 2019; Poulin et al., 2017), two-dimensional convolutional neural networks (CNNs) (Li et al., 2018, 2019; Gong et al., 2018; Gibbons et al., 2018), shallow three-dimensional CNNs (Li et al., 2019; Lin et al., 2019) and recurrent neural networks (Li et al., 2018). q-DL also proposed to use multi-contrast data as inputs to a neural network.

Extending these lines of research, we present a robust framework for DTI processing called “DeepDTI” that extracts both high-fidelity scalar and orientational DTI metrics using only six diffusion-weighted measurements required by conventional voxel-wise methods to fit the six unique unknowns in a diffusion tensor, achieved with data-driven supervised deep learning. DeepDTI uses a deep 3-dimensional CNN to map the input DWIs sampled along six optimized diffusion-encoding directions to the residuals between the input and output high-quality DWIs, which enables residual learning to boost the performance of CNN and tensor fitting on the resultant high-quality DWIs to generate any scalar and orientational DTI metrics. We systematically quantify the similarity of the voxel-wise, tractography and tract-specific analysis results of DeepDTI compared to those from over-sampled DTI scans (ground truth) and show that the results of DeepDTI are comparable to those of fully-sampled DTI scans acquired in routine practice and outperform those of the state-of-the-art denoising algorithm. We anticipate the immediate benefits of DTI scan time reduction to enable a broader range of clinical and research applications of DTI and DTI-based structural connectome mapping and tract-specific analysis.

2. Methods

2.1. DeepDTI pipeline

We carefully formulate the inputs and outputs of the DeepDTI pipeline based on in-depth knowledge of the underlying diffusion MRI physics. Instead of learning the DTI metrics directly as in previous works, the DeepDTI pipeline learns the residuals between the input and output non-diffusion-weighted (b = 0) image and DWIs. Residual learning is widely recognized as a powerful strategy to boost the performance of CNNs and accelerate the training process for tasks such as object recognition (He et al., 2016), image super-resolution (Kim et al., 2016; Pham et al., 2019) and denoising (Zhang et al., 2017). The resultant high-quality DWIs can be used for tensor model fitting to generate any orientational and scalar DTI metrics and directly used by existing software packages, such as DTI-based tractography software for surgical planning, for streamlined acquisition and processing.

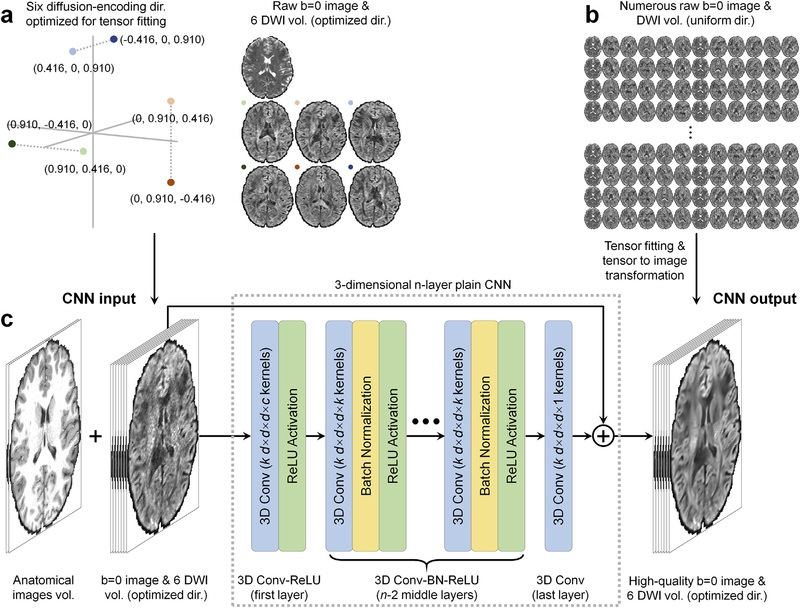
Specifically, the inputs to the DeepDTI pipeline are: a single b = 0 image volume, six DWI volumes sampled along optimized diffusion-encoding directions (Fig. 1a), and anatomical (T₁-weighted and T₂-weighted) image volumes (total of nine input channels). Anatomical images are included as inputs as they are routinely acquired and help delineate boundaries between anatomical structures while preventing blurring in the results (Golkov et al., 2016).

Fig. 1. Diffusion physics-informed and convolutional neural network-based DeepDTI pipeline.

The input is a single b = 0 image and six diffusion-weighted image (DWI) volumes sampled along optimized diffusion-encoding directions (a) as well as anatomical (T₁-weighted and T₂-weighted) image volumes. The output is the high-quality b = 0 image volume and six DWI volumes sampled along optimized diffusion-encoding directions transformed from the diffusion tensor fitted using all available b = 0 images and DWIs (b). A deep 3-dimensional convolutional neural network (CNN) comprised of stacked convolutional filters paired with ReLU activation functions (n = 10, k = 190, d = 3, c = 9, p = 7) is adopted to map the input image volumes to the residuals between the input and output image volumes (c).

The six optimized diffusion-encoding directions were selected to minimize the condition number of the diffusion tensor transformation matrix (A) (i.e., 1.3228) while are as uniform as possible (Skare et al., 2000). The chosen diffusion-encoding scheme improves not only the robustness to experimental noise but also rotational invariance of measurement precision (Skare et al., 2000). The diffusion tensor transformation matrix A defines the linear mapping between the diffusion tensor elements (D) and the apparent diffusion coefficients (ADC) estimates (C) derived from the diffusion-weighted signals (details in Supplementary Information):

$$\mathbf{C}=\mathbf{AD},$$ (1)

where C = [c₁ c₂ c₃ c₄ c₅ c₆]^T with c_i = −ln(S_i/S₀)/b (i = 1, 2, 3, 4, 5, 6), S₀ is the non-diffusion-weighted signal intensity, S_i is the diffusion-weighted signal intensity and b is the b-value. The diffusion tensor transformation matrix A = [α₁ α₂ α₃ α₄ α₅ α₆ ]^T with ${\mathit{\alpha }}_i^T=[g_{ix}^2{g}_{iy}^2{g}_{iz}^{2}2g_{ix}{g}_{iy}2g_{ix}{g}_{iz}2g_{iy}{g}_{iz}](i=1,2,3,4,5,6)$ solely depends on the diffusion-encoding directions (g_ix, g_iy, g_iz)^T (i = 1, 2, 3, 4, 5, 6). D = [D_xx D_yy D_zz D_xy D_xz D_yz ]^T consists six unique elements of a diffusion tensor, which mathematically requires at least six independent ADC measurements (or DWIs) along noncollinear directions to solve using conventional voxel-wise tensor fitting methods (e.g., D = A⁻¹C using linear squares fit).

The use of six optimized diffusion-encoding directions that minimize the condition number of the diffusion tensor transformation matrix A is a key design aspect of the DeepDTI pipeline and has several advantages. First, the diffusion-weighted signal intensities are simply another representation of the diffusion tensor elements in the image space (i.e., S = S₀e^−b·AD, the two spaces are related by logarithmic operation) and therefore the end-to-end training in the image space optimizes the diffusion tensor elements directly for improved performance. In the meanwhile, the diffusion tensor fitting of the resultant images is robust to any imperfection introduced by the CNN.

Second, it simplifies the acquisition and processing of the training data. For using the trained CNN to reduce the scan time, only one b = 0 image and six DWI volumes sampled along optimized directions need to be acquired for each subject. To obtain the training data to optimize CNN parameters, the use of six optimized diffusion-encoding directions allows the input DWIs sampled along optimized directions to be transformed from the DWIs sampled along rotational variations of the six optimized diffusion-encoding directions, which can be extracted from a routinely acquired single-shell multi-directional diffusion dataset without amplifying experimental noise and artifacts. Because the transformed input images have the same image contrast as the ground-truth images but with different observed noise characteristics and artifacts, many sets of input DWIs can be selected from a single-shell multi-directional diffusion MRI dataset of a single subject (e.g., ~130 sets out of 90 uniform directions), which is particularly useful for augmenting the training data when the number of subjects for training is limited. It is also easier to acquire and process new training data using standard single-shell protocol already available on scanners and pre-processing software packages such as the FMRIB Software Library software (Smith et al., 2004; Jenkinson et al., 2012; Andersson and Sotiropoulos, 2016) (FSL, https://fsl.fmrib.ox.ac.uk) or use legacy single-shell data as training data.

Specifically, for each brain voxel, the transformed diffusion-weighted signal intensities S_trans along the six optimized diffusion-encoding directions is calculated as:

$${\mathbf{S}}_{trans}=S_{0,rot}{e}^{-b\cdot {\mathbf{A}}_{opt}{\mathbf{D}}_{rot}}=S_{0,rot}{e}^{-b\cdot {\mathbf{A}}_{opt}{\mathbf{A}}_{rot}^{-1}{\mathbf{C}}_{rot}},$$ (2)

where A_opt is the diffusion tensor transformation matrix associated with the six optimized directions, D_rot is the diffusion tensor derived from the DWIs along an rotational variant of the six optimized directions ($={\mathbf{A}}_{rot}^{-1}{\mathbf{C}}_{rot}$), A_rot is the diffusion tensor transformation matrix associated with the rotational variant of the six optimized directions, and C_rot is a vector of the measured diffusivity. Because the tensor transformation matrix of the optimized directions has a low condition number of 1.3228, the transformation does not amplify noise and artifacts in the measured diffusivities C_rot and therefore minimizes the difference between S_trans and the ground truth for residual learning. In practice, even though the six optimized diffusion-encoding directions are prescribed for acquiring the training data, the acquired b-values and diffusion-encoding directions have to be corrected to account for subject motion and hardware imperfection (e.g., gradient non-linearity) (Bammer et al., 2003; Leemans and Jones, 2009; Sotiropoulos et al., 2013; Guo et al., 2018). The input images still need to be obtained from the transformation of acquired images.

The outputs of the DeepDTI pipeline are: the average of all b = 0 image volumes to yield a high-quality b = 0 image and six ground-truth DWI volumes sampled along optimized diffusion-encoding directions (total of seven output channels). The ground-truth DWIs are generated by fitting the tensor model to all available b = 0 and DWIs and inverting the diffusion tensor transformation to generate a set of DWIs sampled along the six optimized diffusion-encoding directions as:

$${\mathbf{S}}_{gt}=S_{0,gt}{e}^{-b\cdot {\mathbf{A}}_{opt}{\mathbf{D}}_{gt}},$$ (3)

where S_gt is a vector of six ground-truth signal intensities, S_0,gt is the ground-truth non-diffusion-weighted signal obtained by averaging all b = 0 images, and D_gt is the ground-truth diffusion tensor derived from a large number of images. Because the input and output ground-truth b = 0 image and DWIs have identical contrast, the residuals between the input and output images are sparse and consist of high-frequency noise and artifacts, thereby facilitating the CNN to learn a reduced amount of information.

A 10-layer three-dimensional CNN (Simonyan and Zisserman, 2014) was adopted to learn the mapping from the input image volumes to the residuals between the input and output b = 0 image and DWI volumes (Fig. 1c). The network architecture of the CNN is very simple, comprised of stacked convolutional filters paired with batch normalization functions and non-linear activation functions (rectified linear unit). The plain network coupled with residual learning has been shown to be effective for image de-noising (Zhang et al., 2017) and super-resolution (Kim et al., 2016; Chaudhari et al., 2018).

2.2. Human Connectome Project data

Pre-processed diffusion, T₁-weighted and T₂-weighted MRI data of 70 unrelated subjects (40 for training, 10 for validation, 20 for evaluation) from the Human Connectome Project (HCP) WU-Minn-Ox Consortium public database (https://www.humanconnectome.org) were used for this study. The acquisition methods were described in detail previously (Sotiropoulos et al., 2013; Glasser et al., 2013; Ugurbil et al., 2013). Parameter values and processing steps relevant to this study are briefly listed below.

Whole-brain diffusion MRI data were acquired at 1.25 mm isotropic resolution with fourb-values (0, 1, 2, 3 ms/μm²) and two phase-encoding directions (left–right and right–left). The b = 0 image volumes were interspersed between every 15 DWI volumes. For each non-zero b-value, 90 uniformly distributed diffusion-encoding directions were acquired in increments such that the acquired diffusion-encoding directions of prematurely aborted scans were still uniformly distributed on a sphere (Caruyer et al., 2013). The image volumes were corrected for susceptibility and eddy current induced distortions and co-registered using the FSL software. The image volumes acquired with opposite phase-encoding directions were combined into a single image volume, resulting in 18 b = 0 image volumes and 90 DWI volumes for each non-zero b-value. Only the b = 0 image volumes and DWI volumes at b = 1 ms/μm² of each subject were used in this study.

The T₁-weighted and T₂-weighted MRI data were acquired at 0.7 mm isotropic resolution. The two acquired repetitions of the T₁-weighted and T₂-weighted images were averaged. The T₁-weighted, T₂-weighted and diffusion MRI data of every subject were co-registered.

2.3. Image processing

The diffusion data were corrected for spatially varying intensity biases using the averaged b = 0 images with the unified segmentation routine implementation in the Statistical Parametric Mapping software (SPM, https://www.fil.ion.ucl.ac.uk/spm) with a full-width at half-maximum of 60 mm and a sampling distance of 2 mm.

For comparison, diffusion data were denoised using the state-of-the-art block-matching and 4D filtering (BM4D) denoising algorithm (Dabov et al., 2007; Maggioni et al., 2012) (https://www.cs.tut.fi/~foi/GCF-BM3D), an extension of the BM3D algorithm for volumetric data. Briefly, the BM4D method groups similar 3-dimensional blocks into 4-dimensional data arrays to enhance the data sparsity and then performs collaborative filtering to achieve superior denoising performance. The BM4D denoising was performed assuming Rician noise with an unknown noise standard deviation and was set to estimate the noise standard deviation and perform collaborative Wiener filtering with “modified profile” option.

The T₁-weighted and T₂-weighted images were down-sampled to the diffusion image space at 1.25 mm isotropic resolution using cubic spline interpolation. The provided volumetric brain segmentation results (i.e., aparc + aseg.mgz) from the T₁-weighted data of the FreeSurfer software (Fischl et al., 1999; Dale et al., 1999; Fischl, 2012) (https://surfer.nmr.mgh.harvard.edu) were down-sampled to the diffusion image space at 1.25 mm isotropie resolution using nearest neighbor interpolation. Binary masks of brain tissue that excluded the cerebrospinal fluid (CSF) were obtained using FreeSurfer’s “mri_binarize” function with “–gm” and “–all-wm” options.

2.4. Data formatting

To obtain the ground-truth DTI metrics for each subject, diffusion tensor fitting was performed on all the diffusion data (18 b = 0 images and 90 DWI volumes) using ordinary linear squares fitting using FSL’s “dtifit” function with the provided gradient non-linearity correction file to derive the diffusion tensor, primary eigenvector (V1), fractional anisotropy (FA), mean diffusivity (MD), axial diffusivity (AD), and radial diffusivity (RD).

The ground-truth b = 0 image volumes were computed by averaging all 18 b = 0 image volumes. The ground-truth DWIs along the six optimized diffusion-encoding directions were then calculated from the ground-truth diffusion tensor following Equation (3) using in-house code written in MATLAB software (MathWorks, Natick, Massachusetts).

To obtain the input data of DeepDTI for each subject, DWI volumes along rotational variants of the six optimized diffusion-encoding directions (Fig. 1) were selected from the 90 DWI volumes acquired along uniformly distributed directions as follows. Specifically, the six optimized directions were rotated in a random fashion to six new directions, and the set of the six nearest directions were selected if the mean absolute angle compared to the rotated directions was lower than 5° and the condition number of the corresponding diffusion tensor transformation matrix was lower than 2. Out of 90 uniformly distributed directions, ~130 such rotational variants of the six optimized directions could be selected. Due to the limited graphical processing unit (GPU) memory, five sets of images comprising six DWIs along a rotational variant of the optimized directions and the b = 0 image acquired immediately preceding the chosen DWIs were randomly selected for each of the 50 subjects for training and validation. Consequently, a total of 250 sets of input images (5 sets per subject for 50 subjects) were selected for training and validation, with each set consisting of six DWIs and one b = 0 image. When the number of subjects for training and validation is limited, more input image sets can be used to augment the training data. One such image set was randomly selected for each of the 20 evaluation subjects to serve as an evaluation dataset.

For each selected image set comprising one b = 0 and six DWIs, diffusion tensor fitting was performed using ordinary linear squares fitting using in-house MATLAB code with the provided gradient non-linearity correction file to derive the diffusion tensor, V1, FA, MD, AD and RD. The input DWIs to DeepDTI were then calculated from the fitted diffusion tensor following Equation (2) using in-house MATLAB code.

2.5. Network implementation

The CNN of DeepDTI was implemented using the Keras application programming interface (API) (https://keras.io) with a Tensorflow back-end (https://www.tensorflow.org). The mean-square-error (L2) loss compared to the ground-truth images was used to optimize the CNN parameters using the Adam optimizer (Kingma and Ba, 2014) with default parameters (except for the learning rate). Only the mean-square-error within the brain mask was used. Currently, the research into more goal-oriented loss functions for diffusion MRI is still not reliably established and therefore L2 loss of image intensity was used in this study. The slightly more goal-oriented loss functions such as the distance functions on the manifold of all possible diffusion tensors (Pennec et al., 2006), or even more goal-oriented ones such as those for the direct prediction of tractography, tissue segmentation, and diagnosis could potentially further improve the CNN results.

To account for subject-to-subject variations in image intensity, the intensities of the input and ground-truth images of DeepDTI were standardized by subtracting the mean image intensity and dividing by the standard deviation of image intensities across all voxels within the brain mask from the input images. Input and ground-truth images were brain masked.

The training was performed on 40 subjects and validated on another 10 subjects using a V100 GPU (NVIDIA, Santa Clara, CA). The learning rate was set empirically, and the number of epochs for each learning rate was selected based on tracking the validation error. The learning rate was first set to 0.0005 for the first 36 epochs, after which the network approached convergence and the validation error did not further decrease. The learning rate was then set to 0.00001 for the last 12 epochi to fine tune the network parameters (~70 hours in total). Only the latesl model with the lowest validation error was saved during the training Blocks of 64 × 64 × 64 voxel size were used for training (8 blocks from each subject) due to limited GPU memory. The learned network parameters were applied to the whole brain volume of each of the evaluation subjects.

2.6. Quantitative comparison

Peak SNR (PSNR) and structural similarity index (SSIM) (Wang et al., 2004) were used to quantify the similarity between the raw input images, DeepDTI-processed images and BM4D-denoised images compared to the ground-truth images. The across-subject mean and standard deviation of the mean absolute difference (MAD) of different DTI metrics, including FA, V1, MD, AD, RD within the brain (excluding the cerebrospinal fluid) of 20 evaluation subjects were computed to evaluate the performance of different methods compared to the ground-truth results and the results from 7 to 96 images (1 leading b = 0 image volume interleaved for every 15 DWI volumes) extracted from the full dataset. Any first N diffusion-encoding directions of the HCP diffusion data are still uniformly distributed for valid diffusion tensor fitting.

2.7. Tract-specific anafysis

Tract-specific analysis was performed on the ground-truth data, raw data, DeepDTI-processed data and BM4D-denoised data using the automated fiber quantification (AFQ) software (https://github.com/yeatmanlab/AFQ). Briefly, diffusion tensor fitting and deterministic tractography were performed to reconstruct the trajectories of white-matter fascicles across the whole brain. Twenty major white-matter tracts from both left and right hemisphere were identified by grouping fascicles passing through two pre-defined way-point regions-of-interest. For each tract, the tract core was created by taking the mean of the central portion of all fascicles traversing both way-point regions-of-interest, with each tract core represented as 100 equally spaced nodes. For each tract, a tract profile of each scalar metric was calculated as a weighted sum of each fascicle’s value at a given node, interpolated from nearby voxels in the FA, MD, AD and RD maps.

The mean distances between the tract cores generated from the ground-truth data and those generated from the raw data, DeepDTI-processed data and BM4D-denoised data were calculated to gauge the accuracy of the tractography. For each of the 100 nodes on a tract core for comparison, its distance to the ground-truth tract core was defined as the shortest Euclidean distance from it to any node on the ground-truth tract core (represented as 10,000 equally spaced nodes). The average of the distances from all 100 nodes on a tract core for comparison was defined as the mean distance between this tract core and the ground-truth tract core.

3. Results

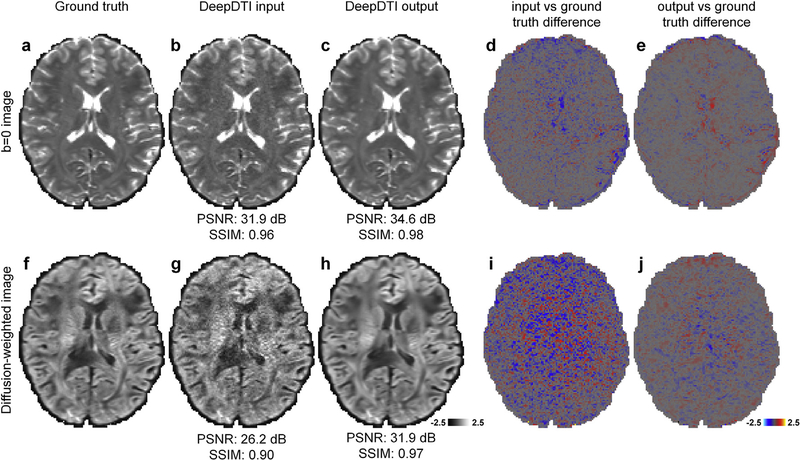
Fig. 2 demonstrates that the output b = 0 image and DWI sampled along one of the six optimized directions from DeepDTI show significantly improved image quality and higher SNR compared to the input images (input and output images along other diffusion-encoding directions available in Supplementary Fig. S1). The improvement is more significant for the DWI, which is much noisier than the b = 0 image. The residual maps between the DeepDTI output images and ground-truth images do not contain anatomical structure or biases reflecting the underlying anatomy (Fig. 2e, j). The DeepDTI output images are visually similar to the ground-truth images, and quantitatively have a high PSNR of 34.6 dB and high SSIM of 0.98 (Fig. 2c) for the b = 0 image and a high PSNR of 31.9 dB and high SSIM of 0.97 for the DWI (Fig. 2h). For the 20 evaluation subjects, the group-level mean (± the group-level standard deviation) of the PSNR is 2.8 dB higher (34.1 ± 1.7 dB vs. 31.3 ± 2.2 dB), and of the SSIM is 0.02 higher (0.98 ± 0.001 vs. 0.96 ± 0.02) for the b = 0 images. The group-level mean (± the group-level standard deviation) of the PSNR is 5.7 dB higher (30.8 ± 0.9 dB vs. 25.1 ± 0.7 dB), and of the SSIM is 0.11 higher (0.97 ± 0.005 vs. 0.86 ± 0.02) for the DWIs.

Fig. 2. Comparison of the input and output images of DeepDTI.

Non-diffusion-weighted (b = 0) images (a–e) and diffusion-weighted images (DWIs) (f–j) sampled along one of the six optimized diffusion-encoding directions (i.e., [0.91, 0.416, 0]) from the ground-truth data (a, f), the input data of DeepDTI (b, g), the output data of DeepDTI (c, h), the residuals between the ground-truth images and DeepDTI input images (d, i) and the residuals between the ground-truth images and the DeepDTI output images (e, j) from a representative subject. The peak signal-to-noise ratio (PSNR) and the structural similarity index (SSIM) are used to quantify image similarity compared to the ground truth.

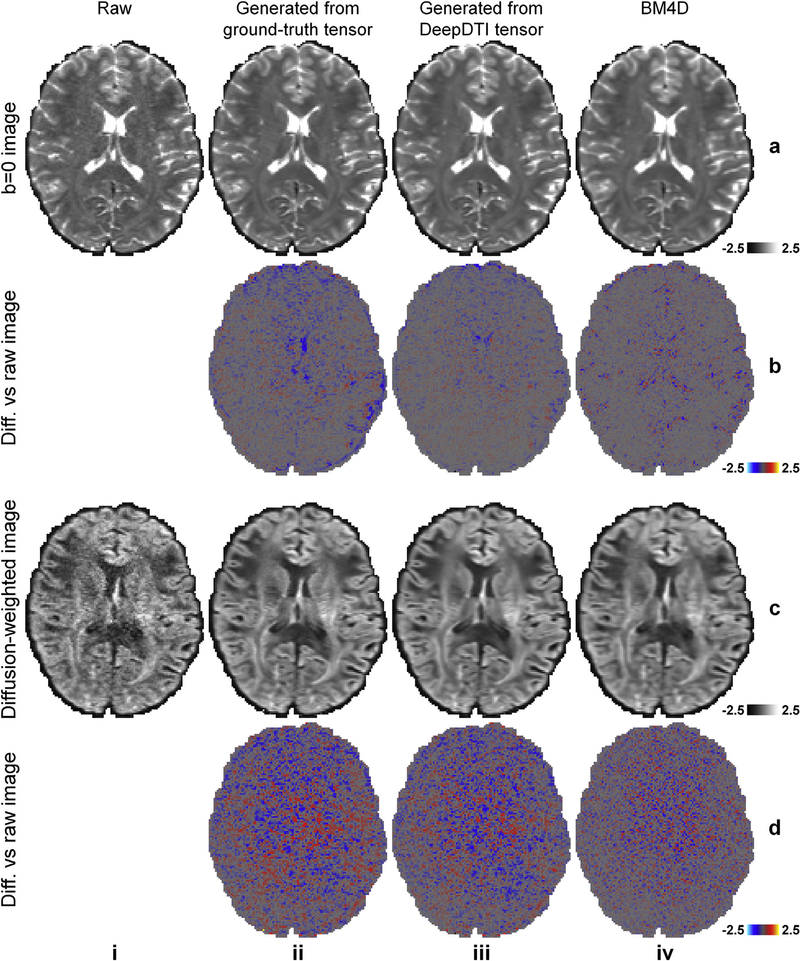
Fig. 3 demonstrates the denoising efficacy of DeepDTI. The DWIs from the ground-truth and DeepDTI results were generated from the diffusion tensor. The residual maps between the DeepDTI-processed images and the acquired raw b = 0 images and DWIs do not contain anatomical structure or biases reflecting the underlying anatomy (Fig. 3, rows b, d, column iii) and are more visually similar to the residual maps from the ground-truth data (Fig. 3, rows b, d, column ii) compared to the residual maps from the BM4D-denoised results (Fig. 3, rows b, d, column iv).

Fig. 3. Comparison of denoising efficacy of different data/methods.

Non-diffusion-weighted (b = 0) images (row a) and diffusion-weighted images (DWIs) (row c) sampled along one of the acquired diffusion-encoding directions (approximately left–right) from the raw data (column i), generated from the ground-truth diffusion tensor (column ii), generated from the tensor fitted on the DeepDTI output images (column iii), and from the BM4D-denoised data (column iv), and their residuals compared to the raw images (rows b, d) from a representative subject.

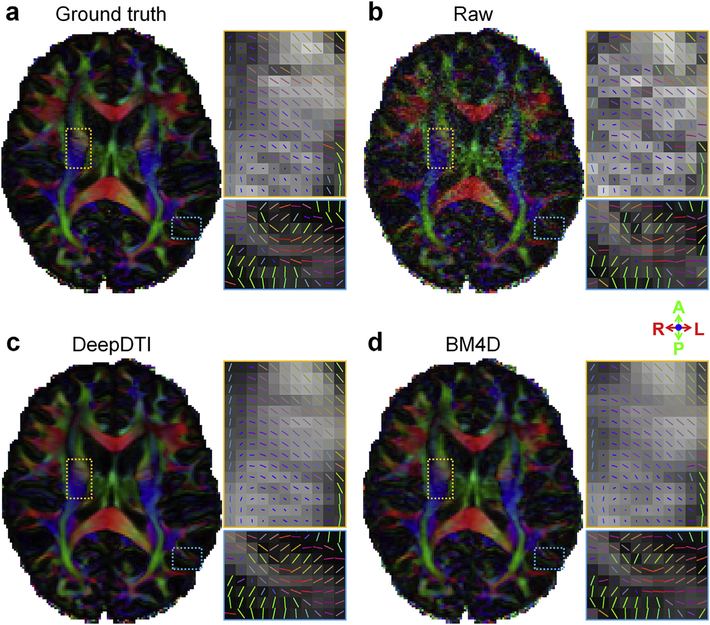
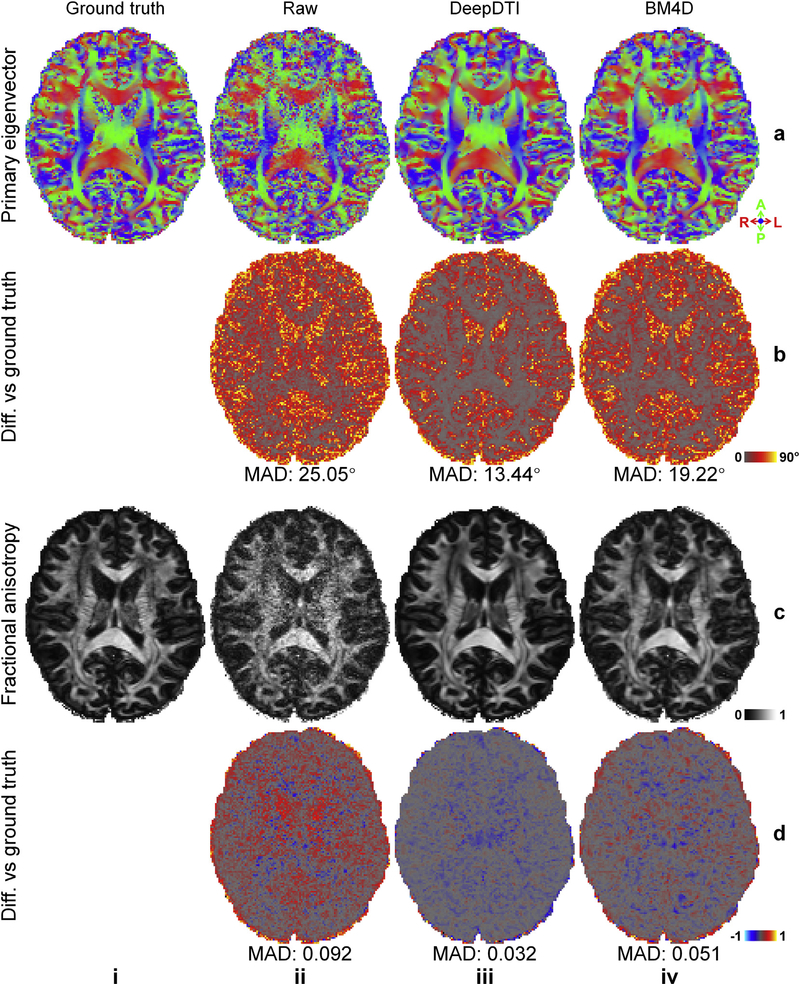
In Fig. 4, we show the ability of DeepDTI to recover detailed anatomical information from the noisy inputs in FA maps, which are color-encoded by the primary eigenvector V1 (individual maps available in Fig. 5). The FA map from DeepDTI significantly improves upon the map derived from the raw data and is far less noisy. It is visually similar and only slightly blurred compared to the ground-truth map, but sharper than the map derived from BM4D denoising. The DeepDTI maps display in exquisite detail the gray matter bridges that span the internal capsule, giving rise to the characteristic stripes seen in the striatum, which are contaminated by noise in the map derived from raw data and blurred out in the map derived from the BM4D-denoised data (Fig. 4 yellow boxes). DeepDTI also visualizes sub-cortical white-matter fascicles coherently fanning into the cortex and the orthogonality between the primary fiber orientations in the cerebral cortex and the cortical surface, which are only roughly preserved in the map from raw data (Fig. 4 blue boxes).

Fig. 4. DeepDTI recovers detailed anatomical Information.

Fractional anisotropy maps color encoded by the primary eigenvector (red: left–right; green: anterior–posterior; blue: superior–inferior) derived from the diffusion tensors fitted using all 18 b = 0 images and 90 diffusion-weighted images (DWIs) (ground truth, a), raw data consisting of 1 b = 0 image and 6 DWIs sampled along an arbitrary rotational variant of the optimized set of diffusion-encoding directions from the full dataset (b), the same 1 b = 0 image and 6 DWIs processed by DeepDTI (c) and denoised by BM4D (d) from a representative subject. Two regions of interest in the deep white matter (yellow boxes) and sub-cortical white matter (blue boxes) are displayed in enlarged views with the primary eigenvectors rendered as color-encoded sticks superimposed on the fractional anisotropy maps.

Fig. 5. Primary eigenvector and fractional anisotropy derived from DeepDTI compared to other data/methods.

Maps of color-encoded primary eigenvector (red: left–right; green: anterior–posterior; blue: superior–inferior) (row a) and fractional anisotropy (row c) derived from the diffusion tensors fitted using all 18 b = 0 images and 90 diffusion-weighted images (DWIs) (ground truth, column i), raw data consisting of 1 b = 0 image and 6 DWIs sampled along an arbitrary rotational variant of the optimized set of diffusion-encoding directions from the full dataset (column ii), the same 1b = 0 image and 6 DWIs processed by DeepDTI (column iii) and denoised by BM4D (column iv), and their residual maps (rows b, d) compared to the ground-truth maps. The mean absolute difference (MAD) of each map compared to the ground truth within the brain (excluding the cerebrospinal fluid) is displayed at the bottom of the residual map.

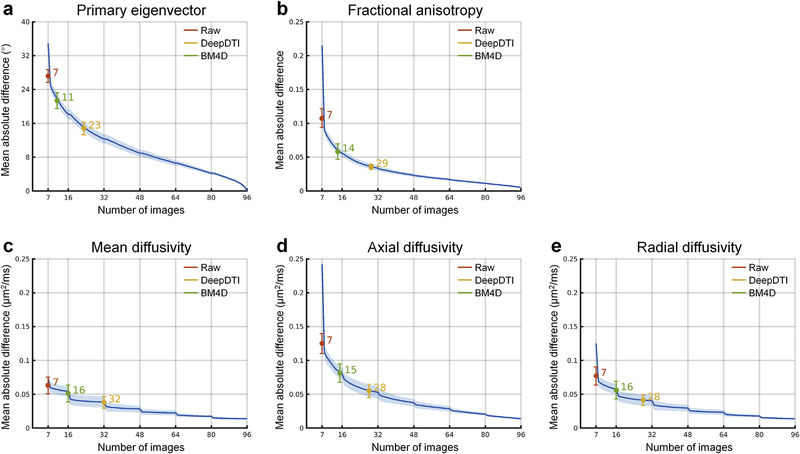
The difference of five common DTI metrics, including V1, FA, MD, AD, RD between the results derived from different methods and ground-truth data is displayed for a representative subject (Fig. 5, Supplementary Fig. S2) and quantified for 20 evaluation subjects (Fig. 6). The group mean (± the group-level standard deviation) of the MAD of V1, FA, MD, AD, RD within the brain (excluding the cerebrospinal fluid) derived from the DeepDTI outputs are 14.83° ± 1.51°, 0.036 ± 0.0038, 0.038 ± 0.0087 μm²/ms, 0.055 ± 0.0097 μm²/ms, and 0.041 ± 0.0081 μm²/ms, respectively, which are in general about half of those from the raw data (27.21° ± 1.54°, 0.11 ± 0.014, 0.064 ± 0.012 μm²/ms, 0.13 ± 0.015 μm²/ms, and 0.077 ± 0.014 μm²/ms) and two thirds of those from the BM4D-denoised data (21.39° ± 1.90°, 0.059 ± 0.012, 0.051 ± 0.013 μm²/ms, 0.081 ± 0.014 μm²/ms, and 0.056 ± 0.013 μm²/ms). The MAD of DeepDTI results for the five commonly DTI metrics of V1, FA, MD, AD and RD are equivalent to the MAD of the results from 2 b = 0 images and 21, 27, 30, 26, and 26 DWIs, respectively, acquired along uniformly distributed directions, achieving 3.3–4.6 × acceleration of scan time (Fig. 6). The acceleration is nearly twice that provided by BM4D, which are equivalent to the MAD of results from one b = 0 image and 10, 13, 15, 14, and 15 DWIs acquired along uniformly distributed directions. The acceleration factor for the primary eigenvector V1 is lower than for the scalar metrics, indicating that orientational metrics involving the estimation of two unique elements are more sensitive to noise and angular under-sampling compared to scalar metrics, which involve the estimation of a single element, since the estimation error of each element of orientational metrics accumulates. This is consistent with prior studies which have shown that a higher number of unique sampling directions are required for robust estimation of orientational measures such as V1 compared to scalar measures such as FA (Jones, 2004).

Fig. 6. Quantification of the accuracy of estimated DTI metrics.

The blue curves and the blue shaded regions represent the group mean and standard deviation of the mean absolute difference (MAD) of different DTI metrics obtained from 7–96 image volumes (1 leading b = 0 image volume interleaved for every 15 diffusion-weighted images (DWIs); DWIs were sampled along uniformly distributed diffusion-encoding directions) extracted from the full dataset compared to the ground-truth values obtained from 108 image volumes (18 b = 0 image and 90 DWI volumes) across 20 evaluation subjects. The colored dots at the center of the error bars and the colored error bars represent the group mean and standard deviation of the MAD of different DTI metrics obtained from the raw data consisting of 1 b = 0 image volume and 6 DWI volumes sampled along an arbitrary rotational variant of the optimized set of diffusion-encoding directions from the full dataset (red), the same 1 b = 0 image and 6 DWI volumes processed by DeepDTI (yellow) and denoised by BM4D (green) compared to the ground truth across 20 evaluation subjects. The numbers above the curves indicate the number of image volumes that would be needed to derive the DTI metrics with equivalent MAD to those derived from 1 b = 0 image and 6 DWI volumes processed by different methods. The MADs within the brain tissue (excluding the cerebrospinal fluid) are reported here.

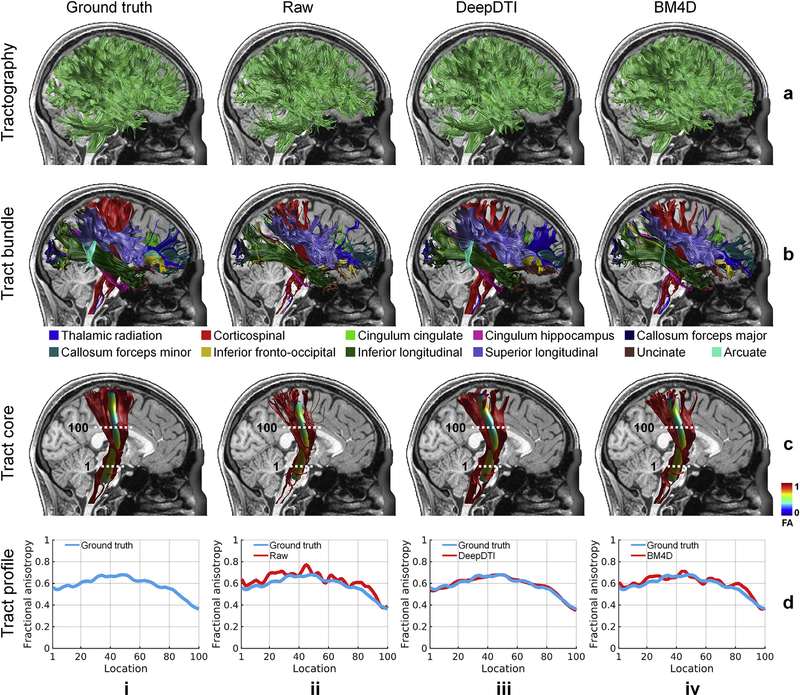
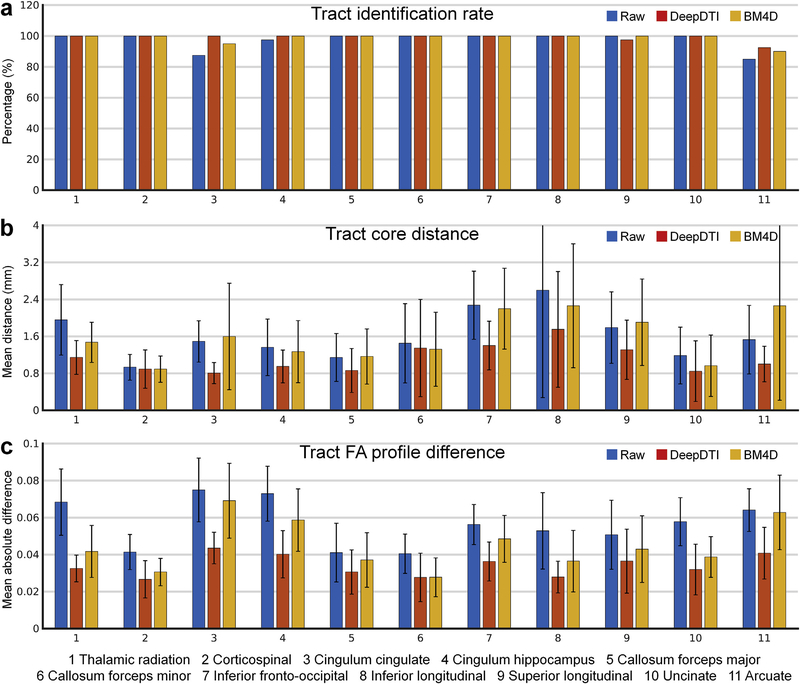
In addition to the voxel-wise performance, DeepDTI also improves tractography and tract-specific analysis. The identified tracts from DeepDTI and BM4D are more similar to the ground truth compared to the raw data (Fig. 7 rows b, c, results of other tracts available in Supplementary Fig. S3). In the representative subject shown in Fig. 7, the arcuate fasciculus could not be delineated from the raw data (Fig. 7, row b, column ii), and only a few fascicles of arcuate fasciculus could be delineated from the BM4D results (Fig. 7, row b, column iv, cyan). DeepDTI identifies the most fascicles of the arcuate fasciculus (Fig. 7, row b, column iii, cyan), similar to those from the ground-truth data. For the 20 evaluation subjects, most of the tracts could be accurately identified from the raw data, DeepDTI-processed data and BM4D-denoised data (Fig. 8a). To exemplify the discriminatory ability of DeepDTI, the rate of identifying the cingulum (cingulate portion) is 12.5% higher with DeepDTI than the raw data (100% versus 87.5%) and 5% higher than with BM4D (100% versus 95%).

Fig. 7. DeepDTI accurately identifies major white-matter tracts.

Whole-brain DTI-based tractography results (row a), 20 representative major white-matter tracts identified using the Automated Fiber Quantification (AFQ) software (row b), the skeleton of a selected tract, the corticospinal tract (row c), and the tract profiles of fractional anisotropy (FA) values along the corticospinal tract (row d) derived from the ground-truth data (column i), raw data consisting of 1 b = 0 image and 6 diffusion-weighted images (DWIs) sampled along an arbitrary rotational variant of the optimized set of diffusion-encoding directions from the full dataset (column ii), the same raw data processed by DeepDTI (column iii) and denoised by BM4D (column iv). Results are shown for the right hemisphere of a representative subject. In row (c), the skeleton of each tract bundle is represented as a 5 mm radius tube color-coded based on the FA value at each point along the tract with the dotted lines representing the way-point regions-of-interest that define the tract core. In row (d), the tract profiles depict the FA values extracted from the tract core of the corticospinal tract.

Fig. 8. Quantification of the accuracy of DTI-based tractography and tract-specific analysis.

The across-subject mean and standard deviation of the Identification rate of the 20 major white-matter tracts determined using the Automated Fiber Quantification (AFQ) software (tracts from the left and right hemisphere are combined except for the forceps major and forceps minor) (a) for the raw data consisting of 1 b = 0 image and 6 diffusion-weighed images sampled along an arbitrary rotational variant of the optimized set of diffusion-encoding directions from the full dataset (blue), the same raw data processed by DeepDTI (red) and denoised by BM4D (yellow) of 20 evaluation subjects. In (b), the mean distance between the tract cores is compared to the ground truth, and in (c), the mean absolute difference of the tract profiles of the fractional anisotropy values are compared to the ground-truth values.

The mean distance between the tract core from DeepDTI and ground truth is more similar than for the raw data and BM4D-denoised data and measures around 1 mm for the thalamic radiation, corticospinal tract, cingulum (cingulate and hippocampal portions), forceps major, uncinate fasciculus and arcuate fasciculus and around 1.5 mm for the forceps minor, inferior fronto-occipital fasciculus, inferior longitudinal fasciculus, and superior longitudinal fasciculus (Fig. 8b). In the representative subject shown in Fig. 7, the tract profile for FA of the corticospinal tract from DeepDTI is more similar to the ground truth compared to other methods and captures the along-tract variation of FA (Fig. 7 row d). For the 20 evaluation subjects, the MAD of the FA tract profiles derived from DeepDTI results is in general half of that derived from the raw data and two thirds to three fourths of that derived from BM4D-denoised data, except for forceps minor (Fig. 8c, MD, AD and RD results available in Supplementary Fig. S4).

4. Discussion

In this study, we have developed a data-driven supervised deep learning approach called DeepDTI for reducing the angular sampling requirement of DTI to six diffusion-encoding directions. Our method maps one b = 0 image and six DWI volumes acquired along optimized diffusion-encoding directions, along with T₁-weighted and T₂-weighted image volumes as inputs, to their residuals with the output high-quality image volumes using a very deep three-dimensional CNN. The performance of DeepDTI was systematically evaluated in terms of the quality of output images, DTI metrics, DTI-based tractography results and tract-specific analysis results, as well as compared to the performance of using different amounts of data and the state-of-the-art BM4D denoising algorithm. The output images of DeepDTI were similar to the ground-truth images obtained from 18 b = 0 images and 90 DWIs, with high PSNR of 34.1 dB and SSIM of 0.98 for the b = 0 images and PSNR of 30.8 dB and SSIM of 0.97 for DWIs at the group level. The whole-brain MADs between DTI metrics from DeepDTI and ground truth were 14.83°, 0.036, 0.038 μm²/ms, 0.055 μm²/ms and 0.041 μm²/ms for the DTI metrics of V1, FA, MD, AD and RD, respectively, at the group level, which were about half of the MADs obtained from the raw data and two thirds of the MADs obtained from BM4D denoising. The accuracy of the DeepDTI-derived DTI metrics were comparable to those obtained with two b = 0 vol and 21 DWI volumes sampled along uniformly distributed directions for DTI V1, and comparable to those estimated from two b = 0 images and 26–30 DWI volumes for DTI FA, MD, AD and RD, achieving 3.3–4.6 × acceleration and outperforming the BM4D denoising algorithm by at least a factor of two. Tractography based on the DeepDTI results accurately identified the twenty major white-matter tracts, with small mean distances of 1–1.5 mm between the core of the white-matter tracts identified from DeepDTI compared to the ground-truth results.

An important design element of the DeepDTI framework is the unique formulation of the inputs and outputs of the CNN to be the DWIs along optimized diffusion-encoding directions that leverages domain knowledge of the underlying diffusion MRI physics. The inability to recover orientational information from diffusion MRI data is an essential limitation of existing machine learning approaches for diffusion MRI. Unlike previous studies that mapped input DWIs directly to metrics derived from a diffusion model, DeepDTI maps the input DWIs to their residuals compared to the ground-truth DWIs. The advantage is that the resultant high-quality DWIs can be used to fit diffusion tensors to generate any scalar metrics and orientational metrics for tractography and are also highly compatible with other advanced analysis methods such as AFQ or DTI-based tractography software for neurosurgical planning. More importantly, residual learning boosts the performance of CNNs and accelerates the training process (He et al., 2016; Kim et al., 2016; Pham et al., 2019; Zhang et al., 2017). While we only used a simple 10-layer plain network (Kim et al., 2016; Zhang et al., 2017; Chaudhari et al., 2018) for the mapping between the inputs and outputs, the formulation of DeepDTI allows more sophisticated CNNs (e.g., even deeper CNNs, U-Net (Ronneberger et al., 2015; Falk et al., 2019), generative adversarial networks (Goodfellow et al., 2014)) to be adopted for further improving the results.

There are several reasons for using the theoretical minimum of one b = 0 image and six DWIs required by conventional voxel-wise tensor fitting methods as input in DeepDTI, acknowledging that a more sophisticated CNN could potentially obtain good DTI results from a smaller number of image volumes, e.g., one b = 0 image and three DWI volumes sampled along orthogonal diffusion-encoding directions. Most importantly, residual learning adopted in DeepDTI requires the number of input and output images to be identical. Since at least one b = 0 image and six DWIs are required to fit the tensor model on the output images, the matched number of b = 0 image and DWIs are used as the input. More than one b = 0 image and six DWIs can be used as input and output, e.g., one b = 0 image and 30 DWIs along uniformly distributed directions, which might require a larger number of CNN parameters to handle the larger number of channels and consequently more GPU memory during training. Second, using fewer than one b = 0 image and six DWIs to obtain a high-quality diffusion tensor (which is of note mathematically impossible using conventional voxel-wise tensor fitting, as detailed in the Supplementary Information), would further reduce the interpretability of the CNN-generated results and might consequently impede the wide adoption of the CNN-based DeepDTI method by users including MRI physicists, psychologists, neuroscientists and clinicians at the present time. Fortunately, numerous efforts have been made to characterize neural networks (Mascharka et al., 2018; Montavon et al., 2018; Lipton, 2018; Mardani et al., 2019; Zhang et al., 2018). These invaluable studies that increase the interpretability of neural networks will improve our understanding of neural networks and facilitate the wider acceptance of the further reduction of the number of required images used in DeepDTI using more advanced neural networks. Furthermore, the acceleration from six DWIs to fewer than six DWIs does not offer a practical time-savings in terms of the acquisition, given that each image volume can be acquired in as little time as ~5 s using modern parallel imaging and slice acceleration methods. Therefore, in considering the tradeoffs between wider acceptance of CNN-based methods and further acceleration of the acquisition, six DWIs sampled along optimized diffusion-encoding directions were considered in our view to be a good balance.

DeepDTI establishes a versatile framework for DTI processing that can be adapted for different purposes by changing the input and output images. Our current approach emphasizes reducing the angular sampling requirement of DTI to six diffusion-encoding directions. Therefore, the input and output DWIs have the same spatial resolution but are obtained using different numbers of DWIs. The end results achieve a combination of angular super-resolution and denoising. For very low-SNR data, such as those with sub-millimeter isotropic resolution, input images can be derived from DWIs acquired along 30 uniformly and fully sampled diffusion-encoding directions to provide the CNN with sufficient directional diffusion contrast to infer the tensor metrics. In this case, DeepDTI performs pure denoising and can achieve a similar acceleration factor given sufficiently high-quality training targets. In applications where high spatial resolution (millimeter or sub-millimeter isotropic) is desired, such as the in vivo mapping of cerebral cortical microstructure (McNab et al., 2013; Kleinnijenhuis et al., 2015; Fukutomi et al., 2018; Calamante et al., 2018; Tian et al., 2017) and the structural connections in the basal ganglia, the input images can be derived from DWIs acquired along 30 uniformly and fully sampled diffusion-encoding directions but with lower spatial resolution than the target images to achieve combined spatial super-resolution and denoising. The specific CNN adopted by DeepDTI is well suited for both spatial super-resolution and denoising, which is often referred to as VDSR (very deep super-resolution) network in the context of super-resolution (Kim et al., 2016; Chaudhari et al., 2018) and DnCNN (denoising CNN) in the context of denoising (Zhang et al., 2017). If the input images are acquired along under-sampled diffusion-encoding directions with spatial resolution lower than the target images, DeepDTI achieves angular super-resolution, spatial super-resolution and denoising simultaneously. Moreover, the DeepDTI pipeline could also be used for mapping high-SNR DWIs obtained by averaging multiple repetitions from single-repetition data without imposing any diffusion models. The input and output DWIs would be expected to incorporate higher b-values, which are needed for mapping crossing fibers and more advanced microstructural metrics. The resultant high-quality DWIs could be used for fitting any preferred advanced diffusion models and model-free metrics as proposed by the q-DL method (Golkov et al., 2015, 2016).

DeepDTI offers a compelling demonstration of the value of deep learning approaches in mining hidden information embedded in imaging data. The success of DeepDTI proves that there is sufficient information in the data from six diffusion-encoding directions to derive high-fidelity DTI metrics that are long believed to require far more data. The requirement for more than necessary data is mainly because the redundant information in the diffusion data has not traditionally been fully exploited. For diffusion MRI, the unique challenge is that the data redundancy traverses a six-dimensional joint image-diffusion space (Callaghan et al., 1988), which is non-trivial to model for microstructural imaging. Previous works partially exploited this data redundancy using techniques such as compressed sensing and low-rank convex optimization (Hu et al., 2020; Shi et al., 2015; Wu et al., 2019; Cheng et al., 2015; Pesce et al., 2017, 2018; Chen et al., 2018). As demonstrated in this work, well-constructed CNNs are better suited to make use of the redundancy in the imaging data and derive more accurate results with fewer input images. Specifically, the use of 3 × 3 × 3 × N (the number of input channels) kernels ensures that information across the six-dimensional image-diffusion space can be jointly utilized. The deep CNN has 10 layers and therefore a 21 × 1.25 mm (the voxel size) receptive field, which is sufficiently large to include similar information contained in non-local voxels. In the input layers, the kernels also use images with other contrasts (Golkov et al., 2016), e.g., T₁-weighted and T₂-weighted images, which is challenging, if not impossible, to be explicitly incorporated into a diffusion model.

The power of deep learning lies in its ability to generalize the inference of any number of diffusion MRI measures beyond the tensor model, given the known limitations of DTI, including the inability to resolve complex fiber configurations such as crossing fibers and not accounting for non-Gaussian diffusion behavior. While we have only focused on the simplest tensor model for applications that are constrained to the Gaussian diffusion regime (i.e., b-value lower than 1,500 s/mm²) because of practical factors such as the limited gradient strength of the MRI scanner, partially utilizing the capability of CNNs, future work is encouraged to leverage this principle to explore further reducing the number of input DWIs to fewer than six DWIs used in this work (e.g., three DWIs along orthogonal directions), the data requirement for more advanced crossing fiber mapping methods (e.g., BEDPOSTX (Behrens et al., 2003; Jbabdi et al., 2012), constrained spherical deconvolution (Tournier et al., 2004, 2007; Jeurissen et al., 2014)), microstructural imaging (e.g., axon diameter index mapping (Huang et al., 2020; Fan et al., 2019)) and advanced diffusion-encoding methods (e.g., q-space trajectory imaging (Westin et al., 2016) and double diffusion encoding (Yang et al., 2018)). More importantly, well-designed CNNs can be used for directly mapping the acquired DWIs to model-free metrics beyond historical models such as DTI, as well as other relevant outcomes of interest such as the segmentation of pathology, diagnosis and prognostication, without imposing any diffusion models, following the model-free argument proposed by the q-DL method (Golkov et al., 2015, 2016). The more goal-oriented mapping potentially further reduces the amount of required DWI data. In general, our work encourages the wider adoption of CNNs as complementary tools to comprehensively understand and extract the hidden information that may be embedded in the data from other forms of imaging, such as functional MRI, for accelerating the acquisition and improving the quality of the results.

Most importantly, DeepDTI enables greater accessibility to DTI for mapping the white-matter tissue properties and tracts in the in vivo whole human brain. DeepDTI only requires one b = 0 image and six DWI volumes of the brain, with the acquisition time of each measurement as short as ~4 s with parallel imaging and simultaneous multislice imaging techniques. The reduction of the entire DTI acquisition to 30–60 s potentially makes high-fidelity DTI a routine modality, along with anatomical MRI, for most MRI scans in both clinical and research settings, which promises to improve scan throughput and enable routine use in previously inaccessible populations, such as motion-prone patients and young children. As a stand-alone post-processing step, DeepDTI only takes in reconstructed images from the MRI scanner as inputs, without any need to intervene in the current imaging flow. Therefore, it can be easily incorporated into or deployed as an add-on of existing software packages, such as DTI-based tractography software for surgical planning, for streamlined acquisition and processing. We anticipate the immediate benefits of more accessible high-quality DTI and DTI-based tractography enabled by deep learning for a wide range of clinical and research neuroimaging studies.

4.1. Summary

This study presents a data-driven supervised deep learning-based method called DeepDTI to enable high-fidelity DTI using only one b = 0 image and six DWI volumes. In distinction to prior studies, DeepDTI maps the input image volumes to their residuals compared to the ground-truth output image volumes using a very deep 10-layer three-dimensional CNN. The rotationally-invariant and robust estimation of DTI metrics from DeepDTI are comparable to those obtained with two b = 0 images and 21 DWIs for estimation of the primary eigenvector V1 and two b = 0 images and 26–30 DWIs for the scalar DTI metrics of FA, MD, AD and RD, achieving 3.3–4.6 × acceleration. DeepDTI outperforms the state-of-the-art BM4D denoising algorithm at the group level by at least a factor of two. DeepDTI enables fast mapping of the whole-brain structural connectome, identification of the major white-matter tracts and tract-specific analysis, which would otherwise not be possible with a sparse acquisition consisting of just one b = 0 image and six DWIs. The mean distance between the core of the major white-matter tracts identified from DeepDTI and those obtained from the ground-truth results using 18 b = 0 images and 90 DWIs measures around 1–1.5 mm. The efficacy of DeepDTI lies in the use of the six optimized diffusion-encoding directions and a very deep 3-dimensional CNN combined with residual learning. DeepDTI promises to benefit a wide range of clinical and neuroscientific studies that require fast and high-quality DTI and DTI-based tractography.

Data availability

The image data including the diffusion, T₁-weighted and T₂-weighted anatomical data from 70 subjects are provided by the Human Connectome Project WU-Minn-Ox Consortium and are available via public database (https://www.humanconnectome.org).

Code availability

The source codes of DeepDTI implemented using MATLAB and Keras application programming interface are available from the corresponding author upon email request.