Abstract
Nanobubbles have gained attention for their use as highly stable ultrasound (US) contrast agents, but assessment of individual nanobubble size remains a challenge. Current sizing techniques require either extensive sample preparation or depend on assumed values of nanobubble density that are not well characterized. An US based approach would be desirable; however, probing individual nanobubbles using US transducers at clinical frequencies is not feasible due to the comparatively long acoustic wavelengths employed. Here we present a technique which can be used to estimate nano- or microbubble size by virtue of the amount of motion detected in an M-Mode image acquired using an acoustic microscope equipped with a 200 MHz transducer. A sample of a bubble-containing solution is incorporated into a phantom composed of molten agarose. The solidified agarose gel contains pores with well-defined sizes dictated by the agarose concentration. Bubbles in the gel matrix that are smaller in diameter than the gel pore size are capable of undergoing stochastic motion which manifests as intensity fluctuations in M-Mode images. Conversely, bubbles which are larger than the agarose pores become trapped and produce static M-Mode intensity patterns. In this study, agarose gels with concentrations ranging from 0.25% to 1.25% (mean pore sizes ranging from 2.68 µm to 0.34 µm) were loaded with either nanobubbles (mean diameter 0.326 µm) or microbubbles (mean diameter 2.71 µm) and imaged at 200 MHz. In the nanobubble loaded gels, M-Mode fluctuations were clearly visible up to a gel concentration of 1% (pore size of 0.39 µm). In contrast, the microbubble loaded gels exhibited minimal M-Mode fluctuation even at agarose concentrations of 0.25% (2.68 µm pore size). Autocorrelation curves generated from the M-Mode data demonstrated a clear trend of curve flattening (loss of motion) when the pore size was comparable to mean bubble diameter, indicating that individual bubbles trapped in the agarose pores are the main source of acoustic backscatter. In the future, decay parameters extracted from the autocorrelation curves could potentially be used as indicators of mean bubble diameter for bubble populations of unknown size.
Graphical Abstract
Detection of the motion of individual nanobubbles and microbubbles in an agarose gel using an ultra-high frequency acoustic microscope.
Introduction
The term nanobubble (NB) is used to refer to a bubble with sub-micron diameter, commonly composed of a lipid shell surrounding a gas-core1. NBs have a wide range of industrial applications including cleaning, disinfection, water treatment, and manufacturing of functional materials2. In biomedical applications, NBs can be used to deliver therapeutic agents into tumors3 while providing enhanced ultrasound (US) contrast for diagnostic purposes4, and assessing treatment efficacy5. When compared to commercial microbubbles (MB), NBs provide similar or better US contrast6, have higher mass transportation efficiencies2, and have greater temporal stability, with decay half-lives over 10 times longer when used in murine models7. As with MBs, the stability and size of a population of NBs is directly related to the composition of their gas core, their shell material, and the presence of membrane stiffeners in their shells1. Recently developed ultra-stable NB formulations, such as PGG (Propylene Glycol and Glycerol) NBs8, contain perfluorocarbon gas and phospholipids including poly-ethylene glycol (PEG) which further increase in vivo half-life and biocompatibility9. Another advantage of NBs is their small diameter (10-1000 nm for NBs vs 1-10 µm for MBs) which allows them to extravasate from the tumor vasculature when used in vivo10, allowing higher uptake in tumor parenchyma.
NBs can be produced via several methods, including: self-assembly1, electrolysis11, cavitation12, and several other processes13. However, determining the approximate size distribution of the NBs in the final preparation remains a challenge, as the diameter of the NBs is typically below the resolving capabilities of conventional microscopy14. Current techniques used to measure bubble size, such as electron microscopy, require sample modification by freeze fracturing and coating with a palladium/gold mixture15. Other techniques like dynamic light scattering or the Coulter Counter can measure the bulk size of particles in an aqueous solution but cannot directly distinguish between bubbles and non-gaseous particles without additionally measuring properties such as zeta potential13. Resonance mass measurement (RMM) devices can measure the buoyant mass of particles and calculate their size based on an assumed particle density16. However, these devices do not directly measure size, but instead estimate particle size based on an assumed density which the user must input into the system manually. Moreover, these systems are costly. Therefore, a technique is needed that can both demonstrate the existence of the NBs and estimate their size. An ultrasound-based technique would potentially be advantageous for these purposes due to the enhanced scattering resulting from the gas core of the NBs.
Acoustic microscopy utilizes single element US transducers with central frequencies in the hundreds of megahertz (MHz) for imaging and material characterization17,18. At these ultra-high frequencies (UHF), spatial resolution that rivals - and in some cases exceeds - that of conventional optical techniques can be achieved, enabling the imaging of samples with sub-micron detail18,19. Analysis of the RF-signals recorded in UHF pulse-echo studies allows for extraction of information such as the mechanical properties of biological cells20, and mitotic cell cycle phase21. Furthermore, when the wavelength of the insonifying acoustic pulse is comparable to the dimensions of the scattering object, unique features in the backscattered power spectrum22–24 enable the sizing of microscopic objects such as spherical microbeads25 and single cells26–28 without the need for 2D scanning. Such techniques have previously been utilized in UHF acoustic flow cytometry systems for the purposes of sizing cancer cells to a high degree of accuracy and demonstrate good agreement with gold standard particle sizing techniques, such as the Coulter Counter29.
A common technique for assessing motion in US studies is to generate a 2D image comprised of RF-lines from a single spatial location as a function of image acquisition time. These Motion Mode, or M-mode, images are commonly used in medicine to monitor organ movements, such as the motion of the heart in echocardiography30. Here we describe a technique which combines UHF US and M-Mode imaging to detect the acoustic backscatter from, and the motion of, individual NBs. For this purpose, UHF US is ideal since the acoustic wavelength is more comparable to the NB size than for traditional clinical frequencies (e.g. ~8 µm for a 200 MHz transducer, vs ~150 µm for a 10 MHz transducer), increasing the amplitude of the backscattered signal. The NBs are embedded in an agarose meshwork with pore sizes ranging from less than 250 nm to larger than 1 µm, depending on the agarose gel concentration used in the experiments31. It has been shown that NBs have very low buoyancy and undergo Brownian motion allowing them to remain dispersed in aqueous solutions for long periods of time32. In low agarose concentrations, the pore sizes are large compared to the NB diameter and the Brownian motion of individual NBs is detected in acquired M-Mode images as fluctuations in the intensity of acoustic backscatter from within the agarose. In gels where the pore size is comparable to the NB diameter, the are no fluctuations in the M-Mode images. In this work, we demonstrate the use of the technique on a preparation of NBs embedded in agarose concentrations ranging from 0.25% to 1.25%. Additionally, autocorrelation curves generated from the acquired M-Mode images were used to quantify the amount of motion within the gel, and thus as an indicator of the NB diameter. Finally, we demonstrate that the technique can readily be used to discriminate between populations of MBs and NBs based on the agarose gel concentration used.
Methodology
Nanobubble Synthesis, Isolation, and Activation
All glassware was washed and cleaned with 70% ethyl alcohol and then air dried. The gas used to form MBs/NBs was octafluoropropane (C3F8) (Synquest Labs, USA). The nanobubble solutions were made following the procedure developed by de Leon et al8. Bubble solutions were prepared by mixing 60.1 mg of 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), 10 mg of 1,2-dipamitoyl-sn-glycero-3-phosphate, sodium salt (DPPA), 10 mg of 1,2-distearoyl-sn-glycero-3-phosphothanolamine-N-[amino (polyethylene glycol)-2000] (DSPE-mPEG) (Avanti Polar Lipids, USA) and 20 mg of 1,2-dipalmitoyl-sn-glycero-3-phosphothanolamine (DPPE) (Sigma, USA) in a glass vial. The mixture was added to 1 mL of propylene glycol (PG) heated to 80°C in a water bath and dissolved by sonicating every 1–2 minutes for 10 minutes. A mixture of 8 mL Phosphate Buffered Saline (PBS) (Wisent Inc, Canada) and 1 mL of glycerol was prepared and heated to 80°C before being adding to the lipid/PG solution. The mixture was placed in the sonicator for 10 minutes at room temperature and was then transferred into serum vials to be capped, sealed, and stored at 4°C until activation.
For activation, a vacuum was induced in a serum vial using a 20 mL syringe with a 25-gauge needle. A 10 mL syringe was then used to inject C3F8 gas into the vial until the pressure of the vial had equalized with ambient pressure. At this point, a second 25-gauge needle was used to puncture the cap and act as a vent while injecting the remaining C3F8 gas. The vial was then shaken for 45 seconds with a mechanical shaker (VialMix, Bristol Myers Squibb, USA). Finally, the vial was inverted and centrifuged at 50g for 5 minutes to isolate NBs below the neck of the vial. “g” in this case represents g-force experienced in the centrifuge by the NBs. Size measurements of NBs were performed using Archimedes RMM system (Malvern Panalytical, United Kingdom) fitted with a nano sensor10. The lower limit of detection for the RMM measurements is set automatically by the system for each sample based on the system noise present at the beginning of the measurement.
Microbubble Isolation & Activation
The synthesis and activation of MBs begins with the same procedure as the NBs. The MB isolation was carried out following the procedure developed by Feshitan et al33. After activation, 2 vials of MBs were drawn into a 3 mL syringe using a 21 gauge needle and then transferred to another beaker and diluted into 100 mL filtered PBS. The solution was slowly swirled by hand in order to mix the MB solution with PBS to obtain a homogenous solution. 30 mL syringes with a length of 8.2 cm were used to draw the solution. A differential centrifugation technique was used to isolate MB of different sizes from the stock solutions. In brief, the syringes were centrifuged at 50g for 2 minutes. After centrifugation, the white layer (cake) resting against the syringe plunger, consisting microbubbles larger than 1 µm in diameter, was re-diluted into 100 mL PBS and the infranatant consisting submicron bubbles was discarded. Next, syringes filled with re-diluted cake were centrifuged at 160g for 2 minutes. The infranatant consisting of bubbles less than 2 µm in diameter was discarded, and the cake was re-diluted into 100 mL PBS. This centrifugation process was repeated an additional two times at 180g and 250g, respectively, before resuspending the final cake into 20 mL of PBS. The final solution was transferred to a 4 mL scintillation vial and then capped and sealed. Size measurements of MBs were performed using a PN A51387A Coulter Counter Multisizer 4 (Beckman Coulter, United States) fitted with a 30 µm aperture.
Phantom Preparation
Five mixtures of low melting point agarose (Sigma, USA) dissolved in PBS were prepared at concentrations of 0.25%, 0.50%, 0.75%, 1.0%, 1.25% w/v, respectively. In brief, a beaker filled with PBS was covered with saran wrap to prevent evaporation and heated in a water bath to a temperature of 100°C. The saran wrap was removed and agarose powder was slowly added to the PBS while stirring the solution with a magnetic stir bar. The beaker containing the mixture was weighed, then re-covered with saran wrap. Several small holes were poked in the saran wrap for ventilation. The solution was mixed in the water bath using a magnetic stirrer hot plate (IKA, Germany) until the agarose had completely dissolved in the PBS (approximately 15 minutes). The beaker was removed from the water bath, uncovered, and weighed a second time. To maintain the desired agarose/PBS concentration, fresh PBS was added to the solution until the initial beaker weight was obtained. The molten agarose mixture was then divided into scintillation vials (VWR, United States) and stored at 4°C. To prepare the phantoms, the solidified agarose mixtures were heated to 70°C until molten and then cooled to 40°C. A pipette was used to mix 5 µL of activated MB or NB solution into 300 µL of molten agarose. The agarose and bubble mixture was then plated on an uncoated 35 mm glass bottom petri dish (MatTek, USA). The phantoms were left to solidify for 15 minutes at room temperature before being placed in a 37°C environment for imaging. It is assumed that integration of the bubbles into the agarose in this way does not modify the bubble size, and that the bubble size distribution in the agarose is representative of the distribution present in the original stock solution. Three phantoms containing MBs and three phantoms containing NBs were prepared for each concentration of agarose.
Scanning Electron Microscopy
For scanning electron microscopy (SEM) imaging, agarose gels were prepared as above and were gelled inside a 24-well plate. Once set, the gels were frozen in liquid nitrogen, freeze-fractured, and lyophilized. Dry gels were then sputter coated with 5 nm of palladium and imaged using an FEI Helios 650 SEM (Hillsboro, OR) with an acceleration voltage of 2.0 kV. Each gel concentration was freeze-fractured and imaged in triplicate. Mean pore size for each agarose gel concentration was quantified using ImageJ software by measuring individual pores at the maximum width (n ≥ 70) for each gel concentration.
Signal Acquisition and Analysis
The phantom petri dishes were topped up with PBS to provide acoustic coupling and then placed on the translation stage of a SASAM (Kibero GmBH, Germany)34,35 scanning acoustic microscope. The SASAM was equipped with a 200 MHz single element transducer that had a 30° semi-aperture angle, −6dB bandwidth of 120 MHz, depth-of-field of 54 µm, and an acoustic focal spot of 7.8 µm. The speed of sound in water is 1527 m•s−1 at 37°C18, corresponding to an acoustic wavelength of approximately 7.6 µm for a pulse with 200 MHz frequency. The transducer was positioned such that the acoustic focus was approximately 100 µm below the surface of the phantom. A custom MATLAB script was used to acquire M-mode images of the phantom. Each M-Mode image consisted of 10,000 RF-lines acquired at a rate of 121 kHz (slow time). Individual RF-lines were recorded using a 10-bit DC252 digitizer (Acqiris, USA) with a sampling rate of 2 GHz (fast time) and were averaged 40x to increase the measurement SNR. In each phantom, 5 unique M-Mode images were acquired at locations separated by at least 500 µm.
The M-Mode RF-data was loaded into MATLAB as an array, with each RF-line corresponding to a column and each row representing the same sample number in the fast-time dimension. A dataset for background subtraction was acquired by performing measurements on a water-filled petri dish with the transducer focus several millimeters above the bottom of the dish. This background was subtracted from the M-Mode dataset to eliminate artifacts attributable to acoustic reflections within the transducer buffer rod18,34. Each RF-line was then enveloped and normalized by the maximum amplitude in the array. To eliminate rows containing only noise and no signal from bubbles, the maximum value for each row (i.e. the largest amplitude for a single fast-time across all RF-lines) was determined. Rows in the array with a maximum value less than 0.15 were comparable to the system noise and were excluded from subsequent analysis. For the remaining rows, the autocorrelation for a given lag, k, was calculated as:
using the built-in MATLAB command autocorr. The autocorrelation curves were normalized to have a value of 1 at zero lag, and average autocorrelation curves from the five measurement locations were computed for each phantom. The zero lag data point does not contain any information pertaining to bubble motion, and as such was excluded from the analysis.
Results
Sizes of Bubble Preparations
Distributions of the NB and MB diameters as determined by RMM (NB) and the Coulter Counter (MB) are shown in Figure 1. For the RMM system, 2 µL of NB stock was diluted in 1 mL of water. A total of 3000 particles were then measured for three separate stock solutions. The Archimedes system used to measure the NB size automatically selected the limit of detection for each experiment, which determined the cutoff of the lower size limit set for the NB size distribution. This resulted in each NB size distribution beginning at a different size bin (140 nm, 266 nm and 185 nm for experiments 1, 2 and 3 respectively). On average, less than 2% of the particles were found to be non-buoyant (i.e. lipid fragments). For all NB preparations, the mean bubble diameter was 326 ± 48 nm, with the largest bubble detected being 1004 nm in diameter. For the Coulter Counter measurements, 1 mL of the isolated MB stock was diluted in 20 mL of isotone prior to measurement. From this dilution, 100 µL was extracted and run through the Coulter Counter device. The mean size of the filtered MB populations as determined using the Coulter Counter were 2.45 ± 0.93 µm, 2.48 ± 1.22 µm, and 3.19 ± 1.56 µm, for the first, second, and third experiment trials, respectively.
Figure 1.
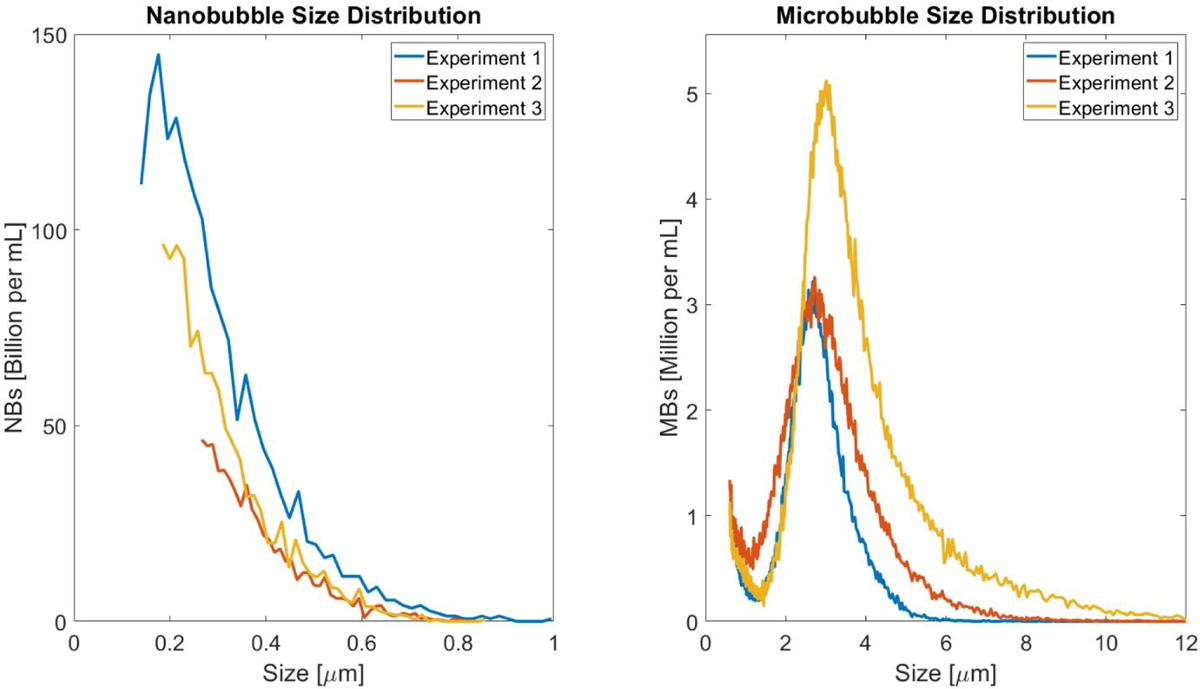
Measurement of bubble size for NB and MB populations. The sizing results of the isolated NB (left) and MB (right) populations were determined using Archimedes resonant mass measurement system and Beckman Coulter Counter Multisizer 4, respectively. NB and MB concentrations were multiplied by factors of 2000 and 20, respectively, to match the concentration of the stock solution prior to dilution.
Agarose Gels
The size distribution of the pores in the agarose gel phantoms determined using SEM, as a function of varying agarose concentration, is shown in Figure 2a. The mean pore size decreased from 2.68 µm at 0.25% agarose concentration to 0.34 µm at 1.25%. A steep decrease in pore size with increasing concentration was observed for concentrations less than 1%, while there was little variation in pore size when increasing agarose concentration from 1% to 1.25%. With the exception of the 0.5% agarose phantoms, the variance in pore sizes also decreased as a function of increasing agarose concentration. Representative SEM images of the 0.25%, 0.75%, and 1.25% gels are shown in Figures 2b–c, 2d–e, and 2f–g, respectively, and demonstrate the change in appearance of the pores in the agarose mesh with increasing agarose concentration.
Figure 2.
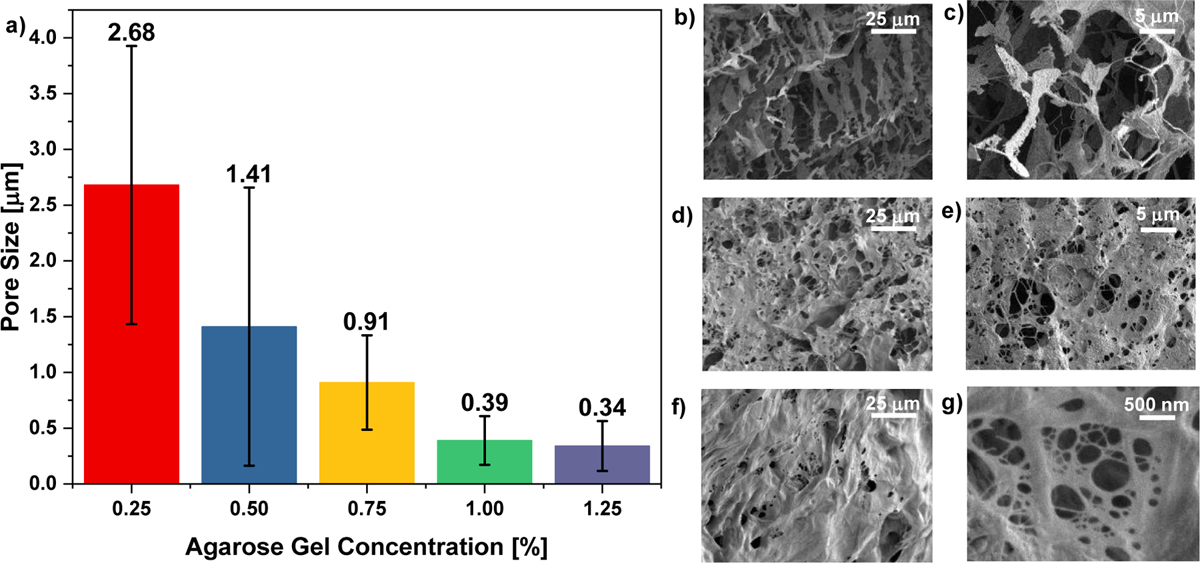
Agarose pore size measurements. a) Bar graph showing the pore size results based on SEM imaging. The mean pore size for each gel concentration is indicated above each bar, and the error bars represent one standard deviation from the mean. SEM image of 0.25% (b,c), 0.75% (d,e), and 1.25% (f,g) agarose phantoms at different magnifications (b,d,f: 250x, c,e: 1000x, and g: 10,000x).
M-Mode Images
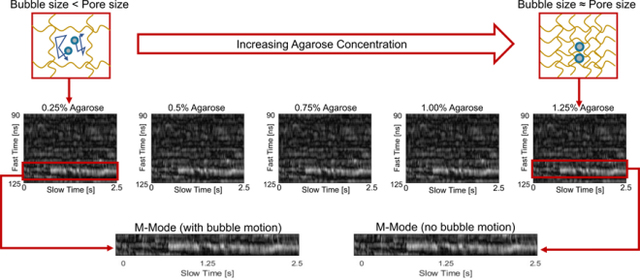
Representative M-Mode images from the NB phantoms with agarose concentrations increasing from 0.25% to 1.25% are shown top-to-bottom in the left-hand column of Figure 3. At concentrations below 0.75% the M-Mode images exhibit a significant amount of fluctuation along the slow time axis. As the agarose concentration increased - so that the average agarose pore size approached the average NB size - the amount of fluctuation in the M-Mode images decreased and exhibited negligible temporal variation. At a concentration of 1.25% (Figure 3i), no motion was apparent in the NB M-Mode image. In comparison, M-Mode images shown on the right-hand side of the Figure are from MB loaded phantoms for the same agarose concentrations. Slight fluctuations were observed in the MB M-Mode images obtained at an agarose concentration of 0.25%. One such fluctuation is indicated with a red contour in Figure 3b, and a zoomed in view of the region is shown in the corresponding figure inset. At higher concentrations the MB M-Mode images exhibited no temporal fluctuation and were indistinguishable from one another.
Figure 3:

Representative M-Mode images of bubble loaded phantoms at varying agarose concentrations. The left column depicts NB loaded phantoms with agarose concentrations of a) 0.25%, c) 0.50%, e) 0.75%, g) 1.00%, and h) 1.25%. The right column displays M-mode images of MB loaded phantoms with agarose concentrations of b) 0.25%, d) 0.50%, f) 0.75%, h) 1.00%, and j) 1.25%. In b), a zoomed-in view of a region that exhibits slight M-Mode fluctuations (indicated with a red contour) is shown in the figure inset.
Autocorrelation Curves
Mean autocorrelation curves from gels of various concentration loaded with NBs from the same stock solution are shown in Figure 4a, and autocorrelation curves from gels loaded with MBs from the same stock solution are shown in Figure 4b. The mean curves were generated by averaging the autocorrelation curves from all measurement locations in a single phantom. In both figures, the curves for different gel concentrations have been offset in the y-axis to intersect at a value of unity. For every agarose concentration examined the ACV curves for the NB phantoms exhibited a faster decorrelation time than the corresponding MB phantoms, indicating greater motion in the NB phantoms than the MB phantoms. As expected from the M-Mode images, for the NB phantoms the slope of the curve decreased with increasing gel concentration, indicating a decrease in motion with increasing agarose concentration. In contrast, for the MB phantoms a curve with a slight slope was observed for a gel concentration of 0.25%, and overlapping horizontal curves - indicative of negligible motion - were observed at all other agarose gel concentrations.
Figure 4:
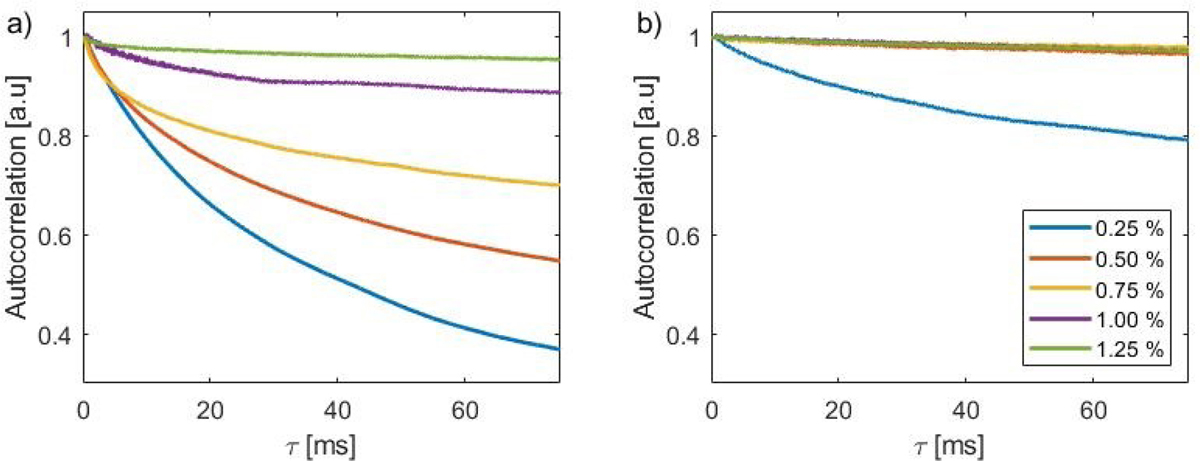
Average autocorrelation curves for agarose gels ranging from 0.25% to 1.25%. a) autocorrelation curves for agarose gels containing nanobubbles from the same stock solution, and b) autocorrelation curves for gels containing microbubbles from the same stock solution. The autocorrelation curves have been offset vertically to intersect the ordinate at unity. The legend in b) is applicable to both graphs.
To examine the relationship between the autocorrelation decay and the agarose concentration, every autocorrelation curve acquired from each phantom across all experiments was fit to an exponential equation of form:
The fit variable ‘b’, which represents the decay parameter of the autocorrelation curve, was then extracted as a function of concentration for each curve. M-Mode images which exhibited spurious noise artifacts or low SNR produced artificially high b values and were excluded from the final population statistics. The resultant boxplots depicting the distribution of b values are shown in Figure 5. The mean value of b was found to decrease with increasing agarose concentration for the NB loaded gels, but was insensitive to gel concentration for the MB populations.
Figure 5:
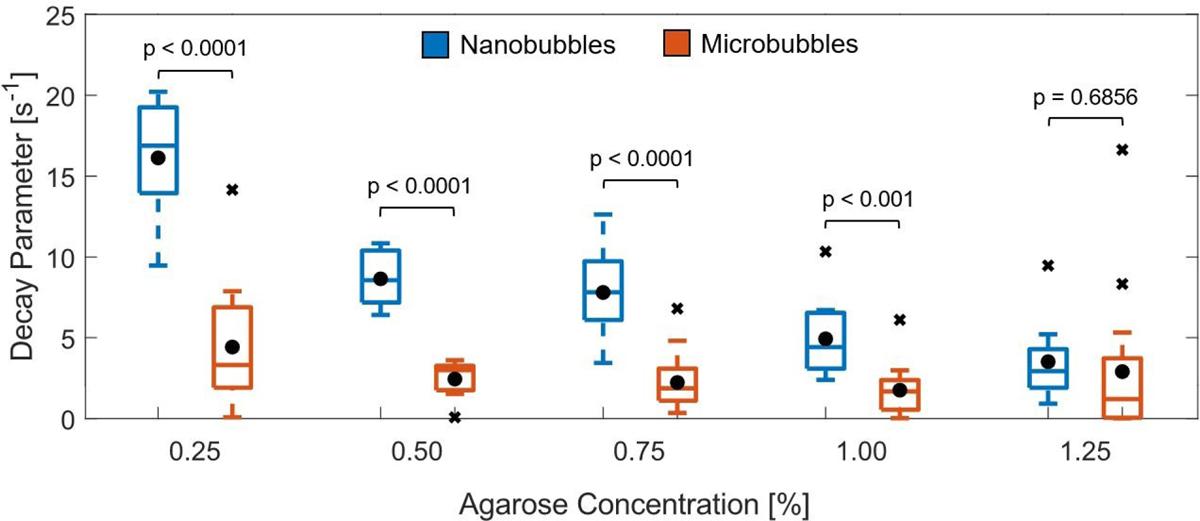
Box-and-whisker plot of decay parameters for varying agarose concentrations averaged over 3 experiments. For each concentration, the average decay parameter for both the NB (blue) and MB (orange) loaded phantoms are indicated by black circles. The p-values from a two-sample t-test comparing the populations at the same agarose concentration are indicated above each pair of box-and-whisker plots.
Discussion
Agarose gels are commonly used in techniques such as gel electrophoresis36, and as a result, agarose gel pore sizes are well characterized. Pore sizes ranging from several nanometers to approximately 600 nm for concentrations between 1–3% w/v agarose in PBS have been reported for low melting point agarose at a setting temperature of 22°C37. The size of the agarose pores in this work as measured using SEM are shown in Figure 2. The measured pore sizes range between 0.34 µm and 2.68 µm depending on the gel concentration and are consistent with the values reported in the literature.
The mean diameter of the bubbles in the NB preparation was on the order of 300 nm, in good agreement with previous RMM experiments reporting a NB mean diameter of 290 nm10. The mean diameter of the bubbles in the MB populations was 2.5 µm. No bubbles less than 600 nm in diameter were detected in any MB population, due to the minimum detection size limitations of the device. Comparing the mean bubble diameter with the average pore size provides an explanation for the appearance of the M-Mode images. Our hypothesis is that individual bubbles undergo motion in the matrix for gel concentrations which yield pore sizes larger than the mean bubble size; however, when the gel pore size is comparable to the mean bubble size the bubble motion will be restricted by the agarose matrix. For the NB populations, when the agarose concentration is 0.25% the mean pore size is much larger than the mean NB size, but is comparable to the average MB size. This explains the drastic difference in appearance of Figures 3a and 3b. As the agarose concentration is increased and the pore size decreases, the appearance of the M-Mode images for the MB loaded phantoms remains constant as the pores in the agarose matrix are already smaller than the mean bubble size. In comparison, the NB gel phantoms exhibit substantial motion at low concentrations, but as the gel concentration is increased and the mean pore size approaches that of the mean NB size, the motion decreases and the qualitative features of the M-Mode images from the two bubble populations begin to resemble one another.
The autocorrelation curves were generated to quantify the amount of motion present in the M-Mode images. In agarose concentrations where the mean pore size was larger than the mean bubble diameter, a large value for b was obtained, indicating a significant amount of variation in the autocorrelation curve. In contrast, as the pore size decreased and became comparable to the diameter of the bubble, the b values decreased. A two-sample t-test was performed comparing the NB and MB populations at the same agarose gel concentration. A statistically significant difference in the decay parameter (p<0.001) was observed for corresponding agarose concentrations below 1%, with no statistically significant difference in the NB and MB decay parameters at 1.25% (p = 0.6856), indicating marked differences in the amount of motion present in gels of the same concentration for the bubble different populations. For gel concentrations that exhibited barely discernable M-Mode motion (i.e. above 1% for NBs and 0.25% for MBs), the corresponding mean decay parameter values for all measurement locations were comparable. Although it is not possible to determine the exact size of individual NBs using this technique, insight into the mean size, and certainly the maximum size, of the bubble population can be obtained. In the future, we plan to further investigate the relationship of the decay parameter and bubble diameter, and perhaps use it as a predictor for the average bubble size. For example, we envision a technique which uses a well-defined threshold to monitor bubble motion. When several gels loaded with bubbles from the same stock solution are analyzed using the approach described in this work, a mean bubble size for the population could be determined by finding the concentration of gel for which the decay parameter falls below the threshold.
While previous works have reported in great detail the interactions which occur with acoustic waves and aggregates of NBs8,19,38–40 to our knowledge, this is the first work reporting ultrasound backscatter from individual NBs. We believe this to be the case for the following reason. Due to the small size of the agarose pores, clusters of NBs would be constrained in the matrix, unable to undergo motion and producing nearly flat autocorrelation curves in the M-Mode images even at low agarose concentrations. The fact that significant motion is present in agarose gels with average pore sizes of 390 nm thus points towards individual NBs being the dominant source of detected scatter in the images. While a single resolution volume (approximately 8 µm laterally with a depth-of-field of 54 µm) may itself contain many NBs, we posit that each individual pore within the volume would only contain a single bubble. While it could be argued that constructive/destructive interference should occur when more than one bubble is present in the transducer field of view, with a lack of motion, this would generate a static pattern in the M-Mode image instead of fluctuating intensity patterns such as those shown in the left-hand column of Figure 3.
The backscattering of an acoustic wave by a liquid sphere is dictated by the product of the incoming wave’s wavenumber (k) and the radius of the scattering sphere (a) 26. If the product ka << 1, the degree of scattering of the wave is negligible. As the value of ka approaches 1, acoustic scattering from the sphere rapidly increases. In this work, we used a 200 MHz transducer to insonify the nanobubbles. Assuming a speed of sound of 1527 m/s in water at 37°C, this yields a k ≈ 8.23E5 m−1. For a 300 nm bubble, the resultant ka is approximately 0.123. This value is comparable to the values of ka observed in techniques such as super-resolution US microscopy which utilize bubbles with 1 – 5 µm diameter and transducers with central frequency of 15 MHz41. It is thus reasonable to assume that with our technique acceptable SNR could be expected even in the case where there is a single NB in the transducer focal zone; potentially opening up the way for future studies which examine the properties of individual NBs. The other parameter which dictates the magnitude of scattering is the acoustic impedance of the scattering body. For an object with acoustic impedance equal to that of the surrounding medium (i.e. a situation where the region can be considered acoustically homogenous) no scattering will be observed regardless of the ka value. Therefore, the ultrasound-based technique is insensitive to the lipid fragments and other non-buoyant particulates which are generated as a result of the bubble synthesis process. Other bulk particle sizing techniques, such as DLS, are sensitive to these inhomogeneities and report a mixed result describing both bubble and particulate size. In the future, if individual NBs can be isolated and measured individually, for example by flowing a diluted sample of bubbles through an acoustic flow cytometer29, the feasibility of applying backscattering models such as those that are used for sizing biological cells26–28 for the purposes of sizing individual NBs can also be investigated.
The UHF M-Mode approach described here does have some caveats with respect to interpretation of experimental results. One such consideration is that the granularity in the precision of the technique is dictated by the number of unique agarose concentrations used in the measurement, as well as their corresponding pore sizes. In the current study, average pore sizes of 2.68 µm (0.25%), 1.41 µm (0.50%), 0.91 µm (0.75%), 0.39 µm (1.00%), and 0.34 µm (1.25%) were used. With these concentrations, hypothetical monodisperse NB populations having diameters of 500 nm and 700 nm, respectively, could both be expected to cease motion at a gel concentration of 1%. In such a case, additional gel concentrations between 0.75% and 1% would be necessary in order to further fine tune the measurements and allow for differentiation of the two populations. Another consideration is that the technique it currently derives its results from a select number of samples within the phantom to ensure acceptable scanning times. This should not be a problem assuming homogeneity of bubble size distribution; however, in some instances incorrect conclusions could be drawn by randomly selecting several points in the phantom which have unrepresentative large/small bubble sizes. This drawback could be overcome by increasing the number of sampling points within the phantom; however, it comes at the expense of increased signal acquisition time.
Conclusion
The main goal of this work was to devise a rapid, inexpensive technique for detecting the backscatter from NBs, and to demonstrate the feasibility of using the technique to determine a rough approximation of the size of a population of NBs. Acoustic backscatter from NBs immobilized in the agarose gel phantoms was recorded and used to generate M-Mode images depicting bubble motion. Comparison of the M-Mode images from the NB and MB loaded phantoms demonstrated a relationship between the agarose concentration (i.e. the average pore size) and the diameter of the bubble population. The motion can be characterized by extracting the decay parameter from the corresponding autocorrelation curves, which can potentially be used as an indicator for the size of an unknown bubble population. In the future we plan to investigate the potential of applying this technique to US systems which use linear array transducers at sub-UHF frequencies to decrease scanning time and expand the applicability of the technique to conventional US systems utilizing transducers with central frequencies below 10 MHz.
Acknowledgements
This research was supported, in part, by: the Natural Sciences and Engineering Research Council of Canada [grant no. RGPIN-2017-06496 (MCK)], the Canadian Cancer Society [grant no. 702161 (MCK)], the Canadian Foundation for Innovation [grant no. 30994 (MCK)], the Ontario Ministry for Research and Innovation [grant no. 30994 (MCK)], the Terry Fox Foundation [grant no. 1034 (MCK)], the National Institutes of Health [grant no. R01EB025741 (AE)], and the Office of the Assistant Secretary of Defense for Health Affairs, through the Prostate Cancer Research Program [award No. W81XWH-16-1-0371 (AE)]. Views and opinions of, and endorsements by the author(s) do not reflect those of the National Institutes of Health or of the Department of Defense.
Footnotes
Publisher's Disclaimer: This is an Accepted Manuscript, which has been through the Royal Society of Chemistry peer review process and has been accepted for publication.
Publisher's Disclaimer: Accepted Manuscripts are published online shortly after acceptance, before technical editing, formatting and proof reading. Using this free service, authors can make their results available to the community, in citable form, before we publish the edited article. We will replace this Accepted Manuscript with the edited and formatted Advance Article as soon as it is available.
Bibliography:
- 1.Khan MS, Hwang J, Lee K, Choi Y, Kim K, Koo H-J, Hong JW and Choi J, Molecules, 2018, 23, 2210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Meegoda JN, Aluthgun Hewage S and Batagoda JH, Environ. Eng. Sci, 2018, 35, 1216–1227. [Google Scholar]
- 3.Yuan F, Dellian M, Fukumura D, Leunig M, Berk DA, Torchilin VP and Jain RK, Cancer Res, 1995, 55, 3752–3756. [PubMed] [Google Scholar]
- 4.Cai WB, Yang HL, Zhang J, Yin JK, Yang YL, Yuan LJ, Zhang L and Duan YY, Sci. Rep, 2015, 5, 13725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Peiris PM, Toy R, Doolittle E, Pansky J, Abramowski A, Tam M, Vicente P, Tran E, Hayden E, Camann A, Mayer A, Erokwu BO, Berman Z, Wilson D, Baskaran H, Flask CA, Keri RA and Karathanasis E, ACS Nano, 2012, 6, 8783–8795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Perera RH, Solorio L, Wu H, Gangolli M, Silverman E, Hernandez C, Peiris PM, Broome A-M and Exner AA, Pharm. Res, 2014, 31, 1407–1417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Perera RH, de Leon A, Wang X, Wang Y, Ramamurthy G, Peiris P, Abenojar E, Basilion JP and Exner AA, Nanomedicine Nanotechnol. Biol. Med, 2020, 28, 102213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.de Leon A, Perera R, Hernandez C, Cooley M, Jung O, Jeganathan S, Abenojar E, Fishbein G, Sojahrood AJ, Emerson CC, Stewart PL, Kolios MC and Exner AA, Nanoscale, 2019, 11, 15647–15658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Abou-Saleh RH, Swain M, Evans SD and Thomson NH, Langmuir, 2014, 30, 5557–5563. [DOI] [PubMed] [Google Scholar]
- 10.Hernandez C, Abenojar EC, Hadley J, de Leon AC, Coyne R, Perera R, Gopalakrishnan R, Basilion JP, Kolios MC and Exner AA, Nanoscale, 2019, 11, 851–855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Svetovoy VB, Sanders RGP and Elwenspoek MC, J. Phys. Condens. Matter, 2013, 25, 184002. [DOI] [PubMed] [Google Scholar]
- 12.Oliveira H, Azevedo A and Rubio J, Miner. Eng, 2018, 116, 32–34. [Google Scholar]
- 13.Ushikubo FY, Furukawa T, Nakagawa R, Enari M, Makino Y, Kawagoe Y, Shiina T and Oshita S, Colloids Surf. Physicochem. Eng. Asp, 2010, 361, 31–37. [Google Scholar]
- 14.Hell SW, Science, 2007, 316, 1153–1158. [DOI] [PubMed] [Google Scholar]
- 15.Owen J and Stride E, Ultrasound Med. Biol, 2015, 41, 3253–3258. [DOI] [PubMed] [Google Scholar]
- 16.Alheshibri M and Craig VSJ, J. Phys. Chem. C, 2018, 122, 21998–22007. [Google Scholar]
- 17.Kolios MC, Strohm EM and Czarnota GJ, Quantitative Ultrasound in Soft Tissues, Springer Netherlands, Dordrecht, 2013, pp. 315–341. [Google Scholar]
- 18.Briggs A, Acoustic Microscopy, University of Oxford, Second Edition, 2002. [Google Scholar]
- 19.Zhang J, Chen Y, Deng C, Zhang L, Sun Z, Wang J, Yang Y, Lv Q, Han W and Xie M, Front. Pharmacol, 2019, 10, 610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Strohm EM and Kolios MC, Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. IEEE Eng. Med. Biol. Soc. Annu. Int. Conf, 2009, 2009, 6042–6045. [DOI] [PubMed] [Google Scholar]
- 21.Pasternak MM, Strohm EM, Berndl ES and Kolios MC, Cell Cycle, 2015, 14, 2891–2898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Faran JJ, J. Acoust. Soc. Am, 1951, 23, 405–418. [Google Scholar]
- 23.Anderson VC, J. Acoust. Soc. Am, 1950, 22, 426–431. [Google Scholar]
- 24.Frey HG and Goodman RR, J. Acoust. Soc. Am, 1966, 40, 417–420. [Google Scholar]
- 25.Baddour RE, Sherar MD, Hunt JW, Czarnota GJ and Kolios MC, J. Acoust. Soc. Am, 2005, 117, 934–943. [DOI] [PubMed] [Google Scholar]
- 26.Saha RK, Sharma SK and Kolios MC, Can. Acoust, 2010, 38, 31–34. [Google Scholar]
- 27.Moore MJ, Strohm EM and Kolios MC, Int. J. Thermophys, 2016, 37, 118. [Google Scholar]
- 28.Moore MJ, Sebastian JA and Kolios MC, J. Biomed. Opt, 2019, 24, 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Strohm EM, Gnyawali V, Sebastian JA, Ngunjiri R, Moore MJ, Tsai SSH and Kolios MC, Sci. Rep, 2019, 9, 4775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Riccabona M, Sorantin E and Ring E, Eur. Radiol, 1998, 8, 1457–1461. [DOI] [PubMed] [Google Scholar]
- 31.Narayanan J, Xiong J-Y and Liu X-Y, J. Phys.: Conf. Ser, 2006, 28, 83–86. [Google Scholar]
- 32.Azevedo A, Etchepare R, Calgaroto S and Rubio J, Miner. Eng, 2016, 94, 29–37. [Google Scholar]
- 33.Feshitan JA, Chen CC, Kwan JJ and Borden MA, J. Colloid Interface Sci, 2009, 329, 316–324. [DOI] [PubMed] [Google Scholar]
- 34.Strohm E, Czarnota GJ and Kolios MC, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 2010, 57, 2293–2304. [DOI] [PubMed] [Google Scholar]
- 35.Moore MJ, Strohm EM and Kolios MC, Opt. Express, 2018, 26, 22315–22326. [DOI] [PubMed] [Google Scholar]
- 36.Lee PY, Costumbrado J, Hsu C-Y and Kim YH, J. Vis. Exp. JoVE, 2012, 3923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Narayanan J, Xiong J-Y and Liu X-Y, J. Phys. Conf. Ser, 2006, 28, 83–86. [Google Scholar]
- 38.Wu H, Rognin NG, Krupka TM, Solorio L, Yoshiara H, Guenette G, Sanders C, Kamiyama N and Exner AA, Ultrasound Med. Biol, 2013, 39, 2137–2146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Yin T, Wang P, Zheng R, Zheng B, Cheng D, Zhang X and Shuai X, Int. J. Nanomedicine, 2012, 7, 895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bing C, Hong Y, Hernandez C, Rich M, Cheng B, Munaweera I, Szczepanski D, Xi Y, Bolding M, Exner A and Chopra R, Sci. Rep, 2018, 8, 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Errico C, Pierre J, Pezet S, Desailly Y, Lenkei Z, Couture O and Tanter M, Nature, 2015, 527, 499–502. [DOI] [PubMed] [Google Scholar]


