Using the Causal Inference Framework to Support Individualized Drug Treatment Decisions Based on Observational Healthcare Data

Abstract

When healthcare professionals have the choice between several drug treatments for their patients, they often experience considerable decision uncertainty because many decisions simply have no single “best” choice. The challenges are manifold and include that guideline recommendations focus on randomized controlled trials whose populations do not necessarily correspond to specific patients in everyday treatment. Further reasons may be insufficient evidence on outcomes, lack of direct comparison of distinct options, and the need to individually balance benefits and risks. All these situations will occur in routine care, its outcomes will be mirrored in routine data, and could thus be used to guide decisions. We propose a concept to facilitate decision-making by exploiting this wealth of information. Our working example for illustration assumes that the response to a particular (drug) treatment can substantially differ between individual patients depending on their characteristics (heterogeneous treatment effects, HTE), and that decisions will be more precise if they are based on real-world evidence of HTE considering this information. However, such methods must account for confounding by indication and effect measure modification, eg, by adequately using machine learning methods or parametric regressions to estimate individual responses to pharmacological treatments. The better a model assesses the underlying HTE, the more accurate are predicted probabilities of treatment response. After probabilities for treatment-related benefit and harm have been calculated, decision rules can be applied and patient preferences can be considered to provide individual recommendations. Emulated trials in observational data are a straightforward technique to predict the effects of such decision rules when applied in routine care. Prediction-based decision rules from routine data have the potential to efficiently supplement clinical guidelines and support healthcare professionals in creating personalized treatment plans using decision support tools.

Introduction

While it is commonly agreed that informed medical decisions require profound understanding of specific benefits and risks of treatments, conclusive information for a specific situation is often lacking.¹ As an example, this was the case in about half of the 3000 treatment options compiled in the BMJ Clinical Evidence compendium 2013 with another seven percent requiring (individualized) trade-offs between benefits and harms.² Thus, when prescribing drugs, clinicians constantly need to make treatment decisions for patients without knowing the best choice of often multiple available options.³ This is especially important if different patients respond differently to distinct treatment options, ie, if treatment effect measure modifiers⁴ such as patient characteristics can cause heterogeneous treatment effects (HTE, for a comprehensive list of abbreviations, see also Suppl. Table 1).⁵ As a consequence, most patients under a given treatment will not experience the average effect.⁶ In addition, individually varying probabilities of treatment response and also of potential treatment-related harm may have to be weighed against each other.^7,8 In such common situations, decisions cannot simply rely on averaged results of clinical trials,^6,9 but rather require individualized decisions to avoid mistakes and are thus depending on the physicians’ preference when personalizing their decisions (precision medicine).¹⁰

A central goal of precision medicine is therefore the derivation of individualized treatment rules (ITR) that maximize the benefit of respective treatments in situations with HTE.^11,12 ITR thus go beyond classical subgroup analyses, which generally stratify by only one or two characteristics to define treatment recommendations.⁶ In ITR, estimated individual treatment responses are used to determine the allocation rule according to the most desirable predicted outcome.¹³ There are numerous examples for heterogeneous responses to treatment that hold the promise for improvements through ITR: a relevant example is the use of antiplatelet drugs such as prasugrel and clopidogrel in secondary prevention after acute coronary syndromes,¹⁴ the choice of which depends on individual patient characteristics. The greatest benefit of prasugrel over clopidogrel was observed in patient subgroups with diabetes and myocardial infarction (STEMI) in whom ischemic events appear to be more effectively reduced than in others without concurrently increasing the risk for major bleeding.¹⁵ In contrast, older patients (despite concomitantly increased effectiveness), underweight patients, or patients with a history of stroke or transient ischemic attack experienced a net harm by prasugrel due to major bleeding events. While the resulting complexity in treatment decision can be mapped by simple decision rules, more complex situations (such as those associated with multimorbidity) can hardly be addressed by generalizing guidelines, especially if numerous diverse subgroup effects contribute to individual treatment success. When multiple subgroup variables impact the outcome, it will be difficult to define a single reference class that should guide the choice of therapy (“reference class problem”).¹⁶ What would be needed instead is a kind of “multivariate” individualized risk estimate,⁶ which can be used for model-assisted decision support by personalized evidence targeting the particular healthcare situation.

Admittedly, treatment decisions have always been personalized, simply because they are made for a particular patient. They could become more precise though and potentially result in improved effectiveness and increased safety, if clinicians integrated not only signs and symptoms, generalized treatment guidelines, personal experience, and patient preferences, but also exploited real-world evidence from routine data that more closely reflect the inter-patient variability and can thus better account for individual patient conditions. Data from randomized controlled trials (RCTs) do not necessarily provide the best basis for investigating HTE, especially if a subpopulation is excluded or underrepresented in these trials.^8,17 While HTE occurs independent of the data source or quality of evidence,^6,8 it is debatable whether highly controlled experimental evidence can be reasonably generalized to fit a particular situation in day-to-day healthcare.⁶ In contrast, routine data collected under exactly these circumstances contain relevant decision factors and could thus enable predicting individual treatment responses and defining suitable decision rules under a causal inference framework.¹⁸ Hence, while modelling HTE is a well-established technique to derive ITR from mainly RCT data, it is rarely applied to non-randomized observational data, in which both effect measure modifiers and confounding variables can be present. Moreover, observational data such as health insurance data have rarely been used to generate missing evidence in drug therapy and have not yet been used to provide individualized suggestions for specific patients. The novelty of this approach thus consists of two aspects. 1) By combining several well evaluated, emerging knowledge-generation techniques, information is to be extracted from health insurance claims data that is hardly ever used for this purpose. 2) In addition, it opens up the additional possibility of developing several competing drug therapy proposals, which subsequently allow for individualization to the needs and preferences of the patient.¹⁹

In our methodological perspective, we show how principles from epidemiology (eg, causal inference framework), statistics, and machine learning can be used to inform clinical medical decisions about drug treatments. In the end, the derived information can be integrated into clinical decision support systems, such as electronic tools that guide physicians during the prescribing process by offering relevant information either on specific risks arising from the prescribed drugs or by suggesting adequate treatment choices and anticipated benefits. Hence, the clinical decision support tool as such offers a structured framework that helps to make clinical treatment decisions according to standardized principles and, thus, reduce variability introduced by variable knowledge and performance of healthcare professionals. This makes it possible to generate more than one treatment option and to create a list of possible treatment strategies with benefits and risk, which helps to reconcile patients’ preferences with individualized treatment options. Along this way, we address the special aspects of the analysis of observational data and present an exemplary situation typical for this field of research, which can be readily adopted in analyses for the improvement of daily healthcare (see also Suppl. Figure 1). We adapt an established simulation framework for a data-generating process involving confounding by indication and effect measure modification. We then apply state-of-the-art methods for simultaneous confounding adjustment, HTE identification, and derivation of ITR as the critical steps to obtain useful predictions for clinical decision support.

State-of-the-Art for Developing Prediction-Based Recommendations

Prediction models attempt to predict a future health state of a patient on the basis of the individual’s current health condition. They are called prognostic if they include patient characteristics to calculate probabilities for a future outcome.²⁰ If they additionally include information influencing the prognosis (eg, treatments), they are called predictive models and patient variables that modulate the effect of treatment effects are called predictive variables.²¹ This means that the effect measure of a (pharmacological) treatment and also the probability of achieving a clinical outcome under these treatments varies individually according to a patient’s health condition or further modifiers. In turn, outcome predictions for individual patients could nicely support and facilitate clinical decision-making by suggesting, which patient should be treated with a particular drug.⁵ Good prediction model accuracy generally ensures good performance of the associated ITR.¹¹ If individuals respond differently to given treatments, such HTE will yield distinct response probabilities whereupon ITR can be defined. In practice, though, clear rules based on these probabilities are often lacking. Moreover, even a predictive model will only become useful once clear decision rules for the clinical context are set.²² To achieve this goal, we provide a working example for individually varying response probabilities due to HTE and apply ITR to these probabilities to decide, which treatment should be preferentially recommended.

Numerous methodological approaches to estimate HTE and define ITR exist and comprehensive reviews can hardly keep pace within this vibrant area of research.²³ Among the multifaceted methods are penalized regression,²⁴ random forests,²⁵ Bayesian additive regression trees (BART),^12,13,26,27 or other machine learning methods as recently summarized.²⁸ However, methods applied to observational data must appropriately handle selection bias, which is all the more relevant in routine claims data, where treatments are administered to patients for a specific reason (ie, the medical indication and co-morbidities).²⁷ Thus, the indication for treatment (and physician knowledge and experience) leads to a selective prescription and confounding by indication can inherently arise if the decision for a particular treatment is also related to the prognosis (ie, benefit and risk of the outcome).^8,29

In the next subsections, we highlight the need for confounder adjustment during HTE exploration, show how individualized recommendations can be obtained, and explain how model-based decision rules would influence the frequency of future clinical events once implemented.

Addressing Confounding and Effect Measure Modification

When models are derived from or applied to observational healthcare data, confounding and effect measure modification can affect their validity and thus require special attention. Confounding occurs when treatment allocation depends on a patient's condition that is also related to the outcome of interest.³⁰ As a result, such confounding by indication can distort the studied drug effect on the outcome if not adequately accounted for. In theory, the actual drug effect is determined by the results a patient would achieve with the different treatment options. However, we do not know what outcome a particular patient would experience under the alternative treatment option, nor can we derive it from averaged treatment effects if treatment allocation was not random. Thus, the underlying problem can be regarded as a missing-data problem because we can only observe the outcome for patients with actually used drugs (formalized in the Roy-Rubin-model^31,32). Formally, we are thus interested in outcomes Y_i of each individual i under a standard treatment (T_i = A) or an alternative (T_i = B) and henceforth denote them Y_i (A) and Y_i (B). The (true) treatment effect for an individual i would correspond to the individual treatment effect (ITE), though not directly observable and denoted as

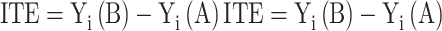(1)

Assuming that individual i actually received treatment B, Y_i (A) is unobservable and called the counterfactual. While it is impossible to calculate the comparisons from Equation (1), one can instead derive the average treatment effect (ATE) from group means defined as

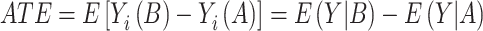(2)

A randomized experiment would provide an unbiased estimate of the ATE, whereas an observational study with confounding by indication would provide biased estimates if treatment allocation was not random but rather depended on patient characteristics with prognostic impact on the outcome. By weighting (or matching) patients according to their propensity (score) for being treated with the respective drug, this source of bias can be reduced by adjusting treatment effect estimates for covariate imbalances between patients treated with drug A or B (ie, treatment allocation in dependence of covariates X). Treatment recommendations can be based on ATE when response-modifying patient characteristics are absent.³³

Effect measure modification is another fundamental issue to be considered in observational data.³⁴ The ITE estimate for an individual i (Equation (1)) by calculating the ATE (Equation (2)) from balanced or weighted groups assumes that all patients respond in the same way (except for unexplained random variability/error). This may not apply if the clinical response is modulated by other (observable) variables Z (called effect modifiers) and if the individual patient deviates significantly from the average through his set of modifiers.³³ A simple example is the different response to prasugrel across several subgroups, which can be attributed to effect modifiers (eg, age, weight, and medical history). More complex cases are often not well described, also because they neither have been identified nor comprehensively evaluated nor adequately reported. To provide an initial glimpse into this emerging field of research, Table 1 lists further candidate effect modifiers extracted from the literature. It should be noted that effect measure modification can arise from both varying baseline risks (making an averaged treatment more or less effective) and varying effectiveness itself.⁶

Table 1.

Examples for Candidate Effect Modifiers Identified from the Literature

Drug (Class)	Potential Effect Modifiers	Major Adverse Events	Exemplary Reference(s)
Anticoagulants (oral)	History of thromboembolism Co-medication	Thromboembolic events Major bleeding	[54,55]
Antidepressants	Sex	Healthcare utilisation (eg, hospitalizations)	[56]
Antidiabetics	History of cardiovascular disease	Major cardiovascular events	[57]
Antithrombotic drugs/antiplatelets (eg, prasugrel)	Co-medication, age Diabetes	Major bleeding Major cardiovascular events	[15,58,59]
Beta-Blockers	Age Heart failure after myocardial infarction	Cardiovascular events Mortality	[60,61]
Drugs acting on the renin-angiotensin-aldosterone-system	Previous stroke Age	Cardiovascular events Mortality	[62,63]
Disease-modifying anti-rheumatic drugs	Sex Disease duration	Non-persistence as a proxy for treatment failure	[64]
Statins	Chronic kidney disease/dialysis Age	Cardiovascular events	[65,66]
Tyrosine kinase inhibitors	Co-medication (eg, proton-pump inhibitors)	Mortality	[67]

Note: The listed examples were identified from a systematic literature search which was adapted from Schandelmaier and co-workers⁶⁸ and extended by adding search terms for the respective drug class.

In many cases, ATE will result in a potentially inaccurate estimate of individual responses. To account for an effect measure modification, we can condition the ATE to the effect modifiers Z to obtain the conditional average treatment effect (CATE) by

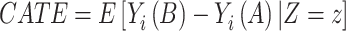(3)

Which is achieved by predicting the respective outcomes (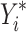) depending on the effect modifiers Z as predicted individual treatment effect (PITE):

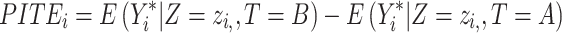(4)

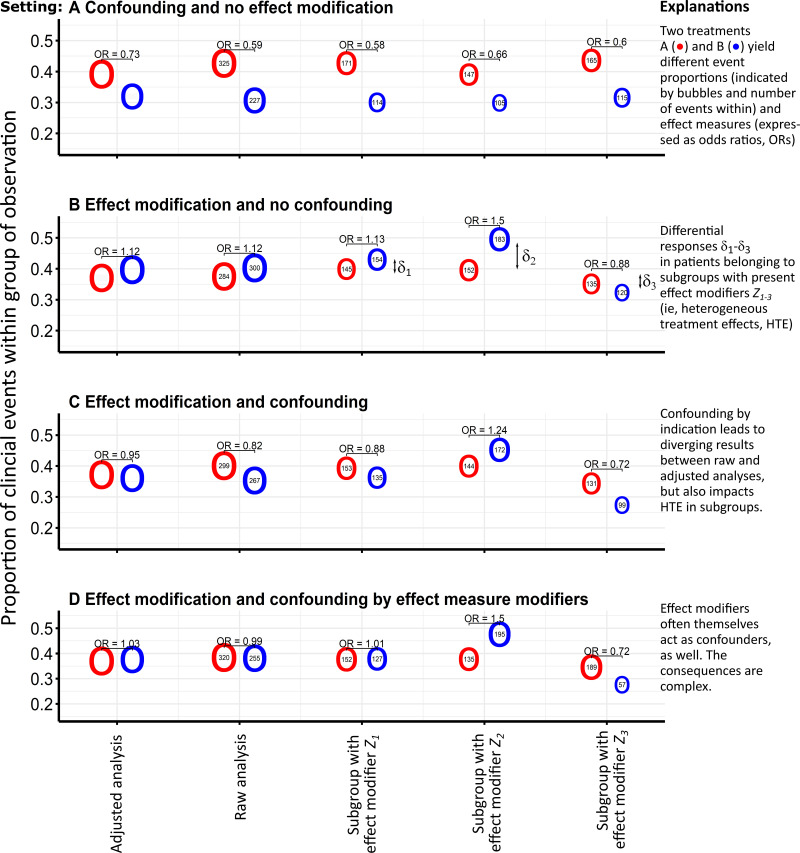
To illustrate the two concepts of confounding and effect measure modification, we adopted the simulation framework proposed by Anoke and co-authors.²⁶ We acknowledge that a real-data example would yet require pre-validated exposure, covariate, and outcome definitions, and would require that HTE are present and are sufficiently large to impact differential ITR (see also Suppl. Figure 1). By simulating such a setting with a known data-generating process, we can be sure to have met these requirements and can readily interpret its results. In particular, we simulated binary outcomes in dependence of nine covariates acting as (continuous) confounders (X), (binary) effect modifiers (Z), or both in 1500 virtual patients (Figure 1). Thus, the data presented in Figures 1 and 2 originate from a simulation study, where treatment allocation may depend on covariates (P_treatment = expit(l₁) with expit(x) = e^x/(1 + e^x) = 1/(1 + e^−x) as the logistic function and the linear predictor l₁ as a combination of covariate influences). Likewise, the likelihood for the binary outcome may be defined by a similar linear predictor (P_outcome = expit(l₁)) including the treatment (main) effect T, further (prognostic) covariates (X and Z), and finally predictive covariates as indicated by product terms T · Z (ie, in a multiplicative interaction). The source code with actual parameters and the simulated data set are available upon request from the first author. In brief, the simulated main treatment effect is identical in all scenarios, but is further modulated by complementary interaction effects with the effect measure modifiers. In Figure 1, the net treatment effect is visualized by the different event proportions attributed to the red and blue bubbles indicating treatments A and B, respectively. The corresponding odds ratio (OR) is proportional and may differ from raw analyses and multivariate analyses adjusted for confounding (first column of the categorical x-axis). Subgroups defined by effect modifiers Z can show pronounced deviations from averaged mean effects in case of HTE presence, which can be further distorted by confounding.

Figure 1.

A simulation study to illustrate the concept of confounding by indication and effect measure modification.

Notes: Presented data originate from a simulation of binary outcomes in dependence of nine covariates acting as (continuous) confounders (X), (binary) effect modifiers (Z), or both in 1500 virtual patients. The simulation framework thus addresses a typical situation of observational data from health insurance claims. The panels below show the results for each simulation scenario (A–D), where event numbers (predicted in adjusted analyses) are given within circles referring to both treatment options A (red) and B (blue) (odds ratios were derived from logistic regression models, the size of the circles is proportional to the absolute numbers of patients, whereas no statistical comparison between the groups is shown).

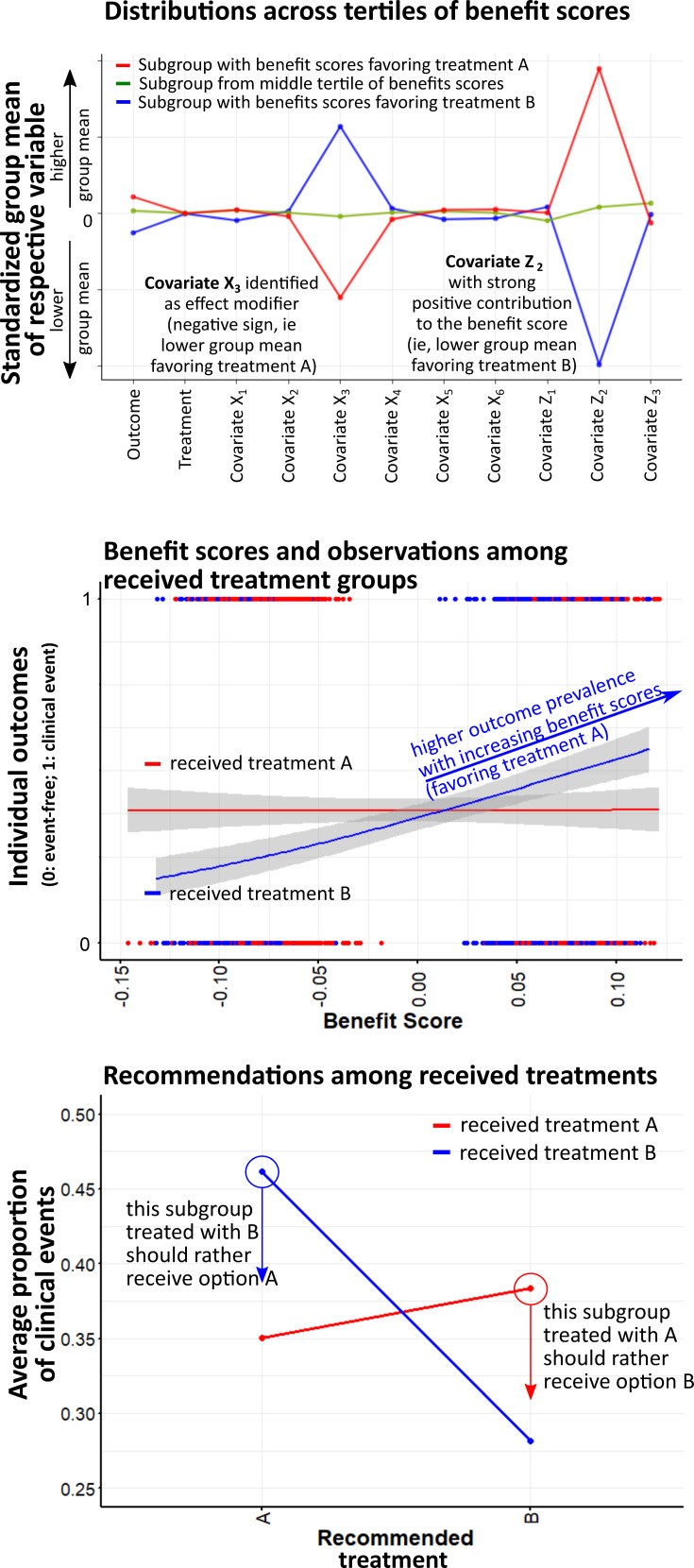
Figure 2.

Prediction of individual treatment effects and recommendations from individualized treatment rules.

Notes: Conditional average treatment effect (CATE) estimation was conducted via LASSO-based penalized regression to provide the predicted individual treatment effect (PITE) expressed as benefit scores.^24,35 A decision rule would suggest selecting treatment A if the benefit score is greater than zero. Classifying individuals according to their benefit scores will yield differing group means in the variables that are effect modifiers (top). Thus, patients under current treatment B (indicated in blue color) may also be recommended the alternative; this applies to those patients having received treatment B whose benefit scores are greater than the decision threshold set to zero (mid). This ITR therefore defines an action space where outcome frequencies above the threshold could be presumably reduced by selecting the alternative. Likewise, this also applies to the opposite case, where such a re-assignment of treatment could reduce outcome frequencies suggesting option B at benefit scores below the threshold of zero (mid, bottom).

Deriving Individualized Treatment Rules

Whenever a prescriber expects that a certain treatment option is more effective than another, confounding by indication occurs.⁸ Physicians are more likely to select treatment options with larger expected benefit, smaller treatment-related harm, and a favourable benefit–risk ratio. If a patient risk profile will modify treatment effects and will thus cause or contribute to interpatient response differences, the crucial patient variables will act as confounders and effect modifiers (ie, representing the most probable scenario D in Figure 1).³⁴

It is therefore essential to account for confounding by indication and effect measure modification when estimating the CATEs or predicting ITEs from observational data (Equations (3) and (4)). While propensity scores represent a well-established strategy to adequately deal with confounding, effect measure modification needs to be accurately quantified to obtain individual response probabilities to possible treatment options. The resulting response probabilities for a given patient can be compared to estimate where treatment benefit is largest. The comparison of the individual response probabilities can be termed benefit score.³⁵

In order to quantify effect measure modification and estimate benefit scores, the literature offers a wide range of regression techniques or supervised learning methods in statistics and machine learning.²⁸ Basic (S-learner or T-learner) and advanced approaches (X-learner) have already been introduced and are promising options to quantify effect measure modification.^5,25,26 The T-learner²⁵ approach fits “two” regression models or (random-forest) trees for patient subgroups treated with either option A or B and thus yields corresponding outcome probabilities. This results in two probabilities of outcome for each patient, one estimated for the treatment actually received and one for the treatment with the alternative option (which provides the potential outcome). The differences between the two probabilities are the expected treatment benefits or risks for individual patients based on their covariates.³⁶ In addition to differences in probabilities, the extended X-learner approach also considers differences between potential and observed outcomes to provide final response estimates.²⁵ Another basic approach called S-learner uses only a “single” estimator to derive response probabilities for all treatment options, for example derived from a single parametric model or single random forest.²⁶ In such parametric models, HTE can be characterized by the interaction of the treatment with (one or more) patient characteristics.

In our example, we apply the framework proposed by Chen and co-authors,³⁵ which uses benefit scores to rank patients according to their PITEs (Equation (4)). In a penalized regression model, the treatment-covariate interactions are selected by the so-called “least absolute shrinkage and selection operator” (LASSO).³⁷ To derive PITEs, these treatment-covariate interactions are the only component beyond the main effect to obtain individual response probabilities, which we denote as benefit scores. These benefit scores thus indicate which patients rather profit from treatment options A or B. In the parametric regression approach, they can stem from a linear predictor with LASSO-selected effect modifiers.²⁴ Given our known data-generating process with linear effect terms, we chose the parametric regression approach also for simplicity. It should be noted that non-linear effects can potentially be predicted much better by machine learning approaches such as random forests, but especially BART^12,13,26,27 as one of the most prominent techniques when deriving ITR from predictions in situations with HTE.¹³

Figure 2 illustrates ITE predicted from a penalized regression model and the resulting treatment recommendations for our exemplary situation with two treatments A and B based on the simulated data from simulation setting D (Figure 1). The benefit scores indicate individual responses to both treatments and guide treatment recommendations based on a decision threshold. By decision threshold, we mean that a certain recommendation results from a cut-off value in the individual response probability. If benefit scores are used to define subgroups, they typically differ in group means of the variables identified as effect modifiers (Figure 2 top). Outcome frequencies might differ across the range of calculated benefit scores for each observed treatment (middle), suggesting that partial re-assignment of these options could have prevented clinical events (bottom).

These aspects directly relate to ITR defined as recommendations that are expected to maximize patient benefit when applied to a population. In its most basic form, an ITR could mean to exclusively address beneficial effects and use a decision threshold above and below which different treatments are suggested. However, treatment assignment should also consider associated risks. For example, a certain treatment option might bring a particular patient substantial expected benefit, but might concurrently increase his likelihood for adverse drug events. In this case, both probabilities (ie, for benefit and harm) are important for decision-making. In addition to the benefit score, treatment effect models should also be developed for adverse events thus providing a “harm score” following similar principles. Then, both scores can be weighed against each other with a threshold to be (empirically) defined. This was applied to a situation for individually weighing the benefit and harms of intensified blood pressure control.^7,38 Thus, the decision threshold could be obtained from a binary logit model on the composite endpoint of the clinical outcome and adverse event with predicted probabilities for benefit and harm as covariates.⁷

Projecting Clinical Utility

ITR are especially useful when HTE is present and large enough to be of clinical relevance. While the model performance in assessing HTE can be described by performance metrics such as the concordance-for-benefit statistics,³⁹ it is also of great interest to quantify the impact of ITR on the implementation of a decision tool. Once threshold-based ITR have been defined to identify the best possible treatment option, their impact on clinical outcomes in the presence and absence of such an implemented decision aid can be projected. A controlled trial would require many additional efforts, but clinical utility of the model can be projected by examining how patient outcomes would have been affected if treatment decisions had been based on prediction-based decision rules compared to the standard of care.⁴⁰ Thus, a prediction-driven trial could be emulated to evaluate the clinical utility of a prediction-based decision rule also in routine claims data.^40–42 In particular, a randomized experiment between the decision aid and standard of care can be emulated in a claims data sample and potential outcomes can be predicted by means of g-computation.⁴³ Such innovative approaches clearly help elucidating the value of prediction-based treatment recommendations albeit without providing ultimate proof.

Discussion

Data-informed medical decision-making for an individual patient requires consideration of the patient’s unique constellation in co-morbidities, co-medication, and other relevant modifiers. Observational data from health insurance claims provide large longitudinal, continuously growing datasets containing fine-grained information about representative patient populations, interventions, and outcomes.²⁵ Such information could be used to weigh risks and benefits of different treatment options and to inform physicians and patients in a shared decision-making process.³ Using documented evidence in routine data, our decision support system would extract and weight possible drug treatment strategies for the complex situation of an individual patient. Based on these data, we suggest to clearly communicate the estimated likelihood of different outcomes, to take into account the patient’s opinion and preferences, and, based on this, to provide treatment advice to support patient and physician in choosing an appropriate (drug) treatment option. Because claims data are a rather rich and comprehensive data source, the methodology described in this paper appears well suited and readily applicable. However, we highlight how necessary it is to simultaneously adjust for confounding when assessing HTE to derive treatment recommendations from such observational data sources. This is particularly important because state-of-the-art methods are rarely applied to non-randomized data.¹⁷

Several use cases describe how decision support can be based on predictive models.^44–46 Predictive models for individual treatment response are particularly useful if individual patients respond differently to pharmacological treatments in a clinically meaningful way. On the one hand, it is a core premise for personalized medicine meaning that the treatment effect varies across individuals depending on particular baseline characteristics (ie, effect modifiers).⁴⁷ On the other hand, individual tailoring of therapies is only advantageous if resulting effect measure modifications are large enough to cause meaningful clinical differences for the patients.⁴⁸ However, one has to consider at least two basic limitations of routine (claims) data. First, relevant information on potential effect modifiers and outcomes is required, which usually excludes laboratory measurements or estimates of quality of life in this data source. This is also important after the implementation of a model, because such additional effect modifiers can actually become available from other sources, so that more precise predictions can be made that go beyond the possibilities of pure routine data. Second, treatment effect modifiers should only be studied in situations with exposure–outcome relationships allowing for valid inferences in routine data. Although health insurance claims contain a wealth of information, it is not always clear how accurate they are with respect to co-morbidities or outcome classification. Although of importance, severity of disease is often difficult to determine, and patient preferences are not available at all. In the end, results obtained from claims databases need to be robust, though, and comparable to gold-standard results from RCTs that could be used for pre-validation. By pre-validation, we mean that promising (literature) findings must demonstrate the consistency in routine claims data and thus indicate that the claims data are suitable for further steps of modelling and HTE assessment. If main effects from RCTs can be consistently replicated in routine claims data, the particular clinical situation can be considered sound for the investigation of individual effects. If the data source turns out to be suitable, it may be further trimmed according to the characteristics of a particular patient's characteristics before the described steps of predictive modeling begin.⁴⁹

Prognostic models and predictive models are abundant in clinical research with steadily growing numbers of articles.⁴⁰ However, they are only rarely applied in health research, reflecting the dilemma that most of these developments never reach routine patient care.⁵⁰ One obvious reason may be that most developments do not define ITR beyond mere probabilities and the models thus lack the necessary “action space” defined as a mapping of the probabilities to the set of all possible medical decisions.⁴⁰ In our envisaged framework, we also present the possibility of extrapolating the clinical utility in the selection of ITR; this could hopefully overcome the reluctance of researchers to define clear “action spaces”. This could indeed help to assess how different decision thresholds affect clinical outcomes. In any case, it matters how the information is presented to the clinician or patient:³ for recommendations to be correctly followed, they need to be readily understood from the visualizing presentation format. Finally, barriers to successful implementation should be addressed when it comes to developing useful predictive models to make treatment decisions based on routine data. Obstacles to the introduction of decision-making rules could arise before implementation (eg, skepticism towards new technologies, conviction that clinical judgment is superior to prediction-based decision rules), during (eg, lack of algorithms to treat potential inconsistencies with the best medical treatment from guideline recommendations and resulting decision conflicts, alert fatigue⁵¹), or after using a decision-making rule (eg, tool is not easy to use, absence of supportive infrastructure, fear of unintended consequences).^19,22 Therefore, the clinical usefulness should be described in terms of how clinical decision-making can be improved by such a predictive decision support tool⁵² and include how the information from predicted probabilities should be presented so that it is well accepted by its users,³ and how the predictive information influences the clinicians’ decisions.^42,43

In summary, our methodological perspective assumes that individual patients respond differently to pharmacological treatments and that thorough (quantitative) knowledge of effect modifiers will help predicting individual responses to medicines (personalized medicine). Validated decision support could efficiently complement clinical guidelines and support the healthcare professional when interpreting complex patient data, weighing the benefit and risks of multiple treatment options, and trying to incorporate patient preferences to finally design a personalized treatment plan. The ultimate goal would be to select the most efficacious therapies (to avoid nonresponse), avert adverse drug events (to avoid harm), and thus reduce costs and improve relevant endpoints (ie, survival or quality of life) for patients and other stakeholders.⁵³

Author Contributions

ADM was responsible for data generation, data analysis, and visualization of results. ADM and WEH drafted the manuscript, all authors critically revised the manuscript. All authors made substantial contributions to conception and design, acquisition of data, or analysis and interpretation of data; took part in drafting the article or revising it critically for important intellectual content; agreed to submit to the current journal; gave final approval of the version to be published; and agree to be accountable for all aspects of the work.

Disclosure

Andreas D. Meid is funded by the Physician-Scientist Programme of the Medical Faculty of Heidelberg University. The funding body did not play any role in the design of the study and collection, analysis, and interpretation of data and in writing the manuscript.

Hanna M Seidling reports grants from Chambers of pharmacists Baden-Württemberg, Chamber of pharmacists Nordrhein, Chamber of pharmacists Hessen, Chamber of pharmacists Niedersachsen, Klaus-Tschira-Stiftung, Förderinitiative Pharmazeutische Betreuung e.V., Dosing GmbH, ABDA – Bundesvereinigung Deutscher Apotheker e.V., g-BA, BMBF, European Commission Horizon 2020, AOKPlus, Dr. August und Dr. Anni Lesmüller Stiftung, personal fees and non-financial support from ADKA e.V.; EAHP; Chamber of Pharmacists, Hessen; Chamber of pharmacists, Baden-Württemberg, Chamber of pharmacists, Westfalen-Lippe, Chamber of pharmacists Nordrhein, Chamber of pharmacists Bavaria, DPhG, ABDA, omnicell, Chamber of pharmacists Niedersachsen, and Chamber of pharmacists Thüringen, Govi Verlag, Deutscher Apotheker Verlag, Wissenschaftliche Verlagsgesellschaft Stuttgart, and Bundesgesundheitsblatt, and non-financial support from VKliPha; AkdÄ; GSASA, APS e.V., NHS, ESCP, BAK, ÄZQ, SFPC, Dosing GmbH, Karolinska Institutet, University of Bonn, and University Hospital Hamburg, outside the submitted work.

Walter E Haefeli reports grants from Landesapothekerkammer BW, Dosing GmbH, Heidelberg, Gemeinsamer Bundesaussschuss (HIOPP, Proper med, PIM Stop), and Smooth ClinicalTrials Ltd., research funding from Sumaya Biotec GmbH & Co. KG, Klaus Tschira Stiftung, Vaxxim GmbH, AOK Baden-Württemberg, Basilea Pharmaceutica Ltd., and Elsevier GmbH, EU Horizon 2020 (PRESTIGE-AF), personal fees from CHIESI GmbH, PIQUR Basel, and Regierungspräsidium Stuttgart, personal fees and non-financial support from BayerPharma AG, personal fees, non-financial support, speaker fee, and traveling expenses from Aqua Institute Göttingen, speaker fee and traveling expenses from Aspen Europe GmbH, Diaplan, MSD Sharp & Dohme GmbH, AstraZeneca GmbH, Grünenthal GmbH, KWHC GmbH, Novartis, Berlin-Chemie AG, and Doctrina Med GmbH & Co.KG, grants and non-financial support from Actelion GmbH, speaker fee and research funding from GSK GER/UK/Slovakia/France/, grants, research funding, speaker fee, and traveling expenses from Daiichi Sankyo GmbH, research funding, speaker fee, and traveling expenses from Bristol-Myers Squibb GmbH, speaker fee, traveling expenses, and consultancy services from Boehringer GmbH, non-financial support, speaker fee, and traveling expenses from Pfizer GmbH, traveling expenses from University Frankfurt, research funding and consultancy services from Heidelberg ImmunoTherapeutics GmbH, personal fees, consultancy services, and traveling expenses from Fresenius Medical Care, consultancy services from Ligatur Verlag and Stiftung Warentest, editorship/authorship royalties from Thieme Verlag and Wissenschaftliche Verlagsgesellschaft Stuttgart, grant numbers TI02.001, TTU05.901,O1ET10048, 01GK0702 from the German Federal Ministry of Education and Research (BMBF) (projects entitled DZIF, ESTHER, Agewell, LipORa, Prima LiveR) J

The authors report no other potential conflicts of interest for this work.