Automated mapping of laboratory tests to LOINC codes using noisy labels in a national electronic health record system database

Abstract

Objective

Standards such as the Logical Observation Identifiers Names and Codes (LOINC^®) are critical for interoperability and integrating data into common data models, but are inconsistently used. Without consistent mapping to standards, clinical data cannot be harmonized, shared, or interpreted in a meaningful context. We sought to develop an automated machine learning pipeline that leverages noisy labels to map laboratory data to LOINC codes.

Materials and Methods

Across 130 sites in the Department of Veterans Affairs Corporate Data Warehouse, we selected the 150 most commonly used laboratory tests with numeric results per site from 2000 through 2016. Using source data text and numeric fields, we developed a machine learning model and manually validated random samples from both labeled and unlabeled datasets.

Results

The raw laboratory data consisted of >6.5 billion test results, with 2215 distinct LOINC codes. The model predicted the correct LOINC code in 85% of the unlabeled data and 96% of the labeled data by test frequency. In the subset of labeled data where the original and model-predicted LOINC codes disagreed, the model-predicted LOINC code was correct in 83% of the data by test frequency.

Conclusion

Using a completely automated process, we are able to assign LOINC codes to unlabeled data with high accuracy. When the model-predicted LOINC code differed from the original LOINC code, the model prediction was correct in the vast majority of cases. This scalable, automated algorithm may improve data quality and interoperability, while substantially reducing the manual effort currently needed to accurately map laboratory data.

BACKGROUND AND SIGNIFICANCE

Multi-site, aggregate data sources are valuable for research, quality, public health, and creating large evidence bases to answer clinical questions.^1,2 Before clinical data can be integrated, institution-specific information must first be mapped to a standardized terminology.^3,4 Laboratory data, an essential domain for assessing patient outcomes, map to the standard code system Logical Observation Identifiers Names and Codes (LOINC^®).⁵ However, mapping laboratory tests to LOINC codes is time consuming and resource intensive,^6–8 highlighting the need for automated methods to facilitate the mapping process.

Electronic health record (EHR) systems are a rich source of data accumulated through routine clinical care.¹ Secondary use of EHR data for analytics, research, quality and safety measurement, and public health is increasingly prevalent.^1,9,10 The Health Information Technology for Economic and Clinical Health (HITECH) Act¹¹ and the meaningful use incentive program¹² facilitated widespread EHR adoption.¹³ Consequently, multi-site data aggregation and centralization are feasible and increasingly common. These aggregate data sources are important for research, quality, public health, and commercial applications.¹ For example, in the public health domain, aggregate data analysis can facilitate early detection of emerging epidemics.¹

Common data models (CDMs), which standardize the format and content of observational data, hold promise for facilitating integration of disparate data sources in healthcare. This process requires mapping institution-specific information to a standardized terminology, without which clinical data cannot be integrated, shared, or interpreted in a meaningful context.^3,4

Laboratory data are essential for performing comparative effectiveness research, assessing patient outcomes, and adverse event monitoring. The standard code system for laboratory observations, LOINC,⁵ aims to facilitate data aggregation.¹⁴ Historically, EHR implementations have used proprietary data mapping with locally defined, idiosyncratic, ambiguous identifiers¹⁵ that make mapping to standard terminologies challenging. Furthermore, even when LOINC codes are used, they are often incorrectly mapped.⁷ As a result, accurately mapping these data to standards for incorporation into CDMs is time consuming and resource intensive.¹⁶ Because local laboratory test information contains the basic information required to map to a LOINC code, the mapping process can theoretically be automated. However, no truly automated methods currently exist. Previous studies attempting to automate LOINC mapping relied upon a local corpus or lexical mapping.^17–19 The corpus method relies upon manually mapping local terms to LOINC codes (eg, a local code “BILID” with description “Bilirubin, Direct” maps to LOINC code 1968-7). The lexical method attempts to map local terms to standard vocabularies, such as the Unified Medical Language System (UMLS) or LOINC (eg, “AST” maps to Aspartate Transaminase in UMLS with Concept Unique Identifier [CUI] C0004002). Previously published corpus-based algorithms correctly classified the single best LOINC code 50% to 79% of the time across 3 to 5 institutions.^17,18 The lexical algorithm correctly mapped 57% to 78% of concepts (average 63%).¹⁹ While the generation of potential mappings in the latter study was automated, the method still required an expert/clinician to choose the correct mapping from a list of candidates. The Regenstrief LOINC Mapping Assistant (RELMA^®) provides a semi-automated platform for mapping local terms to LOINC fields (https://loinc.org/relma), but requires user input when test names or units are not in a normalized format.

Noisy labels have recently gained attention^20,21 because they alleviate the need to perform time-consuming manual gold standard adjudication for label assignment prior to training a model. Noisy labels refer to incorrect class labels resulting from an imperfect labeling process (eg, serum creatinine labeled as urine creatinine). Implicit in noisy labeling, a large volume of training data is necessary to compensate for inaccuracy in labels (noise-tolerant learning).^22,23 Previous studies suggest large-volume, imperfectly labeled training data can compensate for label inaccuracy and outperform models trained on smaller “clean” datasets,^24,25 even when up to 40% of labels are incorrect.^26,27 To our knowledge, no prior studies have used noisy labels to automate mapping of laboratory tests to LOINC codes. Using a dataset containing a mix of labeled and unlabeled data with an unknown labeling error rate, we hypothesized that noisy LOINC labels could be leveraged in a machine learning algorithm to automate mapping of unlabeled data and reclassification of incorrect mappings within labeled data.

MATERIALS AND METHODS

Study setting and design

We collected laboratory data from the Department of Veterans Affairs (VA) Corporate Data Warehouse, which aggregates data from each VA facility’s Veterans Health Information Systems and Technology Architecture (VistA) and Computerized Patient Record System (CPRS) instances.^28,29 Data included all inpatient and outpatient laboratory results from 130 VA hospitals and clinics collected between January 1, 2000, and December 31, 2016. This study was approved by the Institutional Review Board and the Research and Development Committee of the Tennessee Valley Healthcare System VA.

Data collection and aggregation

Within each VA site, we selected the 150 most commonly used laboratory tests with numerically reported results (eg, hemoglobin, sodium). We aggregated the raw data—comprised of individual patient-level measurements—by grouping on the following elements: 1) laboratory test name identifier, 2) specimen type identifier, 3) units of measurement, and 4) LOINC code. Within these groupings, we summarized the numeric test results using mean, median, percentiles (5th, 25th, 75th, 95th), minimum, maximum, count, and normalized frequency (the percentage of all laboratory results at the site attributed to the specific test). Each data row formed by aggregation comprised an instance (example shown in Supplementary Table S1).

Ancillary data sources

We used the publicly available LOINC^® table (version 2.56) for automated feature generation, restricting to the laboratory and clinical observation class types.⁵ We also used the UMLS^® REST API to generate model features containing UMLS CUIs.³⁰

Feature engineering

Automated text processing

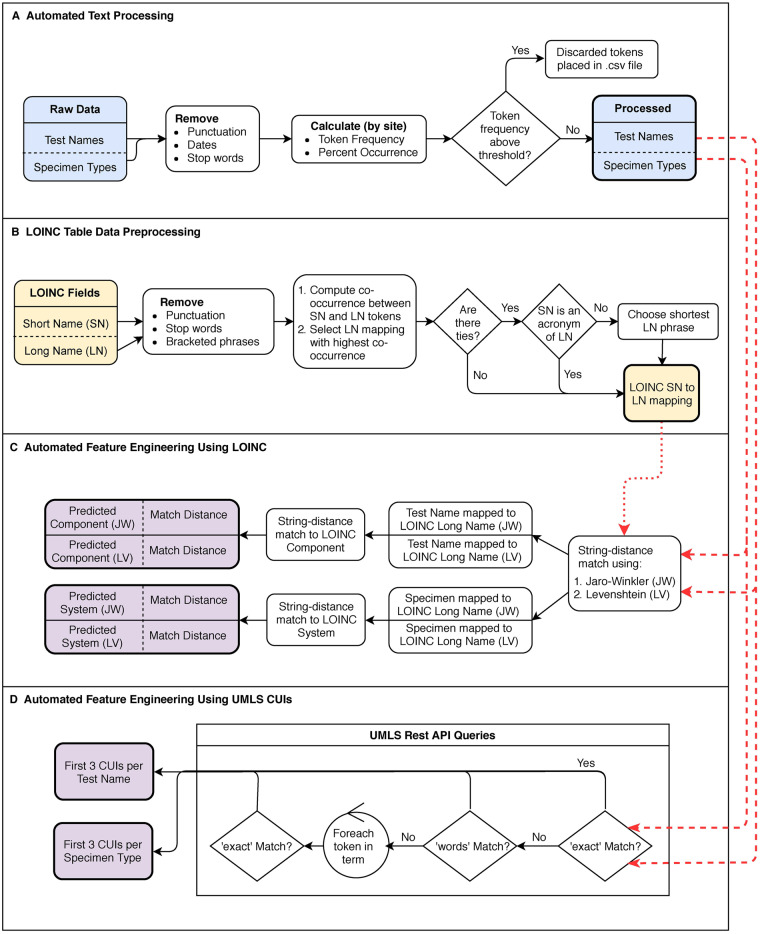
We processed source data test name and specimen type by first removing punctuation, dates, and stop words (Figure 1A). For each token (a string of one or more alphanumeric characters separated by white space) we computed the percent occurrence as a function of the total number of tokens per site. Using a tunable threshold (4% in this study based on manual inspection), tokens occurring above a certain frequency within a site were removed, because high-frequency tokens (ie, “sendout”) may be uninformative for determining what a particular test signifies (Supplementary Table S2).

Figure 1.

A) Raw source data test name and specimen type automated text processing. B) From the publicly available LOINC table, processing of LOINC Short Name (SN) and Long Name (LN) fields and mapping of SN tokens to LN tokens/phrases, C) String distance-matching tokens from the processed source data test names and specimen types (from A) to the tokens derived from the LOINC data preprocessing step (from B), with final mapping to the predicted LOINC Component and System fields. D) Using the UMLS REST API to obtain UMLS CUIs for test names and specimen types (from A).

Feature engineering using UMLS CUIs

With the processed text, we used the UMLS REST API to obtain UMLS CUIs for test names and specimen types, respectively (Figure 1D). We attempted to map the test name or specimen type to a UMLS CUI using the “exact” match search type. If no results were returned, we attempted a “words” search, in which a term is broken into its component parts, and all concepts containing any words in the term are retrieved.³¹ If neither of the initial searches returned results, we iterated over the individual tokens in the test name and performed an “exact” match search for each token. For both test name and specimen type, we retained the first 3 CUIs as model features (Table 1).

Table 1.

Model features

Text features	Numeric features
Test Name mapped to LOINC Long Name (JW)	Test result 5th percentile
Test Name mapped to LOINC Long Name (LV)	Test result 25th percentile
Specimen Type mapped to LOINC System (JW)	Test result median
Specimen Type mapped to LOINC System (LV)	Test result mean
Predicted LOINC Component (JW)	Test result 75th percentile
Component Match Distance (JW)	Test result 95th percentile
Predicted LOINC Component (LV)	Test result minimum
Component Match Distance (LV)	Test result maximum
Predicted LOINC System (JW)	Normalized test frequencya
System Match Distance (JW)
Predicted LOINC System (LV)
System Match Distance (LV)
Units
UMLS Test CUI #1
UMLS Test CUI #2
UMLS Test CUI #3
UMLS Specimen CUI #1
UMLS Specimen CUI #2
UMLS Specimen CUI #3

Abbreviations: CUI, Concept Unique Identifier; JW, Jaro-Winkler; LOINC, Logical Observation Identifiers Names and Codes; LV, Levenshtein; UMLS, (Unified Medical Language System).

^aNormalized test frequency calculation = (Test frequency/Total number of test results within site) x 100.

Automated LOINC table data preprocessing

From the publicly available LOINC table, we preprocessed the Short Name and Long Name fields by removing punctuation, stop words, and bracketed phrases (Figure 1B and Supplementary Figure S1). We computed the co-occurrence between each LOINC Short Name token and a sliding window of 1 to 3 LOINC Long Name tokens (Supplementary Figure S2), using an upper bound of 3 because the long-form components of most medical acronyms are ≤ 3 words. To create a cross-walk from LOINC Short Name tokens/acronyms to Long Name tokens/phrases, we selected the pairing with the highest count by co-occurrence (Supplementary Figure S3).

To handle abbreviations contained in the LOINC System field, we used string distance matching with the Jaro-Winkler metric^32–34 to find the corresponding words with the smallest edit distance in the LOINC Long Name field. We mapped the System token to the resulting distance-matched Long Name token and/or acronym expansion.

Feature engineering using LOINC

Using the Jaro-Winkler and Levenshtein metrics,^32–35 we string distance-matched tokens from the processed source data test names and specimen types to the LOINC Long Name token(s) with the smallest edit distance (Figure 1C). For each test name and specimen type, we concatenated the resulting Long Name tokens to form the 2 “Test Name mapped to LOINC Long Name” features (1 for each distance-matching metric) and the 2 “Specimen Type mapped to LOINC System” features. We distance-matched the resulting mapped test names and specimen types to the LOINC Component and System fields, respectively. We included the predicted Component and System (from the 2 string distance-matching metrics) and their corresponding match distances as model features (Table 1).

Data partitioning

We held out instances with missing specimen type and/or LOINC code in the unlabeled dataset for a separate analysis. We combined data instances containing LOINC codes used at only 1 site or <10 times by test frequency with the unlabeled dataset for reclassification. In the remaining labeled dataset, we partitioned data for 5-fold cross-validation using splits by sites.

Automating LOINC equivalence

Three levels of interoperability may exist between 2 LOINC codes.³⁶ In Level I interoperability, the LOINC Component, Time Aspect, Scale, Property, System, and Method are identical for 2 codes. In Level III interoperability, 2 codes differ only in the LOINC Method (Supplementary Table S3). In the latter scenario, 2 codes can be used interoperably (albeit, with some meaning loss) in cases in which the method is not considered important. In this study we did not consider Level II interoperability, which requires data processing to make codes comparable (eg, log conversion).

To automate the creation of equivalent LOINC code sets, we grouped LOINC codes by Component, Property, Time Aspect, System, and Scale. Within these groups, we created key-value pairs for groups with Level I (identical methods) or Level III (differing methods) interoperability (full description in Supplementary Table S3). Using the LOINC group keys, we “rolled up” all LOINC codes present in the original source data into corresponding LOINC keys where possible. If the original LOINC codes were not part of an interoperable LOINC group, we retained the original LOINC code as the LOINC key.

Machine learning models

We implemented logistic regression (L1 penalized,³⁷ L2 penalized,³⁸ and L1/L2 penalized³⁹), a random forest⁴⁰ multiclass classifier, and a 1-versus-rest ensemble of binary random forest classifiers. Model building and analyses were conducted using scikit-learn in Python.⁴¹ We tuned all models with 5-fold cross-validation using the weighted F1 score as the loss function.

Model performance

Using 5-fold cross-validation by site in the labeled dataset, we estimated performance for each model with the following measures: accuracy, weighted F1 score,^41,42 and micro-averaged F1 score.⁴¹ We included accuracy for intuitive interpretation. Since accuracy can be optimistic with class imbalance (simply predicting the labels of the most common classes), we examined the weighted F1 score and the micro-averaged F1 score. We also calculated expected accuracy with random guessing in proportion to label prevalence.

Within each of the 3 measures (accuracy, weighted F1, and micro-averged F1), we evaluated performance differences among the 5 models using a 1-way anlysis of variance (ANOVA),⁴³ followed by independent 2-sample t tests⁴⁴ between each pair of models when findings from the ANOVA test were significant (P < .05). We also calculated 95% confidence intervals for the performance measures of each of the 5 models using their mean and standard deviation from the 5-fold cross-validation.

Model fitting and label assignment

The model has 2 potential use cases: 1) predicting labels when new sites are added to an existing model, and 2) reclassifying incorrect labels in retrospective multi-site data. We fit the best-performing model to the training data during cross-validation (CV Model) for the first use case, and to the full labeled dataset (Full Model) for the second case. Using the CV Model and the Full Model, we obtained the predicted LOINC keys as described above. In cases in which the predicted LOINC code was not identical to the original LOINC code, but the predicted LOINC code was the key for the group containing the original LOINC code, we retained the original LOINC code. When the predicted code was not interoperable with the original LOINC code, we retained the predicted LOINC code.

Subsequently, the CV Model and the Full Model were used to predict LOINC codes on the holdout dataset comprised of instances with either missing or infrequently used LOINC codes.

Manual validation

We performed manual validation by randomly sampling 2 instances from each of the 130 sites in both the labeled and unlabeled datasets. Using the cumulative sum of test frequency within a site, we selected 1 instance with test frequency ≥50%, and 1 instance with test frequency <50% (Supplementary Table S4). Adjudication label categories are described in Supplementary Tables S5–S7. We examined the accuracy of the labels predicted in the CV Model and the Full Model. Additionally, to explicitly evaluate model utility for reclassifying incorrect LOINC codes in the dataset, we obtained a sample of 260 instances in the labeled dataset where the predicted LOINC code (Full Model) differed from the original source data LOINC code. Two clinicians manually adjudicated a total of 780 records. We report the inter-annotator agreement using Cohen’s kappa. In the case of adjudication disagreement, we used consensus agreement to determine the final adjudication.

Examining model performance by dataset characteristics

From the full labeled dataset, we randomly sampled between 5 and 125 sites (in increments of 5 sites) and fit a random forest multiclass classifier with 5-fold cross-validation split by sites to assess model performance. Within each sampled data subset, we calculated the number of distinct LOINC keys and the number of data instances and examined their relationship with model performance.

All source code was developed in Python 3.6.0, and are available at https://github.com/skparr/ml_loinc_mapping. For string distance matching, we used the R stringdist package^45,46 within Python via the rpy2 package.⁴⁷Supplementary Table S8 contains tool options that can be parameterized to provide flexibility for the user. Once the user specifies the variables in the configuration file (detailed in the README.md file), the program can be run via command line execution of a single Python script.

RESULTS

The raw laboratory data consisted of over 6.5 billion test results, ranging from 2.5 to 184 million results per site (median 41.2 million). After aggregating by laboratory test identifier, specimen type identifier, units, and LOINC code, the analytic dataset consisted of 140 565 instances and 2215 distinct LOINC codes. LOINC codes were missing in 41 301 source data instances (29%), corresponding to 450 million test results.

Of the 1895 distinct LOINC keys remaining after grouping, we combined the data associated with the 707 keys used at only a single site and the 24 low-frequency (ie, <10 times by total test frequency) keys with the unlabeled data for reclassification.

The filtered, labeled dataset consisted of 94 845 data instances, aggregated from approximately 6.1 billion individual test results, with 1164 distinct LOINC keys. The dataset comprised of unlabeled and/or infrequent tests consisted of 42 720 instances, aggregated from approximately 462 million individual test results.

Cross-validated model performance

The random forest models (1-versus-rest and multiclass) significantly outperformed the 3 logistic regression models in all performance measures (Table 2). All models performed considerably better than random guessing in proportion to the prevalence of the 1164 possible class labels, which would yield an accuracy of 0.5%.

Table 2.

Model performance in 5-fold cross-validation

	Accuracy (95% CI)	Weighted F1 score (95% CI)	Micro-averaged F1 (95% CI)
L1	0.568 (0.559–0.578)	0.551 (0.537–0.565)	0.568 (0.559–0.578)
L2	0.606 (0.591–0.621)	0.556 (0.536–0.577)	0.606 (0.591–0.621)
L1-L2	0.607 (0.593–0.621)	0.562 (0.543–0.582)	0.607 (0.593–0.621)
RF (multiclass)	0.638 (0.622–0.653)*	0.612 (0.594–0.630)*	0.638 (0.623–0.654)*
RF (1-versus-rest)	0.649 (0.632–0.666)*	0.621 (0.601–0.640)*	0.649 (0.632–0.666)*

Abbreviations: CI, Confidence Interval. L1, L1 penalized logistic regression; L2, L2 penalized logistic regression; L1-L2, L1-L2 penalized logistic regression; RF, random forest.

^*P-values <0.05 within each of the 3 performance measures for comparisons between RF (multiclass) and, L1, L2, and L1-L2 LR models and for comparisons between RF (1-versus-rest) and, L1, L2, and L1-L2 LR models.

Manual validation

Full model

Unlabeled data

Using the Full Model applied to the unlabeled data, Cohen’s kappa for inter-rater agreement was 0.76 (Supplementary Table S9). The model-predicted label was correct in 84.7% of records by test frequency. Model performance by test frequency was comparable in the infrequent (bottom 50%) and frequent (top 50%) tests, but by instance, the model performed better on the frequent tests (Table 3).

Table 3.

Manual validation in unlabeled data (Full Model)

	Unlabeled Data
	Bottom 50%		Top 50%		Total
	Instances (N = 130)	Tests (N = 944 156)	Instances (N = 130)	Tests (N = 30 776 801)	Instances (N = 260)	Tests (N = 31 720 957)
Total Correct	87 (66.9%)	798 268 (84.5%)	108 (83.1%)	26 054 265 (84.7%)	195 (75.0%)	26 852 533 (84.7%)
Predicted Correct	70 (53.9%)	599 043 (63.4%)	106 (81.5%)	25 910 603 (84.2%)	176 (67.7%)	26 509 646 (83.6%)
No LOINC Coverage, Code Synonymous	17 (13.1%)	199 225 (21.1%)	2 (1.5%)	143 662 (0.5%)	19 (7.3%)	342 887 (1.1%)
Total Incorrect	26 (20%)	114 632 (12.1%)	19 (14.6%)	4 285 372 (13.9%)	45 (17.3%)	4 400 004 (13.9%)
Predicted Incorrect	22 (16.9%)	114 622 (12.1%)	19 (14.6%)	4 285 372 (13.9%)	41 (15.8%)	4 399 994 (13.9%)
No LOINC Coverage, Code Incorrect	4 (3.1%)	10 (<0.1%)	0 (0%)	0 (0%)	4 (1.5%)	10 (<0.1%)
Insufficient or Conflicting Information	17 (13.1%)	31 256 (3.3%)	3 (2.3%)	437 164 (1.4%)	20 (7.7%)	468 420 (1.5%)

Full Model refers to the 1-versus-rest classifier fit to the full labeled dataset.

Label definitions: Predicted Correct: model-predicted label is correct; No LOINC Coverage, Code Synonymous: LOINC code does not exist for the combination of test and specimen type in the source data, but the predicted LOINC code is the most reasonable alternative; Predicted Incorrect: model-predicted label is incorrect; No LOINC Coverage, Code Incorrect: LOINC code does not exist for the combination of test and specimen type in the source data, and the predicted LOINC code is not a reasonable alternative; Insufficient or Conflicting Information: either not enough source data to infer code (ie, units missing and would be necessary to assign code), or source data conflict (ie, test name includes the word “blood” and specimen type is “urine”).

Randomly sampled labeled data

In the labeled dataset, Cohen’s kappa was 0.82 (Supplementary Table S9). The model-predicted label was correct in 95.9% of records by test frequency, with higher accuracy in the frequent tests than in infrequent tests (Table 4).

Table 4.

Manual validation in randomly sampled labeled data (Full Model)

	Randomly Sampled Labeled Data
	Bottom 50%		Top 50%		Total
	Instances (N = 130)	Tests (N = 4 678 607)	Instances (N = 130)	Tests (N = 136 643 970)	Instances (N = 260)	Tests (N = 141 322 577)
Total Correct	81 (62.3%)	3 801 382 (81.3%)	126 (96.9%)	131 790 613 (96.4%)	207 (79.6%)	135 591 995 (95.9%)
Concordant Correct	71 (54.6%)	3 763 546 (80.4%)	124 (95.4%)	129 207 143 (94.6%)	195 (75%)	132 970 689 (94.1%)
Discordant Predicted Correct	7 (5.4%)	37 612 (0.8%)	1 (0.8%)	1 565 720 (1.1%)	8 (3.1%)	1 603 332 (1.1%)
No LOINC Coverage, Code Synonymous	3 (2.3%)	224 (<0.1%)	1 (0.8%)	1 017 750 (0.7%)	4 (1.5%)	1 017 974 (0.7%)
Total Incorrect	31 (23.8%)	876 859 (18.7%)	4 (3.1%)	4 853 357 (3.6%)	35 (13.5%)	5 730 216 (4.1%)
Concordant Incorrect	25 (19.2%)	876 829 (18.7%)	3 (2.3%)	2 782 119 (2.0%)	28 (10.8%)	3 658 948 (2.6%)
Discordant Original Correct	1 (0.8%)	1 (<0.1%)	1 (0.8%)	2 071 238 (1.5%)	2 (0.8%)	2 071 239 (1.5%)
Discordant Neither Correct	1 (0.8%)	15 (<0.1%)	0 (0%)	0 (0%)	1 (0.4%)	15 (<0.1%)
No LOINC Coverage, Code Incorrect	4 (3.1%)	14 (<0.1%)	0 (0%)	0 (0%)	4 (1.5%)	14 (<0.1%)
Insufficient or Conflicting Information	18 (13.8%)	366 (<0.1%)	0 (0%)	0 (0%)	18 (6.9%)	366 (<0.1%)

Full Model refers to the 1-versus-rest classifier fit to the full labeled dataset.

Label Definitions: Concordant Correct: model-predicted label = original label and is correct; Discordant Predicted Correct: model-predicted label ≠ original label, and model-predicted label is correct; No LOINC Coverage, Code Synonymous: LOINC code does not exist for the combination of test and specimen type in the source data, but the predicted LOINC code is the most reasonable alternative; Concordant Incorrect: model-predicted label = original label and is incorrect; Discordant Original Correct: model-predicted label ≠ original label, and original label is correct; Discordant Neither Correct: model-predicted label ≠ original label, and neither label is correct; No LOINC Coverage, Code Incorrect: LOINC code does not exist for the combination of test and specimen type in the source data, and the predicted LOINC code is not a reasonable alternative; Insufficient or Conflicting Information: either not enough source data to infer code (ie, units missing and would be necessary to assign code), or source data conflicts (ie, test name includes the word “blood” and specimen type is “urine”).

Targeted evaluation of discordant labels

In manual validation of cases in which the LOINC code present in the source data (original label) differed from the model-predicted LOINC code, Cohen’s kappa was 0.70 (Supplementary Table S9). The model-predicted LOINC code was correct in 83.2% by test frequency, and the model-predicted LOINC code was better than the original label 71.5% of the time by test frequency (Supplementary Table S10).

CV model

Unlabeled data

Using the CV Model applied to the unlabeled dataset, Cohen’s kappa was 0.73 (Supplementary Table S11). The model-predicted label was correct in 82.3% of records by test frequency, which is similar to the results from the Full Model. Compared to the Full Model, the CV Model performed modestly better in the infrequent tests and slightly worse in the frequent tests (Table 3 and Supplementary Table S12).

Randomly sampled labeled data

Cohen’s kappa was 0.86 in the labeled dataset (Supplementary Table S11). The model-predicted label was correct in 94.8% of records by test frequency, which is similar to the results from the Full Model. Compared to the Full Model, incorrect predictions in the CV Model were driven by more instances in which the original and predicted labels disagreed and were both incorrect (Discordant Neither Correct), but fewer instances in which the original and predicted labels agreed and were incorrect (Concordant Incorrect) (Table 4 and Supplementary Table S13).

Estimated noisy label prevalence

In manual validation of randomly sampled labeled data, noisy labels (incorrect labels in the original source data) are comprised of the Discordant Predicted Correct, Discordant Neither Correct, and Concordant Incorrect categories in Table 4. Considering the 234 instances in which LOINC coverage existed for the source data, and in which there was sufficient information to determine the LOINC code, the noisy label prevalence is 15.8% (Supplementary Table S14).

Examining model performance by dataset characteristics

When the number of sites in the model ranged from 5 to 35, performance improved dramatically with the addition of data in 5-site increments (Supplementary Figure S4A). Increasing the number of sites beyond 35 (up to 125) provided modest, albeit continued, performance improvement. The number of unique LOINC keys in the data also increased most appreciably in the range of 5 to 35 sites, plateauing when approximately 80 sites were included in the model (Supplementary Figure S4B). As sites were added to the dataset, the number of data instances increased linearly across the entire range.

DISCUSSION

In this study we automated feature generation and mapping of laboratory data to LOINC codes using a machine learning algorithm that leverages noisy labels within a large, heterogeneous national EHR system database. We were able to assign LOINC codes to unlabeled data with reasonable performance. We demonstrated comparable label accuracy when the model is fit to the entire dataset or when labels are assigned during cross-validation, suggesting that this model could be used on existing retrospective datasets or applied to new sites. While our manual validation suggested that the prevalence of incorrect existing LOINC codes in the VA Corporate Data Warehouse is non-trivial, inclusion of noisy labels was still effective for classifying previously unlabeled laboratory tests. Additionally, our model demonstrated utility in LOINC code reclassification, which could serve to augment data quality. The latter finding suggests that our algorithm might achieve higher performance if used within an iterative model training/adjudication/re-training framework.

Our results are similar in accuracy to the best reported automated methods for laboratory test mapping.^17–19 Notably, our estimates of model performance may actually be conservative for 2 reasons. First, we did not exclude tests that occurred rarely (ie, <10 results during the 16-year data collection timeframe). Second, during manual validation, we did not consider clinical equivalence in determining label accuracy. For example, using the LOINC Groups classification,⁴⁸ tests for Glucose [Mass/volume] in Capillary blood (LOINC code 32016-8) and Glucose [Mass/volume] in Blood (LOINC code 2339-0) can be grouped by the parent code LG11181-1. However, we considered a label of 2339-0 for the latter test incorrect, because a model would ideally assign the more specific code 32016-8 given the information in the source data. We opted for this stringent assessment, because an ideal model would assign the most granular label that represents the data and allow the end-user to aggregate codes if desired. We chose not to use the LOINC Multi-Axial Hierarchy table, which in some cases, groups LOINC codes with differing property and scale. For example, tests with quantitative results may be grouped with tests reported in ordinal scale. Since we aimed to map laboratory tests in a way that would not require the end-user to filter, sort, or transform tests within a LOINC group, we used the LOINC equivalence algorithm detailed in the Methods section.

In this study, random forest models outperformed penalized logistic regression models, which is not surprising given that random forests are inherently multi-class capable and robust to label noise.⁴⁰ Additionally, random forest models are attractive because they automatically handle non-linear relationships and high-order variable interactions.

Strengths and novelties of this study include: (a) use of a large (6.6 billion laboratory results) heterogeneous data source (130 sites) for model development, (b) implementation of an automated pipeline, (c) generalizable application, and (d) leveraging of noisy labels. Prior to our study, there have been no truly automated methods to map laboratory tests to LOINC codes. Previous methods required manual work by domain experts, either to extensively map local terms to LOINC codes (corpus-based methods),^17,18 or to choose the correct mapping from a list of candidates generated by the mapping tool (lexical method).¹⁹ The method we present fully automates the following steps: source data text processing and normalization, acronym and abbreviation expansion, synonym detection, feature engineering, and mapping/LOINC code assignment.

Our study is not without limitations. First, because this model was developed using a large, national data source, our approach may not be generalizable to organizations with fewer sites. However, in our sensitivity analysis of varying dataset characteristics, performance was reasonable with approximately 35 sites. Furthermore, performance appears to correlate more with the number of distinct LOINC codes in the dataset rather than the number of data instances, suggesting that the model might perform well even in smaller organizations with heterogeneous data. Second, we restricted to common laboratory tests with numeric results at each site, which could limit generalizability. However, because the top 150 tests were not identical across all of the 130 sites, the data used to train and evaluate the model was heterogeneous. Additionally, we selected the 150 most common tests per site based upon the local laboratory test name, which could be associated with different specimen types and/or units, resulting in 219 to 2153 distinct combinations of test name/specimen type/units per site. Furthermore, for our manual validation, we sampled from both commonly (top 50%) and uncommonly (bottom 50%) used tests, explicitly examining model performance with rarer data occurrences. Because we used heterogeneous data with rare occurrences, the model may perform well with addition of more tests. We did not include tests with text-reported results due to the need for normalization. However, Hauser et al. recently reported creating a scalable, generalizable tool to standardize laboratory test fields,⁵⁰ which could potentially be used in conjunction with our method to comprehensively improve data quality and mapping. Another potential limitation is that our model uses LOINC keys, which effectively groups similar LOINC codes via interoperability. This method is likely appropriate for many use cases, but the information contained in the method field of the individual LOINC codes could be important for research questions requiring granular laboratory test information. Finally, by including noisy labels, model performance is inherently dependent upon the quality of the underlying labels. In this data source with an estimated noisy label rate of 16%, model performance was reasonable, and prior research suggests that higher noisy label prevalence may be tolerated by machine learning methods.

CONCLUSION

With widespread EHR adoption, multi-site data aggregation and centralization are feasible and increasingly common. To leverage these data sources for research, quality assessments, and public health, data must be represented accurately and consistently across sites. Currently, there is a paucity of truly automated methods to map disparate data sources to standards that facilitate consistent data representation. The methods we describe incorporate features created from raw source data aggregation, and as such, could be implemented as an initial step in the transformation pipeline for common data models. In summary, this scalable, automated algorithm may improve data quality and interoperability, while substantially reducing the manual effort currently required to accurately map laboratory data.

FUNDING

This work was supported by the Department of Veterans Affairs, Office of Academic Affiliations, Advanced Fellowship Program in Medical Informatics; Vanderbilt University Medical Center Department of Biomedical Informatics; and Veterans Health Administration Health Services Research & Development (HSR&D) Investigator Initiated Research IIR 13-052.

Conflict of interest statement. None declared.

CONTRIBUTORS

SKP and MEM initially designed the study and acquired the data. TAL and MSS contributed to study design, model selection, and data analysis approach. ADJ assisted with manual adjudication. SKP performed all data analysis and drafted the initial manuscript. All authors contributed to interpretation of results and critical revision of the manuscript.