Using electronic health records to identify candidates for human immunodeficiency virus pre-exposure prophylaxis: An application of super learning to risk prediction when the outcome is rare

Abstract

Human immunodeficiency virus (HIV) pre-exposure prophylaxis (PrEP) protects high risk patients from becoming infected with HIV. Clinicians need help to identify candidates for PrEP based on information routinely collected in electronic health records (EHRs). The greatest statistical challenge in developing a risk prediction model is that acquisition is extremely rare.

Methods:

Data consisted of 180 covariates (demographic, diagnoses, treatments, prescriptions) extracted from records on 399 385 patient (150 cases) seen at Atrius Health (2007–2015), a clinical network in Massachusetts. Super learner is an ensemble machine learning algorithm that uses k-fold cross validation to evaluate and combine predictions from a collection of algorithms. We trained 42 variants of sophisticated algorithms, using different sampling schemes that more evenly balanced the ratio of cases to controls. We compared super learner’s cross validated area under the receiver operating curve (cv-AUC) with that of each individual algorithm.

Results:

The least absolute shrinkage and selection operator (lasso) using a 1:20 class ratio outperformed the super learner (cv-AUC = 0.86 vs 0.84). A traditional logistic regression model restricted to 23 clinician-selected main terms was slightly inferior (cv-AUC = 0.81).

Conclusion:

Machine learning was successful at developing a model to predict 1-year risk of acquiring HIV based on a physician-curated set of predictors extracted from EHRs.

1 |. INTRODUCTION

Pre-exposure prophylaxis (PrEP) has been shown to dramatically decrease the risk of becoming infected with Human immunodeficiency virus (HIV) in adherent high risk populations.^1,2 Automated identification of high risk patients could promote health and reduce the spread of HIV. A risk prediction model based on information routinely captured in an electronic health record (EHR) could help physicians offer PrEP to patients most likely to benefit from treatment. One challenge is that HIV acquisition is extremely rare. A second challenge is that although covariates in EHR data are readily available, they are imperfect proxies for behavioral patterns indicative of exposure to the virus.³ CDC criteria for PrEP prescribing rely on behavioral characters such as receptive anal intercourse or number of shared needles that are not routinely captured in the EHR.⁴ Existing HIV risk prediction models also include such covariates and may be developed within a restricted high risk population of men who have sex with men..^5–7 In contrast, our goal was to understand whether routinely collected EHR data could help identify high risk candidates for PrEP within a general population in the United States.

Our data contained information on patients seen between 2007 and 2015 at Atrius Health, a clinical network serving eastern Massachusetts. Among approximately 1.2 million Atrius patients, 150 were newly diagnosed with an incident HIV infection. Observations on each patient consisted of demographic information, diagnosis codes, procedure codes, drug prescriptions, laboratory tests, and results. For clinical aspects of this work and details on the data source, we refer the interested reader to a companion paper in the medical literature.³ In this article, we describe our methodologic approach to risk prediction that harnesses both clinical expertise and the tools of machine learning.

We were interested in predicting 1-year risk of acquiring HIV, that is, the conditional probability of being newly diagnosed as HIV positive within the next calendar year conditional on the patient’s medical history. We define this as $E(Y(t+1)\mid \overline{X}(t))$, the patient-level conditional mean outcome at time t + 1 given covariate history measured through time t, $\overline{X}(t)$.

An important question is how to best capture salient elements of $\overline{X}(t)$ while simultaneously building a model that can be successfully applied across a broad variety of settings. Since a patient’s true risk of acquiring HIV will rise and fall with changes in behaviors that affect exposure to the virus, more recent values of some covariates may supplant values measured long ago. Another advantage of limiting the length of the look back period is that fewer patients will be excluded from our dataset due to inadequate medical history. Finally, we aim to create a tool that can be applied to as broad a patient population as possible, rather than the small subset of patients with lengthy historical EHR data. A disadvantage to limiting the length of the look-back period is the potential for ignoring important predictors of risk. In fact, the length of time covered by the EHR might itself be predictive of risk.

For these reasons, we define a prediction model that conditions on baseline characteristics X(0), information accrued over two calendar years $\tilde{X}(t)=(X(t),X(t-1))$, and summary measures of more distant history, Z(t). For example, $Z(t)=f(\overline{X}(t))$ could include the mean number of annual gonorrhea tests, a binary indicator of ever having had an HIV test, a binary indicator of ever having a positive syphilis test, and so on. Thus, $Z(t)=f(\overline{X}(t))$ summarizes the recorded medical history for each patient over the patient-specific time period for which data are available. Our target parameter is given by $E(Y(t+1)\mid \overline{X}(t))$, with $\overline{X}(t)\equiv (X(0),\tilde{X}(t),Z(t))$. Predictors in our model accurately reflect information recorded in the EHR, not necessarily the true patient history. This does not pose a problem, since recorded information is what will be used to calculate risk when the model is applied in practice.

A traditional approach to risk prediction modeling relies on clinical expertise to identify important predictors, and fitting a logistic regression model to the data. When the outcome is rare relative to the number of available predictors, as it is here, a forward or backward stepwise selection procedure might be used to create a parsimonious model. Instead of relying on a single parametric model specification, a machine learning algorithm adapts to information in the data. Different machine learning algorithms make different use of this information. A practitioner has little way of knowing which approach will work best on any given dataset.

For this reason, we relied on super learning (SL) to predict one year risk of acquiring HIV. SL is an ensemble machine learning algorithm that develops a risk prediction model for each algorithm in a user-specified library, and evaluates the cross validated loss for each one.^8,9 The minimizer of the cross validated loss is the algorithm that produced the best prediction model. However, ensemble SL may possibly improve upon this model by combining predictions from multiple models. SL predictions are calculated as an asymptotically optimal weighted combination of predictions from the individual algorithms. SL has been applied to risk score prediction in several health care settings, including intensive care unit mortality and identifying high risk candidates for PrEP in Uganda and Kenya.^10–14

Cross validation provides an honest assessment of the relative performance of prediction algorithms. Although SL is asymptotically optimal, in finite samples, it is not guaranteed to out-perform each individual learner in the library.¹⁵ For this reason, we compared SL’s cross validated area under the receiver operating curve (AUC), with that of each of the individual algorithms in the library. This allowed us to evaluate whether the SL model is better at discriminating between cases and non-cases than each of the others. If it is not, we are better off choosing the model that is the best. In the SL literature, this process of using cross validation to identify the single best performer is known as discrete super learning (dSL).

While dSL allows us to choose the model that minimizes the cross validated loss (1-AUC), we also want to consider the trade-offs between using an ensemble SL model versus a simpler, more interpretable model. Keep in mind that our ultimate goal is to focus health care providers’ attention on likely candidates for PrEP. All else being equal, we favor a model that is parsimonious, interpretable, and acceptable to clinicians. For example, lasso performs its own internal covariate selection to reduce dimensionality and produce a familiar logistic regression model. The lasso model is transparent, easy to communicate, and easy to update. Implementing the lasso model in practice would require extracting and processing information only for the small number of covariates retained in the model, rather than all covariates originally considered by SL. This would make it an attractive option, particularly when SL’s performance is not appreciably different. On the other hand, if the SL model is vastly superior, its enhanced ability to identify appropriate PrEP candidates could offset the lack of transparency.

2 |. STATISTICAL METHODS

2.1 |. Super learner

The machine learning literature teaches that an alternative to relying on a single parametric model is to combine predictions from multiple models,^16–18 or more generally from multiple predictive algorithms.^19,20 SL is an example of the latter. The analyst assembles a collection of prediction algorithms known as a library, and uses SL to estimate either a class label (classification task, eg, case or control), or conditional mean outcome (regression task). Ensemble SL predictions are a convex combination of the predictions from each algorithm in the library. In contrast, dSL predictions equal those produced by the single best performing algorithm in the library.

Discrete SL converges to the true data model, or true conditional distribution of the data, when the library algorithms search over the portion of the solution space that contains the model. Otherwise, SL will converge to the minimizer of the cross validated loss, $\mathcal{L}(O)$.⁸ Common loss functions include the negative log likelihood, negative sum of squared residuals, and 1-AUC. SL’s reliance on K-fold cross validation confers proven asymptotic oracle properties.¹⁵ At large enough sample size, the distribution of SL risk predictions will approximate the true distribution as closely as possible, given the candidates specified in the library. For example, if the SL library contains only misspecified logistic regression models, dSL will select the one that best fits the data, even though it is incorrect.

Ensemble SL extends dSL by calculating an optimal weighted combination of predictions from the algorithms under consideration.⁹ The intent is to stabilize estimates. However, in finite samples, there is no theoretical guarantee that ensemble SL will out-perform discrete SL, or that it will not overfit the data. For this reason, we evaluated the cross-validated loss of the ensemble SL itself. This allowed us to compare its finite sample performance with that of each of the candidate algorithms in our SL library.

In practice, the key to success with SL is defining an appropriate library of candidate algorithms. In high-dimensional data, the collection of probability distributions under consideration, or solution space, is too large to do an exhaustive search. Note that when we consider the number of potential interaction terms and transforms of the covariates, even moderately sized data are, in fact, high dimensional. The SL library specification constrains the solution space. A rich library might contain parametric, nonparametric, and semiparametric algorithms, some of which model the covariate-outcome relationships, and others that avoid directly modeling the outcome distribution. Searching over the solution space in different ways robustifies SL performance.²¹

Other considerations when defining the SL library include characteristics of the outcome (eg, binary, ordinal, continuous, rare), the number of potential covariates, the number of observations, and the opportunity to incorporate data-adaptive and/or knowledge-based dimension reduction. Theoretical results hold for an SL library allowed to grow polynomially with sample size, so a large library is encouraged. In practice, computation time and resource availability limit the size of the SL library to one that is feasible.

2.2 |. Library algorithms

To better understand performance of individual machine learning algorithms under consideration for inclusion in our SL library, we applied them to simulated data. The goal was to gain insight into method performance in a dataset with a rare outcome under different undersampling schemes. For each algorithm in the SL library, we wanted to better understand sensitivity to changes in the setting for the tuning parameters. We established a plausible set of values for each sensitive tuning parameter, and provided them to machine learning algorithms that perform their own internal cross-validation to choose the best tuning parameter value within a user-specified range. Otherwise, we included multiple variants of the algorithm in our SL library. We also paid attention to how convergence and computation time, and goodness of fit varied at different ratios of cases to controls.

Data were simulated so that the event rate matched the rate in the Atrius population who had at least one HIV-related flag in the EHR (see Section 3). We simulated a binary outcome that followed the logistic distribution. Eighteen correlated binary covariates, X₁, … X₁₈ were generated, and then model coefficients β₁, … β₁₈ were fixed at values between 0.01 and 1, mimicking mild associations with the outcome similar to those observed in the real data. The intercept was set to β₀ = −10 to yield a marginal event proportion on the order of that observed in the Atrius data. Y was generated as a Bernoulli random variable with probability equal to expit(Xβ), where X is the design matrix containing the intercept and covariates X₁, … X₁₈. We evaluated a variety of algorithms using R version 3.3.1,²² assessing the cv-AUC, sensitivity to tuning parameters, computation time, and changes in performance under different ratios of incident HIV cases to controls, ranging from 1:100 to 1:10. Based on this informal assessment, we decided to incorporate variants of the following five types of candidate algorithms in the SL library used to build our risk score model.

2.2.1 |. Logistic regression-based algorithms

The R glm function provides maximum likelihood estimation of parameters of a pre-specified logistic regression model. We also used the step function to data-adaptively select first and second order terms using a stepwise backward selection procedure based on the Akaike Information Criterion (AIC). We incorporated weights into each approach, where cases received a weight of 1 and controls received a weight that was inversely proportional to the conditional probability of being sampled.

2.2.2 |. Regularized regression algorithms

Elastic net estimators are regularized regression algorithms that shrink coefficients in a regression model towards zero. The glmnet package provides a family of elastic net estimators of the form,

$$\widehat{\beta }=\text{arg}{\text{min}}_{\beta }\left(\Vert y-X\beta {\Vert }^2+(1-\alpha )\Vert \beta {\Vert }^2+\alpha \Vert \beta {\Vert }_1\right),$$

where $\Vert \beta {\Vert }_1={\sum }_{j=1}^p\left|{\beta }_j\right|$, and p is the number of terms in the model.²³ Setting α = 0 corresponds to penalizing by the L₂ norm (ridge), while setting α = 1 corresponds to penalizing by the L₁ norm (lasso). The ridge penalty drives coefficient values toward 0, while the lasso penalty allows some coefficients to actually reach 0, effectively excluding some covariates from the model data-adaptively.²⁴ We included lasso and ridge regression in the SL library for developing our HIV acquisition prediction model.

2.2.3 |. Neural networks

Neural networks are machine learning algorithms that (typically) model the regression function as a weighted sum of sigmoid curves.²⁵ The class of feed forward neural nets implemented in the nnet package has an input layer, a single hidden layer, and an output layer. There are weighted directed edges from nodes in the input layer to nodes in the hidden layer, and from nodes in the hidden layer to nodes in the output layer. The nnet package also allows skip-layer connections directly from input nodes to output nodes. This flexibility allows the neural network to approximate complex non-linear functions. Initial weights on the directed edges are updated to minimize an optionally penalized loss function (ie, least squares), where the penalty on the sum of squares of the weights is known as weight decay.²⁵

2.2.4 |. Random forests

Random forests are collections of classification and regression trees that nonparametrically classify observations by reporting the mode of the classifications of the individual trees. Predicted probabilities are the mean of the class predictions across all trees.²⁶ A single tree is created by iteratively dividing the data at each node in the tree in a way that maximally separates the classes. For binary outcomes, these splits are based on the covariate that best discriminates between cases and controls. The splitting process continues until all observations in the node are in the same class, or a specified minimum node size is reached. As implemented in the randomForest package, only a randomly sampled subset of covariates are considered at each node.²⁷ Tree-building inherently models higher order interactions and is not affected by monotone (rank preserving) transforms of the data. Although a single tree can be unstable in the face of small perturbations in the data, random forest overcomes this limitation by aggregating over hundreds or thousands of trees in a forest.²⁶

2.2.5 |. Support vector machines

Support vector machines (SVM) avoid directly modeling the outcome regression. Instead, an SVM identifies vectors in a multidimensional space that maximally separate cases from controls.^28,29 Support vectors are the data points that lie closest to the class boundaries. SVMs try to maximize the minimum distance between these vectors, which leads to identifying the minimum number of support vectors. Soft margins optionally allow solutions to include some misclassification of labeled observations in the training set.²⁸

An equivalence between linear SVMs and lasso solutions has recently been proven.³⁰ Nonlinear transforms of the data through kernel functions allows SVMs to succeed even when classes are not linearly separable. For example, nonlinear SVMs can discover neural network solutions using a sigmoid kernel function.²⁹ The SVMs in our super learner library used a sigmoid kernel.

2.3 |. Rescaling predicted risk scores

A notable feature of our data was that the outcome is extremely rare, occurring in approximately 13 out of 100 000 patients. Algorithms that aim to minimize the proportion of misclassified observations when predicting class probabilities (case or noncase) are difficult to train when there are large imbalances in the outcome classes.^31,32 Improving the balance by undersampling the more prevalent outcome class can improve the discriminatory performance of the classifier. Artificially adjusting the class proportions is a form of biased sampling. Some algorithms, such as classic logistic regression, can incorporate weights equal to the inverse of the conditional probability of being sampled into the estimation procedure to accurately scale predicted probabilities. For algorithms that cannot incorporate weights, the predicted probabilities need to be rescaled to account for the biased sampling of cases and controls. Rescaling can be accomplished via the prior correction method.³³ This simple calculation corrects the intercept in a logistic regression model to account for the actual proportion of cases in the data, rather than the under-sampled proportion. Predicted probabilities,Ŷ, are adjusted to reflect the background prevalence of the outcome, instead of the prevalence in the sampled data. The rescaled predicted probabilities,Ŷ′, are given by,

$${\widehat{Y}}^{\prime }=\mathit{\text{expit}}[\mathit{\text{logit}}(\widehat{Y})-\mathit{\text{logit}}(\pi )+\mathit{\text{logit}}(\tau )],$$

where π is the proportion of cases in the undersampled data and τ is the proportion of cases in the source population.

3 |. DATA ANALYSIS

3.1 |. Data

We had access to EHR data on 399 385 of the 1.2 million patients seen during 2007 to 2015 at Atrius Health. These patients had at least one of 180 clinician-specified risk factors for HIV acquisition and/or were diagnosed with incident HIV. Data on an additional n = 755 579 patients who had 0 recorded risk factors were not available to us (details were previously published³). A patient with at least one risk factor contributed one observation to our dataset for each year there was an encounter with the health care system, for a total of 2.3 million observations. Because the outcome was observed in only 150 observations we decided to create an analytic dataset that included all cases, but undersampled the available controls.

A rule of thumb in a typical case-control study is to sample five controls per case (see ch. 6 of Reference³⁴). We did not want to assume that this low sampling ratio would work equally well for the task of predicting an extremely rare outcome. For example, it is not clear that the distribution of covariates in a subset of only 5 × 150 = 750 controls would faithfully represent the distribution in the entire class. We opted to select 50 controls per case to ameliorate this problem, while preserving the option to further undersample controls when fitting each algorithm in the SL library.

There were 30 female and 120 male cases. Although 80% of cases were male, available controls were predominantly female (62%).To achieve an overall ratio of 1:50 cases to controls, matched on sex, we generated binary inclusion indicators for each control using simple random sampling, stratified by sex. For males, P(Include = 1 male control) = 6000 / 842 332 (the total number of available controls), ≈ 0.71%. For females, P(Include = 1 female control)| = 1500 / 1 366 663 (the total number of available females), ≈ 0.11%. The analytic dataset consisted of n = 7616 observations (n = 150 cases, n = 7466 controls). Participants contributed an observation to the dataset for each year the inclusion criteria were met. Sampling was on the observation level rather than the participant level to mirror the distribution of medical history length in the source population.

Each observation contained information on 134 covariates capturing demographic information (12 variables), medical utilization measures, number of ordered tests for various sexually transmitted diseases in the past 1 and 2 years (70 variables), and ever number of positive or abnormal tests, prescriptions for selected drugs, diagnoses of selected medical conditions and treatments (52 variables) (Table 1). Based on clinical expertise and familiarity with data capture at Atrius, 180 covariates were initially considered for inclusion. Forty six of those were subsequently dropped due to lack of variation in the data, or to collinearity. These 46 variables could provide no additional predictive ability. We removed them from the analytic dataset to facilitate convergence and speed up computation time. We also defined two interaction terms, sex-nongonococcal urethritis and sex-suboxone prescription. Including all 134 covariates in a logistic regression model would lead to overfitting the data, since there are only 150 cases. Following tradition in the nonautomated development of risk prediction models,³⁵ we relied on clinical judgement augmented with empirical correlations in the data to identify 23 potential strong predictors among the listed covariates (Table 2).^36–38 We wanted each algorithm to have the benefit of developing a model based on all covariates, and also based on an expert-selected subset of covariates. Providing too many covariates can sometimes result in overfitting the data, even when learners perform their own internal regularization. At the outset, we did not know which approach would obtain better results, so we tried both.

TABLE 1.

Hundred and thirty-four covariates retained in the analytic dataset

X(0) :	Baseline demographics age, sex,race (6 indicators), language (4 indicators)
$\tilde{X}(t)$ :	Health care utilization during past 1 year and past 2 years
	number of medical encounters, top quartile usage (yes/no), EHR data recorded, HIV counseling
	Number of tests and number of positive tests in past 1 year and past 2 years
	gonorrhea, chlamydia, syphilis, hepatitis B antibody, hepatitis B DNA, hepatitis C antibody, hepatitis C RNA, HIV ELISA test, HIV RNA test
	Diagnoses in past 1 year, 2 years (yes/no)
	syphilis, nongonococcal urethritis, herpes, anogenital warts, anorectal ulcer, pelvic inflammatory disease, venereal disease, anorexia, bulimia, eating disorder, alcohol dependence, opioid dependence, drug dependence, gonorrhea, chlamydia, syphilis, herpes, substance abuse
	Prescriptions in past 1 and/or 2 years
	bicillin, azithromycin, ceftriaxone, methadone, suboxone, cialis/viagra/levitra
Z(t) :	Indicators of ever diagnosed for each condition listed above
	Indicators of ever prescribed for each drug listed above
	high risk sexual behavior, possible transgender, possible homosexual, possible transgender, possible injectable drug use, possible at risk woman, years of available data

TABLE 2.

Twenty-three pre-selected covariates

X(0) :	sex; race asian; race black; race white; english language (y/n)
$\tilde{X}(t)$ :	number of hepatitis C antibody tests in the past year; over the past two years: mean number of HIV tests; HIV counseling; number of tests for gonorrhea; prescription for suboxone; sex-suboxone; chlamydia test diagnosis and treatment; possible at risk woman; possible male sex with male
Z(t) :	total number of recorded HIV RNA tests; positive gonorrhea tests; diagnosis of syphilis; diagnosis of nongonococcal urethritis; sex-nongonococcal urethritis; diagnosis of bulimia; sex-diagnosis of bulimia; exposed to a venereal disease; engaged in high risk sexual behaviors

3.2 |. Model development

All SL analyses relied on 10-fold cross-validation to empirically evaluate the loss function $\mathcal{L}=1-AUC$, using the R SuperLearner package.^22,39 Observations on the same patient were assigned to the same cross-validation fold. The ensemble SL library consisted of 42 machine learning algorithms that are variants of the class of algorithms described in the previous section of the article. Algorithms in the SL library were presented with all covariates or with only the 23 pre-selected covariates, as shown in Table 3. The latter focuses the search on what we suspect is the most fruitful area of the solution space, while the former forces each algorithm to rely on information in the data themselves.

TABLE 3.

Candidate algorithms included in the ensemble Super Learner library

Prediction Algorithm	(approximate) Controls per Case	Eligible Covariates	Notes
Logistic Regression	50, 20, or 10	All	Weighted
(14 variants)	50, 20, or 10	Pre-Selected	Weighted
	50, 20, or 10	All
	50, 20, or 10	Pre-selected
	50	All	Backward selection
	50	Pre-Selected	Backward selection
Lasso	20 or 10	All	Deviance loss
(8 variants)	20 or 10	All	neg AUC loss
	20 or 10	Pre-Selected	Deviance loss
	20 or 10	Pre-Selected	neg AUC loss
Ridge Regression	20 or 10	All	Deviance loss
(8 variants)	20 or 10	All	neg AUC loss
	20 or 10	Pre-Selected	Deviance loss
	20 or 10	Pre-Selected	neg AUC loss
Random Forest	50, 20, or 10	All	10,000 trees, 1/3 of covariates sampled per split
(6 variants)	50, 20, or 10	Pre-Selected	10,000 trees, 1/3 of covariates sampled per split
Support Vector Machine	50	All	Tuning parameters chosen by cross validation
(2 variants)	50	Pre-Selected	Tuning parameters chosen by cross validation
Neural Network	20 or 10	Pre-Selected	10 nodes in 1hidden layer
(4 variants)	20 or 10	Pre-Selected	5 nodes in 1 hidden layer

Note: Risk scores were re-scaled to account for undersampling of controls, except for weighted logistic regression algorithms.

The SL package ordinarily calculates the optimal weighted combination and returns the results. However, because we used different ratios of cases to controls for different algorithms in the library, the raw predictions available internally to SL are not all on the same scale. We evaluated the ensemble SL predictions ourselves. The first step was to use the prior correction method to rescale SL’s matrix of cross validated predictions, Z. We invoked method.AUC, defined in the SL package, to calculate the weights that minimize the loss, based on calibrated matrix, Z^′. This method normalizes the weights, to ensure that the predicted probabilities are a convex combination of predictions from algorithms fit on all the data. SL risk predictions were calculated as the weighted sum of the rescaled predictions from each of the 42 algorithms fit on the entire dataset. The SL package returns the unscaled predictions in a matrix labeled library.predict. If we denote the matrix of calibrated predictions as library.predict^′, then our ensemble SL predictions are set equal the weighted sum of predicted probabilities in library.predict^′.

3.3 |. Cross validating the super learner

In a final step, we used 10-fold cross-validation to obtain an honest estimate of the cv-AUC of the ensemble SL. We use dSL to identify the best performing candidate algorithm. Our dSL library contains 43 candidates—the 42 original algorithms, plus the ensemble SL itself. Because cross-validated loss penalizes overfits, dSL allows us to rank candidates by their ability to discriminate between cases and controls on novel data drawn from the same distribution.

3.4 |. Results

We present and discuss results in terms of maximizing the AUC, which is equivalent to minimizing the loss function, $\mathcal{L}=1-AUC$. We calculated AUC with respect to the general Atrius population where the model will be applied, rather than the sub-population who have at least one recorded risk factor. We are not interested in flagging any patients who have no recorded risk factors (n=755,579), because their EHR provides no justification for considering them to be at high risk. We assigned risk = 0 to these patients, and included them in the AUC calculation. 95% confidence intervals were calculated by incorporating weights into the influence curve-based method of Ledell et al.⁴⁰

Although ensemble SL was among the top performing algorithms (cv-AUC (95% CI) = 0.836, (0.822, 0.851)), several variants of lasso and ridge regression had slightly higher cv-AUCs. The best lasso model (cv-AUC (95% CI) = 0.858 (0.842, 0.874)) was fit on a dataset containing all 134 covariates, and a 1:20 class ratio (Table 4). Overlapping confidence intervals indicate that there is little practical difference in performance between SL and the more interpretable lasso model. All variants of lasso and ridge regression out-performed SVM, neural nets, and logistic regression modeling using stepwise backward selection or an a priori specified model. The choice of deviance-based or AUC-based loss for ridge and lasso had little impact. AUC curves for the best variant of each candidate algorithm in the SL library are shown in Figure 1.

TABLE 4.

Cross-validated area under the receiver-operating curve and 95% confidence interval (CI) for ensemble SL and each of the 42 algorithms in the original super learner library.

Algorithm	cv-AUC (CI)	Algorithm	cv-AUC (CI)
lasso20,dev	0.858 (0.842, 0.874)	rForest10	0.795 (0.778, 0.811)
lasso20,auc	0.855 (0.839, 0.870)	rForest20	0.772 (0.756, 0.788)
lasso10,auc	0.853 (0.836, 0.868)	glm50,pre	0.758 (0.743, 0.773)
lasso10,dev	0.849 (0.833, 0.865)	svm50,pre	0.746 (0.731, 0.760)
ridge20,dev	0.839 (0.824, 0.854)	glmStep50	0.743 (0.729, 0.758)
ridge10,dev	0.839 (0.823, 0.854)	glm50,wt	0.742 (0.728, 0.757)
SL	0.836 (0.822, 0.851)
ridge10,auc	0.836 (0.821, 0.851)	glm20,pre	0.742 (0.728, 0.757)
ridge20,auc	0.831 (0.816, 0.846)	glmStep50,pre	0.737 (0.723, 0.751)
lasso10,pre,auc	0.828 (0.812, 0.845)	glm10	0.736 (0.721, 0.751)
lasso10,pre,dev	0.826 (0.810, 0.842)	glm50	0.707 (0.693, 0.722)
lasso20,pre,dev	0.821 (0.805, 0.837)	rForest50	0.679 (0.666, 0.693)
lasso20,pre,auc	0.821 (0.805, 0.837)	glm20,wt	0.651 (0.638, 0.664)
lasso20,pre,dev	0.818 (0.801, 0.834)	rForest20,pre	0.594 (0.587, 0.601)
glm10,pre	0.814 (0.796, 0.830)	rForest10,pre	0.591 (0.584, 0.598)
ridge10,pre,auc	0.812 (0.796, 0.827)	rForest50,pre	0.588 (0.581, 0.596)
ridge10,pre,dev	0.811 (0.794, 0.826)	glm10,wt	0.552 (0.540, 0.564)
ridge20,pre,auc	0.809 (0.793, 0.825)	nnet10,5h,pre	0.5 (0.490, 0.510)
glm20	0.807 (0.790, 0.823)	nnet10,10h,pre	0.5 (0.490, 0.510)
glm50,pre,wt	0.805 (0.789, 0.821)	nnet20,5h,pre	0.5 (0.490, 0.510)
glm20,pre,wt	0.802 (0.785, 0.817)	nnet20,10h,pre	0.5 (0.490, 0.510)
glm10,pre,wt	0.799 (0.782, 0.815)	svm50	0.424 (0.399, 0.449)

Subscript key: (50, 20,10): # controls per case, pre: 23 pre-selected covariates, auc: neg AUC loss.

dev: deviance loss, wt: weighted regression, 5h, 10h: # nodes in hidden layer.

95% confidence intervals calculated using method of LeDell et al (2015).

FIGURE 1.

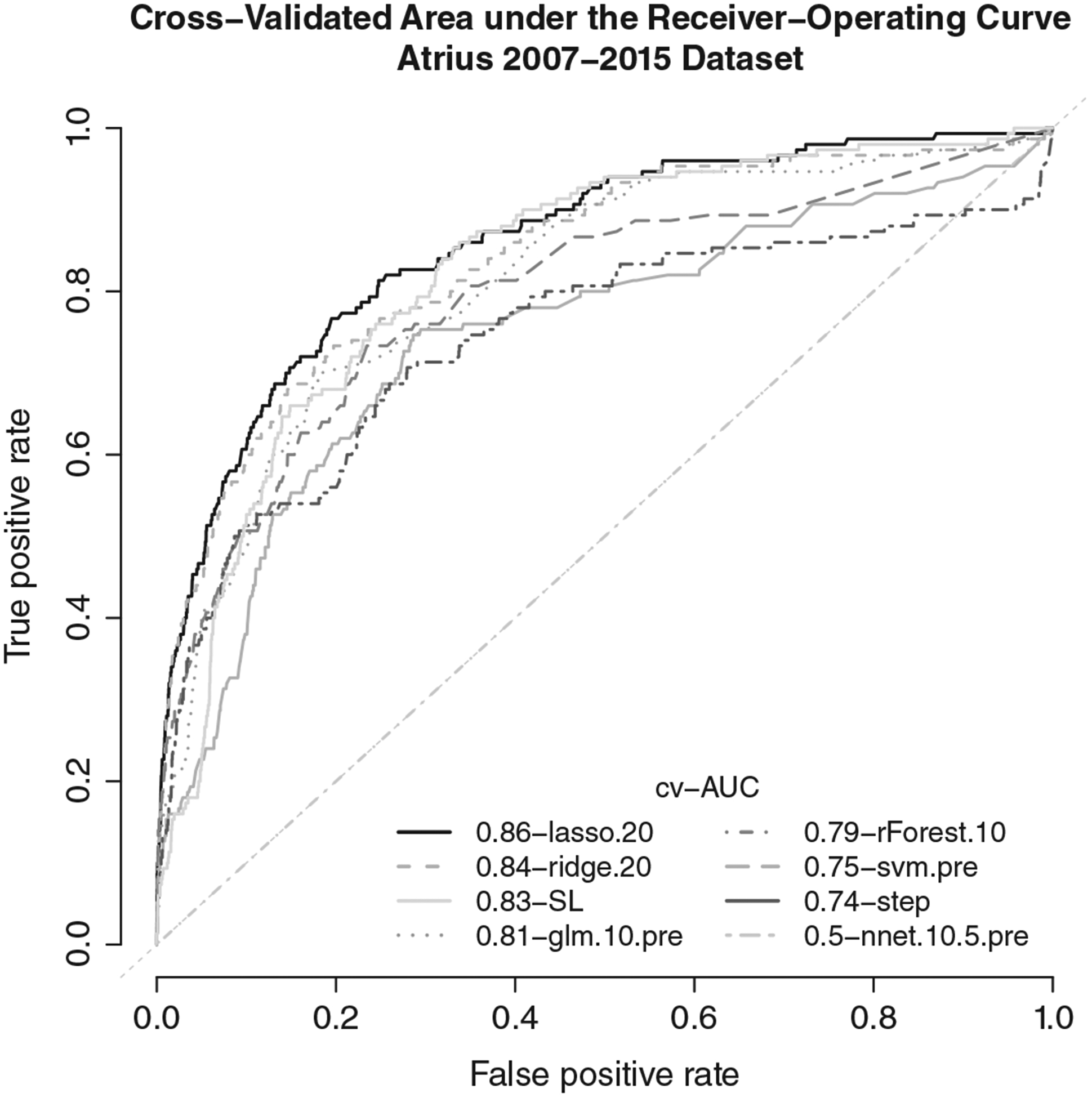
Cross-validated area under the receiver-operating curve for ensemble SL, and the best performing variant of each candidate algorithm in the super learner library

The best maximum likelihood logistic regression-based algorithm we investigated was the a priori specified model containing the pre-selected set of covariates, fit on unweighted data having a 1:10 class ratio, with probabilities re-scaled using the prior correction method. This algorithm was slightly less able to discriminate between high and low risk patients (cv-AUC = 0.814 (0.796, 0.830)) than the penalized regression algorithms. When coefficients in the model were fit on the same data using weighted logistic regression instead of the prior correction method, the cv-AUC (0.799 (0.782, 0.815)) fell slightly.

Random forest, ridge regression, and lasso perform their own variable selection or shrinkage. Granting these algorithms access to all 134 covariates improved performance over allowing them access to only the 23 pre-selected covariates.

4 |. OPTIONALLY AUGMENTING THE SUPER LEARNER LIBRARY

Although it will never be possible to do an exhaustive search over the entire solution space, we tried to see whether we could meaningfully improve SL’s predictive performance by augmenting the SL library. We explored 18 variants of gradient boosting, and revised specifications for nine neural networks. Observations were assigned to the same cross validation folds as in the prior analysis so that the cross validated loss estimates would be comparable.

4.1 |. Gradient boosting

It is an ensemble of weak learning trees that often out-performs random forest in classification tasks.^41,42 We were interested in finding out whether this approach could extract more meaningful information from our data. Each tree is constructed in response to the residual error from the previous tree in the sequence. We defined six variants of gradient boosting that varied the parameters that most affected stability in our simulations using the xgboost package.⁴³ The maximum tree depth was set to either 2 or 4, and the minimum number of observations per node was set to either 10, 25, or 50. We applied these six algorithms to datasets with a case to control ratio of 1:50, 1:20, and 1:10, for a total of 18 variants.

4.2 |. Neural Network

Its performance was poor in our first set of results. We investigated whether reducing the size of the network could improve performance. We began by omitting 74 covariates that were likely to be uninformative, populated almost entirely with zeros (>= 99%). We specified three different architectures: a single hidden layer containing either 1, 2, or 5 nodes. These three algorithms were applied to datasets with a case to control ratio of 1:50, 1:20, and 1:10, for a total of nine variants. This time we used a different R package, the neuralnet package.⁴⁴

4.3 |. Results

Estimated cv-AUCs were obtained using the same assignment of observations to cross-validation folds as in the original analysis. All boosted trees had good performance (Table 5). The best cv-AUC of 0.844 was obtained from a dataset with a 1:10 class ratio, with maximum depth set to 2 and a minimum of 10 observations per node. Neural net performance improved considerably (Table 5). The highest cv-AUC (0.787) was obtained from a dataset with a 1:20 class ratio and 1 node in the hidden layer. Alternative architecture specifications might further improve performance.

TABLE 5.

Cross-validated area under the receiver-operating curve and 95% confidence interval (CI) for gradient boosted (xgb) and neural network (nn) algorithms in the augmented super learner library

Algorithm	cv-AUC (CI)	Algorithm	cv-AUC (CI)	Algorithm	cv-AUC (CI)
xgb10,2,10	0.844 (0.828, 0.859)	xgb20,2,25	0.836 (0.819, 0.853)	nn20,1	0.787 (0.772, 0.802)
xgb50,4,50	0.842 (0.823, 0.861)	xgb20,4,50	0.834 (0.816, 0.852)	nn10,1	0.773 (0.758, 0.788)
xgb50,2,25	0.839 (0.823, 0.856)	xgb50,4,25	0.832 (0.814, 0.849)	nn10,2	0.773 (0.758, 0.787)
xgb20,2,10	0.839 (0.823, 0.855)	xgb20,2,50	0.832 (0.815, 0.848)	nn20,5	0.733 (0.717, 0.749)
xgb10,4,25	0.838 (0.821, 0.855)	xgb50,2,10	0.831 (0.815, 0.847)	nn50,5	0.711 (0.693, 0.729)
xgb50,2,50	0.837 (0.819, 0.856)	xgb10,2,50	0.831 (0.813, 0.848)	nn50,1	0.708 (0.693, 0.724)
xgb10,4,50	0.837 (0.820, 0.854)	xgb20,4,10	0.819 (0.803, 0.836)	nn50,2	0.5 (0.490, 0.510)
xgb20,4,25	0.837 (0.819, 0.854)	xgb10,4,10	0.816 (0.800, 0.832)	nn10,5	0.5 (0.490, 0.510)
xgb10,2,25	0.836 (0.819, 0.853)	xgb50,4,10	0.799 (0.782, 0.815)	nn20,2	0.5 (0.490, 0.510)

xgb subscript key: (a, b, c): a = # controls per case, b=depth, c = min obs per node.

nn subscript key: (a, b): a = # controls per case, b= # nodes in hidden layer.

95% confidence intervals calculated using method of LeDell et al (2015).

Although these results were encouraging, their cv-AUCs are on a par with those of the original individual algorithms. The only remaining question is whether an ensemble of all 69 algorithms (42 original plus 27 new variants) offers a meaningful improvement. The weights were calculated to minimize the cv-AUC, as described earlier. Instead of relying on 10-fold cross validation, we evaluated the loss on an external validation set. The dataset contained information on patients with at least one risk factor seen in Atrius in 2016 (n = 245,475, 16 of whom were cases).³ Two percent of these 2016 patients were also in the 2007–2015 dataset used to fit the model, albeit with different values of time-dependent covariates. This small correlation may cause AUCs to be slightly optimistic. However, it provides a reasonable platform for comparing AUCs of the augmented ensemble SL, the original ensemble SL, and each of the 69 individual algorithms (Table 6). Variants of ridge and lasso had the highest AUC (0.91), confirming the original results. XGBoost was an improvement over random forest (AUC = 0.90 vs 0.66). SL using the augmented library was better than SL on the original library (AUC = 0.88 vs 0.80). However, many algorithms were superior to both.

TABLE 6.

Cross-validated area under the receiver-operating curve (95% CI) for all algorithms based on Atrius 2016 data

Algorithm	cv-AUC	Algorithm	cv-AUC	Algorithm	cv-AUC
ridge10,dev	0.915(0.884, 0.946)	xgb50,4,25	0.862(0.824, 0.899)	xgb20,4,10	0.805(0.762, 0.847)
ridge20,dev	0.909(0.877, 0.941)	xgb20,2,10	0.858(0.820, 0.896)	lasso20,pre,dev	0.803(0.761, 0.846)
lasso20,dev	0.905(0.873, 0.938)	glmStep50	0.857(0.818, 0.895)	lasso10,pre,dev	0.801(0.758, 0.844)
lasso20,auc	0.898(0.865, 0.932)	nn50,5	0.855(0.817, 0.893)	SL42	0.800(0.758, 0.843)
xgb20,4,50	0.895(0.861, 0.929)	xgb10,2,10	0.855(0.816, 0.893)	nn20,2	0.799(0.756, 0.841)
xgb20,2,50	0.895(0.861, 0.929)	glm10,pre	0.848(0.809, 0.887)	glm20,pre,wt	0.798(0.755, 0.841)
ridge20,auc	0.895(0.861, 0.929)	glmStep50,pre	0.843(0.803, 0.882)	lasso20,pre,auc	0.790(0.747, 0.834)
xgb50,2,50	0.893(0.859, 0.927)	glm20	0.839(0.799, 0.879)	svm50,pre	0.783(0.739, 0.827)
xgb50,4,50	0.893(0.859, 0.927)	glm10,pre,wt	0.837(0.797, 0.877)	glm20,wt	0.747(0.702, 0.793)
lasso10,dev	0.892(0.858, 0.926)	glm50,pre,wt	0.836(0.796, 0.876)	glm10	0.739(0.693, 0.785)
xgb10,2,50	0.890(0.856, 0.925)	glm50,pre	0.834(0.794, 0.875)	xgb10,4,10	0.735(0.689, 0.781)
lasso10,auc	0.890(0.856, 0.924)	SL.xgboost	0.825(0.784, 0.866)	glm20,pre	0.692(0.644, 0.739)
xgb10,4,50	0.890(0.855, 0.924)	ridge20,pre,auc	0.823(0.782, 0.864)	svm50	0.680(0.632, 0.728)
ridge10,auc	0.888(0.853, 0.922)	ridge10,pre,auc	0.819(0.777, 0.860)	rForest10	0.664(0.616, 0.712)
xgb50,2,25	0.882(0.847, 0.917)	nn10,2	0.819(0.777, 0.860)	rForest20	0.657(0.609, 0.706)
xgb20,2,25	0.880(0.845, 0.916)	glm50	0.818(0.777, 0.860)	rForest20,pre	0.643(0.594, 0.691)
xgb10,4,25	0.878(0.842, 0.914)	nn10,1	0.817(0.776, 0.859)	rForest10,pre	0.626(0.578, 0.674)
SL69	0.876(0.839, 0.912)	nn20,5	0.817(0.776, 0.859)	rForest50	0.569(0.521, 0.617)
nn50,2	0.873(0.836, 0.909)	nn20,1	0.817(0.775, 0.858)	rForest50,pre	0.569(0.520, 0.617)
xgb20,4,25	0.870(0.833, 0.907)	lasso10,pre,auc	0.816(0.775, 0.858)	glm10,wt	0.515(0.468, 0.562)
xgb50,2,10	0.867(0.830, 0.904)	ridge20,pre,dev	0.815(0.773, 0.856)	nnet10,5h,pre	0.500(0.453, 0.547)
nn50,1	0.864(0.827, 0.902)	glm50,wt	0.812(0.770, 0.854)	nnet10,10h,pre	0.500(0.453, 0.547)
xgb10,2,25	0.862(0.825, 0.900)	nn10,5	0.810(0.768, 0.852)	nnet20,5h,pre	0.500(0.453, 0.547)
		ridge10,pre,dev	0.808(0.766, 0.850)	nnet20,10h,pre	0.500(0.453, 0.547)

Subscript key: (50, 20,10): # controls per case, pre: 23 pre-selected covariates, auc: neg AUC loss.

dev: deviance loss, wt: weighted regression, 5h, 10h: # nodes in hidden layer.

xgb subscript key: (a, b, c): a = # controls per case, b=depth, c = min obs per node.

nn subscript key: (a, b): a = # controls per case, b= # nodes in hidden layer.

95% confidence interval method calculated using Hanley’s method.⁴⁸ Method of LeDell et al (2015) is not applicable to single external validation set.

5 |. DISCUSSION

This project was motivated by a compelling public health need to increase PrEP uptake in vulnerable populations. It demonstrated that information routinely captured in the EHR can play an important role in automated identification of high risk patients. Choosing a risk score threshold to identify patients who should be further evaluated as PrEP candidates involves trading off sensitivity and specificity. This trade-off should take into acount the relative costs of false positives and false negatives, and the availability of local resources to act on the information (see Reference 3).

The target statistical parameter was defined as a function of covariate history that could be applied regardless of the actual length of the medical history. We knew that many of the strong behavioral predictors of HIV risk are not well captured in the EHR. However, we hoped there might be predictive power in variables that are present in the data. We initially created a rich set of covariates that defined a high-dimensional model space. We did not know if it, or any subset of the model space, would have sufficient predictive power.

Using SL allowed us to investigate a diverse set of parametric and machine learning approaches to developing a risk prediction model. This work adds to the body of literature demonstrating that instead of trying to anticipate what will work best for analyzing a given dataset, an analyst can instead use SL to investigate many options simultaneously. Cross validation (discrete SL) allowed us to identify the best performing algorithm among the 71 candidates in a principled manner (42 original algorithms, 27 supplemental algorithms, an ensemble SLs with either 42 or 69 algorithms in the library).

We strove to develop a model with good predictive power that could be easily integrated into the EHR system. A low-dimensional model with good performance characteristics emerged. Because lasso turned out to be the top performing algorithm, we were able to write down a simple logistic regression model for EHRs programmers to implement, and clinicians to assess. We expect this will facilitate adoption of the model and its recommendations in practice. The lasso model is easy to implement and to update, even in small clinics and public health departments in resource-poor areas of the United Sates. We also wanted to be able to compare the performance of sophisticated methods with what might traditionally be done in practice, that is, concerned clinicians using their expertise to select covariates and limited interaction terms for a logistic regression model, then estimating the coefficients from data. For these reasons, we included logistic regression in our SL library. While it did well, more data-adaptive methods were better able to exploit the available information in the data. The distinctions between variants of each library algorithm were often small, but sometimes offered large gains in cv-AUC. Since ensemble SL did not outperform every other candidate, we were spared having to weigh pros and cons of trading off transparency and familiarity with predictive performance.

We found that increasing the balance between cases and controls improved predictive performance of some algorithms, but not others. The ideal class ratio depended on the information content of the data and characteristics of the prediction algorithm. We found it helpful to examine each algorithm’s behavior using simulated data that mimicked salient characteristics of the real world data. This improved our understanding of how different algorithms performed at different ratios of cases to controls when the proportion of outcome events was on the order of 10⁻⁴. We saw that random forest performed much better when presented with a more balanced class ratio than the 1:50 ratio in our original dataset. Internal calculations rely on subsets of the observations that are uninformative if they contain only cases or only controls. Large imbalances will delay convergence. Weighted glm, a maximum likelihood-based algorithm, performed better when more observations were available, even though the imbalance was greater. Promising variants of each of these algorithms were included in our SL library.

An alternate strategy for improving class balance is to oversample the less prevalent class. Another option is the synthetic minority over-sampling technique (SMOTE) that creates synthetic cases with covariate profiles similar to observations already in the data.⁴⁵ While oversampling is often recommended in the literature, some research has shown that cross-validated loss calculations can be overly optimistic when the minority class is oversampled, and that undersampling can sometimes better address class imbalance.^46,47 We chose to undersample rather then oversample because the computational resources needed to analyze the much larger dataset produced by retaining all controls and an appropriate fraction of resampled cases would have forced us to reduce the size of the SL library.

Although the rarity of the outcome suggested that overfitting could be a concern, we also knew that many of the strong behavioral predictors of HIV risk are not well captured in the EHR. We initially created a rich set of covariates that defined a high-dimensional model space. At the outset, we did not know if it, or any subset of the model space, would have sufficient predictive power. However, we were pleased to see that a low-dimensional model with good performance characteristics emerged.

It was not clear at the outset whether the machine learning algorithms would perform better when given access to the entire set of covariates or when restricted to the smaller expert-selected covariate set. We found that the answer depends on the nature of the candidate algorithm. Algorithms that themselves select covariates or shrink coefficients (lasso, ridge, random forest) performed better when provided with the full set of covariates. Logistic regression modeling was improved by relying on the pre-selected subset.

A limitation of our approach is that both our original and augmented SL libraries may have excluded a better-performing algorithm. We tried to include a rich set of algorithms that could feasibly be investigated. Our primary focus was on mitigating the impact of class imbalance without losing the diversity in the distribution of covariates in the large number of available controls. We saw that boosted trees had better discriminatory ability than random forest. Performance approached that of lasso and ridge regression modeling.

The library specification problem is one that analysts have to grapple with every time they use SL. SL enables the analyst to try variants of machine learning algorithms without requiring deep expertise in all of them. When possible, we recommend experimenting on simulated data to develop an understanding of which tuning parameters most impact performance, and then including that algorithm in the SL library several times, with different settings of influential tuning parameters, rather than omitting the algorithm entirely. In our project, SVM and neural network performance might have further improved with other choices of tuning parameters.

There may also be limitations to re-scaling on the logit scale when using the prior correction method. For example, why not the probit scale? These two distributions differ most in the tails. In this application the predicted probability values were quite low, so the choice might affect predictive accuracy. This remains an area of future work, as does improving our understanding of when weighting is preferable to re-scaling.

We previously studied the generalizability of the fitted model.³ The model we developed using data specific to the historical Atrius-based patient mix and standards of care had exceptional performance when applied to Atrius data collected in 2016, but performed less well when applied to data collected 2011–2016 by Fenway Health, an independent community health center specializing in healthcare for sexual and gender minorities. (n = 33,404, 423 cases, AUC = 0.77). This suggests that the model fails to generalize to care settings where covariate-risk associations differ. Predictive accuracy could also change as standard medical practice evolves over time. Even when the model fails to generalize to other patient populations, the approach itself is transferrable. A site-specific risk prediction model could easily be developed by following the steps outlined in this article.