Abstract
Objective
Data integration methods that combine data from different molecular levels such as genome, epigenome, transcriptome, etc., have received a great deal of interest in the past few years. It has been demonstrated that the synergistic effects of different biological data types can boost learning capabilities and lead to a better understanding of the underlying interactions among molecular levels.
Methods
In this paper we present a graph-based semi-supervised classification algorithm that incorporates latent biological knowledge in the form of biological pathways with gene expression and DNA methylation data. The process of graph construction from biological pathways is based on detecting condition-responsive genes, where 3 sets of genes are finally extracted: all condition responsive genes, high-frequency condition-responsive genes, and P-value–filtered genes.
Results
The proposed approach is applied to ovarian cancer data downloaded from the Human Genome Atlas. Extensive numerical experiments demonstrate superior performance of the proposed approach compared to other state-of-the-art algorithms, including the latest graph-based classification techniques.
Conclusions
Simulation results demonstrate that integrating various data types enhances classification performance and leads to a better understanding of interrelations between diverse omics data types. The proposed approach outperforms many of the state-of-the-art data integration algorithms.
Keywords: gene expression, DNA methylation, semi-supervised learning, graph theory, ovarian cancer, data integration
INTRODUCTION
As a fast-growing field, translational bioinformatics translates biomedical and genomic data into applicable medical knowledge that can be further used to investigate the underlying genomic structures of different impairments in the human body.1,2 Such knowledge can be used to predict clinical outcomes or diagnose disease stages to guide medical interventions. Molecular-based data, such as DNA methylation and gene expression, are provided by microarray technology, enabling researchers to analyze the underpinnings of diseases at a genomic level.3,4,37,38
Despite the rich literature available on microarray data analysis and machine learning algorithms, it is a challenge to take advantage of different genomic levels to gain better insight into the structure of a given disease. Each genomic level can provide us with increased information on the tissue of interest. For example, at the genome level, copy number alterations can broaden our knowledge to larger regions of the genome, called chromosomes, even when entire chromosomes are not duplicated. At the epigenome level, DNA methylation plays an important role, and at the transcriptome level, gene expression and microRNA (miRNA) represent the molecular signatures. Transcriptome data has long been the main pillar of translational bioinformatics.5–9
Although omics data can be used directly for diagnostic purposes, a single level of data may not include enough information to elucidate the underlying structure of the disease. Therefore, it seems useful to leverage the hidden knowledge in different omics levels as a whole to make more accurate predictions. During the past few years, integrated omics methods have been introduced in numerous papers. This issue has been addressed from several different points of view. In general, data integration methods can be categorized into 2 groups:10 multistaged analysis and metadimensional analysis. In multistaged analysis, only 2 scales can be used at a time to construct a model in a linear, stepwise, or hierarchical manner. Here, scale means the numerical or categorical features of the data. In metadimensional analysis, all the scales of the data are combined simultaneously.10 Genomic variation analysis methods, such as expression quantitative trait loci and methylation quantitative trait loci,11–13 and domain knowledge–guided analysis methods are examples of multistaged analysis approaches.14–16 Metadimensional analysis approaches are 3-fold:10 concatenation-based integration methods such as Bayesian networks17 and multivariate Cox lasso models,18 transformation-based integration methods such as kernel-based integration methods19 and graph-based semi-supervised learning (SSL) algorithms,20 and model-based integration methods such as majority voting21 and ensemble classifiers.22 Another viewpoint on phenotype classification and disease gene discovery was proposed by Hwang et al.39 Their method, called regularized non-negative matrix tri-factorization (R-NMTF), tries to co-cluster phenotypes and genes along with simultaneous detection of associations between the detected phenotype clusters and gene clusters.
One of the main difficulties in handling microarray data is its complexity and large number of features, eg, genes, compared to the number of samples (the “curse of dimensionality”). An efficient approach to tackle such a computational burden is to employ graph-based approaches that have proven to work well when dealing with complex data such as manifolds. In this regard, Shin et al.23 proposed a graph sharpening approach along with graph integration. In principle, graph sharpening is a method to reduce the noise effects in a scalable manner in order to prune irrelevant and redundant edges in a graph to increase learning. Their method addresses the prediction of protein functions based on graph-based SSL and graph integration in order to provide synergy for better classification. To overcome the inherent effects of noise, they also proposed a method called graph sharpening, which has improved the area under the receiver operating characteristic (ROC) curve by 30%. In another study, Tsuda et al.24 addressed protein classification using multiple protein networks such as physical interaction networks. Due to the sparsity of network edges, the computational time is linear and combinations of the weights of the edges can provide useful information in order to reduce noise.
Synergistic effects of different levels of genomic data have been addressed by Kim et al.,25 where copy number alterations, DNA methylation, gene expression, and miRNA data have been used to classify glioblastoma multiforme into low and high grades. They employ ordinary graph-based semi-supervised methods for each layer and concatenate them via a linear programming model, but do not take into account the interrelationships between different sets of genomic features. To do so, in,26 intrarelation of gene expression was constructed from interrelation between miRNA and gene expression to predict short-/long-term survival of patients with glioblastoma multiforme. In a similar approach,27 interrelationships among multiomics data have been addressed in order to consider such relations contributing to regulation or dysregulation of cancer. By incorporating lateral biological knowledge such as pathway information into the model proposed in,25 a boosted graph-based method is introduced in.28 This method averages expression values of the genes belonging to a pathway and uses them as a single new feature so that each genomic level can be represented by 2 graphs: 1 is constructed from the original data and the other is composed of the same samples plus the new set of features. There are some issues with this approach. Although this method takes the average of the genes belonging to each pathway, not all of those genes will necessarily be upregulated or downregulated with respect to the phenotype. On the other hand, some of the genes in each pathway might not be statistically meaningful, so just taking a simple average may not make biological sense.
To address this issue, we propose a new graph-based semi-supervised approach considering pathway information through employing condition-responsive genes (CORGs).29 CORGs are sets of genes belonging to particular biological pathways. According to,29 to obtain the CORGs of a certain biological pathway, the constituting genes of the pathway are ranked in such a way that their average expression values across all the samples provide the largest degree of discrimination between cases and controls based on statistical 2-sided t test. As a result, for each pathway, the most discriminative set of genes containing the highest statistical signal level are picked. On the contrary, gene set enrichment analysis employs all members of a pathway and incorporates them in the hypergeometric statistical test to measure the pathway activity. In this sense, it is unlikely that the whole genes together provide the largest discrimination between cases and controls. As a result, CORGs can keep the biological meaningfulness of their members while yielding the maximum statistical signal.
After obtaining the CORGs for each pathway, 3 approaches are employed, yielding 3 different sets of features. The 3 approaches are as follows:
Consider all the genes in the obtained CORGs and use them to construct the graph.
Sort all the genes in the CORGs in ascending order based on their P-values and then filter out the genes having P-values larger than a threshold.
Consider high-frequency genes in all the CORGs and use them to construct the graph.
Generally, the main objectives and novelties of this research study can be summarized as follows:
Incorporate CORGs in the form of a graph to be coupled with molecular data types to increase prediction accuracy.
Develop 3 gene selection mechanisms using CORGs to extract highly discriminative biomarkers curated from biological pathways to reflect the impact of latent biological knowledge on phenotype classification.
Provide a more powerful graph-based SSL system than other existing single and multiomics classification algorithms.
The remainder of this paper is organized as follows: In the next section, a brief overview of the currently existing methods being used are provided. Then, the proposed approach will be given under the section ‘The Proposed Approach’ followed by the datasets being used and numerical experiments and comparisons. Finally, conclusion remarks will be discussed.
AN OVERVIEW OF THE METHODS BEING EMPLOYED
In this section, we provide a brief overview of some of the methods used in this paper. First, basics of graph-based SSL are reviewed. Then the optimization framework used to integrate different genomic layers is described.
Graph-based semi-supervised learning
SSL methods stand between unsupervised methods, where training samples are entirely unlabeled, and supervised methods, where all training samples are labeled. SSL algorithms make use of unlabeled data along with labeled samples to enrich the training set and construct a more efficient and reliable classifier, especially when a large amount of unlabeled samples is available. The performance of such classifiers is measured on the unlabeled samples only. According to,30,31,35 the key to SSL approaches is the consistency assumption, which states that (1) points on the same structure (ie, manifolds) are likely to have the same label and (2) nearby points are also likely to have the same label. SSL methods have proven to be quite productive in dealing with complex datasets such as biological data, where data structures are intertwined. Various types of SSL algorithms such as spectral methods,32,33 graph mincuts,34 transductive support vector machines (SVMs),31 and random walks36 can be found in the literature.
In this paper we employed the SSL method proposed by Zhou et al.30 In this approach, each node represents a sample and the edges can be established between nodes using the K nearest neighbors method. In fact, edges between nodes convey the mutual relationship between the samples. The more the weight of the edge, the more likely the nodes it connects to will have the same label.
K nearest neighbors of each sample can be computed by ordinary Euclidean distance, and the weight of the edges obtained using the Gaussian kernel. Suppose is the entire set of samples comprising labeled samples and unlabeled samples. Let denote the class labels. Let be an matrix corresponding to classification of the set , where sample belongs to class if . Here, is a vector function that assigns a vector to each sample . According to,30 the matrix is obtained from (1):
| (1) |
where is an identity matrix and denotes the tradeoff parameter between the 2 conditions of smoothness and loss. Also, denotes the labels where samples are labeled by 1 and −1 and unlabeled samples are represented by 0. Here, is the graph Laplacian matrix, where is the symmetric weight matrix calculated in Eq. 2 and is given by (3).
| (2) |
| (3) |
where .
Graph integration
One of the goals of this paper is to integrate the computed graphs as the result of applying SSL on each genomic level. The purpose of graph integration is to leverage hidden knowledge in the gene expression and DNA methylation data along with biological knowledge such as pathway information to obtain the best classification performance. The integration process can be carried out by finding the optimal combination of each dataset represented by a graph. Suppose that there are graphs. The weights of the combined graphs can be obtained using the following optimization model:28
| (4) |
where and represent the graph Laplacian matrix and the optimum weight coefficient of the graph , respectively.
The final solution of the above-mentioned model can be calculated by Eq. 5:28
| (5) |
THE PROPOSED APPROACH
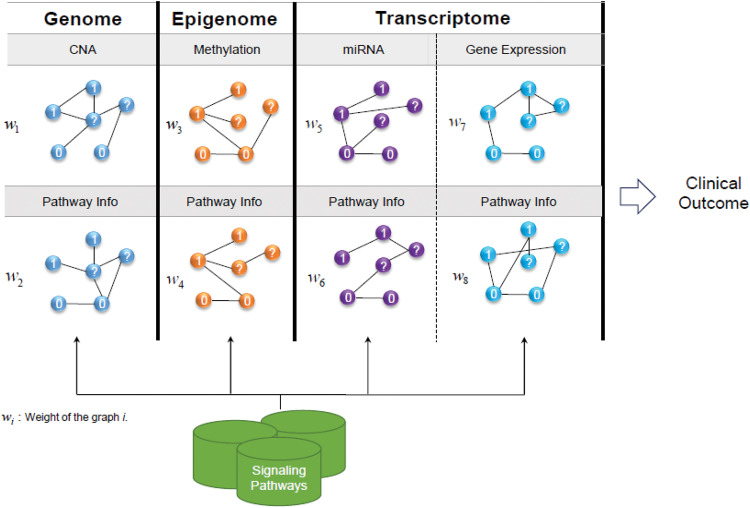
The main contribution of this paper is to provide a systematic approach to incorporating biological knowledge in the form of biological pathways into a graph-based SSL algorithm, to gain better phenotype classification performance. Here, each genomic level, such as gene expression or DNA methylation graph, will have a complementary graph containing its corresponding pathway information. Figure 1 illustrates the overall pipeline of the proposed approach. In this figure, each node represents a sample, where the samples are the same for all genomic levels being considered. Graphs of each level are constructed by the SSL algorithm. It should be mentioned that in the context of SSL, all samples, including labeled and unlabeled, are taken into account during the process of learning. In Figure 1, the 2-class problem is addressed where node classes are represented by “1” and “0” and unlabeled samples are represented by “?.”
Figure 1.
A graphical representation of the graph integration method.
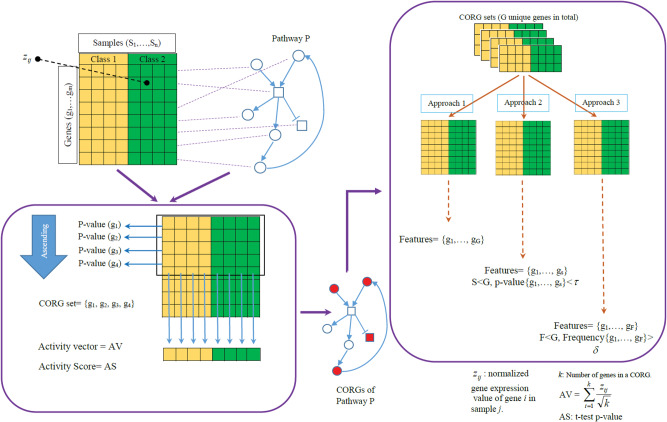
Although construction of the graphs with respect to each dataset is performed by the existing SSL algorithm discussed in the previous section, in order to construct the graphs considering biological pathways, 3 new approaches have been developed based on the set of CORGs.29 The overall pipeline of these approaches is depicted in Figure 2 .
Figure 2.
Gene extraction process from biological pathways.
Given a set of gene-wise normalized samples, each cell member of the data matrix is represented by where and represent the corresponding gene and sample, respectively. As shown in Figure 2, first the set of genes corresponding to the pathway being considered is extracted from the dataset. The extracted genes are then ordered in an ascending manner based on their P-values, computed by the statistical 2-sided t test. In the next step, a loop is applied to the members of the ascending-ordered gene set: starting from the first gene, the activity vector of that gene is constructed, and then its respective activity score is calculated. In the next step, the second gene is considered along with the first one, and their corresponding activity score is calculated. The process of adding new genes to the list of selected genes continues until the activity score no longer improves. Note that in Figure 2, the activity score of the activity vector is the same as the P-value of the vector. It should be mentioned that P-value represents the strength of the statistical discrimination between the cases and controls. In other words, the activity vector of the CORGs (a subset of certain genes belonging to a biological pathway) represents the average expression values of the most influencing genes inside the pathway such that the 2-sided statistical t test assigns the highest difference between cases and controls using this vector. By this, we can come up with a particular set of genes belonging to the same pathway while keeping the average expression levels across all cases and controls as different as possible. Given that the statistical t test is a widely used method for extracting biomarkers, activity score coupled with the t test combines the useful hidden biological knowledge of pathways with characterizing the most powerful discriminatory genes available in the data.
After extracting all the signaling genes (CORGs) of each pathway, 3 approaches were considered to shape the final set of genes for constructing the pathway graphs. In approach 1, all the genes in all the CORGs were listed and used as the final set of features. Note that it is possible that some genes are repeated in various CORGs. In such cases, just 1 of them is adopted. In approach 2, all the unique genes in the CORGs are ordered in an ascending manner based on their P-values. Then, genes with P-values larger than a threshold () are filtered out. The threshold that we set in this paper for filtering genes was 0.001. Finally, in approach 3, we make use of the number of times that each gene has been repeated in the CORGs. The more a gene is repeated, the stronger it is as a biomarker. Finally, a threshold is applied and low-frequency genes are filtered. In this paper, we set the threshold to be = 0.01 × (# pathways).
After constructing all the graphs with respect to each genomic level and biological pathway, these graphs are integrated using the graph-integration method described in the Graph integration section. The resultant graph consists of the hidden knowledge extracted from different genomic levels and biological pathways. In this method, if 2 samples have a large correlation (are closer) with respect to their labels in different levels, this will provide good synergy and the weight of their connecting edge in the final integrated graph will be large, to convey such a mutual relation. On the contrary, if the weights of the connecting edges between 2 nodes in different graphs are negligible, this will be projected onto the final integrated graph, indicating that it is highly probable that these 2 samples belong to different classes.
DATASETS
We applied the proposed approach to normalized ovarian cancer data downloaded from the Human Genome Atlas.36 We used clinical information, gene expression data, and methylation data (Table 1). Using the clinical outcomes, samples were divided into 2 classes: short survival of <3 years (group 1) and long survival of >3 years (group 2). After filtering the samples based on their clinical outcome, we came up with 340 samples, 147 in group 1 and 193 in group 2. Gene expression and methylation data contain around 28 000 and 65 000 probes, respectively.
Table 1.
Data description
| Data | Platform | # Features |
|---|---|---|
| Gene expression | Affymetrix HT Human Genome U133 Array Plate Set | 28 000 |
| DNA methylation | Infinium HumanMethylation27 Beadchip | 65 000 |
For pathway information, we used the C2 curated gene sets from MSigDB v5.0 containing 472 canonical and signaling pathways. The pathways are pooled from 9 manually curated databases. In total, these sets contain 4725 genes.
EXPERIMENTAL RESULTS AND DISCUSSION
To evaluate the performance of the proposed approaches, first the data was perturbed and then split into 2 groups: 80% for training and 20% for validation. The cross-validation process is 2-fold: 5 and 10. During each round of cross-validation, the training data were first perturbed and then 5- or 10-fold cross-validation was applied. The perturbation process was repeated 50 times.
We conducted a series of experiments to determine the behavior of the proposed method compared to other state-of-the-art algorithms. These experiments are listed below:
Implement SSL on DNA methylation data.
Implement SSL on gene expression data.
Implement graph-based integrated model of DNA methylation and gene expression.
Implement graph-based integrated model of DNA methylation data and pathways using the 3 feature selection approaches.
Implement graph-based integrated model of gene expression data and pathways using the 3 feature selection approaches.
Implement graph-based integrated model of DNA methylation, gene expression and pathways using the 3 feature selection approaches.
For each experiment, area under the ROC curve (AUC) and error rate (ER) have been measured. Additional metrics, including true positive rate (TPR), false positive rate (FPR), true negative rate, and false negative rate, are reported. Due to the high dimensionality of the data being used, we applied an initial filtering before conducting the experiments using the 2-sided t test and eliminated features having P-values larger than 0.05. As a result, the DNA methylation and gene expression data had around 4100 and 1000 features, respectively. To have a better understanding of the effects of multiomics data integration compared to other non–graph-based methods, we also repeated the experiments using SVM with radial basis function kernel and artificial neural network (ANN) having 2 hidden layers, each layer with 10 neurons.
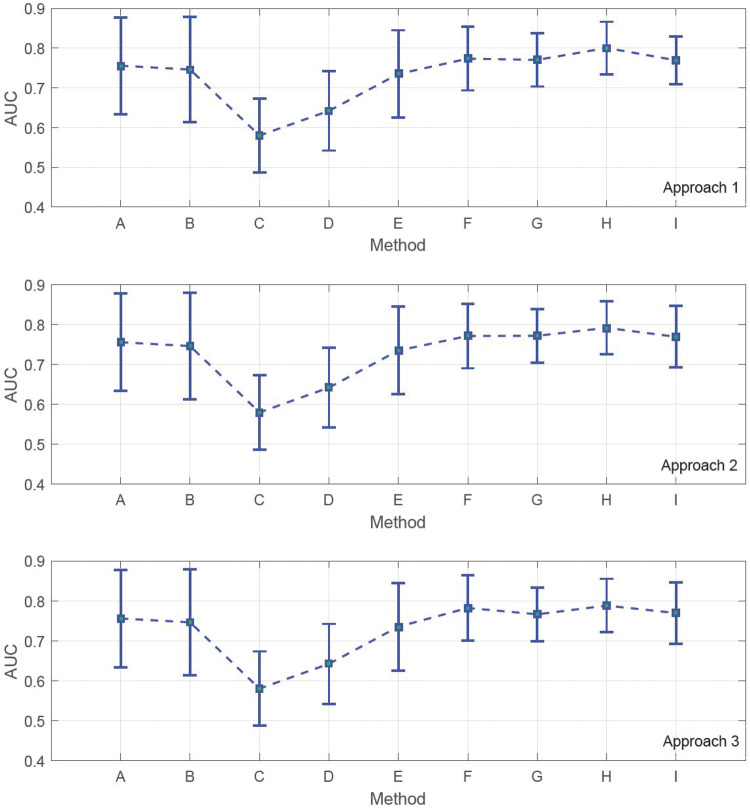
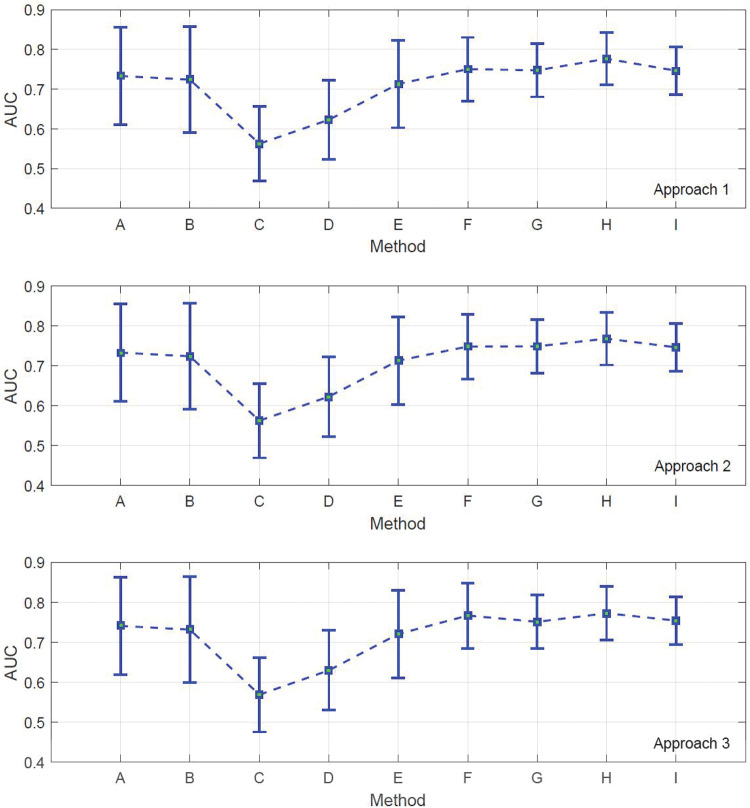
Figure 3 represents the computed AUC values for the defined experiments, along with the standard deviation of the results based on 5-fold cross-validation. The experiments were repeated with 10-fold cross-validation. The results are reported in Figure 4 .
Figure 3.
AUC measurements based on 5-fold cross-validation. Different methods were evaluated: (A) artificial neural network (ANN), (B) support vector machines (SVMs), (C) graph-based SSL on methylation data, (D) graph-based SSL on gene expression data, (E) graph-based SSL on integration of gene expression and methylation data, (F) graph-based integration of methylation data and biological knowledge using the proposed approaches, (G) graph-based integration of gene expression data and biological knowledge using the proposed approaches, (H) graph-based integration of methylation data, gene expression data, and biological knowledge using the proposed approaches, and (I) graph-based method presented in.28
Figure 4.
AUC measurements based on 10-fold cross-validation.
We expected to gain better AUCs by adding more layers of information to the training process, and this expectation was met by the computational results. Note that SVM and ANN were applied on both gene expression and DNA methylation data, but only the gene expression AUCs are reported, since they were larger. In both figures, it can be observed that simple implementation of graph-based SSL on gene expression and methylation provides the lowest AUCs, while integration of gene expression and methylation yields lower performance than SVM and ANN. This can be interpreted as an indication that each genomic level of data might not solely contribute to development of cancer and that synergistic effects of epigenetic and transcriptomic factors can be a better predictive tool.
This synergy yields more boosted AUCs as we incorporate pathway information. For instance, in Figures 3 and 4, SSL implementation on gene expression data gives a higher AUC than on methylation data; nevertheless, integration of methylation data and pathway information based on approaches 2 and 3 produces better classification results than the combination of gene expression and pathway information. This difference implies that in the context of graph-based SSL, integration of methylation and pathway data can result in a higher level of synergy compared to integration of gene expression and pathway information, and can radically boost the predictive power of methylation in classifying samples from ovarian cancer. Therefore, it can be concluded that only a portion of features belonging to the pathway sets are capable of enhancing the discrimination of samples, and the remaining features that were used in approach 1 can have a negative impact on the predictive power of the model. That is why integration of gene expression and pathway information yields better AUCs than its counterpart using DNA methylation, as demonstrated in Figure 3 (approach 1) and Figure 4 (approach 1).
The highest AUC is achieved by integration of gene expression, methylation, and pathway information datasets, which is around 0.80. The ascending trend in AUCs can be perceived as positive effects of data integration on phenotype classification. We also conducted an experiment on the method proposed by Kim et al.28 and showed that the result of this method is no better than integration of all of the data levels using our proposed approaches; however, it still gives significantly large AUCs compared to ANN, SVM, or graph-based SSL implemented independently on gene expression and DNA methylation data. In,28 the integration process is the same as ours, and the main difference is in the construction of graphs corresponding to biological pathways. In,28 genes belonging to each pathway are first extracted, and then their average is used as a new feature. The remaining genes that do not belong to any of the pathways are directly used in the process of graph construction. By averaging the genes, those genes that are not differentially expressed individually might reduce the meaningfulness of the differential expression of the average of genes belonging to a pathway. Indeed, this method yields lower AUCs compared to the 3 approaches presented in this paper, where no averaging on the genes was carried out.
To make a comparison between the 3 proposed approaches, it can be observed that approach 1 gives larger AUCs compared to the other approaches. Also, approach 3 yields slightly better results than approach 2. We can conclude that taking all the computed genes in all the CORGs has more predictive power than selecting a subset of the genes. Nevertheless, high-frequency genes, ie, genes that are repeated more in all the CORGs compared to the other genes present in all the CORGs, in approach 3 still demonstrate better performance than filtering the CORGs based on their P-values.
To get better insight into other classification criteria in addition to AUC, the following measurements were carried out: ER, TPR, FPR, positive predictive value (PPV), and negative predictive value (NPV). The measurements will be presented for both cross-validation and validation sets. According to Figures 3 and 4, our approach 1 led to the best results, so here we will only report the measurements performed in this approach. These results are represented in Tables 2–5. We will refer to our approach as graph-based SSL with pathway information (GSSLPI).
Table 2.
Cross-validation measurements on gene expression data (10-fold)
| Measure | ANN | SVM | SSL | GSSLPI | Kim et al.28 |
|---|---|---|---|---|---|
| AUC | 0.7436 ± 0.0541 | 0.7852 ± 0.1311 | 0.6746 ± 0.1115 | 0.7922 ± 0.122 | 0.7822 ± 0.128 |
| ER | 0.1930 ± 0.0798 | 0.1692 ± 0.0728 | 0.2439 ± 0.0745 | 0.1847 ± 0.0960 | 0.1819 ± 0.1003 |
| PPV | 0.7340 ± 0.2026 | 0.75316 ± 0.1732 | 0.5340 ± 0.1602 | 0.7998 ± 0.1383 | 0.7872 ± 0.1682 |
| NPV | 0.6152 ± 0.0847 | 0.7626 ± 0.1185 | 0.6061 ± 0.0745 | 0.7820 ± 0.0934 | 0.7731 ± 0.0911 |
| TPR | 0.6677 ± 0.0916 | 0.7684 ± 0.1423 | 0.65733 ± 0.1016 | 0.6971 ± 0.1978 | 0.6931 ± 0.1900 |
| FPR | 0.1395 ± 0.0424 | 0.1330 ± 0.0891 | 0.1481 ± 0.0363 | 0.1328 ± 0.1267 | 0.1376 ± 0.1217 |
We should note that in Tables 2–5, ANN, SVM, and SSL were individually implemented on each data type. In Tables 2 and 4, we used gene expression data and pathway information together, in our approach and Kim’s method.28 Similarly, in Tables 3 and 5, we used DNA methylation data and pathway information together in our approach and Kim’s method.28
Table 4.
Validation measurements on gene expression data
| Measure | ANN | SVM | SSL | GSSLPI | Kim et al.28 |
|---|---|---|---|---|---|
| AUC | 0.66924 | 0.70668 | 0.60714 | 0.71298 | 0.70398 |
| ER | 0.253 | 0.2297 | 0.2939 | 0.2447 | 0.2711 |
| PPV | 0.504 | 0.6239 | 0.5003 | 0.7048 | 0.6802 |
| NPV | 0.6142 | 0.7023 | 0.6061 | 0.7022 | 0.7020 |
| TPR | 0.63716 | 0.7175 | 0.6032 | 0.6855 | 0.6704 |
| FPR | 0.1795 | 0.1883 | 0.1901 | 0.1775 | 0.1939 |
Table 3.
Cross-validation measurements on DNA methylation data (10-fold)
| Measure | ANN | SVM | SSL | GSSLPI | Kim et al.28 |
|---|---|---|---|---|---|
| AUC | 0.6746 ± 0.1115 | 0.7608 ± 0.0895 | 0.5276 ± 0.1228 | 0.7821 ± 0.1124 | 0.7722 ± 0.1124 |
| ER | 0.1939 ± 0.0745 | 0.1591 ± 0.0689 | 0.2243 ± 0.0735 | 0.1800 ± 0.0929 | 0.2170 ± 0.0944 |
| PPV | 0.7723 ± 0.1250 | 0.79031 ± 0.0556 | 0.7324 ± 0.1349 | 0.7964 ± 0.1768 | 0.7904 ± 0.0958 |
| NPV | 0.6861 ± 0.0745 | 0.7221 ± 0.0886 | 0.6262 ± 0.1035 | 0.7474 ± 0.1182 | 0.7034 ± 0.0802 |
| TPR | 0.6926 ± 0.1350 | 0.7025 ± 0.1429 | 0.6014 ± 0.0101 | 0.7062 ± 0.1990 | 0.6962 ± 0.1154 |
| FPR | 0.1381 ± 0.0363 | 0.1939 ± 0.07774 | 0.1203 ± 0.0057 | 0.1100 ± 0.1241 | 0.1700 ± 0.1341 |
Table 5.
Validation measurements on DNA methylation data
| Measure | ANN | SVM | SSL | GSSLPI | Kim et al.28 |
|---|---|---|---|---|---|
| AUC | 0.6346 | 0.7133 | 0.5066 | 0.7232 | 0.721 |
| ER | 0.2239 | 0.1801 | 0.3043 | 0.21 | 0.227 |
| PPV | 0.70263 | 0.78031 | 0.6931 | 0.7724 | 0.7414 |
| NPV | 0.6001 | 0.6944 | 0.6062 | 0.7014 | 0.6634 |
| TPR | 0.6126 | 0.6525 | 0.6014 | 0.6462 | 0.6162 |
| FPR | 0.1573 | 0.2139 | 0.1523 | 0.131 | 0.206 |
According to Table 2, our approach ranks first in 4 metrics out of 6. The cross-validation AUC on gene expression data is roughly 0.79, but variation of the AUCs during each iteration in the process of cross-validation is higher than for ANN and SSL. Here, SVM produces the lowest ER along with the smallest standard deviation. GSSLPI exhibits superior accuracy in terms of PPV, NPV, and FPR, with a reasonable standard deviation compared to the other methods. In general, SSL yields the weakest performance across all metrics, while Kim’s method results in relatively similar measures to our approach.
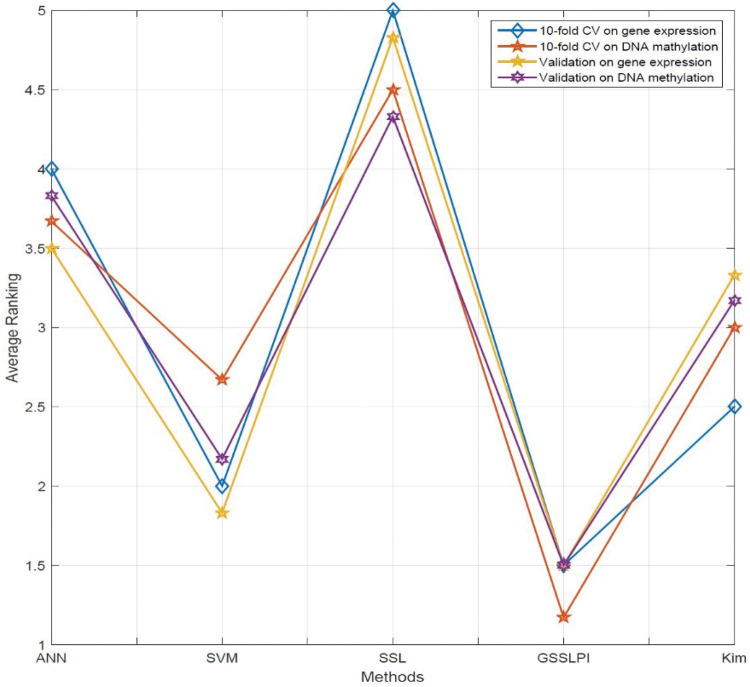
The situation for validation measurements is different. On both gene expression and DNA methylation data, our approach yields the best AUC and FPR, and SVM gives the best ER and TPR. For gene expression data, our method leads to the highest PPV, and SVM yields the highest NPV, while this situation is reversed for the DNA methylation data. In general, in our approach, SVM and Kim’s algorithm produce roughly similar results, while SSL in both datasets gives the worst classification performance. On the other hand, performance of ANN and SSL in both datasets exhibits less variation in cross-validation and validation experiments. In order to gain better intuition for the ranking of each method with respect to each metric, in Figure 5 we provide the average of rankings of each algorithm with regard to the results presented in Tables 2–5. The process of computing the rankings is as follows. Consider Table 2. For the AUC metric, GSSLPI ranking is 1, SVM is 2, Kim’s method is 3, and so on. These ranks are computed for the other 5 metrics across all methods. The obtained ranks are then averaged with respect to each method. This process was repeated for Tables 3–5. Obviously, the smaller the ranking of a method, the better its performance compared to the other methods. It is observed that GSSLPI holds the lowest average ranking across the 6 measurements: AUC, ER, PPV, NPV, TPR, and FPR. In addition to the mentioned method, we repeated the same experiments using the R-NMTF39 and observed roughly identical results. For example, on the validation side, R-NMTF led to AUCs of 0.710 and 0.7075 for the gene expression and methylation datasets, respectively. Both of these numbers are smaller than the obtained AUCs reported in Tables 4 and 5. The same situation can be observed in the 10-fold cross-validation numbers, where R-NMTF shows AUCs about 0.7735 and 0.7655 for gene expression and methylation, respectively. It can be observed that GSSLPI outperforms R-NMTF, though the difference is not significant. One reason for this can be the latent biological knowledge that these 2 methods share, and that has significant positive effects on boosting the computational accuracy.
Figure 5.
Average ranking of each method with respect to different experiments.
Despite employing a single data type, our experiments show that SVM and ANN are still powerful in dealing with the task of phenotype classification using high-throughput data. These methods are easier to implement, and there are plenty of readily available platforms providing versions of these algorithms. When it comes to taking into account molecular interactions in different layers, SVM and ANN by nature are not able to handle multiple data sets. Among multiomics methods, our focus in this research is on graph-based SSL algorithms, and we tried to increase the accuracy of some of the well-known graph-based methods in the literature. According to our numerical experiments, this has been achieved under various circumstances. On the other hand, our proposed feature selection mechanisms from biological knowledge can also be used as means for independent feature selection algorithms. However, multiomics approaches are harder to implement and less public software is available on them. They also produce marginally better classification results compared to single-omics approaches such as SVM. So, if accuracy and readiness are the main priority, then SVM, ANN, or other similar methods can be used, but if one intends to consider interactions among transcriptome, epigenome, genome, etc., while having latent biological knowledge and employ them to make a more accurate prediction, then our proposed approaches can be chosen.
In order to look at the identified driver genes from a biological perspective, we used the obtained genes during the process of model learning and graph construction and performed pathway enrichment analysis. The following top pathways were observed: Wnt signaling pathway (P = 2−10e7), p53 signaling pathway (P = 3−10e7), cell cycle (P = 4−10e7), apoptosis (P = .0000032), mitogen-activated protein kinase signaling pathway (P = .000064), and cell proliferation (P = .000000066). The observed pathways are among the most common pathways underlying a large spectrum of cancers. This finding verifies that the proposed approach is capable of not only providing high-quality classification performance, but also yielding biologically meaningful and related results to the phenotype of interest.
One of the points that can be taken for future extensions of our work is the distance measure being employed for graph construction. In this paper, we used Euclidean distance to measure how far the features were to compute the graph weights. Other measures, from statistical correlation to manifold distances, also are of interest and might be able to enhance the performance of the proposed approaches.
CONCLUSIONS
In this paper we proposed a novel method to incorporate pathway information for constructing graphs in the context of SSL. We made use of an existing graph integration approach to boost the classification performance of graph-based SSL by integrating different layers of genomic information including gene expression, DNA methylation, and their corresponding pathway information. With respect to extracting knowledge from biological pathways, 3 approaches were developed based on the concept of CORGs, where each CORG represents a set of genes belonging to a pathway. These 3 approaches take: (1) all genes in all the CORGs, (2) genes in all the CORGs based on their P-values, and (3) genes in all the CORGs having the highest frequency. Several numerical experiments were conducted on the ovarian cancer dataset downloaded from the Human Genome Atlas data portal. We demonstrated that the proposed approaches outperform other graph-based SSL algorithms and yield high-quality results compared to well-known methods with high-quality performance such as SVM and ANN. We showed that, in contrast, taking into account individual levels of genomic information may not lead to highly accurate phenotype classification. We demonstrated that integrating epigenetic, transcriptomic, and biological knowledge can dramatically boost the discriminatory power of graph-based SSL algorithms.
Funding
This research is supported by the Institute for Collaborative Biotechnologies through grant W911NF-10‐2‐0111 from the US Army Research Office. The content of the information does not necessarily reflect the position or the policy of the government, and no official endorsement should be inferred.
Conflict of Interests
The authors declare no conflict of interest.
Contributors
ADT was in charge of method development, coding, running simulations, and preparing the manuscript. LP supervised editing the manuscript from the technical and writing points of view.
References
- 1. Shah NH, Tenenbaum JD. The coming age of data-driven medicine: translational bioinformatics’ next frontier. J Am Med Inform Assoc. 2012;19 (e1):e2–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Butte AJ, Ohno-Machado L. Making it personal: translational bioinformatics. J Am Med Inform Assoc. 2013;204:595–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Doostparast Torshizi A, Fazel Zarandi MH. Alpha-plane based automatic general type-ii fuzzy clustering based on simulated annealing meta-heuristic algorithm for analyzing gene expression data. Comp Bio Med. 2015;64:347–59. [DOI] [PubMed] [Google Scholar]
- 4. van’t Veer LJ, Dai H, van de Vijver MJ, et al. . Gene expression profiling predicts clinical outcome of breast cancer. Nature. 2002;415:530–36. [DOI] [PubMed] [Google Scholar]
- 5. Fan X, Shi L, Fang H, Cheng Y, Perkins R, Tong W. DNA microarrays are predictive of cancer prognosis: a re-evaluation. Clin Canc Res. 2010;16:629–36. [DOI] [PubMed] [Google Scholar]
- 6. Nguyen T, Khosravi A, Creighton D, Nahavandi S. Hidden Markov models for cancer classification using gene expression profiles. Inf Sci. 2015;316:293–307. [Google Scholar]
- 7. Zhang L, Qian L, Ding C, Zhou W, Li F. Similarity-balanced discriminant neighbor embedding and its application to cancer classification based on gene expression data. Comp Bio Med. 2015;64:236–45. [DOI] [PubMed] [Google Scholar]
- 8. Vidal M, Peg V, Galvan P, Tres A, et al. . Gene expression–based classifications of fibroadenomas and phyllodes tumors of the breast. Mol Onc. 2015;9:1081–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Gillies CE, Siadat MR, Patel NV, Wilson GD. A simulation to analyze feature selection methods utilizing gene ontology for gene expression classification. J Bio Inf. 2013;466:1044–59. [DOI] [PubMed] [Google Scholar]
- 10. Ritchie MD, Holzinger ER, Li R, Pendergrass SA, Kim D. Methods of integrating data to uncover genotype-phenotype interactions. Nat Rev. 2015;16:85–97. [DOI] [PubMed] [Google Scholar]
- 11. Schadt EE, et al. . An integrative genomics approach to infer causal associations between gene expression and disease. Nat Gen. 2005;37:710–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Shabalin AA. Matrix eQTL: ultra fast eQTL analysis via large matrix operations. Bioinformatics. 2012;28:1353–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Abecasis GR, Cardon LR, Cookson WO. A general test of association for quantitative traits in nuclear families. Amer J Hum Gen. 2000;661:279–92. [Google Scholar]
- 14. Wang K, Li M, Hakonarson H. ANNOVAR: functional annotation of genetic variants from high-throughput sequencing data. Nuc Acid Res. 2010;38 (e164). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Ward LD, Kellis M. HaploReg: a resource for exploring chromatin states, conservation, and regulatory motif alterations within sets of genetically linked variants. Nuc Acid Res. 2012;40:D930–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Boyle AP, et al. . Annotation of functional variation in personal genomes using RegulomeDB. Gen Res. 2012;229:1790–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Fridley BL, Lund S, Jenkins GD, Wang LA. Bayesian integrative genomic model for pathway analysis of complex traits. Gen Epi. 2011;364:352–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Mankoo PK, Shen R, Schultz N, Levine DA, Sander C. Time to recurrence and survival in serous ovarian tumors predicted from integrated genomic profiles. PloS One. 2011;611:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Lanckriet GRG, De Bie T, Cristianini N, Jordan MI, Noble WS. A statistical framework for genomic data fusion. Bioinformatics. 2004;2016:2626–35. [DOI] [PubMed] [Google Scholar]
- 20. Tsuda K, Shin H, Schölkopf B. Fast protein classification with multiple networks. Bioinformatics. 2005;21:ii59–65. [DOI] [PubMed] [Google Scholar]
- 21. Draghici S, Potter RB. Predicting HIV drug resistance with neural networks. Bioinformatics. 2003;191:98–107. [DOI] [PubMed] [Google Scholar]
- 22. Akavia UD, et al. . An integrated approach to uncover drivers of cancer. Cell. 2010;1436:1005–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Shin H, Lisewski AM, Lichtarge O. Graph sharpening plus graph integration: a synergy that improves protein functional classification. Bioinformatics. 2007;2323:3217–24. [DOI] [PubMed] [Google Scholar]
- 24. Tsuda K, Shin H, Scholkopf B. Fast protein classification with multiple networks. Bioinformatics. 2007;2123;3217–24. [DOI] [PubMed] [Google Scholar]
- 25. Kim D, Shin H, Song YS, Kim JH. Synergistic effect of different levels of genomic data for cancer clinical outcome prediction. J Biomed Inf. 2012;45:1191–98. [DOI] [PubMed] [Google Scholar]
- 26. Kim D, Shin H, Joung JG, Lee SY, Kim JH. Intra-relation reconstruction from inter-relation: miRNA to gene expression. BMC Syst Bio. 2013;73:1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Kim D, Shin H, Sohn KA, Verma A, Ritchie MD. Incorporating inter-relationships between different levels of genomic data into cancer clinical outcome prediction. Methods. 2014;67:344–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Kim D, Joung JG, Sohn KA, et al. . Knowledge boosting: a graph-based integration approach with multi-omics data and genomic knowledge for cancer clinical outcome prediction. J Am Med Inform Assoc. 2015;22:109–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Lee E, Chuang HY, Kim JW, Ideker T, Lee D. Inferring pathway activity toward precise disease classification. PLoS Comp Bio. 2008;411:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Zhou D, Bousquet O, Lal TN, Weston J, Scholkopf B. Learning with local and global consistency. Proc Adv Neural Inform Process Syst. 2004. [Google Scholar]
- 31. Zhu X, Goldberg AB. Introduction to Semi-Supervised Learning. San Rafael, CA: Morgan and Claypool; 2009. [Google Scholar]
- 32. Belkin M, Niyogi P. Semi-supervised learning on Riemannian manifolds. Mach Lrn. 2004;56:209–39. [Google Scholar]
- 33. Joachims T. Transductive learning via spectral graph partitioning. Proceedings of International Conference on Machine Learning. Washington, DC: ICML; 2003. [Google Scholar]
- 34. Blum A, Chawla S. Learning from labeled and unlabeled data using graph mincuts. Proceedings of International Conference on Machine Learning. Williamstown, MA: ICML; 2001. [Google Scholar]
- 35. Zhu X, Ghahramani Z, Lafferty J. Semi-supervised learning using Gaussian fields and harmonic functions. Proceedings of International Conference on Machine Learning. Washington, DC: ICML; 2003. [Google Scholar]
- 36. Doostparast Torshizi A. http://www.cancergenome.nih.gov/. Accessed October 2016.
- 37. Fazel Zarandi MH, Doostparast Torshizi A. A new validation criteria for type-2 fuzzy c-means and possibilistic c-means. 2012 Annual Meeting of the North American Fuzzy Information Processing Society (NAFIPS). USA; 2012. [Google Scholar]
- 38. Doostparast Torshizi A, Fazel Zarandi MH, Rostam Niakan Kalhori M. A two-stage meta-heuristic approach to general type-ii fuzzy clustering for microarray data analysis. IEEE Conference on Norbert Wiener in the 21st Century (21CW). USA; 2014. [Google Scholar]
- 39. Hwang TH, et al. . Co-clustering phenome–genome for phenotype classification and disease gene discovery. Nucl. Acid Res. 2012;4019:e146. [DOI] [PMC free article] [PubMed] [Google Scholar]