Internet search query data improve forecasts of daily emergency department volume

Abstract

Objective

Emergency departments (EDs) are increasingly overcrowded. Forecasting patient visit volume is challenging. Reliable and accurate forecasting strategies may help improve resource allocation and mitigate the effects of overcrowding. Patterns related to weather, day of the week, season, and holidays have been previously used to forecast ED visits. Internet search activity has proven useful for predicting disease trends and offers a new opportunity to improve ED visit forecasting. This study tests whether Google search data and relevant statistical methods can improve the accuracy of ED volume forecasting compared with traditional data sources.

Materials and Methods

Seven years of historical daily ED arrivals were collected from Boston Children’s Hospital. We used data from the public school calendar, National Oceanic and Atmospheric Administration, and Google Trends. Multiple linear models using LASSO (least absolute shrinkage and selection operator) for variable selection were created. The models were trained on 5 years of data and out-of-sample accuracy was judged using multiple error metrics on the final 2 years.

Results

All data sources added complementary predictive power. Our baseline day-of-the-week model recorded average percent errors of 10.99%. Autoregressive terms, calendar and weather data reduced errors to 7.71%. Search volume data reduced errors to 7.58% theoretically preventing 4 improperly staffed days.

Discussion

The predictive power provided by the search volume data may stem from the ability to capture population-level interaction with events, such as winter storms and infectious diseases, that traditional data sources alone miss.

Conclusions

This study demonstrates that search volume data can meaningfully improve forecasting of ED visit volume and could help improve quality and reduce cost.

INTRODUCTION

Emergency departments (EDs) in the United States have been growing increasingly crowded. From 2001 to 2008, ED visit volume grew roughly twice as fast as the total U.S. population, while the number of total hospital beds shrank by about 198 000_.^1,2 Between 1993 and 2003, the number of EDs in the United States shrank by 425, while total visit volume increased by 26%.³ Similar trends are being reported across the world in studies from the United Kingdom,⁴ Australia,⁵ Singapore,⁶ Brazil,⁷ and South Korea.⁸ Furthermore, the responsibilities of EDs have expanded beyond traditional acute care to include indigent care, disaster response, observational care, mental health services, and other services traditionally associated with primary care.^9,10 For patients, this increased crowding has been shown to be associated with longer patient wait times, worsened quality of care,^11,12 worsened health outcomes,¹³ risks to patient safety,¹⁴ delayed access to life-saving treatment,^15,16 and lower patient satisfaction.¹⁷ For staff, crowding is associated with lower job satisfaction and increased career burnout.¹⁸ Improved forecasting of visit volume could help EDs better manage their staffing and other resources to accommodate fluctuations and reduce crowding. Additionally, improved forecasting accuracy could allow for decreased staffing during times of low demand and reduced departmental costs.

A number of previous studies have examined the relationship of different variables to ED visits. The majority of previous studies attempting to predict ED visit volume are descriptive in nature, assessing correlations among visit volume, calendar variables, and sometimes historical weather data.^19–23 Some of these studies found weather to be correlated with ED visits, whereas others did not. The direction and magnitude of these correlations seems to vary by location. Many of the studies note patterns in ED visits relating to holidays, month of the year, and other special events. Almost all studies agree that day of the week is one of the strongest trends in ED visits, while exactly which particular days are busy seems to vary. Special local events such as flu outbreaks,²⁴ heat waves,²⁵ blackouts,²⁶ sporting events,²⁷ and publicity over Presidential heart surgery²⁸ have also been shown to have effects on local ED visits.

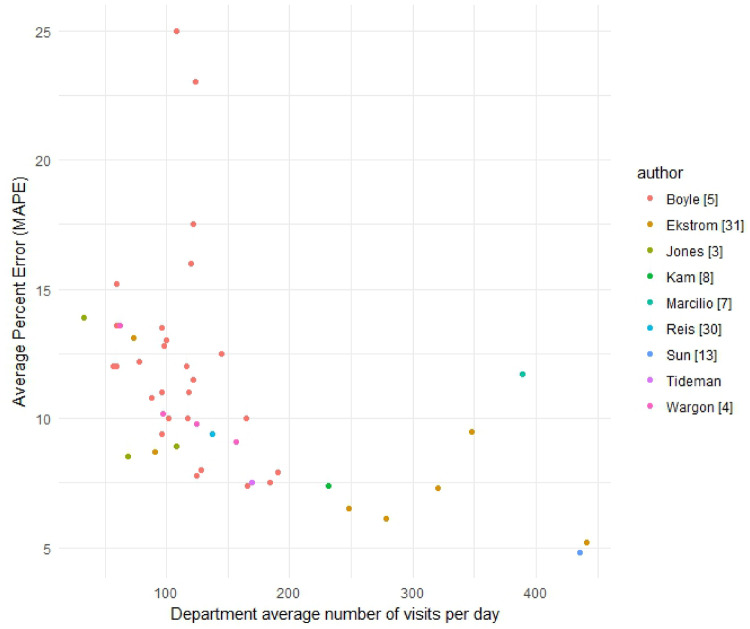
There is a growing body of literature that uses statistical forecasting methods to predict daily ED visit counts, testing model accuracy on an out-of-sample dataset, with generalizable measures of accuracy.^2–8,29,30 We believe that this is the correct approach to allow comparisons across departments, data sources, and modeling techniques and best simulate the real-world performance of a forecasting model. Previous studies represent a diverse collection of EDs from 7 different countries and average daily visit counts ranging from 33 to 441. These studies have used a variety of methods such as linear regression, random forest regression, neural nets, and time series methods such as SARIMA (seasonal autoregressive integrated moving average). While these studies make use of weather and calendar variables, none of them take advantage of the growing number of potential data sources available through the Internet. Ekström et al³¹ utilized novel data sources by using internet traffic to a Swedish health department website to predict ED visits in the Stockholm area. Mean absolute percent error (MAPE), the average percent difference between the forecast and the actual visit count, is the most commonly used metric because it allows comparisons across departments of different sizes. Looking at the results of these previous studies (Figure 1), we can see that despite the diversity in department characteristics and statistical methods, many studies achieve similar overall MAPE. There also appears to be a downward trend with department size, suggesting that forecasts for larger departments can achieve a lower MAPE, as would be expected due to the law of large numbers.

Figure 1.

Accuracy of previous studies. MAPE: mean absolute percent error.

Internet search volume has been seen as a possible additional data source for public health monitoring. In 2008, Polgreen et al³² used Yahoo searches for influenza surveillance. In 2009, Google released Google Flu Trends (GFT), a model based on anonymized, aggregated search activity of selected terms that predicts the official influenza-like illness levels in the United States reported by the Centers for Disease Control and Protection.^33,34 However, GFT’s early predictive performance was disappointing and led to doubts about the validity of its original approach.³⁵ A growing body of research has attempted to expand upon GFT’s results and has demonstrated noticeable improvements.^36–40 Notably, Yang et al⁴¹ demonstrated how LASSO (least absolute shrinkage and selection operator) variable selection of autoregressive linear regression combined with dynamic recalibration can yield substantially better influenza-like illness predictions than can previous approaches.

The methods learned from predicting influenza and other diseases using search volume data^42–47 could also be used to improve forecasts of ED visit volume beyond the accuracy of previous data sources alone. The techniques used in our study can easily be applied to other departments to forecast visit volume and potentially improve staffing practices.

MATERIALS AND METHODS

ED visit volume

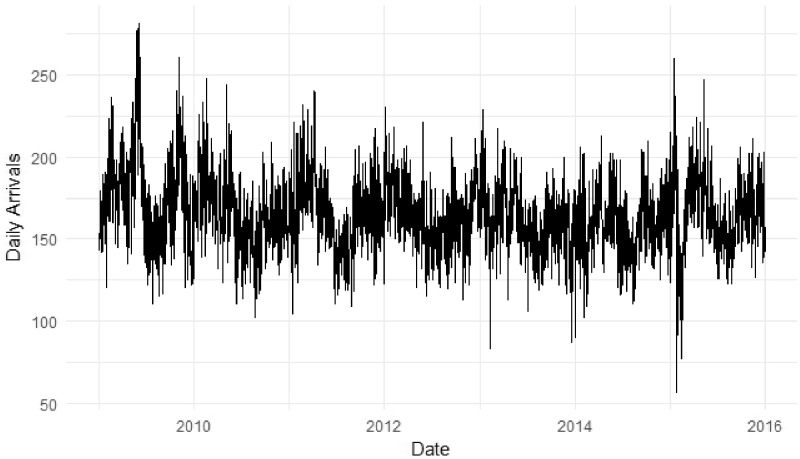
This study was conducted at the Boston Children’s Hospital (BCH) ED, an urban pediatric academic level 1 trauma center in Boston, Massachusetts. The BCH ED treats patients generally 21 years of age and younger, and handles an average of about 60 000 visits every year. The department’s daily arrival counts were collected from BCH’s electronic data warehouse for the dates of January 1, 2009, to December 31, 2015. The local institutional review board approved this study. Visits were classified into days based on the time of arrival as recorded in the electronic medical record. The model used the actual weather and search volume for the day being predicted for the purpose of analyzing the additional usefulness of the search volume data. These data would not be available when making actual predictions about the future. This was a retrospective study with the data split into a training set and an out-of-sample testing set. All models were fit using the training data and tested for accuracy on the testing set. The data used to train each of the proposed models included only historical data before January 1, 2014. The out-of-sample model test period included data from January 2, 2014, to December 31, 2015. We can see in the visit data in Figure 2 that there are 2 extreme events. In the middle of 2009, there is a spike in visits associated with the swine flu epidemic. In early 2015, there is a drop associated with extreme snowfall. This explains the differences in the minimum and maximum values between the training set and test set, as shown in Table 1. The swine flu event shapes the expectations of the trained model and the will models struggle to predict the response to an unprecedented snow storm.

Figure 2.

Daily emergency department arrivals at Boston Children’s Hospital for the whole study period.

Table 1.

Comparison of data in training and test sets

		Training set				Test set
		Mean	SD	Min	Max	Mean	SD	Min	Max
ED visits	Max	166	24.6	83	281	162.5	23.1	57	260
Temperature	Max	60.2	18	13	103	59.1	19.1	14	96
	Mean	53.2	17	6	92	51.8	18.3	8	84
	Min	45.6	16.4	−2	81	43.8	17.9	−3	74
Barometer	Max	30.1	0.2	29.2	30.8	30.1	0.2	29.6	30.9
	Mean	30	0.2	29	30.7	30	0.2	29.1	30.8
	Min	29.9	0.3	28.7	30.6	29.9	0.2	28.8	30.6
Visibility	Max	10	0.5	0	10	9.9	0.6	2	10
	Mean	8.8	2.1	0	10	8.9	2	1	10
	Min	6.5	4	0	10	6.7	4	0	10
Wind speed	Max	20.8	6.2	6	48	20.5	5.9	8	45
	Mean	10.7	3.8	2	31	10.6	3.6	3	26
Snowfall	Total	0.1	0.5	0	10.8	0.1	1	0	13.6
Fever	Vol	2374.1	547.4	798.8	6471.7	2674	517.1	1240.2	4612.4
Flu shot	Vol	555.7	933.8	0	16443.1	486.7	558.4	0	3682.5
Flu	Vol	3557	8722.6	140.2	163310.8	2169	1477.3	209.5	8462.8
Pneumonia	Vol	987.4	399.4	265.2	2960.7	1064	369.9	194.6	2262.4
Bronchitis	Vol	554	242	0	2908	537.2	217.4	136.7	1293.2
Snow	Vol	9964.8	12114.7	2371.6	214082.3	13351.6	19133.6	2628.8	219681.7
Allergies	Vol	920.2	423	166.3	3079.6	982.2	600	186.2	4687.4
Blizzard	Vol	930.4	2901.1	152.2	84259.9	1112.2	4133.1	139.6	72836.5
Forecast	Vol	6680	3111.1	1207.4	31667.9	7699.6	3803.6	2132.9	33665
Humidifier	Vol	612.1	446.7	0	3036	644.1	485.8	121.5	2929.9

Autoregressive variables

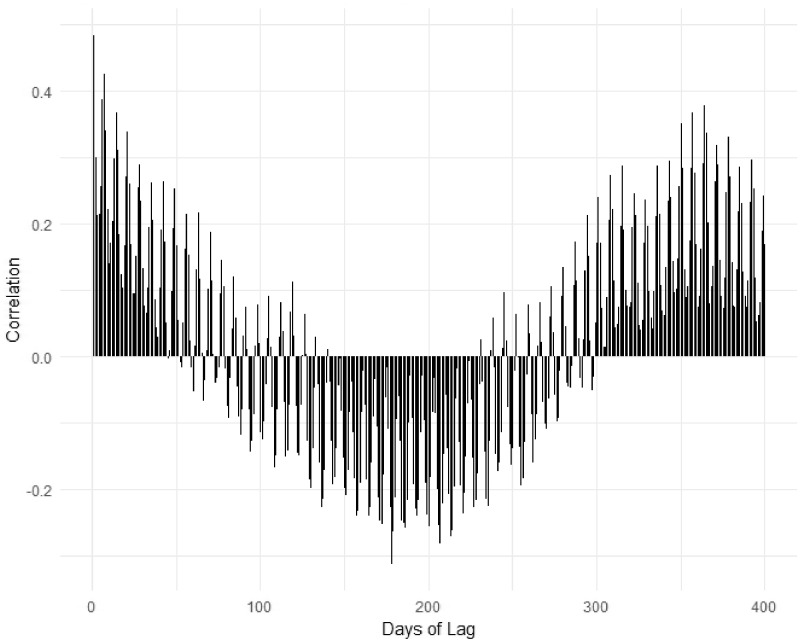
Lag variables representing the visit count from a specified interval of days before the present day were created. Figure 3 shows an autocorrelation function plot of daily ED arrivals from the training set. A strong weekly pattern in the data is evident from the peaks in the autocorrelation function plot for lags divisible by 7. There is also a strong annual trend, with the correlation bottoming out around 182 days in the past and strengthening around 365 days. For the models predicting next-day visits, we created variables for lags from 1 to 14, 21, 350, 357, and 364, corresponding to periods of high autocorrelation in the training set.

Figure 3.

Autocorrelation function plot for training range.

Calendar variables

Indicator variables were created for each day of the week, as well as major holidays: New Year’s Day, Presidents’ Day, July 4th, Halloween, Thanksgiving, Christmas, and New Year’s Eve. Referencing the Boston Public Schools calendar, indicator variables were created for summer vacation, winter vacation, first spring vacation, second spring vacation, holidays, Monday after a long weekend, Tuesday after a long weekend, other day after a long weekend or vacation, and early release days. While most previous studies created indicator variables for each month, we created a sine function with period 365.25 and a cosine function with period 365.25, starting on January 1, 2009. Due to the properties of trigonometric identities, regressing a sine and cosine function with the same period will produce a single sine function with the amplitude and shift that corresponds to the least-squares fit to the outcome variable.

$$a*\hspace{0.17em}\text{sin}(x)+b*\hspace{0.17em}\text{cos}(x)=c*\hspace{0.17em}\text{sin}(x+d)$$

$$c=\sqrt{a^2+b^2}d=\mathit{atan}2(a,b)$$

First, the advantage of this approach over the month indicator variable approach is that a maximum of 2 parameters are being estimated, instead of up to 11. Second, this method demonstrates continuous change throughout the month and into the next month, instead of an abrupt change between the last day of a month and the first day of the next month. One disadvantage is that this model implies a linear relationship between the outcome variable and the annual cycle, while indicator variables for months allow for nonlinear relationships with the annual cycle.

Weather variables

Weather data were downloaded from National Oceanic and Atmospheric Administration⁴⁸ for the Boston Logan Airport weather station. Daily data were collected on minimum, mean, and maximum temperature, barometer, and visibility. Visibility was measured on a 10-point scale with 10 being the clearest visibility. Daily maximum and mean wind speeds were also recorded, but not minimum wind speed, as this was almost always zero. Daily snowfall was also collected. Daily occurrences of weather warnings, watches, and advisories for blizzards, heat, floods, freezing rain, high wind, hurricanes, severe thunderstorms, tornadoes, wind chills, winter storms, and winter weather were represented as binary indicator variables. Table 1 shows that the weather data were very similar between the testing and training sets, with the noticeable exception of snowfall. The average snowfall was more than twice as high in the testing set as in the training set. Furthermore, the maximum snowfall was almost 3 inches higher in the testing set than in the training set. During January and February of 2015, Boston experienced record levels of snowfall (colloquially labeled by the locals as “snowmageddon”).

Google search volume

The daily Google search fraction for a set of weather- and health-related search terms were retrieved through the Google Health application programming interface (API). The structure of the dataset retrieved from the API was the indicator value of the fraction of daily searches containing each selected term for the Google-defined Boston metro area (Google search location code: “eUS-MA-506”). We chose 10 search terms to test in the model: allergies, blizzard, bronchitis, fever, flu, flu shot, forecast, humidifier, pneumonia, and snow. We chose to limit the number of terms to 10 so as to not overwhelm the model selection process. The terms were chosen based on our theory that disease, symptom, and weather-related terms would be most predictive. Google Correlate is a publicly available tool that finds search terms that are most correlated with a weekly time series. We were unable to use Google Correlate to find terms whose Boston-area search volume was correlated with the daily ED visit count at BCH, as Google Correlate is only available for analyzing search volumes at the national level. We did include humidifier in our list of search terms because Google Correlate suggested that it was highly correlated with searches for flu at the national level.

Table 1 shows that the characteristics of the training and testing sets are broadly similar. The most notable exception appears to be flu. The average daily search volume for flu is much higher in the training period, with the maximum indicator value of 163 310 searches on April 30, 2009. This corresponds with the beginning of the media coverage of the swine flu epidemic of 2009. However, the number of ED visits during this period is not particularly high, and the peak number of visits related to flu did not occur until September 2009. This time period serves as a cautionary note that local search volume for terms such as flu can sometimes become disconnected from the conditions generating the local demand for the ED. This may reflect the fact that local search activity is not exclusively related to the actual local prevalence of the disease being searched, but can also reflect general interest in the subject. Some search terms have much higher volume than others: snow, forecast, and fever are the 3 highest in the testing period. Search terms with higher average volumes had lower variance relative to their search volumes, making it easier to identify potentially predictive signals compared with terms with lower volume and higher variance relative to their search volumes. While Yang et al⁴¹ found that dynamic reweighting of search terms was needed to take into account the changing search behavior, our own modeling experiments showed that a dynamic reweighting approach did not significantly increase the forecasting accuracy in comparison to a statically trained model.

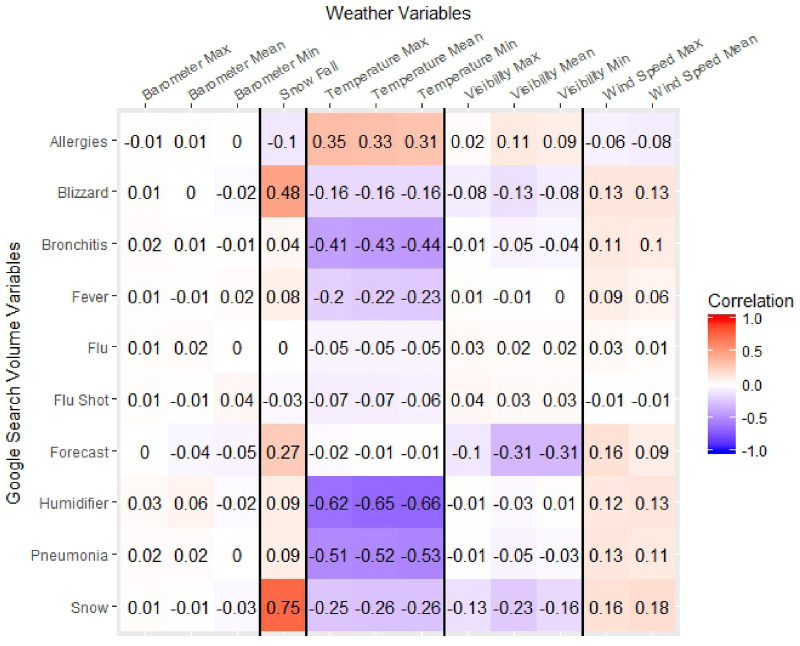
To verify that the weather and search volume datasets contain independent information, we performed pairwise correlations and a principal component analysis. In Figure 4. the highest correlation is between recorded snowfall and searches for snow. Searches for allergies, bronchitis, humidifier, and pneumonia also show positive and negative correlation with the temperature variables. This is likely due the seasonal nature of all these variables. However, most of the variables have little or no pairwise correlation. The principal component analysis yielded similar results. There is some shared information in the weather and search volume datasets, but most of the variables are independent and cannot be reduced.

Figure 4.

Pairwise correlation of weather and search volume data.

Accuracy metrics

A number of accuracy metrics were used to evaluate the performance of each of the models in our study. The formulas associated for these quantities can be found in Yang et al,⁴¹ such as MAPE, a metric that reflects the average prediction error in a percent scale. One hundred percent error suggests over- or underprediction by as much as the observed quantity and zero percent error suggests a perfect prediction. This metric is used frequently and thus, allows for comparison across different studies and departments. Root mean squared error is the cost function minimized during the model fitting process and has the scale of the outcome variable. This metric cannot be used to compare with other studies conducted in different EDs with heterogenous daily visits values. R², or the coefficient of determination, can be interpreted as the percent of the variance in the predicted variable explained by the model. This is a useful measure, as it can be compared across studies and departments. Its limitation is that it does not have a practical application when trying to understand the magnitude of uncertainty in the forecasts. Finally, we used an ad hoc metric, namely, the percent absolute percent error >20%, as a way to measure the percentage of days in which the model prediction error was >20%. After discussing the staffing needs with subject matter experts in the ED, we were informed that on days when staffing was mismatched by >20%, they often had to bring in extra on-call staff. Therefore, we designed this measure as a way to assess how our predictions could have affected staffing strategies in the ED.

Formulation of prediction models

For each of our models, we followed a 2-stage approach that included a variable selection stage and the development of an optimal model.

Variable selection

We used a regularized multivariable linear regression, LASSO, to select the strongest predictors in our set of input variables, and as a way to minimize the use of redundant information in our final models. The benefit of LASSO regression is its ability to zero-out redundant input variables (or predictors), therefore serving as a model selection tool_.³⁶ With nearly 90 covariates in our full model, LASSO provides a systematic form of variable selection. Before performing LASSO regression, all the covariates were normalized so that the coefficients from the LASSO regression could be interpreted as reflecting the parameters’ importance in the model. The optimal parameter was chosen from a series of possible values as the one with the minimum root mean squared error in 10-fold cross validation on the training set. A known downside of using LASSO regression is that the variable selection may be unstable; thus, zeroing out the contribution of useful variables in the optimization process.⁴⁹

Optimal model

To build an optimal model, our second stage consisted of selecting the variables consistently chosen by LASSO and fitted a standard linear regression without regularization.

Gradual incorporation of data sources

To test the contribution of each data source, we classified our variables into 5 groups: day of the week, autoregressive, calendar, weather, and search volume. We used our modeling approach on all 5 groups, adding each data source sequentially to determine its contribution to the forecasting accuracy. We started with day of the week as a baseline, since the BCH ED currently uses long-term, day-of-the-week averages to determine staffing. We then produced retrospective predictions using each resulting model for each of the subsets of data sources. We chose to order the data source categories according to how commonly they were used in the previous literature on the subject_,^2–8 with the search volume data being tested last.

RESULTS

Retrospective simulated predictions for daily visit counts were produced for the testing period using all the data available before the predicted day. Five models were fit on the training set period using different data sources and tested for accuracy on 4 different metrics, as shown in Table 2. Each model also included the data sources listed in the models above it.

Table 2.

Comparison of model accuracy

Model name	MAPE (%)	RMSE	R 2	PAPE > 20% (%)
Day of the week	10.99	16.73	0.135	11.23
Calendar	10.05	15.12	0.213	8.36
Autoregressive	8.41	12.93	0.443	5.21
Weather	7.71	12.29	0.551	3.84
Search volume	7.58	12.08	0.569	3.29

MAPE: mean absolute percent error; PAPE: percent absolute percent error; RMSE: root mean square error.

Variables from each data source were selected and added to the model to improve the out-of-sample accuracy without overfitting the model to the in-sample dataset. Each model with an added data source performed better across all measures of accuracy than the models with fewer data sources. Calendar variables appeared to provide more forecasting improvement in the later models because more calendar terms were included once the model accounts for possible confounding due to weather. Weather variables provided a large improvement in accuracy in an already crowded model reducing MAPE from 8.41% to 7.71%. Weather variables, such as maximum temperature and mean visibility, are among the most important variables in the model.

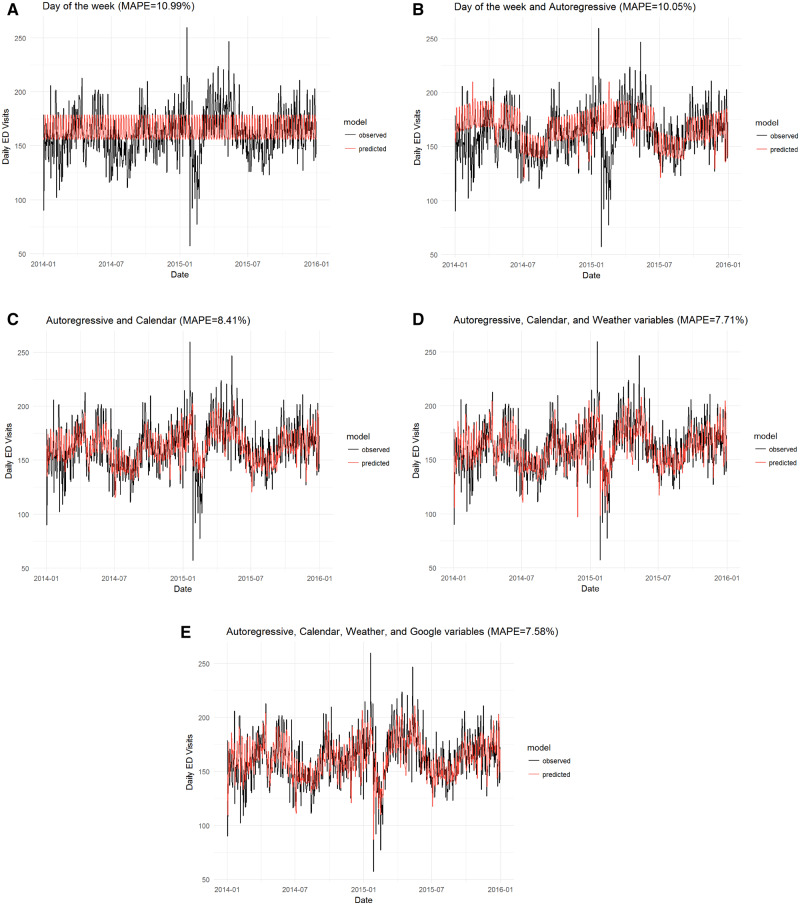
Even in a model with 66 other covariates, the 7 selected search variables provided additional out-of-sample forecasting accuracy, lowering MAPE from 7.71% to 7.58% and root mean squared error from 12.29 to 12.07 (Figure 5). The meaningful impact of adding search variables can be assessed with the metric percent absolute percent error >20%. This corresponds to preventing 2 improperly staffed days a year in comparison with the full model without search volume data.

Figure 5.

Observed and predicted values for different models. ED: emergency department; MAPE: mean absolute percent error.

To further compare the relative value of the weather and search volume datasets, we compared a model using everything but weather to a model using everything but the search volume data. Remarkably, these 2 models achieved the exact same MAPE of 7.71% in the test set. This suggests that the value of these 2 data sources in very similar even though the search volume dataset only contains 10 terms.

Among the search terms included in the final model are terms relating to weather, diseases, and specific symptoms. The word snow was the most important search term (Table 3). Because the outcome is log transformed, the coefficient can be interpreted the as the percent change in the estimated daily ED visit volume associated with a 1-SD increase in search volume with all other variables held equal. On January 27, 2015 Boston experienced 19.7 inches of snowfall. This corresponded to an 18.7-SD increase in search volume relating to the word snow. Accordingly, the final model lowered its estimate by 29.8 visits. While the models without search volume data also had very high estimates for the effect of snowfall, the model with search volume data has higher accuracy. We understand that this demonstrates that search volume data measure the public’s reaction to, and awareness of, these snow storms that weather data alone cannot capture. On May 10, 2015 during the height of the spring pollen season, searches containing the word allergies surged 7.1 SDs above average. Accordingly, the final model raised its estimate by 7.1 visits. This demonstrates how search volume data can capture local population level health information and translate that into associated estimates of its effect on ED visits.

Table 3.

Coefficient estimates and importance rank of search terms in final model

Search term	Coefficient	Rank
snow	–0.00967	13
allergies	0.00557	23
blizzard	–0.00464	28
flu shot	0.00461	29
fever	0.00452	31
forecast	–0.00354	41
pneumonia	0.00329	42
flu	0	N/A
bronchitis	0	N/A
humidifier	0	N/A

N/A: not available.

DISCUSSION

Based on 5 years of historical data, the forecasting model provides good accuracy in predicting daily ED visit volume. In addition to weather data and calendar variables, search volume provides additional useful information that improves the accuracy of the forecasts. Search terms related to weather and allergies were the most useful in our model, suggesting that search volume data provide additional information that can be used to forecast ED visits than weather and calendar data can alone. Our results suggest that over our 2-year test period, the best model would have only 24 instances in which the model was off by more than 20%, probably leading to improperly staffed days in the ED. This is compared with 28 days in the model without search volume data and 82 days in our baseline day-of-the-week model. While in our study we only chose 10 search terms to investigate, using additional search terms could provide further prediction accuracy. Our side-by-side comparison showed that a model with search volume data and without weather data performed equally well as a model with weather data and no search volume data. With the use of the API, Google search volume data could prove to be easier and more valuable than weather data for ED volume prediction.

The 2-step modeling approach of using LASSO regression for variable selection and log-linear regression for model fitting can successfully handle variable selection and model calibration for datasets of many variables. This system reliably chose useful variables from sequentially added data sources and improved out-of-sample forecasting accuracy while reducing the change of overfitting to the new data.

This methodology can be applied widely at other EDs to improve forecasting of patient volumes to improve staff and resource planning and reduce overcrowding. Any ED could attempt to build a similar prediction model with any combination of data sources available. The variables that are important, the relationship between the variables and the outcome, as well as the accuracy, are likely to be unique to each location. To implement this procedure a model would need to be fit on local historical data. This framework can also be used to fit predictions to any amount of time into the future that is desired. In the master’s thesis on which much of this article is based, it was shown that predictions for greater time horizons into the future led to decreases in accuracy_.⁵⁰ The number of days into the future at which the model is calibrated is a choice that each location would need to make after considering the trade-off between the preparation time needed to take meaningful action and the accuracy of those predictions. Once a model is trained, a data pipeline is needed to send clean, up-to-date data to the model to make predictions, most likely on a daily basis. Future work should include validating the methodology at additional diverse sites, incorporating additional novel sources of data, and prospectively testing the models in real time.

CONCLUSION

This study demonstrates that Google search volume data can meaningfully improve forecasting of ED visit volume. Additionally, we describe a broad and flexible methodology that can be used to test at other departments and other possible data sources. This framework could be implemented to help EDs with resource planning to help reduce problems of overcrowding and improve quality and cost.

Contributions

ST, MS, and BR conceived research. JB collected institutional data. ST collected external data and normalized all datasets. ST, MS, and BR contributed to the design of predictive models. ST implemented and analyzed predictive models. ST wrote the first draft of the manuscript. All authors contributed and approved to the final version of the manuscript.

ETHICS APPROVAL

This research was approved by the Institutional Review Board at Boston Children’s Hospital (Protocol number IRB-P00023195) and was determined to not represent human subjects research and informed consent was waived because the data was deidentified.

Conflict of interest statement

None declared.