Unsupervised machine learning and prognostic factors of survival in chronic lymphocytic leukemia

Abstract

Objective

Unsupervised machine learning approaches hold promise for large-scale clinical data. However, the heterogeneity of clinical data raises new methodological challenges in feature selection, choosing a distance metric that captures biological meaning, and visualization. We hypothesized that clustering could discover prognostic groups from patients with chronic lymphocytic leukemia, a disease that provides biological validation through well-understood outcomes.

Methods

To address this challenge, we applied k-medoids clustering with 10 distance metrics to 2 experiments (“A” and “B”) with mixed clinical features collapsed to binary vectors and visualized with both multidimensional scaling and t-stochastic neighbor embedding. To assess prognostic utility, we performed survival analysis using a Cox proportional hazard model, log-rank test, and Kaplan-Meier curves.

Results

In both experiments, survival analysis revealed a statistically significant association between clusters and survival outcomes (A: overall survival, P = .0164; B: time from diagnosis to treatment, P = .0039). Multidimensional scaling separated clusters along a gradient mirroring the order of overall survival. Longer survival was associated with mutated immunoglobulin heavy-chain variable region gene (IGHV) status, absent Zap 70 expression, female sex, and younger age.

Conclusions

This approach to mixed-type data handling and selection of distance metric captured well-understood, binary, prognostic markers in chronic lymphocytic leukemia (sex, IGHV mutation status, ZAP70 expression status) with high fidelity.

INTRODUCTION

With improved data mining of the electronic medical record, the scale of data available for clinical research is increasing dramatically. Expanding size and complexity demand new analytical approaches.^1,2 Techniques refined in bioinformatics to analyze high-throughput data may provide translational methods for large-scale clinical data, if they can be properly transformed. Pattern discovery with unsupervised machine learning (UML), a common approach for multiomics data,^3,4 has the potential to revolutionize understanding of patient phenotypes and clinical outcomes.⁵ However, clinical data, characterized by greater heterogeneity than high-throughput datasets, pose unique problems for UML.¹ Although there are important roles for mixed-data handling in bioinformatics, UML in omics contexts commonly involves the uniform application of a single distance metric to a matrix of homogeneous data, either continuous or binary.⁴ Unlike omics data, clinical data contain mixed data types, which can impede easy application of UML.¹ Heterogeneity of data types raises new challenges in feature selection: choosing a distance metric that captures biological meaning and visualizing clinical data. This study outlines an informatic experiment to address a core problem in the application of UML to clinical data: transforming a heterogeneous dataset to allow rigorous, biologically meaningful discovery by UML algorithms.

UML broadly encompasses algorithms that aim to uncover hidden structure in data from input features alone. Clustering analyses, a subcategory of UML, partition these input data into distinct groups based on calculated similarities between observations.⁶ For 2 decades, UML has been a common tool for pattern discovery in bioinformatics.^3,4 Unsupervised analysis of high-throughput omics experiments uncovered new patterns to annotate the genome, elucidate chromatic structure,⁷ reveal molecular subtypes in cancer from gene expression,⁸ and functionally segment the human genome by understanding histone modification.⁹ Recently, UML began to be applied to clinical data. Due to phenotypic and outcome heterogeneity in many diseases, clustering analyses have found diverse applications. They have improved understanding of the role of comorbidities in atrial fibrillation¹⁰ and chronic obstructive pulmonary disease (COPD), including highlighting the driving role of anxiety and depression on COPD progression in young, female patients.¹¹ Clustering has applications in health services, such as subtyping inpatient e-portal users to improve care delivery.¹² Some analyses of heterogeneous diseases discover subclasses that are fuzzy or not mutually exclusive, both in chronic conditions such as COPD¹³ and acute sepsis.¹⁴ To the best of our knowledge, this is the first application of clustering to clinical data in cancer.

We chose chronic lymphocytic leukemia (CLL), a disease with well-characterized risk factors, to “biologically validate” the discoveries generated by our methodologic approach. For “biological validation,” we propose to use real data with known behavior as a source of “ground truth” to evaluate methods. CLL, the most common leukemia in the Western hemisphere, is characterized by the accumulation of mature-appearing, but malignant, B lymphocytes in blood, bone marrow, and lymph nodes.¹⁵ The disease course is heterogeneous; some patients die from refractory disease within a few years, while others live for decades with indolent disease. However, patients with initially indolent disease remain at risk of disease progression, infections, and secondary malignancies.^16–18 One of the best predictors of prognosis in clinical use is the somatic mutation status of the immunoglobulin heavy chain variable region (IGHV) genes.¹⁹ Somatic mutation of IGHV genes is a normal process that occurs in the germinal center following antigen exposure and enhances antibody affinity. In general, CLL patients with unmutated IGHV genes (U-CLL) have aggressive disease, while patients with mutated IGHV genes (M-CLL) have more indolent disease.^20,21 Chromosomal abnormalities are also strong predictors of disease progression and survival in CLL. Fluorescence in situ hybridization analyses on nondividing interphase nuclei demonstrate that ∼80% of CLL cases contain nonrandom gains or losses of chromosomal material, many with prognostic significance.^22,23 Deletions in 13q14 (del(13q)) are most common, followed by deletions in 11q22.3-q23.1 (del(11q)), trisomy 12 (+12), and deletions in 17p13 (del(17p)). Del(13q), associated with a good prognosis, is the site of DLEU1 and the microRNA genes, miR-15a/16-1, which negatively regulate BCL2 post-transcriptionally.^24,25 In contrast, del(17p), the site of TP53, and del(11q), the site of ATM and the miR34b/c cluster, are markers of poor prognosis. If patients with +12 have an intermediate prognosis, their overall survival (OS) lies between patients with del(13q) and those with del(11q) or del(17p).

Recently, we studied gene expression data from a subset (N = 101) of the CLL patients whose clinical data is available here.²⁶ Using hierarchical clustering (after selecting about 1100 genes associated to time-to-progression after therapy), we found 3 distinct subgroups of CLL with both different gene expression profiles and different response to therapy. We then built a robust classifier to predict membership in these subtypes. This classifier was validated on data from an independent clinical trial, showing that prognostically relevant subtypes of CLL do, indeed, exist. Ideally, the same kind of analysis on clinical data could improve treatment outcomes.

In this experiment, we hypothesized that UML, when applied to clinical data, could discover clusters of patients with different prognoses. Using CLL as a case study, we explored best practices in transformation to a single data type, a common approach seen in the clinical clustering literature, as a method for mixed-data handling for a clustering analysis. We applied k-medoids clustering to a set of clinical features by transforming them to binary vectors, exploring 10 metrics for calculating a distance matrix and 2 common methods of visualization. Implementing 2 parallel approaches to discretization, our analysis revealed statistically significant associations between clusters and important survival outcomes, visualized by MDS as a “spectrum” of subgroups. This analysis captured known, binary markers of prognosis and outcome with high fidelity. Critically, we identify and propose solutions for important limitations within this common methodology for mixed-type data handling, including challenges with information loss and visualization.

RELATED WORK

Unsupervised clustering analyses have been used to uncover subgroups within clinical data since the 1960s.²⁷ Then and now, hierarchical clustering methods have been a dominant approach.^12,27–30 Recently, a few studies have applied k-means and k-medoids algorithms to cluster clinical data.^31–33 Increasingly, studies have emerged comparing traditional hierarchical clustering approaches to k-means and k-medoids.^11,13,34

Studies clustering clinical data apply several approaches to integrating heterogeneous data, but disparities in reporting impede the identification of best practices. In the clinical literature, often no description of mixed data handling is reported.^32,34 Within the studies described here, Euclidean distance, which is best suited for continuous data, was the most commonly employed dissimilarity metric regardless of the data type being clustered.¹¹ Often, no distance metric was reported.^31–33

Approaches for clustering mixed-type data in the literature often use 2 methods of calculating similarity: 1 for continuous and 1 for categorical data. These may combine 2 distance metrics (usually a Minkowski distance for continuous data with the Hamming distance or Gower coefficient for categorical)^35–38 or 2 algorithms, such as Huang’s k-Prototypes algorithm, which implements k-means for continuous data and k-modes for categorical data.^39,40 An alternative approach is to restrict data sets to only 1 data type.^41,42 Clinical applications of this approach include an experiment on Z-normalized continuous data in the critical care setting,³¹ normalizing on frequency,³³ or transforming mixed-type data to categorical.¹¹

When comparing k-means and hierarchical approaches, Pikoula and colleagues¹¹ found k-means clustering recovered more stable clusters than hierarchical methods. Using unsupervised random forests for feature selection and similarity matrix calculation, Castaldi and colleagues¹³ demonstrated similar performance between k-medoids and hierarchical clustering. The team recovered best performance with hierarchical clustering with removal of “poorly classifiable subjects,” but in some experiments this resulted in removal of up to 86% of subjects, which suggests the potential for loss of biological meaning. Clustering these experiments, regardless of type, often produced clusters with limited coherence. When the percentage frequency of a defining feature in a cluster was reported in a study, the most common features defining a cluster had low frequencies, sometimes less than 50%. This indicates that the recovered clusters lacked strong identities and had reduced potential for clinical discovery.^11,31,32

In this study, we propose that transformation to a single data type represents a simple solution to a complex problem if it can be successfully implemented through careful methods. We explore rigorous methods to apply a “simple” set of solutions to produce interpretable results from a process with low computational intensity. Data transformation risks information loss and introduction of bias. However, we argue that complicated solutions, such as those produced by Castaldi and others, run similar risks with an increased burden from impaired interpretation of results.

We used k-medoids clustering in this paper, which produces more stable clinical data clusters.¹¹ The 2 primary challenges to either hierarchical clustering or k-means or k-medoids approaches are solutions for mixed-type data and selection of an appropriate distance metric. In this paper, we transform mixed data to binary features to eliminate conflict from multiple data types and assess 10 distance metrics to make a judicious choice to maximize biological meaning recovery.

MATERIALS AND METHODS

Samples and clinical findings

This study uses deidentified data that were previously published. Originally, peripheral blood samples were obtained from 247 treatment-naïve CLL patients after obtaining informed consent at the University of Texas MD Anderson Cancer Center and processed as described.^43–45 The studies were approved by the Institutional Review Boards and conducted according to the principles expressed in the Declaration of Helsinki. Clinical and routine laboratory data were obtained by review of the medical records (Table 1). Additional information on these data is available in Supplementary File A.1. The somatic mutation status of IGHV genes and ZAP70 expression, measured by either flow cytometry or immunohistochemistry, were assessed on blood or bone marrow samples according to established protocols.^46–48 Common CLL-associated abnormalities (del(11)(q22.3); del(13)(q14.3); del(17)(p13.1); trisomy 12), were assessed by array-based single nucleotide polymorphism genotyping.^43,48 Cases were grouped according to the Döhner hierarchy.²³ Our analysis included 7 measures of outcome collected over 15 years of follow-up: overall survival (OS), time from diagnosis to treatment (TTT), time from sample collection to treatment (TST), event-free survival (EFS), progression-free survival (PFS), time-to-progression (TTP), and survival after treatment (TxOS).

Table 1.

Clinical characteristics of chronic lymphocytic leukemia (CLL) patients

	Patients n (%)
Total	247
Sex
Male	173 (70.0)
Female	74 (30.0)
Race
Asian	1 (0.4)
Black	11 (4.5)
Hispanic	7 (2.8)
White	228 (92.3)
Rai Stage
Low (0–2)	196 (79.4)
High (3–4)	51 (26.0)
Döhner Classification
del13q	90 (36.4)
+12	37 (15.0)
FISH normal	73 (29.6)
del11q	34 (13.8)
del17p	13 (5.3)
IGHV Mutation Status
Mutated	106 (43.1)
Unmutated	140 (56.9)
Treatment Status
Never treated	20 (8.1)
Treated with FCR	227 (91.9)
Age at Diagnosis	Years
Minimum	26.74
Median	55.87
Maximum	82.41

Selected clinical and routine laboratory data, somatic mutation status, and common recurrent cytogenetic abnormalities collected at time of diagnosis on 247 treatment-naïve patients diagnosed with CLL and obtained by chart review.

Clinical data transformation

Our clinical data are heterogeneous, including binary, nominal, ordinal, and continuous features (Supplementary Table A.1). Because our data set was already dominated by binary features, we chose to discretize to binary data, believing that altering fewer features reduces opportunities to introduce bias. The approach for discretization of continuous variables was driven by biological meaningfulness. Reclassifying categorical and continuous data as binary required decision-making steps that inherently result in information loss. So, we compared 2 distinct approaches which we refer to as “Data transformation A” and “Data transformation B.” Further details are in Supplementary Methods A.2.

Both transformations included binary features which can be subclassified into 2 types. For symmetric binary features, such as sex, both values are about equally likely, and there is no reason to prefer coding either value as 0 or 1. In our data, both the IGHV somatic mutation status and ZAP70 expression were symmetric, and either presence or absence is relevant to predict clinical outcome. For asymmetric binary features, 1 of the values tends to be much rarer than the other, and is usually coded as 1. This value is “more informative,” since people who share the attribute have more in common than people who lack it. For example, anemia, splenomegaly, and hypogammaglobulinemia are asymmetric binary features of our clinical data. For symmetric binary features in both transformations, we retained 2 binary vectors—1 for presence and 1 for absence of a feature. For asymmetric binary features, we retained 1 vector capturing a positive result (or presence of a feature).⁴⁹

In data transformation A, we preserved categorical and continuous data in more detail than in data transformation B. For categorical data, we transformed each category into binary dummy variables, retaining a set of vectors for each category. Thus, for the Döhner classification, we retained 5 binary vectors corresponding to 5 cytogenetic categories. We binned continuous data along clinically interpretable lines. We binned age by decade and prolymphocyte count by percentage into 6 categories each. We converted these sets of dummy variables using the same approach that we applied to categorical data. The greatest number of dummy variables for any given category was 6.

In data transformation B, we converted all categorical and continuous features into 2 clinically meaningful binary categories. Each feature was divided along a meaningful clinical cutoff and retained as 2 symmetric binary vectors. For example, the continuous variable “age” was split into 2 vectors corresponding to age greater or less than 65 years. Although this transformation was smoothly applied to continuous data, Döhner classification, an ordinal variable, could not be collapsed into 2 meaningful binary categories. Thus, we retained only the Döhner classification as a nonbinary set of dummy variables, with a total of 5 vectors.

Unsupervised machine learning

We applied an identical UML workflow to both transformations. We began with principal component analysis and clustering using the Thresher R package.^50,51 Using the Mercator R package, we assessed 10 binary distance metrics (Sokal&Michener, Euclidean, Manhattan, Pearson, Hamming, Jaccard, Binary, Canberra, Russell&Rao, and Goodman&Kruskal; see Supplementary Methods A.3.1) representing meaningful groupings of 76 distance metrics.⁵² Mercator provides streamlined tools for principal component analysis from different distance metrics, application of the Thresher algorithm, and multiple visualizations. To select an appropriate metric, we recovered k clusters at a range of k values, calculated the categorical distance between clusters, and visualized the similarity between distance metrics with hierarchical clustering (Supplementary Figure A.1). For analysis of both transformations, we selected the Sokal&Michener distance d_SM for representativeness of trends among recovered clusters. Developed for taxonomy, the Sokal&Michener distance tolerates symmetric binary variables and categorical data.^49,53 It is easily interpretable, calculating dissimilarity as a ratio of concordant matches to all pairs:⁵²

$$d_{SM}=\mathrm{ }\frac{N_{00}+N_{11}}{N_{00}+N_{01}+N_{10}+N_{11}}$$

where $N_{ij}$ counts the number of times the first vector contains the value i while the second vector contains the value j. We recovered clusters using Partitioning Around Medoids (PAM).⁴⁹ Goodness-of-fit for each cluster was determined from the silhouette width (Supplementary Methods A.3.2), which represents the tightness of clustering between groups.⁵⁴ The number of clusters was determined by maximizing the average silhouette width. For each cluster, we defined “salient” features as those that characterize >75% of patients within the cluster (Supplementary Methods A.3.3). We visualized clusters with both linear (MDS) and nonlinear (t-stochastic neighbor embedding [t-SNE]) dimension reduction methods.⁵⁵ To assess prognostic utility, we performed survival analysis using a Cox proportional hazards model, evaluated with the log-rank test and visualized by Kaplan-Meier curves.

RESULTS

Data transformation A

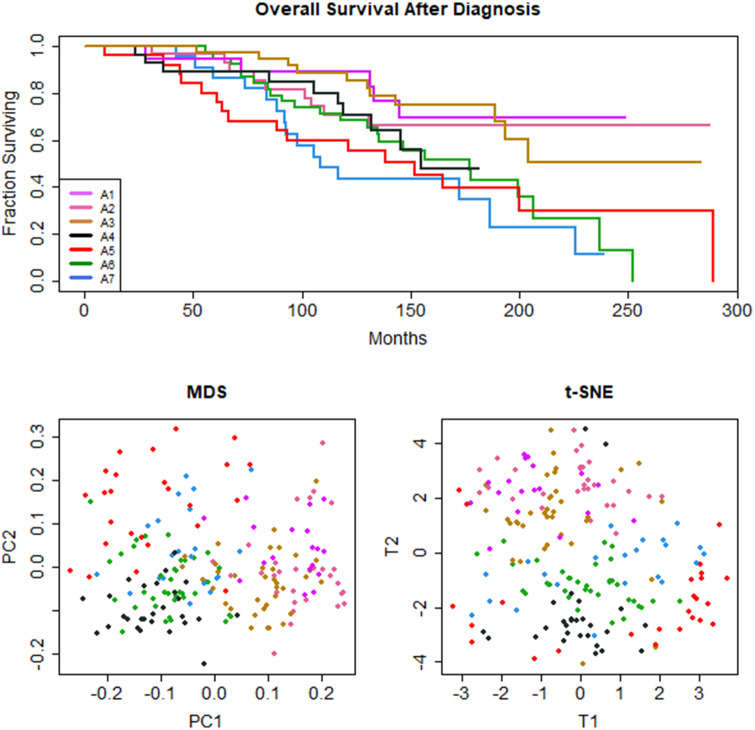
Data transformation A, which preserved categorical features, produced 40 binary vectors. PAM clustering on a Sokal&Michener dissimilarity matrix returned k = 7 clusters (average silhouette width = 0.10). Survival analysis with a Cox proportional hazards model revealed a statistically significant association between 7 clusters and OS from time of diagnosis (logrank = 5.84, P = .016; Figure 1A) Recovered clusters were not significantly associated with other outcome measures (TTT, logrank = 0.04, P = .84; EFS, logrank = 0.63, P = .43; PFS, logrank = 0.26, P = .607; TTP, logrank = 0.27, P = .27; TxOS, logrank = 2, P = .158; TST, logrank = 3.64, P = .06). Visualization by t-SNE (Figure 1B and C) demonstrated loose groupings. Visualized by MDS, these loose clusters were arrayed along a gradient in the first dimension that mirrored the OS order seen in the Kaplan-Meier curves. Visualizations of the other 9 tested distance metrics using MDS (Supplementary Figure B.2) and t-SNE (Supplementary Figure B.3) are available as supplemental files.

Figure 1.

Data transformation A: (A) Kaplan-Meier survival curve, (B) MDS plot, and (C) t-SNE plot for 7 unsupervised clusters of CLL patients. Unsupervised machine learning, using k-means clustering with Partitioning Around Medoids (PAM) and the Sokal&Michener distance yields 7 clinical phenotypes with significant differences in overall survival (OS) (P = .0164). Clusters separated by MDS along the first dimension reflect OS outcomes.

Informative features that varied with survival outcome included IGHV somatic mutation status, sex, ZAP70 expression, immunoglobulin light chain subtype, hypogammaglobulinemia, anemia, and Döhner classification. A subset of informative features is presented in Table 2, with complete results in Supplementary Table B.1. The 3 clusters with the longest survival (A1, A2, A3) were associated with mutated IGHV status and lack of ZAP70 expression. The cluster with second-longest survival was the only cluster associated with female sex. The 2 clusters with shortest survival (A6, A7) were associated with unmutated IGHV status and ZAP70-positivity, regardless of sex. The clusters with second- and third-longest survival were associated with del(13q), the only Döhner classification abnormality identified by the analysis. Only 2 clusters were associated with dummy categorical features, specifically del(13q); all other clusters are based on binary features. Light chain subtypes lambda (A1) and kappa (A4, A6) were identified as salient features.

Table 2.

Informative, identifying features of clusters for data transformations A and B, in order of overall survival

Data Transformation A.
ID	n	Sexa	IGHV Status	ZAP70	Döhner	CD38	Light Chain	Other
A1	19	M	Mutated	−		Low	Lambda	Hypogammaglobulinemia
A2	29	F	Mutated	−	del13q	Low
A3	36	M	Mutated	−	del13q	Low
A4	27	M	Unmutated			High	Kappa
A5	25	M	Unmutated	−		Low		Anemia
A6	38		Unmutated	+		Low	Kappa
A7	22		Unmutated	+		Low		Anemia
Data Transformation B.
ID	n	Sex a	IGHV Status	ZAP70	CD38	Age (yrs)	Prolymphocytes (%)	Light Chain	Otder
B1	46		Mutated	−	Low	< 65	< 10	Lambda
B2	37		Mutated	−	Low	< 65	< 10	Kappa
B3	26	M	Unmutated			< 65	< 10		Anemia
B4	44		Unmutated	+	Low	< 65	< 10	Kappa
B5	12	M	Unmutated	+	Low	≥ 65		Lambda	Anemia
B6	31	M	Unmutated	+	High	< 65	< 10	Kappa

Notes: Clusters are ordered by predicted survival outcome, from longest survival (A1 or B1) to shortest (A7 or B6). Characteristic features of each cluster, defined as a feature present in at least 75% of members of a given cluster, include known indicators of superior prognosis (IGHV-mutated status and female sex) and poor prognosis (ZAP70 positivity). For complete results and percentages, see Supplementary Table B.1.

^aM, male; F, female.

Some common features characterized a majority of patients in many of the recovered clusters. In all clusters, 75% or more patients were diagnosed at low Rai stage (Rai stage < III). All clusters featured low CD38 except for A4, with high CD38. Some clusters were notable only for the absence of a common feature. All clusters except A7 had low beta-2 microglobulin. All clusters had low white blood cell counts at diagnosis except cluster A6. All clusters except A4 and A7 had typical Matutes score.

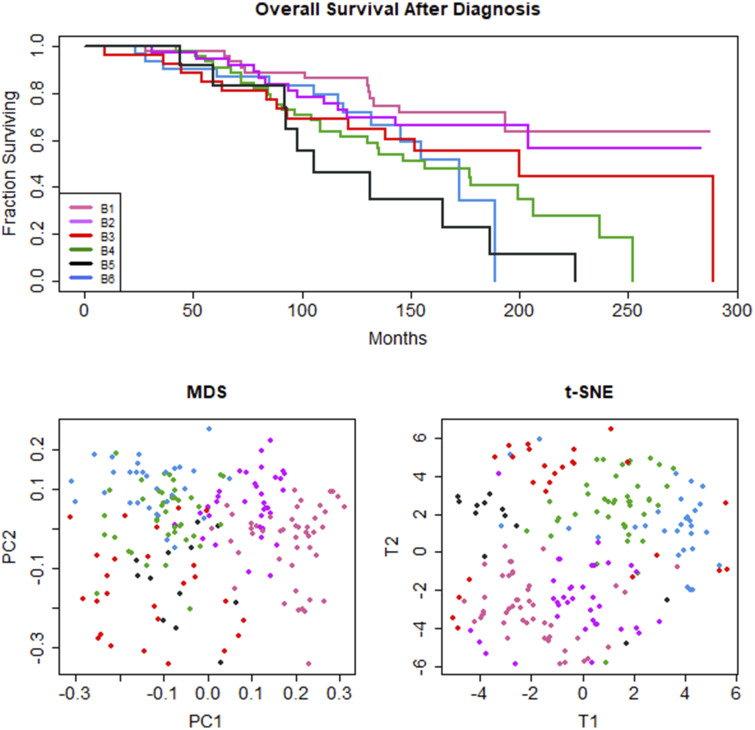
Data transformation B

Collapsing categorical values to binary classifiers reduced transformation B to 32 features. Using the Sokal&Michener distance, PAM recovered k = 6 clusters (average silhouette width = 0.17). Survival analysis by Cox proportional hazards on several outcome measures revealed statistically significant associations between 6 recovered clusters and TTP (logrank = 4.05, P = .0451; Supplementary Figure B.1) and time from diagnosis to treatment (logrank = 8.41, P = .0039; Supplementary Figure B.1), a related measure. Recovered clusters were not significantly associated with other outcomes (OS, logrank = 0.74, P = .39; EFS, logrank = 2.31, P = .129; PFS, logrank = 2.93, P = .088; TxOS, logrank = 2.08, P = .151). t-SNE visualized loose groupings without broad separation. Along the first dimension, MDS separated clusters along a gradient in an order mirroring OS, but not other outcomes such as TTP (Figure 2B and C). Although MDS separated clusters on the first dimension along the order of OS, the association between clusters and OS was not statistically significant.

Figure 2.

Data transformation B: (A) Kaplan-Meier survival curve, (B) MDS plot, and (C) t-SNE plot for 6 unsupervised clusters of CLL patients. Unsupervised machine learning, using k-means clustering with Partitioning Around Medoids (PAM) and the Sokal&Michener distance yields 7 clinical phenotypes with significant differences in time-to-progression (TTP) (P = .0451). (Supplementary Figure 1) Clusters separated by MDS along the first dimension reflect order of overall survival (OS) outcomes.

Informative features defining 75% of the patients in a given cluster are presented in Table 2, with complete results in Supplementary Table B.1. Clusters with improved OS had mutated IGHV status and ZAP70-negativity. Clusters with shorter OS had unmutated IGHV status and ZAP70 positivity. The cluster with the second-shortest survival was associated with older age (> 65 years) at the time of diagnosis. The cluster with shortest survival was associated with CD38 positivity. As in data transformation A, lambda (B1, B5) and kappa (B2, B4, B6) light chains were alternately identified as salient features.

As in data transformation A, some common features were represented in many clusters. For example, most clusters were associated with low Rai stage—except B3 and B5, which did not have a predominant association with any Rai stage. Most clusters had typical immunophenotypes by Matutes score—except B5 and B6, which had fewer than 75% of members with typical immunophenotypes, but no cluster was characterized by atypical immunophenotypes by Matutes.

DISCUSSION

Applying methods common in bioinformatics to clinical data entails potential problems and pitfalls. Difficulties in recovering clusters are rooted in clinical data heterogeneity. Our analysis captured symmetric, binary classifiers with high fidelity but lagged in capturing important prognostic features of other data types. Two of the best-understood prognostic features in CLL are IGHV mutation status and ZAP70 expression. Both transformations identified these features as salient and informative. Some features proved uninformative because they characterized a majority of patients in most or all of the recovered clusters. Binary features for which 1 of the 2 categories predominated within the dataset, such as Rai stage or white blood cell count, were sufficiently common as to be identified as salient features in each cluster by our 75% cutoff. Such features are meaningless due to their frequency across the data as a whole.

In data transformation A, a high proportion of categorical and binned continuous data led to loose clusters and low silhouette widths. Salient clinical features identified by our workflow failed to capture meaningful categorical data, including age, a well-understood prognostic indicator. These limitations led us to explore data transformation B. Collapsing categorical data to binary form improved silhouette width and led to the inclusion of 2 important classifiers, age and prolymphocyte count, in cluster definitions. We believe that the improved results may be due to making binary selections based on clinically meaningful thresholds.

Both data transformations captured light chain subtype (lambda or kappa) as a salient feature for the majority of clusters. Light chain subtype is a commonly recorded variable with known function in physiological B-cell development and differentiation. However, its role as a prognostic indicator is poorly understood. Furthermore, although light chain subtype helps distinguish cluster identities, the alternating pattern of light chain subtype along the survival spectrum in transformation B suggests that association with overall survival is unlikely. Our analysis captured several pairs of clusters differentiated by few features other than light chain subtype. In data transformation B, clusters B1 and B2 are differentiated only by light chain subtype. Thus, although light chain is not a powerful predictor, it does drive clustering. Applications of unsupervised ML to clinical data hold the potential to explore other poorly understood clinical features and their role in predicting treatment response or survival outcomes. Future work remains to refine methodologies to elucidate these clinical features.

Critically, neither transformation captured what is perhaps the most important, best understood, prognostic indicator in CLL: the Döhner classification. Data transformation A identified a Döhner abnormality in 2 clusters only, and data transformation B failed to identify Döhner classification for any cluster at all. The Döhner classification was the only ordinal feature that could not be meaningfully collapsed into binary form, which may explain why it was not captured by either model. Another possible explanation arises because the Döhner classification is strongly associated with both IGHV mutation status and ZAP70 expression. Cases which only have del(13q) tend to be IGHV-mutated and negative for ZAP70 and have good prognosis. Cases with del(17p) or del(11q) tend to be IGHV-unmutated and positive for ZAP70 and have poor prognosis. Nevertheless, this finding suggests that important categorical factors with many levels may have less influence on clustering than associated symmetric binary factors. It also reflects the fact that (by definition) UML methods are inherently less powerful than supervised methods at finding factors relevant to a particular clinical outcome; we know that the Döhner classification is prognostic because it was found during supervised analyses of clinical data from CLL cohorts.

A simple binary transformation and subsequent application of dissimilarity metrics uniformly across a clinical data set is clearly insufficient to capture all medically important facets within the data. Collapsing age to a binary classifier of greater or less than 65 years successfully led to its inclusion as a salient feature in data transformation B. However, patient ages in the data set ranged from less than 40 to over 80 years old at diagnosis. Clearly, rich and important clinical information was lost with at least some binary transformations. Ideally, the power of applying UML to clinical data would be in capturing clinical details not previously identified. Collapsing continuous data to a binary classifier may prevent the realization of this important potential.

Clinical data are inherently complex. Our dataset, though small, is representative of this complexity. These data contain features that are symmetric, balanced, and binary (eg, sex); symmetric and binary, but strongly unbalanced (eg, Rai stage); binary but asymmetric (eg, anemia); nominal (eg, Döhner classification); continuous on an interval scale (eg, age); and continuous on a ratio scale (eg, prolymphocyte count). Any UML approach must capture and leverage this complexity.

Although our methods captured clinical features associated with survival outcomes, visualization by t-SNE and MDS showed loose groupings instead of tight, well-separated clusters. Many diseases present with clinical phenotypes arrayed along spectra, as opposed to fully distinct subgroups. CLL is 1 such disease. Importantly, for both transformations, MDS recovered a spectrum of subgroups that mirrored the outcomes seen in overall survival. These results suggest that some common modes of dimension reduction and subgroup visualization, such as t-SNE, may be inappropriate for diseases with diffuse clinical presentation, failing to visualize clusters even when clinically meaningful subgroups are present. In clinical contexts, there is merit in exploring methods to visualize other patterns within data, such as the spectra of clusters associated with an important clinical outcome visualized here with MDS.

In this article, we explored the concept of “biological validation” to assess a clustering method using real data. In the absence of known “ground truth” clusters, which are never available in real data, testing clustering methods on data from well-understood diseases provides a means to test accuracy and meaningfulness of clusters. Although experiments on well-understood disease may fail to yield a wealth of novel insights, we argue that “biological validation” experiments provide a fruitful avenue for rigorous assessment of unsupervised methods in clinical contexts.

A primary methodological concern of our analysis and future directions is fitting an appropriate distance metric to a given problem. Here, we selected the Sokal&Michener distance for appropriateness of data type, representativeness of other distance metrics, and representativeness of trends within our data. First, the Sokal&Michener distance, although originally developed for small, categorical data,⁵³ is appropriate for use in symmetric binary data,⁴⁹ such as the important features in our data that are prognostically meaningful both when absent or present. Second, the Sokal&Michener distance produces results highly correlated with other well-understood measures of binary distance, including Manhattan, Minkowski, and Gower distances,⁵² so we can view the Sokal&Michener distance as representative of other approaches to calculating dissimilarity. Finally, when visualizing our data across 10 distance metrics (see Supplementary Figures A.2 and A.3), the Sokal&Michener distance qualitatively reproduced plotting trends across multiple methods of calculating dissimilarity.

Although clustering is a common approach in bioinformatics, both current bioinformatics and future clinical informatics applications can benefit from careful attention to this problem. Many distance metrics currently used in bioinformatics have their roots in taxonomic and speciation problems of the early- to mid-twentieth century.^52,53 Clustering remains, in many ways, a taxonomic problem. Creating meaningful biological classifications requires thoughtful assignment of a distance metric to a particular set of data. Although the heterogeneity of clinical data stresses the most complex aspects of this problem, we argue that exploring multiple distance metrics to select the best fitting calculation of dissimilarity for a given data set should be an integral step in any UML workflow.

In bioinformatics, homogeneous datasets can easily be subjected to a single dissimilarity metric. However, analysts typically resort to software defaults, such as the Euclidean distance for continuous metrics as opposed to selecting the metric that best fits the particular experiment. Failure to disclose distance metrics in the construction of a dissimilarity matrix or linkage metrics in hierarchical clustering is an impediment to reproducibility. In 1980, in response to publication of cluster experiments characterized by insufficient methodological reporting to allow reproducibility, Blashfield²⁷ called for reporting of the chosen similarity metric in all published clustering analyses. Forty years later, this recommendation and reporting need still stands. Although using a default measure is convenient, thoughtlessly applying an artificial, mathematically-constructed distance metric may rest on faulty assumptions that an arbitrary metric can correspond to meaningful biological reality.

Any solution for clustering clinical data must capture relationships between data types without information loss. To tackle the heterogeneous data problem, Kaufman and Rousseuw⁴⁹ suggest clustering a dissimilarity matrix, as opposed to raw data. They subcompartmentalize distinct data types—each requiring different solutions and metrics in the construction of a dissimilarity matrix—including symmetric or asymmetric binary data, ordinal, nominal, interval-scale continuous, and ratio-scale continuous. Each data type is subjected separately to targeted distance calculations, then recombined in a dissimilarity matrix for clustering. This methodology and more elegant solutions merit further exploration.

FUNDING

This work was supported by the National Cancer Institute grant number R03 CA235101 and by Pelotonia Intramural Research Funds from the James Cancer Center.

AUTHOR CONTRIBUTIONS

CEC contributed in study design, data analysis, and manuscript preparation. ZBA contributed in data analysis and manuscript preparation. SL contributed in data analysis. LVA contributed in study design, data acquisition, and manuscript preparation. KRC contributed in study design, data analysis, and manuscript preparation. All authors have approved the final version of the manuscript and agree to be accountable for all aspects of the work.

CONFLICT OF INTEREST STATEMENT

None declared.