Fold-stratified cross-validation for unbiased and privacy-preserving federated learning

Abstract

Objective

We introduce fold-stratified cross-validation, a validation methodology that is compatible with privacy-preserving federated learning and that prevents data leakage caused by duplicates of electronic health records (EHRs).

Materials and Methods

Fold-stratified cross-validation complements cross-validation with an initial stratification of EHRs in folds containing patients with similar characteristics, thus ensuring that duplicates of a record are jointly present either in training or in validation folds. Monte Carlo simulations are performed to investigate the properties of fold-stratified cross-validation in the case of a model data analysis using both synthetic data and MIMIC-III (Medical Information Mart for Intensive Care-III) medical records.

Results

In situations in which duplicated EHRs could induce overoptimistic estimations of accuracy, applying fold-stratified cross-validation prevented this bias, while not requiring full deduplication. However, a pessimistic bias might appear if the covariate used for the stratification was strongly associated with the outcome.

Discussion

Although fold-stratified cross-validation presents low computational overhead, to be efficient it requires the preliminary identification of a covariate that is both shared by duplicated records and weakly associated with the outcome. When available, the hash of a personal identifier or a patient’s date of birth provides such a covariate. On the contrary, pseudonymization interferes with fold-stratified cross-validation, as it may break the equality of the stratifying covariate among duplicates.

Conclusion

Fold-stratified cross-validation is an easy-to-implement methodology that prevents data leakage when a model is trained on distributed EHRs that contain duplicates, while preserving privacy.

INTRODUCTION

The large-scale collection of data and its analysis by artificial intelligence (AI) algorithms have led to new scientific discoveries and huge expectations for the near future.^1–5 Although AI algorithms (eg, random forest, gradient boosting, neural networks)⁶ provide powerful tools, they are difficult to develop, as they generally require large training datasets to reach reasonable performances,⁷ and often detailed, high-dimensional records about individuals. Beyond the technical challenges that such a data collection represents, storing and analyzing a large amount of personally identifying information (PII) may moreover imply serious risks regarding privacy, and recent research projects have been hindered by public opinion concerns.^8,9 These concerns are not unfounded, as reidentification attacks have regularly broken the anonymity of large datasets.^10–13 To address these risks, new regulations that impose higher security standards have been introduced.¹⁴ Technically, it moreover appears necessary to complement classical anonymization techniques as they are intrinsically limited in the case of high-dimensional data.^15,16 Handling and analyzing securely such data therefore requires moving from the anonymize, release, and forget approach to configurations in which a data curator secures and controls the use of data that remain to some extent identifying.¹⁷ In the latter configuration, the question arises as to which organization should play the role of the trusted data curator. In the case of medical records, patients and information technology managers have been reluctant to devote this role to centralized private or public organizations,^8,9,18 limiting large-scale research on electronic health records (EHRs). To solve this issue, a technique called federated learning has recently been proposed. This technique enables the training of AI models while keeping records in decentralized trusted data warehouses curated for instance by hospitals.^19–25 Federated learning appears as a promising privacy-enhancing technique that avoids single points of failure, and it is currently being developed and tested in various projects worldwide.^26–30

In addition to privacy concerns, recent controversies indicate that many AI models may have been validated improperly, shedding doubt on the performances that have been advertised.^31–35 One of the most frequent sources of bias in performance estimation is the data leakage that occurs when data used for validation and training are correlated.^36–39 Avoiding data leakage requires building training and validation datasets in such a way that all the data related to a given individual are exclusively in the former or the latter. This dataset building procedure may be compromised by the presence of different records related to the same individual: this risk is far from being negligible, as it has been shown that up to 15% of records in medical information systems are duplicates,⁴⁰ and that many patients have records in multiple hospitals.⁴¹ Data leakage induced by duplicates may be especially important in the case of AI models, as they are often trained on large real-world datasets such as EHRs that have not been curated for research.⁴ To address data leakage caused by duplicates, deduplication algorithms, often called record linkage algorithms, have been developed that rely on various deterministic or probabilistic methods.⁴²

Although federated learning and deduplication algorithms address privacy and validation issues, respectively, they cannot be easily combined. Indeed, deduplication relies on the comparison of PII through the computation of a similarity index established between 2 potentially duplicated records, whereas federated learning avoids PII exchange and therefore prevents their comparison when records are located in different data warehouses. Consequently, detecting duplicates of a given record that are present in 2 different hospitals while preserving their privacy appears challenging. Some solutions to this problem have already been proposed.⁴³ A first solution consists of sharing hashes of identifiers among centers to detect duplicates.⁴⁴ This technique limits the risk of reidentification but can only be used when a shared personal identifier is available. EHRs are often not tagged by such an identifier, limiting the datasets that can be deduplicated by this technique. Moreover, comparison of hashes is vulnerable to some reidentification attacks.⁴³ Another set of solutions consists of cryptographic schemes referred to as secure multiparty computation (SMC). These schemes enable computing in each center the list of its records that are present in at least 1 other center while transferring only encrypted data. SMC has been proven to be secure and scalable but is also limited to the detection of exact matches between 2 identifiers.^45,46 It is not straightforward to extend SMC to approximate matching between records that are note tagged by a shared identifier, and additional researches in that direction are necessary.⁴⁶ In this article, we propose an approach that makes it possible to avoid data leakage in a federated learning setting while not relying on the availability of a shared identifier. Our method is moreover easy to implement and does not rely on cryptographic schemes. We consider the classical cross-validation technique for performance estimation, and complement it by an initial stratification of datasets. Whereas some stratification techniques have already been combined with cross-validation in order to limit disparities between randomly chosen folds,⁴⁷ we extend the use of stratification to avoid data leakage in the case of undetected data duplicates.

The article is organized as follows. In the Materials and Methods, we describe the fold-stratified cross-validation methodology we propose and the simulation methodology we follow to assess its validity on both synthetic and real-world MIMIC-III (Medical Information Mart for Intensive Care-III) records. In the Results, we simulate a data analysis in a federated learning setting following different validation strategies, the performances and limitations of which are detailed in Discussion section.

MATERIALS AND METHODS

Fold-stratified cross-validation

We consider a model $\mathrm{f}$ that computes a predicted $\stackrel{\sim }{\mathrm{y}}$ of an outcome $\mathrm{y}$ using covariates $\mathbf{x}=\left({\mathrm{x}}_1,{\mathrm{x}}_2,\dots ,{\mathrm{x}}_{\mathrm{m}}\right)$: $\stackrel{\sim }{\mathrm{y}}=\mathrm{f}\left(\mathbf{x}\right)$. We consider a performance metric that we want to maximize and that is computed as the expectation of a function $\mathrm{h}\left(\mathrm{y},\stackrel{\sim }{\mathrm{y}}\right)$. In the case of accuracy $\mathrm{h}\left(\mathrm{y},\stackrel{\sim }{\mathrm{y}}\right)=\mathrm{I}\left(\mathrm{y}=\stackrel{\sim }{\mathrm{y}}\right)$, where the function $\mathrm{I}\left(\mathrm{A}\right)$ equals 1 if $\mathrm{A}$ is true and 0 otherwise. A record $\mathrm{r}=\left(\mathbf{x},\mathrm{y}\right)$ is a point in a mathematical space $\mathrm{\Omega }$ that gathers for an individual her covariates $\mathbf{x}$ and her realized outcome $\mathrm{y}$, and a dataset $\mathcal{D}$ is a collection of records. A dataset $\mathcal{D}$ contains duplicates when there are 2 records ${\mathrm{r}}_{\mathrm{i}}$ and ${\mathrm{r}}_{\mathrm{j}}$ with $\mathrm{i} \ne \mathrm{j}$ such that ${\mathrm{r}}_{\mathrm{i}}={\mathrm{r}}_{\mathrm{j}}$. For the sake of simplicity, we limit ourselves to exact duplicates but as discussed later our conclusions apply also to inaccurate duplicates, caused for instance by flawed or incomplete recording of data related to a given individual. We consider hereafter that there are never 2 individuals with perfectly identical records, implying that equal records always relate to the same individual that has been registered more than once. We moreover consider that individuals whose records are duplicated are distributed uniformly in the population.

Cross-validation is a statistical technique commonly used to estimate the performances of a model.⁶ In cross-validation a dataset $\mathcal{D}$ is partitioned in $\mathrm{k}$ folds (disjoint subsets) ${\mathcal{D}}_{\mathrm{i}}$, with $\mathrm{i} = 1,.,\mathrm{k}$. For each fold ${\mathcal{D}}_{\mathrm{i}}$ the statistical model is trained on all the folds apart from fold ${\mathcal{D}}_{\mathrm{i}}$ (training), and its performances are estimated on fold ${\mathcal{D}}_{\mathrm{i}}$ (validation). The average of per-fold estimates is used as the estimate of the performances of the same model that would have been trained on all the records. Classical cross-validation often relies on a random partitioning of the dataset in $\mathrm{k}$ folds. In that case, duplicated records may be simultaneously present in training and validation folds thus inducing data leakage and yielding overoptimistic estimates of performance compared with cross-validation without duplicates, that we consider hereafter as the unbiased estimate.

We consider training and validation of a model in a federated learning setting in which records are distributed in different hospitals. In that case, many datasets related to different hospitals are jointly analyzed by an external data scientist without exchanging PII (see Figure 1). Cross-validation in a federated learning setting involves partitioning the dataset ${\mathcal{D}}^{\left(\mathrm{\alpha }\right)}$ of each hospital $\mathrm{\alpha }$ in $\mathrm{k}$ folds ${\mathcal{D}}_{\mathrm{i}}^{\left(\mathrm{\alpha }\right)}$ with $\mathrm{i} = 1,.,\mathrm{k}$. Folds are then merged over hospitals to obtain global folds: ${\mathcal{D}}_{\mathrm{i}}={\cup }_{\mathrm{\alpha }}{\mathcal{D}}_{\mathrm{i}}^{\left(\mathrm{\alpha }\right)}$. To better characterize the presence of duplicates in a federated learning setting we introduce the following definitions:

Figure 1.

Privacy-preserving federated learning: analysis by a data scientist of medical records (blue and red individuals) distributed in 2 hospitals without extracting personally identifying information. One individual’s record is duplicated in the 2 hospitals (red) (ID4), due for instance to multiple admissions. The performances of a model are estimated through cross-validation, partitioning the datasets in training and validation folds either randomly (left) or through stratification (ie, grouping similar patients in folds) (right). Whereas duplicated records (red) may be simultaneously in training and validation folds when random partitioning is applied, thus causing data leakage, this risk is circumvented by stratification.

Definition 1: Intrahospital deduplication: For all records ${\mathrm{r}}_{\mathrm{i}},{\mathrm{r}}_{\mathrm{j}}\in {\mathcal{D}}^{\left(\mathrm{\alpha }\right)}$ in a hospital $\mathrm{\alpha }$ with $\mathrm{i}\ne \mathrm{j}$ we have ${\mathrm{r}}_{\mathrm{i}}\ne {\mathrm{r}}_{\mathrm{j}}$.

Definition 2: Interhospital deduplication: For all records ${\mathrm{r}}_{\mathrm{i}}\in {\mathcal{D}}^{\left(\mathrm{\alpha }\right)}$, ${\mathrm{r}}_{\mathrm{j}}\in {\mathcal{D}}^{\left(\mathrm{\beta }\right)}$ in different hospitals $\mathrm{\alpha }\ne \mathrm{\beta }$ we have ${\mathrm{r}}_{\mathrm{i}}\ne {\mathrm{r}}_{\mathrm{j}}$.

Datasets $\mathcal{D}$ that jointly fulfill definitions 1 and 2 are completely deduplicated (ie, there are no 2 identical records ${\mathrm{r}}_{\mathrm{i}}={\mathrm{r}}_{\mathrm{j}}$ with $\mathrm{i} \ne \mathrm{j}$ in the whole dataset). As explained previously, although many deduplication techniques have been developed to fulfill definition 1, fulfilling definition 2 remains challenging without losing the privacy-enhancing advantage of federated learning. We therefore consider a weaker definition of deduplication that is sufficient to avoid data leakage between folds:

Definition 3: Interfold deduplication: For all records ${\mathrm{r}}_{\mathrm{i}}\in {\mathcal{D}}_{\mathrm{m}}^{\left(\mathrm{\alpha }\right)}$, ${\mathrm{r}}_{\mathrm{j}}\in {\mathcal{D}}_{\mathrm{n}}^{\left(\mathrm{\beta }\right)}$ related to different fold indexes $\mathrm{m}\ne \mathrm{n}$ we have ${\mathrm{r}}_{\mathrm{i}}\ne {\mathrm{r}}_{\mathrm{j}}$.

Definition 3 is weaker than definitions 1 and 2 as it can be fulfilled without removing all duplicates if one ensures instead that duplicates of a given record are present in the same fold. We propose hereafter a technique to create folds that fulfill definition 3. We consider a partition of the record space $\mathrm{\Omega }$ in $\mathrm{k}$ subspaces ${\mathrm{\Omega }}_{\mathrm{i}}$: $\mathrm{\Omega }={\cup }_{\mathrm{i} = 1}^{\mathrm{k}}{\mathrm{\Omega }}_i$ and ${\mathrm{\Omega }}_i\cap {\mathrm{\Omega }}_i=\mathrm{\varnothing }$ if $\mathrm{i}\mathrm{ }\ne \mathrm{j}$. Such a partition can be realized stratifying $\mathrm{\Omega }$ relatively to 1 covariate, and we refer to such a partition as a stratification. Once a stratification has been defined, each hospital $\mathrm{\alpha }$ dataset ${\mathcal{D}}^{\left(\mathrm{\alpha }\right)}$ can be partitioned in folds $\mathrm{i} = \mathrm{1,2},\dots ,\mathrm{k}$ as follows:

$$\left\{\begin{array}{c}{\mathcal{D}}_1^{\left(\mathrm{\alpha }\right)}={\mathcal{D}}^{\left(\mathrm{\alpha }\right)}\cap {\mathrm{\Omega }}_1\\ ⋮\\ {\mathcal{D}}_i^{\left(\mathrm{\alpha }\right)}={\mathcal{D}}^{\left(\mathrm{\alpha }\right)}\cap {\mathrm{\Omega }}_i\\ ⋮\\ {\mathcal{D}}_k^{\left(\mathrm{\alpha }\right)}={\mathcal{D}}^{\left(\mathrm{\alpha }\right)}\cap {\mathrm{\Omega }}_k\end{array}\right.$$ (1)

Partitioning each hospital dataset ${\mathcal{D}}^{\left(\mathrm{\alpha }\right)}$ using a given stratification leads for $\mathrm{i} \ne \mathrm{j}$ to: ${\mathcal{D}}_{\mathrm{i}}^{\left(\mathrm{\alpha }\right)}\cap {\mathcal{D}}_{\mathrm{j}}^{\left(\mathrm{\beta }\right)}=\left({\mathcal{D}}^{\left(\mathrm{\alpha }\right)}\cap {\mathrm{\Omega }}_{\mathrm{i}}\right)\cap \left({\mathcal{D}}^{\left(\mathrm{\beta }\right)}\cap {\mathrm{\Omega }}_{\mathrm{j}}\right)=\left({\mathcal{D}}^{\left(\mathrm{\alpha }\right)}\cap {\mathcal{D}}^{\left(\mathrm{\beta }\right)}\right)\cap \left({\mathrm{\Omega }}_{\mathrm{i}}\cap {\mathrm{\Omega }}_{\mathrm{j}}\right)=\mathrm{\varnothing }$, and definition 3 is therefore fulfilled. Combining stratification technique equation 1 with classical cross-validation constitutes the validation methodology that we call fold-stratified cross-validation.

Although fold-stratified cross-validation prevents overoptimistic estimates of performance induced by duplicates, it does not systematically provide an unbiased estimator compared with cross-validation in the absence of duplicates. A stratification procedure may indeed induce training and validation folds featuring different covariate distributions and covariate-outcome associations. A model trained and validated on such folds tends to overfit the training population and to be unfit for a generalization to the validation population, and fold-stratified cross-validation appears closer to the external validation on a new population. Validating externally a model on a population coming from a different hospital is commonly recognized as a proof of quality, as it measures the generalizability of a model to new care contexts, but fold-stratified cross-validation unfortunately does not measure this relevant interhospital generalizability, as folds cannot be identified with hospitals. The stratification procedure should therefore be defined as to minimize the irrelevant pessimistic bias associated with the heterogeneity of folds populations. An ideal stratifying covariate would therefore be a covariate shared by duplicates but independent of the other covariates and of the outcome, as it would provide folds that would be statistically equivalent (Figure 2). Such a stratifying covariate is often not available since covariates extracted from EHRs are associated with a patient’s medical condition to some extent. A challenge of fold-stratified cross-validation consists in finding a surrogate stratifying covariate that is weakly correlated to the other covariates and to the outcome. In the following section, we run simulations to investigate and discuss the impact of various stratification strategies.

Figure 2.

Description of fold-stratified cross-validation.

Simulation

In order to study the properties of fold-stratified cross-validation, we simulate data analysis in a federated learning setting in presence of duplicates. We generate synthetic datasets in which a binary outcome $\mathrm{y}$ depends on 10 covariates ${\mathrm{x}}_1,{\mathrm{x}}_2,\dots ,{\mathrm{x}}_{10}$. Covariates are generated randomly following a multivariate gaussian distribution:

$$\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_{10}\end{array}\right]=\mathcal{N}\left(\begin{array}{cc}\left[\begin{array}{c}{\mu }_1\\ {\mu }_2\\ ⋮\\ {\mu }_{10}\end{array}\right],\mathrm{ }& \mathrm{\Sigma }\end{array}\right)$$ (2)

with ${\mathrm{\mu }}_1,{\mathrm{\mu }}_2,\dots ,{\mathrm{\mu }}_{10}$ the covariates means and $\mathrm{\Sigma }$ the covariance matrix. To generate $\mathrm{\Sigma }$, we choose 10 eigenvalues $\left({\mathrm{\lambda }}_1,{\mathrm{\lambda }}_2,\dots ,{\mathrm{\lambda }}_{10}\right)$, and sample a random orthogonal matrix $\mathrm{O}$ of size $9 \times 9$. An intermediate covariance matrix ${\mathrm{\Sigma }}^{\mathrm{\text{'}}}$ is obtained through:

$${\mathrm{\Sigma }}^{\mathrm{\text{'}}}=O\left[\begin{array}{cccc}{\lambda }_1& 0& \cdots & 0\\ 0& {\lambda }_2& \ddots & ⋮\\ ⋮& \ddots & \ddots & 0\\ 0& \cdots & 0& {\lambda }_9\end{array}\right]O^{\mathrm{t}}$$ (3)

The final covariance matrix $\mathrm{\Sigma }$ is then generated concatenating ${\mathrm{\Sigma }}^{\mathrm{\text{'}}}$ with ${\mathrm{\lambda }}_{10}$ in a block-diagonal matrix:

$$\mathrm{\Sigma }=\left[\begin{array}{cc}{\mathrm{\Sigma }}^{\mathrm{\text{'}}}& \begin{array}{c}0\\ ⋮\\ 0\end{array}\\ \begin{array}{ccc}0& \cdots & 0\end{array}& {\lambda }_{10}\end{array}\right]$$ (4)

Generating covariates $\mathrm{x}=\left({\mathrm{x}}_1,{\mathrm{x}}_2,\dots ,{\mathrm{x}}_{10}\right)$ according to equations 2-4 provides a set of 9 correlated covariates ${\mathrm{x}}_1,{\mathrm{x}}_2,\dots ,{\mathrm{x}}_9$ and an independent covariate ${\mathrm{x}}_{10}$. Once covariates have been generated, we randomly generate their associated outcomes $\mathrm{y}$ through a logistic model. We consider a situation where the logarithm of the odds is a strongly nonlinear function of the covariates:

$$\log \frac{\mathrm{p}\left(\mathrm{y}=1|{\mathrm{x}}_1,\dots ,{\mathrm{x}}_{10}\right)}{\mathrm{p}\left(\mathrm{y}=0|{\mathrm{x}}_1,\dots ,{\mathrm{x}}_{10}\right)}={\mathrm{a}}_0+{\mathrm{a}}_1{\mathrm{x}}_1+{\mathrm{a}}_2{\mathrm{x}}_2+{\mathrm{a}}_3{\mathrm{x}}_3+{\mathrm{a}}_4{\mathrm{x}}_1{\mathrm{x}}_2+{\mathrm{a}}_5{\mathrm{x}}_3\mathrm{I}\left({\mathrm{x}}_4>0\right)$$ (5)

$$+{\mathrm{a}}_6{\mathrm{x}}_5^2\mathrm{I}\left({\mathrm{x}}_6>0\right)+{\mathrm{a}}_7{\mathrm{x}}_7\mathrm{I}\left({\mathrm{x}}_8{\mathrm{x}}_9>0\right)$$

with $\left({\mathrm{a}}_0,{\mathrm{a}}_1,\dots ,{\mathrm{a}}_7\right)$ a set of constants. Covariates ${\mathrm{x}}_1$, ${\mathrm{x}}_2$, …, ${\mathrm{x}}_9$ are associated with the outcome $\mathrm{y}$ contrary to ${\mathrm{x}}_{10}$ that remains independent of all other variables. The strongly nonlinear case given by equation 5 corresponds to a generic situation with complex interactions that cannot be accounted for by simple generalized linear models.

Each simulation consists in generating randomly ${\mathrm{n}}_{\mathrm{gen}}=10\mathrm{ }000$ records and then in adding randomly ${\mathrm{n}}_{\mathrm{dup}}=2000$ duplicates (17% of the total number of records). Each of the ${\mathrm{n}}_{\mathrm{gen}}$ original records is drawn from equations 2 and 5, and is then attributed randomly to 1 of the ${\mathrm{n}}_{\mathrm{h}}=5$ hospitals with uniform probability. To generate duplicates, we randomly draw 1 of the ${\mathrm{n}}_{\mathrm{gen}}$ original records and 1 of the ${\mathrm{n}}_{\mathrm{h}}$ hospitals. We then add a duplicate of the drawn record to the drawn hospital unless a duplicate of the original record already exists in the hospital that has been drawn, thus ensuring that definition 1 is fulfilled. We repeat this procedure until ${\mathrm{n}}_{\mathrm{dup}}$ duplicated records have been added.

Unless stated otherwise, we consider centered covariates $\left({\mathrm{\mu }}_1,{\mathrm{\mu }}_2,\dots ,{\mathrm{\mu }}_{10}\right)=\left(0,0,\dots ,0\right)$ generated through equation 2 using eigenvalues $\left({\mathrm{\lambda }}_1,{\mathrm{\lambda }}_2,\dots ,{\mathrm{\lambda }}_{10}\right)=\left(1.0,1.2,1.4,1.6,1.8,2.0,2.2,2.4,2.6,2.8\right)$. Outcomes are generated using equation 5 with parameters $\left({\mathrm{a}}_0,{\mathrm{a}}_1,{\mathrm{a}}_2,{\mathrm{a}}_3,{\mathrm{a}}_4,{\mathrm{a}}_5,{\mathrm{a}}_6,{\mathrm{a}}_7\right)=\left(-2,0.4,0.8,1.2,0.4,1.2,3.0,2.0\right)$, leading to $\sim 47\mathrm{\%}$ of records associated to a positive outcome $\mathrm{y} = 1$. Cross-validation is realized with $\mathrm{k} = 5$ folds. The code used for the simulations is available in the Supplementary Appendix.

We complement the model analysis of synthetic datasets by an analysis of real-world medical records included in the MIMIC-III dataset.⁴⁸ Each record corresponds to the admission of a patient in an intensive care unit (ICU). We focus on admissions either in the medical ICU or in the surgical ICU. When multiple records are related to a given patient, to avoid data leakage we keep at random only 1 of these records, leading to 15 446 and 7232 records in the medical and surgical ICUs, respectively. We duplicate at random 4644 records, thus mimicking data duplication that may be caused by imperfectly traced transfers of patients between 2 ICUs. For each record, we compute the 15 explanatory variables used in the SAPS-II (Simplified Acute Physiology Score-II),⁴⁹ and use them as the training covariates. As stratifying covariate we use (1) the age at admission, (2) the weight at admission, (3) the lowest creatinine value from the first 24 hours after admission, (4) the lowest blood urea nitrogen value from the first 24 hours after admission, or (5) the highest hemoglobin value from the first 24 hours after admission.

Model definition and dataset partitioning strategies

High-dimensional nonlinear problems on tabular data are commonly modeled using gradient boosting, random forests, or support vector machines.⁶ We focus hereafter on gradient boosting and we use its implementation in the XGBoost library.⁵⁰ We consider trees of depth 3 that are added successively during 200 boosting iterations. The learning parameter is set to 0.6 and we use the binary logistic loss function. Although it is currently not possible to apply directly XGBoost in a federated learning setting, protocols are being developed to circumvent this difficulty.^51,52 These computational considerations are not related to the data leakage issue under consideration, and for the sake of simplicity, in our simulations XGBoost is applied on physically centralized datasets, simulating gradient boosting in a federated learning setting.

For each analysis, we start with a deduplicated dataset on which we fit and validate a gradient boosting model using the classical cross-validation methodology. We measure thus an unbiased estimate of the performance reached by a model with a dataset that has been perfectly deduplicated. Having computed this baseline, we consider the case of imperfect deduplication. We add duplicates to the dataset and consider various cross-validation strategies. Random partitioning consists in partitioning randomly each hospital dataset in $\mathrm{k}$ folds of the same size. Stratified partitioning consists in choosing first a stratifying covariate ${\mathrm{x}}_{\mathrm{str}}$ and a set of thresholds $\{{\mathrm{t}}_0,{\mathrm{t}}_1,\dots ,{\mathrm{t}}_{\mathrm{k}}\}$. Each record is then attributed to the fold $\mathrm{i}$ that fulfills ${\mathrm{t}}_{\mathrm{i}}<{\mathrm{x}}_{\mathrm{str}}<{\mathrm{t}}_{\mathrm{i} + 1}$. We choose thresholds ${\mathrm{t}}_{\mathrm{i}}$ in such a way that the number of records in each global fold ${\mathcal{D}}_{\mathrm{i}}$ is the same. Once fold partitioning is realized, gradient boosting models are fitted and validated on these folds.

RESULT

Model training and validation

We consider first the analysis of synthetic datasets. For each $\mathrm{i}\in 1,.,\mathrm{k}$, the model is trained on all the folds apart from fold ${\mathcal{D}}_{\mathrm{i}}$, and its training performances are measured on the same folds. Figure 3 shows the training learning curves obtained during boosting for unbiased (squares), random (circles), and stratified along ${\mathrm{x}}_1$ (triangles) strategies. Training accuracies increase monotonously as the model learns from the training dataset, and the learning speed does not depend on the fold-partitioning strategy that is adopted. Indeed, training accuracies do not depend on strategy-dependent data leakage between training and validation folds.

Figure 3.

Accuracies computed through cross-validation as a function of the number of boosting iterations in the case of synthetic datasets. Symbols and curves correspond respectively to training accuracies and validation accuracies. Green, red, and blue colors correspond to unbiased, random, and stratified, respectively, along ${\mathrm{x}}_1$ fold-partitioning strategies. Unbiased validation accuracy lies between the overoptimistic random and the pessimistic ${\mathrm{x}}_1$-stratified estimates. The horizontal black dashed line indicates the theoretical optimal accuracy $\mathrm{Accurac}{\mathrm{y}}_{\mathrm{opt}}$.

For each $\mathrm{i}\in 1,.,\mathrm{k}$ the model trained on folds ${\mathcal{D}}_{\mathrm{j}}$ with $\mathrm{j} \ne \mathrm{i}$ is validated on fold ${\mathcal{D}}_{\mathrm{i}}$. Figure 3 shows the variation of validation accuracies during training (solid and dashed lines). When a deduplicated dataset is used (green dashed curve), the unbiased validation accuracy increases during the first 50 boosting iterations and then saturates at an $\mathit{Accuracy}=0.84$ that is lower than the optimal $\mathit{Accuracy}=0.88$ that a predictive model could reach (straight dashed black line, see Supplementary Appendix). As expected the validation accuracy remains lower than the optimal accuracy. When duplicates are added and random fold-partitioning strategy is used, the estimated validation accuracy (solid red curve) is biased by data leakage, and it increases monotonously until falsely reaching a high accuracy. When stratified along ${\mathrm{x}}_1$ strategy is adopted, duplicates of a given record are grouped in the same fold and definition 3 is fulfilled: there is consequently no overoptimistic bias, and the estimated accuracy remains close to the unbiased one, but a small pessimistic bias is observed that is due to interfold heterogeneity. Applying a random fold-partitioning strategy on a dataset with duplicates therefore misses the saturation of the performances observed in unbiased and stratified cases.

Bias and feature importance

We ran additional simulations to better understand the implications of the choice of a stratifying covariate. Figure 4 shows validation accuracies obtained after 200 boosting iterations for 30 simulations using the same set of generating parameters $\mathrm{\Sigma }$ and $\left({\mathrm{a}}_0,{\mathrm{a}}_1,\dots ,{\mathrm{a}}_7\right)$ but applying various fold-partitioning strategies. Whereas random fold partitioning always leads to overoptimistic estimates of accuracy (red) compared with the unbiased estimates obtained without duplicates (green), other stratification strategies lead to accuracy estimates that feature pessimistic biases of variable importance (blue). Whereas ${\mathrm{x}}_5$ stratification leads to a pessimistic bias of roughly 5%, stratifying along ${\mathrm{x}}_1$, ${\mathrm{x}}_2$, ${\mathrm{x}}_4$, ${\mathrm{x}}_8$, ${\mathrm{x}}_9$, or ${\mathrm{x}}_{10}$ leads to estimates that are close to the unbiased ones. The arbitrary choice of a stratifying covariate may consequently lead to important pessimistic biases. The closeness with the unbiased estimates of the estimates obtained having stratified along ${\mathrm{x}}_{10}$ was predictable, as ${\mathrm{x}}_{10}$ is an independent variable that does not induce interfold heterogeneity.

Figure 4.

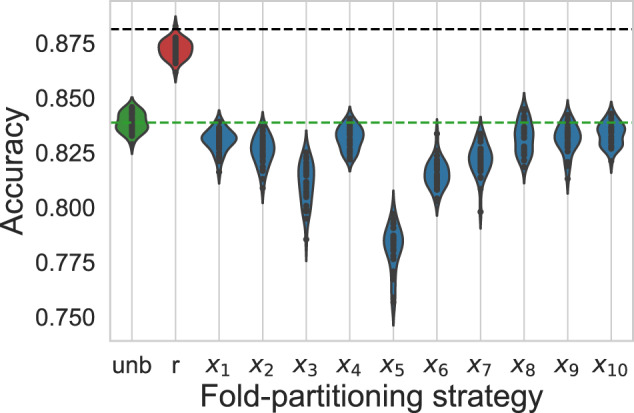
Violin plots for cross-validation estimates of accuracy adopting either an unbiased (green), random (red), or ${\mathrm{x}}_1,{\mathrm{x}}_2,\dots ,{\mathrm{x}}_{10}$–stratified (blue) fold-partitioning strategy and running 30 simulations in the case of synthetic datasets. Horizontal black and green dashed lines correspond to the optimal accuracy that a model could reach $\mathrm{Accurac}{\mathrm{y}}_{\mathrm{opt}}$ and to the mean unbiased estimate of the accuracy $\mathrm{Accurac}{\mathrm{y}}_{\mathrm{unb}}$ reached by the model under consideration, respectively. Whereas random fold partitioning leads to overoptimistic estimates of accuracy, ${\mathrm{x}}_1,{\mathrm{x}}_2,\dots ,{\mathrm{x}}_{10}$–stratified estimates feature pessimistic biases of various sizes.

To better characterize pessimistic biases, we run additional simulations varying also the covariate covariance matrix $\mathrm{\Sigma }$ and the outcome generating parameters $\mathrm{a}=\left({\mathrm{a}}_0,{\mathrm{a}}_1,\dots ,{\mathrm{a}}_7\right)$. We draw 100 different sets of parameters $\{\mathrm{\Sigma },\mathrm{a}\}$ (see Supplementary Material for details), and for each set of generating parameters, we generate a dataset. For each dataset, we fit and validate a gradient boosting model using classical cross-validation and measuring its unbiased validation accuracy $\mathrm{Accurac}{\mathrm{y}}_{\mathrm{unb}}$. We then add duplicates and fit successively 10 gradient boosting models corresponding each to fold-stratified cross-validation having stratified along 1 of the 10 covariates. Figure 5 shows for each one of the 1000 models the validation accuracy $\mathrm{Accurac}{\mathrm{y}}_{\mathrm{str}}$ measured having stratified along ${\mathrm{x}}_{\mathrm{str}}$ divided by the unbiased estimate $\mathrm{Accurac}{\mathrm{y}}_{\mathrm{unb}}$ obtained on the same dataset, plotted with respect to normalized feature importance of ${\mathrm{x}}_{\mathrm{str}}$ measured during the training of the unbiased model—see Hastie et al⁶ for feature importance computation. We observe a negative Pearson correlation coefficient $\mathrm{r}=-0.7$5 between the pessimistic bias on accuracy and the normalized importance of the stratifying covariate.

Figure 5.

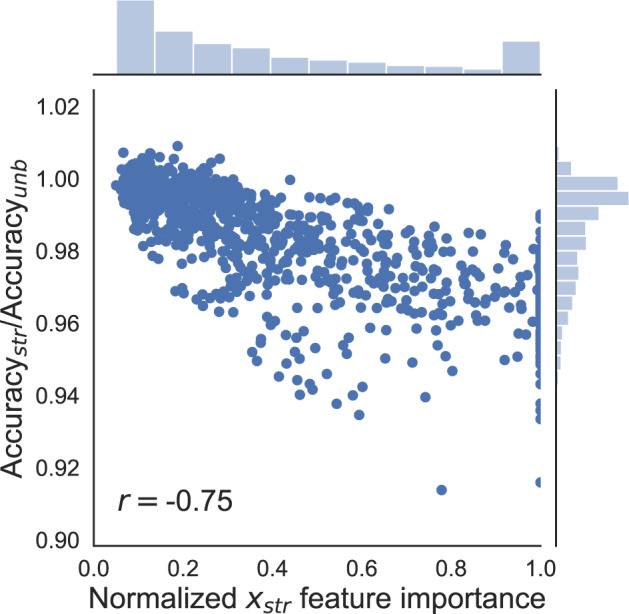
Ratio of ${\mathrm{x}}_{\mathrm{str}}$-stratified estimate of accuracy over the unbiased estimate of accuracy plotted with respect to the normalized importance of the stratifying covariate ${\mathrm{x}}_{\mathrm{str}}$ (see text) in the case of synthetic datasets. A total of 100 datasets are generated corresponding to different $\{\mathrm{\Sigma },\mathrm{a}\}$, and for each dataset, each covariate is taken successively as stratifying covariate. The Pearson correlation coefficient is $\mathrm{r}=-0.77$.

Simulations using real data

We consider now the case of MIMIC-III database.⁴⁸ We reproduce the training and validation of a gradient boosting model,⁵³ that predicts hospital mortality using as performance metric the area under the curve (AUC) of the receiver-operating characteristic curve (Figure 6). We run 30 simulations corresponding each to duplicated records being chosen at random. Applying random cross-validation on the deduplicated dataset, we reproduce the original performance (AUC = 0.826).⁵³ Considering the dataset with added duplicates, random cross-validation leads to a performance (AUC = 0.826) that is overoptimistic compared with the unbiased case, and fold-stratified cross-validation leads to pessimistic performances AUC = 0.806, 0.823, 0.807, 0.798, and 0.820 using age, weight, creatinine, blood urea nitrogen, and hemoglobin, respectively, as stratifying covariates. However, this bias is limited using weight or hemoglobin.

Figure 6.

Violin plots for cross-validation estimates of accuracy adopting either an unbiased (green), a random (red) or a stratified (blue) fold-partitioning strategy and running 30 simulations in the case of MIMIC-III (Medical Information Mart for Intensive Care-III)–based datasets. The horizontal green dashed line corresponds to the mean unbiased estimate of the accuracy $\text{Accurac}{\mathrm{y}}_{\mathrm{unb}}$ reached by the model under consideration. Whereas random fold partitioning leads to overoptimistic estimates of accuracy, stratified estimates feature pessimistic biases of various sizes when the age at admission (age), the weight at admission (wei), the lowest creatinine value from the first 24 hours after admission (cre), the lowest blood urea nitrogen value from the first 24 hours after admission (bun), or the highest hemoglobin value from the first 24 hours after admission (hem) are used as stratifying covariates (see text). Inset shows the ratio of stratified estimate of accuracy over the unbiased estimate of accuracy plotted with respect to the normalized importance of the stratifying covariate $($see text). The Pearson correlation coefficient is $\mathrm{r}=-0.79$. AUC: area under the curve.

DISCUSSION

The data leakage phenomenon at play in our simulations is specific neither to the XGBoost model nor to the data under scrutiny, and the risk of duplicate-caused data leakage should be addressed whatever the scientific problem at stake. Fold-stratified cross-validation methodology avoids data leakage between folds by fulfilling interfold deduplication (definition 3) without requiring full deduplication (definitions 1 and 2), thus providing a validation methodology that is robust to the presence of undetected duplicates (Figures 3 and 4). Although fold-stratified cross-validation avoids an overoptimistic bias due to data leakage between folds, it may be subject to a pessimistic bias due to interfold heterogeneity (Figures 3, 4, and 6). In order to limit this undesired pessimistic bias, it appears optimal to choose a stratifying covariate that is weakly associated to the other covariates and to the outcome (Figures 5 and 6). Determining a priori which covariate is weakly or strongly associated to the other covariates and to the outcome is challenging, and can rely either on prior knowledge of the problem under scrutiny or on preliminary fitting of the model on a local dataset. In the special case of the date of birth or a personal identifier being available, hashing it provides an ideal stratifying covariate that is shared by duplicates. Another difficulty might arise when records related to a given individual are not perfectly equal, as it is the case when duplicated records correspond to different recording events such as hospital admissions. But perfect equality of duplicated records is not necessary to apply fold-stratified cross-validation: identifying a single stratifying covariate, the value of which is shared among records related to a given individual, is indeed sufficient.

Fold-stratified cross-validation methodology presents generic limitations. First, when duplicated records are so different that no shared covariate can be found to stratify, it appears impossible to ensure through stratification that 2 records related to a given individual are present in the same fold. Second, when data curators are not hospitals but instead are directly individuals, such as for instance in the case of data stored in mobile phones,²⁵ it is impossible to partition datasets in folds as each dataset corresponds to a single record. Third, pseudonymization is often applied to records prior to their analysis (eg, date shifting, quantization, noise addition).^54,55 Applying hospital-specific or probabilistic pseudonymization may break the equality of stratifying covariates among duplicates. Last, a subpopulation may be more subject to data duplication, thus inducing its overrepresentation in the validation fold. We moreover underline that the presented simulations are mostly illustrative: the size of biases measured in this article depend strongly on the data, the model, and the metric at stake.

CONCLUSION

When a model is trained and validated in a privacy-preserving federated learning setting, the presence of duplicated records may lead to overoptimistically biased estimates of its performances. We have shown that fold-stratified cross-validation methodology can be used to avoid this overoptimistic bias while not relying on deduplication algorithms, the application of which is often limited to records that are tagged by a shared personal identifier. Fold-stratified cross-validation presents drawbacks, as it may be subject to a pessimistic bias, but this bias can be minimized by carefully choosing the stratifying covariate. We underline that fold-stratified cross-validation, although of special importance in the case of federated learning in which full deduplication is often unfeasible, also applies to the case of a centralized dataset with undetected duplicates and can therefore be used as an easy-to-implement sanity check. Although of possibly broad application, fold-stratified cross-validation is only a partial solution to duplicate problems: tagging records by shared identifiers and applying deduplication algorithms remains optimal to ensure databases integrity.

FUNDING

This project is supported by Bpifrance as part of the HealthChain project, which resulted from the Digital Investments Program for the major challenges of the future RFP. As part of the HealthChain project, a consortium coordinated by Owkin (a private company) has been established, including the Substra association, Apricity (a private company), the Assistance Publique-Hôpitaux de Paris, University Hospital Center of Nantes, Léon Bérard Center, French National Center for Scientific Research, École Polytechnique, Institut Curie, and University of Paris.

AUTHOR CONTRIBUTIONS

RB designed the methodology, conducted the simulations, and wrote the article. RG and MB provided technical advice and article feedback. FG realized the analysis based on the MIMIC-III dataset and provided article feedback. RP oversaw the project and helped with writing the article .

SUPPLEMENTARY MATERIAL

Supplementary material is available at Journal of the American Medical Informatics Association online.