Optogenetic Control Reveals Differential Promoter Interpretation of Transcription Factor Nuclear Translocation Dynamics

SUMMARY

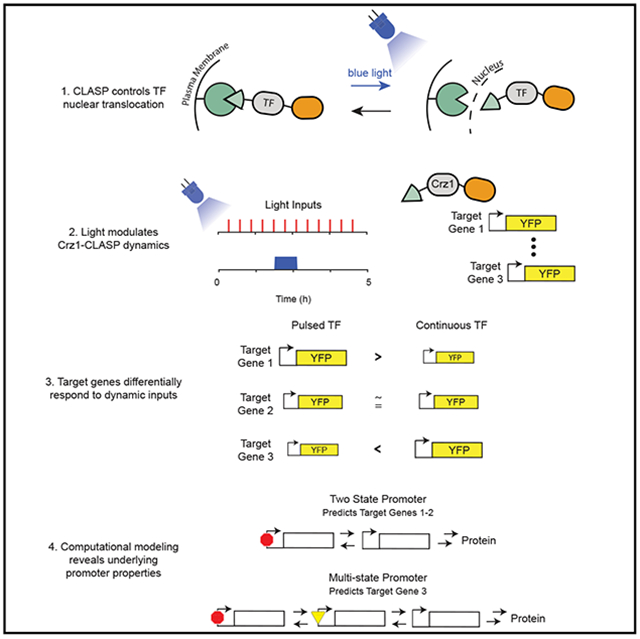
Gene expression is thought to be affected not only by the concentration of transcription factors (TFs) but also the dynamics of their nuclear translocation. Testing this hypothesis requires direct control of TF dynamics. Here, we engineer CLASP, an optogenetic tool for rapid and tunable translocation of a TF of interest. Using CLASP fused to Crz1, we observe that, for the same integrated concentration of nuclear TF over time, changing input dynamics changes target gene expression: pulsatile inputs yield higher expression than continuous inputs, or vice versa, depending on the target gene. Computational modeling reveals that a dose-response saturating at low TF input can yield higher gene expression for pulsatile versus continuous input, and that multi-state promoter activation can yield the opposite behavior. Our integrated tool development and modeling approach characterize promoter responses to Crz1 nuclear translocation dynamics, extracting quantitative features that may help explain the differential expression of target genes.

Graphical Abstract

In Brief

CLASP is a modular optogenetic strategy to control the nuclear localization of transcription factors (TFs) and elicit gene expression from their cognate promoters. CLASP control of Crz1 nuclear localization, coupled with computational modeling, revealed how promoters can differentially decode dynamic transcription factor signals. The integrated strategy of CLASP development and modeling presents a generalized approach to causally investigate the transcriptional consequences of dynamic TF nuclear shuttling.

INTRODUCTION

Transcription factors (TFs) are key mediators in the transmission of information from the internal and external environment of the cell to its genome. Understanding how TFs encode information about the environment in order to coordinate transcriptional programs remains one of the most pressing problems in molecular and systems biology. Many studies have explored how modulation of TF concentration, TF post-translational modifications, and combinatorial TF control can yield differential gene regulation (Czyz et al., 1993; Sadeh et al., 2011; Springer et al., 2003), therefore explaining many important aspects of TF function and their information encoding capacity. These mechanisms, however, may not fully account for the complexity of signal multiplexing that is carried out by TFs. As a result, it has been proposed that TFs might also encode information in their spatiotemporal dynamics.

A number of studies have attempted to elucidate this TF dynamic encoding hypothesis by eliciting different TF dynamic patterns using various environmental inputs and assessing the consequences (Batchelor et al., 2011; Covert et al., 2005; Gotoh et al., 1990; Hoffmann et al., 2002; Nelson et al., 2004; Nguyen et al., 1993; Purvis and Lahav, 2013; Purvis et al., 2012; Tay et al., 2010; Traverse et al., 1992; Werner et al., 2008; Lane et al, 2017; Yissachar et al., 2013). For example, it was shown that p53 exhibits fixed concentration pulses in response to gamma radiation, but implements only one amplitude- and duration-dependent continuous pulse in response to UV (Batchelor et al., 2011). These two pulsing regimes have different physiological outcomes, with the former leading to cell cycle arrest and the latter leading to cell death (Purvis et al., 2012). Other studies programmed different TF nuclear translocation patterns by gaining control of a signaling node upstream of the TF. A prominent example of this approach is the modulation of Msn2 dynamics using an analog-sensitive protein kinase A (PKA) allele (Hansen and O’Shea, 2013, 2015a, 2015b; Hao and O’Shea, 2011; Hao et al., 2013). With this method, it was shown that genes in the Msn2 regulon can be differentially modulated by the amplitude, duration, and frequency of Msn2 nuclear translocation pulses.

In the budding yeast Saccharomyces cerevisiae, there are approximately 200 known TFs, two-thirds of which are constitutively localized to the nucleus; the remaining one-third are located in the cytoplasm during exponential growth in complete media (Chong et al., 2015). At least nine of these basally cytoplasmic TFs transiently localize into the nucleus in response to various stress conditions (Dalal et al., 2014). Furthermore, different environmental conditions elicit a range of pulsing characteristics for these TFs that differ in their duration, amplitude, and frequency (Dalal et al., 2014 and Figure S1), suggesting that reversible TF nuclear localization may encode regulatory information. This information may then be decoded by downstream target genes in order to produce an appropriate response (Granados et al., 2018).

Control of TF localization through modulation of upstream regulators with small molecules or chemicals has been an essential method to put forward such a hypothesis of TF dynamic encoding (AkhavanAghdam et al., 2016; Cai et al., 2008; Hansen and O’Shea, 2013, 2015a, 2015b; Hao and O’Shea, 2011; Lin and Doering, 2016; Purvis et al., 2012; Sen et al, 2020). However, this method produces pleiotropic effects that can be hard to untangle. For example, PKA controls many transcriptional regulators in addition to Msn2. As a result, modulating its activity with a small molecule may yield gene-expression changes that are not solely caused by Msn2 translocation dynamics, but are instead the result of combinatorial gene regulation by other PKA-responsive TFs such as Msn4 (AkhavanAghdam et al., 2016; Garmendia-Torres et al., 2007) and Dot6 (Pincus et al., 2014).

Therefore, to causally and quantitatively probe the relationship between TF nuclear localization dynamics and transcriptional activity, a method by which TFs can be specifically, quickly, and reversibly localized to the nucleus is needed. Specificity is necessary to allow direct regulation of TF nuclear localization without pleiotropic effects, while speed and reversibility are necessary to recapitulate the minutes-level resolution with which TFs translocate into and out of the nucleus in response to environmental inputs. Ideally, this method would also work modularly with many TF cargos, including TFs that are basally nuclear. Optogenetic strategies are ideally suited for this purpose.

There are many general optogenetic tools to control the activity of molecules (Shimizu-Sato et al., 2002; Strickland et al., 2012; Toettcher et al., 2011,2013), as well as published optogenetic strategies to translocate protein cargos to the nucleus (Niopek et al., 2014; Redchuk et al., 2017; Yumerefendi et al., 2015; Gautier et al., 2010). A number of these tools utilized LOV2, a light-responsive protein often isolated from A. sativa, to uncage a nuclear localization sequence (NLS) in response to blue light and translocate the optogenetic molecule to the nucleus along with any appended protein cargo. Light-activated nuclear shuttle (LANS) is an example of this strategy (Yumerefendi et al., 2015) (Figure 1A). The architecture of this class of optogenetic tools may cause leaky nuclear localization based on the protein cargo. An example is the TF Msn2, which when fused to LANS, in many cells exhibited constitutive nuclear localization in the absence of light stimulation (Figure S2A). Moreover, tools such as LANS cannot be used to regulate the localization of basally nuclear TFs.

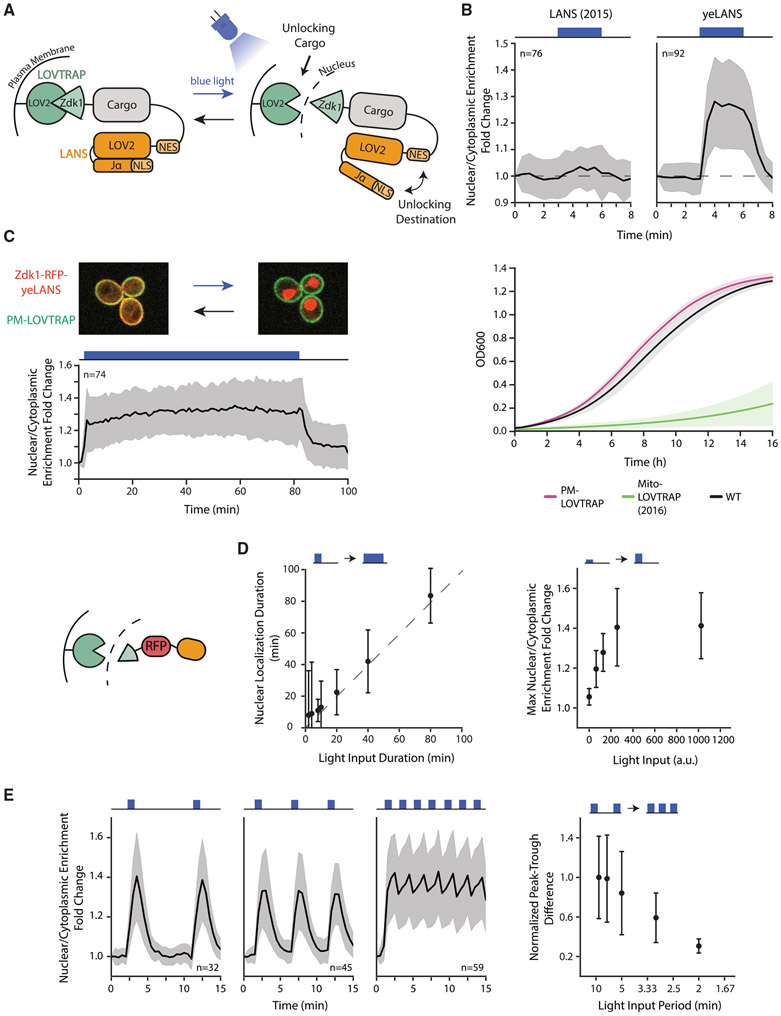
Figure 1. Design, Optimization, and Characterization of CLASP.

(A) Schematic illustrating CLASP mechanism.

(B) Optimization of LANS NLS (top panels) and LOVTRAP localization (bottom panel). Top panels show the mean value of nuclear/cytoplasmic enrichment fold change for original NLS and optimized NLS (yeLANS) as a function of time when given a pulse of blue light. Nuclear/Cytoplasmic enrichment fold change is calculated relative to the nuclear/cytoplasmic enrichment at t = 0. Bottom panel shows the mean of OD600 in 3 independent growth experiments for original LOVTRAP targeted to mitochondria and the optimized plasma membrane-targeted LOVTRAP.

(C) (Top panel) Confocal microscopy image showing mScarlet-CLASP localization at the plasma membrane in the dark (left) and in the nucleus (right) after 3 min of light exposure. Images are an overlay of the mCherry and Cy7 channels. (Bottom panel) Quantification of mean nuclear/cytoplasmic enrichment fold change of mScarlet-CLASP as a function of time in response to a prolonged light input (80 min, 1024 a.u. light input amplitude). Blackline represents the mean of 74 cells.

(D) Quantification of the response of mScarlet-CLASP to light inputs with different dynamic characteristics. The left plot shows median time to return within 25% of basal nuclear/cytoplasmic enrichment for light pulses of different durations and constant 1,024-a.u. amplitude. Median is used to minimize the effect of outliers. The dotted line is Y = X line. The right plot shows the mean response to 1 min light pulses of different amplitudes. Points in both plots represent at least 21 cells.

(E) Nuclear/cytoplasmic enrichment fold change of mScarlet-CLASP in response to light pulsing with different periods. Left three graphs show mean enrichment fold change as a function of time in response to pulsed light inputs (1 min light given in a 9, 5, or 2 min period, respectively) with 1,024-a.u. amplitude. The right plot quantifies median peak-to-trough difference (normalized to the median peak-to-trough difference generated by the longest period). Median is used to minimize the effect of outliers. Each point in the right plot represents at least 32 cells. Error bars and shaded area except where noted, represent standard deviation to show the spread of the data. For all panels, n represents the number of cells tracked and light input regimes are depicted on top of panels. Cartoon (left of D) represents mScarlet-CLASP. yeLANS—yeast enhanced LANS, PM-LOVTRAP—plasma membrane LOVTRAP, Mito-LOVTRAP—mitochondrial LOVTRAP. See also Figures S1 and S2.

A different optogenetic tool, LOVTRAP, a LOV2-based tool for protein sequestration, could be used for rapid translocation of cargo with less leaky basal localization. LOVTRAP is composed of a LOV2 fused to the mitochondria and Zdk1, a small peptide that is fused to the protein cargo. The interaction of LOV2 and Zdk1 in the dark sequesters the cargo to the surface of the mitochondria (Wang et al., 2016) (Figure 1A). However, LOVTRAP alone does not contain targeting information, and hence cannot direct the cargo to the nucleus on demand. Therefore, to enable both robust and targeted optogenetic control of many different cargos, we sought to use LOVTRAP in concert with LANS. The idea of combining optogenetic sequestration and nuclear localization was previously investigated (Redchuk et al., 2017; Yumerefendi et al., 2018). However, the resulting tools either required complex dual-color stimulation (Redchuk et al., 2017), thereby limiting the number of fluorescent proteins that could be used in a cell, or did not demonstrate modularity for different cargos (Yumerefendi et al., 2018). These tools also lacked optimization for use in yeast.

Here, we present CLASP, an optimized optogenetic tool that can exert precise, modular, and reversible control of TF localization. CLASP uses two LOV2 light-responsive domains derived from Avena sativa to sequester a cargo at the plasma membrane in the dark and target it to the nucleus in response to blue light. We demonstrate how CLASP can be used as a general strategy to control many TF cargos without any further optimization.

With CLASP and the use of computational modeling, we investigate the consequences of TF translocation dynamics and delineate the quantitative principles by which these dynamics are interpreted by different promoters. This paper, therefore, contributes an integrated approach through which optogenetic technology development and refinement is coupled tightly to computational modeling in order to answer fundamental questions about promoter principles that allow decoding of dynamic TF inputs. Due to the modularity of CLASP, our integrated approach provides a general strategy for investigating these principles in many systems.

RESULTS

Construction and Optimization of CLASP, a Dual-LOV2 Optogenetic Strategy for Control of Nuclear Shuttling

To construct a modular and specific tool for yeast protein nuclear translocation, we first tackled optimization of the published LANS and LOVTRAP constructs. Fluorescently tagged (mCherry) LANS (Yumerefendi et al., 2015) displayed only a moderate increase (3.4%) in nuclear over cytoplasmic enrichment in response to blue light (Figure 1B, upper left panel). This increase was much weaker than that seen for TFs in response to stress inputs (Figure S1B, 20%–50% increase). Additionally, the published LOVTRAP tool used a TOM20 mitochondrial targeting tag that caused a strong growth defect in yeast at high expression levels (Figure 1B, lower panel). LOVTRAP sequestration had previously been shown to perform best when the mitochondria-bound LOV2 trap was expressed in excess of the Zdk1; as a result, these high expression levels were necessary for trapping many protein cargos and made the growth defect a concrete concern (Wang et al., 2016).

To improve LANS localization properties, we replaced the published LANS NLS with a small library of yeast NLS peptides (Kosugi et al., 2009; Table S1). We then screened blue light-induced nuclear localization of mCherry-LANS constructs that had any one of these different NLS sequences. We identified a number of NLS sequences that showed an improvement in nuclear/cytoplasmic enrichment in response to blue light (Figure S2B), including an NLS that increased the fold change by eight-fold. We chose this NLS sequence to move forward as a yeast enhanced LANS (yeLANS) (Figure 1B). Next, to rectify the growth defect associated with LOVTRAP sequestration to the mitochondria, we swapped the mitochondrial TOM20 tag with a plasma membrane Hs-RGS2 tag (Heximer et al., 2001) to create pm-LOVTRAP. This modification rescued the growth defect of LOVTRAP even at high expression levels (Figure S2C).

Finally, we combined yeLANS and pm-LOVTRAP to form CLASP (controllable light-activated shuttling and plasma membrane sequestration), a construct composed of two AsLOV2 domains. The first AsLOV2 domain is fused to the plasma membrane and sequesters a Zdk1 fused to the N terminus of the cargo (for example, a TF). The second AsLOV2 domain is fused to the C terminus of the cargo. This AsLOV2 domain is preceded by a nuclear export sequence (NES) and has a nuclear localization sequence (NLS) embedded in the Jα helix. Blue light causes a conformational change in both AsLOV2 domains, yielding the simultaneous unlocking of cargo and its targeting to the nucleus (Figure 1A). Strains harboring CLASP did not experience any measurable growth defect (Figure S2D).

We first tested CLASP with a red fluorescent protein (mScarlet) as a cargo. Confocal microscopy showed that mScarlet-CLASP was successfully sequestered at the membrane in the dark and translocates to the nucleus in response to blue light. Furthermore, widefield microscopy showed that nuclear localization could be maintained stably for at least 80 min (Figure 1C). Varying the duration of the light input demonstrated that CLASP could also track shorter light inputs (Figures S2E-S2G). On average, mScarlet-CLASP nuclear localization extended 4 min longer than the duration of the input light pulse, illustrating its rapid shut-off time (Figures 1D and S2E). The maximum nuclear/cytoplasmic enrichment achieved by mScarlet-CLASP was also graded as a function of light amplitude; when subjected to one min pulses of increasing amplitude (64–1,024 a.u.), enrichment increased commensurately for a wide range and saturated after 256 a.u. of light (Figure 1D; Table S4).

Finally, to test the ability of CLASP to respond to repeated light pulses and probe its dependence on their period, we subjected the cells to 1 min pulses of blue light repeated every 2–9 min (Figure 1E, left 3 panels to show 1 min pulses every 9, 5, or 2 min). These experiments revealed that mScarlet-CLASP followed these pulses faithfully until the pulses became too rapid, that is when the next light pulse occurred during the time required for nuclear exit (~4 min). This effect occurred when pulses were repeated every 2 min, at which point nuclear localization became almost continuous at a high level. The mean peak-to-trough difference in the amplitude of nuclear localization of single-cell traces for different periodic light inputs showed a clear dependence on the period of the light pulse (Figure 1E).

Overall, our data indicate that mScarlet-CLASP could be rapidly, reversibly, and repeatedly localized to the nucleus as frequently as every 5 min and that the duration and the magnitude of this translocation could be robustly controlled.

CLASP Achieves Precise, Modular Control of TF Nuclear Translocation and Activation of Target Genes

The usefulness of CLASP depends on its ability to successfully control the translocation of TF cargos while maintaining their function. Our next step was, therefore, to test the ability of CLASP to quickly and reversibly control the translocation of three basally cytoplasmic TFs to the nucleus. We chose a synthetic transcription factor, SynTF, constructed from Cys₂-His₂ zinc finger domains and a VP16 activation domain (Khalil et al., 2012), as well as Msn2, the principal TF in the environmental stress response (Gasch et al., 2000), and Pho4, the principal TF in the phosphate starvation response (Vardi et al., 2014). Both Msn2 and Pho4 have been known to translocate to the nucleus in response to stress (Dalal et al., 2014; Vardi et al., 2014). The three-TF cargos were also tagged with a C-terminal RFP (mScarlet) for visualization.

For all three TFs, TF-CLASP achieved its maximal nuclear localization in response to light within 1 min of blue light exposure. Like the mScarlet cargo, the TF cargos reversibly translocated to the nucleus as frequently as every 5 min when induced with a 1 min pulse of light. Furthermore, a sustained light input produced continuous nuclear localization of the TFs, indicating that CLASP was capable of maintaining robust nuclear localization of associated TF cargos for an extended period of time (Figure 2A). The maximum nuclear/cytoplasmic enrichment fold change achieved with CLASP for Msn2 as cargo was similar to that of Msn2 with a strong osmotic shock using 0.95 M Sorbitol (Figure S1B; Hoffmann et al., 2002).

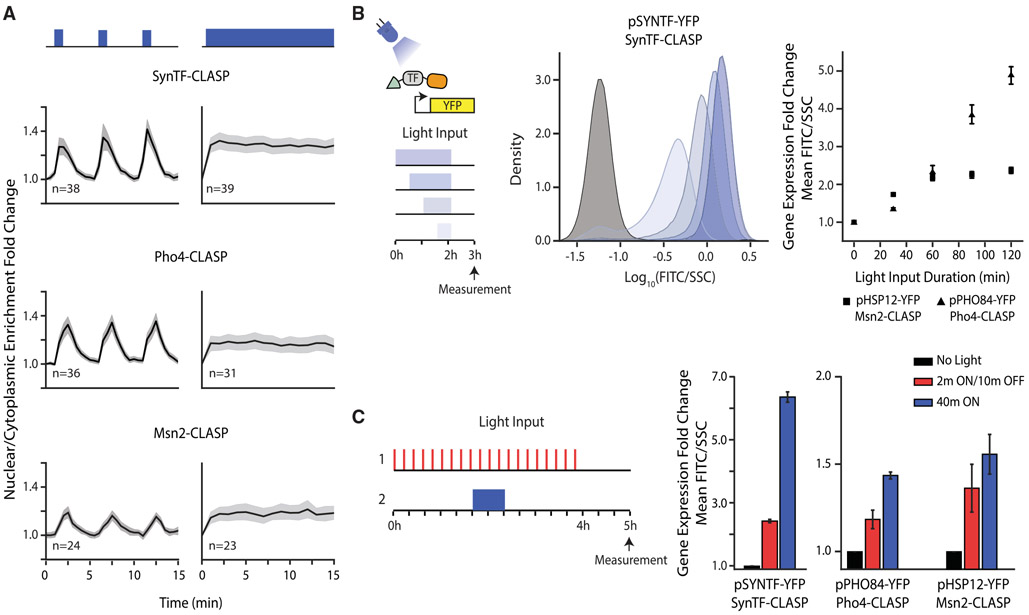
Figure 2. CLASP Can be Used to Control Localization of Many Transcription Factor Cargos.

(A) Nuclear/cytoplasmic enrichment fold change in response to pulsed (left panels) and continuous light (right panels) for several TF-CLASP cargos. Graph shows mean of single-cell traces for TFs tagged with CLASP. Light is delivered for one minute at the start of each 5-min period or continuously. The shaded gray area represents 95% confidence interval and light inputs are represented in blue above graphs. n represents number of cells tracked.

(B) Fluorescent reporter expression due to TF-CLASP localization. The left panel shows a schematic of the experiment—the TF is localized to the nucleus for 0.5, 1, 1.5, or 2 h. A fluorescent reporter is measured via flow cytometry 1 h after light shut-off. Center panel shows the population response of pSYNTF-YFP (promoter downstream of SynTF-CLASP) for inputs shown on the left. Darker blue shades correspond to longer light duration. The black histogram corresponds to no light. The right panel shows quantification of the YFP fold change as a function of light duration for promoters responsive to other TF-CLASP constructs following the same experimental protocol. Fluorescence readings are normalized by side scatter and then normalized to the 0 min dose for each strain to show fold change. Error bars represent standard error of the mean for 9 biologically independent replicates.

(C) Fluorescent reporter response to pulsatile versus continuous localization of different TF-CLASP constructs. TF-CLASP constructs are given either 20 2-min pulses of light or 1 40-min pulse of light, as depicted in the schematic on the left. Reporter expression is measured via flow cytometry 1 h after light shut-off. Right panels show quantification of YFP fold change in response to pulsed light input, continuous light input, or no input. Error bars represent standard error of the mean for 9 biologically independent replicates. In all panels, strains are induced with a given amplitude of light (SynTF-CLASP – 1,024 a.u.; Msn2-CLASP – 2,048 a.u., Pho4-CLASP – 4,095 a.u.). See also Figure S3.

To test whether nuclear localization of the TFs led to concomitant gene expression, we built yeast strains in which YFP was expressed from promoters that were responsive to SynTF (pSYNTF-YFP), Msn2 (pHSP12-YFP), and Pho4 (pPHO84-YFP). We exposed these strains to fixed-amplitude light inputs (Figure S3A) of increasing duration (0.5–2 h) and measured YFP fluorescence via flow cytometry. For all three TFs, increasing the duration of the light input led to increased downstream reporter gene expression, illustrating that the TF was still functional despite its fusion to CLASP. Notably, SynTF-CLASP yielded more than 20-fold activation of pSYNTF-YFP with only 2 h of light activation (Figure 2B). Gene expression in the dark downstream of the three TF-CLASP constructs was similar to basal expression and was also commensurate after light induction to gene expression generated by a constitutively nuclear TF (Figures S3B-S3D; STAR Methods “Measuring the basal and constitutively nuclear gene expression of TFs”).

Next, we explored whether CLASP could control the localization of TFs such as Gal4, which was basally nuclear. Gal4-CLASP was successfully sequestered to the plasma membrane in the dark and reversibly translocated to the nucleus in response to light. Nuclear translocation of Gal4-CLASP also activated expression from pGAL1, a Gal4-responsive promoter (Figures S3E-S3G), indicating that CLASP was able to control TFs irrespective of their endogenous nuclear localization.

Finally, we sought to demonstrate that different TF dynamic translocation patterns generated with CLASP could yield different gene-expression outputs. Several TFs, such as Pho4 following phosphate starvation, translocate into the nucleus in response to a stress input and reside there continuously until the response is completed (Vardi et al., 2014). Others, including Msn2 following a 0.4% glucose input, have been known to translocate into the nucleus with episodic and repeated pulses in response to an activating input (Dalal et al., 2014). Moreover, Msn2 has also been known to translocate with sustained pulses in response to osmotic shock (Figure S1B). As a result, we sought to explore the gene-expression consequences of pulsing relative to continuous localization of the three CLASP-fused TFs (SynTF, Msn2, and Pho4). We delivered two light inputs that had different dynamic patterns but the same cumulative light duration of 40 min. In the first case, the light was switched ON for 40 min, and in the second, the light was given in 20 episodic pulses (2 min ON/10 min OFF) (Figure 2C). Delivery of the same cumulative light input and measurement at the end of the time course were necessary controls to compare the response efficiency of the promoters for pulsed input relative to continuous inputs. YFP fluorescence was measured for both inputs after 5 h using flow cytometry. These data showed unambiguously that continuous nuclear input of SynTF-CLASP, Msn2-CLASP, and Pho4-CLASP produced higher gene expression than pulsed inputs. This directly demonstrates that TF nuclear translocation dynamics could affect downstream reporter gene expression, an idea that we wanted to explore in more depth.

CLASP Control of the Crz1 TF Reveals that Its Target Genes Differ in Their Response Efficiency to Short Pulses

To further explore the modes of decoding of TF dynamics by promoters in a biologically meaningful setting, we chose to focus on Crz1, the main TF in the calcineurin-Crz1 signaling pathway that responds to calcium stress. Crz1 has been shown to exhibit two modes of pulsatile nuclear translocation in response to calcium chloride (CaCl₂) stress—a single long initial pulse (40–60 min) and subsequent episodic repeated pulsing (1–4 min) (Figure S4A). We reasoned that continuous nuclear localization and pulsing of Crz1 could be interpreted differently by different target genes, a behavior that could be revealed and studied by controlling its localization using CLASP.

Crz1 has been shown to undergo phosphorylation on multiple residues to activate gene expression in calcium stress (Figure S4B, Stathopoulos-Gerontides et al., 1999). Therefore, to survey the response of Crz1 target genes to dynamic inputs using CLASP, we needed to adopt a variant of Crz1 that bypassed this regulation, an endeavor that could be necessary for studying the effects of many TFs with CLASP. We therefore, built a strain expressing Crz1*, an alanine mutant with 19 S/T to A substitutions of Crz1, that was basally nuclear (data not shown) and circumvented the post-translational modification requirements for nuclear localization (Figure S4B, Stathopoulos-Gerontides et al., 1999). To verify that Crz1* preserved the transcriptional profile of wild type Crz1, we carried out mRNA sequencing of cell populations in which the wild type allele of Crz1 was knocked out and Crz1* was expressed from a constitutive pADH1 promoter. We compared the up-regulated genes of the Crz1* strain (where Crz1* is basally nuclear) with genes upregulated by Crz1-yeLANS under CaCl2 stress. We found similar gene-expression patterns between these two gene sets as shown in the heatmap of genes that cluster together (Figure S4C). By probing individual Crz1 target genes with fluorescent reporters, we also found that light-induced Crz1*-CLASP, but not light-induced Crz1-CLASP, was able to elicit appreciable gene expression (Figure S4D). For example, Crz1*-CLASP driving pPUN1-YFP, a canonical Crz1-responsive promoter, achieved similar gene-expression fold change as pPUN1-YFP in calcium stress (fold change of 1.8 versus 1.7) (Figure S4E). Importantly, Crz1*-CLASP did not cause increased gene expression in the absence of light, indicating that CLASP was able to successfully sequester the nuclearly localized Crz1* outside of the nucleus in the dark (Figure S4F).

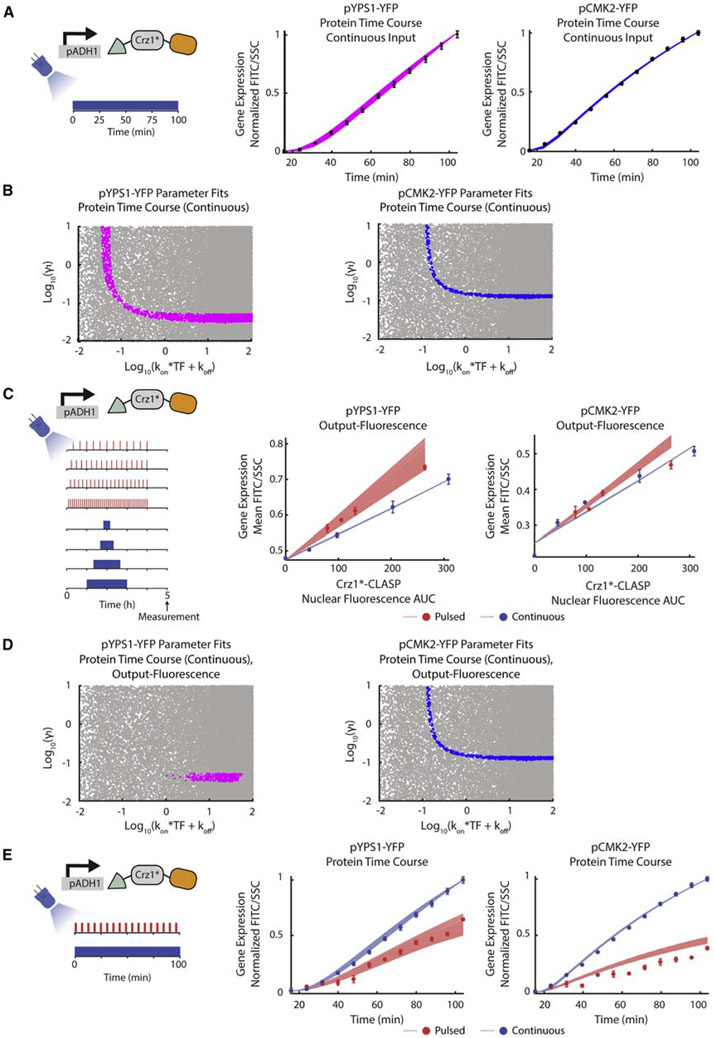
We next identified six Crz1 gene targets (Yps1, Ena1, Mep1, Put1, Cmk2, and Gyp7) for follow up studies. We used the promoters of these genes, which have also been used in previous studies (Stathopoulos and Cyert, 1997; Yoshimoto et al., 2002), to build YFP-expressing promoter fusions, each in a strain with Crz1*-CLASP tagged with mCherry for visualization (Figure 3A). We subjected these cells to two distinct types of inputs that mimic natural Crz1 translocation: 2 min short repeated pulses with different periods or one continuous pulse of varying duration (Figure 3A). We confirmed that extended light exposure did not cause a growth defect in the Crz1 overexpression strain (Figure S4G). We then measured the nuclear fluorescence of mCherry-tagged Crz1*-CLASP continuously at 30-s intervals. We also measured gene expression from all six YFP promoter fusions at 5 h for all inputs given (Figure 3A). Every input (pulsatile or continuous) has a given nuclear fluorescence AUC, which we calculated as the integral of the measured mCherry-tagged Crz1*-CLASP nuclear fluorescence time traces and is a proxy for nuclear concentration. A given nuclear fluorescence AUC was associated with a commensurate gene expression value (measured at 5 h), and these values were plotted against each other for the two input regimes for each of the six promoters. The resulting plot for all nuclear fluorescence AUC values are referred to as the gene output-nuclear fluorescence plot (output-fluorescence plot for short). Exploration of gene expression as a function of nuclear fluorescence AUC allowed a comparison on an equal footing of the overall integrated responses to pulsed and continuous inputs.

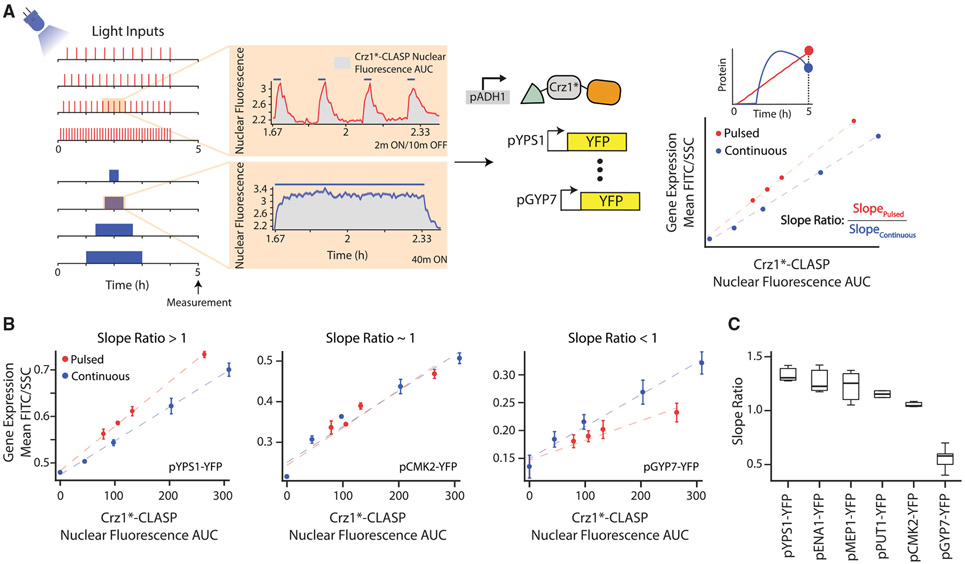
Figure 3. Crz1 Target Genes Show Differing Interpretation of Crz1*-CLASP Short Nucleoplasmic Pulses.

(A) Schematic of the experimental setup used. Two types of light inputs are given to cells expressing Crz1*-CLASP: 2 min pulses with decreasing periods (20, 15, 12, and 6 min periods) and single pulses with increasing durations (20, 40, 80, 120 min). Light-induced Crz1*-CLASP nuclear localization is measured with fluorescence microscopy. The mean of single-cell fluorescence values is plotted (solid red for pulsed input or blue line for continuous inputs), with the shaded area representing 95% confidence interval (red or blue shading). Cells tracked for the pulsed and continuous inputs are 187 and 91 cells, respectively. Crz1*-CLASP nuclear fluorescence AUC (x-axis in a rightmost panel) is quantified as the area under the nuclear fluorescence traces (gray shading in middle panel). Gene expression (mean FITC/SSC) is measured for 6 promoter fusions of target gene driving a fluorescent protein (YFP) at 5 h after light input. A schematic shows gene-expression values for different light input regimes are plotted as a function of nuclear fluorescence AUC, generating the output-fluorescence plot referred to in the text. Each point in the plot is an endpoint measurement of gene expression, as highlighted by the YFP time course schematic above. Red circles represent output fluorescence for short 2 min pulses with an increasing period, and blue circles represent that for continuous single pulse with increasing durations. A best-fit line (red for pulsed inputs and blue for continuous inputs) is fit through the data points for the pulsed and continuous inputs. For each output-fluorescence plot we define the slope ratio as the ratio of the slope of the pulsed to continuous best-fit lines.

(B) Output-fluorescence plot, for three representative Crz1 target promoters pYPS1-YFP, pCMK2-YFP, and pGYP7-YFP. The error bars are the standard deviation of at least 3 biological replicates.

(C) Slope ratios for 6 Crz1 target genes plotted in order of highest to lowest slope ratio. Data for 3 biological replicates are plotted. In all panels, Crz1*-CLASP is induced with a 512 a.u. light input. See also Figure S4.

The Crz1-responsive promoters showed a spectrum of qualitative and quantitative behaviors in the output-fluorescence plots (Figures 3A-3C and S4H-S4J). For pGYP7-YFP, like the promoters shown in Figure 2, a pulsed input generated lower gene-expression output than a continuous input of the same nuclear fluorescence AUC for all values tested (Figure 3B). For pCMK2-YFP, pulsed, and continuous inputs generated almost identical gene-expression output. However, for pYPS1-YFP, pulsed inputs produced higher gene-expression output at all Crz1*-CLASP nuclear fluorescence AUC values tested. These phenotypes were qualitatively reproducible despite the slight quantitative day to day variability in gene expression between experiments (Figures S4H-S4J). The difference in output between pulsed and continuous inputs as a function of nuclear fluorescence AUC was quantified as the ratio of the slopes of the two lines in the output-fluorescence plot (termed the slope ratio) (Figure 3A). This metric showed that the six Crz1-responsive promoters spanned a range that is bracketed by pYPS1-YFP (slope ratio > 1) and pGYP7-YFP (slope ratio <1), going from higher gene expression for pulsed than continuous inputs to the opposite phenotype (Figure 3C) . Since all promoter fusions generated the same YFP as the protein output, these pheno-types must reflect different promoter properties as well as any differential influences of the promoters on mRNA stability. We next turned to data-backed computational modeling to systematically explore and interpret these behaviors.

A Simple Two-State Computational Model of the Promoter Explains pYPS1-YFP and pCMK2-YFP Slope Ratio Data

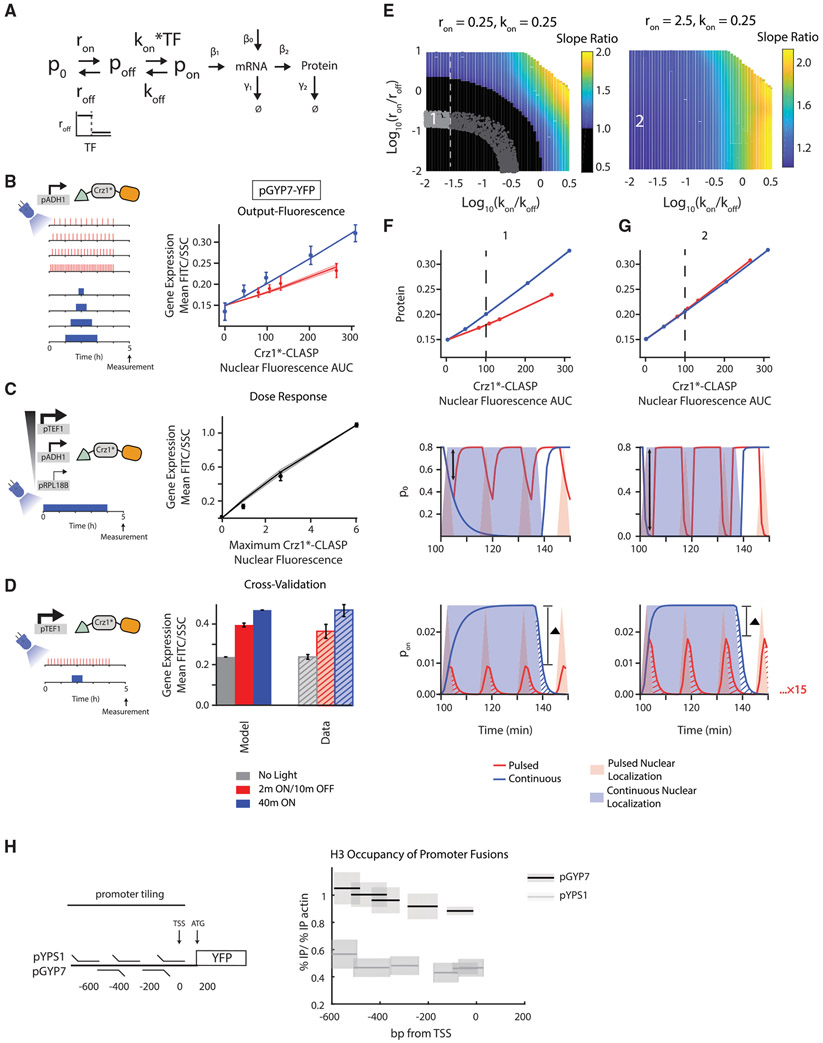
To better understand the difference in slope ratios for pYPS1-YFP and pCMK2-YFP, we represented each gene with a simple two-state promoter computational model. The promoter model (Figure 4A) has an ON state p_on and an OFF state p_off, with p_on + p_off = 1. The time-dependent nuclear concentration of the TF Crz1 is given by the function TF(t). The time-dependent equation for the promoter activity p_on in response to nuclear localization of Crz1 can be written as

$$\begin{gathered} \frac{d{p}_{on}}{dt}=k_{on}{p}_{off}TF(t)-k_{off}{p}_{on} \\ =k_{on}(1-p_{on})TF(t)-k_{off}{p}_{on} \end{gathered}$$ (Equation 1)

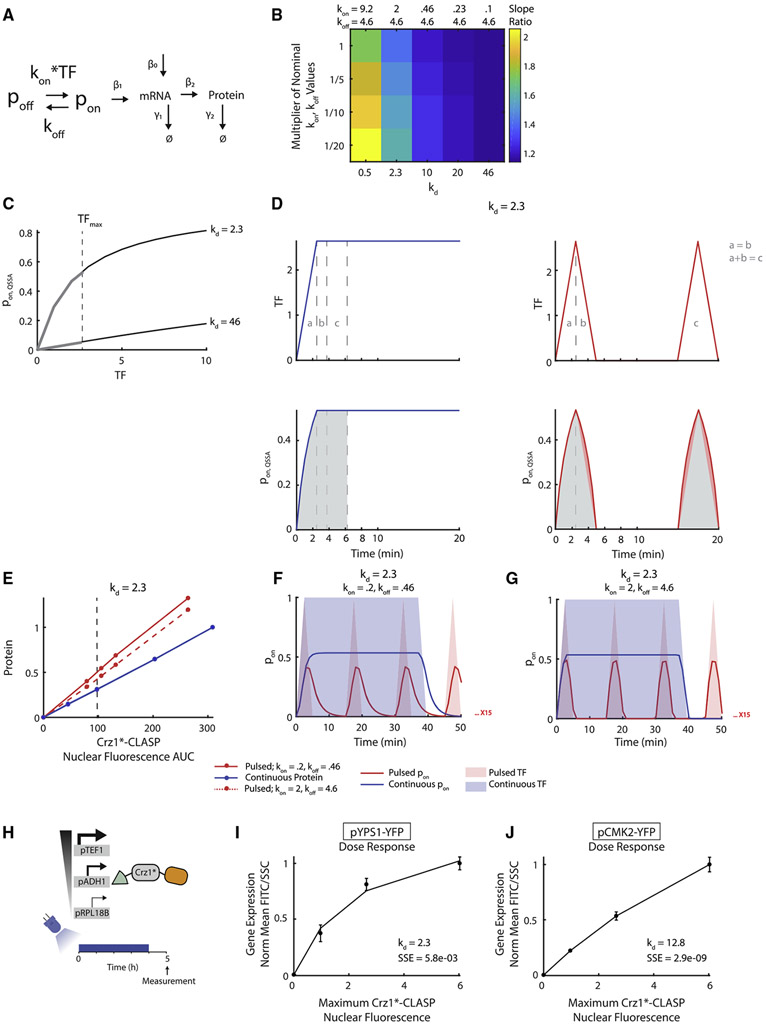
Figure 4. Higher Gene Expression in Response to Short Pulses by Promoters Occurs when the Dose Response Is Saturated at Low TF Concentration.

(A) Schematic of a two-state promoter model, where the input is Crz1*-CLASP nuclear localization (TF) and the output is fluorescent protein level (Protein). The promoter turns ON with rate constant k_on and turns OFF with rate constant k_off.

(B) Heatmap of slope ratio for increasing k_d and different values of k_on and k_off. Each column has a given value of k_d and each row has different values for k_on and k_off that produce the same k_d. The nominal k_on and k_off values used in the first row are noted at the top of each column, and every subsequent row uses a fraction of these values (1/5, 1/10, and 1/20). The values of β₁, β₂ and β₀ are 2.01, 4.92, and 0.0032, respectively.

(C) The plot of p_on as a function of TF for k_d = 2.3 and 46, assuming a fast promoter. This quantity is denoted as p_{on, QSSA}, and calculated as p_{on, QSSA} = TF/(TF+ k_d). The dotted line represents max TF input, TF_max, which is 2.6.

(D) The plot of p_{on, QSSA} as a function of time assuming quasi-steady state of promoter dynamics as in panel (C). In these panels, k_d = 2.3. (Top panels) Red and blue lines represent pulsed and continuous TF inputs, respectively. Gray lines and text denote the equivalent area of TF input. The area labeled “a” represents the rise for both pulsed and continuous inputs. The area labeled “b” represents the fall of the pulsed input, and the equivalent area for the continuous input. The area labeled “c” represents a single pulse of the pulsed input, and the equivalent area of the continuous input. The area labeled “c” is equivalent to the sum of the areas labeled “a” and “b.” The areas labeled “a” and “b” are equivalent to each other. (Bottom panels) Red and blue lines represent p_{on, QSSA} in response to pulsed and continuous TF inputs, respectively. Gray shading denotes the equivalent area of p_{on, QSSA} for continuous and pulsed inputs. Light red shading denotes excess p_{on, QSSA} area resulting from the rise and fall of the pulsed input.

(E) Output-fluorescence plots generated by the model for two parameter sets that qualitatively represent pYPS1-YFP. The solid lines represent k_on = 0.2 and k_off = 0.46. The dashed lines represent k_on = 2 and k_off = 4.6, and k_d = k_off/k_on = 2.3 for both parameter sets. The red lines represent the output of the pulsed input. The blue lines represent the output of the continuous input; for both parameter sets, this output is the same.

(F) Plot of p_on as a function of time for continuous and pulsed inputs for k_d = 2.3 with k_on = 0.2, k_off = 0.46. Red and blue solid lines represent the p_on resulting from pulsed and continuous inputs, respectively. The red and blue shading represents pulsed and continuous TF inputs, respectively.

(G) Same as (F) for k_on = 2, k_off = 4.6.

(H) Schematic of dose-response experiment. Cells with different expression levels of Crz1*-CLASP are induced with light for 4 h and YFP expression is measured after 5 h.

(I) The experimental dose response for pYPS1-YFP was fit to the equation: normalized protein output = C×TF/(TF + k_d) where TF = maximum Crz1*-CLASP nuclear fluorescence, C = scaling factor, and k_d = k_off/k_on. k_d and squared error of prediction (SSE) of the fit for each gene is noted in the bottom right corner of the plot.

(J) Same as (I) for pCMK2-YFP. for (I and J), error bars represent the standard deviation of 3 biologically independent replicates. See also Figures S5, S8, and S9.

The rate constants k_on and k_off are used to describe the transition between the two promoter states. Here, k_on*(1 − p_on)*TF(t) is the ON rate and is nonlinear due to the input TF(t), while the OFF rate, k_off*p_on, is linear. The time-dependent equations for mRNA and Protein are then given by:

$$\frac{dmRNA}{dt}={\beta }_0+{\beta }_1{p}_{on}-{\gamma }_{1}mRNA$$ (Equation 2)

$$\frac{d\text{Pr}otein}{dt}={\beta }_{2}mRNA-{\gamma }_2\text{Pr}otein$$ (Equation 3)

From a wide parameter search across k_on and k_off, we were able to find parameter regimes that qualitatively captured the phenotypes (slope ratio > 1 and slope ratio close to one) observed in the output-fluorescence plots for pYPS1-YFP and pCMK2-YFP in Figure 3 (Figure S5A; example solutions plotted in Figures 4E and S5D). We also found that the quantitative value of the slope ratio obtained from the output-fluorescence plot is dependent on three model parameters—mRNA and protein half-lives, the ratio k_d (k_d = k_off/k_on), and the absolute values of k_on and k_off. We explore these relationships below.

For a Two-State Computational Model of the Promoter, Slope Ratio Increases with Decreasing mRNA Half-Lives but Differences in Half-Lives Cannot Fully Explain the Measured Slope Ratio

Our numerical results indicate that both mRNA and protein degradation values affect slope ratio. Protein degradation of YFP in yeast has been shown to be slow with a value around γ₂ = 0.0083 min⁻¹ (Christiano et al., 2014). This value cannot be different among different promoters since they all produce the same protein (YFP). Therefore, the degradation parameter for YFP cannot explain the effects of slope ratio we are studying, and we will not explore its effects any further.

The mRNA degradation rate, on the other hand, can depend on the identity of the promoter (Bregman et al., 2011; Trcek et al., 2011). The physiological range of mRNA degradation rates in yeast has been experimentally determined to vary between γ₁ = 0.025–10 min⁻¹ (Wang et al., 2002). For values of k_on, k_off, and k_d that span a wide range (k_on from 0.005 to 9.2 min⁻¹a.u.⁻¹, k_off from 0.23 to 4.6 min⁻¹, k_d from 0.5–46 a.u.), changing γ₁ alone cannot span the range of slope ratios we observe for pCMK2-YFP and pYPS1-YFP (Figure S5B). We therefore conclude that while the mRNA degradation rate affects the slope ratio, with increasing slope ratio as the mRNA degradation rate increases, it alone cannot explain the difference between the slope ratios of pCMK2-YFP and pYPS1-YFP without additional differences in the promoter characteristics. We, therefore, turn to investigate the role of promoter dynamics in the slope ratio phenotype.

For a Two-State Computational Model of the Promoter, Slope Ratio Increases with Decreasing k_d

Model simulations for different values of k_d between 0.5 and 46 a.u. revealed that decreasing k_d increases the slope ratio (Figure 4B). To build intuition about this relationship, we first consider an asymptotic regime of extremely fast promoter dynamics, relative to TF dynamics, in which k_on and k_off are large. This results in fast p_on and p_off that equilibrate to a quasi-steady state on the timescale of the TF dynamics. In this regime, p_on ≃ TF(t)/(TF(t) + k_d), where k_d= k_off/k_on. This expression for p_on can then be used in the equation that describes the dynamics of mRNA to determine the number of transcripts made. If k_d is very large compared with the maximum TF concentration (e.g., k_d = 46 a.u. in our system where TF_max = 2.6 a.u.), then p_on is approximately linear as a function of TF and p_on changes proportionally to the TF input (Figure 4C). For a smaller k_d (e.g., k_d = 2.3 a.u.), p_on rises more rapidly as a function of TF because the smaller k_d dictates that this Michaelis-Menten function should saturate faster to 1 as a function of TF.

The fact that p_on grows non-linearly with TF concentration means that there is excess promoter activity derived from the repeated turn-on and shut-off of the pulsed TF input (Figure 4D, excess activity denoted by the light red shading). This allows the promoter to activate more over time than for the continuous input where there is only one activation and shut-off. Therefore, for the continuous input, p_on cannot fully benefit non-linearly from the TF concentration. As a result, for a small k_d, the integral of p_on (its accumulated area as a function of time) is larger for the pulsed input than for the continuous input (Figure 4D, an equivalent area of p_on is denoted by gray shading), therefore resulting in the production of more mRNA. On the other hand, for large k_d (k_d= 46 a.u.), p_on follows TF in a linear way, and hence the difference between its integral for the pulsed and continuous inputs is minimal (Figure S5C). We provide an analytical exposition of the relationship between slope ratio and k_d for a k_on and k_off of any value in STAR Methods (sections “Derivation of expressions of total transcripts from Equation 1 in the main text,” “Derivation of N_p/N_c > 1 in the regime of a fast promoter relative to TF(t)”, and “Derivation of N_p/N_c > 1 for general values of k_on and k_off” with specific examples presented in Figures S8 and S9). We also explore these relationships for smaller k_on and k_off numerically below.

For a Two-State Computational Model of the Promoter, Slope Ratio Increases with Slow k_on and k_off

The results in Figures 4C and 4D represent a promoter that is fast relative to TF(t) (e.g., large k_on and k_off). Next, we explored the slope ratio for small values of k_on and k_off that span different k_d values (Figures 4B and S5B). For a small k_d (k_d = 2.3 a.u.), as k_on and k_off decreased simultaneously (e.g., k_on = 2, k_off = 4.6 versus k_on =.2, k_off =.46), the slope ratio increased (Figure 4E). This is because, for a pulsed input, a slower k_off implies that the promoter stays ON for a period of time beyond the duration of the input. When repeated for every pulse, this residual activity could counteract the amplitude deficiency caused by the decrease in k_on and k_off (Figure 4F). On the other hand, as k_on and k_off increase, p_on follows the input TF(t) pulses more faithfully, minimizing the gains from a pulsed input compared with a continuous one even in the regime of small k_d (Figure 4G). Finally, and as discussed above, for a large value of k_d (e.g., k_d= 46 a.u.), the slope ratio is necessarily close to 1 and is therefore relatively insensitive to the promoter dynamics (see STAR Methods, “Derivation of Np/Nc>1 in the regime of a fast promoter relative to TF(t)” and Figure S8). As a result, in this regime, slowing k_on and k_off will have minimal effects on slope ratio for a value of k_d that is large relative to TF_max (Figure S5D).

Taken together, these analyses indicate that both k_d and the absolute values of k_on and k_off modulate the slope ratio. A small k_d is necessary for higher gene expression in response to short pulses, and a slow k_on and k_off further increase the slope ratio. These conclusions, therefore, point to the necessity of measuring the k_d of these promoters. To do so, we constructed strains that expressed Crz1*-CLASP from constitutive promoters of varying strengths. In each of these strains, we localized Crz1*-CLASP to the nucleus with a continuous light input for 4 h and measured pYPS1-YFP and pCMK2-YFP (Figure 4H), therefore compiling a dose response. Fitting this data to a Michaelis-Menten function, we found that the experimental dose response of pYPS1-YFP had a k_d of 2.3 a.u. (Figure 4I) while the dose response of pCMK2-YFP had a k_d of 12.8 a.u. (Figure 4J).

The small k_d value for pYPS1-YFP and its large slope ratio is in agreement with our analysis showing that small k_d can allow the promoter to differentiate between short pulses and continuous inputs. It also positions the promoter in a regime where the individual values of k_on and k_off might have an important influence on its slope ratio. Moreover, the relatively large k_d for pCMK2-YFP and its slope ratio near 1 is in agreement with our analysis showing that larger k_d restricts the ability of the promoter to differentiate between short pulses and continuous input. Additionally, this relatively large k_d positions the promoter in a regime where the individual values of k_on and k_off have little bearing on its slope ratio. To explore these hypotheses further, we turned to the measurement of protein dynamics in order to further constrain the values of k_on and k_off.

pYPS1 Promoter Dynamics Are Constrained to Be Faster than Its mRNA Decay

To constrain individual parameter values of k_on, k_off, and relate them to the mRNA degradation rate γ₁, we measured protein dynamics for pYPS1-YFP and pCMK2-YFP in response to 2 h of continuous light illumination (Figure 5A). We then used the model to fit these dynamic data by sampling within a wide range of k_on, k_off and γ₁ values (k_on from 0.00–10 (min × a.u.)⁻¹, k_off from 0.000007–100 min⁻¹, and γ₁ from 0.01–10 min⁻¹; Figure 5A, left and right panels, fits sought to maximize fit through the data points within the error bars; model fitting discussed in detail in STAR Methods “Model equations and sampling details of the pYPS1-YFP and pCMK2-YFP phenotypes”). The protein dynamic data revealed a relationship that must exist between k_on×TF+k_off and γ₁ for the data to be explained by the model (Figure 5B). An analysis of mRNA dynamics in the two-state promoter model revealed that this relationship captures an important timescale T_s of the system, which we term the “settling time.” Assuming a very small degradation rate of the protein, T_s is the approximate time at which the mRNA level reaches steady state and the protein production rate becomes constant (see STAR Methods, “Asymptotic Analysis of mRNA Dynamics for the Simple Promoter to a Step Function Input” for analytical derivations of T_s). The T_s relationship captures two characteristic timescales of the system, that of the promoter given by 1/(k_on × TF + k_off) and that of the mRNA, given by 1/γ₁. Their sum determines the timescale of the system (assuming that protein degradation is slow and hence has negligible contribution). Two asymptotic regimes occur if either the promoter or mRNA dynamics dominate the timescale of the system. These asymptotes serve to put a lower bound on the values of k_on×TF + k_off and γ₁. At one extreme where k_on and k_off are large and γ₁ is small, T_s ≃ 1/γ₁ (the asymptote as k_on × TF + k_off goes to infinity in Figure 5B lower-right data points in each panel). Therefore, the protein dynamics data would strongly constrain the values of γ₁ but not k_on and k_off. In the other extreme, for small k_on and k_off and large γ₁, T_s ≃ 1/(k_on×TF +k_off) (the asymptote as γ₁ goes to infinity in Figure 5B, upper left data points in each panel). In this regime, k_on×TF +k_off is well constrained by the protein dynamics data but γ₁ is not constrained. These asymptotes are useful for putting bounds on the parameters.

Figure 5. Time Course Measurements of Protein Output Constrain Parameter Relationships.

(A) (Left panel) Schematic of the input used for protein time course experiment. Cells are induced with constant blue light and pYPS1-YFP or pCMK2-YFP expression is measured continuously (every 8 min) throughout induction for 2 h. (Middle panel) Plot of normalized protein expression (FITC/SSC) as a function of time for pYPS1-YFP. The magenta lines represent fits through the data (plotted as black dots with error bars) for the model in Figure 4A. The model was simulated using 33,000 parameter sets varying k_on, k_off, and γ₁, and fit to the dynamic gene-expression data was assessed. k_on was varied from 0.001–10, k_off from 0.000007–100, and γ₁ from 0.01–10. (Right panel) Same as a middle panel for pCMK2-YFP. For both panels, β₁ was set to 0.1, β₂ set to 0.06, γ₂ set to 0.0083, and β₀ set to 0.001. For middle and right panels, error bars represent standard deviation of 3 biologically independent replicates.

(B) (Left panel) Plot of log₁₀(γ₁) as a function of log₁₀(k_on×TF+k_off) for pYPS1-YFP. Magenta dots represent 2,355 parameter fits to the dynamic protein time course data (continuous input) as discussed in Figure 5A middle panel. Gray dots represent parameters that were tested but did not fit the data. (Right panel) Same as left panel for pCMK2-YFP. Blue dots represent 807 parameter fits to the dynamic protein time course data (continuous input) as discussed in Figure 5A right panel. Gray dots represent parameters that were tested but did not fit the data.

(C) (Left panel) Schematic of input for the output-fluorescence experiment. The experiment is as described in Figure 3A. (Middle panel) Output-fluorescence plot of simulated outputs and data for pYPS1-YFP. Parameters determined to fit the dynamic protein time course with a continuous input are used to predict the output-fluorescence data. Red and blue lines represent the model outputs for all parameters that fit the output-fluorescence and protein time course data from (A). Red and blue circles and error bars represent experimentally measured means and standard deviations for pulsed and continuous inputs, respectively, for 3 biologically independent replicates. (Right panel) Same as the middle panel for pCMK2-YFP.

(D) (Left panel) Plot of log₁₀(γ₁) as a function of log₁₀(k_on×TF+k_off) for pYPS1-YFP, where the magenta dots represent 300 parameters that fit both the output-fluorescence and dynamic protein time course (continuous input). Gray dots represent parameters that were tested but did not fit to the data. (Right panel) Same as the left panel for pCMK2-YFP. The blue dots represent 321 parameters that fit both the output-fluorescence and dynamic protein time course data (continuous input).

(E) (Left panel) Schematic of input for protein time course experiment for pulsed and continuous inputs. Cells were induced with either constant light or pulsed light (2 min ON/4 min OFF) and gene expression was measured every 8 min. (Middle panel) Plot of normalized protein expression (FITC/SSC) as a function of time for pYPS1-YFP for the experiment denoted in the left panel. Red and blue circles and error bars denote experimentally measured means and standard deviations for pulsed and continuous inputs, respectively, for 3 biologically independent replicates. Red and blue lines represent the model outputs for the experiment denoted in the left panel, using parameters that fit the dynamic protein time course (continuous input) and output-fluorescence data. (Right panel) Same as left panel for pCMK2-YFP. See also Figure S8.

T_s can be determined from the protein dynamics data using the mean of the parameter fits. Since T_s has a given value for each gene that can be computed from the protein time course, the relationships between k_on, k_off, and γ₁ are correspondingly constrained for each gene. We found that T_s = 23.8 min (with a range of 18 to 32.8 min) for pYPS1-YFP and T_s = 7.7 min for pCMK2-YFP (with a range of 6.9 to 9 min) (Figure 5B), indicating that the pYPS1 mRNA reaches steady state approximately 3 times slower than the pCMK2 mRNA. These T_s values and their corresponding asymptotes put a lower bound for k_on to be 0.001 min⁻¹a.u.⁻¹, for k_off to be 0.006 a.u.⁻¹ and for γ₁ to be 0.03 min⁻¹ for pYPS1-YFP. These lower bound values for pCMK2-YFP are 0.001 min⁻¹a.u.⁻¹ (k_on), 0.05 a.u.⁻¹ (k_off) and 0.11 min⁻¹(γ₁). Therefore, these constraints predict that all three parameter values might differ between the two promoters, including the mRNA decay rate. However, as we have shown above (Figure S5B), the potential difference in γ₁ values between pYPS1-YFP and pCMK2-YFP contributes to but cannot fully explain the difference in the slope ratio between the two genes.

To further constrain the parameter values for pYPS1-YFP and pCMK2-YFP, we subjected the parameter sets constrained by the protein time course in response to a continuous input to the additional constraint of fitting the output-fluorescence data (Figures 5C and 5D). For pYPS1-YFP, these data constrained k_on×TF + k_off to be larger than 1 and less than 56, and constrained k_on and k_off values to be greater than 0.16 min⁻¹a.u.⁻¹ and 0.6 a.u.⁻¹, respectively. As a result, the γ₁ values were constrained to be between 0.03 and 0.05 min⁻¹, which is approximately an order of magnitude smaller than k_on and k_off (Figure 5D, left panel). For pCMK2-YFP, however, the output-fluorescence data did not further constrain the range of parameters beyond the protein time course data (continuous input) (Figure 5D, right panel). Importantly, the parameters fit to the protein time course (continuous input) and output-fluorescence data for each gene had k_d values comparable to those measured experimentally, which provides a measure of validation for these fits. For pYPS1-YFP, the median k_d for the parameter fits was 1.6 a.u., and for pCMK2-YFP the median k_d value was 14 a.u.

Therefore, for pYPS1-YFP, promoter kinetics (k_on and k_off) are fast relative to mRNA decay (γ₁), indicating that mRNA decay dominates protein dynamics. Taken together with the analyses of the effect of k_d, k_on, and k_off on slope ratio, the small k_d value for this promoter indicates that its slope ratiometric can be strongly affected by its k_on and k_off values and that the large slope ratio is likely the result of the small k_d and large k_on and k_off relative to γ₁. On the other hand, the dynamics and small slope ratio (close to 1) of pCMK2-YFP could be generated by many combinations of parameters γ₁, k_on and k_off that satisfy the T_s relationship (Figure 5D). This finding agrees with the fact that the slope ratio of pCMK2-YFP is minimally affected by the values of k_on and k_off because of its measured large k_d.

Finally, to further cross-validate these insights, we asked whether the parameters identified above, and the accompanying model could predict the outcome of an additional time course experiment on which the model was not trained. In this experiment, protein time course data are collected for cells induced with a pulsed (2 min ON/4 min OFF) light input for 100 min (Figure 5E, data plotted in red as circles and error bars, model predictions plotted in red as lines). As a comparison, the data for the continuous input, which these parameters were fit to previously, are also plotted (data plotted in blue as circles and error bars, model predictions plotted in blue as lines). The output-fluorescence plots show that pYPS1-YFP displays higher gene expression in response to pulsed TF inputs than pCMK2-YFP, given that both inputs have the same area. In this time course, the continuous input has a much greater area than the pulsed input. It is expected that the difference between the protein outputs for the continuous and pulsed inputs would be smaller for pYPS1-YFP than for pCMK2-YFP. Furthermore, it is expected that the parameters identified will be able to predict the gene-expression dynamics for the pulsed input as a result of being fit to the continuous input protein time course data. For both pYPS1-YFP and pCMK2-YFP, the parameter fits produced computational predictions that qualitatively recapitulated the protein outputs in response to pulsed TF inputs for both pYPS1-YFP and pCMK2-YFP (Figure 5E).

Higher Gene Expression in Response to Continuous Inputs by Promoters Can Be Explained by a Model with a Thresholded Transition between the Non-transcribing Promoter States

The simple model from the previous analysis could not produce the pGYP7-YFP phenotype (Figure S6A). In the simple model, even as the output difference between the pulsed and continuous inputs decreased (which occurred when k_on << k_off), the output of the pulsed input was always higher than the continuous input. This is because while decreasing k_on reduced the output of the pulsed input, it also reduced the dynamic range of the output in response to a continuous input. This continued until to a point where k_on was so small that the promoter was barely activated and the much faster k_off quickly shut-off promoter activity, resulting in a promoter that was essentially unresponsive to both continuous and pulsed inputs (Figure S5E).

In order to identify a minimal model that explains the pGYP7-YFP phenotype, we explored eight elaborations of the simple promoter switching model from Figure 4 using a sequence of fitting and cross-validation (Detailed descriptions of all models and their exploration can be found in STAR Methods “Model exploration and sampling details for the pGYP7-YFP phenotype: List of models” and Figure S6). In this process, each model was first fit to the output-fluorescence data in Figure 3; one of the eight models failed to fit. Models that fit the output-fluorescence data were further fit to the dose response of pGYP7-YFP, which was collected in the same way as for pCMK2-YFP and pYPS1-YFP. The pGYP7-YFP dose response was remarkably linear, and four models failed to fit it (Figures S6B-S6E). For the 3 remaining models, the dose-response data served to further constrain parameter sets. For those refined parameters, we cross-validated the models on the data from an additional experiment in which we expressed Crz1*-CLASP from a stronger promoter (pTEF1 versus pADH1), and measured gene expression following a cumulative light induction of 40 min administered either as pulsed or continuous input. Following these rounds of fitting and cross-validation (Figures S6A-S6I), only two of the models surveyed were able to explain all the data we collected (Figures 6A-6E, S6H, and S6I).

Figure 6. Higher Gene Expression in Response to Continuous Inputs by Promoters Can be Explained by a Model with Two Transition States and with a Thresholded Transition between Non-transcribing Promoter States.

(A) Schematic of the three-state model where r_off, the inactivation rate constant from p₀ to p_off, is thresholded by TF concentration and where the activation from p_off to p_on is linearly dependent on TF.

(B) (Left panel) Schematic of the experimental setup. (Right panel) Output-fluorescence plot for pGYP7-YFP. Circles are experimentally measured values while lines denote the mean model output for 96 parameter sets that fit the data points within the error bars, the same metric as used in Figure 5. The solid line denotes the mean and shaded areas denote the standard deviation of the model outputs for these parameter sets. Parameters were sampled (r_on from 0.1–100, r_off from 0.1–100, k_on from 0.0001–1, k_off from 0.0001–1, β₁ from 0.0001–10, β₀ from 0.000001–0.01, threshold from 0–0.5) or set (β₂ = 0.06, γ₁ = 0.05, γ₂ = 0.0083). Red circles, error bars, and lines relate to the pulsed input, while blue circles, error bars, and lines relate to the continuous input. Error bars show standard deviation from 3 biologically independent replicates.

(C) (Left panel) Schematic of the experimental setup. (Right panel) Dose-response plot for pGYP7-YFP. The parameters that fit the output-fluorescence data were used to further fit the dose response of pGYP7-YFP using a least squared error criterion (25 parameter sets). Solid black line is the mean generated by the model. The black circles are the mean of the experimentally measured dose response and error bars are the standard deviation of 3 biologically independent replicates.

(D) (Left panel) Schematic of the experimental setup. (Right panel) The parameters that fit the output-fluorescence are subjected to cross-validation using an experiment where Crz1*-CLASP expression is increased (construct expressed from a pTEF1 promoter), and cells are exposed to either short-pulsed (2 min ON/10 min OFF) or continuous input (40 min of light). The model generated outputs (solid gray, red, and blue bars) are plotted with the experimental data (hashed gray, red, and blue bars). The gray bars correspond to no light input. The error bars are the standard deviation of 3 biological replicates.

(E) (Left panel) Heatmap shown in the log₁₀(k_on/k_off)-log₁₀(r_on/r_off) plane of slope ratio of output-fluorescence relationship resulting from the model in (A). Parameters are sampled (r_off from 0.0025-25, k_off from 0.0025–25) or set (r_on = 0.25, k_on = 0.25, β₁ = 0.0001, β₂ =0.06, γ₁=0.05, γ₂ =0.0083, threshold = 0.5, β₀ = 0.000001). Point 1 highlights a parameter set that fits the output-fluorescence, dose response, and cross-validation datasets for pGYP7-YFP. Black region is where slope ratio < 1. Gray dotted line indicates when log₁₀(k_on/k_off) ≅ −1.5, at which point the dose-response changes from linear to nonlinear with increase in the log₁₀(k_on/k_off) value. All parameters that show a qualitative fit to output-fluorescence data are displayed as light and dark gray dots. The light gray dots represent parameter sets where all pGYP7-YFP data are quantitatively fit. (Right panel) Heatmap of slope ratio as in (E, left panel) with a r_on = 2.5, 10 times larger than that in (E, left panel). k_on is also set to 0.25. Parameters are sampled (r_off from 0.025-250, k_off from 0.0025-25) or set (β₂ = 0.0001, β₂ = 0.06, γ₁ = 0.05, γ₂ = 0.0083, threshold = 0.5, β₀ = 0.000001). Point 2 highlights the effect of increasing both r_on and r_off while maintaining the ratio log₁₀(r_on/r_off).

(F and G) (Upper panels) Output-fluorescence plots generated by the model for different parameter sets that correspond to points 1 and 2 in the heatmaps of (E). The slope ratio for point 1 is 0.51 with log₁₀(k_on/k_off) = −1.58 and log₁₀(r_on/r_off) = −0.89. The slope ratio for point 2 is 1.04 with log₁₀(k_on/k_off) = −1.58 and log₁₀(r_on/r_off) = −0.89. (Middle panels) Example of a time course of promoter state p₀ for a light input that produces the equivalent of 40 min (dotted line in upper panel) in nuclear localization either continuously or in short pulses. Solid lines are the p₀ pulses while shading denotes TF nuclear localization. The black double arrows denote the maximum depletion of the p₀ state for the pulsed input. (Lower panels) Example of a time course of promoter activity p_on for a light input that produces the equivalent of 40 min (dotted line in upper panel) in nuclear localization either continuously or in short pulses, similar to middle panels. The red and blue hashes represent residual promoter activity beyond the TF nuclear localization input. The red residual promoter activity is repeated 15 times while the blue residual activity is repeated one time. The ▲ bar denotes the difference between the amplitudes generated by the 2 min pulsed and 40-min continuous input.

(H) (Left panel) Schematic of chromatin immunoprecipitation experiment. (Right panel) H3 histone occupancy is plotted for regions of the promoter fusions pYPS1-YFP and pGYP7-YFP. H3 histone occupancy is calculated as the ratio of % immunoprecipitation (% IP) of the promoter fusion target to % immunoprecipitation of an actin control. % immunoprecipitation is calculated relative to the input DNA. Black lines show the mean measured value and gray shading shows the standard deviation of 3 biologically independent replicates. See also Figures S6 and S7.

The two models were structurally similar—they both extended the simple two-state model to contain another promoter state, thereby requiring transition through an unproductive promoter state (p_off) before the promoter can be fully activated. Therefore, in these models, the first transition occurred reversibly between promoter state p₀ and a non-transcribing state p_off with rate constants r_on and r_off, while a second transition stage occurred between p_off and p_on with rate constants k_on and k_off. Both models also involved a linear dependence on TF in the second transition stage, whose effect was to prevent the dose response from exhibiting a thresholded behavior. Finally, the two models necessitated a thresholded interaction in the first promoter transition stage, but differed in where it was applied—in one model, r_on was a thresholded function of TF, while in the other model, it was r_off that was thresholded by TF (Figures 6A, S6H, and S6I). The threshold on either r_on or r_off acted as a “reset” for short pulses such that the system quickly returns to the starting p₀ state. Since these two models were able to recapitulate the data gathered for pGYP7-YFP in slightly different parameter regimes, we analyzed the features common to both models rather than focusing on individual values of the model parameters (k_on, k_off, r_on, r_off, γ₁) for pGYP7-YFP.

First, we examined one of these two models, the 3-state r_off-threshold model, in more depth (Figure 6A). To do so, we fixed r_on and k_on to values that fit the data from Figures 6B-6D and varied r_off and k_off within a range of four logs. We then generated output-fluorescence plots for every parameter set and computed its corresponding slope ratio metric, which we plotted in the log₁₀(k_on/k_off) −log₁₀(r_on/r_off) plane (Figure 6E). Overall, we found that this model can generate both higher expression with a continuous input (slope ratio <1, black region in Figure 6E, left panel) and higher expression with short pulses (slope ratio> 1, a colored region on Figure 6E, left and right panels).

Quantitatively, there seemed to be three-parameter constraints for this promoter model to elicit higher gene expression in response to a continuous input than a pulsed one. First, the rate of transition from p₀ to p_off should be slow; second, r_off should be fast relative to r_on; third, k_off should be fast relative to k_on. An analysis of the 3-state r_on threshold model demonstrated similar requirements (Figures S7A and S7B). When r_on and r_off were increased 10-fold, there were no parameter combinations that generated higher expression for continuous inputs than short pulses (Figure 6E, right panel, Figures 6F and 6G, top panel). The difference in the protein outputs between the pulsed and continuous inputs was determined by the amplitude differences of promoter activity p_on (Figures 6F and 6G, bottom panel), which was in turn dictated by the amplitudes of depletion from p₀ for the short-pulsed and continuous inputs (Figures 6F and 6G, middle panel). A slow transition from p₀ prevented the quick and full depletion of this state before a short pulse ended, while p₀ was fully depleted for the continuous input (Figure 6F, middle panel). By contrast, when r_on and r_off were fast, this difference disappeared as the transition from p₀ was now able to reach the same maximal amplitude in the duration of the short input (Figure 6G, middle panel). Hence, the incomplete depletion of the p₀ state in the duration of the short-pulsed input accounted for the difference in protein outputs between the short-pulsed and continuous inputs.

The requirement that the value of r_off be large relative to r_on was motivated by the fact that r_off dictated how quickly the promoter state transitioned back to the initial OFF state p₀ after the end of a short pulse. When the value of r_off decreased relative to r_on (Figure S7C), the depletion of p₀ could proceed to completion during a short pulse (Figure S7C, middle panel), and the resulting maximum amplitudes of the active promoter state p_on were more comparable for a pulsed or continuous input (Figure S7C, bottom panel). Lastly, as k_off was decreased while keeping all other parameters constant, the p_on to p_off switching also slowed, and promoter activity continued unabated between two pulses, hence maximizing the gain of promoter activity from every input pulse and causing stronger gene expression from pulses than from a continuous input (Figure S7D). This was in essence the same mechanism as described in Figures 4E-4G. In summary, slow transition from the initial OFF state (p₀) to the intermediate OFF state (p_off) prevented the short-pulsed input from achieving a quick depletion of the initial OFF state (p₀), essentially creating a filter for short inputs.

Finally, in addition to the constraints above, we found that a threshold of log₁₀(k_on/k_off) ≈> −1.5 seemed to demarcate the transition between a linear and nonlinear promoter dose response in the parameter regime probed (light gray points, Figure 6E, left panel), therefore imposing quantitative bounds on this promoter model to exhibit a graded dose response as seen in the data.

Mechanistically, we hypothesized that the additional promoter state (p₀) and the transition through a non-transcribing promoter state (p_off) of the multi-state models could represent transitions induced by chromatin remodeling at the promoter. This hypothesis was further supported by analysis of previously published nucleosome occupancy data for Crz1 target genes, which showed a negative correlation between nucleosome occupancy and slope ratio (Figures S7E and S7F). To test this hypothesis more specifically, we measured H3 nucleosome occupancy of the pGYP7 and pYPS1 promoter fusions (Figure 6H). H3 occupancy was much greater in pGYP7-YFP than pYPS1-YFP, which recapitulates the nucleosome occupancy profile at the native promoter-ORF junctions previously cited in the literature. This result lends credence to the proposed multi-state model of pGYP7 activation by Crz1.

DISCUSSION

In this work, we devised an integrated approach that combines engineering CLASP, a precise and modular optogenetic tool, with computational modeling and experimentation to investigate the transcriptional consequences of dynamic TF nuclear shuttling. Through precise perturbations afforded by CLASP, we were able to collect data of sufficient resolution to formulate quantitative hypotheses that can explain promoter behaviors. This productive dialog between the technology, the modeling, and the biological findings allowed us to constrain both underlying mechanisms and quantitative parameter relationships in the decoding of dynamic TF signals. Specifically, we showed that some target promoters of Crz1, a naturally pulsatile TF, had higher gene expression in response to short-pulsed inputs compared with a continuous input of the same area. We demonstrated that this behavior could be explained by a two-state promoter model and delineated its quantitative requirements of an easily saturable dose response, fast activation, and slow inactivation. By contrast, pGYP7, which had higher gene expression in response to continuous inputs than pulsed inputs of the same area and also had a linear-dose response, required a more elaborate multi-state model with thresholded activation steps and a dependence on the TF at each step. These insights constitute general principles that would not have been possible without the combined development of CLASP and the organization of the resulting data into computational models.

The quantitative principles delineated by our experiments have clear biological implications. Recent studies have used a 3-state promoter model similar to that used for pGYP7 to recapitulate the decoding of NF-κB dynamics (Sen et al, 2020). The multi-state promoter model we built therefore generated a robust hypothesis that the chromatin structure of pGYP7 was different from the other Crz1 target genes we profiled. To test this hypothesis, we measured nucleosome occupancy for pYPS1-YFP and pGYP7-YFP and analyzed available occupancy data for Crz1 target genes. We found that genes that respond with higher expression to short pulses exhibited lower nucleosome occupancy (Figures 6H, S7E, and S7F). These correlative data suggest the presence of additional promoter regulation, such as a TF-gated promoter transition between non-transcribing promoter states, for promoters that have lower gene expression for short inputs. Phenomenologically, the TF-thresholded transitions between non-transcribing states can represent TF interactions with chromatin remodelers or nucleosomes (Dillon and Festenstein, 2002; Spitz and Furlong, 2012; Lickwar et al., 2012; Platt et al., 2013; Cheng et al., 2011; Gaupel et al., 2014; Steinfeld et al., 2007). However, mechanistic studies, such as direct observation of promoter dynamics, are needed to pinpoint the exact biochemical mechanisms (Cho et al, 2018). Additionally, eukaryotic endogenous gene regulation can be controlled by multiple TFs, phosphorylation, and other factors. Therefore, the study of multiple TF-promoter relationships is needed to reflect the full complexity of gene regulation.

What biological function may differential interpretation of TF dynamic inputs carry for the Crz1 stress response? Under stress, Crz1 undergoes an initial 40–60-min nuclear localization, followed by pulsing in the “maintenance” phase of the calcium response. Cohorts of genes could activate strongly only in the first long pulse, while other genes maintain high expression even in the short pulsing phase of Crz1 response to calcium, therefore programing a staggered response. Moreover, since Crz1 pulses exhibit different amplitudes in the “maintenance” phase (Figure S4A), a 2-state promoter with a dose response that saturates quickly as a function of TF, like pYPSI, would turn on strongly for all pulse amplitudes. By contrast, promoters with a linear-dose response like pCMK2 would activate in a graded fashion, presenting yet another mechanism by which dynamic inputs could be differentially interpreted.

Finally, while our studies focused on the decoding of TF inputs at the promoter level, other modes of differential decoding can be implemented. For example, modulation of translation and degradation of mRNA and protein are alternative strategies for differential decoding. As we discovered for pYPS1-YFP and pCMK2-YFP, different mRNA degradation rates additionally contribute to differential decoding. It will be fascinating to study the bounds of dynamic decoding explored by endogenous genes.

STAR★METHODS

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Hana El-Samad (hana.el-samad@ucsf.edu).

Materials Availability

To request reagents, please submit a form to UCSF at https://ita.ucsf.edu/researchers/mta. Key plasmids have been deposited on Addgene and can be requested from there. For other plasmids (all plasmids listed in Table S3), please contact the Lead Contact.

Data and Code availability

All original microscopy, flow cytometry, RNA-seq, ChIP-qPCR data, and modeling results (except for those for Figures S6A-S6I) have been deposited at Mendeley Data: https://doi.org/10.17632/jxjnjmmj83.1. Raw microscopy images supporting the current study and modeling results for Figures S6A-S6I have not been deposited in a public repository due to file size constraints, but are available from the Lead Contact on request. All code necessary to generate the figures is available via Github at https://github.com/lindseyo/CLASP-Crz1.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Saccharomyces Cerevisiae

Plasmid and Strain Construction

Hierarchical golden gate assembly was used to assemble plasmids for yeast strain construction using the method in Lee et al. Bsal, BsmBI, and NotI cut sites were removed from individual parts to facilitate downstream assembly and linearization. Parts were either generated via PCR or purchased as gBlocks from IDT. For promoters, these parts incorporate the 1000 bp upstream of the open reading frame. These parts were then assembled into transcriptional units (promoter-gene-terminator) on cassette plasmids. These cassettes were assembled together to form multi-gene plasmids for insertion into the yeast genome at the TRP, URA, or LEU locus. Cassette plasmids were grown and prepared from either DH5alpha or Mach1 competent cells (Macrolab, Berkeley, CA). Cassettes were digested with NotI and then transformed into yeast as described in Lee et al. (2013) or (2015).

Yeast Strains, Media, and Growth Conditions

The base S. cerevisiae strain used for experimentation was W303α or BY4741. Base strain for each engineered strain is noted in the strain list. From these base strains, knockout of endogenous transcription factors was done with a one-step replacement using a plasmid that contains 40 base pair overlaps in the 5’ and 3’ UTR of the transcription factor (Gardner and Jaspersen, 2014). The 40 base pair overhangs flank the Candida Albicans HIS selectable marker.

Single colonies were picked from auxotrophic SD (6.7 g/L Bacto-yeast nitrogen base without amino acids, BD Difco, Franklin Lakes, NJ; 2 g/L supplement amino acid mix minus necessary amino acids, MP Biomedical, Irvine, CA; 20 g/L dextrose, Sigma-Aldrich, St Louis, MO) agar plates. For microscopy and growth measurement studies, colonies were picked into 1 ml SDC media. For flow cytometry studies, colonies were picked into 1 ml YPD (yeast extract, Alfa Aesar, Haverhill, MA; peptone, BD Biosciences, Franklin Lakes, NJ; 2% glucose, Sigma-Aldrich, St Louis, MO) or SDC (6.7 g/L Bacto-yeast nitrogen base without amino acids, BD Difco, Franklin Lakes, NJ; 2 g/L complete supplement amino acid mix, MP Biomedical, Irvine, CA; 20 g/L dextrose, Sigma-Aldrich, St Louis, MO) media. Colonies were grown overnight from 30°C to saturation. Prior to the start of an experiment, cells were diluted into 1-3 ml of SDC and grown for 4 h to an OD of 0.05-0.1 prior to the start of an experiment. A TECAN Spark 10M plate reader (TECAN, Mannedorf, Switzerland) was used for growth measurements.

METHOD DETAILS

Microscopy and Blue Light Delivery

Cells were imaged in 96-well Matriplates (MGB096-1-2-LG-L; Brooks Life Science Systems, Spokane, WA). For widefield microscopy, blue light optogenetic stimulation of samples was done using a custom built “optoPlate” as described in Bugaj et al (Bugaj et al., 2018). Individually addressable LEDs (in 96-well format) were controlled by an Arduino Micro microcontroller and programmed with different dynamic light patterns using custom Arduino IDE scripts. Custom adapters for fitting optoPlate on to 96-well matrix plates were designed in AutoCad and 3D printed. For confocal microscopy, blue light stimulation was done using GFP laser illumination. A Nikon Ti inverted scope, with mercury arc-lamp illumination using RFP (560/40 nm excitation, 630/75 nm emission; 572/35 nm excitation, 632/60 nm emission; both manufactured by Chroma, Bellows Falls, VT) and near-infrared FP (640/30 nm excitation, 690/50 nm emission; Chroma, Bellows Falls, VT) filters, was used for widefield microscopy imaging of samples. Images were taken with an Andor EMCCD camera. Automated imaging was controlled and coordinated by custom Matlab (MathWorks, Natick, MA) software interfaced with the μmanager software suite (Edelstein et al., 2014). Confocal microscopy of samples took place on a Nikon Ti inverted scope with a Yokogawa CSU-22 spinning disk confocal scanner unit; cells were excited with laser illumination for Cy3 (561 nm, 100 mW Coherent OBIS; ET610/60nm emission filter) and Cy5 (640 nm,100 mW Coherent OBIS; ET700/75nm emission filter). Imaging was controlled with Nikon Elements 5.02 build 1266 (Nikon Instruments, Melville, NY).

Flow Cytometry

Blue light optogenetic stimulation of samples was done using a custom built “optoPlate” as described in Bugaj et al (Bugaj et al., 2018). Analysis of fluorescent protein reporter expression was performed with a BD LSRII flow cytometer (BD Biosciences, Franklin Lakes, NJ) equipped with a high-throughput sampler. For steady-state measurements, cultures were diluted in TE before running through the instrument. Cultures were run on the instrument 1 h (+/− 20 min) after optical stimulation using the optoPlate, to allow for YFP maturation. YFP (Venus) fluorescence was measured using the FITC channel and RFP (mCherry/mScarlet) was measured using the PE-Texas Red channel. For steady-state measurements, a maximum of 10,000 events were collected per sample.

Growth Assays

Growth was measured using a TECAN Spark 10M plate reader (TECAN, Mannedorf, Switzerland) using 600nm excitation. Cultures were plated into Corning 3904 96-well assay plates (Corning, Corning, NY) and grown at 30°C while shaking until saturation.

Treatment with CaCl₂ Stress

Cells were grown at 30°C in YPD medium to saturation overnight. Cells were then diluted prior to the start of an experiment and grown for 4 h to an OD of 0.05-0.1. For microscopy experiments, cells were plated in SDC with concanavalin A (conA; Sigma-Aldrich, St Louis, MO) for 15 min to adhere them to the bottom of the glass imaging plate. Prior to imaging, the SDC was removed and replaced with a solution of SDC with 0.2M CaCl₂ (Fisher Scientific, Waltham, MA). For flow cytometry experiments, cells in SDC were diluted to OD 0.1 in a media of SDC with 0.2M CaCl₂ and grown in the media for the duration of the experiment. Prior to measurement, the 0.2M CaCl₂ media was removed by centrifugation with 3 washes in 1X TE (Fisher Scientific, Waltham, MA).

Automated Flow Cytometry

Cells were grown at 30°C in YPD medium to saturation overnight. Cells were then diluted prior to the start of an experiment to 0.15 OD and grown for 4 h in SDC media. Cells were then back diluted to 0.2 OD into SDC media with 0.5X Penicillin-Streptomycin to prevent culture contamination (Thermo Fisher Scientific, Waltham, MA; 10,000 U/mL). Cells were then outgrown for 1 h at 30°C while shaking on the automated flow cytometer setup (described in Harrigan et al, 2018). Following the outgrowth, cells were illuminated with 40 mA pulsed or continuous blue light (455 nm) and sampled every 8 min for 6 h using custom LabView scripts.

Chromatin Immunoprecipitation

Chromatin Immunoprecipitation (ChIP) followed by qPCR was performed as described in Greenstein et al (2018) with the following modifications. S.cerevisiae cells were grown at 30°C in YPD overnight to saturation. Cells were then diluted prior to experiment to 0.2 OD and then grown for 4 h in SDC media. To fix cells, 1% formaldehyde (Thermo Fisher Scientific, Waltham, MA) was added directly to the media and cultures were incubated with shaking for 15 min at 30°C. Fixation was quenched with 0.25M glycine (Fisher Scientific, Waltham, MA) for 5 min at 30°C. Cell pellets were washed twice with cold 1xTBS(Teknova, Hollister, CA) and flash frozen prior to lysis. Cells were lysed using a Mini Bead-Beater (Biospec, Bartlesville, OK) with 7 rounds of 1 min ON followed by 2-minute incubations on ice. Sonication was performed using a Diagenode BioRuptor Standard machine (Diagenode, Liege, Belgium) for 30 rounds of 30s ON/30s rest at 4°C. The insoluble fraction was removed by centrifugation and then pre-cleared with Protein A Dynabeads (Thermo Fisher Scientific, Waltham, MA) for 3 h with rotation. Beads were then removed with a magnetic stand (Dynal/Thermo Fisher Scientific, Watham, MA). 2.1 μg of H3 antibody (Active Motif, Carlsbad, CA; 39064) was added per ChIP sample after a 25% was set aside as Input/WCE. Following overnight incubation with antibody, immune complexes were collected with Protein A Dynabeads (Invitrogen) and washed as described (Greenstein et al, 2018) with the exception that the wash buffer step was performed twice. DNA was quantified by RT-qPCR and %IP (ChIP DNA / Input DNA) was calculated as described (Greenstein et al, 2018). %IP values for each qPCR target were normalized to the %IP value for ACT1, an internal positive control.

RNA-Seq of Crz1 19A and 5A Mutant

Single colonies were picked and grown to saturation in YPD at 30°C overnight. Cells were then diluted in SDC and grown for 4 h to an OD of 0.3. Cells were harvested by centrifugation and frozen with liquid nitrogen. RNA was extracted using phenol chloroform (Sambrook and Russell, 2006; Thermo Fisher Scientific, Waltham, MA). RNA quality was assessed using the Agilent RNA Pico kit (Agilent, Santa Clara, CA). The Lexogen Quantseq 3’ mRNA-Seq Library Prep Kit (Lexogen, Vienna, Austria) was used for RNA preparation. mRNA libraries were quantified using Qubit dsDNA HS Assay Kit (Thermo Fisher Scientific, Waltham, MA) and subject to single-end sequencing on an Illumina HiSeq 4000.

Delivery of Stress Inputs for Microscopy

For each environmental perturbation, cells were grown overnight to saturation in YPD, diluted in SDC prior to the experiment, and grown to an OD of 0.1. 200ul cells were plated with conA. Just before imaging, the SDC media was removed from the microscopy well and the appropriate environmental stress media was applied to the cells.The media for glucose depletion consisted of 0.67% YNB w/o AA w/ ammonium sulfate, 0.79% CSM, 0.05% glucose. The media for osmotic shock was composed of 0.67% YNB w/o AA w/ ammonium sulfate, 0.79% CSM, 2% glucose, and 0.95M sorbitol (Gasch et al., 2000; Sigma-Aldrich, St Louis, MO).

Measuring Basal and Constitutively Nuclear Gene Expression of TFs

To further assess how TF-CLASP-induced expression compares to endogenous gene expression, we measured the level of reporter gene expression when the TFs were constitutively localized to the nucleus by C-terminally tagging them with the same NLS used in yeLANS (TF-NLS), or in their basal localization by C-terminally tagging them with only mScarlet. All TF-NLS, TF-mScarlet, and TF-CLASP constructs were expressed from pRPL18b. We compared this value to expression achieved when TF-CLASP was induced with 2 h of blue light. SynTF-CLASP achieved 52% of pSYNTF-YFP expression produced through constitutive nuclear localization of SynTF (Figure S3B). Furthermore, the mean SynTF-CLASP-induced gene expression in the dark (.09) was similar to the mean basal gene expression in a strain in which the SynTF was only tagged with mScarlet (.07) (Figure S3B). Pho4-CLASP activated pPHO84-YFP to 14% of the gene expression achieved with constitutive nuclear localization (Figure S3C) while Msn2-CLASP was more efficient at inducing pHSP12-YFP gene expression than constitutive Msn2 nuclear localization (23% greater expression, Figure S3D). Since Msn2 is subject to faster degradation in the nucleus (Chi et al., 2001; Durchschlag et al., 2004), transient localization with CLASP may be more efficient at inducing gene expression. For both pHSP12-YFP and pPHO84-YFP, reporter expression in the dark was lower in a strain that had either Msn2-CLASP or Pho4-CLASP than in their respective controls with either Msn2 or Pho4 when only tagged with mScarlet (28% and 88% lower, respectively). In fact, pPHO84-YFP showed basal bimodal expression in the constitutively expressed Pho4 strain, but not in the Pho4-CLASP strain (Figure S3C). These data suggest that CLASP can potently sequester TFs in the dark.

Effect of Protein and mRNA Half-Lives on Slope Ratio

Large degradation rates (hence short half-lives) of mRNA and protein result in large slope ratio, which decreases as these rates decrease (Figure S5B). This is not unexpected given that the continuous input ends before the pulsed input. Since the slope ratio is a comparison of the continuous and pulsed inputs measured one hour after the experiment ends, with larger degradation rates, the protein output of the continuous input is reduced more than the output of the pulsed input.

Computational Modeling

Ordinary differential equation (ODE) models of gene expression focusing on promoter kinetics were constructed. For the simple kinetic model that described higher gene expression in response to short pulses, a model was constructed with three state variables and seven parameters. Nine models were constructed and tested for higher gene expression in response to continuous pulses. These models either contained three or five state variables with up to ten parameters. Latin hypercube sampling was done to randomly sample parameters. ODE solvers 45 and 113 in Matlab were used. Least squared error and fit within the error bars of the data were metrics used to obtain model fits. More details of the modeling methods are below.

Model Equations and Sampling Details of the pYPS1-YFP and pCMK2-YFP Phenotypes

Simple Two-State Promoter Model

This model described the higher gene expression in response to short pulses for pYPS1-YFP. The model described a two-state promoter that activates mRNA production which then activates protein production and is depicted in Figure 4A. We modeled these interactions using Equations S1, S2, and S3, which are detailed in the main text as Equations 1, 2, and 3:

$$\frac{d{p}_{on}}{dt}=k_{on}TF(1-p_{on})-k_{off}{p}_{on}$$ (Equation S1)

$$\frac{dmRNA}{dt}={\beta }_0+{\beta }_1{p}_{on}-{\gamma }_{1}mRNA$$ (Equation S2)

$$\frac{d\text{Pr}otein}{dt}={\beta }_{2}mRNA-{\gamma }_2\text{Pr}otein$$ (Equation S3)

In these equations, p_on represented promoter activity due to increased nuclear localization of Crz1*, while mRNAand Protein represented concentration of mRNA and protein, respectively. Here we assumed that promoter activity was conserved such that 1 = p_on + p_off. TF represented the concentration, or nuclear fluorescence, of nuclear transcription factor. The model was characterized by 7 parameters. Most of the activation/inactivation and production/degradation terms were modeled by first-order mass action kinetics. The parameter β₀ was zeroth-order, to reflect basal promoter activity. We chose this simple model form because we were interested in a parsimonious model that could explain the experimental phenotype of pYPS1-YFP. Note that the rate of promoter activation was dependent on TF concentration because Crz1 has been shown to activate genes through binding of a known promoter element, the calcineurin-dependent response element (CDRE), through its zinc finger domain (Stathopoulos-Gerontides et al., 1999). The input to the model was the concentration, or nuclear fluorescence, of nuclear transcription factor (TF), while the output represented protein concentration (Protein).

Dose Response Fitting - The experimental dose response was fit to the equation protein output = C*TF/(TF + k_d) where TF = amplitude of transcription factor input, C = scaling factor, and k_d = k_off/k_on. The model fit showed a k_d of 2.3 for pYPS1-YFP (with a squared error of prediction (SSE) of 5.8e-03) and a k_d of 12.8 for pCMK2-YFP (with an SSE of 2.9e-09).

Parameter Search for Figure S5

The equations were numerically solved by the ODE solver ode113 for nonstiff differential equations via MATLAB. Parameters k_on, k_off, β₀,and β₁ were sampled over 4-5 orders of magnitude systematically and randomly using Latin Hypercube Sampling (LHS). k_on and k_off varied from 1e-1 to 1e2. β₀ was varied from 1e-6 to 1e-2. β₁ was varied from 1e-4 to 1e1. Parameters β₂ = 0.06, γ₁ = 0.06, and γ₂ =0.0083 were fixed to values according to literature (Hansen and O’Shea, 2013; Wang et al., 2002). From the parameter sets sampled, the slope ratio (defined in Figure 3), a summary metric for the degree of efficiency in response to short pulses, was calculated for each parameter set. The parameter search yielded model outputs that qualitatively recapitulate the pYPS1-YFP and pCMK2-YFP slope ratios.

Model Fitting

The model was used to fit the experimental data. Fits of the experimental data to the simple two-promoter state model (Figure 4) were obtained by the following procedure: 1. 10000 parameters were randomly sampled using LHS with the aforementioned parameter ranges (Figure S5A) or more comprehensively sampled using 33,000 parameter sets varying k_on, k_off, and γ₁, (k_on was varied from 0.001-10, k_off from 0.000007-100, and γ₁ from 0.01-10, Figure 5). 2. Fits were determined to be model outputs that fit through ten or more data points within error of the dynamic protein time course data (Figure 5B) or seven or more data points within error of the Output-Fluorescence data (Figure 5D). Note that the ability of the model to fit the data was the same regardless of the criteria of fit used – whether the criteria was the model output fit within the error bars of the data or least squared error of the model to the best fit line to the data. 3. Cross-validation of parameter fits to the dynamic protein time course for light input of 2 minute ON/4 minutes OFF was done. From this procedure, we identified parameter sets that recapitulated all of the experimental data for both pYPS1-YFP and pCMK2-YFP.

Derivation of Expressions of Total Transcripts from Equation 1 in the Main Text

In this section, we derive expressions for the total mRNA produced by the promoter. Using these expressions, we then study properties of total transcripts produced from pulsed and continuous inputs. Starting with the mRNA equation

$$\frac{dmRNA}{dt}={\beta }_1{p}_{\text{on}}-{\gamma }_{1}mRNA$$ (Equation S4)

where there is an instantaneous transcript creation rate β₁p_on, with β₁ being the maximum transcription rate. The instantaneous mRNA loss rate is γ₁mRNA. We will calculate the total integrated output of the promoter, that is the total number of transcripts produced over the entire experiment. By comparing this output for pulsed and continuous inputs that have the same Nuclear Fluorescence AUC, we will be able to link the promoter properties to the ability of producing more transcripts from either pulsed or continuous inputs.

The expression for the total number of transcripts, N, produced over the entire experiment for a given finite input function TF(t) is described by the equation

$$N={\int }_0^5{\beta }_1{p}_{\text{on}}dt$$ (Equation S5)

In the particular setting of our experiments, light input of constant amplitude is administered either continuously (with TF input denoted by TF_c(t), and maximum TF input reaching TF_max) or pulsed (with TF input denoted by TF_p(t)) for a period of time (a maximum of 4 hours), after which the light is shut-off and the output is measured at 5 hours. For the pulsed experiment, light is given in pulses, which yields a TF input of approximately triangular pulses. Each triangular pulse reaches a maximum amplitude of TF_max after which the light is shut-off. By design, for a given Nuclear Fluorescence AUC value, the integrals of TF_c(t) and TF_p(t) are the same, i.e. ${\int }_0^{5}T{F}_p(t)dt={\int }_0^{5}T{F}_c(t)dt$. Dynamic protein measurements (Figure 5B) indicate that the combined timescales of promoter and mRNA decay are faster than 25 minutes (for pYPS1-YFP and pCMK2-YFP). Therefore, p_on and mRNA levels will have decayed to zero at the time of measurement. In addition, prior to any inputs at t = 0, we assume that p_on is zero. As a result, p_on(5) = 0 and p_on(0) = 0.

Equation 1 in the main text indicates that:

$$\frac{d{p}_{\text{on}}}{dt}=k_{\text{on}}(1-p_{\text{on}})TF(t)-k_{\text{off}}{p}_{\text{on}}$$ (Equation S6)

Integrating this equation from t = 0 to t = 5 hours:

$${\int }_0^5\frac{d{p}_{\text{on}}}{dt}dt={\int }_0^5{k}_{\text{on}}(1-p_{\text{on}})TF(t)dt-{\int }_0^5{k}_{\text{off}}{p}_{\text{on}}dt$$ (Equation S7)

Now, ${\int }_0^5\frac{d{p}_{\text{on}}}{dt}dt=p_{\text{on}}(5)-p_{\text{on}}(0)=0$. Thus, setting the two terms on the right side equal to each other and multiplying by β₁/k_off we get

$$N={\int }_0^5{\beta }_1{p}_{\text{on}}dt={\int }_0^5\frac{{\beta }_1}{k_d}(1-p_{\text{on}})TF(t)dt$$ (Equation S8)

where k_d = k_off/k_on. The left two expressions are Equation S5 while the rightmost expression describes how p_on negatively impacts N, for a given input TF(t), through the term (1 − p_on).

To assess the value of N, we use the rightmost expression of Equation S8. We further denote the total number of transcripts generated by TF_p(t) to be N_p and that generated by TF_c(t) to be N_c. Before we delve into the thorough mathematical treatment, we make two arguments. The first is an intuitive illustration of why the ratio N_p/N_c is larger than 1 for the two-state promoter model and the second with respect to how the ratio of total transcripts can be extrapolated to the analysis of the slope ratio we measure, which is that of the protein.

Intuitive Explanation of N_p/N_c > 1 for Two-State Promoter Model

Irrespective of the input, p_on starts at zero and cannot exceed the steady-state solution of p_on from Equation S6 evaluated at TF_max. This steady-state for p_on is given by TF_max/(TF_max + k_d). Fora non-zero TF_c(t), after the initial rise, TF_c(t) is primarily equal to TF_max (Figure 4G (blue shading)) and p_on is primarily equal to TF_max/(TF_max + k_d) (Figure 4G (blue curve)). This is of course assuming that the promoter dynamics allow for reaching steady-state well before the input shuts off. On the other hand, for the pulsed input, the transcription factor input will spend more of its time in the state where TF_p (t)<TF_max (Figure 4G (red shading)) and therefore, p_on will satisfy p_on<TF_max/(TF_max + k_d) (Figure 4G (red curve)) for more of the time course. Accordingly, the (1 − p_on) term on the right hand side of Equation S8 will predominantly be greater for the pulsed input than the continuous input when TF(t) is non-zero. Taken together with the fact that ∫TF_p(t)dt = ∫ TF_c(t)dt, then, according to Equation S8, one might postulate that N_p is larger than N_c. We also prove this to be mathematically true in STAR Methods Sections "Derivation of N_p/N_c>1 in the regime of a fast promoter relative to TF(t) "(fast promoter) and "Derivation of N_p/N_c>1 for general values of k_on and k_off" (general case). A limiting scenario occurs when TF_max ℚ k_d, where TF_max/(TF_max + k_d), the upper bound of p_on, remains much smaller than one (heat map of N_p/N_c in Figure S8A). In this case, the right hand side of Equation S8 dictates that N_p/N_c will be close to one independent of the magnitudes of the rate constants k_on and k_off (see Figure S8B, k_d = 46).

N_p/N_c Can Be Used to Understand Slope Ratio

We can use the ratio of N for the pulsed input to N for the continuous input, i.e. N_p/N_c, to infer the characteristics of the protein slope ratio, which is the quantity experimentally measured (compare Figures 4B and S8A). This is not surprising since transcripts are causal to proteins. This correlation between N_p/N_c and protein slope ratio can also be gleaned from the plot of N as a function of nuclear fluorescence AUC by comparing Figure S8B with the plot of protein as a function of nuclear fluorescence AUC data (Figure 4E (k_d = 2.3) and Figure S5D (k_d = 46)). Furthermore, for all parameters of the model that fit pYPS1-YFP and pCMK2-YFP experimental data, we computed N_p/N_c and the slope ratio of the protein output to compare their relationships. The results in Figures S8A and S8B show that much like for proteins, pulsed inputs yield more transcripts per nuclear fluorescence AUC than continuous inputs. Furthermore N_p/N_c linearly correlates with slope ratio for both pYPS1-YFP and pCMK2-YFP (Figure S8C). Fitting both plots to a line shows that the value of N_p/N_c is generally smaller than slope ratio. Thus, protein and mRNA degradation increase the slope ratio for the protein output.

Derivation of N_p/N_c >1 in the Regime of a Fast Promoter Relative to TF(t)

In the case that the promoter dynamics are much faster than those of the transcription factor nuclear dynamics, p_on reaches pseudosteady state on the timescale of TF(t) such that $p_{\text{on}}\approx \frac{TF(t)}{TF(t)+k_d}$. Using this equation, we can write the middle expression in Equation S8 as

$${\beta }_1{\int }_0^5{p}_{\text{on}}dt={\beta }_1{\int }_0^5\frac{TF(t)}{TF(t)+k_d}dt$$ (Equation S9)

And the right side of Equation S8 is

$$\begin{gathered} \frac{{\beta }_1}{k_d}{\int }_0^5(1-p_{\text{on}})TF(t)dt=\frac{{\beta }_1}{k_d}{\int }_0^5(1-\frac{TF(t)}{TF(t)+k_d})TF(t)dt \\ =\frac{{\beta }_1}{k_d}{\int }_0^5(\frac{TF(t)+k_d}{TF(t)+k_d}-\frac{TF(t)}{TF(t)+k_d})TF(t)dt \\ =\frac{{\beta }_1}{k_d}{\int }_0^5\frac{k_d}{TF(t)+k_d}TF(t)dt \\ ={\beta }_1{\int }_0^5\frac{TF(t)}{TF(t)+k_d}dt \end{gathered}$$ (Equation S10)

Accordingly, Equation S9 is identical to Equation S10 as is required by Equation S8.

To begin, for the continuous TF input, the initial rise of TF_c(t) ends at t = τ_r,c (‘r’ corresponds to rise, and ‘c’ corresponds to continuous). After this rise, TF_c(t) = TF_max until the input starts shutting off at t = τ_f,c (Figure S8D) (where ‘f’ corresponds to fall). We will divide N_c into three parts as follows

$$\begin{gathered} N_c={\beta }_1{\int }_0^{{\tau }_{r,c}}\frac{T{F}_c(t)}{T{F}_c(t)+k_d}dt+{\beta }_1{\int }_{{\tau }_{r,c}}^{{\tau }_{f,c}}\frac{T{F}_c(t)}{T{F}_c(t)+k_d}dt+{\beta }_1{\int }_{{\tau }_{f,c}}^5\frac{T{F}_c(t)}{T{F}_c(t)+k_d}dt \\ =N_r+N_{c,m}+N_f \end{gathered}$$ (Equation S11)

where N_r is the transcriptional contribution due to the rise of the TF pulse, N_f is the transcriptional contribution during the fall of this pulse, and N_c,m is the contribution in between where TF assumes its maximum value TF_max (where ’m’ in N_c,m corresponds to middle).

The maximum amplitude for the pulsed input TF_p(t) is also TF_max. The initial rise of TF_p(t) is the same as that of TF_c(t), and the final decay of the continuous and pulsed inputs are also the same (Figure S8D). If τ_r,p is the initial rise time of TF_p(t) and τ_f,p is the time at which the final pulse starts decaying, then ${\int }_0^{{\tau }_{r,c}}T{F}_c(t)dt={\int }_0^{{\tau }_{r,p}}T{F}_p(t)dt$ and ${\int }_{{\tau }_{f,c}}^{5}T{F}_c(t)dt={\int }_{{\tau }_{f,p}}^{5}T{F}_p(t)dt$.

We again divide N_p into three parts:

$$\begin{gathered} N_p={\beta }_1{\int }_0^{{\tau }_{r,p}}\frac{T{F}_p(t)}{T{F}_p(t)+k_d}dt+{\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{T{F}_p(t)+k_d}dt+{\beta }_1{\int }_{{\tau }_{f,p}}^5\frac{T{F}_p(t)}{T{F}_p(t)+k_d}dt \\ =N_r+N_{p,m}+N_f \end{gathered}$$ (Equation S12)

Where N_p,m is the contribution of the series of pulses occurring between τ_r,p and τ_f,p. Therefore, in order to show that N_p/N_c> 1, we just have to show that N_p,m/N_c,m>1.

To begin, it is important to note that

$${\int }_{{\tau }_{r,c}}^{{\tau }_{f,p}}T{F}_c(t)dt={\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}T{F}_p(t)dt$$ (Equation S13)

For the continuous input, TF_c(t) = TF_max between τ_r,c≤t≤τ_f,c. Accordingly,

$$\begin{gathered} N_{c,m}={\beta }_1{\int }_{{\tau }_{r,c}}^{{\tau }_{f,c}}\frac{T{F}_c(t)}{T{F}_c(t)+k_d}dt \\ ={\beta }_1{\int }_{{\tau }_{r,c}}^{{\tau }_{f,c}}\frac{T{F}_c(t)}{T{F}_{max}+k_d}dt \\ ={\beta }_1\frac{T{F}_{max}[{\tau }_{f,c}-{\tau }_{r,c}]}{T{F}_{max}+k_d} \end{gathered}$$ (Equation S14)

In the steps above we left TF_c(t) in the numerator of the integrand term without replacing it with TF_max in the middle step from Equation S14 in order to use the equality in Equation S13 such that N_c,m becomes:

$$\begin{gathered} N_{c,m}={\beta }_1{\int }_{{\tau }_{r,c}}^{{\tau }_{f,c}}\frac{T{F}_c(t)}{T{F}_{max}+k_d}dt \\ ={\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{T{F}_{max}+k_d}dt \end{gathered}$$ (Equation S15)

On the other hand, the expression for N_p,m is given by:

$$N_{p,m}={\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{T{F}_p(t)+k_d}dt$$ (Equation S16)

Since TF_p(t) + k_d≤TF_max + k_d for every value of t, then $\frac{T{F}_p(t)}{T{F}_p(t)+k_d}\ge \frac{T{F}_p(t)}{T{F}_{max}+k_d}$ for every value of t. In particular, since TF_p(t) is pulsing, then TF_p(t) + k_d<TF_max + k_d for most of τ_r,p≤t≤τ_f,p. We can therefore write down the inequality

$$N_{p,m}={\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{T{F}_p(t)+k_d}dt>{\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{T{F}_{max}+k_d}dt=N_{c,m}$$ (Equation S17)

As a result, $\frac{N_{p,m}}{N_{c,m}}>1$ and thus $\frac{N_p}{N_c}>1$. It should be noted that an important requirement for Equation S17 and all following expressions is that the pulses in TF_p(t) transition from zero to TF_max at a finite speed (e.g, less than infinitely fast). This allows finite integral contributions to the left side of Equation S17 during this transition when 0<TF_p(t)<TF_max. This ensures the inequality. However for rectangular pulses with no transition time, i.e TF_p(t) jumps infinitely fast from zero to TF_max, the left side of Equation S17 will equal the right side and thus N_p = N_c, for this special case.

The ratio $\frac{{\mathit{N}}_{\mathit{p}}}{{\mathit{N}}_{\mathit{c}}}$ is a monotonically decreasing function of k_d and approaches 1 as k_d becomes very large compared to TF_max

One can see on the left side of Equation S17 that the $\frac{T{F}_p(t)}{T{F}_p(t)+k_d}$ term becomes larger in magnitude as k_d decreases for all t when TF_p(t)>0. This implies that N_p,m increases for decreasing k_d for a given TF_p(t). Likewise, N_c,m increases for decreasing k_d. We will next show however that $\frac{N_p}{N_c}$ itself decreases and approaches the value of 1 as k_d increases and becomes large relative to TF_max. Under this constraint Equation S17 becomes

$$N_{p,m}={\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{T{F}_p(t)+k_d}dt\approx {\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{k_d}dt\approx {\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{T{F}_{max}+k_d}dt=N_{c,m}$$ (Equation S18)

Therefore N_p,m≈N_c,m and hence Np ≈ N_c

As mentioned above, the contribution to N_c from the initial rise and final fall of TF_c(t) corresponds to one full pulse of a pulsed input TF_p(t). Therefore, since $N_p={\beta }_1{\int }_0^5\frac{T{F}_p(t)}{T{F}_p(t)+k_d}dt$, then if TF_p(t) consists of M pulses, then one pulse would be the equivalent of $\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{T{F}_p(t)+k_d}dt$. Furthermore, as also explained above: N_r,c = N_r,p and N_f,c = N_f,p and we will refer to both as N_r and N_f, respectively. We will therefore represent N_c as:

$$\begin{gathered} N_c=N_r+N_{c,m}+N_f \\ =\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{T{F}_p(t)+k_d}dt+{\beta }_1{\int }_{{\tau }_{r,c}}^{{\tau }_{f,c}}\frac{T{F}_c(t)}{T{F}_{max}+k_d}dt \end{gathered}$$ (Equation S19)

where we have used Equation S14. Similarly, we represent N_p as

$$\begin{gathered} N_p=N_r+N_{p,m}+N_f \\ =\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{T{F}_p(t)+k_d}dt+{\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{T{F}_p(t)+k_d}dt \\ =\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{T{F}_p(t)+k_d}dt+\frac{M-1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{T{F}_p(t)+k_d}dt \end{gathered}$$ (Equation S20)

The derivative of N_c with respect to k_d would be

$$\begin{gathered} \frac{d{N}_c}{d{k}_d}=\frac{d{N}_r}{d{k}_d}+\frac{d{N}_{c,m}}{d{k}_d}+\frac{d{N}_f}{d{k}_d} \\ =-\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt-{\beta }_1{\int }_{{\tau }_{r,c}}^{{\tau }_{f,c}}\frac{T{F}_c(t)}{(T{F}_{max}+k_d{)}^2}dt \end{gathered}$$ (Equation S21)

Therefore,

$$\frac{d{N}_r}{d{k}_d}=\frac{d{N}_f}{d{k}_d}=-\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt$$ (Equation S22)

and

$$\begin{gathered} \frac{d{N}_{c,m}}{d{k}_d}=-{\beta }_1{\int }_{{\tau }_{r,c}}^{{\tau }_{f,c}}\frac{T{F}_c(t)}{(T{F}_{max}+k_d{)}^2}dt \\ =-\frac{N_{c,m}}{(T{F}_{max}+k_d)} \end{gathered}$$ (Equation S23)

Likewise, the derivative of N_p with respect to k_d would be

$$\begin{gathered} \frac{d{N}_p}{d{k}_d}=\frac{d{N}_r}{d{k}_d}+\frac{d{N}_{p,m}}{d{k}_d}+\frac{d{N}_f}{d{k}_d} \\ =-\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt-{\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt \\ =-\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt-\frac{M-1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt \end{gathered}$$ (Equation S24)

where

$$\begin{gathered} \frac{d{N}_{p,m}}{d{k}_d}=-{\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt \\ =-\frac{M-1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt \end{gathered}$$ (Equation S25)

We will next compute the derivative of N_p/N_c with respect to k_d, and use the expressions above to assess its sign, demonstrating that it is negative. The derivative of N_p/N_c with respect to k_d is given by:

$$\begin{gathered} \frac{d\frac{N_p}{N_c}}{d{k}_d}=\frac{\frac{d{N}_p}{d{k}_d}{N}_c}{N_c^2}-\frac{\frac{d{N}_c}{d{k}_d}{N}_p}{N_c^2} \\ =\frac{1}{N_c^2}\left[(\frac{d{N}_{p,m}}{d{k}_d}+\frac{d[N_r+N_f]}{d{k}_d})(N_{c,m}+[N_r+N_f])-(\frac{d{N}_{c,m}}{d{k}_d}+\frac{d[N_r+N_f]}{d{k}_d})(N_p+[N_r+N_f])\right] \\ =\frac{1}{N_c^2}[\frac{d{N}_{p,m}}{d{k}_d}{N}_{c,m}+\frac{d[N_r+N_f]}{d{k}_d}{N}_{c,m}+\frac{d{N}_{p,m}}{d{k}_d}[N_r+N_f]+\frac{d[N_r+N_f]}{d{k}_d}[N_r+N_f]\phantom{]} \\ \phantom{[}-\frac{d{N}_{c,m}}{d{k}_d}{N}_{p,m}-\frac{d[N_r+N_f]}{d{k}_d}{N}_{p,m}-\frac{d{N}_{c,m}}{d{k}_d}[N_r+N_f]-\frac{d[N_r+N_f]}{d{k}_d}[N_r+N_f]] \\ =\frac{1}{N_c^2}[\frac{d{N}_{p,m}}{d{k}_d}{N}_{c,m}+\frac{d[N_r+N_f]}{d{k}_d}{N}_{c,m}+\frac{d{N}_{p,m}}{d{k}_d}[N_r+N_f]\phantom{]} \\ -\phantom{[}\frac{d{N}_{c,m}}{d{k}_d}{N}_{p,m}-\frac{d[N_r+N_f]}{d{k}_d}{N}_{p,m}-\frac{d{N}_{c,m}}{d{k}_d}[N_r+N_f]] \end{gathered}$$ (Equation S26)

We will now analyze different pairs of terms from the right hand side of Equation S26. We will start with

$$\begin{gathered} \frac{d{N}_{p,m}}{d{k}_d}{N}_{c,m}-\frac{d{N}_{c,m}}{d{k}_d}{N}_{p,m}=-N_{c,m}{\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt+N_{p,m}{\beta }_1{\int }_{{\tau }_{r,c}}^{{\tau }_{f,c}}\frac{T{F}_c(t)}{(T{F}_{max}+k_d{)}^2}dt \\ =-N_{c,m}{\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt+\frac{N_{p,m}}{T{F}_{max}+k_d}{\beta }_1{\int }_{{\tau }_{r,c}}^{{\tau }_{f,c}}\frac{T{F}_c(t)}{T{F}_{max}+k_d}dt \\ =-N_{c,m}{\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt+\frac{N_{p,m}}{T{F}_{max}+k_d}{N}_{c,m} \\ =-N_{c,m}{\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt+N_{c,m}\frac{N_{p,m}}{T{F}_{max}+k_d} \\ =-N_{c,m}{\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt \\ +N_{c,m}{\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{(T{F}_p(t)+k_d)(T{F}_{max}+k_d)}dt \end{gathered}$$ (Equation S27)

where in the third line we have used the relationship $N_{c,m}={\beta }_1{\int }_{{\tau }_{r,c}}^{{\tau }_{f,c}}\frac{T{F}_c(t)}{T{F}_{max}+k_d}dt$ from Equation S14. In the last line we used the relationship $N_{p,m}={\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{T{F}_p+k_d}dt$ from Equation S20. When TF_p(t) is non-zero, $\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}>\frac{T{F}_p(t)}{(T{F}_{(p)}+k_d)(T{F}_{max}+k_d)}$ for all t except when TF_p(t) = TF_max which occurs only at the peak of the pulse. Therefore, $\frac{d{N}_{p,m}}{d{k}_d}{N}_{c,m}-\frac{d{N}_{c,m}}{d{k}_d}{N}_{p,m}<0$. Next, the second pair of terms is

$$\frac{d[N_r+N_f]}{d{k}_d}{N}_{c,m}-\frac{d[N_r+N_f]}{d{k}_d}{N}_{p,m}=\left[-N_{c,m}+N_{pm}\right]\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt$$ (Equation S28)

Where we have used the expression for $\frac{d{N}_r+d{N}_f}{d{k}_d}$ from above. Finally, the third pair is

$$\begin{gathered} \frac{d{N}_{p,m}}{d{k}_d}\left[N_r+N_f\right]-\frac{d{N}_{c,m}}{d{k}_d}\left[N_r+N_f\right]=\left[N_r+N_f\right]\left[-{\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt+{\beta }_1{\int }_{{\tau }_{r,c}}^{{\tau }_{f,c}}\frac{T{F}_c(t)}{(T{F}_{amx}+k_d{)}^2}dt\right] \\ =\left[N_r+N_f\right]\left[-{\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt+\frac{N_{c,m}}{(T{F}_{max}+k_d)}\right] \\ =\frac{1}{M}{N}_p\left[-{\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt+\frac{N_{c,m}}{(T{F}_{max}+k_d)}\right] \\ =\frac{1}{M}{N}_p\left[-\frac{M-1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt+\frac{N_{c,m}}{(T{F}_{max}+k_d)}\right] \\ =-\frac{M-1}{M}{N}_p\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt+\frac{1}{M}{N}_p\frac{N_{c,m}}{(T{F}_{max}+k_d)} \\ =-N_{p,m}\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt+\frac{1}{M}{N}_p\frac{N_{c,m}}{(T{F}_{max}+k_d)} \\ =-N_{p,m}\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt+N_{c,m}\frac{1}{M}\frac{N_p}{(T{F}_{max}+k_d)} \\ =-N_{p,m}\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt \\ +N_{c,m}\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d)(T{F}_{max}+k_d)}dt \end{gathered}$$ (Equation S29)

where in the second line we have used the relationship ${\beta }_1{\int }_{{\tau }_{r,c}}^{{\tau }_{f,c}}\frac{T{F}_c(t)}{(T{F}_{max}+k_d{)}^2}dt=\frac{N_{c,m}}{(T{F}_{max}+k_d)}$ from Equation S23. In the fourth line we have used the relationship $-{\beta }_1{\int }_{{\tau }_{r,p}}^{{\tau }_{f,p}}\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt=-\frac{M-1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p}{(T{F}_p(t)+k_d{)}^2}dt$ from Equation S25. In the last line we used the relationship $N_p={\beta }_1{\int }_0^5\frac{T{F}_p(t)}{T{F}_p(t)+k_d}dt$. We can now add Equations S28 and S29 to get

$$\begin{gathered} \frac{d[N_r+N_f]}{d{k}_d}{N}_{c,m}-\frac{d[N_r+N_f]}{d{k}_d}{N}_{p,m}+\frac{d{N}_{p,m}}{d{k}_d}[N_r+N_f]-\frac{d{N}_{c,m}}{d{k}_d}[N_r+N_f] \\ =\left[-N_{c,m}+N_{p,m}\right]\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt \\ -N_{p,m}\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt+N_{c,m}\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d)(T{F}_{max}+k_d)}dt \\ =-N_{c,m}\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}dt+N_{c,m}\frac{1}{M}{\beta }_1{\int }_0^5\frac{T{F}_p(t)}{(T{F}_p(t)+k_d)(T{F}_{max}+k_d)}dt \\ >0 \end{gathered}$$ (Equation S30)

since $\frac{T{F}_p(t)}{(T{F}_p(t)+k_d{)}^2}>\frac{T{F}_p(t)}{(T{F}_p(t)+k_d)(T{F}_{max}+k_d)}$ for all t and when TF_p(t) is non-zero, except when TF_p(t) = TF_max which occurs only at the peak of the pulse. Thus, from the results in Equations S27 and S30, we can conclude that $\frac{d\frac{N_p}{N_c}}{d{k}_d}<0$, Therefore, N_p/N_c is a monotonically decreasing function of k_d as is demonstrated in Figures 4 and S4 in the main text.

Derivation of N_p/N_c >1 for General Values of k_on and k_off

Below we derive the result that N_p, the total transcripts for the pulsed input TF_p(t), is always greater than N_c, the total transcripts for the continuous input TF_c(t). The first section below (STAR Methods Section "Treatment of a Class of Inputs whose Decreasing Edge Proceeds through Steps") introduces a class of inputs and subsequent analysis and simulation results that form the foundation of this proof. This section continues at a high level to describe the construction of more complex classes of inputs, related analysis, and simulation results. The extremes of these classes represent the continuous and pulsed inputs. We leave the detailed mathematical derivations, analysis, and technical formulation of the proof for later sections, but each derivation is referenced in the appropriate area in STAR Methods Section "Treatment of a Class of Inputs whose Decreasing Edge Proceeds through Steps". This serves as a road-map to understand the complete proof for those interested. Otherwise, STAR Methods Section "Treatment of a Class of Inputs whose Decreasing Edge Proceeds through Steps" by itself serves as a high level intuitive summary of the proof that is aimed to be accessible to a more general audience.

Treatment of a Class of Inputs whose Decreasing Edge Proceeds through Steps

We first consider an ensemble of inputs TF(t) that will become instrumental in the general demonstration, and derive properties generated by the two-state promoter model when stimulated with these inputs. The first class of inputs is shown in the top panel of Figure S9A. After an initial rise of the pulse, all the inputs decrease by a step except one which remains constant (Figure S9A, top plot, blue), reminiscent of the continuous input. The other inputs then remain constant for a duration and then decrease by a step except for one which remains constant (Figure S9A, top plot, red). This behavior repeats itself until the last remaining input step decreases to zero and remains at zero (Figure S9A, top plot, light blue), representing a single pulse. This produces a series of inputs, where each plateaus (indefinitely) at a different value. Simulation results of the model with this input ensemble show that each input’s corresponding p_on trajectory maintains the same relative order to the other inputs’ p_on trajectories as the inputs do with each other (Figure S9A, second panel from the top, compare for example light blue and green traces). This is a general property of the system regardless of the values of k_on and k_off. We provide a proof in STAR Methods Section "Proof showing that p_on(t, α₁)>p_on(t, α₂) for t>t₀ and α₁>α₂" using the analytical results derived in STAR Methods Section "Derivation of an Expression for p_on(t) in Response to a Step Input Starting from an Initial Condition p_on(t₀)".

Then we plot p_on versus accumulated TF area (defined as ${\int }_0^{t}TF(v)dv$) for each input. This plot (Figure S9A, second panel from the bottom) shows that the relative order is the same as it was for p_on versus accumulated time. We derive these results in STAR Methods Section "Proof showing that $p_{\text{on}}(t_0+\sigma ,{\alpha }_1)>p_{\text{on}}(t_0+\frac{{\alpha }_1}{{\alpha }_2}\sigma ,{\alpha }_2)$ for σ>0, where σ is proportional to accumulated TF area". These results are then used to prove, as we observe in our simulations, that for accumulated transcripts versus accumulated TF area, the relative order is reversed from the first three panels (Figure S9A, bottom plot). Intuitively this makes sense since total transcripts from the right hand side of Equation S8 is a function of 1 – p_on (multiplied by TF(t)) and not p_on. Overall, these results show that the lower the plateau value is for this class of inputs, the higher the accumulated transcripts as a function of accumulated area (see STAR Methods Section "Deriving relationships for the number of transcripts, specifically ΔN_α2(σ)>ΔN_α1 (σ) for σ>0" for derivation).

Towards the construction of multiple pulses, in STAR Methods Section "Analysis of a class of inputs that relate the number of transcripts of the continuous input TF_c(t) to that of pulsed input TF_p(t) for the two pulse case" we extend our analysis to a class of inputs that initially follow the same trajectories as Figure S9A (top plot), where each plateaus at a different value, but then rise again to TF_max before shutting off (Figure S9B, top plot). Here the input with the highest valued plateau represents the continuous input TF_c(t) while the input with the lowest valued plateau represents the pulsed input TF_p(t) (two pulses). Importantly, all inputs share the same total TF area. Through a similar analysis as above, we show that the lower the plateau value of an input, the more total transcripts that are produced (Figure S9B, inputs (top panel), transcripts (bottom panel)). Finally, in STAR Methods Section "Extending the Approach to a Higher Number of Pulses" we extend this approach first to three pulses and then to arbitrary numbers of pulses to demonstrate the generality of the two pulse result (examples in Figure S9C, inputs (top panel), accumulated transcripts (bottom panel), and Figure S9E, inputs (left panel), accumulated transcripts (right panel)).

Finally, in our examples we used I = 6 inputs to visually demonstrate our approach. As I gets larger, each step change is smaller and better represents a smooth input, but the conclusions of our proof do not change. Thus, we can take the limit of steps becoming infinitesimally small to represent smooth pulses with large I to prove that for smooth inputs, N_p>N_c.

Derivation of an Expression for p_on(t) in Response to a Step Input Starting from an Initial Condition p_on(t₀)

For the two-state promoter model that experiences a step input TF(t) = α₁TF_max for t ≥ t₀ and where 0 ≤ α₁ ≤ 1, and starting from an initial condition p_on(t₀), the dynamic equations for t ≥ t₀ are given by:

$$\begin{gathered} \frac{d{p}_{\text{on}}}{dt}=k_{\text{on}}TF(t)(1-p_{\text{on}})-k_{\text{off}}{p}_{\text{on}} \\ =k_{\text{on}}{\alpha }_{1}T{F}_{\max }(1-p_{\text{on}})-k_{\text{off}}{p}_{\text{on}} \\ =-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}]p_{\text{on}}+k_{\text{on}}{\alpha }_{1}T{F}_{\max } \end{gathered}$$ (Equation S31)

We seek the time dependent solution of this equation, which we denote by p_on(t, α₁). This is a linear first order ordinary differential equation, whose solution takes the form p_on = a₀ + a₁ exp(−[k_onα₁TF_max + k_off][t – t₀]) for t≥t₀. Following standard procedure, we solve for the constants a₀ and a₁ by evaluating the system at t = t₀ and t = ∞. At t = ∞, $\frac{d{p}_{\text{on}}}{dt}=0$ therefore dictating that $a_0=\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}$. At t = t₀ to the solution must equal the initial condition, that is a₀ + a₁ = p_on(t₀). Thus, $a_1=p_{\text{on}}(t_0)-\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}$ and the full solution becomes:

$$\begin{gathered} p_{\text{on}}(t,{\alpha }_1)=\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}+\left[p_{\text{on}}(t_0)-\frac{k_{\text{on}}{\alpha }_{1}T{F}_{max}}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}\right]\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}][t-t_0]) \\ =\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}+\left[p_{\text{on}}(t_0)-\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}\right]\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}][t-t_0]) \\ +p_{\text{on}}(t_0)-p_{\text{on}}(t_0) \\ =p_{\text{on}}(t_0)+(\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0))\times (1-\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}][t-t_0])) \end{gathered}$$ (Equation S32)

Proof Showing that p_on (t, α₁) >p_on (t, α₂) for t>t₀ and α₁ >α₂

Simulation results of the model with the input ensemble in Figure S9A (top panel) show that each input’s corresponding p_on time trajectory maintains the same relative order to the other inputs’ p_on trajectories as the inputs do with each other (Figure S9A, second panel from the top, compare for example light blue and green traces). This is a general property of the system regardless of the values of k_on and k_off. We now provide a proof of this observation. First, for any pair of inputs with adjacent plateaus (Figure S9A (top plot), blue/red, red/orange, orange/purple, purple/green, green/light blue), the point in time where they diverge we’ll denote as t = t₀. Like-wise, since the pair have identical input behavior up until t = t₀, the value of p_on(t) at t = t₀ will be the same for both. We’ll denote this shared value as p_on(t₀). For t>t₀, the first (upper) input has TF(t) = α₁TF_max while the second (step down, lower) input has TF(t) = α₂TF_max. Accordingly, α₁>α₂. We’ll apply the analytical solution from STAR Methods Section "Derivation of an Expression for p_on(t) in Response to a Step Input Starting from an Initial Condition p_on(t₀)" to compare the solutions of p_on(t) for the upper and lower inputs, which we’ll refer to as p_on(t, α₁) and p_on(t, α₂), respectively. We’ll then prove that p_on(t, α₁)>p_on(t, α₂) for t>t₀. We begin by subtracting the analytical solution of p_on(t, α₂) from that of p_on(t, α₁) to get

$$\begin{gathered} p_{\text{on}}(t,{\alpha }_1)-p_{\text{on}}(t,{\alpha }_2)=p_{\text{on}}(t_0)+(\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0))\times (1-\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}][t-t_0])) \\ -p_{\text{on}}(t_0)-(\frac{k_{\text{on}}{\alpha }_{2}T{F}_{\max }}{k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0))\times (1-\text{exp}(-[k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}][t-t_0])) \\ =(\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0))\times (1-\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}][t-t_0])) \\ -(\frac{k_{\text{on}}{\alpha }_{2}T{F}_{\max }}{k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0))\times (1-\text{exp}(-[k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}][t-t_0])) \end{gathered}$$ (Equation S33)

There are three cases to consider depending on the value of the initial condition p_on (t₀).

1. $\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)>\frac{k_{\text{on}}{\alpha }_{2}T{F}_{\max }}{k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)>0$: In this case, p_on(t, α₁) – p_on(t, α₂)>0 for t>t₀. This is because $1-\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}][t-t_0])>1-\text{exp}(-[k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}][t-t_0])$, since by definition α₁>α₂.

2. $\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)>0$ and $\frac{k_{\text{on}}{\alpha }_{2}T{F}_{\max }}{k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)<0$: In this case, all terms are positive, thus, p_on(t, α₁) – p_on(t, α₂)>0 for t> t₀.

3. $0>\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)>\frac{k_{\text{on}}{\alpha }_{2}T{F}_{\max }}{k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)$. For this case, we will present a more detailed analysis.

To simplify notation, we will rewrite Equation S33 as:

$$p_{\text{on}}(t,{\alpha }_1)-p_{\text{on}}(t,{\alpha }_2)=b_2(1-\text{exp}(-c_2[t-t_0]))-b_1(1-\text{exp}(-c_1[t-t_0]))$$ (Equation S4)

where $b_1=p_{\text{on}}(t_0)-\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}$ and $b_2=p_{\text{on}}(t_0)-\frac{k_{\text{on}}{\alpha }_{2}T{F}_{\max }}{k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}}$, with b₂>b₁>0. Also, c₁ = [k_onα₁TF_max + k_off] and c₂ = [k_onα₂TF_max + k_off], with c₁>c₂>0.

Since the initial conditions for both inputs is the same, the initial condition of their difference in Equation S34 is zero at t = t₀. We therefore need to show that the slope of Equation S34 evaluated for t≥t₀ is positive.

Taking the derivative of Equation S34 we get:

$$\frac{d[p_{\text{on}}(t,{\alpha }_1)-p_{\text{on}}(t,{\alpha }_2)]}{dt}=b_2{c}_2\text{exp}(-c_2[t-t_0])-b_1{c}_1\text{exp}(-c_1[t-t_0])$$ (Equation S5)

We evaluate this expression at t = t₀ to get:

$${\phantom{\mid }\frac{d[p_{\text{on}}(t,{\alpha }_1)-p_{\text{on}}(t,{\alpha }_2)]}{dt}\mid }_{t=t_0}=b_2{c}_2-b_1{c}_1$$ (Equation S36)

We now use the expressions for b₁, c₁, b₂, c₂ in the above equation, to get that:

$$\frac{d[p_{\text{on}}(t,{\alpha }_1)-p_{\text{on}}(t,{\alpha }_2)]}{dt}{\mid }_{t=t_0}=k_{\text{on}}T{F}_{\max }(1-p_{\text{on}}(t_0))({\alpha }_1-{\alpha }_2)$$ (Equation S37)

Which is positive since α₁>α₂. Furthermore, exp(−c₂t) decays slower than exp( – c₁t), and thus exp( –c₂t)>exp( −c₁t) for all t. Therefore, it follows that b₂c₂>b₁c₁, and that b₂c₂ exp( − c₂t)>b₁c₁ exp( − c₁t). This concludes our proof that p_on(t, α₁) − p_on(t, α₂)>0 for t>t₀. As discussed above, in Figure S9A (top plot), this result applies to any pair of inputs with adjacent plateaus (blue/red, red/orange, orange/purple, purple/green, green/light blue). That is, for a given pair, p_on(t) due to the upper input (α₁) remains higher over time relative to p_on(t) due to the lower input (α₂). Now for the sequence of plateaued input pairs, the lower input in one pair is the upper input for the next pair (e.g., blue/red then red/orange in Figure S9A). Thus, this observation combined with the analytical results implies that the observed order of inputs (Figure S9A, top plot) must be shared by their corresponding p_on trajectories (Figure S9A, second panel from the top). Furthermore, this means that the input with the highest valued plateau (Figure S9A, top plot, blue, continuous-like input) produces the highest p_on(t), and the input with the lowest-valued plateau (zero) input (Figure S9A, top plot, light blue, single pulse input) produces the lowest.

Furthermore, since all times of t₀ and values of α_i are arbitrary in the analytical treatment, these conclusions hold for input sequences that step down with any resolution, and therefore for any input that has a decreasing edge. We use I = 6 inputs to visually demonstrate our approach (Figure S9A). As I gets larger, where each step change is smaller and better represents a smooth input, the conclusions of our proof do not change. Our results are invariant to I. Thus, we can represent smooth pulses with large I.

Proof Showing that ${\mathit{p}}_{\mathit{on}}({\mathit{t}}_0+\sigma ,{\alpha }_1)>{\mathit{p}}_{\mathit{on}}({\mathit{t}}_0+\frac{{\alpha }_1}{{\alpha }_2}\sigma ,{\alpha }_2)$ for σ>0, where σ Is Proportional to Accumulated TF Area

In Figure S9A (second panel from the bottom), we plot p_on versus accumulated TF area for each input. This plot shows that the relative order is the same as it was for p_on versus accumulated time. To understand this, we will prove that this observed result must hold for any pair of inputs with adjacent plateaus (Figure S9A (top plot), blue/red, red/orange, orange/purple, purple/green, green/light blue) regardless of the values of k_on and k_off. With the same definitions for p_on(t₀), t₀, α₁, and α₂ as in STAR Methods Section "Proof showing that p_on(t, α₁)>p_on(t, α₂) for t>t₀ and α₁>α₂" we now proceed.

For the α₁TF_max input, over the duration t₀<t<t₀ + σ, the accumulated TF(t) area, denoted as A_α1(σ), can formally be written in integral form as

$$\begin{gathered} A_{{\alpha }_1}(\sigma )={\int }_{t_0}^{t_0+\sigma }{\alpha }_{1}T{F}_{\max }dt \\ ={\alpha }_{1}T{F}_{\max }\sigma \end{gathered}$$ (Equation S38)

Similarly, for the α₂TF_max input, over the duration t₀<t<t₀ + σ′, the accumulated TF(t) area is α₂TF_maxσ′. If we required that the two inputs have equal accumulated area then α₁TF_maxσ = α₂TF_maxσ′. Accordingly, ${\sigma }^{\prime }=\frac{{\alpha }_1}{{\alpha }_2}\sigma$, i.e. σ′ must be larger than σ in order to have the same area since the transcription factor amplitude is lower.

Here one can see that σ is a variable that can be used to transform both inputs (α₁ and α₂) from time to equal accumulated TF(t) area. This allows us to analyze quantities such as p_on(t) and accumulated transcripts as a function of σ. Now, we derive a relationship between the value of p_on evaluated at t₀ + σ for an input α₁TF_max input (which we denote p_on (t₀ + σ, α₁)) and its value evaluated at $t_0+\frac{{\alpha }_1}{{\alpha }_2}\sigma$ for an input α₂TF_max (which we denote by $p_{\text{on}}(t_0+\frac{{\alpha }_1}{{\alpha }_2}\sigma ,{\alpha }_2)$). These two p_on values are therefore generated by two inputs of identical area.

Using the analytical solutions derived above, we can write:

$$\begin{gathered} p_{\text{on}}(t_0+\sigma ,{\alpha }_1)-p_{\text{on}}(t_0+\frac{{\alpha }_1}{{\alpha }_2}\sigma ,{\alpha }_2)=p_{\text{on}}(t_0)+(\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0))\times (1-\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}]\sigma )) \\ -p_{\text{on}}(t_0)-(\frac{k_{\text{on}}{\alpha }_{2}T{F}_{\max }}{k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0))\times (1-\text{exp}(-[k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}]\frac{{\alpha }_1}{{\alpha }_2})) \\ =(\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0))\times (1-\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}]\sigma )) \\ -(\frac{k_{\text{on}}{\alpha }_{2}T{F}_{\max }}{k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0))\times (1-\text{exp}(-[k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}]\frac{{\alpha }_1}{{\alpha }_2}\sigma )) \end{gathered}$$ (Equation S39)

There are 3 possibilities for the relationship between p_on(t₀ + σ, α₁) and $p_{\text{on}}(t_0+\frac{{\alpha }_1}{{\alpha }_2}\sigma ,{\alpha }_2)$.

1. $\frac{k_{\text{on}}{\alpha }_{2}T{F}_{\max }}{k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)<\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)<0$: Here, the expression in Equation S39 is greater than zero. This is because $1-\text{exp}\left(-[k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}]\frac{{\alpha }_1}{{\alpha }_2}\sigma \right)>1-\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}]\sigma )$ for t>t₀.

2. $\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)>0$ and $\frac{k_{\text{on}}{\alpha }_{2}T{F}_{\max }}{k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)<0$: Here, all terms in Equation S39 are positive and thus greater than zero.

3. $\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)>\frac{k_{\text{on}}{\alpha }_{2}T{F}_{\max }}{k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)>0$: For this case, we will present a more detailed analysis.

To begin we’ll differentiate Equation S39 with respect to σ. We get

$$\begin{gathered} \frac{d\left[p_{\text{on}}(t_0+\sigma ,{\alpha }_1)-p_{\text{on}}(t_0+\frac{{\alpha }_1}{{\alpha }_2}\sigma ,{\alpha }_2)\right]}{d\sigma }=\frac{d\left[(\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0))\times (1-\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}]\sigma ))\right]}{d\sigma } \\ -\frac{d\left[(\frac{k_{\text{on}}{\alpha }_{2}T{F}_{\max }}{k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0))\times (1-\text{exp}(-[k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}]\frac{{\alpha }_1}{{\alpha }_2}))\right]}{d\sigma } \\ =[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}](\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0))\times \text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}]\sigma ) \\ -[k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}]\frac{{\alpha }_1}{{\alpha }_2}(\frac{k_{\text{on}}{\alpha }_{2}T{F}_{\max }}{k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0))\times \text{exp}(-[k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}]\frac{{\alpha }_1}{{\alpha }_2}\sigma ) \\ =(k_{\text{on}}{\alpha }_{1}T{F}_{\max }-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}]p_{\text{on}}(t_0))\times \text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}]\sigma ) \\ -(k_{\text{on}}{\alpha }_{1}T{F}_{\max }-\left[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+\frac{{\alpha }_1}{{\alpha }_2}{k}_{\text{off}}\right]p_{\text{on}}(t_0))\times \text{exp}(-[k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}]\frac{{\alpha }_1}{{\alpha }_2}\sigma ) \end{gathered}$$ (Equation S40)

Because $\frac{{\alpha }_1}{{\alpha }_2}>1$, then $k_{\text{on}}{\alpha }_{1}T{F}_{\max }-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}]p_{on}(t_0)>k_{on}{\alpha }_{1}T{F}_{max}-\left[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+\frac{{\alpha }_1}{{\alpha }_2}{k}_{\text{off}}\right]p_{\text{on}}(t_0)>0$ and also $\text{exp}(-[k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}]\frac{{\alpha }_1}{{\alpha }_2}\sigma )$ is smaller than exp(−[k_onα₁TF_max + k_off]σ) for all σ greater than zero. Therefore, the expression in Equation S40 is greater than zero. This taken together with the fact that the initial condition in Equation S39 at σ = 0 is equal to zero dictates that Equation S39 is greater than zero for σ>0. Thus, $p_{\text{on}}(t_0+\sigma ,{\alpha }_1)>p_{\text{on}}(t_0+\frac{{\alpha }_1}{{\alpha }_2}\sigma ,{\alpha }_2)$ for σ>0. Thus, this analytical result implies that the observed order of inputs (Figure S9A, top plot) which are shared by their corresponding time-dependent p_on trajectories (Figure S9A, second panel from the top) must also be shared by the corresponding σ -dependent p_on trajectories. Indeed, when we plot p_on versus accumulated TF area for each input (Figure S9A, second panel from the bottom) the relative order is the same as it was for p_on versus accumulated time.

Deriving for the Number of Transcripts, Specifically ΔN_α2 (σ)>ΔN_α1 (σ) for σ>0

With the same definitions for σ, p_on(t₀), t₀, α₁ and α₂, we now calculate the number of transcripts produced for a given value of σ. We will denote ΔN_α1 (σ) as accumulated transcripts for the α₁TF_max input. We will also denote by ΔN_α2 (σ) the number of accumulated transcripts for the α₂TF_max input over the same input area as for the α₁TF_max input. Applying the right hand side of Equation S8 to the α₁TF_max input we get

$$\begin{gathered} \Delta N_{{\alpha }_1}(\sigma )={\int }_{t_0}^{t_0+\sigma }\frac{{\beta }_1}{k_d}(1-p_{\text{on}}(t,{\alpha }_1)){\alpha }_{1}T{F}_{\max }dt \\ ={\int }_{t_0}^{t_0+\sigma }\frac{{\beta }_1}{k_d}(1-p_{\text{on}}(t_0)-(\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)) \\ \times (1-\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}](t-t_0)))){\alpha }_{1}T{F}_{\max }dt \\ =\frac{{\beta }_1}{k_d}[{\alpha }_{1}T{F}_{\max }\sigma -p_{\text{on}}(t_0){\alpha }_{1}T{F}_{\max }\sigma \phantom{]} \\ -(\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)) \\ \times \phantom{[}({\alpha }_{1}T{F}_{\max }\sigma -\frac{1-\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}]\sigma )}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}{\alpha }_{1}T{F}_{\max })] \end{gathered}$$ (Equation S41)

Likewise, ΔN_α2 (σ) is given by:

$$\begin{gathered} \Delta N_{{\alpha }_1}(\sigma )={\int }_{t_0}^{t_0+\sigma }\frac{{\beta }_1}{k_d}(1-p_{\text{on}}(t,{\alpha }_1)){\alpha }_{1}T{F}_{\max }dt \\ ={\int }_{t_0}^{t_0+\sigma }\frac{{\beta }_1}{k_d}(1-p_{\text{on}}(t_0) \\ -(\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)) \\ \times (1-\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}](t-t_0)))){\alpha }_{1}T{F}_{\max }dt \\ =\frac{{\beta }_1}{k_d}[{\alpha }_{1}T{F}_{\max }\sigma -p_{\text{on}}(t_0){\alpha }_{1}T{F}_{\max }\sigma \phantom{]} \\ -(\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)) \\ \times \phantom{[}({\alpha }_{1}T{F}_{\max }\sigma -\frac{1-\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}]\sigma )}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}{\alpha }_{1}T{F}_{\max })] \end{gathered}$$ (Equation S42)

Next we must show that ΔN_α2 – ΔN_α1>0. Explicitly this expression (divided by $\frac{{\beta }_1}{k_d}$) is

$$\begin{gathered} \frac{k_d}{{\beta }_1}[\Delta N_{{\alpha }_2}(\sigma )=\Delta N_{{\alpha }_1}(\sigma )]=(\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)) \\ \times ({\alpha }_{1}T{F}_{\max }\sigma -\frac{1-\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}]\sigma )}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}{\alpha }_{1}T{F}_{\max }) \\ -(\frac{k_{\text{on}}{\alpha }_{2}T{F}_{\max }}{k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)) \\ \times ({\alpha }_{1}T{F}_{\max }\sigma -\frac{1-\text{exp}(-\left[k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}\right]\frac{{\alpha }_1}{{\alpha }_2}\sigma )}{k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}}{\alpha }_{2}T{F}_{\max }) \\ ={\alpha }_{1}T{F}_{\max }[(\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0))\phantom{]} \\ \times (\sigma -\frac{1-\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}]\sigma )}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}) \\ -(\frac{k_{\text{on}}{\alpha }_{2}T{F}_{\max }}{k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)) \\ \times \phantom{[}(\sigma -\frac{1-\text{exp}(-\left[k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}\right]\frac{{\alpha }_1}{{\alpha }_2}\sigma )}{\left[k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}\right]\frac{{\alpha }_1}{{\alpha }_2}})] \end{gathered}$$ (Equation S43)

At α = 0, Equation S43 is zero as it should be. We just need to show that the slope of Equation S43 is positive with respect to σ. The expression for the slope is

$$\begin{gathered} \frac{k_d}{{\beta }_1}\frac{d[\Delta N_{{\alpha }_2}(\sigma )-\Delta N_{{\alpha }_1}(\sigma )]}{d\sigma }={\alpha }_{1}T{F}_{\max }[(\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)) \\ \times (1-\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}]\sigma ))\phantom{]} \\ -(\frac{k_{\text{on}}{\alpha }_{2}T{F}_{\max }}{k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)) \\ \phantom{[}\times (1-\text{exp}(-\left[k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}\right]\frac{{\alpha }_1}{{\alpha }_2}\sigma ))]= \\ ={\alpha }_{1}T{F}_{\max }[p_{\text{on}}(t_0)+(\frac{k_{\text{on}}{\alpha }_{1}T{F}_{\max }}{k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0))\phantom{]} \\ \times (1-\text{exp}(-[k_{\text{on}}{\alpha }_{1}T{F}_{\max }+k_{\text{off}}]\sigma )) \\ -p_{on}(t_0)-(\frac{k_{\text{on}}{\alpha }_{2}T{F}_{\max }}{k_{\text{on}}T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0)) \\ \times \phantom{[}(1-\text{exp}(-\left[k_{\text{on}}{\alpha }_{2}T{F}_{\max }+k_{\text{off}}\right]\frac{{\alpha }_1}{{\alpha }_2}\sigma ))] \\ ={\alpha }_{1}T{F}_{\mathrm{amx}}\left[p_{\text{on}}(t_0+\sigma ,{\alpha }_1)-p_{\text{on}}(t_0+\frac{{\alpha }_1}{{\alpha }_2}\sigma ,{\alpha }_2)\right] \\ >0 \end{gathered}$$ (Equation S44)

This is because for $\sigma >0,p_{\text{on}}(t_0+\sigma ,{\alpha }_1)-p_{\text{on}}(t_0+\frac{{\alpha }_1}{{\alpha }_2}\sigma ,{\alpha }_2)>0$ as demonstrated above. Thus, ΔN_α2(σ) − ΔN_α1 (σ)>0 for σ> 0. This inequality verifies that more transcripts are produced from an input TF whose amplitude is reduced (α₂TF_max input) and which extends more in time relative to a shorter but higher TF amplitude input (α₁TF_max input) when the TF input area is equal between the two inputs. These results imply that given the relative order of the inputs (Figure S9A, top plot) the associated order of accumulated transcripts versus accumulated TF area must be reversed (compare the top plot in Figure S9A to the bottom plot). Overall, these results show that the lower the plateau value is for this class of inputs, the higher the accumulated transcripts as a function of accumulated area.

Analysis of a Class of Inputs that Relate the Number of Transcripts of the Continuous Input TF_c (t) to that of Pulsed Input TF_p(t) for the Two Pulse Case

Here, we will start using all the properties derived above to establish relationships between the number of transcripts generated by a continuous input TF_c(t) and that of a pulsed input TF_p(t) for M = 2 pulses. Figure S9B (top plot) shows the classes of inputs we will consider here. These are similar to those in Figure S9A (top plot), in that the inputs descend to their respective plateaus in exactly the same manner, but later rise to TF_max and then shut off. Here the input with the highest valued plateau represents the continuous input TF_c(t) (Figure S9B (top plot, dark blue)) while the input with the lowest valued plateau represents the pulsed input TF_p(t) (Figure S9B (top plot, light blue, two pulses)). Importantly, the inputs are constructed such that the total TF area is the same for all inputs. As we did for the analysis above, we analyze each pair of inputs with adjacent plateau values (Figure S9B (top plot, blue/red, red/orange, orange/purple, purple/green, green/light blue)) where the input with the higher plateau value will be called TF_α1 (t) and the input with the lower plateau value is TF_α2 (t). Similar to the above analysis, we’ll denote the corresponding p_on for each these inputs as p_on(t, α₁) and p_on(t, α₂), respectively. To begin, we will first consider a continuous input that rises, plateaus to a value α₁TF_max, (α₁ = 1 in this case for illustration purposes) and then shuts off (Figure S9B (top middle plot), dark blue, TF_α1 (t)). The input with a plateau value adjacent to the continuous input (Figure S9B (top middle plot), red, TF_α2 (t)) rises in the same fashion, plateaus, and then drops at time t₀ to a lower plateau value of α₂TF_max, staying there until time $t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }$. The input then jumps up to TF_max and then shuts off. The total accumulated TF area for TF_α1 (t) at t = t₀ + σ* is identical to that for TF_α2(t) at $t=t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }$. The shut-off for the two TF inputs are identical, albeit shifted in time with respect to each other. That is, $T{F}_{{\alpha }_1}(t_0+{\sigma }^{\ast }+\tau )=T{F}_{{\alpha }_2}(t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }+\tau )=T{F}_{off}(\tau )$ for τ>0.

We know from our discussion and derivations above that the total transcripts produced from TF_α1 (t) at t = t₀ + σ* is less than that of $T{F}_{{\alpha }_2}(t)\text{at}t=t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }$. To analyze the transcripts produced from the shut-off of the input for each case, we will begin by first showing that for the identical shut-off of the TF inputs, $p_{\text{on}}(t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }+\tau ,{\alpha }_2)$ for $T{F}_{{\alpha }_2}(t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }+\tau )$ is always less than the p_on(t₀ + σ* + τ, α₁) for TF_α1 (t₀ + σ* + τ) at every τ for τ>0. Let us first model TF_off (τ) for τ>0 as a series of step changes with arbitrary resolution. This allows us to apply our analytical solutions over the duration of each step for two different initial conditions where we will show that the lower initial condition will remain lower over the duration of the step. To derive this result, consider p_on(t, α) which has the initial condition p_on(t₀) at t = t₀, and which has the solution for the input TF(t) = αTF_max for 0≤α≤1 and for t>t₀ is

$$p_{\text{on}}(t,\alpha )=p_{\text{on}}(t_0)+(\frac{k_{\text{on}}\alpha T{F}_{\max }}{k_{\text{on}}\alpha T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0))\times (1-\text{exp}(-[k_{\text{on}}\alpha T{F}_{\max }+k_{\text{off}}][t-t_0]))$$ (Equation S45)

Likewise consider ${\tilde{p}}_{\text{on}}(t,\alpha )$ which has initial condition ${\tilde{p}}_{\text{on}}(t_0)$ at t = t₀ and where ${\tilde{p}}_{\text{on}}(t_0)<p_{\text{on}}(t_0)$. The solution for ${\tilde{p}}_{\text{on}}(t,\alpha )$ would be

$${\tilde{p}}_{\text{on}}(t,\alpha )={\tilde{p}}_{\text{on}}(t_0)+(\frac{k_{\text{on}}\alpha T{F}_{\max }}{k_{\text{on}}\alpha T{F}_{\max }+k_{\text{off}}}-{\tilde{p}}_{\text{on}}(t_0))\times (1-\text{exp}(-[k_{\text{on}}\alpha T{F}_{\max }+k_{\text{off}}][t-t_0]))$$ (Equation S46)

Now, $p_{\text{on}}(t,\alpha )-{\tilde{p}}_{\text{on}}(t,\alpha )$ is given by:

$$\begin{gathered} p_{\text{on}}(t,\alpha )-{\tilde{p}}_{\text{on}}(t,\alpha )=p_{\text{on}}(t_0)+(\frac{k_{\text{on}}\alpha T{F}_{\max }}{k_{\text{on}}\alpha T{F}_{\max }+k_{\text{off}}}-p_{\text{on}}(t_0))\times (1-\text{exp}(-[k_{\text{on}}\alpha T{F}_{\max }+k_{\text{off}}][t-t_0])) \\ -{\tilde{p}}_{\text{on}}(t_0)-(\frac{k_{\text{on}}\alpha T{F}_{\max }}{k_{\text{on}}\alpha T{F}_{\max }+k_{\text{off}}}-{\tilde{p}}_{\text{on}}(t_0))\times (1-\text{exp}(-[k_{\text{on}}\alpha T{F}_{\max }+k_{\text{off}}][t-t_0])) \\ =[p_{\text{on}}(t_0)-{\tilde{p}}_{\text{on}}(t_0)][1-(1-\text{exp}(-[k_{\text{on}}\alpha T{F}_{\max }+k_{\text{off}}][t-t_0]))] \end{gathered}$$ (Equation S47)

Now recall that we are modeling TF_off (τ) for τ>0 as a series of step changes with arbitrary resolution. This analytical result implies that the function with the lower initial condition at $\tau =0,p_{\text{on}}(t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }+\tau ,{\alpha }_2)$, will remain lower over the series of steps in TF_off (τ) for τ>0. This is simply because at the end of a given step, the lower valued function at this point in time represents the lower initial condition for the next step and will remain lower over that step. Thus, the lower valued function must remain lower through the whole series of steps until the input shuts off. To reiterate, since $p_{\text{on}}(t_0+{\sigma }^{\ast }+\tau ,{\alpha }_1)>p_{\text{on}}(t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }+\tau ,{\alpha }_2)$ at τ = 0, and since both are experiencing TF_off(τ), our results above imply that $p_{\text{on}}(t_0+{\sigma }^{\ast }+\tau ,{\alpha }_1)>p_{\text{on}}(t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }+\tau ,{\alpha }_2)$ for τ>0. Importantly, this is independent of the shape of TF_off (τ).

We are now poised to determine which input, TF_α1 (t) or TF_α2 (t), produces more total transcripts. For the TF_α1 (t) input, applying the right hand side of Equation S8, we have

$$\begin{gathered} N_{{\alpha }_1}={\int }_0^5\frac{{\beta }_1}{k_d}(1-p_{\text{on}}(t,{\alpha }_1))T{F}_{{\alpha }_1}(t)dt \\ ={\int }_0^{t_0+{\sigma }^{\ast }}\frac{{\beta }_1}{k_d}(1-p_{\text{on}}(t,{\alpha }_1))T{F}_{{\alpha }_1}(t)dt+{\int }_{t_0+{\sigma }^{\ast }}^5\frac{{\beta }_1}{k_d}(1-p_{\text{on}}(t,{\alpha }_1))T{F}_{{\alpha }_1}(t)dt \\ =N_{{\alpha }_1}(t_0+{\sigma }^{\ast })+{\int }_0^{5-[t_0+{\sigma }^{\ast }]}\frac{{\beta }_1}{k_d}(1-p_{\text{on}}(t_0+{\sigma }^{\ast }+\tau ,{\alpha }_1))T{F}_{off}(\tau )d\tau \end{gathered}$$ (Equation S48)

And for the TF_α2(t) input we have

$$\begin{gathered} N_{{\alpha }_2}={\int }_0^5\frac{{\beta }_1}{k_d}(1-p_{\text{on}}(t,{\alpha }_2))T{F}_{{\alpha }_2}(t)dt \\ ={\int }_0^{t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }}\frac{{\beta }_1}{k_d}(1-p_{\text{on}}(t,{\alpha }_2))T{F}_{{\alpha }_2}(t)dt+{\int }_{t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }}^5\frac{{\beta }_1}{k_d}(1-p_{\text{on}}(t,{\alpha }_2))T{F}_{{\alpha }_2}(t)dt \\ =N_{{\alpha }_2}\left(t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }\right)+{\int }_0^{5-\left[t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }\right]}\frac{{\beta }_1}{k_d}\left(1-p_{\text{on}}\left(t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }+\tau ,{\alpha }_2\right)\right)T{F}_{off}(\tau )d\tau \end{gathered}$$ (Equation S49)

We have previously shown that $N_{{\alpha }_2}(t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast })>N_{{\alpha }_1}(t_0+{\sigma }^{\ast })$ (Equation S44). Since $p_{\text{on}}(t_0+{\sigma }^{\ast }+\tau ,{\alpha }_1)>p_{\text{on}}(t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }+\tau ,{\alpha }_2)$ for τ> 0, this means that $1-p_{\text{on}}(t_0+{\sigma }^{\ast }+\tau ,{\alpha }_1)<1-p_{\text{on}}(t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }+\tau ,{\alpha }_2)$ for τ>0. Thus, the integral term on the last line of the N_α2 equation, Equation S49, will be greater than that of the N_α1 equation, Equation S48. We can therefore conclude that N_α2 >N_α1 for α₁ > α₂. Additionally, analysis of the next pair of inputs with adjacent plateau values (Figure S9B (bottom middle plot), red (TF_α1 (t)) and orange (TF_α2 (t))) follows exactly the same logic and will yield the same result. This remains true for every subsequent pair of inputs with adjacent plateau values from Figure S9B (top plot) where the TF_α2 (t) input always produces more total transcripts than the TF_α1 (t) input. Thus, for this class of inputs, the lower an input’s plateau value, the more total transcripts that are produced (Figure S9B (bottom plot)), with the continuous input TF_c(t) producing the least and the pulsed input TF_p(t) producing the most.

Extending the Approach to a Higher Number of Pulses

This analysis also applies to inputs with larger numbers of pulses. We’ll first start with the three pulse input (Figure S9C). We extend the analysis from the two pulse input for the first two adjacent input pairs (Figure S9B (middle plots)) to accommodate the three pulse input (Figure S9C (middle plots)). As above with the two pulse input, t = t₀ represents the time at which divergence of the inputs TF_α1 and TF_α2 occurs, and where TF_α2 drops to its plateau value. Additionally, at t = t₀, both TF_α1 (t) and TF_α2 (t) have the same TF area. As above with the two pulse input, at $t=t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }$, TF_α2 (t) jumps back up to TF_α1 (t), and where TF_α1 (t) at t = t₀ + σ* has the same corresponding accumulated TF area as TF_α2 (t) does at $t=t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }$. For the three pulse input, unlike the two pulse input, TF_α2 (t) then drops a second time to its plateau value at t = t₁(α₂). Correspondingly, the TF area at t = t₁(α₁) for TF_α1 (t) is the same as the TF area at t = t₁ (α₂) for TF_α2 (t). For the first adjacent input pair, $t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }$ happens to share the same value as t₁ (α₁) (Figure S9C (top middle plot)). This is the result of the particular choice we make– i.e. triangular pulses, that we are modeling with steps. However, the second adjacent input pair does not exhibit this equality (Figure S9C (bottom middle plot)) nor would any succeeding pair.

Given the analysis above for the two pulse input, we already know that for the three pulse input, the total transcripts produced from TF_α1 (t) at t = t₀ + σ* is less than that of TF_α2(t) at $t=t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }$ (Figure S9C (middle plots)). Then, similar to the two pulse input, the inputs are identical but shifted, i.e. $T{F}_{{\alpha }_1}(t_0+{\sigma }^{\ast }+\tau )=T{F}_{{\alpha }_2}(t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }+\tau )$, but only over the duration $0<\tau \le t_1({\alpha }_1)-[t_0+{\sigma }^{\ast }]=t_1({\alpha }_2)-\left[t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }\right]$ (Figure S9C (middle plots)). From the general implications of Equation S47, we know that since $p_{\text{on}}(t_0+{\sigma }^{\ast },{\alpha }_1+\tau )>p_{\text{on}}(t_0+\frac{{\alpha }_1}{{\alpha }_2}{\sigma }^{\ast }+\tau ,{\alpha }_2)$ at τ = 0, this relationship must hold over the duration of τ. TF_α2(t) will therefore yield more transcripts through the right-hand side of Equation S8 over this duration. Thus, for the same accumulated TF area, i.e. TF_α1 (t) up until t = t₁ (α₁) and TF_α2 (t) up until t = t₁(α₂), TF_α2 (t) produces more transcripts.

Now for the three pulse input, TF_α1 (t₁ (α₁) + τ) is identical to TF_α1 (t₀ + τ) for the two pulse input for τ>0. Additionally, for the three pulse input, TF_α2 (t₁ (α₂) + τ) is identical to TF_α2(t₀ + τ) for the two pulse input for τ>0. For the two pulse input, p_on(t₀, α₁) = p_on(t₀, α₂) and TF_α2 (t) produces more transcripts. However, p_on(t₁(α₁), α₁)>p_on(t₁ (α₂), α₂) for the three pulse input. Thus, TF_α2 (t) must produce more transcripts for τ>0. We can therefore conclude that TF_α2 (t) produces more transcripts than TF_α1 (t) for the three pulse input, i.e. N_α2>N_α1. This same analysis can then be applied to each successive pair of inputs with adjacent plateau values to ultimately show that the pulsed input TF_p(t) yields the most transcripts for this class of inputs while the continuous input TF_c(t) yields the least (Figure S9C (bottom plot)).

The logic and analysis developed for the three pulse input can be applied to the same class of inputs with an arbitrary number of pulses to show that TF_p(t) yields the most transcripts for this class of inputs while the continuous input TF_c(t) yields the least, regardless of the number of pulses. To begin, we discuss the first two adjacent input pairs (Figure S9D) where we plot just past the beginning of the third drop to its plateau value for TF_α2 (t). As above, t = t₀ represents the time where TF_α2 (t) first drops to its plateau value, and at which both TF_α1 (t) and TF_α2(t) have the same TF area. In general, all successive drops to the plateau value of TF_α2(t) start at t = t_i(α₂), where 1≤i≤M – 2, where M is the total number of pulses for this class of inputs. Given t = t_i(α₂) for TF_α2(t), the time that corresponds to the same TF area for TF_α1 (t) is t = t_i(α₁).

For the three pulse input, we used the right-hand side of Equation S8 to show that the transcripts produced from t = t₀ to t = t₁ (α₁) for TF_α1 (t) is less than that for TF_α2 (t) from t = t₀ to t = t₁ (α₂). This comparison is over equivalent TF area. Now for TF_α1 (t) from t = t₁ (α₁) to t = t₂(α₁), the input is the same as it was from t = t₀ to t = t₁ (α₂). Similarly, for TF_α2 (t) from t = t₀ (α₂) to t = t₂(α₂), the input is the same as it was from t = t₀ to t = t₁(α₂). This repeats at every t = t_i(α₁) for TF_α1 (t) and every t = t_i(α₂) for TF_α2(t) until i = M – 2 just prior to shutoff. Importantly, at t = t₀, p_on(t₀, α₁) = p_on(t₀, α₂), but at the beginning of every succeeding repeated sequence pair, p_on (t_i(α₁), α₁)<p_on(t_i (α₂), α₂) for all 1≤i≤M – 2. Hypothetically, if p_on(t_i (α₁), α₁) = p_on(t_i(α₂), α₂), we know that TF_α2(t) will yield more transcripts through Equation S8 from t = t_i(α₂) to t = t_i+1 (α₂) than TF_α1 (t) from t = t_i(α₁) to t = t_i+1(α₁). Thus, since p_on(t_i(α₁), α₁)>p_on(t_i(α₂), α₂), this must still hold. We can therefore conclude that over every succeeding repeated sequence pair, TF_α2(t) will always yield more transcripts. Furthermore, we can apply the shutoff results from the three pulse input above to conclude that TF_α2(t) will yield more transcripts for t>t_M–2(α₂) (through shutoff) than TF_α1 (t) for t>t_M–2(α₁) (through shutoff). Thus, in general, for any number of pulses M, N_α2>N_α1. This same analysis can then be applied to each successive pair of inputs with adjacent plateau values to ultimately show that the pulsed input TF_p(t) yields the most transcripts for this class of inputs while the continuous input TF_c(t) yields the least (see twenty pulse example in Figure S9E).

Finally, this analysis proves that the continuous input TF_c(t) will always produce less total transcripts than the pulsed input TF_p(t), given the constraint of equal TF area. Thus, the slope ratio of the total transcripts, N_p/N_c, will remain greater than one. Importantly, while we use triangle-like pulses as a visual example, the analysis is general for any pulse type that has a single rise (step-ups allowed as in the examples presented) followed by a fall (step-downs allowed as in the examples).

Asymptotic Analysis of mRNA Dynamics for the Simple Promoter to a Step Function Input

We can evaluate the promoter model (Figure 4A; Equation 1 in the main text) and the resulting mRNA dynamics for a step input using linear systems analysis. For a four hour constant input experiment, TF(t) ≈ TF_maxu(t), a step function, since TF(t) equilibrates to TF_max within two minutes (Figure 3A). The solution for p_on would be

$$p_{\text{on}}(t)=\frac{T{F}_{max}}{T{F}_{max}+\frac{k_{\text{off}}}{k_{\text{on}}}}u(t)[1-\text{exp}(-[k_{\text{on}}T{F}_{max}+k_{\text{off}}]t)]$$ (Equation S50)

The mRNA equation would then be

$$\frac{dmRNA}{dt}={\beta }_1{p}_{\text{on}}(t)-{\gamma }_{1}mRNA$$ (Equation S51)

where β₁ is the production rate of the promoter and γ₁ is the mRNA decay rate. The solution for the mRNA equation would then be

$$\begin{gathered} mRNA(t)={\beta }_1\frac{T{F}_{max}}{T{F}_{max}+\frac{k_{\text{off}}}{k_{\text{on}}}}[u(t)-u(t)\text{exp}(-[k_{\text{on}}T{F}_{max}+k_{\text{off}}]t)]\ast u(t)\text{exp}(-{\gamma }_{1}t) \\ ={\beta }_1\frac{T{F}_{max}}{T{F}_{max}+\frac{k_{\text{off}}}{k_{\text{on}}}}u(t)[\frac{1}{{\gamma }_1}-\frac{1}{{\gamma }_1}\text{exp}(-{\gamma }_{1}t)-\frac{1}{{\gamma }_1-[k_{\text{on}}T{F}_{max}+k_{\text{off}}]}\text{exp}(-[k_{\text{on}}T{F}_{max}+k_{\text{off}}]t)\phantom{]} \\ \phantom{[}+\frac{1}{{\gamma }_1-[k_{\text{on}}T{F}_{max}+k_{\text{off}}]}\text{exp}(-{\gamma }_{1}t)] \end{gathered}$$ (Equation S52)

where ’*’ denotes convolution. Here we have used the formula

$$[u(t)\text{exp}(-{\lambda }_{1}t)]\ast [u(t)\text{exp}(-{\lambda }_{2}t)]=\frac{1}{{\lambda }_2-{\lambda }_1}[u(t)\text{exp}(-{\lambda }_{1}t)-u(t)\text{exp}(-{\lambda }_{2}t)]$$ (Equation S53)

for λ₁ ≠ λ₂. Now let’s look at two extreme regimes. The first being k_onTF_max + k_off>>γ₁ (where k_onTF_max + k_off>>1 is also true). For this case

$$mRNA(t)\approx {\beta }_1\frac{T{F}_{max}}{T{F}_{max}+\frac{k_{\text{off}}}{k_{\text{on}}}}u(t)\left[\frac{1}{{\gamma }_1}-\frac{1}{{\gamma }_1}\text{exp}(-{\gamma }_{1}t)\right]$$ (Equation S54)

Here the dominant effect in the time signal mRNA(t) is the slow γ₁ with exponential timescale T_s = 1 /γ₁. The other extreme regime is k_onTF_max + k_off<<γ₁ (where γ₁>>1 is also true). For this case

$$mRNA(t)\approx {\beta }_1\frac{T{F}_{max}}{T{F}_{max}+\frac{k_{\text{off}}}{k_{\text{on}}}}u(t)\left[\frac{1}{{\gamma }_1}-\frac{1}{{\gamma }_1}\text{exp}(-[k_{\text{on}}T{F}_{max}+k_{\text{off}}]t)\right]$$ (Equation S55)

Here the dominant effect in the time signal mRNA(t) is the slow k_onTF_max + k_off with exponential timescale T_s = 1/(k_onTF_max + k_off). We denote T_s as the settling time for the dynamic data presented in Figure 5 in the main text.

Model Exploration and Sampling Details for the pGYP7-YFP Phenotype: List of Models

Two-state models with either k_off or k_on thresholding (Figures S6C and S6D) -

These models involved a TF concentration gated activation, k_on, or inactivation, k_off, rate constant. The kinetic model with k_off thresholding consisted of Equations S1, S2, and S3, but utilized the following equation instead of Equation S1:

$$\frac{d{p}_{on}}{dt}=k_{on}TF(1-p_{on})-k_{off}^{\ast }{p}_{on}$$ (Equation S56)

where ${\mathrm{k}}_{\text{off}}^{\star }=0$ when TF ≥ threshold. Otherwise ${\mathrm{k}}_{\text{off}}^{\star }={\mathrm{k}}_{\text{off}}$. threshold is a parameter value which denoted the threshold TF concentration at which ${\mathrm{k}}_{\text{off}}^{\star }$ switches from 0 to k_off.

The kinetic model with k_on thresholding consisted of Equations S1, S2, and S3, and utilized the following equation in place of Equation S1:

$$\frac{d{p}_{on}}{dt}=k_{on}^{\ast }TF(1-p_{on})-k_{off}{p}_{on}$$ (Equation S57)

where ${\mathrm{k}}_{\text{on}}^{\star }={\mathrm{k}}_{\text{on}}$ when TF ≥ threshold. Otherwise ${\mathrm{k}}_{\text{on}}^{\star }=0$.

These two models could represent a binary interaction of the transcription factor (TF) with promoter elements, where below a TF concentration, the TF had no effect on promoter activity and above a TF concentration, the promoter turned on at its maximal rate.

The same parameter ranges were sampled in this model as in the simple kinetic model. The additional parameter threshold was sampled randomly from TF = 0 to 2.6, the maximum value of the TF input to the model.

Cooperative Model (Figure S6B) -

Similar to the two-state thresholded models, the cooperative model described a nonlinear relationship between TF concentration and protein output. The model was represented by the equations:

$$\frac{dmRNA}{dt}={\beta }_0+{\beta }_1\frac{T{F}^n}{T{F}^n+k_d^n}-{\gamma }_{1}mRNA$$ (Equation S58)

$$\frac{d\text{Pr}otein}{dt}={\beta }_{2}mRNA-{\gamma }_2\text{Pr}otein$$ (Equation S59)

where n is the Hill coefficient, and ${\mathrm{k}}_{\mathrm{d}}=\frac{k_{off}}{k_{on}}$.

The same parameter ranges were sampled in this model as in the simple kinetic model. The additional parameter n was sampled randomly from n = 0.5 to 4, a biologically relevant range (Hansen and O’Shea, 2013).

3-State Models -

We considered five 3-state models with different relationships of TF and the rate constants for the transition between promoter states. The first such model was a 3-state model (Figure S6F). An additional promoter state, p₀, was added. The rate equations describing this model were:

$$\frac{d{p}_0}{dt}=r_{off}{p}_{off}-r_{on}{p}_0$$ (Equation S60)

$$\frac{d{p}_{off}}{dt}=k_{off}{p}_{on}+r_{on}{p}_0-(r_{off}+k_{on}TF)p_{off}$$ (Equation S61)

$$\frac{d{p}_{on}}{dt}=k_{on}TF{p}_{off}-k_{off}{p}_{on}$$ (Equation S62)

$$\frac{dmRNA}{dt}={\beta }_0+{\beta }_1{p}_{on}-{\gamma }_{1}mRNA$$ (Equation S63)

$$\frac{d\text{Pr}otein}{dt}={\beta }_{2}mRNA-{\gamma }_2\text{Pr}otein$$ (Equation S64)

In this model, the p₀ and p_off could be thought of as non-transcribing promoter states that represented nucleosome occluded and open states, respectively. p_on represented an active transcribing promoter state. The rate constants r_off and r_on described the transitions between the occluded and open promoter states. The promoter underwent a transition between p₀ and p_off (with rate constants, r_on and r_off, respectively), but p_off was still not a promoter state conducive for transcription. A second transition from p_off to p_on (with rate constants, k_on and k_off, respectively) was needed to start transcription.

3-state model with r_off threshold but no linear TF dependence of k_on (Figure S6E) -

This model was the same as the 3-state model with r_off threshold, except there was no linear dependence of the TF in the transition from p_off and p_on. The model was described by Equations S60, S61, S62, S63, and S64; the following equations replaced Equations S60, S61, and S62:

$$\frac{d{p}_0}{dt}=r_{off}^{\ast }{p}_{off}-r_{on}{p}_0$$ (Equation S65)

$$\frac{d{p}_{off}}{dt}=k_{off}{p}_{on}+r_{on}{p}_o-(r_{off}^{\ast }+k_{on})p_{off}$$ (Equation S66)

$$\frac{d{p}_{on}}{dt}=k_{on}{p}_{off}-k_{off}{p}_{on}$$ (Equation S67)

where ${\mathrm{r}}_{\text{off}}^{\star }=0$ when TF ≥ threshold. Otherwise ${\mathrm{r}}_{\text{off}}^{\star }={\mathrm{r}}_{\text{off}}$.

3-state model with r_on threshold (Figure S6H) -

This model contained a TF concentration threshold dependence of r_on between the occluded p₀ and open p_off promoter states, and was described by Equations S60, S61, S62, S63, and S64; where model Equations S60 and S61 were replaced by:

$$\frac{d{p}_0}{dt}=r_{off}{p}_{off}-r_{on}^{\ast }{p}_0$$ (Equation S68)

$$\frac{d{p}_{off}}{dt}=k_{off}{p}_{on}+r_{on}^{\ast }{p}_0-(r_{off}+k_{on}TF)p_{off}$$ (Equation S69)

where ${\mathrm{r}}_{\text{on}}^{\star }={\mathrm{r}}_{\text{on}}$ when TF ≥ threshold. Otherwise ${\mathrm{r}}_{\text{on}}^{\star }=0$.

For this model, the transcription factor modulated the rate of transition from p₀ to p_off such that when TF concentration reached the threshold concentration, threshold, the transition rate switched from zero to a value. Biologically, this model could represent TF interaction with chromatin acetylators and other modifiers that could promote an open chromatin conformation on the promoter.

3-state model with r_off threshold (Figure S6I) -

Similarly, the model with a threshold dependence on the inactivating transition from the open p_off to occluded p₀ states was described by the model Equations S60, S61, S62, S63, and S64; where Equations S60 and S61 were replaced by:

$$\frac{d{p}_0}{dt}=r_{off}^{\ast }{p}_{off}-r_{on}{p}_0$$ (Equation S70)

$$\frac{d{p}_{off}}{dt}=k_{off}{p}_{on}+r_{on}{p}_0-(r_{off}^{\ast }+k_{on}TF)p_{off}$$ (Equation S71)

where ${\mathrm{r}}_{\text{off}}^{\star }=0$ when TF ≥ threshold. Otherwise ${\mathrm{r}}_{\text{off}}^{\star }={\mathrm{r}}_{\text{off}}$.

For this model, the transcription factor modulated the rate of transition from p_off to p₀ such that when TF concentration reached the threshold concentration, threshold, the transition rate switched from a value to zero. Biologically, this model could represent either physical hindrance of closed chromatin formation or TF-modulated repression of a chromatin de-acetylase. The parameters r_on and r_off were randomly sampled in the range from 10e-4 to 1.

3-state model with linear TF dependence of r_on and k_on (Figure S6G) -

This model contained a linear dependence on TF for the transitions between both p₀ to p_off and p_off to p_on. This model was described by the model Equations S60, S61, S62, S63, and S64; where Equations S60 and S61 were replaced by:

$$\frac{d{p}_0}{dt}=r_{off}{p}_{off}-(r_{on}TF)p_0$$ (Equation S72)

$$\frac{d{p}_{off}}{dt}=k_{off}{p}_{on}+(r_{on}TF)p_0-(r_{off}+k_{on}TF)p_{off}$$ (Equation S73)

Parameter Search and Model Fitting -

Parameter search and model fitting were done in a similar way as for modeling of pYPS1-YFP and pCMK2-YFP in the section above, except two rounds of fitting were done with the Output-Fluorescence and dose response data of pGYP7-YFP. Fits to the dose response were determined to be parameter sets whose least squared error was 0.8 standard deviations below the mean of the least squared error distribution. An experiment with a strain expressing pTEF1 driven Crz1*-CLASP exposed to short pulsed and continuous inputs, as described in the main text, was used to cross-validate the model fits.

Detailed exploration of model fits to the pGYP7-YFP data -

The simple kinetic model that described the pYPS1-YFP and pCMK2-YFP phenotypes produced no parameter sets for which a pulsed input generated lower gene expression output than a continuous input (Figure S6A). Hence, we explored model elaborations, introduced in the previous section, of the simple promoter switching model.

We first tested whether the two-state models with either k_off or k_on thresholding (Figures S6C and S6D), or the cooperative model (Figure S6B), could generate a promoter that responded with higher gene expression to continuous pulses. The rationale here was that if the promoter spent some time below its threshold of activation for any input, then the effect of this TF concentration thresholding would be smaller for a continuous pulse that does this once, than for a sequence of short pulses where this would be done repeatedly. In agreement with this intuition, this suite of models was able to generate Output-Fluorescence plots that mirrored the pGYP7-YFP experimental data for many parameters (Figures S6B-S6D, left middle panel). Figure S6D shows an illustrative example of this class of models, where many parameters sets (380) were shown to maximize fits through the data points within the error bars (Figure S6D, left middle panel). Upon further fitting with independently-obtained dose response data for pGYP7-YFP (obtained in the same way as explained above for pYPS1-YFP and pCMK2-YFP), this model however failed to fit the data, as did all models with only two promoter states (Figures S6B-S6D, middle right panel). The failure of these models to fit the pGYP7-YFP dose response showed a characteristic pattern – while the pGYP7-YFP dose response was linear in the TF regime we measured, the computationally predicted dose response was thresholded given the model structure we imposed (Figures S6B-S6D, middle right panel).

Next, we increased the complexity of the model by adding a second layer of promoter transitions to generate the 3-state model (Figure S6F). This model had the same linear structure as the two-state promoter model of Figure 4, and hence could not produce higher gene expression in response to continuous input over the pulsed one (Figure S6F).

We also tested whether a 3-state model with r_off threshold but no linear TF dependence on k_on could produce better fits (Figure S6E). This model was indeed able to generate Output-Fluorescence plots that match the pGYP7-YFP experimental data (423 parameter sets within error) (Figure S6E, middle left panel), but with these parameters, it again produced a thresholded dose response that failed to fit that of pGYP7-YFP (Figure S6E, middle right panel).

Following these results, we reasoned that the introduction of a linear dependence on TF concentration in the immediate step before promoter activation could mitigate the effects of a threshold on an earlier promoter transition step, therefore producing a linear dose response. Hence, the 3-state model with r_off threshold was tested (Figure 6A and S6I). With this addition, the model was able to generate Output-Fluorescence plots that maximized fit to the experimental data for many parameters (96 parameter sets) and for a subset of those (25 parameter sets), was also able to recapitulate the pGYP7-YFP dose response (Figures 6A and S6I, middle right panel). The 3-state model with r_on threshold was similarly able to recapitulate the data (Figure S6H), albeit with a poorer fit for the Output-Fluorescence plot. Finally, we tested the 3-state model with linear TF dependence of r_on and k_on (Figure S6G). This model was also able to produce qualitative fits to the Output-Fluorescence plot (Figure S6G, middle left panel) and dose response data (Figure S6G, middle right panel).

To further test these three successful models and also further invalidate the discarded models, we subjected them to cross-validation using an independent experiment in a strain where Crz1*-CLASP expression was increased (now expressed from pTEF1 instead of pADH1). We subjected these cells to either short pulses (2 minutes ON/10 minutes OFF) or a continuous input (40 minutes of light) in a timespan of 4 hours, and measured pGYP7-YFP levels at 5 hours. These data revealed that the higher gene expression in response to continuous input was still preserved at the higher pTEF1 expression level. All discarded models (Figure S6, right panels) were inconsistent with these data, predicting instead a reversal of the phenotype with an increase in the TF concentration. Notably, the 3-state model with linear TF dependence of r_on and k_on (Figure S6G, right panel) also failed this cross-validation because the dependence on TF caused the rate of transition from p₀ to p_off to increase with increased TF, and thus the higher gene expression in response to continuous inputs could only be produced for relatively low TF concentrations. Hence, only two minimal models were able to explain all the data we collected (Figures S6H, S6I, and 6B-6D).

QUANTIFICATION AND STATISTICAL ANALYSIS

Nuclear Localization Quantification

The software tool “ilastik” was used for image segmentation to determine nuclear fluorescence (Sommer et al., 2011). Time lapse images of the IRFP nuclear marker were used to identify nuclei objects for strains with iRFP nuclear marker. Otherwise, the 5% brightest pixels per cell were denoted as the nucleus. Nuclear fluorescence of each nucleus was defined as the mean pixel intensity of this nucleus. Cell tracking of nuclear/cytoplasmic enrichment was done using automated yeast cell tracking software implemented in Matlab (Doncic et al., 2013). Photobleaching was corrected for cells that underwent constant illumination and frequent imaging. This correction was done by fitting an exponential decay function to each nuclear and cytoplasmic trace and then dividing each trace by its decay function. For all microscopy analysis, “nuclear/cytoplasmic enrichment” represented the mean pixel intensity of the nucleus divided by the mean pixel intensity of the cytoplasm, and “fold change” represented division by the value of the signal at t=0. Nuclear localization duration was defined as the time from light ON to the time when the nuclear/cytoplasmic enrichment has returned to 75% of the starting (t=0) value. Normalized peak-trough difference was quantified across all pulses for single cell traces, and represented the difference between the local maximum (the peak) and the local minimum (the trough) values divided by the maximum peak-trough difference in the population-averaged traces.

Flow Cytometry Quantification

All analysis of flow cytometry data was performed in Python 2.7 using the package FlowCytometryTools or Matlab using custom scripts. Fluorescence values were calculated using the height (H) measurement for the appropriate channel and normalized to cell size by dividing by side scatter (SSC-H).

Growth Assays Quantification

Data was analyzed in Python 2.7 or Matlab using custom scripts. To quantify log phase growth rate, only the OD600 measurements which were between. 1 and 1 for each strain were used. A linear regression was then fit to the natural logarithm of the log phase OD600 values (as y) and time (as x). The slope from this regression was plotted as the log phase growth rate.

RNA Sequencing Quantification

Genomic alignment was performed using STAR (Dobin et al., 2013), using the UCSC S. cerevisiae annotation file. Log counts were calculated using the variance stabilizing transform from DESeq2 (Love et al., 2014). For more details on quantification, please see Mace et al, 2020 on bioRxiv. Hierarchical clustering using Matlab was performed on the normalized counts from the RNA sequencing.

ChIP-seq Analysis from Published Literature

A ChIP-seq dataset (Sen et al., 2015) and TSS dataset (Malabat et al., 2015) were used to identify the nucleosome occupancy of Crz1 target genes. The SRA toolkit was used to convert .sra files to .fastq files. The ChIP-seq data was then aligned using STAR (Dobin et al., 2013) and then further processed and visualized using Deeptools (Ramírez et al., 2014).

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Histone H3 Antibody (mAb)	Active Motif	Cat No. 39064
Bacterial and Virus Strains
DH5alpha (competent cells)	Macrolab	https://qb3.berkeley.edu/macrolab/
MACH1 (competent cells)	Macrolab	https://qb3.berkeley.edu/macrolab/
Biological Samples
None
Chemicals, Peptides, and Recombinant Proteins
Conconvalin A	Sigma-Aldrich	Cat No. C2272
YNB w/o AA	BD Difco	Cat No. 233520
Glucose	Sigma-Aldrich	Cat No. D9434
Ammonium sulfate	Sigma-Aldrich	Cat No. 7783-20-2
Sorbitol	Sigma-Aldrich	Cat No. S1876
YNB w/o AA & ammonium sulfate	Life Sciences	Cat No. Y2030-02
Calcium chloride	Fisher Scientific	Cat No. 50995817
Complete supplement mixture	MP Biomedical	Cat No. MP114560122
Dextrose	Sigma-Aldrich	Cat No. 50-99-7
Yeast extract	Alfa Aesar	Cat No. 26769
Peptone	BD Biosciences	Cat No. 211677
Penicillin-Streptomycin (10,000 U/mL)	Thermo Fisher Scientific	Cat No. 15140122
Formaldehyde	Thermo Fisher Scientific	Cat No. 28908
20X TBS, pH 7.4	Teknova	Cat No. T1680
Glycine	Fisher Scientific	Cat No. BP381
Phenol-Chloroform	Thermo Fisher Scientific	Cat No. AM9720
TE Buffer	Fisher Scientific	Cat No. BP24771
Critical Commercial Assays
Quantseq 3’ mRNA-seq library prep kit FWD for Illumina	Lexogen	https://www.lexogen.com/quantseq-3mrna-sequencing/#quantseqdescription
Agilent RNA 6000 Pico Kit	Agilent Technologies	Cat No. 5067-1513
Qubit dsDNA HS Assay Kit	Thermo Fisher Scientific	Cat No. Q32851
Deposited Data
CLASP-Crz1 Data	This manuscript	http://dx.doi.org/10.17632/jxjnjmmj83.1
Experimental Models: Cell Lines
None
Experimental Models: Organisms/Strains
Strain list, see Table S2	This manuscript	N/A
Oligonucleotides
None
Recombinant DNA
Plasmid list, see Table S3	This manuscript	N/A
Software and Algorithms
Matlab	Mathworks	https://www.mathworks.com/downloads/
uManager	uManager	https://micro-manager.org/
ilastik	ilastik	https://www.ilastik.org/
FlowCytometryTools	Python	https://pypi.org/project/FlowCytometryTools/
Python 2.7.12	Python	https://docs.conda.io/projects/conda/en/latest/user-guide/install/index.html
LabView	National Instruments	https://www.ni.com/en-us/shop/labview/upgrade.html
STAR	Dobins 2013	https://github.com/alexdobin/STAR
DESeq2	Love 2014	https://bioconductor.org/packages/release/bioc/html/DESeq2.html
SRA Toolkit	NCBI	https://www.ncbi.nlm.nih.gov/sra/docs/toolkitsoft/
deepTools	deepTools	https://deeptools.readthedocs.io/en/develop/
Arduino IDE	Arduino	https://arduino.en.softonic.com
CLASP-Crz1 Code	This manuscript	https://github.com/lindseyo/CLASP-Crz1
Other
PhosphoGRID	PhosphoGRID - Mike Tyers	https://phosphogrid.org/
CYCLoPs	University of Toronto - Andrews Lab	https://thecellvision.org/cyclops/

Highlights.

• CLASP, an optogenetic tool, translocates TFs to the nucleus with minute-level resolution

• Crz1 genes show different expression for pulsatile or continuous Crz1-CLASP inputs

• Modeling reveals quantitative promoter features required for TF input decoding

• Two- and three-state promoter models explain differential gene expression