Identifying Modifiable Predictors of Patient Outcomes after Intracerebral Hemorrhage with Machine Learning

Abstract

Background/Objective:

Demonstrating a benefit of acute treatment to patients with intracerebral hemorrhage (ICH) requires identifying which patients have a potentially modifiable outcome, where treatment could favorably shift a patient’s expected outcome. A decision rule for which patients have a modifiable outcome could improve the targeting of treatments. We sought to determine which patients with ICH have a modifiable outcome.

Methods:

Patients with ICH were prospectively identified at two institutions. Data on hematoma volumes, medication histories, and other variables of interest were collected. ICH outcomes were evaluated using the modified Rankin Scale (mRS), assessed at 14-days and 3-months after ICH, with “good outcome” defined as 0–3 (independence or better) and “poor outcome” defined as 4–6 (dependence or worse). Supervised machine learning models identified the best predictors of good vs. poor outcomes at Institution 1. Models were validated using repeated five-fold cross-validation as well as testing on the entirely independent sample at Institution 2. Model fit was assessed with area under the ROC curve (AUC).

Results:

Model performance at Institution 1 was strong for both 14-day (AUC of 0.79 [0.77, 0.81] for decision tree, 0.85 [0.84, 0.87] for random forest) and 3-month (AUC of 0.75 [0.73, 0.77] for decision tree, 0.82 [0.80, 0.84] for random forest) outcomes. Independent predictors of functional outcome selected by the algorithms as important included hematoma volume at hospital admission, hematoma expansion, intraventricular hemorrhage, overall ICH Score, and Glasgow Coma Scale. Hematoma expansion was the only potentially modifiable independent predictor of outcome and was compatible with “good” or “poor” outcome in a subset of patients with low hematoma volumes, good Glasgow Coma scale and premorbid modified Rankin Scale scores. Models trained on harmonized data also predicted patient outcomes well at Institution 2 using decision tree (AUC 0.69 [0.63, 0.75]) and random forests (AUC 0.78 [0.72, 0.84]).

Conclusions:

Patient outcomes are predictable to a high level in patients with ICH and hematoma expansion is the sole modifiable predictor of these outcomes across two outcome types and modeling approaches. According to decision tree analyses predicting outcome at 3-months, patients with a high Glasgow Coma Scale score, less than 44.5 mL hematoma volume at admission, and relatively low premorbid modified Rankin Score in particular have a modifiable outcome and appear to be candidates for future interventions to improve outcomes after ICH.

Intracerebral hemorrhage (ICH) is the most morbid form of stroke and has no specific treatment.¹ Patient outcomes after ICH are predictable with severity of injury scores, which generally include clinical severity (e.g., Glasgow Coma Scale) and neuroimaging (e.g., hematoma volume). The ICH Score, a composite prognostic scale, is predictive of functional outcome at hospital discharge and follow-up.^2,3 Other severity of injury scales are similar, despite slight differences in accuracy.^4,5 However, severity of injury scales for ICH identify neither modifiable predictors of outcome nor patient subgroups who might benefit from treatment. Improved techniques to identify patients with modifiable outcome are needed to select patients most likely to benefit from treatments.

Most interventions improve patient outcomes in some subgroups of patients more than others. Therefore, if a treatment is administered to a group of patients in which a substantial subgroup has a non-modifiable poor outcome, the treatment will be deemed ineffective. Previous attempts to improve outcomes after ICH included reducing inflammation (e.g., deferoxamine),^6,7 surgical drainage (e.g., MISTIE III),^8,9 and reducing hematoma expansion (e.g., FAST trials of Factor VII).^10,11 The inclusion of patients with ICH who were highly unlikely to have a good outcome with any putative treatment (e.g., hematoma volume >60 mL) in previous trials to reduce hematoma expansion may have obscured the benefit that was realized in those with modifiable outcomes, despite rapid initiation of therapy and hemostatic efficacy.^12,13

Previous studies on severity of injury scales in ICH have relied on regression models to identify outcome predictors. While regression models (e.g., logistic regression) identify the contribution of independent predictors toward an outcome in the entire cohort, they do not readily identify subgroups in the cohort, which must be identified post-hoc, which form the basis for a subsequent trial.¹⁴ To identify subgroups, decision-tree based methods are more intuitive and appropriate, as they operate by segmenting the observations into subgroups that maximize differences between groups. This enables group-assignment predictions to be easily made in different subgroups of patients, which is the goal of the current study.

Identifying effective ICH therapies may depend on the ability to determine which subgroups of patients have a potentially modifiable outcome to focus on patients most likely to benefit. Our objective was to identify independent predictors of outcomes in ICH that are potentially modifiable to select patients for targeted treatment.

MATERIALS AND METHODS

Study Overview

This study included the same patients as a previous study.¹⁵ In brief, patients with spontaneous acute ICH were prospectively identified and enrolled in a registry between 2006 and 2016 at two unrelated institutions. ICH cases were diagnosed using CT by a board-certified neurologist and patients were admitted to the ICU. Data were subsequently collected from patients, including Glasgow Coma Scale (GCS) scores, hematoma volume, hematoma expansion, demographics, and pre-ICH modified Rankin Scale (mRS) scores. The mRS, an ordinal scale from 0 (no symptoms) to 6 (death) was obtained at 14-day (or hospital discharge, whichever came first) and at 3-months follow-up, as previously reported. “Good outcome” was defined as mRS 0 – 3 (independence or better) and “poor outcome” as mRS 4–6 (dependence or death). This dichotomization has previously been implemented for trials with ICH patients^16,17 and represents a common method of analyzing mRS results that can be implemented in binary classification algorithms.¹⁸ Aspirin use was coded as over-the-counter use or as directed by a physician, and is a predictor of hematoma expansion and the mRS in patients with ICH.¹⁹ Other variables were selected based on a combination of theoretical associations with ICH patient outcomes and the pattern of missingness across variables. Only complete observations were used in the final analyses, which meant that variables with large amounts of missingness were not included. In total, 19 features were included in the analyses for Institution 1.

The analyses for this project can be broken into two main stages. In the first stage of analysis, we trained models on a single cohort of patients from Northwestern Memorial Hospital (Institution 1). Model construction was completed using a five-fold cross-validation framework replicated ten times with random splitting, with nested cross-validation within each of the outer folds implemented for parameter tuning. The outer fold of the cross-validation was used to estimate out-of-sample performance and to select parameters, which were then used to construct models on the entire training dataset. In the second stage of analysis, we provided further evaluation of model predictive performance by testing a representative predictive model in a cohort of patients from the Johns Hopkins Hospital and Johns Hopkins Bayview Medical Center, part of Johns Hopkins Medicine (Institution 2). At Institution 2, only discharge disposition was available (i.e., no mRS scores for Institution 2), so discharge disposition was used instead, as this outcome was present in both datasets. Discharge at both institutions corresponded to “good outcome” (discharged to home or rehabilitation) or “poor outcome” (discharged for long term acute care, nursing facility, or death).

In order to estimate model performance on unknown data, we implemented the abovementioned five-fold cross-validation framework. In this approach, the dataset is split into five equally sized parts, hereafter referred to as a “fold.” Subsequently, one of the folds is temporarily designated the “test” or “validation” fold (i.e., the data on which a model is evaluated) and the observations within that fold are left out of the model construction process. The observations in the remaining four folds of the dataset then serve as the training data (i.e., the data on which the model is built) and model construction proceeds on these data without the inclusion of the observations in the test fold. Upon completion of model training, the final model is evaluated on the data in the test fold, producing predictions that are entirely separated from the model-construction process. Once the model is evaluated on the test fold, a new fold is selected as the test fold and the other four folds—including the fold that was previously the test fold—are considered the training data for a new round of model construction. This process continues until each of the five folds has been considered the test dataset once. As a result of the cross-validation procedure, predictions are made for each of the observations in the dataset based on models that maintain training-test separation. In other words, the models are not built and evaluated on the same observations, thus reducing overfitting and enhancing the potential generalizability of the results beyond training data. Within a given loop, parameter tuning occurred through a separate cross-validation procedure. This form of nested cross-validation ensures that the same separation between training and test data implemented for generalization predictions applies to the process of parameter tuning, thus reducing the bias of the models towards the training data.²⁰ The cross-validation process was repeated ten times with different splits each time to reduce the likelihood that a given split improperly influenced the results.

In addition to the repeated cross-validated analyses, we went one step further in the second stage of analysis, isolating an additional dataset on which to test the models built on the data from Institution 1. We did this additional step as a further test of generalizability, as there could be characteristics of Institution 1 shared across folds that might artificially enhance confidence in the generalizability of our results. By testing our models on data from a separate institution, we alleviate this concern, as characteristics that are shared amongst patients at Institution 1 may be less likely to be shared with patients at Institution 2. In summary, we used five-fold cross-validation from Institution 1 to construct models, and subsequently used the dataset from Institution 2 as a pure test set drawn from a different sample of patients.

Algorithms

To identify the independent predictors of good or poor outcome, we used decision tree-based algorithms to automatically classify subjects, based on values of the independent variables. Specifically, the algorithm automatically selected the binary splits on variable values that led to the largest reduction in the Gini Impurity index—a measure of impurity within nodes in a tree, with smaller values indicating observations that are more likely to be a part of a shared class—at a given step along the tree.²¹ Node splits were determined using a standard binary recursive partitioning algorithm, splitting the dataset into two groups at each node in a recursive manner and selecting the split on a variable’s values among all possible variables that led to the largest Gini decrease. The decision trees were overgrown and subsequently pruned using a cost-complexity pruning parameter determined by using nested cross-validation and selecting the value of the complexity parameter that led to the overall highest average cross-validated area under the receiver operating characteristic curve (AUC). AUC is a single numerical value to quantify the relationship expressed in the ROC curve, which represents the relationship between the false positive and true positive rates across a variety of probability cutoffs. In concrete terms, AUC represents the probability that, when looking at two randomly chosen observations known to be from the “poor” and “good” outcome groups, the “good” outcome example will be more likely to be classified as “good” than the “poor” outcome. Final model performance was quantified using AUC across all models. Decision tree algorithm results can be visualized by a diagram in which each variable split is represented by branches that segment the sample into increasingly smaller partitions according to specific variable values.

To increase the confidence in our results, we also performed a random forest analysis, which is an ensemble method that includes bootstrapping and averaging multiple decision trees to build a more powerful predictive model.^22,23 Random forest algorithms construct many possible trees by sampling observations with replacement from the overall sample and building decision trees based on these bootstrapped samples. Trees are de-correlated from each other by a process of randomly sampling variables at each node split, meaning that individual trees could be based on different sets of predictor variables. Results from these trees are averaged together to create a final model that uses the information from all constituent trees to make a classification decision. The final model classifies individual observations according to a majority vote process, meaning that each observation is assigned to the category that it was assigned in the majority of the constituent trees. As this is a “black box” method, the individual steps in the random forest process cannot be illustrated in the same format as an individual decision tree. However, variables important to the overall model performance can be summarized across the constituent trees. Predictions from random forest models tend to be more generalizable as they are less prone to the overfitting that can occur in individual decision trees.

We further tested decision tree and random forest algorithms in data from 206 patients from Institution 2 to test generalizability of the model. As machine learning algorithms mandate identical variables across training and testing samples and there is not a standardized set of variables collected on all ICH patients at every institution, this meant that some amount of variable harmonization was necessary before the algorithm could be tested on the independent dataset. Thus, variables between Institution 1 and Institution 2 were harmonized to ensure the same meaning (e.g., the same definition and measurement of hematoma expansion across institutions)²⁴ so that models trained on variables from Institution 1 could be applied to predict outcomes from observations in Institution 2. This harmonization process involved considering each of the variables across both datasets that were identical in essence, if not identical in measurement and changing the measurements of the variable to match across datasets. For example, both Institution 1 and Institution 2 had a measure of hematoma expansion; however, Institution 1 measured expansion as a continuous variable in milliliter units, while Institution 2 measured the presence of hematoma expansion as a true/false dichotomous variable using a previously validated definition.²⁴ For harmonization, hematoma expansion at Institution 1 was re-coded to match the definition at Institution 2. A similar process was conducted across the other variables, with each one changed so that measurements were identical across both datasets. Of note, Institution 2 did not have mRS scores, meaning the outcome variable across datasets was different than described previously. Specifically, the outcome used in both cases was the disposition of the patient at hospital discharge. “Good” disposition was described at both institutions as being discharged to one’s home or to rehab; “Poor” disposition was described as including long-term accurate care, nursing facility, or death. In total, 15 features were included in the analyses for Institution 2. Decision tree and random forest models were then derived as described above for Institution 1, and tested in data from Institution 2.

We used standard statistical software to construct decision trees (R package “rpart”²⁵) and random forests (R package “randomForest”²⁶) implemented in R version 3.5.3²⁷. We implemented five-fold nested cross-validation to optimize parameters and minimize overfitting (a model that is more accurate in the data from which it is derived because it fits noise in addition to signal) using the tuning framework from the “caret” package in R²⁸ for both the decision tree and random forest algorithms. An overfit model would tend to be predictive in the training cohort, but not in external data, as these models fit random variation in addition to true relationships in the data. Pruning of trees was explored to further reduce the likelihood of overfitting.

Standard Protocol Approvals, Registrations, and Patient Consents

The study was approved by the institutional review board (IRB). Written informed consent was obtained from the patient or a legally authorized representative. The IRB approved a waiver of consent for patients who died during initial hospitalization and those who were incapacitated and for whom a legal representative could not be located. Separately, identification of patients and collection of data in the Hopkins cohort were approved by the Johns Hopkins IRB.

Data Sharing

Qualified investigators who wish to reproduce the analysis or utilize the code should contact the corresponding author.

RESULTS

Demographics of the cohort are shown for the 278 included ICH patients from Institution 1 (Table 1a) and the 206 included ICH patients from Institution 2 (Table 1b) stratified by outcome. From Institution 1, the decision tree algorithm selected initial hematoma volume, hematoma expansion, intraventricular hemorrhage (IVH), and Glasgow Coma Scale (GCS) scores as the most important predictors of 14-day outcome at each node, where variable importance is defined as the relative reduction in the loss of function of a variable at each node across the overall tree.²⁵ The model to predict good or poor patient outcome at 3-months was similar, with most important variables chosen being Glasgow Coma Scale (GCS) scores, hematoma volume at admission, and hematoma expansion. The decision tree for prediction of outcomes at 3-months can be found in Figure 1. Hematoma expansion is the only modifiable outcome that can impact predicted outcomes in this tree. Of particular note is a subset of patients who have a GCS score of 13 or higher, hematoma volume at admission less than 44.5 mL, and premorbid modified Rankin Scale score of less than 4. For these patients, hematoma expansion is a critical predictor of outcome, with hematoma expansion greater than 6.65 mL leading to the prediction of poor outcome for 5% of the total sample (10 patients). These patients may be of particular interest for future clinical intervention.

Table 1a.

Characteristics of the 278 Patients from Institution 1, stratified by “poor” (mRS 0–3) and “good” (mRS 4–6) outcomes. Percentages are rounded to the nearest whole number. Footnotes are provided by variable names to indicate significant differences in medians between groups at an α level of .05 using Mood’s median test using the “RVAideMemoire” package in R³³.

		“Poor” outcome N = 204	“Good” Outcome N = 74
Variable	Details	N (%) or Median [IQR]
Age, Years1	Continuous	66 [55.75 – 77.25]	60 [49.25 – 70.00]
Gender	Categorical
Male		90 (44.1)	43 (58.1)
Female		114 (55.9)	31 (41.9)
Race	Categorical
White		104 (51)	38 (51.4)
Black or African American		91 (44.6)	30 (40.5)
Asian		3 (1.5)	2 (2.7)
Native Pacific Islander		4 (2)	4 (5.4)
American Indian/Native Alaskan		0 (0)	0 (0)
Not Reported		2 (0.9)	0 (0)
ICH Score, Total	Ordinal
0		39 (19.1)	45 (60.8)
1		61 (29.9)	24 (32.4)
2		53 (26)	5 (6.8)
3		34 (16.7	0 (0)
>=4		17 (8.3)	0 (0)
Glasgow Coma Scale	Ordinal
13–15		111 (54.4)	68 (91.9)
5–12		73 (35.8)	6 (8.1)
3–4		20 (9.8)	0 (0)
Intraventricular Hemorrhage	Categorical
Yes		105 (51.5)	9 (12.2)
No		99 (48.5)	65 (87.8)
Large Hematoma Volume	Categorical
At least 30 cc		56 (27.5)	2 (2.7)
Less than 30 cc		148 (72.5)	72 (97.3)
Initial Hematoma Volume, mL2	Continuous	12 [6.0 – 30.00]	4 [1.4 – 11.35]
Located in Infratentorial Region	Categorical
Yes		24 (11.8)	10 (13.5)
No		180 (88.2)	64 (86.5)
Hematoma Expansion, mL3	Continuous	0.185 [−1.23 – 3.05]	−0.10 [−0.38 – 0.28]
Seizure	Categorical
Has had a seizure		10 (4.9)	3 (4.1)
Has not had a seizure		194 (95.1)	71 (95.9)
Reversal of Anticoagulation	Categorical
Presence of reversal		14 (6.9)	5 (6.8)
No reversal		190 (93.1)	69 (93.2)
Desmopressin	Categorical
Given		29 (14.2)	9 (12.2)
Not given		175 (85.8)	65 (87.8)
Historical Modified Rankin,	Ordinal
0		151 (74)	62 (83.8)
1		18 (8.8)	7 (9.4)
2		7 (3.4)	3 (4.1)
3		8 (3.9)	2 (2.7)
4		19 (9.3)	0 (0)
5		1 (0.5)	0 (0)
Novel Oral Anticoagulant	Categorical
Given		0 (0)	1 (1–4)
Not given		204 (100)	73 (98.6)
Warfarin Use	Categorical
Usage		23 (11.3)	5 (6.8)
No usage		181 (88.7)	69 (93.2)
International Normalized Ratio	Continuous	1.1 [1 – 1.2]	1.1 [1 – 1.2]
Statin	Categorical
Usage		33 (16.2)	11 (14.9)
No usage		171 (83.8)	63 (85.1)
Aspirin Use Prior to ICH	Categorical
Usage		70 (34.3)	24 (32.4)
No usage		134 (65.7)	50 (67.6)
Diabetes by History	Categorical
Diagnosis		35 (17.2)	15 (20.3)
No diagnosis		169 (82.8)	59 (79.7)
Hypertension by History	Categorical
Diagnosis		148 (72.5)	52 (70.3)
No diagnosis		56 (27.5)	22 (29.7)

¹χ² (1, 278) = 4.68 , p = .03

²χ² (1, 278) = 17.46 , p < .001

³χ² (1, 278) = 8.12 , p = .004

Table 1b.

Characteristics of the 206 Patients from Institution 2, broken out into “poor” (discharged to acute care or death) and “good” (discharged to home or rehab) outcomes. Footnotes are provided by variable names to indicate significant differences in medians between groups at an α level of .05 using Mood’s median test using the “RVAideMemoire” package in R³³.

		“Poor” Outcome N = 105	“Good” Outcome N = 101
Variable	Details	N (%) or Median [IQR]
Age, years	Continuous	62 [54 – 80]	59 [51 – 69]
Gender	Categorical
Male		63 (60)	58 (57.4)
Female		42 (40)	43 (42.6)
Race	Categorical
White		60 (57.1)	38 (37.6)
Black or African American		44 (41.9)	61 (60.4)
Asian		1 (1.0)	1 (1.0)
Hispanic		0 (0)	1 (1.0)
ICH Score, Total	Ordinal
0		12 (11.4)	38 (37.6)
1		20 (19)	38 (37.6)
2		31 (29.5)	19 (18.8)
3		34 (32.4)	5 (5)
>=4		8 (7.7)	1 (1)
Glasgow Coma Scale	Ordinal
13–15		49 (46.7)	83 (82.2)
5–12		6 (5.7)	6 (5.9)
3–4		50 (47.6)	12 (11.9)
Intraventricular Hemorrhage	Categorical
Yes		54 (51.4)	27 (26.7)
No		51 (48.6)	74 (73.3)
Large Hematoma Volume	Categorical
At least 30 mL		42 (40)	15 (14.9)
Less than 30 mL		63 (60)	86 (85.1)
Initial Hematoma Volume, mL4	Continuous	22 [6 – 47]	8 [4 – 19]
Hematoma Location	Categorical
Infratentorial		21 (20)	18 (17.8)
Supratentorial		84 (80)	83 (82.2)
Hematoma Expansion	Categorical
Presence		18 (17.1)	8 (7.9)
Absence		87 (82.9)	93 (92.1)
Seizure	Categorical
Has had a seizure		15 (14.3)	6 (5.7)
Has not had a seizure		90 (85.7)	95 (90.5)
Warfarin or Novel Oral Anticoagulant	Categorical
Given		11 (10.5)	8 (7.9)
Not given		94 (89.5)	93 (92.1)
International Normalized Ratio	Continuous	1.1 [1 – 1.2]	1.1 [1 – 1.1]
Statin	Categorical
Usage		26 (24.8)	25 (24.8)
No usage		79 (75.2)	76 (75.2)
Aspirin Use Prior to ICH	Categorical
Usage		36 (34.3)	37 (36.6)
No usage		69 (65.7)	64 (63.4)
Diabetes by history	Categorical
Diagnosis		30 (28.6)	12 (11.9)
No diagnosis		75 (71.4)	89 (88.1)
Hypertension by history	Categorical
Diagnosis		86 (81.9)	82 (81.2)
No diagnosis		19 (18.1)	19 (18.8)

⁴χ² (1, 206) = 15.23 , p < .001

Figure 1.

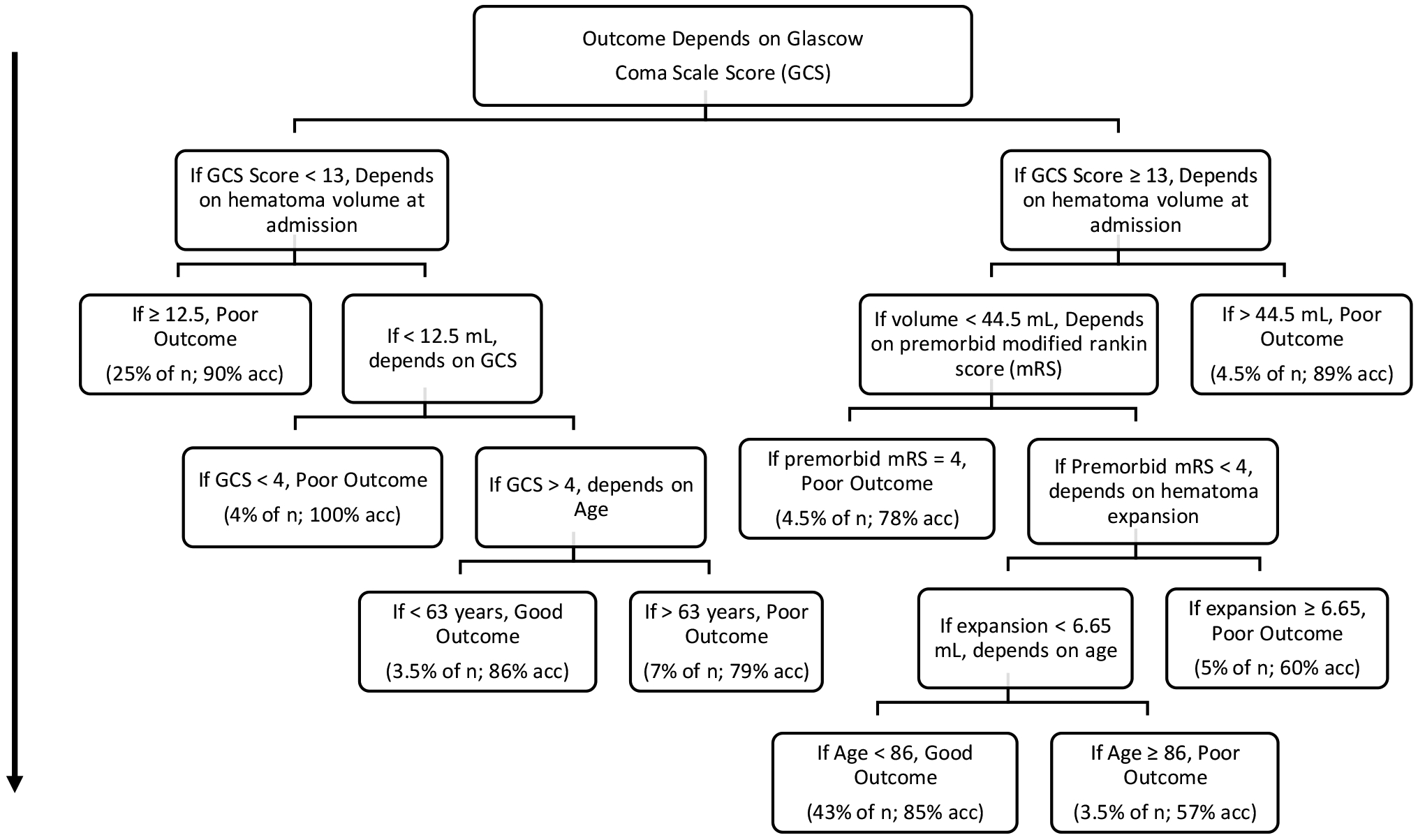
Decision tree predicting good or poor outcome at 3-months, fit on the entire training dataset after repeated five-fold cross-validation to tune parameters and estimate model performance. Classification starts at the top and each observation works its way down the branches until it hits a terminal node (i.e., node in which there are no further nodes going down). At this point, the observation is classified as either Good Outcome or Poor Outcome. Percentages of the total sample size are included in the terminal nodes to represent the number of observations in a given node, with the percentage of these observations that are accurately classified following a semicolon. This decision tree is provided to illustrate what one of the algorithms selected as the best way to classify patients at discharge and is not recommended for prescriptive use without further testing.

Random forest models performed better than the decision trees across both outcome types in Institution 1. The cross-validated performance (measured using AUC) of decision tree and random forest algorithms on the validation data from Institution 1 are shown in Table 2, along with 95% confidence intervals (CIs) derived using stratified bootstrap resampling. For 14-day outcomes, the AUC for the decision tree approach was 0.79, with a 95% CI of [0.77, 0.81], compared to an AUC of 0.85 and a 95% CI of [0.84, 0.87] for the random forest. For 3-month outcomes, the AUC for the decision tree approach was 0.75, with a 95% CI of [0.73, 0.77], compared to an AUC of 0.82 with a 95% CI of [0.80, 0.84] for 3-month outcomes. Accuracy rates assuming a 50% classification cutoff point are provided in Table 3, along with proportional confusion matrix information.

Table 2.

Area under the receiver operating characteristic curve (AUC) by each model in Institution 1. 95% Confidence Intervals derived via 5000 stratified bootstrap replications are included below each AUC value, calculated using the pROC package in R³⁵.

Model Type	14-Day Decision Tree	14-Day Random Forest	3-Month Decision Tree	3-Month Random Forest
AUC	0.79	0.85	0.75	0.82
95% CI:	[0.768, 0.807]	[0.838, 0.867]	[0.728, 0.771]	[0.800, 0.836]

Table 3.

Proportional confusion matrix information for all four models after 5-fold cross-validation repeated 10 times. Accuracy is provided at the default classification cutoff point of 0.50, rounded to the nearest hundredth. Matrix information is provided in terms of average proportions of cell counts across resamples. For example, a true positive value of .50 would suggest that on average across resamples 50% of the observations were classified as positive cases when in fact they were positive cases (i.e., they were classified correctly). Positive classification in this case refers to a classification of “Good Outcome,” while negative refers to “Poor Outcome.” The summation of true positives and true negatives equals the accuracy, which is presented at the top alongside the corresponding 95% confidence interval.

Model Type:	14-Day Decision Tree	14-Day Random Forest	3-Month Decision Tree	3-Month Random Forest
Accuracy	0.745	0.787	0.720	0.730
95% CI:	[0.728, 0.761]	[0.771, 0.802]	[0.699, 0.739]	[0.710, 0.750]
True Positive Proportion:	.138	.108	.350	.371
True Negative Proportion:	.607	.679	.369	.359
False Positive Proportion:	.127	.054	.143	.153
False Negative Proportion:	.128	.158	.137	.117

Models also weighted similar variables as being important for inclusion, as determined from the variable importance values produced by both modeling approaches. To predict good or poor outcome at 14-days, both decision tree and random forest algorithms selected hematoma volume at admission, hematoma expansion, Intraventricular Hemorrhage (IVH), GCS scores, and age as the most important predictors. To predict good or poor outcome at 3-months, the algorithm selected GCS score, hematoma volume at admission, hematoma expansion, age, premorbid mRS scores, and IVH as the most important variables. There was remarkable consistency across outcomes and modeling approaches in these importance values, suggesting generalizability across time and predictive approaches. These results can be seen in graphical format in Figure 2.

Figure 2.

Variable importance values for decision tree and random forest results predicting outcome at 14-days and 3-months.

We then turned to establishing generalizability in an independent dataset. Upon completion of variable harmonization using the process described above, data from Institution 1 were treated as the training dataset and data from Institution 2 were utilized as a test dataset. In training, the analysis procedure mimicked the analyses described above for the full Institution 1 analyses. Namely, repeated five-fold cross-validation was implemented to train both decision tree and random forest algorithms. Final models were evaluated on the test data from Institution 2. Predictions of discharge outcome in the test data resulted in an AUC value of 0.69 (95% CI: [0.63, 0.75]) for the decision tree and an AUC value of 0.78 (95% CI: [0.72, 0.84]) for the random forest model. Data on outcomes at 3-months were not available for the creation of comparison models. Similar to the models derived and validated at Institution 1, the most important variables were GCS scores, initial hematoma volume, age, and hematoma expansion. Additionally, age was an important variable in the random forest analyses.

Institution 2 did not have mRS data. In data from Institution 1, the mRS at 14-days was correlated with the mRS at 3-months (Spearman rho = 0.85, P<0.001).

DISCUSSION

We identified patients whose outcome could be either good or poor after ICH. Decision tree and random forest models consistently identified initial hematoma volume, hematoma expansion, GCS score, age, and intraventricular hemorrhage as the most important variables for the prediction of ICH outcomes at both 14-days and 3-months. Hematoma expansion was the only potentially modifiable predictor of patient outcome identified for these patients across modeling approaches and time periods. A subset of patients was identified, consisting of patients who have a GCS score of 13 or higher, hematoma volume at admission less than 44.5 mL, and premorbid modified Rankin Scale score of less than 4 (see Figure 1). These patients’ outcome depended on hematoma expansion and thus serve as a potential target for clinical intervention. In sum, across modeling approaches, datasets, and time periods, these data suggest that a subset of patients with ICH have a potentially modifiable outcome by reducing hematoma expansion.

Hematoma expansion predicts poor outcome after ICH. Most definitions of hematoma expansion have a similar predictive value (e.g., 26% of the initial hematoma volume, an absolute increase of ≥3 mL).²⁹ Clinical trials of blood pressure control,³⁰ Factor VII,^10,11 and tranexamic acid³¹ have sought to improve patient outcomes by reducing the likelihood of hematoma expansion, but have had mixed results on preventing hematoma expansion and improving the odds of good outcome. Our findings suggest that in each of the clinical trials conducted to date, many randomized patients may already have been highly likely to have a poor outcome at follow-up because of large initial hematoma volume or IVH, regardless of hematoma expansion. These results suggest that future research might further narrow eligibility for a clinical trial in order to select patients with an outcome that is potentially modifiable from poor outcome to good outcome. While we are not the first group to suggest restricting inclusion criteria for clinical trials in patients in ICH,¹³ we are suggesting an innovative method for selecting those criteria using a generalizable model from existing data sets.

Decision tree-based algorithms are different from regression models. Regression models determine the marginal attribution of variance in the data from independent variables (e.g., patient age for each additional year) on a dependent variable (e.g., good or poor outcome), and are intuitive for determining the effect of independent variables generally in a cohort. In patients with ICH, predictors of patient outcome considered in logistic regression models are unlikely to be truly independent (e.g., larger hematoma volume eventually impairs consciousness), even if interaction terms do not significantly improve a statistical model. We chose decision tree-based algorithms because they are intuitively more appropriate for subgrouping subjects, as our goal was to identify patients with a potentially modifiable outcome.

The methods described in this paper are intended to inform further mechanistic research to improve patient outcomes after ICH. Specifically, these data suggest which patients are most likely to transition from “poor” to “good” outcome, particularly for patients in whom hematoma expansion might be reduced. Additionally, these data may be helpful for prognostication after accounting for hematoma expansion, a potential improvement over scales that are measured at admission and do not account for hematoma expansion.

There are potential limitations to these data. The sample size may not be adequate to detect prognostic factors with smaller effects on functional outcome. Transitioning a patient from “poor” to “good” outcome requires a substantial effect size¹² and more sensitive patient outcomes might increase the power to detect an effect of treatment. The results of the analysis across two independent datasets somewhat allay concerns about model generalizability, as the model performed similarly even though it was arguably handicapped by the harmonization process reducing the number and specificity of the variables. The mRS is also insensitive to certain domains of function that are important from a patient’s perspective (e.g., cognitive function) and, as a result, to predictors of disability in those domains.³² We used repeated five-fold cross-validation and found very strong performance of decision tree and random forests models, as well as reasonable performance of a less-specific model on a separate dataset. Additional validation in external cohorts would be helpful, however, some of these are costly and might have different independent variables that would require reconciliation before analysis. Our results should be generalizable, however, given the efforts made to examine performance on data unimplicated in the model construction process. The cohort used in this analysis included a small proportion of patients who were known to take anticoagulant medication (warfarin or a novel oral anticoagulant) with ICH, however, the effect of anticoagulant medication is likely mediated through hematoma expansion, which is modifiable with specific treatment (e.g., prothrombin complex concentrate).³³

In sum, we found that a subset of patients with ICH has a potentially modifiable outcome. Hematoma expansion is the prominent modifiable determinant of patient outcome. Future research to develop or evaluate therapies for ICH might focus on a smaller subset of patients with potentially modifiable outcome.