Suppress, and Not Just Flatten: Strategies for Rapid Suppression of COVID19 Transmission in Small World Communities

Abstract

Many countries have introduced Lockdowns to contain the COVID19 epidemic. Lockdowns, though an effective policy for containment, imposes a heavy cost on the economy as it enforces extreme social distancing measures on the whole population. The objective of this note is to study alternatives to Lockdown which are either more targeted or allows partial opening of the economy. Cities are often spatially organized into wards. We introduce Multi-lattice small world (MLSW)  network as a model of a city where each ward is represented by a 2D lattice and each vertex in the latex represents an agent endowed with SEIR dynamics. Through simulation studies on MLSW, we examine a variety of candidate suppression policies and find that restricting Lockdowns to infected wards can indeed out-perform global Lockdowns in both reducing the attack rate and also shortening the duration of the epidemic. Even policies such as partial opening of the economy, such as Two-Day Work Week, can be competitive if augmented with extensive Contact Tracing.

Introduction

The World Health organization(WHO) on March 12, 2020 declared COVID-19 outbreak as a pandemic1. The virus first emerged in China in late December¹⁸, and since then has invaded more than 150 countries posing an unprecedented threat to global public health. As of 19th April, more than 2 million people have been infected globally and more than 100 thousand deaths have taken place. The Director of WHO recently warned that The worst is yet to come (Press). Several countries have suffered massive loss of human lives, but there are far greater number of countries where COVID19  has just arrived. The anticipated cumulative loss of lives in these countries could be apocalyptic unless urgent measures are taken. There is now a growing view among scientists (Press) and many world leaders (UN press release) that Rapid Suppression of COVID19transmission must be the way forward.

In the absence of any vaccine, governments across the globe are announcing various forms of moderate to extreme Social Distancing measures for containing this pandemic which ranges from Self-Isolation to imposing Lockdowns. Lockdown was first used in China for fighting the COVID19 pandemic. The effectiveness of such Lockdowns is still being evaluated⁶, but there is now global consensus that it is probably the best tool for containment. Despite the success of Lockdown, there are, however, growing concerns that Lockdown may have unintended consequences which could be devastating to the economy (Press). Unemployment is an inevitable outcome of economic downturn and it is no surprise that Lockdowns have resulted in significant job losses. For instance, in France, half of private sector employees have been unemployed because of Coronavirus-related Lockdown (Press). There is, thus, an immediate need for seeking effective alternatives to Lockdowns.

Targeted Social Distancing, such as isolating individuals who are in the contact network of an infected individual, fares better than Population-wide measures in treating specialized diseases¹⁰. Usually, the contact network of an individual is rarely known. However, in recent times, one can use Contact Tracing using GPS-enabled smartphones to discover the underlying contact network. Preliminary results suggest that contact tracing and Case isolation tools can help in containing COVID19 if applied very early. However, if applied even slightly later than 3 weeks, the epidemic spirals out of control^{8, 11}.

In this note, we seek to exploit the contact network of individuals to obtain a comparative assessment of various Non-Pharmaceutical Policies (NPIs) as suitable alternatives to Lockdowns when applied in the early stages of the epidemic.

A summary of the main findings is as follows

1. Cities are spatially organized into Wards. Restricting the imposition of a Lockdown to infected wards seems to be the best suppression strategy and can be more efficient than Lockdowns.

2. Opening up the economy, like a 2-Day work week, can be competitive with global lockdowns if there is extensive contact tracing.

3. Contact Tracing involves checking the state of the persons in the contact network of the suspect and then isolating them if necessary. Our empirical results suggest that this may not be as effective as Tracing the Contacts and their Contacts (TC2S). The suggested TC2S  strategy can substantially lower the attack rate, by more than 30%, over the prevalent Contact Tracing approach.

4. Apart from the study, we also contribute MLSW, a flexible mathematical model, which can be used for studying policy interventions in a city.

Disclaimer The aim of this report to make authorities aware of policy alternatives to Lockdown. The conclusions we draw are about the relative efficacy of various strategies and not about their absolute predictability. Also, our study does not consider ethical factors, issues related to civil liberties, and economic hardships of the proposed interventions.

Methods

Understanding the spread of Infectious Disease on a Network has emerged as an active area of research in Mathematical Epidemiology (see^{12, 17} for a survey). Compared to traditional compartmental models¹³, these models incorporate contact structure and are, thus, considered as more realistic for explaining epidemics. Empirical modeling of COVID19  outbreak suggests that Network-based models such as Small world networks can be a better candidate to explain the spread of the disease²². Small world networks²¹ was first introduced in epidemiology by¹ for understanding epidemic spread on networks. Since then, there has been substantial interest in using Small World Networks in modeling specialized disease outbreaks^{15, 16, 19}. To the best of our knowledge, no study has attempted to understand the spread of COVID19  on small world networks. Previously, studies of epidemic modeling on Small World Networks have used SEIR, as a compartmental model, on 1D and 2D lattice-based models⁴.

In this note, we simulate a SEIR model on a Small World network to assess several NPIs as sustainable strategies for hindering the progress of COVID19 in a city. Small world networks posit a 1D or 2D lattice structure on the entire population with occasional long edges. Such networks will miss the point that the cities are not necessarily homogeneously structured but are often organized into spatial clusters, for example, the city of London has 25 wards. The motivation for modeling the ward structure arises from the need for containment of disease at the ward level. Directing measures to target affected individuals should have the most effect in containment but unfortunately there may not be enough technological support for executing such measures. Imposing a coarse measure such as Lockdown on an entire city is unsustainable as it would face compliance issues from the broader population. Ward-level interventions may strike the right compromise in deriving sustainable containment policies. It is also to be noted that ward-wise containment policies are already being considered in several Indian cities including Bengaluru (Press). Our aim is to compare such strategies to Lockdown.

Urban Environments as Multi-Lattice Small Worlds

We develop a small world model which involves modeling a ward as a 2D lattice. The city of Bengaluru is divided into 198 wards. Neighboring wards are naturally defined and they create edges in the resulting neighborhood graph of the city. Each ward is replaced by a population between 400 and 800 people in direct proportion to the population of each ward to simulate a city of roughly (see Fig.  1) ${10}^5$ citizens.

Figure 1:

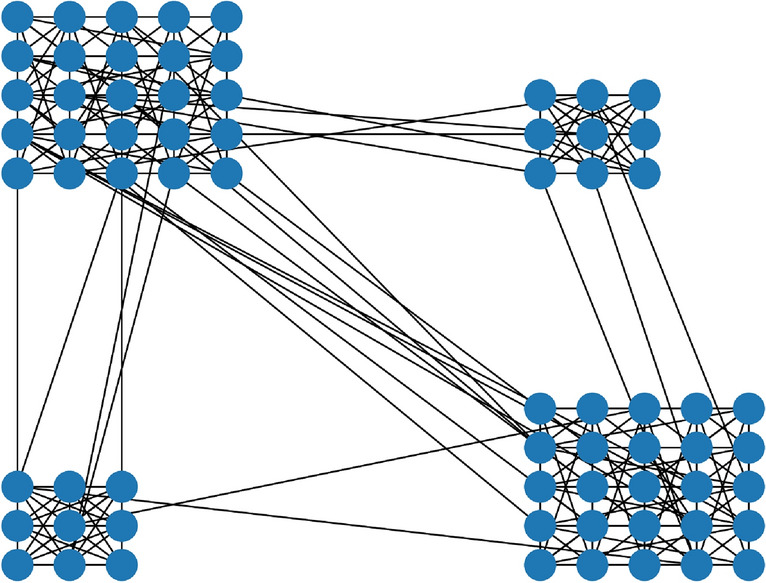
A multi-lattice small world example with four wards. Each ward is a 2D torus.

We will now describe a small world model of a city consisting of wards . At each ward, the population is a regular 2D lattice with edges to all eight neighbors. This models local spatial interaction. The lattice is also wrapped around (it is a torus) so that it has no boundary. If two wards are neighbors, $\mathbf{e}$ vertex pairs are chosen at random across the two wards and an edge is inserted across each of the five pairs. These edges model interaction between adjacent wards. This is done for every pair of neighboring wards. In this way, the graph is created. What this graphs lacks are long edges. Inspired by the small world model, we rewire an edge in this graph with probability $p_0$. We cycle through all the edges. Every edge (u, v), is rewired with probability $p_0$. Here, we choose a new vertex $v^{\prime }$ randomly from the entire graph and the edge (u, v) is replaced by this edge $(u,v^{\prime })$. These edges capture non-local contact interaction.

This procedure results in a graph which at one level contains neighborhood information of the city and at another, the small world characteristics due to the long edges. Since we have a collection of lattices in our graph (instead of one), we call it Multi-Lattice Small World (MLSW). MLSW is parametrized by $\{n_1,\dots ,n_W,\mathbf{W},\mathbf{e},p_0\}$ where $\mathbf{W}$ is the number of Lattices. A Lattice $w\in \{1,\dots ,\mathbf{W}\}$ has  $n_w$ vertices which reflects the population in the ward. Inter lattice edges are parametrized by $\mathbf{e}$ and finally $p_0$ is the rewiring probability.

The city of Bengaluru when viewed as MLSW have $W=198,\mathbf{e}=5,400\le n_w\le 800,p_0=0.1$. The resulting graph has 116, 631 vertices and 472, 319 edges. This model can be enhanced in several ways by using detailed knowledge of the city such as transportation patterns to determine the long edges. Modeling Epidemics in Urban networks is not new (see⁷ and citations therein). However, we are unaware of any work which tries to account for the ward structure. The proposed model, MLSW, is novel not only in epidemiology but also in the area of small world models. MLSWcan be viewed as a special instance of Random Spatial Networks². A detailed mathematical study comparing MLSW with such networks will be presented elsewhere. In this note, we present a simulation study for assessing different NPIs as suppression policies.

Disease Progression and Transmission

In this section, we develop an SEIR-based state model of an stochastic Agent which resides in one of the vertices of MLSW and interacts with its neighbors. The parameters of the agent are adjusted to model the progression of the disease in an individual and the interaction between the agents are modeled to suit the transmission dynamics of COVID19.

Disease Progression

We develop a state-based model for Disease Progression in an Individual based on the following assumptions based on existing literature, also summarized in Table  1.

Table 1:

Assumptions on COVID 19 Disease Progression.

Incubation period18	5 days
Onset of Symptoms after Infection20	5 days
Infected people requiring Hospitalization20	4.4 %
Hospitalized people requiring ICU20	30%
No. of days in Hospital for Severe patients20	8 days
No. of days in ICU20	10 days
IFR20	1%

Assumptions Incubation period of the virus is assumed to be 5 days. $4.4\%$ of infected patients require hospitalization in 5 days after showing signs of infection. $30\%$ of hospitalized patients may require ICU admission or ventilator access; and half of the ICU patients die.

The State Model Each vertex can be in one of the seven states. All nodes start as susceptible S, and eventually end as either dead D or recovered R. In between a vertex will be either exposed E or infected I. We have three levels of infection, mild IM, severe IS, and critical IC. The entire state transition diagram including transition probabilities is defined in Fig.  2. Based on the probabilities on the self loops, it is clear that the expected number of days to escape at nodes E, IM, IS, IC is 5, 5, 8, 10, respectively. These numbers are in tune with the number in⁵.

Figure 2:

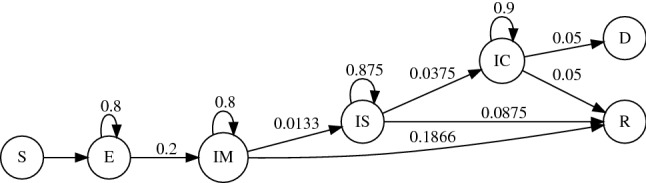
State transition diagram.

Disease Transmission

To describe the spread of the disease, we consider the following approach. When one end of an edge is infected (i.e., in state IM, IS, or IS), and the other end is susceptible S, with some probability, vertex at the other end transitions to E. This probability depends on the nature of infection and we will parameterize the probability of IM infecting a susceptible person to be ${\beta }_{\mathrm{M}}$. Similarly, we also introduce parameters ${\beta }_{\mathrm{S}},{\beta }_{\mathrm{C}}$ to measure probability of infection by a patient in state IS and IC respectively. We will calibrate $\beta ={[{\beta }_{\mathrm{M}},{\beta }_{\mathrm{S}},{\beta }_{\mathrm{C}}]}^{\top }$ to match the basic reproduction rate, $R_0$, assumed to be 2.8¹⁴.

Simulating the Progress of COVID19  on MLSW

The simulation begins by initializing the states of INDEX number of nodes to IM in MLSW. This state serves as introducing INDEX number of Index patients in the population.

A day in the Simulation consist of two steps, namely Edge Sweep and Node Sweep.

Edge Sweep All the edges in MLSW  are inspected in an arbitrary order. If edge (u, v) has one of its endpoints (say v) as susceptible S, and the other endpoint (u) as infected (there are three possibilities here: IM, IS, IC). Then, the infection will spread to v with a probability that depends on the nature of the infection at u. Let $\beta ={[{\beta }_{\mathrm{M}},{\beta }_{\mathrm{S}},{\beta }_{\mathrm{C}}]}^{\top }$ be a vector of parameters where ${\beta }_{\mathrm{M}},{\beta }_{\mathrm{S}},{\beta }_{\mathrm{C}}$ are probabilities of infecting a node with vertex S corresponding to states IM, IS, IC respectively. If the infection should spread, the new state of the node v would be exposure E.

Node Sweep All nodes of MLSW  are inspected in arbitrary order. Each node u is in one of seven states. Unless the states are in R or D where nothing happens as these are final states, in all other cases, the node transitions to a new state or stays put according to the probabilities assigned in Fig. 2. This mimics the progression of the disease in an individual.

The simulation runs through several days till there are no infected patients in the network, i.e., all states are in any one of the R, S, D states.

Model Calibration

The Edge Sweep requires $\beta$. The state transition has 11 parameters as can be read from Fig.  2. Additionally, there is the rewiring probability $p_0$. Each of these sets of parameters plays a unique role.

The rewiring probability $p_0$ determines how fast the disease can spread in the network. If the long edges are missing, we are left with lattices connected to their neighbors and this takes infection a long time to propagate. Long edges shorten this time. Even mild values of $p_0$ show rapid ability to mix. Large $p_0$ essentially results in a random graph.

The Edge Sweep parameters ${\beta }_M,{\beta }_S,{\beta }_C$ determine how fast the infection actually propagates on MLSW. The state transition matrix determines how long a person is active to infect. It also determines the death rate amongst the people who do get infected.

The lattice we have chosen has 8 neighbors corresponding to the eight immediate vertices around a fixed vertex on a 2D grid. Let us fix a vertex. It has typically 8 neighbors on an average (the specific degree will change a bit depending on the rewiring). Suppose the vertex is in state IM. Then, the probability of propagating the infection to a fixed neighbor is ${\beta }_{\mathrm{M}}$. If the number of susceptible neighbors is d then the expected number of infections is $d{\beta }_{\mathrm{M}}$. If the probability of exiting IM is ${\gamma }_{\mathrm{M}}$ (this value can be read from the state transition diagram), the number of days it takes to exit the state is $\frac{1}{{\gamma }_{\mathrm{M}}}$. This means the total number of neighbors infected in expectation is $d\frac{{\beta }_{\mathrm{M}}}{{\gamma }_{\mathrm{M}}}$. The process repeats itself for severe and critical infections but the dominant term is $d\frac{{\beta }_{\mathrm{M}}}{{\gamma }_{\mathrm{M}}}$. We now match this to the assumed value of $R_0=2.8$ to obtain ${\beta }_{0M}=0.07$. In the absence of any other data on hospital infections, we set the value of ${\beta }_{0S}=0.02$ and ${\beta }_{0C}=0.001$. Hence, we will assume that $\beta ={\beta }_0={[{\beta }_{0M},{\beta }_{0S},{\beta }_{0C}]}^{\top }$.

An important parameter to match is the Infection Fatality Rate (IFR) rate. The IFR rate is the probability of transitioning from E to D in the state transition diagram. We match IFR rate, the percentage of total infected patients match, along with active infected patients peaking around 75 days, with those of⁵. In all our simulation, $\mathtt{INDEX}$ is set to 5.

Intervention Policies for Rapid Suppression

We are seeking policy alternatives to Lockdown which can rapidly suppress the COVID19 pandemic. Lockdown measures, though extremely effective, involve extreme social distancing measures for the entire population hence making them unsustainable for long duration. Policy alternatives to Lockdowns should, therefore, seek more targeted Social distancing, or aim to limit the amount of time for continuous lockdown. Keeping this in mind we explore two kinds of strategies. The first kind of strategy, called Targeted Interventions, involve either Contact Tracing and Isolation or Hotspot-specific interventions. The second kind of strategy involves limiting the severity of Lockdowns by various means such as opening the economy for a few days in the week, or relaxing the lockdown. A list of few envisaged policies are mentioned in Table  2.

Table 2.

List of Interventions.

Policy	Type	Description
LD		Lockdown
LD(mild)	RD	Mild lockdown
FDLD	RD	40-day lockdown
TDWW + LD	RD	Two-day week followed by a strict lockdown
TC2S	TI	Tracing and sealing of neighbors and their neighbors of Infected patients
WSO	TI	Ward-level sealing and opening with different relaxation factors

TI targeted Interventions, RD relaxed LockDowns

Metrics for Evaluating Suppression Policies

Any suppression policy needs to be effective and sustainable. The effectiveness of any policy would depend on its ability to contain the infection to a small fraction of the population. Often, such measures could be extreme in nature and thus sustainability depends on the duration of the time it is enforced, shorter the better. To evaluate both these aspects, one can consider the following metrics for evaluating a policy A.

• The length of the epidemic,denoted by $T_{\text{epi}}(A)$ , is defined as the duration of the epidemic starting with few infected patients and ending when there are no infected people in the population. For sustainability purposes $T_{\text{epi}}(A)$ should be low.

• Attack rate, measured as follows

  $$\begin{array}{cc}\hfill I_{\infty }(A)=& \frac{100}{N}(\text{Number}\text{of}\text{infected}\hfill \\ \hfill & \text{people}\text{till}\text{time}{T}_{\text{epi}})\hfill \end{array}$$ 1

  Since infected people either recover or die, $I_{\infty }(A)=R_{\infty }(A)+D_{\infty }(A)$, where

  $$\begin{array}{cc}\hfill R_{\infty }(A)=& \frac{100}{N}(\text{Number}\text{of}\text{recovered}\hfill \\ \hfill & \text{people}\text{till}\text{time}{T}_{\text{epi}})\hfill \end{array}$$ 2

  and $D_{\infty }(A)$ denotes the percentage of Deaths due to policy A. A good suppression policy should ensure that $I_{\infty }$ is low which implies that both $D_{\infty }$ and $R_{\infty }$ are low.

From these observation, one can draw the insight that a policy would gain acceptability if it is as effective as a lockdown but it is enforced for a shorter length of time than Lockdown. We encapsulate this insight via preference score, defined as follows.

The preference score of a policy $\mathbf{A}$ with respect to a base policy ${\mathbf{A}}_0$ is defined as

$$\begin{array}{c}\hfill \mathtt{score}(\mathbf{A};{\mathbf{A}}_0)=\frac{1}{2}\left(\frac{I_{\infty }(\mathbf{A})}{I_{\infty }({\mathbf{A}}_0)},+,\frac{T_{\text{epi}}(\mathbf{A})}{T_{\text{epi}}({\mathbf{A}}_0)}\right)\end{array}$$ 3

This score can be used to evaluate preference of a policy over the base policy ${\mathbf{A}}_0$. A policy $\mathbf{A}$ would be preferable to ${\mathbf{A}}_0$ if $\mathtt{score}(\mathbf{A};{\mathbf{A}}_0)$ is less than 1.

Description of Intervention Policies

Using the designed metrics, we will study the acceptability of the following policies, also summarized in Table  2.

Lockdown (LD) Lockdowns have been enforced in different ways across the globe. For example, in UK (Press), it is allowed to go out for a walk or exercise once a day, while in India this is not allowed. To model this varied degree of Lockdown we introduce a parameter called relaxation factor, $\eta$, which is allowed to vary between [0, 1]. This parameter modulates the transmission parameter to obtain an effective transmission rate of $\beta =\eta {\beta }_0$, The value of $\eta =0$ corresponds to perfect lockdown and $\eta =1$ represents the other extreme with no lockdown. Perfect lockdown corresponds to the entire population being quarantined. As practiced in many places, LD is enforced by shutting down all but essential services. This should definitely lower ${\beta }_M$ considerably and getting such estimates would be difficult. One can assume that Lockdown will correspond to a small $\eta$. A small $\eta$ corresponds to lowering of the reproduction rate in the network. (We hesitate to use $R_0$ here because reproduction rate has meaning at any instant of time in a network.) In the absence of clear guidelines, in this note, we will define LD as any measure which can achieve $\eta \le 0.5$. It would be useful to know how long should such a lockdown need to continue.

Fixed Duration Lockdown(FDLD) As an alternative to LD , one can consider a fixed duration Lockdown (FDLD). In India, the Government announced a lockdown for 21 days on March 23rd and then extended it for another 20 days. Keeping this in mind, we simulated a FDLD of 40 days and applied it after 20 days of onset of the pandemic.

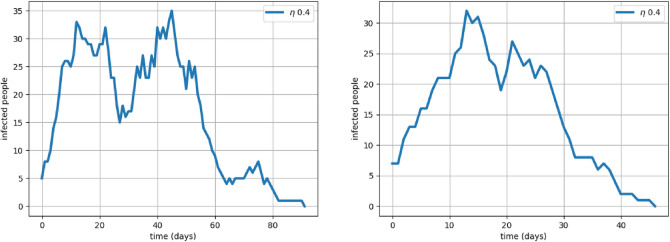
Tracing the Contacts and their Contacts and Sealing (TC2S) Contact Tracing and Case Isolation is an important tool in the fight against this epidemic. It is long argued that Targeted Social Distancing may be more effective than social distancing measures imposed on the whole population¹⁰. Contact Tracing usually involves checking for infections in all persons who have come in the contact of an infected person. Based on the empirical results (see Fig. 4), we propose a two-level strategy—not only trace the contacted persons of the patient, but also trace their contacts as well. We call this policy Tracing the Contacts and their Contacts (TC2S) and implement it as follows. The trigger is when a node u becomes severe (IS) or critical (IC). In this case, we look at all its neighbors v and seal it if it is state IM. We then look at the neighbors of v and then seal all their neighbors who is in state IM. Finding the neighbors of u and their neighbors are part of the tracing mechanism. Sealing means the node will not have any connections with its neighbors and it could be implemented by either self-isolation or being admitted to Quarantine facilities. Here is a reason for doing this two-level tracing. The node u must have got infected by one of its neighbors $u_{\mathrm{p}}$ (who may have recovered since), who could have infected other neighbors as well. We cannot reach these neighbors by merely sealing the neighbours of u, hence the two-level tracing and sealing.

Figure 4:

Tracing and Sealing helps but the peaks are still substantial. TC1S (trace and seal immediate contacts) does worse than the two-level tracing, TC2S.

For such a scheme to be viable, it is important that the number of people who are traced and isolated is small. We introduce a percentage measure of efficiency for TC2S  as follows

$$\begin{array}{c}\hfill T_e=\frac{1}{N}\text{Total}\text{number}\text{of}\text{people}\text{traced}\times 100,N=\text{Size}\text{of}\text{Population}\end{array}$$ 4

Very few countries have the ability to implement TC2S  at the whole population scale and it is reasonable to assume that most countries can do it only when $T_e$ is a small fraction of the population.

Ward Seal and Open(WSO) In LD , an entire city will be under lockdown. Instead of shutting the entire city, one can enforce lockdowns in Infection Hotspots, in case of Bengaluru it could be wards with infected patients. Such strategies are already being considered (Press).

A ward can be isolated by removing all edges to other wards. In our case, we merely change ${\beta }_M$ by an $\eta$ factor to account for account for delivery boys, health officials, stray travel to groceries, etc. The difference to the global lockdown is that the ${\beta }_M$ is lowered only for those nodes in wards that are in lockdown.

The opening and closing of ward are guided by a low-water mark and a high-water mark, denoted WSO(low, high). It will be assumed that once the infections in a ward cross the high-water mark, the epidemic surveillance triggers are activated and the ward is declared as a Hotspot which requires intervention. The ward will be sealed, that is lockdown will be imposed till such time that the infections subside to a low-water mark which signifies tolerable level. To measure the economic efficiency of WSO, we introduce

$$\begin{array}{cc}& W_l=\frac{{\sum }_{i=1}^W{T}_i}{W·T_{\text{epi}}(\mathit{LD})},\hfill \\ \hfill T_i=& \text{Total}\text{number}\text{of}\text{days}\text{the}\text{ward}i\text{was shut},\hfill \\ \hfill W=& \text{Total}\text{number}\text{of}\text{wards}\hfill \\ \hfill T_{\text{epi}}(\mathit{LD})=& T_{\text{epi}}\text{for}\mathit{LD}\hfill \end{array}$$ 5

To explain the motivation for $W_l$, we consider the following. Assume that loss to the economy incurred by shutting down one ward for 1 day is c units. The loss incurred by WSOis then ${\sum }_{i=1}^{W}c{T}_i$. The loss incurred by LD policy is $c{T}_{\text{epi}}W$. Thus, $W_l$ measures the relative loss to the economy compared to LD.

Thus, any ward-specific policy requiring the wards to be shut down should be considered practical only if $W_l$ is low. For our implementation, we have chosen low $=0$, and high $=3$. For values of low other than 0, the system becomes unstable. Ideally one should aim for the highest value of the upper limit to minimize the duration of the lockdown.The chosen number 3 seems to be the best possible.

Two-day work week followed by a Lockdown(TDWW+LD) In spirit of WSO  one can withdraw the lockdown for some amount of time and re-impose it after sometime. It is clear that with the infection doubling every 5 days [9], if left unchecked, it maybe risky to withdraw the lockdown for a whole week. Assuming that first symptoms will occur after 5 days, one could potentially allow a 2-day work week. The policy intervention is to impose a lockdown for 5 days and open the economy for 2 days.

Other variations of the policies such as one Lockdowns on alternate weeks or three day week do not seem to work as well as the two-day work week. So we do not consider these alternatives here.

Do Nothing(DN) This is the base case where no interventions are done and the population achieves immunity after getting infected by the virus.

Remarks We want to re-emphasize that we have taken a uniform approach to various stages of lockdown using a single factor $\eta$. For example, in a global- or a ward-level lockdown, it is natural to expect all long edges emanating from the ward to be ineffective. Instead, we retain the edges but dampen the probability of infection propagating to account for the delivery boys, the local police, the health workers, etc. who still move through the ward.

Results

In this section, we present the results of simulation studies of various policies mentioned in Table 2 on Small world network. One run of the algorithm starts with 5 index patients and iterates till there are no infected patients in the population. In Table  3, we report the median over 11 runs of relevant parameters namely projected number of deaths per million, $R_{\infty }$, and $T_{\text{epi}}$. We also report $W_l$ and $T_e$ wherever applicable.

Table 3:

$R_{\infty },T_e,W_l$ are reported in percentages (see (2),(4), and (5) respectively).

	$\eta$	Deaths	$R_{\infty }$	$T_{\text{epi}}$	$T_e$	$W_l$
		per million	%	(days)	%
DN	1	8702	84.96	178
FDLD	0.4	8479	84.88	232
TC1S	1	7528	74.77	209	11
TC2S	1	5642	55.63	303	15.3
WSO(0,3)(mild)	0.6	2992	29.97	480		3.78
LD(mild)	0.6	2675	25.75	557
TDWW+LD	0.4	1354	12.55	675
LD(mild)+TC2S	0.6	103	1.09	184	0.15
WSO(0,3)(mild)+TC2S	0.6	171	1.05	274	0.2	0.43
LD	0.4	51	0.52	115
TDWW+LD+TC2S	0.4	34	0.35	107	0.05
LD+TC2S	0.4	43	0.35	83	0.07
WSO(0,3)	0.4	18	0.33	124		0.18
WSO(0,3)+TC2S	0.4	18	0.09	65	0.02	0.04

$T_{\text{epi}}$ is the length of epidemic measured in days. All numbers reported are median values of 11 runs. BoldItalic cells indicate that the value in the cell is acceptable. italicized cells indicate that the value can be considered, while underlined cells indicate unacceptable values. For more discussion on the acceptable, unacceptable, can be considered see results. The policy acronyms are mentioned in Table  2

For the sake of comparison between policies, we have color-coded the values in the table. Red indicates unacceptable, Green indicates acceptable and Yellow indicates can be considered. We assume that a city’s Healthcare system can deal with patients comfortably if the percentage of infected population is less than $5\%$($I_{\infty }$ is less than 5%). In case of epidemic outbreaks, it can be pushed to higher values for a short amount of time say 15%. To assess the suitability of the duration of the policy, $T_{\text{epi}}$, one could compare it with $T_{\text{epi}}$ for LD. From our simulations it seems that a strict Lockdown may take around 4 months(median value) to make the population Infection free. We rounded all $T_{\text{epi}}$ estimates to nearest months, and decide that all values less than 4 months are acceptable, as it is more efficient than LD. If $T_{\text{epi}}$ is more than double the duration during Lockdown, i.e. more than 8 months, we can consider it as unacceptable. Values in between can be deemed as can be considered. To assess the suitability of $T_e$, we assume that only a small fraction of the population can be contact traced and isolated. We set this limit to less than $0.5\%$. Any number more than $1\%$ would be unacceptable. For $W_l$ one can argue that a policy should not be as expensive as LD. Any acceptable value must be necessarily less than 1. As lockdowns are expensive, one can argue that any policy should incur a loss which is a small fraction of the loss incurred by LD. We set the threshold for $W_l$ to be 0.1 for being acceptable. Any value between 0.1 and 1 can be considered. A value more than 1 is not acceptable. These thresholds are only notionally set to enable comparison. They can be set more precisely using information from Health Departments from respective cities.

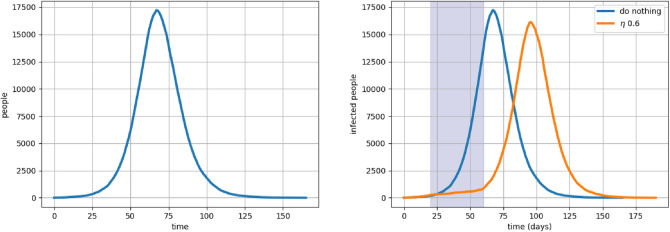
Do Nothing, the base case Figure  3 shows the number of infections with time for DN  when no interventions are applied. The peak occurs at about 67 days on an average. The number of deaths is 8702 per million and around $85\%$ of the people have been infected and recovered. These numbers are in line with [5] and serves as a sanity check. The longevity of the virus seems to be roughly six months. The transmission parameters are unmodified with $\eta =1$. Our numbers are slightly higher than that of [5] as we allow for Infections to be propagated by severely and critically ill patients as well.

Figure 3:

DN vs FDLD: on the left is the infection curve with no interventions. On the right is a forty-day lockdown.

Tracing and Sealing As can be see from Fig. 4, TC2S as a stand-alone strategy brings down the total infected population to less thab 2/3 of DN  resulting in significant reduction of deaths per million. It also prolongs the life of the epidemic to a little less than a year. Fatality rate at 5650 deaths/million, though lower than DN, but still is unacceptably high. Also, it is to be noted that roughly $15\%$ population needed to be sealed. To compare, the TC1S numbers are these: 7528 deaths/million while sealing $11\%$ of the population. This is a $33\%$ increase in death/million without a dramatic decrease in the percentage of population sealed. Hence, we discard TC1S in favour of TC2S. As we will see, TC2S  works even better when it augments other strategies.

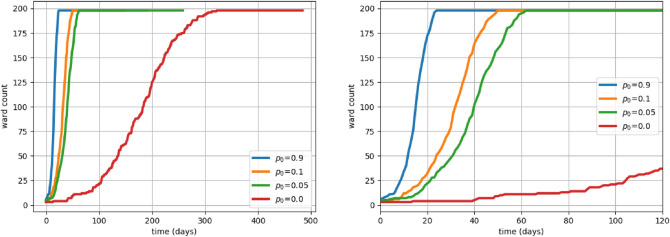
The effect of $p_0$ on the graph Figure 5 shows rewiring is a sensitive parameter. A moderate number of edges rewired results in speeding up the spread of the epidemic. The graphs show how fast an epidemic can sweep through the different wards of the city by simply tuning the rewiring parameter, $p_0$.

Figure 5:

The rewiring parameter $p_0$ has a role to play in how far the disease spreads across the wards. Right: Zoomed version of the graph to show even a small amount of rewiring has a huge effect on the speed of disease spread.

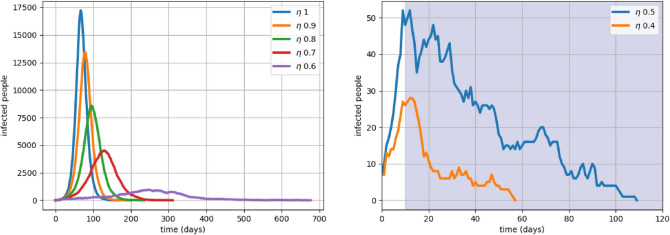
The effect of relaxation factor, $\eta$ The aim of the most Intervention strategies is to reduce the $\beta$s so that the effective transmission comes down. The relaxation factor, $\eta$, takes values between 1 and 0 and serves to reduce the transmission parameters $(\eta {\beta }_M,\eta {\beta }_S,\eta {\beta }_C).$ This allows to model various Interventions designed to hinder the transmission by a single parameter $\eta$. Figure  6 shows plots of the number of infected persons with time for various values of $\eta$. As $\eta$ decreases the speed of progression becomes slower and the disease takes longer time and the peak infection also comes down. However, it effects most of the population, almost the same death and recovery rates. As reported elsewhere (for, e.g.,⁵), such reductions in transmission rates could be obtained by various social distancing measures. These interventions ensure that the peak infection rate comes down but overall a large fraction of population gets infected. These kinds of measures help in flattening the curve and do not help in Suppression. The results show that the strategies of suppression belong to the regime of $\eta <0.5$. In this regime, both $R_{\infty }$ is extremely low and length of the epidemic is reduced to below the base case. The figure in the right-hand side of Fig. 6 shows that the longevity of the epidemic reduces as $\eta$ decreases. Thus suppression strategies should aim for Interventions which can halve the transmission rate. Such strategies would be difficult to achieve without extreme social distancing, such as Lockdowns.

Figure 6:

The effect of $\eta$ Figure on the left shows infection over time for $\eta \ge 0.6$. Any policy which yields $1\ge \eta \ge 0.6$ will help in flattening the curve. Figure on the right shows Lockdown implemented after 20 days from the onset of the pandemic for $\beta =0.5$ and $\beta =0.4$. It shows that the suppression is achieved. Smaller values of $\eta$ yield quicker suppression.

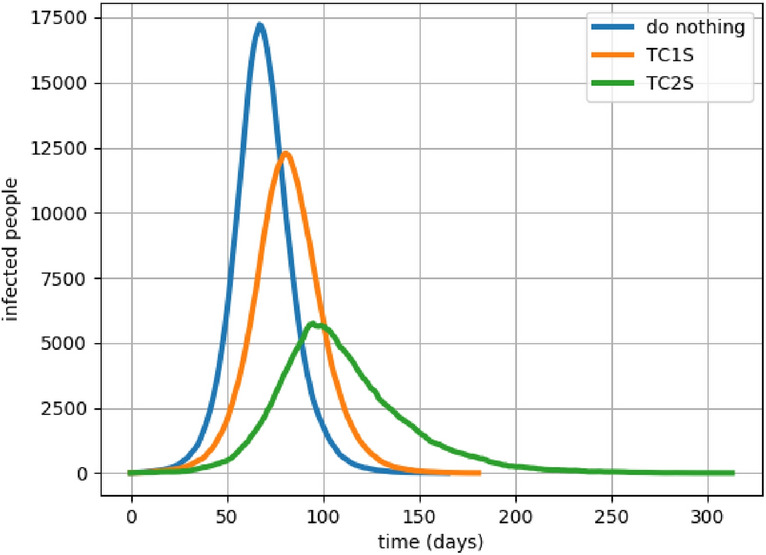
Lockdowns LD is an extreme social distancing measure which can reduce the transmission rate. In absence of any known reliable data, we assume that a Lockdown can reduce the transmission rate to less than half. In this setup, this corresponds to assuming that LD is a measure corresponding to $\eta <0.5$. In particular we will use $\eta =0.4$. Figure on the right in Fig. 6 shows that it is possible that the disease dies out within 4 months. Simulation results suggest that this can be achieved by affecting only $0.52\%$ of the population and the pandemic can end in 115 days, both values are median. Adding TC2S  to LD  significantly improves the infection rate by bringing it down to half. The effectiveness of any other policy can be evaluated against these set of numbers.

Mild lockdown Instead of LD, a mild lockdown with parameter $\eta =0.6$ reduces $R_{\infty }$ to $25.75\%$, much lower than DN , but still it is much higher than that achieved by  LD. However, if we use it along with TC2S, then it becomes a very effective strategy, reducing the infection rate to $1\%$.

Fixed duration lockdown Figure  3 compares it with DN. Instead of seeing the peak of infection after 67 days in DN the new peak is shifted by 30 days approximately. It does not yield any reduction in infection rates or in number of deaths. If the policy is to be used only once, then it should not be used early. To avoid the peak of infection, one should apply the FDLD a little later. The exact time to apply such a policy is still open. [3] recommends that it should be used closer to the peak. This will avoid the second peak but as a policy, FDLDis not acceptable as it will anyway lead to significant infections and many deaths.

Two-day work week with 5-day lockdown Figure 8 shows TDWW  policy is better than mild lockdown. This is not surprising as the lockdown is withdrawn only for 2 days but is enforced for the remaining 5 days. It is still not practical as it gives a very high value of $T_{\text{epi}}$ and also a infection rate of more than $12\%$. However, when enforced with TC2S  it becomes an acceptable policy with $R_{\infty }$ coming down to 0.35 and it takes the same time as LD.

Figure 8:

TDWW-policy: it prolongs the epidemic. Also, on the right is the zoomed version where one can clearly see oscillations due to lifting and imposing of ban.

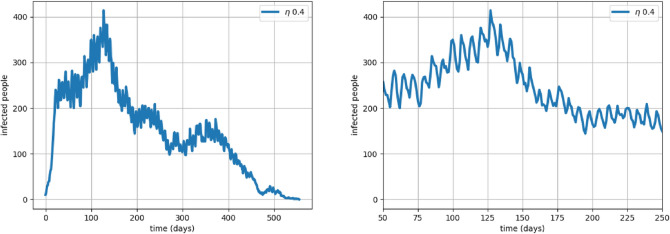
Ward-level interventions WSO(0,3) policy performs extremely well when strict lockdowns are enforced inside the wards. The policy lowers the infection rate to 2/3 of that achieved by LD  with similar values of $T_{\text{epi}}$. As soon as the infection rises the respective affected wards are locked down. Figure  7 shows a typical run of WSO(0,3). It exhibits multiple peaks of infection but the number of infections at the peak is much lower than DN. The $W_l$ loss value is $16.52\%$ implying that most of the wards are open most of the time. Coupling with TC2S  further lowers the infection rate by a factor of 3 and also halves $T_{\text{epi}}$. As an icing on the cake it reduces the $W_l$ loss value by almost a factor of 3. However, if the lockdowns are not enforced, strictly the policy can be dangerous. It is slightly better than TC2S , and moreover with a $W_l$ value of 3.77, it can be interpreted that policy results in closure of the large parts of the city for a prolonged period of time. The mild lockdown version of WSO(0,3) is significantly improved if used alongside with TC2S.

Figure 7:

WSO(0,3): on the left, different wards lockdown at different times and these account for multiple peaks. On the right, when TC2S is imposed as well.

Discussion

Important insights drawn from the study are summarized by the following points.

1. Doing Nothing (DN) and allowing infection to spread in the hope of growing Herd Immunity is clearly not acceptable as it results in far too many infections and death.

2. The study confirms that Lockdown (LD) is an acceptable strategy with and without contact tracing as it reduced the attack rate to $0.52\%$ compared to $85\%$ with no interventions. When used with TC2S  it further improves to $0.35\%$.

3. Lockdowns of limited duration or relaxed Lockdowns are not acceptable even in the early stages. However, Lockdowns of limited duration are extremely useful to bring down the infections temporarily.

4. Releasing the lockdown for a few days in a week (TDWW) can be considered but it can be risky. Contact Tracing should be a must for such policies.

5. TC2S when used as a stand-alone strategy may not be effective but when used with some of the other alternatives it can generate much improved policies. Mild lockdowns, which on its own are not acceptable, but when coupled with TC2S  produce an acceptable policy. Another intervention, shortened week with lockdown (TDWW+LD) is risky but when applied with TC2S  becomes very effective. When used with $\mathbf{TC}\mathbf{2}\mathbf{S}$ , it reduces the attack rate by 1/3 that of Lockdown. The effectiveness of TC2S, as proposed here, would depend on not only identifying the complete list of infected people in the contact network but also would require identifying any infected people in the network of the contacts. These findings are similar to [8, 11] where it is argued that extensive contact tracing and case isolation may help

6. WSO(0,3) appears to be the most promising alternative to LD. It not only outperforms LD on attack rate but also reduces the duration of the epidemic by 1/2 when augmented with contact tracing. Even mild lockdowns with contact tracing in WSO  can be an acceptable alternative.

Preferred Suppression Strategy Alternatives to Lockdown

Figure  9 shows a bar-chart of preference scores, $\mathtt{score}(\mathbf{A};\mathbf{LD})$ (defined in (3)) of all considered policies. Any policy with score less than 1 should be preferred over LD. From the chart, two distinct policy alternatives emerge which could match the effectiveness of Lockdown when applied as Intervention measures in early stages of the pandemic.

1. Shortened work week (TDWW + LD + TC2S) can be considered as an alternative to full Lockdown. The policy advocates a 2-day week where the economy is open but for the remaining 5 days a week, a strict lockdown is enforced.

2. Opening and closing hotspots depending on Infection levels (WSO) can be a better alternative to TDWW. This policy only constrains the residents inside the ward and rest the remaining populace go about their business. TDWW  would enforce lockdowns for most of the week and hence it is more constraining than WSO. Our study shows that if implemented in early stages, very few wards need to be shut down.

The success of WSO  policy crucially depends on the ability to Test all residents in the hotspots. While Contact tracing is not necessary it will definitely help in improving the WSO  policy outcomes. An interesting insight is since we can target the tracing to the ward it even requires less number of contacts to be traced then implementing LD. If there is substantial shortage of Testing kits making WSO unviable then one can consider the alternative policy of opening the economy for two days a week. If the two policies are weighed in terms of their economics, then one can say that WSO though opens the economy much more than the 2-day week policy but also requires some investment in Testing, which could be a challenge in densely populated urban wards of metropolises. But for both the interventions, Contact Tracing is required.

Figure 9:

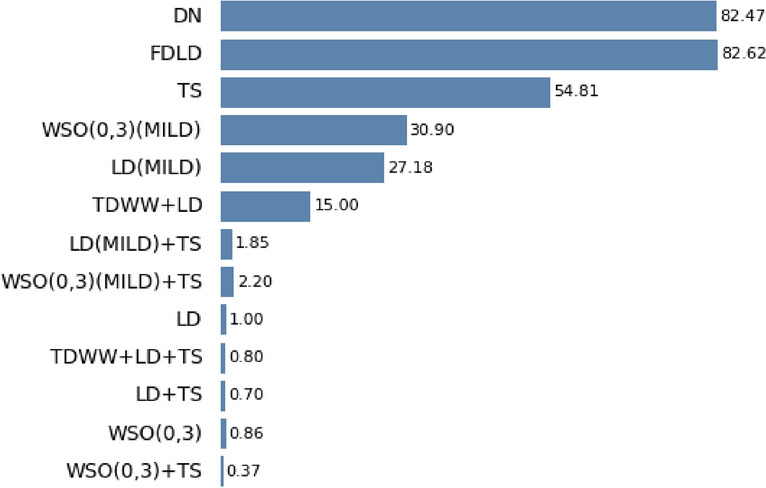
Interventions and their preference scores, $\mathtt{score}(\mathbf{A};\mathbf{LD})$. Smaller score indicate that policy $\mathbf{A}$ is better than LD.

Conclusions

In this note, we reported an empirical study of various policy alternatives to Lockdown for suppressing COVID19 pandemic on a city modeled by MLSW, a small world model. This type of small world model does not seem to have been investigated before and a detailed mathematical study of the properties should be an important area of investigation. Our results indicate three interesting highlights. First, Tracing the Contacts and their Contacts shows substantial benefits over the usual practice of Tracing the Contacts. Second, opening the economy partially, say 2 days a week followed by a Lockdown, could be more effective than Lockdown. Third, and most importantly, the most preferred strategy should be to do hotspot surveillance. The results suggest that WSO, a hotspot surveillance strategy, not only has lower attack rates, but also is much faster in destroying the virus. On top of these two things, it is also economically far more efficient. If the policy is introduced early enough, it is possible that the pandemic can be suppressed in the early stages at a far lesser time than the currently practiced Lockdowns.

Biographies

Chiranjib Bhattacharyya

is currently Professor in the Department of Computer Science and Automation, Indian Institute of Science. His research interests are in foundations of Machine Learning, Optimisation and their applications to Industrial problems. He has authored numerous papers in leading journals and conferences in Machine Learning. Some of his results have won best paper awards. He joined the Department of CSA, IISc, in 2002 as an Assistant Professor. Prior to joining the Department he was a postdoctoral fellow at UC Berkeley. He holds BE and ME degrees, both in Electrical Engineering, from Jadavpur University and the Indian Institute of Science, respectively, and completed his PhD from the Department of Computer Science and Automation, Indian Institute of Science. He is also a fellow of Indian Academy of Engineering. For more information about his work please see http://mllab.csa.iisc.ernet.in.

V. Vinay

has been an academic and an entrepreneur. He was a former professor of Computer Science at the Indian Institute of Science, co-invented the Simputer and was a co-founder of Strand Life Sciences. He is an adjunct faculty at the Chennai Mathematical Institute and recently founded Ati Motors, an autonomous industrial vehicle company.