Anomalous versus Normal Room-Temperature Diffusion of Metal Adatoms on Graphene

Abstract

Fabrication of high-performance heterostructure devices requires fundamental understanding of the diffusion dynamics of metal species on 2D materials. Here, we investigate the room-temperature diffusion of Ag, Au, Cu, Pd, Pt, and Ru adatoms on graphene using ab initio and classical molecular dynamics simulations. We find that Ag, Au, Cu, and Pd follow Lévy walks, in which adatoms move continuously within ∼1–4 nm² domains during ∼0.04 ns timeframes, and they occasionally perform ∼2–4 nm flights across multiple surface adsorption sites. This anomalous diffusion pattern is associated with a flat (<50 meV) potential energy landscape (PEL), which renders surface vibrations important for adatom migration. The latter is not the case for Pt and Ru, which encounter a significantly rougher PEL (>100 meV) and, hence, migrate via conventional random walks. Thus, adatom anomalous diffusion is a potentially important aspect for modeling growth of metal films and nanostructures on 2D materials.

Fabrication of multifunctional metal contacts in heterostructure devices based on two-dimensional (2D) materials necessitates growth of vapor-deposited metal films in a controlled fashion on 2D crystal substrates.^1,2 A key step toward achieving this control is to fundamentally understand the dynamics of adatom surface diffusion, the atomic-scale process that leads to island nucleation and thereby largely sets the lateral length scale of film morphology.^3,4

During epitaxial metal and semiconductor growth, at temperatures that are typical for thin-film deposition experiments, adatom diffusion is described as a thermally activated chain of uncorrelated jumps, so that adatoms execute a random walk on the substrate surface.⁵ Within this framework, the diffusivity of an adatom transitioning between surface sites separated by a mean square distance l² at rate ν is calculated as 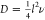. The temperature-dependent jump rate ν is typically approximated by the Arrhenius equation, in which the static (i.e., 0 K) surface migration barrier is determined by ab initio or classical computational methods,⁶⁻¹⁶ while the jump attempt frequency is estimated via (quasi-)harmonic transition-state theory approaches.^17,18 Alternatively, D can be computed using Einstein’s equation ⟨x²(t)⟩ = 4Dt, where ⟨x²(t)⟩ is the adatom mean square displacement (MSD) after time t, with ⟨x²(t)⟩ being measured either experimentally or estimated via classical molecular dynamics simulations.^5,19

At temperatures significantly higher than those used for thin-film synthesis experiments, the above-described notion of random walk can be inadequate²⁰⁻²⁵ because ⟨x²(t)⟩ may not vary as ∼t. Such nonlinear ⟨x²(t)⟩ versus t dependence is indicative of anomalous diffusion and has been attributed to vibrational entropy modifying the potential energy landscape (PEL) of the substrate surface, thereby allowing for long and correlated adatom jumps.²⁶⁻³¹ As 2D materials are intrinsically inert^32,33 they often interact weakly with adatoms and their PEL is markedly flat, so that the onset of anomalous diffusion may take place at temperatures that are within experimentally relevant ranges (e.g., room temperature). Moreover, 2D materials, owing to their reduced dimensionality and the smaller density of vibrational modes they host in their lattice, are intuitively expected to dissipate adatom energies less efficiently as compared to bulk crystals, which may further enhance the tendency for anomalous surface diffusion.

In the present work, we explore the propensity of metal adatoms for anomalous diffusion on 2D crystals at room temperature. To this purpose, we study surface migration dynamics of silver (Ag), gold (Au), copper (Cu), palladium (Pd), platinum (Pt), and ruthenium (Ru) adatoms on single-layer graphene (SLG)³⁴ via ab initio and classical (semiempirical) molecular dynamics simulations. The choice of the six metals is motivated by the fact that (i) the reported estimates of their static surface migration barriers on graphene range from 0.004 to 0.188 eV³⁵ and hence represent a multitude of expected dynamic diffusive behaviors and (ii) they are relevant as metal contacts in nanoelectronics, sensing, and catalysis.³⁶⁻³⁹

We first perform ab initio molecular dynamics (AIMD) simulations of monomer diffusion on SLG for times up to 0.2 ns (see later in the text for simulation details and detailed explanation of the reasons behind the selection of the simulation times for the various adatoms). The trajectories are displayed in Figure 1, which shows that Pt and Ru diffuse within areas of ∼0.04–0.09 nm². Closer inspection of the trajectories (enlarged sections presented as insets in the Pt and Ru trajectory panels) reveals that the adatoms spend most of the simulation trapped in specific surface sites, and for the case of Pt, random jumps among neighboring adsorption sites are observed. All the above-described features are consistent with a random walk. In contrast, Ag, Au, Cu, and Pd atoms move continuously across the surface without being halted by adsorption sites, diffuse within relatively short-range domains (marked with circles in Figure 1) during time frames of ∼0.04 ns, and occasionally perform long jumps that cover multiple adsorption sites (the distance between adjacent adsorption sites is ∼0.12–0.24 nm). This anomalous behavior corresponds to superdiffusion. Moreover, visual inspection of the trajectories reveals that both the areas of the domains and the jump lengths for Ag and Cu trajectories (the approximate mean values for these quantities are ∼4 nm² and ∼4 nm, respectively) are significantly larger than those for Au and Pd (∼1 nm² and ∼2 nm). The distinctly different normal versus superdiffusive behavior exhibited by the various adatoms is further illustrated in Figure S1 in the Supporting Information which plots trajectories of all metals after a 0.02 ns simulation time.

Figure 1.

Ab initio MD diffusion trajectories for Pt (0.04 ns); Ru (0.02 ns); and Ag, Au, Cu, and Pd (0.2 ns). The circles in the trajectories for Ag, Au, Cu, and Pd mark a short-range diffusion domain (see text for more details).

To estimate the diffusivity D and quantify the migration dynamics of single adatoms, we compute, for each one of the anomalous trajectories in Figure 1, the time-averaged adatom mean square displacement⁴⁰

1

In eq 1, Δt is the simulation time step, τ a variable representing a specific observation time scale, and N the total number of subtrajectories with a duration τ that can be defined over the total atomic trajectory (note that two different subtrajectories defined in this way may partially overlap). For a total simulation time T and an observation scale τ consisting of N_T and N_τ time steps Δt, respectively, N = N_T – N_τ + 1. Thus, each point on a versus τ curve corresponds to an average entailing information on all subtrajectories with a duration τ. From the latter it follows that the statistical significance of a given value decreases with increasing τ, because larger τ values yield a smaller number of subtrajectories available for calculating . Moreover, it is worth pointing out that the analysis on the data in Figure 1 is based on 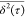, instead of ⟨x²(t)⟩, because an accurate calculation of the latter quantity would require data from multiple simulated trajectories.

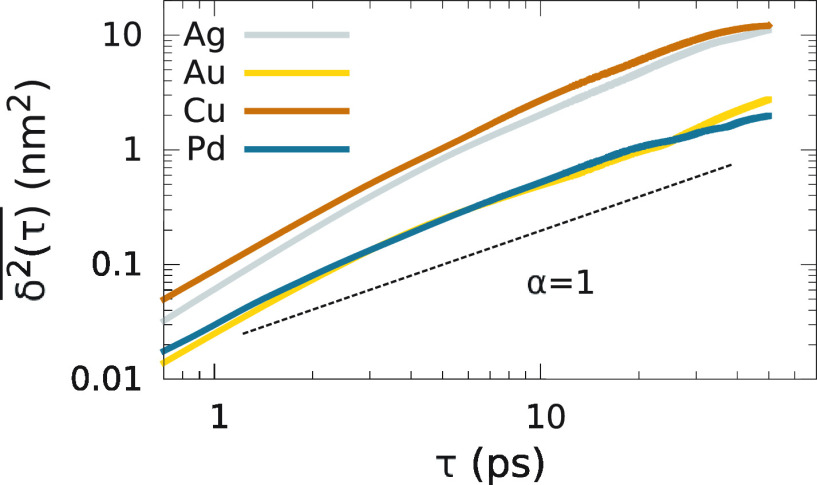
The versus τ curves (0 < τ ≤ 50 ps; a detailed explanation for the selection of τ range is provided later in the text) for Ag, Au, Cu, and Pd are plotted in log–log scale in Figure 2. The data reveal that Ag and Cu exhibit larger values over the entire τ range, which is in line with the differences in the jump length magnitudes seen in Figure 1. Furthermore, irrespective of the atomic displacement magnitude, the versus τ curves exhibit a nonlinear behavior with slopes α larger than one (the α = 1 slope is represented by the dashed line in Figure 2), which is consistent with the superdiffusive nature of the atomic trajectories in Figure 1.⁴¹ Note that α ≈ 1 as τ → 50 ps. We attribute this to the limited statistical significance of 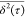at large τ values, e.g., 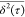for τ = 50 ps is calculated using 4 subtrajectories (see eq 1).

Figure 2.

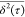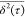versus τ curves (plotted in log–log scale) extracted from the AIMD trajectories presented in Figure 1 for Ag, Au, Cu, and Pd. All lines exhibit a slope α > 1 which is consistent with the superdiffusive nature of adatom motion. This is in contrast to random walk trajectories which exhibit a versus τ slope of α = 1 (represented by the dashed line). A more detailed discussion on the correlation among α and diffusion nature can be found in the text.

On the basis of the nonlinear behavior established in Figure 2, we conclude that we cannot use the Einstein equation for correlating 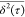versus τ curves and D. For this reason, in the remainder of the Letter we use the continuous time random walk formalism as an alternative framework to treat anomalous diffusion.⁴² This formalism assumes that 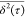exhibits a power law dependence on time

2

where the exponent 1 < α < 2 denotes the superdiffusive character of the monomer (α = 2 corresponds to a ballistic trajectory, whereas α = 1 corresponds to a random walk) and D_α is a generalized diffusion coefficient with physical dimensions nm²·ps^–α.

The task of extracting relevant values for α and D_α is not straightforward, because each point at the versus τ curves has a different statistical significance (see eq 1). Thus, following the methodology proposed by Saxton,⁴⁰ only 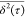points within an interval [0: τ_cut] are considered. The value τ_cut is a time cutoff here taken to be equal to 50 ps (see Figure 2), to exclude all points averaged over less than 4 independent subtrajectories. Moreover, this choice has a physical justification: τ_cut is of the same order of magnitude as the typical time required for an adatom to transition between superdiffusive domains—note that the trajectories in Figure 1 consist of ∼3–4 domains—and is thus representative of the adatom migration dynamics at the time scale of several tens of picoseconds. We also notice in Figure 2 that the slope of log–log 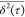versus τ curves is not constant. Hence, in order to extract α we perform a linear fit of the curves for multiple time intervals [0: τ*] with 0 < τ*≤ 50 ps as explained by Kepten et al.⁴³ Then, the most probable value from the statistical distribution of α is selected (see Figure S2 in the Supporting Information), from which D_α is calculated using eq 2.

Table 1 lists the numerical values of α and D_α for Ag, Au, Cu, and Pd. With regards to the scaling exponents, we see that Ag and Cu have an exponent α = 1.4, whereas for Au α = 1.2, and for Pd α = 1.1. Table 1 also presents the static (0 K) adsorption energies E_ads^0K (see later in the text for details) of all metals (Pt, Ru, Ag, Cu, Au, and Pd) on the hollow, bridge, and top site of graphene (hollow, above center of a C6 ring; bridge, above midpoint of C=C bond; top, above a C atom). The E_ads values are validated against high accuracy static relaxations and are compared to data for both SLG and multilayer graphene from the literature (see Table S1 in the Supporting Information).^7,38,44,45 We note that the energy values in Table 1 are shifted with respect to the most stable site for which E_ads^0K is set equal zero. By comparing α and E_ads, we conclude that the propensity of an adatom toward anomalous diffusion can be correlated with the flatness of the surface PEL: (i) for Pt and Ru, the smallest energy difference between adsorption sites ΔE_ads^0K is in the range ∼200 to ∼600 meV, yielding a random walk behavior; (ii) while for Ag, Cu, Au, and Pd, ΔE_ads is considerably lower (∼1 to ∼50 meV), which offers more and easier transition pathways and promotes superdiffusive behavior, as seen by the α > 1 values. Moreover, the PEL can also be correlated with the degree of anomaly of the different metals that exhibit superdiffusion: the markedly flat PEL for Ag and Cu (ΔE_ads^0K of the order of a few millielectronvolts) induces long atomic jumps, large diffusion domains (∼4 nm and ∼4 nm², respectively), and α = 1.4; whereas the somewhat rougher PEL of Au and Pd (ΔE_ads up to 1 order of magnitude larger) results in relatively smaller jump lengths and domain areas for Au and Pd (∼2 nm and ∼1 nm²), and yields α = 1.2 and α = 1.1, respectively. Hence, by computing the static PEL of an adatom on a 2D material, we can qualitatively assess the adatom tendency for exhibiting anomalous diffusion patterns. However, it is important to emphasize that the adatom jump lengths and the specific dynamic diffusion behavior established for the various adatom-on-SLG systems should be considered in relation to the mean separation between islands observed in experiments³⁵

Table 1. Exponents α, Diffusivities (D_α, nm²·ps^–α), and Adsorption Energies at 0 and 300 K (E_ads^0K and E_ads, meV) of Metal Adatoms on the Graphene Surface^a.

			Eads0K			Eads300K
	α	Dα	hollow	bridge	top	hollow	bridge	top
Ag	1.4(×1.07±1)	0.016	9	1	0	6	0	3
Au	1.2(×1.08±1)	0.007	22	5	0	∼33	6	0
Cu	1.4(×1.07±1)	0.024	184	0	8	∼171	4	0
Pd	1.1(×1.09±1)	0.008	290	0	53	∼660	0	19
Pt	1		894	0	215
Ru	1		0	641	664

^aThe adsorption energies refer to the hollow, bridge, and top positions, whereby energies are shifted with respect to the most stable adsorption site for which E_ads is set equal zero.

The normal (i.e., random walk) diffusive behavior of Pt and Ru adatoms at 300 K can be explained by the fact that the thermal energy k_BT (≈ 25 meV) is signifficantly smaller than the minimum ΔE_ads^0K that separates stable adsorption sites. In contrast, the collective motion of substrate surface atoms may play a decisive role on the dynamics of adatoms interacting weakly with the substrate, whereby the minimum ΔE_ads may become comparable with the thermal energy k_BT. The latter is particularly relevant for strongly anharmonic materials like graphene,⁴⁶ in which out-of-plane vibrations are relatively larger compared to those on surfaces of bulk crystals. To qualitatively understand the effects induced by graphene vibrations on the PEL, we calculate the adsorption energy of hollow, bridge, and top graphene sites at 300 K (see later in the text for details). Table 1 shows that, for the cases of Ag, Au, and Cu, the numerical accuracy of DFT for adsorption-energy values (a few millielectronvolts) is comparable with the differences between ΔE_ads^0K and ΔE_ads. The influence of temperature is more pronounced for the case of Pd, where ΔE_ads^300K between bridge and top sites decreases by ∼30 meV compared to ΔE_ads. This temperature-induced effect may explain the fact that Pd exhibits a diffusion behavior fairly similar to that of Au, despite having a notably larger 0 K PEL corrugation (∼50 vs ∼5 meV). It is important to note that atomic vibrations do not only affect adatom migration dynamics by modifying the effective PEL; they may also alter the adatom preferences for occupying the different adsorption sites because of entropy effects, as explained in the Supporting Information (Section S4 and Table S2).

Besides AIMD, we employ classical molecular dynamics (CMD) to model multiple Ag trajectories of 3 ns and a long one of 30 ns (see later in the text for details). By using the same methodology as that in the AIMD simulations to analyze the 30 ns long trajectory (see Figure S3 in the Supporting Information), we extract a versus τ exponent α = 1.3, which shows that CMD also predicts anomalous diffusion behavior for Ag. This can be understood in light of the shallow PEL that CMD yields (see Table S3 in the Supporting Information), which is consistent with AIMD (i.e., millielectronvolt difference between adsorption sites). Because both simulation approaches yield a qualitatively consistent physical behavior, we take advantage of the higher computational efficiency of CMD, to gather statistics and further our understanding of the type of diffusion that adatoms perform on SLG.

We analyze the trajectories by computing the ensemble mean 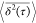of the time-averaged 3 ns trajectories and compare it with the ⟨x²(t)⟩ of the same trajectories in order to confirm or refute the ergodic character⁴⁷ of the diffusion dynamics. Figure 3a shows that the two averages differ by a small factor from the simulations start until 0.1 ns, after which they converge. This discrepancy at short and medium time scales indicates that, because of the tendency of adatoms to perform long jumps, the expansion rate of the area that an adatom may visit is greater than its mean diffusion rate. The adatom is, thus, unable to access all points of the phase space, which renders the motion nonergodic.

Figure 3.

(a) Ensemble average and ⟨x²(t)⟩ for the 30 CMD diffusion trajectories (3 ns long) and (b) jump length distribution for the 30 ns long CMD trajectory of Ag at 300 K.

Moreover, we calculate the adatom jump length probability distribution

3

of the 30 ns run for time sampling intervals Δt_S = 7.5, 10, 12.5, and 15 ps, and fit a regression line for each of the p(l) data sets, which are plotted in Figure 3b. For all the cases, the slope of the regression lines takes values 1.4 < μ < 1.7. We conclude from these results that the adatom motion is an intermediate case between ballistic motion (μ = 1) and random walk (μ = 3).

The nonergodic character and the specific jump length distribution established by the analysis presented in Figure 3 indicate that Ag adatoms follow a fractal movement pattern known as Lévy walk,^41,42,48 which is also observed in other phenomena in physical and biological sciences, including light propagation in optical media,⁴⁹ animal foraging,⁵⁰ or human travel.⁵¹ We expect that Au, Cu, and Pd also perform a Lévy walk, owing to the qualitative resemblance of their AIMD trajectories to that of Ag, as well as because for Ag, Au, Cu, and Pd we find that α > 1. Lévy walks have an effective upper limit for their jump lengths,⁵² which allows treating the correlated long-range adatom motion between diffusive domains (marked with circles in Figures 1 and S3a) as a random walk⁵³ and hence extracting effective diffusivities from the Einstein equation. These diffusivities, however, cannot be directly correlated with static activation barriers as diffusive domains are not adsorption sites with an associated PEL. Moreover, the relevance of effective diffusivities should be seen in relation to the mean density of surface defects,⁵⁴⁻⁵⁶ because these defects may hinder the atomic motion and inhibit the transition to quasi-random walk behavior.

In summary, we study, via AIMD and CMD simulations, the diffusion of Ag, Au, Cu, Pd, Pt, and Ru adatoms on monolayer graphene at 300 K, a temperature that is relevant for thin-film synthesis experiments. We find that, while Pt and Ru exhibit typical features of a random walk, Ag, Au, Cu, and Pd move continuously across the surface unhindered by adsorption sites, and follow a superdiffusive motion pattern known as Lévy walk. This motion is characterized by a wide distribution of jump lengths, often on the order of several nanometers. We also establish that the type of motion undergone by the adatoms is correlated with the PEL they experience on the SLG surface: diffusion resembles a random walk when the energy differences between adsorption sites are of the order of hundreds of millielectronvolts and turns into superdiffusive when these differences become of the order of 10 meV. The overall results of our work highlight that knowledge of static (i.e., 0 K) surface migration barriers that are readily available⁶⁻¹⁶ and govern the kinetics of random walks between adjacent adatom sites is not sufficient to describe the complex surface diffusion dynamics of adatoms on 2D-materials that exhibit flat PELs. Instead, modeling approaches that take into account the superdiffusive nature of adatom motion are required for guiding knowledge-based synthesis of metal-layers nanostructures with controlled morphology^35,57−59 in nanoelectronic, optoelectronic, and catalytic devices based on weakly interacting substrates.³⁶⁻³⁹

Computational methods

We use AIMD simulations to study atomistic diffusion mechanisms with density functional theory (DFT) accuracy. All AIMD simulations are performed using the Vienna ab initio simulation package (VASP).⁶⁰ Core electrons are replaced by the projector augmented wave (PAW) pseudopotentials and the generalized gradient approximation of Perdew, Burke, and Ernzerhof (PBE).⁶¹ We use an energy cutoff of 400 eV for the plane waves and a 3 × 3 × 1 Γ-centered k-point mesh for the Brillouin zone integration. The monolayer graphene substrate is implemented as a hexagonal supercell containing 72 carbon atoms, between two vacuum layers of 10 Å thickness, and periodic boundary conditions are established in all three directions. We model the van der Waals forces using the DFT-D3 method with Becke–Johnson (BJ) damping,⁶² which accurately describes the properties of both graphite and diamond.⁶³ All simulations are spin-polarized. Initial test simulations showed that Ru and Pt exhibit diffusion patterns that are encountered in classical homoepitaxial growth systems, while Ag, Au, Cu, and Pd diffuse considerably faster and execute jumps across multiple adsorption sites. Hence, we focus on Ag, Au, Pd, and Cu adatoms, the diffusion of which is simulated for 0.2 ns, while reference simulations are performed for Pt and Ru adatoms for times of 0.02 and 0.04 ns, respectively.

We calculate the PEL at 0 K by computing the ground-state energies E_ads of the monomers on the hollow, top, and bridge sites using standard DFT static structure relaxations, and the PEL at room temperature, by averaging E_ads over the configurations of the AIMD simulations for which the monomer is found on each of the main adsorption sites.

AIMD runs are complemented by CMD simulations of Ag adatom diffusion on a graphene sheet of 680 atoms. These simulations are performed using LAMMPS.⁶⁴ The C–C and Ag–C interactions are described using AIREBO⁶⁵ and Lennard-Jones⁶⁶ potentials, respectively. The AIREBO potential is well-established in the literature for simulating carbon-based materials⁶⁷⁻⁷⁰ and, together with Lennard-Jones, is used to study the diffusion of noble metals (including Ag) clusters on graphite surfaces.⁷¹ More information about CMD validation can be found in the Supporting Information. We run a long simulation of 30 ns and 30 statistically independent simulations of 3 ns, both with a time step of 0.25 fs. We use canonical sampling (Nosé–Hoover thermostat) of the configurational space for all MD simulations. AIMD and CMD outputs are visualized using the Ovito freeware.⁷²

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.0c02375.

• Comparison of 0.02 ns long AIMD trajectories (S1); calculation of scaling exponent α (S2); high-accuracy calculation of static (0 K) adsorption energies (S3); entropy effects on diffusion dynamics (S4); potential energy landscape using classical interatomic potentials and CMD simulation analysis (S5) (PDF)

The authors declare no competing financial interest.