Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Oct 14;11(21):9152–9158. doi: 10.1021/acs.jpclett.0c02319

Full-Harmonics Phasor Analysis: Unravelling Multiexponential Trends in Magnetic Resonance Imaging Data

Wouter M J Franssen †,*, Frank J Vergeldt †, Arjen N Bader †,‡, Herbert van Amerongen †,‡, Camilla Terenzi †,*
PMCID: PMC7649845  PMID: 33053305

Abstract

graphic file with name jz0c02319_0004.jpg

Phasor analysis is a robust, nonfitting, method for the study of multiexponential decays in lifetime imaging data, routinely used in Fluorescence Lifetime Imaging Microscopy (FLIM) and only recently validated for Magnetic Resonance Imaging (MRI). In the established phasor approach, typically only the first Fourier harmonic is used to unravel time-domain exponential trends and their intercorrelations across image voxels. Here, we demonstrate the potential of full-harmonics (FH) phasor analysis by using all frequency-domain data points in simulations and quantitative MRI (qMRI) T2 measurements of phantoms with bulk liquids or liquid-filled porous particles and of a human brain. We show that FH analysis, while of limited advantage in FLIM due to the correlated nature of shot noise, in MRI outperforms single-harmonic phasor in unravelling multiple physical environments and partial-volume effects otherwise undiscernible. We foresee application of FH phasor to, e.g., big-data analysis in qMRI of biological or other multiphase systems, where multiparameter fitting is unfeasible.

Phasor representation of exponential decays is a robust and nonfitting method designed for describing multicomponent decays from lifetime imaging data.1−3 The established phasor method maps the time-domain decay from each voxel to only two numbers, the real and imaginary parts of the first Fourier Transform (FT) harmonic of the raw lifetime imaging data. Those points can all be displayed in a collective two-dimensional (2D) phasor plot, where mono- as well as multicomponent trends from all voxels are displayed and discerned. Remarkably, unique information about intervoxel correlations, inaccessible by fitting analysis, is unraveled in a phasor plot; in this way, multicomponent trends can be unmixed by establishing the relative amplitudes of their underlying monoexponential terms.

The single-harmonic phasor approach is used extensively in fluorescence lifetime imaging microscopy (FLIM), where accurate description of multicomponent decays in images is highly desirable.1,4−7 The well-established advantage of quantitative phasor analysis of lifetime images, as compared to multivoxel multiexponential fitting, lies in the fact that it enables the study of exponential decays within all voxels of an imaging data set simultaneously, without any prior assumption or knowledge about the number of lifetimes present within each voxel. In addition, being a nonfitting procedure based solely on an exact FT mathematical procedure, phasor does not introduce any further errors during data analysis.

Very recently, standard single-harmonic phasor analysis has been introduced and validated for the analysis of quantitative Magnetic Resonance Imaging (qMRI) data, either in vivo or from other multiphase heterogeneous systems, under the influence of T2 relaxation or diffusion.8−10 Current data analysis methods in all applications of qMRI rely solely on per-voxel iterative approximations, either by ill-posed Inverse Laplace Transform algorithms,11−16 to extract distributions of lifetimes, or mostly by drastic simplifications to single-exponential fitting for the scope of faster data analysis.17,18 It has been shown that, in qMRI, phasor processing excels compared to multiparameter fitting in unravelling multiexponential trends,8 as well as partial-volume effects9 that are otherwise not recognized by fitting. Yet, the accuracy of the established single-harmonic phasor analysis is severely limited, in qMRI more than in FLIM data, by the low signal-to-noise ratio (SNR) typical of in vivo, or other types of fast, measurements.19,20 One of the main reasons behind the limited accuracy of standard phasor analysis lies in the fact that just a single Fourier harmonic, often either the first or the second, is used for the construction of a phasor plot:21,22 the information from all other higher harmonics, which also could contribute to increasing the SNR, is usually discarded. This loss of information in the phasor plot, and the associated SNR reduction, is a key limiting factor10 to unlocking the full advantage of using phasor analysis for its most interesting potential applications in qMRI, namely, for real-time measurements or big-data acquired in suboptimal conditions of SNR and/or of time-domain sampling.

Here, we set out to reduce the effect of noise in phasor analysis of qMRI data in order to improve the accuracy and information content of phasor plots. To this aim, we introduce a new full-harmonics (FH) phasor approach based on off-axis projections of the full phasor space. We show that our proposed FH method (i) uses all the available Fourier harmonics present in the frequency domain and (ii) yields a 2D phasor representation with optimized information content about multicomponent decays from any lifetime imaging data set, without requiring changes on the acquisition parameters. This advancement will be useful in a wide range of applications of qMRI, from porous media to biological tissues, with possible extension to data sets with other time dependences, such as kinetics studies.23−27 Specifically, we envision useful applications in the emergent field of big-data analysis of medical qMRI data, with either relaxation or diffusion contrast, where using multicomponent fitting procedures is often unfeasible due to the low robustness and prohibitively long analysis time involved.

For an exponential decay sampled with an even number N of real data points, there is a maximum of N/2 + 1 harmonics in the Fourier series. In phasor analysis, the intensity of the zeroth-order harmonic is used as a normalization value for all other harmonics. Therefore, N/2 harmonics can be used for the plot with both a real and imaginary part, and the full phasor space is therefore N-dimensional.

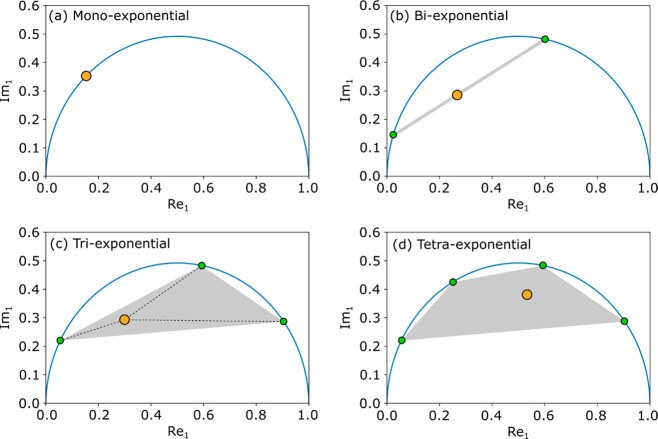
In the conventional phasor representation, the real part of the first harmonic (Re1) is plotted vs the respective imaginary part (Im1). In such a phasor plot, each monoexponential decay shows up as a point on a semicircle of radius 1/2, if equidistant sampling in the time domain is used, and on a distorted semicircle otherwise. Multiexponential decays give rise to a cloud of points within the area defined by this semicircle, in a polygon whose vertices represent the lifetimes of each single-exponential component of the multicomponent decay. For instance, a biexponential decay with lifetimes τ1 and τ2 leads to a point on the line connecting the two points on the semicircle that represent the two lifetimes τ1 and τ2. The position of this point along the biexponential line is determined by the relative population of the two lifetimes. A distribution of the relative populations, as occurs, e.g., due to partial-volume effects, will manifest as a series of data points along this line. Triexponential decays fall within a triangle, tetraexponentials fall within a tetragon, and so on. Figure 1 shows examples of first-harmonic phasor plots for the cases discussed above. For up to three-component decays, and if the underlying lifetimes are known, the relative populations of single-component terms can be determined, i.e., unmixed, on the basis of the position in the phasor plot. For decays with four or more components, the position within the polygon is not uniquely determined, making unmixing not possible from the 2D representation. This unmixing is, however, possible from a 4D representation, by using two harmonics simultaneously.28

Figure 1.

Figure 1

Open in a new tab

From (a) to (d): examples of first-harmonic phasor plots for mono-, bi-, tri- and tetraexponential decays, respectively. The lifetime (orange dot) falls on the semicircle (blue line) in (a), on a line (gray line) in (b), and within a polygon (gray area) in (c) and (d). For (b) and (c) the position of the lifetime uniquely arises from the positions of the lifetimes for the underlying monoexponential decays (green dots) on the semicircle, and their relative populations.

Considering the full set of Fourier harmonics as a multidimensional variable space, a plot of Re1 versus Im1 is a projection of the full data set on the Re1–Im1 plane. From a set of Ren and Imn variables, with n varying from 1 to N/2, one can in principle make O(N2) different 2D phasor plots. In a higher-harmonic plot, where Ren vs Imn (n > 1) is reported, the same grouping of points along lines or within polygons as shown in Figure 1 occurs. However, the position of each lifetime along the semicircle shifts anticlockwise when compared to the first-harmonic plot, except for very long or very short lifetimes compared to the sampling interval, which will remain at positions [0,0] and [1,0], respectively. The amount of this shift depends on the length of the lifetime, because using higher harmonics essentially corresponds to sampling a Lorentzian function, which is the Fourier pair of an exponential decay, further towards higher frequencies. The largest shift occurs for lifetimes where Re1 ≈ 0.7, as there the slope of the Lorentz function is highest. This shift also affects the representation of multiexponential patterns, which can stretch or contract in the phasor plot depending on the underlying lifetimes. Ultimately, this affects the accuracy of phasor analysis, and thus the optimal harmonic to plot depends on the data.

Other combinations of real and imaginary parts of the harmonics are also possible, for instance Ren vs Imm or Ren vs Rem, with n ≠ m (see example in Figure S1). Each projection of the full phasor data has the same properties as those shown in Figure 1, but with a different shape of the “semicircle”. We will, however, keep calling it the “semicircle”, in order to use established terminology.

How well a specific data set is described will depend on the chosen axes, and therefore on the shape of the semicircle. For biexponential data, there are two criteria for optimizing the choice of the axes of the FH phasor plot: (i) the two points representing the underlying monoexponential trends should be as far as possible from each other, with respect to the experimental noise, to enable the most accurate unmixing; (ii) the line connecting these points should be as distant as possible from the semicircle, compared to the experimental noise, to facilitate identification of biexponential trends. The effect of the above-mentioned criteria is shown in some examples of projections of 3D phasor data in Figure S1b–d.

So far, only phasor plots whose x and y axes are single Ren or Imm values have been considered. However, also linear combinations of all such harmonics can be used for both axes in order to optimize the 2D phasor projection for each given data set. Here, we refer to this as our proposed FH phasor approach.

The selection of these linear combinations of harmonics can be done by defining three points in the N-dimensional phasor space, as any plane can be mathematically defined by three points. For phasor data, this is best done by selecting three points on the semicircle, each representing a different lifetime, which can be readily calculated in N dimensions. The three selected lifetimes then define the projection plane of the phasor plot. The algorithm developed to achieve this can be found in the Supporting Information section 2 and Figure S2.

For biexponential data, two of the selected projection lifetimes should coincide with the lifetimes of the underlying monoexponential decays. The third projection lifetime should be between these, making sure that the longest distance between the line on which the biexponential data falls and the semicircle is maximized. For triexponential data, the surface area of the “triangle” (Figure 1) should be maximized to enable the most accurate unmixing, and this is achieved by selecting the three underlying lifetimes as the projection lifetimes.

The selection of the projection plane can also be done automatically, for example by Principle Component Analysis (PCA). PCA can be used to find the projection plane with the highest information content. Yet, PCA does not maximize the distance between the biexponential data and the semicircle, because the semicircle is not part of the data and is therefore not taken into account by PCA. The algorithm and examples of PCA application to phasor data can be found in the Supporting Information (section 3 and Figure S3).

As stated above, the accuracy of unmixing for biexponential data depends on the separation of the phasors associated with the two constitutive monoexponential decays, with respect to the experimental noise. For qMRI data, the noise in the phasor space is the same for each Fourier harmonic and is uncorrelated, when assuming Gaussian noise. Therefore, the average noise level in the phasor plot is independent of the chosen axes and this means that, for qMRI data, the best unmixing accuracy can therefore be obtained by choosing axes that yield the largest separation of the two lifetimes in the resulting phasor plot. We note here that if the qMRI images are processed in magnitude mode, part of each decay can be affected by Rician, and not Gaussian, noise, which would require offset correction prior to the phasor analysis.29 For FLIM data the situation is different, because shot noise is correlated over the harmonics, and hence it increases in a FH view (see the Supporting Information section 4 and Figure S4). In our opinion, this is likely the reason why the FH approach has thus far not been developed for FLIM studies.28 We note that for camera-based FLIM measurements, where shot noise is less relevant, FH processing might still be advantageous; further elaboration on this is beyond the scope of this work.

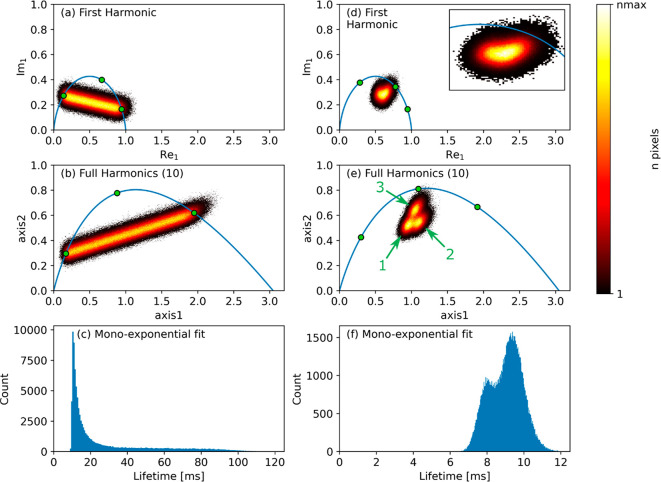
In the following, we focus on validating the FH method for qMRI applications. Figure 2 demonstrates the improvement that can be obtained by using FH processing compared to first-harmonic phasor plots for two sets of simulated data. Panels a–c of Figure 2 show biexponential data sets with a randomly chosen fraction of the two decay rates. The FH approach increases the separation of the underlying monoexponential decays, and thus the unmixing accuracy, by a factor of 2.2. This implies that the experimental time could be reduced by a factor (2.2)2 = 4.8 in this case for obtaining the same accuracy as in Figure 2a. The maximum distance between the biexponential line and the semicircle has improved by a factor of 1.5. Compared to the commonly used monoexponential fit (see Figure 2c), the biexponential nature of the imaging data set is much better visualized in the phasor plot, and this representation is optimized even further in the FH view.8

Figure 2.

Figure 2

Open in a new tab

Phasor analysis and monoexponential fitting results of simulated data with biexponential decays (left column) or with three different multicomponent decays (right column). The time axis consisted of 20 points, with sampling interval Δt. The first row shows the first-harmonic phasor plots, while the second row shows the FH plots. In the last row, the results of a monoexponential fit of the data are displayed. In (b) and (e) the lifetimes used for the definition of the projection plane are indicated by green dots, which are at (Δt, 2.6·Δt, 10·Δt) for (b) and at (Δt, 2·Δt, 6·Δt) for (e). The number of used harmonics is shown in brackets in the legend. The insert in (d) shows a zoom in of the cloud.

Panels d–f of Figure 2 demonstrate FH processing on a simulated data set consisting of three distinct populations, described by either two or three lifetimes each. The populations that are overlapping in the single-harmonic phasor plot can be separated using FH processing. Considering the multiexponential nature of the data set, the advantage of using phasor in separating these populations is remarkable. By using mono- or biexponential fitting (see respectively Figure 2f and Figure S5), these populations cannot be readily separated.

The improvement in unmixing accuracy for biexponential data depends on the number of sampled points in the time domain, as well as on the length of the two lifetimes relative to the sampling interval Δt (see Figure S6). The SNR of the data set is of no relevance in this respect. Indeed, the improvement factor, namely, the ratio between the unmixing accuracy using FH and only the first-harmonic, cannot be lower than 1, as FH processing always adds information and increases the SNR. Yet, for cases where both lifetimes are long compared to Δt, the improvement might be too low to be of any interest. The maximum improvement factor, for very short lifetimes, is roughly equal to the number of sampled points in the time domain. FH processing may also be used to aid in choosing optimal sampling strategy for known lifetimes, but the discussion of this topic is beyond the scope of the present work.

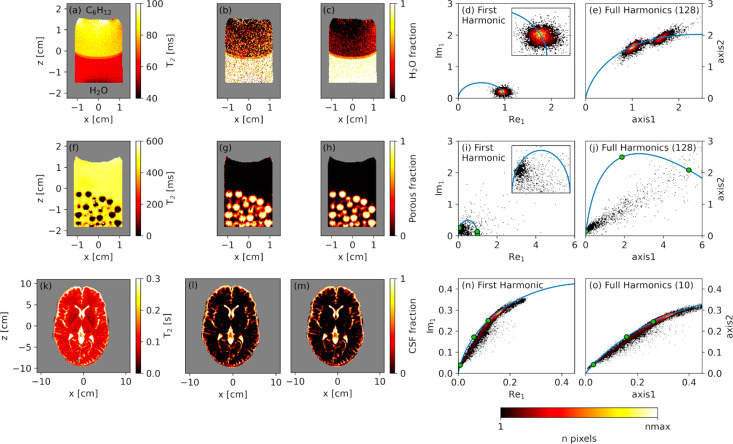
To best visualize the physical insight provided by FH phasor analysis, both in phasor plots and in respective unmixing imaging results, we show FH processing on two phantoms and also validate the FH analysis on an in vivo human brain data set, previously already analyzed by a single-harmonic phasor by Vergeldt et al.8 The data sets for phantoms I and II were acquired at SNR values of 30–50 in the first echo image, to match the SNR condition of the human brain data set. We further underline that improvement in unmixing accuracy is independent of SNR, although more visible in low-SNR images, while it may depend on data sampling (see Figure S6 in the Supporting Information). The above examples of T2 MRI data were here chosen, respectively, with the aim to (I) disentangle overlapping lifetimes in low-SNR data from bulk liquids, (II) reveal partial-volume effects in low-SNR data from a liquid/solid phantom, and (III) increase unmixing accuracy in data from biological tissues. System I is a bulk liquid phantom consisting of two immiscible liquids, namely, a cyclohexane layer on top of distilled water, vertically stacked inside a 25 mm NMR tube (see Figure 3a). In this case, each liquid yields a well-defined single-exponential decay. A low-SNR data set was recorded by an excitation flip angle of 7° and an excessive number of echoes. System II is a phantom consisting of porous alumina pellets immersed in excess bulk cyclohexane, the latter forming an additional bulk-only layer on top of the particles (see Figure 3f). In this case, partial-volume effects are expected to occur due to the fact that voxels contain both bulk and intra-particle cyclohexane, the latter having a much shorter T2 than the bulk phase. Also in this case, a low flip angle of 4° was used to reduce the SNR. System III is the in vivo qMRI measurement of a human brain (see Figure 3k).8 Data sets I and II consisted of phased real data, while the brain data were acquired in magnitude mode. Owing to the long lifetimes and short sampling of the brain data set, the noise can be assumed to be Gaussian with no issues due to Rician noise typical of magnitude data.29 The results of the single-harmonic and FH phasor analyses are displayed in Figure 3, along with the T2 maps obtained by monoexponential fitting.

Figure 3.

Figure 3

Open in a new tab

For a two-layer liquid phantom with water and cyclohexane (first row), a cyclohexane layer with porous alumina pellets (second row), and a human brain (third row): experimental T2 MRI maps obtained by monoexponential fitting ((a), (f) and (k)); unmixing results from the first-harmonic phasor plot ((b), (g), and (l)); unmixing results from the FH phasor plot ((c), (h), and (m)); respective first-harmonic ((d), (i), and (n)) and FH ((e), (j), and (o)) phasor plots. In the images in the first three columns, masked areas are depicted in gray. The green dots in the phasor plots represent the three lifetimes used to define the projection plane, namely (58, 70, and 85 ms) in (e), (6.1, 20, and 490 ms) in (j), and (97, 150, and 700 ms) in (o).

Panels a–e of Figure 3 demonstrate the capability of FH phasor in separating the two populations present in phantom I. We note that the short apparent T2 values in system I are caused by the strong field gradients used during the measurement. While the T2 decays for water and cyclohexane appear overlapping in the single-harmonic view, they are readily separated in FH analysis with a remarkable accuracy improvement by a factor of 8.6. Unmixing the phasor information from single- and full-harmonics analysis, to obtain the water/cyclohexane fraction in every voxel, leads respectively to Figure 3b,c. From these images, it is clear that the FH method is much less influenced by noise than single-harmonic phasor. We note that by reducing the excessively large number of recorded echoes (256) to the minimum number of echoes (64) needed to observe the full T2 decay, we obtain a lower factor, 1.9 improvement in unmixing accuracy by FH: this is due to the fact that first-harmonic phasor performs relatively well for these particular sampling conditions.

Panels f–j of Figure 3 demonstrate the advantage of FH phasor processing when describing partial-volume effects in system II. Due to the high amount of noise in this data set, the first-harmonic phasor is not able to visualize the line indicative of a biexponential decay, as was explained in Figure 1b. FH processing does reveal this trend, yielding an increased unmixing accuracy by a factor 6.3, as well as a factor 4.4 improvement of the maximum distance between the biexponential line and the semicircle. This increase in unmixing accuracy is well visible in Figure 3g,h, where the fraction of intra-pore cyclohexane signal is mapped.

For the final validation on in vivo brain data in Figure 3k–o, whose improved accuracy is expected not to be readily visible from the images with phasor unmixing due to their high SNR, a biexponential trend is observed in the phasor plots due to partial-volume effects of cerebral spinal fluid (CSF) and white matter. The separation of the two lifetimes is improved by a factor 1.3 in the FH view when compared to the first-harmonic plot, as is demonstrated in Figure 3n,o. The same unmixing accuracy as in Figure 3l could therefore be obtained by 1.32 = 1.7 times faster image acquisition. The more modest improvement factor in this data set, when compared to phantoms I and II, is due to the longer lifetimes in this data set, relative to the echo time used. Unmixing this data yields the data shown in Figure 3l,m, using first harmonic and FH processing, respectively. Unmixing can also be done by global fitting of the time-domain data with a biexponential function, which leads to similar results (see Figure S7). We note, however, that segmentation and model selection in this case is still based on the phasor analysis and that fitting is more computationally involved compared to unmixing from the phasor plot.

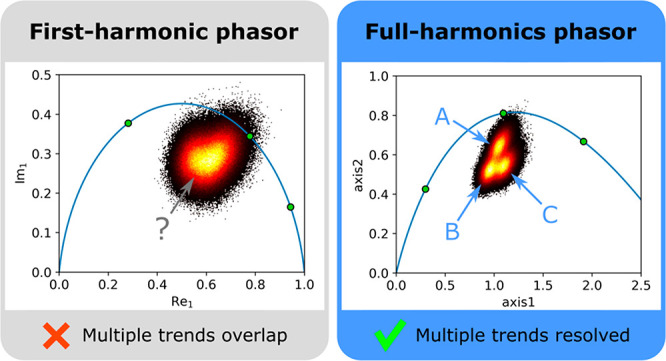
In all cases shown in Figure 3, the phasor plot is considerably improved by utilizing the information from all Fourier harmonics simultaneously. This allows for better separation of different physical environments, and identification of partial-volume effects that are not unveiled by first harmonic phasor analysis. In cases where SNR is low, even the unmixing images are significantly improved, which in turn is of great value for aiding segmentation analysis.

In conclusion, we have shown that our proposed FH phasor analysis enables increasing both SNR and unmixing accuracy in phasor plots as compared to the established single-harmonic phasor method, as well as to enable unravelling partial-volume effects otherwise undiscernible. In our FH analysis, a projection plane must be defined in the phasor space either manually, by selecting three lifetimes, or automatically, by using PCA. In all cases, the information content of the FH phasor plots is enhanced, without changing the sampling scheme of the experiment, while retaining the linear property of the phasor plot (Figure 1), even in cases where suboptimal time-domain sampling schemes are used and/or a data exhibit poor SNR. In the experimental applications considered in this paper, an improvement of 1.3—8.6 in separating populations was obtained with respect to single-harmonic phasor.

Thanks to this advancement, FH phasor of qMRI data is able to provide, for all voxels in the lifetime imaging data set and without recurring to any fitting procedure, additional physical insight on multicomponent decays and/or partial-volume effects otherwise not accessible in conventional phasor analysis. We foresee that the unique information provided by the FH phasor, without the need to make any a priori assumption on the number of lifetimes, can help by optimizing (i) multicomponent fitting, by providing suitable input for model selection, and (ii) the design of faster measurements in multiphase materials, in terms of both sampling strategy of time-domain data points and required SNR. Ultimately, our FH method enables more accurate analysis of lifetime imaging data and will be useful in a wide range of relevant applications of qMRI, from porous media up to biological tissues. Specifically, this method development is expected to have considerable impact in the field of big-data analysis in medical MRI, where data processing by multiparameter iterative fitting is not robust as well as time-consuming.

Experimental and Computational Methods

The 2D T2-MRI images of a sample of cyclohexane (J. T. Baker, >99%) on top of distilled water were recorded on a Bruker Ascend 300 WB magnet using an Avance III console. Excitation and detection of the H1 signal were performed using a Bruker MICWB 40 RF probe inside a Micro 2.5 gradient WB system with maximum gradient strength of 1.5 T/m. The signal was recorded using a multislice-multiecho (MSME) imaging sequence.30 Examination parameters were 256 echoes with echo time 8 ms, field of view 45 × 30 mm, 128 × 128 voxels, slice thickness 1 mm, bandwidth 50 kHz, repetition time 8 s, number of averages 1, and total time 17 min 4 s. A low flip angle (7°) was used to simulate a low SNR case. The data were used in real (phased) mode.

The 2D T2-MRI images of the alumina pellets (spherical, 5 mm diameter, uniform pore size of about 180 nm; see the Ssupporting Information), soaked for several days in cyclohexane were recorded on the same system using the same MSME sequence. For this data set, the examination parameters were 256 echoes with echo time 3.2 ms, field of view 45 × 30 mm, 128 × 128 voxels, slice thickness 1 mm, bandwidth 100 kHz, repetition time 8 s, number of averages 1, and total time 17 min 4 s. A low flip angle (4°) was used to simulate a low SNR case. The data were used in real (phased) mode.

Multislice 2D T2-MRI images of the brain of a healthy human volunteer were acquired on a 3 T whole body MR system (Magnetom TimTrio, Siemens Healthcare, Erlangen, Germany). Examination parameters were 20 echoes with echo times 8.7 ms, field of view 220 × 220 mm, 256 × 256 voxels, 15 slices, slice thickness 3 mm, interslice gap 3 mm, repetition time 3 s, number of averages 1, and total time 7 min 58 s. The data were used in magnitude mode. For the phasor images, a 5 × 5 mean filter was used in the spatial domain. For the T2 and unmixing images no filter was applied.8 The experiment was carried out in accordance with relevant guidelines and regulations. The MRI examination of the healthy volunteer was approved by the local institutional review board (METC CMO Regio Arnhem-Nijmegen) and the volunteer gave written informed consent prior to the MR exam.

The data shown in Figure 2 were simulated using Python 3.8 scripts. The data in Figure 2a–c are biexponential, with lifetimes Δt and 10·Δt, with 20 sampling points and Δt = 5 ms. All 1 million simulated decays have a random combination of the two underlying single-exponential decays with added Gaussian noise. The FH plot in Figure 2b uses lifetimes Δt, 2.6·Δt, and 10·Δt to define the projection plane and utilizes all 10 harmonics. Gaussian noise was added to time-domain data, with relative amplitude of 0.1.

For Figure 2d–f the data consist of three different populations with Gaussian noise added (relative width 0.1, time domain). Each population consists of a mixture of two or three monoexponential decays with a constant intensity ratio. Each of these monoexponential decays was normalized to its sum before use. In total, 5 million decays were simulated. Population 1 is biexponential (lifetimes 6·Δt and Δt, 0.41 and 0.59 intensity), population 2 is biexponential (lifetimes 6·Δt and Δt, 0.5 and 0.5 intensity), and population 3 is triexponential (lifetimes 6·Δt, 2·Δt, and Δt, 0.32, 0.41, and 0.27 intensity). The time axis consisted of 20 points with Δt = 5 ms. The FH plot in (e) uses lifetimes Δt, 2·Δt, and 6·Δt to define the projection plane, and all 10 harmonics were used.

The monoexponential fits in Figure 2c,f were performed on 100 000 decays using the Levenberg–Marquardt algorithm. Processing of the experimental data was performed using Python 3.8 scripts developed in-house.

Acknowledgments

We thank Tom Scheenen (Department of Radiology and Nuclear Medicine, Radboud UMC, Nijmegen, The Netherlands) for supplying the brain MRI data. This work is part of the 4TU Precision Medicine program supported by High Tech for a Sustainable Future, a framework commissioned by the four Universities of Technology of The Netherlands (https://www.4tu.nl/en/news/!/393/awarding_hightech/).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.0c02319.

  • Description of the FH phasor algorithm, illustration of the use of PCA in phasor, explanation of the effect of shot noise in fluorescence, illustrations on projection plane definition in three dimensions, results of biexponential fitting for the data in Figure 2, plots of the improvement of unmixing accuracy of biexponential data for a range of lifetimes with respect to first-harmonic processing, and approximate estimation of the pore size of the alumina pellets by 1H NMR T2 relaxation data from Figure 3 (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz0c02319_si_001.pdf (995.4KB, pdf)

References

  1. Clayton A. H.; Hanley Q. S.; Verveer P. J. Graphical representation and multicomponent analysis of single-frequency fluorescence lifetime imaging microscopy data. J. Microsc. 2004, 213 (1), 1–5. 10.1111/j.1365-2818.2004.01265.x. [DOI] [PubMed] [Google Scholar]
  2. Fereidouni F.; Bader A. N.; Gerritsen H. C. Spectral phasor analysis allows rapid and reliable unmixing of fluorescence microscopy spectral images. Opt. Express 2012, 20 (12), 12729–41. 10.1364/OE.20.012729. [DOI] [PubMed] [Google Scholar]
  3. Stefl M.; James N. G.; Ross J. A.; Jameson D. M. Applications of phasors to in vitro time-resolved fluorescence measurements. Anal. Biochem. 2011, 410 (1), 62–69. 10.1016/j.ab.2010.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Leray A.; Spriet C.; Trinel D.; Usson Y.; Heliot L. Generalization of the polar representation in time domain fluorescence lifetime imaging microscopy for biological applications: practical implementation. J. Microsc. 2012, 248 (1), 66–76. 10.1111/j.1365-2818.2012.03651.x. [DOI] [PubMed] [Google Scholar]
  5. Digman M. A.; Caiolfa V. R.; Zamai M.; Gratton E. The phasor approach to fluorescence lifetime imaging analysis. Biophys. J. 2008, 94 (2), L14–16. 10.1529/biophysj.107.120154. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Ranjit S.; Dobrinskikh E.; Montford J.; Dvornikov A.; Lehman A.; Orlicky D. J.; Nemenoff R.; Gratton E.; Levi M.; Furgeson S. Label-free fluorescence lifetime and second harmonic generation imaging microscopy improves quantification of experimental renal fibrosis. Kidney Int. 2016, 90 (5), 1123–1128. 10.1016/j.kint.2016.06.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Iermak I.; Vink J.; Bader A. N.; Wientjes E.; van Amerongen H. Visualizing heterogeneity of photosynthetic properties of plant leaves with two-photon fluorescence lifetime imaging microscopy. Biochim. Biophys. Acta, Bioenerg. 2016, 1857 (9), 1473–1478. 10.1016/j.bbabio.2016.05.005. [DOI] [PubMed] [Google Scholar]
  8. Vergeldt F. J.; Prusova A.; Fereidouni F.; Van Amerongen H.; Van As H.; Scheenen T. W. J.; Bader A. N. Multi-component quantitative magnetic resonance imaging by phasor representation. Sci. Rep. 2017, 7 (1), 861. 10.1038/s41598-017-00864-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Deng R.; Janssen A. E. M.; Vergeldt F. J.; Van As H.; de Graaf C.; Mars M.; Smeets P. A. M. Exploring in vitro gastric digestion of whey protein by time-domain nuclear magnetic resonance and magnetic resonance imaging. Food Hydrocolloids 2020, 99, 105348. 10.1016/j.foodhyd.2019.105348. [DOI] [Google Scholar]
  10. van Rijssel M. J.; Froeling M.; van Lier A.; Verhoeff J. J. C.; Pluim J. P. W. Untangling the diffusion signal using the phasor transform. NMR Biomed. 2020, e4372 10.1002/nbm.4372. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Venkataramanan L.; Song Y.-Q.; Hurlimann M. D. Solving Fredholm integrals of the first kind with tensor product structure in 2 and 2.5 dimensions. IEEE Trans. Signal Process 2002, 50 (5), 1017–1026. 10.1109/78.995059. [DOI] [Google Scholar]
  12. Reci A.; Sederman A. J.; Gladden L. Obtaining sparse distributions in 2D inverse problems. J. Magn. Reson. 2017, 281, 188–198. 10.1016/j.jmr.2017.05.010. [DOI] [PubMed] [Google Scholar]
  13. Ioannidis G. S.; Nikiforaki K.; Kalaitzakis G.; Karantanas A.; Marias K.; Maris T. G. Inverse Laplace transform and multiexponential fitting analysis of T2 relaxometry data: a phantom study with aqueous and fat containing samples. Eur. Radiol. Exp. 2020, 4, 28. 10.1186/s41747-020-00154-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Bai R.; Koay C. G.; Hutchinson E.; Basser P. J. A framework for accurate determination of the T2 distribution from multiple echo magnitude MRI images. J. Magn. Reson. 2014, 244, 53–63. 10.1016/j.jmr.2014.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Benjamini D.; Basser P. J. Water mobility spectral imaging of the spinal cord: Parametrization of model-free Laplace MRI. Magn. Reson. Imaging 2019, 56, 187–193. 10.1016/j.mri.2018.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. de Almeida Martins J. P.; Topgaard D. Multidimensional correlation of nuclear relaxation rates and diffusion tensors for model-free investigations of heterogeneous anisotropic porous materials. Sci. Rep. 2018, 8 (1), 2488. 10.1038/s41598-018-19826-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Akçakaya M.; Basha T. A.; Weingärtner S.; Roujol S.; Berg S.; Nezafat R. Improved quantitative myocardial T2 mapping: Impact of the fitting model. Magn. Reson. Med. 2015, 74 (1), 93–105. 10.1002/mrm.25377. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Whittall K. P.; MacKay A. L.; Li D. K. Are mono-exponential fits to a few echoes sufficient to determine T2 relaxation for in vivo human brain?. Magn. Reson. Med. 1999, 41 (6), 1255–1257. . [DOI] [PubMed] [Google Scholar]
  19. Leray A.; Spriet C.; Trinel D.; Blossey R.; Usson Y.; Heliot L. Quantitative comparison of polar approach versus fitting method in time domain FLIM image analysis. Cytometry, Part A 2011, 79 (2), 149–158. 10.1002/cyto.a.20996. [DOI] [PubMed] [Google Scholar]
  20. Rowley M. I.; Barber P. R.; Coolen A. C.; Vojnovic B. In Bayesian analysis of fluorescence lifetime imaging data, Multiphoton Microscopy in the Biomedical Sciences XI; International Society for Optics and Photonics, 2011; p 790325. [Google Scholar]
  21. Sanchez S.; Bakas L.; Gratton E.; Herlax V. Alpha hemolysin induces an increase of erythrocytes calcium: a FLIM 2-photon phasor analysis approach. PLoS One 2011, 6 (6), e21127 10.1371/journal.pone.0021127. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Cutrale F.; Salih A.; Gratton E. Spectral phasor approach for fingerprinting of photo-activatable fluorescent proteins Dronpa, Kaede and KikGR. Methods Appl. Fluoresc. 2013, 1 (3), 035001. 10.1088/2050-6120/1/3/035001. [DOI] [PubMed] [Google Scholar]
  23. Xiao D.; Balcom B. J. Ultra-short echo time imaging with multiple echo refocusing for porous media T2 mapping. J. Magn. Reson. 2019, 299, 33–41. 10.1016/j.jmr.2018.12.003. [DOI] [PubMed] [Google Scholar]
  24. Xiao D.; Balcom B. J. Two-dimensional T2 distribution mapping in rock core plugs with optimal k-space sampling. J. Magn. Reson. 2012, 220, 70–78. 10.1016/j.jmr.2012.04.003. [DOI] [PubMed] [Google Scholar]
  25. Song Y.-Q. Recent progress of nuclear magnetic resonance applications in sandstones and carbonate rocks. Vadose Zone J. 2010, 9 (4), 828–834. 10.2136/vzj2009.0171. [DOI] [Google Scholar]
  26. Poonoosamy J.; Haber-Pohlmeier S.; Deng H.; Deissmann G.; Klinkenberg M.; Gizatullin B.; Stapf S.; Brandt F.; Bosbach D.; Pohlmeier A. Combination of MRI and SEM to Assess Changes in the Chemical Properties and Permeability of Porous Media due to Barite Precipitation. Minerals 2020, 10 (3), 226. 10.3390/min10030226. [DOI] [Google Scholar]
  27. Gore J.; Anderson A.; Does M.; Gochberg D.; Joers J. M.; Kennan R.; Parsons E.; Schachter M. The relationship of problems in biomedical MRI to the study of porous media. Magn. Reson. Imaging 2001, 19 (3–4), 295–300. 10.1016/S0730-725X(01)00239-9. [DOI] [PubMed] [Google Scholar]
  28. Vallmitjana A.; Dvornikov A.; Torrado B.; Jameson D. M.; Ranjit S.; Gratton E. Resolution of 4 components in the same pixel in FLIM images using the phasor approach. Methods Appl. Fluoresc. 2020, 8 (3), 035001. 10.1088/2050-6120/ab8570. [DOI] [PubMed] [Google Scholar]
  29. Gudbjartsson H.; Patz S. The Rician distribution of noisy MRI data. Magn. Reson. Med. 1995, 34 (6), 910–914. 10.1002/mrm.1910340618. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Edzes H. T.; van Dusschoten D.; Van As H. Quantitative T2 Imaging of Plant Tissues By Means Of Multi-Echo MRI Microscopy. Magn. Reson. Imaging 1998, 16 (2), 185–196. 10.1016/S0730-725X(97)00274-9. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz0c02319_si_001.pdf (995.4KB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES