Ambient PM_2.5 exposure and rapid spread of COVID-19 in the United States

Abstract

It has been posited that populations being exposed to long-term air pollution are more susceptible to COVID-19. Evidence is emerging that long-term exposure to ambient PM_2.5 (particulate matter with aerodynamic diameter 2.5 μm or less) associates with higher COVID-19 mortality rates, but whether it also associates with the speed at which the disease is capable of spreading in a population is unknown. Here, we establish the association between long-term exposure to ambient PM_2.5 in the United States (US) and COVID-19 basic reproduction ratio R₀– a dimensionless epidemic measure of the rapidity of disease spread through a population. We inferred state-level R₀ values using a state-of-the-art susceptible, exposed, infected, and recovered (SEIR) model initialized with COVID-19 epidemiological data corresponding to the period March 2–April 30. This period was characterized by a rapid surge in COVID-19 cases across the US states, implementation of strict social distancing measures, and a significant drop in outdoor air pollution. We find that an increase of 1 μg/m³ in PM_2.5 levels below current national ambient air quality standards associates with an increase of 0.25 in R₀ (95% CI: 0.048–0.447). A 10% increase in secondary inorganic composition, sulfate-nitrate-ammonium, in PM_2.5 associates with ≈10% increase in R₀ by 0.22 (95% CI: 0.083–0.352), and presence of black carbon (soot) in the ambient environment moderates this relationship. We considered several potential confounding factors in our analysis, including gaseous air pollutants and socio-economical and meteorological conditions. Our results underscore two policy implications – first, regulatory standards need to be better guided by exploring the concentration-response relationships near the lower end of the PM_2.5 air quality distribution; and second, pollution regulations need to be continually enforced for combustion emissions that largely determine secondary inorganic aerosol formation.

Graphical abstract

1. Introduction

In December 2019, a new strain of coronavirus, SARS-CoV-2, began infecting residents of Wuhan Province, China (Chinazzi et al., 2020; Li et al., 2020b; Wu et al., 2020a; Xu et al., 2020). In the following months, the disease caused by SARS-CoV-2 – coronavirus disease 2019 (COVID-19) – has spread to nearly every country around the globe, and the situation had rapidly evolved into a global pandemic (Chinazzi et al., 2020; Gilbert et al., 2020). The viral entry of SARS-CoV-2 has been shown to use Angiotensin-converting enzyme 2 (ACE2) as its co-host receptor (Wan et al., 2020). ACE2 plays a crucial role in lung protection by cleaving and converting angiotensin II (Ang II) to the cardioprotective angiotensin 1–7 (Ang 1–7) (Tikellis and Thomas, 2012). Clinical observations of COVID-19 patients (Guan et al., 2020) suggest a mechanism involving viral loads of SARS-CoV-2 depleting residual ACE2 activity and impairing host defenses. This causes an imbalance between Ang II and Ang 1–7, resulting in high circulating levels of Ang II, which induces pulmonary vasoconstriction, inflammation, and oxidative stress (Derouiche, 2020). Consequently, depleted lungs, typically in the form of acute lung injury or its most serious form, acute respiratory distress syndrome, manifest in patients with COVID-19 (Li et al., 2020a).

A recent study by Italian medical researchers posited a causal link between SARS-CoV-2 infection rate and long-term air pollution exposure in a population (Frontera et al., 2020). They postulated a “double-hit phenomenon”: patients chronically exposed to high levels of fine particulate matter (PM_2.5; particulate matter with aerodynamic diameter 2.5 μm or less) present themselves with an overexpression of ACE2 (Lin et al., 2018), which readily facilitates penetration of the viral infection. This in turn depletes ACE2 receptors and gives rise to more severe forms of the disease. Subsequently, the spread of the disease accelerates among the population.

Exposure to PM_2.5 has a well-established association with increased risks and severe outcomes during infectious disease outbreaks, including COVID-19, the 2009 H1N1, and the 1918 Spanish influenza pandemics (Clay et al., 2018; Clay et al., 2019; Morales et al., 2017; Wu et al., 2020b) Exposure to PM_2.5 has been causally linked to occurrences of chronic respiratory disease, infectious respiratory disease, asthma, inflammation, and decreased lung function (Zhou et al., 2020). Recent studies have have strongly associated COVID-19 mortality with long-term air pollution exposure in the US (Wu et al., 2020b), as well as identifying that long-term meteorological and climatic variables play a minor role in comparison to the amount of susceptible population for fundamentally driving the pandemic dynamics (Baker et al., 2020). Yet, no study to our knowledge has examined the association between long-term PM_2.5 exposure and the exponentially fast spread of COVID-19 in a population (Ferguson et al., 2020).

The spread of a disease through a population is estimated using the dimensionless epidemiological parameter R ₀ – the basic reproduction ratio (Griffin et al., 2011; Liu et al., 2020b; Ridenhour et al., 2018). It is defined as the average number of individuals that an infected individual would infect in an entirely susceptible population. Thus, this parameter is of utmost importance for public health officials and policymakers because it indicates the onset of an outbreak based on the threshold value of 1.0. With increasing R ₀ >1, disease spread in a population becomes more rapid, and it becomes harder to control the outbreak.

Here, we establish the association between R ₀ and long-term ambient PM_2.5 exposure in the United States of America (US), where the impact of the pandemic has been most severe. Using robust and established statistical analysis, we elucidate the role of PM_2.5 mass concentration and composition in COVID-19's rapid spread across the US. We estimate the state-specific values of R ₀ using an established epidemic progression model involving the susceptible–exposed–infected–recovered (SEIR) dynamics, the age-stratified disease transmissibility, and the possible large-scale undocumented (i.e., asymptomatic and/or untested) transmission of COVID-19 taking place in the US (Brockmann and Helbing, 2013; Li et al., 2020c; Liu et al., 2020a; Wallinga et al., 2006). We inferred the state-wise R ₀ values by fitting the prediction of SEIR model with US COVID-19 recorded data corresponding to the period March 2–April 30 (Dong et al., 2020). This period was characterized by a rapid surge in COVID-19 cases across the US states and the implementation of strict social distancing measures. We calculated state-level long-term PM_2.5 exposure (from 2012 to 2017) using an established and cross-validated exposure prediction model that innovatively fuses ground-based and satellite observations, and chemical transport modeling output (Van Donkelaar et al., 2019; Wu et al., 2020b). We fit a general additive model (GAM) (Ma et al., 2020; Wood, 2001; Zhang et al., 2019) using state-level R ₀ values as the outcome and state-level long-term average PM_2.5 mass concentrations and composition as the exposure. We use the Johnson-Neyman technique (Carden et al., 2017) to explore how the relationship between PM_2.5 exposure and R ₀ is moderated by PM_2.5 composition and other socio-economic and demographic variables. We considered 43 potential confounding factors in our analysis including gaseous air pollutants, meteorological variables, race, population density, age distribution, hospital and ICU beds, median household size and income, and time delay in state's issuance of stay-at-home orders (Wu et al., 2020b).

2. Methods

2.1. Inference of the COVID-19 basic reproduction ratio

We inferred state-wise R ₀ values by fitting the prediction of a susceptible-exposed-infected-recovered (SEIR) model (Li et al., 2020c; Liu et al., 2020a) to confirmed COVID-19 cases (Dong et al., 2020). Our epidemic model accounts for the age-stratified disease transmissibility (Wallinga et al., 2006), and possible large-scale undocumented transmission (Li et al., 2020c) of COVID-19 in the US. The detailed model structure and parameterization follow that outlined in recent publications (Li et al., 2020c; Liu et al., 2020a), except that here we neglected the influence of interstate mobility of COVID-19 carriers on long-term disease progression, considering the rapid decline in domestic traffic after the nationwide implementation of stay-at-home orders. The inference timespan was set between March 02 and April 30 (coinciding the nationwide social distancing period), so as to minimize the influences of other human behaviors and social activities on epidemic dynamics. The daily number of confirmed COVID-19 cases was acquired from a real-time epidemic tracking dashboard published by Johns Hopkins University (Dong et al., 2020).

The fitting procedure can be described as such: First, the daily number of state-wise confirmed-and-active COVID-19 cases (Dong et al., 2020) was tracked and recorded, which can be written as a time-series j _n ^r(t) (subscript n denotes each US state, superscript r indicates “reported”, and t is time incrementing with a unit of days between March 02 and April 30). Next, the SEIR prediction was fitted with the ground truth using twenty consecutive days of epidemic size data. Specifically, we took twenty consecutive elements from the j _n ^r(t) time series, generating a “minibatch” written as j _n ^r(t _i : t _i+19). Here, t _i is defined as an initial date. A total of 41 minibatches can be generated, where i increments between 1 and 41. For each minibatch j _n ^r(t _i : t _i+19), we initialize the SEIR model with j _n ^r(t _i), and then the model guessed a value for R ₀ and predicted the epidemic trends on the following nineteen days, written as $\widehat{j_n^r}\left(t_i:t_{i+19}\right)$. The values of R ₀ were inferred in a trial-and-error manner, by minimizing the root-mean-square-error between j _n ^r(t _i : t _i+19) and $\widetilde{j_n^r}\left(t_i:t_{i+19}\right)$. This process can be formally written as:

$$\underset{R_{0,n,t_i},{\eta }_{n,t_i},{\zeta }_{n,t_i}}{\text{argmin}}{‖\widetilde{j_n^r}\left(t_i:t_{i+19}\left|R_{0,n,t_i},{\eta }_{n,t_i},{\zeta }_{n,t_i}\right)\right)-j_n^r\left(t_i:t_{i+19}\right)‖}_2.$$ (1)

Here, R _{0, n, ti} represents the basic reproduction ratio values inferred for state n within the timespan between t _i and t _i+19; η _{n, ti} and ζ _{n, ti} respectively denote the unknown documentation ratio and exposure ratio³⁴, which were simultaneously inferred along with R _{0, n, ti}. Finally, for each state n, we calculated a time-averaged reproduction ratio ${\overline{R}}_{0,n}$ by taking the arithmetic mean values of the R _{0, n, ti} series.

2.2. Acquisition of PM_2.5 exposure profiles

We calculated the state-level long-term (averaged between 2012 and 2017) PM_2.5 exposure profiles using recently published datasets (Van Donkelaar et al., 2019). The PM_2.5 exposure levels were estimated monthly across the entire continental United States by combining observations from ground-based monitors, GEOS-Chem model outputs, and satellite observations. The original dataset provides annually-resolved PM_2.5 mass concentration, along with the fraction of constituent species, as functions of geographic coordinates at a grid resolution of 0.01° × 0.01° (Van Donkelaar et al., 2019). This spatiotemporal distribution can be written as x _{longitude, latitude, year}, where x generically denotes PM_2.5 concentration or composition. Next, we labelled each data point x per the state n wherein x resides, such as x _{n, k, year} (where k denotes the kth point residing within state n). We then aggregated and averaged PM_2.5 exposure profile within each n, and obtained the state-level yearly-resolved dataset, ${\overline{x}}_{n,\text{year}}=K^{-1}\sum _{k=1}^K{x}_{n,k,\text{year}}$ (where K is the total number of data points residing in state n). Finally, we obtained the state-level long-term exposure profile by averaging the data across time, such as ${\stackrel{̿}{x}}_n=\left(1/18\right)\ast \sum _{\text{year}=2000}^{2017}{\overline{x}}_{n,\text{year}}$. In the following text, we omit subscript n in the notation if there is no need to discriminate the state-wise statistics.

2.3. Associating PM_2.5 exposure and COVID-19 transmission

We examine association between long-term state-level PM_2.5 exposure $\stackrel{̿}{x}$ and the state-wise COVID-19 transmissibility ${\overline{R}}_0$. The correlation between $\stackrel{̿}{x}$ and ${\overline{R}}_0$ was quantified with the widely-adoped GAM model (Wood, 2001; Zhang et al., 2019). The core function used in the GAM can be expressed as:

$${\overline{R}}_0=b+s\left(\stackrel{̿}{x},d_f=4\right)+\epsilon ,$$ (2)

where b denotes a constant intercept; s(,) denotes a thin-plate basis smooth function; ε denotes a zero centered Gaussian noise; d _f stands for degrees of freedom, and d _f = 4 was chosen because no high-level of nonlinearity was observed in the data trends. The restricted maximum likelihood method was adopted in the optimization to prevent overfitting. The GAM fitting and analysis were conducted using R software and the “mgcv-1.8-31” package.

2.4. Moderation analysis

We used the Johnson-Neyman technique to investigate two-way interactions between PM_2.5 composition and their effect on ${\overline{R}}_0$. The Johnson-Neyman technique allows one to investigate the size of effect that an independent “predictor” variable has on the dependent “response” variable (in this case ${\overline{R}}_0$), given the value of a second “moderating” variable (Carden et al., 2017). Details on the Johnson-Neyman technique can be found in the work by Carden et al. (Carden et al., 2017) When the moderating variable has a statistically significant effect on the relationship between the predictor and the response variable, there is said to be a two-way interaction between the predictor and moderating variable (Carden et al., 2017).

2.5. Potential confounders

We considered the following 43 state-level variables as potential confounders (see Supplementary material Table S10): population, population density, percent of the population ≤9 years of age, percent of the population 10–19 years of age, percent of the population 20–29 years of age, percent of the population 30–39 years of age, percent of the population 40–49 years of age, percent of the population 50–59 years of age, percent of the population 60–69 years of age, percent of the population 70–79 years of age, percent of the population ≥80 years of age, number of people tested, fraction of people tested, hospital beds, ICU beds, liquid asset poverty rate, total healthcare and social services workers, total essential workers, fraction of total healthcare and social services workers, fraction of total essential workers, average household size, average family size, number of households, total number of families, households with elderly resident, renter-occupied housing units, lapse in state's issuance of stay-at-home order, residents in two-or-more unit structures, median income for single earner household, median income for working age individuals, fraction of white population, fraction of African American population, fraction of Asian population, fraction of Native American Indian population, fraction of Pacific Islander population, and fraction of other race, and daily measurements of ozone, NO₂, temperature, pressure, NO_y, NO_x, relative humidity, and SO₂ which have been averaged annually between 2012 and 2017.

3. Results

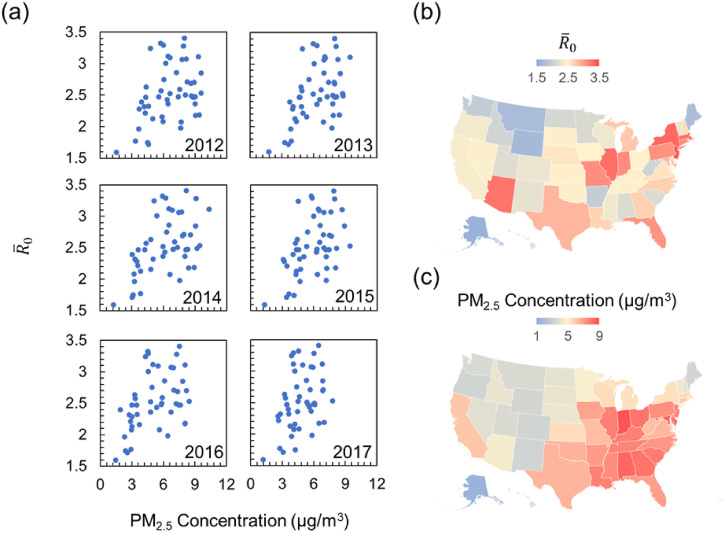
The complete inference results for ${\overline{R}}_0$ (time-averaged R ₀ between March 2 and April 30) and the PM_2.5 composition profiles corresponding to each US state are tabulated in Supplementary information (Tables S1-S9). Although real-time values of ${\overline{R}}_0$ were always greater than 1 during the two-month investigation period, the parameter's rapidly declining trend (Supplementary Table S1) suggests that the implemented non-pharmaceutical intervention strategies—such as school and business closure—were effective in altering the disease dynamics. Fig. 1 shows the correlation between state-wise ${\overline{R}}_0$ and the annual average PM_2.5 concentration. A positive correlation between ${\overline{R}}_0$ and PM_2.5 concentration can be observed from all the past 6-year datasets. The correlation between ${\overline{R}}_0$ and long-term average (between years 2012 and 2017) PM_2.5 exposure profile for the entire continental US are shown in Fig. 1(b) and (c). A qualitative comparison of the color-coded continental US maps reveals the overall spatial pattern of ${\overline{R}}_0$ coinciding with that of the PM_2.5 exposure levels.

Fig. 1.

Correlation of yearly PM_2.5 exposure levels with state-wise COVID-19 reproduction number ${\overline{R}}_0$ (a) plot of state-wise ${\overline{R}}_0$ as a function of the yearly-resolved PM_2.5 concentration. The year corresponding to the PM_2.5 datasets is written on each sub-panel. (b) The map of continental US colored according to the state-wise time-averaged (between March 2 and April 30, 2020) COVID-19 basic reproduction ratio ${\overline{R}}_0$, (c) the map of continental US colored according to state-level long-term average (between 2012 and 2017) PM_2.5 concentration.

Table 1 summarizes the Pearson correlation coefficient (PCC) between ${\overline{R}}_0$ and PM_2.5 composition including black carbon (BC), organic matter (OM), sulfate (SO₄ ²⁻), nitrate (NO₃ ⁻), ammonium (NH₄ ⁺), Sulfate-Nitrate-Ammonium (SNA). Among all factors, ${\overline{R}}_0$ is observed to be positively associated with PM_2.5 concentration (PCC ≈ 0.47), NH₄ ⁺ fraction (PCC ≈ 0.37), SO₄ ²⁻ fraction (PCC ≈ 0.37), and NO₃ ⁻ fraction (PCC ≈ 0.29); whereas a negative correlation is observed between ${\overline{R}}_0$ and OM fraction (PCC ≈ −0.42). The correlation between ${\overline{R}}_0$ and BC are statistically insignificant (p-value >0.05). Henceforth in this paper, we treat the sulfate-nitrate-ammonium (SNA) ionic composition of PM_2.5 as a whole, that is, SNA denotes the summation of the fraction of each individual species.

Table 1.

Pearson correlation between COVID-19 basic reproduction ratio and PM_2.5 composition.

	PM2.5	BC	OM	SO42−	NO3−	NH4+	SNA
PCC with ${\overline{R}}_0$	0.47	−0.20	−0.42	0.37	0.29	0.37	0.44
p-Value	0.0006⁎	0.1592	0.0029⁎	0.0081⁎	0.0396⁎	0.0095⁎	0.0016⁎

COVID-19, Corona Virus Diseases 2019; PCC, Pearson correlation coefficient; PM_2.5, mass concentration of particular matter with aerodynamic diameter ≤ 2.5 μm; BC, black carbon fraction; OM, organic matter fraction; SO₄²⁻, sulfate fraction; NO₃⁻, nitrate fraction; NH₄⁺, ammonium fraction; MD, mineral dust fraction; SS, sea salt fraction.

^⁎p-Value <0.05 is considered statistically significant.

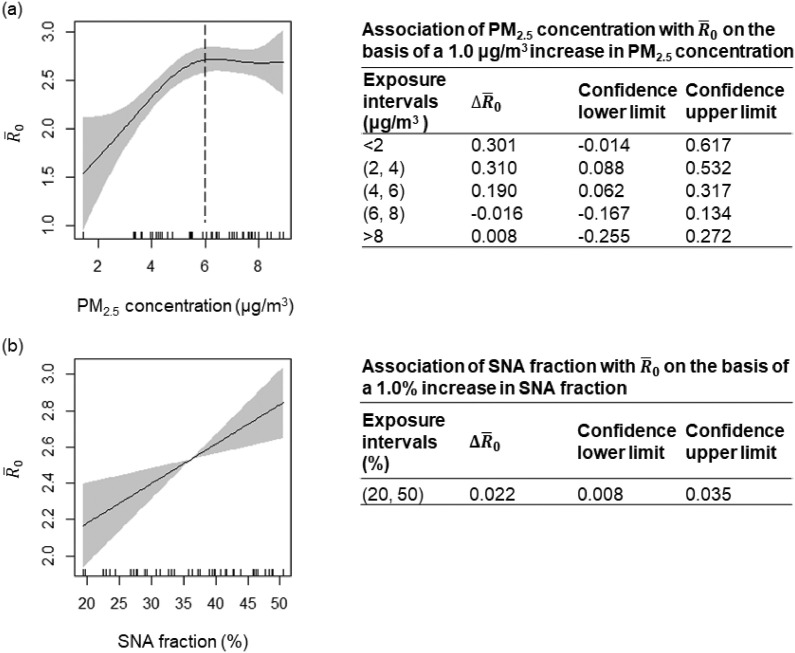
We next quantitatively establish the link between ${\overline{R}}_0$ and the composition-specific PM_2.5 exposure by fitting the GAM (Wood, 2001; Zhang et al., 2019). Fig. 2 shows the output of GAM with PM_2.5 concentration and SNA fraction as the input. Panel (a) again shows that the relationship between ${\overline{R}}_0$ and PM_2.5 concentration demonstrates a “two-regime” behavior: First, when PM_2.5 concentration is below 6 μg/m³, a rapid increase in ${\overline{R}}_0$ can be observed along with increasing PM_2.5 concentration; This increasing trend slows down upon reaching its plateau (at PM_2.5 concentration ≈ 6 μg/m³). A spline analysis shows that a 1.0 μg/m³ increase in PM_2.5 concentration was associated with increase in ${\overline{R}}_0$ by 0.310 (95% CI: 0.088–0.532) and 0.190 (95% CI: 0.062–0.317), when PM_2.5 concentration ∈(2, 4) μg/m³ and ∈(4, 6) μg/m³, respectively. When PM_2.5 concentration > 6 μg/m³, the increasing trend starts to reach its plateau, and the correlation becomes statistically insignificant. Panel (b) shows that the positive relationship between ${\overline{R}}_0$ and SNA fraction takes up a near linear functionality. Throughout the entire range of SNA fraction, a 10% increase in SNA fraction associates with an increase in ${\overline{R}}_0$ by 0.218 (95% CI: 0.083–0.352). The GAM analysis on the ${\overline{R}}_0$-BC fraction and ${\overline{R}}_0$-OM fraction correlation can be found in the Supplementary materials (Fig. S1).

Fig. 2.

Quantitative relationship between COVID-19 reproduction ratio and PM_2.5 exposure levels and composition. Partial response plot and 95% confidence intervals (shaded region) for the transmissibility of COVID-19 with respect to PM_2.5 concentration (a) and sulfate-nitrate-ammonium (SNA; secondary inorganic aerosol) fraction (b). Tables next to the figures show the results of association analysis based on GAM fitting. For example, for PM_2.5 concentration ∈(2, 4) μg/m³, a 1.0 μg/m³ increase in PM_2.5 concentration is associated with a 0.310 (95% CI: 0.088–0.532) increase in ${\overline{R}}_0$.

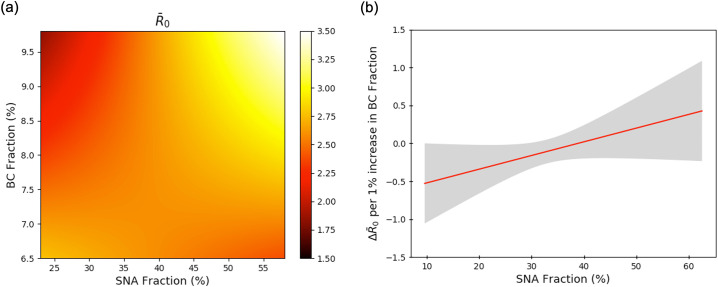
Fig. 3 shows the results of Johnson-Neyman analysis (Carden et al., 2017), where SNA fraction is the predictor variable and BC fraction is the moderating variable. These results indicate that the direct relationship between SNA fraction and ${\overline{R}}_0$ is dependent on BC fraction. Fig. 3(a) shows the value of ${\overline{R}}_0$ as a function of SNA fraction and BC fraction. Fig. 3 shows that in areas where a large portion of PM_2.5 is made up of SNA, an increase in BC fraction leads to an increase in ${\overline{R}}_0$. However, if SNA makes up a smaller portion of PM_2.5, an increase in BC fraction leads to a decrease in ${\overline{R}}_0$. Alternatively, as BC fraction increases, the positive relationship between ${\overline{R}}_0$ and SNA fraction becomes more prominent. Fig. 3(b) elaborates on this phenomenon by plotting the ${\overline{R}}_0$ gradient value along the direction of changing BC fraction. This result shows that for SNA fraction greater than 38.8%, a 1% increase in BC fraction leads to an increase in ${\overline{R}}_0$ (upper and lower 95% CI are given by grey shaded region). State-wise population density also weakly moderated the association between ${\overline{R}}_0$ – PM_2.5 and ${\overline{R}}_0$ – SNA fraction, respectively (see Fig. S2 in Supplementary information).

Fig. 3.

Black carbon concentration levels modulate the interaction between R₀ and inorganic ionic PM_2.5 composition. Johnson-Neyman analysis of the response of ${\overline{R}}_0$, where the predictor variable is sulfate-nitrate-ammonium (SNA) mass fraction and the moderator variable is black carbon (BC) mass fraction. (a) Plot of predicted ${\overline{R}}_0$ as a function of SNA fraction and BC fraction. (b) Plot of slope of panel (a) for constant SNA fraction. Grey shaded area shows the 95% confidence interval.

Given that we find both population density and SNA fraction to be highly correlated with ${\overline{R}}_0$, a logical argument might arise regarding the relation of ${\overline{R}}_0$ with SNA simply being a compositional surrogate for population density. Especially since SNA aerosol precursors are closely linked to urbanization, one might argue that it is difficult to delineate the effect of SNA fraction and population density on ${\overline{R}}_0$. We aim to address this concern and strengthen our argument by citing specific examples wherein confounding relationship of ${\overline{R}}_0$ with population density and SNA with population density do not hold valid. A justified comparison would be between Alabama and Louisiana, two states that are similar climatically, socioeconomically, and demographically (see Table S11). In comparing these states, we find that their population densities differ by only 1.04%, but Louisiana has 5% higher fraction of SNA. Despite their similarity in population density, ${\overline{R}}_0$ in Louisiana is 20.7% higher than Alabama. This example shows that when comparing two states that differ only in SNA fraction, the positive association between SNA fraction and ${\overline{R}}_0$ still holds.

4. Discussion

To the best of our knowledge, this is the first nationwide study to estimate the relationship between long-term exposure to PM_2.5 and the rapidity of COVID-19 spread in the US. Up to 6 μg/m³ PM_2.5 ambient concentrations, which is below current regulatory standards (EPA, 2019), we find that a 1.0 μg/m³ increment in long-term exposure associates with a 0.25 increase in ${\overline{R}}_0$. Short-term exposure due to outdoor air pollution dropped significantly during the months of March and April in the US (Tanzer-Gruener et al., 2020), yet our findings suggest that long-term exposure to pollutants had rendered the nationwide population susceptible to the virus spread. Although our study design cannot provide insights into potential biological mechanisms, the results indicate that long-term exposure to fine particulate matter air pollution increases COVID-19 spread plausibly via the “double hit phenomenon” (Frontera et al., 2020).

Our observation of a high degree of association between long-term exposure to low ambient PM_2.5 and ${\overline{R}}_0$ has major policy implications. The 2019 policy assessment review for the PM_2.5 National Ambient Air Quality Standards (NAAQS) in the US recommended a revision to the annual PM_2.5 concentration standards from 12 μg/m³ to 9 μg/m³ (EPA, 2019). This recommendation was primarily guided by general observations of positive and statistically significant health effect associations for PM_2.5 air quality distributions characterized by overall mean (or median) concentrations at or above 9.6 μg/m³ (EPA, 2019). It is noteworthy to recognize the limitations of these approaches–epidemiologic studies evaluate associations between distributions of ambient PM_2.5 and health outcomes and do not necessarily identify the specific exposures that cause reported effects. In reality, associated health effects and risk factors could occur over the entire distribution of ambient PM_2.5 concentrations evaluated, and past studies have not necessarily identified a population level threshold below which PM-associated health effects cease to occur. Thus, our findings contribute to the growing body of evidence of PM_2.5 concentration-response relationships near the lower end of the PM_2.5 air quality distribution by providing new evidence of a relationship of PM_2.5 with ${\overline{R}}_0$ at levels below the current NAAQS (Dirgawati et al., 2019; Makar et al., 2017; Pinault et al., 2016).

With respect to PM_2.5 composition, we find a 10% increase in sulfate-nitrate-ammonium (SNA) ionic fractions to be associated with a 0.218 (≈10%) increase in ${\overline{R}}_0$ (95% CI: 0.083–0.352). This strong association of ${\overline{R}}_0$ with secondary inorganic fraction in PM_2.5, which could be modulated in the presence of BC aerosol, highlight the long-term health risks associated with combustion emissions by fossil fuels (EPA, 2019). The formation pathways of secondary inorganic aerosol in the atmosphere involve the photochemical oxidation of gaseous sulfur dioxide (SO₂) and nitrogen dioxide (NO₂), both of which are predominantly emitted from coal-fired power plants and vehicles. While the oxidation chemistry of NO₂ to form nitric acid (HNO₃) is relatively straight forward, partitioning of nitrate to sol phase depends on a number of factors including temperature (Kroll et al., 2020). NO₂ has also been shown to accelerate the oxidation of SO₂ to form sulfates (Wang et al., 2020). Not surprisingly, this study finds a positive correlation between ${\overline{R}}_0$ and NO₂ emissions and annual temperature variations, respectively (see Supplementary material Table S10). Although decades of strict air quality regulations in the US have resulted in significant reductions of NO₂ levels (Kroll et al., 2020), recent reversal of environmental regulations which weaken limits on gaseous emissions from power plants and vehicles threaten the country's future air quality scenario (Pulido et al., 2019).

We consider it important to acknowledge the limitations of this study. First, the robustness of our model prediction could be limited by the coarse-grain spatial representation of model variables, such as the PM_2.5 exposure profile and ${\overline{R}}_0$. County-level distribution of PM_2.5 composition and ${\overline{R}}_0$ values are readily washed away upon averaging the data points residing within the state boundaries. Based on past findings (Crouse et al., 2020), we anticipate a county-level analysis will not alter the nature of the relationship established between the variables in this study, although the strength of their associations might vary.

The inherent ability to accurately quantify the number of COVID-19 cases due to limited testing capacity during the March–April timeframe presents another potential limitation. The large uncertainty represented by the shaded area in Fig. 3 suggests that the variation in ${\overline{R}}_0$ is not fully accounted for by the PM_2.5 exposure profile. Caution must be taken when extrapolating results from this study to generalize the virus spread in other countries and drive public health responses. The basic reproduction ratio is a complex property of an epidemic and is highly sensitive to the underlying model used to estimate it, the specific population demographic, and time period of study (Ridenhour et al., 2018).

Future analysis should include COVID-19 epidemic parameters and PM_2.5 exposure data at finer-grain levels, e.g. county-level (Wu et al., 2020b). Research on disproportionate impacts of air pollution on at-risk populations, including minority populations and populations with lower socioeconomic status, during the epidemic is another understudied area. Synergistic analysis of air quality and population demographic information suggest that the highest PM_2.5 concentrations in a given area tended to be measured at locations where populations lived or were more likely to below the poverty line and constituted larger percentages of racial and ethnic minorities. Last but not least, the design limitations of this study calls for detailed research on biological mechanisms responsible for the observed associations.

Data availability

The epidemiological COVID-19 data used in this study can be accessed at https://github.com/pliu1991/COVID19PM25_supporting_data_and_files. The historical PM_2.5 exposure data (V4.NA.02.MAPLE) can be accessed at: https://sites.wustl.edu/acag/datasets/surface-pm2-5/. The data was produced as part of the following paper: van Donkelaar, A., R. V. Martin, C. Li, R. T. Burnett, (2019) Regional Estimates of Chemical Composition of Fine Particulate Matter using a Combined Geoscience-Statistical Method with Information from Satellites, Models, and Monitors, Environ. Sci. Technol., 53, 5, 2595–2611. Gaseous air pollutant and annual meteorological datasets were obtained from the Environmental Protection Agency at: https://aqs.epa.gov/aqsweb/airdata/download_files.html.

Code availability

The epidemic dynamic model and statistical analysis codes can be accessed at https://github.com/pliu1991/COVID19PM25_supporting_data_and_files.

CRediT authorship contribution statement

Rajan K. Chakrabarty: Conceptualization, Methodology, Writing - original draft. Payton Beeler: Writing - original draft, Software, Methodology, Data curation. Pai Liu: Writing - original draft, Software, Methodology, Data curation. Spondita Goswami: Software, Methodology. Richard D. Harvey: Supervision. Aaron van Donkelaar: Writing - review & editing. Randall V. Martin: Writing - review & editing.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Editor: Jay Gan

Appendix A. Supplementary data

Supplementary Data consists of a) notes 1 ~ 3, b) figures S1 and S2, and c) tables S1 ~ S11.