A General Framework for Application of Prestrain to Computational Models of Biological Materials

Abstract

It is often important to include prestress in computational models of biological tissues. The prestress can represent residual stresses (i.e. stresses that exist after the tissue is excised from the body) or in situ stresses (i.e. stresses that exist in vivo, in the absence of loading). A prestressed reference configuration may also be needed when modeling the reference geometry of biological tissues in vivo. This research developed a general framework for representing prestress in finite element models of biological materials. It is assumed that the material is elastic, allowing the prestress to be represented via a prestrain. For prestrain fields that are not compatible with the reference geometry, the computational framework provides an iterative algorithm for updating the prestrain until equilibrium is satisfied. The iterative framework allows for enforcement of two different constraints: elimination of distortion in order to address the incompatibility issue, and enforcing a specified in situ fiber strain field while allowing for distortion. The framework was implemented as a plugin in FEBio (www.febio.org), making it easy maintain the software and to extend the framework if needed. Several examples illustrate the application and effectiveness of the approach, including the application of in situ strains to ligaments in the Open Knee model (simtk.org/home/openknee). A novel method for recovering the stress-free configuration from the prestrain deformation gradient is also presented. This general purpose theoretical and computational framework for applying prestrain will allow analysts to overcome the challenges in modeling this important aspect of biological tissue mechanics.

1. Introduction

Experimental observations show that connective tissues such as ligaments, tendons and skeletal muscle retract when excised from the body. This retraction is due to in situ strain -strain that exists in vivo in the absence of loading in the reference configuration. The strain and associated stress is relieved when the tissue is removed from the body, yielding a relatively stress-free configuration. In situ strains for ligaments in diarthrodial joints are in the range of 3–10% (Gardiner et al., 2001; Woo et al., 1990) and it has been shown that they contribute to the stability of joints (Ellis et al.; Lujan et al.). Residual strain (i.e. strain that exists in the tissue after it is excised from the body) is observed in many tissues such as arteries (Chuong and Fung, 1986), mitral leaflets (Rausch and Kuhl, 2013) and myocardium (Guccione et al., 1991; Omens and Fung, 1990; Wang et al., 2014). Often, geometries of biologically tissues are acquired in vivo and consequently the reference configuration cannot be assumed stress-free. All these various forms of prestrain, i.e. strain that exists in the reference configuration of the body of interest, can contribute significantly to the mechanical response of the system. Inclusion is often necessary in computational models of biological tissues to obtain reasonable predictions of tissue mechanics.

One class of previously reported methods for accommodating prestrain in finite element modeling can be described as deforming a stress-free configuration to induce stress in a desired/known reference configuration. For example, in (Balzani et al., 2006) this is accomplished by closing the geometry representing a radially cut artery, using a special type of spring element. In (Rausch and Kuhl, 2013), a stress-free configuration of mitral leaflets is stretched to conform to the in-vivo reference configuration. In this case, the deformation map from stress-free to prestressed reference configuration was assumed to be known. This class of methods requires a sequence of forward analyses and can be executed with any finite element analysis software. The drawback is that they rely on the existence and knowledge of a stress-free configuration. In practice however, obtaining a stress-free configuration can be challenging, and there is no guarantee that it exists. For instance, in the case of arteries, the opening angle experiment was once believed to relieve the residual stress (Fung and Liu, 1989). However, it was later shown that a single cut does not relieve all the residual stress (Greenwald et al., 1997; Vossoughi et al., 1993).

In another class of methods, prestress is accounted for directly in the reference configuration without the requirement that a stress-free state exists or is known a priori. These methods are especially useful in the context of patient- and subject-specific modeling, since in these cases finite element models are often constructed based on image data acquired in the reference configuration. Usually the materials are assumed to be elastic and the prestress is then defined via a prestrain. The methods in this class primarily differ from each other in the definition of the prestrain. In (Alastrue et al., 2007), the deformation gradient is taken from an analytical solution for the bending of a cylinder. In (Weiss et al., 2005) and (Dhaher et al., 2010) it was obtained indirectly from experimental data. In (Gee et al., 2010) and later in (Weisbecker et al., 2014) and (Grytz and Downs, 2013), the prestrain deformation gradient was obtained by solving an inverse finite element problem: given the in-vivo reference configuration and the in-vivo loads, find the deformation gradient that generates the stresses in the reference configuration required to balance the applied loads. This approach requires an iterative solution due to the nonlinearity of large deformation elasticity. The method by (Bols et al., 2013) is also similar in that regard, except that it attempts to recover the stress-free configuration. In general, biological tissues can have residual stresses in addition to prestress, and the methods mentioned above can be used to accommodate all forms of prestrain in a single analysis. For instance in (Pierce et al., 2015) the general prestressing algorithm by (Weisbecker et al., 2014) is used to account for both the residual stress and the prestress in the reference configuration of an artery. A shortcoming of the methods that start from a prestrain deformation gradient is that it cannot always be guaranteed that the induced prestress is in equilibrium with the given reference configuration. Thus, it must be verified that the applied prestrain results in equilibrated stresses. Ideally, a method to compensate for any incompatibility should be available.

The objective of this study was to develop and implement a general purpose computational framework for modeling prestrain in finite element models of biological tissues. The framework uses a prestrain gradient approach that does not require the knowledge or computability of a stress-free reference configuration. The manuscript details the theoretical foundation as well as the computational aspects of the framework. We demonstrate that some of the previously reported methods for applying prestrain can be recovered as special cases of the framework. We also describe a method for recovering prestrain from sparse experimental data, and a method for recovering the global stress-free state from its deformation gradient. Examples illustrate the application of the framework to several test problems, including the application of prestrain to a finite element model of the knee from the Open Knee project (Erdemir, 2013, 2015; Erdemir and Sibole, 2010). The framework was implemented in the freely available finite element software FEBio (Maas et al., 2012) and can be used with any of the elastic constitutive models.

2. Methods

2.1. Theoretical background

Consider a body in its prestressed reference configuration that is subjected to applied loading and subsequently deforms into a loaded configuration (Figure 1). The deformation map $\mathbf{\phi }\left(\mathbf{X}\right)$, which maps the material coordinates $\mathbf{X}$ to the corresponding spatial coordinates $\mathbf{X}=\mathbf{\phi }\left(\mathbf{X}\right)$, has a deformation gradient $\mathbf{F}={\nabla }_0\mathbf{\phi }$. It is assumed that for each material point, a local stress-free virtual configuration can be found in the sense of (Johnson and Hoger, 1995). The gradient of the local mapping from the stress-free to the prestressed reference configuration is represented by ${\mathbf{F}}_p$, which will be referred to as the prestrain gradient.

Figure 1.

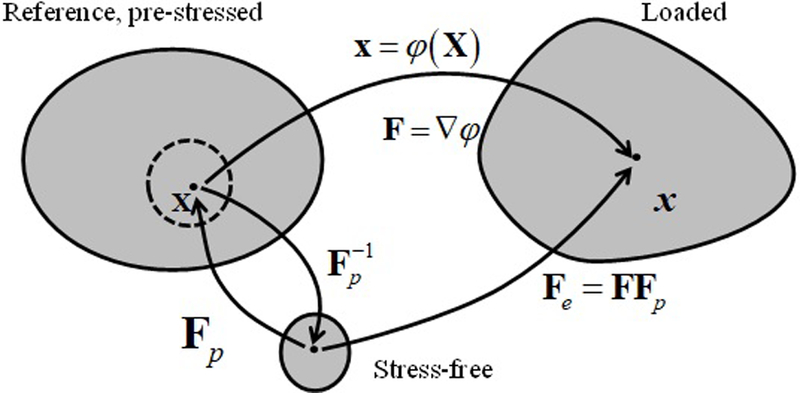
Schematic showing the pre-stressed reference configuration and the loaded, deformed configuration. At each point in the reference configuration, it is assumed that a small (potentially infinitesimal) neighborhood can be found for which a local deformation map exists that takes the neighborhood to a stress-free state.

The total elastic deformation gradient ${\mathbf{F}}_e$ is determined by the composited deformation gradient,

$${\mathbf{F}}_e=\mathbf{F}{\mathbf{F}}_p.$$ (1)

It is further assumed that the constitutive response of the material is hyperelastic. As shown by (Johnson and Hoger, 1995) in this case the Cauchy stress $\mathbf{\sigma }$ and spatial elasticity tensor $\text{c}$ can now be evaluated using ${\mathbf{F}}_e$:

$$\mathbf{\sigma }=\mathcal{\text{F}}\left({\mathbf{F}}_e\right),\hspace{0.17em}\hspace{1em}\text{c}=\mathcal{\text{T}}\left({\mathbf{F}}_e\right),$$ (2)

where $\mathcal{\text{F}}$ and $\mathcal{\text{T}}$ denote the “natural” material response functions (i.e. the response functions obtained from deforming the material from a stress-free reference configuration). For a finite element software such as FEBio that evaluates these quantities in the spatial frame, accommodating prestrain via the prestrain gradient approach is relatively straightforward.

In general, the inverse deformation gradient ${\mathbf{F}}_p^{-1}$ that renders the neighborhood of a point in the reference configuration stress-free can only be defined locally. Thus ${\mathbf{F}}_p$ cannot be obtained from the derivative of a mapping from a stress-free configuration to the prestressed configuration. This is a strong motivation for using the prestrain gradient approach in this work. Of course, if such a mapping is available, its gradient can be computed directly and then used to evaluate the material response via Eq. (2).

Finally, the Cauchy stress in the prestressed configuration ${\mathbf{\sigma }}_p=\mathcal{\text{F}}\left({\mathbf{F}}_p\right)$ must satisfy equilibrium in the absence of any subsequent deformation (i.e. $\mathbf{F}=\mathbf{1}$). This implies that, in the absence of body forces, ${\mathbf{\sigma }}_p$ must satisfy the equations representing conservation of linear and angular momentum in the interior of the prestressed domain:

$$\begin{gathered} \mathrm{div}\left({\mathbf{\sigma }}_p\right)=\mathbf{0}, \\ {\mathbf{\sigma }}_p={\mathbf{\sigma }}_p^T. \end{gathered}$$ (3)

In addition, the free boundaries must be traction free:

$${\mathbf{\sigma }}_p\cdot \mathbf{n}=\mathbf{0}.$$ (4)

Here, $\mathbf{n}$ is the unit outward normal vector at the boundary. When the stress induced by the prestrain gradient satisfies Eqs. (3) and (4) the prestrain gradient is considered compatible with the reference geometry.

2.2. The prestrain gradient approach

The proposed framework starts from knowledge of an initial target for the prestrain gradient, an initial reference configuration, and the boundary conditions and loads that exist in this configuration. As noted above, this is the most convenient starting point when the prestrain gradient is known (e.g. from a forward FE analysis or from an analytical solution) or can be obtained from experiment. At the same time, experimental measurement of the complete prestrain gradient can be difficult, so the full prestrain gradient may not always be available. For instance, when measuring ligament strain, often the fiber stretch is measured (Dhaher et al., 2010; Ellis et al., 2006; Gardiner and Weiss, 2003; Gardiner et al., 2001; Lujan et al., 2007; Lujan et al., 2005; Weiss et al., 2005). In this case, additional modeling assumptions are necessary to fill in the missing information. Similarly, assumptions are often made about the form of the prestrain gradient when measuring strain in arteries (Balzani et al., 2006, 2007; Holzapfel and Ogden, 2010; Labrosse et al., 2009; Raghavan et al., 2004) and the heart (Omens et al., 2003; Taber and Chabert, 2002; Taber et al., 1993; Wang et al., 2014). The result of these assumptions is an approximate prestrain field that may not be compatible with the initial reference configuration. In a finite element analysis, the application of an incompatible prestrain field results in a distortion of the reference geometry which also alters the effectively applied prestrain gradient. It is usually not desirable to have both a distortion of the reference configuration and an effective prestrain gradient that differs from the applied prestrain gradient as this may complicate the interpretation of the results. Depending on the specific goal and the input data, the analyst may wish to eliminate distortion and thus needs to find an alternative prestrain gradient field that is compatible with the original reference configuration. Alternatively, the goal may be to enforce the given prestrain gradient field as closely as possible and in this case a new reference configuration needs to be found that is compatible with the applied prestrain gradient field.

For both goals, the framework uses an iterative mechanism that updates the prestrain gradient field in order to accomplish the desired goal. In the following sections the deformation gradient that corresponds to the distortion of the geometry is denoted by $\mathbf{F}$. Our computational framework assumes that the user provides an initial target for the prestrain gradient, notated as ${\widehat{\mathbf{F}}}_p$. Then the prestrain gradient ${\mathbf{F}}_p$ that results in an effective prestrain gradient ${\mathbf{F}}_{p,eff}$ is:

$${\mathbf{F}}_{p,eff}=\mathbf{F}{\mathbf{F}}_p,$$ (5)

such that ${\mathbf{F}}_{p,eff}$ is compatible with the possibly distorted reference configuration is calculated using an iterative algorithm (Figure 2). Users can provide either the full tensor ${\widehat{\mathbf{F}}}_p$ or provide a simplified functional form that calculates ${\widehat{\mathbf{F}}}_p$ from given data. In either case, ${\widehat{\mathbf{F}}}_p$ is held constant during the iterative loop. A forward finite element analysis is then executed which results in a distortion of the mesh with deformation gradient ${\mathbf{F}}^k$. After the forward analysis, ${\mathbf{F}}_p$ is updated. Since the update depends on the desired goal, the user selects one of the by default provided update rules (or implements a new one). After ${\mathbf{F}}_p$ is updated, a new forward analysis is performed. This iterative procedure continues until ${\mathbf{F}}_p$ converges to a stable value. In our current implementation, the convergence criterion is

$$\Vert {\mathbf{F}}_p^{k+1}-{\mathbf{F}}_p^k\Vert <\epsilon .$$ (6)

After the algorithm converges, the initial reference geometry is replaced with the distorted geometry, ${\mathbf{F}}_p\leftarrow \mathbf{F}{\mathbf{F}}_p$.$\mathbf{F}$, which measures the deformation of the final distortion, is reset to the identity tensor. Now ${\mathbf{F}}_p$ is compatible with the new reference geometry. This step is necessary to ensure that any subsequent loading is applied to the compatible reference geometry and not the incompatible initial reference geometry.

Figure 2.

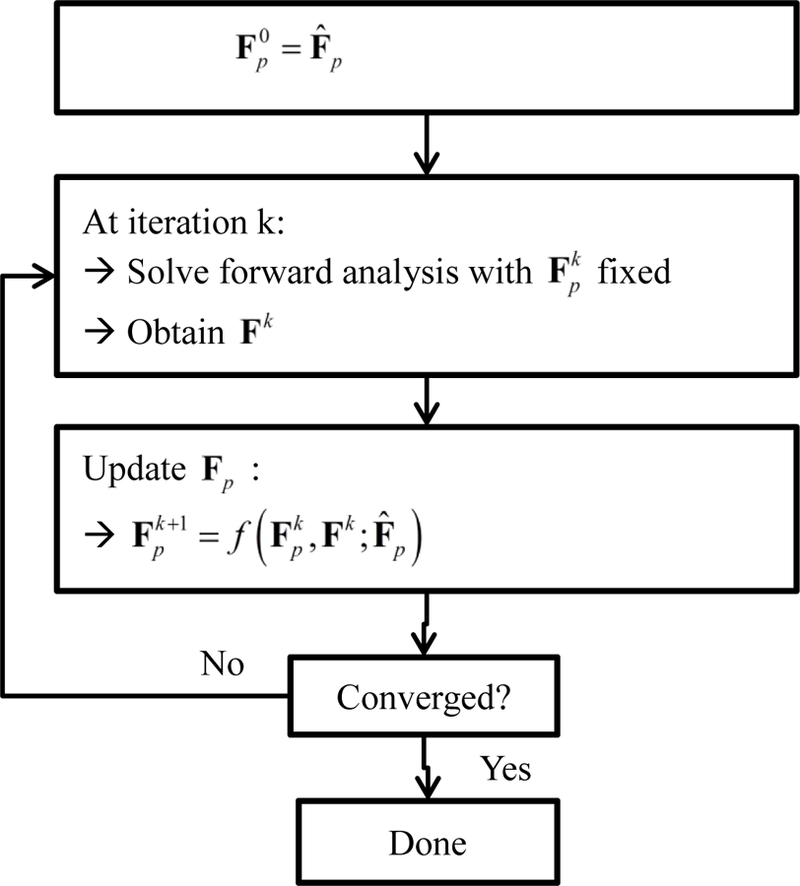
Flowchart of numerical algorithm, showing how the prestrain gradient is found iteratively by solving a series of forward FE problems. In the forward FE model, the prestrain gradient is held constant. After each forward analysis, the prestrain gradient is updated.

This approach offers a very flexible approach to applying a prestrain gradient field and, as illustrated below, can be used to implement different algorithms for applying prestrain in a finite element model. The main difference between these algorithms will lie in two aspects: how ${\widehat{\mathbf{F}}}_p$ is constructed from given data and how ${\mathbf{F}}_p$ is updated. In Sections 2.2.1 and 2.2.2, two particular update rules will be considered as examples that illustrate the possible applications of the proposed framework. In Section 2.2.3 a form for ${\widehat{\mathbf{F}}}_p$ written in terms of fiber stretches will be presented, and that form will be used in the examples in Section 3.

2.2.1. Elimination of distortion

In this application the goal is to eliminate the distortion induced by the incompatibility of the initial prestrain gradient. As explained in Section 2.1, the iterative algorithm alternates between a forward FE analysis (with ${\mathbf{F}}_p$ fixed) and an update to ${\mathbf{F}}_p$. At iteration k, the forward analysis induces a distortion of the reference geometry, characterized by a deformation gradient ${\mathbf{F}}^k$. This is approximately equivalent to distorting the initial reference configuration backwards via ${\left({\mathbf{F}}^k\right)}^{-1}$, such that the distorted geometry coincides with the given geometry. From this altered initial reference configuration, the effective prestrain gradient is given by ${\mathbf{F}}_{p,eff}^k={\mathbf{F}}^k{\mathbf{F}}_p^k$. The update rule then follows by requiring that the new prestrain gradient coincides with the effective prestrain gradient, i.e. ${\mathbf{F}}_p^{k+1}={\mathbf{F}}_{p,eff}^k$. From this, the update rule follows directly:

$${\mathbf{F}}_p^{k+1}={\mathbf{F}}^k{\mathbf{F}}_p^k.$$ (7)

A new forward analysis is then executed. The process is repeated until ${\mathbf{F}}_p$ converges. The result of this approach is a prestrain gradient field that is compatible with the original reference configuration, thus eliminating distortion.

Note that the ${\mathbf{F}}_p$ in general will not be identical to ${\widehat{\mathbf{F}}}_p$. This is the price that must be paid for a prestrain field that is compatible with the original reference configuration. An obvious question is then is it possible to find a reference configuration that allows initial prestrain to be enforced exactly. This question motivates the next application.

2.2.2. Enforcement of a prestrain gradient field

Enforcing the initial prestrain gradient ${\widehat{\mathbf{F}}}_p$ is equivalent to stating that a reference configuration is to be found in which the effective prestrain gradient is equal to the initial prestrain gradient, i.e.

$${\mathbf{F}}_{p,eff}={\widehat{\mathbf{F}}}_p.$$ (8)

At iteration k of the algorithm, the mesh will distort with deformation gradient ${\mathbf{F}}^k$ and the effective prestrain will be ${\mathbf{F}}_{p,eff}^k={\mathbf{F}}^k{\mathbf{F}}_p^k$. Keeping ${\mathbf{F}}^k$ fixed during the update phase, Eq. (8) can be enforced by choosing ${\mathbf{F}}_{p,eff}^{k+1}={\mathbf{F}}^k{\mathbf{F}}_p^{k+1}={\widehat{\mathbf{F}}}_p$. Solving this equation for ${\mathbf{F}}_p^{k+1}$ yields the following update rule:

$${\mathbf{F}}_p^{k+1}={\left({\mathbf{F}}^k\right)}^{-1}{\widehat{\mathbf{F}}}_p.$$ (9)

In general, exact enforcement of a particular ${\widehat{\mathbf{F}}}_p$ is an ill-posed problem. Small variations in ${\widehat{\mathbf{F}}}_p$ can lead to large distortions of the mesh, or in the worst case, may prevent the algorithm from converging. This is expected as an arbitrary prestrain gradient cannot be enforced on an arbitrary reference geometry. Progress can be made by appropriate regularization. For instance, instead of enforcing the full initial prestrain gradient, only part of the tensor is enforced. This compromise allows some distortion, but still enforces part of the initial prestrain gradient that is most important for reproducing e.g. experimental measurements. In the examples below it is assumed that the local fiber stretch is known (e.g. from experimental data). Thus, an update rule that only enforces the given fiber stretches is derived next.

The fiber stretch ${\widehat{\lambda }}_p$ induced by the initial prestrain gradient ${\widehat{\mathbf{F}}}_p$ is given by

$${\widehat{\lambda }}_p{\widehat{\mathbf{a}}}_p={\widehat{\mathbf{F}}}_p\cdot {\mathbf{a}}_0.$$ (10)

Here, ${\mathbf{a}}_0$ is the fiber vector in the stress-free configuration and is in general unknown. Since the fiber vector ${\widehat{\mathbf{a}}}_p$ in the initial reference configuration is usually known, we can solve for the initial fiber stretches using ${\widehat{\lambda }}_p^{-1}{\mathbf{a}}_0={\widehat{\mathbf{F}}}_p^{-1}\cdot {\widehat{\mathbf{a}}}_p$.

At iteration k the effective fiber stretch ${\lambda }_{eff}$ is determined by,

$${\lambda }_{eff}^k{\mathbf{a}}^k={\mathbf{F}}^k{\mathbf{F}}_p^k\cdot {\mathbf{a}}_0.$$ (11)

Again, keeping ${\mathbf{F}}^k$ fixed during the update phase, the initial fiber stretch can be enforced by setting ${\lambda }_e^{k+1}={\widehat{\lambda }}_p$. Using this as well as ${\mathbf{F}}_p^{k+1}=\mathrm{\Delta }{\mathbf{F}}_p^{k+1}{\widehat{\mathbf{F}}}_p$, and eliminating the unknown quantity ${\mathbf{a}}_0$ using Eq. (10), Eq. (11) can be rewritten as follows.

$${\mathbf{a}}^k={\mathbf{F}}^k\mathrm{\Delta }{\mathbf{F}}_p^{k+1}\cdot {\widehat{\mathbf{a}}}_p$$ (12)

Note that this also eliminates ${\widehat{\lambda }}_p$. Although we believe that Eq. (12) is the most general way to write an update rule that enforces a given fiber stretch, it is not sufficient to define the update rule uniquely and further assumptions must be made. In the remainder of this section it is assumed that the update rule for $\mathrm{\Delta }{\mathbf{F}}_p^{k+1}$ is such that the orientation of the fiber vectors in the initial reference configuration are unaltered. In other words,

$${\lambda }_p^{k+1}{\widehat{\mathbf{a}}}_p=\mathrm{\Delta }{\mathbf{F}}_p^{k+1}\cdot {\widehat{\mathbf{a}}}_p.$$ (13)

Secondly, since only materials that are (nearly-) incompressible will be considered in this manuscript it is required that $\det \left(\mathrm{\Delta }{\mathbf{F}}_p^{k+1}\right)=1$. A form of $\mathrm{\Delta }{\mathbf{F}}_p^{k+1}$ that accomplishes all of this is given by

$$\mathrm{\Delta }{\mathbf{F}}_p^{k+1}={\lambda }_p^{k+1}{\widehat{\mathbf{a}}}_p\otimes {\widehat{\mathbf{a}}}_p+{\lambda }_2^{k+1}{\widehat{\mathbf{a}}}_2\otimes {\widehat{\mathbf{a}}}_2+{\lambda }_3^{k+1}{\widehat{\mathbf{a}}}_3\otimes {\widehat{\mathbf{a}}}_3.$$ (14)

Here, ${\widehat{\mathbf{a}}}_p,{\widehat{\mathbf{a}}}_2,{\widehat{\mathbf{a}}}_3$ form a right-handed coordinate system and ${\lambda }_2^{k+1},{\lambda }_3^{k+1}$ are such that ${\lambda }_p^{k+1}{\lambda }_2^{k+1}{\lambda }_3^{k+1}=1$. This does not determine ${\lambda }_2^{k+1},{\lambda }_3^{k+1}$ uniquely, and a final assumption is necessary, namely that ${\lambda }_2^{k+1}={\lambda }_3^{k+1}={\left({\lambda }_p^{k+1}\right)}^{-1/2}$. Next, by choosing ${\lambda }_p^{k+1}={\left({\lambda }^k\right)}^{-1}$ where ${\lambda }^k$ is the fiber stretch induced by ${\mathbf{F}}^k$ (i.e. ${\lambda }^k{\mathbf{a}}^k={\mathbf{F}}^k\cdot {\widehat{\mathbf{a}}}_p$). The resulting update rule (using ${\mathbf{F}}_p^{k+1}=\mathrm{\Delta }{\mathbf{F}}_p^{k+1}{\widehat{\mathbf{F}}}_p$) becomes

$${\mathbf{F}}_p^{k+1}=\left[{\left({\lambda }^k\right)}^{-1}{\widehat{\mathbf{a}}}_p\otimes {\widehat{\mathbf{a}}}_p+{\left({\lambda }^k\right)}^{1/2}\left(\mathbf{I}-{\widehat{\mathbf{a}}}_p\otimes {\widehat{\mathbf{a}}}_p\right)\right]{\widehat{\mathbf{F}}}_p.$$ (15)

This can be written more concisely by constructing an orthogonal tensor $\mathbf{Q}$ of which the columns are formed by the vectors ${\widehat{\mathbf{a}}}_p,{\widehat{\mathbf{a}}}_2,{\widehat{\mathbf{a}}}_3$. In that case, Eq. (15) can be rewritten as

$${\mathbf{F}}_p^{k+1}=\mathbf{Q}\left[\begin{array}{ccc}{\lambda }^{-1}& & \\ & {\lambda }^{1/2}& \\ & & {\lambda }^{1/2}\end{array}\right]{\mathbf{Q}}^T{\widehat{\mathbf{F}}}_p,$$ (16)

where the superscript k on ${\lambda }^k$ was dropped for clarity. It can easily be verified that this particular update rule satisfies Eq. (12) and thus effectively enforces the given fiber stretches. Note that in this case however, the distortion of the geometry is not eliminated, so the reference geometry is altered. This is necessary since the initial reference geometry was not compatible with the given fiber stretches and a new geometry was sought that is compatible.

2.2.3. Defining prestrain in terms of fiber stretches

Aside from providing an update rule for ${\mathbf{F}}_p$, the user must also provide an initial estimate of the prestrain gradient. Although a full 3×3 tensor can be provided, the framework allows the user to express ${\widehat{\mathbf{F}}}_p$ in terms of other quantities. This is useful in the case ${\widehat{\mathbf{F}}}_p$ is constructed from experimental data when knowledge of the full tensor may not be available. For example, consider the case where the fiber stretches ${\widehat{\lambda }}_p$ along the material fibers were determined from experiment. The selection of the form for ${\widehat{\mathbf{F}}}_p\left({\widehat{\lambda }}_p\right)$ follows the approach in (Weiss et al., 2005). It is assumed that the material is transversely isotropic and that the fibers carry most of the load, which implies that the stress in the material is determined predominantly from the fiber stretches ${\widehat{\lambda }}_p$. Furthermore, it is assumed that the material is incompressible and thus the deformation induced by ${\widehat{\mathbf{F}}}_p$ must be isochoric (i.e. $\det \left({\widehat{\mathbf{F}}}_p\right)={\widehat{J}}_p=1$). These assumptions are not sufficient to determine ${\widehat{\mathbf{F}}}_p$ uniquely (in fact, in general the prestrain gradient cannot be determined uniquely), but we argue that, if the stress of the material is determined mostly by ${\widehat{\lambda }}_p$ and ${\widehat{J}}_p$, then any form of ${\widehat{\mathbf{F}}}_p$ that results in the given fiber stretches ${\widehat{\lambda }}_p$ and whose determinant satisfies ${\widehat{J}}_p=1$, results in the same prestress and is thus a valid prestrain gradient. Thus, given the fiber stretches ${\widehat{\lambda }}_p$ and the fiber vectors in the prestressed reference configuration ${\widehat{\mathbf{a}}}_p$, a form of ${\widehat{\mathbf{F}}}_p$ that satisfies these requirements is given by,

$${\widehat{\mathbf{F}}}_p={\widehat{\lambda }}_p{\widehat{\mathbf{a}}}_p\otimes {\widehat{\mathbf{a}}}_p+{\widehat{\lambda }}_p^{-1/2}\left(\mathbf{I}-{\widehat{\mathbf{a}}}_p\otimes {\widehat{\mathbf{a}}}_p\right).$$ (17)

Using similar arguments as presented in Section 2.2.2, this can be rewritten more concisely using

$${\widehat{\mathbf{F}}}_p=\mathbf{Q}\left[\begin{array}{ccc}{\widehat{\lambda }}_p& & \\ & {\widehat{\lambda }}_p^{-1/2}& \\ & & {\widehat{\lambda }}_p^{-1/2}\end{array}\right]{\mathbf{Q}}^T,$$ (18)

where $\mathbf{Q}$ is an orthogonal tensor whose columns are formed from the vectors ${\widehat{\mathbf{a}}}_p,{\widehat{\mathbf{a}}}_2,{\widehat{\mathbf{a}}}_3$ that define a right-handed coordinate system.

Combining this particular form of ${\widehat{\mathbf{F}}}_p$ (Eq. (18)) and the update rule described in Section 2.2.1. (Eq. (16)) essentially recovers the method by (Weiss et al., 2005) which has been used successfully used to enforce the experimental fiber stretches. This application of the framework is illustrated in the example of Section 3.4.

2.3. Compatibility and recovery of the displacement field

As noted above, the prestrain gradient approach does not rely on the existence of a stress-free configuration. However, given a prestrain gradient field, we can test whether a corresponding stress-free configuration exists, and if it does, it can be recovered.

If ${\mathbf{F}}_p$ is in fact the gradient of a deformation map, then it must satisfy the following conditions:

$$\det {\mathbf{F}}_p>0,$$ (19)

$$\nabla \times {\mathbf{F}}_p=\mathbf{0}.$$ (20)

The first condition ensures that ${\mathbf{F}}_p$ corresponds to a physically possible state, and it must be true even if ${\mathbf{F}}_p$ is not the gradient of a deformation map. The second condition will only be true if ${\mathbf{F}}_p$ is the gradient of a deformation map. In other words, if $\mathbf{X}=\eta \left(\mathbf{y}\right)$, then ${\mathbf{F}}_p={\nabla }_{\mathbf{y}}\eta$. Thus, Eq. (20) can be used to determine if the prestrain gradient field is in fact the derivative of a deformation map.

The following algorithm recovers the displacement field from ${\mathbf{F}}_p$ for the case when it is the derivative of a deformation map. Assume the displacement field $\mathbf{u}\left(\mathbf{y}\right)$ from the (unknown) stress-free configuration is written in terms of the shape functions in a finite element formulation:

$$\mathbf{u}\left(\mathbf{y}\right)=\sum _a{N}_a\left(\mathbf{y}\right){\mathbf{u}}_a.$$ (21)

Here, $N_a$ are the shape functions of node a and ${\mathbf{u}}_a$ are the values of the nodal displacements. Inside an element e, the gradient of this displacement field at node b of element e is given by

$${\nabla }_{\mathbf{y}}^e\mathbf{u}\left({\mathbf{y}}_b\right)=\sum _a{\mathbf{u}}_a\otimes {\nabla }_{\mathbf{y}}^e{N}_a\left({\mathbf{X}}_b\right).$$ (22)

Since the shape function derivatives are in general not continuous across element boundaries, Eq. (22) evaluated at the same node b, but from a different element will yield a different result. Thus, in the following the value of all elements that contain node b must be considered. The set of all elements that connect to node b is referred to as the star of b and denoted by $S_b=\left\{e|b\in e\right\}$. Then, the least-squares error at node b is defined as follows:

$$E_b=\frac{1}{2}\sum _{e\in S_b}{\Vert {\nabla }^e\mathbf{u}\left({\mathbf{y}}_b\right)-\mathbf{G}\left({\mathbf{y}}_b\right)\Vert }_F^2.$$ (23)

Here, the sum is taken over the star of node b and, ${\Vert •\Vert }_F$ is the Fröbenius norm and $\mathbf{G}={\mathbf{F}}_p-\mathbf{I}$. The total error is then defined by summing over all the nodes. Using Eq. (22), this can be written as follows:

$$E=\frac{1}{2}\sum _b\sum _{e\in S_b}{\Vert \sum _{a\in e}{\mathbf{u}}_a\otimes {\nabla }^e{N}_a\left({\mathbf{y}}_b\right)-\mathbf{G}\left({\mathbf{y}}_b\right)\Vert }_F^2.$$ (24)

By solving this least squares problem, a set of linear equations is recovered that can readily be solved for the nodal displacements ${\mathbf{u}}_a$. See the Appendix for details.

2.4. Implementation aspects

The framework described above was implemented in the FEBio finite element software (Maas et al., 2012) as a plugin, which is an extension to FEBio that is developed and maintained independently from the main FEBio source code. The prestrain plugin defines a new material (called prestrain elastic) that is a wrapper around the FEBio elastic materials. The purpose of this material is twofold: to allow the user to define the initial guess for the prestrain gradient ${\widehat{\mathbf{F}}}_p$, and to pass the total elastic deformation gradient ${\mathbf{F}}_e$ to the functions that calculate the stress and elasticity tensors. FEBio evaluates these tensors in the spatial frame directly using Eq. (2). Unlike other approaches that are based on an iterative method for obtaining the prestrain gradient, this approach does not require any change to the existing FEBio source code. In fact, the code that evaluates the constitutive response does not know if the model is being analyzed for a standard forward analysis or a prestrain analysis. Any of the available constitutive (hyperelastic) models in FEBio can be used without modification. This is in part made possible by the ability to define material data hierarchically in FEBio. New element data (in this case the prestrain gradients ${\widehat{\mathbf{F}}}_p$ and ${\mathbf{F}}_p$) can be defined without changing any existing data structures.

The initial prestrain gradient ${\widehat{\mathbf{F}}}_p$ can be defined as constant over the entire domain, it can be defined for each element, or it can be defined via the fiber stretch. The prestrain plugin can also be expanded and users can create new ways to define the initial prestrain gradient (for instance, a mathematical expression representing the solution of an idealized geometry). The iterative update algorithm described in Section 2.2 is implemented as a nonlinear constraint and accomplishes its goal by using the augmentation mechanism in FEBio. This mechanism allows constraints to evaluate and modify the state of the model at the end of each converged time step. If a constraint modifies the state of the model, then the time step is re-evaluated. This mechanism is often used in FEBio to determine Lagrange multipliers using the augmented Lagrangian method; in this case it is used to update the prestrain gradient. During the augmentation phase, the prestrain gradient is updated and the convergence is checked. If convergence is met, the augmentation loop finishes and the time step ends. The default implementation does not provide a specific update rule (the base class is an abstract class) and specific update rules are implemented by subclassing the base class. The two update rules discussed in Sections 2.2.1 and 2.2.2 are available as part of the plugin distribution and can be used as examples that show how to define new update rules.

In general, applying prestrain using this plugin requires a two-step analysis. In the first step, the initial prestrain gradient is given and, if necessary, the update algorithm is applied to find a compatible prestrain gradient. Then, subsequent loading of the model is applied in the second step during which the prestrain gradient is held fixed. The prestrain plugin, associated documentation and example problems are available for download at the FEBio web page (www.febio.org/plugins).

3. RESULTS

3.1. Verification analysis

This example demonstrates that in the case of a compatible prestrain gradient, Eq. (2) indeed results in the correct Cauchy stress. This example uses a hexahedral mesh of a tensile test specimen with dogbone geometry. A transversely isotropic hyperelastic constitutive model was used (Weiss et al., 1996) - material “coupled trans-iso Mooney-Rivlin” in FEBio (Maas et al., 2012). The strain energy is defined as:

$$W=c_1\left(I_1-3\right)+c_2\left(I_2-3\right)+W_f\left(\lambda \right)+U\left(J\right)$$ (25)

Here, $I_1$ and $I_2$ are the first and second invariants of the right Cauchy-Green tensor $\mathbf{C}$ and $J$ is the determinant of the deformation gradient. The fiber stretch $\lambda$ is given by ${\lambda }^2={\mathbf{a}}_0\cdot \mathbf{C}\cdot {\mathbf{a}}_0$. The strain energy function for the fibers, $W_f$, is more easily expressed in terms of its derivative with respect to the fiber stretch, but grows exponentially as a function of the fiber stretch. See (Weiss et al., 1996) for more details. The term $U\left(J\right)=\frac{1}{2}k\ln {\left(J\right)}^2$ is the volumetric strain energy function and k is the bulk modulus. The material parameters were c₁=1.44 MPa, c₂=0 MPa, c₃=0.57 MPa, c₄=48, c₅=467.1 MPa, k=1000 MPa and are representative for MCL ligament (Gardiner et al., 2001). The fiber direction was aligned along the long axis of the model.

First, a forward FE analysis was performed, which applied a 10% uniaxial stretch to the sample along the long axis. This was followed by a shear of 10% in the short axis direction (Figure 3A). Then, the nodal coordinates and the deformation gradients were extracted from the forward analysis at the end of the uniaxial stretch and taken as the starting geometry for the prestrain analysis. The deformation gradient of the forward model was used as the initial prestrain gradient of the prestrain analysis. The prestrain model then underwent the same 10% shear. Eq. (2) was used for evaluating the stress and spatial tangents in the prestrain analysis. The predicted stresses for the prestrain analysis were nearly identical to those from the forward analysis (Figure 3B). The maximum error in the effective stress was 4×10⁻⁵ MPa. As a point of reference, the maximum effective stress for both models was 54 MPa.

Figure 3.

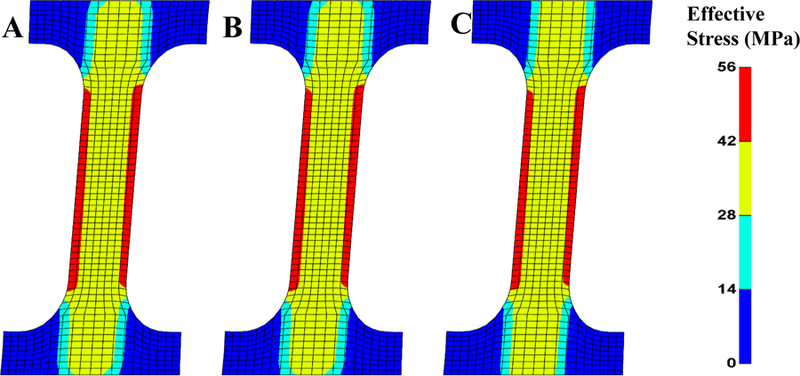
Verification example of the prestrain gradient approach for the case where the prestrain gradient is kinematically compatible. (A) In the forward model, a uniaxial stretch is applied, followed by a shear. The plot shows the effective (von Mises) stress at the end of the analysis. (B) Result for the prestrain analysis where the deformation gradient and nodal coordinates at the end of the uniaxial stretch were taken as the inputs. The prestrain analysis then underwent the same shear step. (C) A similar analysis was performed but using only the fiber stretches instead of the entire deformation gradient from the forward analysis. Again the shear is applied and the effective stress is shown at the end of the shear step.

Similarly, the nodal coordinates and the fiber stretches were taken from the forward analysis at the end of the uniaxial stretch and used as the input of an in situ stretch model. The in situ stretch model then underwent the same 10% shear, using Eq. (18) to evaluate the initial prestrain gradient. Since only the fiber stretches were given, the iterative procedure described in Section 2.2.2 was used at the start of the analysis to find a compatible prestrain gradient. Again the effective stresses were compared to the results of the forward analysis (Figure 3C). Without the iterative update procedure, the in situ strain model resulted in a maximum error of 8 MPa and a maximum effective stress of 53 MPa. The largest errors occurred near the top and bottom of the model geometry. With the iterative procedure, the results improved slightly: the error in the effective stress reduced to 7.4 MPa and the maximum effective stress was 53.2MPa.

3.2. Incompatible Strain field

This example demonstrates the outcome of applying a prestrain field that is incompatible with the reference configuration. The geometry, representing a medial collateral ligament (MCL) model, and the material properties were taken from published experimental data (Gardiner et al., 2001). The MCL was discretized using hexahedral elements and the material was represented using the same transversely-isotropic Mooney-Rivlin constitutive model in Section 3.1 (Eq. (25)). The material properties were c₁=4.6 MPa, c₂=0 MPa, c₃=2.4 MPa, c₄=30.6, c₅=323.7 MPa, and k=1,000 MPa.

A heterogeneous in situ fiber stretch field was obtained by first applying a prescribed displacement of approximately 5% of total length to the undeformed MCL geometry. In order to simulate experimental uncertainty, the fiber stretch field was smoothed using six iterations of a Laplacian smoothing algorithm (Figure 4A).

Figure 4.

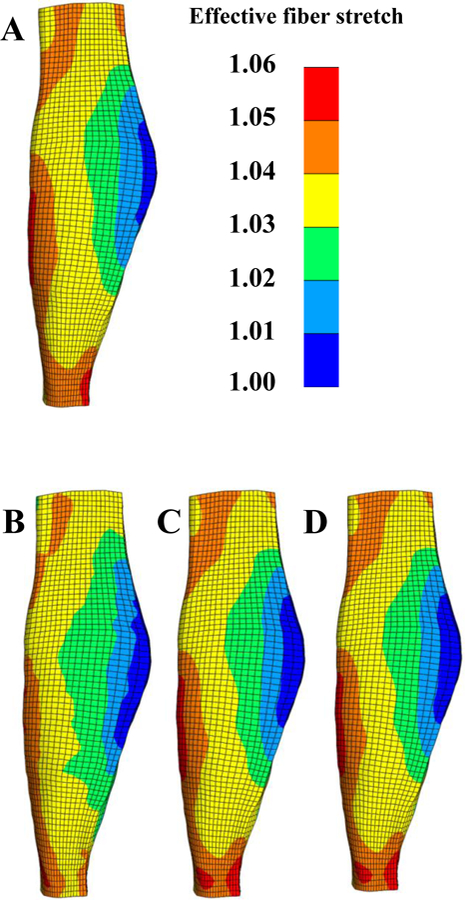
Effects of applying in situ stretch to a reference geometry that is kinematically incompatible. (A) Reference geometry with target in situ fiber stretch. (B) Deformed state and effective fiber stretch without updates. (C) Effective fiber stretch after eliminating distortion. (D) Effective fiber stretch after enforcing the target in situ stretch.

The deformed geometry and smoothed fiber stretches from this forward analysis were then used as the starting point of the prestrain analysis. In the prestrain analysis, the ends of the MCL were held fixed and no external loads were applied. Since the applied prestrain was incompatible with the prestressed reference geometry, the mesh distorts and the effective fiber stretches were altered. Visual inspection of the effective fiber stretch (Figure 4B) shows the qualitative difference compared to the applied fiber stretches. The error in the in situ stretch was measured by taking the absolute value of the difference:

$$\text{in-situ error}=\left|{\widehat{\lambda }}_p-{\lambda }_{eff}\right|.$$ (26)

Here, the effective fiber stretch is defined via ${\lambda }_{eff}\mathbf{a}=\mathbf{F}{\widehat{\mathbf{F}}}_p\cdot {\widehat{\mathbf{a}}}_p$, with $\mathbf{F}$ the deformation gradient of the distortion and ${\widehat{\mathbf{a}}}_p$ the fiber vectors in the initial reference configuration. The in situ error ranged over the entire mesh between 0 and 0.014.

The distortion of the mesh was quantified by inspecting the effective Lagrange strain $E_{eff}$,

$$E_{eff}=\sqrt{\frac{3}{2}\tilde{\mathbf{E}}:\tilde{\mathbf{E}}}$$ (27)

where $\tilde{\mathbf{E}}=\text{DEV}\left(\mathbf{E}\right):=\mathbf{E}-\frac{1}{3}\left(\mathrm{tr}\left(\mathbf{E}\right)\right)\mathbf{I}$ and calculated from the deformation gradient of the mesh distortion. The observed distortion ranged between 0 and about 0.136. The largest errors occurred near the insertion sites.

3.3. Elimination of distortion

For this example the same geometry and in situ fiber stretch data were taken from Section 3.2. The application described in Section 2.2.1 was then applied in order to eliminate the distortion induced by the incompatibility of the prestrain field. As a consequence, the effectively applied prestrain will be different than the initial prestrain field. Qualitatively the effective fiber stretch is noticeably different from the applied fiber stretches (Figure 4C). The maximum in situ error, evaluated using Eq. (26), grew slightly to 0.016 compared to the example of Section 3.2. The maximum distortion error, evaluated by Eq. (27) and measured over the entire mesh was reduced to 1.24E-3 and is effectively eliminated.

3.4. Enforcement of a prestrain deformation gradient field

This example used the same MCL model as Section 3.2., but this time the initial heterogeneous in situ fiber stretches were enforced using the algorithm in Section 2.2.2. Visual comparison of the resulting effective fiber stretches shows qualitatively the excellent agreement with the applied fiber stretches (Figure 4D). The maximum error in the in situ, evaluated by Eq. (26), and measured over the entire mesh was reduced to 0.0039. However, the mesh distortion evaluated by Eq. (27) increased to 0.193.

3.5. Recovering displacement map from deformation gradient

Using the dogbone mesh from the verification example in Section 3.1., the final, deformed geometry and the final deformation gradient were used as the starting point for recovering the original, reference geometry. The deformation gradient from the forward analysis was inverted since the goal was to find the displacement map from the deformed to the reference geometry. Then, the least-squares method described in Section 2.3 was applied to the deformed geometry and the displacement field was recovered. The original reference geometry from the dogbone model was effectively recovered. The maximum displacement of the forward analysis was 1.415 mm and the maximum displacement of the inverse method was 1.405 mm with a maximum relative error of 0.007 (Figure 5). The error is most likely caused by the post-processing step that mapped the deformation gradients from the integration points of the forward analysis to the nodal quantities needed by the inverse method.

Figure 5.

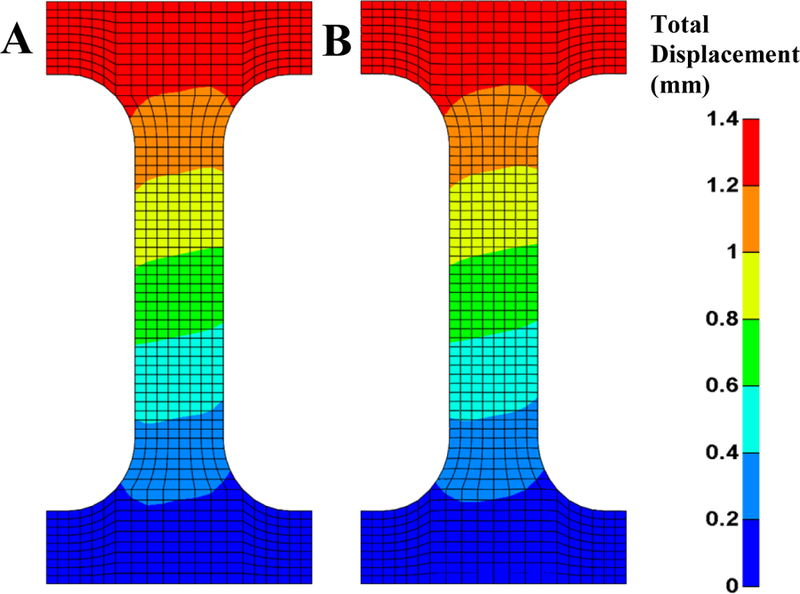
Example illustrating the method to recover the displacement map from the deformation gradient. (A) The reference geometry of the model used in the verification example. (B) The geometry recovered by taking the final, deformed geometry of the verification example and the deformation gradient field and then applying the inverse least-squares method described in the methods section. The fringe plot corresponds to the total displacement (in mm).

3.6. Open Knee Example

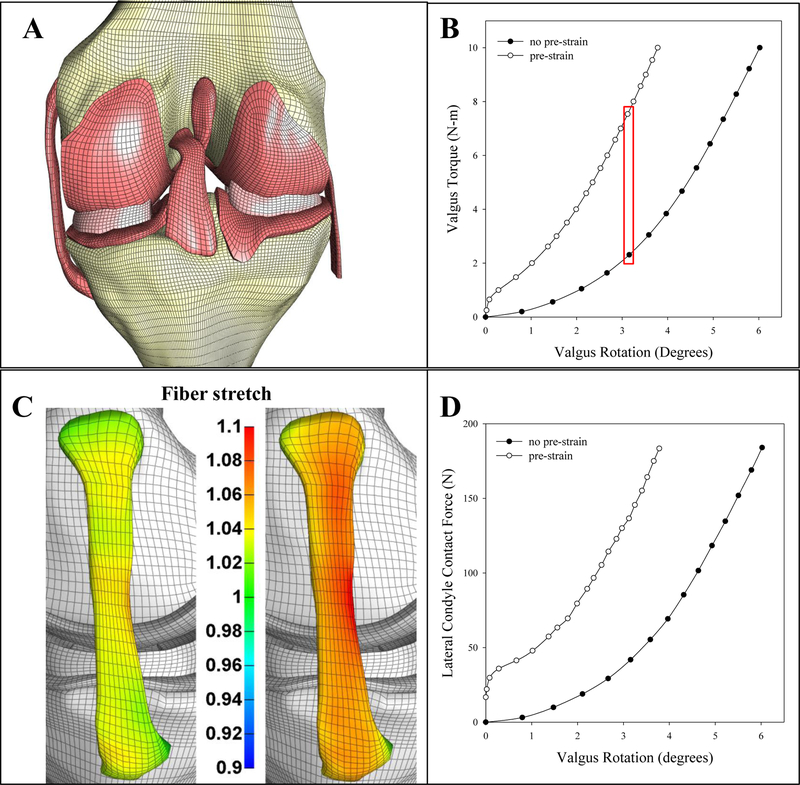
In the final example, a given in situ fiber strain was applied on the ligaments of the Open Knee computational model of the knee joint (Erdemir, 2015; Erdemir and Sibole, 2010; Sibole et al., 2010). The Open Knee model contains the femur and tibia, both assumed rigid, femoral and tibial cartilage, the menisci, and the four major knee ligaments (MCL, ACL, PCL, and LCL). The geometry was meshed with hexahedral elements. Springs are used to connect the meniscal horns to the tibial plateau. The ligaments were modeled using a transversely isotropic material with an isotropic Mooney-Rivlin matrix. The fiber orientations were defined along the long-axis mesh lines. The menisci were modeled with a Fung orthotropic material and the cartilage layers were represented with a Mooney-Rivlin material. Detailed information regarding material coefficients and constitutive models can be found in the Open Knee User’s Guide (https://simtk.org/home/openknee). All four cruciate ligaments were prestrained by applying in situ strain data taken from published experimental data (Dhaher et al., 2010) and mapped onto the four ligaments. The loading scenario considered was valgus loading to a torque of 10 Nm. The resulting torque on the femur as a function of valgus rotation was compared between the prestrained model and the model without prestrain applied. Similarly, the averaged contact force on the lateral condyle and the effective fiber strains on the MCL were also compared.

Application of prestrain to the knee model, shown in Figure 6, resulted in a much stiffer joint torque-rotation response under valgus loading than the model without prestrain. This can be seen by comparing the valgus torque as a function of valgus rotation (Figure 6B). Similarly, the average contact force over the lateral condyle grew more quickly in the prestrained model (Figure 6D). When compared at a specific angle of valgus rotation (red box in Figure 6B), the predicted fiber strains on the MCL (the primary restraining ligament to valgus rotation in the knee) much higher in the prestrained model (Figure 6C).

Figure 6.

Finite element analysis of the Open Knee model under 10 Nm of valgus torque. A) The Open Knee finite element model, including articular cartilage, menisci, and the four major knee ligaments. B) Valgus torque as a function of valgus rotation for both the prestrained model and the model without prestrain. The red box shows the two points where the fiber strains are compared in panel C. C) Effective fiber stretch at ~3.1 degrees valgus rotation. Left, without prestrain. Right, with prestrain. D) The contact reaction force across the lateral condyle. Results demonstrate that the structural behavior of the joint and predicted ligament strains are dramatically different without prestrain field to the ligaments, and in particular the response is too soft under valgus torque without prestrain.

4. Discussion

A general framework was developed to apply prestrain (and therefore prestress) to finite element models in the context of simulating the mechanics of biological structures. The method can solve prestrain problems in a “traditional” manner, where the prestrain deformation gradient field is known (e.g. from analytical solution or recovered from a forward analysis of a global stress-free configuration). In addition, in the case where the applied prestrain field is unknown or just an initial guess, the framework can be used to recover a prestrain gradient field that is compatible with the (possibly altered) reference geometry. Definition of the initial guess and the update rule for the prestrain field are controlled by the user and result in different applications of the framework. Two possible applications were illustrated for the case of applying in situ fiber stretches to a model of a MCL. In the first application, the distortion of the mesh was eliminated. In the second application, the distortion was retained and used to find an alternative reference configuration in which the given fiber stretches could be enforced exactly. These two applications demonstrate the great practical use of the proposed framework in applying prestrain.

Although the framework was illustrated in the context of applying fiber stretches by choosing a particular functional form for the prestrain gradient, other forms (e.g. a prestrain field that is the analytical solution of a simplified geometry) can easily be used with the framework. Similarly, other update rules for the prestrain gradient can be implemented easily. However, the two particular update rules considered in Section 2.2 reflect the two ends of the spectrum in terms of applying an incompatible prestrain field: either find an alternative prestrain field that eliminates the distortion or enforce the desired prestrain field in an altered reference geometry. The choice of which path to take depends on the goals of the analyst. It can be influenced by the estimated error in the reference geometry compared to the estimated error in the prestrain field. For instance, if the geometry is carefully segmented from high-resolution image data, and thus represents a high-fidelity model of the geometry, it might be important to reduce the induced distortion and to retain the unaltered reference geometry. Alternatively, if the distortion of the reference geometry is small, it may be desirable to enforce the prestrain field without alteration. It might be tempting to ask for both, i.e. can a given prestrain field be enforced on the reference geometry? The answer is “no” in general, unless the applied prestrain field is compatible with the reference geometry in the first place. If the prestrain field is not compatible with the reference geometry, the discrepancies need to be compensated by adjusting either the prestrain field, or the reference geometry, or both as in the case where the prestrain gradient is not updated. The latter case could make interpretation of the results difficult.

It is important to point out that, in general, enforcing a given prestrain field by finding an altered reference geometry (as discussed in Section 2.2.2) is an ill-posed inverse problem. The solution may not be unique or worse, may not exist. This poses challenges to applying experimentally obtained prestrain data to a finite element model. If the experimentally obtained prestrain data is too sparse, or the variance in the experimental data is too large, the enforcement of this prestrain may not be possible. On the other hand, the failure of the algorithm in Section 2.2.2 to converge indicates that the prestrain data is too inaccurate or incomplete and suggests that additional data (e.g. more accurate fiber stretches or measuring the inhomogeneity in the material parameters) is necessary in order to apply the given prestain.

The general framework recovers other methods for applying prestrain that have been proposed in the literature. For example, consider the problem of applying prestress to an in vivo model, where the goal is to determine the stresses when only the deformed geometry and the applied loads are known. Methods for solving these type of problems were presented by (Gee et al., 2010) and expanded on by (Weisbecker et al., 2014) and (Grytz and Downs, 2013). These methods attempt to find the deformation gradient iteratively, without recovering the stress-free reference configuration. Our framework can similarly be used to solve this type of problem. In fact, the algorithm described in Section 2.2.1 effectively recovers such a method if the initial guess for the prestrain field is taken to be the identity tensor. In that case, the recovered prestrain gradient is in fact the effective prestrain gradient that generates the in vivo prestress.

A method was also presented for recovering the displacement field from a given deformation gradient, if the deformation gradient satisfies the kinematic compatibility conditions. This can also be seen as a type of inverse finite element method where the deformation gradient is known as well as the deformed configuration and the reference configuration is sought. This can be of interest in studies where a prestrain field is proposed based on an analytical formulation and the stress-free reference configuration is needed for use in a forward FE analysis (e.g. (Rausch and Kuhl, 2013)).

To demonstrate the effect of prestrain on the mechanical response of a biological system, the framework was used on an Open Knee model where in situ fiber strains were applied to the four knee ligaments. As expected, application of prestrain to the knee ligaments resulted in a stiffer response for the torque-rotation curve, higher strains on the MCL, and higher contact stresses on the articular cartilage in the lateral compartment under valgus loading. Thus, the in situ strains increased the stability of the knee joint. This further demonstrates that the inclusion of prestrain in computational models is often a necessary requirement to obtain reasonable predictions of subsequent loading conditions of interest.

In summary, the framework presented in this manuscript provides a powerful tool to apply prestrain in large-deformation finite element analysis of biological structures. It is especially useful when the reference configuration in which anatomy is acquired may not be a stress-free state and the stress-free state may not be computable. A significant advantage of the framework is the ease with which it can be customized to recover existing methodologies for applying prestrain, while still allowing new approaches for applying prestrain to be explored.

Appendix

This appendix details how to obtain the linear system of equations to solve for the unknown nodal displacement values, given a compatible deformation gradient tensor $\mathbf{F}$ and the deformed geometry. The goal is to find the displacement values that minimize the following least squares error E:

$$E=\frac{1}{2}\sum _b\sum _{e\in S_b}{\Vert \sum _{a\in e}{\mathbf{u}}_a\otimes {\nabla }^e{N}_a\left({\mathbf{y}}_b\right)-\mathbf{G}\left({\mathbf{y}}_b\right)\Vert }_F^2.$$ (1)

In order to minimize this expression, the derivative with respect to the unknown nodal deformations must be equated to zero:

$$\frac{dE}{d{\mathbf{u}}_c}=\sum _b\sum _{e\supset b,c}\left(\sum _{a\in e}{\mathbf{u}}_a\otimes {\nabla }^e{N}_a\left({\mathbf{y}}_b\right)-\mathbf{G}\left({\mathbf{y}}_b\right)\right){\nabla }^e{N}_c\left({\mathbf{y}}_b\right)=\mathbf{0}.$$ (2)

This can be rewritten as follows,

$$\sum _b\sum _{e\supset b,c}\left(\sum _{a\in e}{\mathbf{u}}_a\left({\nabla }^e{N}_a\left({\mathbf{y}}_b\right)\cdot {\nabla }^e{N}_c\left({\mathbf{y}}_b\right)\right)-\mathbf{G}\left(y_b\right){\nabla }^e{N}_c\left({\mathbf{y}}_b\right)\right)=\mathbf{0}.$$ (3)

Bringing all the known quantities to the right-hand side, results in

$$\sum _{e\supset c}\sum _{a,b\in e}{\mathbf{u}}_a\left({\nabla }^e{N}_a\left({\mathbf{y}}_b\right)\cdot {\nabla }^e{N}_c\left({\mathbf{y}}_b\right)\right)=\sum _{e\supset c}\sum _{b\in e}\mathbf{G}\left({\mathbf{y}}_b\right){\nabla }^e{N}_c\left({\mathbf{y}}_b\right).$$ (4)

This is a linear system of equations, which can be solved for ${\mathbf{u}}_a$. In fact, these are three linear systems of equations with the same coefficient matrix:

$$\begin{gathered} \mathbf{A}{\mathbf{u}}_x={\mathbf{R}}_x, \\ \mathbf{A}{\mathbf{u}}_y={\mathbf{R}}_y, \\ \mathbf{A}{\mathbf{u}}_z={\mathbf{R}}_z. \end{gathered}$$ (5)

Since the coefficient matrix is the same, the LU decomposition of A only needs to be computed once to solve for the ${\mathbf{u}}_a$.